组合图形的面积-组合图形的面积

发布时间：2018-01-06 所属栏目：教案

一 : 组合图形的面积

人教版五年级数学上册第五单元

岳溪小学黄良清

正方形

长方形

平行四边形

梯形

三角形

你还记得吗？
长方形的面积 = 长 ×宽正方形的面积 = 边长×边长

S=ab
S=a×a S=ah S=ah÷2

平行四边形的面积= 底×高
三角形的面积 = 底×高÷2

梯形的面积 = (上底+下底）×高÷2 S=(a+b)h÷2

下面这些物品里有哪些图形？

由两个完全一样的梯形组合成的

由一个长方形和两个完全一样的三角形组合成的

由几个简单的图形拼出来的图形，我们把它们叫做组合图形。

例2、右图表示的是一间房子侧面墙的形状。它的面积是多少平方米？
你能想出几种方法？

可以把它看成一个正方形和一个三角形的组合。

方法一：

5米

2 2 2 2
米

5 5
米

方法一：
2米

5米 2 米 5米

5米

＝

＋
5 米

5 米

5×2÷2＋5×5 =5+25 =30(平方米) 答：它的面积是30平方米。

我把它分成两个完全一样的梯形。

方法一：

5米

2 2 2 2
米

5 5
米

方法二：
2 米 52 米米 5米（5÷2）米 2 米 5 米（5÷2）米 5 5 米米

＝

+

（5＋5＋2）×（5÷2）÷2×2 ＝12×2.5÷2×2 ＝30（平方米）答：它的面积是30平方米。

你是怎样想的？

可以把它看成一个长方形挖去两个个三角形后剩下的组合。

方法三：

5米

2 2 2 2
米

5 5
米

方法三：
2 米
5米 5 米

=

-

(5+2)×5 －(5÷ 2)×2÷2×2 =35-5

=30(平方米）

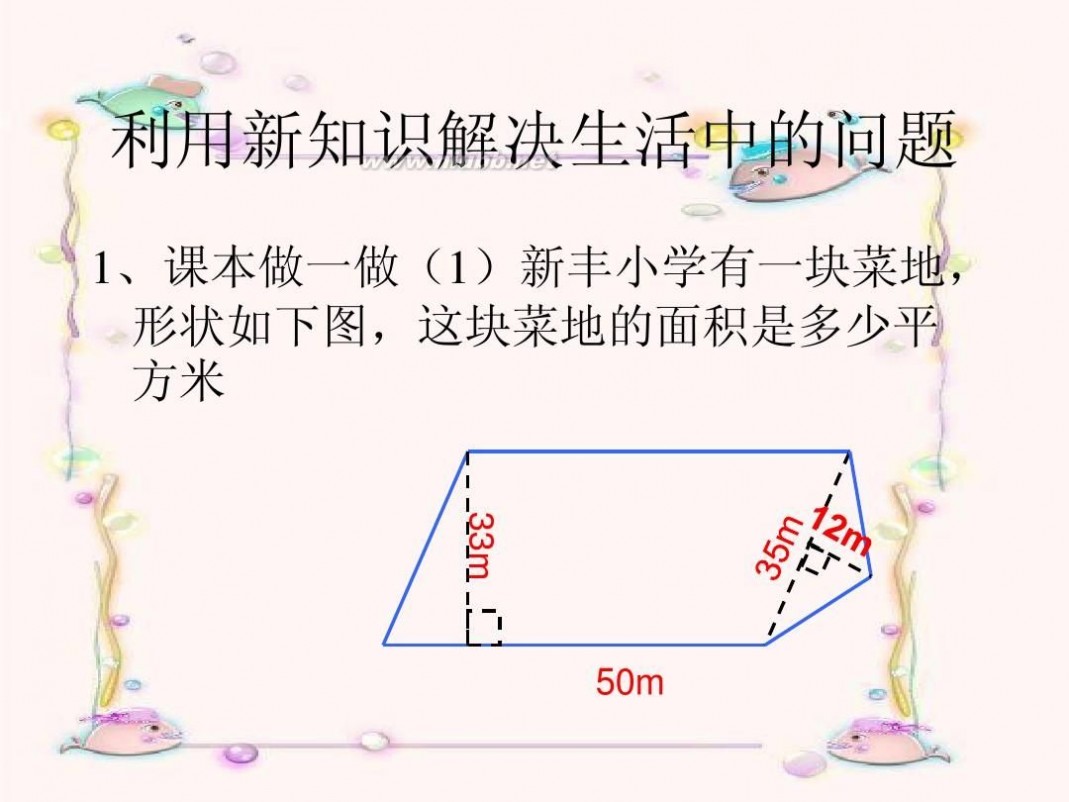
想：这块菜地的面积 = 平行四边形面积＋三角形面积

50×33＋35×12÷2 ＝1650＋210 ＝1860（平方米）

学校开运动会要制作一些锦旗，式样如图所示。一面锦旗需要多少平方厘米的布料？

45cm

60cm

60×30 －30×(60－45) 2 ÷ = 1800－225 =1575(cm2)

⑵爱动脑筋的学生
要做一面这样的队旗需要多什么布？你能想出几种方法？（课本P94页第2题）

中队旗面积 = 梯形面积 + 梯形面积

S=（a+b)h÷2=(80+60) ×30÷2
=140 ×30÷2=4200÷2=2100平方厘米
中队旗面积 = 梯形面积 + 梯形面积

队旗面积=2100 ×2=4200平方厘米

中队旗面积 = 长方形面积 + 三角形面积 × 2

S=ab+ah÷2×2

=(80-20) ×（30+30） +20 ×30÷2×2 =4200平方厘米

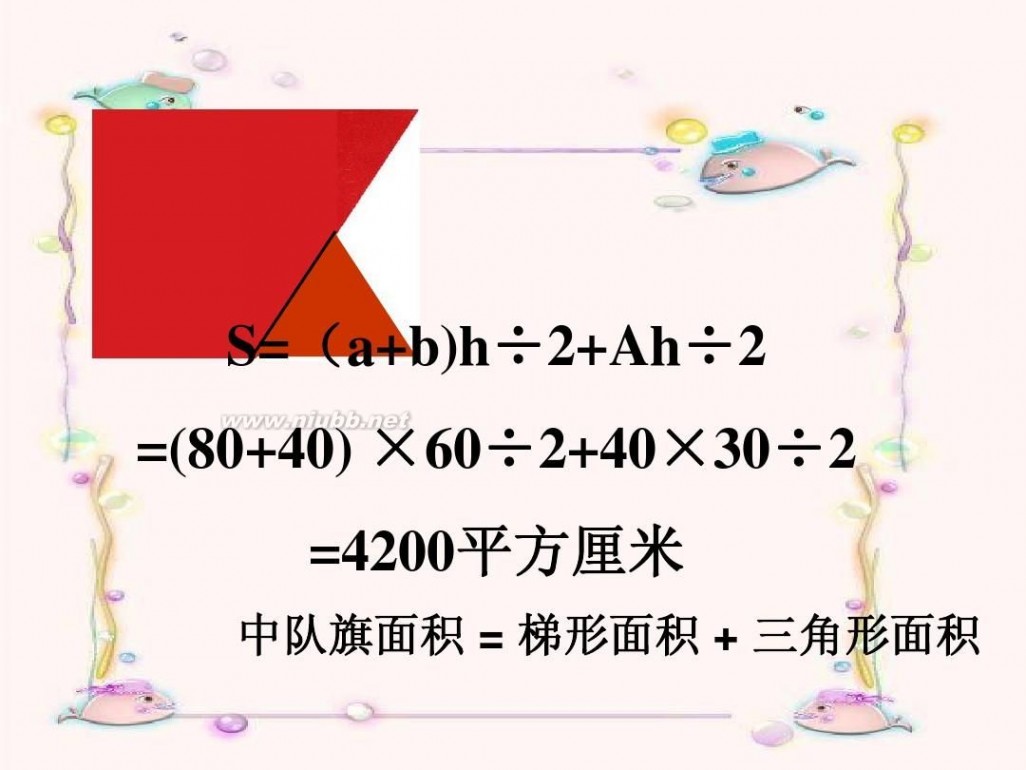
中队旗面积 = 梯形面积 + 三角形面积

S=（a+b)h÷2+Ah÷2
=(80+40) ×60÷2+40×30÷2 =4200平方厘米
中队旗面积 = 梯形面积 + 三角形面积

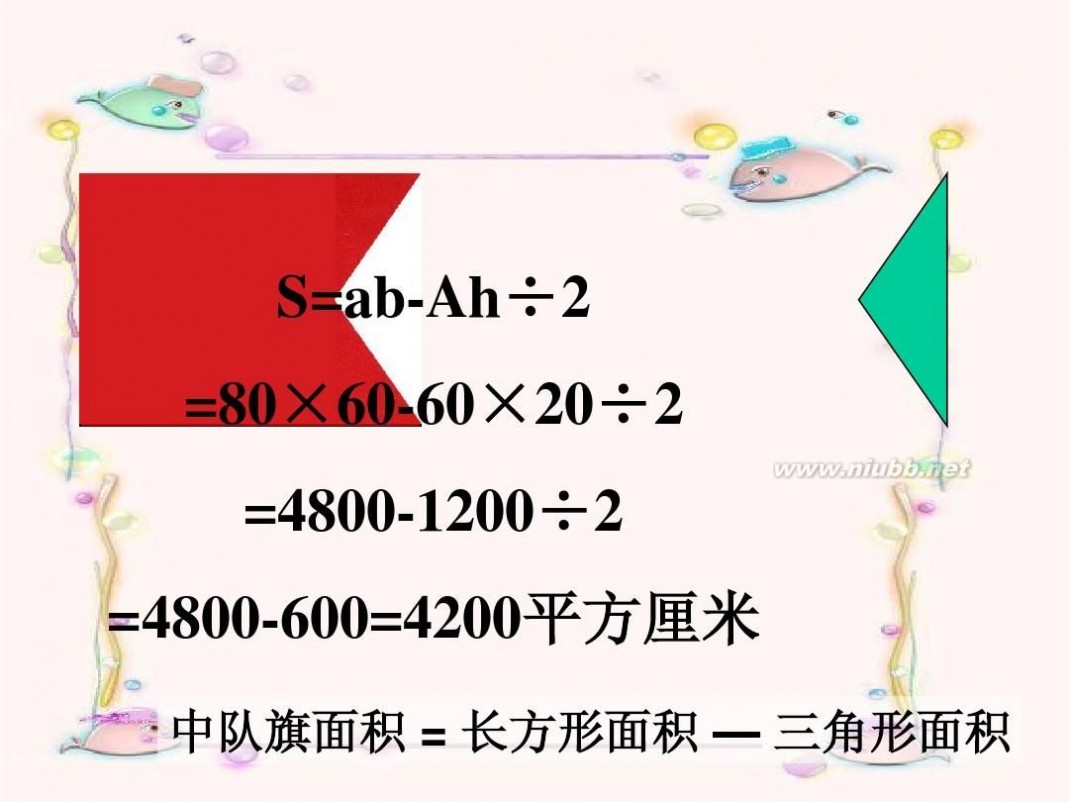
中队旗面积 = 长方形面积 — 三角形面积

S=ab-Ah÷2

=80×60-60×20÷2
=4800-1200÷2

=4800-600=4200平方厘米
中队旗面积 = 长方形面积 — 三角形面积

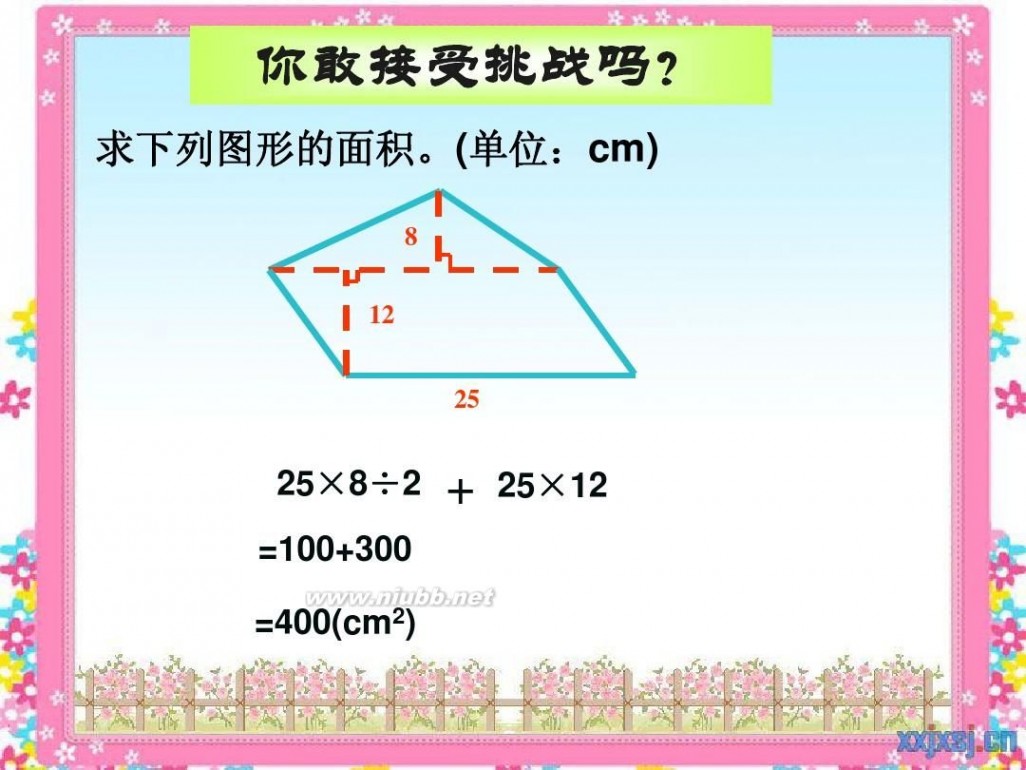
你敢接受挑战吗？
求下列图形的面积。(单位：cm)
8 12 25

25×8÷2 =100+300 =400(cm2)

+

25×12

怎么计算组合图形的面积？
1、分图形：用分割法或添补法把组合图形分成我们会计算的简单图形。 2、找条件，算面积：分别计算简单图形的面积。 3

、最后求和或差。

利用新知识解决生活中的问题
1、课本做一做（1）新丰小学有一块菜地，形状如下图，这块菜地的面积是多少平方米
33m 50m

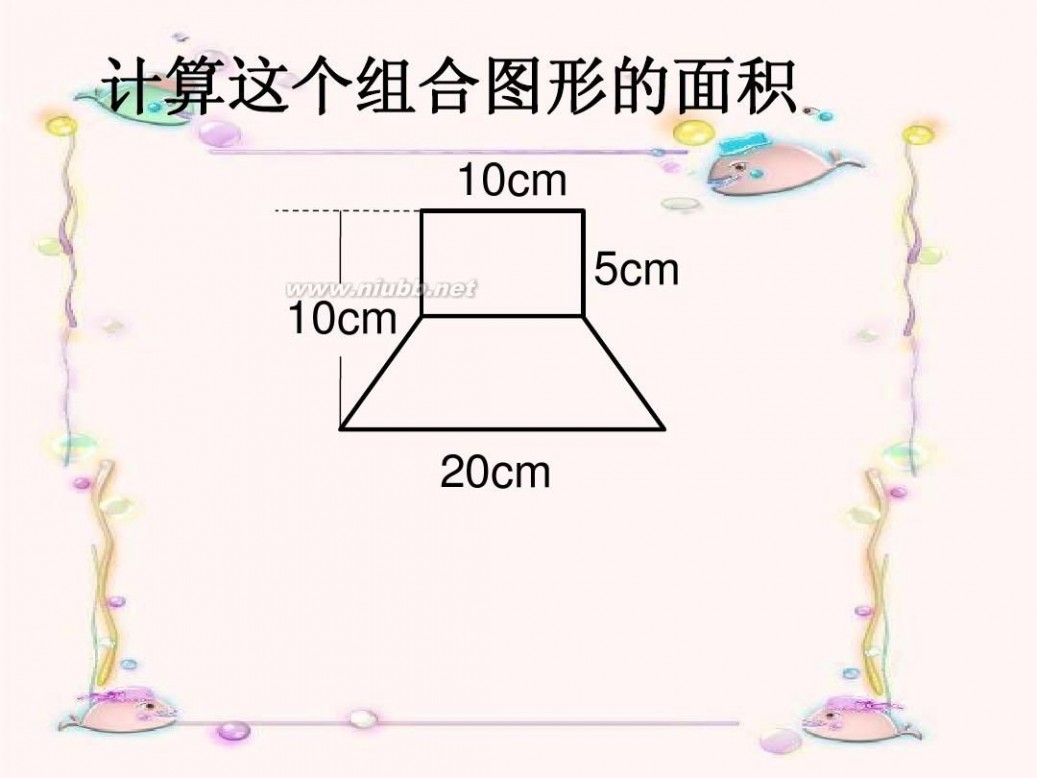
计算这个组合图形的面积
10cm 5cm

10cm
20cm

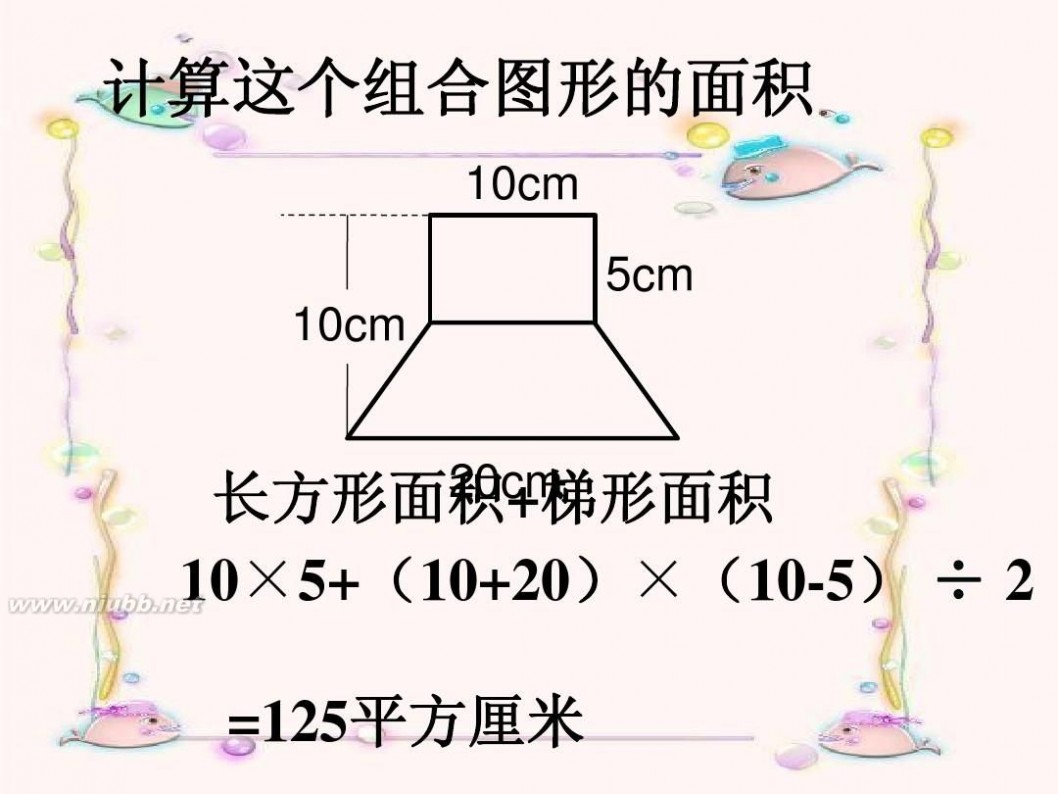
计算这个组合图形的面积
10cm 5cm

10cm
20cm 长方形面积+梯形面积

10×5+（10+20）×（10-5） ÷ 2

=125平方厘米

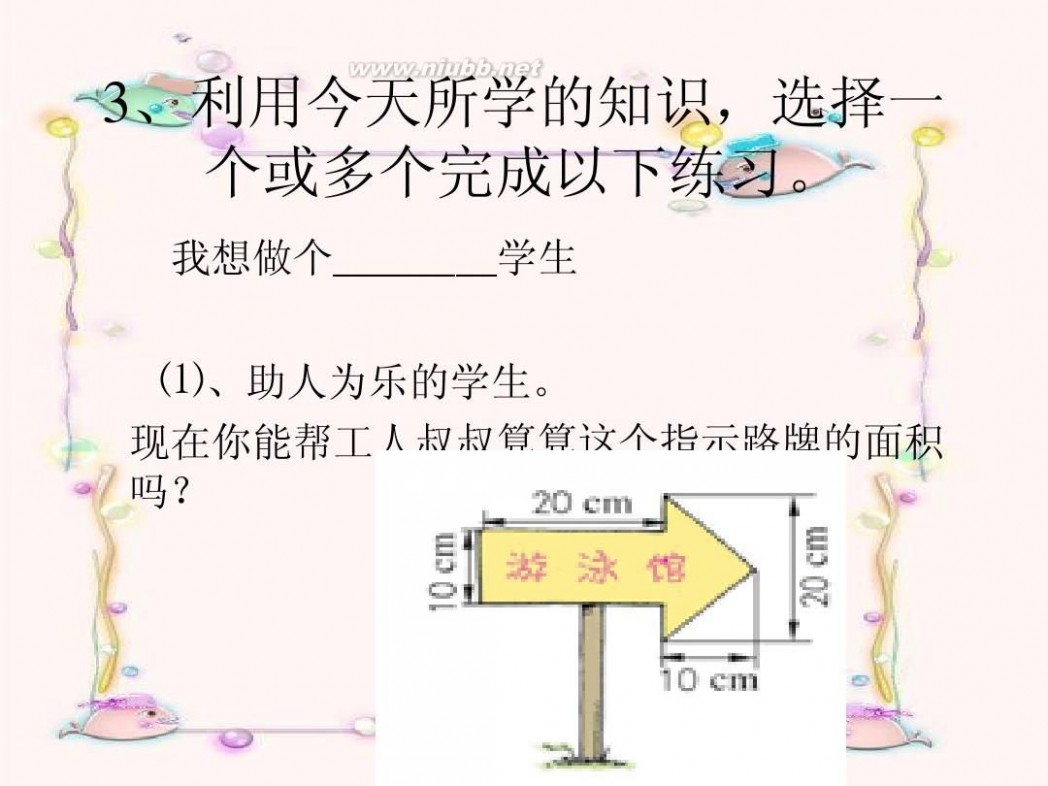
3、利用今天所学的知识，选择一个或多个完成以下练习。
我想做个________学生

⑴、助人为乐的学生。
现在你能帮工人叔叔算算这个指示路牌的面积吗？

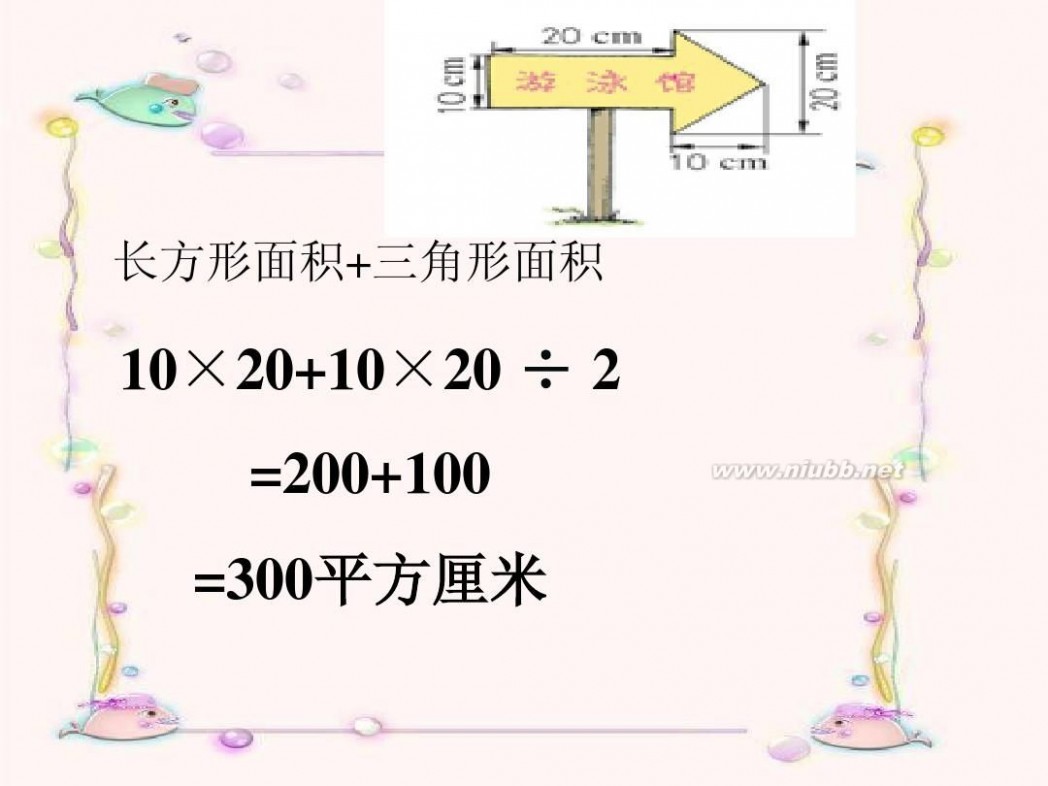
长方形面积+三角形面积

10×20+10×20 ÷ 2
=200+100

=300平方厘米

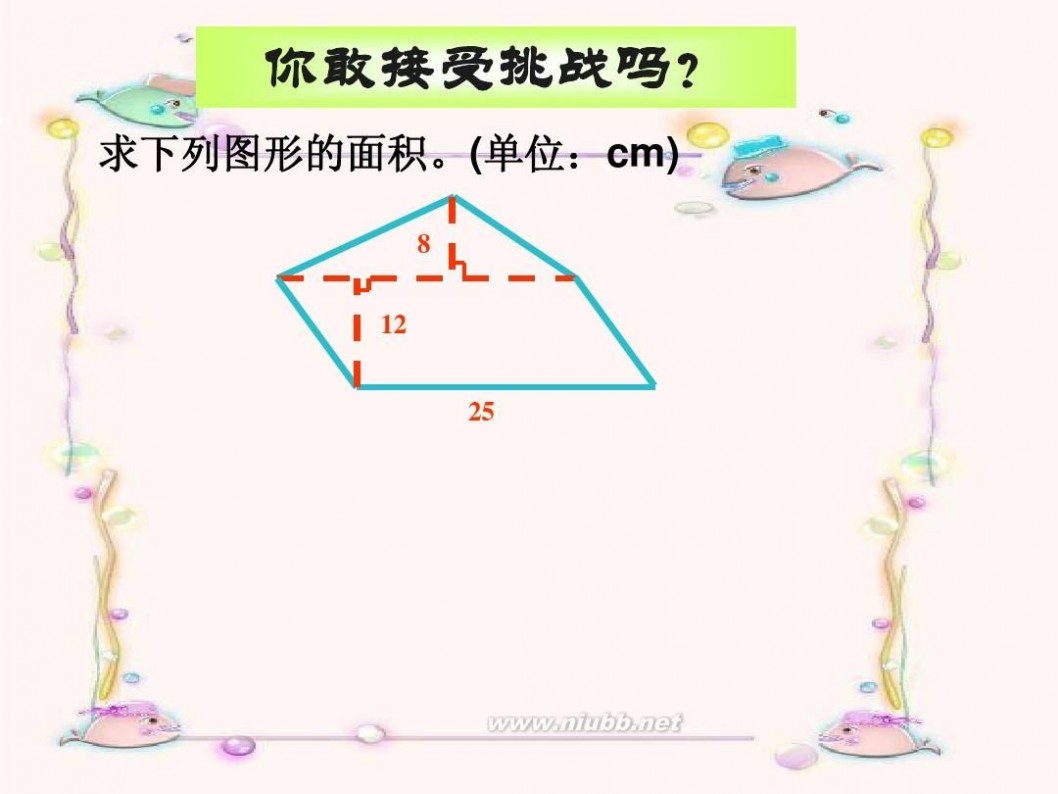
你敢接受挑战吗？
求下列图形的面积。(单位：cm)
8 12 25

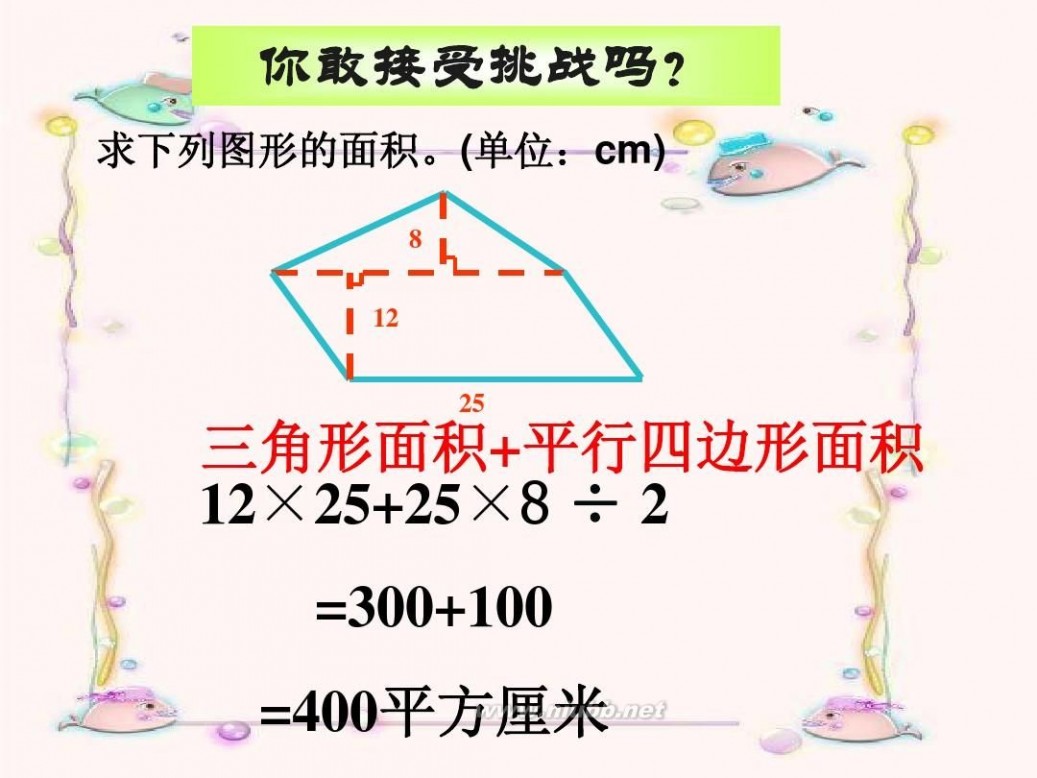
你敢接受挑战吗？
求下列图形的面积。(单位：cm)
8 12 25

三角形面积+平行四边形面积 12×25+25×8 ÷ 2
=300+100 =400平方厘米

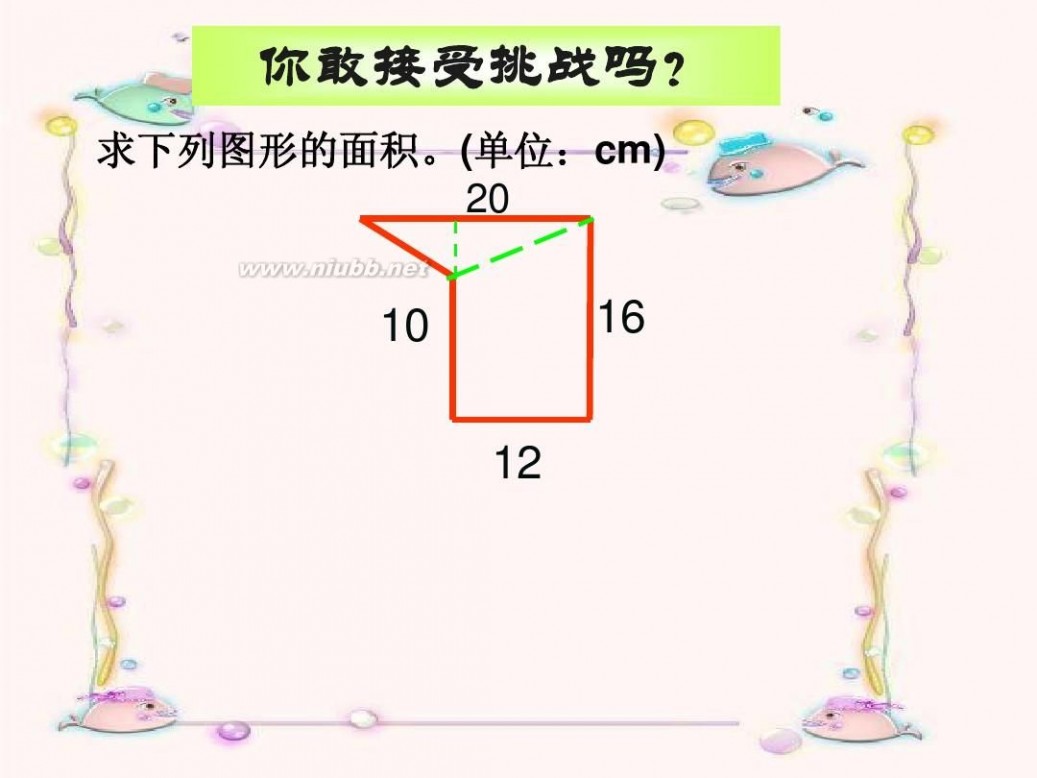
你敢接受挑战吗？
求下列图形的面积。(单位：cm) 20

10

16

12

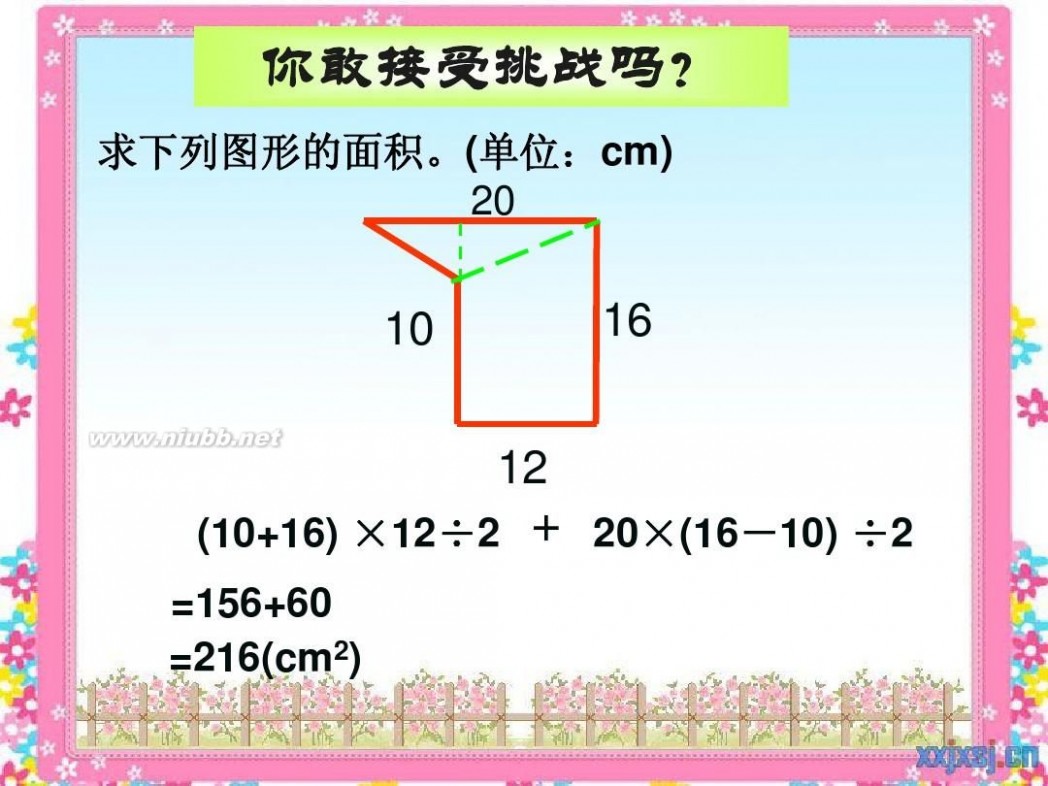
你敢接受挑战吗？
求下列图形的面积。(单位：cm) 20

10

16

12
(10+16) ×12÷2 =156+60 =216(cm2)

+

20×(16－10) ÷2

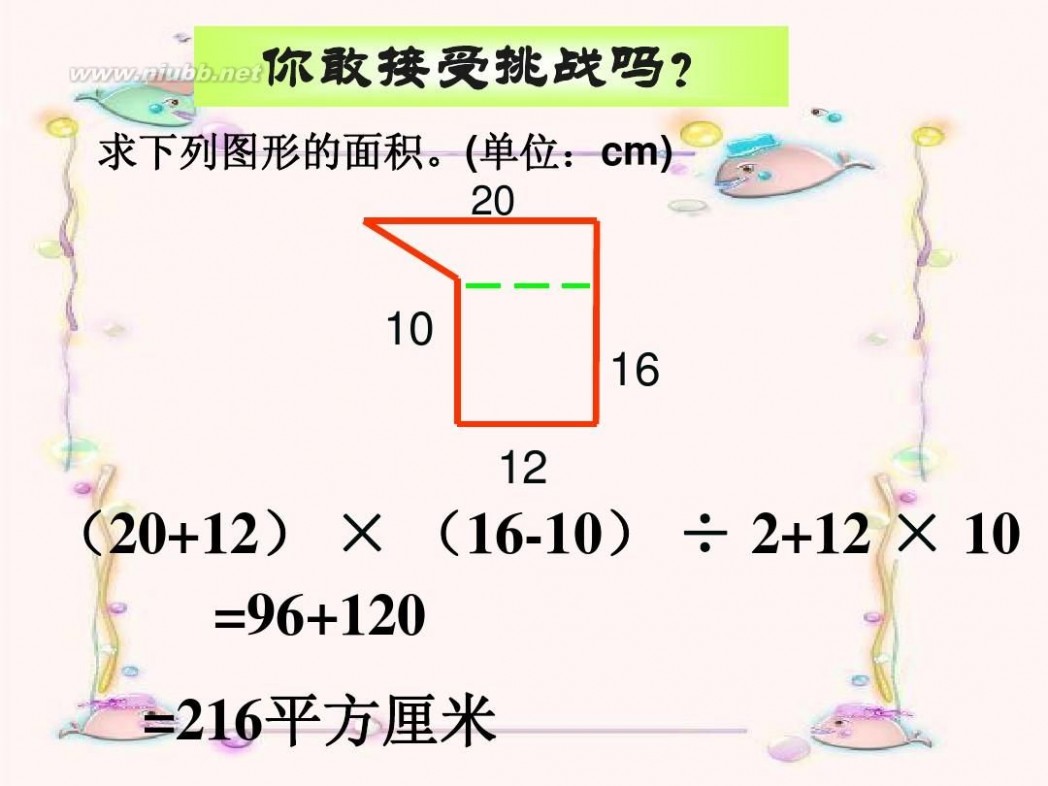
你敢接受挑战吗？
求下列图形的面积。(单位：cm) 20

10

16

12

（20+12） × （16-10） ÷ 2+12 × 10 =96+120

=216平方厘米

老师家新买了住房，计划在客厅铺地板。至少要买多大面积的地板呢？
4m

7m

3m

客厅平面图

6m

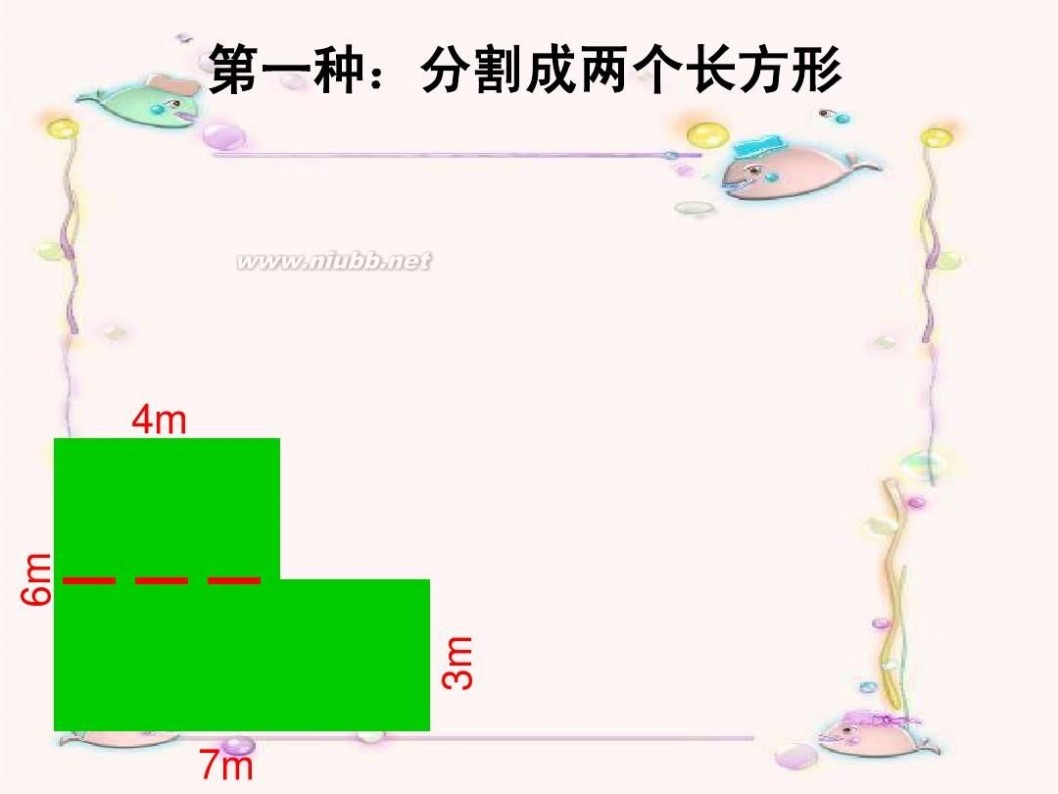
第一种：分割成两个长方形

4m

6m

7m

3m

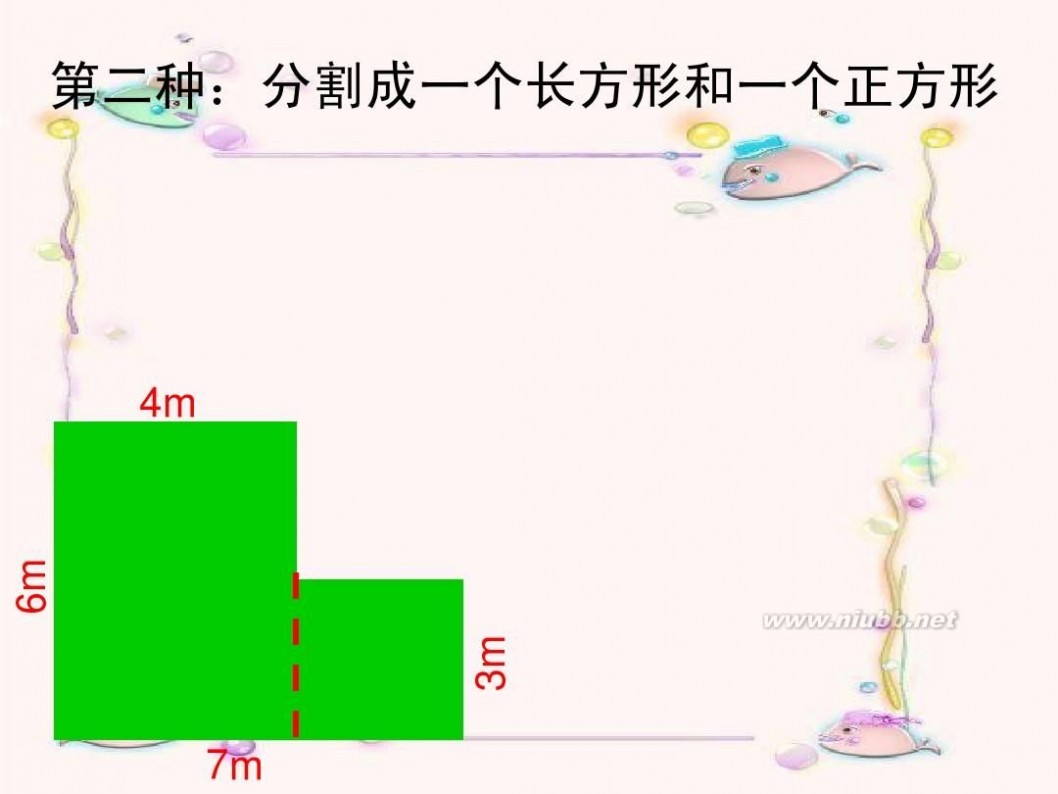
第二种：分割成一个长方形和一个正方形

4m

6m

7m

3m

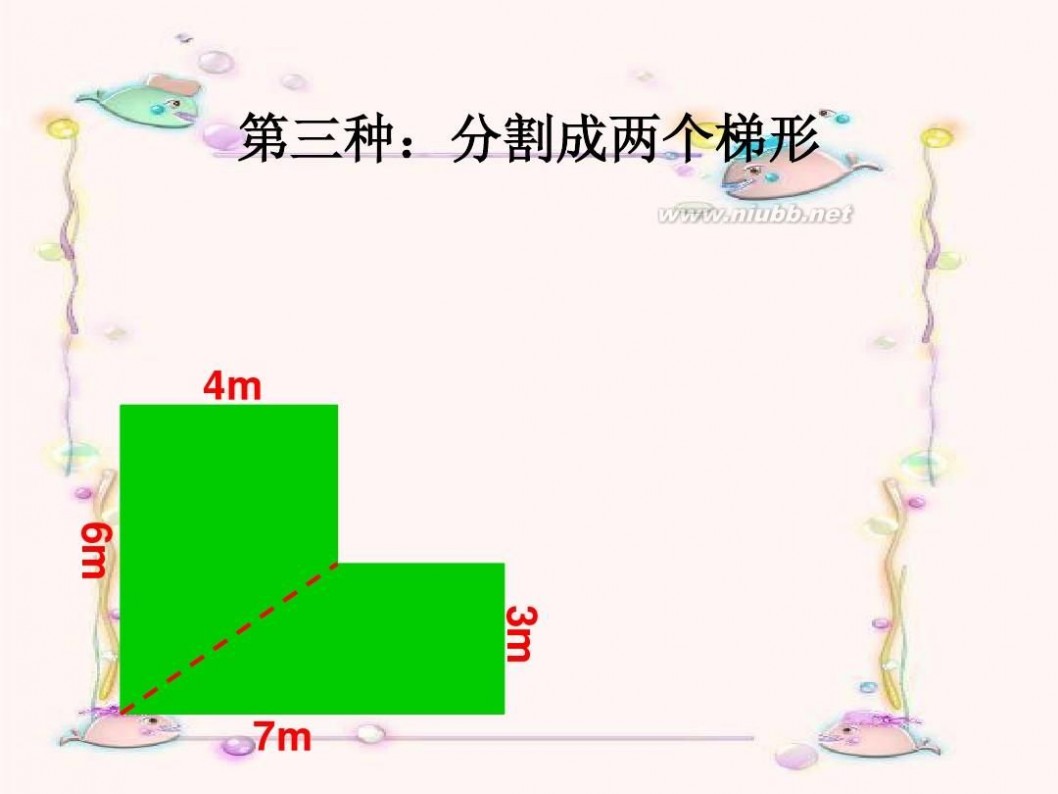
第三种：分割成两个梯形

4m

6m 3m
7m

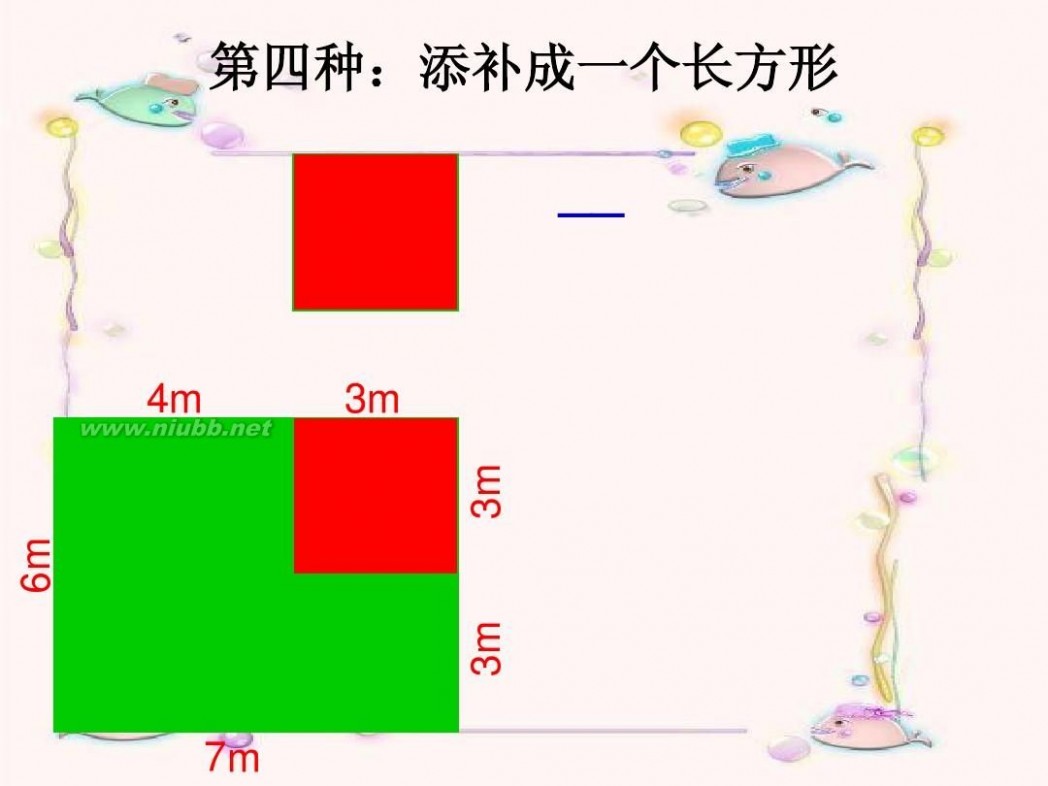
第四种：添补成一个长方形

__

4m

3m

6m

7m

3m

3m

4m 6m

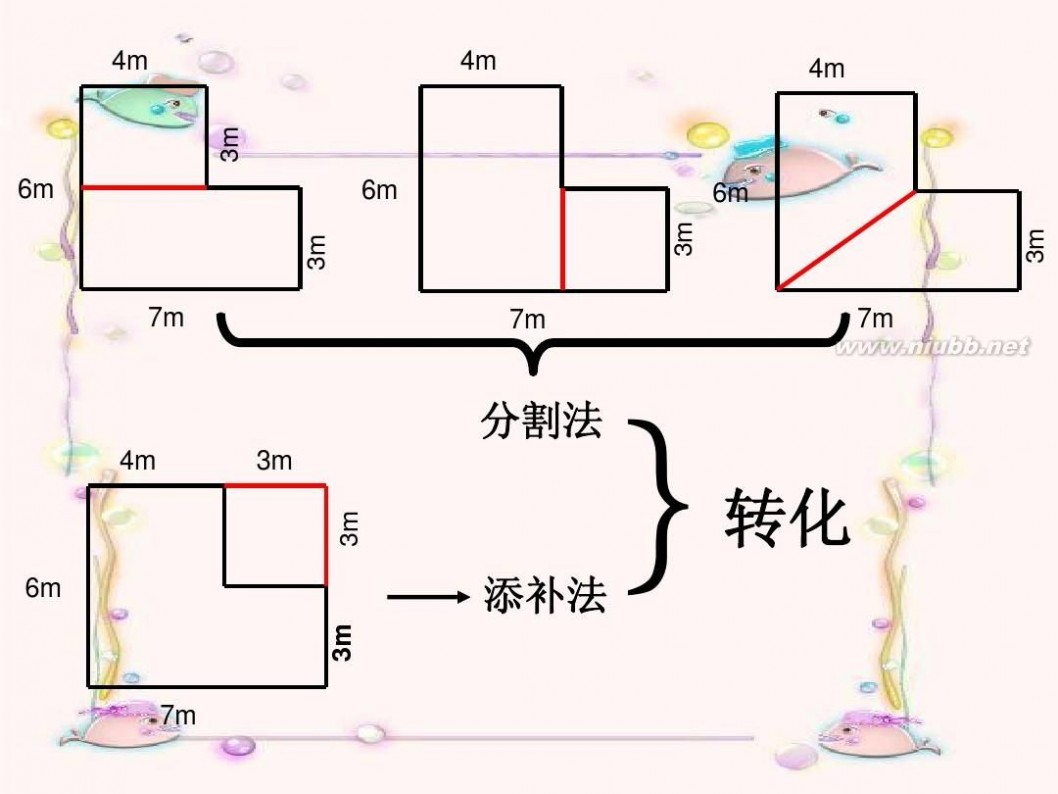
算一算
6m 3m

4m

3m

7m （一） 4m 6m 6m 7m （三） 3m 3m

7m （二） 4m

3m 7m （四）

4m 3m

4m

4m

6m 3m

6m 3m

6m 3m 7m

7m

7m

分割法
4m 3m 3m

6m 3m

添补法
7m

｝

转化

小结

方法：一分图形二找条件三算面积

关键：学会运用“分割”与“添补” 的方

法计算组合图形面积．

2、某工厂有一种用铁皮剪成的零件。（如图）请计算做一个这样的零件要用多少铁皮（单位：米）
先仔细观察图形，然后用你熟悉的方法去完成这道题。

2m 3m
3m 3m 3m 3m

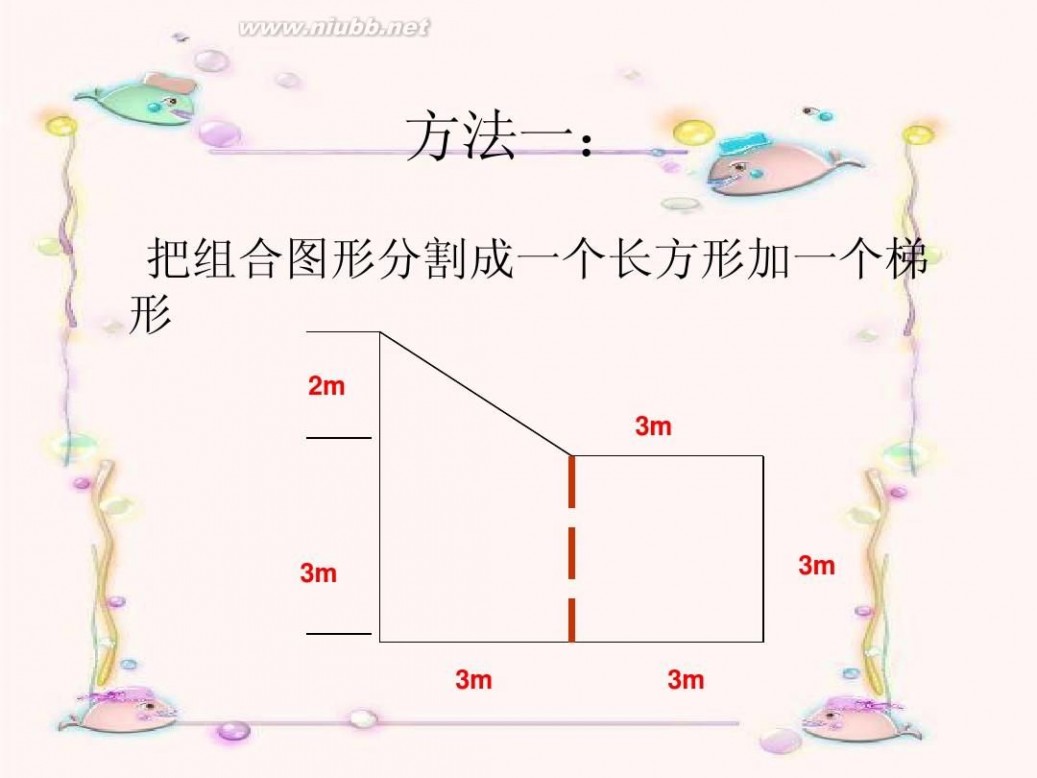
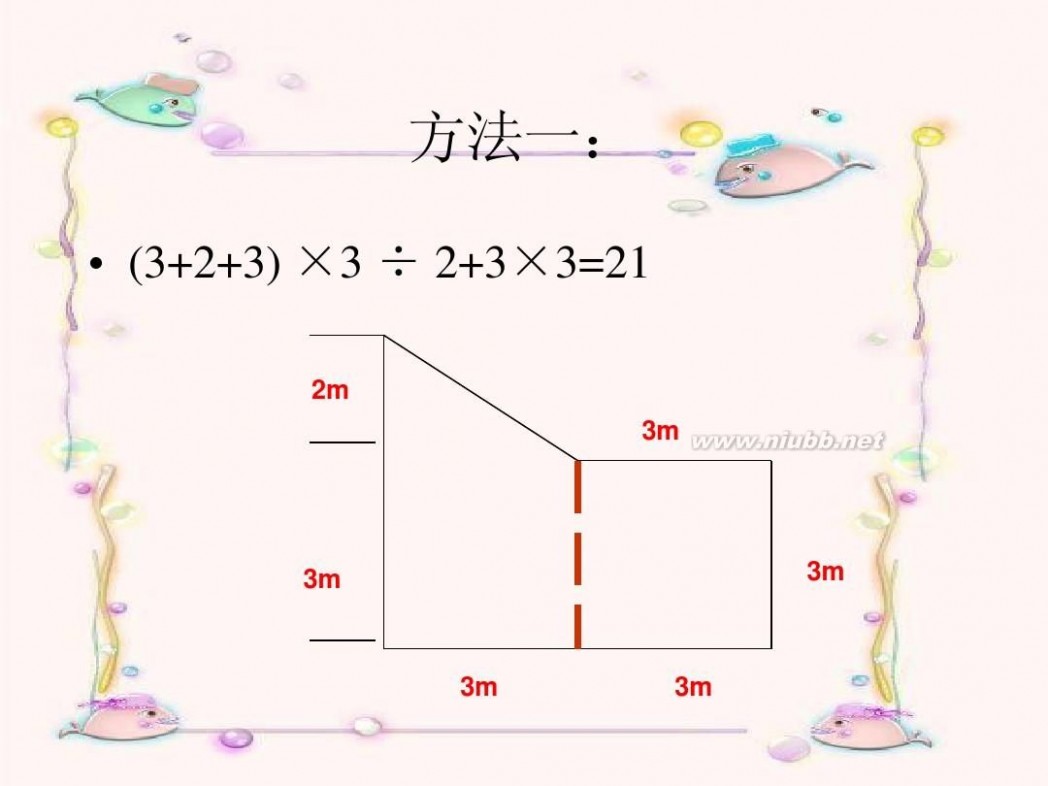
方法一：
把组合图形分割成一个长方形加一个梯形
2m 3m

3m

3m

3m

3m

方法一：
? (3+2+3) ×3 ÷ 2+3×3=21
2m 3m

3m

3m

3m

3m

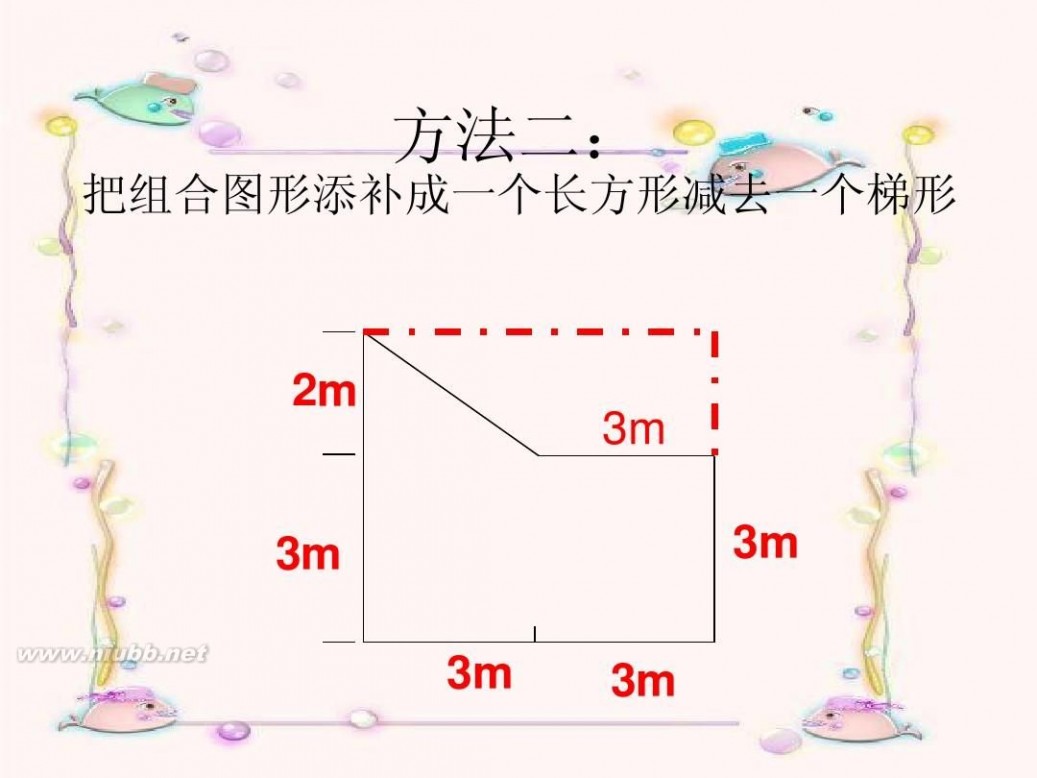
方法二：
把组合图形添补成一个长方形减去一个梯形

2m

3m 3m 3m
3m

3m

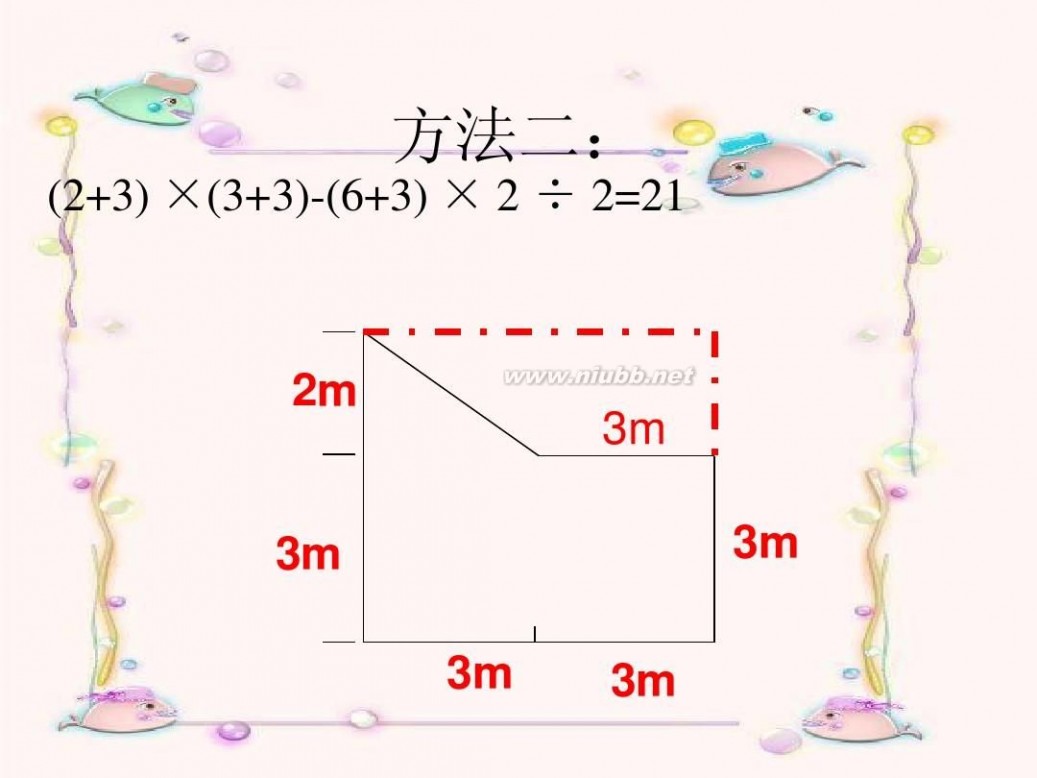
方法二：
(2+3) ×(3+3)-(6+3) × 2 ÷ 2=21

2m

3m 3m 3m
3m

3m

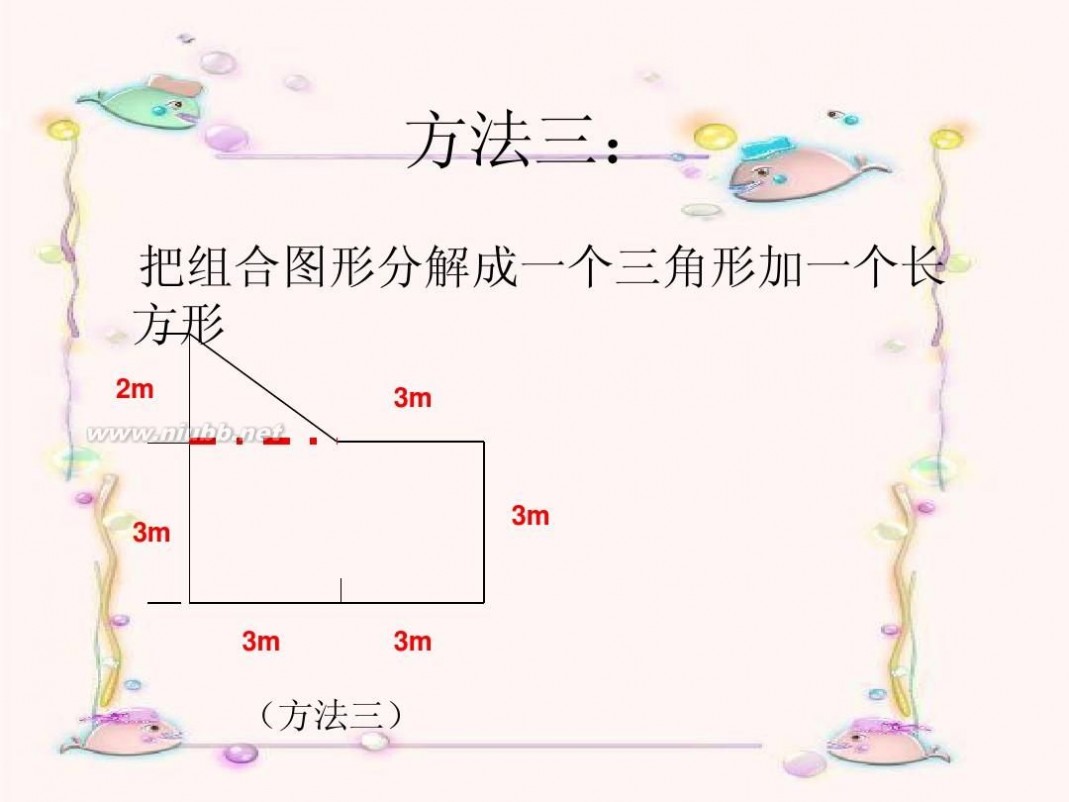
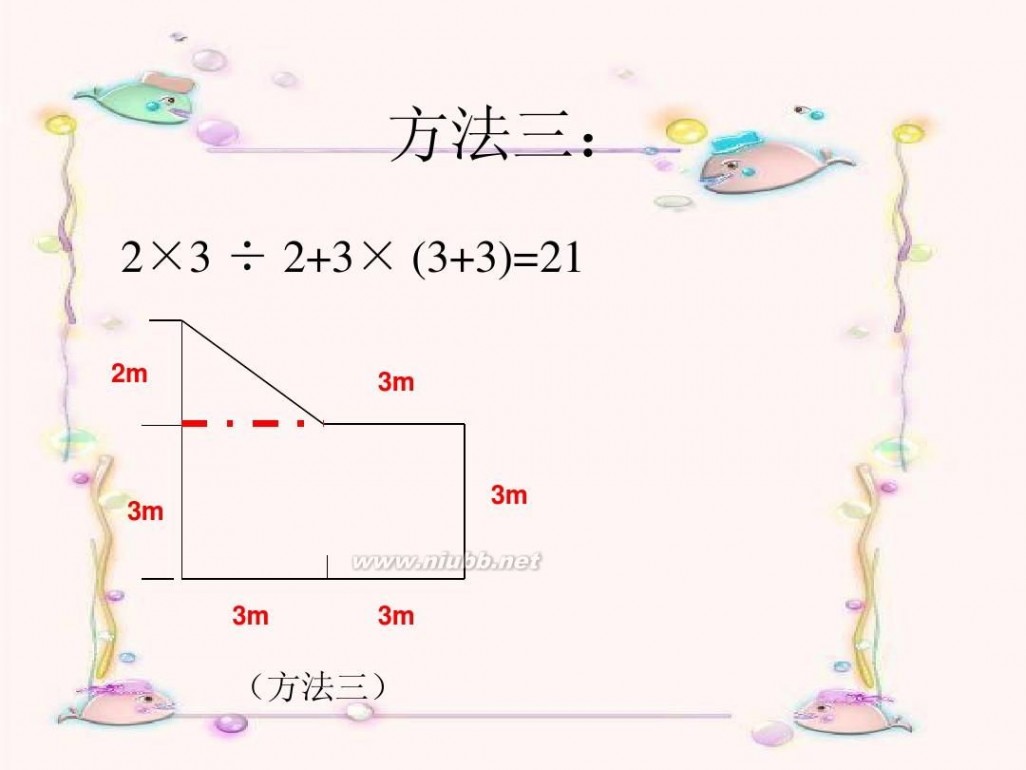
方法三：
把组合图形分解成一个三角形加一个长方形
2m 3m

3m

3m

3m

3m

（方法三）

方法三：
2×3 ÷ 2+3× (3+3)=21
2m 3m

3m

3m

3m

3m

（方法三）

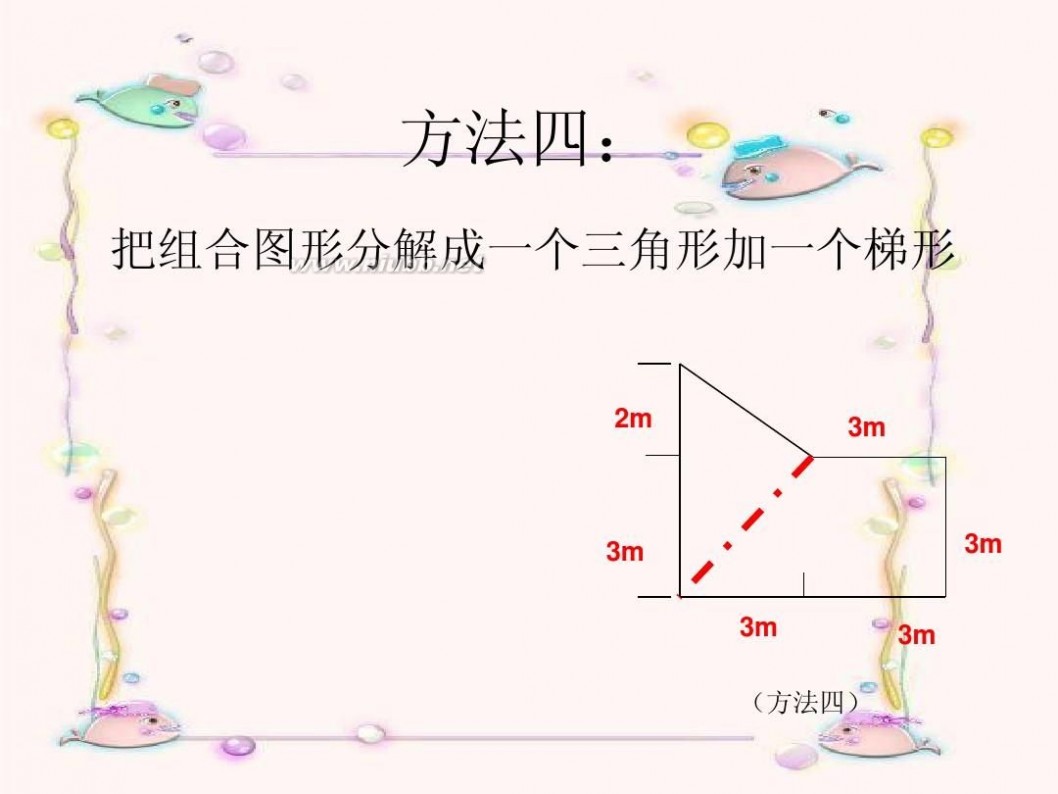
方法四：
把组合图形分解成一个三角形加一个梯形

2m

3m

3m 3m （方法四） 3m

3m

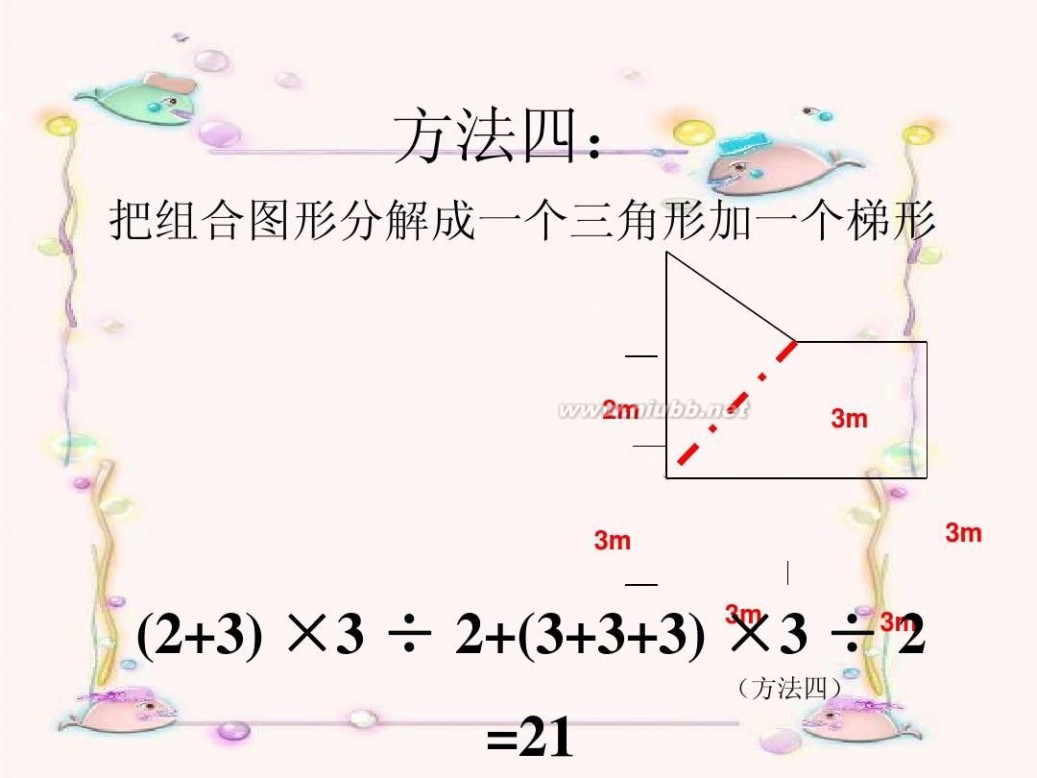
方法四：
把组合图形分解成一个三角形加一个梯形

2m

3m

3m

3m 3m

(2+3) ×3 ÷ 2+(3+3+3) ×3 ÷ 2
3m （方

法四）

=21

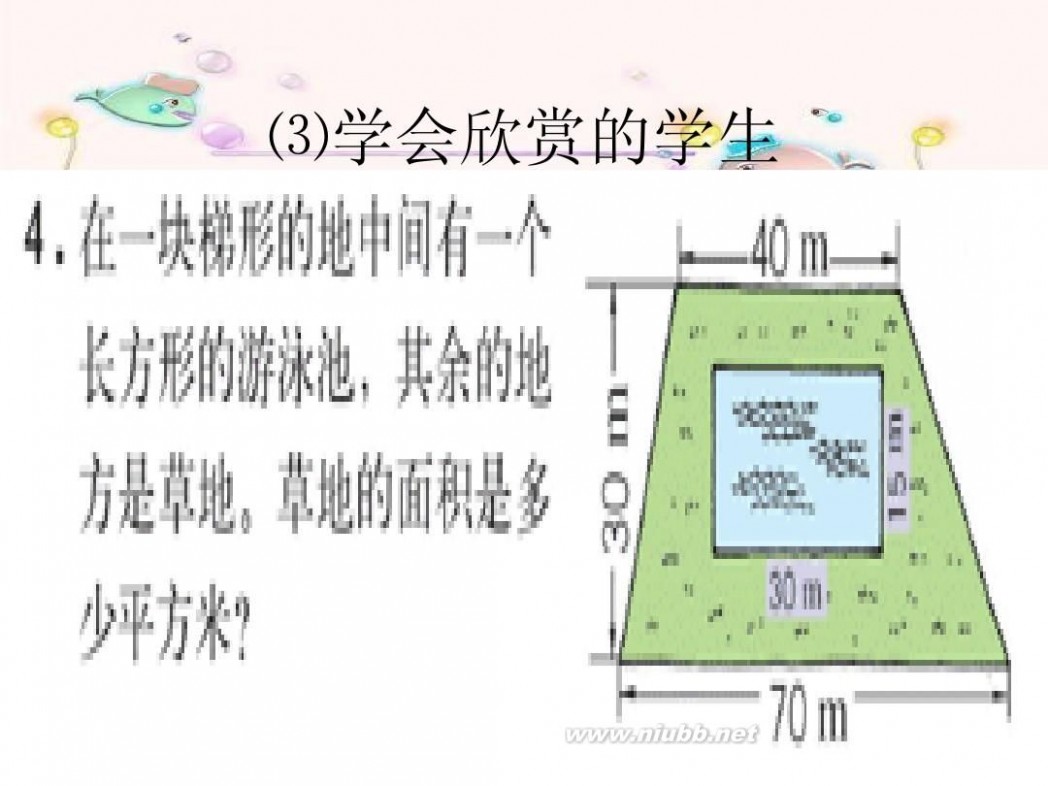
⑶学会欣赏的学生
P94页第4题欣赏利用组个图形拼成的图案及其

在生活中的应有

。

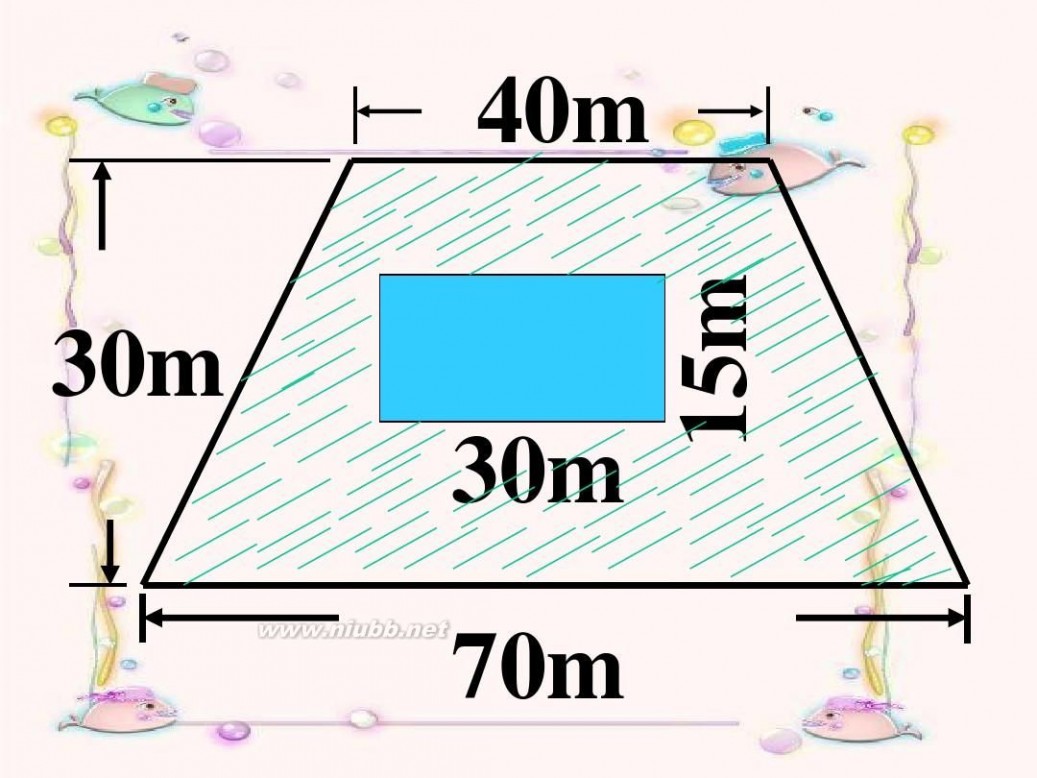
40m 30m
30m 70m 15m

(70+40) × 30 ÷ 2 -30 × 15
=1650-450 =1200平方米

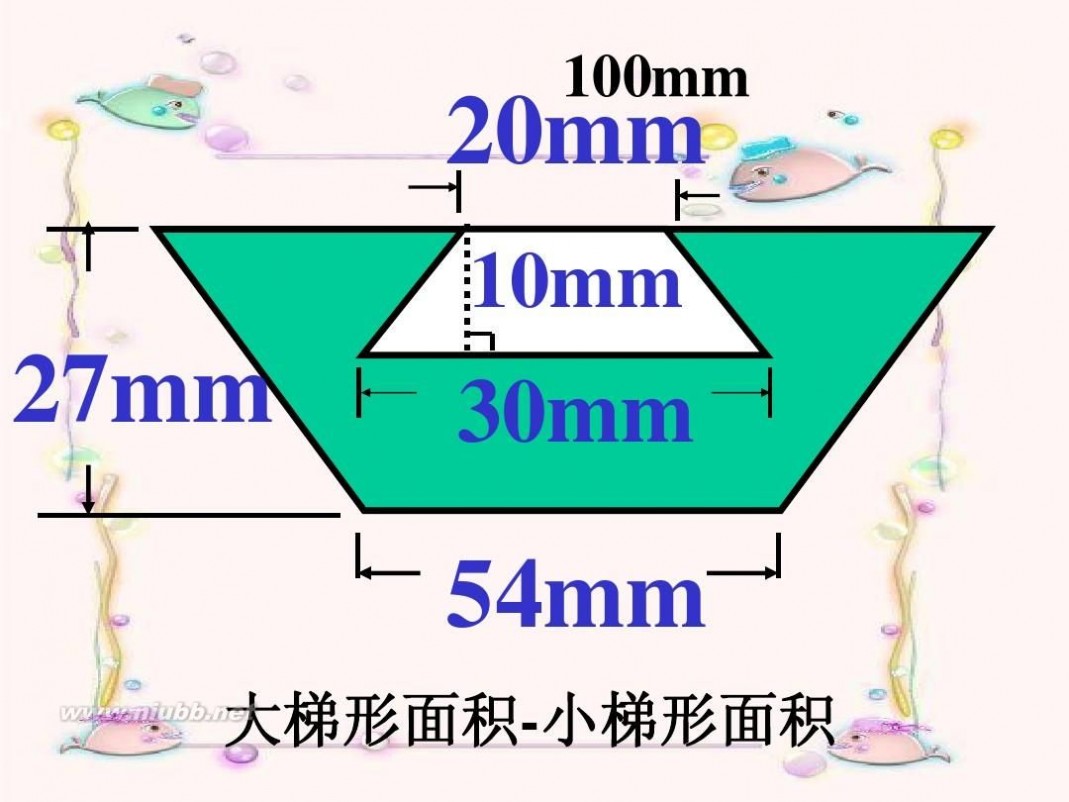
（4）下图是一个零件的横截面，计算它的面积。

20mm
10mm

27mm

30mm

54mm
100mm

20mm
10mm

100mm

27mm

30mm

54mm
大梯形面积-小梯形面积

(54+100) × 27 ÷ 2 -（20+30）× 10 ÷ 2

=2079-250
=1829平方毫米

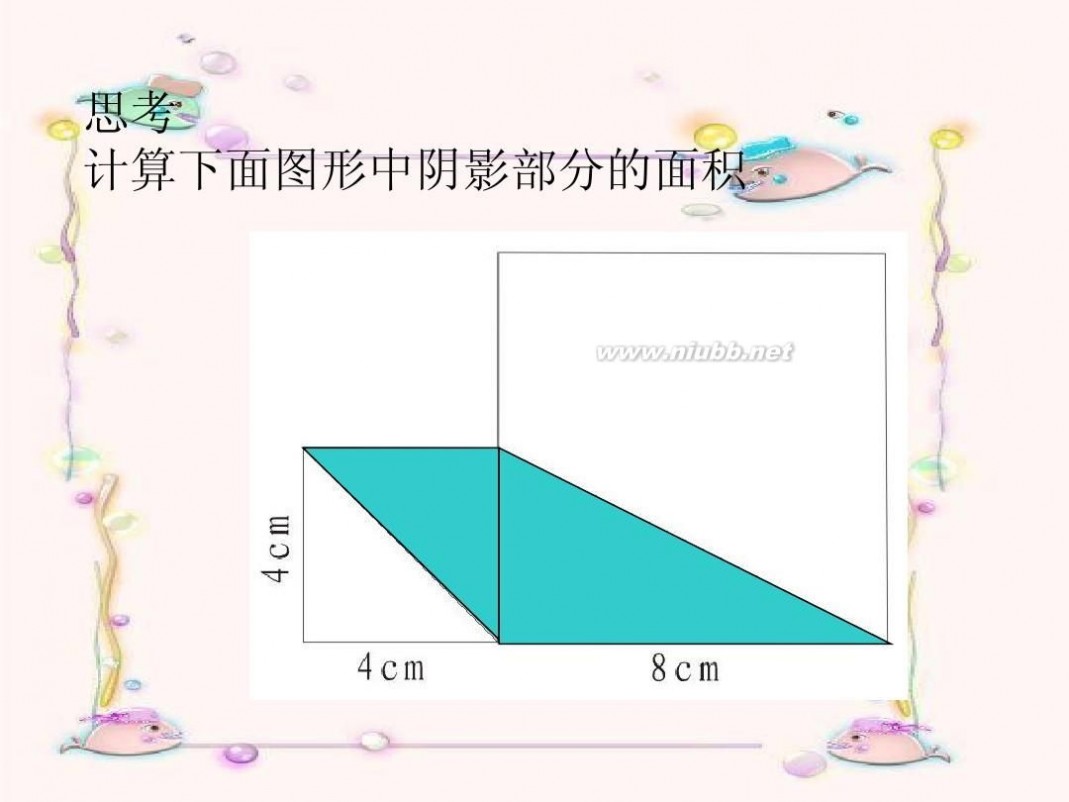
思考计算下面图形中阴影部分的面积

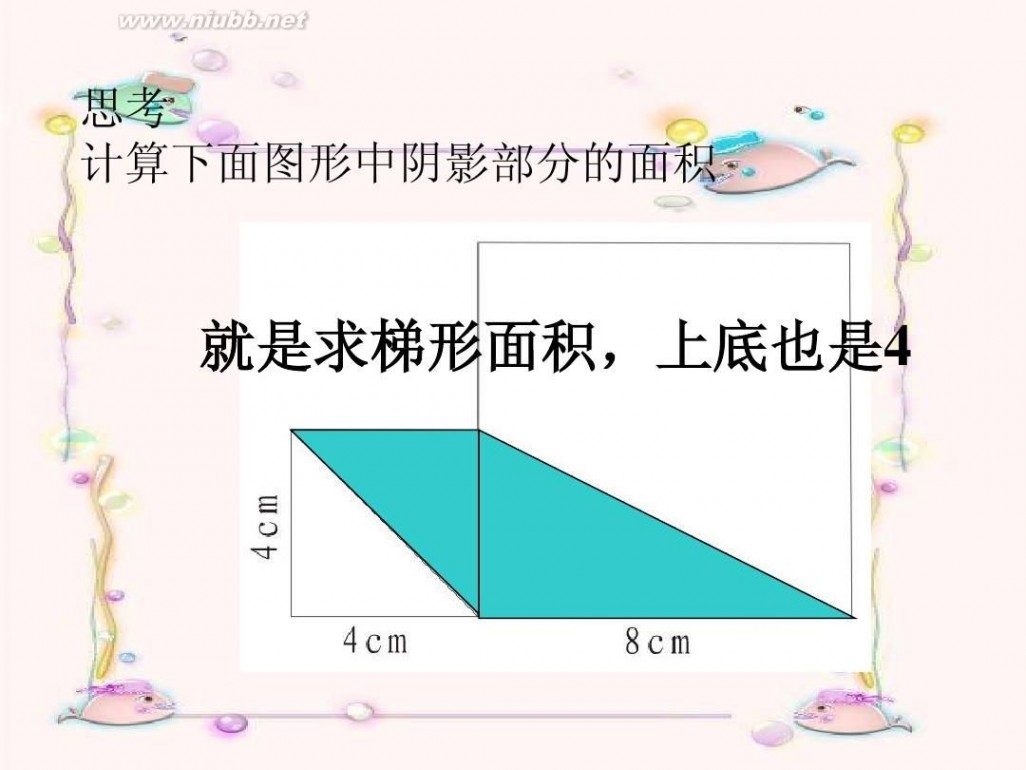
思考计算下面图形中阴影部分的面积

就是求梯形面积，上底也是4

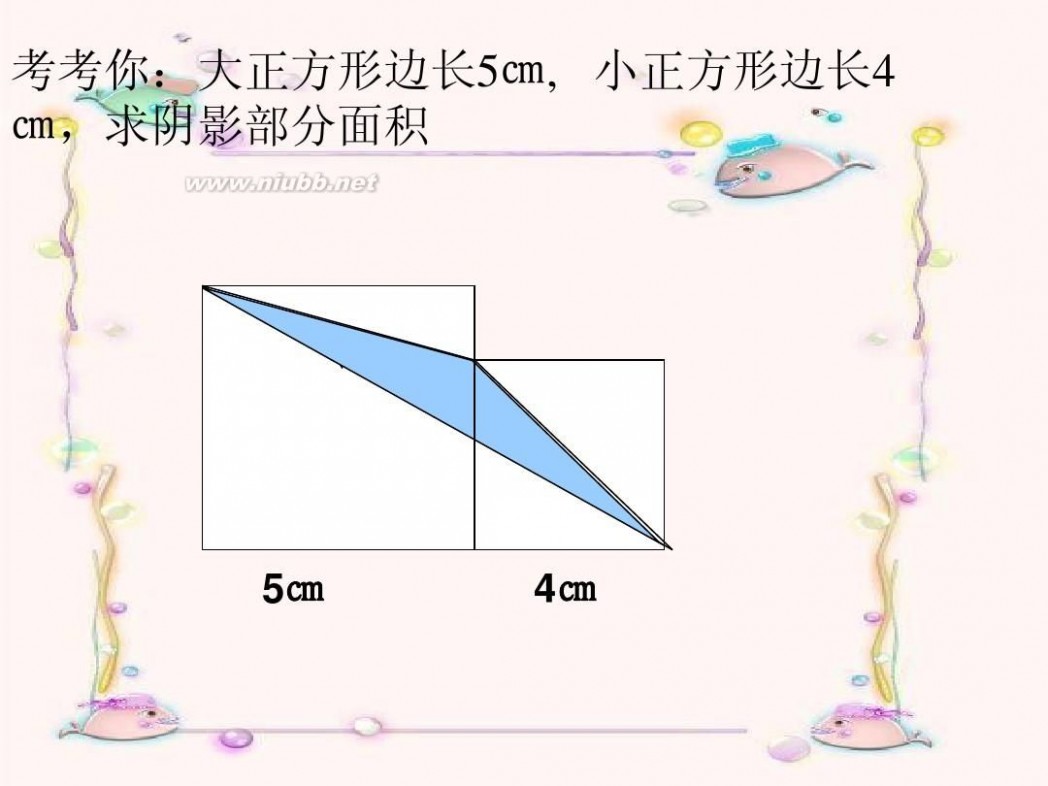
考考你：大正方形边长5㎝, 小正方形边长4 ㎝，求阴影部分面积

5㎝

4㎝

5 × 5+4 × 4-(5+4) × 5 ÷ 2

-（5-4）× 5 ÷ 2-4 × 4 ÷ 2
=25+16-22.5-2.5-8 =8平方厘米

六、如图，一块草地，长32，宽24，中间有一条宽为4的小路。求草地（阴影）面积。（单位：米）

?32 ? 4 ? ? ?24 ? 4 ?
? 28 ? 20 ? 560 ( m 2 )
答：草地的面积是560m2。

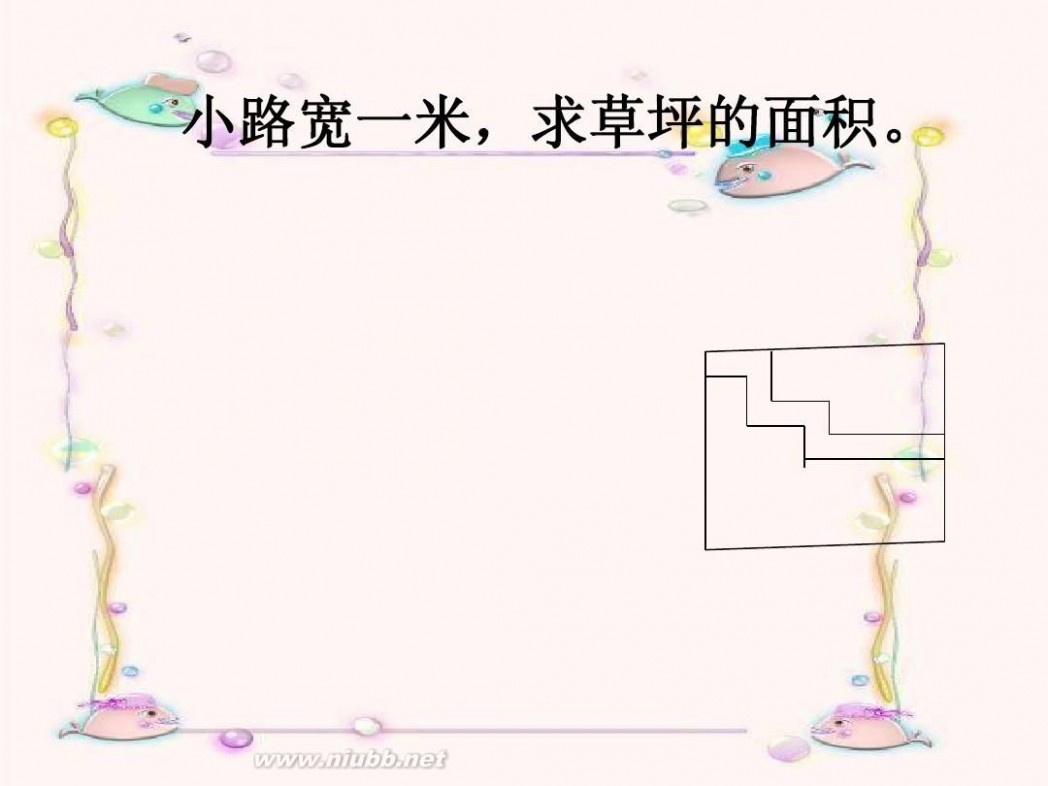
小路宽一米，求草坪的面积。

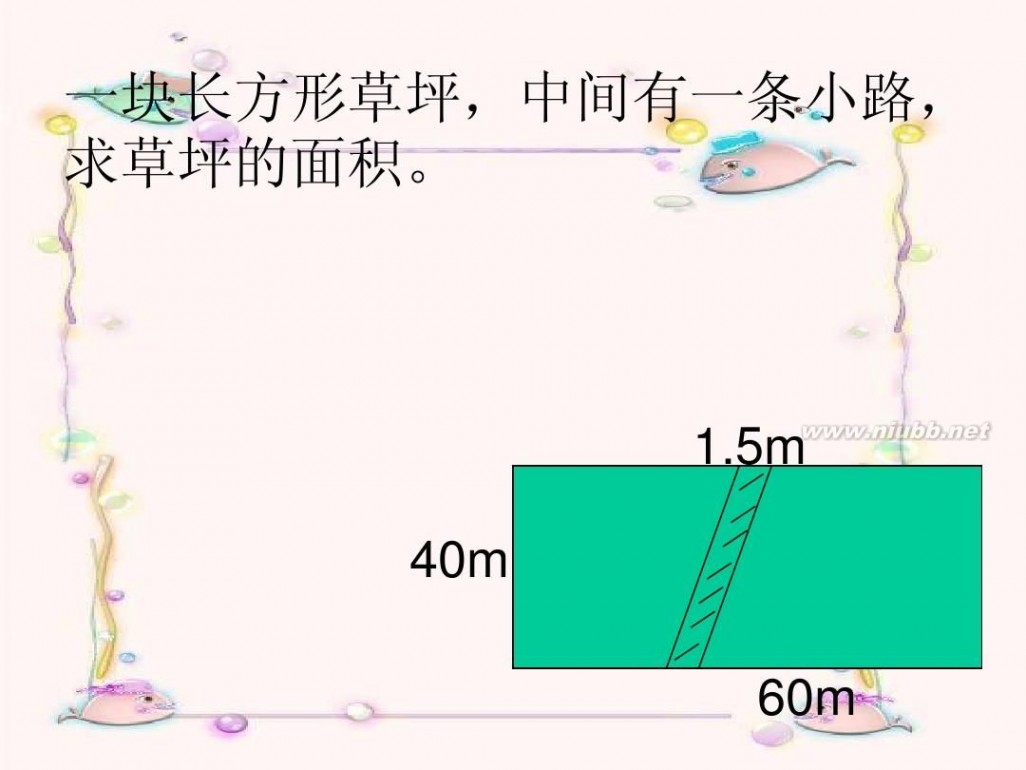
一块长方形草坪，中间有一条小路，求草坪的面积。

1.5m 40m 60m

一块长方形草坪，中间有一条小路，求草坪的面积。就是把平行四边形的底减去1.5后再计算
1.5m 40m 60m

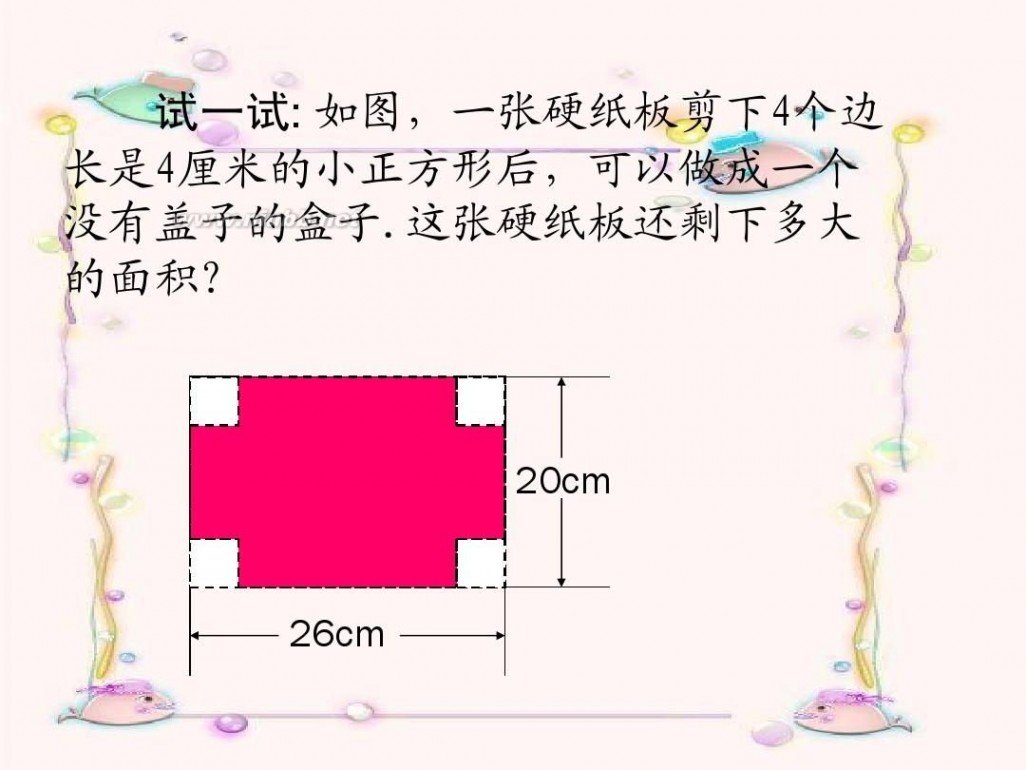
试一试: 如图，一张硬纸板剪下4个边长是4厘米的小正方形后，可以做成一个没有盖子的盒子.这张硬纸板还剩下多大的面积?

20cm

26cm

二 : “组合图形的面积”说课稿

一、教材分析
“组合图形的面积”是小学数学人教版第九册第五单元的内容。教材把这一内容安排在平行四边形、三角形和梯形面积计算之后学习，让学生知道在进行组合图形面积计算中，要把一个组合图形分解成已学过的平面图形并进行计算，这样可以巩固对各种平面图形特征的认识和面积公式的运用，又有利于发展学生的空间观念。教材在内容呈现上突出了两个部分，一是感受计算组合图形面积的必要性，也是日常生活中经常需要解决的问题。二是针对组合图形的特点强调学生学习的自主探索性。因此可以确立这课时的教学重点与难点，就是：探索并理解掌握组合图形面积的计算方法。
组合图形的面积计算方法有两种：分割法和添补法。在这个内容上我把它分为两个课时来讲授，而这节课时是讲分割法。
基于以上的分析，我确立本节课的教学目标：
1、知识目标
（1）认识简单的组合图形，会把组合图形分解成已学过的平面图形并计算出它的面积。
（2）能运用所学的知识，解决生活中有关组合图形面积的实际问题。
2、技能目标
（1）让学生在观察、列举中认识简单的组合图形，在尝试、交流中探索组合图形面积的计算方法。
（2）学会用分割法计算组合图形的面积。
3、情感目标
（1）结合具体的题例，感受计算组合图形面积的必要性，产生积极的数学学习情感。
（2）渗透转化的数学思想和方法。
二、学情分析
本课的授课对象是五年级的学生，学生通过之前的学习，对于平面图形直观感知和认识上已有了一定的基础，也掌握了一些基本图形面积的计算方法。作为五年级的学生，应进一步提高知识的综合运用能力，在学习中去探索掌握解决问题的思考策略。
三、教学方法与手段
（一）教法
根据《数学课程标准》的要求：“教学要贯彻直观性、趣味性实践性的原则，教学方法要多样、灵活、有趣。”因此在教学中我有意识地利用直观的图形，与有趣的“七巧板”进行导入，利用多媒体课件、学具，让学生通过动手实践、操作、亲身体验知识的获取过程。
（二）学法
根据新课程对学生学习方式的改变，结合这节课的内容，课堂上学生学习方式主要是由独立思考与合作学习相结合。学生通过自己来观察组合图形的特点，思考解题的方法，逐步构建自己的知识体系；通过与他人的合作获取更多的方法，找到合适、有效的解决问题的方法，进一步完善自己的知识形成过程。
基于以上的教法与学法，我对本节课建构了一个基本的组织教学过程：复习与设问——探索与交流——归纳与应用——总结与提升。
四、教学过程
（一）复习旧知：
出示以前学过的图形：长方形、正方形、平行四边形、三角形、梯形，让学生写一写以上图形的面积计算公式，并用字母公式表示。
（这样做是为了让学生回顾以前的知识，在内心萌发出对各种基本图形的直观感，为下一步新课的学习奠定基础。）
（二）拼图活动导入新课：
同桌合作利用事先准备好的七巧板，任选其中的若干个，拼成一个学生喜欢的图案，并让学生说一说你拼的图案像什么？是由哪些基本图形组成的？
通过学生的拼图与老师的引导，让学生发现这些图形都有一个共同的特点：就是都由以前学过的基本图形组成的，从而揭示课题：组合图形的面积。
（根据新课标提倡的“自主、合作、探究”的理念，我进行第三个环节）
（三）自主探索新知，小组合作学习：
课件出示例题（右图表示的是一间房子侧面墙的形状。它的面积是多少平方米？）
先让学生观察图形，独立思考问题：对于这个组合图形，该怎样去计算它的面积？这个组合图形能看作由哪些基本图形组合而成的？
学生独立计算后，再小组交流解决这个组合图形面积的计算方法。
（在这个过程中，我会在下面巡视学生做题的情况，接下来我就结合学生做题的具体情况，边讲解边板书这个组合图形面积的计算方法）
（可能会出现两种方法：1、是把这个组合图形分解成一个三角形和一个正方形来计算，这种方法能直接利用已知条件进行计算；
2、是把这个组合图形分解成两个梯形，这种方法就要先利用已知条件求出梯形的下底和高才能进行计算，相对第一种方法要复杂一点。）
（正因为如此，在讨论解决这道题的过程中，对于“分割法”的含义，有两个要点务必要让学生明白：）
1、对组合图形的分割，必须有其分割的合理性，让学生明白，分割的图形越简洁，其解题的方法也将越简单。
2、要考虑分割的图形与所给条件的关系。有些图形分割后找不到相关的条件就是失败的。
（四）实际应用，体会乐趣
在学生充分理解了“分割法”的含义之后，我就拿一些练习来考考他们是否真正掌握了这种方法，具体是利用课本上的习题（p95第6、7题），因为这两道题比较贴切生活，做这样的练习，可以使他们经历一个学以致用的过程，体会用学到的知识来解决实际问题的乐趣。
（五）质疑问难，提升自我
在教学的最后，为了激发学生对学习数学的乐趣，我会安排一个让学生“自问自答”的环节，即让一个学生提出对本节课所学的知识有哪些不明白的地方，接着由其他学生来解决回答，这样的一个环节，目的是让学生在一个完善自我的学习过程的同时，也能与其他同学互助互学，感受帮助别人解决问题的快乐与成就感。
（我的说课完毕，谢谢大家！）

三 : 组合图形的面积

《》教学设计

一、激趣导入：

师：同学们，在前一段时间我们共同探究了一些平面图形的面积，现在请同学们回忆一下，我们一共研究过哪几种平面图形？它们的面积分别怎样求？

师：同学们，你可不要小巧了这五个基本的平面图形，它能把我们带到神奇的图形世界。在XX年的春节晚会上，我们亿万观众一起领略了刘谦的魔法带给我们的巨大震撼，现在这五种图形同样会带给你美的震撼！现在，就让我们一起走进魅力而神奇的图形世界！说一说画面上分别有哪些美丽的图案？它是由我们学过的哪些平面图形组成的？

师：同学们，只要你开动聪明的小脑袋，动手拼一拼，也能设计出美丽的图案。相信一定会比老师设计的还棒！现在请各组组长拿出材料一（基本图形），我们看看哪个小组设计的多、设计的好、设计的美。各小组开始活动吧！

师：哪个小组想第一个把你们的作品展示给大家看？你能告诉大家你拼的是什么？它是由那些图形组成的吗？

师：同学们认为他设计的美不美？既然美，掌声还不快响起来！

师：哪个小组还想展示？

师：同学们，刚才我们一起展示了这么多美丽的图案，他们的形状虽然不一样，可他们都有没有共同的特点呢？

师：对，他们都是由两个或两个以上的平面图形组成的。像这样由几个简单图形组成的复杂图形我们把它叫做组合图形，今天我们就一起来研究组合图形的面积。

二、自主探究、学习新课：

师：刚才，我们每个人都做了一次小小设计师，设计出了许多美丽的图案，那大家能不能从一些复杂的组合图形中发现基本图形呢？下面就来考考大家的眼力，谁能一眼就看出这个图形是由哪些基本图形组成的？（课件：动脑筋）。

师：说的不错，为了便于观看，请大家动手分一分，看一看你有几种分法？分完后先在组内互相交流，看看谁的方法多，谁的方法巧？好，下面组长拿出材料二（动脑筋），开始吧！

师：哪个组的同学先来展示？哪个小组还有不同的补充？

师：同学们的眼力真棒，只要你从不同的角度观察，同一种图形可以分成多种基本图形。

师：同学们，老师前一段时间在昌盛花园新买了一套房子，客厅的地面就是一个组合图形，我想过两天装修一下，想请同学们帮忙算一下客厅的面积。我们一起来看。请你先自己独立的探究，想一想可以有几种方法？然后在小组内交流，在交流时注意认真倾听同学的意见，咱们比比看哪个组用的方法多。

师：哪个组先把你们的方法展示给大家看？你能说说你是怎样想的吗？哪个组还有补充？把你的方法介绍给大家！

师：刚才我们选用了四种方法都可以求出他的面积，现在，我们一起来比较一下这四种方法，看看他们之间有没有相同点和不同点？（小组同学可以讨论一下）。

师：谁想说一说？

师：对，像前三个，对原图进行了分割，从而求出他们的面积，我们把这种方法叫做分割法。第四种对原图进行了添补，我们把这种方法叫做添补法。虽然我们采用了不同的方法解决了这个问题，但是结果都是一样的，因此，在解题过程中要多角度思考问题，寻求多种方法解决问题。那么，同学们，如果要求你只选择一种方法，你会选哪一种？为什么？在计算组合图形的面积时，可能有多种方法，我们要仔细观察图形，多动脑筋，选择自己喜欢的、简便的方法进行计算。

三、应用练习

师：同学们，今天我们研究了组合图形，想一想，除了客厅的地面，在我们的生活中还有哪些物体的形状也是组合图形？（平房的墙、少先队队旗、风筝等）

师：下面请同学们选择自己最喜欢的一个组合图形做一做。（出示墙、队旗）

师：哪位同学先来展示？能说说你应用的是分割法还是添补法？谁还有不同的方法？

师：看来，同学们对今天的知识掌握得非常好了，下面，我来考一考大家，看看谁最棒。（出示我能行）

四、总结：

同学们，通过这次学习，你有什么收获？能谈一谈你在组内的表现吗？

四 : 组合图形的面积

组合图形的面积组合图形的面积