一 : 课题:4.1.2频数与频率
教学目标
1通过掷硬币的实验理解频数与频率的意义。2 知道重复试验中,各试验结果的频数之和等于实验的总次数,各试验结果的频率之和等于教学重点、难点重点:1 理解频数和频率的意义,2知道重复试验中,各试验结果的频数之和等于实验的总次数,各试验结果的频率之和等于1.难点:理解频数与频率的意义。教学过程一 创设情境,导入新课在一次象棋比赛中,有两个最优秀的选手始终是平局,于是决定用掷硬币的方法来确定谁是第一名,把硬币抛掷地面,只有两种可能性,有国徽的一面朝上或者另一面朝上,猜中者为冠军,假设你是这两个选手中的一员,你认为怎么样猜好?为什么呢?下面就让我们来通过试验感受抛掷硬币时,出现有国徽的一面朝上的可能性。二 合作交流,探究新知1 掷一枚硬币的试验(1)体会频数与频率的概念请你抛掷一枚硬币10次,并纪录抛掷结果,填入下表:次数12345678910结果统计:① 在这10次试验中,正面朝上的有____次,反面超上的有____次。指出:正面朝上的次数和反面朝上的次数也叫频数。思考:正面朝上的次数和反面朝上的次数以及总次数有什么关系?指出:在一组重复实验中,各结果的频数之和等于试验的总次数。② 在这10试验中,正面朝上的次数占总次数的几分之几?反面朝上的次数占总次数的几分之几?指出:正面朝上的次数占总次数的比例叫正面朝上的频率,反面朝上的次数占总次数的比例教反面朝上的频率。思考:正面朝上的的频率和反面朝上的频率之和等于______指出:在一组重复实验中,各结果的频率之和等于1 请把你统计的结果填入下表频数频率正面朝上反面朝上和(2)统计20位同学的结果填入下表(体会正面朝上和反面朝上的频率差距大不大?)频数频率正面朝上反面朝上说一说:上面用抛掷硬币的实验来决定冠军时,猜哪面朝上好呢?2 掷两枚硬币的试验如果是抛掷两枚硬币来决定冠军,两枚硬币有可能出现哪些情况呢?(交流讨论)a 两枚硬币都是正面朝上, b 两枚硬币都是反面朝上,c 一枚硬币正面朝上,另一枚硬币反面朝上每次抛掷硬币都发生a,b,c三种情形中的一种,并且只发生一种,猜那种正面朝上好呢?我们来试验:每个同学抛掷一次,填写p121表格。思考:通过试验你发现了什么?发现:出现c的可能性多一些。为什么出现c的可能性会多一些呢?你只原因吗?三 课堂练习,巩固提高 p 122四 反思小结,拓展提高这节课你有什么收获?五 作业练创考 p 65---65二 : 应用概率统计习题解答(全)
习 题 一 解 答
1. 设A、B、C表示三个随机事件,试将下列事件用A、B、C及其运算符号表示出来:
(1) A发生,B、C不发生;
(2) A、B不都发生,C发生;
(3) A、B中至少有一个事件发生,但C不发生;
(4) 三个事件中至少有两个事件发生;
(5) 三个事件中最多有两个事件发生;
(6) 三个事件中只有一个事件发生.
解:(1)ABC (2)ABC (3)?A?BC (4)ABC?ABC?ABC (5)ABC (6)ABC?ABC?ABC
――――――――――――――――――――――――――――――――――――――― 2. 袋中有15只白球 5 只黑球,从中有放回地抽取四次,每次一只.设Ai表示“第i次取到白球”(i=1,2,3,4 ),B表示“至少有 3 次取到白球”. 试用文字叙述下列事件:
(1) A?4?A , (2) A ,(3) , (4) Ai
i?12?A3 .
解:(1)至少有一次取得白球
(2)没有一次取得白球
(3)最多有2次取得白球
(4)第2次和第3次至少有一次取得白球
――――――――――――――――――――――――――――――――――――――― 3. 设A、B为随机事件,说明以下式子中A、B之间的关系.
(1) A?B=A (2)AB=A
解:(1)A?B (2)A?B
――――――――――――――――――――――――――――――――――――――― 4. 设A表示粮食产量不超过500公斤,B表示产量为200-400公斤 ,C表示产量低于300公斤,D表示产量为250-500公斤,用区间表示下列事 件:
(1) AB, (2) BC,(3) B?C,(4)(B?D)C,(5)A.
解:(1)?200,450?; (2)?200,300? (3)?0,450? (4)?200,300? (5)?0,200?
――――――――――――――――――――――――――――――――――――――― 5. 在图书馆中任选一本书,设事件A表示“数学书”,B表示“中文版”, C表示“ 1970 年后出版”.问:
(1) ABC表示什么事件?
(2) 在什么条件下,有ABC=A成立? (3) ?B表示什么意思?
(4) 如果A=B,说明什么问题?
解:(1)选了一本1970年或以前出版的中文版数学书
(2)图书馆的数学书都是1970年后出版的中文书
(3)表示1970年或以前出版的书都是中文版的书
(4)说明所有的非数学书都是中文版的,而且所有的中文版的书都不是数学书
――――――――――――――――――――――――――――――――――――――― 6. 互斥事件与对立事件有什么区别?试比较下列事件间的关系.
(1) X < 20 与X≥ 20 ;
应用概率统计 应用概率统计习题解答(全)
(2) X > 20与X< 18 ;
(3) X > 20与X ≤ 25 ;
(4) 5 粒种子都出苗与5粒种子只有一粒不出苗;
(5) 5 粒种子都出苗与5粒种子至少有一粒不出苗.
解:(1)对立; (2)互斥;(3)相容;(4)互斥;(5)对立
――――――――――――――――――――――――――――――――――――――― (古)7. 抛掷三枚均匀的硬币,求出现“三个正面”的概率. 11??0.125 382
――――――――――――――――――――――――――――――――――――――― (古)8. 在一本英汉词典中,由两个不同的字母组成的单词共有 55 个,现从?26个英文字母中随机抽取两个排在一起,求能排成上述单词的概率. 55解:p??0.0846 26?25
――――――――――――――――――――――――――――――――――――――― (古)9. 把 10 本书任意地放在书架上,求其中指定的三本书放在一起的概率是多少? 解:首先将指定的三本书放在一起,共3!种放法,然后将7?(1)?8进行排列,共有8!种不解:p?
3!8!61???0.067 10!9015
――――――――――――――――――――――――――――――――――――――― (古)10. 电话号码由 6 位数字组成,每个数字可以是 0,1,2,3,4,5,6,7,8,9 共 10 个数字中的任何一个数字(不考虑电话局的具体规定),求:
(1) 电话号码中 6 个数字全不相同的概率;
(2) 若某一用户的电话号码为 283125 ,如果不知道电话号码,问一次能打通电话的概率是多少?
6P10?6解:(1) p?6?0.1512,(2) p?10 10
――――――――――――――――――――――――――――――――――――――― (古)11. 50 粒牧草种子中混有3粒杂草种子,从中任取4粒,求杂草种子数分别为0,1,23 粒的概律
k4?k4k?0,1,2,3 解: P{X?k}?C3C27/C50,同排列方法。[www.61k.com]故p?
――――――――――――――――――――――――――――――――――――――― (古)12. 袋内放有两个伍分、三个贰分和五个壹分的硬币,从中任取五个,求钱额总和超过一角的概率.
解:设A为事件“钱额总和超过一角”,则A={两个五分其余任取3个+一个五分3个两分
123131122P(A)?5C2C8?C2C3C5?C2C3C5一个一分+一个五分2个两分2个一分},故:=0.5 C10??
――――――――――――――――――――――――――――――――――――――― (古)13. 10 把钥匙中有3把能打开门,今任取两把,求能打开门的概率. 1371168211???解:P(A)?2C3?C3C7,或P(A)?=0.53 101033015C10??
――――――――――――――――――――――――――――――――――――――― (古)14. 求习题 11 中至少有一粒杂草种子的概率.
解:本题与11解法有关,即为1?P(X?0)?0.2255
――――――――――――――――――――――――――――――――――――――― (几)15.有一码头,只能停泊一艘轮船,设有甲、乙两艘轮船在0道T小时这段时间内等
应用概率统计 应用概率统计习题解答(全)
可能地到达这个码头,到后都停T1小时,求两船不相遇的概率.
解:设x,y分别为甲、乙船到达码头的时刻,A为事件“两船相遇”。(www.61k.com)则
???(x,y)|0?x?T,0?y?T?,??(x,y)|x?y?T1?。 所求概率为P(A)?1?P(A)?1?1
T2?T2?(T?T1)2??T1????1?T?? ??2
――――――――――――――――――――――――――――――――――――――― (几)16.(蒲丰投针问题)设平面上画着一些有相等距离2a(a>0)的平行线。向此平面上投一枚质地均匀的长为2l(l<a)的针,求针与直线相交的概率。
解:设x为针的中点到最近一条直线的距离(0?x?a),?为针与直线的夹角,则 ???(x,?)|0?x?a,0?????, A??(x,?)|0?x?lsin?,0?????,于是有
P(A)?L(A)1?L(?)a???
0lsin?d??2l a?
―――――――――――――――――――――――――――――――――――――――
17. 某种动物由出生活到20岁的概率为0.8, 活到25岁的概率为0.4,求现在20岁的这种动物能活到25岁的概率。
解:设A为该动物能活到20岁,B为能活到25岁,则B?A,已知P(A)?0.8,P(B)?0.4,所求概率为
P(AB)P(B)P(B|A)???0.5 P(A)P(A)
―――――――――――――――――――――――――――――――――――――――
18.由长期统计资料表明,某一地区6月份下雨(记为事件A)的概率为4/15,刮风(记为事件B)的概率为7/15,既下雨又刮风的概率为1/10,求P(A|B),P(B|A),P(A?B) 解:由条件概率公式知
1P?AB?3P?A|B?????0.2143 14PB15
1P?AB?3 P?B|A?????0.375 PA8
15
47119 P?A?B??P?A??P?B??P?AB??????0.6333 15151030
―――――――――――――――――――――――――――――――――――――――
19.为防止意外,在矿内设有两种报警系统,单独使用时,系统A有效的概率为 0.92 ,系统B有效的概率为 0.93 ,在系统A失灵的条件下,系统B有效的概 率为 0.85,求:
(1) 发生意外时,这两种系统至少有一个系统有效的概率.
(2) 系统B失灵的条件下,系统A有效的概率. 解:由题意P(A)?0.92,P(B)?0.93,P(B|A)?0.85。
(1)所求概率为:P(A?B)?P(A)?P(B?A)?P(A)?P(B)?0.92?0.068?0.988, 其中:P(B)?P(B|)P()?0.85?(1?0.92)?0.068
(2)所求概率为 P(A|)?1?P(|)?1?P()
P()?1?0.012?0.82857, 0.07
其中 P()?P(?B)?P()?P(B)?0.08?0.068?0.012
―――――――――――――――――――――――――――――――――――――――
应用概率统计 应用概率统计习题解答(全)
20. 100件产品中有10件次品,用不放回的方式从中每次取1件,?连取3 次,求第三次才取得正品的概率.
解:设第三次才取得正品的概率为A,样本空间为A100
12C90A1090?10?9??0.0083 所以P?A??3100?99?98A1003
――――――――――――――――――――――――――――――――――――――― (条件)21. 在空战中,甲机先向乙机开火,击落乙机的概率为 0.4 ;?若乙机未被击落,就进行还击,击落甲机的概率为 0.5 ;若甲机仍未被击落,则再进攻乙机,击落乙机的概率为 0.6 .求在这几个回合中
(1) 甲机被击落的概率;
(2) 乙机被击落的概率.
解:设A为甲机第一次被击落,Bi为乙机第i次被击落,这里A,B1,B2互不相容。[www.61k.com)依题义有
P(B1)?0.4,P(A|1)?0.5,P(B2|1)?0.6
(1)所求概率为 P(A)?P(A|B1)P(B1)?P(A|1)P(1)?0?0.4?0.5?0.6?0.3
(2)所求概率为 P(B1?B2)?P(B1)?P(B2),其中
P(B2)?P(B2|1)P(1)?P(B2|1)P(|1)P(1)?0.6?0.5?0.6?0.18
故所求概率为P(B1?B2)?P(B1)?P(B2)?0.4?0.18?0.58
――――――――――――――――――――――――――――――――――――――― (全概)22. 一个袋子中装有6只白球,4只黑球,从中任取一只,然后放回,并同时加进2只与取出的球同色的球,再取第二只球,求第二只球是白色的概率.
解:设A为“第一次取得白球”,B为“第二次取得白球”(共4白2黑),则
P(B)?P(B|A)P(A)?P(B|)P()?8664????0.4?0.2?0.6 12101210
―――――――――――――――――――――――――――――――――――――――
23. 10 张娱乐票中有4张电影票, 10个人依次抽签.?问第一个人与第二个人抽到电影票的概率是否相同?
解:设Ai为事件“第i个人抽到电影票”,则 P(A1)?4 10
P(A2)?P(A2|A1)P(A1)?P(A2|1)P(1)?34464???? 91091010
―――――――――――――――――――――――――――――――――――――――
24. 发报台分别以概率 0.6 和 0.4发出信号“ .”和“ - ”,?由于通信系统受到干扰,当发出信号“ .”时,收报台分别以概率 0.8 及 0.2 收到信号 “ .”和“ - ”,同样,当发报台发出信号“ - ”时,收报台分别以概率 0 .9 和 0.1 收到信号“ - ”和“ .”.求
(1) 收报台收到信号“ .”的概率.
(2) 当收报台收到信号“ .”时,发报台确系发出信号“ .”的概率.
解:设A,B分别为发出和接受信号“。”,A,分别为发出和接受信号“-”则依题意有
P(A)?0.6,
P(B|A)?0.8,
P(|)?0.9,
(1)
(2) P(A)?0.4,P(|A)?0.2, P(B|)?0.1所求概率为 P(B)?P(B|A)P(A)?P(B|)P()?0.8?0.6?0.1?0.4?0.52, 所求概率为 P(A|B)?P(AB)P(B|A)P(A)48???0.923 P(B)P(B)52
―――――――――――――――――――――――――――――――――――――――
25. 某工厂有甲、乙两车间生产同一种产品,两车间产品的次品率分别为?0 .03 和 0.02 ,
应用概率统计 应用概率统计习题解答(全)
生产出来的产品放在一起,且知甲车间的产量比乙车间的产量多一倍,求:
(1) 该厂产品的合格率;
(2) 如果任取一个产品,经检验是次品,求它是由甲车间生产的概率. 解:设A,分别为甲、乙车间生产的产品,B为次品,则依题义有
(1)
(2) 21,P(A)?,P(B|A)?0.03,P(B|A)?0.02 33所求概率为 P()?1?P(B)?1?[P(B|A)P(A)?P(B|A)P(A)?0.973 P(AB)P(B|A)P(A)6???0.75 所求概率为 P(A|B)?P(B)P(B)8P(A)?
―――――――――――――――――――――――――――――――――――――――
26. 在习题20 中,若第二只取到的是白球,问第一只球是白球的概率大还是黑球的概率大? 解:已知第二只球是白球的概率P?B??0.6
假设第一只球是白色时为事件A1,第一只球是黑球时为事件A2
32??PAP?????A?1P?A1B??1??2PA|B?????所以 1PBPB0.63
又因为A1,A2是对立事件,而且事件B对A1,A2都无影响 P?A2|B??1?p?A1|B??1?
P?A2|B??P?A2|B? 21? 33
所以 第一只球是白球的概率大
―――――――――――――――――――――――――――――――――――――――
27. 两射手彼此独立地向同一目标射击,设甲击中的概率为 0.9 ,?乙击中的概率为 0.8 .求
(1) 目标被击中的概率;
(2) 两人都击中的概率;
(3) 甲中、乙不中的概率;
(4)甲不中、乙中的概率.
解:A为甲击中,B为乙击中,则A,B独立,且所求概率分别为
(1)P(A?B)?P(A)?P(B)?P(A)P(B)?0.9?0.8?0.72?0.98,
(2)P(AB)?P(A)P(B)?0.72, (3)P(A)?P(A)P()?0.9?0.2?0.18, (4)P(B)?P()P(B)?0.1?0.8?0.08
―――――――――――――――――――――――――――――――――――――――
28. 加工一个零件要经过三道工序,各道工序的合格率分别为 0.95,0.9,0.85,设各道工序是否合格是独立的,求加工出来的零件的合格率.
解:设A1,A2,A3分别表示第一,第二,第三道工序出现的合格品,则依题意
A1,A2,A3相互独立,且P?A1??0.95,P?A2??0.9,P?A3??0.85
又设A表示加工出来的零件是合格品,则A?A1?A2?A3
所以P?A??P?A1A2A3??P?A1??P?A2??P?A3??0.95?0.9?0.85?0.727 ―――――――――――――――――――――――――――――――――――――――
29. 某厂用两种工艺生产一种产品,第一种工艺有三道工序,各道工序出现废品的概率为0.05,0.1,0.15;第二种工艺有两道工序,?各道工序出现废品的概率都是 0.15 ,各道工序独立工作.设用这两种工艺在合格品中得到优等品的概率分别为0.95,0.85.试比较
应用概率统计 应用概率统计习题解答(全)
用哪种工艺得到优等品的概率更大?
解:第一道工序的合格率为0.95?0.9?0.85?0.72675,优等品率为0.72675?0.95?0.69 第二道工序的合格率为0.853?0.614125,优等品率为0.52
―――――――――――――――――――――――――――――――――――――――
30. 三个人独立地破译一个密码,他们能单独译出的概率分别为111,,. 求此密码被534
译出的概率.
解:设A,B,C分别为甲、乙、丙三人能单独译出的事件,则A,B,C相互独立,所求概率为
P(A?B?C)?P(A)?P(B)?P(C)?P(A)P(B)?P(A)P(C)?P(B)P(C)?P(A)P(B)P(C) 代入数据即可。[www.61k.com)
或
考虑逆事件的概率:
P(A?B?C)?1?P(A?B?C)
?1?P()P()P()
111?1?(1?)(1?)(1?)
534
3?5
―――――――――――――――――――――――――――――――――――――――
31. 某动物的成活率为60% ,现饲养5只,设各动物是否成活互不影响,求:(1)恰有2只成活的概率; (2) 至少有2只成活的概率.
解:设A为动物能成活,则p?P(A)?0.6,设X为5只中的成活数,则X~b(n,p),其中n?5,p?0.6
(1) 所求概率为
?5?25?223?P(X?2)??p(1?p)?10?(0.6)?(0.4)?0.2304 ?2???
(2) 所求概率为
P(X?2)?1?P(X?0)?P(X?1)?0.913
―――――――――――――――――――――――――――――――――――――――
32. 某单位有 12 台个人计算机,各计算机是否被使用是独立的.设计算机的使用率为 0.7 ,求在同一时刻有 9 台或更多计算机在使用的概率.
解:设A为事件“计算机被使用”则p?P(A)?0.7,设X为同时使用的计算机数目,则X~b(12,0.7),所求概率为
?12?k12?k??0.492 ?p(1?p)
k?9??
―――――――――――――――――――――――――――――――――――――――
33.爱滋病普查 使用一种血液试验来检测人体内是否携带爱滋病病毒.设这种试验的假阴性比例为5%(即在携带病毒的人中,有5%的试验结果为阴性),假阳性比例为1%(即在 不携带病毒的人中,有1%的试验结果为阳性).据统计人群中携带病毒者约占1?,若某人的血液检验结果呈阳性,试问该人携带爱滋病毒的概率.
,P(A|B)?0.05,解:设A为检查为阳性,B为携带病毒,求P(B|A)。已知P(B)?0.001
P(A|)?0.01,由贝叶斯法则有 P(X?9)????k12
应用概率统计 应用概率统计习题解答(全)
P(B|A)?P(AB)P(A|B)P(B)?P(A)P(A|B)P(B)?P(A|)P() 0.95?0.001??0.0868370.95?0.001?0.01?0..999
习 题 二 解 答
1. 五张卡片上分别写有号码1,2,3,4,5。(www.61k.com]随即抽取其中三张,设随机变量X表示取出
三张卡片上的最大号码。
(1) 写出X的所有可能取值;(2)求X的分布率。
解:(1)显然是:3,4,5。
(2) X的分布律

2. 下面表中列出的是否时。某个随机变量的分布律
(1)

(2)
答:(1)是
(2)不是
3.一批产品共有N件,其中M件次品。从中任意抽取n(n<=M)件产品,求这n件产品中次品数X的分布律。(此分布律为超几何分布)
解:抽取n件产品的抽法有CN种,抽取到次品的抽法有CMCN?M种,所以所求概率为: kn?kCMCN?MP?X?k?=,k=0,1,2,3……..n nCNnkn?k
―――――――――――――――――――――――――――――――――――――――
k,k=1,2,3,4,5. 15
15 求:(1)P{X=1或X=2}; (2)P{?X?}; (3)P{1?X?2}. 22
121 解:(1)P{X=1或X=2}=P{X=1}+ P{X=2}=+=。 15155
15121 (2)P{?X?}=P{1?X?2}=P{X=1}+ P{X=2}=+=。 2215155
121 (3)P{1?X?2}=P{X=1}+ P{X=2}=+=。 151554.设随机变量X的分布律为P={X=k}=
―――――――――――――――――――――――――――――――――――――――
5.一批产品共10件,其中7件正品,3件次品。从该批产品中每次任取一件,在下列两种

应用概率统计 应用概率统计习题解答(全)
情况下,分别求直至取得正品为止所需次数X的分布律。[www.61k.com)
(1)每次取后不放回; (2)每次取后放回。
解:(1)P(X?1)?7,10P(X?2)?3?773?2?77?, P(X?3)??, 10?93010?9?81207?3? (2) P?X?k????10?10?k?1 (k=1,2,?)
―――――――――――――――――――――――――――――――――――――――
6.某射手每发子弹命中目标概率为0.8,现相互独立地射击5发子弹,
求:(1)命中目标弹数地分布律; (2)命中目标的概率。
解:(1)设X为命中目标的弹数,则其分布律为
P{X=K}=C5?0.8?kk?0.2?5?k,(k=0,1,2,3,4,5).
00 (2)P{命中目标}=1-P{X=0}=1-C5?0.8??0.2?5?0=0.99968
―――――――――――――――――――――――――――――――――――――――
7.设随机变量X服从泊松分布P(?),且P{X=1}=P{X=2},求P{X=4}.
?1
???2
?? 解:由P{X=1}=P{X=2}得:e=e解得:?=2或?=0(舍弃)。 2!1!
24
故:P{X=4}=4!e?2= 2e?2 3
―――――――――――――――――――――――――――――――――――――――
8.设随机变量X的分布律为:
(1)P{X=k}=a,k=1,2,…..N N
(2) P{X=k}=a
试确定常数a
解:(1)由?kk!,k=0,1,2,…… ?P{X?k}=1 得:N *
k?1
????Na=1,解得:a=1 N (2) 由?P{X?k}=1 得:?a
k?0k?0?kk!=1,解得:a= e??

应用概率统计 应用概率统计习题解答(全)
―――――――――――――――――――――――――――――――――――――――
9. 某车间有同类设备100台,各台设备工作互不影响。[www.61k.com)如果每台设备发生故障得概率是0.01且一台设备的故障可由一个人来处理,问至少配备多少维修工人,才能保证设备发生故障但不能及时维修的概率小于0.01(利用泊松定理近似计算)。
解:设X为发生故障设备得台数,则X~B(100,0.01)??(1),即X近似服从参数为??1的poisson分布。设设备需要N个人看管“才能保证设备发生故障但不能及时维修的概率小于0.01”,则
P(X?N)?1?1?0.01 k!k?N?!??
查表得N?5
―――――――――――――――――――――――――――――――――――――――
10.设随机变量X的密度函数为f(x)=c e
(1)常数c;
解:(1)因为
即:?x (-?<x<+?),求: (3)P{X?5} (2)X落在区间(0,1)内的概率; ??????
0f(x)dx?f(x)dx+?????
00??0f(x)dx=1 0????cexdx+?ce?xdx=1, cex?ce?x??0=1,解得:c=1 2
(2)P{0?X?1}=?1
0f(x)dx=?1?xe?1 edx=022e1
(3)P{X?5}=P{X??5或X?5}=
=?5??5??f(x)dx+???5f(x)dx ??11x?x?5+= e edxedx???2?52
―――――――――――――――――――――――――――――――――――――――
11.设随机变量X的密度函数为f(x)???cx,x?(0,1),求
?0,其他
(1)常数c; (2)P{0.3<X<0.7}; (3)常数a,使得P{X>a}=P{X<a}; (4)常数b,使得
P{X>b}=0.64; (5)X分布函数。
解:(1) ???
??1??f(x)dx=?0??0dx+?0cxdx+?00dx
=?1
0cxdx
=1
所以,解得
C=2
(2) P{0.3<X<0.7}=?
=x0.70.32xdx 20.7
0.3
=0.49-0.09
=0.4
应用概率统计 应用概率统计习题解答(全)
(3)由P{X?a}?P{X?a}得: 当
a
<
0a
时
?0
,
P(?
??
a
??
X)?a?
??(??f
)???x, 0d,x
当a > 1时,P(X?a)?0,故,a不可能小于0或大于1;
当0≤a≤1时,
P(X?a)?1
P{X?a}??
2
??
a
f(x)dx??2xdx?1?a,P{X?a}??f(x)dx??2xdx?a2
a
??
1
2
aa
所以,1?a?a,即得:a=
2
2 2
(4)由题设可知,b的取值范围为:0≤b≤1
P{X?b}??
??
b
f(x)dx??2xdx?1?b2?0.64,所以b=0.6
b
1
(5)当x < 0时,F(x)=0;当0≤x≤1时,F(x)=2xdx?
??
x
1
?
x
?
x
2xdx?x2
当x > 1时,F(x)=2xdx?
??
??2xdx?1
?0?
?F(x)??x2
?1?
,,,
x?00?x?1 x?1
――――――――――――――――――――――――――――――――――――――― 12.解:
由题设可知,把X的分布函数的取值范围分为四段: 当x ≤ -1时,F(x)=0;
1; 6
111
当0 < x≤ 1时,F(x)=??
632
当-1 < x ≤0时,F(x)=当x > 1时,F(x)=1
?0?1??6
?F(x)??
?1?2?1?
,,,,
x??1?1?x?0
0?x?1x?1
应用概率统计 应用概率统计习题解答(全)

――――――――――――――――――――――――――――――――――――――
13.解:
-2 (1)P{X?2} = F(2) = 1-e=0.8647 ;
P{X > 2} = 1-P{X?2}=1-0.8647=0.1353;
(2)设X的密度函数为f(x).
当X<0时,f(x)=F?(x)=0;
当X≥0时,f(x)=F?(x)?(1?e
-x? x?0?e , ?f(x)=? x?0??0 ,?x)??e?x;
――――――――――――――――――――――――――――――――――——――
14.解:
(1)lim(A?Barctanx)=1;即:A?x????2B?1 ① ;
B?0 ② ; lim(A?Barctanx)=0;即:A?x????2
由①②式得:A=11,B= 2?
11?11?1+×)-(-×)= 2?2?244(2)P{-1≤X﹤1}=F(1)-F(-1)=(
(3)X的密度函数:
f(x)=F?(x)?(?1
21?arctanx)??1
?1?x2.1
?f(x)?1 ?(1?x2),(???x???)
―――――――――――――――――――――――――――――――――――――――
?f(x)dx=0; 1??当?≤x≤时,F(x)=(cosx)dx=??22215.解:当x<??2时,F(x)=x??111x(cosx)dx??sinx==(sin x+1) ???22?222x
应用概率统计 应用概率统计习题解答(全)
?当x>时,F(x)=2?1(cosx)dx=
??2x?
211=?sinx2?=1 (cosx)dx??22?222???1,???1?F(x)??(sinx?1),2??0,??
图如下: x????x??2?2 x???2
题15的图:
―――――――――――――――――――――――――――――――――――――――
16.解:
(1)由?????f(x)dx?1得,c????xe?dx??c?0????x0??x?xe?d(?)??c??e???c??1 ?????0??
所以,c?1
?
(2)因为P{X > a}=1-P{X < a}=1?
所以,a???ln??0a1e?x?dx?e?a?=1 21??ln2 2
――――――――――――――――――――――――――――――――――――――――
17.解:设乘客候车时间为X分。(www.61k.com)由于乘客到达该汽车站的任一时刻是等可能的,且公共汽车每隔5分钟通过车站一次,所以,X在区间[0,5]内均匀分布。所以X的密度函数为
?1?,f(x)??5??0,0?x?5其他
所以,乘客候车时间不超过3分钟的概率为:F(x)??3
013dx?=0.6 55
―――――――――――――――――――――――――――――――――――――――――
应用概率统计 应用概率统计习题解答(全)
18.解:
?1?,
因为X在[-2 , 5]上服从均匀分布,所以,X的密度函数为:f(x)??7
??0,
2
2
?2?x?5其他
而要方程4??4?X?X?2?0有实根,则要求△=16X?16(X?2)?0,即得:X≤-1或X≥2
1
即,方程有实根的概率为:P{X≤-1}+P{X≥2}=dx?
?27
?
?1
?
5
2
14dx? 77
―――――――――――――――――――――――――――――――――――――――
――― 19.解:
X?2
~N(0,1) 0.3
(1)P{X?1}?1?P{X?1}?1??((
1?2
)?1??(?3.33)??(3.33)=0.9996 0.3
2
)
P{?1?X?1.2}?P{X?1.2}?P{X??1}??(
??(10)??(2.67)?1?0.9962?0.0038
1.2?2?1?2
)??()??(?2.67)??(?10)0.30.3
――――――――――――――――――――――――――――――――――――――――――――― 20.解:
(1)P{??k??X???k?}??(k)??(?k)?2?(k)?1?0.8 , 所以?(k)?0.9 查表可得:k的最大取值为:k=1.28
(2)P{X???k?}?1?P{X???k?}?1??(k)?0.95 , 所以?(?k)?0.95 查表可得:k的最大取值为:k=-1.65
――――――――――――――――――――――――――――――――――――――――――――― 21.解:
由题设得:P{X?c}?1?P{X?c}?P{X?c},即:P{X?c}?查表得:
1c?31,即:?()? 222
c?3
=0,所以c=3 2
―――――――――――――――――――――――――――――――――――――――――――――
应用概率统计 应用概率统计习题解答(全)
22.解:(1)Y?
X?5000
?
~N(0,1)
P{4500?X?5500}?P{X?5500}?P{X?4500}??(
??(
即:?((
5500?5000
?
)??(
4500?5000
?
)
500
?
)??(?
500
?
)?2?(
500
?
)?1?0.9
500
?
)?0.95; 查表并计算得:?=303
2
)
P{X?4000}?1?P{X?4000}?1??(
4000?5000
?
)?1??(?
1000
?
1000
)??()?0.95
?
查表并计算得:?=606
――――――――――――――――――――――――――――――――――――――――――――― 23.解:要该种配件是合格品,那么,该配件的长度X的范围应该在:9.93≤X≤10.17 (单位:cm)
所以,生产该种配件是合格品的概率为:
10.17?10.059.93?10.05
P{9.93?X?10.17}?P{X?10.17}?P{X?9.93}??()??()??(2)??(?2)?2?(2)?
0.060.06
查表得:?(2)?0.9773,所以概率为:0.9546
――――――――――――――――――――――――――――――――――――――――――――――― 24.解:
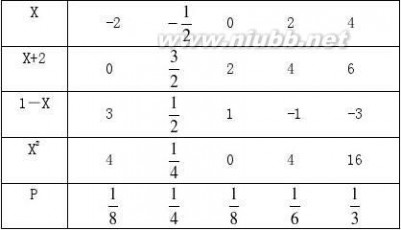
―――――――
25.解:因为Y=1-X是严格单调的函数,所以:
当0<y<1时,即,0<x<1时,fY(y)?fX(1?y)(1?y)??3(1?y)
2
应用概率统计 应用概率统计习题解答(全)
当Y为其他值时,即,X在区间〔0,1〕外时,fY(y)?fX(1?y)(1?y)??0
所以:Y=1-X的密度函数为:
?3(1?y)2
fY(y)??0?
或:
解 Y=1-X的分布函数FY(y)为
,,0?y?1其他 FY(y)?P(Y?y)?P(1?X?y)?P(X?1?y)
?1?P(X?1?y)?1?FX(1?y),
其中FX(x)是X的分布函数,它满足
?(x)?FXdFX(x)?fX(x), dx
而
?dF(y)d?3(1?y)2YfY(y)??[1?FX(1?y)]?fX(1?y)??dydy??00?y?1其它
―――――――――――――――――――――――――――――――――――――――――――――
26.解:
(1)由题设可得:
150?50?150?50P{X?150}?P{?150?X?150}??()??()100100
??(1)??(2)?1?0.8413?0.97725?1
?0.81855
(2)由(1)可知误差的绝对值不超过150cm的概率为:p=0.81855
那么在三次测量中至少有一次的概率:1?C3p(1?p)?1?(1?0.81855)?0.9940
(3)由题设可得:P{X?0}?1?P{X?0}?1??(?
习 题 三 解 答
1:设二维随变量(X,Y)只能取下列数组中的值:(0,0),(-1,1),(-1,1/3),(2,0),且取这几组值的概率依次为1/6,1/3,1/12,5/12。[www.61k.com)求此二维随机变量(X,Y)的分布列。 解:此二维随机变量(X,Y)的分布列是:

003350)??(0.5)?0.6915 100
应用概率统计 应用概率统计习题解答(全)

2.一袋中有四个球,它们依次标有数字1,2,2,3。(www.61k.com)从这袋中任取一球后,不放回袋中,再从袋中任取球,设每次取球时,袋中每个球被取到的可能性相同。以X,Y分别记第一、二次取得的球上标有的数字,求(X,Y)的概率分布。
解:由题意得:(X,Y)的可能取值为:(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2)。
则由概率的乘法公式得:P{X=1,Y=2}=(1/4)×(2/3)=1/6
P{X=1,Y=3}=(1/4)×(1/3)=1/12
P{X=2,Y=1}=(2/4)×(1/3)=1/6
P{X=2,Y=2}=(2/4)×(1/3)=1/6
P{X=2,Y=3}=(2/4)×(1/3)=1/6
P{X=3,Y=1}=(1/4×(1/3)=1/12
P{X=3,Y=2}=(1/4)×(2/3)=1/6
而事件(1,1),(3,3)为不可能事件,所以P{X=1,Y=1}=0,P{X=3,Y=3}=0。
则(X,Y)的联合分布列为:
――――――――――――――――――――――――――――――――――――――― 3在一个箱子里装有12只开关,其中2只是次品,在其中随机地取两次,每次取一只,考虑两种试验,(1)有放回抽样,(2)无放回抽样,我们定义随机变量X,Y如下
?0X???1表示第一次取出的是正品表示第一次取出的是次品
?0Y? ??1
表示第二次取出的是正品表示第二次取出的是次品 解:(


(2)所求联合概率分布为:
应用概率统计 应用概率统计习题解答(全)
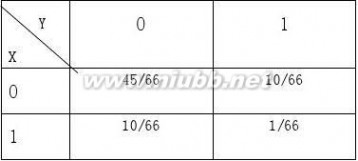
―――――――――――――――――――――――――――――――――――――――
4.设二维随机变量(X,Y)的概率密度为
?ke?(3x?4y),x?0,y?0 f(x,y)=? 0,其他?
(1)确定常数k;(2)求(X,Y)的分布函数;(3)求P{0<X≤1,0<Y≤2}。(www.61k.com] 解:(1)由概率密度函数的性质知
??????
????f(x,y)dxdy????0???0ke?(3x?4y)dxdy
??
0 =k???0e?3xdx?e?4ydy
=k*
=1
即 k=12.
(2)由定义,有
F(x,y)?
当x?0或y?0时
F(x,y)?
当x?0,y?0时 11? 34??yxyx????f(u,v)dudv ??
y????f(u,v)dudv??y?????x0dudv?0 F(x,y)?12?du?e?(3u?4v)dv00
xy????11?12??e?3u|???e?4v|? ????3400????x
??1?e?3x??1?e?4y?
于是
?(1?e?3x)(1?e?4y)F(x,y)??0?y?0,x?0其它
应用概率统计 应用概率统计习题解答(全)
(3)P?0?X?1,0?Y?2???2
0dy?12e?(3x?4y)dx 0
?3?81 =(1?e)(1?e)
―――――――――――――――――――――――――――――――――――――――
5.随机变量(X,Y)的分布密度为
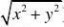
??C(Rf(x,y)??x2?y2?R2??0,x2?y2?R2
(1)求系数C;(2)求随机变量(X,Y)落在x?y?r(r?R)内的概率。[www.61k.com) 222
解:(1)由???
???????f(x,y)dxdy?1
(利用极坐标运算)得
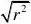
2??R2?R3
d??CR?d???0C2?3? ?2?0d??CR0R?rdr??2?0
?C
于是 C??3R3?13 3?R
(2)利用极坐标运算得:
3r22r =3(1-) R3R
―――――――――――――――――――――――――――――――――――――――
6.求出在D上服从均匀分布的随机变量(X,Y)的分布密度及分布函数,其中D为x轴,y轴及直线y=2x+1围成的三角形区域.
解:由于面积S=1/4,所以(X,Y)的联合密度函数为
?4(x,y)?Df(x,y)?? 0其它?
分布函数分区域讨论
(1) 当x??或y?0, f(x,y)=0 1
2
应用概率统计 应用概率统计习题解答(全)
从而 F(x,y)=??yx
-?-?f(x,y)dxdy=?y-?-??x0dxdy=0
1-<x?0,或0<y?2x?1, (2) 当2
F(x,y)=?
(3) 当?y-?-??xf(x,y)dxdy=?dyy-14dx=4xy+2y-y2 02yx1?x?0,2x?1?y 2
y
-?-?F(x,y)=??xf(x,y)dxdy=?1dx?-2x2x+104dy=?1?8x+4?dx??2x?1? ?2x2
(4) 当0?x,0?y?1
F(x,y)=?y
-?-??xf(x,y)dxdy=?dy?y-14dx=1-?1-y? 02y02
(5) 当0?x,1?y F(x,y)=
综上可得: ??yx-?-?f(x,y)dxdy=?1dx?-202x+104dy=1
?0???4xy?y2?2y?? F(x,y)??2??2x?1???1??1?y?2
?1??
7. 设随机变量(X,Y)的概率密度为 1x??或y?02?1?x?0,0?y?2x?12 1??x?0,2x?1?y20?x,0?y?10?x,1?y
?2xy?x?,0?x?1,0?y?2f(x,y)?? 3
??0,其他
求P{X+Y?1}.
解:P{X+Y?1}=1–P{X+Y<1} =1–?1
0dx?1?x0(x2?xy65 )dy=372
28:设二维随机变量(X,Y)要区域D上服从均匀分布,其中D 是曲线y=x和 y=x所围成,
应用概率统计 应用概率统计习题解答(全)
试求(X,Y)的分布密度及边缘分布密度。(www.61k.com)
解:面积Sd?21dxdy?dxdy?x?x??dx??????D0x201x11 6
?6(x,y)?D则 f(x,y)?? 0其他?
(a)关于X的边缘概率密度
当0?x?1时,
??
fX(x)?
???f(x,y)dy??6dy?6?x?x2? x2x
当x?0或x?1时
fX(x)?0
所以
2??6?x?x?0?x?1 fX(x)??0其他??
(b)关于Y的边缘概率密度
当0?y?1时,
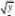
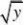
?? fY(y)?
???f(x,y)dxdx?6yy ?
当y?0或y?1时
fY(y)?0
所以
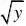
??6fY(y)????y0?0?y?1其他
9.(1)第1题中的随机变量X和Y是否相互独立(提示:考虑事件{X=-1,y=1})?
(2)第6题中的随机变量X与Y是否相互独立(提示:考虑事件 ?X???
?11?,Y??)? 42?
解:(1)P?X??1??0?11515??,P?Y?1??0??0? 12312312
1而 P?X??1,Y?1?? 3
?P?X??1,Y?1??P?X??1?P?Y?1?
应用概率统计 应用概率统计习题解答(全)
根据定义得:X与Y不相互独立。(www.61k.com)
(2) 由第6题得, ?4,(x,y)?D f(x,y)?? ?0,其他
11P{X??,Y??0 42
而
11111P{X???4???? 42424 11111P{Y??4???? 22424 1111?P{X??,Y??P{X??}P{Y? 4242 ?X与Y不相互独立
10.已知二维随机变量(X,Y)的概率密度为:
?6xy(2?x?y),f(x,y)???0,
求边缘概率密度fX?x?与fY?y?;
(1) fX|Y(x|y),fY|X(y|x)
(2) 问X和Y是否相互独立?
解:(1)0?x?1,0?y?1其它 fX(x)??f(x,y)dy ????
当0≤x≤1时,
fX?x???6xy(2?x?y)dy?4x?3x012
其它, f(x,y)?0,
所以
fX?x??0
所以关于X的概率密度为
?4x?3x2,0?x?1fX(x)??
?0,其它
类似地,fY?y??
当0≤y≤1, ?????f(x,y)dx
应用概率统计 应用概率统计习题解答(全)
fY?y???6xy(2?x?y)dx?4y?3y2 01
其它, f(x,y)?0
fY?y??0
所以
?4y?3y2,0?y?1fY?y???
?0,其它
(3) 故由条件概率密度的定义可知,
?6x(2?x?y),0?x?1,0?y?1f(x,y)?4?3yfX|Y(x|y)??? fY(y)??0,其它
?6x(2?x?y),0?x?1,0?y?1f(x,y)?fY|X(y|x)???4?3x fX(x)??0,其它
(3)x=1,y=1时,fX(x)×fY(y)=(4y-3y)(4x-3x)=1 22
f(x,y)?0
此时fX(x)?fY(y)?f(x,y)
所以X和Y不相互独立。(www.61k.com)
―――――――――――――――――――――――――――――――――――――――
11.(1)如果(X,Y)在以原点为中心,边长为2的正方形内服从均匀分布,问X和Y是否相互独立?(2)如果(X,Y)在以原点为中心,R为半径的圆内服从均匀分布,问X和Y是否相互独立?
解:(1)因为(X,Y)服从均匀分布,故
?1?f(x,y)??4??0?1?x?1,?1?y?1其它
当x<-1或x>1时,f(x,y)=0
所以
fX(x)??0dy?0 ????
当?1?x?1时, fX(x)????
??f(x,y)dy??11? ?1421
于是得关于X的概率密度为
应用概率统计 应用概率统计习题解答(全)
?1?fX(x)??2??0?1?x?1其它
同理可得关于Y得概率密度为
?1?fY(y)??2??0?1?y?1其它
fX(x)?fY(y)?f(x,y),故X和Y是相互独立。[www.61k.com)
(2)因为(X,Y)服从均匀分布,故
?1?f(x,y)???R2
??0
当x<-R或x>R时, x2?y2?R2其它
f(x,y)?0,所以 fX(x)??0dy?0 ????
当?R?x?R时,
fX(x)??R2?x2
_12R2?x2dy?R2?x2?R2?R2 ?2R2?x2?即fX(x)???R2
?0?
同理得: ?R?x?R 其它
22?R2?y212R?y?fY(y)???_R2?y2?R2dx??R2
?0??R?y?R 其它fX(x)?fY(y)?f(x,y), ,故X和Y不相互独立。
12.设X和Y相互独立,它们的概率密度分别为
?e?y,?1,0?x?1,fX(x)??fY(y)??0,其他,??0,
求Z=X+Y的概率密度.
解:因为X和Y相互独立,所以有 y?0,y?0,
fZ(z)??fX(x)fY(z?x)dx ????
应用概率统计 应用概率统计习题解答(全)
当0?z?1时
fZ(z)??1?ex?zdx?1?e?z 0z
当z?1时
fZ(z)??1?ex?zdx?(e?1)e?z 01
?1?e?z0?z?1,? fZ(z)??(e?1)e?zz?1,
?0其他,?
―――――――――――――――――――――――――――――――――――――――
13.设随机变量(X,Y)的概率密度为 f(x,y)?
2212??2ex?y?222?,???x???,???y??? 求Z?X?Y的概率密度。[www.61k.com]
解:Z的分布函数为
F(z)?P?Z?z??PX?Y?z?22
22????f(x,y)dxdyG 式中,G是xOy平面内由不等式x?y?z所确定的区域,
当z<0时,F(z)=0;求导得fZ?z??0
当z>0时,
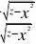
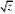
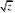
FZ(z)???f(x,y)dy]dx 再用极坐标来求积分
FZ?
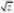

z???d??002?12??
ze2?r22?0dr??1?e2?r22?dr
求导得 fZ?z??
所以 12?2e?2?2
?0,?fZ?z??FZ??z???1?z
2??2e?2?z?0z?0
――――――――――――――――――――――――――――――――――――――― 14设(X,Y)的分布密度为
?(x?y)?,x?0,y?0?e f(x,y)?? ??0,其他
应用概率统计 应用概率统计习题解答(全)
求Z=X?Y的概率密度。(www.61k.com] 2
FZ(z)?P(X?Y?z)???f(x,y)dxdy 2x?y?2z解:Z的分布函数为
当z?0时,FZ?z??0;
当z?0时,
FZ(z)??
所以 2z0?2z?y0e?(x?y)dxdy?1?2ze?2z?e?2z '
fZ(z)?FZ'(z)?4ze?2z
综上得
fZ(z)???0
?2zz?0z?0?4ze
―――――――――――――――――――――――――――――――――――――――
15.设(X,Y)的联合分布密度为
?kxy,f(x,y)???0,
求k值。
解:由概率密度f(x,y)的性质
由题意得,
????31x?[0,1],y?[1,3]其他 ??????????f(x,y)dxdy?F(??,??)?1, ??????f(x,y)dxdy??dy?kxydx??(1013ky2x2)1
0dy??3
1kkydy?2432y)
1?2k?1,
所以 k=1。 2
16求15题中X和Y的边缘分布。
解 (1)因为当x<0或x>1时,f(x,y)=0,
所以
fX(x)??0dy?0 ????
当0?x?1时,
fX(x)????
??f(x,y)dy??31113xydy?xy2|1?2x 24
应用概率统计 应用概率统计习题解答(全)
(2) 因为当y<1或y>3时,f(x,y)=0,
所以
fY(y)??0dx?0 ????
当1?y?3时,
fY(y)??f(x,y)dx??????111xydx?x2y|1?y 002441
由上可知
?2xfX(x)???0
?1?yfY(y)??4??00?x?1其它1?y?3其它
习 题 四 解 答
1. 解:由数学期望的定义知:
EX=?XiPi=-1?0.2+0?0.3+1?0.4+2?0.1=0.4
因为
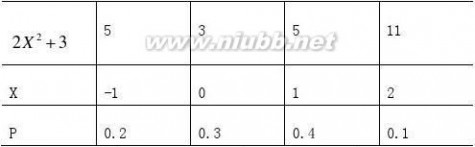

所以 E(2X2+3)=3?0.3+5?0.6+11?0.1=5
D?X??E?X?EX? 2
=(-1-0.4)2?0.2+(0-0.4)2?0.3+(1-0.4)2?0.4+(2-0.4)2?0.1
=0.84
―――――――――――――――――――――――――――――――――――――――
2. 解:甲品种母猪产仔的期望为
应用概率统计 应用概率统计习题解答(全)
EX=?XiPi
=7?0.03+8?0.05+9?0.08+10?0.16+11?0.2+12?0.2+13?0.14
+14?0.08+15?0.04+16?0.02
=11.39
乙品种母猪产仔的期望为
EY=?YiPi
?7?0.04+8?0.06+9?0.07+10?0.1+11?0.15+12?0.16+13?0.14
+14?0.12+15?0.1+16?0.06
=11.92
由于EX<EY, 因此乙种母猪平均产仔数多。(www.61k.com)
―――――――――――――――――――――――――――――――――――――――
3. 解:设在取得合格品以前已取出的废品数为X,
则X的可能取值为0,1,2,3
1C93 且 P?X?0??1? C124
11C3C9399P?X?1??1?1??? C12C11121144
111C3C9C23299P?X?2??1?1?1???? C12C11C10121110220
1111C3C9C2C132191P?X?3??1?1?1?1??????

C12C11C10C91211109220
E?X??0? +1? +2? +3? =444220220110399
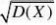
19E?X2??0? +1? +4? +9? = 44422022022
D?X??E?X2 ???EX?29?33??????0.319 22?110?2
?0.565
―――――――――――――――――――――――――――――――――――――――
应用概率统计 应用概率统计习题解答(全)
4.解:设孵出小鸡的个数为X,则X~B?50,0.9?
EX?np?50?0.9?45 DX?npq?50?0.9??1?0.9??4.5
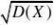
4.5=2.12
―――――――――――――――――――――――――――――――――――――――
5.解:(1)EX) ?

??
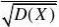

E*
?E?

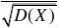
?
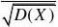
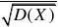
E ?E?
(2) ??0 D?
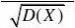
X*??E((X*)2)?(E(X*))2
?E2]?0 1?E[(X?E(X))2]D(X)
D(X)??1D(X)
―――――――――――――――――――――――――――――――――――――――
6.解:E?X?????
??xf(x)dx=?1500
03000?3000?x?x2xdx?xdx 22?150015001500
=1500
―――――――――――――――――――――――――――――――――――――――
7.设测量真实值为Y,则m?Y
此时候,?0.5?
同,于是X?m?1,故X=Y-(m+0.5) X?0.5,且Y在[m,m+1]之间是均匀分布,因为取每一个点的可能性相?U(?0.5,0.5).故
应用概率统计 应用概率统计习题解答(全)
0.5?(?0.5)?02
(0.5??0.5)21
D(X)??1212E(X)?
―――――――――――――――――――――――――――――――――――――――
8. (1)由规范性
901????
??f(x)dx??30k(x?30)(90?x)dx
1?36000k,故k?36000
(2) E?X???????xf(x)dx
??90
30 x(x?30)(90?x)dx?6036000
――――――――――――――――――――――――――――――――――――――― 9. E?X?????
??xf(x)dx ??1?x1x=?x?edx??x?edx ??202
=000???x??11(xex|?ex|)?(?)(xe?x|?e|) ????0022
=?=0 11? 22
??2xf(x)dx ??
0x2??21?x1xedx??xedx 022E(X2)??=???
=0x2?????x212x01(xe|??edx)?(?)(x2e?x|??edx) ????0022
00???x??11(0?2xex|?2ex|)?(?)(0?2(xe?x|?e|) ????0022=
=1+1
=2
D?X??E?X2???EX??2?0?2 2
―――――――――――――――――――――――――――――――――――――――
应用概率统计 应用概率统计习题解答(全)
10.解:
??e??t
f(t)?F?(t)???0
按定义有
t?0t?0 E(T)????????????t1tf(t)dt??t?e??tdt=?te??t|??edt= ??000?
??2t??e??tdt 0 E(T2)??
??2????t2??t=? (?e)dt?t(?e)|0?0?
= 2
?2
由公式D?T??ET?2???ET??22
?2?1?2?1?2
―――――――――――――――――――――――――――――――――――――――
11.解:设球的直径为R,则R~U?a,b?,
所以
?1a?R?b?f(R)??b?a ?其他?0
4?R?又因为球的体积为V???? 3?2?
3?4?R?3???4?R?? 所以E?V??E????????f(R)dR ?3?2????3?2????3
E?V???
ba4?R?1???dR 3?2?b?a3??
24?b?a??b2?a2?
――――――――――――――――――――――――――――――――――――――― 12
应用概率统计 应用概率统计习题解答(全)
E?Y??E?T(1?e?aX)??TE?1?e?aX?
?T(1?E(e?aX)),由于X?P(?)
故E(e?aXe??
k?ak)??e
k?0k!?
?ak
?e???(?e)
k!k?0?
?a ?e??e?e?e?(e?a?1)
?a故 E?Y??T(1?e?(e?1))
―――――――――――――――――――――――――――――――――――――――
13. 解:由期望的性质和题设条件知
(1)E?X1?X2??E?X1??E?X2?
?
????????x1f1(x1)dx1??x2f2(x2)dx2 ?????0x12e?2x1dx1??x24e?4x2dx2 0??
?1?1?2x1????4x2??? =2?(?2x1?1)e?+4?(?4x2?1)e ?00416????
=
(2)E2X1?3X2
113?? 2442???2E?X??3E?X? 212??2?4x21?2??3??4x2edx2 02
=1?3 ???
02(?x2)d(e?4x2)
=1?3??x2e2??4x2??
0????
0?e?4x22d(?x2)?
=1?3???1(?x2)d(e?4x2) 02
3???4x2?1?4x2???=1?3??x2e?0?2?0edx2 2??
=1+0- 35 = 88
应用概率统计 应用概率统计习题解答(全)
―――――――――――――――――――――――――――――――――――――――
14.解: 由期望的定义得
1121E?X1???x?2xdx?,E(X12)??x2?2xdx? 0032
由公式有D?X1??EX12??EX1??
而E(X2)???2141?? 2918???(x?5)5???xx?edx?exe?5?5dx?5?1?6
??2?(x?5)5??2?xE?X??x?edx?e?xedx?25?10?2?37 552
2
22所以D?X2??EX2??EX2??37?6?1 ??2
于是
2?6?4 3
119(2)D(X1?X2)?D(X1)?D(X2)??1? 1818(1)E(X1X2)?E(X1)E(X2)?
(15)略
(16)
E(X)??=1?0.4+2?0.6=1.6; E(Y)=1?0.5+2?0.5=1.5
E(X2)?1?0.4+4?0.6=2.8; E(Y2)=1?0.5+4?0.5=2.5
故

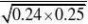
D(X)=2.8-2.56=0.24
D(Y)=2.5-2.25=0.25
E(XY)=1?0.1+2?0.3?2?0.4?4?0.2?2.3
Cov(X,Y)?E(XY)?E(X)E(Y)=0.1 ?(X,Y)?
(17) ???0.48x7?(x?y)dxdy?0?086
22y7E?Y?????(x?y)dxdy?0086
22xy4E(XY)????(x?y)dxdy?0083E?X???22
cov(X,Y)?E(XY)?E?X?E?Y???1
36
应用概率统计 应用概率统计习题解答(全)
E?X2???2
E?Y2???
20x25?(x?y)dxdy? ?08322y5?(x?y)dxdy??0832
11?D(Y) 36
1?(X,Y)???11D(X)?E?X2??(E?
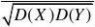
X?)2?
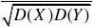
(18)
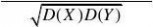
E(XY)?EXEY?(X,Y)??11111111而E(XY)?1??0???0??0?0???0???088888888
323E?X???1??0??1??0,故E(XY)?E?X?E?Y??0,X与Y不相关 888
13但P{X??1,Y??1}?,P{X??1}??P{Y??1},88
故
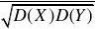
P{X??1,Y??1}?P{X??1}?P{Y??1},故不相互独立
(19)
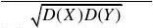
?(X,Y)?E(XY)?EXEY? 而E(XY)?E?X?E?Y??E(X3)?E?X?EX221x1xx3
?????故X与Y不相关?12?12?121
应用概率统计 应用概率统计习题解答(全)
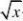
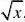
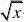


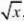
但当0<x<1时,P{Y<x,X?x}?P{?X?x}
11?(x?2
P{Y<x}=P{??? x11P{X<x}=??(x?1),则P{Y<x,X?x}?P{Y<x}?P{X<x}?122
故X与Y不相互独立?P{?x}??x
20. D(X)=25, D(Y)=36, D(X+Y)=D(X)+D(Y)+2cov(X,Y) ?(X,Y)?
故
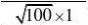
cov(X,Y)??(X,Y?5?6?0.4?12从而D(X?Y)?25?36?12?85
D(X?Y)?E[(X?Y)2]?[E(X?Y)]2
?E(X2?2XY?Y2)?[E(X)]2?2E(X)E(Y)?[E(Y)]2?D(X)?D(Y)?2cov(X,Y)
从而D(X?Y)?25?36?12?37
P{?Xi?120}????(2)?0.9772i?1
22.
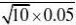
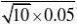
n 21.
的方法来求)???? ?2??1?0.4714P{|X?20|?0.1}(用?
23设X表示良种的粒数,则
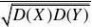
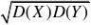
应用概率统计 应用概率统计习题解答(全)
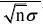


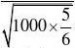
P{|X1?|?0.01}60006
的方法来求)???? ?2??1?0.9624?P{940?X?1060}(用?
24.设所求 为 a,则
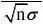
P{|
X1?|?a}60006
?P{1000?6000a?X?1000?6000a}(用?的方法来求)
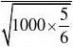
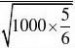
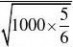
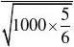
?????2??1?0.99
则a?0.0124,故|?2.58X1?|?0.0124,得925<X<107460006
25.设不发芽种子数为X,则p=0.2.(注意不发芽的概率为1-0.8)


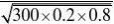
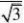
P{40?X?60}(用???的方法来求)?? ??(0)??(?0.498126.设X为不短于3m的木柱的数目,注意到长度不少于3m的目住的概率为p=0.80
应用概率统计 应用概率统计习题解答(全)
题目要求至少有30根木柱短于3m,相当于求至多 有70根木柱长于3m的概率,故
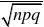
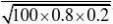
P{X?70}(用???的方法来求) ??(?2.5)?1??(2.5)?0.00621
27.设X表示每毫升血液所含白细胞数,则
P{5200?X?9400},
?P{|X-7300|?2100}
?1?P{|X-7300|?2100}
70028?1??210029
28.设X表示虫食豆的数目,则
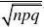

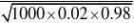
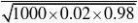
P{20?X?40}(用???的方法来求)?? ????(0)?0.529.设要配置a条外线才满足题目要求,X为200台分机某时刻使用的外线数目,则
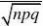
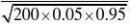
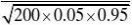
P{X?a}(用???的方法来求)?0.9 ?1.28得a?13.945,故至少要14条
30.设该10000人中每年的死亡人数为X
(1)要使得亏本,必须1000X>120000,即x>120,故
应用概率统计 应用概率统计习题解答(全)
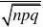
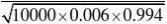
P{X?120}
?1?P{X?120}(用? 的方法来求)?1??(7.765)?1?1?0?1??
(2)
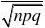
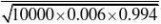
要使得利润不少于40000元,必须120000-1000X?40000,则X?80,
P{X?80}(用?的方法来求)
??(2.589)?
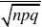
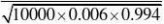
0.9951
要使得利润不少于60000元,必须120000-1000X?60000,??则X?60,
P{X?60}(用???的方法来求)
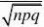
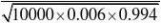
??(0)?0.5
要使得利润不少于80000元,必须120000-1000X?80000,则X?40,
P{X?40}(用???的方法来求) ?1?0.9951?0.0049
31.设X表示有这种血液的人数,则

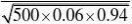

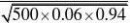
P{40?X?500}(用???的方法来求)?? ?1???0.04504
应用概率统计 应用概率统计习题解答(全)
32.设X表示1万个件中的次品数,则
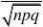

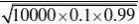
P{1000?X?1050}(用???的方法来求)?? ?0.46047
习 题 五 解 答
2 解: ?
x1?x2?x3?x4?x5417.3?418.1?419.4?420.4?412.5??417.54 55
1512???x1??2??x2??2??x3??2??x4??2??x5??2?9.353s?x???in?1i?15?12??
?6.32?2?52,~N52,1.053 解: ~N? 即 ??36????
?50.8?52??53.8?52?P?50.8??53.8??P???????1.71?????1.14????1.71????1.14??1?1.05??1.05
查表得 ?0.95637?0.8729?1?0.82927 4 解: 依题意 ~N?80,22? ?P?80?3?1?P??83??P??77??1?P?
=2?2??1.5??0.13362 ??????????1.5??P???1.5? ??????
5 解: 依题意 ?X~N?0,0.32? ?
?X?2 ?1?~??1? ?0.3?2X ~N?0,1?,由标准正态分布和?2的关系知:0.3
?X??X?222 同理可得 ?2?~??1?,???10?~??1?.由?的可加性知: ?0.3??0.3?22
1102Xi~?2?10? ?0.09i?1
应用概率统计 应用概率统计习题解答(全)
?102??11021.44?2Xi? ?P??Xi?1.44??P???P??10??16?0.100 ?0.09??i?1??0.09i?1??
26 解: 查表可得 (1)?0.05?9??16.92
(2)?0.99?21??8.92 2(3?0.9?18??10.86 2
(4)t0.05?30??1.697 (5)t0.025?16??2.120
(6)t0.01?34??2.4411 (7)F0.05?12,20??2.28
(8)F0.95?12,20??0.3937 (9)F0.025?12,20??2.68
??2?7 解: 依题意可得?X~N?,?,?X~N???,n?? ???2?
???
n~N?0,1? ,由标准正态分布和?2分布之间的关系知:
?????????????U?????nn??n??
(2)由2~?2?1? 5.2可得,当X1,X2?Xn来自总体X~N?,??2?的样本,则
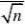
有??
~N(0,1)(n?1)S2?2~t(n?
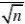
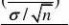
1)
???????V??~F?1,n?1? ???????2(n?1)??2
?n?1?S2
8 解:(1)根据定理5.1 有?2~?2?n?1? 9?S29?2.92
2 P{S>2.9}=P{>}=P???9??18.92??0.025(查表得) 44
应用概率统计 应用概率统计习题解答(全)
(2) 根据定理5.1 有 ??~t?n?1? S
n
?????46.5?4??? P??6.5??P???Pt?9???0.005 2.52.5????????
定理5.3的证明:
由于
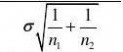
~N(?1,?2
n1),~N(?2,?2n2
n2),)(利用一开始给出的那个性质), 则?~N(?1??2,
?2n1??2~N(0,1)由定理5.1可知
(n1?1)S12
?

且S12和S22相互独立,由?2分布的可加性有
(n1?1)S12(n2?1)S22?~?2(n1?n2?2)22?2~?(n1?1),2(n2?1)S222~?2(n2?1),??
由t分布的定义可知
?t(n1?n2?2) 从而定理5.3成立
应用概率统计 应用概率统计习题解答(全)
1证明:F1???n1,n2??F?n2,n1由定义可知1???P{F?F1???n1,n2?}
1111P{??1?P{?FF1??n1,n2FF1??n1,n21111故?????.................(1)FF1??n1,n2FF1??n1,n211但?,依定义有FF?n2,n1 1P{?F??n2,n1?}??............................................................(2)F
比较(1)和(2)就有
1F1???n1,n2??F?n2,n1li习 题 六 解 答
2、解:由例3(P114)知:?,?的矩法估计分别为 2
1n??, ????(Xi?)2 ?ni?12
代入数据得样本均值为:
?
且 x1?x2?x3?x4?x52781+2836+2807+2763+2858??2809 55
1n1?222222x??x1????x2????x3????x4????x5????1206.8 ????i?ni?15?
应用概率统计 应用概率统计习题解答(全)
于是?,?的矩估值分别为2809, 1206.8
―――――――――――――――――――――――――――――――――――――――
3、解:似然函数为
n2
L(?)??i?11?xi???1?????e???n?x1?x2??xn??1?1??i?
? ???e???n?xin
对其求对数得: ??1??x1?x2??xn? lnL(?)?nln?????nln??i?1
?????
求导,并令其为0 nxi
xidlnL(?)1?
??n?i?1
2?0 d???
解得: n
??1X? (即为?的极大似然估计) ??ini?1
―――――――――――――――――――――――――――――――――――――――
4、解:因为X~N(?,1),可知样本X1,X2,X3均服从N(μ,1) n
?1??E? E??31?131?1X1?X2?X3????????? 102?5102?5
1515?1?1?2??E?X1?X2?X3?????????E??412?3412?3
111137?1?1?3??E?X1?X2?X3????????E??? 3512351260??
?1,??2是?的无偏估计量。[www.61k.com] 所以 ?
?1??D??191D?X1??D?X2??D?X3?251004 19119????25100450
应用概率统计 应用概率统计习题解答(全)
?2??D??
1125D?X1??D?X2??D?X3?916144 112525????91614472
?2??D???1? 于是 D??
即?2的无偏估计量方差较小。[www.61k.com)
―――――――――――――――――――――――――――――――――――――――
5、解:设总体X~N?,?0
为1??的置信区间为 (?u?
2?2?,因为总体方差??0n) 20?502已知,所以总体均值?的置信水平?0
n,?u?
2
又已知n=25,?500(样本均值),1???0.95,从而得u??u0.025?1.96
2
故得
?

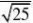
得置信下限为:?u?
2?500?1.96?480.4 ?519.6 ?

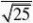
得置信上限为:?u?
2?500?1.96故?的置信水平为95%的置信区间为(480.4,519.6)
―――――――――――――――――――――――――――――――――――――――
6.由于已知n=100,?10(样本均值),S=3,1???0.99,从而得u??u0.005?2.58
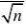
2
利用置信区间(?t?(n?1)
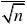
2?t?(n?1)) 2
代入相关数据后可得置信区间 (10?2.58?33,10?2.58?)即(9.23, 10.77) 1010
从而10000*9.23=92300
―――――――――――――――――――――――――――――――――――――――
7. 直接计算可知n=15,?4.25(样本均值),S?71.88 ,1???0.95,查表得2
t0.025(14)?2.145,把相关数据代入置信区间
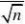
(?t?(n?1)
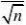
2?t?(n?1)) 2
应用概率统计 应用概率统计习题解答(全)
可得
(420.3, 429.7)
――――――――――――――――――――――――――――――――――――――― 8. 由于?=13,则有置信区间(i?1
2?(x?7i??)21??/2(n),?(xi?17i??)2) ?2
?/2(n)
查表可知?2
0.95(7)?2.17,?20.05(7)?14.07
代入相关数据后可得 (1515,)=(1.066,6.912) 14.072.17
―――――――――――――――――――――――――――――――――――――――
9、解:(1)μ的置信水平为0.95
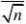
的置信区间长度为2u?
2
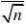
,即2?1.96 ∴要使置信区间长为5
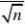
,则令2?1.96?5 nmin?62
(2)若置信水平为99

%,则有2u?
2?
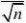
5,即2?2.58?5 nmin?107
―――――――――――――――――――――――――――――――――――――――
11、解:因为总体方差?未知,所以用样本方差s来代替总体方差。[www.61k.com]从而总体均值?的置信水平为1??的置信区间为
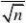
(?t?(n?1)

222?t?(n?1)) 2
2其中1???0.95,??0.05,t??n?1??t0.025?5??2.571,n=6,
?
2x1?x2?x3?x4?x5?x6221+191+202+205+256+236??218.5 661n1?2222222??585.9s?x??x??x??x??x??x??x????????????????i123456??n?1i?16?1
从而 s?24.2
代入数据得:?的置信水平为95%的置信区间为
(218.5-2.571×9.88,218.5+2.571×9.88)
即
应用概率统计 应用概率统计习题解答(全)
(193,244)
―――――――――――――――――――――――――――――――――――――――
12、解:因为总体方差?未知,所以用样本方差s来代替总体方差。[www.61k.com)从而总体均值?的置信水平为1??的置信区间为
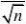
(?t?(n?1)
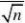
222?t?(n?1)) 2
2其中1???0.95,n=81,s=15.3,?98.5 ??0.05,t??n?1??t0.025?80??u0.025?1.96,代入数据得:?的置信水平为95%的置信区间为
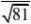
(98.5-1.96
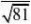
,98.5+1.96) 即 (95.2,101.8)
―――――――――――――――――――――――――――――――――――――――
13、解:当总体均值?未知时,总体方差?的置信水平为1??的置信区间为 2
n?1?S2n?1?S2??(2,2) ??n?1??n?11?22
其中1???0.95,??0.05,n=10, 查表得:
2?2
??n?1???0.975?10?1??2.70。 1?222???n?1???0.025?10?1??19.02,2
?
2482+493+457+471+510+446+435+418+394+496?460.2 101n11022s??xi????xi?460.2??1382 ??n?1i?110?1i?1
代入数据得总体方差?的置信水平为95%的置信区间为
(653.92, 4607.26)
――――――――――――――――――――――――――――――――――――――― 2
n?1?S2n?1?S2??14. ?的估计用(2,2) ??n?1??n?11?222
?的估计用
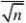
(?t?(n?1)
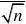
2?t?(n?1)) 2
代入相关数据即可
应用概率统计 应用概率统计习题解答(全)
―――――――――――――――――――――――――――――――――――――――
15.由定理5.3可知
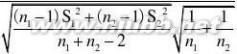
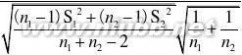
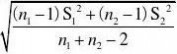
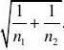
由于
?t(n1?n2?2)t?(n1?n2?2)}2
故?1??2的置信度为1??的置信区间为
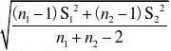
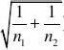
(??t?(n1?n2?2)2
??t?(n1?n2?2)2
直接计算可得
12?0.089
22?0.0447
查表可知t0.025(17)?2.11
代入到置信区间可得所求区间为 (0.031, 0.537)
习 题 七 解 答
1、由经验知某零件重量X~N?,? ?2?,??15,?2?0.052,技术革新后,抽出6个零件,测得重量为(单位:g)
14.7 15.1 14.8 15.0 15.2 14.6
已知方差不变,试统计推断,平均重量是否仍为15g(??0.05)?
解:此题是正态总体方差?2?0.052已知时,关于总体均值?的双侧检验,故采用U检验。(www.61k.com] 假设 H0:???0?15 H1:??15
因为 ?2?0.052已知,故应选择统计量
应用概率统计 应用概率统计习题解答(全)
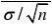
U?
又??0.05,且U~N(0,1),所以查正态分布表得U0.025?1.96,故拒绝域为 ?1.96
由题设条件知:n=6,??0.05,样本均值为
1n1??xi??14.7+15.1+14.8+15.0+15.2+14.6??14.9 ni?16
于是统计量得观测值

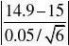
???4.902?1.96 即U落在拒绝域中,故否定H0,即认为平均重量不为15g.
―――――――――――――――――――――――――――――――――――――――
2.由于方差已知,用U检验
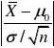
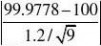
U???0.06?1.64?u0.05 即U落在接受域中,故接受H0,即认为平均重量为100千克
―――――――――――――――――――――――――――――――――――――――
3.由于方差已知,用U检验

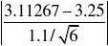
U???0.31?1.96?u0.025 即U落在接受域中,故接受H0,即认为平均重量为3.25
―――――――――――――――――――――――――――――――――――――――
4. 由于方差已知,用U检验
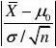
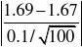
U???2?1.96?u0.025 即U落在拒绝域中,故拒绝H0,即认为平均身高不是1.67m
―――――――――――――――――――――――――――――――――――――――
5、已知健康人的红血球直径服从均值为7.2?m的正态分布,今在某患者血液中随机测得9个红血球的直径如下:
7.8 9.0 7.1 7.6 8.5 7.7 7.3 8.1 8.0
应用概率统计 应用概率统计习题解答(全)
问该患者红血球平均值与健康人的差异有无统计意义(??0.05)?
解:由于方差未知,所以采用T检验。[www.61k.com)
假设:
H0:???0?7.2 H1:??7.2
由题中数据得: 1n1样本均值:??xi??7.8+9.0+7.1+7.6+8.5+7.7+7.3+8.1+8.0??7.9 ni?19
样本方差:S?0.587
于是 检验统计量
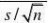
t??7.9?7.2?3.58 0.587/3
2当??0.05时,自由度n-1=8,查t分布表得t??n?1??t0.025?8??2.306,于是得拒绝
域为 T?2.306
因为t?6.071落在拒绝域内,所以拒绝H0,即该患者红血球平均值与健康人的差异在??0.05下有统计意义。
―――――――――――――――――――――――――――――――――――――――
6.由于方差不知道,用T检验
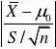
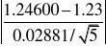
T???1.24183? 2.77645?t0.025(4) 因为落在接受域内,所以接受H0,即实际面积为1.23平方千米
―――――――――――――――――――――――――――――――――――――――
7.由于方差不知道,用T检验

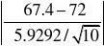
T???2.45? 2.26216?t0.025(9) 因为落在拒绝域内,所以拒绝H0,有统计意义
―――――――――――――――――――――――――――――――――――――――
8.由于方差不知道,用T检验
应用概率统计 应用概率统计习题解答(全)

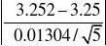
T??? 0.34?4.60409?t0.005(4) 因为落在接受域内,所以接受H0。(www.61k.com)
―――――――――――――――――――――――――――――――――――――――
9. 由于方差不知道,用T检验而且是单侧T检验
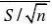

T??? -4.15?-2.13185?t0.05(4) 因为落在拒绝域内,所以拒绝H0。
―――――――――――――――――――――――――――――――――――――――
10. 由于方差不知道,用T检验
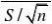

|T|?|?||? 1.11803?2.00958?t0.025(49) 因为落在接受域内,所以接受H0。
―――――――――――――――――――――――――――――――――――――――
11.期望未知,对方差检验,用卡方检验法 由于(n?1)S2
?24?0.2282? ?17.854? 11.1??20.025(4) 2(0.108)
故拒绝原假设
――――――――――――――――――――――――――――――――――――――― 12(1)由于期望不知道,对方差检验用卡方检验 ?2
0.925(11)?3.8157?(n?1)S2
?211?2.26722? ?17.45?21.92??0.025(11) 接受原2(1.8)
假设
(2)由于方差知道,用U检验
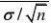
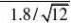
|U|?||?||? 3.85?1.96?u0.025 因为落在拒绝域内,所以拒绝H0。
―――――――――――――――――――――――――――――――――――――――
13、由于期望不知,对期望检验,用卡方分布
应用概率统计 应用概率统计习题解答(全)
2.7??2
0.975(9)?(n?1)S2?29?81.72? ?10.688?19.02??20.025(9) 5625
接受原假设
―――――――――――――――――――――――――――――――――――――――
14、(1) 方差不知,对期望检验,用F分布
S2
xF0.975(4,4)?0.1?|F|?|2|?0.224882?9.6?F0.025(4,4) Sy
接受原假设
(2)方差不知但相等,对期望检验,用T分布

|T|?||?3.31152? 2.306?t0.025(8) 拒绝原假设
―――――――――――――――――――――――――――――――――――――――
15、方差不知但相等,对期望检验,用T分布
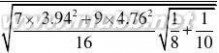
|T|?|?1.07? 2.12?t0.025(16)
接受原假设,其中 X?499.4,Y?501.64,Sx?3.94,Sy?4.76
―――――――――――――――――――――――――――――――――――――――
16、(1) 期望不知,对方差检验,用F分布
S2
x 4.212
|F|?|2|?= 26.6185?14.62?F0.025(7,3),拒绝原假设 2Sy 0.816
接受原假设,其中 X?21,Y?25,Sx?3.94,Sy?4.76
―――――――――――――――――――――――――――――――――――――――
17、方差已知,对期望检验用U检验法

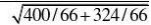
|U|?||?||? 3.07362?1.96?u0.025 拒绝原假设,说明有影响
―――――――――――――――――――――――――――――――――――――――
18、期望不知,对方差检验,用F分布
S2
xF|?|2|?5.66?4.823?F0.025(9,7) Sy
拒绝原假设,说明有统计意义
――――――――――――――――――――――――――――――――――――――
19、(1)期望不知,对方差检验,用F分布
应用概率统计 应用概率统计习题解答(全)
S2x
F0.995(9,9)?0.153?F|?|2|? 2.20661?6.541?F0.005(9,9)
Sy
接受原假设,说明方差相等
(2)方差不知但相等,对期望检验,用T分布

|T|?|
?3.29543? 2.878?t0.005(18)
拒绝原假设,说明有统计意义
―――――――――――――――――――――――――――――――――――――― 20、期望不知,对方差检验,用F分布
S2x
F0.975(5,5)?0.14?F|?|2|? 1.108?7.15?F0.025(5,5)
Sy
接受原假设,说明方差相等,其中X?0.14067,Y?0.13850,Sx?0.00280,Sy?0.00266 ―――――――――――――――――――――――――――――――――――――― 21、期望不知,对方差检验,用F分布
S2x
F|?|2|? 0.262?0.32?F0.95(9,10)
Sy
拒绝原假设,说明方差不相等
―――――――――――――――――――――――――――――――――――――― 22、期望不知,对方差检验,用F分布
S2x
F0.95(6,5)?0.228?F|?|2|? 3.426?4.95?F0.05(6,5),其中Sx?6.83,Sy?3.69
Sy
接受原假设,说明方差相等
―――――――――――――――――――――――――――――――――――――― 23、期望不知,对方差检验,用F分布
S2x
F0.95(7,7)?0.264?F|?|2|? 1.069?3.787?F0.05(7,7),其中Sx?0.941,Sy?0.91
Sy
接受原假设,说明方差相等
习 题 八 解 答
1、今有不同温度处理的鱼卵胚胎发育速度(从受精到孵化所需时间)数据如下表,试做方差分析。(www.61k.com]

应用概率统计 应用概率统计习题解答(全)
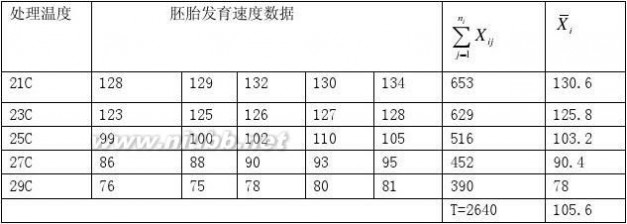
假设鱼卵胚胎发育速度服从方差相等的正态分布,依题意r?5,n1?n2?n3?n4?n5?5,
n?n1?n2?n3?n4?n5?25,它们在不同温度下,发育速度均值分别为?1,?2,?3,?4,?5。[www.61k.com)
(1)需检验假设
H0:?1??2??3??4??5
(2)首先计算离差平方和自由度
2
?T21?rni1
????Xij???26402?278784 nn?i?1j?1
?25
??x
i?1j?1r
rni
2ij
?1282?1292???812?289138
r
Ti21ni653262925162452239022
??(?xij)??????288942 ?nn55555i?1i?1ij?1i
于是
Ti2T2SSA????288942-278784=10158
ni?1ni
r
Ti2
SSE???x???289138-288942=196
ni?1j?1i?1i
r
2
ij
r
ni
SST?SSA?SSE?10158+196=10354
自由度:
dfA?r?1?5?1?4 dfE?n?r?25?5?20
应用概率统计 应用概率统计习题解答(全)
dfT?n?1?25?1?24


统计意义。(www.61k.com]
――――――――――――――――――――――――――――――――――――――― 2、A、B、C三种饲料喂猪,得一个月后每猪所增体重(单位:500g)于下表,试作方差分析。 解:
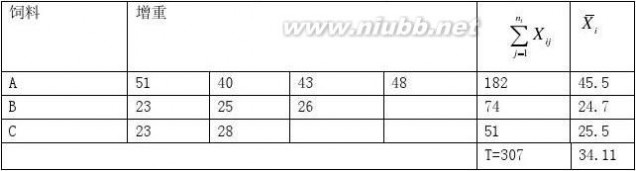
依题意有r?3,n1?4,n2?3,n3?2,n?n1?n2?n3?9,假设在不同的饲料下,一个月所增体重均值为?1,?2,?3。 (1)需检验假设
H0:?1??2??3
(2)首先计算离差平方和自由度
2
?1T1?rni
????Xij???3072?10472.11 nn?i?1j?1
?9
2
??x
i?1j?1r
rni
2ij
?512?402???282?11497
r
Ti21ni18227425122
??(?xij)????11406.83 ?nn432i?1i?1ij?1i
应用概率统计 应用概率统计习题解答(全)
于是
Ti2T2
SSA????11406.83-10472.11=934.72
ni?1ni
r
Ti2
SSE???x???11497-11406.83=90.17
ni?1j?1i?1i
r
2
ij
r
ni
SST?SSA?SSE?934.72+90.17=1024.89
自由度:
dfA?r?1?3?1?2 dfE?n?r?9?3?6 dfT?n?1?9?1?8

(4)因为F?31.10?F0.05?2,6??5.14,故拒绝H。[www.61k.com),即用三种不同的饲料喂猪对猪所增体重的影响具有统计意义。
―――――――――――――――――――――――――――――――――――――――
3、列出方差分析表
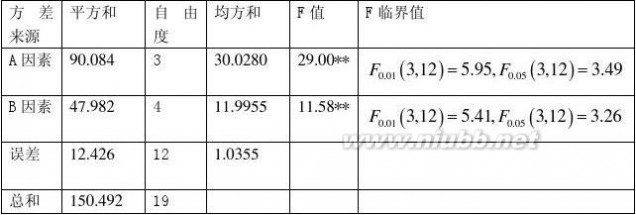
(4)因为FA?29?F0.01?3,12??5.95,故拒绝H。,天数对菌的生长量的影响极有统计意义。
因为FB?11.58?F0.01?4,12??5.41,故拒绝H。,温度对菌的生长量的影响极有统计意义。
应用概率统计 应用概率统计习题解答(全)
―――――――――――――――――――――――――――――――――――――――

――――――――――――――――――――――――――――――――――――――― 6、ancova c7=c1|c2 c1|c4 c2|c4
Source DF SS MS F P
a 1 1250.00 1250.00 277.78 0.038
b 1 1860.50 1860.50 413.44 0.031
a*b 1 1352.00 1352.00 300.44 0.037
c 1 32.00 32.00 7.11 0.228
a*c 1 180.50 180.50 40.11 0.100
b*c 1 2.00 2.00 0.44 0.626
Error 1 4.50 4.50
Total 7 4681.50
发现A*B的F值小于1,于是去掉A*B再做方差分析,用以下命令
ancova c7=c1|c2 c1|c4 c4;
mean c1|c2 c1|c4 c4.
ANCOVA: data versus a, b, c
Factor Levels Values
a 2 1, 2
b 2 1, 2
c 2 1, 2
Analysis of Variance for data
Source DF SS MS F P
a 1 1250.00 1250.00 384.62 0.003
b 1 1860.50 1860.50 572.46 0.002
应用概率统计 应用概率统计习题解答(全)
a*b 1 1352.00 1352.00 416.00 0.002
c 1 32.00 32.00 9.85 0.088
a*c 1 180.50 180.50 55.54 0.018
Error 2 6.50 3.25
Total 7 4681.50
Means
a N data
1 4 414.75
2 4 389.75
b N data
1 4 387.00
2 4 417.50
a b N data
1 1 2 386.50
1 2 2 443.00
2 1 2 387.50
2 2 2 392.00
c N data
1 4 400.25
2 4 404.25
a c N data
1 1 2 417.50
1 2 2 412.00
2 1 2 383.00
2 2 2 396.50
考虑a b 和 a*b发现a1和b2的组合最好,然后考虑a和c的交互作用发现a1和c1的组合最好,所以最好的处理是a1b2c1
三 : 新编计算机科学概论 刘艺、蔡敏 习题与答案
第0章习题
(1) 复习题
1、简述计算机科学的研究领域。(www.61k.com]
数值和符号计算、算法和数据结构、体系结构、操作系统、程序设计语言、软件方法学和工程、数据库和信息检索、计算理论、人工智能和机器人学等。(P2)
2、简述现代计算机的发展简史。
计算机发展经历了算盘时代、机械时代和机电时代这些原始阶段。自从电子计算机问世以来,计算机经历了电子管时代、晶体管时代、集成电路时代和大规模、超大规模集成电路时代等,发展速度越来越快。(P8-16)
3、试分析计算机对社会的影响。
计算机的产生与发展使得社会对计算机产生了依赖,也改变了我们人类的生活方式,并带来了许多有关于伦理和犯罪的问题。(P16-P17)
4、试列出与计算机科学相关的学科及技术。
计算机科学是一门实用性很强、发展极其迅速的面向广大社会的学科,它建立在数学、电子学 (特别是微电子学)、磁学、光学、精密机械等多门学科的基础之上, 与数学、计算机程序设计、软件工程和计算机工程等学科之间存在不同程度的交叉和覆盖。(P2)
5、尝试到网络上搜索关于计算机学科中几个典型问题的资料。
提示本书P4-P7页列出了一些经典问题,大家可以查找相关的情况
6、简述电子数字计算机的发展趋势。.
计算机将向更高性能、更加易用、联网更广泛和更专业的应用发展。随着硬件技术和算法设计的进步,计算机的处理能力将进一步提高,计算机有能力处理更加复杂和规模更大的问题。
随着计算机向智能化方向发展,计算机具有人的某些智能,如学习和推理的能力。(P14-P15)
7、谈谈你对电子计算机的印象。
提示:可从计算机的应用、能力、社会影响等方面考虑
8、试述计算机模型与计算机的联系和区别。
图灵设想所有的计算都可能在一种特殊的机器上执行,通用图灵机是对现代计算机的首次描述,该机器只要提供了合适的程序就能做任何运算。而计算机只是一种计算的工具。(P4)
9、列举出你所知道的操作系统。
提示:可从互联网上了解,或向周围的人们打听
(2) 练习题
(1)填空题
1、ACM是____________组织的简称。
国际计算机组织
计算机科学概论 新编计算机科学概论 刘艺、蔡敏 习题与答案
第一章习题
(1) 复习题
1、试述数制的概念。[www.61k.com]
位置化数字系统中,在数字中符号所占据的位置决定了其表示的值。大多数人使用的数字系统是以10为底的,也就是十进制。二进制数字系统是最简单的数字系统。(P21-23)
2、列举出你所知道的数字系统。
提示:根据本章内容和自己接触过的情况,也可以上网搜索有关资料。
3、谈谈二进制、八进制和十六进制等数字表示方法各有什么有点和缺点。
八进制就是逢8进位,十六进制就是逢16进位,2、8、16,分别是2的1次方,3次方,4次方。这三种进制之间可以非常直接地互相转换。八进制数或十六进制数实际上是缩短了的二进制数,但保持了二进制数的表达特点。(P23-P25)
4、为什么使用二进制计算的时候会出现溢出?
因为存储空间大小(即存储单元的位的数量)的限制,可以表达的整数范围是有限的。二进制补码中两个整数相加的法则是,2个位相加,将进位加到下一列。如果最左边的列相加后还有进位,则舍弃它。如果在最高位有进位,那就会产生溢出。(P29-32)
5、反码和补码相对于原码有什么优点?计算机中的数是用原码表示的还是用反码、补码表示的?
数值的反码表示法是用最高位存放符号,并将原码的其余各位逐位取反。反码的取值空间和原码相同且一一对应。在补码表示法中,正数的补码表示与原码相同,即最高符号位用0表示正,其余位为数值位。而负数的补码则为它的反码、并在最低有效位(即D0位)加1所形成。处理器内部默认采用补码表示有符号数。(P29)
6、汉字编码有哪几种?各自的特点是什么?
汉字的编码有国际码、机内码等。在国标码的字符集中共收录了6763个常用汉字和682个非汉字字符,汉字机内码是与ASCII对应的,用二进制对汉字进行的编码。由于汉字数量多,一般用2个字节来存放汉字的内码,即双字节字符集(double-byte character set,简称DBCS)。(P36-37)
7、图像是如何压缩存储的?哪一种图像占用空间最小,为什么?图形压缩编码的考虑主要由于位图文件体积太大,人们研究通过编码的形式,在保证图像具备一定质量的前提下,缩小图像文件的大小。压缩编码按其对图像质量的影响可分为无损压缩和有损压缩两类。当前最主流的图像压缩方式是JPEG ,JPEG压缩技术十分先进,即能支持无损压缩,也支持大压缩比的有损压缩。(P40-P41)
8、ASCII码是什么编码?为什么国际上推行Unicode码?
ASCII编码是由美国国家标准学会制定的标准单字节字符编码方案,用于基于文本的数据。ASCII码是计算机世界里最重要的标准,但它存在严重的国际化问题Unicode扩展自ASCII
计算机科学概论 新编计算机科学概论 刘艺、蔡敏 习题与答案
第二章习题
(1) 复习题
1.简述冯?诺依曼原理,冯?诺依曼结构计算机包含哪几部分部件,其结构以何部件为中心? 答:冯?诺依曼理论的要点包括:指令像数据那样存放在存储器中,并可以像数据那样进行处理;指令格式使用二进制机器码表示;用程序存储控制方式工作。[www.61k.com)这3条合称冯?诺依曼原理
冯?诺依曼计算机由五大部分组成:运算器、控制器、存储器、输入设备、输出设备,整个结构一般以运算器为中心,也可以以控制器为中心。 (P52-P55)
2.简述计算机体系结构与组成、实现之间的关系。
答:计算机体系结构通常是指程序设计人员所见到的计算机系统的属性,是硬件子系统的结构概念及其功能特性。计算机组成(computer organization)是依据计算机体系结构确定并且分配了硬件系统的概念结构和功能特性的基础上,设计计算机各部件的具体组成,它们之间的连接关系,实现机器指令级的各种功能和特性。同时,为实现指令的控制功能,还需要设计相应的软件系统来构成一个完整的运算系统。计算机实现,是计算机组成的物理实现, 就是把完成逻辑设计的计算机组成方案转换为真实的计算机。计算机体系结构、计算机组成和计算机实现是三个不同的概念,各自有不同的含义,但是又有着密切的联系,而且随着时间和技术的进步,这些含意也会有所改变。在某些情况下,有时也无须特意地去区分计算机体系结构和计算机组成的不同含义。 (P48-P52)
3.根据指令系统结构划分,现代计算机包含哪两种主要的体系结构?
答:根据指令系统结构划分,现代计算机主要包含:CISC和RISC两种结构。 (P57)
4.简述RISC技术的特点?
答:从指令系统结构上看,RISC 体系结构一般具有如下特点:
(1) 精简指令系统。可以通过对过去大量的机器语言程序进行指令使用频度的统计,来选 取其中常用的基本指令,并根据对操作系统、高级语言和应用环境等的支持增设一些最常用的指令;
(2) 减少指令系统可采用的寻址方式种类,一般限制在2或3种;
(3) 在指令的功能、格式和编码设计上尽可能地简化和规整,让所有指令尽可能等长;
(4) 单机器周期指令,即大多数的指令都可以在一个机器周期内完成,并且允许处理器在同一时间内执行一系列的指令。
(P59-60)
5.有人认为,RISC技术将全面替代CISC,这种观点是否正确,说明理由?
答:不正确。与CISC 架构相比较,RISC计算机具备结构简单、易于设计和程序执行效率高的特点,但并不能认为RISC 架构就可以取代CISC 架构。事实上,RISC 和CISC 各有优势,CISC计算机功能丰富,指令执行更加灵活,这些时RISC计算机无法比拟的,当今时代,两者正在逐步融合,成为CPU设计的新趋势。 (P60-62)
6.什么是流水线技术?
答:流水线技术,指的是允许一个机器周期内的计算机各处理步骤重叠进行。特别是,当执行一条指令时,可以读取下一条指令,也就意味着,在任何一个时刻可以有不止一条指令在“流水线”上,每条指令处在不同的执行阶段。这样,即便读取和执行每条指令的时间保持不变,而计算机的总的吞吐量提高了。 (P60-61)
7.并行处理结构包含哪几种主要的体系结构,分别有什么特点?
计算机科学概论 新编计算机科学概论 刘艺、蔡敏 习题与答案
第三章习题
(1) 复习题
1.计算机由哪几部分组成,其中哪些部分组成了中央处理器?
答:计算机硬件系统主要由运算器、控制器、存储器、输入设备、输出设备等五部分组成 其中,运算器和控制器组成中央处理器(CPU)。[www.61k.com] (P69)
2.试简述计算机多级存储系统的组成及其优点?
答:多级存储系统主要包括:高速缓存、主存储器和辅助存储器。
把存储器分为几个层次主要基于下述原因:
(1)合理解决速度与成本的矛盾,以得到较高的性能价格比。
(2)使用磁盘、磁带等作为外存,不仅价格便宜,可以把存储容量做得很大,而且在断电时它所存放的信息也不丢失,可以长久保存,且复制、携带都很方便。 (P74-P75)
3.简述Cache的工作原理,说明其作用。
答:Cache的工作原理是基于程序访问的局部性的。即主存中存储的程序和数据并不是CPU每时每刻都在访问的,在一段时间内,CPU只访问其一个局部。这样只要CPU当前访问部分的速度能够与CPU匹配即可,并不需要整个主存的速度都很高。
Cache与虚拟存储器的基本原理相同,都是把信息分成基本的块并通过一定的替换策略,以块为单位,由低一级存储器调入高一级存储器,供CPU使用。但是,虚拟存储器的替换策略主要由软件实现,而Cache的控制与管理全部由硬件实现。因此Cache效率高并且其存在和操作对程序员和系统程序员透明,而虚拟存储器中,页面管理虽然对用户透明,但对程序员不透明;段管理对用户可透明也可不透明。
Cache的主要作用是解决了存储器速度与CPU速度不匹配的问题,提高了整个计算机系统的性能。 (P77)
4.描述摩尔定律的内容,并说明其对于计算机的发展具有怎样的指导意义?
答:摩尔定律(Moore law)源于1965年戈登·摩尔(GordonMoore,时任英特尔(Intel)公司名誉董事长)的一份关于计算机存储器发展趋势的报告。根据他对当时掌握的数据资料的整理和分析研究,发现了一个重要的趋势:每一代新芯片大体上包含其前一代产品两倍的容量,新一代芯片的产生是在前一代产生后的18-24个月内。
随着计算机技术的发展,摩尔定律得到业界人士的公认,并产生巨大的反响,逐渐成为硬件领域最重要的规律。许多基于未来预期的研究和预测都是以它为理论基础。这里需要特别指出,摩尔定律并非数学、物理定律,而是对发展趋势的一种分析预测,因此,无论是它的文字表述还是定量计算,都应当容许一定的宽裕度。
从某种意义上说,摩尔定律是关于人类创造力的定律,而不是物理学定律。摩尔定律实际上是关于人类信念的定律,当人们相信某件事情一定能做到时,就会努力去实现它。摩尔当初提出他的观察报告时,在某种程度上是给了人们一种信念,使大家相信他预言的发展趋势一定会持续。而所以摩尔定律在长达40多年的时间里不断被证实,正是由于人们这些年来的不懈努力。摩尔提出的周期可以认为是英特尔公司芯片研发的基本计划周期。 (P72-P73)
5.与主存相比Cache具有哪些特点?
答:主存相比Cache具有以下特点:
(1)Cache一般用存取速度高的SRAM元件组成,其速度已经与CPU相当。
(2)Cache与虚拟存储器的基本原理相同,都是把信息分成基本的块并通过一定的替换策略,以块为单位,由低一级存储器调入高一级存储器,供CPU使用。但是,虚拟存储器的替换策略主要由软件实现,而Cache的控制与管理全部由硬件实现。因此Cache效率高并且其存在和操作对程序员和系统程序员透明,而虚拟存储器中,页面管理虽然对用户透明,但对程序员不透明;段管理对用户可透明也可不透明。
(3)Cache的价格较贵,为了保持最佳的性能价格比,Cache的容量应尽量小,但太小会影响命中率,所以Cache的容量是性能价格比和命中率的折衷。 (P77)
计算机科学概论 新编计算机科学概论 刘艺、蔡敏 习题与答案
第五章习题
(1) 复习题
1、试述数据和数据结构的概念及其区别。(www.61k.com]
数据是对客观事物的符号表示,是信息的载体;数据结构则是指互相之间存在着一种或多种关系的数据元素的集合。(P113)
2、列出算法的五个重要特征并对其进行说明。
算法具有以下五个重要的特征:有穷性:一个算法必须保证执行有限步之后结束。确切性:算法的每一步骤必须有确切的定义。输入:一个算法有0个或多个输入,以刻画运算对象的初始情况,所谓0个输入是指算法本身定除了初始条件。输出:一个算法有一个或多个输出,以反映对输入数据加工后的结果。没有输出的算法没有实际意义。可行性:算法原则上能够精确地运行,而且人们用笔和纸做有限次运算后即可完成。(P115)
3、算法的优劣用什么来衡量?试述如何设计出优秀的算法。
时间复杂度 空间复杂度(P117)
4、线性和非线性结构各包含哪些种类的数据结构?线性结构和非线性结构各有什么特点? 线性结构用于描述一对一的相互关系,即结构中元素之间只有最基本的联系,线性结构的特点是逻辑结构简单。所谓非线性结构是指,在该结构中至少存在一个数据元素,有两个或两个以上的直接前驱(或直接后继)元素。树型和图型结构就是其中十分重要的非线性结构,可以用来描述客观世界中广泛存在的层次结构和网状结构的关系。(P118 P122)
5、简述树与二叉树的区别;简述树与图的区别。
树用来描述层次结构,是一对多或多对一的关系;二叉树(Binary Tree)是个有限元素的集合,该集合或者为空、或者由一个称为根(root)的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成。二叉树是有序的,即若将其左、右子树颠倒,就成为另一棵不同的二叉树。图也称做网,是一种比树形结构更复杂的非线性结构。在图中,任意两个节点之间都可能相关,即节点之间的邻接关系可以是任意的,图表示的多对多的关系。(P121-P124)
6、请举出遍历算法在实际中使用的例子。
提示:根据实际生活中需要逐个访问处理的情况举例。
7、编写一个算法,统计在一个输入字符串中各个不同字符出现的频度。用适当的测试数据来验证这个算法。
提示:根据查找算法和串中求子串的算法,查找输入串中以单个字符形式的子串。
8、若对有n个元素的有序顺序表和无序顺序表进行顺序搜索,试就下列三种情况分别讨论两者在等搜索概率时的平均搜索长度是否相同?
(1) 搜索失败;
(2) 搜索成功,且表中只有一个关键码等于给定值k的对象;
(3) 搜索成功,且表中有若干个关键码等于给定值k的对象,要求一次搜索找出所有对
计算机科学概论 新编计算机科学概论 刘艺、蔡敏 习题与答案
第4章 操作系统习题
(1) 复习题
1、什么是操作系统?
答:操作系统(Operating System,简称OS)是管理计算机系统资源、控制程序执行,改善人机界面,提供各种服务,合理组织计算机工作流程和为用户使用计算机提供良好运行环境的一类系统软件。(www.61k.com)(P89)
2、操作系统的基本功能是什么?
答:操作系统是用户与计算机硬件之间的接口。使得用户能够方便、可靠、安全、高效地操纵计算机硬件和运行自己的程序。操作系统合理组织计算机的工作流程,协调各个部件有效工作,为用户提供一个良好的运行环境。操作系统是计算机系统的资源管理者,负责管理包括处理器、存储器、I/O设备等硬件资源和程序和数据等软件资源,跟踪资源使用情况,监视资源的状态,满足用户对资源的需求,协调各程序对资源的使用冲突;为用户提供简单、有效使用资源统一的手段,最大限度地实现各类资源的共享,提高资源利用率。(P90-91)
3、操作系统的基本组成有哪些?
答:操作系统构成的基本单位包括内核和进程、线程。内核对硬件处理器及有关资源进行管理,给进程的执行提供运行环境。进程是程序动态执行的过程。(P91)
4、操作系统如何分类?
答:根据系统运行的方式分类,操作系统的基本类型有三种:批处理系统、分时系统和实时系统。具备全部或兼有两者功能的系统称通用操作系统。根据系统的运行环境分类的操作系统有:微机操作系统、网络操作系统、分布式操作系统和嵌入式操作系统。(P92-94)
5、什么是进程?它与程序是什么关系?
答:进程是一个可并发执行的具有独立功能的程序关于某个数据集合的一次执行过程,也是操作系统进行资源分配和保护的基本单位。程序是静态的概念,它以文件形式存在于辅助存储器中,进程是动态的概念,程序执行时创建进程,一个程序多次执行创建多个进程,这多个进程可同时存在于机器的内存中。进行执行完成后结束,进程终止,但程序本身仍然存在,并不因进程的终止而消失。(P91,96-98)
6、什么是死锁?死锁产生的原因是什么?
答:在系统运行过程中,多个进程间相互永久等待对方占用的资源而导致各进程都无法继续运行的现象称为“死锁”。发生死锁后,实际上各进程都占有一定的资源而都不能正常使用,系统的资源实际上被罢占并空闲的,是严重的资源的浪费;若无外力作用,进程不能自己从死锁中解脱出来。
产生死锁的原因主要是:系统资源不足,进程会因争夺有限的资源而陷入死锁;进程运行推进的顺序不合适,进程运行推进顺序与速度不同,也可能产生死锁;资源分配不当等。 (P99-100)
计算机科学概论 新编计算机科学概论 刘艺、蔡敏 习题与答案
第六章习题
(1) 复习题
1、简述自然语言与形式语言的概念以及区别、汇编语言与机器语言的概念及区别。[www.61k.com) 自然语言是某一社会发展中形成的一种民族语言,而形式语言是进行形式化工作的元语言,它是以数学和数理逻辑为基础的科学语言。用机器指令形式编写的程序称为机器语言, 用带符号或助记符的指令和地址代替二进制代码成为语言进化的目标。这些使用助记符语言的语言后来就被称之为汇编语言。
(P135 P136)
2、什么是高级程序设计语言?它有什么特点?
高级语言是汇编语言的一种抽象。高级语言的设计目标就是使程序员摆脱汇编语言细节的繁琐。高级语言同汇编语言都有一个共性,那就是:它们必须被转化为机器语言,这个转化的过程称为解释或编译。
(1)高级语言接近算法语言,易学、易掌握;
(2)高级语言设计出来的程序可读性好,可维护性强,可靠性高;
(3)高级语言与具体的计算机硬件关系不大,其程序可移植性好,重用率高;
(4)高级语言自动化程度高,开发周期短,利于提高程序的质量。
(P138)
3、列举程序设计语言的几种范型。
程序语言大致分为命令式程序设计语言、面向对象的程序设计语言、函数式程序设计语言和逻辑型程序设计语言等范型。
(P138-140)
4、简述语言虚拟机。
提示:语言虚拟机是某种语言的解释器。语言虚拟机是建立在硬件和操作系统之上,针对不同的硬件和操作系统有不同的虚拟机,通过语言虚拟机屏蔽掉硬件的差异。这样使得硬件系统能够支持这种语言编写的程序的有效执行。目前最流行的语言虚拟机是Java虚拟机。 (P147)
5、计算机执行用高级语言编写的程序有哪些途径?它们之间的主要区别是什么? 提示:主要有编译、解释等方式,也有两种方式的混合使用的形式。
编译是使用编译器将高级语言编写的源程序转换成计算机可以执行的机器语言可执行程序,也可以理解为用编译器产生可执行程序的动作。编译方式是一次编译,然后执行程序可以反复多次执行。
解释是另一种将高级语言转换为可执行程序的方式。与编译不同,解释性语言的程序不需要编译,省了道工序,解释性语言在运行程序的时候才翻译,每个语句都是执行的时候才翻译。这样解释性语言每执行一次就要翻译一次,效率比较低。
近来随着网络的发展,为了实现跨平台但同时又保证一定的效率,出现了编译、解释混合的方式,先用伪编译形成效率较高中间代码,再用语言虚拟机进行解释执行,以屏蔽掉硬件的差异。
计算机科学概论 新编计算机科学概论 刘艺、蔡敏 习题与答案
第七章习题及解答
(1) 复习题
1、关系模型由哪三部分组成?
关系模型的概念是建立在实体——关系方法基础上的。(www.61k.com)数据模型通常由数据结构、数据操作和完整性约束三部分组成。(P159)
2、关系的完整性分为哪三类?
关系数据模型的操作必须满足关系的完整性约束条件。完整性是指数据的精确性和可靠性。完整性约束是防止数据库中存在不符合语义规定的数据和防止因错误信息的输入/输出造成无效操作或错误信息而提出的。数据完整性分为四类:实体完整性、域完整性、参照完整性、用户定义的完整性。(P161)
3、常见的关系数据库产品有哪些?
提示:本书第7.2节(P159)介绍了一些产品,可以通过网络、专业报纸杂志再了解一些情况
4、什么是表?什么是记录?两者的区别是什么?
提示:表和记录是关系数据库中用于记录数据的两种数据结构。表是记录的上层结构,表示关系,记录是表的一行,表示一个关系的实例。
P160-161
5、数据模型的组成要素是什么?
提示:数据模型是严格定义的一组概念的集合。这些概念精确地描述了系统的静态特征、动态特性与完整性约束条件。因此数据模型通常由数据结构、数据操作和完整性约束三部分组成。
数据结构:数据结构是所研究的对象类型的集合。这些对象是数据库的组成成分,它们包括两类:一类是与数据类型、内容、性质有关的对象;另一类是与数据之间联系有关的对象。数据结构是刻画一个数据模型性质最重要的方面。在数据库系统中,人们通常按照其数据结构的类型来命名数据模型。例如层次结构、网状结构和关系结构的数据模型分别命名为层次模型、网状模型和关系模型。数据结构是对系统静态特征的描述。
数据操作:数据操作是针对数据库中各种对象(类型)的实例(取值)允许执行的操作的集合,包括操作及有关的操作规则。数据库主要有检索和更新(包括插入、删除、修改)两大类操作。数据模型必须定义这些操作的确切含义、操作符号、操作规则(如优先级)以及实现操作的语言。数据操作是对系统动态特性的描述。
数据的约束条件:数据的约束条件是一组完整性规则的集合。完整性规则是给定的数据模型中数据及其关系所具有的制约和依存规则,用以限定数据模型的数据库状态以及状态的变化,以保证数据的正确、有效、相容。
(P157)
6、数据字典是什么?数据字典有几类?
提示:数据字典是系统中各类数据描述的集合,是进行详细的数据收集和数据分析所获得的
计算机科学概论 新编计算机科学概论 刘艺、蔡敏 习题与答案
本章习题
(1) 复习题
1.简述软件的特点
答:
软件相对硬件而言有许多不同特点。[www.61k.com)了解这些特别之处能够帮助我们全面、正确地理解计算机软件。
(1)软件是一种逻辑实体,而不是具体的物理实体,具有很强的抽象性。我们只能把它记录在介质上,或在系统上运行,但却无法直接通过我们的眼睛看到软件的形态。
(2)软件是一个逻辑上复杂而规模上庞大的系统,涉及技术、管理等多方面的问题。如果将代码比作零件,则一个软件是由成百上千万个零件组成的复合体,而且其结构远较机械装置复杂。应该说软件的复杂程度高于同等规模的硬件产品。
(3)软件是智力产品,其价值体现在解决问题的知识和能力,而并不体现在软件载体本身。软件的生产方式与硬件明显不同,设计方法和制造阶段不同;软件的生成成本主要在研发设计上,而大量复制几乎没有成本。
(4)在软件的运行和使用期间,没有硬件的磨损、老化问题。但软件维护比硬件维护要复杂得多,软件的故障主是由于对软件的改变和使用环境的变化引起的。
(5)软件的开发和运行对硬件有较强依赖关系。在软件开发有可移植性的问题,现在通常把软件的可移植性作为衡量软件质量的重要因素之一。
(6)软件工作涉及许多社会因素。软件与人的关系密切,涉及到语言、文化等多方面,甚至关系到的道德领域。
{P175}
2.什么是软件危机?主要有哪些表现?其产生的原因是什么?
答:
软件危机是软件开发领域,特别是在大型软件开发和维护过程中遇到的一系列严重问题的统称。
软件危机主要表现为费用高、开发过程不易控制、工作量估计困难、软件质量低、软件项目失败率高、无法判断大型系统能否正常工作以及软件维护任务重等现象。
产生软件危机的主要原因,一方面是软件本身所固有的抽象性、复杂性等特性;另一方面是人们当时对软件和软件开发过程的不正确认识。
{P175}
3.简述什么是软件工程
答:
软件工程是应用计算机科学、数学及管理科学等原理开发软件的工程。它借鉴系统工程的原则、方法,以提高质量,降低成本为目的。软件工程是从管理和技术两方面研究如何更好地开发和维护计算机软件的一门学科。采用工程化方法和途径来开发与维护软件。 {P175-176}
4.简述软件工程研究的基本内容与目标
答:
计算机科学概论 新编计算机科学概论 刘艺、蔡敏 习题与答案
第9章 计算机网络
(1) 复习题
1、什么是计算机网络,它是如何分类的?
答:计算机网络是计算机技术与通信技术紧密结合的产物,是计算机通信网络发展的高级阶段。[www.61k.com]现在的计算机网络尚未具备完善的网络操作系统。仅实现了一定程度的资源共享,所以,它们仍是计算机通信网,也称为广义计算机网络。
计算机通信网是一种地理上分散的、具有独立功能的多台计算机通过通信设备和线路连接起来,在配有相应的网络软件(网络协议、操作系统等)的情况下实现资源共享的系统。 计算机网络按其覆盖范围大小可分为局域网(LAN)、城域网(MAN)、广域网(WAN)三大类,Internet属于广域网,从使用范围和用途来分,计算机网络又可分为校院网、企业网、公用网、专用网、以及内联网(intranet)和外联网(extranet)等。
2、什么是以太网,如何分类?
答:以太网是基带系统,采用曼彻斯特编码。以太网的核心技术是采用一种称为载波监听多路访问/冲突检测CSMA/CD(Carrier Sense Multiple Access/Collision Detection)的共享访问方案,即多个工作站都连接在一条总线上,所有的工作站都不断向总线上发出监听信号,但在同一时刻只能有一个工作站在总线上进行传输,而其他工作站必须等待其传输结束后再开始自己的传输。
以太网按传输速率可分为早期以太网10Mbps、快速以太网100Base-T和千兆以太网1 Gbps。
3、什么是计算机网络的体系结构,分层结构的主要特点有哪些?
答:
计算机网络系统是一个很复杂的信息系统,需要用高度结构化的方式来进行设计,即将一个比较复杂的系统设计问题分解成一个个容易处理的子问题,“分而治之”逐个地加以解决。从功能上,一个网络系统的总体结构,可以用如下“体系结构”来描述: A={S,E,L,P}
其中,A——网络体系结构, S——系统,E——实体,L——层,P——协议,所谓网络体系的分层结构,就是指把网络系统所提供的通路分成一组功能分明的层次,各层执行自己所承担的任务,依靠各层之间的功能组合,为用户或应用程序提供与另一端点之间的访问通路。在同一体系结构中的上层与下层之间,下层为上层提供服务,上层为下层的用户,上下层之间靠预先定义的接口联系。不同计算机之间的通信在同等的层之间进行,同等层之间的连接和信息由通信协议来定义。
层次化网络体系结构具有以下优点:
各层相互独立。某一高层只需通过接口向下一层提出服务请求,并使用下层提供的服务,并不需要了解下一层执行时的细节。
灵活性好。如果某一层发生变化,只要层间接口不变,则相邻层就不会受影响,这样有利于技术进步和模型的修改。例如当某一层的服务不再需要时,可以取消这层提供的服务,对其他层不会造成任何影响。
易于通信系统的实现和维护。整个系统被分割为多个容易实现和维护的小部分,使得整个庞大而复杂的系统容易实现、管理和维护,有利于标准化的实现,由于每一层都有明确的定义,即功能和所提供的服务都很确切,因此非常有利于系统标准化的实施。
4、网络一般有哪几部分组成,网络互连设备有哪些?
答:一个基本的计算机网络由服务器、工作站、网络接口卡、传输介质和共享的资源与外围设备组成。网络互连设备主要有集线器、中继器、网桥、路由器、交换机等。
计算机科学概论 新编计算机科学概论 刘艺、蔡敏 习题与答案
第10章 计算机信息系统安全习题
(1) 复习题
1、计算机网络系统主要面临哪些威胁?
答:由于黑客的攻击、管理的欠缺、网络的缺陷、软件的漏洞或“后门”,还有网络内部的威胁(比如用户的误操作,资源滥用和恶意行为使得再完善的防火墙也无法抵御来自网络内部的攻击,也无法对网络内部的滥用做出反应)等安全问题的根源。[www.61k.com)网络信息安全主要面临以下威胁。
非授权访问:非授权访问主要有以下几种形式:假冒、身份攻击、非法用户进入网络系统进行违法操作、合法用户以未授权方式进行操作等。非授权访问的威胁涉及到受影响的用户数量和可能被泄露的信息。入侵是一件很难办的事,它将动摇人的信心。而入侵者往往将目标对准政府部门或学术组织。
信息泄漏或丢失:指敏感数据在有意或无意中被泄漏出去或丢失,它通常包括,信息在传输中丢失或泄漏,信息在存储介质中丢失或泄漏,通过建立隐蔽隧道等窃取敏感信息等。具有严格分类的信息系统不应该直接连接Internet。
破坏数据完整性:以非法手段窃得对数据的使用权,删除、修改、插入或重发某些重要信息,以取得有益于攻击者的响应;恶意添加,修改数据,以干扰用户的正常使用。 拒绝服务攻击:拒绝服务攻击不断对网络服务系统进行干扰,改变其正常的作业流程,执行无关程序使系统响应减慢甚至瘫痪,使合法用户被排斥而不能进入计算机网络系统或不能得到相应的服务。
利用网络传播病毒,通过网络传播计算机病毒,其破坏性大大高于单机系统,而且用户很难防范。
2、简述计算机网络信息系统的安全服务与安全机制。
答:通常将为加强网络信息系统安全性及对抗安全攻击而采取的一系列措施称为安全服务。ISO7498-2中定义的5类安全服务是:数据完整性,鉴别,数据保密,访问控制,不可否认,这5类安全服务同面的安全目标的5个方面基本对应。
安全机制是实现安全服务的技术手段,表现为操作系统、软硬件功能部件、管理程序以及它们的任意组合。信息系统的安全是一个系统的概念,为了保障整个系统的安全可以采用多种机制。ISO7498-2中定义了8类安全机制:加密机制,数字签名机制,访问控制机制,数据完整性机制,鉴别机制,通信业务填充机制,路由控制机制,公证机制。
以上是特定安全机制,可以嵌入到合适的协议层提供一些OSI安全服务。另外还有五种安全机制如下:可信功能度,安全标志,事件检测,安全审计跟踪,安全恢复。一种安全机制可以提供多种安全服务,而一种安全服务也可采用多种安全机制。
3、什么是对称密钥,什么是非对称密钥,各有何特点?
答:现代密码术是根据密约规则和密钥算法将人可阅读的明文与不可阅读的密文相互转换的技术。将明文变为密文的过程称为加密;将密文译回明文的过程称为解密。密钥是随机的长数列比特数位串,它和算法结合,完成加/解密的过程。
在对称密钥密码术中,用相同的密钥来锁和打开“箱子”。 这种技术无论加密还是解密都是用同一把钥匙。这种方法快捷简便,即使传输信息的网络不安全,被别人截走信息,加密后的信息也不易泄露。但对称密钥密码术这在使用方便的同时,也带来了一系列问题,一
四 : 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版
[www.61k.com)概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
概率论与数理统计习题及答案
习题一
1.?略.见教材习题参考答案.
2.设A,B,C为三个事件,试用A,B,C的运算关系式表示下列事件:
(1)A发生,B,C都不发生;
(2)A与B发生,C不发生;
(3)A,B,C都发生;
(4)A,B,C至少有一个发生;
(5)A,B,C都不发生;
(6)A,B,C不都发生;
(7)A,B,C至多有2个发生;
(8)A,B,C至少有2个发生.
【解】(1)ABC(2)ABC(3)ABC(4)A∪B∪C=C∪BC∪ABC∪BC∪AC∪ABC∪ABC=ABC
(5)ABC=A∪B∪C
(7)(6)ABC BC∪AC∪ABC∪C∪ABC∪BC∪ABC=ABC=∪∪C
∪ABC(8)AB∪BC∪CA=ABC∪AC∪BC
3.?略.见教材习题参考答案
4.设A,B为随机事件,且P(A)=0.7,P(A?B)=0.3,求P(
【解】P()=1?P(AB)=1?[P(A)?P(A?B)]
=1?[0.7?0.3]=0.6
5.设A,B是两事件,且P(A)=0.6,P(B)=0.7,求:
(1)在什么条件下P(AB)取到最大值?
(2)在什么条件下P(AB)取到最小值??).
【解】(1)当AB=A时,P(AB)取到最大值为0.6.
(2)当A∪B=Ω时,P(AB)取到最小值为0.3.
6.设A,B,C为三事件,且P(A)=P(B)=1/4,P(C)=1/3且P(AB)=P(BC)=0,
P(AC)=1/12,求A,B,C至少有一事件发生的概率.
1
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
【解】P(A∪B∪C)=P(A)+P(B)+P(C)?P(AB)?P(BC)?P(AC)+P(ABC)
=11113++?=443124
7.?从52张扑克牌中任意取出13张,问有5张黑桃,3张红心,3张方块,2张梅花的概率
是多少?
【解】5332p=C13C13C13C13/C1352
8.?对一个五人学习小组考虑生日问题:
(1)求五个人的生日都在星期日的概率;(2)求五个人的生日都不在星期日的概率;
(3)求五个人的生日不都在星期日的概率.
【解】(1)设A1={五个人的生日都在星期日},基本事件总数为75,有利事件仅1个,故
P(A1)=115=()577(亦可用独立性求解,下同)
(2)设A2={五个人生日都不在星期日},有利事件数为65,故
6565P(A2)=5=()77
(3)设A3={五个人的生日不都在星期日}
9.?略.见教材习题参考答案.
10.一批产品共N件,其中M件正品.从中随机地取出n件(n<N).试求其中恰有m件(m≤M)正品(记为A)的概率.如果:
(1)n件是同时取出的;
(2)n件是无放回逐件取出的;
(3)n件是有放回逐件取出的.
mn?mn【解】(1)P(A)=CMCN?M/CN P(A3)=1?P(A1)=1?(15)7
n(2)由于是无放回逐件取出,可用排列法计算.样本点总数有PN种,n次抽取中有m
m次为正品的组合数为Cn种.对于固定的一种正品与次品的抽取次序,从M件正
mn?m品中取m件的排列数有PM种,从N?M件次品中取n?m件的排列数为PN?M种,
故
mmn?mCnPMPN?MP(A)=nPN
由于无放回逐渐抽取也可以看成一次取出,故上述概率也可写成
mn?mCMCN?MP(A)=nCN
可以看出,用第二种方法简便得多.
(3)由于是有放回的抽取,每次都有N种取法,故所有可能的取法总数为Nn种,n
2
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
m
次抽取中有m次为正品的组合数为Cn种,对于固定的一种正、次品的抽取次序,
m次取得正品,都有M种取法,共有Mm种取法,n?m次取得次品,每次都有N?M种取法,共有(N?M)n?m种取法,故
m
P(A)=CnMm(N?M)n?m/Nn
此题也可用贝努里概型,共做了n重贝努里试验,每次取得正品的概率为
M
,则取得N
m件正品的概率为
M?m?M??P(A)=Cn1??N??N?????
mn?m
11.?略.见教材习题参考答案.
12.?50只铆钉随机地取来用在10个部件上,其中有3个铆钉强度太弱.每个部件用3只铆
钉.若将3只强度太弱的铆钉都装在一个部件上,则这个部件强度就太弱.求发生一个部件强度太弱的概率是多少?【解】设A={发生一个部件强度太弱}
13.?一个袋内装有大小相同的7个球,其中4个是白球,3个是黑球,从中一次抽取3个,
计算至少有两个是白球的概率.【解】设Ai={恰有i个白球}(i=2,3),显然A2与A3互斥.
1
C2184C3
P(A2)=3=,
C735
33P(A)=C110C3/C50=
1
1960
C344
P(A3)=3=
C735
2235
故
P(A2∪A3)=P(A2)+P(A3)=
14.?有甲、乙两批种子,发芽率分别为0.8和0.7,在两批种子中各随机取一粒,求:
(1)两粒都发芽的概率;
(2)至少有一粒发芽的概率;(3)恰有一粒发芽的概率.【解】设Ai={第i批种子中的一粒发芽},(i=1,2)
(1)P(A1A2)=P(A1)P(A2)=0.7×0.8=0.56(2)P(A1∪A2)=0.7+0.8?0.7×0.8=0.94(3)P(A12∪1A2)=0.8×0.3+0.2×0.7=0.38
15.?掷一枚均匀硬币直到出现3次正面才停止.
(1)问正好在第6次停止的概率;
(2)问正好在第6次停止的情况下,第5次也是出现正面的概率.【解】(1)p1=C52()2(3
1
21215=232
1131C1()(4
=2(2)p2=
5/325
3
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
16.?甲、乙两个篮球运动员,投篮命中率分别为0.7及0.6,每人各投了3次,求二人进球
数相等的概率.
【解】设Ai={甲进i球},i=0,1,2,3,Bi={乙进i球},i=0,1,2,3,则
212P(∪AiBi3)=(0.3)3(0.4)3+C130.7×(0.3)C30.6×(0.4)+3i=0
22233C2
3(0.7)×0.3C3(0.6)0.4+(0.7)(0.6)
=0.32076
17.?从5双不同的鞋子中任取4只,求这4只鞋子中至少有两只鞋子配成一双的概率.【解】1111C4CCCC13p=1?52
4222=C1021
18.?某地某天下雪的概率为0.3,下雨的概率为0.5,既下雪又下雨的概率为0.1,求:
(1)在下雨条件下下雪的概率;(2)这天下雨或下雪的概率.
【解】设A={下雨},B={下雪}.
(1)p(BA)=P(AB)0.1==0.2P(A)0.5
(2)p(A∪B)=P(A)+P(B)?P(AB)=0.3+0.5?0.1=0.7
19.?已知一个家庭有3个小孩,且其中一个为女孩,求至少有一个男孩的概率(小孩为男
为女是等可能的).
【解】设A={其中一个为女孩},B={至少有一个男孩},样本点总数为23=8,故
P(BA)=P(AB)6/86==P(A)7/87
6
7或在缩减样本空间中求,此时样本点总数为7.P(B?A)=
20.?已知5%的男人和0.25%的女人是色盲,现随机地挑选一人,此人恰为色盲,问此人是
男人的概率(假设男人和女人各占人数的一半).
【解】设A={此人是男人},B={此人是色盲},则由贝叶斯公式
P(A)P(BA)P(AB)P(AB)==P(B)P(A)P(BA)+P(A)P(BA)
=0.5×0.0520=0.5×0.05+0.5×0.002521
21.?两人约定上午9∶00~10∶00在公园会面,求一人要等另一人半小时以上的概率.
4
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
题21图题22图
【解】设两人到达时刻为x,y,则0≤x,y≤60.事件“一人要等另一人半小时以上”等价于|x?y|>30.
如图阴影部分所示. 3021P=2=604
22.?从(0,1)中随机地取两个数,求:
6的概率;5
1(2)两个数之积小于的概率.4(1)两个数之和小于【解】设两数为x,y,则0<x,y<1.
6(1)x+y<.5
144
17p1=1?==0.68125
1(2)xy=<.4
1?1?11p2=1??1dx1dy?=+ln2?44x?42
23.?设P()=0.3,P(B)=0.4,P(A)=0.5,求P(B|A∪)【解】P(BA∪B)=P(AB)P(A)?P(AB)=P(A∪B)P(A)+P(B)?P(AB)
5
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
=
0.7?0.51
=
0.7+0.6?0.54
24.?在一个盒中装有15个乒乓球,其中有9个新球,在第一次比赛中任意取出3个球,比
赛后放回原盒中;第二次比赛同样任意取出3个球,求第二次取出的3个球均为新球的概率.
【解】设Ai={第一次取出的3个球中有i个新球},i=0,1,2,3.B={第二次取出的3球均为新
球}
由全概率公式,有
P(B)=∑P(BAi)P(Ai)
i=0
3
21
C3C3C1C3C2C3C3C3699C689C679
=3?3+3?3+3?3+3?36
C15C15C15C15C15C15C15C15
25.按以往概率论考试结果分析,努力学习的学生有90%的可能考试及格,不努力学习的学
生有90%的可能考试不及格.据调查,学生中有80%的人是努力学习的,试问:(1)考试及格的学生有多大可能是不努力学习的人?(2)考试不及格的学生有多大可能是努力学习的人?【解】设A={被调查学生是努力学习的},则
=0.089
={被调查学生是不努力学习的}.由题意知P
(A)=0.8,P()=0.2,又设B={被调查学生考试及格}.由题意知P(B|A)=0.9,P(|)=0.9,故由贝叶斯公式知
P(A)P(BA)P(AB)
(1)P(AB)==
P(B)P(A)P(BA)+P(A)P(BA)
=
0.2×0.11
==0.02702
0.8×0.9+0.2×0.137
即考试及格的学生中不努力学习的学生仅占2.702%(2)
P(A)=
=
P(A)P(BA)P(=P(B)P(A)P(BA)+P(A)P(BA)0.8×0.14
==0.3077
0.8×0.1+0.2×0.913
即考试不及格的学生中努力学习的学生占30.77%.
26.将两信息分别编码为A和B传递出来,接收站收到时,A被误收作B的概率为0.02,而
B被误收作A的概率为0.01.信息A与B传递的频繁程度为2∶1.若接收站收到的信息是A,试问原发信息是A的概率是多少?
【解】设A={原发信息是A},则={原发信息是B}
6
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
C={收到信息是A},则={收到信息是B}由贝叶斯公式,得
om
P(AC)=
=
P(A)P(CA)
P(A)P(CA)+P(A)P(CA)
kh
daw.c
2/3×0.98
=0.99492
2/3×0.98+1/3×0.01
27.?在已有两个球的箱子中再放一白球,然后任意取出一球,若发现这球为白球,试求箱
子中原有一白球的概率(箱中原有什么球是等可能的颜色只有黑、白两种)?【解】设Ai={箱中原有i个白球}(i=0,1,2),由题设条件知P(Ai)=
出一球为白球}.由贝叶斯公式知
1
,i=0,1,2.又设B={抽3
P(A1B)=
P(BA1)P(A1)P(A1B)=2
P(B)
∑P(BAi)P(Ai)
i=0
=
28.?某工厂生产的产品中96%是合格品,检查产品时,一个合格品被误认为是次品的概率
为0.02,一个次品被误认为是合格品的概率为0.05,求在被检查后认为是合格品产品确是合格品的概率.
【解】设A={产品确为合格品},B={产品被认为是合格品}
由贝叶斯公式得
课后答案网 www.61k.com
P(AB)=
=
2/3×1/31
=
1/3×1/3+2/3×1/3+1×1/33
P(A)P(BA)P(AB)
=
P(B)P(A)P(BA)+P(A)P(BA)
0.96×0.98
=0.998
0.96×0.98+0.04×0.05
=
0.2×0.05
=0.057
0.2×0.05+0.5×0.15+0.3×0.3
kh
30.?加工某一零件需要经过四道工序,设第一、二、三、四道工序的次品率分别为
0.02,0.03,0.05,0.03,假定各道工序是相互独立的,求加工出来的零件的次品率.【解】设Ai={第i道工序出次品}(i=1,2,3,4).
da
w.c
P(A|D)=
P(AD)P(A)P(D|A)
=P(D)P(A)P(D|A)+P(B)P(D|B)+P(C)P(D|C)
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
om
7
29.?某保险公司把被保险人分为三类:“谨慎的”,“一般的”,“冒失的”.统计资料表明,上
述三种人在一年内发生事故的概率依次为0.05,0.15和0.30;如果“谨慎的”被保险人占20%,“一般的”占50%,“冒失的”占30%,现知某被保险人在一年内出了事故,则他是“谨慎的”的概率是多少?
【解】设A={该客户是“谨慎的”},B={该客户是“一般的”},
C={该客户是“冒失的”},D={该客户在一年内出了事故}则由贝叶斯公式得
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
P(∪Ai)=1?P(A1A2A3A4)
i=1
4
om
3
=1?P(A1)P(A2)P(A3)P(A4)
=1?0.98×0.97×0.95×0.97=0.124
khdaw.c
即为【证】亦即因此
故A与B相互独立.
31.?设每次射击的命中率为0.2,问至少必须进行多少次独立射击才能使至少击中一次的概
率不小于0.9?
【解】设必须进行n次独立射击.
1?(0.8)n≥0.9
(0.8)n≤0.1
n≥11
故
至少必须进行11次独立射击.
32.?证明:若P(A|B)=P(A|),则A,B相互独立.
课后答案网 www.61k.com
P(AB)P()=P(P(B)
P(A|B)=P(A|)即
P(AB)P(AB)
=P(B)P(B)
P(AB)[1?P(B)]=[P(A)?P(AB)]P(B)
P(AB)=P(A)P(B)
33.?三人独立地破译一个密码,他们能破译的概率分别为的概率.
,则【解】设Ai={第i人能破译}(i=1,2,3)
111
,,,求将此密码破译出534
P(∪Ai)=1?P(A1A2A3)=1?P(A1)P(A2)P(A3)
i=1
i=0
kh
=(0.4×0.5×0.3+0.6×0.5×0.3+0.6×0.5×0.7)0.2+
(0.4×0.5×0.3+0.4×0.5×0.7+0.6×0.5×0.7)0.6+0.4×0.5×0.7
8
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
da
P(A)=∑P(A|Bi)P(Bi)
3
w.c
34.?甲、乙、丙三人独立地向同一飞机射击,设击中的概率分别是0.4,0.5,0.7,若只有一人
击中,则飞机被击落的概率为0.2;若有两人击中,则飞机被击落的概率为0.6;若三人都击中,则飞机一定被击落,求:飞机被击落的概率.【解】设A={飞机被击落},Bi={恰有i人击中飞机},i=0,1,2,3
由全概率公式,得
om
423
=1?××=0.6
534
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
khdaw.c
【解】(1)p1=
∑C
k=0
k
10
3
(2)p2=
k=4
∑C
10
36.?一架升降机开始时有6位乘客,并等可能地停于十层楼的每一层.试求下列事件的概率:
(1)A=“某指定的一层有两位乘客离开”;
(2)B=“没有两位及两位以上的乘客在同一层离开”;(3)C=“恰有两位乘客在同一层离开”;(4)D=“至少有两位乘客在同一层离开”.
【解】由于每位乘客均可在10层楼中的任一层离开,故所有可能结果为106种.
4C269(1)P(A)=,也可由6重贝努里模型:610
(2)6个人在十层中任意六层离开,故
课后答案网 www.61k.com
1294()()P(A)=C26
1010
6P10
P(B)=6
10
(3)由于没有规定在哪一层离开,故可在十层中的任一层离开,有C1种可能结果,再从10
六人中选二人在该层离开,有C2.其余4人中不能再有两人同时离开的情?6种离开方式况,因此可包含以下三种离开方式:①4人中有3个人在同一层离开,另一人在其余
31
8层中任一层离开,共有C1种可能结果;②4人同时离开,有C1种可能结果;9C4C89
om
k
10
=0.458
35.?已知某种疾病患者的痊愈率为25%,为试验一种新药是否有效,把它给10个病人服用,
且规定若10个病人中至少有四人治好则认为这种药有效,反之则认为无效,求:(1)虽然新药有效,且把治愈率提高到35%,但通过试验被否定的概率.(2)新药完全无效,但通过试验被认为有效的概率.
(0.35)k(0.65)10?k=0.5138
(0.25)k(0.75)10?k=0.2241
2131146
P(C)=C110C6(C9C4C8+C9+P9)/10
(4)D=.故
6
P10
P(D)=1?P(B)=1?6
10
kh
9
37.n个朋友随机地围绕圆桌而坐,求下列事件的概率:(1)甲、乙两人坐在一起,且乙坐在甲的左边的概率;
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
da
w.c
om
③4个人都不在同一层离开,有P94种可能结果,故
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
(2)甲、乙、丙三人坐在一起的概率;
(3)如果n个人并排坐在长桌的一边,求上述事件的概率.khdaw.c(3)p1′=
构成的图形,即
【证】(2)p2=3!(n?3)!,n>3(n?1)!(n?1)!13!(n?2)!=;p2′=,n≥3n!nn!38.?将线段[0,a]任意折成三折,试求这三折线段能构成三角形的概率?【解】设这三段长分别为x,y,a?x?y.则基本事件集为由0<x<a,0<y<a,0<a?x?y<a所构成的图形,有利事件集为由om?x+y>a?x?y?x+(a?x?y)>y???y+(a?x?y)>x【解】(1)p1=1n?1 课后答案网 www.61k.com 如图阴影部分所示,故所求概率为p=a?<x<0?2??0<y<a?2?a?<x+y<a??21.4?39.某人有n把钥匙,其中只有一把能开他的门.他逐个将它们去试开(抽样是无放回的).证明试开k次(k=1,2,…,n)才能把门打开的概率与k无关.Pnk??111?p=k=,k=1,2,?,n?Pnn
小立方体是无色的,故所求概率为41.对任意的随机事件A,B,C,试证
kh512384=0.512,P(A1)==0.384,10001000968P(A2)==0.096,P(A4)==0.008.10001000da
10P(A0)=
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com .c40.把一个表面涂有颜色的立方体等分为一千个小立方体,在这些小立方体中,随机地取出一个,试求它有i面涂有颜色的概率P(Ai)(i=0,1,2,3).?【解】设Ai={小立方体有i面涂有颜色},i=0,1,2,3.在1千个小立方体中,只有位于原立方体的角上的小立方体是三面有色的,这样的小立方体共有8个.只有位于原立方体的棱上(除去八个角外)的小立方体是两面涂色的,这样的小立方体共有12×8=96个.同理,原立方体的六个面上(除去棱)的小立方体是一面涂色的,共有8×8×6=384个.其余1000?(8+96+384)=512个内部的om
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
P(AB)+P(AC)?P(BC)≤P(A).
【证】
P(A)≥P[A(B∪C)]=P(AB∪AC)
khdaw.c
因此或
42.?将3个球随机地放入4个杯子中去,求杯中球的最大个数分别为1,2,3的概率.【解】设Ai={杯中球的最大个数为i},i=1,2,3.
将3个球随机放入4个杯子中,全部可能放法有43种,杯中球的最大个数为1时,每个杯中最多放一球,故
om
=P(AB)+P(AC)?P(ABC)≥P(AB)+P(AC)?P(BC)
C33!3
P(A1)=43=
48
而杯中球的最大个数为3,即三个球全放入一个杯中,故
课后答案网
www.61k.com
319
P(A2)=1?P(A1)?P(A3)=1??=
81616
21
C194C3C3
P(A2)==
4316
C114
P(A3)=3=
416
43.?将一枚均匀硬币掷2n次,求出现正面次数多于反面次数的概率.
【解】掷2n次硬币,可能出现:A={正面次数多于反面次数},B={正面次数少于反面次数},
C={正面次数等于反面次数},A,B,C两两互斥.
可用对称性来解决.由于硬币是均匀的,故P(A)=P(B).所以
1?P(C)
P(A)=2
由2n重贝努里试验中正面出现n次的概率为
n1n1n
P(C)=C2n((22
11
P(A)=[1?Cn]2n2n
22
故
n112
P(A)=[1?n)n]
22
45.?设甲掷均匀硬币n+1次,乙掷n次,求甲掷出正面次数多于乙掷出正面次数的概率.
11
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
kh
da
w
.c
44.?掷n次均匀硬币,求出现正面次数多于反面次数的概率.
【解】设A={出现正面次数多于反面次数},B={出现反面次数多于正面次数},由对称性知
P(A)=P(B)
(1)当n为奇数时,正、反面次数不会相等.由P(A)+P(B)=1得P(A)=P(B)=0.5(2)当n为偶数时,由上题知
om
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
【解】
=(甲正≤乙正)=(n+1?甲反≤n?乙反)(甲正>乙正)
khdaw.c因此P(甲正>乙正)==(甲反≥1+乙反)=(甲反>乙反)由对称性知P(甲正>乙正)=P(甲反>乙反)46.?证明“确定的原则”(Sure?thing):若P(A|C)≥P(B|C),P(A|C)≥P(B|C),则P(A)≥P(B).【证】由P(A|C)≥P(B|C),得om12令甲正=甲掷出的正面次数,甲反=甲掷出的反面次数.乙正=乙掷出的正面次数,乙反=乙掷出的反面次数.显然有
P(AC)P(BC)≥,P(C)P(C)
即有
同理由
得
故P(AC)≥P(BC) 课后答案网 www.61k.com P(A|)≥P(B|P(≥P(P(A)=P(AC)+P()≥P(BC)+P()=P(B)
k(n?1)1k?P(Ai)==(1?)kn?n?2P(AiAj)=(1?)k
n
?
n?1kP(Ai1Ai2?Ain?1)=(1?)n47.一列火车共有n节车厢,有k(k≥n)个旅客上火车并随意地选择车厢.求每一节车厢内至少有一个旅客的概率.?【解】设Ai={第i节车厢是空的},(i=1,…,n),则
kh
12
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com .c其中i1,i2,…,in?1是1,2,…,n中的任n?1个.显然n节车厢全空的概率是零,于是om
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
khdaw.c
?
om
11k
S1=∑P(Ai)=n(1?)k=C1(1?)n
nni=1
2k
S2=∑P(AiAj)=C2(1?)n
n1≤i<j≤n
n
Sn?1=
1≤i1<i2<?in?1≤n
∑
?1
P(Ai1Ai2?Ain?1)=Cnn(1?
n?1k
n
Sn=0
ni=1
P(∪Ai)=S1?S2+S3??+(?1)n+1Sn
1k2kn?1k2nn?1
=C1(1?)?C(1?)+?+(?1)C(1?)nnn
nnn
1k2n?1k2n?1)+Cn(1?)i??+(?1)n+1Cn(1?)nnn
故所求概率为
1
1?P(∪Ai)=1?Cn(1?
n
i=1
48.设随机试验中,某一事件A出现的概率为ε>0.试证明:不论ε>0如何小,只要不断地独立地重复做此试验,则A迟早会出现的概率为1.?【证】
在前n次试验中,A至少出现一次的概率为
49.袋中装有m只正品硬币,n只次品硬币(次品硬币的两面均印有国徽).在袋中任取一只,
将它投掷r次,已知每次都得到国徽.试问这只硬币是正品的概率是多少?【解】设A={投掷硬币r次都得到国徽}
课后答案网 www.61k.com
1?(1?ε)n→1(n→∞)
B={这只硬币为正品}
由题知
P(B)=
mn
,P(?B)=m+nm+n
1
P(A|B)=r,P(A|B)=1
2
则由贝叶斯公式知
kh
50.巴拿赫(Banach)火柴盒问题:某数学家有甲、乙两盒火柴,每盒有N根火柴,每次用
火柴时他在两盒中任取一盒并从中任取一根.试求他首次发现一盒空时另一盒恰有r根的概率是多少?第一次用完一盒火柴时(不是发现空)而另一盒恰有r根的概率又有多少?
da
w.c
m1
r
m==r
m+2nr+1m+n2m+n
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
om
13
P(B|A)=
P(AB)P(B)P(A|B)
=
P(A)P(B)P(A|B)+P(B)P(A|B)
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
【解】以B1、B2记火柴取自不同两盒的事件,则有P(B1)=P(B2)=
1
.(1)发现一盒已空,2
khdaw.c
式中2反映B1与B2盒的对称性(即也可以是B2盒先取空).
(2)前2n?r?1次取火柴,有n?1次取自B1盒,n?r次取自B2盒,第2n?r次取自B1
盒,故概率为
51.?求n重贝努里试验中A出现奇数次的概率.【解】设在一次试验中A出现的概率为p.则由
00nn?12n?2nn0
(q+p)n=Cnpq+C1+C2+?+Cnpq=1npqnpq00nn?122n?2nnn0(q?p)n=Cnpq+C1pq+Cpq??+(?1)Cnpqnn
以上两式相减得所求概率为
课后答案网 www.61k.com
n?13n?3
p1=C1+C3+?npqnpq
若要求在n重贝努里试验中A出现偶数次的概率,则只要将两式相加,即得
om
另一盒恰剩r根,说明已取了2n?r次,设n次取自B1盒(已空),n?r次取自B2盒,
第2n?r+1次拿起B1,发现已空。[www.61k.com)把取2n?r次火柴视作2n?r重贝努里试验,则所求概率为
1n1n?r11n
p1=2Cn((i=C2n?rn?r2r?r
2222
1n?11n?r112n?r?1?1?1
p2=2Cn(=Cn2n?r?1(2n?r?1(2222
1
=?(q?p)n]21
=?(1?2p)n]2
1
p2=+(1?2p)n].
2
52.设A,B是任意两个随机事件,求P{(
+B)(A+B)(+)(A+)}的值.
【解】因为(A∪B)∩(∪)=A∪B
(∪B)∩(A∪)=AB∪
所求
(+B)(A+B)(+)(A+)=[(AB∪AB)∩(AB+AB)]=?
kh
【解】由P(A∪B∪C)=P(A)+P(B)+P(C)?P(AB)?P(AC)?P(BC)+P(ABC)
da
故所求值为0.
53.设两两相互独立的三事件,A,B和C满足条件:
ABC=Φ,P(A)=P(B)=P(C)<1/2,且P(A∪B∪C)=9/16,求P(A).
w.c
14
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
om
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
=3P(A)?3[P(A)]2=
916
54.设两个相互独立的事件A和B都不发生的概率为1/9,A发生B不发生的概率与B发生A
不发生的概率相等,求P(A).
khdaw.c
om
故P(A)=
1311或,按题设P(A)<,故P(A)=.4424
【解】
P(AB)=P(A∪B)=1?P(A∪B)=
P()=P()
1
9
①②
故故
P(A)?P(AB)=P(B)?P(AB)
P(A)=P(B)
1
=1?P(A)?P(B)+P(A)P(B)9
③
由A,B的独立性,及①、③式有
故故
课后答案网 www.61k.com
=[1?P(A)]2
1?P(A)=±
13
24
P(A)=或P(A)=(舍去)
33
2
.3
)内掷一点,点落在半圆内任何区域的概率与2ax?x2(a为正常数
=1?2P(A)+[P(A)]2
即P(A)=
55.随机地向半圆0<y<
区域的面积成正比,则原点和该点的连线与x轴的夹角小于π/4的概率为多少??【解】利用几何概率来求,图中半圆面积为
1
2
πa2.阴影部分面积为
故所求概率为
kh
15
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
da
56.?设10件产品中有4件不合格品,从中任取两件,已知所取两件产品中有一件是不合格
品,求另一件也是不合格品的概率.
【解】设A={两件中至少有一件是不合格品},B={另一件也是不合格品}
w.c
π212a+a
=1+1p=22ππa2
om
π212a+a42
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
khdaw.c
则
3
57.设有来自三个地区的各10名、15名和25名考生的报名表,其中女生的报名表分别为3
份、7份和5份.随机地取一个地区的报名表,从中先后抽出两份.?(1)求先抽到的一份是女生表的概率p;
(2)已知后抽到的一份是男生表,求先抽到的一份是女生表的概率q.【解】设Ai={报名表是取自第i区的考生},i=1,2,3.
Bj={第j次取出的是女生表},j=1,2.
(1)p=P(B1)=
(2)q=P(B1|B2)=
而
课后答案网 ∑ www.61k.com
P(B1B2)P(B2)
3
P(2)=
om
i=1
C242
P(AB)C101
P(B|A)===
P(A)C256
1-2
C10
1
P(Ai)=,i=1,2,3
3
375
P(B1|A1)=,P(B1|A2)=,P(B1|A3)=
101525137529=++=P(B|A)(∑1i
310152590i=1
P(2|Ai)P(Ai)
1782061
=(++=310152590
P(B12=∑P(B12|Ai)P(Ai)
i=1
3
故
58.设A,B为随机事件,且P(B)>0,P(A|B)=1,试比较P(A∪B)与P(A)的大小.(2006研考)
P(AB)=P(B)?P(AB)=P(B)
所以
P(A∪B)=P(A)+P(B)?P(B)=P(A).
kh
16
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
da
w.c
解:因为
P(A∪B)=P(A)+P(B)?P(AB)
om
137785202=(×+×+×=3109151425249
2
P(B1B2)20q===
61P(B2)6190
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
习题二
1.一袋中有5只乒乓球,编号为1,2,3,4,5,在其中同时取3只,以X表示取出的3只
球中的最大号码,写出随机变量X的分布律.【解】
khdaw.c
故所求分布律为
X=3,4,5
1
=0.1C353
=0.3C35
P(X=3)=
P(X=4)=
C24
P(X=5)=3=0.6
C5
30.1
40.3
50.6
XP
2.设在15只同类型零件中有2只为次品,在其中取3次,每次任取1只,作不放回抽样,以X表示取出的次品个数,求:(1)X的分布律;
(2)X的分布函数并作图;(3)
课后答案网 www.61k.com
133
.P{X≤P{1<X≤},P{1≤X≤},P{1<X<2}
222
【解】
om
X=0,1,2.
C322
P?(X=0)=13=.3
C1535
2
C1122C13
P(X=1)=3=.
C1535
故X的分布律为
P
22
351235135
(2)当x<0时,F(x)=P(X≤x)=0
当0≤x<1时,F(x)=P(X≤x)=P(X=0)=
kh
1
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
2235
da
w.c
X012
om
C11
P(X=2)=13=3
C1535
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
当1≤x<2时,F(x)=P(X≤x)=P(X=0)+P(X=1)=34
35
khdaw.c(3)
故X的分布律为
X0
0.0083.射手向目标独立地进行了3次射击,每次击中率为0.8,求3次射击中击中目标的次数的分布律及分布函数,并求3次射击中至少击中2次的概率.【解】设X表示击中目标的次数.则X=0,1,2,3. 课后答案网 www.61k.com P(X=0)=(0.2)3=0.0082P(X=1)=C130.8(0.2)=0.0962P(X=2)=C(0.8)0.2=0.384?231122P(X≤)=F=,2235333434P(1<X≤)=F)?F(1)=?=02235353312P(1≤X≤)=P(X=1)+P(1<X≤)=2235341P(1<X<2)=F(2)?F(1)?P(X=2)=1??=0.3535om当x≥2时,F(x)=P(X≤x)=1故X的分布函数x<0?0,?22?,0≤x<1?F(x)=?35?34,1≤x<2?35?1,x≥2??P(X=3)=(0.8)?3=0.51210.09623
分布函数
P(X≥2)=P(X=2)+P(X=3)=0.896
4.(1)设随机变量X的分布律为kh
2
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com <0?0,?0.008,0≤x<1??F(x)=?0.104,1≤x<2?0.488,2≤x<3?x≥3??1,w.comP0.3840.512
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
λk
P{X=k}=a,
k!
其中k=0,1,2,…,λ>0为常数,试确定常数a.
(2)设随机变量X的分布律为
P{X=k}=a/N,k=1,2,…,N,
试确定常数a.【解】(1)由分布律的性质知
khdaw.c
故(1)
23
om
∞2
λk
1=∑P(X=k)=a∑=aieλ
k=0k=0k!
∞
a=e?λ
(2)由分布律的性质知
1=∑P(X=k)=∑
k=1
N
a
=ak=1N
N
即a=1.
5.甲、乙两人投篮,投中的概率分别为0.6,0.7,今各投3次,求:(1)两人投中次数相等的概率;(2)甲比乙投中次数多的概率.
【解】分别令X、Y表示甲、乙投中次数,则X~b(3,0.6),Y~b(3,0.7)
P(X=Y)=P(X=0,Y=0)+P(X=1,Y=1)+P(X=2,Y=2)+
P(X=3,Y=3)
21
=(0.4)3(0.3)3+C1C30.7(0.3)2+?30.6(0.4)
课后答案网 www.61k.com
C(0.6)0.4C(0.7)?20.3+(0.6)3(0.7)3
2
3
=0.32076
(2)P(X>Y)=P(X=1,Y=0)+P(X=2,Y=0)+P(X=3,Y=0)+
P(X=2,Y=1)+P(X=3,Y=1)+P(X=3,Y=2)
=C30.6(0.4)(0.3)+C3(0.6)0.4(0.3)+
212
(0.6)3(0.3)3+C23(0.6)0.4C30.7(0.3)+2322(0.6)3C130.7(0.3)+(0.6)C3(0.7)0.31
2
3
2
2
3
kh
=0.243
6.设某机场每天有200架飞机在此降落,任一飞机在某一时刻降落的概率设为0.02,且设各
3
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
da
w.c
om
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
om
飞机降落是相互独立的.试问该机场需配备多少条跑道,才能保证某一时刻飞机需立即降落而没有空闲跑道的概率小于0.01(每条跑道只能允许一架飞机降落)?
【解】设X为某一时刻需立即降落的飞机数,则X~b(200,0.02),设机场需配备N条跑道,
则有
P(X>N)<0.01
k200
khdaw.c
即
利用泊松近似
k=N+1
∑C
200
(0.02)k(0.98)200?k<0.01
λ=np=200×0.02=4.
e?44k
P(X≥N)?∑<0.01
k!k=N+1
∞
查表得N≥9.故机场至少应配备9条跑道.
7.有一繁忙的汽车站,每天有大量汽车通过,设每辆车在一天的某时段出事故的概率为0.0001,在某天的该时段内有1000辆汽车通过,问出事故的次数不小于2的概率是多少(利用泊松定理)?
【解】设X表示出事故的次数,则X~b(1000,0.0001)
课后答案网 www.61k.com
P(X≥2)=1?P(X=0)?P(X=1)
=1?e?0.1?0.1×e?0.1
4223
C15p(1?p)=C5p(1?p)
8.已知在五重贝努里试验中成功的次数X满足P{X=1}=P{X=2},求概率P{X=4}.
【解】设在每次试验中成功的概率为p,则
故所以
p=
13
14210
.P(X=4)=C4=5)
33243
k
P(X≥3)=∑C5(0.3)k(0.7)5?k=0.16308
k=3
(2)令Y表示7次独立试验中A发生的次数,则Y~b(7,0.3)
k7?kP(Y≥3)=∑Ck(0.3)(0.7)=0.352937
k=37
10.某公安局在长度为t的时间间隔内收到的紧急呼救的次数X服从参数为(1/2)t的泊松分
4
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
kh
da
w
.c
5
om
9.设事件A在每一次试验中发生的概率为0.3,当A发生不少于3次时,指示灯发出信号,(1)进行了5次独立试验,试求指示灯发出信号的概率;(2)进行了7次独立试验,试求指示灯发出信号的概率.【解】(1)设X表示5次独立试验中A发生的次数,则X~6(5,0.3)
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
om
32
布,而与时间间隔起点无关(时间以小时计).
(1)求某一天中午12时至下午3时没收到呼救的概率;
(2)求某一天中午12时至下午5时至少收到1次呼救的概率.【解】(1)P(X=0)=e
?
(2)
P(X≥1)=1?P(X=0)=1?e
?
5
2
khdaw.c
m4?m
P{Y=m}=Cm,4p(1?p)
k2?k11.设P{X=k}=Ck,k=0,1,22p(1?p)
m=0,1,2,3,4
分别为随机变量X,Y的概率分布,如果已知P{X≥1}=
5
,试求P{Y≥1}.9
【解】因为P(X≥1)=
而
54,故P(X<1)=.99
P(X<1)=P(X=0)=(1?p)2
4
(1?p)2=,
91p=.
3
故得即从而
12.某教科书出版了2000册,因装订等原因造成错误的概率为0.001,试求在这2000册书中
恰有5册错误的概率.
【解】令X为2000册书中错误的册数,则X~b(2000,0.001).利用泊松近似计算,
课后答案网 www.61k.com
P(Y≥1)=1?P(Y=0)=1?(1?p)4=
65
≈0.8024781
λ=np=2000×0.001=2
得
e?225
=0.0018P(X=5)≈
5!
31
13.进行某种试验,成功的概率为,失败的概率为.以X表示试验首次成功所需试验的次?44
数,试写出X的分布律,并计算X取偶数的概率.【解】X=1,2,?,k,?
13
P(X=k)=(k?1
44
kh
5
131313
=+(3+?+(2k?1+?444444
131=i=41?(25
4
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
da
w.c
P(X=2)+P(X=4)+?+P(X=2k)+?
om
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
khdaw.c
1014.有2500名同一年龄和同社会阶层的人参加了保险公司的人寿保险.在一年中每个人死亡的概率为0.002,每个参加保险的人在1月1日须交12元保险费,而在死亡时家属可从保险公司领取2000元赔偿金.求:(1)保险公司亏本的概率;(2)保险公司获利分别不少于10000元、20000元的概率.【解】以“年”为单位来考虑.(1)在1月1日,保险公司总收入为2500×12=30000元.设1年中死亡人数为X,则X~b(2500,0.002),则所求概率为由于n很大,p很小,λ=np=5,故用泊松近似,有om
∞
?∞P(2000X>30000)=P(X>15)=1?P(X≤14)e?55kP(X>15)≈1?∑≈0.000069k!k=014(2)P(保险公司获利不少于10000)=P(30000?2000X≥10000)=P(X≤10)e?55k≈∑≈0.986305k!k=0即保险公司获利不少于10000元的概率在98%以上?P(保险公司获利不少于20000)=P(30000?2000X≥20000)=P(X≤5) 课后答案网 www.61k.com e?55k≈∑≈0.615961k!k=05∞即保险公司获利不少于20000元的概率约为62%?15.已知随机变量X的密度函数为??∞<x<+∞,f(x)=Ae?|x|,?(2)P{0<X<1};(3)F(x).求:(1)A值;?【解】(1)由∫?∞f(x)dx=1得1=∫Ae?|x|dx=2∫Ae?xdx=2A0∞
kh1.211?x1?1(2)p(0<X<1)=edx=(1?e)∫022x11(3)当x<0时,F(x)=∫exdx=ex?∞22x101x1?|x|x?x当x≥0时,F(x)=edx=dx+e∫?∞2∫?∞2∫02dx1=1?e?x2故A=da
6
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com .com
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
om
150
故
?1x
e,??2
F(x)=?
?1?1e?x??2
x<0x≥0
kh
daw.c
100??x≥100,f(x)=?x2?x<100.?0,
(1)P(X≤150)=
故
16.设某种仪器内装有三只同样的电子管,电子管使用寿命X的密度函数为
求:(1)在开始150小时内没有电子管损坏的概率;(2)在这段时间内有一只电子管损坏的概率;(3)F(x).【解】
1001
dx=.∫100x2
328
p1=[P(X>150)]3=)3=
327
1224
(2)p2=C1(=3
339
(3)当x<100时F(x)=0
当x≥100时F(x)=
x
课后答案网 ∫
www.61k.com ∫∫
?∞
f(t)dt
=
100
?∞
f(t)dt+
x
100
f(t)dt
=∫
100100
t=?1100t2x
x
?1?100,x≥100?F(x)=?x
??x<0?0,
17.在区间[0,a]上任意投掷一个质点,以X表示这质点的坐标,设这质点落在[0]中任意小区间内的概率与这小区间长度成正比例,试求X的分布函数.
【解】由题意知X~∪[0,a],密度函数为
故当x<0时F(x)=0当0≤x≤a时F(x)=当x>a时,F(x)=1即分布函数
∫
x
?∞
f(t)dt=∫f(t)dt=∫
xx
1xt=aa
kh
7
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
da
w.c
om
?1,0≤x≤a?f(x)=?a
?0,其他?
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
om
?0,??xF(x)=??a??1,
x<0
0≤x≤a
x>a
kh
daw.c
故所求概率为
18.设随机变量X在[2,5]上服从均匀分布.现对X进行三次独立观测,求至少有两次的观测
值大于3的概率.【解】X~U[2,5],即
?1,2≤x≤5?f(x)=?3
?其他?0,
P(X>3)=∫
5
3
12
dx=33
22120323
p=C2)+C(=33
33327
19.设顾客在某银行的窗口等待服务的时间X(以分钟计)服从指数分布E().某顾客在窗口
等待服务,若超过10分钟他就离开.他一个月要到银行5次,以Y表示一个月内他未等
到服务而离开窗口的次数,试写出Y的分布律,并求P{Y≥1}.【解】依题意知X~E(,即其密度函数为
课后答案网 www.61k.com
15
?1?x
?e5,x>0f(x)=?5
?0,x≤0?
x
5
15
该顾客未等到服务而离开的概率为
P(X>10)=∫
∞1
10
5
edx=e?2
?
Y~b(5,e?2),即其分布律为
P(Y≥1)=1?P(Y=0)=1?(1?e?2)5=0.5167
kh
x?4060?40?
P(X<60)=P??10<10?=Φ(2)=0.97727
??
da
20.某人乘汽车去火车站乘火车,有两条路可走.第一条路程较短但交通拥挤,所需时间X服
从N(40,102);第二条路程较长,但阻塞少,所需时间X服从N(50,42).(1)若动身时离火车开车只有1小时,问应走哪条路能乘上火车的把握大些?(2)又若离火车开车时间只有45分钟,问应走哪条路赶上火车把握大些?【解】(1)若走第一条路,X~N(40,102),则
w
.c
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
om
8
?2k?25?k
P(Y=k)=Ck,k=0,1,2,3,4,55(e)(1?e)
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
若走第二条路,X~N(50,42),则故走第二条路乘上火车的把握大些.
(2)若X~N(40,102),则
khdaw.cX?4045?40?P(X<45)=P??10<10?=Φ(0.5)=0.6915??X?5045?50?P(X<45)=P?=Φ(?1.25)?4<?4??=1?Φ(1.25)=0.1056若X~N(50,42),则
故走第一条路乘上火车的把握大些.
21.设X~N(3,22),
(1)求P{2<X≤5},P{?4<X≤10},P{|X|>2},P{X>3};
(2)确定c使P{X>c}=P{X≤c}.
【解】(1)P(2<X≤5)=P? 课后答案网 www.61k.com ?2?3<X?3≤5?3?
22??2?
?1??1?=Φ(1)?Φ???=Φ(1)?1+Φ???2??2?
=0.8413?1+0.6915=0.5328
?4?3X?310?3?P(?4<X≤10)=P?<≤??222???7???Φ??7?=0.9996=Φ??2??2??????omX?5060?50?P(X<60)=P??4<4?=Φ(2.5)=0.9938++??
P(|X|>2)=P(X>2)+P(X<?2)
?X?32?3??X?3?2?3?=P?>+P??2<2?22????
?1??5??1??5?=1?Φ??+Φ???=Φ??+1?Φ??2??2??2??2?
=0.6915+1?0.9938=0.6977
P(X>3)=P(
kh(2)c=322.由某机器生产的螺栓长度(cm)X~N(10.05,0.062),规定长度在10.05±0.12内为合格品,
9
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com ?33-3>=1?Φ(0)= www.61k.com
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
求一螺栓为不合格品的概率.【解】P(|X?10.05|>0.12)=P?
khdaw.c
故(3)
23.一工厂生产的电子管寿命X(小时)服从正态分布N(160,σ2),若要求P{120<X≤200}
≥0.8,允许σ最大不超过多少?
【解】P(120<X≤200)=P?
om
?X?10.050.12?
>
0.06??0.06?
=1?Φ(2)+Φ(?2)=2[1?Φ(2)]
=0.0456
?120?160<X?160≤200?160?
?σσσ??
40???40?=2Φ?40??1≥0.8=Φ??Φ?σ??σ??σ?
??????
σ≤
40
=31.251.29
24.设随机变量X分布函数为
(1)求常数A,B;
(2)求P{X≤2},P{X>3};(3)求分布密度f(x).
课后答案网 www.61k.com
?A+Be?xt,x≥0,
F(x)=?(λ>0),
00.,x<?
F(x)=1??A=1?xlim→+∞
【解】(1)由?得?
limF(x)=limF(x)?B=?1??x→0+x→0?
(2)P(X≤2)=F(2)=1?e?2λ
P(X>3)=1?F(3)=1?(1??e?3λ)=e?3λ
?λe?λx,f(x)=F′(x)=?
?0,
x≥0x<0
0≤x<1,1≤x<2, .
25.设随机变量X的概率密度为
当0≤x<1时F(x)=
kh
10
∫
x
?∞
f(t)dt=∫
?∞
f(t)dt+∫f(t)dt
x
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
da
求X的分布函数F(x),并画出f(x)及F(x).
【解】当x<0时F(x)=0
w.c
?x,?
f(x)=?2?x,
?0,?
om
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
x2
=∫tdt=02
x
当1≤x<2时F(x)=
om
∫
x?∞0
f(t)dt
1
khdaw.c
当x≥2时F(x)=
=∫
?∞1
f(t)dt=∫f(t)dt+∫f(t)dt
1
x
=∫tdt+∫(2?t)dt
1
x
1x23=+2x??222x2
=?+2x?1
2
x?∞
∫
f(t)dt=1
x<0
0≤x<1
故
26.设随机变量X的密度函数为
(1)f(xe?l|x|,λ>0;
课后答案网 www.61k.com
1≤x<2
?0,?2?x,?2F(x)=?2
??x+2x?1,?2??1,
x≥2
(2)
?bx,0<x<1,?1f(x)=?2,1≤x<2,
x?
?0, .
试确定常数a,b,并求其分布函数F(x).【解】(1)由
故
∫
∞
?∞
f(x)dx=1知1=∫ae
?∞
∞
?λ|x|
dx=2a∫e?λxdx=
∞
2a
λ
a=
λ2
x>0x≤0
即密度函数为
kh
11
λλx1λxdx=e∫?∞?∞22
x0λxλλx?λx
当x>0时F(x)=f(x)dx=dx+∫?∞∫?∞2∫02dx
1=1?e?λx
2
当x≤0时F(x)=
x
f(x)dx=∫
x
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
da
w.c
?λ?λx
e,??2
f(x)=?
?λeλx??2
om
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
故其分布函数
omkhdaw.c
(2)由1=
?1?λx1?e,??2
F(x)=?
?1eλx,??2
21
x>0x≤0
∫
∞
?∞
f(x)dx=∫bxdx+∫
1
1b1
dx=+x222
得
即X的密度函数为
b=1
0<x<1?x,??1
f(x)=?2,1≤x<2
?x
其他??0,
当x≤0时F(x)=0当0<x<1时F(x)=
当1≤x<2时F(x)=
∫ 课后答案网 ∫∫∫∫
www.61k.com
=
x0
∫
x
?∞
f(x)dx=∫
?∞
f(x)dx+∫f(x)dx
x
x2
xdx=
2
x
?∞
f(x)dx=
?∞
0dx+
1
xdx+
x
1
1dxx2
=
31?2x
当x≥2时F(x)=1故其分布函数为
27.求标准正态分布的上α分位点,(1)α=0.01,求zα;(2)α=0.003,求zα,zα/2.【解】(1)P(X>zα)=0.01
即即
1?Φ(zα)=0.01
Φ(zα)=0.09
kh
12
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
da
w
.c
om
x≤0?0,
?2x,?0<x<1?2F(x)=?
3?1,1≤x<22x?1,x≥2?
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
故
zα=2.33
om
?11/6
01/541/5
(2)由P(X>zα)=0.003得
1?Φ(zα)=0.003
khdaw.c
即查表得即查表得
Φ(zα)=0.997zα=2.75
由P(X>zα/2)=0.0015得
1?Φ(zα/2)=0.0015
Φ(zα/2)=0.9985
zα/2=2.96
11/15
311/30
28.设随机变量X的分布律为
XPk
?21/5
求Y=X2的分布律.
【解】Y可取的值为0,1,4,9
课后答案网 www.61k.com
P(Y=0)=P(X=0)=
15
117
P(Y=1)=P(X=?1)+P(X=1)=+=
61530
1
P(Y=4)=P(X=?2)?=
5?11
P(Y=9)=P(X=3)=
30
故Y的分布律为
Pk
1/57/3011/30
29.设P{X=k}=(
?1,当X取偶数时Y=?
??1,当X取奇数时.
求随机变量X的函数Y的分布律.【解】P(Y
=1)=P(X=2)+P(X=4)+?+P(X=2k)+?
kh
13
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
da
w.c
1k
),k=1,2,…,令2
om
Y019
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知! om
=∫
lny
?∞111=(2+(4+?+(2k+?222111=(/(1?=443khdaw.cP(Y=?1)=1?P(Y=1)=2330.设X~N(0,1).(1)求Y=eX的概率密度;(2)求Y=2X2+1的概率密度;(3)求Y=|X|的概率密度.【解】(1)当y≤0时,FY(y)=P(Y≤y)=0当y>0时,FY(y)=P(Y≤y)=P(ex≤y)=P(X≤lny)fX(x)dx
故
(2)P(Y=2X2+1≥1)=1
当y≤1时FY(y)=P(Y≤y)= www.61k.com fY(y)=
?y?1??2=P?X≤=P≤X≤???2????
=
dFY(y)1?ln2y/2=fx(lny)=,y>0dyy当y>1时FY(y)=P(Y≤y)=P(2X2+
1≤y)fX(x?)dx
??+fX???????d故fY(y)=FY(y)=dy=
(3)P(Y≥0)=1?(y?1)/4,y>1当y>0时FY(y)=P(|X|≤y)=P(?y≤X≤y)
kh
14
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com 当y≤0时FY(y)=P(Y≤y)= www.61k.com ??fX??
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知! =∫故fY(y)=y?yfX(x)dx
khdaw=【解】(1)故?y2/2,y>031.设随机变量X~U(0,1),试求:(1)Y=eX的分布函数及密度函数;(2)Z=?2lnX的分布函数及密度函数.P(0<X<1)=1P(1<Y=eX<e)=1
当y≤1时FY(y)=P(Y≤y)=0当1<y<e时FY(y)=P(eX≤y)=P(X≤lny)当y≥e时FY(y)=P(eX≤y)=1即分布函数 课后答案网 ∫ www.61k.com =lny0omdFY(y)=fX(y)+
fX(?y)dydx=lny
y≤1?0,?FY(y)=?lny,1<y<e
?1,y≥e?
故Y的密度函数为
1?1<y<efY(y)=?y,
?0,其他?
P(Z>0)=1
当z≤0时,FZ(z)=P(Z≤z)=0当z>0时,FZ(z)=P(Z≤z)=P(?2lnX≤z)
e
kh
15=∫?z/2dx=1?e?z/21
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com =P(lnX≤?)=P(X≥e?z/2) www.61k.com (2)由P(0<X<1)=1知
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
即分布函数
故Z的密度函数为
khdaw.c
【解】P(0<Y<1)=1
故Y
的密度函数为
om
=
arcsiny
z≤0?0,
FZ(z)=?-z/2
?1-e,z>0
?1?z/2?e,
fZ(z)=?2
??0,
z>0z≤0
32.设随机变量X的密度函数为
?2x
?,0<x<π,f(x)=?π2
?其他.?0,
试求Y=sinX的密度函数.
当y≤0时,FY(y)=P(Y≤y)=0
当0<y<1时,FY(y)=P(Y≤y)=P(sinX≤y)
课后答案网 www.61k.com ∫∫
=P(0<X≤arcsiny)+P(π?arcsiny≤X<π)
2x
dx
0π?arcsinyπ21122=2arcsiny)+1-2π-arcsiny)ππ2
=arcsiny?π
π
2xdx+2π
当y≥1时,FY(y)=1
试填上(1),(2),(3)项.
【解】由limF(x)=1知②填1。[www.61k.com)
x→∞
kh
16
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
da
?1
,?
F(x)=?1+x2
??(2),
x<(1)x≥
,
(3).
w
.c
33.设随机变量X的分布函数如下:
om
?20<y<1?πfY(y)=??0,其他?
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
由右连续性limF(x)=F(x0)=1知x0=0,故①为0。[www.61k.com)+
x→x0
khdaw.c
抛掷出现6点}。则
34.同时掷两枚骰子,直到一枚骰子出现6点为止,求抛掷次数X的分布律.
om
=
从而③亦为0。即
?1,x<0?
F(x)=?1+x2
?1,x≥0?
1
.且A1与A2相互独立。再设C={每次6
【解】设Ai={第i枚骰子出现6点}。(i=1,2),P(Ai)=
P(C)=P(A1∪A2)=P(A1)+P(A2)?P(A1)P(A2)
111111
+?=666636
11
故抛掷次数X服从参数为的几何分布。
36
35.随机数字序列要多长才能使数字0至少出现一次的概率不小于0.9?【解】令X为0出现的次数,设数字序列中要包含n个数字,则
X~b(n,0.1)
0n
P(X≥1)=1?P(X=0)=1?C0n(0.1)(0.9)≥0.9
即
课后答案网 www.61k.com
(0.9)n≤0.1???0,
??1
F(x)=?x+,
2??1,??
得n≥22
即随机数字序列至少要有22个数字。36.已知
x<0,
0≤x<1x≥.
2
1,2
【解】因为F(x)在(?∞,+∞)上单调不减右连续,且limF(x)=0
x→?∞
kh
但是F(x)在x=0处不连续,也不是阶梯状曲线,故F(x)是非连续亦非离散型随机变量的分布函数。选(C)
37.设在区间[a,b]上,随机变量X的密度函数为f(x)=sinx,而在[a,b]外,f(x)=0,则区间[a,b]
17
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
da
x→+∞
limF(x)=1,所以F(x)是一个分布函数。
w.c
om
则F(x)是()随机变量的分布函数.(A)连续型;(B)离散型;(C)非连续亦非离散型.
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
等于()(A)[0,π/2];
(B)[0,π];(D)[0,
【解】在[0,上sinx≥0,且
khdaw.c
π2
在[0,π]上在[?
∫
π
π
,0]上sinx≤0,故f(x)不是密度函数。(www.61k.com)233
在[0,π]上,当π<x≤π时,sinx<0,f(x)也不是密度函数。
22
故选(A)。
38.设随机变量X~N(0,σ2),问:当σ取何值时,X落入区间(1,3)的概率最大?
om
∫
π/20
(C)[?π/2,0];
3
π].2
sinxdx=1.故f(x)是密度函数。
sinxdx=2≠1.故f(x)不是密度函数。
【解】因为X~N(0,σ2),P(1<X<3)=P(
利用微积分中求极值的方法,有
课后答案网 g′(σ)=(?
=3311
′′Φ(+
Φ()22
σσσσ?9/2σ2?1/2σ2
令
?1/2σ2?8/2σ2
=[1?3e]=04,则ln3
1X3<<σσσ31
=Φ()?Φ)令g(σ)
σσ
2
得σ
0=σ0=
又故
σ0<
g′′(σ0)<0
故当σ=
时X落入区间(1,3
)的概率最大。
39.设在一段时间内进入某一商店的顾客人数X服从泊松分布P(λ),每个顾客购买某种物
品的概率为p,并且各个顾客是否购买该种物品相互独立,求进入商店的顾客购买这种物品的人数Y的分布律.
e?λλm
【解】P(X=m)=,m=0,1,2,?
m!
设购买某种物品的人数为Y,在进入商店的人数X=m的条件下,Y~b(m,p),即
kh
da
18
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
w.c
om
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
k
P(Y=k|X=m)=Cmpk(1?p)m?k,k=0,1,?,m
om
=∫
由全概率公式有
P(Y=k)=∑P(X=m)P(Y=k|X=m)
m=k
∞
khdaw.c
e?λλmkk
=∑Cmp(1?p)m?k
m!m=k
∞
λm
=e∑pk(1?p)m?k
m=kk!(m?k)!
?λ
∞
=e
?λ
(λp)kk!
[λ(1?p)]m?k∑(m?k)!m=k
∞
(λp)k?λλ(1?p)=ee
k!
(λp)k?λp=e,k=0,1,2,?
k!
此题说明:进入商店的人数服从参数为λ的泊松分布,购买这种物品的人数仍服从泊松分布,但参数改变为λp.
40.设随机变量X服从参数为2的指数分布.证明:Y=1?e?2X在区间(0,1)上服从均匀分布.【证】X的密度函数为
课后答案网 www.61k.com
?2e?2x,x>0
fX(x)=?
x≤0?0,
由于P(X>0)=1,故0<1?e?2X<1,即P(0<Y<1)=1
当y≤0时,FY(y)=0当y≥1时,FY(y)=1
?2x
当0<y<1时,FY(y)=P(Y≤y)=P(e≥1?y)
1
=P(X≤?ln(1?y))
2
1
?ln(1?y)2
2e?2xdx=y
即Y的密度函数为
即Y~U(0,1)
41.设随机变量X的密度函数为
kh
19
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
da
w.c
?1,0<y<1
fY(y)=?
?0,其他
om
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
khdaw.c
?1
?3,0≤x≤1,??2f(x)=?,3≤x≤6,?9
其他.?0,
??
(2000研考)
若k使得P{X≥k}=2/3,求k的取值范围.
【解】由P(X≥k)=
若k<0,P(X<k)=0
1k1dx=∫033≤31
当k=1时P(X<k)=
3
11k1
若1≤k≤3时P(X<k)=∫dx+∫0dx=
031311k2211
若3<k≤6,则P(X<k)=dx+dx=k?≠∫03∫39933
若0≤k≤1,P(X<k)=
k
若k>6,则P(X<k)=1
故只有当1≤k≤3时满足P(X≥k)=42.设随机变量X的分布函数为
课后答案网 www.61k.com
2.3
求X的概率分布.(1991研考)
【解】由离散型随机变量X分布律与分布函数之间的关系,可知X的概率分布为
om
XP
21知P(X<k)=33
x<?1,?0,
?0.4,?1≤x<1,?F(x)=?
?0.8,1≤x<3,?x≥3.?1,
?1
0.410.430.2
故p=
13
44.若随机变量X在(1,6)上服从均匀分布,则方程y2+Xy+1=0有实根的概率是多少?【解】
kh
20
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
da
w.c
由P(X≥1)=
198知P(X=0)=(1?p)3=2727
om
43.设三次独立试验中,事件A出现的概率相等.若已知A至少出现一次的概率为19/27,求A
在一次试验中出现的概率.
【解】令X为三次独立试验中A出现的次数,若设P(A)=p,则
X~b(3,p)
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
om?1?,1<x<6f(x)=?5?0,其他?4
5P(X2?4≥0)=P(X≥2)+P(X≤?2)=P(X≥2)=
khdaw.c45.若随机变量X~N(2,σ2),且P{2<X<4}=0.3,则P{X.【解】0.3=P(2<X<4)=P(2?2X?24?2<<)σσσ22=Φ(?Φ(0)=Φ)?0.5σσ2故Φ()=0.8σ
X?20?22因此P(X<0)=P(<=Φ(?σσσ
2=1?Φ(=0.2σ
46.假设一厂家生产的每台仪器,以概率0.7可以直接出厂;以概率0.3需进一步调试,经调
试后以概率0.8可以出厂,以概率0.2定为不合格品不能出厂.现该厂新生产了n(n≥2)台仪器(假设各台仪器的生产过程相互独立).求
(1)全部能出厂的概率α;
(2)其中恰好有两台不能出厂的概率β;
(3)其中至少有两台不能出厂的概率θ.
【解】设A={需进一步调试},B={仪器能出厂},则 课后答案网 www.61k.com
={能直接出厂},AB={经调试后能出厂}由题意知B=∪AB,且P(A)=0.3,P(B|A?)=0.8
P(AB)=P(A)P(B|A)=0.3×0.8=0.24
P(B)=P(A)+P(AB)=0.7+0.24=0.94
令X为新生产的n台仪器中能出厂的台数,则X~6(n,0.94),
故
α=P(X=n)=(0.94)n
2β=P(X=n?2)=Cn(0.94)n?2(0.06)2
θ=P(X≤n?2)=1?P(X=n?1)?P(X=n)
kh47.某地抽样调查结果表明,考生的外语成绩(百分制)近似服从正态分布,平均成绩为72分,96分以上的占考生总数的2.3%,试求考生的外语成绩在60分至84分之间的概率.【解】设X为考生的外语成绩,则X~N(72,σ2)da=1?n(0.94)n?10.06?(0.94)nw.c
21
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
24?X?7296?72?
0.023=P(X≥96)=P?≥=1?Φ(?σ?σ?σ
om
故查表知
Φ(
24
=0.977σ
khdaw.c
24
=2,即σ=12σ
从而X~N(72,122)故P(60≤X≤84)=P?
?60?72X?7284?72?
≤≤?121212??
=Φ(1)?Φ(?1)=2Φ(1)?1=0.682
48.在电源电压不超过200V、200V~240V和超过240V三种情形下,某种电子元件损坏的概
率分别为0.1,0.001和0.2(假设电源电压X服从正态分布N(220,252)).试求:(1)该电子元件损坏的概率α;
(2)该电子元件损坏时,电源电压在200~240V的概率β【解】设A1={电压不超过200V},A2={电压在200~240V},
A3={电压超过240V},B={元件损坏}。[www.61k.com)由X~N(220,252)知
课后答案网 www.61k.com
P(A1)=P(X≤200)
?X?220200?220?=P?≤?2525??=Φ(?0.8)=1?Φ(0.8)=0.212
P(A2)=P(200?≤X≤240)
?200?220≤X?220≤240?220?
=P??252525??=Φ(0.8)?Φ(?0.8)=0.576
由全概率公式有
α=P(B)=∑P(Ai)P(B|Ai)=0.0642
i=1
由贝叶斯公式有
β=P(A2|B)=
P(A2)P(B|A2)
≈0.009
P(B)
49.设随机变量X在区间(1,2)上服从均匀分布,试求随机变量Y=e2X的概率密度fY(y).
22
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
kh
da
w.c
3
om
P(A3)=P(X>240)=1?0.212?0.576=0.212
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
【解】fX(x)=?
?1,1<x<2?0,其他
因为P(1<X<2)=1,故P(e2<Y<e4)=1当y≤e2时FY(y)=P(Y≤y)=0.
khdaw.c
即故
当e2<y<e4时,FY(y)=P(Y≤y)=P(e2X≤y)
om
=∫
1?y21
=P(1<X≤
dx=
1
lny)21
lny?12
当y≥e4时,FY(y)=P(Y≤y)=1
50.设随机变量X的密度函数为
课后答案网 www.61k.com
?124,e<y<e
fY(y)=?2y
?0,其他??e?x,x≥0,fX(x)=?
?0,x<0.
?0,y≤e2??1
FY(y)=?lny?1,e2<y<e4
?241,y≥e??
求随机变量Y=eX的密度函数fY(y).
【解】P(Y≥1)=1
当y≤1时,FY(y)=P(Y≤y)=0
(1995研考)
当y>1时,FY(y)=P(Y≤y)=P(eX≤y)=P(X≤lny)
=∫
lny
e?xdx=1?
即
y>1y≤1
y>1
故
kh
23
?1?,
fY(y)=?y2
?0,?
y≤1
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
da
w.c
?1?1?,
FY(y)=?y
?0,?
om
1y
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
51.设随机变量X的密度函数为
求Y=1?x的密度函数fY(
y).
khdaw.c
=∫=
∞
【解】FY(y)=P(Y≤y)=P(1≤y)=P(X≥(1?y)3)
11
dx=x
(1?y)3π(1+x2)π?π3?
?arctg(1?y)???2?
om
fX(x)=
1
,
π(1+x2)
∞
(1?y)3
1π
故
3(1?y)2
fY(y)=
π1+(1?y)6
52.假设一大型设备在任何长为t的时间内发生故障的次数N(t)服从参数为λt的泊松分布.
(1)求相继两次故障之间时间间隔T的概率分布;
(2)求在设备已经无故障工作8小时的情形下,再无故障运行8小时的概率Q.(1993
研考)
【解】(1)当t<0时,FT(t)=P(T≤t)=0
课后答案网 www.61k.com
当t≥0时,事件{T>t}与{N(t)=0}等价,有
FT(t)=P(T≤t)=1?P(T>t)=1?P(N(t)=0)=1?e?λt
?1?e?λt,t≥0
FT(t)=?
t<0?0,
即
即间隔时间T服从参数为λ的指数分布。[www.61k.com)(2)
e
Q=P(T>16|T>8)=P(T>16)/P(T>8)=
?16λ?8λ
e
=e?8λ
当?1<x<1时,P(X≤x|?1<X<1)=此时F(x)=P(X≤x)
x+12
kh
24
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
da
w.c
由题知P(?1<X<1)=1?
115?=848
om
53.设随机变量X的绝对值不大于1,P{X=?1}=1/8,P{X=1}=1/4.在事件{?1<X<1}出现的条
件下,X在{?1,1}内任一子区间上取值的条件概率与该子区间长度成正比,试求X的分布函数F(x)=P{X≤x}.(1997研考)【解】显然当x<?1时F(x)=0;而x≥1时F(x)=1
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
=P(X≤,?1<X<1)+P(X≤x,X=?1)+P(X≤x,X=1)=P(X≤x,?1<X<1)+P(X≤x,x=?1)
=
x+15151
+=(x+1)+288168
1
8
khdaw.c
故X的分布函数
解:
依题意
所以有
当x=?1时,F(x)=P(X≤x)=P(X=?1)=
54.设随机变量X服从正态分N(μ1,σ12),Y服从正态分布N(μ2,σ22),且P{|X-μ1|<1}>P{|Y-μ2|<1},试比较σ1与σ2的大小.(2006研考)
课后答案网 www.61k.com
P{X?μ1<1}=PX?μ11
<,σ1σ1Y?μ21
<.σ2σ2
P{Y?μ2<1}=P{
因为P{X?μ1<1}>P{Y?μ2<1},即
om
P{
=P(X≤x|?1<X<1)P(?1<X<1)+P(X=?1)
x<?1?0,
?1?5
F(x)=?(x+1)+,-1≤x<1
8?16
x≥1??1,
X?μ1Y?μ2
~N(0,1),~N(0,1),则σ1σ2
X?μ11?Y?μ11
<>P{<,σ1σ1?σ2σ2
11
,即σ1<σ2.>
σ1σ2
kh
25
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
da
w.c
om
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
习题三
khdaw.c
Y
X
00
om
1
1.将一硬币抛掷三次,以X表示在三次中出现正面的次数,以Y表示三次中出现正面次数与
出现反面次数之差的绝对值.试写出X和Y的联合分布律.【解】X和Y的联合分布律如表:
2
30
1
1113C1i××=3
2228111C2i××=3/83
222
3
18
1111××=2228
2.盒子里装有3只黑球、2只红球、2只白球,在其中任取4只球,以X表示取到黑球的只数,以Y表示取到红球的只数.求X和Y的联合分布律.【解】X和Y的联合分布律如表:
Y
X
00
10
2
2
C233iC2
=C4357
3
1
C323iC2
=4
C735
10
课后答案网
www.61k.com
12
C163iC2iC2
=4
C735
21
C3iC1122iC2
=C4357
1
C323iC2
=4
C735
2P(0黑,2红,2白)=
24
C22iC2/C7=
1
21
C163iC2iC2
=4
C7352
C233iC2
=C4357
3.设二维随机变量(X,Y)的联合分布函数为
【解】如图P{0<X≤
kh
1
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
da
πππ
,<Y≤公式(3.2)463
ππππππF(,?F(?F(0,+F(0,434636
w
.c
求二维随机变量(X,Y)在长方形域?0<x≤
??
ππ
<y≤46
π?
内的概率.3?
om
ππ??sinxsiny,0≤x≤,0≤y≤F(x,y)=?22
?其他.?0,
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
ππππππ=sinsin?sinsin?sin0i
sin+sin0i434636=
www.61k.com 题3图?1).4说明:也可先求出密度函数,再求概率。[www.61k.com)
4.设随机变量(X,Y)的分布密度
?Ae?(3x+4y),f(x,y)=??0,
求:(1)常数A;
(2)随机变量(X,Y)的分布函数;
(3)P{0≤X<1,0≤Y<2}.
【解】(1)由+∞+∞
?∞?∞x>0,y>0,其他.
得A=12
(2)由定义,有 课后答案网 ∫∫∫∫ www.61k.com f(x,y)dxdy=+∞+∞00Ae-(3x+4y)dxdy=A=112
F(x,y)=∫y
?∞?∞∫xf(u,v)dudv
yy??∫0∫012e?(3u+4v)dudv?(1?e?3x)(1?e?4y)y>0,x>0,=?=??0,其他???0,
(3)P{0≤X<1,0≤Y<2}
=P{0<X≤1,0<Y≤2}
5.设随机变量(X,Y)的概率密度为
kh
2(1)确定常数k;(2)求P{X<1,Y<3};(3)求P{X<1.5};(4)求P{X+Y≤4}.【解】(1)由性质有
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com .cf(x,y)=??k(6?x?y),0<x<2,2<y<4,其他.?0,om=∫10∫2012e?(3x+4y)dxdy=(1?e?3)(1?e?8)≈0.9499.
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
∫∫?∞+∞+∞?∞f(x,y)dxdy=∫20∫42k(6?x?y)dydx=8k=1,
(2)P{X<1,Y<3}=om∫∫
313故1R=?8?∞?∞f(x,y)dydx
khdaw.c(3)P{X<1.5}=x<1.5=∫∫∫13k(6?x?y)dydx=0∫288f(x,y)dxdy如图af(x,y)dxdy1D1=∫dx∫01.5(4)P{X+Y≤4}=
X+Y≤4
2∫∫127(6?x?y)dy=.2832f(x,y)dxdy如图b∫∫f(x,y)dxdy4D2=∫dx∫04?x212?x?y)dy=.83
题5图
6.设X和Y是两个相互独立的随机变量,X在(0,0.2)上服从均匀分布,Y的密度函数为 课后答案网 www.61k.com
?5e?5y,y>0,fY(y)=?其他.?0,
求:(1)X与Y的联合分布密度;(2)P{Y≤X}.
kh
3
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com 而da?1,0<x<0.2,fX(x)=?0.2?其他.?0,w.c题6图【解】(1)因X在(0,0.2)上服从均匀分布,所以X的密度函数为om
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
所以
f(x,y)X,Y独立fX(x)ifY(y)
khdaw.c(2)P(Y≤X)=y≤x?1×5e?5y?25e?5y,0<x<0.2且y>0,?=?0.2=?其他.?0,?0,?om∫∫00.2?5e?5y,y>0,fY(y)=?其他.?0,f(x,y)dxdy如图∫∫25e?5ydxdyDx-5y0.200=∫dx∫25edy=∫(?5e?5x+5)dx
=e-1≈0.3679.
7.设二维随机变量(X,Y)的联合分布函数为
求(X,Y)的联合分布密度.?2F(x,y)?8e?(4x+2y),x>0,y>0,【解】f(x,y)==??x?y其他.?0,
8.设二维随机变量(X,Y)的概率密度为 课后答案网 www.61k.com
f(x,y)=??(1?e?4x)(1?e?2y),F(x,y)=??0,x>0,y>0,其他.?4.8y(2?x),0≤x≤1,0≤y≤x,
其他.?0,
求边缘概率密度.
【解】fX(x)=∫+∞
?∞f(x,y)dy
x??∫04.8y(2?x)dy?2.4x2(2?x),0≤x≤1,=?=?其他.?0,??0,
?∞f(x,y)dx
kh
4
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com .c12??∫y4.8y(2?x)dx?2.4y(3?4y+y),0≤y≤1,=?=?其他.?0,??0,omfY(y)=∫+∞
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
khdaw.c题8图9.设二维随机变量(X,Y)的概率密度为om题9图?e?y,0<x<y,f(x,y)=? .?0,求边缘概率密度.
【解】fX(x)=∫+∞
?∞f(x,y)dy
fY(y)=∫ 课后答案网 ∫ www.61k.com +∞?∞+∞??∫xe?ydy?e?x,x>0,=?=?其他.?0,??0,f(x,y)dx
yyx??0e?dx?ye?,y>0,=?=?其他.?0,??0,
题10图
10.设二维随机变量(X,Y)的概率密度为
?cx2y,x2≤y≤1,f(x,y)=? .?0,
【解】(1)
D
=∫dx∫2cx2ydy=-111x4c=1.21
得?c=
?∞
kh
5(2)fX(x)=∫+∞f(x,y)dy
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com .4w.c∫∫?∞+∞+∞?∞f(x,y)dxdy如图∫∫f(x,y)dxdyom(1)试确定常数c;(2)求边缘概率密度.
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
fY(y)=
∫
khdaw【解】fX(x)=+∞
?∞?x2ydx?75??y2,0≤y≤1,=?=?2??0, 其他.?0,?11.设随机变量(X,Y)的概率密度为om+∞?∞?1212?2124?∫x2xydyx(1?x),?1≤x≤1,=?4=?8?0,?0,其他.??f(x,y)dxf(x,y)=?y<x,0<x<1, .?0,?1,求条件概率密度fY|X(y|x),fX|Y(x|y). 课后答案网 www.61k.com ∫题11图f(x,y)dy
x??1dy=2x,0<x<1,=?∫?x
?其他.?0,
fY(y)=∫?∞+∞
所以
kh
6
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com .c?1f(x,y),|y|<x<1,fY|X(y|x)==?2xfX(x)?其他.?0,om??11dx=1+y,?1<y<0,?∫?y?1?f(x,y)dx=?∫y1dx=1?y,0≤y<1,?其他.?0,??
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
khdaw.c
3
?1
?1?y, y<x<1,?
f(x,y)?1
fX|Y(x|y)==?,?y<x<1,
fY(y)?1+y
?0,其他.??
12.袋中有五个号码1,2,3,4,5,从中任取三个,记这三个号码中最小的号码为X,最大
的号码为Y.
(1)求X与Y的联合概率分布;(2)X与Y是否相互独立?【解】(1)X与Y的联合分布律如下表
Y
om
45
X
P{X=xi}
6
10310110
1
11=C3105
22
=C310511=C3105
33
=C310522=C310511=C2105
2
3
课后答案网
www.61k.com
P{Y=yi}
110310
610
(2)因P{X=1}iP{Y=3}=
故X与Y不独立
13.设二维随机变量(X,Y)的联合分布律为Y0.40.8
X
2
5
6161×=≠=P{X=1,Y=3},1010100108
(2)X与Y是否相互独立?
【解】(1)X和Y的边缘分布如下表
Y0.40.8
0.150.05
0.300.12
0.350.03
kh
da
X
258
w
.c
P{Y=yi}0.80.2
7
0.150.300.350.050.120.03
(1)求关于X和关于Y的边缘分布;
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
om
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
课后答案网 www.61k.com
若侵犯了您的版权利益,敬请来信告知!
P{X=xi}
(2)因P{X
0.20.420.38
khdaw.c
【解】(1)因fX(x)==?
故X与Y不独立.
14.设X和Y是两个相互独立的随机变量,X在(0,1)上服从均匀分布,Y的概率密度为
om
=2}iP{Y=0.4}=0.2×0.8=0.16≠0.15=P(X=2,Y=0.4),
1??e?y/2,
fY(y)=?2
??0,
y>0,
其他.
(1)求X和Y的联合概率密度;
(2)设含有a的二次方程为a2+2Xa+Y=0,试求a有实根的概率.
?1,0<x<1,?0,其他;
?1?y
?e2,y>1,
fY(y)==?2
?0,其他.?
0<x<1,y>0,其他.
课后答案网
www.61k.com
题14图
(2)方程a2+2Xa+Y=0有实根的条件是
2?4Y≥0?=(2X)
?1e?y/2
?
故f(x,y)X,Y独立fX(x)ifY(y)=?2
??0,
故
从而方程有实根的概率为:
X≥Y,
2
x2≥y
15.设X和Y分别表示两个不同电子器件的寿命(以小时计),并设X和Y相互独立,且服
从同一分布,其概率密度为
kh
8
若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com
da
w.c
1?y/2edy
002
=1Φ(1)?Φ(0)]=0.1445.=∫dx∫
1
x2
om
P{X2≥Y}=
∫∫
f(x,y)dxdy
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
似然函数 L =∏ P( x ,θ ) = 4θi =16(1 ?θ 2 )(1 ? 2θ ) 4 .kh解 6 ? 28θ + 24θ 2ln L = ln 4 + 6 ln θ + 2 ln(1 ? θ ) + 4 ln(1 ? θ ), d ln L 6 2 8 6 ? 28θ + 24 θ 2 = ? ? = = 0, dθ θ 1 ? θ 1 ? 2θ θ (1 ? θ )(1 ? 2θ )=0θ1,2 =7 ± 13 . 2得由于课后答案网 www.61k.com + 13 1 > , 12 2 ? 7 ? 13 . θ= 2 ? αβ ?1 ? β , x > α , F (x,β)= ? x ? 0, x ≤ α. ?所以θ的极大似然估计值为 15.设总体 X 的分布函数为kh7? 2α 2 , x ≥ α; ? 当β=2 时, f ( x ,α ) = Fx1 (x ,α , 2) = ? x3 ? 0, x <α. ?若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com ? β , x ≥ 1; ? 当α=1 时, f ( x , β ) = F ( x ,1, β ) = ? x β +1 ? 0, x < 1. ?1 xw.c其中未知参数β>1,α >0,设 X 1, X2 ,…, Xn 为来自总体 X 的样本 (1) 当α=1 时,求β的矩估计量; (2) 当α=1 时,求β的极大似然估计量; (3) 当β=2 时,求α 的极大似然估计量. 【解】om 课后答案网 www.61k.com 若侵犯了您的版权利益,敬请来信告知!?? ?(1) E ( X ) =∫+∞1β β 1? β dx = x β x 1?β X , X ?1+∞ 1=β β ?1? 令 E ( X ) = X ,于是 β =? 所以 β 的矩估计量 β =da(2) 似然函数w .cnomX . X ?1i =1khL = L( β ) = ∏? n ? n ?( β +1) x ?β f ( xi , β ) = ? ? ∏ i ? i =1 ? 0, ?n i =1? ? , xi > 1, ( i = 1, 2, ?, n); ? 其他.ln L = n ln β ? ( β +1) ∑ ln xi , d ln L n n = ? ∑ ln xi = 0, dβ β i =1 ? 所以 β 的极大似然估计量 β =(3) 似然函数课后答案网 ∑ www.61k.com xii =1nL=∏i =1? 2n α 2 n , xi ≥ α , ( i = 1, 2,? , n); ? n 3 ?? ? f ( xi ,α ) = ? ? ∏ xi ? ? ? i =1 ? ? 0, 其他. ?显然 L = L(α ) ↑,? ? 那么当 α = min{xi } 时, L = L(α ) = max L (α ) ,1≤ i ≤ na> 01≤i ≤ n?∞z?(z)1.28 0.91.645 0.951.960.975【解】 X ~ N ? 3.4,? ?62 ? ,则 Z = X ? 3.4 ~ N (0,1), ? 6/ n n?kh8若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com .33 0.99? ( z) = ∫z1 ? t2 / 2 e dt 2π.c16.从正态总体 X~ N(3.4,62 )中抽取容量为 n 的样本,如果其样本均值位于区间(1.4,5.4) 内的概率不小于 0.95,问 n 至少应取多大?om? 所以 α 的极大似然估计量 α = min{ xi} . 课后答案网 www.61k.com 若侵犯了您的版权利益,敬请来信告知!?? ?于是 Φ ?∴ n≥35.kh17. 设总体 X 的概率密度为da? n? n ? ≥ 0.975 则 3 ≥ 1.96 , ? 3 ?w .c5.4 ? 3.4? ?1.4 ? 3.4 P{1.4 < X < 5.4} = P ? <Z < ? 6/ n ? ? 6/ n ? ? = P ?? n < Z < n ? ? 3 3 ? ? ? ? ? ? ? = Φ ? n ? ? Φ ? ? n ? = 2Φ ? n ? ?1 ≥ 0.95
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
? 3 ? ? 3 ? ? 3 ?omEX =? θ, ? f(x,θ)= ?1 ? θ , ? 0, ?0 < x < 1, 1 ≤ x < 2, 其他.其中 θ是未知参数( 0<θ <1), X1 ,X 2,…, X n 为来自总体 X 的简单随机样本,记 N 为样本值x1 ,x2 ,…,xn 中小于 1 的个数.求: (1) θ的矩估计; (2) θ的最大似然估计. ) 解 (1) 由于课后答案网 www.61k.com ∫ ∫ ∫+∞ ?∞xf ( x; θ )d x = θ xd x +0121(1 -θ ) xd x1 3 3 = θ + (1 ? θ ) = ?θ . 2 2 2 3 3 ? θ = X ,解得 θ = ? X , 2 2 所以参数 θ 的矩估计为令? 3 θ = ?X . 2(2) 似然函数为ni =1取对数,得令所以 θ 的最大似然估计为kh9d ln L(θ ) N n ? N = ? . dθ θ 1?θ d ln L(θ ) N = 0, 得 θ = , dθ n若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com 两边对 θ 求导,得.cln L(θ ) = N lnθ + (n ? N )ln(1 ? θ ),omL(θ ) = ∏ f ( xi ; θ ) = θ N (1 ? θ ) n ? N , 课后答案网 www.61k.com 若侵犯了您的版权利益,敬请来信告知!?? ?? N θ= . nkh课后答案网 www.61k.com .comkh10若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com .com 课后答案网 www.61k.com 若侵犯了您的版权利益,敬请来信告知!?? ?习题八1. 已知某炼铁厂的铁水含碳量在正常情况下服从正态分布 N (4.55,0.1082).现在测了 5 炉铁 水,其含碳量(%)分别为 4.28 4.40 4.42 4.35 4.37 问若标准差不改变,总体平均值有无显著性变化( α =0.05)? 【解】dakh所以拒绝 H0,认为总体平均值有显著性变化. 2. 某种矿砂的 5 个样品中的含镍量(%)经测定为: 3.24 3.26 3.24 3.27 3.25 设含镍量服从正态分布,问在 α =0.01 下能否接收假设:这批矿砂的含镍量为 3.25. 【解】设所以接受 H0,认为这批矿砂的含镍量为 3.25. 3. 在正常状态下,某种牌子的香烟一支平均 1.1 克,若从这种香烟堆中任取 36 支作为样本; 测得样本均值为 1.008(克) ,样本方差 s2=0.1(g2 ).问这堆香烟是否处于正常状态 .已知香烟 (支)的重量(克)近似服从正态分布(取 α =0.05). 【解】设w .c课后答案网 www.61k.com 0 : μ = μ 0 = 3.25; H1 : μ ≠ μ 0 = 3.25. n = 5,α = 0.01,tα / 2 (n ? 1) = t 0.005 (4) = 4.6041 x = 3.252, s = 0.013, x ? μ0 (3.252 ? 3.25) t= = × 5 = 0.344, 0.013 s/ n t < t0.005 (4).omH 0 : μ = μ 0 = 4.55; H1 : μ ≠ μ 0 = 4.55. n = 5, α = 0.05, Z α / 2 = Z 0.025 =1.96, σ = 0.108 x = 4.364, x ? μ0 (4.364 ? 4.55) Z= = × 5 = ? 3.851, 0.108 σ/ n Z > Z0.025.H 0 : μ = μ 0 = 1.1; H1 : μ ≠ μ 0 = 1.1. n = 36, α = 0.05,tα / 2 (n ? 1) = t 0.025 (35) = 2.0301,n = 36, x = 1.008, s 2 = 0.1, x ? μ 0 (1.008 ? 1.1) t= = × 6 = 1.7456, s/ n 0.1 t = 1.7456 < t 0.025(35) = 2.0301.kh所以接受
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
H0,认为这堆香烟(支)的重要(克)正常. 4.某公司宣称由他们生产的某种型号的电池其平均寿命为 21.5 小时, 标准差为 2.9 小时.在实 验室测试了该公司生产的 6 只电池,得到它们的寿命(以小时计)为 19,18,20,22,16, 25, 问这些结果是否表明这种电池的平均寿命比该公司宣称的平均寿命要短?设电池寿命近1若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com .com 课后答案网 www.61k.com 若侵犯了您的版权利益,敬请来信告知!?? ?似地服从正态分布(取 α =0.05). 【解】kh所以接受 H0,认为电池的寿命不比该公司宣称的短. 5.测量某种溶液中的水分, 从它的 10 个测定值得出 x =0.452(%),s =0.037(%).设测定值总体为 正态,μ为总体均值,σ为总体标准差,试在水平 α =0.05 下检验. (1) H0 :μ=0.5(%);H1 :μ<0.5(%).(2) H 0 : σ =0.04(%); H 1′ : σ <0.04(%). ′ 【解】(1)da所以拒绝 H0,接受 H1. (2)H 0 : σ = σ 0 = 0.005; H1 : σ = σ 0 ≠ 0.005. n = 9, α = 0.05, s = 0.008,2 2 2 χα / 2 (8) = χ 0.025(8) = 17.535, χ 1?α / 2 (8) = χ 2 (8) = 2.088, 0.975第二批棉纱样本:n2 =200, y =0.57kg,s 2=0.176kg.kh故应拒绝 H0,不能认为这批导线的电阻标准差仍为 0.005. 7.有两批棉纱,为比较其断裂强度,从中各取一个样本,测试得到: 第一批棉纱样本:n1 =200, x =0.532kg, s 1=0.218kg;da2若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com ( n ?1) s 2 8 × 0.0082 2 χ = = = 20.48, χ 2 > χ0.025 (8). 2 2 σ0 (0.005)2.com所以接受 H0,拒绝 H1. 6.某种导线的电阻服从正态分布 N( μ,0.0052).今从新生产的一批导线中抽取 9 根,测其 电阻,得 s=0.008 欧.对于 α =0.05,能否认为这批导线电阻的标准差仍为 0.005? 【解】w .cχ2 =μ0 = 21.5, n = 6,α = 0.05, z0.05 = 1.65,σ = 2.9, x = 20, x ? μ0 (20 ? 21.5) z= = × 6 = ?1.267, 2.9 σ/ n z > ?z 0.05 = ?1.65.μ0 = 0.5; n = 10, α = 0.05, tα ( n ?1) = t0.05 (9) = 1.8331,课后答案网 www.61k.com σ 02 = (0.04) 2 , n = 10,α = 0.05,χ12 α = χ 0.95 (9) = 3.325, ? x = 0.452, s = 0.037,x = 0.452, s = 0.037, x ? μ0 (0.452 ? 0.5) t= = × 10 = ?4.10241, 0.037 s/ n t < ?t 0.05 (9) = ?1.8331.2 χ 2 > χ0.95 (9).omH 0 : μ ≥ 21.5; H1 : μ < 21.5.( n ?1) s 2 9 × 0.0372 = = 7.7006, 2 σ0 0.042 课后答案网 www.61k.com 若侵犯了您的版权利益,敬请来信告知!?? ?设两强度总体服从正态分布,方差未知但相等,两批强度均值有无显著差异?( α =0.05) 【解】n1 = n2 = 200,α = 0.05, tα / 2 ( n1 + n2 ? 2) = t 0.025(398) ≈ z 0.025 = 1.96,kh【解】所以接受 H0,认为两批强度均值无显著差别. 8.两位化验员 A ,B 对一种矿砂的
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
含铁量各自独立地用同一方法做了 5 次分析,得到样本方 差分别为 0.4322(%2 )与 0.5006(%2).若 A ,B 所得的测定值的总体都是正态分布,其方差分别 为σA2 ,σB2 ,试在水平 α =0.05 下检验方差齐性的假设daw .csw = t= t < t0.025 (398). F=所以接受 H0,拒绝 H1. 9~12. 略2 (n1 ? 1)s12 + (n 2 ? 1)s 2 199 × (0.2182 + 0.1762 ) = = 0.1981, n1 + n2 ? 2 398x?y (0.532 ? 0.57) = = ?1.918; 1 1 1 1 sw + 0.1981× + n1 n2 200 200课后答案网 www.61k.com n1 = n2 = 5, α = 0.05, s12 = 0.4322, s 2 = 0.5006,那么 F0.975 (4, 4) < F < F0.025 (4, 4).omH 0 : μ 1 = μ 2; H1 : μ 1 ≠ μ 2.2 2 2 2 H 0 : σ A = σ B ; H1 : σ A ≠ σ B .Fα / 2 ( n1 ?1, n2 ?1) = F0.025(4, 4) = 9.6, 1 1 F0.975 (4, 4) = = = 0.1042, F0.025(4.4) 9.6 s12 0.4322 = = 0.8634. 2 s2 0.5006kh3若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com .com 课后答案网 www.61k.com 若侵犯了您的版权利益,敬请来信告知!?? ?习题九1? 灯泡厂用 4 种不同的材料制成灯丝,检验灯线材料这一因素对灯泡寿命的影响.若灯泡寿 命服从正态分布,不同材料的灯丝制成的灯泡寿命的方差相同,试根据表中试验结果记录, 在显著性水平 0.05 下检验灯泡寿命是否因灯丝材料不同而有显著差异?w .c1 1600 1580 1460 1510om2 1610 1640 1550 1520试验批号 3 1650 1640 1600 1530 4 1680 1700 1620 1570 5 1700 1750 1640 1600 6 1720 1660 1680 7 1800 1740 8灯丝 材料 水平khdaA1 A2 A3 A41820【解】rr = 4, n = ∑ ni = 26;i =1T..2 =69895900-69700188.46=195711.54, ST = ∑∑ x ? n i =1 j =14 4 2 ij 4SA = ∑i =11 2 T..2 Ti . ? =69744549.2-69700188.46=44360.7, ni n课后答案网 www.61k.com = ST ? S A =151350.8, S A /(r ? 1) 44360.7 / 3 = = 2.15 , S E /(n ? r ) 151350.8 / 22 F0.05 (3, 22) = 3.05 > F. F=故灯丝材料对灯泡寿命无显著影响. 表 9-1-1 方差分析表方差来源 因素影响 误差 总和 平方和 S 44360.7 151350.8 195711.54 自由度 3 22 25 均方和 S 14786.9 6879.59F值2.1573 89 8266 60 4588 78 4877 31 78da68 79 56ⅠⅡkhwⅢ2. 一个年级有三个小班,他们进行了一次数学考试,现从各个班级随机地抽取了一些学生, 记录其成绩如下:41 59 68.c若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com 课后答案网 www.61k.com 若侵犯了您的版权利益,敬请来信告知!?? ?43 80 7393 36 7791 51 85 7462 76 96 8091 71 71 8753 79 15差相等. 【解】r = 3, n = ∑ ni = 40,i =1da3kh3ni2 ST = ∑∑ xij ?i =1 j =11 2 T..2 S A = ∑ Ti . ? =186112.25-185776.9=335.35, n i =1 niSE = ST ? S A =13349.65, F=S A /(r ? 1) 167.7 = = 0.465 S E /(n ? r ) 360.8 F0.05 (2, 37) = 3.23 > F .故各班平均分数无显著差异.w .cr
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
56 试在显著性水平 0.05 下检验各班级的平均分数有无显著差异.设各个总体服从正态分布, 且方T..2 =199462-185776.9=13685.1, n课后答案网 www.61k.com 表 9-2-1 方差分析表平方和 S 335.35 13349.65 13685 自由度 2 37 39 均方和 S 167.68 360.80方差来源 因素影响 误差 总和omF值0.4653. 下面记录了 3 位操作工分别在不同机器上操作 3 天的日产量.操 机 器T... ,Tij ,Ti.. ,T. j. 的计算如表 9-3-1.kh2若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com 取显著性水平α=0.05,试分析操作工之间,机器之间以及两者交互作用有无显著差异? 【解】 由已知 r=4,s =3,t=3.wA3 A415 1817 2016 2218 1517 1616 1718 17.c18 17 18 17A1 A215 1715 1717 1719 1519 1516 1516 1918 22om21 22作工甲乙丙 课后答案网 www.61k.com 若侵犯了您的版权利益,敬请来信告知!?? ?表 9-3-1omTij操 作 工Ti ..乙 丙甲机 器w .cA147 51 48 60 20654 45 51 48 19855 63 54 51 223156 159 153 159 627khdaA3 A4 T. j .r sA2课后答案网 ∑ www.61k.com ∑2 ST = ∑∑∑ xijk ?ti =1 j =1 k =1 r2 i..T...2 = 11065 ?10920.25 = 144.75, rst1 SA = stT...2 T ? = 10923 ?10920.25 = 2.75, rst i =1s2 . j.1 SB = rtT...2 T ? = 10947.42 ?10920.25 = 27.17, rst j =1?1 r s T2 ? S A× B = ? ∑∑ Tij2. ? ... ? ? S A ? SB = 73.50, rst ? ? t i =1 j =1 SE = ST ? S A ? SB ? SA ×B = 41.33.表 9-3-2 得方差分析表方差来源 因素 A(机器) 因素 B(操作工) 交互作用 A×B 误差 总和 平方和 S 2.75 27.17 73.50 4.33 1094.75 自由度 3 2 6 24 均方和 S 0.92 13.58 12.25 1.72 F值FA =053 FB =7.89 FA× B =7.12即机器之间无显著差异,操作之间以及两者的交互作用有显著差异.3若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com 接受假设 H 01 ,拒绝假设 H 02 , H 03 .daF0.05 (3, 24) = 3.01, F0.05 (2, 24) = 3.40, F0.05 (6, 24) = 2.51.w.com 课后答案网 www.61k.com 若侵犯了您的版权利益,敬请来信告知!?? ?om4. 为了解 3 种不同配比的饲料对仔猪生长影响的差异,对3 种不同品种的猪各选 3 头进行试 验,分别测得其 3 个月间体重增加量如下表所示,取显著性水平 α =0.05,试分析不同饲料与 不同品种对猪的生长有无显著影响?假定其体重增长量服从正态分布,且各种配比的方差相 等.体重增长量 因素 A (饲料) 因素 B(品种)【解】由已知 r=s=3,经计算 x =52, x1. =50.66, x2. =53khx3. =52.34, x.1 =52, x.2 =57, x.3 =47,r sST = ∑∑ ( xij ? x ) 2 = 162;i =1 j =1 rS A = s∑ ( xi . ? x )2 = 8.73,i =1 r j =1SB = r ∑ ( x. j ? x ) 2 = 150, SE = ST ? S A ? SB = 3.27.方差来源 饮料作用 品种作用
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
试验误差 总和daw .cA1 A2 A3B1 51 53 52B2 56 57 58B3 45 49 47课后答案网 www.61k.com 表 9-4-1 得方差分析表自由度 2 2 4 平方和 S 8.68 150 3.32 162 均方和 S 4.34 75 0.83F值 5.23 90.36由于 F0.05 (2, 4) = 6.94 > FA , F0.05 (2, 4) < FB . 因而接受假设 H 01 ,拒绝假设 H 02 . 即不同饲料对猪体重增长无显著影响,猪的品种对猪体重增长有显著影响. 5.研究氯乙醇胶在各种硫化系统下的性能(油体膨胀绝对值越小越好)需要考察补强剂(A )、 防老剂(B) 、硫化系统( C )3 个因素(各取 3 个水平) ,根据专业理论经验,交互作用全忽 4)表作 9 次试验及试验结果见下表: 略,根据选用 L9 (3列号 试验号 1 2 3 4 5 1 1 1 1 2 2 2 1 2 3 1 2 3 1 2 3 2 3 4 1 2 3 3 1 结果 7.25 5.48 5.35 5.40 4.424若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com .c表头设计试验om 课后答案网 www.61k.com 若侵犯了您的版权利益,敬请来信告知!?? ?6 7 8 923125.90 4.68 5.90 5.63w .c18.08 15.72 16.21 2.36(2) 给定α=0.05,作方差分析与(1)比较. 【解】(1) 对试验结果进行极差计算,得表 9-5-1. 表 9-5-117.33 15.80 16.88 1.53 19.05 16.51 14.45 4.46 17.30 16.06 16.65 1.24khdaT1 j T2 j T3 j Rjom3 1 3 2 3 2 1 3 3 3 2 1 (1) 试作最优生产条件的直观分析,并对 3 因素排出主次关系.T=50.01由于要求油体膨胀越小越好,所以从表 9-5-1 的极差 Rj 的大小顺序排出因素的主次顺序 为:主→次 B, A, C 最优工艺条件为: A2 B2 C3 .(2) 利用表 9-5-1 的结果及公式 S j =课后答案网 ∑ www.61k.com rrTij2 ?i =1T2 ,得表 9-5-2. PC 33.539表 9-5-2A 1B 20.4124 0.256Sj1.034ST = 5.241 Se =0.128 方差分析 fe表 9-5-2 中第 4 列为空列,因此 Se = S 4 = 0.256 ,其中 f e = 2 ,所以 表如表 9-5-3.sj方差来源fjsj / f jF=sj fj/A B C e1.034 0.412 3.539 0.2562 2 2 20.517 0.206 1.769 0.1284.039由于 F0.05 (2, 2) = 19.00 ,故因素 C 作用较显著,A 次之,B 较次,但由于要求油体膨胀5若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com .609 13.828w.cse feom显著性表 9-5-3 课后答案网 www.61k.com 若侵犯了您的版权利益,敬请来信告知!?? ?om越小越好,所以主次顺序为:BAC,这与前面极差分析的结果是一致的. 6. 某农科站进行早稻品种试验(产量越高越好) ,需考察品种(A) ,施氮 肥 量( B ) ,氮、磷 、 钾肥比例(C ) ,插植规格( D)4 个因素,根据专业理论和经验,交互作用全忽略,早稻试 验方案及结果分析见下表:因素试验号 1 2 3 4 5 6 7 8khA 品种 1(科 6 号) 1 2(科 5 号) 2 1(科 7 号) 1 2(珍珠矮) 2B 施氮肥量 1(20) 2(25) 1 2 1 2 1 2C
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
氮、磷、钾肥比例 1(2∶2∶1) 2(3∶2∶3) 1 2 2 1 2 1D 插植规格 1(5×6) 2(6×6) 2 1 1 2 2 1w .c试验指标 产量 19.0 20.0 21.9 22.3 21.0 21.0 18.0 18.2(1) 试作出最优生产条件的直观分析,并对 4 因素排出主次关系. (2) 给定α =0.05,作方差分析,与(1)比较. , 【解】被考察因素有 4 个:A ,B ,C ,D 每个因素有两个水平,所以选用正交表 L8(27) 进 行极差计算可得表 9-6-1. 表 9-6-1列号 水平 试验号 1 2 3 4 5 6 7 8da课后答案网 www.61k.com 1 1 1 1 2 2 2 2 83.2 78.2 5.0 A 2 1 1 2 2 1 1 2 2 81.0 80.4 0.6 3 1 1 2 2 2 2 1 1 75.2 86.2 11.0 B 4 1 2 1 2 1 2 1 2 79.9 81.5 1.6 C 5 1 2 1 2 2 1 2 1 80.1 81.3 1.2主 →次D 6 1 2 2 1 1 2 2 17 1 2 2 1 2 1 1 2试验结果 19.0 20.0 21.9 22.3 21.0 21.0 18.0 18.2T1j T2j Rj80.5 80.9 0.480.3 81.1 0.8T=161.4从表 9-6-1 的极差 Rj 的大小顺序排出因素的主次为: B, C, A, D 最优方案为: A1 B2 C2 D2 (2) 利用表 9-6-1 的结果及公式 s j =表 9-6-213khA 2B 4C 5D 6da76若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com n 2 T2 ∑ T ? 得表 9-6-2. r i =1 ij P.com 课后答案网 www.61k.com 若侵犯了您的版权利益,敬请来信告知!?? ?sj3.1250.04515.1250.3200.1800.0200.080ST = 18.895表 9-6-2 中第 1,3,7 列为空列,因此 se=s 1+s 3+s7 =18.330, fe=3,所以他列中fjw .csj<se .故将所有次均并入误差,可得 fe seΔ = sT = 18.895, f eΔ = 7.表 9-6-3整理得方差分析表为表 9-6-3.khdaomse =6.110.而在上表中其 fesjfj方差来源sj fj0.045 0.320 0.180 0.020 6.110F=s j seΔ / f j f eΔ显著性A B C D e0.045 0.320 0.180 0.0201 1 1 1 3 70.017 0.119 0.067 0.007eΔ课后答案网 www.61k.com .330 18.895 2.699主 →次由于 F0.05 (1.7) = 5.59 ,故 4 因素的影响均不显著,但依顺序为: B, C, A, D 与(1)中 极差分析结果一致.kh7若侵犯了您的版权利益,敬请来信通知我们! ℡ www.61k.com .com
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
概率论与数理统计试题及答案 概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社
抱歉,获取内容失败请稍后刷新尝试
本文标题:概率论与数理统计课后习题答案-课题:4.1.2频数与频率61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1