一 : 高中数学必修五数列测试题

高二数学单元测试题（数列）

班级________ 学号________ 姓名___________成绩___________

10.已知等比数列{an}满足an?0,n?1,2,?，且a5?a2n?5?22n(n?3)，则当n?1时，

（ ） log??lo2gan??2a1?log2a3?21

一．选择题：本大题共10小题，每小题5分，共50分．

1．数列1111

2,?4,8,?16,?的一个通项公式可能是（ ）

A．(?1)n12n B．(?1)n12n C．(?1)n?112n D．(?1)n?112n

2．在等差数列?a?中，a

n2?2，a3?4,则a10＝( )

A．12

B．14

C．16

D．18

3．如果等差数列?an?中，a3?a4?a5?12，那么a1?a2?...?a7?( ) （A）14 （B）21 （C）28 （D）35 4.设数列{a3n}的前n项和Sn?n，则a4的值为( )

（A） 15 (B) 37 (C) 27 （D）64

5.设等比数列{a的公比q?2，前n项和为SS

n}n，则4a?（ ）

2

A．2 B．4

C．152

D．172

6.设Sn为等比数列?an?的前n项和，已知3S3?a4?2，3S2?a3?2，则公比q?（（A）3 （B）4 （C）5 （D）6 7. 已知a?

1?2

,b?

1?2

,则a,b的等差中项为（ ）

A． B．2

C

D

．

2

8．已知{an}是等比数列，a2?2，a5?

1

4

，则a1a2?a2a3???anan?1?（ ） A．323(1?2?n) B．16(1?4?n) C．16(1?2?n) D．32

3

(1?4?n) 9.若数列?

an

n?的通项公式是an?(?1)(3n?2)，则a1?a2?????a20? ( )

（A）30 （B）29

（C）-30 （D）-29

1

A. n(2n?1) B. (n?1)2 C. n2 D. (n?1)2

二11.已知数列?an?满足: a3?5,an?1?2an?1 (n∈N*)，则a1? ________.

12.已知?an?

为等比数列,a4?a7?2,a5a6??8,则a1?a10?________.

13.设等差数列?an?的公差d不为0，a1?9d．若ak是a1与a2k的等比中项，则k?______. 14. 已知数列{an}的首项a2an

1?2，an?1?

a，n?1,2,3,…,则 a2012? ________. n?2

三．解答题：本大题共6小题，满分80分．

15．（12分）一个等比数列?an?中，a1?a4?28，a2?a3?12，求这个数列的通项公式.

16．（12分）有四个数：前三个成等差数列，后三个成等比数列。（www.61k.com)首末两数和为16，中间两数和为12.求这四个数.

2

）

高中数学必修5数列 高中数学必修五数列测试题

17.（14分）等差数列?an?满足a5?14，a7?20，数列?bn?的前n项和为Sn，且bn?2?2Sn. (Ⅰ) 求数列?an?的通项公式； (Ⅱ) 证明数列?bn?是等比数列.

18.（14分）已知等差数列?an?满足：a2?5，a5?a7?26，数列?an?的前n项和为Sn． （Ⅰ）求an及Sn；

（Ⅱ）设?bn?an?是首项为1，公比为3的等比数列，求数列?bn?的前n项和Tn.

19. （14分）设{an}是公比为正数的等比数列，a1?2，a3?a2?4. （Ⅰ）求{an}的通项公式； （Ⅱ）求数列{(2n?1)an}的前n项和Sn.

3

20．（14分）已知数列?a?S

?

n?的前n项和为Sn，点?n,n

?n

??

在直线y?12x?112上.

（Ⅰ）求数列?an?的通项公式； （Ⅱ）设b3n?

(2a11)，求数列?b，并求使不等式Tk

n?的前n项和为Tnn?20

对一切

n?11)(2an?1?n?N*都成立的最大正整数k的值．

4

高中数学必修5数列 高中数学必修五数列测试题

高二数学单元测试题（数列）

班级________ 学号________ 姓名___________成绩___________

10.已知等比数列{an}满足an?0,n?1,2,?，且a5?a2n?5?22n(n?3)，则当n?1时，

（ ）C log??lo2gan??2a1?log2a3?21

一．选择题：本大题共10小题，每小题5分，共50分．

1．数列1111

2,?4,8,?16,?的一个通项公式可能是（ ）D

A．(?1)n12n B．(?1)n12n C．(?1)n?112n D．(?1)n?112n

2．在等差数列?a中，a

n?2?2，a3?4,则a10＝( ) D

A．12

B．14

C．16

D．18

3．如果等差数列?an?中，a3?a4?a5?12，那么a1?a2?...?a7?( ) C （A）14 （B）21 （C）28 （D）35 4.设数列{an}的前n项和Sn?n3，则a4的值为( ) 答案：B （A） 15 (B) 37 (C) 27 （D）64

5.设等比数列{a}的公比q?2，前n项和为SS

4nn，则a?（ ）C

2

A．2 B．4

C．15

D．1722

6.设Sn为等比数列?an?的前n项和，已知3S3?a4?2，3S2?a3?2，则公比q?（ （A）3 （B）4 （C）5 （D）6 7. 已知a?

1?2

,b?

1?2

,则a,b的等差中项为（ ）A

A． B．2

C

D

．

2

8．已知{a}是等比数列，a1

n2?2，a5?4

，则a1a2?a2a3???anan?1?（ ）D

A．323(1?2?n) B．16(1?4?n) C．16(1?2?n) D．32

3

(1?4?n) 9.若数列?

an

n?的通项公式是an?(?1)(3n?2)，则a1?a2?????a20? ( ) A

（A）30 （B）29

（C）-30 （D）-29

5

B

A. n(2n?1) B. (n?1)2 C. n2 D. (n?1)2

二11.已知数列?an?满足: a3?5,an?1?2an?1 (n∈N*)，则a1? ________.2

12.已知?an?

为等比数列,a4?a7?2,a5a6??8,则a1?a10?________. -7

13.设等差数列?an?的公差d不为0，a1?9d．若ak是a1与a2k的等比中项，则k?______.4 14. 已知数列{a2an

n}的首项a1?2，an?1?

a，n?1,2,3,…,则 a12012? ________.

n?2

1006三．解答题：本大题共6小题，满分80分．

15．（12分）一个等比数列?an?中，a1?a4?28，a2?a3?12，求这个数列的通项公式。（www.61k.com]

解：???a?a3

11q?28

?q?3或1?a2

，（3分） 两式相除得， …………6分 1q?a1q?12

3代入a1?a4?28，可求得a1?1或27， …………9分

n?4

?an?1或a???1?

n?3n?3?

?

…………12分

16．（12分）有四个数：前三个成等差数列，后三个成等比数列。首末两数和为16，中间两数和为12.求这四个数.

解：设此四数为：x，y，12-y，16-x。所以2y=x+12-y且（12-y）2

= y（16-x）. ……6分 把x=3y-12代入，得y= 4或9.解得四数为15，9，3，1或0，4，8，16 . …………12分

6

）

高中数学必修5数列 高中数学必修五数列测试题

17.（14分）等差数列?an?满足a5?14，a7?20，数列?bn?的前n项和为Sn，且bn?2?2Sn. (Ⅰ) 求数列?an?的通项公式； (Ⅱ) 证明数列?bn?是等比数列.

(Ⅰ) 解：数列?a1

n?为等差数列，公差d?2

(a7－a5)?3 ,a1?2,所以an?3n?1. …6分

(Ⅱ) 由bn?2－2Sn， 当n?2时，有bn?1?2－2Sn?1，可得

b?bb1

nn?1??2(Sn?Sn?1)??2bn.即nb＝. 所以?bn?是等比数列. …………14分

n－13

18.（14分）已知等差数列?an?满足：a2?5，a5?a7?26，数列?an?的前n项和为Sn． （Ⅰ）求an及Sn；

（Ⅱ）设?bn?an?是首项为1，公比为3的等比数列，求数列?bn?的前n项和Tn. 解：（Ⅰ）设等差数列?an?的公差为d，因为a3?7，a5?a7?26，所以

??

a1?d?5

，( 2分) 解得?2aa1?3,d?2， …………4分 1?10d?26

所以an(n-1)

n?3?（2n?1)=2n+1；( 6分) Sn=3n+

2

?2=n2+2n. …………8分 （Ⅱ）由已知得bn?1

n?an?3

，由（Ⅰ）知abn?1

n?2n+1，所以 n?an?3

， …………11分

T=S3n?1

)?n2

?2n?3n?1

nn?(1?3?????2

. …………14分 19. （14分）设{an}是公比为正数的等比数列，a1?2，a3?a2?4. （Ⅰ）求{an}的通项公式；

（Ⅱ）求数列{(2n?1)an}的前n项和Sn.

解：（I）设q为等比数列{an}的公比，则由a1?2,a3?a2?4得2q2?2q?4，…………2分

即q2

?q?2?0，解得q?2或q??1（舍去），因此q?2. …………4分 所以{an}的通项为an?2?2n?1?2n(n?N*). …………6分

7

（II）T3n?3?2?5?22?7?2???(2n?1)?2n …………7分

2Tn?

3?22?5?23???(2n?1)?2n?(2n?1)?2n?1 …………8分

?Tnn?3?2?2（22?23???2）-(2n?1)?2n?1 …………10分

?6?2?4(1?2n?1)

?2

?(2n?1)2n?1??（2n?1）?2n?11?2 …………12分

∴ Sn?（2n?1）?2n?1+2. …………14分

20．（14分）已知数列?a?S

?

n?的前n项和为Sn，点??n,n

n

??

在直线y?12x?112上.

（Ⅰ）求数列?an?的通项公式； （Ⅱ）设b3n?

(2a?11)(2a，求数列?b?的前n项和为Tk

nn，并求使不等式Tn?对一切

nn?1?11)20

n?N*都成立的最大正整数k的值．

解：（Ⅰ）由题意，得Sn?111111

2n?2,即S2nn?2n?2

n. …………2分

故当n≥2时，aS?111??111?

n?n?Sn?1???2n2?2n?????2(n?1)2?2(n?1)??

?n?5. …………5分

当n=1时，a1?S1?6?1?5, 所以 an?n?5(n?N*). …………6分 （Ⅱ）b3(2aa?3n?1)?3?n?

2?1?2n?1?1?

2n?1??

. …………8分 n?11)(2n?1?11)(2n?1)(2所以Tb3??

1??1

1?

?1

1

??

3?

1

?

3n

n?1?b2???bn?2????1?3?????3?5???????2n?1?2n?1?????2??1?2n?1??

?

2n?1.…10分 由于Tn?1?Tn?3（

n?12n?3?n2n?1）?3(2n?3)(2n?1)

?0，因此Tn单调递增， …………12分 故(Tn)min?1.令1?k

20

，得k?20，所以kmax?19. …………14分

8

二 : 高一数学必修1期末测试题

高一数学必修1期末测试题

考试时间：90分钟

试卷满分：100分

一、选择题：本大题共14小题，每小题4分，共56分．在每小题的4个选项中，只有一项是符合题目要求的．

1．设全集U＝R，A＝{x|x＞0}，B＝{x|x＞1}，则A∩UB＝( )． A．{x|0≤x＜1}

B．{x|0＜x≤1}

C．{x|x＜0}

D．{x|x＞1}

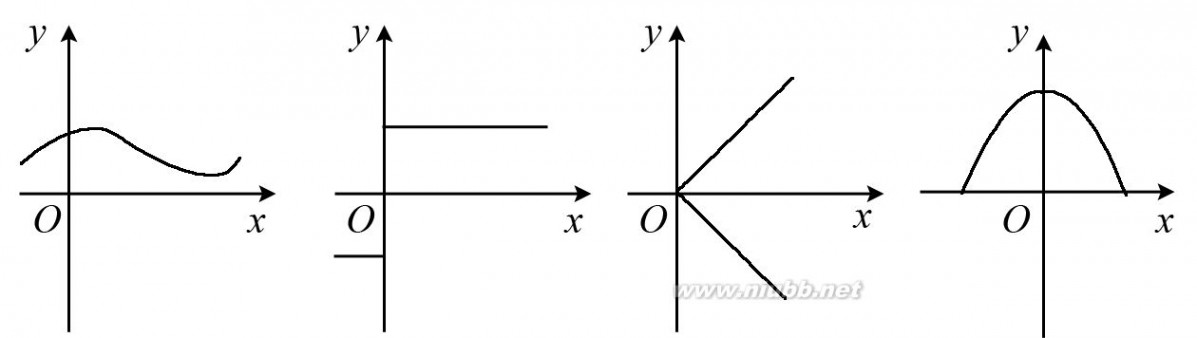
2．下列四个图形中，不是以x为自变量的函数的图象是( )． ．．

A B C D 3．已知函数 f(x)＝x2＋1，那么f(a＋1)的值为( )． A．a2＋a＋2

B．a2＋1

C．a2＋2a＋2

D．a2＋2a＋1

4．下列等式成立的是( )． A．log2(8－4)＝log2 8－log2 4 C．log2 2＝3log2 2

3

B．

loglog

22

84

＝log

8

2

4

D．log2(8＋4)＝log2 8＋log2 4

5．下列四组函数中，表示同一函数的是( )． A．f(x)＝|x|，g(x)＝x2 B．f(x)＝lg x2，g(x)＝2lg x C．f(x)＝

x－1x－1

2

，g(x)＝x＋1

D．f(x)＝x＋1·x－1，g(x)＝x2－1 6．幂函数y＝xα(α是常数)的图象( ). A．一定经过点(0，0) C．一定经过点(－1，1)

B．一定经过点(1，1) D．一定经过点(1，－1)

第 1 页 共 6 页

高中数学必修一测试题 高一数学必修1期末测试题

7．国内快递重量在1 000克以内的包裹邮资标准如下表：

如果某人从北京快递900克的包裹到距北京1 300 km的某地，他应付的邮资是( ).

A．5.00元 B．6.00元 C．7.00元 D．8.00元

8．方程2x＝2－x的根所在区间是( ).

A．(－1，0)

9．若 bB．(2，3) C．(1，2) D．(0，1) ?1?log2 a＜0，???2?＞1，则( ).

B．a＞1，b＜0 D．0＜a＜1，b＜0 A．a＞1，b＞0 C．0＜a＜1，b＞0

10．函数y＝－4x的值域是( ).

A．[0，＋∞) B．[0，4] C．[0，4) D．(0，4)

11．下列函数f(x)中，满足“对任意x1，x2∈(0，＋∞)，当x1＜x2时，都有f(x1)＞f(x2)的是( ).

A．f(x)＝1

x

B．f(x)＝(x－1)2 D．f(x)＝ln(x＋1) C ．f(x)＝ex

12．奇函数f(x)在(－∞，0)上单调递增，若f(－1)＝0，则不等式f(x)＜0的解集是

( ).

A．(－∞，－1)∪(0，1)

C．(－1，0)∪(0，1)

13．已知函数f(x)＝?

A．－2 ?log2 B．(－∞，－1)∪(1，＋∞) D．(－1，0)∪(1，＋∞) x，x＞00?f(x＋3)，x≤ ，则f(－10)的值是( ). B．－1

x C．0 D．1 14．已知x0是函数f(x)＝2＋

有( ).

A．f(x1)＜0，f(x2)＜0 11－x的一个零点．若x1∈(1，x0)，x2∈(x0，＋∞)，则 B．f(x1)＜0，f(x2)＞0

第 2 页 共 6 页

高中数学必修一测试题 高一数学必修1期末测试题

C．f(x1)＞0，f(x2)＜0 D．f(x1)＞0，f(x2)＞0

二、填空题：本大题共4小题，每小题4分，共16分．将答案填在题中横线上．

15．A＝{x|－2≤x≤5}，B＝{x|x＞a}，若A?B，则a．

16．若f(x)＝(a－2)x＋(a－1)x＋3是偶函数，则函数f(x)的增区间是 ．

17．函数y＝log2x－2的定义域是．

?1?

?4?x－82218．求满足??＞4－2x的x．

三、解答题：本大题共3小题，共28分．解答应写出文字说明、证明过程或演算步骤．

19．(8分) 已知函数f(x)＝lg(3＋x)＋lg(3－x)．

(1)求函数f(x)的定义域；

(2)判断函数f(x)的奇偶性，并说明理由．

第 3 页 共 6 页

高中数学必修一测试题 高一数学必修1期末测试题

20．(10分)已知函数f(x)＝2|x＋1|＋ax(x∈R)．

(1)证明：当 a＞2时，f(x)在 R上是增函数．

(2)若函数f(x)存在两个零点，求a的取值范围．

21．(10分)某租赁公司拥有汽车100辆．当每辆车的月租金为3 000元时，可全部租出．当每辆车的月租金每增加50元时，未租出的车将会增加一辆．租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元．

(1)当每辆车的月租金定为3 600元时，能租出多少辆车？

(2)当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？

第 4 页 共 6 页

高中数学必修一测试题 高一数学必修1期末测试题

参考答案

一、选择题

1．B 解析：

2．C

3．C

4．C

5．A

6．B

7．C

8．D

9．D

解析：由log2 a＜0，得

10．C

x解析：∵ 4x＞0，∴0≤16－ 4x＜16，∴－4∈[0，4)． UB＝{x|x≤1}，因此A∩UB＝{x|0＜x≤1}． ?1?0＜a＜1，由???2?b＞1，得b＜0，所以选D项．

11．A

解析：依题意可得函数应在(0，＋∞)上单调递减，故由选项可得A正确．

12．A

13．D

14．B

解析：当x＝x1从1的右侧足够接近1时，

f(x1)＜0；当x＝x2足够大时，

选项是B．

二、填空题

15．参考答案：(－∞，－2)．

16．参考答案：(－∞，0)．

第 5 页 共 6 页 11－x11－x是一个绝对值很大的负数，从而保证 可以是一个接近0的负数，从而保证f(x2)＞0．故正确

高中数学必修一测试题 高一数学必修1期末测试题

17．参考答案：[4，＋∞)．

18．参考答案：(－8，＋∞)．

三、解答题

19．参考答案：(1)由??3＋x＞0

?3－x＞0，得－3＜x＜3，

∴ 函数f(x)的定义域为(－3，3)．

(2)函数f(x)是偶函数，理由如下：

由(1)知，函数f(x)的定义域关于原点对称，

且f(－x)＝lg(3－x)＋lg(3＋x)＝f(x)，

∴ 函数f(x)为偶函数．

20．参考答案：(1)证明：化简f(x)＝?

因为a＞2，

所以，y1＝(a＋2)x＋2 (x≥－1)是增函数，且y1≥f(－1)＝－a；

另外，y2＝(a－2)x－2 (x＜－1)也是增函数，且y2＜f(－1)＝－a．

所以，当a＞2时，函数f(x)在R上是增函数．

(2)若函数f(x)存在两个零点，则函数f(x)在R上不单调，且点(－1，－a)在x轴下方，所以a的取值应满足??(a＋2)(a－2)＜0

?－a＜0 －1?(a＋2)x＋2，x≥?(a－2)x－2，x＜－1 解得a的取值范围是(0，2)．

3 600－3 000

5021．参考答案：(1)当每辆车的月租金定为3 600元时，未租出的车辆数为

＝12，所以这时租出了100－12＝88辆车．

(2)设每辆车的月租金定为x元，则租赁公司的月收益为

f(x)＝?100－

??1x－3 000?x－3 000×50＝－(x－4 050)2＋307 050． ?(x－150)－505050?

所以，当x＝4 050 时，f(x)最大，其最大值为f(4 050)＝307 050．

当每辆车的月租金定为4 050元时，月收益最大，其值为307 050元．

第 6 页 共 6 页

三 : 高中数学必修4测试题及答案

高中数学必修4测试试题

第Ⅰ卷（选择题 共60分）

一、选择题：本答题共12小题，每小题5分，共60分。（www.61k.com］在每小题给出的四个选项中，只有一项是符合题目要求的。

4?5?2?5?1.-300°化为弧度是 （ ） A.? B.? C．? D．? 3336

2.为得到函数y?sin(2x?)的图象，只需将函数y?sin(2x?)的图像（ ） 36

??A．向左平移个单位长度 B．向右平移个单位长度 44

??C．向左平移个单位长度 D．向右平移个单位长度 22

3.函数y?sin(2x?)图像的对称轴方程可能是（ ） 3

????A．x?? B．x?? C．x? D．x?612612

x4．若实数x满足㏒2=2+sin?,则 x?1?x?10?( ) ???

A. 2x-9 B. 9-2x C.11 D. 9

y5.点A(x,y)是300°角终边上异于原点的一点，则值为( ) x

A.3 B. - 3 C. D. - 33

6. 函数y?sin(2x?)的单调递增区间是（ ） 3?

?5???A．?k??,k?? k?Z ?1212???5???B．?2k??,2k??? 1212??k?Z ?5???C．?k??,k??? k?Z 66??

7．sin(－

?5???D．?2k??,2k??? k?Z 66??31011π)的值等于（ ） A． B．－ C． D．－ 22223

8．在△ABC中，若sin(A?B?C)?sin(A?B?C)，则△ABC必是（ ）

A．等腰三角形 C．等腰或直角三角形 B．直角三角形 D．等腰直角三角

9.函数y?sinx?sinx的值域是 （ ）

高中数学必修四答案 高中数学必修4测试题及答案

A．0 B．??1,1? C．?0,1? D．??2,0?

10.函数y?sinx?sinx的值域是 （ ）

A．??1,1? B．?0,2? C．??2,2? D．??2,0?

11.函数y?sinx?tanx的奇偶性是（ ）

A．奇函数 B．偶函数 C．既奇又偶函数 D．非奇非偶函数

12.比较大小，正确的是（ ）

A．sin(?5)?sin3?sin5

第Ⅱ卷（非选择题 共90分）

二、填空题（每小题6分，共30分）

13.终边在坐标轴上的角的集合为_________.

14.时针走过1小时50分钟，则分钟转过的角度是______.

15. 已知扇形的周长等于它所在圆的周长的一半，则这个扇形的圆心角是C．sin3?sin(?5)?sin5 B．sin(?5)?sin3?sin5 D． sin3?sin(?5)?sin5 ________________.

16.已知角?的终边经过点P(-5,12),则sin?+2cos?的值为______.

17.一个扇形的周长是6厘米，该扇形的中心角是1弧度，该扇形的面积是________________.

三、解答题：本大题共4小题，共60分。（www.61k.com］解答应写出文字说明及演算步骤.。

18.已知sin?是方程5x2?7x?6?0的根，求

高中数学必修四答案 高中数学必修4测试题及答案

3???3?sin???????sin??????tan2(2???)22

??????cos?????cos?????cot(???)?2??2?

的值.(14分)

19.求函数y=-cos2x+3cosx+5的最大值及最小值，并写出x取何值时 4

函数有最大值和最小值。［www.61k.com) (15分)

20.已知函数y=Asin(?x??) （A＞0,? ＞0,??）的最小正周期为2?， 3

最小值为-2，图像过（

21.用图像解不等式。(16分)

①sinx?

5?，0），求该函数的解析式。 (15分) 931 ②cos2x? 22

参考答案

一、选择题（每小题5分，共60分）

1----6、BBDCBA 7----12、CCDCAB

二、填空题（每小题6分，共30分）

n?13.??|??,n?Z? 14. -660° 15.(??2)rad 2

216. 17. 2 13

三、解答题（共60分）

18．（本小题14分）

解：由sin?是方程5x2?7x?6?0的根，可得

3 sin?=? 或sin?=2（舍） -----------3分 5

3?3??sin(??)?sin(??)?(?tan?)2

原式= sin??(?sin?)?(?cot?)

cos??(?cos?)?tan2? = sin??(?sin?)?(?cot?)

高中数学必修四答案 高中数学必修4测试题及答案

=-tan? ------------10分

3 由sin?=?可知?是第三象限或者第四象限角。［www.61k.com] 5

33 所以tan?=或? 44

3 即所求式子的值为 ? -------------14分 4

19．（本小题15分）

解：令t=cosx, 则t?[?1,1] -------------2分 所以函数解析式可化为：y??t2?t?

=?(t?5 432)?2 ------------6分 2

因为t?[?1,1]， 所以由二次函数的图像可知：

当t?3?11? 时，函数有最大值为2，此时x?2k??或2k??，k?Z 266

1 当t=-1时，函数有最小值为?，此时x?2k???，k?Z 4

------------15分

20.（本小题15分）

2?2?2? 解：? ， ?T??即??3 ------------3分 3?3

又?函数的最小值为?2， ?A?2 ------------5分 所以函数解析式可写为y?2sin(3x??) 又因为函数图像过点（

所以有：2sin(3?5?，0）， 95?5? ---------9分 ??)?0 解得??k??93

?2? ------------13分 ????,???或?33

?2? 所以，函数解析式为：y?2sin(3x?)或y?2sin(3x?) -------------15分 33

21.（每小题8分，共16分）

（1）、图略 ------------3分

?5??? 由图可知：不等式的解集为?2k??,2k???,k?Z ----------8分 66??

（2）、图略 -------------11分

高中数学必修四答案 高中数学必修4测试题及答案

?11??? 由图可知：不等式的解集为?k??,k??,k?Z ---------16分 ?1212??

《试卷编写说明》

本试卷三角函数的大框架下，主要借助正弦函数和余弦函数这两种模型，从函数的定义域、值域、单调性、奇偶性，特别是新学习内容-----周期性出发，以这五个方面为主要内容而命制。（www.61k.com）

试卷中首先突出了弧度制的应用，函数状态下，弧度制的应用显然多于角度制，所以对这一学生较难接受的新概念，要在应用中体现其重要性。其次，重基础，试卷加强了对知识形成过程的重视及拓宽。优适当加强试题的灵活性。第三，对数形结合的数学思想试题也比较突出。第21题用单位圆可以做，用函数图像也可以做。第四，体现了数学模型之间的互相转化。反映出普遍联系的客观规律。

四 : 成都49中2014级高一上期9月必修1质量检测

成都49中2014级高一上期9月质量检测

数 学

一、选择题：（每小题5分，共60分）

1．集合{x?N?|x?5}的用列举法表示为--------------------------（ ）

A．{0，1，2，3，4} B.{1，2，3，4}

C.{0，1，2，3，4，5} D.{1，2，3，4，5}

2.

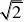
若A?x|0?x?

A．?x|x?0? ?,B??x|1?x?2?，则A?B? -------------- ( ) B．?x|x?2? C

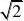
．0?x?? D．?x|0?x?2?

3.在下列四组函数中，f（x）与g（x）表示同一函数的是----------------（ ）

A．y?1,y?x xB．y?x?1?x?1,y?x2?1

C．y?x,y?x3

4．函数f(x)??x?D．y?|x|,y?(x)2 x?3?1的定义域是-------------------------（ ）

A [1,??) B [?3,??) C [?3,1] D (??,1]?[?3,??)

?x?1,x?015.已知函数f(x)??，则f[f()]?（ ） 2?x?1,x?0

A 1133 B ? C D ? 2222

6.若?1,a,??0,a,a?b，则a?b的值为------------------------ ( )

A．0 B．1 C．?1 D．1或?1

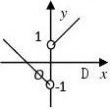
7.函数y?

??b?a??2?x?x

的图象是

---------------------------------------（ ）

B?y0?y?2。8.设A?x0?x?6，从A到B的对应法则f不是映射的是（ ） ????

11x B．f:x???y?x 32

11?y?x D．f:x???y?x C．f:x??46?y?A．f:x??

9.已知集合A?{x|1?x?2},B?{x|x?a}，若A?B??，则实数a的集合为（ ）．

A {a|a?2} B {a|a?1} C {a|a?1} D {a|1?a?2}

10.若f(x?1)的定义域为[1，2]，则f(x?2)的定义域为--------------------（ ）

A．[0，1] B．[2，3] C．[－2，－1] D．无法确定

11、设全集U={1,2,3,4,5,6,7}，A={2,4,5,7}，B={3,4,5}，定义A*B={x∈U|x?A或x?B}，则A*B等于--------------------------------------------------------- ( )

A、{1,6} B、{4,5} C、{1,2,3,6,7} D、{2,3,4,5,7}

12、已知集合A?xy??2x?x2,B?yy?a?2x?x2，若A?B?A，则a的取值范围是--------------------------------------------------------（ ）

A、[2,??) B、 [?6,??) C、 [?6,2? D、(??,?6)?[2,??)

二、填空题（每小题4分，共16分） ????

?,则A?(B?C)= . 13. 已知A=?1,2,3,4,5,6,7,8,9?,B=?1,2,3?,C=?3,4,5,6

14. 已知x+bx+c<0的解集是{x|1<x<3}，则b+c等于_________. 2

?x2＋2(x?2)，15.设函数f（x）＝? 若f（x0）＝8，则x0＝2x(x?2)，?

16. 对于函数f(x)?1(x?0)定义域中任意x1,x2(x1?x2)有如下结论： x

①f(x1?x2)?f(x1)?f(x2)； ②f(x1x2)?f(x1)f(x2) ③x?xf(x1)?f(x2)f(x1)?f(x2)?0； ④f(12)?。 22x1?x2

上述结论中正确结论的序号是 。

本文标题：高中数学必修一测试题-高中数学必修五数列测试题
本文地址： http://www.61k.com/1143042.html