一 : 集合定义1

集合的定义 集合定义1

集合的定义 集合定义1

集合的定义 集合定义1

集合的定义 集合定义1

集合的定义 集合定义1

集合的定义 集合定义1

集合的定义 集合定义1

集合的定义 集合定义1

二 : 集合的定义

集合的定义 集合的定义

集合的定义 集合的定义

集合的定义 集合的定义

集合的定义 集合的定义

集合的定义 集合的定义

集合的定义 集合的定义

集合的定义 集合的定义

集合的定义 集合的定义

集合的定义 集合的定义

集合的定义 集合的定义

集合的定义 集合的定义

集合的定义 集合的定义

集合的定义 集合的定义

集合的定义 集合的定义

集合的定义 集合的定义

集合的定义 集合的定义

集合的定义 集合的定义

集合的定义 集合的定义

集合的定义 集合的定义

集合的定义 集合的定义

集合的定义 集合的定义

集合的定义 集合的定义

集合的定义 集合的定义

集合的定义 集合的定义

集合的定义 集合的定义

集合的定义 集合的定义

集合的定义 集合的定义

三 : 集合定义1

集合
?集合 ?元素 ?集合的性质

复习回顾
我们初中在一些数学概念中用过的 “集合”这个词， （1）不等式x-3>2解的集合

（2）平面内到一个定点的距离等 于定长的点的集合（即圆）

引例：
（1）城阳职专高一年级学生的全体 （2）方程x2=4的所有实数根 （3）所有的平行四边形 （4）平面上到一条线段的两个端点距离相等的点的全体 例（1）中我们把城阳职专高一年级的每一个学生作为一个 确定的对象，这些对象的全体就构成一个集合；例（2）中， 把方程x2=4的每一个实数根作为一个确定的对象，这些对象 的全体也构成一个集合。同样地，例（3） （4）中的对象的 全体也分别构成一个集合

定义：
一般地，把一些能够确定的对象看成一个整 体，就说这个整体是由这些对象的全体构成 的集合（简称为集）。构成集合的每个对象 都叫做集合的元素。
引例中的四个集合中的元素分别是什么？幻灯 片3

（1）城阳职专高一年级的每一个学生 （2）2，-2 （3）每一个平行四边形 （4）这条线段的垂直平分线
练习P3 1

集合的性质
（1）确定性：作为集合的元素，必须是完全 确定的。这就是说，不能完全确定的对象，不能 构成集合。例如，高一(1)班高个子同学的全体， 就不能构成集合。这是由于没有规定多高才算是 高个子，因而“高个子同学”不能确定。 （2）互异性：一个给定集合中的元素，是 互不相同的。也就是说，集合中的元素不能重复 出现。
练习P3 3

集合表示方法：大写英文字母A,B,C…

元素表示方法：小写英文字母a,b,c?
若a是集合A的元素，就说a属于集合A，记作a∈A若a不是 集合A的元素，就说a不属于集合A，记作a?A
含有有限个元素的集合叫做有限集，含有无限个 元素的集合叫做无限集。 想一想：引例中四个集合中，哪些是有限集？哪 些是无限集？幻灯片 3

常用的数集及其记法
? 非负整数集（或自然数集）：全体非负整数 的集合，记作N; ? 正整数集：非负整数集内排除0的集，记作N* 或N+; ? 整数集：全体整数的集合，记作Z; ? 有理数集：全体有理数的集合，记作Q; ? 实数集：全体实数的集合，记作R. 特别的，我们把不含任何元素的集合叫做空集， 记作?。例如，由平方等于-1的所有实数组成的集 合就是空集。

例题讲解：
用符号∈或?填空 （1）2 ___N, （2）2 ___Z, （3）2 ___Q, （4）2 ___R,
练习P3 2

-3 ___N, 0.5 ___N, 3 ___N -3 ___Z, 0.5 ___Z,
3

___Z

-3 ___Q, 0.5 ___Q, 3 ___Q -3 ___R, 0.5 ___R,
3

___R

总结：

?集合元素 ?集合的性质 ?常见的数集
作业： 练习册P2 1,2

四 : 集合的定义

知识点
集 合
1. 正整数1, 2, 3, ?? ; 2. 中国古典四大名著; 3. 高一10班的全体学生; 4. 我校篮球队的全体队员; 5. 到线段两端距离相等的点.

1.集合的概念:

一般地，指定的某些对象的全体 称为集合，简称“集”.
集合中每个对象叫做这个集合的 元素.

练习1.下列指定的对象，能构成一个集合 ( B ) 的是 ①很小的数 ②不超过 30的非负实数 ③直角坐标平面的横坐标与纵坐标相等的点 ④?的近似值 ⑤高一年级优秀的学生 ⑥所有无理数 ⑦大于2的整数 ⑧正三角形全体 A. ②③④⑥⑦⑧ C. ②③⑥⑦ B. ②③⑥⑦⑧ D. ②③⑤⑥⑦⑧

练习1.下列指定的对象，能构成一个集合 ( B ) 的是 ①很小的数 ②不超过 30的非负实数 ③直角坐标平面的横坐标与纵坐标相等的点 ④?的近似值 ⑤高一年级优秀的学生 ⑥所有无理数 ⑦大于2的整数 ⑧正三角形全体 A. ②③④⑥⑦⑧ C. ②③⑥⑦ B. ②③⑥⑦⑧ D. ②③⑤⑥⑦⑧

2.集合的表示: 集合常用大写字母表示，元素常用小 写字母表示.

2.集合的表示: 集合常用大写字母表示，元素常用小 写字母表示. 3.集合与元素的关系: 如果a是集合A的元素，就说a属于集 合A，记作a∈A. 如果a不是集合A的元素，就说a不属 于集合A，记作a?A. 例如：A表示方程x2＝1的解. 2?A，1∈A.

4.集合元素的性质: ⑴确定性: 集合中的元素必须是确定的. 如: x∈A与x?A必居其一. ⑵互异性: 集合的元素必须是互异不相同 的. 如:方程 x2－?x＋?＝0的解集为{1} 而非{1，1}. ⑶无序性: 集合中的元素是无先后顺序的. 如:{1，2}，{2，1}为同一集合.

4.集合元素的性质: ⑴确定性: 集合中的元素必须是确定的. 如: x∈A与x?A必居其一. ⑵互异性: 集合的元素必须是互异不相同 的. 如:方程 x2－?x＋?＝0的解集为{1} 而非{1，1}. ⑶无序性: 集合中的元素是无先后顺序的. 如:{1，2}，{2，1}为同一集合.
?那么{(1，2)}，{(2，1)}是否为同一集合?

5.集合的表示方法: 描述法、列举法、图表法

5.集合的表示方法: 描述法、列举法、图表法

问题1：用集合表示 ①x2－3＝0的解集; ②所有大于0小于10的奇数; ③不等式2x－1＞3的解.

6.集合的分类:

有限集、无限集 问题2：我们看这样一个集合： { x |x2＋x＋1＝0}，它有什么特征？

6.集合的分类:

有限集、无限集 问题2：我们看这样一个集合： { x |x2＋x＋1＝0}，它有什么特征？
?显然这个集合没有元素.我们把这样的

集合叫做空集，记作?. 练习2：⑴ 0 ⑵{0} ? (填∈或?) ? (填＝或≠)

6.集合的分类:

有限集、无限集 问题2：我们看这样一个集合： { x |x2＋x＋1＝0}，它有什么特征？
?显然这个集合没有元素.我们把这样的

集合叫做空集，

记作?. ? ? (填∈或?) 练习2：⑴ 0 ⑵ { 0 } ≠ ? (填＝或≠)

7.重要的数集:
? N：自然数集(含0)

? N+：正整数集(不含0)
? Z：整数集

? Q：有理数集
? R：实数集

例题
例1若x∈R，则数集{1，x，x2}中元素x

应满足什么条件.

例题
例1若x∈R，则数集——文章窝——{1，x，x2}中元素x

应满足什么条件. 解：∵x≠1且x2≠1且x2≠x，

例题
例1若x∈R，则数集{1，x，x2}中元素x

应满足什么条件. 解：∵x≠1且x2≠1且x2≠x，
∴ x≠1且x≠－1且x≠0.

例2设x∈R，y∈R，观察下面四个集合 A＝{ y＝x2－1 } B＝{ x | y＝x2－1 } C＝{ y | y＝x2－1 } D＝{ (x, y) | y＝x2－1 } 它们表示含义相同吗?

例3若方程x2－5x＋6＝0

和方程x2－x－2＝0的解为元素的集为
M，则M中元素的个数为 A.1 B.2 C.3 D.4 ( C )

例3若方程x2－5x＋6＝0

和方程x2－x－2＝0的解为元素的集为
M，则M中元素的个数为 A.1 B.2 C.3 D.4 ( C )

例4已知集合
A＝{x|ax2＋4x＋4＝0，x∈R，a∈R} 只有一个元素，求a的值与这个元素.

例4已知集合
A＝{x|ax2＋4x＋4＝0，x∈R，a∈R} 只有一个元素，求a的值与这个元素.

解：当a＝0时，x＝－1.

例4已知集合
A＝{x|ax2＋4x＋4＝0，x∈R，a∈R} 只有一个元素，求a的值与这个元素.

解：当a＝0时，x＝－1.
当a≠0时，?＝16－4×4a＝0. a＝1. 此时x＝－2.

例4已知集合
A＝{x|ax2＋4x＋4＝0，x∈R，a∈R} 只有一个元素，求a的值与这个元素.

解：当a＝0时，x＝－1.
当a≠0时，?＝16－4×4a＝0. a＝1. 此时x＝－2. ∴a＝1时这个元素为－2. ∴a＝0时这个元素为－1.

课堂练习
1.教科书5面练习第1、2题
2.教科书11面习题1.1第1、2题

课堂小结
1.集合的定义 2.集合元素的性质 3.集合与元素的关系 4.集合的表示 5.集合的分类

课后作业
教科书12面习题1.1第3、4题

五 : 集合中的新定义(精华)

集合中的新定义

1、设整数n?4,集合X??1,2,3,?,n?.令集合

S???x,y,z?|x,y,z?X,且三条件x?y?z,y?z?x,z?x?y恰有一个成立?， 若?x,y,z?和?z,w,x?都在S中,则下列选项正确的是( )

A . ?y,z,w??S,?x,y,w??S B．?y,z,w??S,?x,y,w??S

C．?y,z,w??S,?x,y,w??S D．?y,z,w??S,?x,y,w??S

2、设S是整数集Z的非空子集，如果?a,b?S,有ab?S，则称S关于数

的乘法是封闭的．若T,V是Z的两个不相交的非空子集，T?U?Z,且?a,b,c?T,有 abc?T;?x,y,z?V,有xyz?V，则下列结论恒成立的是（ ）

A．T,V中至少有一个关于乘法是封闭的B．T,V中至多有一个关于乘法是封闭的

C．T,V中有且只有一个关于乘法是封闭的D．T,V中每一个关于乘法都是封闭的

3、已知集合A＝{1,2,3,4,5}，B＝{(x，y)|x∈A，y∈A，x－y∈A}，则B中所含元素的个数为( )．A．3 B．6 C．8 D．10

24、设非空集合S?xm?x?n满足：当x?S时，有x?S，给出如下三个命题： ??

①若m?1,则S??1?；②若m??其中正确的命题的个数为（ ） 111?m?0． ,则?n?1；③若n?

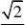
,则422

A.① B.①② C.②③ D.①②③

5、在整数集Z中，被5除所得余数为k的所有整数组成一个“类”，记为[k]， 即[k]＝{5n＋k|n∈Z}，k＝0,1,2,3,4.给出如下四个结论：

①2011∈[1]; ②－3∈[3]；③Z＝[0]∪[1]∪[2]∪[3]∪[4]；

④“整数a，b属于同一‘类’”的充要条件是“a－b∈[0]”．

其中，正确结论的个数是( )A．1 B．2 C．3 D．4

6、已知集合M?{(x,y)|y?f(x)}，若对于任意(x1,y1)?M，存在(x2,y2)?M，使得x1x2?y1y2?0成立，则称集合M是“好集合”．给出下列4个集合： ①M?{(x,y)|y? ②M?{(x,y)|y?e?2}

1xx

集合的定义 集合中的新定义(精华)

③M?{(x,y)|y?cosx} ④M?{(x,y)|y?lnx}

其中所有“好集合”的序号是（ ）

A．①②④ B．②③ C．③④ D．①③④

a7、设P是一个数集，且至少含有两个数，若对任意a、b∈R，都有a＋b、a－b, abP(除b

数b≠0)，则称P是一个数域．例如有理数集Q是数域；数集F＝{a＋b2|a，b∈Q}也是数域．有下列命题： ①整数集是数域；②若有理数集Q?M，则数集M必为数域；

③数域必为无限集；④存在无穷多个数域．其中正确的命题的序号是________．

8、设M,P是两个非空集合，定义M与P的差集为M?P??x|x?M,x?P?，则M?(M?P)等于（ ）A.P B.M?P C.M?P D.M

9、设M,P是两个非空集合，定义M与P的差集为M?P??x|x?M,x?P?。［www.61k.com]已知A??1,3,5,7?,B??2,3,5?，则集合A?B的子集个数为( )

A.1 B.2 C.3 D.4

10、对集合A??1,2,3,?,2001?及每一个非空子集，定义一个唯一确定的“交替和”如下：按照递减的次序重新排列该子集，然后从最大的数开始，交替的减或加后继的数所得的结果。例如，集合?1,2,4,7,10?的“交替和”为10?7?4?2?1?6，集合?7,10?的“交替和”为10?7?3,?5?的“交替和”为5，等等，试求A的所有子集的“交替和”的总和。

11、若集合A1,A2满足A1?A2?A，则称(A1,A2)为集合A的一个分拆，并规定：当且仅当

A1?A2时，(A1,A2)与(A2,A1)为集合A的同一种分拆，则集合A??a1,a2,a3?的不同分拆种数是 A.27 B.26 C.9 D.8

12、定义集合A,B的一种运算：A?B??x|x?x1?x2,x1?A,x2?B?，A??1,2,3?,B??1,2?，则A?B中的所有元素之和为( ) A.9 B.14 C.18 D.21

3113、设数集M?{x|m?x?m?N?{x|n??x?n}，且M,N都是集合{x|0?x?1}的43

子集，如果把b?a叫做集合?x|a?x?b?的“长度”，那么集M?N的长度的最小值是 。

14、设I??1,2,3,4?,A与B是I的子集，若A?B??1,3?，则称(A,B)为一个“理想配集”。那么符合此条件的“理想配集”的个数是（规定(A,B)与(B,A)是两个不同的“理想配集”）

( )A.4 B.8 C.9 D.16

15、对于平面上的点集?，如果连接?中任意两点的线段必定包含于?，则称?为平面上

集合的定义 集合中的新定义(精华)

的凸集，给出平面上4个点集的图形如下（阴影区域及其边界）：

其中为凸集的是

16、设S,T是R的两个非空子集,如果存在一个从S到T的函数y?f(x)满足:①

T?{f(x)|x?S}；②对任意x1,x2?S，当x1?x2时,恒有f(x1)?f(x2),那么称这两个集合“保序同构”。[www.61k.com]以下集合对不是“保序同构”的是( )

A.A?N?,B?N B.A?{x|?1?x?3},B?{x|x??8或0?x?10}

C.A?{x|0?x?1},B?R D.A?Z,B?Q ??17、设M为平面内一些向量组成的集合,若对任意正实数?和向量a?M,都有?a?M，则称M为“点射域”,则下列平面向量的集合为“点射域”的是

??x?y?0???A.{(x,y)|y?x2} B.?(x,y)|?? x?y?0?????C.{(x,y)|x2?y2?2y?0} D.{(x,y)|3x2?2y2?12?0}

18、非空集合G关于运算?满足：⑴对任意a,b?G，都有a?b?G；⑵存在c?G，使得对一切a?G，都有a?c?c?a?a，则称G关于运算?为“融洽集”。

现给出下列集合和运算：①G?{非负整数}，?为整数的加法；②G?{偶数}，?为整数的乘法；③G?{平面向量}，?为平面向量的加法；④G?{二次三项式}，?为多项式的加法；⑤G?{虚数}，?为复数的乘法。其中G关于运算?为“融洽集”的是

19、设全集I??1,2,3,?,9?，A,B是I的子集，若A?B??1,2,3?，就称集合对(A,B)为好集，那么所有的好集个数为（ ）

A.720 B.36 C.64 D.729

20、定义集合A与B的运算：A?B?{x|x?A或x?B,x?A?B}，已知集合

A??1,2,3,4?,B??3,4,5,6,7?,则(A?B)?B?( )

A.?1,2,3,4,5,6,7? B.?1,2,3,4? C.?1,2? D.?3,4,5,6,7?

21、定义：若平面点集A中的任一个点(x0,y0)，总存在正实数r，

使得集合

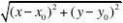
?(x,y)?r?A则称A为一个开集．给出下列集合： ?

22①(x,y)|x?y?1；② ?(x,y)|x?y?2?0?③(x,y)x?y?6； ???

④

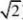
(x,y)|0?x?(y??1．其中是开集的是．

22、函数f(x)???22??x, x?P，其中P、M为实数集R的现，两个非空子集，又规定??x, x?M

A?{y|y?f(x),x?P},B?{y|y?f(x),x?M}，给出下列三个判断：

①若P?M??，则A?B??；②若P?M?R，则A?B?R；

③若P?M?R，则A?B?R.

其中错误的判断是________(只需填写序号).

本文标题：集合的定义-集合定义1
本文地址： http://www.61k.com/1169234.html