一 : 分析计算题训练

2011中考复习专题三分析计算题训练

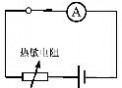
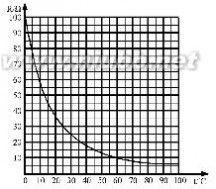
1.热敏电阻可以用来测量温度的变化，且反应快，精度高。（www.61k.com］黄非同学为了检测他家蔬菜大棚内的温度变化，他用热敏电阻设计了一个下图左所示的电路，其中电源电压是3V,热敏电阻的阻值随温度变化的图像下图中所示，电流表的量程是0－100mA。为了能从电流表直接读出大棚内的气温，他将电流表的刻度盘改画成温度的刻度，这样改造后的电流表就成了气温表。 （1）请你帮他计算,改造成的气温表能测量的最高温度是多少？写出计算过程。

（2）结合图像分析，你认为黄非设计的电路有什么不妥之处?

（3）在保持现有元件不变的条件下，再增添一个电阻，你能想办法使该气温表的量程扩大到60℃吗？请在方框中画出你设计的电路图，并通过计算求出新增电阻的阻值。

（4）根据你设计的电路，通过计算说明，此气温表的0℃应与电流表刻度盘的什么刻度对应？

第36题图

2．１０月２４日１８时０５分，在西昌这个被称为“月亮女儿的故乡”的地方，长征三号甲运载火箭托举着嫦娥一号卫星顺利升空——“嫦娥”就这样开始了奔月之旅。 “嫦娥一号”卫星本次的任务主要有三个：一是探测月球三维全息图像；二是探测月球资源成分、密度和进行物质光谱分析；三是探测地球到月球之间的空间环境，为以后的登月载人飞船打下基础。

（1）中秋节的月相是______________

(2)“嫦娥一号”发射升空时，“长征三号”捆绑式火箭尾部的火焰如果直接喷射到发射台，发射架要被熔化。为了保护发射架，就在发射架的台底建了一个大水池，让火焰喷射到水池中。建造大水池的主要原因是利用了水 时要吸热，从而使周围环境温度不致太高。

(3)火箭上升时，燃料燃烧释放的__________能转化为飞船的 能；

(4)我国计划在2020年登陆月球，但要把人类送去月球，还有许多航天技术问题需要解决，如：如何提供在往返路程中宇航员呼吸所需要的氧气和消除呼吸过程中产生的二氧化碳就是一个值得研究的问题。已知一个成年人平均每天要呼吸空气飞船飞往月球考．．18000升左右，

察来回一趟需要的时间较长，如果在飞船发射时携带全部所需的氧气，则数量很大，

将大大 1

西昌地震 分析计算题训练

提高发射的成本和难度。［www.61k.com］

① 若飞船上有三名宇航员，登月时间为15天，请计算理论上需要氧气________________

千克。(氧气的密度是1．43g／L，答案取整数) ②有人提出在飞船上供氧的两个方案：

方案一：通过太阳能电池产生的电流来电解水

方案二： 通过下列化学反应产生氧气2Na2O2+2CO2＝2Na2CO3+O2

从减轻飞船发射重量和消除呼吸过程中产生的二氧化碳的角度请你评价这两个方案最主要的优缺点(

③也有科学家提出研究使宇航员人工冬眠的技术或加快飞船速度，缩短航行时间来减少氧气的携带量。你是否有较好的方案，请举一例___________________；你提出该方案的简要理由是________________________________________。

④我国已成功启动 “嫦娥工程”。现已知月球的体积是地球的四十九分之一，上面没有空气，也没有磁场，同一物体在月球上与地球上所受的重力之比为1∶6 。下列说法正确的是 A．月相的变化是由于月球被太阳照亮部分的形状变化而引起的； B．月球上没有昼夜之分；

C．两物体在月球上所受重力之比为1∶6，则它们在地球上的质量之比也为1∶6； D．在月球上没有空气，所以宇航员登上月球将不能听到任何声音。

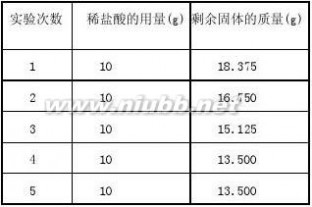
3.某化学兴趣小组的同学为测定假黄金(铜锌合金)组成元素的质量分数，称取20克假黄金置于烧杯中，用某浓度的稀盐酸50克，分5次加入，每次充分反应后，取出固体，经过滤、于燥等操作后称重，各次稀盐酸用量和剩余固体质量记录如下：

1)求铜锌合金中锌的质量分数 ▲ ；

2)从图可知，当所用合金与稀盐酸的质量比为 ▲ 时，表明锌恰好完全溶解； 3)计算稀盐酸中溶质的质量分数。

2

西昌地震 分析计算题训练

4. 2011年，3月15日下午，日本地震进入第五天，最新的消息显示，地震海啸造成的死亡人数已经达到3079人，而且日本的核电站也遭受地震破坏，相继发生了氢气爆炸，让日本进一步笼罩在核辐射的阴影下。(www.61k.com]

（1）地震时震源的振动以横波和纵波两种形式向外传播，速度分别约为3.4km/s和5.6km/s。震源正上方的地方称为震中，若地震时测出纵波和横波到达震中的时间差为2秒，那么，震源到震中的距离大致是 ▲ km。

（2）救援的最佳时间应在震后72小时以内。长时间缺水是威胁生命的最重要原因，请说出水对人体的一项重要作用 ▲ 救援时急需要大量的血液，医生要对自愿献血的人进行体检，并验血型。那么，献血前先进行体检的主要目的是为了防止___▲____。

（3）核电站发电的原理是 ▲ 产生巨大的能量。

（4）本次灾区消毒多采用“84”消毒液。实际使用时，质量分数一般为0.2％～0.5％。若需配制溶质的质量分数为0.5％的消毒液，取100毫升原液加水至1000毫升即得，那么若要配制质量分数为0.2％的消毒液16升，需要取原液___▲___毫升(消毒液密度均取1克／毫升)。

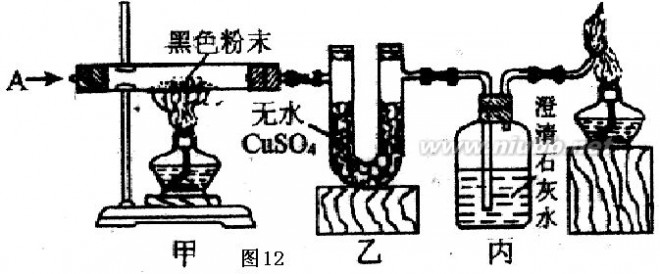
5、按图12进行实验，已知A为H2、CO中的一种或两者的混合物，甲装置中的黑色粉末为CuO、炭粉中的一种或两者的混合物。

61阅读提醒您本文地址：

（1）若黑色粉末是纯净物，甲、乙、丙装置中

的固体或溶液依次出现红色、蓝色、浑浊，

则气体A是 ，黑色粉末为 。

（2）若A为纯净物，反应现象与（1）同，则A

是 ，黑色粉末为 。

（3）若第（1）问中：乙装置的物质增重1.8g，

丙装置中的物质增重2.2g，假设气体与固体反应完全，则通入气体的质量可能是 。

（A）0.8g （B）1.6g （C）3g （D）2.5g

（4）若第（2）问中：充分反应后，甲装置得到6.4g红色固体，乙装置中物质增重0.9g，则黑色固体的质量为_________g。

6.如图所示的电动观光车，有关技术参数如下表。

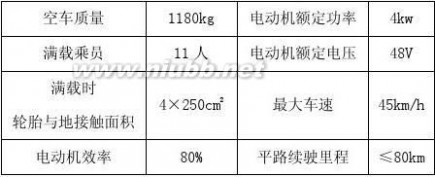
根据技术参数，求解下列问题：（g 取10N/kg）

（1）设乘员质量均为60kg，求满载时车对水平路面的压强。

（2）电动机以额定功率工作半小时消耗多少电能？电动机对外做了多

少功？若这一过程中，观光车以36km/h的速度沿水平路面匀速行驶，

求车在行驶过程中受到的阻力。

3

西昌地震 分析计算题训练

6．2008年5月12日14时28分，中国汶川发生了8．0级大地震。［www.61k.com]党和政府立刻作出重要部署，一场围绕“救人为本”的抗震救灾工作迅速有序展开。地震无情人有情，一方有难八方支援。

(1)减少地震给人类造成灾难的关键是提高人类防震抗灾能力，下列措施可以减少地震灾害的是:

A．提高地震预报水平

B．建造抗震建筑物

C．发生地震时，跑到空旷处或躲到面积

较小的房间

(2)如图是正在救灾现场工作的挖掘机，

画出图中放大部分杠杆的动力、动力臂和阻力臂；

7．小敏设计了

一种“闯红

灯违规证据

模拟记录

器”，如图

甲，拍摄照

片记录机动

车辆闯红灯

时的情景。

工作原理：当光控开关接收到某种颜色光时，开关自动闭合，且当压敏电阻受到车的压力，它的阻值变化引起电流变化到一定值时，继电器的衔铁就被吸下，工作电路中的电控照相机工作，拍摄违规车辆。光控开关未受到该种光照射自动断开，衔铁没有被吸引，工作电路中的指示灯发光。

回答下列问题：

(1)根据工作原理，将电路连接完整。

(2)要记录违规闯红灯的情景，光控开关应在接收到_______光(填“红”、“绿”或“黄”)时，自动闭合。

(3)由图乙可知，压敏电阻R的阻值随受到压力的增大而________________。

(4)已知控制电路电压为6V，继电器线圈电阻10欧，当控制电路中电流大于0.06安时，

衔铁被吸引。通过计算说明，只有质量超过多少千克的车辆违规时才会被拍照记录。

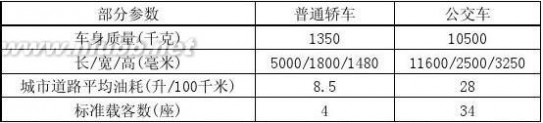
8．以车代步给人们带来便捷、舒适的同时，也带来了空气污染、道路拥挤等社会问题，需要我们去解决和管理。

(1)全班52位师生准备去离校10千米的市内德育基地参观。提出乘出租车(普通轿车)和

公交车二种出行方法，请你从师生最小人均耗油量和人均占有路面面积的角度，通过计算说明选择公交车的优点。(人均占有路面面积＝车辆占有道路面积/载客人数，假设城市中两种车速度相同)

下表是某普通轿车和城市常见公交车的部分数据：

4

西昌地震 分析计算题训练

(2)汽车的尾气排放已成为城市空气污染的重要来源之一，请写出其中的一种污染物：__________。（www.61k.com]汽车最理想的清洁燃料是氢气，科学家发明了一种车用制氢装置，其原理是硼(B)和水在高温下反应，生成氢气和X，化学方程式是2B+6H22。则

X的化学式是_______________。 (3)我国研制的某款纯电动汽车，最大功率是27千瓦。电池充满电后行驶里程约200千米，能满足城市特定交通圈及上班族的基本需要。试计算：当电机工作电压为320伏，工作电流为30安时的功率为多大?

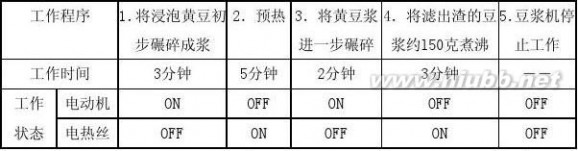
9.小琪家里新买回来一个豆浆机，其外形、工作电路和铭牌如图l4所示：

2

(1)豆浆机底部与水平桌面的接触面积为0.02米，则豆浆机对桌面的压强大小为多少

帕?(请简要书写计算过程，其中g取l0牛／千克)

(2)将豆浆机装满清水，但未加装黄豆，则此时它们受到的总重力为＿＿＿＿＿＿牛。(3)

为安全起见，应将豆浆机接入下面给出的第＿＿＿＿＿＿种插座(选填“Ⅰ”或“Ⅱ”)

(4)以下是小琪制作豆浆时，豆浆机的工作程序表，那么在正常工作的情况下，制作150克豆浆需要消耗多少电能?(请书写必要的计算过程，其中0N：表示开启工作；0FF：表示断电．．．．．．．．．．．．．．．．．．不工作)

．．．

5

西昌地震 分析计算题训练

6

61阅读提醒您本文地址：

二 : 初中八年级数学专项训练-题谷网提供

初中八年级数学专项训练

一、选择题。［www.61k.com］

1、若?a?1??b?2=0，则a6??a?2b?等于2（）

D.-3

）A.5B.-5C.32.当m，n为自然数时，多项式xm?yn?2m?n的次数应当是（

A.mB.nC.m,n中较大的

）D.m+n3.当x分别等于2或-2时，代数式x3?5x的值（

A.相等B.互为相反数C.互为倒数D.互为相反数

）.4.设a是一个负数，则数轴上表示数－a的点在（

A.原点的左边

B.原点的左边和原点的右边B.原点的右边D.无法确定）.5.下列图形中，表示南偏西60°的射线是（

a

ABC

)D6.下列图形中,能够折叠成正方体的是(ABCD

7.如图,OB平分∠AOC,OD平分∠EOC,∠1=20°,∠AOE=88°,则∠3为

题谷网初中数学 初中八年级数学专项训练-题谷网提供

ED

CB3421()OAA.24°B.68°C.28°D.都不对

8.某种商品的标价为120元，若以九折降价出售，相对于进价仍获利20%，则该商品的进价是（

A.95元

9.解方程B.90元）.C.85元）.D.80元x?1x?2??2,去分母正确的是（36A.2x?1?x?2?2

C.2x?2?x?2?6B.2x?1?x?2?12D.2x?2?x?2?12

10.有一些分别标有6，10，14，18的卡片，后一张卡片上的数比前一张卡片上的数大4，小红拿到了相邻的3张卡片，且这些上的数字之和为282，那么小红拿到的3张卡片为（）

A.88,92,96

C.90,94,98

二、填空题.

11.-3,-(-1),+(-5),-2.15,0,?1.5,-3.2中整数有

个，负数有个。[www.61k.com］个，正整B.100,104,108D.88,98,106

12.用一个平面去截长方体、五棱柱、圆柱和圆锥，不能截出三角形。

。13,若x2?2y?5的值是7，则代数式3x2?6y?4的值是

题谷网初中数学 初中八年级数学专项训练-题谷网提供

14．若│x+2│+（y-3）=0,则xy=____.15.一个多项式与?3x2?x?5的和是?2x2

?x?3，则这个多项式是。（www.61k.com]16.下图是某几何体分别从正面左面及上面看到的平面图形，则这个几何体是。2

17.一家商店将某种服装按成本价提高40%标价，又以8.5折优惠卖出，结果每件仍获利12元，若设每件服装的成本为x元，则可列方程

18.。它们是按一定规律排列的，依照此规律，第8个图形共有_____枚五角星。

三、解答题

19.计算下列各题。

（1）?1.3?2.8??2.7??4.2

题谷网初中数学 初中八年级数学专项训练-题谷网提供

(2)?14?(3*2)3?162÷(-8)

20.解下列方程

(1)4x?3(5?x)?6;(2)3x?13x?22x?3?2??2105

21．已知有三个有理数a，b，c，其积是负数，其和是正数，当x?a

a?b

b?c

c时，求x19?95x?1082的值。[www.61k.com)

22.某人用400元，购买了八套儿童服装，准备以一定价格出售，如果以每套儿童服装55元的价格为标准，超出的记作正数，不足的记作负数，记录如下：

题谷网初中数学 初中八年级数学专项训练-题谷网提供

+2，-3，+2，+1，-2，-1,0,-2（单位：元）

（1）当他卖完这8套儿童服装后是盈利还是亏损？

（2）盈利（或亏损）了多少钱？

23.下面是小马虎解的一道题

题目：在同一平面上，若∠BOA=70°，∠BOC=15°求∠AOC的度数。[www.61k.com)

解：根据题意可画出图

∵∠AOC=∠BOA－∠BOC

=70°－15°

=55°

∴∠AOC=55°

CB

若你是老师，会判小马虎满分吗？若会，说明理由。若不会，请将小马虎的的错误指出，并给出你认为正确的解法。

24.王老师购买一套教师住宅，采取分期付款的方式，一种付款方式

题谷网初中数学 初中八年级数学专项训练-题谷网提供

是第一年付四万元，以后每一年付一万元；另一种付款方式是前一半时间每年付款一万四千元，后一半时间每年付款一万一千元。(www.61k.com］两种付款方式中付款钱数和付款时间都相同，假设一次性付清房款，可以少付一万六千元，现在王老师一次性付出购房款，要付房款多少万元？

25.美化城市，改善人们的居住环境已成为城市建设的一项重要内容。某市区近几年来，通过拆迁旧房，植草，栽树，修建公园等措施，使城区绿地面积不断增加．

（1）根据图中所提供的信息，回答下列问题：2002年底的绿地面积为公顷，比2001年底增加了公顷；在2000年，2001年，2002年这三年中，绿地面积增加最多的是年；

（2）为满足城市发展的需要，计划到2004年底使城区绿地总面积达到72.6公顷，试求2004年底绿地面积比2002年底增长了百分之几？

60

56

51

48

1999200020012002年份绿地面积（公顷）

城区每年年底绿地面积统计图

题谷网初中数学 初中八年级数学专项训练-题谷网提供

26.光明中学七年级组织课外活动，准备举行一次羽毛球比赛，于是到商店购买羽毛球拍和羽毛球，走两家商店得知：每副球拍25元，每个球2元，但甲商店说：“买羽毛球拍和羽毛球都打九折”优惠；乙商店说：“买一副球拍送两个球”优惠。（www.61k.com）

（1）准备花90元钱全部用于买2副球拍及若干个球，问到哪家商店购买更合算？

（2）若必须买2副球拍，则再买多少个球时到两家商店一样合算？

参考答案

一．1-5：ACBBD6-10：CABDC

二．11.414

16.圆锥12.圆柱13.1014.-615.x2?218.2517.（1+40%）x×85%-x

题谷网初中数学 初中八年级数学专项训练-题谷网提供

三．19.（1）-3（2）-249

20.（1）x=3

21.934

22.（1）盈利（2）盈利16元（2）x=716

23.不会给小马虎满分

原因是：小马虎没有把问题考虑全面，他只考虑了OC落在∠AOB的内部，还有OC落在∠AOB的外部的情况（图略）

当OC落在∠AOB的外部时，∠AOC=∠AOB+∠BOC=85°

24.134000

25.（1）60，4，2001；72.6?60?100%?21%．60

答：2004年底绿地面积比2002年底增长为21%．

26.（1）应到甲商店购买（2）15个（2）

更多试题解析，请关注题谷网

三 : 初一数学计算题练习

?11?

?1.5?1.4?4.3?5.2?3.6 ??6?????

?32?

11??1??

??0.5?????? ?2.5?7.3?2.5?(?2.4)?2.5?(?1.7)

36??24??

???3???12???5?

?3???5??1?0.2?????2?? ?|?5|??1????1??????

5???23???3????

2

?1??1?22

?????2??????? －9+5×(－6) －(－4)÷(－8) 4?2??4???

3

?

2x?111??

?3 ??0.3?3?????2? 4?6x?

212?33?

1

x?12

?

2?3x3

94?49

?1 15＋(―1)―15―(―0.25)

4

(?81)?

?(?32) —48 × (

14

?

136

?

16

?

112

)

??4?2???

?

?

?5??2

????? （2m＋2）×4m 4?8??3

13

(2x＋y)2－(2x－y)2 (xy)2·(－12x2y2)÷(－

43

x3y)

[(3x＋2y)(3x－2y)－(x＋2y)(3x－2y)]÷3x

先化简后求值：

m(m－3)－(m＋3)(m－3)，其中m＝－4．

4312

4×(－3)2－13＋(－－|－43| －32 －［（－2）－（1－×）÷（－2）］

254

2x-19=7x+31

2

2

2

3x?14

2

－

5x?76

= 1

化简（求值）2(xy?xy)?2(xy?x)?2xy

?21?16?(?

12

2

?2y的值，其中x??2,y?2

3

)?4?(?3) 5x?6?3x

?

2

???x

3

?2x?3

2

?

先化简，再求值，已知a = 1，b = —的值

13

，求多项式?a3?2b3??2?ab2?

?

?

12

ab??2ab?b

2

??

?

23

?

-22-（-3）3×（-1）4-（-1）5 -1-（1-0.5）×

1

13

×[2-（-3）2]

22

11＋(－22)－3×(－11) (2)(?3)?()??6??

293

322

3

－2(x－1)＝4 －8x＝3－1/2x

48?(?

16?14?112

) 18?6???2????

??1?

? 3?13

(?

13

)?3

2

-（-6） -12-（1-0.5）×（-1）×[2-（-3）2]

－2-3×(-2)-(-1)

12

14

18

334

32216

(－)??|-3|?(?0.25)?()

232

13?(?3) 16

)?(?6)]?(?7)

34.

2

2

?1?

2

?? (?2)?

2

?3?2?3?(?2) [50?(

79

?

1112

?

先化简，再求值：3(x?y)?2(x?y)?2，其中x??1，y?

74?78?23

?(?6) 化简：(4a?3a)?(2a?a?1)?(2?a?4a)

2222

先化简，再求值：

2(x－2)＋2＝x＋1

2x－15x－1

－ ＝1 36

1

212??312??

x?2?x?y????x?y?，其中x=－2，y=。

3233???2?

2

?1?41

6?2?(?3)?2? (?4)2?(?3

4)?30?(?6)

解方程：4?3(2?x)?5x 解方程：

3

2?5

6?7

12?9

20?11

30?13

42?15

562x?13?x?22?1 (3

4?1

6?1

12)?8?(?48)

?11

2?[3?(?2

3)2?1] －2+2×[(－1)+|－1|] 02210

3

512712371757) 3(2?3

4?1

6)?(?24)

(??)?(60??60??60?

3

?6?(?1

5)?2?(?1.5)

?36?4?(?2.5)?(?0.1)

?(?3)2?32??(?3)?(?4)?? ?1.5?1.4?4.3?5.2?3.6

先化简，再求值：?(2x?3y)?(2x?2y)?1，其中

?1?513?313?221?????24??5?4???5??4??2?4 ??????????84?24?864??22x??14,y?15

2?x?3x?2y22??3?4?3x?2x2? 3xy?2?xy??xy?22?

???12?2?x??2x? 4??

??6???

?1?3?1?? 2?4

11??1????0.5?????? ?2.5?7.3?2.5?(?2.4)?2.5?(?1.7) 36??24??

??3???3???5??1?0.2?????2?? 5????

化简求值.2xy+[7x－3(2x－1)－2xy]＋y，其中x?2,y??

2212。

??8????1? 8?(?10)?(?2)?(?5)

??5????

??5??131?? ?24?????? 4??243?

8?（?4

5）??16 ?36?(?6)?72?(?8)

5

四 : 初一数学计算题练习19

初一数学计算题测试（面积-乘法公式）

【知识梳理】 1.整式的乘除法:

①几个单项式相乘除,系数与系数相乘除,同底数的幂结合起来相乘除.

②单项式乘以多项式,用单项式乘以多项式的每一个项. 再把所得的积相加 ③多项式乘以多项式,用一个多项式的每一项分别乘以另一个多项式的每一项. 再把所得的积相加

④多项式除以单项式,将多项式的每一项分别除以这个单项式. 2.乘法公式

平方差公式：两个数的和与这两个数的差的积等于这两个数的平方， 即(a?b)(a?b)?a2?b2；

完全平方公式：两数和（或差）的平方，等于它们的平方和，加上（或减去）它们的积的2倍，即(a?b)2?a2?2ab?b2

3．分解因式：把一个多项式化成几个整式的积的形式，这种变形叫做把这个多项式分解因式．

4．分解因式的方法：

⑴提公团式法：如果一个多项式的各项含有公因式，那么即可把这个公因式提出来，从而将多项式化成两个因式乘积的形式，这种分解因式的方法叫做提公因式法． ⑵运用公式法：公式a2?b2?(a?b)(a?b) ； a2?2ab?b2?(a?b)2

5．分解因式的步骤：分解因式时，首先考虑是否有公因式，如果有公因式，一定先提取公团式，然后再考虑是否能用公式法分解． 6．分解因式时常见的思维误区：

⑴ 提公因式时，其公团式应找字母指数最低的，而不是以首项为准． ⑵ 提取公因式时，若有一项被全部提出，括号内的项“ 1”易漏掉． ⑶ 分解不彻底，如保留中括号形式，还能继续分解等 【考点例题】

1 计算（1） (-x)5·(xy)2·x3y （2）(2a2b3)3·(-3a2b)2·

（3）3x(1?2x)?2x(3x?x?1) （4）2a-a(2a-5b)-b(5a-b)

（5）(4m-3)2+(4m+3)(4m-3) （6）(3x-4y)2-(3x+4y)2-xy （7）(x-2y+4)(x+2y-4)

2 因式分解

（1）(a+b)2－2(a+b) （2）a(x－y)+b(y－x)+c(x－y)

2

2

2

1

abc （3）(-ab+2)(ab+2) 72

（3）(x+2)2－9 （4）4(a+b)2－9(a－b)2

（5）x3－25x；

（6）x2y2－1

3.（1）已知a2-2a+b2+4b+5=0，求(a+b)2005的值。

（2）已知m、n为自然数，且m(m－n)－n (n－m)=7，求m、n的值。

（3）已知a、b、c分别为三角形的三条边，试说明：a2?b2?c2

?2bc?0

（4）若a、b、c为△ABC的三边，且满足a2＋b2＋c2＝ab＋ac＋bc，试判断△ABC 的形状。

【课堂巩固】 一、 填空

（1）若x2

?mx?15?(x?3)(x?n)，则m

（2）已知(a+b)2=7，(a—b)2

=3，则 （3）若x2+mx+1是完全平方式，则； （4）已知4x2?mxy?9y2

是关于x,y的完全平方式，则（5）若二项式4m2+1加上一个单项式后是一含m（6）若m2+n2－6n＋4m＋13＝０，则m2－n2 =_________；

（7）若a?b??3,ab?2，则a2?b2

?，?a?b?2

?

（8）若a?b?2,a?c?1,则(2a?b?c)2?(c?a)2

?

（9）已知2m＝x，43m＝y，用含有字母x 的代数式表示y，则y＝_____________。

（10）如上图所示的正方形和长方形卡片若干张，拼成一个长为(2a+b)，宽为(a+b)的矩形，

需要B类卡片_______张． 二、计算

（1）3x2(1?2x)?2x(3x2?x?1) （2）2a2-a(2a-5b)-b(5a-b)

（3）(x?2y?z)(?x?2y?z) （4）（a+2b－3c）（a－2b+3c）

（5）(2?1)(22?1)(24?1)???(22n?1)

三、因式分解

（1）4x4－4x3＋x2； （2）ab＋a＋b＋1

（3）?x—1??x—2?—2?2—x?2； （4）a2?ab?b2

??

2

—9a2b2

111??2

（5）a2－3a＋1＝0．求a?、a?2和?a??的值；

aaa??

【课后练习】

一、耐心填一填

1、计算：??2a2?2??3a3? ； (2x＋5)(x－______． 2、计算：?5?104???3?102??；（用科学记数法表示）

a?a?b??b?a?b?=___________．

3、⑴·3ab2c?—24a3b5c； ⑵?—a—b?2?a22ab?b2

4、（1）如图1，可以求出阴影部分的面积是（写成两数平方的差的形式）； （2）如图2，若将图1的阴影部分裁剪下来，重新拼成一个矩形，它的宽是 ，长是 ，面积是 （写成多项式乘法的形式）； （3）比较图1、图2的阴影部分面积，可以得到乘法公 式 （用式子表达）．

n

5、我国宋朝数学家杨辉在他的著作《详解九章算法》中提出右表，此表揭示了(a+b)（n为非负整数）展开式的各项系数的规律．

1

例如：(a+b)=a+b，它有两项，系数分别为1，1；

222

(a+b)=a+2ab+b，它有三项，系数分别为1，2，1；

32223

(a+b)=a+3ab+3ab+b，它有四项，系数分别为1，3，3，1；??

根据以上规律，

2

(a+b)展开式共有五项，系数分别为

6、观察：3-1=8;5-3=16; 7-5=24;9-7=32.??根据上述规律，填空：

2

2

2

2

2

2

2

2

4

132-112= ,192-172= .请用含n的等式表示这一规律 ；

7、若a—b=2，3a+2b=3，则3a(a—b)+2b(a—

8、数学家发明了一个魔术盒，当任意数对?a,b?进入其中时，会得到一个新的数：?a?1??b?2?.现将数对?m,1?放入其中得到数n，再将数对?n,m?放入其中后，如果最后得到的数是 .（结果要化简）

2

9、多项式4x+1加上一个单项式后，使它成为一个完全平方式，那么加上的单项式可以是

（填上一个你认为正确的就可以）

二、精心选一选

10、下列各式中，是完全平方式的是 （ ）

11222222

A、m-mn+n B、x-2x-1 C、x+2x+ Db-ab+a

44

11、下列各式中计算正确的是 （ ） A.(a?b)?a?b B.(a?2b)2?a2?2ab?4b2

C. (a?1)?a?2a?1 D.(?m?n)2?m2?2mn?2n2

12、下列多项式, 在有理数范围内不能用平方差公式分解的是： （ ）

2222

A．—x2?y2 B．a—8b C．4a2—?a?b?2 D． xy—1 13、通过计算几何图形的面积可表示代数恒等式，右图 可表示的代数恒等式是： （ ）

A．?a—b?2?a2—2ab?b2 B．?a?b??a2?2ab?b2

2

222

2242

C．2a?a?b??2a2?2ab D．?a?b??a—b??a2—b2

14、设A=（x-3）(x-7)，B=(x-2)(x-8)，则A，B的大小关系为 （ ） A．A＞B B．A＜B C．A=B D．无法确定

15、?x2?mx?1??x?2?的积中x的二次项系数为零，则m的值是： （ ） A．1 B．–1 C．–2 D．2

16、如图是长10cm，宽6cm的长方形，在四个角剪去4个边长为xcm的小正方形，按折痕做一个有底无盖的长方体盒子，这个盒子的容积是 （ ） A.?6?2x??10?2x? B.x?6?x??10?x? C.x?6?2x??10?2x? D.x?6?2x??10?x?

17、如果a?b?3,a?c?1，那么?a?b?2??b?c?2??c?a?2的值是 （ ） A.14 B.13 C.12 D.11

22

18、已知a?a?3?0，那么a?a?4?的值是 （ ） A.9 B.?12 C.?18 D.?15

19、已知9x?kxy?4y是一个完全平方式,那么k的值是 ( ) A.12 B.24 C.?12 D.?24

2222

20、若x?4y?(x?2y)?A?(x?2y)?B, 则A,B各等于 ( ) A.4xy,4xy

8

22

B.4xy,?4xy C.?4xy,4xy D.?4xy,?4xy

21、已知6-1能被30~40之间的两个整数整除，这两个整数是 ( )

A.31, 33

B.33,35

C.35,37

D.37,39

三、用心做一做

22、用简便方法计算：

（1）198 （2）10.5×9.5 （3） 20122-4024×2011+2011

1281?1???1??（4）（1+2）(1+22)(1+24)??(1+2) （5）??1?2??1?2??1?2????1?

22

?2??3??4?

?

1

20102? ??

23、利用乘法公式计算：

(1) ?2x?3y???y?3x??3x?y? (2) (x＋y) ( x2＋y2) ( x－y)(x4?y4)

2

(3) (a－2b＋3)(a＋2b－3) (4) [(x－y)2＋(x＋y)2](x2－y2)

(5) (m－2n－3)2 (5) (2x-3)2(-2x-3)2

222

24、先化简，再求值：(x+5)-(x -5)-5(2x+1)(2x- 1)+ x·(2x), 其中x=-1

25、已知?a?b??7，?a—b??4，求a?b和ab的值．

2

2

22

26、下面是小明和小红的一段对话：

13??13?小明说：“我发现，对于代数式?当n?2010和?m?2n??m?2n??(2n?4)(4?2n)的值，?4??4?

n?2011时，值居然是相等的.”小红说：“不可能，对于不同的值，应该有不同的结果.”在此问题中，你认为谁说的对呢？说明你的理由.

初一数学计算题练习19_初一数学计算题

111??2227、已知a－3a＋1＝0．求a?、a?2和?a??的值； aaa??

2

28、已知a2?b2?4a?2b?5?0,求a,b.的值。

29、已知x?y?1,xy?1，求：（1）x2y?xy2;（2）(x2?1)(y2?1) 5

m 30、若我们规定三角“ ”表示为：abc ; 方框“ n ”表示为：（x m + y n）.y x 例如： b

4 1

÷ 3 =1×19×3÷(2 4+31)=3 .请根据这个规定解答下列问题： 2 19

1 4

（1）计算： -3 × － 1 3 = ；

2 2

x （2）代数式： 3y + k 为完全平方式，则k = ;

1 1 (3)解方程： － = 6x2+7 . (x+2)(3x-2) 3x-2

31、 观察下列等式

(x?1)(x?1)?x2?1;(x?1)(x2?x?1)?x3?1;(x?1)(x3?x2?x?1)?x4?1；??

nn?1n?2（1）请你猜想一般规律：(x?1)(x?x?x????x2?x?1)? ；

322008（2）已知x?x?x?1?0，求x的值.

33、在x+px+8与x-3x+q的积中不含x与x项，求p，q的值．

223

五 : 初一数学计算题练习

?11?

?1.5?1.4?4.3?5.2?3.6 ??6?????

?32?

11??1??

??0.5?????? ?2.5?7.3?2.5?(?2.4)?2.5?(?1.7)

36??24??

???3???12???5?

?3???5??1?0.2?????2?? ?|?5|??1????1??????

5???23???3????

2

?1??1?22

?????2??????? －9+5×(－6) －(－4)÷(－8) 4?2??4???

3

?

2x?111??

?3 ??0.3?3?????2? 4?6x?

212?33?

1

x?12

?

2?3x3

94?49

?1 15＋(―1)―15―(―0.25)

4

(?81)?

?(?32) —48 × (

14

?

136

?

16

?

112

)

??4?2???

?

?

?5??2

????? （2m＋2）×4m 4?8??3

13

(2x＋y)2－(2x－y)2 (xy)2·(－12x2y2)÷(－

43

x3y)

[(3x＋2y)(3x－2y)－(x＋2y)(3x－2y)]÷3x

先化简后求值：

m(m－3)－(m＋3)(m－3)，其中m＝－4．

4312

4×(－3)2－13＋(－－|－43| －32 －［（－2）－（1－×）÷（－2）］

254

2x-19=7x+31

2

2

2

3x?14

2

－

5x?76

= 1

化简（求值）2(xy?xy)?2(xy?x)?2xy

?21?16?(?

12

2

?2y的值，其中x??2,y?2

3

)?4?(?3) 5x?6?3x

?

2

???x

3

?2x?3

2

?

先化简，再求值，已知a = 1，b = —的值

13

，求多项式?a3?2b3??2?ab2?

?

?

12

ab??2ab?b

2

??

?

23

?

-22-（-3）3×（-1）4-（-1）5 -1-（1-0.5）×

1

13

×[2-（-3）2]

初一数学计算题 初一数学计算题练习

22

11＋(－22)－3×(－11) (2)(?3)?()??6??

293

322

3

－2(x－1)＝4 －8x＝3－1/2x

48?(?

16?14?112

) 18?6???2????

??1?

? 3?13

(?

13

)?3

2

-（-6） -12-（1-0.5）×（-1）×[2-（-3）2]

－2-3×(-2)-(-1)

12

14

18

334

32216

(－)??|-3|?(?0.25)?()

232

13?(?3) 16

)?(?6)]?(?7)

34.

2

2

?1?

2

?? (?2)?

2

?3?2?3?(?2) [50?(

79

?

1112

?

先化简，再求值：3(x?y)?2(x?y)?2，其中x??1，y?

74?78?23

?(?6) 化简：(4a?3a)?(2a?a?1)?(2?a?4a)

2222

先化简，再求值：

2(x－2)＋2＝x＋1

2x－15x－1

－ ＝1 36

1

212??312??

x?2?x?y????x?y?，其中x=－2，y=。(www.61k.com］

3233???2?

2

初一数学计算题 初一数学计算题练习

?1?41

6?2?(?3)?2? (?4)2?(?3

4)?30?(?6)

解方程：4?3(2?x)?5x 解方程：

3

2?5

6?7

12?9

20?11

30?13

42?15

562x?13?x?22?1 (3

4?1

6?1

12)?8?(?48)

?11

2?[3?(?2

3)2?1] －2+2×[(－1)+|－1|] 02210

3

512712371757) 3(2?3

4?1

6)?(?24)

(??)?(60??60??60?

3

初一数学计算题 初一数学计算题练习

?6?(?1

5)?2?(?1.5)

?36?4?(?2.5)?(?0.1)

?(?3)2?32??(?3)?(?4)?? ?1.5?1.4?4.3?5.2?3.6

先化简，再求值：?(2x?3y)?(2x?2y)?1，其中

?1?513?313?221?????24??5?4???5??4??2?4 ??????????84?24?864??22x??14,y?15

2?x?3x?2y22??3?4?3x?2x2? 3xy?2?xy??xy?22?

???12?2?x??2x? 4??

??6???

?1?3?1?? 2?4

初一数学计算题 初一数学计算题练习

11??1????0.5?????? ?2.5?7.3?2.5?(?2.4)?2.5?(?1.7) 36??24??

??3???3???5??1?0.2?????2?? 5????

化简求值.2xy+[7x－3(2x－1)－2xy]＋y，其中x?2,y??

2212。［www.61k.com]

??8????1? 8?(?10)?(?2)?(?5)

??5????

??5??131?? ?24?????? 4??243?

8?（?4

5）??16 ?36?(?6)?72?(?8)

5

初一数学计算题 初一数学计算题练习

3

?2?2

1

?4?2

???????2????5? 3x－2（x－3y） 2?3?

( x2?y )?4 ( 2x2

?3y )

?12

?(

23

?

12

)?(?5)

?21

?(42

?11

1

1

236?32)?(?23)

??4.5??(?5)?(1?1?0.7)??

?2 ???25???5?

5

12?(?2)?0?147?2

4

?(?29)?(?2)?(32?23

)

6

?|?5|???12?????5??1????1????

?

?23???3??0.53?(?2)3??1?

3??(??

3)2??32?

??21?326

3??(0.2)?

?2?3(?1)??25??

??

2

4

初一数学计算题 初一数学计算题练习

??(?3?2)3?(?43)2?(?12)?32?(?3)2??(?1)?

(?3)

2

?(?32)?(2?3)

2

?2?3

2

；

1+（－2）+︱－2－3︱－5

??

1?1?3??

64?

??

??48?

?1

2009

???5?2??5???

??0.8?1 ?3?

2

?14????(13?2)??(?1)3

；

??

16?(?1)215

?152?

9

；

（?23

）÷（?

58

）÷（－0.25）

︱?97︱×(23－15)―13× (－1) 2008

?40?28???19????24?

7

117

初一数学计算题 初一数学计算题练习

11?2

???

?

????60? 23????2?

3

???4?

?

?31215

?

?22?2?3???1?2

?16???2?3????1?

?8???

??4?

12???1?2?1??432? ?

32÷[（－2）3－（－4）]

?3

62

??1

2?

2

3

???3????

3?

2

5

－7＋3.4

?32????1???24

????1??

?3??2?化简：－3（2x－5）+6x 8

5.6

初一数学计算题 初一数学计算题练习

（－14）－（－16）－（+6） 解方程：5（8－3x）=x

58

?(?4)?0.25?(?5)?(?

2

12

)

3

先化简，再求值： 当x??

2

3×(－4)＋(－28) ÷7 4×(－3)－15÷(－3)－50

先化简，再求值： 2x2+(－x2+3xy+2y2)－(x2－xy+2y2),其中x=

4x＋3＝2(x－1)＋1

x?13

?x?26

?4?x2

12

x?(2x?

23

y)?(

2

32

x?

13

y)，其中x??

2

14

,y??

12

12

,y??3时，求代数式3(x?2xy)?[3x?2y?2(xy?y)]的值

22

12

，y=3.

9

初一数学计算题 初一数学计算题练习

(13?4

78?31)?27

8

2

) (?1)?[(?2)?3]?(?7

332

4x?3(20?x)?3

x?1

2x?13

?x?

2?3x6

?1

6x－7＝4x-5

(?4)?(?

2

2

?

3?2x3

?1

34

)?30?(?6)

先化简，再求值：(5a+2a2－3+4a3)－(－a+4a3+2a2)，其中a＝1

(?4)??8?(?3)

3

?(?3) 42?(?

23

)?(?

34

)?(?0.25)

10

初一数学计算题 初一数学计算题练习

?2?34

9?(?2

3)?(?1) 7a?5b?(15a?b) 24

?3(2x2?xy)?4(x2?xy?6)

先化简，再求值：

(?2)?[(?11325141172)?()]?|?|?(?5) 9?(?15)?(2.5??3?1) 2242582814(?4a2?2a?8)?(12a?1)，其中a?12

当x??

(?2)?2?(?4)?312,y??3时，求代数式3(x?2xy)?[3x?2y?2(xy?y)]的值。[www.61k.com］ 221

4 ?10?[(?4)?(1?3)?2] 322

22化简求值： 5a?[3a?2(2a?3)?4a]，其中a??1

2

11

初一数学计算题 初一数学计算题练习

?20?(?14)?(?18)?13 ?1.6?[(?

2)?(?3)?(?2)]

2

3

2

2(3y?1)?7(y?2)?3

(－8)+10+2+(－1) 5+(

(－0.8)+1.2+(－0.7)+(－2.1)+0.8+3.5

(－17)+59+(－37) (

3

xx?13?32

?4?

5x?36

－6)+3+9+(－4)+(－7) 1242

+(－

3

)+

5

+(－

12

)+(－

13

)

－18.65)+(－6.15)+18.15+6.15 12

初一数学计算题 初一数学计算题练习

(－4

(－1.9)+3.6+(－10.1)+1.4 (－7)+(+11)+(－13)+9 33

31123

13

12

14

14

12

)+(－3)+6+(－2) (－0.5)+3+2.75+(－5)

+(－2.16)+9

811

+(－3

2125

) 49

1921

+(－78.21)+27

221

+(－21.79)

先化简再求值：4a2b＋(－2ab2＋5a2b)－2(3a2b－ab2),其中a=－1,b=－

4x-3(5-x)=6

x-35

-x-43

=1

23

(-3+3)×[(-1)

2

2008

-(1-0.5×

13

)]

13

初一数学计算题 初一数学计算题练习

-22×|-3|+(-6) ×(-

3(-2x-5)+2x=9 2x-

化简求值：2x2+(-x2+3xy+2y2)-2(0.5x2-

0.4x?0.9

0.5?0.03?0.02x

0.03?x?5

2（- ?4?3

7+3

4-5

14）?（-7） 512)-|+18|÷(-12) 13=2x?16-1 12xy+y2),其中x=12,y=3.

33?3?1???1??1?（0.28-14+4） ?1???2?????2? 1432??2???4???12

35?31

4?0.71?1

4?3.5?（-32.5）-7.1?0.075

212???1?(?3)2?2?????4?22???? 4?3??3?

14

初一数学计算题 初一数学计算题练习

化简求值 ?8xy?3x2??5x?2?3xy?2x2?，其中x=－1，y=1

（－3）2

－2 3

÷13

×3 （1－16

＋

34

）×（－48） 2x

27

（3x＋7）＝2－1.5x

80% ·x ＝（x＋22）·75%

?3???1??1?3??

?1?

?5?3?

?

9? ?

2

12

－[2－(1－

123

×0.5)]×[3－（－2）2

]

＋3＝x－1

2x?1x?13

－

56

＝1

?4133

?4

4

?2

13

?(?3

14

)

15

－

初一数学计算题 初一数学计算题练习

?4??3???0.8???3?1??2362 ?(?2)?3?(?2)?(?1)??(?3)?3?(?2)???5?6??

3x?7?14?4x x

3?1?2??4????4 2?3?

2x?3

3?1?2?3x

2

222先化简，再求值3x?(2x?x?1)?2(?3?x?x)，其中x??3

[15.25－13－（－14.75）]×（－0.125）÷

－12?[1

16 123 （34?56?712）÷32 34?8×（－3）]×0－（－5） 3225?6÷（－2）?（－4）×212

初一数学计算题 初一数学计算题练习

x?2(x?1)?3x ?(y?x)?(5x?2y)

3x?4?7x?8

3?x2

?23

(x?4)

-14-（-2）3×5+0.25÷（-1）2 2

-42

×538

??5?(-4)×

122÷4 4

?

x?(7?8x)?3(x?2)

x?

x?12

?2?

x?23

25?

34

???25??

1

2?25????1?

?4??

－12

－[2－(1－

13

×0.5)]×[32－（－2）2

]

17

初一数学计算题 初一数学计算题练习

1311??2362

(－+－)×（－48） ?3?(?2)??(?1)??(?3)??3?(?2)

66412??

15＋(―14

)―15―(―0.25) 292324

×(-12) 25

（—5.3）+（—3.2）—（—2.5）—（+4.8）

??48??6???25????4?

18

(?81)?

944

?

9

?(?32)

×3―(―25)×1＋25×(－14

2

4

)

（—314

）+（+8

12

）—（—5

34

）(?

253

?

34

?

6

)?(?12)

初一数学计算题 初一数学计算题练习

-2 +|5-8|+24÷（-3） ??1??1?1?11??3??1?????2????3????1?

?77

100?2004?100

?121

3??1??1

??8?2?

?10?3??3

?3?3??

(?1.25)?8?1.25?(?8) -2

(-56)+(+3.5)+(-1

6)

?2?4?2??4??4??1.5?1.4???3.6??4.3???5.2? 13?16?14)?(-24) 2-1?1?38???2? ???5.7????1.8??2.3 19 (

初一数学计算题 初一数学计算题练习

31111?1?

8???????5?? ???

?4?

4

32

?(?4)3

?3?843?(?6)?(?13?18);

(10x3

?6x2

?5x?4)?(?9x3

?2x2

?4x?2)

15?(7?5x)?2x?(5?3x)

1?3?y?13?y?8??

?1 ???

20

3243|?32?(?3)2

|?101

202

2

21

?

3

8x?[3x?(7x?2)?4]

2x?16

?5x?18

?1

x0.18?0.03x0.5?0.02?1

初一数学计算题 初一数学计算题练习

?3?2???3?12?(?8)?(?11)?(?6) ?5???7?????7?

???2?3?1?

12?

??? ?34?24?

?31?36?(?2)2?2?(?6)

x?(?215

3)?6

(?3)2?[(?21

3)?(?4)]?1

12

?8?3???8??4.5?295?8 ?14?16??2???3?2? 2x?1?1 ÷4.5-3×| - 19 | 21 3.6

初一数学计算题 初一数学计算题练习

??2?2???4?2???1

??1??1?22??3??2?2???2????? 2??2???

??3??322?5????2???1?0.8????2???2?? 4??????

(－3)×(－9)－8×(－5) －63÷7+45÷(－9)

－3×22－(－3×2)3 (－0.1)3－

－23－3×(－2)3－(－1)4 (－)?23214?(－35) 2216?|-3|?(?0.25)?() 32

[11×2－|3÷3|－(－3)2－33］÷

22 34 229?(-112)－(－1.2)?0.4 ) 322

初一数学计算题 初一数学计算题练习

0.25???2?32???2???4?????1? ?3?????

?3?1.2???0.3?223?1??????3?22???3????1? ??2??2??32521

4???10? 2

1?32??2??0.5??2???8? ????????2

?3?4 2-7+4-3 2

4-（-2）3-33÷（-1） （-5）2×（-

(-2）2-（-1）3×（

35）÷（-925） 12-13）÷16-?1 25×34－（-25）×12－25×14

23

初一数学计算题 初一数学计算题练习

1÷[(-2)×0.5-(-2.24)÷(-2)]-12237 {41+[-9×(+1)-0.8]}÷(-52) 8

(-16)+(+27)+(+9)+(一24) (

(一3)×18+14

(?11

5)?(?34

5)

?36?(11

9?6?1

18)；

295一5)+(一2)+(+9)一(一8) ?9?40?25； (?2)?13?(?3) ?134?213?(?32)???3?； 24

初一数学计算题 初一数学计算题练习

22?3?2?3?(?2) ?20?(?14)?(?18)?13

2

5??11

2?(?21

4)?(?2.75) （－24）×（1

6－1

4+1

2）

-14-（-2）3×5+0.25÷（-1

2）2 25?3

4???25??1?1??25????2?4?

设A=2x3+3x2-x, B=4x3+8x2-2x+6,当x=

12时，求A-12B的值

(5a－3b)＋[(a＋b)－(5a＋3b)]，其中a＝－1，b＝1

222222

—

25 25?(?110) 9—（—3）

初一数学计算题 初一数学计算题练习

（—5）—5 （—3

14

）+（+8

12

）—（—5

34

）

（—5.3）+（—3.2）—（—2.5）—（+4.8） 15＋(―1)―15―(―0.25)

4

(?81)?

94?49

?(?32) 29

2324

×(-12)

4

2

4

25×3―(―25)×1＋25×(－1) ??48??6???25????4?

12—（—18）+（—7）—15 (?

23?34?56

)?(?12)

26

初一数学计算题 初一数学计算题练习

5?122?2??2x?x?1??6?x?x?2?，其中x??33 ?2?

-2+|5-8|+24÷（-3） ??1??1?2? ?1?11??3??1?????2????3????1? 4?2??4??4?

?7

100?2004?7

100 ?1.5?1.4?3.6????4.3?? 5.2??

?12

1?1?1?2???10???8??3? ??9????19?3?3?3?3????2?9……???99?

??1????2????3????4??……???99????100? (

(?1.25)?8?1.25?(?8) 13?16?14)?(-24)

27

初一数学计算题 初一数学计算题练习

51?1? -2-??? (-)+(+3.5)+(-) 213

8?2?

??5.7????1.8??2.3

1

3?1

2?1

4?1

3

2

|?32?(?3)2|?10120

21?2

3

8x?[3x?(7x?2)?4]

668????1?34?? ????5??432?(?4)3?3?843?(?6)?(?13?18); (10x3?6x2?5x?4)?(?9x3?2x2?4x?2) 15?(7?5x)?2x?(5?3x) 28

初一数学计算题 初一数学计算题练习

2x?1?5x?1?1 1?1???y?y?8?1 68

x18?0.03x0.5?0.

0.02?1

3??3??29

本文标题：初中数学计算题训练-分析计算题训练
本文地址： http://www.61k.com/1095380.html