一 : 2006年药学专业知识（一）药物分析部分模拟试题一答案

二 : 数学分析_各校考研试题及答案

2003南开大学年数学分析.

一、设w?

f(x?y,x?y,x)其中f(x,y,z)有二阶连续偏导数，求wxy

解：令u=x+y,v=x-y,z=x则wx?fu?fv?fz；

wxy?fuu?fuv(?1)?fvu?fvv(?1)?fzu?fzv(?1)

二、设数列{an}非负单增且liman

n??

?

1

nnnn?a2???an]a，证明lim[a1

n??

?a

1

nnn

解：因为an非负单增，故有an?[a1?a2???an]n1nn

?(nan)

由

n??

liman?a；据两边夹定理有极限成立。［www.61k.com]

?2

三、设f(x)??xln(1?x),x?0试确定?的取值范围，使f(x)分别满足：

?

0,x?0?

（1） 极限limf(x)存在

x?0?

（2） f(x)在x=0连续

（3） f(x)在x=0可导 解：（1）因为

xxlimf(x)=limx?ln(1?x2)=limx?[x2????(?1)n?1?o(x2n)]极限存在则

x?0x?0x?02n

?

?

42n

?

2+??0知???2

??2

x?0

?

(2)因为limf(x)=0=f(0)所以要使f(x)在0连续则?

?(0)?0所以要使f(x)在0可导则?（3）f?

四、设f(x)在R连续，证明积分?解；令U=x

2

??1

22

f(x?y)xdx?ydy与积分路径无关 l

?y2则?lf(x2?y2)xdx?ydy=1?lf(u)du又f(x)在R上连续故存在F（u）

2

使dF(u)=f(u)du=f(x2?y2)xdx?ydy

所以积分与路径无关。 （此题应感谢小毒物提供思路） 五、

设

f(x)在

M

[a,b]上可导，

f(

a?b

)?02

且

f?(x)?M

,证明

b2 ?af(x)dx?4(b?a)

证：因f(x)在[a,b]可导，则由拉格朗日中值定理，存在

数学分析试题 数学分析_各校考研试题及答案

??(a,b)使f(x)?f(a?ba?b)?f?(?)(x?)22

a?b)dx2即有?b

abf(x)dx?

b

aa?f?(?)(x?a?ba?ba?ba?bMb?2??f(?)(x?)dx?M[?a(?x)dx??a?b(x?)dx]?(b?a)2

22242

六、设{an}单减而且收敛于0。[www.61k.com）

a) 证明?ansinn发散 ?ansinn收敛

unli?1n??vn其中b) 证明un??(aksik?aksikn)；

vn??(aksink?aksink)

证：（1）因为?sink?1

1s2而{an}单减而且收敛于0据狄利克莱判别法知

?ansinn收敛

（2）因为正项级数?ansinn发散则?aksink??(n??)又由上题知

un?1 n??vn?aksink有界故有lim

??1e?tx??七、设F(t)sinxdx 证明 x

???txe（1）1?sinxdx在[0,??)一致收敛 x

（2）F(t) 在[0,??)连续

证：（1）因???sinx?tx收敛（可由狄利克莱判别法判出）故在t>=0上一致收敛；又e1x

在x>=1,t>=0 单调且一致有界0?

（2）?t0e?tx?1(?x?1,t?0)由阿贝尔判别法知一致收敛 ?[0,??),??,??0使t0?[?,?]由上题知，F（t）在[?,?]一致收敛，

数学分析试题 数学分析_各校考研试题及答案

且由e?txsinx在（x,t）?[1,??)?[?,?]上连续知F（t）在[?,?]连续所以在t0连x

续，由t0的任意性得证

八、令{fn(x)}是[a,b]上定义的函数列，满足

（1）对任意x0?[a,b]{fn(x0)}是一个有界数列

（2）对任意??0，存在一个??0,当x,y?[a,b]且x?y??时，对一切自然数n,有fn(x)?fn(y)??求证存在一个子序列{fnk(x)}在[a,b]上一致收敛

证：对任意x?[a,b]，{fn(x)}是一个有界数列故由致密性定理存在一收敛子列，设为{fn(x)}，又令U={u(x,?x)x?[a,b]}则U为[a,b]的一个开覆盖集，由有限覆盖定

k

理，存在有限个开区间覆盖[a,b]，不妨设为u(x1,?x

于是对1)?u(xm,?x) m???0,能找到N一>0，?nk,nk?N，?xi,(i?1,2,?,m)12有

fn(xi)?fn(xi)?k2k2?3令??min{?x,?,?x}则由条件（2）知对上述???0 1m

???0,?x?[a,b],?xl使x?xl??，对一切自然数n,有fn(x)?fn(xl)?于是???3?0,?K?0,?k,t?K有nk,nt?N,?x?[a,b],?xl?[a,b]有

kttlkkkfn(x)?fn(x)?fn(x)?fn(xl)?fn(xl)?fn(xl)?fn(xl)?fn(x)t

?fn(x)?fn(xl)+fn(xl)?fn(xl)+fn(xl)?fn(x)??ttlkkk由柯西准则得

证。（www.61k.com）

2004年南开大学数学分析试题答案 ?f(x)??1. lim?x?a?f(a)???

2. 1x?aln?limex?af(x)f(a)x?a?ef'(a)f(a)?1 ?zy?fxy?2fy, ?xx

数学分析试题 数学分析_各校考研试题及答案

1y?2zy1yy?fx?yxfxx?fxy?2fy?fyx?3fyy=fx?yxfxx?2fy?3fyy xx?x?yxxxx

2ln(1?x)11?1?，即证2ln(1?x)?x?1? x1?x1?x

1设f(x)?2ln(1?x)?x?1?，f(0)?0， 1?x3.即证明

21?x2

f'(x)??1???0，f(x)?f(0)?0，证完。[www.61k.com） 221?x(1?x)(1?x)

4.2222xyln(x?y)dxdy??D=?2?0sin2?cos2?d??r5lnr2dr01=

?

08?2sin2?cos2?d??r5lnrdr= ?01? 72

5.设P=x2?y2，Q=?2xy，?Q?P??2y?，积分与路径无关，则 ?x?y

J??xdx?0

?2?33lnn?1n 6. n?1e??n?n??lnnlnnlnn???1??0??0??时，n?1n??1收敛，当时，级数n?1n??1发散，n,又当

原题得证

7.由拉格朗日定理，f(2n)?f(n)?f'(?n)n，其中n??n?2nlimf'(?n)?limn??n??f(2n)?f(n)?0，原题得证 n

时命题成立，

也成立，则当8.（1）应用数学归纳法，当若当n?1n?k时命题n?k?1时，

Fk?1?m

（2）

（3）由Fik,nfk?1}{?(Fk?fk?1)?Fk?fk?12F(x)，由归纳假设Fk?1连续。 {Fk?1(x)}单调递减趋于，{Fk?1(x)}与F(x)都连续，由地尼定理，该收敛为一致收敛。

9.(1)证明：?x0?(a,b),?x0?x1?x2

数学分析试题 数学分析_各校考研试题及答案

取??x1?x0,x1?x2,x2?x0，代入式中得， x2?x0

x1?x0f(x1)?f(x0)f(x2)?f(x0)，所以函数[f(x2)?f(x0)]即?x2?x0x1?x0x2?x0f(x1)?f(x0)?

g(x)?f(x)?f(x0)单调递增有下界，从而存在右极限，则 x?x0

f(x)?f(x0)； x?x0

f(x1)?f(x2)f(x2)?f(x3)f(x3)?f(x4)， ??x1?x2x2?x3x3?x4f?'(x0)?limx?x0??x1?x2?x3?x4，由题设可得

即f(x3)?f(x4)f(x3)?f(x4)f(x1)?f(x2)f(x1)?f(x2)从而lim， ??limx?xx?x2143x1?x2x3?x4x1?x2x3?x4所以导函数递增。（www.61k.com]

(2)参考实变函数的有关教材。

2005年南开大学数学分析试题答案

1.由于D关于x轴对称，被积函数关于y成奇函数，所以该积分为0 ?y?z?gz?0?y?zdu?y?z?x?x,由 ?fx?fy?fz2.，其中 求出 ?y?z?x?xdx?x?xhx?hy?hz?0?x?xgx?gy

?yhxgz?hzgx?zhxgy?hygx ?,??xgyhz?gzhy?xgyhz?gzhy

1n

3.lim?n??nk?1

M1k4?()2n??1dx4?x20??? 234.?0sintdt?2,1在x?(0,??)上单调一致趋于0，则f(x)在x?(0,??)上一致收x?t

敛，又sint在x?(0,??)上连续，则f(x)在x?(0,??)上连续。 x?t

泰勒公式5.由111e?

e?1?????1!2!n!(n?1)!，则

数学分析试题 数学分析_各校考研试题及答案

111e?e，后者收敛，则原级数收敛。［www.61k.com) e?1??????1!2!n!(n?1)!(n?1)!

6.由拉格朗日中值定理，

定理，原级数一致收敛。

?1xf()?nn1xf'(?)nn?MxM?2,后者收敛，由魏尔特拉斯2nn

由s(x)一致收敛，则可以逐项求导，s'(x)?

导

7.反证：设存在(x0,y0)有(?n?1xf'()也一致收敛且连续，故s(x)连续可n2?Q?P?Q?P?)(x0,y0)?0，不妨设(?)(x0,y0)?0，由连?x?y?x?y

?Q?P?)(x,y)?0，则存在?x?y续函数的局部保号性，知道存在一个邻域?,当(x,y)??时(

一个圆周C0??,

8.当0?x?Pdx?Qdy???D(?Q?P?)dxdy?0与已知矛盾。 ?x?ya时，f'(x)?f''(?)x?x 2

a?x?a时，f'(x)?f''(?)(x?a)?a?x，综上，f'(x)?g(x) 2

a(2)若对任意的x?(0,a)有f'(x)?g(x)，则在x?时，f''(x)不存在，矛盾。 2

(3)设当x?U时，f'(x)?g(x)?0当x?(0,a)\U时f'(x)?g(x)?0，两边对x积分即可

6.f(x)?g(x0)?g(x0)(x?x0) ，f(x0)?f(x)?g(x)(x0?x)，由g(x)在(a,b)上有定义，则g(x)在(a,b)上有界，则可以得到f(x)在(a,b)上连续。

(2)x0?x1?x2，则f(x1)?f(x0)f(x2)?f(x1)?g(x1)?x1?x0x2?x1，则

f(x1)?f(x0)f(x2)?f(x0)f(x)?f(x0)'则单调递增有下界，存在右极限，f?(x0)?x1?x0x2?x0x?x0

存在，同理f?(x0)存在，由极限的保不等式性可得

'

2003年中国科学院数学研究院数学分析试

数学分析试题 数学分析_各校考研试题及答案

题答案

A

1. limln(e?e)?limln(1?ex?0?x?0?x

A

x

AxBxB?Ax

)

B?Ax

A

（1）当B?A?0时，limln(e?e)?limln(1?e

x?0?x?0?xA

当A?0时，limln(e?e)?limln(1?e

x?0?x?0?xA

当A?0时，limln(e?e)?limln(1?e

x?0?x?0?x

A

x

Bx

Ax

Bx

B?Ax

Bx

)

)???

B?Ax

)???

A

当A?0时，limln(e?e)?limln(1?e

x?0?x?0?x

（2）当B?A?0时，

A

xBxB?Ax

)?0

A

limln(e?e)?limln(1?ex?0?x?0?x

A

xBxB?Ax

Ae

)?limx?0?x

B?A

x

?Alime

x?0?

B?Ax

A?B

= x2

A(A?B)lim

x2e

(A?B)x2

x???

?0

Ax

Bx

Ax

（3）当B?A?0时，limln(e

x?0?Ax

Bx

?e)?limln(2e)?limln2?

x?0?

x?0?

Ax

A x

当A?0时，limln(e?e)?limln(2e)?limln2?

x?0?

x?0?

x?0?

Ax

Bx

Ax

A

??? xA

??? xA

?ln2 x

当A?0时，limln(e

x?0?

?e)?limln(2e)?limln2?

x?0?

x?0?

Bx

Ax

当A?0时，limln(e?e)?limln(2e)?limln2?

x?0?

x?0?

x?0?

Ax

2. 当??0时， limf(x)?0，从而f(x)连续；

x?0

1

?0，f'(0)存在；

x?0x

11??1??2

cos 当??2时，f'(x)??xsin?x

xx

??1

当??1时，f'(0)?limxsin

limf'(x)?0,

x?0

数学分析试题 数学分析_各校考研试题及答案

3.即证：yx?xy?lny?ylnx?lnx?xlny， yx

f(t)?lny?ylnt?lnt?tlny，f(1)?0，f(y)?0 f'(t)?y?1?lny t

y?111?lny，g'(y)???0，g(y)?g(1)?0， tty当1?t?y时，设g(y)?

所以f'(t)?y?1?lny?0f(t)?f(1)?0， t

y?111?lny，g'(y)???0，g(y)?g(1)?0， tty当0?t?y?1时，设g(y)?

所以f'(t)?

4. y?1?lny?0f(t)?f(y)?0， t?

?

02?0??d?d?d????2? ??2?cos?02?cos?2?cos??

??d?d?1?4d?d?dtan?2?22?????4?4??04?cos2??04tan2??3202?cos?2?cos?204?cos2???2?

0d?2?? 2?cos?3

f'(x)?M，积分lnf(b)?lnf(a)?M(b?a)矛盾 f(x)5.假设存在常数M，0?

?z?1?rcos??6.作代换?x?rsin?cos?

?y?rsin?sin??

V??d??02?120r2sin?d??

d??2cos?2cos?02(?1?rcos?) rsin?=?2?

0d??1200(?2r?2r2cos?)dr=

1

2?2?

0d??1arctan20161?cos2?1642[?(2cos?)?cos?d??2??()2?2(1?cos2?)]d?0332

数学分析试题 数学分析_各校考研试题及答案

=

xx2

?y2?z2?1的切向量为(,y,z) 7.椭球面9696

x

?y?z，切点为x?9,y?1,z?3和x??9,y??1,z??3 88883412

d?196260,D? 1313

8. ???0,???0,当???x??时，

???f(2x)?f(x)?A?? x

xf(x)?f()1?A?1? ???x22

2

xxf()?f()1?A?1? ?2??x222

4?

xxf(n?1)?f(n)1?A?1? ?n??x22n

2n

相加：

n

??k?11??k4f(x)?f(xx)n?nA1?? ??kkk?12k?14n令n??，所以f'(0)?A ???1yf(x)dx?????? 9?2?1x?y2?1???1

???1yf(x)dx?lim?lim?lim ?1x2?y2?1?y?0?y?0???y?0?1lim?y?0

数学分析试题 数学分析_各校考研试题及答案

由含参量积分的性质，limy?0??1?0lim???y?0?1?0

??

0?yf(x)y?dx?f(?)dx?f(0)y?0 1?0y2?x22y2?x2

0yf(x)y?dx?f(?)dx?f(0)y?0 2?2222??2y?xy?x???0

科院2006年数学分析试题参考解答

1求a,b使下列函数在x=0处可导:

?ax?b当x?0; y??2x?1当x<0.?

解：由于函数在x=0处可导，从而连续，由f(0?0)?b,f(0?0)?1得到b=1;

又由f?(0)?a,f?(0)?0得到a=0.即得。[www.61k.com]

?112 已知an?0,级数?,求证级数?.

n?1ann?1an?1?

证明: 用反证法。 ?11 由an?0知级数?，?均为正项级数。 n?1ann?1an?1?

假设级数11收敛，则lim?0，于是有?n??a?1a?1n?1nn?

1

?an111lim?lim?lim?1，从而由正项级数的比较判别法知级数?收n??n??n??nn?1an1?an?1an?1an?1

敛，矛盾，从而得证。

1

3 设m,n?0为整数,求积分xm(1?x)ndx的值. ?0

解：

数学分析试题 数学分析_各校考研试题及答案

1

设I(m,n)=?xm(1?x)ndx,则由分部积分法有0

m?111xm?1xm?1nnxn?1I(m,n)=?(1-x)d?(1?x)|??n(1?x)(?1)dx?I(m?1,n?1).m?1m?100m?1m?10n 1

从而

I(m,n)?

nnn?1nn?11I(m?1,n?1)?I(m?2,n?2)????I(m?n,0)m?1m?1m?2m?1m?2m?nn!1m!n!即得解。(www.61k.com） ??m?n?1(m?n?1)!

m!

（利用余元公式、换元、?函数更为简单）

f(x)4 设a>0,f(x)是定义在[-a,a]上的连续的偶函数,则?dx??f(x)dx. x1+e?a0

证明：由f(x)是定义在[-a,a]上的连续的偶函数知f(?x)?f(x),从而令x??t有aa f(x)f(?t)etf(t)dx??(?dt)??dt x?tt?1+e1?e1?e?aa?a

aaaaa?aaf(x)1f(x)etf(t)1从而?dx?(dx?dt)?f(x)dx xxt???1+e2?a1+e1?e2?a?a?a

11?[?f(x)dx??f(x)dx]?[?f(x)dx??f(x)dx]??f(x)dx得证。 2?a20000

5设函数f(x)在含有[a,b]的某个开区间内二次可导且f?(a)=f?(b)=0,0aaaa

则存在??(a,b)使得|f??(??|?

证明: 4|f(b)?f(a)|. (b?a)2

数学分析试题 数学分析_各校考研试题及答案

由Tayler定理,

a+b对x=?(a,b)有2

1f''(?1)(x?a)2,2!

1f(x)?f(b)?f'(b)(x?b)?f''(?2)(x?b)2.2!

而f'(a)?f'(b)?0,故有f(x)?f(a)?f'(a)(x?a)?

|f(b)?f(a)|?1|f''(?1)(x?a)2?f''(?2)(x?b)2|2!

令|f(?)|?max{|f''(?1)|,|f''(?2)|},则有

1b?a2(b?a)2

|f(b)-f(a)|?|f''(?)2()?|f''(?)|2!24

4即|f''(?)|?|f(b)?f(a)|.2(b?a)

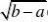
设实值函数f(x)及其一阶导数在区间[a,b]上连续,

而且f(a)=0,则

b

x?[a,b]

b126 max|f(x)|?|f'(t)|2dt),?a

?a1f(x)dx?(b?a)2?|f'(t)|2dt.2a2b

证明: 我们先来证明一个不等式，一般的称为Cauchy---Schwarz不等式，即

bb

定理1 ?af(x)g(x)dx?(?f2(x)dx)(?g2(x)dx)(f,g是[a,b]上的可积函数) aa1b212

数学分析试题 数学分析_各校考研试题及答案

设h(x)?f(x)?tg(x),则

h2(x)?f2(x)?2tf(x)g(x)?t2g2(x),两边从a到b取积分,有

b

2b2b2b2g?(x)dx

a?h(x)dx??f(x)dx?2t?f(x)g(x)dx?taaa

由等式右边对?t??都成立,知

b

2b2b??(2?f(x)g(x)dx)?4?f(x)dx?g2(x)dx?0.即证.

aaa

下面我们来证明题目:

(1)设max|f(x)|?|f(x0)|,则有Newton?Leibniz公式有x?[a,b]

x0x0

|f(x0)|?|f(a)|??|f(t)|dt??|f(t)|dt

aa

x0

即|f(x0)|?(?|f(t)|dt)2

a

x0

2x0

2x02

??|f(t)|dt?1dt?(x0?a)?|f(t)|2dtaaa

b

?(b?a)?|f(t)|2dt

a

两边开方即得证。(www.61k.com］

(2)同样，由Newton-Leibniz公式有

xx

f(x)=f(a)+?f'(t)dt??f'(t)dt

aa

xxx

即f2(x)?(?f'(t)dt)2??f'2(t)dt?12dt

aaa

等式两边x从a到b积分有

bb

2x?af'(x)dx??[(x?a)?f'2(t)dt]dxaa

bx

2 (x?a)2

??[?f'(t)dt]d2aa

x

??ab(x?a)2b(x?a)22f'(t)dt|??f'(x)dxaa222

b(b?a)2

?2

?f'(t)dt又得证。a2

数学分析试题 数学分析_各校考研试题及答案

设n是平面区域D的正向边界线C的外法线，则

7 ?u?2u?2uds???(2?2)dxdy???n?u?uCD

证明：

由Green公式有

?u?u?u?2u?2uds??dy?(?dx)???(2?2)dxdy ????n?x?y?u?uCCD

x2y2

8 设曲线?:2?2?1的周长和所围成的面积分别为L和S，还令ab

J???(bx?2xy?ay)ds，则J?

?

222222S2L?22. ?2a2b2S2LL?2 证明：由对称性知J??(bx?2xy?ay)ds??abds?abL?2??????22222

?dx(?1)n?1

9 计算积分? ?31+xn?13n?201

解：设I=

1dx 3?01+x

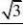
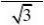
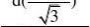
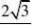
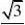
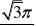
11dxdx则I???3?0(1?x)(1?x?x2)1?x0

1

??(

0111x?2?)dx31?x3x2?x?1

1112x?1?31?ln(1?x)|??2dx060x?x?13

1111112?ln2?ln(x?x?1)|??2dx020x?x?136

1?ln2?30

1?ln2?31 1?ln2?231?

数学分析试题 数学分析_各校考研试题及答案

(?1)n?1

为证明?=I，我们先来证明一个定理： 3n?2n?1?

Rn?1

定理2 设f(x)??anx在|x|<R内收敛，若?an也收敛，则 n?1n?0n?0?n?

R

?0

xRn?1 f(x)dx??ann?1n?0?事实上,f(x)在(?R,R)上收敛,从而内闭一致收敛,对于任何x?(-R,R),都有xn?1

f(t)dt???antdt???antdt??an,?n?1n?00n?000n?0nn?

?xn?1Rn?1

即有幂级数?an在(?R,R)上收敛,而?an,n?1n?1n?0n?0?x??x 从而在[0,R]上一致收敛,和函数在x=R处左连续,便有

R

?0?xn?1Rn?1f(x)dx?lim?an??anx??R?0n?1n?0n?1n?0?

??(?1)n?1

n?13n?3回到题目，看数项级数?收敛，设f(x)=?(?1)x，|x|<1,由定理2即知 3n?2n?0n?1

(?1)n?1

?=?f(x)dx=I.

n?13n?20?1

10 求曲线x?acost,y?asint(a?0)绕直线y?x旋转所成的曲面的表面积.

解: 这是星形线，充分考虑到对称性(x=0,y=0,x=y,x=-y)，有

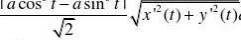
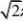
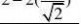
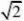
33

表面积S?2?2??

43?4

?

?a[?(?cos3t?sin3t)sintcostdt?

?

4223?4(cos??23t?sin3t)sintcostdt]

?a2?3?a2

5

北京大学2005

数学分析试题 数学分析_各校考研试题及答案

1设f(x)?

解x2sinx?1x?sinx2sinx，试求limsupf(x)和liminff(x). x???x???:

x2sinx?1首先我们注意到.f(x)?2sixn在x?sinxsxi?n的时候是单调增的(0,1] .

x2sinx?1x2sinxx2

并且在x充分大的时候显然有.sinx?2sinx?2,2x?sinxx?1x?1

所以易知在x???时,limsupf(x)?1.x???

当然此上极限可以 令x?2k???

2,k???这么一个子列得到.

sinxx2sin2x对于f(x)的下极限.我们注意到lim2?0,而liminf2?0,x???x?sinxx???x?sinx

所以有liminff(x)?0.x???

此下极限当然可以

令x?(2k?1)?,k???这么个子列得到.

1. (1)设f(x)在开区间(a,b)可微，且f?(x)在(a,b)有界。［www.61k.com]证明f(x)在(a,b)一致连续. 证明:设f?(x)在x?(a,b)时上界为M.因为f(x)在开区间(a,b)上可微.

对于?x1,x2?(a,b),由Lagrange中值定理,存在

??(x1,x2),使得f(x1)?f(x2)?f?(?)x1?x2?Mx1?x2.

这显然就是

Lipschitz条件,所以由x1,x2任意性易证明.f(x)在(a,b)上一致收敛.

(2) 设f(x)在开区间(a,b)(???a?b???)可微且一致连续，试问f?(x)在(a,b)是否一定有界。（若肯定回答，请证明；若否定回答，举例说明）

证明:否定回答.f?(x)在(a,b)上是无界的.

设f(x)?(1?x),显然此f(x)在[0,1]上是连续的根据.Cantor定理,闭区间上连续函数一致连续.所以f(x)在(0,1)上一致连续.

显然此1f(?x)?(在(x1上是可微的)1?11x而)2?x(1).

数学分析试题 数学分析_各校考研试题及答案

f?(x)??1

2(1?x)1在(0,1)上是无界的.

3．设f(x)?sin2(x2?1).

(1)求f(x)的麦克劳林展开式。［www.61k.com]

(2)求f(n)(0)。(n?1,2,3?)

解: 这道题目要是直接展开是很麻烦的.先对原式做一下变形.有f(x)?11?cos[2(x2?1)].再由cosx的Maclaurin展开式.有 22

???. 又由于

f(x)是偶函数，所以其展开式形式应该为：

f(x)?k0?k1x2?k2x4???knx2n??

比较系数有：k0?0，接下来，若p为奇数，则由

2k22k1?2pk?12(x?1)中x项系数为： f(x)??(?1)2i?1(2k)!

k2p????(?1)k?1?1???22k?1???C2pk?22k?(?1)k?1? ，此时令 ????????2k?p?1(2k)!2k?p?1(2k?p)!p!?????2??2?

p?1. 22k?p?2t?1,?k?t?

有k2p?2?(?1)2p!pp?12???t?122t?1?(?1)2?(?1)?sin2。 ?(2t?1)!2p!

2?(?1)?cos2 。综合得： 2p!pp?12t?1pp?12 同理可得：p为偶数时，k2p?

数学分析试题 数学分析_各校考研试题及答案

p?1??2p?1?(2p)!2(?1sin?2p为奇数??p!??f2p(0)?k2p?(p2?)?!pp?1??12?(2p)!?2?（-1cos2?p为偶数?p!???(n)2?1 f(0) ??fp(0?)0

?其中p?1,2,?3??????

4．试作出定义在R中的一个函数f(x,y)，使得它在原点处同时满足以下三个条件：

（1）f(x,y)的两个偏导数都存在；（2）任何方向极限都存在；（3）原点不连续 2

?xy?x2?y2?0?22 解： f(x,y)??x?y 。(www.61k.com)显然这个函数在 xy?0 的时候，有偏导

?0?x?y?0?

数存在

??fy(x,y)?? ??f(x,y)?x??

点也成立。 x(x2?y2)(x2?y2)2y(y2?x2)(x2?y2)2 ，而对于xy?0的时候，有??fy(x,y)?0 ，此式在原?fx(x,y)?0

?2?cos?sin? 对于任意方向极限，有limf(?cos?,?sin?)?lim?cos?sin?。??0??0?2

显然沿任意方向趋于原点。

此函数的方向极限都存在。最后，因为沿不同方向???趋向原点。不妨设

??，??（0），显然有不同的极限 4

cos?si?n与c?os。且其都不为0。所以该函数在原点不连续。 s?in

2225．计算xds.其中L是球面x?y?z?1与平面x?y?z?0的交线。 ?2

L

222 解：首先，曲线L是球面x?y?z?1与平面x?y?z?0的交线。因为平面

x?y?z?0过原点，球面x2?y2?z2?1中心为原点。

所以它们的交线是该球面上的极大圆。再由坐标的对称性。易知有

数学分析试题 数学分析_各校考研试题及答案

?

L

x2ds??y2ds??z2ds。（www.61k.com]

L

L

因此有

?

L

x2ds=

12?1222

ds(x?y?z)ds==。 ??LL333

6．设函数列{fn(x)}满足下列条件：（1）?n，fn(x)在[a,b]连续且有fn(x)?fn?1(x)（x?[a,b]）

（2）{fn(x)}点点收敛于[a,b]上的连续函数s(x)

证明：{fn(x)}在[a,b]上一致收敛于s(x)

证法1：首先，因为对任意x0??a,b?,有fn(x0)?S(x0)。且有fn(x0)?fn?1(x0)，所以

?nk，对于任意n?nk，有0?S(x0)?fn(x0)?

?

3

。

又因为fn(x)与S(x)在x0点连续。所以可以找到?x?0，当

x?x0??x0,且x??a,b? 时。有fnk(x)?fnk(x0)?

S(x)?S(x0)?有

?

3

，以及

?

3

同时成立。因此，当n?nk，x?x0??x0,且x??a,b? 时，

S(x)?fn(x)?S(x)?fnk(x)?S(x)?S(x0)?S(x0)?fnk(x0)?fnk(x)?fnk(x0)??。

如此，令?x0?{x:x?x0??x0}，所以有开区间族 {?x0:x0??a,b?} 覆盖了

?a,b?区间。

而S(x)在闭区间?a,b?上连续。由Heine-Borel 定理，从开区间族

{?x0:x0??a,b?}中可以选出有限个?x1,?x2,?x3,??xk，

使 ?a,b??

??

i?1

k

xi

。由?xi的选法。可由相应?xi与nki，当x??xi??a,b?，且

n?nki时，有S(x)?fn(x)??。

取N?max{nki:1?i?k}，当n?N时，且x??a,b?，有S(x)?fn(x)立。所以{fn(x)}在?a,b?上一致收敛于S(x)。 证毕。

?? 成

数学分析试题 数学分析_各校考研试题及答案

证法2：反证法.设存在某?0?0，对于任意n，有一xn，使得fn(xn)?S(xn)??0．又{xn}有界，由Bolzano-Weierstrass定理，所以其必存在

收敛子列{xnk}收敛于

?a,b?

中某值x0．因为对任意

x0??a,b?,有fn(x0)?S(x0)。（www.61k.com］

且有

fn(x0?)fn?x?nkp

1(，)所以

，当

nk?nkp

时，有

S(x0?)fnkx?0fn(x)??S)xk

p

?0

3

( ．)

p1

设某nk?nk，由S(x)与fnk(x)连续性．存在一

p1p

?0，当

x?x0??0,且x??a,b?时

有S(x)?S(x0)?

?0

3

以及fnk(x)?fnk(x0)?

p1

p1

?0

3

同时成立．显然，又因为

{xnk}?x0．所以存在K值，K?kp1 ．

当nk?nK时， xnk?x0??0成立．最后，当nk?nK时，有

S(xnk)?fnk(xnk)?S(xnk)?fnk(xnk)?S(xnk)?S(x0)?S(x0)?fnk(x0)?fnk(x0)?fnk(xnk)

p1

p1

p1

p1

＜?0．这与假设矛盾．

所以在?a,b?上，{fn(x)}是一致收敛于s(x)．证毕．

大连理工大学2005试题

数学分析试题解答

一、 计算题

1、

求极限：lim解：

a1?2a2?...?nan

,其中liman?a

n??n??n2

lim

a1?2a2?...?nan(n?1)an?1(n?1)ana

?lim?lim?(利用Stolz公式)

n??n??(n?1)2?n2n??2n?1n22

1x2

2、求极限：lime(1?)

x??x

?x

解：

数学分析试题 数学分析_各校考研试题及答案

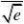
lime?x(1?1)x2(1?1x)

x??x?lim(x??e)x

(1?1)x?e(1?1)x(ln(1?1)1??)x??lim1?limx??1

x?x2

(1?111 ?elim2?o(2))?x????e?2

x2

(1?1)xe

?lim?x12e?x

x??e(1?x)?lim()x?lim()x?x??ex??e3、证明区间（0，1）和（0，+?）具有相同的势。(www.61k.com］ 证明：构造一一对应y=arctanx。

4、计算积分??1

Dy2?xdxdy，其中D是x=0,y=1,y=x围成的区域

解：

??1

y2?xdxdy??1

0?y11y0y2?xdxdy?

D?0ln(x?y2)|0dy??1 0ln(1?y)dy??10lnydy

?[(1?y)ln(1?y)?(1?y)?ylny?y]|1

?2ln2

5、计算第二类曲线积分：I???ydx?xdyC:x2?2y2

Cx2?y2，?1方向为逆时针。

解 ：

数学分析试题 数学分析_各校考研试题及答案

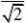
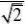
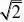
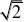
?x?cos??,??[0,2?)?y????

2??ydx?xdy换元

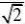
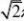
2?cos2?I????????d?22?C00x?y3?cos2??cos2?22

1?x2322(2?x)?(1?x)????2x?tan???????darctanx??dx2万能公式代换2??1?x(2?x)(1?x2)??3?1?x2

????16??dx?d???2???6???1?x2

1?

b?1b?a?1?6、设a>0,b>0,证明：???b?1?

证明： ?a????。[www.61k.com) ?b?

x?a?1????b?1?

?a?1????b?1?

bb?1?a??a?b????，构造函数f(x)??1??x??b???a?b???1???b?1?bb?1bb?1?f(b?1)

?a??a?b?????1???f(b)b??b??

a?ba?b?a?b?f'(x)??1?[ln(1?)?]?0(Taylor展开可以证明)?xxx?(a?b)??

所以f(x)递增，从而得证

二、 设f(x)为[a,b]上的有界可测函数，且

[a,b]x?f2(x)dx?0,证明：f(x)在[a,b]上几乎

处处为0。

证明：

反证法，假设A={x|f(x)≠0}，那么mA>0。

??1An?{x|f(x)?A??An。必然存在某个An,mAn?0nn?1 mAn2f(x)dx??0,矛盾2?n[a,b]

数学分析试题 数学分析_各校考研试题及答案

三、 设函数f(x)在开区间（0，+?）内连续且有界，是讨论f(x)在（0，+?）内的一

致连续性。［www.61k.com)

讨论：非一致连续，构造函数：

1

x

显然，f(x)连续且有界。但是f(x)在x?0时非一致连续f(x)?sin

反证法：如果一致连续，对???0,x?0,???0,当|x'?x"|??

11 ?sin|??.取??1x'x"

211令x'?,x"?。当n足够大的时候|x'?x"|???(2n?1)?n?(2n?1)n?

11|sin?sin|?1??x'x"|sin

?2x,y)?(0,0)四、

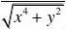
设f(x,y)?，讨论函数的连续性和可微性。

?0,(x,y)?(0,0)

解：

1）连续性：连续

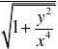
x?0y?2?x?0y?0?0

2）可微性：可微

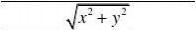
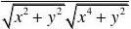
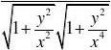
f(x,0)?f(0,0)?0x?0xf(0,y)?f(0,0)fy(0,0)?lim?0x?0yf(x,y)?f(x,y)?f(x,y)2?x?0x?0y?y?fx(0,0)?lim

?x?0y??0

五、 设f(x)在（a,b）内二次可微，求证：

a?b(b?a)2

???(a,b)，满足f(a)?2f()?f(b)?f"(?) 24

数学分析试题 数学分析_各校考研试题及答案

证明：

b?a)?f(x)，利用Cauchy中值定理：2

g(x)?g(a)b?a?g'(?)?f(??)?f(?),??(a,x)x?a2

利用Lagrange中值定理：令g(x)?f(x?

b?ab?ab?a)?f(?)?f"(?),??(?,??)222

b?ab?a2令?=,原式?g(x)?g(a)?()f"(?)22f(??

六、 f(x)在R上二次可导，?x?R，f"(x)?0,?x0?R,f(x0)?0

x???limf'(x)???0,limf'(x)???0，证明：f(x)在R上恰有两个零点。[www.61k.com） x???

证明：

(1)先证：当x???的时候，f(x)?0

?limf'(x)??,所以，当x的绝对值足够的时候,不妨设x?x1?0,x???

f'(x)??

2

当x?x1时，f(x)?f(x1)?(x?x1)

当x??2f(x1)?2.

??x1的时候，f(x)?0

(2)同理,当x???的时候，f(x)?0

又f"(x)?0?f'(x)为递增函数?f(x)先单调减少，在单调递增?f(x0)?0，根据连续函数的介值定理，在(??,x0),(x0,??)各有一个零点

七、 设函数f(x)和g(x)在[a,b]内可积，证明:对[a,b]内任意分割

?:a?x0?x1?...?xn?b,??i,?i?[xi,xi?1],i?0,1,2,....有|?|?0lim?f(?i)g(?i)?xi??f(x)g(x)dx

i?0an?1b

证明：

数学分析试题 数学分析_各校考研试题及答案

根据定义

?b

af(x)g(x)dx?lim?f(?i)g(?i)?xi|?|?0i?0

n?1

i?0n?1i?0n?1|?f(?i)g(?i)?xi??f(?i)g(?i)?xi|?|?f(?i)[g(?i)?g(?i)]?xi|i?0n?1

?max{|f(?i)|}?|g(?i)?g(?i)|?xiii?0n?1

n?1

i?0由于g(x)可积，所以?|g(?i)?g(?i)|?xi???i?xi?0，(?i为振幅)i?0n?1

?lim|?f(?i)g(?i)?xi??f(?i)g(?i)?xi|?0，从而得证|?|?0i?0i?0n?1n?1

(?1)n

八、 求级数：?

n?03n?1?

解：

?(?1)nx3n?1(?1)n(x3)n

?x?(?1,1]内收敛?3n?13n?1n?0n?0?

?(?1)(x)在

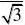
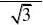
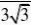
(?1,1]内一致收敛，所以可以逐项求导n3n

n?0

M(?1)n(x3)n1?(?x)3M?3

n3n(x?)'??(?1)(x)?3n?11?x3n?0n?0M

11?(?x)(?1)?lim??M???03n?11?x3n?0?nM?1?112 x?111)dxdx??dx??(?301?x01?x1?x?x2

ln(1?x)11d(x2?x)1111????d(x?)3601?x?x22?0?(x?)22

42

ln21ln2??|0??33

九、 讨论函数项级数?x(n2e?nx?(n?1)2e?(n?1)

n?1

2222??2222x)在(0,1)和(1,+∞)的一致收敛性 讨论：

1） ?x(n2e?nx?(n?1)2e?(n?1)n?1??x)?xlim(n2e?nx) n??220<x<1

数学分析试题 数学分析_各校考研试题及答案

xlim(ne

n??

2?n2x2

)?0

级数收敛，但不一致收敛。（www.61k.com］

1

取xn?,|Sn(xn)?0|?n不趋近于0，所以不一致收敛

n

2）

x>1

22

xlim(n2e?nx)?0

n??

(xe

?x2

)'?e

22

?x2

(1?2x)?0即xe

2

?n2x22

2

?

2

?x2

?

?

1e

n24

nn

?xn2e?nx?e?e?e

ee

????0,?x?1,?N??n?N,Sn(x)??

十、 计算

n22

??

?

x2dyd?z

2

2

ydz?dxz，其中dxdy?为圆锥曲面z2?x2?y2被平面

z=0,z=2所截部分的外侧。

解：

??

?

????(rcos??rsin??z)rd?drdz

?

??dz?rdr?(cos??sin?)d???zdz?

?

V

2

2

2

2

z

2

2

2

x2dydz?y2dzdx?z2dxdy????(x?y?z)dxdydz

z

rdr?d?

2?

?4?

十一、设f(x)在[0,1]上单调增加,f(0)>=0,f(1)<=1,证明：???[0,1],f(?)??

证明：

3

M?{x|f(x)?x3,x?[0,1]}m?infM

显然M非空,下证:f(m)?m3

反证法：如果命题不成立，那么显然f(m)?m3,不妨设f(m)?m3?r?0?x?m,f(x)?x

3

f(x)?f(m)?r?x3?m3

由于y?x3是连续函数，所以，对?r>0存在x'x'3?m3?r?0,与单调性矛盾。

十二、设f(x)在[0,+∞]上连续，

?

??

?(x)dx绝对收敛，证明：

数学分析试题 数学分析_各校考研试题及答案

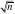
limx??0??xf()?(x)dx?f(0)??(x)dx 0n

证明：

limx??0??xf()?(x)dx?f(0)??(x)dx0n

??因为??(x)dx绝对收敛，当n足够大的时候(x)dx???(x)dx<?，000??

x因为f(x)连续，所以，当n足够大的时候f()?f(0)??n

??xx|f()?(x)dx?f(0)??(x)dx|?|f()?f(0)]?(x)dx|?f(0)?000nn

???|?(x)dx|?f(0)?0??

由于?的任意性，所以命题成立

十三、设an?0，证明：

??ln(1/an)?1时，级数?an收敛 当下极限liminfn??lnnn?1

??ln(1/an)?1时，级数?an发散 当上极限limsupn??lnnn?1

证明：（1）

ln(1/an)?1?2r?1n??lnn

ln(1/an)即n足够大的时候?1?r?1?1/an?n1?r lnn

an?n?(1?r)liminf

根据积分判别公式，知命题成立

（2）

ln(1/an)?1n??lnn

ln(1/an)即n足够大的时候?1?r?1?1/an?n1?r lnn

an?n?(1?r)limsup

根据积分判别公式，知命题成立

苏州大学2004年数学分析解答

1.(20’)

数学分析试题 数学分析_各校考研试题及答案

x2?(arctanx)2

（）求极限1limx?0(arcsinx)4

解：原式=limx?04x3

12?6x2?2222x(1?x)?2(arctanx)?lim?limx?0x?04x3(1?x2)12x2?20x5

(2?6x2)(1?x2)?28x2?6x4

?lim?lim2x?0(1?x2)(12x2?20x5)x?0x(1?x2)(12?20x3)

8?6x282?lim??x?0(1?x2)(12?20x3)123x?(arctanx)?lim4x?0x222x?2(arctanx)1

(2)证明对任意自然数n，方程xn?xn?1?……?x?1在区间[0，上总有1]

唯一实根xn,并求limxnn??

证明：令f(x)?xn?xn?1?……?x?1

则f(0)??1?0,f(1)?n?1?0,x?[0，1]

因此f(x)在[0，上有零点1]

又f?(x)?nxn?1?(n?1)xn?2……?2x?1?0,x?[0，1]

所以f(x)在[0，上单调1]

从而f(x)在[0，上存在唯一的零点，1]也即方程xn?xn?1?……?x?1在区间[0，上总有1]唯一实根xn

因此xnn?xnn?1?……?xn?1

两边令n???,则有limxn1?1?limxn?n??1?xn??2n

2.(20')

数学分析试题 数学分析_各校考研试题及答案

1证明函数sin在区间（0，??）上不一致连续，但是对于任意a?0，在x

[a,??)上一致连续。［www.61k.com]

证明：（）法一：1

1111取x1?,x2?,则limsin?1?limsin?0n??n????2n?x1x2?2n?2

1从而sin在区间（0，??）上不一致连续x

111法二：取?0?，则???0,取x1?,x2?2??4n??2n?2

111x1?x2??,取N???4n?4n?4n?

11sin?sin?1??0x1x2

1从而sin在区间（0，??）上不一致连续x

(2)当x?[a,??)时

???0,???0,当x1?x2??时，有

sin111111?sin???x1?x2?2x1?x2x1x2x1x2x1x2a

11?sin??x1x2 取??a2?时，有sin

1即sin在[a,??)上一致连续。x

数学分析试题 数学分析_各校考研试题及答案

3.证明不等式tanxx??,x?(0,)xsinx2

tanx

x?sin2x?在x?(0,)上>0,令f(x)??2,显然f(x)在(0,)连续xsinx2xcosx2

sinx

下证f(x)>1

2sinxcosx?x2cosx?sin2x(2xcosx?x2sinx)f?(x)=x4cos2x

2xsinxcos2x?2sin2xcosx?xsin3x2xsinxcos2x?2sin2xcosx?xsinx(1?cos2x)??32xcosxx3cos2x

sinx(xcos2x?2sinxcosx?x)?x3cos2x

令h(x)?(xcos2x?2sinxcosx?x),x?(0,)2

h?(x)?cos2x?2xcosxsinx?2cos2x?2sin2x?1?2xcosxsinx?3sin2x

?sinx(2xcosx?3sinx)?0,x?(0,)2

所以h(x)单调递增，h(x)?limh(x)?0x?0??

从而xcos2x?2sinxcosx?x?0

又sinx?0,x3cos2x?0,x?(0,)2

所以f?(x)?0,即f(x)在(0,)单调递增2

sin2x所以f(x)>limf(x)?lim2?1x?0x?0xcosx

即f(x)?1

tanxx?从而?,x?(0,)xsinx2

??

数学分析试题 数学分析_各校考研试题及答案

4.(20')(1)设f(x)在[1，+?）上非负递减，证明n?+?时?f(k)??k=1nn1f(x)dx有极限L，且0?L?f(1)

111??……??lnlnn,n?2,3……2ln23ln3nlnn

证明数列{an}收敛。[www.61k.com](2)设an?

证明：（）令1an??f(k)??f(x)dx

k=11nn

则an??f(k)??f(x)dx??f(k)???k=11k=1k?1nnnn?1k?1kf(x)dx??f(k)??f(k)(k?1?k)?f(n)?0k=1k=1nn-1所以an有下界

又an?1?an?f(n?1)??

从而an单调递减

因此{an}收敛且a1?f(1)?an?0,两边令n??,有0?L?f(1)

（2）.令f(x)=

nn?1nf(x)dx?f(n?1)?f(?),其中??（n,n+1)由于f(x)在[1，+?）上非负递减，所以f(n?1)?f(?)?01xlnxnn?1n?1

1k?10an??f(k)??f(x)dx??f(k?1)??k?2f(x?1)dx

??f(k?1)??k?1

n?1n?1n?11f(x?1)dx??f(x?1)dx0n?1

1

11有（）知道1?f(k?1)??k?11f(x?1)dx收敛1dx00(x?1)ln(x?1)

11可以知道0是g(x)的瑕点，x?0?(x?1)ln(x?1)x(1?x)

1111而?dx收敛，所以?收敛0x(1?x)0(x?1)ln(x?1)又令g(x)=?f(x?1)dx??

因此{an}收敛

数学分析试题 数学分析_各校考研试题及答案

5.（20’）设u(x,y)在平面上二次连续可微，x=rcos?,y=rsin?,(r?0)

?u(1)用u关于r,?的偏导数表示?x

?2u(2)用u关于r,?的一，二阶偏导数表示2?x

?u?u?u1?cos??rsin??x?r??

?2u?u?u?2u?2u?2u?2u(2)2?(cos??rsin?)??2cos??(?sin?)?sin??2rcos??x?r???r?r???r????2u

?r??2?2u

?r??sin???2u

2cos??2rcos?

?

6.(15')设a?0,求级数?n2

(1?a)nn=1

?

解：设f(x)??n2xn,f(x)的收敛区间为（-1，1）

n=1

f(x)?2n?1f(x?

x??nx,令g?(x)?),则g(

n=1xx)??nxn

n=1

令h?(x)?g(x)?x

x,则h(x)??xn?

n=11?x

则h?(x)?1

（1?x）2，g(x)?x（1?x）2

g?(x)?1?x

（1?x）3,从而f(x)?x(1?x)（1?x）3

1

??n21(1?1)(1?a)(2?a)

n?f(n=1(1?a)1?a)?

(1?1?

3a3

1?a)

??

数学分析试题 数学分析_各校考研试题及答案

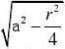
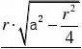
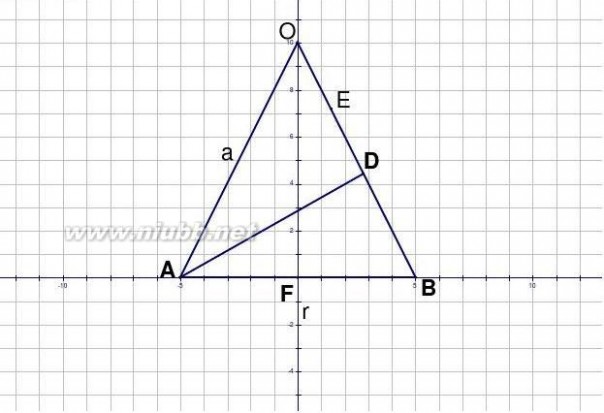
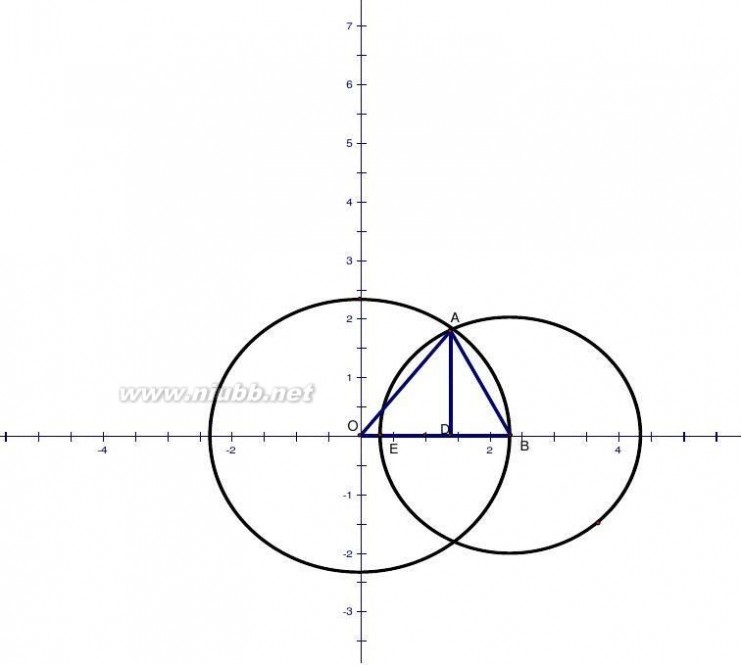
7.（20 ）设半径为r的球面s的球心在半径为常数a的定球面上，问：r为何值时，s位于定球面内部部分面积最大？

解：设s位于定球面内部部分面积为S,S为一球冠，则S=2?rh,其中h为球冠的高如图，ED=h,BE=r,AB=r

作OF?AB,则OF?ABAD?OB?OF?AB?AD??OBr2

BD??2a

r2

所以DE?r?2a

r2?因此S?2?rh=2?r(r?)?2?r2?r3

2aa

3?24令S??4?r?r?0?r?aa3

6?S??|4?4??r|4??4??0r?ar?aa33所以当r?4a时，S最大

3

数学分析试题 数学分析_各校考研试题及答案

数学分析试题 数学分析_各校考研试题及答案

８（.15')设函数f,g在x0的某个领域上可导，且g?(x)?0,limg(x)??x?x0如果limx?x0f?(x)f(x)?A,证明lim?A，其中A是实数。[www.61k.com）x?x0g(x)g?(x)

证明：取x0?x?x1,由Cauchy中值定理，令x1?x0

f(x)-f(x1)f?(?)有??A,(x1?x0)g(x)?g(x1)g?(?)

f(x)?

从而

所以f(x)-f(x1)(g(x)?g(x1))?f(x1)g(x)?g(x1)g(x1)f(x1)f(x)f(x)-f(x1)?(1?)?g(x)g(x)?g(x1)g(x)g(x)f(x)-f(x1)g(x1)f(x1)?Ag(x1)f(x)?A?(?A)(1?)?g(x)g(x)?g(x1)g(x)g(x)

令x1?x0，则???0,??1?0,使得当x0?x?x1?A??1时，有f(x)-f(x1)?－A?g(x)?g(x1)4

将x1固定，令x?x0，则由　g(x)??知道???0(??x1?A)使a?x??,有

g(x1)f(x1)?Ag(x1)??1,?g(x)g(x)2

于是

f(x)-f(x1)g(x1)f(x1)?Ag(x1)?f(x)??A?－A）＋??2???g(x)g(x)?g(x1)g(x)g(x)42

所以limx?x0 f(x)?Ag(x)

05苏州大学

数学分析试题 数学分析_各校考研试题及答案

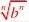
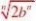
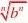
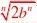
1.(20')求下列极限

（）1?a?b)n而??bnn因此?bn(2)lim(x?a11?),其中f?(a)?0,f??(a)存在f(x)?f(a)(x?a)f?(a)

(x?a)2

解：由于f?(a)?0,f??(a)存在，从而f(x)=f(a)+f?(a)(x-a)+f??(a)?o((x?a)2)2

11(x?a)f?(a)?(f(x)?f(a))lim(?)?lim()x?af(x)?f(a)x?a(x?a)f?(a)(f(x)?f(a))(x?a)f?(a)

(x?a)2

(x?a)f?(a)?(f?(a)(x-a)+f??(a)?o((x?a)2))?lim(x?a(x?a)2

(x?a)f?(a)(f?(a)(x-a)+f??(a)?o((x?a)2))2

(x?a)2

-f??(a)?o((x?a)2)?limx?a(x?a)2

(x?a)f?(a)(f?(a)(x-a)+f??(a)?o((x?a)2))2

1?f??(a)f??(a)?lim??x?a?(a)]22[f????f(a)(f(a)?f(a)?o((x?a))2

2.(18')设f(x)在[0，上可微，且1]f(x)的每一个零点都是简单零点，即若f(x0)?0则f?(x0)?0.证明：f(x)在[0,1]上只有有限个零点。［www.61k.com］

证明：设若不然f(x)在[0,1]上有无穷多个零点，不妨设{xn}?[0,1],f(xn)?0,n?1,2 则存在{xn}的一个子列{xnk},使得xnk?x0(k??)且f(xnk)?0，从而f(x0)?0

f(xnk)?f(x0)f(x)?f(x0)则f?(x0)?lim?lim?0与题设相矛盾！x?x0x?x0x?x0x?x0

所以f(x)在[0,1]上只有有限个零点。

数学分析试题 数学分析_各校考研试题及答案

3.(20')设f(x)是R上的2?周期函数，满足：（）1?

2?0

f(x)dx?0

(2)f(x)?f(y)?Lx?y,?x,y?R

证明：（1）f(x)在R上可以取到最大值，最小值 （2）maxx?Rf(x)??L

证明：（1）由f(x)?f(y)?Lx?y,?x,y?R知

???0,???0,取x0?[0,2?],?x?[0,2?],当x?x0??时，有f(x)?f(x0)?Lx?x0,则有f(x)?f(x0)??,

L

从而f(x)在[0,2?]上连续，既f(x)在[0,2?]上可以取到最大值，最小值又f(x)是R上的2?周期函数，所以f(x)在R上可以取到最大值，最小值。[www.61k.com）（2）令f(xM)?maxx?[0,2?]f(x)由?

2?0

取??

?

f(x)dx?0知?x0?[0,2?]，使得f(x0)?

12?

?

2?

f(x)dx?0

以下分三种情况讨论：(a)当xM?x0时

f(xM)?f(x0)?0?maxx?[0,2?]f(x)?0??L(b)当xM?x0时,由f(x)的周期性，得

2f(x0)?f(xM)?f(x0)?f(xM)?f(x0?2?)?f(xM)?L(x0?xM)?L(x0?2??xM)?2?L(c)当xM<x0时,由f(x)的周期性，得

2f(x0)?f(xM)?f(xM)?f(x0)?f(xM?2?)?f(x0)?L(x0?xM)?L(xM?2??x0)?2?L从而由(a)，(b)，(c)知道maxx?Rf(x)??L

4.（16?）将方程x?

?u?u

?y??0变为以极坐标r,?为自变量的形式，其中极坐标?y?x

变换为x=rcos?,y=rsin?,(r?0)

解：

?u?u?u??cos???r?(?sin?)?x?r???u?u?u??sin???r?cos??y?r??

?u?u?u?u?u?u?u

因此x??y??r?cos???sin??r2cos2???rsin?cos??r2sin2??r2

?y?x?r???r????

?u

所以方程为r2?0

??

数学分析试题 数学分析_各校考研试题及答案

5.（20?）设数列{an}有极限L，证明

（1）f(x)=?anxn在（?11，）上有定义

n=1?

（2）lim（1?x)f(x)?L?x?1

证明：（）因为1liman?L,若L?0,则有limn??an?1?1n??an

(事实上a?L?an?Lan?1a?a1?1?n?1n?n?1??2?)anananA

?

n=1所以L?0时，f(x)=?anxn的收敛区间为（?11，）

从而f(x)=?anxn在（?11，）上有定义

n=1?

若L=0,则liman?0，?N,当n?N时，（?11，）)?anxn?0,(当x?n??n2n

所以L=0时f(x)=?anxn在（?11，）上有定义

n=1

n?1（2）lim（1?x)f(x)?lim（f(x)-xf(x))=lim(ax?ax)??nn???nx?1x?1x?1

?n=1n=1???

?lim(an?1x??x?1n=0

?

x?1?n?1??anxn=1?n?1)?lim(a1x??an?1x?x?1n=1?n?1??anxn?1)n=1n????lim(a1x??(an?1?an)x?n=1n?1)?a1??(an?1?an)?a1?lim(an?1?a1)?Ln=1

数学分析试题 数学分析_各校考研试题及答案

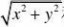
6.(20')求由圆锥体z?x2?y2?(z?a)2?a所围成的立体体积，其中a?0.

z?解：{?2z2?2az?a2?a?0x2?y?(z?a)2?a

(1)当2a?a2?0时，即a?2,or,a?0时

圆锥体与球体不相交，从而所围体积为0

（2）当2a?a2?0时，即a?2,or,a?0时

（a)a?0时，球体缩为一个点，从而所围体积为0

（b)a?2时,

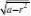
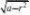
圆锥体与球体相切，此时z=1

令{x=rcos?,0?r?1,0???2?y=rsin?

331111V????dxdydz??d??dr??2?(a?(a?1)2??a2)00r2333

(3)当2a?a2?0时，即0<a<2时，圆锥体与球体相交2?1aV????dxdydz??d??dr?002?1ar331111?2?(a?(a?1)2??a2)2333

数学分析试题 数学分析_各校考研试题及答案

?,???x?0

7.（18‘）将函数f(x)?{4展成Fourier级数，

?

,0?x??4

?

1

并求?2

n=1(2n?1)解：显然f(x)在[??，?]上是奇函数因此an?0bn?21

?

?

???

?

f(x)sin(nx)dx?

2

???

?

1

?

f(x)sin(nx)dx?

??

1

?

f(x)sin(nx)dx

1?1

??f(x)sin(nx)dx??sinnxdx??sin(nx)dnx?0?0420n1111111n?11?(?1)cos(nx)|???cos(n?)??(?1)??02n2n2n2n2n2n?1

?

1

所以f(x)??sinnx

n?12n?1

?

?

1

(2)因为?sin(nx)单调递减?（0n??）

2n?1n=1

?

1

所以由Arbel判别法知?sinnx收敛

n?12n?11

?

?

??

?

?

[f(x)]2dx?

2

a0

??(an2?bn2)2n?1

2?

11

即??2

?n=1(2n?1)

?

）dx???[f(x)]dx???（?4

?

?

?

1

?

?

2

?2

8

?

?

3???

8.(18分)设f?x?在R上二次连续可微(其中x?(x1,x2,x3)),且在x处的梯度

0??

?

?

?????2f

,Hesse矩阵Q=?⑴f(x)在()?为正定矩阵.证明：

??x?xx0?

ij??

?

?f(x0)?0x

?0

处取到极小值；

⑵若?是Q的最大特征值，?是Q对应于?的特征向量，则f(x)从

?

x

?0

处沿着?方向增长

?

浙江师范大学2005年研究生

一（每小题8分，共48分）计算题

1、求极限 解

x?0x3(

lim

x2?sin2x?x??x)

.

数学分析试题 数学分析_各校考研试题及答案

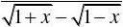
原式?limx?0x?sinxx?sinxlim 3分 3x?0x?0xx?2lim1?cosx

3x2x?0?x??x 5分 lim2x?0

sinx1?2lim? 8分 x?06x3

?

2、求级数 n2xn的和.

n??1

?

解 作f?x???n2xn?1，则

n?1

x??

?f(t)dt?nxn 0n?1

??

作g?x?

n?nxn?1，则 ?1

x?

?g(t)dt??xn ?x

0n1?x

?1

因此g?x??1

(1?x)2 x

?f(t)dt?x

0(1?x)

f?x??dx12x

dx(1?x)2?(1?x)2?x(1?x)3?1?(1?x)

于是 ，原式?xf?x??x?x2

(1?x) 2分 5分8分

数学分析试题 数学分析_各校考研试题及答案

???1?k?1?3、求级数 ???的和. ?kk?1?k?12k?1???

?111?1??1 2分 解 因?，故?n?1k?1kk?1k?1kk?1??1??1?x2k?1??为了求?，作f?x???， 4分 2k?1k?12k?1k?1?

2?x12k??1 5分 则f??x?????1?x?221?x1?xk?1?knkk

x1??dt?[?t?arctant]??x?arctanx 6分 f?x?????1?2?01?t?0?x

f(1)??1?π 4

π 8分 4因此，原式?f(1)?1?

11

4、求dyedx的值.

0y

1x

x2??x2解 原式?dxedy 4分

00??

2?exx?xedx????2012??e?1 8分 ??2??0

n15、求极限 limlim?cosm!πx? m??n??

解 因cosm!πx的周期为2m!， 2分 故当x为有理数时，存在正整数

n

n??qp和整数q使得x?p，这时当m?p时，cosm!πx?1，lim?cosm!πx??1， 4分

而当x为无理数时，cosm!πx?1，lim?cosm!πx??0 6分 n??n

数学分析试题 数学分析_各校考研试题及答案

?1,当x为有理数时因此，原式?? 8分 ?0，当x为无理数时

6、求极限 11??1lim?????? n?n?n???n?1n?2

解 原式?11 4分 ?kn??k?11?nlim

1n1dx ????ln?1?x???ln2 8分 1?x00

二（14分）已知实数列{an}收敛于a，且

a?a???aSn?n，用定义证明{Sn}也收敛于a.

证记bi?ai?a，K?b1?b2???bk，则???0，?正整数k，使得

an?a??

2(n?k), 3分 1K?因?0，故?正整数k1，使得?， 8分 nn2

令k2?max{k,k1}，则当n?k2时，有

Kn?k????? 14分 nn2a1?a2???anKb?bk?2??bn?a??k?1

nnn

三（20分）设??t?和??t?为二次可微函数，

u?x,y??x??x?y??y??x?y? ?2u?2u?2??0 证明?x?y?y?x

证 ?2u

ux???x???y??，uy?x?????y?? 5分 uxx?2???x????y??? ，uxy????x???????y???

数学分析试题 数学分析_各校考研试题及答案

uyy?x????2???y??? 15分

因此，左?2???x????y????2(???x???????y???)

?x????2???y????0?右 20分

四（20分）设

πf?x?在?0,π?上连续，证明 ππ⑴?xf?sinx?dx?20

⑵若

则?f?sinx?dx 0π0f?x??0，x??0,π?，且?f?x?dx?0， f?x??0，x??0,π?，

π

证 记I??xf?sinx?dx

ππ (1) 令x?π?t，则 π

I??xf?sinx?dx??(π?t)f?sint?dt?π?f?sint?dt?I 000

ππ因此，左?I?2?f?sint?dt?右 10分

（2）（用反证法）若不然，则?x0??0,π?使得f?x0??0，

由极限的保号性，存在开区间(a,b)使得x0??a,b???0,π?，且当x?(a,b)时，有f(x)?

πf(x)， 16分 2

这与?f?x?dx?0矛盾. 20分

ax2?bx?c五（16分）若不定积分?2dx为有理式，则a,b,c应满足什么条件？ xx?1ax2?bx?ccax?b?c解 因2，故 ??2?xx?1xx(x?1)

数学分析试题 数学分析_各校考研试题及答案

?a?0ax2?bx?c当且仅当?时，不定积分?2dx为有理式. 16分 xx?1?b?c?0

六（16分）若f?x?在?0,???上可微，lim

n??一个数列{?n}，使得{?n}单调，

证法1 因f(x)?0，求证?0,???内存在x??xlim?n???，且limf?(?n)?0. n??n?1n?2,2f?x?在?0,???上可微，故?n?Z?，f?x?在???上连续，在?2n?1,2n?内可导，从而由拉格朗日中值定理知，??n? ?2n?1,2n?使 f(2n)?f(2n?1)f(2n)?f(2n?1)f(2n)f(2n?1)?f?(?n)，即f?(?n)??2n?n?1 9分 2n?2n?12n?122而

n??f(x)f(2n)n2???，故由海涅归结原则知，limn?0，从因lim?0，limn??n??2x??xlimf?(?n)?0. 16分

f(x)证法2 由lim?0知，???0，?K?0，使得当x?K时， x??x

f(x)?? 2分 x

f(x)?1，?K2?2K1，使当x?K2时，?K1?0，使当x?K1时，x

f(x)1?，?Kn?2Kn?1，使得当x?Kn时， x2

f(x)1? 6分 xn

用数学归纳法，得到一个数列{Kn}，在闭区间[Kn,2Kn]上应用拉格朗日中值定理，??n??Kn,2Kn?，使得

f?(?n)?f(2Kn)?f(Kn) 10分 2Kn?Kn

由?n?2Kn??n?1知，数列{?n}单调增，由数列{Kn}满足Kn?2Kn?1?2n?1K1和

数学分析试题 数学分析_各校考研试题及答案

K1?0知n??lim?n??? 13分 f(2Kn)?f(Kn)f(2Kn)f(Kn)213????? 2Kn?KnKnKnnnn由f?(?n)?

知

n??limf?(?n)?0 16分

n?1

七（16分）设un(x)

证法1 ?k?1kn?kx(1?x)，证明un(x)在?0,1?上一致收敛. ?

nn?1x?x?1??2? ?0???，当x??0,??时，un(x)??xk?1?x1??6k?1

当x?1??,1时，由对称性知 un(x)?

当x????(1?x)k?1n?kn?1k?2? ??,1???时， un(x)??x(1?x)k

k?1n?1??(1??)k(1??)n?k k?1n?1

?(n?1)(1??)n 6分 因lim(n?1)(1??)?0，故对上述的?，?正整数K使得当n?K时， n??n

(n?1)(1??)n?2? 14分

n?1

综上，当n?K时，un(x)

这表明un(x)在?k?1kn?kx(1?x)?2?，对?0,1?中的一切x成立，??0,1?上一致收敛. 16分

1时 2证法2当x?

un(x)?x(1?x)?xk(1?x)n?k?2?

k?0n?2x(1?x)?n?11?x?xn?1? 3分 ???1?2x?

由Dini定理，要证un(x)在

下面分0?x??0,1?上一致收敛.只需证明un(x)在[0,1]上 11，?x?1，x?0，x?1这四种情形来证明 22

数学分析试题 数学分析_各校考研试题及答案

n??

即知极限函数一定连续. 7分 limun(x)?0

1而当x?(0,)时， 2

x2(1?x)2?1?x?n?2?xn?2?0 un(x)?un?1(x)?1?2x

1当x?(,1)时， 2??

x2(1?x)2?1?x?n?2?xn?2?0 un(x)?un?1(x)?1?2x

1当x?0或x?1时，un(x)?0，而当x?时， 2

n?1111n?1un()??kn?k?n 22k?122??

11n?1nn?2un()?un?1()?n?n?1?n?1?0 10分 22222

于是，?x?[0,1]，有un(x)?un?1(x)，

即un(x)关于n单调， 16分

武汉大学2003年

一、 判断下列命题是否正确（共5小题，每小题6分，共30分）：

1）单调序列{an}中有一子列{ani}收敛，则序列{an}收敛。[www.61k.com］

正确。不妨设{ani}收敛于a，利用单调性那么不难证明{an}也收敛于a

2）子列{an}的子序列{a2n}和{a2n?1}收敛，则序列{an}也收敛 不正确。只要{a2n}和{a2n?1}收敛于不同的极限，A、B那么{an}不收敛

3）序列{an}收敛，则序列{an}收敛，其逆命题也成立

不正确。序列{an}收敛=〉序列an收敛，但反之命题不成立如{an}:an?(?1)n

数学分析试题 数学分析_各校考研试题及答案

14）?an收敛，则an?o().

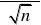
n

n

不正确。（www.61k.com)可以找到莱布尼兹级数{an}:an?

5）函数序列{un(x)}，x?[a,b]，满足对任意的自然数p和任意x?[a,b]，有以下性质：limun(x)?un?p(x)?0，则{un(x)}一致收敛。 n??

不正确。不妨设x?[0,1]，{un(x)}:un(x)?xn，

limun(x)?un?p(x)?lim(1?xp)xn?0。显然{un(x)}并非一致收敛。 n??n??

二、 计算题（每小题8分，共32分）

1

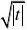
）设F(x)??

F(x)??x

?x?tdt,求

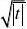
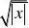
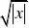
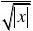
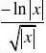
F'(0) xtdt?F'(x)?

F'(0)?x?0lnxx?lim??0（应用L’Hospital法则） x?0xxex?ln(1?x)2）求极限：lim x??x2

x2

x(1?x?o(x))?(x??o(x2))xxe?ln(1?x)lim?lim22x??x??xx（应用Taylor展开） 2xx2?o(x2)??3?limx??x22

3）

2222222计算积分：(x?y?z)dV,其中V是球面

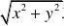
x?y?z?a和圆???V

锥面z?

数学分析试题 数学分析_各校考研试题及答案

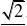
???(x

V

2

?y2?z2)dV????(x2?y2?z2)dxdydz????r2r2sin?drd?d?

V

V

??

2?

?

??

40

a

rsin?drd?d???d??4sin?d??

4

2?

?

a

a5

rdr?2??(1

5

4

(2?a5?

5

4）计算曲面积分I???x3dydz?y3dzdx?z3dxdy，S为球面x2?y2?z2?1的

S

外侧

I???x3dydz?y3dzdx?z3dxdy????(3x2?3y2?3z2)dxdydz?

S

V

???3r

V

4

sin?drd?d???3rdr?sin?d??

1

4

?2?

12?d??

5

三、 判断级数与反常积分的敛散性（共4小题，每小题9分，共36分）

1）?

??

1

sin2x

dx x

2）?

??

1

sinx

dx x?x

?

??

1

??1?cos2xsin2x

dx??dx

1x2x

?

??

1

??1?cos2xsin2x

dx??dx

1x2x

sin2(x?)sin2(x?)??1????1???d(x?) ?d(x??) ??dx??dx??12x?1112x442(x?)?2(x?)?

4242

??1??sin2x??1??sin2x??dx???dx。（www.61k.com］发散??dx???dx。发散11?11?2x2x42x?42x?

22

??

3

）n

4）?

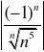
1

lnn

(lnn)

1(e

lnnlnn

?(lnn)

1

lnn

??

)

ln

?1，从而知发散 ??

1n

lnlnn

1nln

1?。收敛lnn

n

当n足够大时

数学分析试题 数学分析_各校考研试题及答案

22??x?y?2az四、 设a>0,求曲线?2上的点到xy-平面的最大最小距离 22??x?y?xy?a

解1：

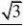
Lagrange乘子法：A?z??(x2?y2?2az)??(x2?y2?xy?a2)

?A???2(???)x??y?0???x?22??(???)(x?y)?0??A??2(???)y??x?0???y???(a,?a)取到最大值a????A?(x,y)??1?2a??0??a?z)取到最小值??3???A22?x?y?2az?0?????A??x2?y2?xy?a2?0????

解2：（初等数学的不等式方法）当z取到最值，即xy取到最值

1)xy?0时,x2?y2?2xy,

32x2?y2a2a?x?y?xy?(x?y)?z??22a3 222)xy?0时,x?y??2xy,222

12x2?y2

2a?x?y?xy?(x?y)?z??a22a222

ccan2五、 设0<c<1, a1=，an?1??。（www.61k.com)证明{an}收敛，并求其极限

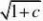
222

分析：只须满足a1?1

证明：

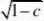
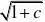
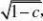
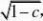
归纳法，假设an?1?can2an?1??22

an2?2an?can?1?an??0?an?1?1?2

又an?0。所以有界单调数列必然存在极限。

??1a1?1?解得极限=???1a1?1?

数学分析试题 数学分析_各校考研试题及答案

xn

六、 设f(t)在R上连续，证明：lim?f()dx?f(0)

n??1?x0

xn

证明：（考虑在（0，1）趋近于0）

1?x

1

对???0,?x?[0,?],?N,?n?N,xn??xn

递增1?x?

xn?nf()dx??f(?1),其中?1?(0,)?(0,?)?1?x1??0

1

?

?

1

xn?n1f()dx?(1??)f(?2),其中?1?(,)1?x1??2xnf()dx??f(?1)?(1??)f(?2)1?x

??0,??1

??0,??1

?

根据连续性f(?2)有界，lim?f(?1)?(1??)f(?2)?lim

f(?1)?f(0)

七、

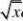
证明含参量非正常积分：?

?xydy，对任意??0在[?,??]一致收敛，

2

而在[0,??]上不是一致收敛的 证明：1）

?

?xy2

??

dy?

?e

?xy2

M

?lim

M???

?

?e

?xy2

?lim

M???

e?ydy

2

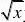
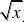
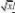
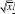
当x?[?,??)时，lim

M???

e

?y

2

dy??e

?y2

dy

显然是一致收敛的。[www.61k.com］

2）

数学分析试题 数学分析_各校考研试题及答案

?

?xy2

??

dy?

?e

?xy2

M

?lim

M???

?e

?xy2

?lim

M???

e?ydy

2

当x?(0,??)时，根据定义，利用反证法，如果一致收敛对于???0,?x?(0,??),?N,?n,M?N时

y2

??

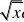
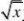
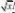
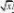
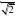
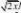
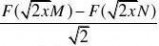
e?ydyedt?

?

t22

F(x)为标准正态分布的x上位数1

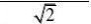
,右式?2N2显然与上述不等式矛盾。(www.61k.com］从而命题成立令M?N2,x?

武汉大学2004年攻读硕士学位研究生入学考试试题

科目代码：369

科目名称：数学分析

一、计算下列各题：

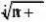
1．

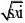
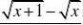
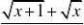
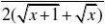
2.

lim(1n)

12nx??

lim(?2

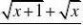
?...?n),(a?1)n??aaa?lim1 x??1?()n

1na?)??lim(n2?limn??1a?1a(a?1)x??1?a

?0

3.

4.

x0

?lim

x?0

sin(t2)dt

x3k?1

?

sin(x2)?lim(L'Hospital法则) ??arctan(2k?1)?arctan(2k?1) 2x?03xk?11???????3244

?arctan

?

1

2k2

5.

数学分析试题 数学分析_各校考研试题及答案

???...A(?)！?1?4?8?12B(?)????...3!7！11!15!

e?e??A(x)??3B(x)?sinxA(?)?2x?x?????e?e?3B(?)e?e??A(x)??B(x)??24?3

6. ???1??4?8?12

"设：F(x,y)??x(x?yz)f(z)dz,其中f(z)为可微函数，求Fxy(x,y)

yxy

F'(x,y)?y

"Fxy(x,y)??xyxy(?z)f(z)dz?(x?xy2)xf(xy) xx22'f()?(2x?3y)f(xy)?xy(1?y)f(xy)2yy

二、设x1?0，xn?1?

证明：

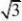
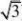
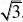
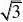
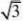
3(1?xn)，(n?1,2,3...)，证明：limxn存在，并求出极限 n??3?xn

23(1?xn)3?xnxn?1?xn??xn?3?xn3?xn

xn?1?(3xn?3?xn

(1)当xn?不难证明xn?xn?1?(2)当xn?不难证明xn?xn?1?

(a,b)内可导，g'(x)?0，三、设f(x),g(x)在[a,b]上连续，

证明：???(a,b)，使f(a)?f(?)f'(?)? g(?)?g(b)g'(?)

证明：（另外，还可以用上下确界的方法做）

数学分析试题 数学分析_各校考研试题及答案

构造辅助函数H(x)?f(x)g(x)?f(x)g(b)?f(a)g(x)

H(a)??f(a)g(b)?H(b)

根据Rolle中值定理，存在??(a,b),

H'(?)?f'(?)g(?)?f(?)g'(?)?f'(?)g(b)?f(a)g'(?)?0

整理：f(?)g'(?)?f(a)g'(?)?f'(?)g(b)?f'(?)g(?)

?g'(?)(f(?)?f(a))?f'(?)(g(b)?g(?))

?g'(x)?0,从而g(x)单调，g(b)?g(?)?0

从而原式成立

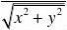
x,y)?(0,0)四、讨论f(x,y)?在（0，0）点的连续性和可微性

0,(x,y)?(0,0)?

解：（1）连续性：

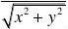
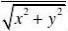
x,y)?(0,0)f(x,y)?0,(x,y)?(0,0)?0?limf(x,y)?lim?lim?limy?0 (x,y)?(0,0)(x,y)?(x,y)?(x,y)?(0,0)从而知连续

（2）可微性

?f3

??x?f3

??y

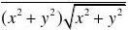
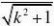
(x,y)?(ky,y)

?f?3显然不连续?x同样?f不连续。［www.61k.com］所以不可微?y

五、计算曲线积分I? ??ydx?zdy?xdz，其中L为圆周：L

?x2?y2?z2?a2(a?0)，L的方向是：从x轴的正方向看过去为逆时针方向。 ??x?y?z?0解：

数学分析试题 数学分析_各校考研试题及答案

?x2?y2?z2?a2

??

?x?y?z?0

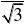
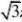
I???ydx?zdy?xdz???y(?dz?dy)?zdy?(y?z)dz

L

L

???(z?y)dy?(2y?z)dz,L'为L在yz平面的投影

L'

????3dydz??3?aS

?a22

六、计算曲面积分I?

??yzdxdy?zxdydz?xydzdx,其中S为由：x

S

?y2?R2,z?h

（h,R>0）及三个坐标面所围的第一卦限部分的外侧。(www.61k.com） 解：另外可以用Stokes公式做

I???yzdxdy?zxdydz?xydzdx

S

????(y?z?x)dxdydz??

Vh

h

?

??

20a0

a

(rcos??rsin??z)drd?dz

h

?20

?20

a0

??dz?(cos??sin?)d??rdr??zdz?d??dr

?ha?

七、证明：

解：

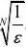
2

?h2a

4

?

?x

n?1

n

(1?x2)在[0,1]上一致收敛

(1)对???0,取?1-M

n

2

N

?

2

???1,x?[0,?],?N?2

?M

1?xM?N

x(1?x)?x(1?x)?xN???1?xn?N

(2)取?1-M

n

?

2

???1,x?[???，1],?N?1,?M

2

N

2

1?xM?Nx(1?x)?x(1?x)?(1?x)???1?xn?N

所以，对???0,只要N?

八、证明积分

根据Cauchy收敛准则知一致收敛

?

??

cos(x2)

dx在|p|?p0?1上一致收敛 xp

数学分析试题 数学分析_各校考研试题及答案

解：另外可以用积分判别法的Dirichlet定理做

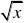
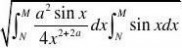
2??cos(x)??cos(x)dx??0xp?0px2

??cosx??cosx??dx?p?1?02xadx02x2

p?1a??(0,1)2

??cosxsinx????asinxdx?|??dx a01?a?02xa02x2x

对任意??0,不难证明N足够大的时候：

asinx?N2x1?adx?

从而得证M??

武 汉 大 学2005 年

|xn?xn?1|,|qn|?r?1 ，证明{xn}收敛。(www.61k.com) 一、设{xn}满足: |xn?1?xn|?|qn|?

证明：（分析：压缩映像原理）

1?r,则显然|qn|?m?12

|xn?1?xn|?|qn|?|xn?xn?1|?m?|xn?xn?1|令：m?

(此即压缩映像原理证明)以下证明压缩映像原理利用Cauchy收敛准则，对??,

n?p?1

|xn?p?xn|?

i?n?1?|x?xii?1|?(1?m?...?mp?1)|xn?1?xn|

mn?1|x2?x1|1?mp

n?1?m|x2?x1|?1?m1?m

1?m?ln|x2?x1|取N?+1,对任意的n?Nlnm

|xn?p?xn|??。从而知命题收敛

二、对任意δ > 0。证明级数?n?0??1在(1,1+δ)上不一致收敛。 xn

证明：（利用反证法，Cauchy收敛准则和定义证明。）

数学分析试题 数学分析_各校考研试题及答案

如果级数收敛，

那么对于???0,?x?(1,1??),?N,当n,M?N时

11?()M?N?1M111???n?n?n1xxn?Nx1?x

只需令x?(1,min{1??从而知非一致收敛

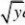
?(1,1??),代入上式，矛盾

三、设f(x)??|x?y|,求f"(x) 01

解，（本题利用莱布尼兹求导法则：）

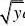
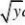
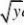
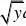
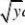
F(x，?)??b(x)

a(x)f(x，?)dx

b(?)?f(x，?)?F?b(?)?a(?)???f(b(?)，

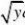
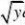
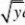
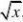
?)?f(a(?)，?)a(?)????????f(x)??|x?y|sin01

?x(x?y)sin?1(y?x)sin,x?[0,1]?x??0

?1f(x)???(x?y)sin,x?(1,??)0?1?(y?x)sin,x?(??,0)??0

?x?1x,x?[0,1]?x??0

?1f'(x)???,x?(1,??)0?1??sin,x?(??,0)??0

?2sinx?[0,1]?f"(x)??0,x?(1,??)

?0,x?(??,0)?

四、判断级数?lnlnnsinn的绝对收敛性和相对收敛性

n?2lnn??

解：（1）绝对收敛性：（主要使用放缩法）

数学分析试题 数学分析_各校考研试题及答案

首先，不难证明对于?n?N,|sinn|?|sin(n?1)|?2sin当M足够大的时候,lnlnM?1

????lnlnnlnlnnlnlnn|sinn|?|sinn|?|sinn|???lnnn?Mn?Mlnnn?Mlnn??1?A2

?

n??ln2n。(www.61k.com)显然，该级数发散。即不绝对收敛M

2??A

（2）相对收敛性：（A-D判别法）

<1>{an}收敛于0，?bn有界

<2>{an}有界，?an收敛

满足上述任意一个条件?anbn收敛

1

??1sinn?sinn?(积化和差)??11n?2cosn?2cos22

lnlnn1lim?lim?0(L'Hospital法则) n??lnnn??lnn

根据Dirichlet判别法，知该级数收敛??cos

五、计算I??(y2?z)dx?(x?2yz)dy?(x?y2)dz，其中Γ为曲线 ?

2222??x?y?z?a,z?0,0?2b?a，从z轴的正方向看过去，Γ是逆时针方向 ?22??x?y?2bx

解：（利用奇偶性做）

数学分析试题 数学分析_各校考研试题及答案

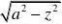
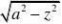
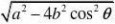
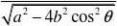
?x?????y??,代入方程得到?z?z??

?

?dx??4bcos?sin?d???2yd??x?2bcos2?

?????

??[?,]??dy?2b(1?2sin2?)d??2(x?b)d??y?2bcos?sin?

22??24byz???dz???d?

z??I??(y2?z)dx?(x?2yz)dy?(x?y2)dz

?

?

??2?xdy,(利用奇偶性，第一第三个积分为0)

?2

?

?b

2

??(cos2??1)cos2?d2??b??cos

2?2

?

2

?

2

?d?

?b2?

1?cos2?

2??b2?

??4

?

六、设f(x)在[0,1]上变号，且为连续函数，求证：minf(x)???|f'(t)|dt

[0,1]

01

证明：（画出函数图像，分两段讨论：） 利用介值定理，取??[0，1]，??inf{x|f(x)?0},不难证明f(?)?0

(1)xmin?[0,?]?f(x)min???(2)xmin?[?，1]?f(x)min??

??xmin

f'(t)dt???

?

?

xmin

|f'(t)|dt???|f'(t)|dt

010

1

xmin

f'(t)dt???

xmin

|f'(t)|dt???|f'(t)|dt

七、证明含参变量反常积分?

??

sinxy

dy在[?，??]上一致收敛，其中δ>0，但是

x(1?y)

在(0, ??)内不一定一致收敛。［www.61k.com］ 证明：

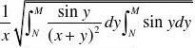
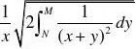
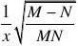
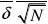
(1)?

??0

?Msinysinxy1??sinxy

dy??dxy?lim?dy

M???0x(1?y)x0x?xyx?y

?2

根据定义,???0,?N?2,?M?N

?

1Msiny|?dy|?xNx?y????。（利用了Cauchy-Schwarz不等式）

数学分析试题 数学分析_各校考研试题及答案

（2）???

0sinxydy在[0，??]不一致收敛x(1?y)

反证法：根据Cauchy收敛准则，??>0,?N,?M?N,当x?

xM?M时sinydyMsinxyxMsiny?xMxNM|?dxy|?dy?yNx?xyxNx?y?xNdyM2?MN??????xxxx1?M

当M足够大时，上式显然不成立，矛盾。(www.61k.com]故原命题成立

八、在底面半径为a，高为h的正圆锥内作长方体，其一面与圆锥地面重合，对面

四个顶点在锥面上，求长方体的最大体积。 解：

首先，由于顶点所在的平面和圆锥的交线为一个圆A，四个顶点组成在圆上。所以，易知长方体的底面中点和圆锥底面的中点重合。

另外，顶面的长方形对角线为圆A的直径d，即为定值。

1S顶?sin??d2,当且仅当底面为正方形的时候取到。2

不妨设，高为h'

12?V?Sh'?dh'顶?2122a?dhddhdd8a2h?3?V?d(h)?(2a?d)?(??(2a?d))??122aa22a2227?h?h'd

??a?h

本题还可以用Lagrange乘子法解决。但是，我觉得用初等方法也可以。

我不用Lagrange乘子法用意是学习了高等数学不应该把初等数学方法忘记了。

1)，f(x)在[0,a]上连续，在(0,a),在（0，a）内可导，以及在(0,a)九、设a?(0，

内取到最值，且满足f(0)=0,f(a)=a。证明：

1）???(0,a),使得f(?)?a?； 2）???(0,a),使得f'(?)?a

证明：1）命题有问题，取a=1/2,f(x)=5x-8x2

f(0)=0,f(1/2)=1/2

f(x)在5/16取到最值，但是f(x)-ax只在x=0,x=9/16等于0，与命题1矛盾。

数学分析试题 数学分析_各校考研试题及答案

2）构造函数g(x)?f(x)?ax。（www.61k.com］

由于f(x)为连续函数，所以g(x)在[0,a]上为连续函数，且一致连续反证法：如果命题不正确，那么g(x)?0,x?(0,a)

根据题设，存在??(0,a),使得f'(?)?0?g'(?)??a

由于g(?)?0,加上一致连续的条件，存在?'??,g(?')?g(?)

由于g(0)?0,利用连续性和介值定理，存在??(0,?'),g(?)?g(?)

根据Rolle中值定理，得到??(?,?),g'(?)?0?f'(?)?a

2004年上海交通大学 数学分析 一（14）设liman?a，证明limn??n??a1?2a2???nana? 22n

证 因xn?n2?? ，故利用Stolz公式，limn??y?yy?lim，得xn?1?xnn??xn

a1?2a2???nan(n?1)an?1n?1alim?lim?liman?1? 222n??n??n??n(n?1)?n2n?1n??2

二（14）证明sin(x2)在?0,???上不一致连续.

证

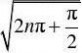
因xn?

22yn?sinxn?sinyn?1，

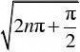
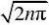
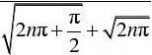
xn?yn????0， 故sin(x2)在?0,???上不一致连续.

三（14）设f(x)在?0,2a?上连续，且f(0)＝f(2a)，证明?x0??0,a?，使

f(x0)＝f(x0?a)

证 作g(x)?f(x?a)?f(x)（x??0,a?），则g(x)在?0,a?上连续，因f(0)＝f(2a)，故g(2a)??g(0)，

情形1 若g(0)?0，则取x0?0，则f(x0)＝f(x0?a)，

情形2 若g(0)?0，则因g(2a)g(0)??g2(0)?0，故由介值定理知，存在x0??0,a?，使得g(x0)?0，即f(x0)＝f(x0?a).

数学分析试题 数学分析_各校考研试题及答案

2??四（14）证明不等式x＜sinx＜x，x???0,? ??2?

证 作f(x)?sinx?π?，x??0,?，则因 x?2?

f?(x)?xcosx?sinxcosx?2(x?tanx)?0， 2xx

2sinx?π?在?0,?上严格单调减少，而limf(x)?1，， limf(x)?πx?0πx?2?x?2故f(x)?2sinx?π?2因此，在?0,?上，有?f(x)??1，即x＜sinx＜. ?πx?2?五 (14) 设收敛,且在上一致连续，证明= 0.

证 因在上一致连续，故，，使得当且时，有， 令，则由积分第一中值定理得，

，使得.

因收敛，故级数收敛，从而，即

，也即，故对上述的，存在，使得

当时，.

取，则当时，因

故存在惟一的，使得，易见，且，从而

六（14）设，，，证明级数收敛.

解. ，因，故只要证

收敛即可.

数学分析试题 数学分析_各校考研试题及答案

七（14）设在上连续，= 0 , ，，

证明在上一致收敛.

八（12）设在上连续，证明＝.

证 （1）（令，则，

（2）因在上连续，故，使得，，（3），记，不妨设，则

，

（4）

（5）因在上连续，故在上一致连续，故对上述的正数，，当且时，有

（6）因，记，则存在正整数，使得当时，有，

（7）当时，有，从而当时，有

（8）由（3）和（7）知，当时，有

九（12）设>0，＝＋，证明＝1

证 （1）要证＝1 ，只要证，

即只要证，即证

（2）因＝＋，故，

因此只要证，即只要证

（3）由知，单调增加，假如有上界，则必有极限，由＝＋知，＝＋，因此，矛盾.

数学分析试题 数学分析_各校考研试题及答案

这表明单调增加、没有上界，因此. （证完）

十（28）计算下述积分：

1．，其中D是矩形区域，

解 记

，

2．，其中S是曲面上的那部分正侧.

解 记（取下侧），

，则，由高斯公式知，

华中科技大学2004年《数学分析》试题及解答

数学分析试题 数学分析_各校考研试题及答案

以下每题15分

1．设，（），（）．求级数之和．

解 由（），得

．

2．设，（）．证明（）．此估计式能否改进？

证明 将、在点（）用Taylor公式展开并相减，则得

（），由于，因此得

．

此不等式可以改进为：（），因为时，上式．

3．设有处处连续的二阶偏导数，．证明

．

证明

4．设在上连续，在内可微，存在唯一点，使得，．设，（），

，证明是在上的最大值．

证明 （反证法），假设不是在上的最大值。(www.61k.com］由于，存在，当时，。

考察闭区域，显然，由已知在上连续，从而在上取得最大值，设为。显然在上，总有，因而必有：。当时，，因此

是在上的最大值。由假设，。

这与已知矛盾，可知假设不真。

5．设处处有．证明：曲线位于任一切线之上方，且与切线有唯一公共点．

证明 设为曲线上任一点，在该点处曲线的切线方程为

对曲线上任意点，按Taylor公式展开，得

由知，当时，，而为唯一公共点．得证．

6．求，是取反时针方向的单位圆周．

解 的参数方程：

7．设是连续正值函数，

．

证明（）是严格单调减函数．

证明 ，当

因此，（）是严格单调减函数。

数学分析试题 数学分析_各校考研试题及答案

8．设级数收敛，证明．

证明 由收敛知，在上一致收敛，从而左连续，即．对，有，

于是．

9．设在上连续，其零点为，．证明：积分收敛级数收敛．

证明 ，若收敛，则

，即收敛。[www.61k.com］

若不收敛，同理可知不收敛。

10．设，在上连续，（），当时，在上一致收敛于．证明：至少存在一点，使得．

证明 由在上一致收敛于，得知在上连续，且数列收敛于，即，由于，得，至少存在一点

，使得．

注 或用反证法：若对，有，由的连续性得，与上面相同证法，推出矛盾．

数学分析试题 数学分析_各校考研试题及答案

（www.61k.com]

数学分析试题 数学分析_各校考研试题及答案

(www.61k.com）

数学分析试题 数学分析_各校考研试题及答案

（www.61k.com)

数学分析试题 数学分析_各校考研试题及答案

(www.61k.com］

三 : 数值分析试题及答案

数值分析考试试题纸（A卷）

课程名称 专业年纪 一、计算题（本题满分100分，共5小题，每小题20分）

1． 已知函数表

(1) 求f(x)的三次Lagrange型插值多项式及其插值余项（要求化成最简形式）.

(2) 求f(x)的Newton插值多项式（要求化成最简形式）.

212

2. 已知A= 013 ，求 A 1， A ∞，A的LU分解.

612

3. 叙述m阶代数精度的定义，写出求 af x dx 的Simpson公式，并验证Simpson公式的代数精度为3阶.

12 4. 设矩阵A= ，求当α为何值时，解线性方程组Ax=b的Gauss-Seidel迭代法收敛. α1

5. 叙述最小二乘法的基本原理，并举例说明其应用.

b

数值分析试卷 数值分析试题及答案

(www.61k.com] 本文标题：分析化学试题及答案-2006年药学专业知识（一）药物分析部分模拟试题一答案
本文地址： http://www.61k.com/1063247.html