一 : 高一数学对数函数的图象及性质测试题及答案9

1．函数f(x)＝lg(x－2)＋5－x的定义域为(　　)
A．(2,5] B．(2,5)
C．[2,5] D．[2,5)
【解析】　要使函数有意义，只须使
x－2>05－x≥0，∴x>2x≤5
∴2<x≤5，函数定义域为(2,5]．故选A.
【答案】　A
2．函数y＝log13x在(0,3]上的值域是(　　)
A．R B．[－1，＋∞)
C．(－∞，－1] D．[0,1]
【解析】　由y＝log13x在(0,3]上单调递减，
∴ymin＝log133＝－1.∴函数值域为[－1，＋∞)．故选B.
【答案】　B
3．已知对数函数f(x)的图象过点P(8,3)，则f(132)＝________.
【解析】　设f(x)＝logax，则loga8＝3，∴a3＝8，
∴a＝2即f(x)＝log2x，
∴f(132)＝log2132＝－5.
【答案】　－5
4．已知f(x)＝lg1＋x1－x，x∈(－1,1)，若f(a)＝12，求f(－a)．
【解析】　∵f(－x)＝lg1－x1＋x＝－lg1＋x1－x＝－f(x)，
∴f(x)是奇函数，
∴f(－a)＝－f(a)＝－12.

一、选择题(每小题5分，共20分)
1．若某对数函数的图象过点(4,2)，则该对数函数的解析式为(　　)
A．y＝log2x B．y＝2log4x
C．y＝log2x或y＝2log4x D．不确定
【解析】　由对数函数的概念可设该函数的解析式为
y＝logax(a>0，且a≠1，x>0)，则2＝loga4＝loga22＝2loga2，即loga2＝1，a＝2.故所求解析式为y＝log2x.故选A.
【答案】　A
￥资%源~网2．函数f(x)＝lg|x|为(　　)
A．奇函数，在区间(0，＋∞)上是减函数
B．奇函数，在区间(0，＋∞)上是增函数
C．偶函数，在区间(－∞，0)上是增函数
D．偶函数，在区间(－∞，0)上是减函数
【解析】　已知函数的定义域为(－∞，0)∪(0，＋∞)，关于原点对称，且f(－x)＝lg|－x|＝lg|x|＝f(x)，所以它是偶函数．
当x>0时，|x|＝x，即函数y＝lg|x|在区间(0，＋∞)上是增函数，
又f(x)为偶函数，所以f(x)＝lg|x|在区间(－∞，0)上是减函数．故选D.
【答案】　D.
3．若函数g(x)＝logx(1－x)的定义域为M，函数f(x)＝
ln(1－|x|)的定义域为N，则M∩N为(　　)
A．[0,1) B．(0,1)
C．[0,1] D．(－1,0]
【解析】　由题意得x>0x≠11－x>0∴0<x<1.
∴M＝(0,1)
由1－|x|>0得－1<x<1，
∴N＝(－1,1)，
∴M∩N＝(0,1)．故选B.
【答案】　B
4．函数f(x)＝log2(x＋1)＋1(3≤x≤7)的值域是(　　)
A．[3,4] B．[2,3]
C．(0，＋∞) D．(1，＋∞)
【解析】　当3≤x≤7时，4≤x＋1≤8,2≤log2(x＋1)≤3.
【答案】　A
二、填空题(每小题5分，共10分)
5．若函数f(x)＝ax(a>0，且a≠1)的反函数的图象过点(3,1)，则a＝________.
【解析】　函数f(x)的反函数为y＝logax，由题意，loga3＝1，
∴a＝3.
【答案】　3
6．设g(x)＝ex　　　(x≤0)lnx　　　(x>0)，则g(g(12))＝________.
【解析】　g(12)＝ln12<0，
g(ln12)＝eln12＝12，
∴g(g(12))＝12.
【答案】　12
三、解答题(每小题10分，共20分)
7．求下列函数的定义域：
(1)y＝log3(2x－1)＋1log4x；
(2)y＝log(x＋1)(16－4x)；
【解析】　(1)要使函数有意义，则
2x－1>0，log4x≠0，x>0，即x>12，x≠1，x>0，

∴x>12，且x≠1.
故所求函数的定义域是12，1∪(1，＋∞)．
(2)要使函数有意义，则
16－4x>0，x＋1>0，x＋1≠1，即x<2，x>－1，x≠0，
∴－1<x<2且x≠0.
故所求函数的定义域是{x|－1<x<2，且x≠0}．
8．求函数y＝log13(x2＋2x＋4)的值域．
【解析】　∵x2＋2x＋4＝(x＋1)2＋3≥3，
∴定义域为R，∴f(x)≤log133＝－1，
∴函数值域为(－∞，－1]．

9．(10分)当x∈(1,2)时，不等式(x－1)2<logax恒成立，求a的取值范围．
【解析】　设f1(x)＝(x－1)2，f2(x)＝logax，要使当x∈(1,2)时，不等式(x－1)2<logax恒成立．只需f1(x)＝(x－1)2在(1,2)上的图象在f2(x)＝logax的下方即可．
当0<a<1时，由图象知显然不成立．当a>1时，如图所示，要使在(1,2)上，f1(x)＝(x－1)2的图象在f2(x)＝logax的下方，只需f1(2)≤f2(2)，即(2－1)2≤loga2，loga2≥1，∴1<a≤2.

二 : 小学生的数学题在一次测试中有38人参加，答对第一题的有26人，答

小学生的数学题

在一次测试中有38人参加，答对第一题的有26人，答对第二题的有24人，两题都答对的有18人，有多少人两题都答得不对？
注：该题是印刷题，小学三年级用。

---

1。根椐答对第1题的26人；答对第2题的24人；1和2题都答对的18人。则26+24-18=32人，也就是32人中，不是答对1题的就是答对2题的，没有空手的。

2。38-32=6人。这6人就是都没答对的。

答：有6人两题都没答对。

三 : 实数单元复习与测试题三套(含答案)

《实数》复习与回顾

一、知识梳理

1.平方根

（1）算术平方根的定义：一个正数x的平方等于a,即_____，那么这个正数x就叫做a

的________.0的算术平方根是_____。［www.61k.com)

（2）平方根的定义：如果一个数x的平方等于a，即_____，那么这个数x就叫做a的_______。

（3）平方根的性质：一个正数有_____个平方根，它们________； 0只有_____个平方根，它是_____；负数_____平方根。

（4）开平方：求一个数a的________的运算，叫做开平方。

2.立方根

（1）立方根的定义：如果一个数x的_____等于a，即_____，那么这个数x就叫做a的立方根。

（2）立方根的性质：每个数a都只有_____个立方根。正数的立方根是_____；0的立

方根是_____；负数的立方根是_____。

（3）开立方：求一个数a的________的运算叫做开立方。

3.实数

（1）无理数的定义：无限不循环小数叫做_____。

（2）实数的定义： _____和_____统称实数。

（3）实数的分类：①按定义分：________________________；②按性质分：________________________。

（4）实数与数轴上的点的对应关系：_____与数轴上的点是_____对应的。

（5）有关概念：在实数范围内，相反数、倒数、绝对值的意义和有理数范围内的意义_____。

4.实数的运算：

（1）实数的加、减、乘、除、乘方运算和_______一样，而且有理数的运算律对__________仍然适用。

（2）两个非负数的算术平方根的积等于这两个数积的算术平方根，算术平方根的商等

- 1 -

实数 实数单元复习与测试题三套(含答案)

于这两个数商的算术平方根，用式子表示为__________；__________。(www.61k.com）

二、考点例析

考点1 平方根、立方根的定义与性质

例1 （1）下列各数是否有平方根？若有，求出其平方根；若没有，说明理由。

①625 ②（－2）2 ③（－1）3

（2）下列各数是否有立方根？若有，求出其立方根。 ①1 ②－343 ③－22 27

分析：（1）要判断一个对象有无平方根，首先要对这个对象进行转化，直到能看出它

的符号，然后依据平方根的性质进行判断。（2）因为正数、0、负数均有立方根，所以所给各数都有立方根。

解：（1）①因为625>0，故其平方根有两个，即625=±25；②因为（－2）2=4>0，

故其平方根有两个，即±(?2)

平方根。

（2）由立方根的性质可知，所给各数均有立方根。 ①2=±2；③因为（－1）3=－1<0, 故其不存在11?； ②?343??7 ； 273

③－22的立方根?4。

说明：只有非负数才有平方根，这一点同学们一定要牢固掌握。

考点2 实数的分类与性质

例2 下列各数中： ?1－，7，3.14159, －π,,－4,0,0.3,8,,2.121122111222… 34

其中有理数有__________________________；

无理数有__________________________。

分析：对于、等应先化简再判断。 解：有理数：－1，3.14159,0,0.3,, 4

- 2 -

实数 实数单元复习与测试题三套(含答案)

无理数有：7,－π,10,－4,2.12112111222…… 3

说明：本题考查有理数和无理数的概念，要正确判断一个数属于哪一类，理解各数的意义是关键。（www.61k.com］

例3

分析：如果a表示一个正实数，那么－a就表示一个负实数，a与－a互为相反数；0

的相反数依然是0。一个正实数的绝对值是它本身；一个负实数的绝对值是它的相反数，0的绝对值是0。非零实数a的倒数是?1的相反数是 ；?的绝对值是 ；－81的倒数是 1211。 a

981=－，所以－11121解：2?1的相反数是1－2；?的绝对值是；－

1181的倒数是－。 9121

说明：解决此问题要牢记实数的性质，实数范围内一个数的相反数、倒数、绝对值的意

义和在有理数范围内的意义是一样的。

考点3 实数的运算

例4 （1

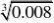
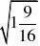
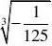
（2）化简?2(2?2)得（ ）

（A）－2 （B）2?2 （C）2 （D）42?2

分析：有理数的运算法则、性质、运算律等在实数范围内仍然适用，本例根据运算顺序直接计算即可。

解：（1）原式=0.2×?225?(?)=5

4151511??15?(?5)??75?75； 5444

（2）8?2(2?

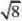
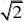
2)?

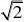
2??2?=－2。故选（A）。

说明：在实数范围内进行加、减、乘、除、乘方和开方运算，运算顺序依然是从高级到

低级。值得注意的是，在进行开方运算时，正实数和零可以开任何次方，负实数能开奇次方，但不能开偶次方。

- 3 -

实数 实数单元复习与测试题三套(含答案)

考点4 非负数

例5 已知x，y

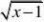
3(y?2)2?0，则x?y的值为（ ）.

（A）3 （B）－3 （C）1 （D）－1

分析：本题主要考查非负数的性质及其应用，非负数，即不是负数，也即正数和零，常

见的非负数主要有三种：实数的绝对值、实数的算术平方根、实数的偶次方。(www.61k.com）它有一个非常重要的性质：若干个非负数的和为0，这几个非负数均为零。利用这个性质可解本题，

解：由题意，得x?1?0，y?2?0，即x?1，y?2，所以x?y??1。故选（D）。 说明：非负数是中考常考的知识点，同学们应从其意义入手，理解并掌握它。 考点5 数形结合题

例6 已知实数 a、b 在数轴上的位置如图所示：试化简：｜a－b｜－｜a＋b｜ b的位置判断a－b和a+b的符号。 分析：要化简｜a－b｜－｜a＋b｜，需根据数轴上a、a∣<∣b∣解：因为a>0，b<0，且∣，所以a－b>0，a+b<0， 所以原式=（a－b）+（a+b）=a－b+a+b=2a

说明：数形结合是解决数学问题常用的思想方法，解题时必须通过所给图形抓住相关数的信息。 考点6 探究题

例7 阅读下列解题过程：

?

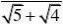
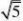
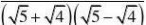
1?

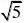
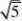
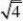
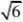
1?

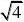
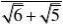
?2

?

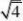
2

?

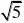
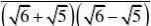
?请回答下列问题：

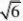
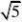
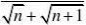
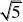
?2

?

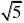
2

?（1（2

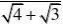
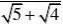
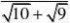
）、利用上面所提供的解法，请化简：

?

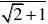
?n?2?

? - 4 -

实数 实数单元复习与测试题三套(含答案)

分析：通过阅读解题过程不难发现，每个式子的结果都等于分母中两个式子的差。(www.61k.com] 解：（1

?n?1?n。

（2）原式=2?1??2?4???4??????=?1。 说明：这类题目需要我们细心观察及思考，探究其中的规律，寻找解决问题的途径。

三、易错点例析

1、对平方根、算术平方根、立方根的概念与性质理解不透

理解不透平方根、算术平方根、立方根的概念与性质，往往出现以下错误：求一个正数的平方根时，漏掉其中一个，而求立方根时，又多写一个；求算术平方根时前面加上“?”成了平方根等等。

例1 （1）求61的平方根 （2）求的算术平方根 4

错解：（1）61?4255?；（2）81的算术平方根是9 42

错解分析：错解（1）中混淆了平方根和算术平方根；错解（2）中=9，81的算术平方根其实是9的算术平方根，而9的算术平方根是3。

正确解法：（1）?61255????；（2）的算术平方根是3。 442

例2 求64与－27的立方根。

错解：64的立方根是±4，－27没有立方根。

错解分析：64的立方根是4，只有一个，认为64的立方根有两个且互为相反数，是

与正数的平方根相混淆；－27的立方根是－3，错误地认为－27没有立方根是与负数没有平方根相混淆。

正确解法：因为43=64，所以64的立方根是4。因为（－3）3=－27，所以－27的立方根是－3。

2、忽略平方根成立的条件

只有非负数才能开平方，这一条件解题时往往被我们忽略。

例3 当m取何值时，?m2有意义？

- 5 -

实数 实数单元复习与测试题三套(含答案)

错解：不论m取何值时，?m2都无意义。［www.61k.com］

错解分析：考虑不全，漏掉了m=0时的情况。

正确解法：当m=0时，－m2=0，此时?m2有意义。

3、实数分类时只看表面形式

对实数进行分类不能只看表面形式，应先化简，再根据结果去判断。

例4 下列各数－2、

?1、3.14159

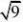
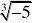
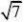
2、、中无理数有53

错解：无理数有?

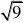
2、。 3

错解分析：这种错误认为带根号的数都是无理数。其实能化简的应先化简，

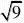
－3，

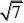
2=7，=2，所以它们是有理数。 正确解法：无理数有

4、运算错误

在进行实数的运算时要注意运算法则与公式的正确应用，千万不要忽略公式的应用条件。

例5 化简（1）5a?9a （2）(?9)?(?25)

错解：（1）5a?a=5a?3a=2；

（2）(?9)?(?25)=(?9)??25)=（－3）×（－5）=15

错解分析：（1）中合并同类二次根式时丢掉了?

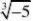
3a从而出错；（2）中忽略了公式

a?b?a?b的应用条件，即a≥0，b≥0，因为负数没有平方根，虽然最后结果正确，但解法是错误的。

正确解法：（1）5a?9a=5a?3a=2a；

（2）(?9)?(?25)=?25=?25=3×5=15。

- 6 -

实数 实数单元复习与测试题三套(含答案)

四、考点链接

中考中对于实数一章的考查，其题型主要有选择题、填空题、解答题。(www.61k.com］近几年题型变化比较大，创设了一些新的情境，考查学生灵活运用所学知识的能力，这也是近几年考查的热点和趋势。下面是2007年各省市关于实数的中考题的归类说明。

1、利用平方根、算术平方根、立方根的定义与性质解题

（1）（资阳市）如果某数的一个平方根是－6，那么这个数为________．

（2

．

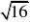
（3）(南京市)1的算术平方根是（ ） 4

111Ａ．? Ｂ． Ｃ．? 222 Ｄ．1 16

（4）(遵义市)8的立方根是 ．

3（5）(永州市)0.001＝________。

（6）（南宁市）若(x?1)2?1?0，则x的值等于（

A．?1 B．?2 C．0或2 ） D．0或?2

分析：本组题目主要考查平方根、算术平方根、立方根的定义与性质，其中（6）小题与方程相结合，可由(x?1)?1?0得（x+1）2=1，又由（±1）2=1得x+1=±1，再进一步求出x即可。

解：（1）36；（2）±2；（3）选B；（4）2；（5）0.1；（6）选D

2、考查实数的有关概念及实数大小的比较

（7）(金华市

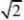
． 2

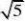
个． （8）（旅顺口）如图，在数轴上，A，B两点之间表示整数的点有

（9）（江西省）

．

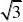
（10）(河北省)比较大小：

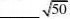
“＞”、“＝”或“＜”）

（11）(广州市)下列各数中，最小的数是（ ） ．．

A．－2 B．－1 C．0

D(12)(中山市)在三个数0.5、51、?中，最大的数是（ ）。 33

- 7 -

实数 实数单元复习与测试题三套(含答案)

A、0.5 B、51 C、? D、不能确定 33

分析：涉及数轴、相反数、绝对值、无理数等实数的有关概念及实数大小的比较历来是

中考考查的基本内容。［www.61k.com)实数进行大小比较的基本原则是：数轴上右边的数总是大于左边的数。

解：（7

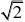
）8）4；（9）2；（10）＜；（11）A；(12) B

3、考查非负数的性质及其应用

（13

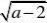
(b?5)2?0，那么a?b的值为． 分析：先根据非负数的性质求出a、b的值，然后代入代数式求解即可。

解：由题意，得a－2=0，b+5=0，即a=2，b=－5，所以a?b=2+(－5)=－3。故a?b的值为－3。

4、考查实数的化简与运算

（14）（潍坊市）化简40的结果是（ ）

A．10 B．2 C．45 D．20

（15

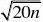
n为（ ）

A．2 B．3 C．4 D．5

（16

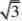
）（南京市）下列各数中，与 ）

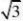
Ａ．2

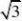
Ｂ．2

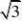
Ｃ．?2（17）（荆门市）下列计算错误的是( )

A．?7?72

B．60?5?23 D.2?2?3 C．9a?25a?8a

（18）（青岛市）

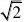
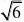
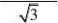
?1＝

（19）（黄冈市）计算：（+2）（5－2）=

（20）（临沂市）计算(?31?}的结果是（ ） 3

- 8 -

实数 实数单元复习与测试题三套(含答案)

A．6 B．43 C．2?6 D．12

2（218＋(－1)3－． 2

分析：中考中，有关实数运算的题目一般难度不大。(www.61k.com）要注意：化简时把能开得尽方的因

数都开出来，使结果成最简形式；运算时一定要注意运算顺序，另外，应用乘法公式可简化计算，如（19）小题可使用平方差公式。

解：（14）B；（15）D；（16）D；（

式=22?1?2?2?1

17）D（18）1；（

- 9 - 19）1；（20）D；（21）原

实数 实数单元复习与测试题三套(含答案)

第13章《实数》随堂小测（A 卷）

（本试卷满分100分） 班级_______ 姓名_______ 分数_______

一、仔细选一选：（每题4分，共24分）

1．16的平方根是

A、4 B、－4 C、±4 D、±2

2．立方根等于3的数是（ ）

A、9 B、?9 C、27 D、?27

3、有下列说法：①有理数和数轴上的点一一对应；②不带根号的数一定是有理数；③负数没有立方根；④?是17的平方根。（www.61k.com］其中正确的有（ ）

（A）0个 （B）1个 （C）2个 （D）3个

4、下列各式中，正确的是（ ） A. (?2)2??2 B.?32?3 C. ?9??3 D. ???3

5、估计 的大小应在( )

A.7～8之间 B.8.0～8.5之间 C. 8.5～9.0之间 D. 9.0～9.5之间

6、下列计算中，正确的是（ ） A.23+32=55 B.（3+7）==10

C.（3+2）（3－2）=－3 D.（2a?）(2a?b)=2a+b

二、细心填一填：（每题5分，共30分）

1

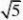
2的相反数是；绝对值是

2、下列各数：1??、?、－22

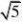
0.01020304…中是无理数的有_____________. 、0.3227

3、比较大小，填＞或＜号：

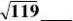
11；

3．

4、利用计算器计算3.142≈；≈（结果保留4个有效数字）。

5、一个正数x的平方根是2a?3与5?a，则a的值为____________．

6、绝对值小于7的整数有____________．

三、用心解一解：（共46分）

- 10 -

实数 实数单元复习与测试题三套(含答案)

1、求下列各式中未知数x的值（每小题4分，共8分）

（1）16x

2、化简（每小题5分，共20分）

（1）48－3 （2）×+5

（3）

3、（8分）用铁皮制成一个封闭的正方体，它的体积是1.331立方米，需要多大面积的铁皮

才能制成？

4、（10分）观察

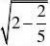
2?25?0 （2）?x?1??83 1 (2－) （4）(3?)(2?) 3

?

???

????

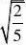
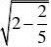
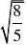
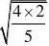
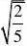
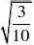
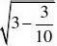
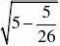
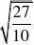
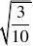
并通过计算验证你的猜想。（www.61k.com)

- 11 -

实数 实数单元复习与测试题三套(含答案)

随堂小测（A卷）答案：

一、CCBDCC

二、1、2－5

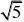
2 2、?

0.01020304… 3、＜；＞

4、1.773；4.344 5、－2 6、－2、－1、0、1、2

三、1、（1）x=±（2）x=3

2、（1）原式=?3?3???33?43??3

（2）原式=?3?5?36?5?6?5?11； 52

（3）原式=211?12??75?24?25?4?5??1； 33

（4）原式=6－35?25?5?1?

3、设正方体的边长为x米，则x3=1.331，x=1.1，1.12×6=7.26平方米。［www.61k.com]

4

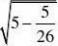
5

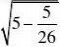
25?55=5。 ?26262626

- 12 -

实数 实数单元复习与测试题三套(含答案)

第13章《实数》随堂小测（B 卷）

（本试卷满分100分） 班级_______ 姓名_______ 分数_______

一、仔细选一选：（每题4分，共20分）

1、的平方根等于（ ）

（A）9 （B）±9 （C）3 （D）±3

2、下列说法正确是（ ）

A 不存在最小的实数 B 有理数是有限小数

C 无限小数都是无理数 D 带根号的数都是无理数

3、下列计算正确的是（ ）

A

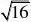
4 B．

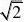
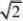
C．

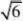
=4 D

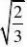
4、若m是9的平方根，n=（）2，则m、n的关系是（ ）

（A）m=n （B）m=－n （C）m=±n （D）｜m｜≠｜n｜

5、已知.28?1.738，a?0.1738，则a的值为（ ）

（A）0.528 （B）0.0528 （C）0.00528 （D）0.000528

二、细心填一填：（每题5分，共25分）

1、请你任意写出三个无理数：

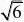
2、满足?2?x?3的整数是

3、化简4?6得y?3?0,则x=________，y=________.

=3；= 33；=333；…….44、若x?1?5、观察下列式子，根据你得到的规律回答：

请你说出的值是

三、用心解一解：（共55分）

1、计算：（1）（6

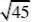
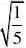
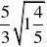
- 13 -

实数 实数单元复习与测试题三套(含答案)

（2）（7

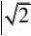
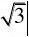
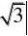
分）?

??2?

2、（10分）若xy=－2,x－y=52－1,求(x+1)(y－1)的值。（www.61k.com）

3、（10分）已知2a－1的平方根是±3，3a+b－1的平方根是±4，求a+2b的平方根.

4、（1）计算（12分）32?____,0.72?____,

1(?6)2?____,(?)2?____,(?0.28)2?____,02?____。 2

（2）（6分）根据（1）中的计算结果可知，a2一定等于a吗？你发现其中的规律了吗？请你用自己的语言描述出来。

2（3）（4分）利用上述规律计算：(3.14??)。

- 14 -

实数 实数单元复习与测试题三套(含答案)

随堂小测（B卷）答案：

一、DADCC

二、1、答案不唯一，如π 21 0 1. 3、66. 2,5,等。(www.61k.com]、－

4、－1，3. 5、33…3(共n个3)

三、1、（1）原式=35?5?5??25。

（2）原式=2?1?3?2?2?=1。

2、(x+1)(y－1)=xy－x+y－1= xy－(x－y)－1

=－2－(52－1)－1=－2－52+1－1=－62

3、由2a－1的平方根是±3得2a－1=9，故a=5；由3a+b－1的平方根是±4得3a+b－1=16，

故3×5+b－1=16，得b=2。所以a+2b=5+2×2=9，它的平方根是±3.

1

4、（1）3，0.7，6，2，0.28，0.

（2）不一定等于a.规律：当a≥0时a2=a，当a≤0时a2=－a.

2（3）由3.14－?≤0得(3.14??)=－（3.14－?）=?－3.14.

- 15 -

实数 实数单元复习与测试题三套(含答案)

第13章《实数》实战演练

（本试卷满分100分）

班级_______ 姓名_______ 分数_______

考场秘诀：谁沉着、冷静、认真、细心，谁就一定能够在考场上赢得最大的胜利！！祝你成功！！

一、 仔细选一选：（每题3分，共30分）

?2?1．下列实数: ?，0，?3.141592,2.95，，25，3， 0．020020002……中,无32

理数有( )个．

A.2 B.3 C.4 D.5

2．25表示的意义是( )

A.25的立方根 B.25的平方根 C.25的算术平方根 D.5的算术平方根

3．下列语句正确的是( )

A. －2是－4的平方根; B. 2是(－2)2的算术平方根;

C. (－2)2的平方根是2; D. 8的立方根是±2．

4．下列各数中，互为相反数的是( )

A.－2与(?2)2； B.－2与?8； C.－2与?

5.算术平方根等于它本身的数是（ ）

A .1和0 B .0 C . 1 D . ?1和0

6. 某位老师在讲“实数”时，画了一个图（如图1），即“以数轴的单位线段为边做一个正方形，然后以O为圆心，正方形的对角线长为半径画弧交x轴上于一点A”。（www.61k.com）则OA的长就

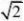
A.数轴上的点和有理数一一对应

B.数轴上的点和无理数一一对应

C.数轴上的点和实数一一对应

D.不能说明什么

7．实数a、b、c在数轴上的位置如图2: 则化简 a?b?c的结果

是(

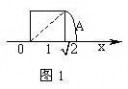
) 图2 1； D.?2与2． 2

- 16 -

实数 实数单元复习与测试题三套(含答案)

A.a－b－c; B.a－b+c; C.－a+b+c; D.－a+b－c．

8．绝对值小于5的所有实数的积为 ( )

A.24; B.576; C.0; D. 10

9、若实数x满足｜x｜+x=0，则x是（ ）。(www.61k.com］

A. 零或负数 B. 非负数 C. 非零实数 D.负数． 10. 的整数部分为a，小数部分为b，则b2为( )

B．20 C．20－6 D．20+6 A．2

二、细心填一填（每题4分，共32分）

1、－3的倒数是________，绝对值是________

2．9

______

3．若x?3=－2，则x的值是4、如果a?3=3，那么（a+3）2的值为

5、计算：37?1＝64

26、(?4)? .

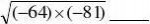
7、若三角形的三边a、b、c满足a2－4a+4+b?3=0,则笫三边c的取值范围是_____________ 8、计算: (?2)(3?2)=_____,(2?)(2?3)=_____,(?2)(?2)=

____;……．通过以上计算,试用含n(n为正整数)的式子表示上面运算揭示的规律:__________________

三、解答题：（共38分）

1、（6分）求下列各式的值：

（1）?49； （2）

121； （3）－0.09 256

- 17 -

实数 实数单元复习与测试题三套(含答案)

2、（6分）化简:（1）27?23?45 （2）3?（23?）

3、（6分）已知x?1=x－1，求x的值。[www.61k.com]

4、（6分）一个长方体的长为5 cm，宽为2 cm，高为3 cm，而另一个正方体的体积是它的3倍，求这个正方体的棱长(结果精确到0.01 cm).

5、(7分) 已知三角形的三边a、b、c的长分别为45cm、cm、cm，求这个三角形的周长和面积.

- 18 - 图3

实数 实数单元复习与测试题三套(含答案)

6、（7分）．如图3所示，某计算装置有一数据入口A和一运算结果的出口B，下表给出的是

小红输入的数字及所得的运算结果：

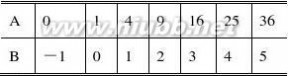
若小红输入的数为48，输出的结果应为多少？若小红输入的数字为a,你能用a表示输出结果吗？

《实数》实战演练参考答案

一、BCBAA，CCCAC

二、1、－33; 2、±3； 3、－5 4、81 5、?3

4 6、4；72 7、1<c<5

1,1,1, (n?1?n)(n?1?n)?1.

三、1、（1）?7 （2）11

16 （3）－0.3

2、（1）原式=?2?3??3

（2）原式=?23??6?6－32。[www.61k.com）

3、因为立方根等于它本身的数是1,－1,0，所以有x－1=1, x－1=－1或x－1=0, 所以x=2,0或1

4

、

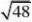
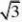
?2?3?3=≈4.48cm

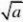
5、周长=45++=12cm；

因为（45）2+（）2=125=（）2，

所以三角形是直角三角形，故面积=145×80=30cm2

2

6、（11?1 （21(a?0)

- 19 - 8、

本文标题：一次函数测试题含答案-高一数学对数函数的图象及性质测试题及答案9
本文地址： http://www.61k.com/1105186.html