一 : 六个常用分布的数学期望和方差

指数分布的方差 六个常用分布的数学期望和方差

指数分布的方差 六个常用分布的数学期望和方差

指数分布的方差 六个常用分布的数学期望和方差
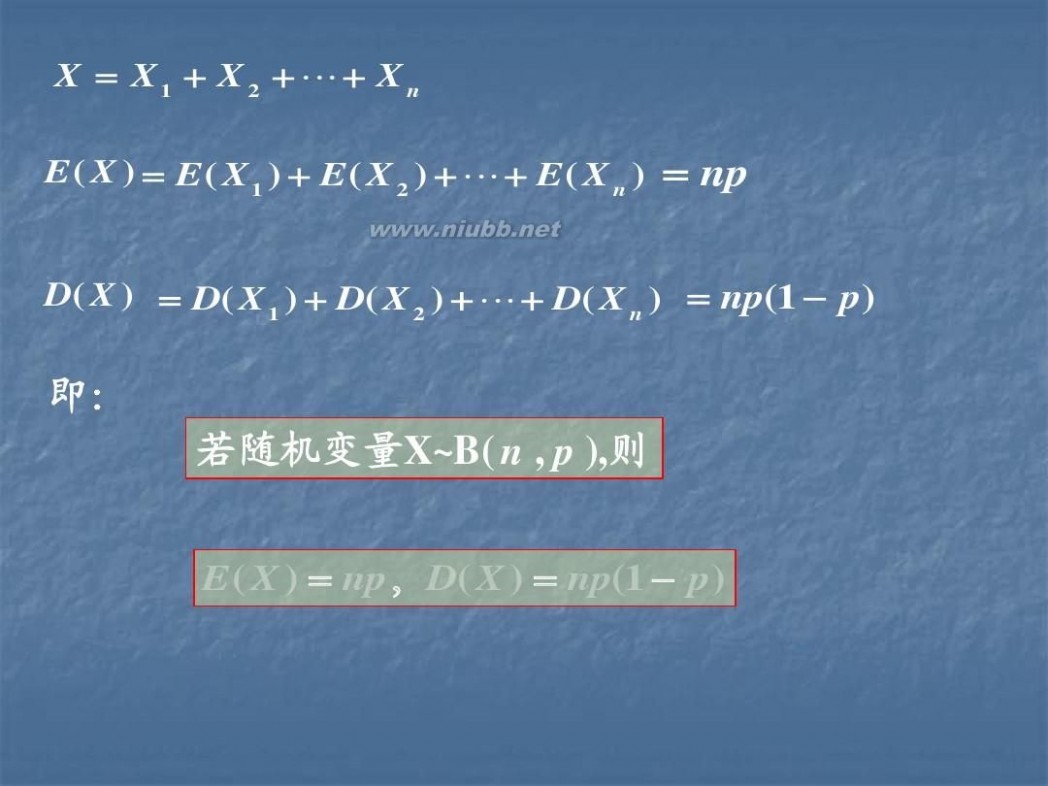
指数分布的方差 六个常用分布的数学期望和方差

指数分布的方差 六个常用分布的数学期望和方差

指数分布的方差 六个常用分布的数学期望和方差

指数分布的方差 六个常用分布的数学期望和方差

指数分布的方差 六个常用分布的数学期望和方差

指数分布的方差 六个常用分布的数学期望和方差

指数分布的方差 六个常用分布的数学期望和方差

指数分布的方差 六个常用分布的数学期望和方差

指数分布的方差 六个常用分布的数学期望和方差
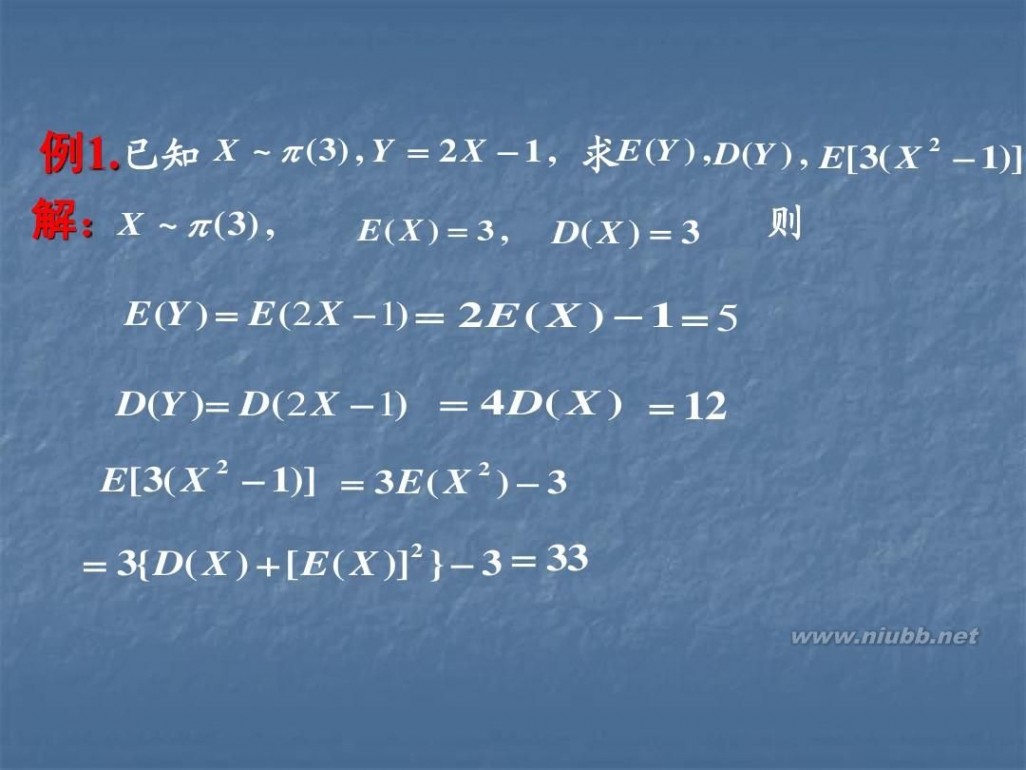
指数分布的方差 六个常用分布的数学期望和方差

指数分布的方差 六个常用分布的数学期望和方差

二 : Gamma分布的k阶矩、期望和方差及特征函数
Gamma?ù??k??Y!?"ú???9A???ê?
Mà|
¥I???‰?????)??
2010c10??10F
á?
????L??E5y2‰?Gamma?ù??k??YúA???ê§ó??‰??"ú???.
·????§??3???m(R+,BR+)t????V??ùx
λαα?1?λxxe:α>0,λ>0}P={p(x;α,λ)=Γ(α)
′Gamma?ùx§P?P={Ga(α,λ):α>0,λ>0}.Gamma?ù??k??Y?dXe?n‰?.
?n1.e‘?CtX~Ga(α,λ)§KX??k??Y?
EXk=Γ(α+k)1(α+k?1)(α+k?2)···α=Γ(α)λλT?n??y2é{ü§?wXey2.
y2.dX~Ga(α,λ)?X??—Y?êp(x)?
λαα?1λxxeI(x≥0)p(x;α,λ)=Γ(α)
Kùk??Y
EX=
?k??+∞?∞αkλxxα?1eλxI(x≥0)dx=Γ(α)??0+∞λαα?1λxxxedxΓ(α)k??{0μMà|§¥I???‰?????)??êt2L?Ea2LX2009?a???)?????ü §¥I???‰???êt2L?Ea2L??¤?;’§êt2L??????μêt7K???‰§?9?ó§???O??‰??EaX.
1
什么是gamma分布 Gamma分布的k阶矩、期望和方差及特征函数
u-x=§K
11EXk=Γ(α)λ??0+∞uα+k?1e?udu
=
EXk=Γ(α+k)1(α+k?1)(α+k?2)···α=Γ(α)λkλ
k
e?′d?n1???????í?§Tí?′k'Gamma?ù???"??????.
í?1.e‘?CtX~Ga(α,λ)§KX???"?????
EX=α
λ
α
λVar(X)=|^?n1éTí???y2é{ü§??l?.e????n‰???Gamma?ù??A???ê/a.
?n2.eX~Ga(α,λ)§X??A???êf(t)?
f(t)=(1?it?α)λ
y2.dX~Ga(α,λ)§9A???ê??
??+∞αitXitxλf(t)=Ee=exα?1e?λxI(x≥0)dxΓ(α)?∞
=
f(t)=
???
itf(t)=(1?)?α
λ
?ò′
f(t)=(1???0+∞λαα?1?λ(1?it)xdxxeΓ(α)tα[λ(1?i)]α?1?λ(1?it)xdxxeΓ(α)??0+∞it?
α)λ
2
扩展:gamma分布的期望 / gamma分布的方差 / gamma分布期望
三 : 第四讲 常见分布的期望 方差

指数分布的方差 第四讲 常见分布的期望 方差

指数分布的方差 第四讲 常见分布的期望 方差

指数分布的方差 第四讲 常见分布的期望 方差

指数分布的方差 第四讲 常见分布的期望 方差

指数分布的方差 第四讲 常见分布的期望 方差

指数分布的方差 第四讲 常见分布的期望 方差

指数分布的方差 第四讲 常见分布的期望 方差

指数分布的方差 第四讲 常见分布的期望 方差
指数分布的方差 第四讲 常见分布的期望 方差

指数分布的方差 第四讲 常见分布的期望 方差

指数分布的方差 第四讲 常见分布的期望 方差

指数分布的方差 第四讲 常见分布的期望 方差

指数分布的方差 第四讲 常见分布的期望 方差
指数分布的方差 第四讲 常见分布的期望 方差

四 : 六个常用分布的数学期望和方差
附: 几种重要随机变量的数学期望和方差
一.二点分布 二.二项分布 四.均匀分布 五.正态分布 六.指数分布
三.泊松分布
一.二点分布
若随机变量X服从二点分布,其分布律为:
X Pk 0 1-p 1
p
E( X ) ? p
E( X ) ? p
2
D( X ) ? p(1 ? p)
二.二项分布
随机变量X~B(n,p),其分布律为:
P{ X ? k } ? C n p (1 ? p)
k k n? k
,
k ? 1,2,?, n
由二项分布定义可知,X是n重贝努利试验中事件A发
生的次数,且在每次试验中A发生的概率为p,设
Xk ?1 ?? ?0 A在第k次发生 A在第k次不发生 , k ? 1,2, ? , n
则Xk服从二点分布,其分布律为:
E( X k ) ? p ,
D( X k ) ? p(1 ? p)
X Pk
0
1
1-p
p
X ? X1 ? X 2 ? ?? X n
E ( X ) ? E ( X 1 ) ? E ( X 2 ) ? ? ? E ( X n ) ? np
D( X ) ? D( X 1 ) ? D( X 2 ) ? ? ? D( X n ) ? np(1 ? p)
即: 若随机变量X~B( n , p ),则
E ( X ) ? np,D( X ) ? np(1 ? p)
三.泊松分布
随机变量
P{ X ? k } ?
X ~ ? (? ) ,其分布律为:
λ e
k ?λ
,
k ? 0,1,2,? ,
k!
E( X ) ?
?k
k ?0
?
? e
k
??
? ?e
??
k!
? (k ? 1)!
k ?1
?
?
k ?1
? ?e
??
e
?
??
2 E ( X ) ? E[ X ( X ? 1) ? X ] ? E[ X ( X ? 1)] ? E ( X )
?
? k (k ? 1 )
k ?0
?
? e
k
??
??
?? e
2
??
k!
? (k ? 2)! ? ?
k ?2
?
?
k ?2
?? e
2
??
e ?? ?? ??
2
?
D( X ) ? E ( X ) ? [ E ( X )]
2
2
??
即:
若随机变量X~π(λ),则
E ( X ) ? λ , D( X ) ? λ
四.均匀分布
设随机变量X在区间(a,b)上服从均匀分布,其概率
密度为
? 1 ? f ( x) ? ? b ? a ? 0 ?
??
a? x?b 其它
,
E( X ) ?
?
?
??
xf ( x )dx ?
?
b
x
1 b?a
dx
a
?
1 b?a
x
2
b
?
a?b 2
2 a
E( X ) ?
2
?
b
x
2
1 b?a
dx ?
b ?a
3
3
a
3(b ? a )
a ? ab ? b
2 2
?
a ? ab ? b
2
2
3
a ? 2ab ? b
2 2
D( X ) ? E ( X ) ? [ E ( X )] ?
2 2
?
3
4
?
(b ? a ) 12
2
即 若随机变量X~U( a , b ),则
E( X ) ?
a?b 2
, D( X ) ?
(b ? a ) 12
2
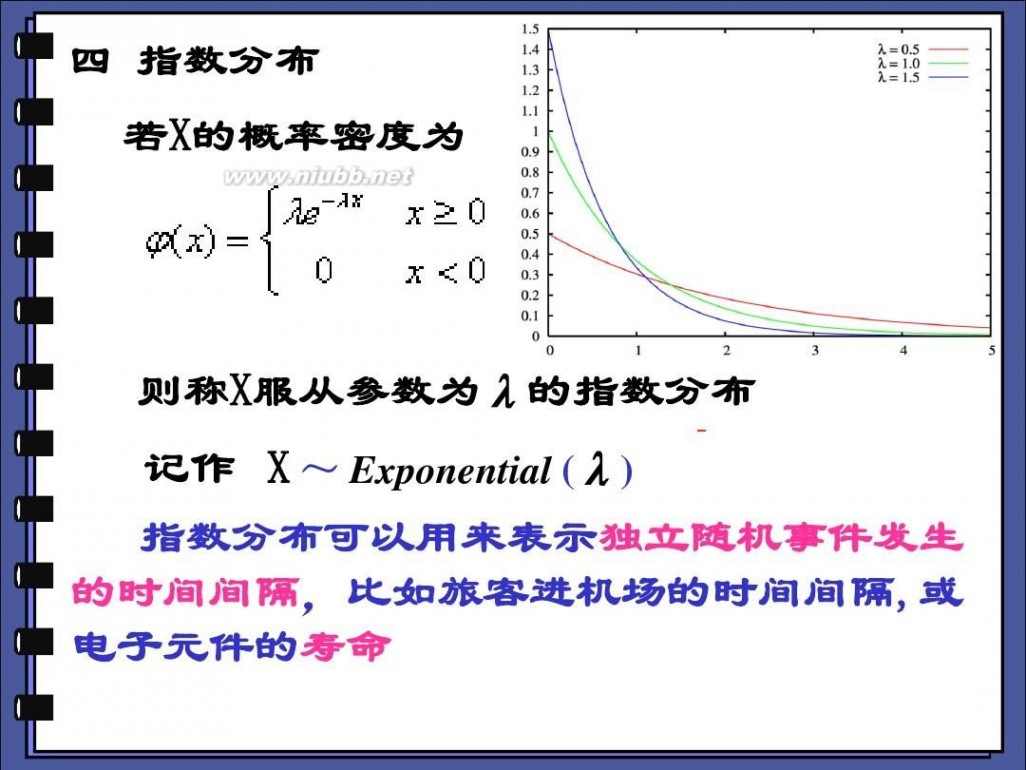
五.指数分布
随机变量X服从参数为λ的指数分布,其概率密度为:
?1 ?x ? e θ f ( x) ? ? θ ? 0 ? x?0 x?0
? x θ
E( X ) ?
?
??
??
xf ( x )dx ?
??
?
x
??
x?
1 θ
e
dx ?
? x
0
?
??
( ? x)de
?
x θ
0
? ? x) ( e
?
x
??
?
0
??
??
?
e
?
dx
? ??e
?
0
?θ
0
E( X ) ?
2
?
2
??
??
x f ( x )dx ?
? x θ
2
?
??
x ?
2
? x
1 θ
?
x θ
e
dx
? x
0
??
?
?
0
??
( ? x )de
? ? x) ( e
2
?
0
0
x
??
??
??
2 xe
??
?
dx
x
0
?
?
??
( ? 2θx)de
? x ??
?
x θ
? ? 2?x) ( e
?
?
0
? 2? ?
?
e
?
dx
0
? ?2? e
2
?
0
2 ? 2θ , D( X ) ? E ( X 2 ) ? [ E ( X )]2 ?θ
2
即
若随机变量X服从参数为λ的指数分布,则
E ( X ) ? θ,D( X ) ? θ
2
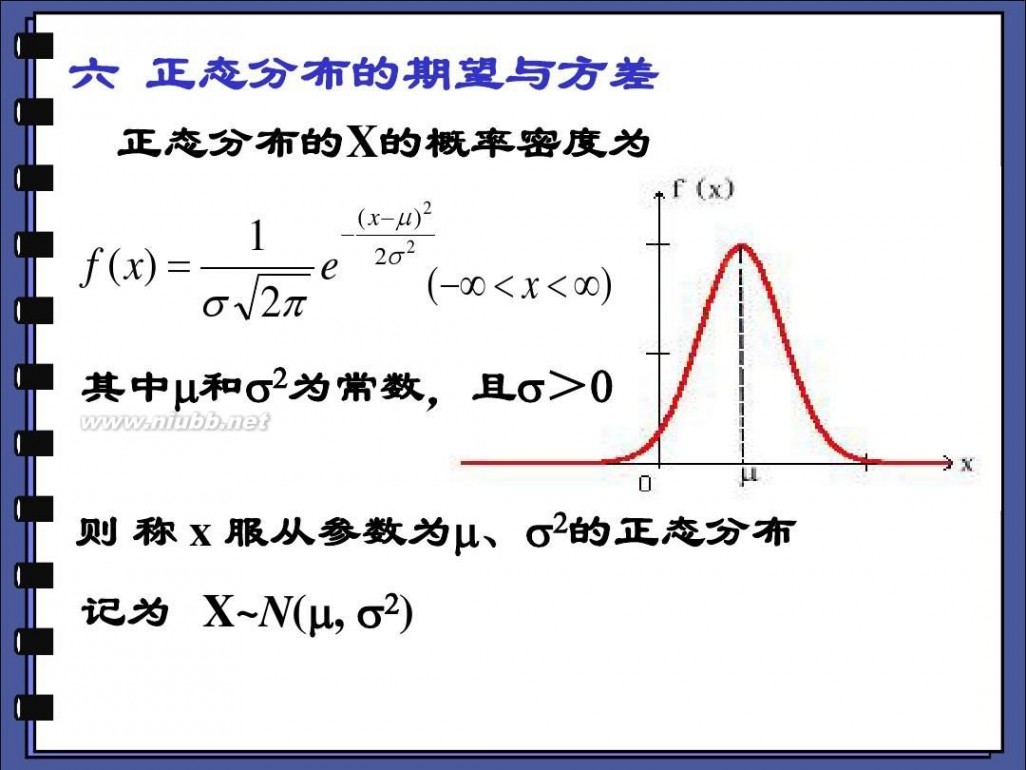
六.正态分布
随机变量 X ~ N ( ? ,? 2 ) ,其概率密度为:
f ( x) ? 1 2? ?
? ( x?? ) 2?
2 2
e
,
? ? ? x ? ??
( x?? ) 2?
2 2
E( X ) ?
1
?
??
??
xf ( x )dx ?
??
?
??
??
x?
1 2? ?
?
e
dx (令 t ?
?? ? t
2
x??
?
)
?
2? ?
?
??
(? t ? ? )e
?
t
2
2
? dt ?
?
2?
?
??
e
2
dt
??
? D( X ) ? E{[ X ? E ( X )] }
2
?
??
??
(x ? ?) ?
2
1 2? ?
?
( x?? ) 2?
2
2
e
dx
?
?
2
2?
?
?
?
??
??
t e
2
?
t
2
2
d t (令
? t
2
t?
x??
?
2
)
?
?
?
2
??
2?
2
??
( ? t )de
2
t ? ?? ? ? 2 ? ? te ? ? ?? 2? ? ? 2
?
??
?
t
2
??
e
2
? d t? ? ?
?
2?
2?
??
2
即
若随机变量X~N(μ,σ2 ), 则
E ( X ) ? μ , D( X ) ? σ
2
例1.已知 X ~ ? (3) , Y ? 2 X ? 1 , 求E (Y ) , D(Y ) , E[3( X 2 ? 1)] 解:X ~ ? (3) , 则 E ( X ) ? 3 , D( X ) ? 3
E (Y ) ? E ( 2 X ? 1) ? 2 E ( X ) ? 1 ? 5
D(Y )? D( 2 X ? 1) ? 4 D( X ) ? 12
E[3( X ? 1)] ? 3 E ( X 2 ) ? 3
2
2 ? 3{ D( X ) ? [ E ( X )] } ? 3 ? 33
例2.已知X和Y相互独立,且X在区间(1,5)上服从
均匀分布, Y ~ N ( 1 , 9 ) , 求(1) (X,Y)的联合概率
Y ~ N (1, 9 ) ,
1? 5 2
(5 ? 1) 12
密度;(2) E ( 3 X ? 4Y ? 2) , D( 3 X ? 4Y ? 2)
解: X在区间(1,5)上服从均匀分布,
?1 ? f X ( x) ? ? 4 ?0 ? 1? x ? 5 其它
? ( y ?1) 18
2
,
E( X ) ? D( X ) ?
?3
2
?
4 3
fY ( y ) ?
1 3 2?
e
,
? ? ? y ? ?? ,
E (Y ) ? 1 ,
D(Y ) ? 9
由X和Y相互独立得:
f ( x, y ) ? f X ( x ) ? f Y ( y )
? ? 1 e ? ? ? 12 2? ? 0 ?
( y ?1 ) 18
2
,
1 ? x ? 5 , ? ? ? y ? ?? 其它
E ( 3 X ? 4Y ? 2) ? 3 E ( X ) ? 4 E (Y ) ? 2 ? 3
D( 3 X ? 4Y ? 2) ? 9 D( X ) ? ( ?4) 2 D(Y ) ? 156
五 : 期望 方差公式的证明全集
期望与方差的相关公式的证明
-、数学期望的来由
早在17世纪,有一个赌徒向法国著名数学家帕斯卡挑战,给他出了一道题目,题目是这样的:甲乙两个人赌博,他们两人获胜的机率相等,比赛规则是先胜三局者为赢家,赢家可以获得100法郎的奖励。[www.61k.com]当比赛进行到第三局的时候,甲胜了两局,乙胜了一局,这时由于某些原因中止了比赛,那么如何分配这100法郎才比较公平?
用概率论的知识,不难得知,甲获胜的概率为1/2+(1/2)*(1/2)=3/4,或者分析乙获胜的概率为(1/2)*(1/2)=1/4。因此由此引出了甲的期望所得值为100*3/4=75法郎,乙的期望所得值为25法郎。
这个故事里出现了“期望”这个词,数学期望由此而来。
i=1,i=1,定义1 若离散型随机变量?可能取值为a(2,3 ,?),其分布列为p(ii
2,3, ?),则当?
i?1?则称?aipi<?时,存在数学期望,并且数学期望为E?=?aipi,i?1?
如果?
i?1?aipi=?,则数学期望不存在。?1?
定义2 期望:若离散型随机变量ξ,当ξ=xi的概率为P(ξ=xi)=P(2,?,ii=1,n,?),则称Eξ=∑xi pi为ξ的数学期望,反映了ξ的平均值.
期望是算术平均值概念的推广,是概率意义下的平均.Eξ由ξ的分布列唯一确定.
二、数学期望的性质
(1)设C是常数,则E(C)=C 。
(2)若k是常数,则E(kX)=kE(X)。
(3)E(X1?X2) ? E(X1)?E(X2)。
三、 方差的定义
前面我们介绍了随机变量的数学期望,它体现了随机变量取值的平均水平,是随机变量一个重要的数字特征。但是在一些场合下,仅仅知道随机变量取值的 1
方差公式 期望 方差公式的证明全集
平均值是不够的,还需要知道随机变量取值在其平均值附近的离散程度,这就是方差的概念。[www.61k.com]
2定义3方差:称Dξ=∑(xi-Eξ)pi为随机变量ξ的均方差,简称方差.D?
叫标准差,反映了ξ的离散程度.
定义4设随机变量X的数学期望E(X)存在,若E[(X
2?E(X))]存在,则称 2E[(X?E(X))]
为随机变量X的方差,记作D(X),即D(X)?
方差的算术平方根D(X)E[(X?E(X))]。 2称为随机变量X的标准差,记作?(X),即
D(X)?(X)?
由于?(X)与X具有相同的度量单位,故在实际问题中经常使用。
Dξ表示ξ对Eξ的平均偏离程度,Dξ越大表示平均偏离程度越大,说明ξ的取值越分散.
方差刻画了随机变量的取值对于其数学期望的离散程度,若X的取值相对于其数学期望比较集中,则其方差较小;若X的取值相对于其数学期望比较分散,则方差较大。若方差D(X)=0,则随机变量X 以概率1取常数值。
由定义4知,方差是随机变量X的函数g(X)?[X
??2??[xk?E(X)]pk, 当X离散时D(X)??k?1
?2?[x?E(X)]f(x)dx, 当X连续时k?????E(X)]2的数学期望,故
; 当X离散时, X的概率函数为P(xk)?P(X?xK)?PK, k?1, 2, ?
当X连续时,X的密度函数为f(x)。
求证方差的一个简单公式:
公式1:D(X)?
证明一:
D(X)?E[(X?E(X))]
?E[X2
22E(X)?[E(X)]22 ?2XE(X)?[E(x)]] 22?E(X)?[E(X)]
2
方差公式 期望 方差公式的证明全集
证明二:D?
n
?
?(x
i?1
i
?E?)?pi
2
2
n
??
?[x
i?1n
2i
?2xiE??(E?)]?pi
n
n2
?x
i?1
22
2i
pi?2E???xipi?(E?)??pi
i?12
2
i?1
?E??2(E?)?(E?)?E??(E?)
2
2
?D??E??(E?)
2
可以用此公式计算常见分布的方差
四、方差的性质
(1)设C是常数,则D(C)=0。(www.61k.com] (2)若C是常数,则D(CX
)?CD(X)。
2
(3)若X与Y 独立,则
公式2: D(X?Y)?D(X)?D(Y)。
证 由数学期望的性质及求方差的公式得
D(X?Y)?E[(X?Y)]?[E(X?Y)]
?E[X
22
2
2
2
2
?Y
2
?2XY]?[E(x)?E(Y)]
2
?E(X)?E(Y)?2E(X)E(Y)?[E(X)]?[E(Y)]?2E(X)E(Y)?E(X)?[E(X)]?D(X)?D(Y)
2
?
22
???E(Y2)?[E(Y)]2?
可推广为:若X1,X2,?,Xn相互独立,则
n
D[?Xi]?
i?1
n
n
?D(X)
i
i?12i
n
D[?CiXi]?
i?1
?C
i?1
D(Xi)
(4) D(X)=0 ?P(X= C)=1, 这里C =E(X)。
五、常见的期望和方差公式的推导过程
(一)离散型随机变量的期望和方差的计算公式与运算性质列举及证明
3
方差公式 期望 方差公式的证明全集
1.由概率的性质可知,任一离散型随机变量的分布列具有下述两个性质: (1)pi≥0,i=1,2,?; (2)p1+p2+?=1。[www.61k.com]
2.离散型随机变量期望和方差的性质: E (a?+b)=aE?+b,D (a?+b)=a2 D?。
(1) 公式3:E(aξ+b)=aEξ+b,
证明:令?
?a??b
a,b为常数 ?也为随机变量
P(axi?b)?P(??xi)
i?1,2,3...
所以 ?的分布列为

E??(ax1?b)p1?(ax2?b)p2?...?(axn?b)pn
=a(x1p1?x2p2?...xnpn?...)?b(p1?
E?
p2?...?pn?...)
=aE??b
的线性函数?
?a??b
E(a??b)?aE??b说明随机变量?的期望等于随机变量?
期望的线性函数
(2) 公式4:D(aξ+b)=a2Dξ(a、b为常数).
证法一: 因为
n
D??
n
?(x
i?1
i
?E?)?pi
2
2
??
?[x
i?1n
2i
?2xiE??(E?)]?pi
n
n2
?x
i?1
22
2i
pi?2E???xipi?(E?)??pi
i?12
2
i?1
?E??2(E?)?(E?)?E??(E?)
2
4
方差公式 期望 方差公式的证明全集
?D??E??(E?)
22
n2
所以有:D(a?
n
?b)?
?[ax
i?1
i
?b?(aE??b)]?pi?a
2
?(x
i?1
i
?E?)?pi?aD?
22
证毕
2
证法二:Dξ=?(xi?E?)
i?1
nn
2
n
2i
n2
?pi?
?x
i?1
pi?2E??xipi?(E?)
i?1
?
i?1
pi?E??(E?)
2
.
E(aξ+b)=aEξ+b, D(aξ+b)=a2Dξ.
n
n
i
D(a??b)?
?[ax
i?1
?b?(aE??b)]?pi?a
22
?(x
i?1
i
?E?)?pi?aD?
22
(二)二项分布公式列举及证明
1.二项分布定义:若随机变量?的分布列为:P (?=k)=Cnk pk qn-k。[www.61k.com](k=0,1,2,?,n,0<p<1,q=1-p,则称?服从二项分布,记作?~B (n,p),其中n、 p为参数,并记Cnk pk qn-k=b(k;n,p)。
2.对二项分布来说,概率分布的两个性质成立。即:
(1)P (?=k)=Cnk pk qn-k>0,k=0,1,2,?,n; (2)?P (?=k)=?Cnk pk qn-k=(p+q) n=1。
k?0
k?0
n
n
二项分布是一种常见的离散型随机变量的分布,它有着广泛的应用。 3.服从二项分布的随机变量?的期望与方差公式: 若ξ~B(n,p),则Eξ=np,Dξ=npq(q=1-p).
(3) 公式5:求证:Eξ=np
方法一:
在独立重复实验中,某结果发生的概率均为p(不发生的概率为q,有p?q?1),那么在n次实验中该结果发生的次数?的概率分布为

5
方差公式 期望 方差公式的证明全集
服从二项分布的随机变量?的期望E??np.证明如下:
预备公式
kck
n?nck?1
n?1
(p?q)
n?1
?(c0
q
n?1
20n?2
k?1k?1
n?1)?(n?k)
n?1p?c10n?2
n?1pq
?cn?1pq
?...?cn?1p
q
(?...?cn?1?1
n?1p
nq0
)
因为p(??k)?ck
k
n?k
k
k
n?k
np(1?p)
?cnpq
,
所以
E??0?c0
p0
qn
?1?c1
1
n?1
2
2
q
n?2
nnpq
??2?cnp?...?k?ckkn?k
npq
?...?ncn0npq
n
=np(c
0n?1)?(n?k)
n?1
n?1
p0q
n?1
?c1n?2
k?1
k?1
n?1
n?1p0
q
?c20n?1pq
n?2
?...?cn?1p
q
(?...?cn?1p
q0
)
=np(p?q)n?1?np 所以
E?
=
np
得证
方法二: 证明:若 X~B(n,p),则
X表示n重贝努里试验中的“成功” 次数,
现在我们来求X的数学期望。(www.61k.com)
若设X??1如第i次试验成功i
? i=1,2,?,n
?0
如第i次试验失败
则X
?X1?X2?...?Xn,因为 P(Xi?1)?P,P(X
i
?0)?1?P?q
所以E(Xi)?0?q?1?p?p,则
n
n
E(X)?E[?Xi]?
?E(X
i
)?np
i?1
i?1
可见,服从参数为n和p的二项分布的随机变量X的数学期望是np 。
需要指出,不是所有的随机变量都存在数学期望。
公式6
k2
Ck
k?1
k?2
n?nCn?1?n(n?1)Cn?2
k2Ckk?1
n?knCn?1
?n[(k?1)?1]Ck?1
n?1
?nCk?1k?1
n?1?n(k?1)Cn?1
?nCk?1
n?1?n(n?1)Ck?2
n?2
?k2
Ck
k?1
n?nCn?1?n(n?1)Ck?2
n?2
6
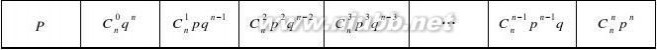
方差公式 期望 方差公式的证明全集
求证:服从二项分布的随机变量?的方差公式7:Dξ=npq(q=1-p). 方法一:
n
证明: E??
2
?i
i?0
1n
2
Cnpq
n
iin?i
n
i?1n?1
?Cpq?npq?npq?npq
n?1
?
?
i?2n
nCpqp
i?1
in?i
?
?
i?2
n(n?1)Cn?2pq
0n?1
i?2in?i
n
i?1n?1
n?1
?np?C
i?1
q
n?i
?npC
n?1
q
n?1
?n(n?1)p
2
2
?C
i?2
i?2n?2
p
i?2
q
n?i
n?1n?1
?np(p?q)?np?npq
2
2
22
n?1
?npq?n(n?1)p(p?q)
2
n?2
n?1
?n(n?1)p
?np?np?np
2
?np(1?p)?np?npq?np
2
2
22
由公式1知D??E??(E?)
?npq?np?(np)?npq
222
表示n重贝努里试验中的“成功” 次数。[www.61k.com] i=1,2,?,n
,故
方法二: 设?
?1
若设Xi??
?0
~B(n,p), 则X
如第i次试验成功如第i次试验失败
则?
?
??是n次试验中“成功”的次数,E(?
i
i?1
2
2
2
i
n
i
)?0?q?1?p?p
D(?
)?E(?i)?[E(?i)]?p?p?p(1?p), i?1,2,?,n
n
由于?1,?2,...,?n相互独立,于是D(?)??D(?i)= np(1- p)。
i?1
(三) 几何分布的期望与方差的公式列举及证明
1. 定义5:几何分布(Geometric distribution)是离散型概率分布。
定义6:在第n次伯努利试验,才得到第一次成功的机率。
P(Xn次伯努利试验,前n-1次皆失败,第n次才成功的概率。
?k)?(1?p)
k?1
61阅读请您转载分享:
p
7
方差公式 期望 方差公式的证明全集
若P(?
?k)?q
k?1
p,则(1)E??
1p
,(2)D?
?
1?pp
2
。[www.61k.com]
1p
求证:(1)几何分布的期望 公式8:E?
?
,
若某射击手击中目标的概率为P,求证:从射击开始到击中目标所需次数?的期望
E??
1p
证明:依题意分布列为

由P(?
?k)?q
k?1
p,知
2
K?1
E??1?P?2P(1?P)?3P(1?P)?...?KP(1?P)
E??p?2pq?3qp?...?kq
2
k?1
2
?...
?...)p
p?...?(1?2q?3q?...?kq
k?1
下面用错位相减法求上式括号内的值。 记S
k
?1?2q?3q?...?kq
2k?1
k
qSk?q?2q?...?(k?1)q
2k?1
?kq
2
k?1
两式相减,得(1?q)S
Sk?
1?q
k2
k
?1?q?q?...?q?kq
k
(1?q)
?
kq
k
1?q
k
k
由0?
p?1,知0?q?1,则limq?0及limkq
k??
k??
?0(可用L'Hospital法则证明)
故1?2p?3q2?...?kqk?1?...?limSk
k??所以E?
?
1(1?q)
2
?
1p
2
,
?
1p
8
方差公式 期望 方差公式的证明全集
求证:(2)p(??k)?g(k,p) 几何分布的方差 公式9:D??1?p?q
2 p2
证明:利用导数公式(xn)'?nxn?1,推导如下: 1?2x?3x2?...?kxk?1?...
?x'?(x2)'?(x3)'?...?(xk)'?...
?(x?x2?x3?...?xk?...)'
?(x
1?x)'?(1?x)?(?x)
(1?x)2
?1
(1?x)2
上式中令x?q,则得 1?2q?3q2?...?kqk?1?...?11
(1?q)2?p2
(2)为简化运算,利用性质D??E?2?(E?)2来推导。(www.61k.com] E?2?p?22qp?32q2p?...?k2qk?1p?...
?p(1?22q?32q2?...?k2qk?1?...)
对于上式括号中的式子,利用导数,关于q求导:k2qk?1?(kqk)',并用倍差法求和,有1?22q?32q2?...?k2qk?1?...
?(q?2q2?3q3?...?kqk?...)'
2
?[q
(1?q)2]'?(1?q)?2(1?q)q(1?q)4
1?q21?q ?(1?q)4?(1?q)3?2?pp3
则E?2?p(2?p2?p
p3)?p2,
9 p
方差公式 期望 方差公式的证明全集
因此D??E?2?(E?)2?2?p
p2?(1p
?)2?1?pp2 ?证明二: ?
E(?)?2?k
K?12pqk?1?p[?k(k?1)qk?1k?1??kqk?1k?1]
=qp(?qk)n?E?
k?1?
=qpD??E?22(1?p)2?p
p23?1p2?2pp2?1p ?(E?)2??(1p)?1?p
p2
10
61阅读请您转载分享:
本文标题:泊松分布的期望和方差-六个常用分布的数学期望和方差61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1