一 : 2011年无锡市化学中考17题D选项求详细解析
2011年无锡市化学中考17题D选项求详细解析
25、将一定量的丙醇(C3H8O)和氧气置于一个封闭的容器中引燃,测得反应前后各物质的质量如下表:
物质x05 丙醇x05 氧气x05水x05二氧化碳 x05X
反应前质量/gx05 6.0x05 12.8x050x050x05 0
反应后质量/gx05 0x05 0x05 7.2x058.8x05 a
下列判断正确的是
A.表中a的值为2.8 x05B.X一定是该反应的催化剂
C.X可能含有氢元素 x05D.若起始时氧气的质量是14.4g,则无X生成
我认为这道题选AD
既然楼主明白ABC,那很容易就可以推算出x的组成是CO,CO的产生是因为燃烧的不完全,若氧气的质量改为14.4g,设无CO生成,则
C3H8O+O2——CO2+H2O
因为在化学方程式中物质的质量和他的相对质量之比是相等的,已知丙醇和氧气的质量所以2C3H8O+9O2——CO2+H2O
配平可得2C3H8O+9O2——8CO2+6H2O
发现丙醇和氧气恰好完全反应,且未生成CO,所以选AD
选我哦!这么晚给你打!若不懂可以追问,我再详细的给你讲.
二 : 高中数学必修一函数大题(含详细解答)
高中函数大题专练
1、已知关于x的不等式(kx?k2?4)(x?4)?0,其中k?R。(www.61k.com] ⑴试求不等式的解集A;
⑵对于不等式的解集A,若满足A?Z?B(其中Z为整数集)。试探究集合B能否为有限集?若能,求出使得集合B中元素个数最少的k的所有取值,并用列举法表示集合B;若不能,请说明理由。
2、对定义在[0,1]上,并且同时满足以下两个条件的函数f(x)称为G函数。
① 对任意的x?[0,1],总有f(x)?0;
② 当x1?0,x2?0,x1?x2?1时,总有f(x1?x2)?f(x1)?f(x2)成立。 已知函数g(x)?x2与h(x)?a?2x?1是定义在[0,1]上的函数。
(1)试问函数g(x)是否为G函数?并说明理由;
(2)若函数h(x)是G函数,求实数a的值;
(3)在(2)的条件下,讨论方程g(2x?1)?h(x)?m(m?R)解的个数情况。
3.已知函数f(x)?2x?1
2|x|.
(1)若f(x)?2,求x的值;
(2)若2tf(2t)?mf(t)?0对于t?[2,3]恒成立,求实数m的取值范围.
?11?,x?0;?4.设函数f(x)是定义在R上的偶函数.若当x?0时,f(x)?? x
?0,x?0.?
(1)求f(x)在(??,0)上的解析式.
(2)请你作出函数f(x)的大致图像.
(3)当0?a?b时,若f(a)?f(b),求ab的取值范围.
(4)若关于x的方程f(x)?bf(x)?c?0有7个不同实数解,求b,c满足的条件.
5.已知函数f(x)?a?b
|x|(x?0)。 2
(1)若函数f(x)是(0,??)上的增函数,求实数b的取值范围;
(2)当b?2时,若不等式f(x)?x在区间(1,??)上恒成立,求实数a的取值范围;
(3)对于函数g(x)若存在区间[m,n](m?n),使x?[m,n]时,函数g(x)的值域也是
[m,n],则称g(x)是[m,n]上的闭函数。若函数f(x)是某区间上的闭函数,试探求a,b应满足的条件。
高中数学必修一 高中数学必修一函数大题(含详细解答)
6、设f(x)?
ax2求满足下列条件的实数a的值:至少有一个正实数b,使函数f(x)?bx,的定义域和值域相同。(www.61k.com]
7.对于函数f(x),若存在x0?R ,使f(x0)?x0成立,则称点(x0,x0)为函数的不动点。
(1)已知函数f(x)?ax2?bx?b(a?0)有不动点(1,1)和(-3,-3)求a与b的值;
(2)若对于任意实数b,函数f(x)?ax2?bx?b(a?0)总有两个相异的不动点,求a的取值范围;
(3)若定义在实数集R上的奇函数g(x)存在(有限的)n 个不动点,求证:n必为奇数。
8.设函数f(x)?x?1
x,(x?0)的图象为C1、C1关于点A(2,1)的对称的图象为C2,
C2对应的函数为g(x).
(1)求函数y?g(x)的解析式;
(2)若直线y?b与C2只有一个交点,求b的值并求出交点的坐标.
9.设定义在(0,??)上的函数f(x)满足下面三个条件:
①对于任意正实数a、b,都有f(a?b)?f(a)?f(b)?1;
②f(2)?0;
③当x?1时,总有f(x)?1.
(1)求f(1)及f()的值; 21
(2)求证:f(x)在(0,??)上是减函数.
10. 已知函数f(x)是定义在??2,2?上的奇函数,当x?[?2,0)时,f(x)?tx?
常数)。
(1)求函数f(x)的解析式;
(2)当t?[2,6]时,求f(x)在??2,0?上的最小值,及取得最小值时的x,并猜想f(x)
在?0,2?上的单调递增区间(不必证明);
(3)当t?9时,证明:函数y?f(x)的图象上至少有一个点落在直线y?14上。
12x(t为3
高中数学必修一 高中数学必修一函数大题(含详细解答)
11.记函数f?x??2?x?7
x?2的定义域为A,g?x??lg??2x?b??ax?1???b?0,a?R?的定
义域为B, (1)求A:
(2)若A?B,求a、b的取值范围
12、设f?x??a?1
xx1?a
(1)求f?x?的反函数f?a?0,a?1?。(www.61k.com] ?1?x?:
(2)讨论f?1?x?在?1.???上的单调性,并加以证明:
(3)令g?x??1?logax,当?m,n???1,????m?n?时,
?g?n?,g?m??,求a 的取值范围。
13.集合A是由具备下列性质的函数f(x)组成的:
(1) 函数f(x)的定义域是[0,??);
(2) 函数f(x)的值域是[?2,4); f?1?x?在?m,n?上的值域是
(3) 函数f(x)在[0,??)上是增函数.试分别探究下列两小题:
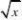
(Ⅰ)判断函数f1(x)?1x2(x?0),及f2(x)?4?6?()(x?0)是否属于集合A?并简2
要说明理由.
(Ⅱ)对于(I)中你认为属于集合A的函数f(x),不等式f(x)?f(x?2)?2f(x?1),
是否对于任意的x?0总成立?若不成立,为什么?若成立,请证明你的结论.
14、设函数f(x)=ax2+bx+1(a,b为实数),F(x)=??f(x)
??f(x)(x?0)(x?0)
(1)若f(-1)=0且对任意实数x均有f(x)?0成立,求F(x)表达式。
(2)在(1)的条件下,当x???2,2?时,g(x)=f(x)-kx是单调函数,求实数k的取值范围。
(3)(理)设m>0,n<0且m+n>0,a>0且f(x)为偶函数,求证:F(m)+F(n)>0。
15.函数f(x)=x
ax?b(a,b是非零实常数),满足f(2)=1,且方程f(x)=x有且仅有一个解。
(1)求a、b的值;
(2)是否存在实常数m,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立?为什么?
(3)在直角坐标系中,求定点A(–3,1)到此函数图象上任意一点P的距离|AP|的最小值。
高中数学必修一 高中数学必修一函数大题(含详细解答)
函数大题专练答案
1、已知关于x的不等式(kx?k2?4)(x?4)?0,其中k?R。[www.61k.com]
⑴试求不等式的解集A;
⑵对于不等式的解集A,若满足A?Z?B(其中Z为整数集)。试探究集合B能否为有限集?若能,求出使得集合B中元素个数最少的k的所有取值,并用列举法表示集合
B;若不能,请说明理由。
解:(1)当k?0时,A?(??,4);当k?0且k?2时,A?(??,4)?(k?
4k
,??);
当k?2时,A?(??,4)?(4,??);(不单独分析k?2时的情况不扣分) 当k?0时,A?(k?
4k,4)。
(2) 由(1)知:当k?0时,集合B中的元素的个数无限;
当k?0时,集合B中的元素的个数有限,此时集合B为有限集。 因为k?
4k
??4,当且仅当k??2时取等号,
所以当k??2时,集合B的元素个数最少。 此时A???4,4?,故集合B???3,?2,?1,0,1,2,3?。
2、对定义在[0,1]上,并且同时满足以下两个条件的函数f(x)称为G函数。 ① 对任意的x?[0,1],总有f(x)?0;
② 当x1?0,x2?0,x1?x2?1时,总有f(x1?x2)?f(x1)?f(x2)成立。 已知函数g(x)?x2与h(x)?a?2x?1是定义在[0,1]上的函数。 (1)试问函数g(x)是否为G函数?并说明理由; (2)若函数h(x)是G函数,求实数a的值;
(3)在(2)的条件下,讨论方程g(2x?1)?h(x)?m(m?R)解的个数情况。 解:(1) 当x??0,1?时,总有g(x)?x2?0,满足①,
当x1?0,x2?0,x1?x2?1时,
g(x1?x2)?x1?x2?2x1x2?x1?x2?g(x1)?g(x2),满足②
2
2
2
2
(2)若a?1时,h(0)?a?1?0不满足①,所以不是G函数;
1?x2
若a?1时,h(x)在x?[0,1]上是增函数,则h(x)?0,满足①
x
由h(x1?x2)?h(x1)?h(x2) ,得a?2
?1?a?2
x1
?1?a?2
x2
?1,
即a[1?(2所以 0?2
?a?
x1
x1
?1)(2
x2
?1)]?1,
x
x1
x1
因为 x1?0,x2?0,x1?x2?1
?1?1 0?22?1? 1 x1与x2不同时等于1 ?0?(21
1?(2
x1
?1)(2?1)?1
?1)(2
x1
?1)
1
)min?1 ?a?1,
当x1?x2?0时,(
1?(2
x1
?1)(2
x1
?1)
综合上述:a?{1} (3)根据(2)知: a=1,方程为4x?2x?m,
高中数学必修一 高中数学必修一函数大题(含详细解答)
?0?2x?1?1由? 得 x?[0,1] ?0?x?1
11令2x?t?[1,2],则m?t2?t?(t?)2? 24
由图形可知:当m?[0,2]时,有一解; 当m?(??,0)?(2,??)时,方程无解。[www.61k.com) 3.已知函数f(x)?2x?1
|x|2
(1)若f(x)?2,求x的值; .
(2)若2tf(2t)?mf(t)?0对于t?[2,3]恒成立,求实数m的取值范围.
[解] (1)当x?0时,
由条件可知 2x
解得 2x
?2xf(x)?0;当x?0时,f(x)?2?2,即 22xxx?12x. ?12x?2?2?1?0, ?1?2.
2?0,?x?log?1?
?
?22t2?. 1?1??t?m2?????02tt2?2?? (2)当t?[1,2]时,2t?
即 m?22t
?2t?,
??. 2?1?0, ? m???2?1?. t?[2,3],???1?2??[?65,?17], ?1??24t???12t2t
故m的取值范围是[?17,??).
?1?,x?0;?4.设函数f(x)是定义在R上的偶函数.若当x?0时,f(x)?? x
?0,x?0.?
(1)求f(x)在(??,0)上的解析式.
(2)请你作出函数f(x)的大致图像.
(3)当0?a?b时,若f(a)?f(b),求ab的取值范围.
(4)若关于x的方程f(x)?bf(x)?c?0有7个不同实数解,求b,c满足的条件. 2
[解](1)当x?(??,0)时,f(x)?f(?x)??
(2)
f(x)的大致图像如下:. 1?x??1x.
高中数学必修一 高中数学必修一函数大题(含详细解答)
0?a?bf(a)?f(b)1?1?11??
?1?????1????1?????2,
aba?b?ab??
?a?b?2ab?11
22
解得ab的取值范围是(1,??).
(4)由(2),对于方程f(x)?a,当a?0时,方程有3个根;当0?a?1时,方程有4个根,当a?1时,方程有2个根;当a?0时,方程无解.…15分
所以,要使关于x的方程f(x)?bf(x)?c?0有7个不同实数解,关于f(x)的方程
f(x)?bf(x)?c?0
2
2
有一个在区间(0,1)的正实数根和一个等于零的根。(www.61k.com)
所以c?0,f(x)??b?(0,1),即?1?b?0,c?0. 5.已知函数f(x)?a?
b|x|
(x?0)。
(1)若函数f(x)是(0,??)上的增函数,求实数b的取值范围;
(2)当b?2时,若不等式f(x)?x在区间(1,??)上恒成立,求实数a的取值范围; (3)对于函数g(x)若存在区间[m,n](m?n),使x?[m,n]时,函数g(x)的值域也是
[m,n],则称g(x)是[m,n]上的闭函数。若函数f(x)是某区间上的闭函数,试探
求a,b应满足的条件。
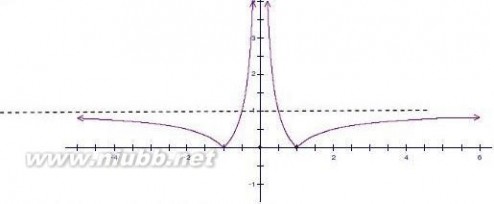
解:(1) 当x?(0,??)时,f(x)?a?
bx
设x1,x2?(0,??)且x1?x2,由f(x)是(0,??)上的增函数,则f(x1)?f(x2)
f(x1)?f(x2)?
b(x1?x2)x1x2
?0
由x1?x2,x1,x2?(0,??)知x1?x2?0,x1x2?0,所以b?0,即b?(0,??)

高中数学必修一 高中数学必修一函数大题(含详细解答)
(2)当b?2时,f(x)?a?
2
x2x2|x|?x在x?(1,??)上恒成立,即a?x?2x
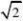
因为x??,当x?
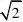
2
x即x?时取等号,
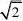
(1,??),所以x?在x?(1,??
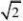
)上的最小值为
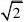
a?(3) 因为f(x)?a?b
|x|的定义域是(??,0)?(0,??),设f(x)是区间[m,n]上的闭函
数,则mn?0且b?0
(4) ①若0?m?n
?f(m)?m当b?0时,f(x)?a?是(0,??)上的增函数,则?, f(n)?n|x|?b 所以方程a?bx?x在(0,??)上有两不等实根, 即x2?ax?b?0在(0,??)上有两不等实根,所以
?a2?4b?0
?2?x1?x2?a?0,即a?0,b?0且a?4b?0
?x?x?b?0?12
当b?0时,f(x)?a?b
|x|?a??b
x在(0,??)上递减,则??f(m)?n
?f(n)?m,即 b?a??n??a?0?m,所以a?0,b?0 ???bmn??b??a??m?n?
②若m?n?0
?f(m)?n当b?0时,f(x)?a?,即?a?是(??,0)上的减函数,所以?f(n)?m|x|x?bb
b?a??n??a?0?m?,所以a?0,b?0 ???mn?b?a?b?m?n? 6、设f(x)?ax2?bx,求满足下列条件的实数a的值:至少有一个正实数b,使函数
f(x)的定义域和值域相同。(www.61k.com]
高中数学必修一 高中数学必修一函数大题(含详细解答)
解:(1)若a?0,则对于每个正数b,f(x)?bx的定义域和值域都是[0,??)
故a?0满足条件
(2)若a?0,则对于正数b,f(x)?
ax
2
b??
?bx的定义域为D????,????0,???,
a??
但f(x)的值域A??0,???,故D?A,即a?0不合条件;
(3)若a?0,则对正数b,定义域D?[0,?
ba
] (f(x))max?
b2?a
,
?a?0
???a??4 ],??f(x)的值域为[0,
a2?a2?a?2?a??a
bbb
综上所述:a的值为0或?4
7.对于函数f(x),若存在x0?R ,使f(x0)?x0成立,则称点(x0,x0)为函数的不动点。[www.61k.com] (1)已知函数f(x)?ax2?bx?b(a?0)有不动点(1,1)和(-3,-3)求a与b的值; (2)若对于任意实数b,函数f(x)?ax2?bx?b(a?0)总有两个相异的不动点,求a的取值范围;
(3)若定义在实数集R上的奇函数g(x)存在(有限的)n 个不动点,求证:n必为奇数。 解:(1)由不动点的定义:f(x)?x?0,∴ax2?(b?1)x?b?0 代入x?1知a?1,又由x??3及a?1知b?3。 ∴a?1,b?3。
2
(2)对任意实数b,f(x)?ax?bx?b(a?0)总有两个相异的不动点,即是对任意的实数b,方程f(x)?x?0总有两个相异的实数根。
∴ax
2
?(b?1)x?b?0中??(b?1)?4ab?0,
2
22
即b?(4a?2)b?1?0恒成立。故?1?(4a?2)?4?0,∴0?a?1。
故当0?a?1时,对任意的实数b,方程f(x)总有两个相异的不动点。 ………...................1’
(3)g(x)是R上的奇函数,则g(0)?0,∴(0,0)是函数g(x)的不动点。 若g(x)有异于(0,0)的不动点(x0,x0),则g(x0)?x0。 又g(?x0)??g(x0)??x0,∴(?x0,?x0)是函数g(x)的不动点。
高中数学必修一 高中数学必修一函数大题(含详细解答)
∴g(x)的有限个不动点除原点外,都是成对出现的, 所以有2k个(k?N),加上原点,共有n?2k?1个。(www.61k.com]即n必为奇数 8.设函数f(x)?x?1
x(2,1)的对称的图象为C2,,(x?0)的图象为C1、C1关于点A
C2对应的函数为g(x).
(1)求函数y?g(x)的解析式;
(2)若直线y?b与C2只有一个交点,求b的值并求出交点的坐标.
解.(1)设p(u,v)是y?x?1
x上任意一点,?v?u?1
u ①
设P关于A(2,1)对称的点为Q(x,y),??
1
4?x?u?x?4?u?4?x?? ?v?y?2?v?2?y1x?4代入①得2?y?4?x?
?g(x)?x?2?1
x?4?y?x?2? (x?(??,4)?(4,??));
?y?b?2 (2)联立?1?x?(b?6)x?4b?9?0, ?y?x?2?x?4?
???(b?6)?4?(4b?9)?b?4b?0?b?0或b?4, 22
(1)当b?0时得交点(3,0); (2)当b?4时得交点(5,4).
9.设定义在(0,??)上的函数f(x)满足下面三个条件:
①对于任意正实数a、b,都有f(a?b)?f(a)?f(b)?1; ②f(2)?0;
③当x?1时,总有f(x)?1.
(1)求f(1)及f()的值; 21
(2)求证:f(x)在(0,??)上是减函数. 解(1)取a=b=1,则f(1)?2f(1)?1.故f(1)?1 又f(1)?f(2?11)?f(2)?f()?1.
22 且f(2)?0.
高中数学必修一 高中数学必修一函数大题(含详细解答)
得:
1
f()?f(1)?f(2)?1?1?1?2 2
(2)设0?x1?x2,则:f(x2)?f(x1)?f(x2?x1)?f(x1)?[f(x2)?f(x1)?1]?f(x1)
x1
x1
?f(
x2x1
)?1 依0?x1?x2,可得
x2x1
?1
再依据当x?1时,总有f(x)?1成立,可得f(
x2x1
)?1
即f(x2)?f(x1)?0成立,故f(x)在(0,??)上是减函数。(www.61k.com]
10. 已知函数f(x)是定义在??2,2?上的奇函数,当x?[?2,0)时,f(x)?tx?常数)。
(1)求函数f(x)的解析式;
(2)当t?[2,6]时,求f(x)在??2,0?上的最小值,及取得最小值时的x,并猜想f(x)
在?0,2?上的单调递增区间(不必证明);
(3)当t?9时,证明:函数y?f(x)的图象上至少有一个点落在直线y?14上。 解:(1)x??0,2?时,?x???2,0?, 则 f(?x)?t(?x)?
12
(?x)??tx?
3
12
x(t为
3
1212
12
x, ∵函x,即 x ,
33
3
数f(x)是定义在??2,2?上的奇函数,即f??x???f?x?,∴?f?x???tx?
f(x)?tx?
12
x,又可知 f?0??0,∴函数f(x)的解析式为 f(x)?tx?
3
x???2,2?;
(2)f?x??x?t?
?
?1
122?
x?,∵t?[2,6],x???2,0?,∴t?x?0,
22?
3
∵ ?f?x??
2
1212??2
2?x?t?x?t?x?3
12?8t122?2
???x?t?x???,∴x?t?x,
2?3272???
????
6t3
6t3
???2,0?)时,fmin??
??
即 x?
2
2t3
,x??(?
269
tt 。
猜想f(x)在?0,2?上的单调递增区间为?0,(3)t?9时,任取?2?x1?x2?2,∵
6t?
?。 3?
高中数学必修一 高中数学必修一函数大题(含详细解答)
1?22?f?x1??f?x2???x1?x2??t?x1?x1x2?x2??0, 2????
∴f?x?在??2,2?上单调递增,即f?x???f??2?,f?2??,即f?x???4?2t,2t?4?,t?9,∴4?2t??14,2t?4?14,
∴14??4?2t,2t?4?,∴当t?9时,函数y?f(x)的图象上至少有一个点落在直线y?14上。(www.61k.com)
11.记函数f?x??2?x?7
x?2的定义域为A,g?x??lg??2x?b??ax?1???b?0,a?R?的定
义域为B, (1)求A:
(2)若A?B,求a、b的取值范围
解:(1)A??x2??x?7??x?3??0???x?0?????,?2???3,???, x?2???x?2?
b1(2)?2x?b??ax?1??0,由A?B,得a?0,则x?orx??,即 2a
b?10??3??a?1??b????2。 ??B????,????,???, ?2a??2???0?b?6??2??1?0??a?
12、设f?x??a?1
xx1?a
(1)求f?x?的反函数f?a?0,a?1?。 ?1?x?:
(2)讨论f?1?x?在?1.???上的单调性,并加以证明:
(3)令g?x??1?logax,当?m,n???1,????m?n?时,
?g?n?,g?m??,求a 的取值范围。
解:(1)f?1f?1?x?在?m,n?上的值域是?x??logx?1
ax?1?x?1或x??1?
(2)设1?x1?x2,∵
∴0?a?1时,f?1x1?1x1?1?x2?1x2?1?2?x1?x2??x1?1??x2?1??0 ?x1??f?1?x2?,∴f?1?x?在?1.???上是减函数:a?1时,
?1?1?1f?x1??f?x2?,∴f?x?在?1.???上是增函数。
?1(3)当0?a?1时,∵f?x?在?1.???上是减函数,
?1?x?1x?1?f?m??g?m?2?1?logax得?ax,即ax??a?1?x?1?0, ∴?,由loga ?1x?1x?1??f?n??g?n?
高中数学必修一 高中数学必修一函数大题(含详细解答)
?
???0?可知方程的两个根均大于1,即?f?1??0?0?a?3?22,当a?1时,∵f
?1?a??1?2a
??f上是增函数,∴?1.??????f?1?x?在?m??g?n???1?n??g?m??1?m?1?amn?an?a??1(舍去)。(www.61k.com) 综??n?1?amn?am
上,得 0?a?3?22。
13.集合A是由具备下列性质的函数f(x)组成的:
(1) 函数f(x)的定义域是[0,??);
(2) 函数f(x)的值域是[?2,4);
(3) 函数f(x)在[0,??)上是增函数.试分别探究下列两小题:
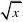
(Ⅰ)判断函数f1(x)?1x2(x?0),及f2(x)?4?6?()(x?0)是否属于集合A?并简2
要说明理由.
(Ⅱ)对于(I)中你认为属于集合A的函数f(x),不等式f(x)?f(x?2)?2f(x?1),
是否对于任意的x?0总成立?若不成立,为什么?若成立,请证明你的结论.
解:(1)函数f1(x)?
f1(x)?x?2不属于集合A. 因为f1(x)的值域是[?2,??),所以函数x?2不属于集合A.(或?当x?49?0时,f1(49)?5?4,不满足条件.)
1xf2(x)?4?6?()(x?0)在集合A中, 因为: ① 函数f2(x)的定义域是[0,??);② 函2
数f2(x)的值域是[?2,4);③ 函数f2(x)在[0,??)上是增函数.
(2)f(x)?f(x?2)?2f(x?1)?6?()(?21x14)?0,
?不等式f(x)?f(x?2)?2f(x?1)对于任意的x?0总成立
14、设函数f(x)=ax2+bx+1(a,b为实数),F(x)=??f(x)
??f(x)(x?0)(x?0)
(1)若f(-1)=0且对任意实数x均有f(x)?0成立,求F(x)表达式。
(2)在(1)的条件下,当x???2,2?时,g(x)=f(x)-kx是单调函数,求实数k的取值范围。
(3)(理)设m>0,n<0且m+n>0,a>0且f(x)为偶函数,求证:F(m)+F(n)>0。
解:(1)?f(-1)=0 ∴b?a?1由f(x)?0恒成立 知△=b2-4a=(a+1)2-4a=(a-1)2?0
(x?0)?(x?1)2∴a=1从而f(x)=x+2x+1 ∴F(x)=? , 2?(x?1)(x?0)?
(2)由(1)可知f(x)=x2+2x+1 ∴g(x)=f(x)-kx=x2+(2-k)x+1,由于g(x)在??2,2?上是单调函数,知-2?k
2??2或-2?k
2?2,得k?-2或k?6 ,
(3)?f(x)是偶函数,∴f(x)=f(x),而a>0∴f(x)在?0,???上为增函数
对于F(x),当x>0时-x<0,F(-x)=-f(-x)=-f(x)=-F(x),当x<0时-x>0,F(-x)=f(-x)=f(x)=-F(x),
高中数学必修一 高中数学必修一函数大题(含详细解答)
∴F(x)是奇函数且F(x)在?0,???上为增函数, ?m>0,n<0,由m>-n>0知F(m)>F(-n)∴F(m)>-F(n) ∴F(m)+F(n)>0 。(www.61k.com] 15.函数f(x)=
xax?b
(a,b是非零实常数),满足f(2)=1,且方程f(x)=x有且仅有一个解。
(1)求a、b的值;
(2)是否存在实常数m,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立?为什么? (3)在直角坐标系中,求定点A(–3,1)到此函数图象上任意一点P的距离|AP|的最小值。 解 (1)由f(2)=1得2a+b=2,又x=0一定是方程所以
1ax?b
xax?b
=x的解,
=1无解或有解为0,若无解,则ax+b=1无解,得a=0,矛盾,若有解为0,则
12
b=1,所以a=(2)f(x)=
2xx?2
。
,设存在常数m,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立,
2mm?2
取x=0,则f(0)+f(m–0)=4,即f(x)+f(–4–x)=
2xx?2
2
=4,m= –4(必要性),又m= –4时,
?
2(?4?x)?4?x?2
2
=……=4成立(充分性) ,所以存在常数m= –4,使得对定
义域中任意的x,f(x)+f(m–x)=4恒成立, (3)|AP|=(x+3)+(|AP|=(t+1)+(, 所以当t–
4t
2
22
x?2
x?2t?422t
),设x+2=t,t≠0, 则
8t
)=t+2t+2–+
16t
2
=(t+
2
16t
2
)+2(t–
4t
)+2=(t–
4t
)+2(t–
2
4t
)+10=( t–
4t
+1)+9
2
+1=0时即t=
2x
?1?2
2
,也就是x=
?5?2
时,|AP| min = 3 。
16、已知函数f(x)??log
1?mx1?x
是奇函数。
(1)求m的值;
(2)请讨论它的单调性,并给予证明。
解(1)?f(x)是奇函数,?f(?x)?f(x)?0; 即(?
2x?log
1?mx
2
1?x
)?(
2x
?log2x
1?mx
2
1?x
2
)?0,解得:m?1,其中m??1(舍); (x???1,0???0,1?)确是奇函数。
经验证当m?1时,f(x)??log
1?x1?x
(2)先研究f(x)在(0,1)内的单调性,任取x1、x2∈(0,1),且设x1<x2 ,则
高中数学必修一 高中数学必修一函数大题(含详细解答)
f(x1)?f(x2)?
?(
由2
x1?2x22x12x1?log?2x221?x121?x1?(22x22?log1?x221?x221?x1?1)], )?[log1?x2?1)?log2(2?0,log2(1?x2?1)?log2(1?x1?1)?0,
得f(x1)?f(x2)>0,即f(x)在(0,1)内单调递减; 由于f(x)是奇函数,其图象关于原点对称,所以函数f(x)在(-1,0)内单调递减。[www.61k.com)
三 : 2011年湖北武汉中考数学16题怎么做要详细的解答过程,谢谢
2011年湖北武汉中考数学16题怎么做
要详细的解答过程,谢谢
如图,过C、D两点作x轴的垂线,垂足为F、G,DG交BC于M点,过C点作CH⊥DG,垂足为H,
∵ABCD是平行四边形,
∴∠ABC=∠ADC,
∵BO∥DG,
∴∠OBC=∠GDE,
∴∠HDC=∠ABO,
∴△CDH≌△ABO(ASA),
∴CH=AO=1,DH=OB=2,
设C(m+1,n),D(m,n+2),
则(m+1)n=m(n+2)=k,
解得n=2m,则D的坐标是(m,2m+2),
设直线AD解析式为y=ax+b,将A、D两点坐标代入得
﹛-a+b=0………①
﹛ma+b=2m+2…②
由①得:a=b,代入②得:mb+b=2m+2,
即b(m+1)=2(m+1),解得b=2,
∴a=2,b=2
∴y=2x+2,E(0,2),BE=4,
∴S△ABE=1/2×BE×AO=2,
∵S四边形BCDE=5S△ABE=5×1/2×4×1=10,
∴S△ABE+S四边形BEDM=10,
即2+4×m=10,
解得m=2,
∴n=2m=4,
∴k=(m+1)n=3×4=12.
本文标题:中学数学题详细解答-2011年无锡市化学中考17题D选项求详细解析61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1