一 : 经典数学问题----费马最後定理

被公认执世界报纸牛耳地位地位的纽约时报於1993年6月24日在其一版头题刊登了一则有关数学难题得以解决的消息，那则消息的标题是「在陈年数学困局中，终於有人呼叫「我找到了」」。时报一版的开始文章中还附了一张留着长发、穿着中古世纪欧洲学袍的男人照片。这个古意盎然的男人，就是法国的数学家费马（pierre de fermat）（费马小传请参考附录）。费马是十七世纪最卓越的数学家之一，他在数学许多领域中都有极大的贡献，因为他的本行是专业的律师，为了表彰他的数学造诣，世人冠以「业余王子」之美称，在三百六十多年前的某一天，费马正在阅读一本古希腊数学家戴奥芬多斯的数学书时，突然心血来潮在书页的空白处，写下一个看起来很简单的定理这个定理的内容是有关一个方程式 x2 + y2 =z2的正整数解的问题，当n=2时就是我们所熟知的毕氏定理（中国古代又称勾股弦定理）：x2 + y2 =z2，此处z表一直角形之斜边而x、y为其之两股，也就是一个直角三角形之斜边的平方等於它的两股的平方和，这个方程式当然有整数解（其实有很多），例如：x=3、y=4、z=5；x=6、y=8、z=10；x=5、y=12、z=13…等等。

　　费马声称当n>2时，就找不到满足xn +yn = zn的整数解，例如：方程式x3 +y3=z3就无法找到整数解。当时费马并没有说明原因，他只是留下这个叙述并且也说他已经发现这个定理的证明妙法，只是书页的空白处不够无法写下。始作俑者的费马也因此留下了千古的难题，三百多年来无数的数学家尝试要去解决这个难题却都徒劳无功。这个号称世纪难题的费马最後定理也就成了数学界的心头大患，极欲解之而後快？

　　十九世纪时法国的法兰西斯数学院曾经在一八一五年和一八六0年两度悬赏金质奖章和三百法郎给任何解决此一难题的人，可惜都没有人能够领到奖赏。德国的数学家佛尔夫斯克尔（p？wolfskehl）在1908年提供十万马克，给能够证明费马最後定理是正确的人，有效期间为100年。其间由於经济大萧条的原因，此笔奖额已贬值至七千五百马克，虽然如此仍然吸引不少的「数学痴」。

二 : 家装水电问题的经典问答

问：改水时冷热水管一定要间距10cm吗？我家工头说间距4－5cm就足够了，不知道对不对啊？

答：做好保温管就可以了

问：PVC排水管渗水的主要原因有哪些？

答：做10公斤水压测试，30分钟，查漏，有可能接头没封好

问：我的装修工人开槽的时候，把承重墙的钢筋露出来了，但是要埋暗盒，是不是不能在承重墙上挖暗盒的洞？ 时间久了会不会有影响啊？

答：这没问题！挖好补平就可以。时间久了没关系。

问：请问如果先不考虑价格因素的话，是否铜管比PPR更好？

答：铜管好．但是有铜锈．而且还有毒。

问：为什么改动下水管会返异味？

答：没装U型弯，最好再装防臭地漏

问：到底选择什么样的水管：

答：目前市场上水路改造主流水管是PPR水管和铜管，铝塑管已经慢慢的少了。

PPR水管采用先进的热熔技术，一般都说终身不漏水，不过PPR水管在低温下会变脆，高温下也会出现一定的变化，所以购买时要注意选择品牌，看见过一些品牌的PPR水管，包括一些网上做的风风火火的品牌的水管和接头莫名其妙的出现裂纹的情况，所以大家选择水管需谨慎。一般PPR水管分冷热水管，冷水管管壁薄，热水管管壁厚，在抗断裂性方面热水管性能好很多，当然价格也是热水管比冷水管贵一些，

就铜管而言，价位高是它的最大缺点，是目前最高档的水管，通常采用焊接工艺安装之后会终身不漏水，另外也不会象不好的PPR一样会裂，甚至有说法铜还有一定的杀菌作用，有些还在使用的铜管，已经有80多年了，应该是值得信赖的。

问：我家里的水管需要改造吗？

答：如果你家里从水表之后没有水管，或者有水管，但是不好，比如是镀锌管，PVC管，或者水管的位置不合理，想重新做，那么就需要改造。

问：水管改造需要多长时间？

答：这个问题很难说，根据你家的情况，时间可长可短，没有标准定义的。

问：水路改造到底应该留出来什么样的接头？

答：一般座便器的位置需要留一个冷水管出口，脸盆、厨房水槽、淋浴或浴缸的位置，都需要留冷热水两个出口。需要注意的是不要出口留少了或者留错了，所以最好要叮咛水路改造工人一定要注意，并且最好改造结束后测试一下，看看各个出口出水是否正常，是不是热水管出水的时候热水表转，冷水管出水的时候冷水表动。

另外一般水管出口都是4分标准接口。

问：我可以按照我的要求想让哪里出水就哪里出水吗？

答：当然可以，不过你要注意，你把水管出水的位置改变的，那么相应的下水管是不是也需要改变，这需要你综合考虑，有人将面盆位置从一面墙挪到另外一面墙上，瓷砖什么的都弄好了，就差最后安装洁具了，安装面盆的时候才意识到下水没有挪过来，

水路改造，客户要自己上心，毕竟家是你自己的，其实水路改造无非就是在哪里要留出水口，出什么水的问题，至于管路怎么样走，一般水管公司也都是建议，比如是走吊顶还是地面呀，你可以根据自己的判断选择最好的方案。

问：水管到底是走吊顶还是地面：

答：一般情况下，走吊顶会费水管，走地面省管，但是走吊顶，将来有维修的话方便，如果走地面，铺上瓷砖后很难维修，有时还需要地面开槽，包括做防水等等，有的人喜欢从棚上走管线的。

建议，如果水管需要走过房间的话，最好走上面，不要走地面，多花点钱，图个心里踏实，其实家庭装修最麻烦的就是水路、电路和暖气改造，不要在这上面省钱。

问：水路改造需要征求物业意见吗？

答：水路改造涉及到上水和下水，有些需要挪动位置的，包括水表位置，出水口位置、下水管位置等等，都最好在准备改造前咨询一下物业有什么是能动的，有什么是不能动的，目前来说，大家买的都不是别墅，这也就意味着你家的房子并不是你完全能够说了算的，物业公司需要审查你的改动，以决定是否会对你的邻居造成影响。

大家装修之前都要到物业那里签个协议，物业一般会要求你写出来家里需要做什么样的装修项目，我建议大家不要把这件事情当成走过场，我建议大家都实实在在的写，而且对于象水电改造、暖气改造、拆墙等项目，更要跟物业人员深入沟通，以免出现问题无法挽救。

以后在墙上打洞的时候.很可能打到管.如果走到墙边角打到的机会就会少很多.因为你会知道这个插座的上方或下方垂直线的区域可能有线管.

注意

关于水电改造，还有几点需要注意：

1、设计的时候一定要设计师到现场去测量，最好带一个水电工，先想好自己的要求，一定要反复推敲，省得施工开始后再改来改去；

不要听任设计师或施工队的摆布，哪里该和哪里不该，你要静一静，尤其是对方极力鼓动的部位，说不定是最没必要的；建议也找有过装修经历或懂装修的朋友参考：

2、水电线路改造的价格一定要讲清楚，最好在合同中注明电路改造所用的电线的品牌。我本人一般用的电线是远东，水路是金牛或金德PP-R管，无论用什么品牌的，一定要在合同中注明。

3、全屋的开关应基本处于同一水平位置，插座距宜为30公分，开关距地宜为140公分。 特殊插座如空调、冰箱及有特殊要求的例外。

4、电路改造中的住宅相线、零线、地线的颜色一定要统一

5、插座线（包括空调冰箱）最好用3线4.0多股，照明线用2线2.5多股就可以了。而且空调线走专线，无论几匹的空调，都最好用4.0的线。

6、用好一点的底盒。

7、关于音响线，如果你不是专业的发烧友，音响线使用6元一米左右的就差不多了：

8、强电与弱电不能走同一条管子。

9、水路改造，入墙的部分一定要用PPR管。

10、水路方面，厨房的冷热水接口、下水管位置特别重要，另外生活阳台的接排水管位置也十分重要；

11、无论水管、线管、底座，你都有要一一检查质量，要不然埋到了地上或墙里面就是一辈子的事了；

12、安装安以后你一定要亲自动手量，不要听他报数字；

13、跟施工方说好，重复性改造的费用由他们承担，改造若留下问题，扣款；

14。机器开槽好看，但因边缘太光滑，批荡以后容易产生裂缝，建议采用手工开槽。

15。电话线、网络线价钱差不多，建议用网络线代替电话线，将来你的灵活性大很多。

16。开槽一定注意躲开水管和原来的线管。

水电改造注意要点

有许多工程队喜欢在水电改造时穿“马甲”，而业主往往事情教忙忽略了这个问题。

马甲是怎么回事呢？也就是铺线时不套管,乘业主不注意的时候，迅速封上水泥，然后

在离接线合的位置约10公分的地方开始套管，蒙蔽业主的双眼。

装修前说好，不检查就不许封水泥。

2316539058329176405.jpg (22.87 KB)

下载次数:0

前天19:37

 

水路改造实图



收藏 分享 评分

三 : 函数定义域、值域经典习题及答案

复合函数定义域和值域练习

搜集整理

向真贤

一、 求函数的定义域

1、求下列函数的定义域：

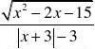
⑴y?

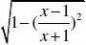
⑵y?

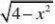
⑶y?1

1?x?1?(2x?1)0

2、设函数f(x)的定义域为[0，1]，则函数f(x2)的定义域为_ _ _；函数f(?2)的定义域为________；

1f(x?1)的定义域为[?2，3]，则函数f(2x?1)的定义域是 ；函数f(?2)的定义域x3、若函数

为 。[www.61k.com]

4、 知函数

二、求函数的值域

5、求下列函数的值域：

⑴

⑵

⑶f(x)的定义域为[?1, 1]，且函数F(x)?f(x?m)?f(x?m)的定义域存在，求实数m的取值范围。 y?x2?2x?3 (x?R) y?x2?2x?3 x?[1,2] y?3x?1 x?1

3x?1⑷y? (x?5) x?1

⑸

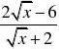
y? ⑹ 5x2＋9x?4y? x2?1

⑺

⑻y?x?3?x?1 y?x2?x

⑼

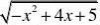
⑽

y? y?4

1

函数定义域 函数定义域、值域经典习题及答案

⑾y?x2x2?ax?bf(x)?的值域为[1，3]，求a,b的值。(www.61k.com） x2?16、已知函数

三、求函数的解析式

1、 已知函数

2、 已知f(x?1)?x2?4x，求函数f(x)，f(2x?1)的解析式。 f(x)是二次函数，且f(x?1)?f(x?1)?2x2?4x，求f(x)的解析式。

3、已知函数

4、设

f(x)满足2f(x)?f(?x)?3x?4，则f(x)= 。 f(x)是R上的奇函数，且当x?[0,??)时，

f(x)?x(1，则当x?(??,0)时f(x)=____ _ f(x)在R上的解析式为

f(x)与g(x)的定义域是{x|x?R,且x??1}，f(x) 是偶函数，g(x)是奇函数，且f(x)?g(x)?1，x?15、设

求f(x)与g(x) 的解析表达式

四、求函数的单调区间

6、求下列函数的单调区间：

⑴

⑵

⑶ y?x2?2x?3

y? y?x2?6x?1

f(x)在[0,??)上是单调递减函数，则f(1?x2)的单调递增区间是

y?2?x的递减区间是

；函数y?3x?6 7、函数8、函数

五、综合题

9、判断下列各组中的两个函数是同一函数的为 （ ）

⑴y1?(x?3)(x?5)， y2?x?5； ⑵y1?x?1x?1 ， y2?x?1)(x?1) ； x?3

⑶f(x)?x， g(x)?x2； ⑷f(x)?x，

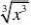
g(x)? ⑸f1(x)?(2x?5)2， f2(x)?2x?5。

A、⑴、⑵ B、 ⑵、⑶ C、 ⑷

10、若函数

D、 ⑶、⑸ f(x)= A、(－∞,+∞) x?4 的定义域为R,则实数m的取值范围是 （ ） mx2?4mx?3333] C、(,+∞) D、[0, ) B、(0,444

11

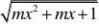
、若函数f(x)?的定义域为R，则实数m的取值范围是（ ）

2

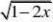
函数定义域 函数定义域、值域经典习题及答案

(A)0?m?4 (B)

12、对于?1?

(A)

13

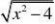
、函数0?m?4 (C) m?4 (D) 0?m?4 a?1，不等式x2?(a?2)x?1?a?0恒成立的x的取值范围是（ ） (B) 0?x?2 x?0或x?2 (C) x?1或x?3 (D) ?1?x?1 f(x)?的定义域是（ ）

A、[?2,2] B、(?2,2) C、(??,?2)?(2,??) D、{?2,2}

14、函数1f(x)?x?(x?0)是（ ） x

A、奇函数，且在(0，1)上是增函数 B、奇函数，且在(0，1)上是减函数

C、偶函数，且在(0，1)上是增函数 D、偶函数，且在(0，1)上是减函数

15、函数?x?2(x??1)?f(x)??x2(?1?x?2) ，若f(x)?3，则x=

?2x(x?2)?

1(x)?fxafxa(??)(?)(?a?0)的定义域为 。（www.61k.com) f(x)的定义域是(0，1]，则g2

mx?n17、已知函数y?2的最大值为4，最小值为 —1 ，则m= ，n= x?1

118、把函数y?的图象沿x轴向左平移一个单位后，得到图象C，则C关于原点对称的图象的解析式为 x?116、已知函数

19、求函数

20、若函数

复合函数定义域和值域练习题

答 案

一、 函数定义域：

1、（1）{x|x?5或x??3或x??6} （2）{x|

2、[?1,1]； f(x)?x2?2ax?1在区间[ 0 , 2 ]上的最值 f(x)?x2?2x?2,当x?[t,t?1]时的最小值为g(t)，求函数g(t)当t?[-3,-2]时的最值。 5[4,9 ] 3、[0,]; 21x?0} （3）{x|?2?x?2且x?0,x?,x?1} 211(??,?]?[,??) 4、?1?m?1 32

二、 函数值域：

7y??4} （2）y?[0,5] （3）{y|y?3} （4）y?[,3) 3

1 （5）y?[?3,2) （6）{y|y?5且y? （7）{y|y?4} （8）y?R 2

1 （9）y?[0,3] （10）y?[1,4] （11）{y|y? 25、（1）{y|

6、a??2,b?2

3

函数定义域 函数定义域、值域经典习题及答案

三、 函数解析式：

1、22 2、f(x)?x?2x?1 3、f(x)?3x?f(x)?x2?2x?3 ； f(2x?1)?4x? 4

?1x?x(1x?0) 5、f(x)?2 g(x)?2 f(x)??x?1x?1??x(1x?0)4 34

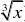
、f(x)?x(1

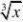
；四、 单调区间：

6、（1）增区间：[?1,??) 减区间：(??,?1] （2）增区间：[?1,1] 减区间：[1,3]

（3）增区间：[?3,0],[3,??) 减区间：[0,3],(??,?3]

7、[0,1] 8、(??,?2),(?2,??)

五、 综合题：

C D B B D B

14

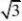
(?2,2] 15、(?a,a?1] 16、m??4 n?3 17、y?1 x?2

18、解：对称轴为x?a （1）a?0时，

（2）0?f(x)min?f(0)??1 ， f(x)max?f(2)?3?4a a?1时，f(x)min?f(a)??a2?1 ，f(x)max?f(2)?3?4a

?2时，f(x)min?f(a)??a2?1 ，f(x)max?f(0)??1 （3）1?a

（4）a?2时 ，f(x)min?f(2)?3?4a ，f(x)max?f(0)??1

?t2?1(t?0)?219、解：g(t)??1(0?t?1) ? t?(??,0]时，g(t)?t?1为减函数

?t2?2t?2(t?1)?

?

? 在[?3,?2]上，g(t)?t2?1也为减函数 g(t)min?g(?2)?5， g(t)max?g(?3)?10

4

四 : 小学全部奥数题及答案_经典奥数题目

六年级奥数题及答案

1、电影票原价每张若干元,现在每张降低3元出售,观众增加一半,收入增加五分之一,一张电影票原价多少元？

解：设一张电影票价x元

(x-3)×（1+1/2）=(1+1/5)x

(1+1/5)x这一步是什么意思，为什么这么做

(x-3){现在电影票的单价}×（1+1/2){假如原来观众总数为整体1，则现在的观众人数为（1+2/1)}

左边算式求出了总收入

(1+1/5）x{其实这个算式应该是：1x*（1+5/1） 把原观众人数看成整体1，则原来应收入1x元，而现在增加了原来的五分之一，就应该再*（1+5/1），减缩后得到（1+1/5x）}

如此计算后得到总收入，使方程左右相等

2、甲乙在银行存款共9600元，如果两人分别取出自己存款的40%，再从甲存款中提120元给乙。（www.61k.com）这时两人钱相等，求 乙的存款

答案

取40％后，存款有

9600×（1－40％）＝5760（元）

这时，乙有：5760÷2＋120＝3000（元）

乙原来有：3000÷（1－40％）＝5000（元）

3、由奶糖和巧克力糖混合成一堆糖，如果增加10颗奶糖后，巧克力糖占总数的60%。再增加30颗巧克力糖后，巧克力糖占总数的75%,那么原混合糖中有奶糖多少颗？巧克力糖多少颗？

答案

加10颗奶糖，巧克力占总数的60%，说明此时奶糖占40%，

巧克力是奶糖的60/40=1。5倍

再增加30颗巧克力，巧克力占75%，奶糖占25%，巧克力是奶糖的3倍 增加了3-1.5=1.5倍，说明30颗占1.5倍

奶糖=30/1.5=20颗

巧克力=1.5*20=30颗

奶糖=20-10=10颗

4、小明和小亮各有一些玻璃球，小明说：“你有球的个数比我少1/4！”小亮说：“你要是能给我你的1/6，我就比你多2个了。”小明原有玻璃球多少个？ 答案

小明说：“你有球的个数比我少1/4！”，则想成小明的球的个数为4份，则小亮的球的个数为3份

4*1/6＝2/3 （小明要给小亮2/3份玻璃球）

小明还剩：4-2/3＝3又1/3（份）

小亮现有：3+2/3＝3又2/3（份）

1

小学奥数题及答案 小学全部奥数题及答案_经典奥数题目

这多出来的1/3份对应的量为2，则一份里有：3*2＝6（个）

小明原有4份玻璃球，又知每份玻璃球为6个，则小明原有玻璃球4*6＝24（个）

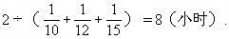
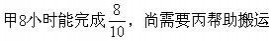
5、搬运一个仓库的货物，甲需要10小时，乙需要12小时，丙需要15小时.有同样的仓库A和B，甲在A仓库、乙在B仓库同时开始搬运货物，丙开始帮助甲搬运，中途又转向帮助乙搬运.最后两个仓库货物同时搬完.问丙帮助甲、乙各多少时间？

解：设搬运一个仓库的货物的工作量是1.现在相当于三人共同完成工作量2，所需时间是

答：丙帮助甲搬运3小时，帮助乙搬运5小时

解本题的关键，是先算出三人共同搬运两个仓库的时间.本题计算当然也可以整数化，设搬运一个仓库全部工作量为 60.甲每小时搬运 6，乙每小时搬运 5，丙每小时搬运4

三人共同搬完，需要

60 × 2÷（6+ 5+ 4）= 8（小时）

甲需丙帮助搬运

（60- 6× 8）÷ 4= 3（小时）

乙需丙帮助搬运

（60- 5× 8）÷4= 5（小时）

2

小学奥数题及答案 小学全部奥数题及答案_经典奥数题目

6、一件工作,若由甲单独做72天完成,现在甲做1天后,乙加入一起工作,合作2天后,丙也一起工作,三人再一起工作4天,完成全部工作的1/3,又过了8天,完成了全部工作的5/6,若余下的工作由丙单独完成,还需要几天?

答案

甲乙丙3人8天完成 :5/6-1/3=1/2

甲乙丙3人每天完成 :1/2÷8=1/16，

甲乙丙3人4天完成 :1/16×4=1/4

则甲做一天后乙做2天要做 :1/3-1/4=1/12

那么乙一天做 :[1/12-1/72×3]/2=1/48

则丙一天做 :1/16-1/72-1/48=1/36

则余下的由丙做要 :[1-5/6]÷1/36=6天

答：还需要6天

7、股票交易中，每买进或卖出一种股票都必须按成交易额的1％和2％分别交纳印花税和佣金（通常所说的手续费）。(www.61k.com)老王10月8日以股票10.65元的价格买进一种科技股票3000股，6月26日以每月13.86元的价格将这些股票全部卖出，

价2.8元出售，很快售完。第二次购书时，每本的批发价比第一次增多了0.5元，用去150元，所购数量比第一次多10本，当这批书售出4/5时出现滞销，便以定价的5折售完剩余图书。试问该老板第二次售书是赔钱还是赚钱，若赔，赔多少，若赚，赚多少

答案

（100+40）/2.8=50本 100/50=2 150/(2+0.5）=60本 60*80%=48本 48*2.8+2.8*50*12-150=1.2 盈利1.2元

一件工程原计划40人做,15天完成.如果要提前3天完成,需要增加多少人 解: 设需要增加x人

(40+x)(15-3)=40*15

x=10

所以需要增加10了

9、仓库有一批货物，运走的货物与剩下的货物的质量比为2：7.如果又运走64吨，那么剩下的货物只有仓库原有货物的五分之三。仓库原有货物多少吨？ 3

小学奥数题及答案 小学全部奥数题及答案_经典奥数题目

解：第1次运走：2/（2+7）=2/9.

64/（1-2/9-3/5）=360吨。［www.61k.com）

答：原仓库有360吨货物。

10、育才小学原来体育达标人数与未达标人数比是3：5，后来又有60名同学达标，这时达标人数是未达标人数的9/11，育才小学共有学生多少人？ 答案

原来达标人数占总人数的

3÷（3＋5）＝3/8

现在达标人数占总人数的

9/11÷（1＋9/11）＝9/20

育才小学共有学生

60÷（9/20－3/8）＝800人

61阅读提醒您本文地址：

11、小王，小李，小张三人做数学练习题，小王做的题数的一半等于小李的1/3,等于小张的1/8,而且小张比小王多做了72道,小王,小张,小李各做多少道? 答案

设小王做了a道，小李做了b道，小张做了c道

由题意1/2a=1/3b=1/8c

c-a=72

解得a=24 b=36 c=96

甲乙二人共同完成242个机器零件。甲做一个零件要6分钟，乙做一个零件要5分钟。完成这批零件时，两人各做了多少个零件？

答案

设甲做了X个，则乙做了（242-X）个

6X=5（242-X）

X=110

242-110=132（个）

答：甲做了110个，乙做了132个

12、某工会男女会员的人数之比是3：2，分为甲乙丙三组，已知甲乙丙三组人数之比是10:8:7，甲组中男女比是3：1，乙组中男女比是5：3。求丙组男女人数之比

答案

设男会员是3N，则女会员是2N，总人是：5N

甲组有：5N*10/[10+8+7]=2N，其中：男：2N*3/4=3N/2，女：2N*1/4=N/2 乙级有：5N*8/25=8/5N，其中男：8/5N*5/8=N，女：8/5N*3/8=3/5N 丙级有：5N*7/25=7/5N

丙级中男有：3N-3N/2-N=N/2，女有：2N-N/2-3/5N=9/10N

那么丙组中男女之比是：N/2：9/10N=5：9

13、甲乙丙三个村合修一条水渠，修完后，甲乙丙村可灌溉的面积比是8：7：5原来三个村计划按可灌溉的面积比派出劳力，后来因为丙村抽不出劳力，经协 4

小学奥数题及答案 小学全部奥数题及答案_经典奥数题目

商，丙村应抽出的劳力由甲乙两村分担，丙村付给甲乙两村工钱1350元，结果，甲村共派出60人，乙村共派出40人，问甲乙两村各应分得工钱多少元？ 答案

根据甲乙丙村可灌溉的面积比算出总份数：8+7+5=20份

20=5人 每份需要的人数：（60+40）÷

5=40人，多出劳力人数：60-40=20人 甲村需要的人数：8×

5=35人，多出劳力人数：40-35=5人 乙村需要的人数：7×

5=25人 或 20+5=25人 丙村需要的人数：5×

25=54元 每人应得的钱数：1350÷

20=1080元 甲村应得的工钱：54×

5=270元 乙村应得的工钱： 54×

14、题李明的爸爸经营已个水果店，按开始的定价，每买出1千克水果，可获利0.2元。(www.61k.com]后来李明建议爸爸降价销售，结果降价后每天的销量增加了1倍，每天获利比原来增加了50%。问：每千克水果降价多少元？

答案

设以前卖出X 降价a 那么0.2X * (1+0.5)=(0.2-a) * 2x

则0.1X=2aX a=0.05

15、哈利.波特参加数学竞赛，他一共得了68分。评分的标准是：每做对一道得20分，每做错一道倒扣6分。已知他做对题的数量是做错题的两倍，并且所有的题他都做了，请问这套试卷共有多少道题？

解：设哈利波特答对2X题，答错X题

20×2X-6X=68

40X-6X=68

34X=68

X=2

答对：2×2=4题

共有：4+2=6题

16、爸爸妈妈和奶奶乘飞机去旅行，三人所带行李的质量都超过了可免费携带行李的质量，要另付行李费，三人共付了4元，而三人行李共重150千克，如果这些行李让一个人带，那么除了免费部分，应另付行李费8元，求每人可免费携带行李的质量。

答案

设可免费携带的重量为x kg，则：

（150-3x）/4=(150-x)/8 //等式两边非免费部分单价相同； 解方程：x=30

5

小学奥数题及答案 小学全部奥数题及答案_经典奥数题目

17、一队少先队员乘船过河，如果每船坐15人，还剩9人，如果每船坐18人，刚好剩余1只船，求有多少只船？

答案

解法一：

设船数为X，则

（15X+9）/18=X-1

15X+9=18X-18

27=3X

X=9

答：有9只船。［www.61k.com）

解法二：

(15+9)÷（18-15）=8只船 --每船坐18人时坐了8只船

8+1=9只船

18、建筑工地有两堆沙子,一堆比2堆多85吨,两堆沙子各用去30吨后,一堆剩的是2堆的2倍,两堆沙子原来各有多少吨?

答案

设2堆为X吨,则一堆为X+85吨

X+85-30=2(X-30)

x=115(2堆)

x+85=115+85=200(1堆)

19、自然数1-100排列，用长方形框出二行六个数，六个数和为432，问这六个数最小的是几

答案

六个数分别是46 47 48 96 97 98

20、甲乙两地相距420千米,其中一段路面铺了柏油,另一段是泥土路.一辆汽车从甲地驶到乙地用了8小时,已知在柏油路上行驶的速度是每小时60千米,而在泥土路上的行驶速度是每小时40千米.泥土路长多少千米?

答案

两段路所用时间共8小时。

柏油路时间：（420－x）÷60

泥土路时间： x÷40

7-(x÷60)+(x÷40)=8

有x÷120=1

所以x=120

21、一少先队中队去野营,炊事员问多少人,中队长答: 一个人一个碗,两个人一只菜碗,三个人一只汤碗,放在你这儿有55只碗,你算算有多少人?

设有x个人

x＋x／2＋x／3＝55

x＝30

6

小学奥数题及答案 小学全部奥数题及答案_经典奥数题目

22、学校购买840本图书分给高、中、低三个年级段，高年级段分的是低年级段的2倍，中年级段分的是低年级段的3倍少120本。(www.61k.com)三个年级段各分得多少本图书？

设低年级段分得x本书，则高年级段分得2x本,中年级段分得（3x-120）本 x+2x+3x-120=840

6x-120=840

6x=840+120

6x=960

x=960/6

x=160

高年级段为：160*2=320( 本) 中年级段为：160*3-120=360(本)

答：低年级段分得图书160本，中年级段分得图书360本，高年级段分得图书320本.

23、学校田径组原来女生人数占1/3,后来又有6名女生参加进来,这样女生就占田径组总人数的4/9。现在田径组有女生多少人?

解 设 原来田径队男女生一共x人

1/3x+6= 4/9(x+6)

x=30

1/3x+6=30*1/3+6=16

女生16人

小华有连环画本数是小明6倍如果两人各再买2本那么小华所有本数是小明4倍两人原来各有连环画多少本？

解：设小华的有x本书

4(x+2)=6x+2

4x+8=6x+2

x=3

6x=18

24、小春一家四口人今年的年龄之和为147岁，爷爷比爸爸大38岁，妈妈比小春大27岁，爷爷的年龄是小春与妈妈年龄之和的2倍。小春一家四口人的年龄各是多少？

61阅读提醒您本文地址：

答案

1、设小春x岁，则妈妈x+27岁，爷爷(x+x+27)*2=4x+54岁，爸爸4x+54-38=4x+16岁

x+x+27+4x+54+4x+16=147,x=5

所以小春5岁，妈妈32岁，爷爷74岁，爸爸36岁。

2、爷爷+爸爸+（妈妈+小春）

=爷爷+（爷爷-38）+（爷爷/2)=147

爷爷=74岁

爸爸=36岁

妈妈+小春=小春+27+小春=74/2=37

小春=5岁

妈妈=5+27=32岁

小春一家四口人的年龄各是74，36，32，5岁

7

小学奥数题及答案 小学全部奥数题及答案_经典奥数题目

(2×2+1)=37(岁） 3、(147+38)÷

36×2＝74（岁） 爷爷的年龄

74－38＝36（岁） 爸爸的年龄

（37+27）÷2＝32（岁） 妈妈的年龄

32－27＝5（岁） 小华的年龄

25、甲乙两校共有22人参加竞赛，甲校参加人数的5分之1比乙校参加人数的4分之1少1人，甲乙两校各多少人参赛？

解：设甲校有x人参加，则乙校有（22-x）人参加。［www.61k.com）

0.2 x=（22-x）×0.25-1

0.2x=5.5-0.25x-1

0.45x=4.5

x=10

22-10=12（人）

答： 甲校有10人参加，乙校有12人参加。

26、在浓度为40%的盐水中加入千克水,浓度变为30%,再加入多千克盐,浓度变为50%?

答案1

解

设原有盐水x千克，则有盐40％x千克，所以根据关系列出方程：

(40％x)/(x＋1)＝30％ 得出x＝3，再设须加入y千克盐，则有方程： （1.2＋y）/(4+y)=50%得出y＝1.6

54比45多20％，算法，设所求为x，x（1＋20％）=54 算出结果45 答案2

设原有溶液为x千克，加入y千克盐后，浓度变为50%

由题意，得溶质为40%x，则有

40%x/(x+5)=30%

解之得

x=15千克

则溶质有15*40%=6千克

由题意，得

（6+y）/(15+5+y）=50%

解之得

y=8千克

故再加入8千克盐，浓度变为50%

27、某人到商店买红蓝两种钢笔，红钢笔定价5元，蓝钢笔定价9元，由于购买量较多，商店给予优惠，红钢笔八五折，蓝钢笔八折，结果此人付的钱比原来节省的18%，已知他买了蓝钢笔30枝，那么。他买了几支红钢笔？ 答案

红笔买了x支。

（5x+30×9）×（1-18%)=5x×0.85+30×9×0.8

x=36.

8

小学奥数题及答案 小学全部奥数题及答案_经典奥数题目

28、甲说：“我乙丙共有100元。（www.61k.com)”乙说：“如果甲的钱是现有的6倍，我的钱是现有的1/3，丙的钱不变，我们仍有钱100元。”丙说：“我的钱都没有30元。”三人原来各有多少钱？

答案

乙的话表明：甲钱5倍与乙钱2/3一样多

所以，乙钱是3*5=15的倍数，甲钱是偶数

丙钱不足30，所以，甲乙钱和多于70，

而乙多于甲的6倍，

所以，乙多于60

设乙=75，甲=75*2/3÷5=10,丙=100-10-75=15

设乙=90，甲=90*2/3÷5=12,90+12>100,不行

所以，三人原来：甲10元，乙75元，丙15元

29、某厂向银行申请甲乙两种贷款共30万，每年需支付利息4万元,甲种贷款年利率为12%，乙种贷款年利率为14%，该厂申请甲乙两种贷款金额各多少元？ 答案

设：甲厂申请贷款金额x万元,则乙厂申请贷款金额（30-x）万元。 列式：x*0.12+(30-x)*0.14=4

化简：4.2-0.02x=4

0.02x=0.2

解得：x=10(万元)

30、某书店对顾客有一项优惠，凡购买同一种书100本以上，就按书价的90%收款。某学校到书店购买甲、乙两种书，其中乙种书的册数是甲种书册数的3/5只有甲种书得到了90%的优惠。其中买甲种书所付的钱数是买乙种书所付钱数的2倍。已知乙种书每本1.5元，那么甲种书每本定价多少元？

答案1

根据题意，

甲种超过了100本，乙种不到100 本

甲乙花的总钱数比为2:1

那么甲打折以前，和乙的总钱数比为：

（2÷0.9）：1=20:9

甲乙册数比为5:3

甲乙单价比为（20÷5）：（9÷3）=4:3

优惠前，甲种每本：1.5×4/3=2元

答案2

设甲买了x本,则乙为3/5x,x>100

买乙共付了:3/5x*1.5=0.9x元

则甲共付了:0.9x*2=1.8x元

所以甲优惠后每本为:1.8x/x=1.8元

则优惠前:1.8/0.9=2元

31、两支成分不同的蜡烛,其中1支以均匀速度燃烧,2小时烧完,另一支可以燃烧3小时,傍晚6时半同时点燃蜡烛，到什么1支剩余部分正好是另一支剩余的2倍？

答案

9

小学奥数题及答案 小学全部奥数题及答案_经典奥数题目

两支蜡烛分别设为A蜡烛和B蜡烛，其中A蜡烛是那支烧得快点的 A蜡烛，两小时烧完，那么每小时燃烧1/2

B蜡烛，三小时烧完，那么每小时燃烧1/3

设过了x小时以后，B蜡烛剩余的部分是A的两倍

2（1—x/2）=1—x/3

解得x=1.5

由于是6点半开始的，所以到8点的时候刚刚好

32、学校组织春游，同学们下午1点从学校出发，走了一段平路，爬了一座山后按原路返回，下午七点回到学校。［www.61k.com）已知他们的步行速度平路4Km/小时，爬山3Km/小时，下山为6Km/小时，返回时间为2.5时。问：他们一共行了多少路 答案1

设走的平路是X公里 山路是Y公里

因为1点到七点共用时间6小时 返回为2.5小时 则去时用3.5小时 Y/3-Y/6=1小时

Y=6公里

去时共用3.5小时 则X/4+Y/3=3.5 X=6

所以总路程为2（6+6）=24km

答案2

解：春游共用时：7：00－1：00＝6（小时）

上山用时：6－2.5＝3.5（小时）

上山多用：3.5－2.5＝1（小时）

山路：（6－3）×1÷（3÷6）＝6（千米）

下山用时：6÷6＝1（小时）

平路：（2.5－1）×4＝6（千米）

单程走路：6＋6＝12（千米）

共走路：12×2＝24（千米）

答：他们共走24千米。

10

61阅读提醒您本文地址：

本文标题：经典数学问题及答案-经典数学问题----费马最後定理
本文地址： http://www.61k.com/1083097.html