一 : 自动控制原理课后习题答案

第一章 引论

1-1 试描述自动控制系统基本组成，并比较开环控制系统和闭环控制系统的特点。 答：

自动控制系统一般都是反馈控制系统，主要由控制装置、被控部分、测量元件组成。控制装置是由具有一定职能的各种基本元件组成的，按其职能分，主要有给定元件、比较元件、校正元件和放大元件。如下图所示为自动控制系统的基本组成。

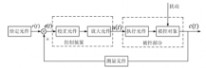
开环控制系统是指控制器与被控对象之间只有顺向作用，而没有反向联系的控制过程。此时，系统构成没有传感器对输出信号的检测部分。开环控制的特点是：输出不影响输入，结构简单，通常容易实现；系统的精度与组成的元器件精度密切相关；系统的稳定性不是主要问题；系统的控制精度取决于系统事先的调整精度，对于工作过程中受到的扰动或特性参数的变化无法自动补偿。

闭环控制的特点是：输出影响输入，即通过传感器检测输出信号，然后将此信号与输入信号比较，再将其偏差送入控制器，所以能削弱或抑制干扰；可由低精度元件组成高精度系统。

闭环系统与开环系统比较的关键，是在于其结构有无反馈环节。

1-2 请说明自动控制系统的基本性能要求。

答：

自动控制系统的基本要求概括来讲，就是要求系统具有稳定性、快速性和准确性。 稳定性是对系统的基本要求，不稳定的系统不能实现预定任务。稳定性通常由系统的结构决定与外界因素无关。对恒值系统，要求当系统受到扰动后，经过一定时间的调整能够回到原来的期望值（例如恒温控制系统）。对随动系统，被控制量始终跟踪参量的变化（例如炮轰飞机装置）。

快速性是对过渡过程的形式和快慢提出要求，因此快速性一般也称为动态特性。在系统稳定的前提下，希望过渡过程进行得越快越好，但如果要求过渡过程时间很短，可能使动态误差过大，合理的设计应该兼顾这两方面的要求。

准确性用稳态误差来衡量。在给定输入信号作用下，当系统达到稳态后，其实际输出与所期望的输出之差叫做给定稳态误差。显然，这种误差越小，表示系统的精度越高，准确性越好。当准确性与快速性有矛盾时，应兼顾这两方面的要求。 1-3 请给出图1-4炉温控制系统的方框图。

答：

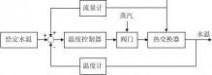
1-4 请给出图1-7热工水温控制系统方框图，说明系统如何工作以保持热水温度为期望值，并指出被控对象、控制装置、测量装置及输入量和输出量。

答：

冷水

冷水在热交换器中由通入的蒸汽加热，得到一定温度的热水，冷水流量变化用流量计测量，温度传感器不断测量热水温度，并在温度控制器中与给定温度比较，当实际水温高于设定温度值时，输出的偏差会控制蒸汽阀门关小，进入热交换器的蒸汽量减少，水温降低，直至偏差为零。在该系统中，冷水流量为扰动量，当冷水流量变大时，热水温度将有所降低。当流量计测得冷水流量变化时，系统按前馈控制温度控制器，使其阀门开大或关小来改变蒸汽量，从而补偿因冷水流量变化引起的热水温度变化。

被控对象：热交换器；控制装置：温度控制器；测量装置：流量计和温度计；输入量：给定水温；输出量：实际水温。

1-5 如图

1-12所示的家用电冰箱控制系统示意图，请画出电冰箱温度控制系统原理方框图，并说明其工作原理。

答：

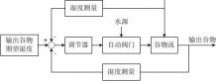
控制盒是一个控制装置。冰箱室温由控制盒中元件设定，温度检测转换装置反应冰箱实际室温的变化。室温的设定值与实际值比较，其偏差通过控制盒校正装置，控制继电器闭合或断开，从而控制压缩机的运行或停止。由于压缩机的作用，管道内循环气体的温度得到改变，蒸发器向室内散发冷气，直至箱体室温与设定室温一致。 1-6 图1-13为谷物湿度控制系统示意图。在谷物磨粉生产过程中，磨粉前需控制谷物湿度，以达到最多的出粉量。谷物按一定流量通过加水点，加水量由自动阀门控制。加水过程中，谷物流量、加水前谷物湿度及水压都是对谷物湿度的扰动。为提高控制精度，系统中采用了谷物湿度顺馈控制，试画出系统方框图。

答：

输入谷物

第二章 控制系统数学模型

2-1 请列写出图2-53的系统传递函数，输入量为ui(t)，输出量为uo(t)。 答：

1

Ci1dt?R1?i1?i2??0 1?

ui?R1?i2?i1??uo uo?R1

2i2?

Ci2dt 2?

1

sCI1?s??R1I1?s??R1I2?s??0 1

Ui?s??R1I2?s??R1I1?s??Uo?s? U1

o?s??R2I2?s??sCI2?s? 2

I2?s??

1

?Uo?s? ??

R1?

2?sC?

2?I1?s??

R1

?Uo?s? ?1?sC?R??1?

1??R2?1??

sC?2??1??1?

U???R1??R2??

o?sUs??sC1??sC2?? ?1?sC?R??1?R i1

1??R2?1??

sC???

2sC12-3 试推出图2-55中无源网络的微分方程。 答：

Uo?s?2?R1R2Cs

URR is?

R1?2?R1R2Cs

R1R2CsUo?s???R1?R2?Uo?s??R1R2CsUi?s??R2Ui?s? R1R2Cuo?t???R1?R2?uo?t??R1R2Cui?t??R2ui?t? 1）

2）3）

4）

5）6）

7）8）9）1）2）3）

（ （

（ （ （

（ （

（

（ （

（

（

2-5 已知系统的传递函数为：系统的单位阶跃响应。 答：

C?s?Rs?

2

，系统初始条件为C?0???1，C?0??0，试求

s2?3s?2

?s2?3s?2

（1） C?s??

ss?1s?2??1e?ate?bte?ctF??? （2） ??

?s?as?bs?c??b?ac?aa?bc?ba?cb?c?

?1

C?s??

142

（3） ??

ss?1s?2

C?t???2e?t?e?2t, constant??1 （4）

2-6 某系统在阶跃信号r(t)=1(t)、零初始条件下的输出响应c?t??1?e?2t?e?t，试求系统的传递函数G(s)和脉冲响应c??t?。 答：

c?s??r?s??

111

?? （1） ss?2s?1

1

（2） s

s2?4s?2

（3） G?s???

rss2?3s?2

c?s?

c??t??c?t????t??2e?2t?e?t （4）

2-7 系统微分方程组：

x1?t??r?t??c?t??n1?t?

x2?t??K1x1?t? x3?t??x2?t??x5?t?

?x3?t?

dt

x5?t??x4?t??K2n2?t? T

dx4?t?

d2c?t?dt2

?

dc?t?dt

?K0x5?t?

式中，K0、K1、K2和T均为常数，试建立以r?t?、n1?t?、n2?t?为输入量，以c?t?为输出量的系统结构图。 答：

n2?s?

r?s?

2-8 已知系统结构图如图2-56所示，当R?s??0、N?s??0时，试求：

（1）E?s?到C?s?的前向通道传递函数G?s?；

（2）E?s?到B?s?的开环传递函数GK?s?；

（3）R?s?到E?s?的误差传递函数GE?s?；

（4）R?s?到C?s?的闭环传递函数GB?s?。

答：

G?s??K1 （1） Ts?1

K1K2 （2） Ts?1GK?s??

GE?s??1 （3） 121?Ts?1

K1

GB?s?? （4）121?Ts?1

2-9 试通过结构图等效变换，求图2-57所示各控制系统传递函数C?s?/R?s?。 答：

Ga?s??

Gb?s??

Gc?s??

Gd?s??G1G2?G2G3 （1） 1?G2H1?G1G2H2G1G2?G2G3 （2） 1?G1G2H1G1G2G3 （3） 1?G1H1?G2H2?G3H3?G1H1G3H3G1G2G3G4 （4） 1?G1G2G3G4H3?G2G3H1?G3G4H2

2-10 用结构图化简的方法，将图2-58所示结构图化简，并求出其给定信号和扰动信号的闭环传递函数。

答：

GR?s??

GN?s??G1G2G3G4?G1G2G5 （1） 1?G1G2G3G4?G1G2G5?G2G3HGNG1G2G3G4?GNG1G2G5?G3G4?G5 （2） 1?G1G2G3G4?G1G2G5?G2G3H

2-11 试通过对结构图的化简，求图2-59所示系统的传递函数。

答：

C?s?

RsC?s?

RsE?s?

Rs???G1G2G3 ?G4 （1）1?G1G2H1?G2H1?G2G3H2G1G2G3G4 （2） 1?G2G3H1?G3G4H2?G1G2G3G4H31 （3） 1?G2G3H1?G3G4H2?G1G2G3G4H3

2-12 绘制图2-60系统结构图对应的信号流图，并用梅逊公式求系统传递函数。

答：

R?

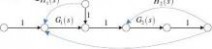
sNsC?s?

3

C?s?

RsC?s?

Ns??G1G2 （1） 1?G2H2?G1G2H3G1G2H1?G2 （2） 1?G2H2?G1G2H3

2-14 有一个复杂液位被控对象，其液位阶跃响应实验结果如表2-4所示：

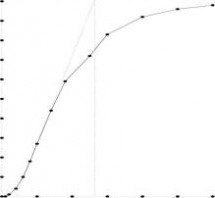
试：（1）画出该液位被控对象的阶跃响应曲线；

（2）若该对象用有延迟的一阶惯性环节近似，请用近似法确定延迟时间?和时间常数T。

答：

??40s，T?270s。

2-15 使用梅逊公式求图2-62系统信号流图的传递函数。 答：

C?s?RsC?s???

G1G2G3G4G5

（1）

1?G2H1?G3H2?G4H3?G2G3G4G6?G2H1G4H3

abcd

（2）

Rs1?af?bg?ch?abce?afch

第三章 控制系统时域分析法

3-1 已知系统脉冲响应分别为

k?t??0.0125e?1.25t，k?t??5t?10sin(4t?45?)

试求系统闭环传递函数。 答：

?1?s??

0.0125s?1.25，?1s?4

2?

s??s2?s2?16

3-2 已知二阶系统的单位阶跃响应为

c?t??1?1.25e?1.2tsin(1.6t?0.93)

试求系统的动态性能指标?%和ts。 答：

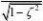
1???nt?????

?1?1.25e?1.2tsin?1.6t?0.93? ??0.6，?n?2.0，??0.93 3??%?e

100%?e

?

4

ts?

3

???2.5s n

3-3 已知控制系统的单位阶跃响应为

h?t??1?0.2e?60t?1.2e?10t

试确定系统的阻尼比和自然频率。 答：

h??t???12e?60t?12e?10t h??s??

600

s2

?70s?600

?2n600

s2?2??2

?2

s?600

ns??ns?703-4 已知单位反馈系统的开环传递函数为

G?s??

K

sTs?1

1）

2）

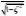
3）

4）

1）

2）

3） （ （ （ （ （ （ （

其中，K?3.2，T?0.2。求：?、?n、?%、ts。

答：

Gc?s??3.2 （1） 0.2s?s?3.22

??0.625，?%?e?n?

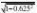
4，ts?1.2s （2）

3-5 设图3-35(a)所示系统的单位阶跃响应如图3-35(b)所示，试确定系统参数。

答：

??s??K2K1 （1）

s2?as?K1

?%?e

tp??1 （2）

3 ?0.1 （3）

??0.33，?n?33.3 （4） K2?3，K1?1109，a?22 （5） 3-6 设角速度指示随动系统结构图如图3-36所示。若要求系统单位阶跃响应无超调，且调节时间尽可能短，问开环增益应取何值，调节时间是多少？

答：

??s??K （1） 0.1s2?s?K

K?2.5，ts?3

??n ?0.6s （2）

3-7 已知系统的特征方程，试判别系统的稳定性，并确定在右半s平面根的个数及纯虚根。 答：

D?s??s5?2s4?s?2?0，系统不稳定，s?1，s?i，s??i；

D?s??s5?2s4?24s3?48s2?25s?50?0，系统不稳定，s?1，s?5i，s??5i；

D?s??s5?3s4?12s3?24s2?32s?48?0，系统临界稳定，s?2i，s??2i；

D?s??s5?2s4?2s3?4s2?11s?10?0，系统不稳定，具有2个正实数根。

3-8 图3-37是某垂直起降飞机的高度控制系统结构图，试确定使系统稳定的K值范围。 答：

??s??K?4s2?2s?1?

s5?s4?4s3?4Ks2?2Ks?K （1）

0.5361?K?0.9326 （2）

3-9 图3-38是核反应堆石墨棒位置控制闭环系统，其目的在于获得希望的辐射水平，增益

4.4是石墨棒位置和辐射水平的变换系数，辐射传感器的时间常数为0.1，直流增益为1，设控制器传递函数为1。

（1）求使系统稳定的功率放大器增益K的取值范围；

（2）设K=20，传感器的传递函数

H?s??1 ?s?1

?不一定是0.1，求使系统稳定的?值取值范围。

答：

??s??2.64K??s?1?

?s3?1?6?s2?6s?2.64K （1）

0?K?36.36 （2）??0.1，

（3） K?20，0???0.3571

3-10 单位反馈系统的开环传递函数为

G?s??K ss?3s?5要求系统特征根的实部不大于-1，试确定开环增益的取值范围。

答：

??s??K （1） ss?3s?5?K

K （2） s1?1s1?2s1?4?K??s1?1??

8?K?18 （3）

3-11 水银温度计的传递函数为1，若用其测量容器内的水温，当插入水中4min才能显Ts?1

示出该水温度的98%的数值（设温度计插入水前处在0℃的刻度上）。若加热容器使水温按2℃/min的速度匀速上升，问温度计的稳态指示误差有多大？

答：

e?240

T ?0.02，T?61.35s （1）

111t，R?s???2 （2） 3030s r?t??

E?s??1Ts （3） ?Ts?11??Ts

Ts11T??2? （4） Ts?130s30limsE?s?R?s??s?s?0

3-12 已知单位反馈系统的开环传递函数为

G?s??ss?4s2?2s?27?s?1?

试分别求出当输入信号r?t??1?t?、t和t2时系统的稳态误差。

答：

limsE?s?R?s??s?s?01 ?R?s? （1）1?Gsess1?0 （2） ess2?7 （3） 8

ess3?? （4）

3-13 单位反馈系统的开环传递函数为

G?s??25 ss?5求各静态误差系数和r?t??1?2t?0.5t2时稳态误差。

答：

limsE?s?R?s??s?s?01 ?R?s? （1）1?GsKv?5，Ka?0 （2）Kp??，

1ABCr?t??A?Bt?Ct2，ess? （3） ??21?KpKvKa

3-14 系统结构图如图3-39所思。已知r?t??n1?t??n2?t??1?t?，试分别计算r?t?、n1?t?和n2?t?作用时的稳态误差，并说明积分环节设置位置对减小输入和干扰作用下的稳态误差的影响。 答：

E?s?

Rs?1

1???T1s?1sT2s?1 （1）

11?E?s?sT2s?1 （2） ??N1s1???T1s?1sT2s?1

1

E?s?T2s?1 （3） ??K11N2s1???T1s?1sT2s?1

essr?0，essn1??1essn2?0 （4）， K

3-15 大型天线伺服系统结构图如图3-40所示，其中??0.707、?n?15、??0.15s。当干扰信号n?t??10?1?t?，输入r?t??0时，试确定能否调整Ka的值使系统的稳态误差小于0.01？

答：

E?s?

Ns2?n2ss2?2??ns??n?nKa1??22ss?2??ns??n?s?1?? （1）

Ka?1000 （2） 3-16 系统结构图如图3-41所示。

（1）为确保系统稳定，如何取K值？

（2）为使系统特征根全部位于s=-1的左侧，K应取何值？

（3）若r?t??2t?2时，要求系统稳态误差ess?0.25，K应取何值？

答：

0?K?15 (1)

1.02?K?9.3 （2） 8?K?15 （3）

3-17 复合控制系统结构图如图3-42所示，图中K1、K2、T1、T2均为大于零的常数。 （1）确定当闭环系统稳定时，参数K1、K2、T1、T2应满足的条件；

（2）当输入r?t??V0t，选择校正装置Gc?s?，使得系统无稳态误差。 答：

C?s?Gc?s??T1s?1??K1K2Rs?

sT 1s?1T 2s?1?K1K2

K1K2TT12?T1?T2 ?G?

K2

c?s?E?s??R?s??

sT?1

2s?1 1? 12

T?

1s?1sT2s?1Gs?1?c?s??

s?T2K 2

3-18 设计题 答：

??s??

Ka

s2

?1?KK aK2s?aK1

e

??0.1 3.5

????9s n

K??2

an 1?KaK2?2??n ???0.6，?n??0.65 rads，K1?1，Ka?0.42，K2?0.5238 第四章 控制系统的根轨迹法

4-1 已知系统开环零点分布如图4-28所示，试绘制相应的根轨迹图。 答：

(a)

(b)

1）

2）

3） 4）

1）

2）

3）

4）

5）

6）

（ （ （（ （ （ （（ （ （

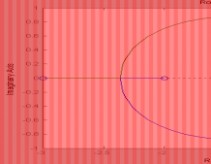
(c)

(d)

(e)

(f)

4-2 已知单位反馈控制系统的前向通道传递函数如下：

（1）G?s??

（3）G?s??K?s?1?s2s?2s?4 （2）G?s??（4）G?s??K ss?1s?2s?5ss?1s2?4s?16K?s?1?K s?s?4?s2?4s?20 K>=0，画出系统的根轨迹图。

答：

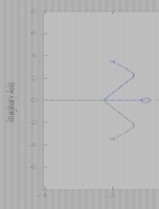
（1） （4）

4-3 给定系统如图4-29所示，K>=0，试画出系统的根轨迹，并分析增益对系统阻尼特性的影响。

答：

随着K值的增加，系统的阻尼越小，系统将产生振荡，但结构参数决定了系统稳定。

4-4 已知系统的开环传递函数为

G?s?H?s??Kr?s?2?

s2s?1s?4

试画出系统根轨迹的渐近线。

答：

??nm?p??zi

i?1j?1j

n?m??1 （1）

???2k?1????,??,? （2） n?m33

4-5 已知系的开环传递函数为

G?s?H?s??Kr s?1s?2s?3试画出该系统根轨迹与虚轴的交点。

答：

4-6 同4-5，求相应的开环根轨迹增益的临界值。

答：

Kr?60 （1） 4-7 给定控制系统如图4-30所示，K>=0，试用系统的根轨迹图确定速度反馈增益K为何值时能使闭环系统极点阻尼比等于0.7。

答：

1?10Ks?0 （1）

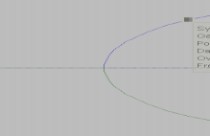
s?s?102

4-8 已知系统的开环传递函数为

G?s?H?s??Kr ss?1s?2试绘制该系统完整的根轨迹图。

答：

4-9 已知系统的开环传递函数为

G?s?H?s??Kr ss?2s2?2s?2试绘制该系统的根轨迹图。

答：

4-8 4-9

4-10 已知单位反馈系统的开环传递函数为

G?s??K ss?10.5s?1

试用根轨迹法确定系统在稳定欠阻尼状态下的开环增益K的范围。 答：

4-11 已知系统的开环传递函数为

G?s??K s0.05s?10.05s2?0.2s?1

画出系统概略的根轨迹。

答：

G'?s??K （1） s0.05s2?0.2s?14-12 已知单位反馈系统的开环传递函数为

G'?s??K ss?10.5s?1要求系统的闭环极点有一对共轭复数极点，其阻尼比为0.5。试确定开环增益K，并近似分析系统的时域性能。

答：

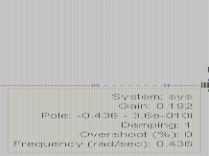
4-13 已知单位反馈系统的开环传递函数为

G?s??K?s2?2s?4?

s?s?4??s?6?s2?1.4s?1，K??0

试画出系统的根轨迹图，并分析系统稳定时K的取值范围。

答：

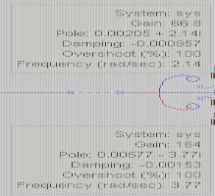
0?K?17.8，66.8?K?164

4-14 已知单位反馈系统的开环传递函数为 1） （

G?s??K ss?1s?2K>=0，试画出系统的根轨迹图。

答：

第五章 控制系统的频域分析

5-1 试求图5-65的频率特性。

答：

G?s??R2?R1R2Cs （1） R1?R2?R1R2Cs

R2?R1R2Cj? （2） R1?R2?R1R2Cj?

G?j???A???

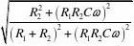
?????arctanR1C??arctanR1R2C? （3） R1?R2

1，试根据频率特性的物理意义，求在输入s?1

信号为r?t??sin?4t?作用下系统的稳态输出c?t?和e?t? 5-2 单位负反馈系统的开环传递函数为G?s??答：

2e?2t?2cos4t?sin4t （1） c?t??10

e?t??r?t??c?t??9sin4t?2cos4t （2） 10

5-3 已知单位负反馈的开环传递函数为G?s??K，当系统输入r?t??sin?10t?时，闭环系sTs?1统的稳态输出为c?t??sin?10t?90??，试计算参数K和T的数值。（提示：可根据频率特性的物理意义求解。）

答：

A????1

2?j????j???1KK?1 （1）

?????1?? ?? （2）22???j????j???1??K?K?

K?10， T?0.1s （3）5-4 试绘制下列开环传递函数的幅相特性，并判断其负反馈闭环时的稳定性。

（1）G?s?H?s??

答：

250 ss?5s?15 （2）G?s?H?s??250?s?1?s2s?5s?15

（1）系统稳定

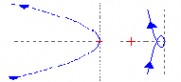
（2）系统稳定

5-5 已知系统开环传递函数为

G?s?H?s??K?s?2?

ss?1

试用乃奎斯特稳定判据判断闭环系统的稳定性，并确定使系统稳定的K的取值范围。 答：

K?1时系统稳定

5-6 已知最小相位系统的幅相特性，如图5-66所示。

（1）试写出该幅相特性相应的传递函数；

（2）用奈奎斯特判据判断闭环系统的稳定性；

（3）标出增益交界频率、相位交界频率、相位裕量，并写出幅值裕量表达式。 答：

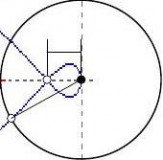
G?s?H?s??K?s??2??s??3?

ss??1s??4s??52?1??2??3??4??5 （1），

GM??20lgG?j?g?H?j?g? （2）

5-7 若单位负反馈的开环传递函数

Ke?0.8s，K?0 G?s??s?1

试确定使系统稳定的K值范围。

答：

G?j???K （1） j??1

????arctan?g?0.8?g （2）K??g，

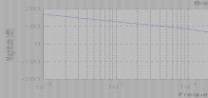
??0，0?K?3.5872 （3） 5-8 试绘制下列传递函数的对数幅频特性渐近曲线。

（1）G?s??2

2s?18s?140?s?0.5?（3）G?s?? ss?0.2s2?s?18?s?0.1?（5）G?s??2 2ss?s?1s?4s?25 （2）G?s??（4）G?s??200 ss?110s?12s26s?1s2?4s?2510s?120?3s?1?

答：

（1）

（2）

（3）

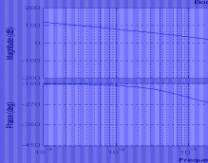
（4）

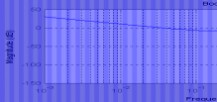
（5）

5-9 若传递函数

G?s??KG0?s? s?

证明

1

?g?K

5-10 已知最小相位系统的对数幅频特性渐近曲线如图5-68所示，试确定系统的开环传递函数。

答：

100G1?s?? ?1??1??s?1??s?1???c3?1?s?1??1??2??1?s2?s?1?1 G2?s?? G3?s???1s

??1??1?s?1??s?1? ??1???2???1???2???3

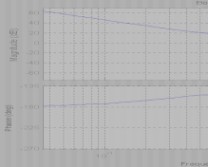
5-11 已知某最小相位系统的开环对数幅频特性如图5-69所示。

（1）写出其开环传递函数；

（2）画出相频特性图，并从图上求出和标明相角裕量和幅值裕量；

（3）求出该系统达到临界稳定时的开环比例系数K；

（4）在复数平面上画出奈奎斯特曲线，并标明点?1?j0的位置。

答：

G?s??2?2s?1?

s20.5s?10.2s?1

（2）

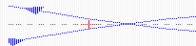
（3） （4） ?（1）

5-12 已知G1?s?、G2?s?和G3?s?均为最小相位系统的传递函数，其对数幅频特性渐近曲线如图5-70所示。试概略绘制传递函数

G1?s?G2?s?4?s??

G1?G2sG3s

的对数幅频、对数相频和幅相特性曲线。 答：

G1?s??K1?180，G2?s??

1

s1.25s?1，G?s??1803?s??9s，G4s??1?

?8s?1??

5-13 已知系统开环传递函数，试根据奈氏判据，确定其闭环稳定的条件：G?s??

K

sTs?1s?1，K?0，T?0

（1）T?2时，K值的范围； （2）K?10时，T值的范围； （3）K、T值的范围。 答：

G?j???K

j?2j??1j??1??1?j0 G?j???10

j?Tj??1j??1??1?j0 G?j???

K

j?Tj??1j??1??1?j0 5-14 已知系统开环传递函数

G?s??

10?s2?2s?5?

s?2s?0.5

试概略绘制幅相特性曲线，并根据奈氏判据判定闭环系统的稳定性。 答：

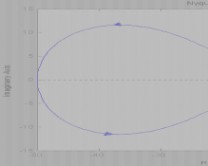
P?1,R??1,Z?P?R,Z?2,系统不稳定

1）

2）

3）

（ （ （

5-15 典型二阶系统的开环传递函数

G?s??

2?n

ss?2??n若已知10%??%?30%，试确定相角裕量的范围；若给定?n?10，试确定系统带宽的范围。 答：

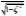
?%?e （1）

1

（2）

??

?

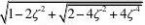
?arctan

2

2?

?b?? 5-16 设单位反馈控制系统的开环传递函数

G?s??

as?1

s2

试确定相角裕量为45度时的参数值。 答：

?g?1，??arctan?a?g??

?

4

a?1 5-17 已知系统中

G?s??

10

ss?1，H?s??1?Khs 试确定闭环系统临界稳定时的Kh。 答：

G?j??H?j???10?1?Khj??j?j??1??1?j0 Kh??0.1

5-18 某最小相位系统的开环对数幅频特性如图5-71所示。要求： （1）写出系统开环传递函数； （2）利用相角裕度判断系统的稳定性；

（3）将其对数幅频特性向右平移十倍频程，试讨论对系统性能的影响。 答：

G?s??

10

s10s?10.05s?1 ??

g?1，?2?

2

?arctan?10?g??arctan?0.05?g? G?s??

100

ss?10.005s?1，?3??2 5-19 对于典型二阶系统，已知参数?n?3、??0.7，试确定截止频率和相角裕度。 答：

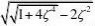
?g??

??

?

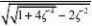
?g2??n

2

?arctan

2???arctan?n?g

3）

1）

2）

1）

2）

1）

2）

3）

（ （ （ （ （ （ （ （

5-20 对于典型二阶系统，已知?%?15%、ts?3s，试计算截止频率和相角裕度。 答：

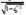
?%?e

ts??5% （1） （2）

?3??n

?g????（3）

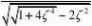
（4）

5-21 某控制系统，其结构图如图5-72所示，图中

G1?s??10?1?s?

1?8s，G2?s??4.8

s??s?1??20??

试按：（1）?、?g，（2）Mr、?g，来估算时域指标?%和ts。

答：

?%?0.16?0.4?

K??1? ?1? （1-1）sin???2?1??1??1??2.5??1? （1-2），K?2?1.5? ts??g?sin???sin??

?%?0.16?0.4?Mr?1? （2-1）

ts?K?

?g，K?2?1.5?Mr?1??2.5?Mr?1? （2-2） 2

5-22 单位负反馈系统的闭环对数幅频特性如图5-73所示。若要求系统具有30度的相角裕度，试计算开环增益应增大的倍数。

答：

Gc?s??1 （1） s?10.8s?10.2s?1Go?s??0.5 （2） s0.08s2?0.508s?11?0.08?c2?

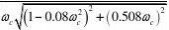
??arctan? （3）0.508?c6

?1 （4）

二 : 自动控制原理 课后答案(孙亮 杨鹏 着) 北京工业大学出版社

三 : 自动控制原理_胡寿松第5版_课后习题及答案_完整_

四 : 自动控制原理_胡寿松第5版_课后习题及答案_完整_

本文标题：自动控制原理课后答案-自动控制原理课后习题答案
本文地址： http://www.61k.com/1106043.html