假设检验的基本步骤-假设检验的基本步骤

发布时间：2017-08-13 所属栏目：理学

一 : 假设检验的基本步骤

假设检验的基本步骤：

1.建立假设，确定检验水准α

假设有零假设（H0）和备择假设（H1）两个，零假设又叫作无效假设或检验假设。H0和H1的关系是互相对立的，如果拒绝H0，就要接受H1.根据备择假设不同，假设检验有单、双侧检验两种。

检验水准用α表示，通常取0.05或0.10.检验水准说明了该检验犯第一类错误的概率。

2.根据研究目的和设计类型选择适合的检验方法

这里的检验方法，是指参数检验方法，有u检验、t检验和方差分析三种，对应于不同的检验公式。对双样本资料，要注意区分成组设计和配对设计的资料类型。如果资料里有"配成对子"字样，或者是对同一对象用两种方法来处理，一般就可以判定是配对设计资料。

3.确定P值并作出统计结论

u检验得到的是u统计量或称u值，t检验得到的是t统计量或称t值。方差分析得到的是F统计量或称F值。将求得的统计量绝对值与界值相比，可以确定P值。

当α＝0.05时，u值要和u界值1.96相比较，确定P值。如果u＜1.96，则P＞0.05.反之，如u＞1.96，则P＜0.05.t值要和某自由度的t界值相比较，确定P值。如果t值＜t界值，故P＞0.05.反之，如t＞t界值，则P＜0.05.相同自由度的情况下，单侧检验的t界值要小于双侧检验的t界值，因此有可能出现算得的t值大于单侧t界值，而小于双侧t界值的情况，即单侧检验显著，双侧检验未必就显著，反之，双侧检验显著，单侧检验必然会显著。即单侧检验更容易出现阳性结论。

当P＞0.05时，接受零假设，认为差异无统计学意义，或者说二者不存在质的区别。当P＜0.05时，拒绝零假设，接受备择假设，认为差异有统计学意义，也可以理解为二者存在质的区别。但即使检验结果是P＜0.01甚至P＜0.001，都不说明差异相差很大，只表示更有把握认为二者存在差异。

二 : 第一节假设检验的基本思想与步骤

第八章
§8.1

假设检验
假设检验的基本思想与步骤

一、问题的提出根据样本的信息检验关于总体的某个假设是否正确. 否正确.这类问题称作假设检验问题假设检验

{

参数假设检验非参数假设检验

罐装可乐的容量按标准应在350毫升例、罐装可乐的容量按标准应在毫升毫升之间.生产流水线上罐装可乐不和360毫升之间生产流水线上罐装可乐不毫升之间断地封装，然后装箱外运. 怎么知道这批断地封装，然后装箱外运罐装可乐的容量是否合格呢？罐装可乐的容量是否合格呢？现在要检验的假设是：现在要检验的假设是： H0： = μ0（ μ0 = 355） μ ）它的对立假设是：它的对立假设是： H1： ≠ μ0 μ 在实际工作中，往往把不轻易否定的命题作为原假设. 原假设

称H0为原假设（或零假设，解消假设）；为原假设（或零假设，解消假设）；称H1为备选假设（或对立假设）. 为备选假设（或对立假设）

二、假设检验的基本思想与步骤 1、假设检验的基本思想、是正态分布的期望值，由于μ是正态分布的期望值，它的估计量是样本均值 X ，因此可以根据 X 与 μ0的差距 | X - μ0| 来判断 0 是否成立来判断H 是否成立. 当H0成立时 X 的观测值 x 应接近 μ 0，若 x 远离 μ 0，成立时,
不真。则有理由怀疑 H 0不真。

当 | X - μ0| 较小时，可以认为H0是成立的；较小时，可以认为是成立的；当 | X - μ0| 较大时，应认为 0不成立，即较大时，应认为H 不成立，生产已不正常. 生产已不正常

提出假设

H0： μ = 355

H1：μ ≠ 355

X ? μ0 ~ N(0,1) 选检验统计量 U = σ n 它能衡量差异 | X ? μ0 | 大小且分布已知 .

已知，由于σ 已知，

可以在N(0,1)表对给定的显著性水平α，可以在表中查到分位点的值 u 2 ，使 α

P{| U |> uα 2} = α

P{| U |> uα 2} = α
是一个小概率事件也就是说,“ 也就是说 “| U |> uα 2 ”是一个小概率事件. 故我们可以取拒绝域为：故我们可以取拒绝域为： W： | U |> uα 2 ：如果由样本值算得该统计量的实测值落入区域W，则拒绝H 否则，不能拒绝H 区域，则拒绝 0 ；否则，不能拒绝 0 .

统计假设的分类
1）单边假设（显著地大、显著地小、提高、降低））显著地大、显著地小、提高、降低）如：

H 0：μ = μ 0 ; H 1：μ > μ 0 ( 右边假设 )
H 0： = μ 0 ; H 1：μ < μ 0 (左边假设 ) μ
?

μ0 ?
μ0

2）双边检验（显著地改变、是否正常、是否合格））显著地改变、是否正常、是否合格）

μ 如： H 0： = μ 0 ； H 1： ≠ μ 0 μ
可省略不写。注：在双边假设中，通常备择假设 H 1可省略不写。在双边假设中，

3、假设检验的基本步骤、第一步：第一

步：提出原假设和备择假设第二步：建立检验统计量，第二步：建立检验统计量，在H0成立下求出它的分布第三步：确定检验的否定域。第三步：确定检验的否定域。构造小概率事件对给定的显著性水平α及检验统计量的分布，对给定的显著性水平α及检验统计量的分布，查表确定临界值，从而得到否定域。查表确定临界值，从而得到否定域。第四步：对原假设作出统计推断。第四步：对原假设H0作出统计推断。如果检验统计量的观测值落入否定域，则否定H 验统计量的观测值落入否定域，则否定 0

三、两类错误假设检验会不会犯错误呢？假设检验会不会犯错误呢？由于作出结论的依据是——小概率原理小概率原理由于作出结论的依据是小概率事件在一次试验中基本上不会发生 . 不是一定不发生因此作出的判断不可能绝对正确，因此作出的判断不可能绝对正确，有可能会出现误判，而可能出现的错误有两类：出现误判，而可能出现的错误有两类：

1、第一类错误、为真时，却错误地拒绝了它,称这类弃真” 称这类“ 当H0为真时，却错误地拒绝了它称这类“弃真” 的错误为第一类错误，记为α 的错误为第一类错误，记为α。为真}= P{拒绝 0 | H0为真 α 拒绝H 拒绝 2、 2、第二类错误为第二类错误，的错误为第二类错误，记为β。 P{接受 0 | H0不真 β 接受H 不真}= 接受为犯第一类错误的概率。显著性水平 α为犯第一类错误的概率。
P {| U |> u α } = α
2

当H0为不真时,却错误地接受了它称这类 “取伪” 为不真时却错误地接受了它,称这类取伪” 却错误地接受了它

三 : 8.1 假设检验的基本思想与步骤

假设检验基本思想

Dec-10

第八章假设检验
§8.1 假设检验的基本思想与步骤 §8.2 正态总体的参数检验
电子科技大学

假设检验基本思想

Dec-10

§8.1 假设检验的基本思想与步骤一.假设检验的基本思想引例1 已知一个暗箱中有100个白色与黑引例已知一个暗箱中有个白色与黑色球，不知各有多少个. 色球，不知各有多少个.现有人猜测其中有 95个白色球，是否能相信他的猜测呢？个白色球，个白色球是否能相信他的猜测呢？他相当于提出假设：他相当于提出假设： p=P(A)=0.05，A={任取一球是黑球，任取一球是黑球}. 任取一球是黑球
电子科技大学

假设检验基本思想

Dec-10

现随意从中抽出一个球, 发现是黑球, 现随意从中抽出一个球发现是黑球怎样解释这一事实？解释这一事实？可有两种解释：可有两种解释： 1）他的猜测是正确的,恰抽得黑球是随机性）他的猜测是正确的, 所致；所致； 2）他的猜测错了. ）他的猜测错了. 应接受哪一种呢？应接受哪一种呢？

小概率事件原理, 根据小概率事件原理事件A的发生不能不根据小概率事件原理, 事件的发生不能不使人们怀疑他的猜测, 倾向于认为箱中白球使人们怀疑他的猜测,更倾向于认为箱中白球个数不是95个. 个数不是个
电子科技大学

假设检验基本思想

Dec-10

引例 2 假设检验基本思想：提出统计假设假设检验基本思想：提出统计假设, 根据小概率事件原理对其进行检验. 概率事件原理对其进行检验二、基本概念工件直径的假设检验 1. 参数与分布的假设检验 1）关于总体参数的假设检验, 如 H0:μ=μ0 ）关于总体参数的假设检验
电子科技大学

假设检验基本思想

Dec-10

2）关于总体分布的假设检验,如）关于总体分布的假设检验如 H0: F(x)=Ψ(x;μ,σ2) 2. 原假设与备择假设根据问题的需要提出的一对对立的假设，根据问题的需要提出的一对对立的假设，原假设或零假设；记H0为原假设或零假设；与原假设H0相对立的假设称为备选假设，与原假设相对立的假设称为备选假设，备选假设记为H 记为 1. 相对于原假设, 可考虑不同的备选假设, 相对于原假设可考虑不同的备选假设如
电子科技大学

假设检验基本思想

Dec-10

1) H0：μ=μ0， H1： μ≠μ0； 2) H0：μ=μ0， H1： μ=μ1； 3) H0：μ≤μ0， H1： μ＞μ0；＞ 4) H0：μ=μ0， H1： μ＜μ0；……. ＜ 3. 检验统计量用做检验统计推断的统计量. 用做检验统计推断的统计量. 4. 假设检验的接受域和拒绝域根据假设检验目的，根据假设检验目的，由样本去推断是否接受原假设H0 .
电子科技大学

假设检验基本思想

Dec-10

接受域使H0得以接受的检

验统计量取值的区域A. 区域否定域：否定域：使H0被否定的检验统计量取值的区域R 区域 . 假设检验的基本步骤三.假设检验的基本步骤包装机工作正常与否的判断 1.提出原假设：根据实际问题提出原假设 .提出原假设： H0和备选假设 1; 和备选假设H
电子科技大学

假设检验基本思想

Dec-10

2. 建立检验统计量：寻找参数的一个良好建立检验统计量：估计量，估计量，据此建立一个不带任何未知参数的统计量U作为检验统计量，并在成立的条件下，计量作为检验统计量，并在H0成立的条件下，作为检验统计量确定U的分布(或近似分布) 确定的分布(或近似分布)；的分布 2

3.确定 0的否定域：根据实际问题选定显确定H 的否定域：确定著性水平α，依据检验统计量的分布与著性水平，依据检验统计量的分布与H0的内确定H 的否定域；容，确定 0的否定域； 3
电子科技大学

假设检验基本思想

Dec-10

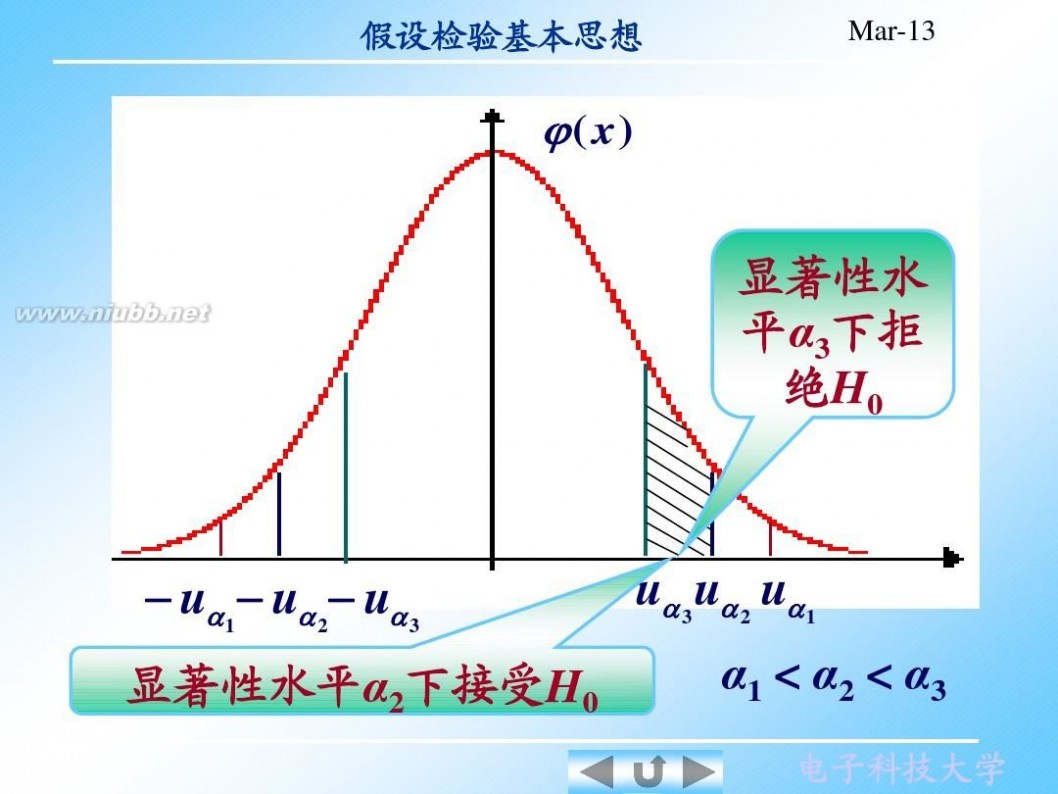
4. 对H0作判断：根据样本值算出检验统作判断：计量的统计值u，判断u是否落在拒绝域是否落在拒绝域，计量的统计值，判断是否落在拒绝域，以 4 确定拒绝或接受H 确定拒绝或接受 0 . 对原假设H 做出判断，称为对H 对原假设 0做出判断，称为对 0做显著性检验， 1?α称为置信水平称为置信水平. 检验， ? 称为置信水平注1 对不同的显著性水平α，有不同的否对不同的显著性水平，定域，从而可能有不同的判断结论. 定域，从而可能有不同的判断结论如在工件直径的假设检验问题中，如在工件直径的假设检验问题中，设α1 < α2 < α3, 对不同的分位数
电子科技大学

假设检验基本思想

Dec-10

?(x)

显著性水平α3下拒绝 H0

? uα1? uα2? uα3
显著性水平α 下接受H 显著性水平 2下接受 0

uα3uα2 uα1
α1 < α2 < α3
电子科技大学

假设检验基本思想

Dec-10

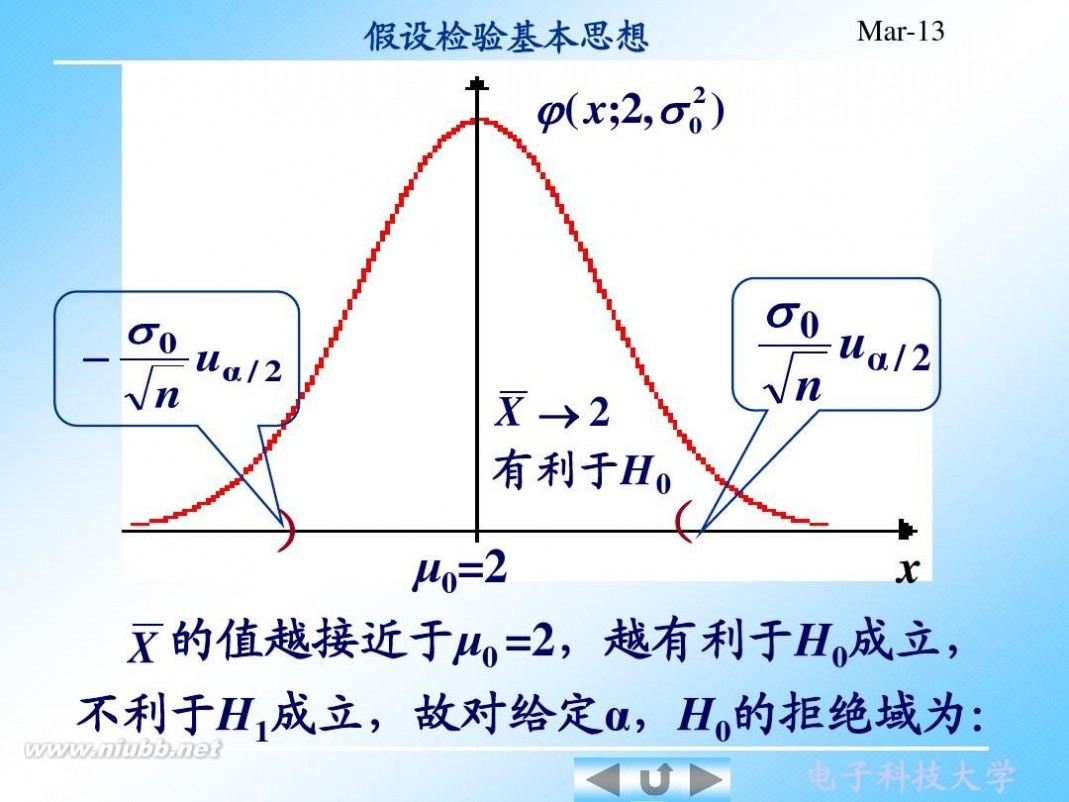
在确定H 的拒绝域时应遵循有利准则有利准则：注2 在确定 0的拒绝域时应遵循有利准则：将检验统计量对H 将检验统计量对 0有利的取值区域确定为接受成立有利的区域作为拒绝域. 域，对H1成立有利的区域作为拒绝域. 如在工件直径假设检验问题中 1）若检验 H0：μ=μ0=2，H1：μ≠μ0=2；），；取检验统计量

X ?2 U= σ0 n
电子科技大学

假设检验基本思想
2 ?( x;2,σ0 )

Dec-10

?

σ0
n

uα / 2

σ0
X →2 有利于H0

n

uα / 2

）

（
x

μ0=2

的值越接近于μ ，越有利于H 成立， X 的值越接近于 0 =2，越有利于 0成立，不利于H 成立，故对给定α，的拒绝域为：不利于 1成立，故对给定，H0的拒绝域为：
电子科技大学

假设检验基本思想

Dec-10

x ? μ0 >
或

σ0
n

uα/ 2

u=

x ? μ0

σ0 / n

> uα/ 2

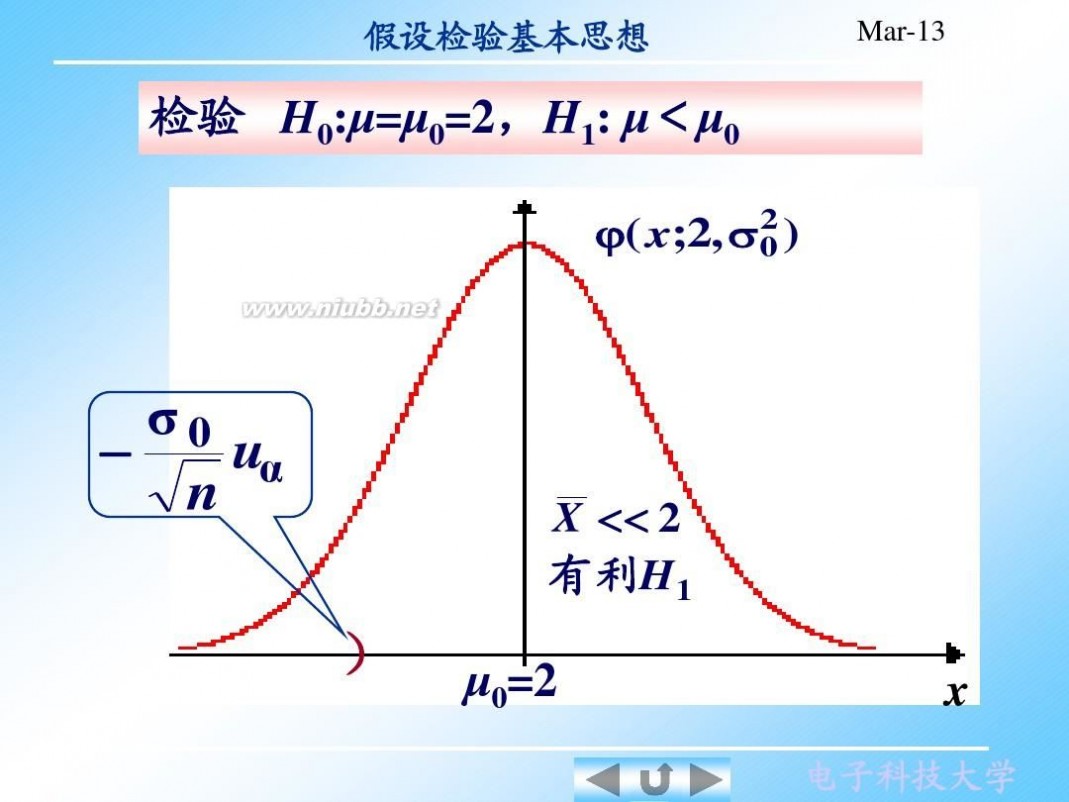
2）若检验 H0

：μ=μ0=2，H1：μ<μ0；），取检验统计量

X ?2 U= σ0 n
电子科技大学

假设检验基本思想

Dec-10

检验 H0:μ=μ0=2，H1: μ＜μ0 ，＜
2 ?( x;2, σ0 )

σ0 u ? α n
）

X << 2 有利H1

μ0=2

x
电子科技大学

假设检验基本思想

Dec-10

给定α，的否定域为：给定，H1的否定域为：

x ? μ0 < ?
例中

σ0

n

uα
u0.05 = ?0.0165

n 拒绝H 即认为新工艺使工件直径偏小. 拒绝 0，即认为新工艺使工件直径偏小.

x ? 2 = ?0.022 < ?

σ0

大样本假设检验例
电子科技大学

假设检验基本思想

Dec-10

四、两类错误 1）假设检验的主要依据是“小概率事件原）假设检验的主要依据是“ 理”，而小概率事件并非绝对不发生. 而小概率事件并非绝对不发生. 2）假设检验方法是依据样本去推断总体，样）假设检验方法是依据样本去推断总体，本只是总体的一个局部，本只是总体的一个局部，不能完全反映整体特性. 特性

无论接受或拒绝原假设H 无论接受或拒绝原假设 0 都可能做出错误的判断
电子科技大学

假设检验基本思想

Dec-10

检验 H0:μ=μ0，H1:μ≠μ0；来自正态总体 N(μ1,σ2) 的可能性也很大. 也很大

不否定 H0 uα/2

μ0

电子科技大学

假设检验基本思想

Dec-10

第一类错误(弃真：成立的情况下，第一类错误弃真)：在H0成立的情况下，弃真错误地否定了H 错误地否定了 0；第二类错误(纳伪：不成立的情况下，第二类错误纳伪)：在H0不成立的情况下，纳伪错误地接受了H 错误地接受了 0. 检验假设 H0：μ=μ0， H1：μ≠μ0 ，当 H0 成立时，

X ? μ0 U= ~ N(0,1) σ0 n
电子科技大学

假设检验基本思想

Dec-10

成立时，若H1 成立时，(即μ≠μ0)

μ ? μ0 X ? μ0 X ? μ μ ? μ0 ~ N( ,1) U= = + σ0 n σ0 n σ0 n σ0 n
犯第一类错误的概率为

P{ U > uα H0真 = α } 2
犯第二类错误的概率β(μ)

显著性水平

Pμ {U ≤ uα } = β (μ), μ ≠ μ0 2
电子科技大学

假设检验基本思想

Dec-10

两类错误判断真实情况判断正误拒绝H 拒绝 0 接受H 接受 0 H0 真犯第一类错弃真）误（弃真）判断正确 H1 真判断正确犯第二类错纳伪）误（纳伪）

不可能使两类错误同时都尽可能小！不可能使两类错误同时都尽可能小！减小一类错误，必然使另一错误增大. 减小一类错误，必然使另一错误增大
电子科技大学

假设检验基本思想

Dec-10

在一次社交聚会中，例8.1.1 在一次社交聚会中，一位女士宣称她能区分在熬好的咖啡中，她能区分在熬好的咖啡中，是先加奶还是先加并当场试验，糖，并当场试验，结果 8 杯中判断正确 7 杯.但但因她未完全说正确，有人怀疑她的能力！因她未完全说正确，有人怀疑她的能

力！该如何证明她的能力呢？何证明她的能力呢？在场的一位统计学家给出了如下的推理思路推理思路：在场的一位统计学家给出了如下的推理思路：设该女士判断正确的概率为p 设该女士判断正确的概率为原假设H 即该女士凭猜测判断，原假设 0 ： p=1/2 即该女士凭猜测判断，对立假设H1： p>1/2 对立假设即该女士确有判断力. 即该女士确有判断力
电子科技大学

假设检验基本思想

Dec-10

在假设H 杯中猜对7杯以上的概率为在假设 0下，8杯中猜对杯以上的概率为杯中猜对 0.0352 (用二项分布计算用二项分布计算). 用二项分布计算正确，则小概率事件发生！若H0正确，则小概率事件发生！ — 故拒绝 0，即认为该女士确有鉴别能力故拒绝H 即认为该女士确有鉴别能力.

#
电子科技大学

假设检验基本思想

Dec-10

8.1.2 工厂生产的工件直径标准为 0=2 工厂生产的工件直径标准为μ （cm)，现从采用新工艺生产的产品中抽取出， 100个，算得直径 x = 1.978(cm)，问 x 与μ0 个，的差异是否反映了工艺条件的改变引起工件直径发生了显著的变化？(已知已知σ=σ0=0.1). 直径发生了显著的变化？已知表示新工艺生产的工件直径总体，解用X 表示新工艺生产的工件直径总体，设X～N(μ,σ2). ～提出统计假设 H0:μ=2；(原假设 , H1:μ≠μ0=2 (备择假设）原假设) 备择假设）；原假设备择假设
电子科技大学

假设检验基本思想

Dec-10

原假设H 相当于“ 原假设 0相当于“新工艺对工件直径无显著影响” 影响”. 标准化成立，若H0 成立，则有 X ?2 U= ~ N(0,1) σ0/ n

由于而

X ?2 P{ < 1.96} = 0.95, σ0/ n 1.978 ? 2 x ?2 u= = = 2.2 > 1.96, 0.1/100 σ0/ n
电子科技大学

假设检验基本思想

Dec-10

小概率事件在一次试验中竟发生，小概率事件在一次试验中竟发生，无理由接受原假设H 接受原假设 0，即认为新工艺对工件有显著的影响. 的影响

#
电子科技大学

假设检验基本思想

Dec-10

某车间有一台葡萄糖自动包装机, 例8.1.3 某车间有一台葡萄糖自动包装机额定标准为每袋重500克设每袋产品重量额定标准为每袋重克.设每袋产品重量 X~N(μ,152)，某天开工后，为了检验包装机，某天开工后，工作是否正常，随机取得9袋产品袋产品，工作是否正常，随机取得袋产品，称得重量数据为(单位单位：：量数据为单位：克)：
497 506 518 524 498 511 520 515 512

这天包装机是否工作正常？问：这天包装机是否工作正常？分析：分析：若μ=500(克)，则包装机工作正常克，则包装机工作正常, 否则认为不正常. 否则认为不正常
电子科技大学

假设检验基本思想

Dec-10

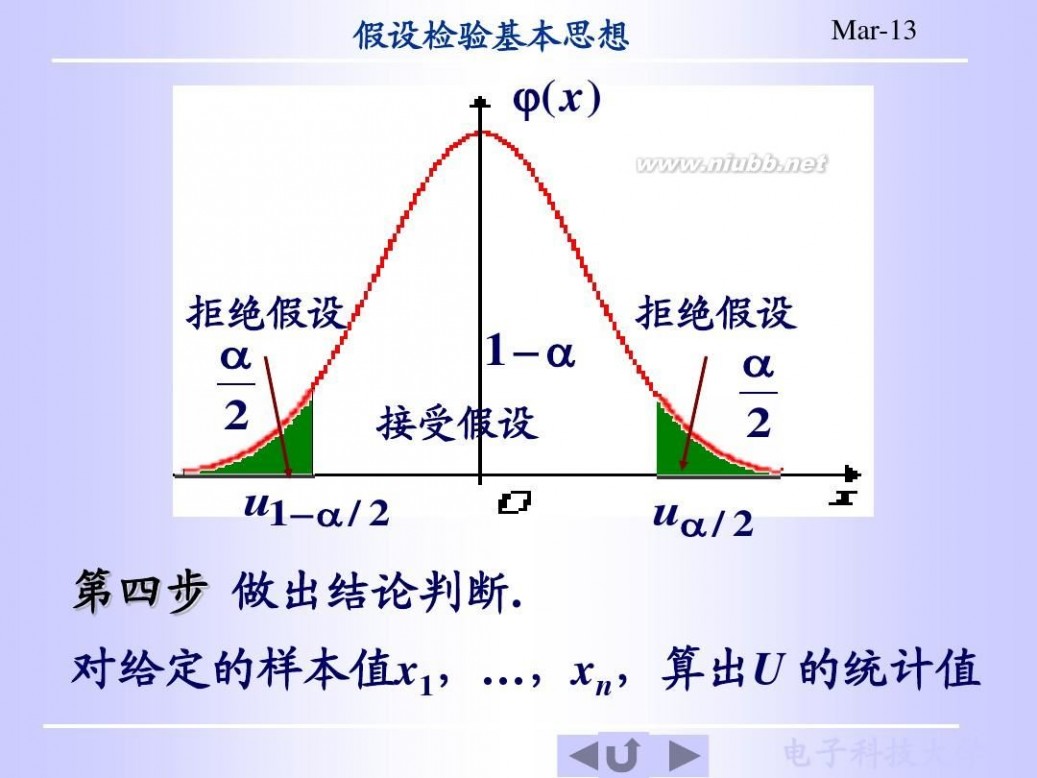
第一步根据实际问题提出

一对假设 H0：μ=500=μ0; H1：μ≠μ0; 若拒绝H 表明包装机工作很可能不正常；若拒绝 0 , 表明包装机工作很可能不正常；否则，可认为包装机工作正常. 否则，可认为包装机工作正常第二步构造适当的检验统计量构造适当的检验统计量. 的良好估计量，由于 X 是μ的良好估计量，且σ02=152，当的良好估计量 H0 成立时，有成立时，

U=

σ0

X ? μ0

X ? 500 ~ N(0,1), = n σ0 n
电子科技大学

假设检验基本思想

Dec-10

第三步确定 0 的拒绝域确定H 对给定的显著水平对给定的显著水平α(0<α<1), 由正态分布表可显著水平查得u 查得 α，使得 P{│U│> uα/2 }=α 即 P{│U│≤ uα/2 }=1－α －

于是H 拒绝域为于是 0的拒绝域为 (－, －uα/2)∪( uα/2 ，+∞) － ∪
电子科技大学

假设检验基本思想

Dec-10

?(x)

拒绝假设

α 2

1? α
接受假设

拒绝假设

α 2

u ?α / 2 1

uα/ 2

第四步做出结论判断做出结论判断. 对给定的样本值x 算出U 对给定的样本值 1，…，xn，算出的统计值，
电子科技大学

假设检验基本思想

Dec-10

x ? μ0 1 , 其中x = ∑xi u= n i=1 σ0 n
n

则拒绝H 而接受而接受H 若│u│>uα/2 则拒绝 0 (而接受 1 ); 否则接受H 否则接受 0. 因若原假设H 成立，因若原假设 0 成立，小概率事件P{│U│> uα/2 }=α 率事件发生，发生，有理由怀疑原假设 H0是错误的. 是错误的
电子科技大学

假设检验基本思想

Dec-10

若取α=0.05，查表得： uα/2 =1.96，由样本可算，查表得：若取，得：

511? 500 11 x ? μ0 u= = = = 2.2, 15 / 3 5 σ0 n
由于│u│=2.2> 1.96，故在显著性水平由于，故在显著性水平α= 0.05 之下拒绝 0 ，即认为包装机工作不正常之下拒绝H 即认为包装机工作不正常.

电子科技大学

#

假设检验基本思想

Dec-10

某系统中装有1024个同类元件，对系个同类元件，例8.1.4 某系统中装有个同类元件统进行一次周期性检查，更换了其中18个元件个元件，统进行一次周期性检查，更换了其中个元件，是否可认为该批元件的更新率p为是否可认为该批元件的更新率为0.03.(取取 α=0.01））解 1）需检验 H0：p=0.03 ； H1: p≠0.03。）。 2）用Y表示表示1024个元件中需更换的个数，个元件中需更换的个数，）表示个元件中需更换的个数为真，若H0为真，则有 Y～B（1024，0.03）～（，）由D—L中心极限定理知中心极限定理知
电子科技大学

假设检验基本思想

Dec-10

Y ? np ～N(0, 1) U= np(1 ? p) 近似成立. 近似成立

3）对给定α(0＜α＜1)，有） (0＜ 1)，
Y ? np P{U ≥ uα } = P{ ≥ uα } ≈α 2 2 np1? p)

当α=0.01，uα/2=u0.005=2.575, H0的拒绝域为， (－∞, －2.575)∪(2.575, ＋∞). － ∪
电子科技大学

假设检验基本思想

Dec-10

4）统计量的统计值）统计量U的统计值 y ? np 18 ?1024×0.03 u= = = ?2.330, np(1? p) 1024×0.03×0.97 －2.330∈(－2.575，2.575), ∈－，无理由拒绝 0，即在α=0.01的显著性水平无理由拒绝H 即在的显著性水平拒绝可认为元件更新率为0.03. 下，可认为元件更新率为若取α=0.05， uα/2=u0.025=1.96，则因，若取，（－1.96，1.96）无理由接受 0，接受H －2.330 ?（－，）无理由接受即认为更新率不是0.03. 即认为更新率不是
电子科技大学

#

四 : 8.1 假设检验的基本思想与步骤

假设检验的基本步骤 8.1 假设检验的基本思想与步骤