一 : C4D人物头部建模基础篇
原文
作者:不详
翻译:lyc
这个教程展示了如何制作人物的头部,教程的要点是利用少量的必须的多边形来创造一个真实的头部模型.当然,这将帮助你制作你自已的人物。[www.61k.com)

1..关键是你要把握好整个物体的平衡,而不是改变他的形状。 首先把立方体放在曲面样条之下,然后使之可编辑。 受曲面影响的立方体就成为了圆润流畅的了

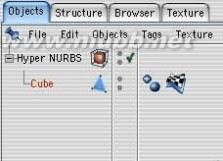
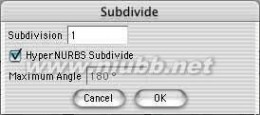
2..在我们把多边形调整成头的形状之前,需要细分这个多边形。在多边形编辑模式下,使用"细分块面"功能,在对话框的细分数中输入1,并勾选HyperNURBS细分,现在这个立方体就成了更加光滑的球形。
c4d教程 C4D人物头部建模基础篇

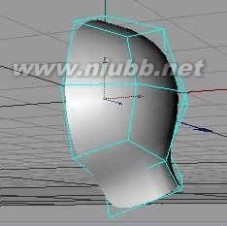
3..我们需要作一个脖子使头部更加完整。(www.61k.com]
选择脖子部位的面,使用挤压工具。如果你不需要脖子,可以在完成建模后删掉它。

4..为了节省时间,提高效率,删掉左半部分。在正视图中,使用矩形选择工具,去掉“仅选择可见元素”选项,选择Y轴左边的点,删掉。
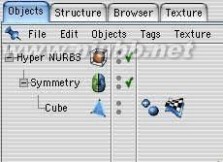
5..在对象管理中,把右半部分拖入一个“对称对象”下。层级关系如图示。
c4d教程 C4D人物头部建模基础篇
6..通过多边形和点的调整,我们把它作成一个头部的外形。[www.61k.com)在后面我们将继续细分和调整来制作头部的细节,因此,要注意中间点的X轴坐标必须为0,否则在“对称对象”作用下,头部就要出现破洞。
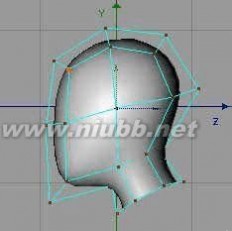
7.. 成型后,利用”功能”里的“细分”工具再次细分。
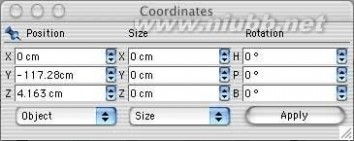
8..如果细分后,中间点的X轴坐标不是0,可以通过坐标管理器把点的X轴数值置0来移动它到正确的位置。(我用R9版没出现这个情况)
c4d教程 C4D人物头部建模基础篇
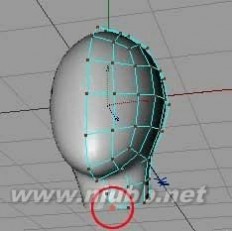
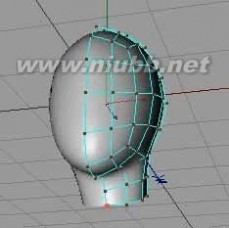
9..对于冠和后脑勺,少量的多边形已经足够,但眼睛,鼻子和嘴巴需要进一步的决策。(www.61k.com)多边形细分中的相应部分。
因此,“切断与刀工具”
c4d教程 C4D人物头部建模基础篇
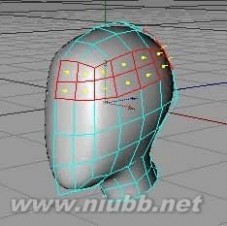
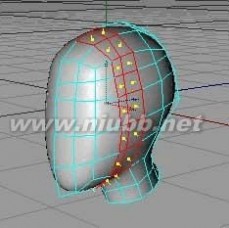

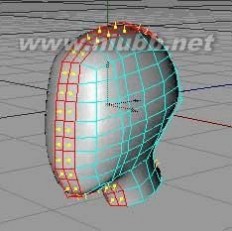
10..从现在开始,我们将制作眼睛、鼻子和嘴这些细节部分。[www.61k.com)注意整体的比例以及对称。

11..选择眼睛的部位,使用内部挤压两次来产生更多的面,如图的选择部分
c4d教程 C4D人物头部建模基础篇

12..在点模式下,通过移动点来塑造整个眼部的外形。[www.61k.com]
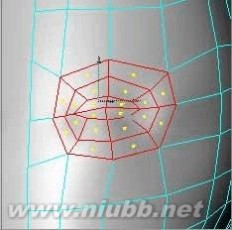
13..在调整嘴的部位之前,我们需要把这个构成头部的对称对象转为一个单一对象一会儿。然后,使用内部挤压三次来产生更多的面。

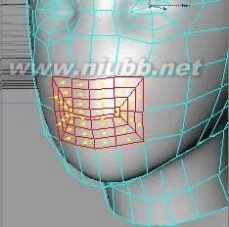
14..接下来要制作一部分嘴的内部空间,可以用来放置牙齿,使用挤压工具把选定的
c4d教程 C4D人物头部建模基础篇
面向后推(推向头的内部)。(www.61k.com)

15..使用法线缩放把被挤出的面放大一些,然后删掉它们。

16..再次删掉头部的左半部分,并放入一个对称对象下。通过调整嘴部的点,制作嘴的形状。
扩展:c4d头部建模 / c4d人物建模 / c4d人物建模教程

c4d教程 C4D人物头部建模基础篇
17..选择鼻子到脸颊的部位,使用循环切刀(勾选限制到选择)来一次切割,来增加面。(www.61k.com]
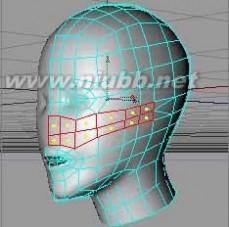
18..现在我们已经有了眼睛、鼻子和嘴的大致外形,进一步的,通过点面的调整,来调整它们的比例,塑造更真实的脸部的外形。
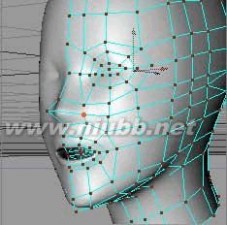
19..再继续制作眼部的细节.选择眼部的面,使用内部挤压三次来增加面.
c4d教程 C4D人物头部建模基础篇
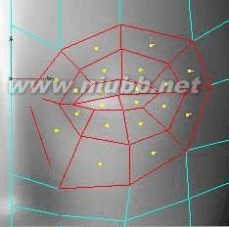
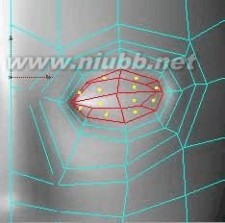
20..调整点
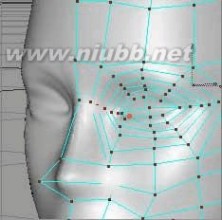
.
21..造择眼睛部分(眼球露出的部位),使用挤压工具向后推(向头的内部),然后删掉这些面

.
c4d教程 C4D人物头部建模基础篇
22..使用切刀,在眼的四周切出更多的面.
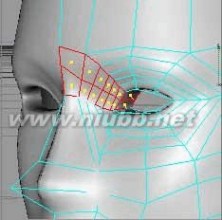
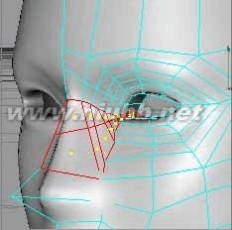

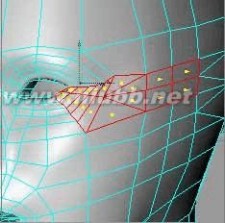
23..如果,在图示的部位出现了三角形的面,那么在加入HyperNURBS后会出现褶皱,在渲染中会出现不正常的现象,我们最好把它们转为四边形,使用功能菜单中的四角形化命令,并去掉"估计角度"选项.
(在耳朵部位,我们切割面时出现的三角形面不必理会,这些面在连接耳朵时是要删掉的.
当然在R9版中,使用切刀时,如果没有去掉"创建N-GONS"选项,三角形面一般不会显现出来,但在加入HyperNURBS后同样面是不光滑的,N-GONS功能并不能对会出现问题的三角形面自动地进行彻底地优化,C4D对面的要求还是比较严谨的.)
c4d教程 C4D人物头部建模基础篇
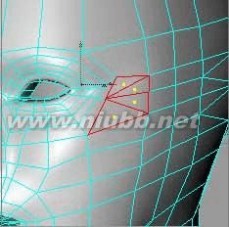
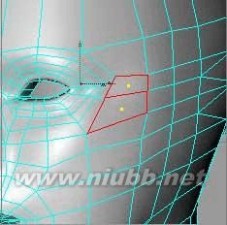
24..为了更方便的工作,选择眼的部位的面后,使用选择菜单中的"设置选集"命令来设定一个选集,在选集的属性面板重命名为"eye",并点击"选择并隐藏其他"按钮,把除眼部的其它面隐藏起来。[www.61k.com]
c4d教程 C4D人物头部建模基础篇
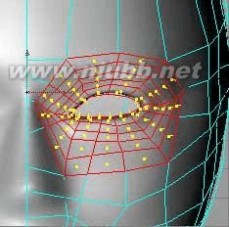
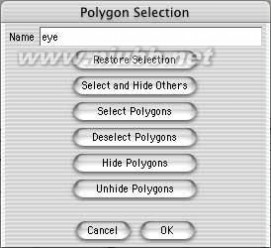
25..调整出眼角的形状.接着要制作眼睑(上下眼皮),选择面,使用内部挤压一次。[www.61k.com)
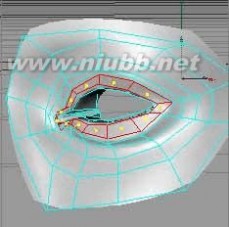
26..调整点来塑造眼睑的形状,我们要注意上下眼皮是用来遮盖眼球的,要作出这种感觉。
c4d教程 C4D人物头部建模基础篇

27..接下来,让我们继续刻画鼻子的细节.选择从鼻子到嘴的面(一直延伸到脖子),应用一下切刀。[www.61k.com)

28..如果出现三角形面,注意优化。

c4d教程 C4D人物头部建模基础篇
29..继续切割鼻孔部位,注意面的优化。[www.61k.com]

30..使用切刀进一步细分面,注意面的优化
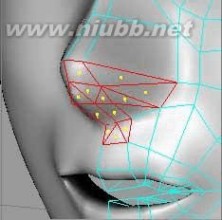
.
31..选择要制作鼻孔的部位,应用一次内部挤压
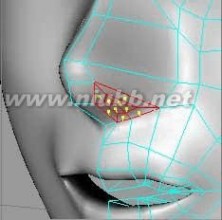
.
c4d教程 C4D人物头部建模基础篇
32..再使用挤压工具作出鼻孔

.
33..继续使用切刀细分图示的鼻梁等部位的面
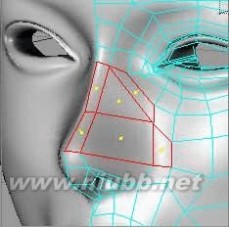
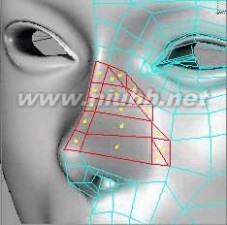

扩展:c4d头部建模 / c4d人物建模 / c4d人物建模教程

.
c4d教程 C4D人物头部建模基础篇
34..使用"四角形化"命令,或者删除面后用"桥接"工具重建面,尽可能地把三角形面转为四角形,以取得光滑的表面

.
35..用切刀切割鼻孔部分的面,来制作鼻翼,并对三角形面进行尽可能的优化
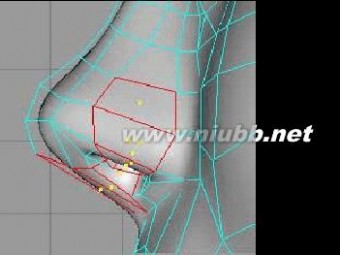
.
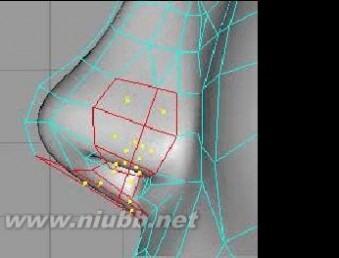
36..在对点进行仔细的调整后,鼻子终于完成了。(www.61k.com)

c4d教程 C4D人物头部建模基础篇
37..现在,让我们对嘴部进行最终的刻画.首先,用切刀切割从嘴部到颊部的面
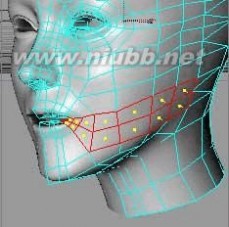
.
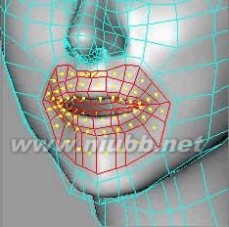
38..再次把对称对象转为单一对象.选择嘴部的面,应用一次内部挤压
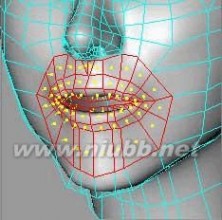
.
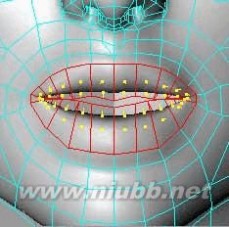
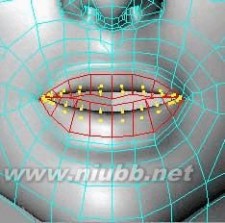
39..选择嘴唇部分,应用两次内部挤压。[www.61k.com)
c4d教程 C4D人物头部建模基础篇
40..删掉左半部分,建立一个对称对象.点模式下,仔细调整嘴部的形状。(www.61k.com]
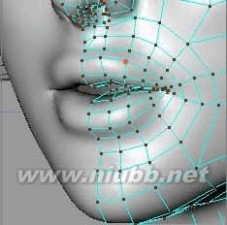
41..最后,删掉在应用内部挤压时在嘴的内部形成的多余的点.嘴over了。

c4d教程 C4D人物头部建模基础篇
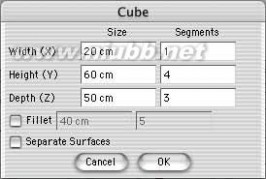
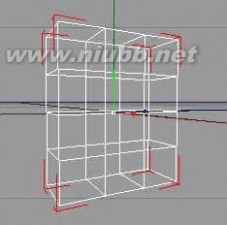
STEP42:下一步将耳朵。(www.61k.com) 如头,案例让我们开始与立方原始细分一步一步。 首先设定在一个对话框中的大小和部分号码。
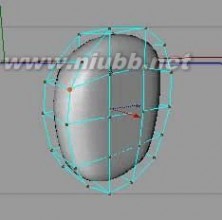
STEP43:置于一个超曲面影响对象,然后进行编辑。 使用点工具,你可以随意塑造成类似的耳朵上。
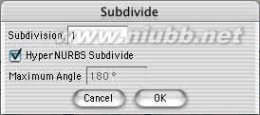
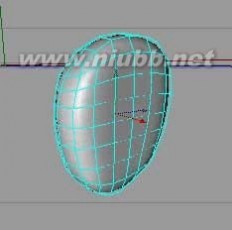
STEP44:进一步细分与段分成工具。
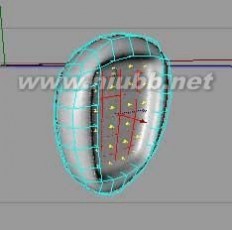
STEP45:选择任何多边形,击退他们使用挤出内。
c4d教程 C4D人物头部建模基础篇
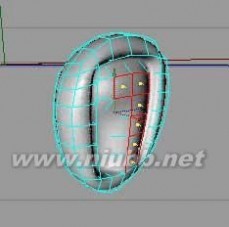


STEP46:编辑点和多边形塑造成耳朵一样的对象之一。[www.61k.com) 由于耳朵形状复杂,你最好仔细观察自己的耳朵结构。

STEP47:让我们消除不必要的多边形,以便把耳朵和头部部份。
c4d教程 C4D人物头部建模基础篇
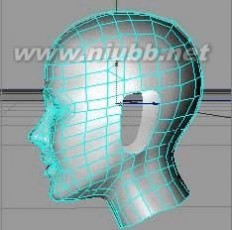
STEP48:删除头部耳朵区域多边形。(www.61k.com)
STEP49:不要“组对象”的头和耳朵部分,或把它作为另一个子对象之一,然后执行连接命令来获得一个新的合并对象。

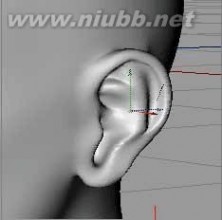
STEP50:让我们绑耳朵一部分与桥工具头。 当所有的工作已经完成,你应该选择所有的多边形,并调整它们的法线方向。 这将阻止
渲染错误。
c4d教程 C4D人物头部建模基础篇

STEP51:将超曲面的多边形,使头发盘。(www.61k.com)

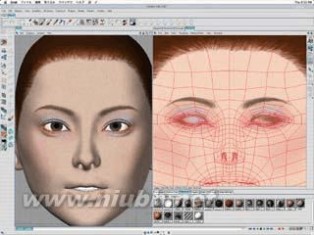
扩展:c4d头部建模 / c4d人物建模 / c4d人物建模教程
c4d教程 C4D人物头部建模基础篇
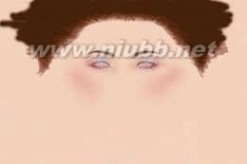
STEP52:使用BodyPaint三维,您可以为面的纹理。[www.61k.com) 您可以直接画的对象,因为如果你的工作是一个真正的人体模型构成。
STEP53:由于唇质地的面孔不同的参数,你必须作出新的和运用额外的脸上。

c4d教程 C4D人物头部建模基础篇

STEP54:应用纹理也对头发,并设置三个灯,你会得到一个字符的图片。(www.61k.com) “眼睛”是的因素很多,使它成为一个可爱的性格,这是其他真实于CG。 让我们创建一个字符是迷人的,生动,而且很可能与您交谈!
扩展:c4d头部建模 / c4d人物建模 / c4d人物建模教程
二 : 数学建模入门基础
数学建模
小册子
目录
第一章优化模型………………………………………………………………………………(02)
第二章统计分析………………………………………………………………………………(05)
第三章层次分析法……………………………………………………………………………(13)
第四章数值计算………………………………………………………………………………(25)
第五章微分方程………………………………………………………………………………(26)
第六章差分方程………………………………………………………………………………(28)
第七章图论……………………………………………………………………………………(31)
第八章BP人工神经网络……………………………………………………………………(34)
第九章GM(1,1)灰色预测……………………………………………………………………(37)
1
第一章优化模型:用LINGO
简单的优化模型:
简单的优化模型,归结为微积分中的函数极值问题,可以直接用微分法求解。简单优化模型的灵敏度分析:
设有一个未知量为x的函数f(x,a1,a2...an)=0,其中a1,a2...an是未知系数(事实上是已知的),这个函数必定存在最值,最值的求法:
?f(x,a1,a2...a)=0?x(a1,a2...an是各自独立的变量)
得到x的函数x(a1,a2...an),未知数是a1,a2...an,用相对改变量衡量结果对参数的敏感程度,下面进行灵敏度分析:x对a1的敏感度记作S(x,a1),定义为
S(x,a1)=?x/xdxa≈?a1/a1da1x(dxdx(a1,a2...an)=da1da1
把a1,a2...an和x代入上式,可解得实值s=S(x,a1),即解释为当x增加1%,当s为正值时,就增加s%;当s为负值时,就减少s%。
同理可得x对a2的敏感度记作S(x,a2)。
数学规划模型:
在很多实际问题中,所能够提供的决策变量取值受到很多因素的制约,这样就产生了一般的优化模型,统称为数学规划模型。按照数学规划模型的具体特征,可以将数学规划分为:线性规划模型(目标函数和约束条件都是线性函数的优化问题);
非线性规划模型(目标函数或者约束条件是非线性的函数);
整数规划(决策变量是整数值得规划问题);
多目标规划(具有多个目标函数的规划问题);
目标规划(具有不同优先级的目标和偏差的规划问题);
动态规划(求解多阶段决策问题的最优化方法)
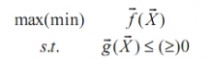
数学规划问题的基本形式为:
其中为决策变量向量,为目标函数(单目标规划只有一个函数,多目标规划可以理为一个向量函数的最优化问题),≤

(≥)0为约束条件,记()
2
D=()≤(≥)0为可行集,因此规划的本质就是在可行集中选择使得目标最优的点。若D=R,则该问题为无条件约束问题,可以用微分法解决(有时仅有关于决策变量的非负约束也可以归结为该类型);若D中的约束都是等式约束,则可以用Lagrange乘数法解决。但是在实际问题中,D的结构往往非常复杂,不能使用普通的微分方法解决,这时候n{}必须借助于计算软件。
规划模型的LINGO求解:
求解线性规划问题:
min=?x2+x3
s..t
x1?2x2+x3=2
x2?3x3+x4=1
x2?x3+x5=2
xj≥0,j=1,...,5
Model
min=-x2+x3;
x1-2*x2+x3=2;
x2-3*x3+x4=1;
x2-x3+x5=2;
end
result:
Globaloptimalsolutionfound.
Objectivevalue:-2.000000
Infeasibilities:0.000000
Totalsolveriterations:2
VariableValueReducedCost
X22.5000000.000000
X30.50000000.000000
X16.5000000.000000
X40.0000000.000000
X50.0000001.000000
RowSlackorSurplusDualPrice
1-2.000000-1.000000
20.0000000.000000
30.0000000.000000
40.0000001.000000
3
Rangesinwhichthebasisisunchanged:
ObjectiveCoefficientRangesCurrent
Variable
X2X3X1X4X5
Coefficient-1.0000001.000000
0.00.00.0
Allowable
Increase0.66666672.0000000.4000000INFINITYINFINITY
RighthandSideRanges
Row234
Current
RHS2.0000001.0000002.000000
AllowableIncreaseINFINITY1.000000INFINITY
AllowableDecrease6.500000INFINITY1.000000Allowable
Decrease
0.00.00.00.01.000000
Variable表示目标函数;Row表示约束条件
分析报告:LINGO经过2次迭代后得到全局最优解,目标值Objectivevalue为-1.5,全局最优解为X=(6.5,2.5,0.5,0,0),ReducedCost列出最优单纯形表中判别数所在行的变量的系数,表示当变量有微小变动时,目标函数的变化率。其中基变量的reducedcost值应为0,对于非基变量Xi,相应的reducedcost值表示当某个变量Xi增加一个单位时目标函数减少(max型问题)或增加(min型问题)的量。SlackorSurplus给出松弛变量的值。DUALPRICE(对偶价格)表示当对应约束有微小变动时,目标函数的变化率。输出结果中对应于每一个约束有一个对偶价格。若其数值为p,表示对应约束中不等式右端项若增加1个单位,目标函数将增加(max型问题)或减少(min型问题)p个单位。(基变量【有实值】时为0;非基变量【为0值】时不为0)
Rangesinwhichthebasisisunchanged:即研究当目标函数的系数和约束右端在什么范围变化时,最优基保持不变。(CurrentCoefficient【CurrentRHS】-AllowableIncrease,CurrentCoefficient【CurrentRHS】+AllowableIncrease)。INFINITY表示无穷大。
4
第二章统计分析:用matlab或SAS

统计学知识总结:
1、统计的几个基本名词:总体、样本、样本值
2、统计推断就是利用样本值来对总体的分布类型、未知参数进行估计和推断。明确的说:
由样本统计量(样本均值、样本比例、样本方差)推断总体(总体均值、总体比例、总体方差)
3、统计过程:样本—>统计量—>抽样分布—>总体分布
4、抽样分布:单正态总体的抽样分布(3个):均值未知、方差未知、均值与方差均未知
双正态总体的抽样分布(2个):均值差、方差比
5、参数估计:
正态分布的置信区间(6中情况):
单正态总体均值(方差已知)
单正态总体均值(方差未知)
单正态总体方差
6、假设检验:
单正态总体的假设检验
双正态总体的假设检验
7、方差分析(单因素)
8、回归分析正双态总体均值差(方差已知)正双态总体均值差(方差已知正双态总体方差比
判别分析:
判别分析法就是利用原有的分类信息,得到体现这种分类的函数关系式(称为判别函

5
数),然后利用该函数去判别未知样品属于哪一类。
聚类分析:
分类问题分为判别分析和聚类分析。判别分析研究事先已经建立类别的情况,即将样品或指标按已知的类别进行归类。聚类分析适用于实现没有分类的情况,即如何将样品或指标进行分类的问题。聚类分析包含的范围很广,可以有系统聚类法、动态聚类法、分裂法、最优分割法、模糊聚类法、图论聚类法、聚类预报等多种方法。
聚类分析法的原理试:首先将一定数量的样品各自看成一类,然后根据样品的亲疏程度,将亲疏程度最高的两类进行合并。然后考虑合并后的类与其他类之间的亲疏程度,再进行合并。重复这一过程,直至将所有的样品合并为一类。
主成分分析:注意建模步骤
在统计分析中有一类问题就是抽取信息的精华,这就是因子分析和主成分分析。
当要研究一个问题时,通常的做法是抽取大量的变量信息,例如,为了准确预报天气,我们抽取了大量的数据,如有1000个变量的抽样数据,然而这些数据中很多是相关的,这就是信息的冗余。信息冗余不仅带来计算上的复杂性,甚至导致计算误差增加。
主成分分析法就是从大量的信息中,选择一组个数少,且互不相关,并带有原样本的大部分的信息另一组变量。简单的说,主成分分析就是把多个指标化为少数几个综合指标的一种统计方法。
主成分分析计算步骤:
①计算相关系数矩阵
?r11?r21R=??M??rp1?r12r22Mrp2Lr1p?Lr2p??MM??Lrpp??(1)
在(3.5.3)式中,rij(i,j=1,2,…,p)为原变量的xi与xj之间的相关系数,其计算公式为
n
rij=(xki?i)(xkj?j)∑k=1
∑(xki?i)
k=1n22(x?)∑kjjnk=1(2)
因为R是实对称矩阵(即rij=rji),所以只需计算上三角元素或下三角元素即可。②计算特征值与特征向量
6
首先解特征方程λI?R=0,通常用雅可比法(Jacobi)求出特征值λi(i=1,2,L,p),并使其按大小顺序排列,即λ≥λ≥L,≥λ≥0;然后分别求出对应12p
于特征值λi的特征向量ei(i=1,2,L,p)。这里要求ei=1,即
量ei的第j个分量。∑ej=1p2ij=1,其中eij表示向
③计算主成分贡献率及累计贡献率
主成分zi的贡献率为
λi
∑λ
k=1p(i=1,2,L,p)k
累计贡献率为
∑λ
∑λ
k=1k=1pik(i=1,2,L,p)k
一般取累计贡献率达85—95%的特征值λ1,λ2,L,λm所对应的第一、第二,…,第m(m≤p)个主成分。
④计算主成分载荷
其计算公式为
lij=p(zi,xj)=λieij(i,j=1,2,L,p)(3)
得到各主成分的载荷以后,还可以按照(3.5.2)式进一步计算,得到各主成分的得分
7
?z11?z21Z=??M??zn1z12z22Mzn2Lz1m?Lz2m??MM??Lznm?(4)
更多的时候我们需要对数据进行标准化,也就是将数据归一化,即对每一列的数据除上它们的标准差,然后进行主成分分析。
在matlab中进行主成分分析:
[pc,score,latent,tsquare]=princomp(x)
PC:相对于特征值latent的特征向量。根据数据矩阵X返回因子成分PC,也就是主成分。score:主成分Yi中的元素。通过将原始数据转换到因子成分空间中得到的数据。也就是原始数据在由主成分所定义的新坐标系中的确定的数据,其大小与输入数据矩阵的大小相同。
latent:存放从大到小的特征值。
tsquare:t平方统计量,它是描述每一测量值与数据中心距离的统计量,用它可以找到数据中的极值点。
在SAS系统中主成分分析通过procprincomp过程来实现。
主成分分析方法应用实例:
1)实例1:流域系统的主成分分析(张超,1984)
表3.5.1(点击显示该表)给出了某流域系统57个流域盆地的9项变量指标。其中,x1代表流域盆地总高度(m),x2代表流域盆地山口的海拔高度(m),x3代表流域盆地周长(m),x4代表河道总长度(m),x5代表河道总数,x6代表平均分叉率,x7代表河谷最大坡度(度),x8代表河源数,x9代表流域
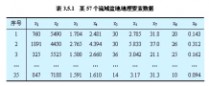
盆地面积(km2)。
(1)分析过程:
①将表3.5.1中的原始数据作标准化处理,然后将它们代入相关系数公式计算,得到相关系数矩阵(表3.5.2)。
8
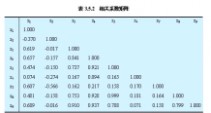
②由相关系数矩阵计算特征值,以及各个主成分的贡献率与累计贡献率(见表
3.5.3)。由表3.5.3可知,第一,第二,第三主成分的累计贡献率已高达86.5%,
故只需求出第一、第二、第三主成分z1,z2,z3
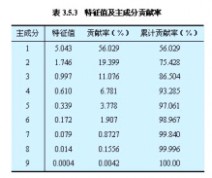

即可。
z3上的载荷(表3.5.4)。
最重要的就是回归分析:
回归分析是指对具有相关关系的现象,根据其关系形态,选择一个合适的数学模型,用来近似地表示变量间的平均变化关系的一种统计方法。
回归分析的分类:按照回归模型中变量个数分(一元回归,多元回归);按照回归曲线的形态分(线性回归,非线性回归);按照是否要求总体分布类型已知分(参数回归,非参数回归)
主要学习一元线性回归和多元线性回归
9
建模过程:①模型的参数估计②检验、预测和控制
一元线性回归模型:
模型的参数估计:
一般地,称由y=β0+β1x+ε确定的模型为一元线性回归模型,记为
?y=β0+β1x+ε?2?Eε=0,Dε=σ
其中固定的未知参数β0,β1称为回归系数,自变量x也称为回归变量,y=β0+β1x称为y对x的回归直线方程。
一元线性回归分析的主要任务
1、用试验值(样本值)对β0,β1和σ作点估计;
2、对回归系数β0,β1作假设检验;
3、在x=x0处对y作预测,对y作区间估计。
回归系数的最小二乘估计
有n组独立观测值,(xi,yi),i=
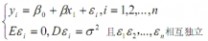
1,2,...,n。
设
记Q=Q(β0,β1)=∑ε=∑(yi?β0?β1xi)。最小二乘法就是选择β0和β12inn2
i=1i=1
?,β?=minQ(β,β)。计算得到?,β?使得Qβ的估计β010101β0,β1()
?=?β??β01???xy?xy?β1=22x?x?
1n1n1n21n2其中x=∑xi,y=∑yi,x=∑xi,xy=∑xiyi。(经验)回归方程为:ni=1ni=1ni=1ni=1
?+β?x=+β?(x?)。?=βy011
?,β?=记Qe=Qβ∑yi?β?0?β?1xi01
i=1()n(?))=∑(y?y2n2ii,称Qe为残差平方和i=1
?=Qe/(n?2)。或剩余平方和。σ的无偏估计为σ22
10
回归方程的显著性检验:
对回归方程Y=β0+β1x的显著性检验,归结为对假设H0:β1=0;H1:β1≠0进行检验。
假设H0:β1=0被拒绝,则回归显著,认为y与x存在线性关系,所求的线性回归方程有意义;否则回归不显著,y与x的关系不能用一元线性回归模型来描述,所得的回归方程也无意义。
n
U2
?i?)(回归平F检验法:当H0成立时,F=~F(1,n?2),其中U=∑(y
Qe/n?2i=1
方和)。若F>F1?α(1,n?2),拒绝H0,否则就接受H0。回归系数的置信区间:
β0和β1置信水平为1?α的置信区间分别为
???t(
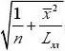
n?2)σ?+t(
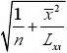
n?2)σ??β?β和0α0α
1?1??22???????β0?t1?α(
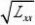
n?2)σβ0+t1?α(
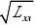
n?2)σ;?22??
QQ??
。σ2的置信水平为1?α的置信区间为?2e,2e
?χαn?2χαn?2???1?22?
预测:
?+β?x作为y的预测值。y的置信水平为1?α的预测区间为?0=β用y0的回归值y01000?0?δ(x0),y?0+δ(x0)????y?,其中δ(x0)=t1?α(

n?2)σ
2
。特别,当n很大且x0在附近取值时,y的置信水平为1?α的预测区间近似为
??
????y?σu,y+σu?eαeα?。1?1??22?
多元线性回归:
Y=Xβ+ε?
一般称?为高斯—马尔柯夫线性模型(k元线性回归模2
Eε=0,COVε,ε=σI()()n?
型),并简记为Y,Xβ,σIn。
(
2
)
11
?y1??1x11???...1x21其中Y=??,X=??...??......???y?n??1xn1x12x22...xn2x1k??β0??ε1??????...x2k?βε21,β=??,ε=??,?...??...?......??????...xnk?β?k??εn?...
y=β0+β1x1+...+βkxk称为回归平面方程。
线性模型Y,Xβ,σIn考虑的主要问题是:
(1)用试验值(样本值)对未知参数β和σ2作点估计和假设检验,从而建立y与(2)x1,x2,...,xk之间的数量关系;
(2)在x1=x01,x2=x02,...,xk=x0k处对y的值作预测与控制,即对y作区间估计。对βi和σ作估计,用最小二乘法求β0,...,βk的估计量:作离差平方和2
Q=∑(yi?β0?β1xi1?...?βkxk)
i=1n2
?=XTX选择β0,...,βk使Q达到最小。解得估计值β()(XY),得到的β?代入回归平方?1T
i
?+β?x+...+β?x,称为经验回归平面方程。β?称为经验回归系数。程得y=β011kki
多元线性回归中的检验与预测:
假设H0:β0=β1=...=βk=0。
当H0成立时,F=U/k~F(k,n?k?1)。如果F>F1?α(k,n?k?1),则Qe/n?k?1拒绝H0,认为y与x1,x2,...,xk之间显著地有线性关系;否则就接受H0,认为y与x1,x2,...,xk之间线性关系不显著。
?+β?x+...+β?x,对于给定自变量的值x,x,...,x,用?=β求出回归方程y011kk12k***
?+β?x*+...+β?x*来预测y?+β?x*+...+β?x*+ε。称y?*=β?*=β?*为y*的点预测。y011kk011kk
多元线性回归matlab命令:
确定回归系数的点估计值:b=regress(Y,X)
12
???β0?????βb=?1?
?...??β???k?
?Y1???Y2
Y=??
?...????Yn??1x11?
1x21
X=?
?......??1xn1?
x12x22...xn2
x1p??
...x2p?......?
?
...xnp??
...
求回归系数的点估计和区间估计、并检验回归模型:
[b,bint,r,rint,stats]=regress(Y,X,alpha)
Stats给出用于检验回归模型的统计量,有三个数值:相关系数r2、F值、与F对应的概率p。
判别规则:相关系数r2越接近1,说明回归方程越显著;F>F1?α(k,n?k?1)时拒绝
H0,F越大,说明回归方程越显著;与F对应的概率p<α时拒绝H0,回归模型成立。
第三章层次分析法
层次分析法(AHP-AnalyticHierachyprocess)----多目标决策方法
70年代由美国运筹学家T·L·Satty提出的,是一种定性与定量分析相结合的多目标决策分析方法论。吸收利用行为科学的特点,是将决策者的经验判断给予量化,对目标(因素)结构复杂而且缺乏必要的数据情况下,採用此方法较为实用,是一种系统科学中,常用的一种系统分析方法,因而成为系统分析的数学工具之一。基本内容:(1)多目标决策问题举例AHP建模方法
(2)AHP建模方法基本步骤(3)AHP建模方法基本算法一、问题举例:
假期旅游地点选择
暑假有3个旅游胜地可供选择。例如:P1:苏州杭州,P2北戴河,P3桂林,到底到哪个地方去旅游最好?要作出决策和选择。为此,要把三个旅游地的特点,例如:①景色;②费用;③居住;④环境;⑤旅途条件等作一些比较——建立一个决策的准则,最后综合评判确定出一个可选择的最优方案。
目标层
准则层
方案层

13
二、问题分析:
例如旅游地选择问题:一般说来,此决策问题可按如下步骤进行:
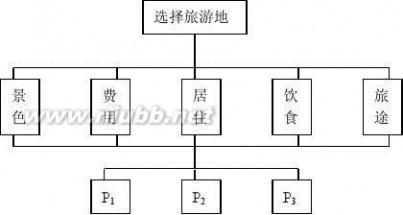
(S1)将决策解分解为三个层次,即:
目标层:(选择旅游地)
准则层:(景色、费用、居住、饮食、旅途等5个准则)
方案层:(有P1,P2,P3三个选择地点)
并用直线连接各层次。
(S2)互相比较各准则对目标的权重,各方案对每一个准则的权重。这些权限重在人的思
维过程中常是定性的。
例如:经济好,身体好的人:会将景色好作为第一选择;
中老年人:会将居住、饮食好作为第一选择;
经济不好的人:会把费用低作为第一选择。
而层次分析方法则应给出确定权重的定量分析方法。
(S3)将方案后对准则层的权重,及准则后对目标层的权重进行综合。
(S4)最终得出方案层对目标层的权重,从而作出决策。
以上步骤和方法即是AHP的决策分析方法。
三、确定各层次互相比较的方法——成对比较矩阵和权向量
在确定各层次各因素之间的权重时,如果只是定性的结果,则常常不容易被别人接受,因而Santy等人提出:一致矩阵法
即:1.不把所有因素放在一起比较,而是两两相互比较
2.对此时採用相对尺度,以尽可能减少性质不同的诸因素相互比较的困难,提高准确度。——成对比较矩阵法:
目的是,要比较某一层n个因素C1,C2, L, Cn对上一层因素O的影响(例如:旅游决策解中,比较景色等5个准则在选择旅游地这个目标中的重要性)。
採用的方法是:每次取两个因素Ci和Cj比较其对目标因素O的影响,并用aij表示,全部比较的结果用成对比较矩阵表示,即:
A=(aij)nxn, aij>0, aji=1(或aij?aij=1)aij
1
aji(1)由于上述成对比较矩阵有特点:A=(aij) , aij>0, aij=
故可称A为正互反矩阵:显然,由
例如:在旅游决策问题中:aij=1,即:aij?aji=1,故有:aji=1aji
14
C(景色)
a12==1
C(费用)2
表示:?
(?C1 景色)对目标O的重要性为1
O的重要性为2?C(费用)对目标2
故:a12=(即景色重要性为1,费用重要性为2)
a13=4==
C(景色)1
C(居住条件)3
表示:
?C1(景色)对目标O的重要性为4
?
O的重要性为1?C(居住条件)对目标3
即:景色为4,居住为1。
a23=7==
C(费用)2
C(居住条件)3
表示:
?C2(费用)对目标O的重要性为7
?
O的重要性为1?C(居住条件)对目标3
即:费用重要性为7,居住重要性为1。
?1
??2?因此有成对比较矩阵:A=?????147123
33?
?55???11?
?11?
?
??问题:稍加分析就发现上述成对比较矩阵的问题:①即存在有各元素的既然:a12=
C11C411=?a21=2; a13=1=?a31==C22C31a134
C2a2112
====8=C3a31C3
1
C2
所以应该有:a23=
而不应为矩阵A中的a23=2
,因:n个元素比较次数为:Cn=
②成对比较矩阵比较的次数要求太次,
n(n?1)
2!
因此,问题是:如何改造成对比较矩阵,使由其能确定诸因素C1, L, Cn对上层因素O的权重?
对此Saoty提出了:在成对比较出现不一致情况下,计算各因素C1, L, Cn对因素(上
15
层因素)O的权重方法,并确定了这种不一致的容许误差范围。
为此,先看成对比较矩阵的完全一致性——成对比较完全一致性四:一致性矩阵
Def:设有正互反成对比较矩阵:
???aWWW?11=1W=1 a112==1 , L , a1n=1?1W?
2Wn??a=W2W?A=?Wa2W1 , L , aW22122==2n=
??12Wn?
?? L L aWi
?ij=?WL
?j?
???an1=W?
nWan2=Wn L a=Wn=11Wnn2W ?
n??
除满足:(i)正互反性:即
a1
ij>0 aij=
a( 或 aij?aji=1)ji
而且还满足:(ii)一致性:即
aaiij=
a=a? aaih
ikkj=i, j=1, 2, L njajh
则称满足上述条件的正互反对称矩阵A为一致性矩阵,简称一致阵。一致性矩阵(一致阵)性质:
性质1:A的秩Rank(A)=1
A的唯一非0的特征根为n
性质2:An的特征向量:
即有(特征向量、特征值):
??W1W1L
W1??WWW??W1W2A=?22?W
1WLWn??W12?r??
?2W??W2?n?LL?,则向量W=??
?WWL?nn?WL
WL??M
??n??W3??1
W2Wn??
??W1
W1??WWL
W12W??=?1
n
满足:AM??W1????nW1??M
LM
??WnW?2??2?
?WWn??=nW?nWWL
Wn
??1
2
Wn
??M?=???L?
?
??Wn????
?nWn??(4)
16
即:(A?nI)=0
W2,W3,…Wn启发与思考:既然一致矩阵有以上性质,即n个元素W1,构成的向量
?W1????W2?W=??L???W??n?
是一致矩阵A的特征向量,则可以把向量W归一化后的向量ω,看成是诸元素W1,W2,W3,…Wn
目标的权向量,因此,可以用求A的特征根和特征向量的办法,求出元素W1,W2,W3,…Wn相对于目标O的劝向量。
解释:一致矩阵即:n件物体M1, M2, L,Mn,它们重量分别为W1, W2 , L,Wn,将他
?W1????W2?们两两比较重量,其比值构成一致矩阵,若用重量向量W=?右乘A,则?L???W??n?
?A的特征根为n,??W1??????W2??以n为特征根的特征向量为:重量向量 W=??,则归一化后的特征向量L????W??:??n?
??W???1??W=?L?(ΣWi=1),就表示诸因素C1,C2,L,Cn对上层因素O的权重,即为???W????权向量,此种用特征向量求权向量的方法 称特征根法,?
分析:
?W1????W2?若重量向量W=?未知时,则可由决策者对物体M1, M2, L,Mn之间两两相比?M???W??n?
关系,主观作出比值的判断,或用Delphi(调查法)来确定这些比值,使A矩阵(不一定有一致性)为已知的,并记此主观判断作出的矩阵为(主观)判断矩阵,并且此(不的一致)在不一致的容许范围内,再依据:A的特征根或和特征向量W连续地依赖于矩阵连续地依赖于矩阵的
元素aij,即当aij离一致性的要求不太远时,的特征根i和特征值(向量)W与一致矩阵A的特征根λ和特征向量W也相差不大的道理:由特征向量W求权向量W的方法即为
17
三 : 数学建模入门基础
数学建模
小册子
数学建模基础 数学建模入门基础
目录
第一章优化模型………………………………………………………………………………(02)
第二章统计分析………………………………………………………………………………(05)
第三章层次分析法……………………………………………………………………………(13)
第四章数值计算………………………………………………………………………………(25)
第五章微分方程………………………………………………………………………………(26)
第六章差分方程………………………………………………………………………………(28)
第七章图论……………………………………………………………………………………(31)
第八章BP人工神经网络……………………………………………………………………(34)
第九章GM(1,1)灰色预测……………………………………………………………………(37)
1
数学建模基础 数学建模入门基础
第一章优化模型:用LINGO
简单的优化模型:
简单的优化模型,归结为微积分中的函数极值问题,可以直接用微分法求解。[www.61k.com]简单优化模型的灵敏度分析:
设有一个未知量为x的函数f(x,a1,a2...an)=0,其中a1,a2...an是未知系数(事实上是已知的),这个函数必定存在最值,最值的求法:
?f(x,a1,a2...a)=0?x(a1,a2...an是各自独立的变量)
得到x的函数x(a1,a2...an),未知数是a1,a2...an,用相对改变量衡量结果对参数的敏感程度,下面进行灵敏度分析:x对a1的敏感度记作S(x,a1),定义为
S(x,a1)=?x/xdxa≈?a1/a1da1x(dxdx(a1,a2...an)=da1da1
把a1,a2...an和x代入上式,可解得实值s=S(x,a1),即解释为当x增加1%,当s为正值时,就增加s%;当s为负值时,就减少s%。
同理可得x对a2的敏感度记作S(x,a2)。
数学规划模型:
在很多实际问题中,所能够提供的决策变量取值受到很多因素的制约,这样就产生了一般的优化模型,统称为数学规划模型。按照数学规划模型的具体特征,可以将数学规划分为:线性规划模型(目标函数和约束条件都是线性函数的优化问题);
非线性规划模型(目标函数或者约束条件是非线性的函数);
整数规划(决策变量是整数值得规划问题);
多目标规划(具有多个目标函数的规划问题);
目标规划(具有不同优先级的目标和偏差的规划问题);
动态规划(求解多阶段决策问题的最优化方法)

数学规划问题的基本形式为:
其中为决策变量向量,为目标函数(单目标规划只有一个函数,多目标规划可以理为一个向量函数的最优化问题),≤

(≥)0为约束条件,记()
2
数学建模基础 数学建模入门基础
D=()≤(≥)0为可行集,因此规划的本质就是在可行集中选择使得目标最优的点。[www.61k.com]若D=R,则该问题为无条件约束问题,可以用微分法解决(有时仅有关于决策变量的非负约束也可以归结为该类型);若D中的约束都是等式约束,则可以用Lagrange乘数法解决。但是在实际问题中,D的结构往往非常复杂,不能使用普通的微分方法解决,这时候n{}必须借助于计算软件。
规划模型的LINGO求解:
求解线性规划问题:
min=?x2+x3
s..t
x1?2x2+x3=2
x2?3x3+x4=1
x2?x3+x5=2
xj≥0,j=1,...,5
Model
min=-x2+x3;
x1-2*x2+x3=2;
x2-3*x3+x4=1;
x2-x3+x5=2;
end
result:
Globaloptimalsolutionfound.
Objectivevalue:-2.000000
Infeasibilities:0.000000
Totalsolveriterations:2
VariableValueReducedCost
X22.5000000.000000
X30.50000000.000000
X16.5000000.000000
X40.0000000.000000
X50.0000001.000000
RowSlackorSurplusDualPrice
1-2.000000-1.000000
20.0000000.000000
30.0000000.000000
40.0000001.000000
3
数学建模基础 数学建模入门基础
Rangesinwhichthebasisisunchanged:
ObjectiveCoefficientRangesCurrent
Variable
X2X3X1X4X5
Coefficient-1.0000001.000000
0.00.00.0
Allowable
Increase0.66666672.0000000.4000000INFINITYINFINITY
RighthandSideRanges
Row234
Current
RHS2.0000001.0000002.000000
AllowableIncreaseINFINITY1.000000INFINITY
AllowableDecrease6.500000INFINITY1.000000Allowable
Decrease
0.00.00.00.01.000000
Variable表示目标函数;Row表示约束条件
分析报告:LINGO经过2次迭代后得到全局最优解,目标值Objectivevalue为-1.5,全局最优解为X=(6.5,2.5,0.5,0,0),ReducedCost列出最优单纯形表中判别数所在行的变量的系数,表示当变量有微小变动时,目标函数的变化率。(www.61k.com)其中基变量的reducedcost值应为0,对于非基变量Xi,相应的reducedcost值表示当某个变量Xi增加一个单位时目标函数减少(max型问题)或增加(min型问题)的量。SlackorSurplus给出松弛变量的值。DUALPRICE(对偶价格)表示当对应约束有微小变动时,目标函数的变化率。输出结果中对应于每一个约束有一个对偶价格。若其数值为p,表示对应约束中不等式右端项若增加1个单位,目标函数将增加(max型问题)或减少(min型问题)p个单位。(基变量【有实值】时为0;非基变量【为0值】时不为0)
Rangesinwhichthebasisisunchanged:即研究当目标函数的系数和约束右端在什么范围变化时,最优基保持不变。(CurrentCoefficient【CurrentRHS】-AllowableIncrease,CurrentCoefficient【CurrentRHS】+AllowableIncrease)。INFINITY表示无穷大。
4
数学建模基础 数学建模入门基础
第二章统计分析:用matlab或SAS

统计学知识总结:
1、统计的几个基本名词:总体、样本、样本值
2、统计推断就是利用样本值来对总体的分布类型、未知参数进行估计和推断。(www.61k.com]明确的说:
由样本统计量(样本均值、样本比例、样本方差)推断总体(总体均值、总体比例、总体方差)
3、统计过程:样本—>统计量—>抽样分布—>总体分布
4、抽样分布:单正态总体的抽样分布(3个):均值未知、方差未知、均值与方差均未知
双正态总体的抽样分布(2个):均值差、方差比
5、参数估计:
正态分布的置信区间(6中情况):
单正态总体均值(方差已知)
单正态总体均值(方差未知)
单正态总体方差
6、假设检验:
单正态总体的假设检验
双正态总体的假设检验
7、方差分析(单因素)
8、回归分析正双态总体均值差(方差已知)正双态总体均值差(方差已知正双态总体方差比
判别分析:
判别分析法就是利用原有的分类信息,得到体现这种分类的函数关系式(称为判别函

5
数学建模基础 数学建模入门基础
数),然后利用该函数去判别未知样品属于哪一类。[www.61k.com]
聚类分析:
分类问题分为判别分析和聚类分析。判别分析研究事先已经建立类别的情况,即将样品或指标按已知的类别进行归类。聚类分析适用于实现没有分类的情况,即如何将样品或指标进行分类的问题。聚类分析包含的范围很广,可以有系统聚类法、动态聚类法、分裂法、最优分割法、模糊聚类法、图论聚类法、聚类预报等多种方法。
聚类分析法的原理试:首先将一定数量的样品各自看成一类,然后根据样品的亲疏程度,将亲疏程度最高的两类进行合并。然后考虑合并后的类与其他类之间的亲疏程度,再进行合并。重复这一过程,直至将所有的样品合并为一类。
主成分分析:注意建模步骤
在统计分析中有一类问题就是抽取信息的精华,这就是因子分析和主成分分析。
当要研究一个问题时,通常的做法是抽取大量的变量信息,例如,为了准确预报天气,我们抽取了大量的数据,如有1000个变量的抽样数据,然而这些数据中很多是相关的,这就是信息的冗余。信息冗余不仅带来计算上的复杂性,甚至导致计算误差增加。
主成分分析法就是从大量的信息中,选择一组个数少,且互不相关,并带有原样本的大部分的信息另一组变量。简单的说,主成分分析就是把多个指标化为少数几个综合指标的一种统计方法。
主成分分析计算步骤:
①计算相关系数矩阵
?r11?r21R=??M??rp1?r12r22Mrp2Lr1p?Lr2p??MM??Lrpp??(1)
在(3.5.3)式中,rij(i,j=1,2,…,p)为原变量的xi与xj之间的相关系数,其计算公式为
n
rij=(xki?i)(xkj?j)∑k=1
∑(xki?i)
k=1n22(x?)∑kjjnk=1(2)
因为R是实对称矩阵(即rij=rji),所以只需计算上三角元素或下三角元素即可。②计算特征值与特征向量
6
数学建模基础 数学建模入门基础
首先解特征方程λI?R=0,通常用雅可比法(Jacobi)求出特征值λi(i=1,2,L,p),并使其按大小顺序排列,即λ≥λ≥L,≥λ≥0;然后分别求出对应12p
于特征值λi的特征向量ei(i=1,2,L,p)。[www.61k.com)这里要求ei=1,即
量ei的第j个分量。∑ej=1p2ij=1,其中eij表示向
③计算主成分贡献率及累计贡献率
主成分zi的贡献率为
λi
∑λ
k=1p(i=1,2,L,p)k
累计贡献率为
∑λ
∑λ
k=1k=1pik(i=1,2,L,p)k
一般取累计贡献率达85—95%的特征值λ1,λ2,L,λm所对应的第一、第二,…,第m(m≤p)个主成分。
④计算主成分载荷
其计算公式为
lij=p(zi,xj)=λieij(i,j=1,2,L,p)(3)
得到各主成分的载荷以后,还可以按照(3.5.2)式进一步计算,得到各主成分的得分
7
数学建模基础 数学建模入门基础
?z11?z21Z=??M??zn1z12z22Mzn2Lz1m?Lz2m??MM??Lznm?(4)
更多的时候我们需要对数据进行标准化,也就是将数据归一化,即对每一列的数据除上它们的标准差,然后进行主成分分析。(www.61k.com)
在matlab中进行主成分分析:
[pc,score,latent,tsquare]=princomp(x)
PC:相对于特征值latent的特征向量。根据数据矩阵X返回因子成分PC,也就是主成分。score:主成分Yi中的元素。通过将原始数据转换到因子成分空间中得到的数据。也就是原始数据在由主成分所定义的新坐标系中的确定的数据,其大小与输入数据矩阵的大小相同。
latent:存放从大到小的特征值。
tsquare:t平方统计量,它是描述每一测量值与数据中心距离的统计量,用它可以找到数据中的极值点。
在SAS系统中主成分分析通过procprincomp过程来实现。
主成分分析方法应用实例:
1)实例1:流域系统的主成分分析(张超,1984)
表3.5.1(点击显示该表)给出了某流域系统57个流域盆地的9项变量指标。其中,x1代表流域盆地总高度(m),x2代表流域盆地山口的海拔高度(m),x3代表流域盆地周长(m),x4代表河道总长度(m),x5代表河道总数,x6代表平均分叉率,x7代表河谷最大坡度(度),x8代表河源数,x9代表流域
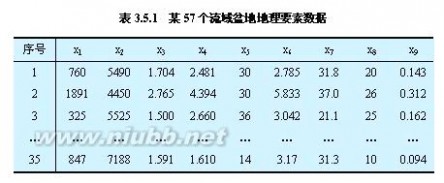
盆地面积(km2)。
(1)分析过程:
①将表3.5.1中的原始数据作标准化处理,然后将它们代入相关系数公式计算,得到相关系数矩阵(表3.5.2)。
8
数学建模基础 数学建模入门基础
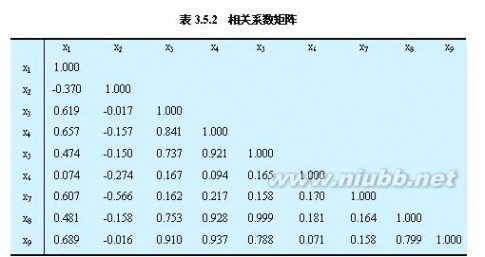
②由相关系数矩阵计算特征值,以及各个主成分的贡献率与累计贡献率(见表
3.5.3)。(www.61k.com]由表3.5.3可知,第一,第二,第三主成分的累计贡献率已高达86.5%,
故只需求出第一、第二、第三主成分z1,z2,z3
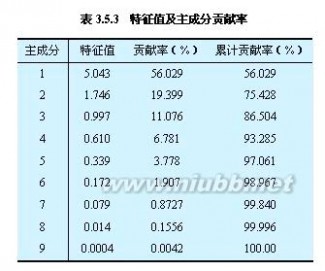

即可。
z3上的载荷(表3.5.4)。
最重要的就是回归分析:
回归分析是指对具有相关关系的现象,根据其关系形态,选择一个合适的数学模型,用来近似地表示变量间的平均变化关系的一种统计方法。
回归分析的分类:按照回归模型中变量个数分(一元回归,多元回归);按照回归曲线的形态分(线性回归,非线性回归);按照是否要求总体分布类型已知分(参数回归,非参数回归)
主要学习一元线性回归和多元线性回归
9
数学建模基础 数学建模入门基础
建模过程:①模型的参数估计②检验、预测和控制
一元线性回归模型:
模型的参数估计:
一般地,称由y=β0+β1x+ε确定的模型为一元线性回归模型,记为
?y=β0+β1x+ε?2?Eε=0,Dε=σ
其中固定的未知参数β0,β1称为回归系数,自变量x也称为回归变量,y=β0+β1x称为y对x的回归直线方程。(www.61k.com)
一元线性回归分析的主要任务
1、用试验值(样本值)对β0,β1和σ作点估计;
2、对回归系数β0,β1作假设检验;
3、在x=x0处对y作预测,对y作区间估计。
回归系数的最小二乘估计
有n组独立观测值,(xi,yi),i=
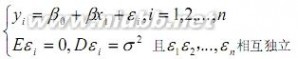
1,2,...,n。
设
记Q=Q(β0,β1)=∑ε=∑(yi?β0?β1xi)。最小二乘法就是选择β0和β12inn2
i=1i=1
?,β?=minQ(β,β)。计算得到?,β?使得Qβ的估计β010101β0,β1()
?=?β??β01???xy?xy?β1=22x?x?
1n1n1n21n2其中x=∑xi,y=∑yi,x=∑xi,xy=∑xiyi。(经验)回归方程为:ni=1ni=1ni=1ni=1
?+β?x=+β?(x?)。?=βy011
?,β?=记Qe=Qβ∑yi?β?0?β?1xi01
i=1()n(?))=∑(y?y2n2ii,称Qe为残差平方和i=1
?=Qe/(n?2)。或剩余平方和。σ的无偏估计为σ22
10
数学建模基础 数学建模入门基础
回归方程的显著性检验:
对回归方程Y=β0+β1x的显著性检验,归结为对假设H0:β1=0;H1:β1≠0进行检验。[www.61k.com]
假设H0:β1=0被拒绝,则回归显著,认为y与x存在线性关系,所求的线性回归方程有意义;否则回归不显著,y与x的关系不能用一元线性回归模型来描述,所得的回归方程也无意义。
n
U2
?i?)(回归平F检验法:当H0成立时,F=~F(1,n?2),其中U=∑(y
Qe/n?2i=1
方和)。若F>F1?α(1,n?2),拒绝H0,否则就接受H0。回归系数的置信区间:
β0和β1置信水平为1?α的置信区间分别为
???t(
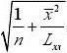
n?2)σ?+t(
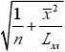
n?2)σ??β?β和0α0α
1?1??22???????β0?t1?α(
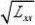
n?2)σβ0+t1?α(
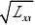
n?2)σ;?22??
QQ??
。σ2的置信水平为1?α的置信区间为?2e,2e
?χαn?2χαn?2???1?22?
预测:
?+β?x作为y的预测值。y的置信水平为1?α的预测区间为?0=β用y0的回归值y01000?0?δ(x0),y?0+δ(x0)????y?,其中δ(x0)=t1?α(
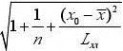
n?2)σ
2
。特别,当n很大且x0在附近取值时,y的置信水平为1?α的预测区间近似为
??
????y?σu,y+σu?eαeα?。1?1??22?
多元线性回归:
Y=Xβ+ε?
一般称?为高斯—马尔柯夫线性模型(k元线性回归模2
Eε=0,COVε,ε=σI()()n?
型),并简记为Y,Xβ,σIn。
(
2
)
11
数学建模基础 数学建模入门基础
?y1??1x11???...1x21其中Y=??,X=??...??......???y?n??1xn1x12x22...xn2x1k??β0??ε1??????...x2k?βε21,β=??,ε=??,?...??...?......??????...xnk?β?k??εn?...
y=β0+β1x1+...+βkxk称为回归平面方程。(www.61k.com]
线性模型Y,Xβ,σIn考虑的主要问题是:
(1)用试验值(样本值)对未知参数β和σ2作点估计和假设检验,从而建立y与(2)x1,x2,...,xk之间的数量关系;
(2)在x1=x01,x2=x02,...,xk=x0k处对y的值作预测与控制,即对y作区间估计。对βi和σ作估计,用最小二乘法求β0,...,βk的估计量:作离差平方和2
Q=∑(yi?β0?β1xi1?...?βkxk)
i=1n2
?=XTX选择β0,...,βk使Q达到最小。解得估计值β()(XY),得到的β?代入回归平方?1T
i
?+β?x+...+β?x,称为经验回归平面方程。β?称为经验回归系数。程得y=β011kki
多元线性回归中的检验与预测:
假设H0:β0=β1=...=βk=0。
当H0成立时,F=U/k~F(k,n?k?1)。如果F>F1?α(k,n?k?1),则Qe/n?k?1拒绝H0,认为y与x1,x2,...,xk之间显著地有线性关系;否则就接受H0,认为y与x1,x2,...,xk之间线性关系不显著。
?+β?x+...+β?x,对于给定自变量的值x,x,...,x,用?=β求出回归方程y011kk12k***
?+β?x*+...+β?x*来预测y?+β?x*+...+β?x*+ε。称y?*=β?*=β?*为y*的点预测。y011kk011kk
多元线性回归matlab命令:
确定回归系数的点估计值:b=regress(Y,X)
12
数学建模基础 数学建模入门基础
???β0?????βb=?1?
?...??β???k?
?Y1???Y2
Y=??
?...????Yn??1x11?
1x21
X=?
?......??1xn1?
x12x22...xn2
x1p??
...x2p?......?
?
...xnp??
...
求回归系数的点估计和区间估计、并检验回归模型:
[b,bint,r,rint,stats]=regress(Y,X,alpha)
Stats给出用于检验回归模型的统计量,有三个数值:相关系数r2、F值、与F对应的概率p。[www.61k.com]
判别规则:相关系数r2越接近1,说明回归方程越显著;F>F1?α(k,n?k?1)时拒绝
H0,F越大,说明回归方程越显著;与F对应的概率p<α时拒绝H0,回归模型成立。
第三章层次分析法
层次分析法(AHP-AnalyticHierachyprocess)----多目标决策方法
70年代由美国运筹学家T·L·Satty提出的,是一种定性与定量分析相结合的多目标决策分析方法论。吸收利用行为科学的特点,是将决策者的经验判断给予量化,对目标(因素)结构复杂而且缺乏必要的数据情况下,採用此方法较为实用,是一种系统科学中,常用的一种系统分析方法,因而成为系统分析的数学工具之一。基本内容:(1)多目标决策问题举例AHP建模方法
(2)AHP建模方法基本步骤(3)AHP建模方法基本算法一、问题举例:
假期旅游地点选择
暑假有3个旅游胜地可供选择。例如:P1:苏州杭州,P2北戴河,P3桂林,到底到哪个地方去旅游最好?要作出决策和选择。为此,要把三个旅游地的特点,例如:①景色;②费用;③居住;④环境;⑤旅途条件等作一些比较——建立一个决策的准则,最后综合评判确定出一个可选择的最优方案。
目标层
准则层
方案层
13
数学建模基础 数学建模入门基础
二、问题分析:
例如旅游地选择问题:一般说来,此决策问题可按如下步骤进行:
(S1)将决策解分解为三个层次,即:
目标层:(选择旅游地)
准则层:(景色、费用、居住、饮食、旅途等5个准则)
方案层:(有P1,P2,P3三个选择地点)
并用直线连接各层次。[www.61k.com]
(S2)互相比较各准则对目标的权重,各方案对每一个准则的权重。这些权限重在人的思
维过程中常是定性的。
例如:经济好,身体好的人:会将景色好作为第一选择;
中老年人:会将居住、饮食好作为第一选择;
经济不好的人:会把费用低作为第一选择。
而层次分析方法则应给出确定权重的定量分析方法。
(S3)将方案后对准则层的权重,及准则后对目标层的权重进行综合。
(S4)最终得出方案层对目标层的权重,从而作出决策。
以上步骤和方法即是AHP的决策分析方法。
三、确定各层次互相比较的方法——成对比较矩阵和权向量
在确定各层次各因素之间的权重时,如果只是定性的结果,则常常不容易被别人接受,因而Santy等人提出:一致矩阵法
即:1.不把所有因素放在一起比较,而是两两相互比较
2.对此时採用相对尺度,以尽可能减少性质不同的诸因素相互比较的困难,提高准确度。——成对比较矩阵法:
目的是,要比较某一层n个因素C1,C2, L, Cn对上一层因素O的影响(例如:旅游决策解中,比较景色等5个准则在选择旅游地这个目标中的重要性)。
採用的方法是:每次取两个因素Ci和Cj比较其对目标因素O的影响,并用aij表示,全部比较的结果用成对比较矩阵表示,即:
A=(aij)nxn, aij>0, aji=1(或aij?aij=1)aij
1
aji(1)由于上述成对比较矩阵有特点:A=(aij) , aij>0, aij=
故可称A为正互反矩阵:显然,由
例如:在旅游决策问题中:aij=1,即:aij?aji=1,故有:aji=1aji
14
数学建模基础 数学建模入门基础
C(景色)
a12==1
C(费用)2
表示:?
(?C1 景色)对目标O的重要性为1
O的重要性为2?C(费用)对目标2
故:a12=(即景色重要性为1,费用重要性为2)
a13=4==
C(景色)1
C(居住条件)3
表示:
?C1(景色)对目标O的重要性为4
?
O的重要性为1?C(居住条件)对目标3
即:景色为4,居住为1。(www.61k.com]
a23=7==
C(费用)2
C(居住条件)3
表示:
?C2(费用)对目标O的重要性为7
?
O的重要性为1?C(居住条件)对目标3
即:费用重要性为7,居住重要性为1。
?1
??2?因此有成对比较矩阵:A=?????147123
33?
?55???11?
?11?
?
??问题:稍加分析就发现上述成对比较矩阵的问题:①即存在有各元素的既然:a12=
C11C411=?a21=2; a13=1=?a31==C22C31a134
C2a2112
====8=C3a31C3
1
C2
所以应该有:a23=
而不应为矩阵A中的a23=2
,因:n个元素比较次数为:Cn=
②成对比较矩阵比较的次数要求太次,
n(n?1)
2!
因此,问题是:如何改造成对比较矩阵,使由其能确定诸因素C1, L, Cn对上层因素O的权重?
对此Saoty提出了:在成对比较出现不一致情况下,计算各因素C1, L, Cn对因素(上
15
数学建模基础 数学建模入门基础
层因素)O的权重方法,并确定了这种不一致的容许误差范围。(www.61k.com)
为此,先看成对比较矩阵的完全一致性——成对比较完全一致性四:一致性矩阵
Def:设有正互反成对比较矩阵:
???aWWW?11=1W=1 a112==1 , L , a1n=1?1W?
2Wn??a=W2W?A=?Wa2W1 , L , aW22122==2n=
??12Wn?
?? L L aWi
?ij=?WL
?j?
???an1=W?
nWan2=Wn L a=Wn=11Wnn2W ?
n??
除满足:(i)正互反性:即
a1
ij>0 aij=
a( 或 aij?aji=1)ji
而且还满足:(ii)一致性:即
aaiij=
a=a? aaih
ikkj=i, j=1, 2, L njajh
则称满足上述条件的正互反对称矩阵A为一致性矩阵,简称一致阵。一致性矩阵(一致阵)性质:
性质1:A的秩Rank(A)=1
A的唯一非0的特征根为n
性质2:An的特征向量:
即有(特征向量、特征值):
??W1W1L
W1??WWW??W1W2A=?22?W
1WLWn??W12?r??
?2W??W2?n?LL?,则向量W=??
?WWL?nn?WL
WL??M
??n??W3??1
W2Wn??
??W1
W1??WWL
W12W??=?1
n
满足:AM??W1????nW1??M
LM
??WnW?2??2?
?WWn??=nW?nWWL
Wn
??1
2
Wn
??M?=???L?
?
??Wn????
?nWn??(4)
16
数学建模基础 数学建模入门基础
即:(A?nI)=0
W2,W3,…Wn启发与思考:既然一致矩阵有以上性质,即n个元素W1,构成的向量
?W1????W2?W=??L???W??n?
是一致矩阵A的特征向量,则可以把向量W归一化后的向量ω,看成是诸元素W1,W2,W3,…Wn
目标的权向量,因此,可以用求A的特征根和特征向量的办法,求出元素W1,W2,W3,…Wn相对于目标O的劝向量。[www.61k.com)
解释:一致矩阵即:n件物体M1, M2, L,Mn,它们重量分别为W1, W2 , L,Wn,将他
?W1????W2?们两两比较重量,其比值构成一致矩阵,若用重量向量W=?右乘A,则?L???W??n?
?A的特征根为n,??W1??????W2??以n为特征根的特征向量为:重量向量 W=??,则归一化后的特征向量L????W??:??n?
??W???1??W=?L?(ΣWi=1),就表示诸因素C1,C2,L,Cn对上层因素O的权重,即为???W????权向量,此种用特征向量求权向量的方法 称特征根法,?
分析:
?W1????W2?若重量向量W=?未知时,则可由决策者对物体M1, M2, L,Mn之间两两相比?M???W??n?
关系,主观作出比值的判断,或用Delphi(调查法)来确定这些比值,使A矩阵(不一定有一致性)为已知的,并记此主观判断作出的矩阵为(主观)判断矩阵,并且此(不的一致)在不一致的容许范围内,再依据:A的特征根或和特征向量W连续地依赖于矩阵连续地依赖于矩阵的
元素aij,即当aij离一致性的要求不太远时,的特征根i和特征值(向量)W与一致矩阵A的特征根λ和特征向量W也相差不大的道理:由特征向量W求权向量W的方法即为
17
数学建模基础 数学建模入门基础
,并由此引出一致性检查的方法。[www.61k.com)特征向量法特征向量法,并由此引出,并由此引出一致性检查的方法一致性检查的方法。
问题:Remark
以上讨论的用求特征根来求权向量W的方法和思路,在理论上应解决以下问题:1.一致阵的性质1是说:一致阵的最大特征根为n(即必要条件),但用特征根来求特征
向量时,应回答充分条件:即正互反矩阵是否存在正的最大特征根和正的特征向量?且如果正互反矩阵A的最大特征根λmax=n时,A是否为一致阵?
2.用主观判断矩阵的特征根λ和特征向量W连续逼近一致阵A的特征根λ和特征向量W时,即:由limk=λk→k
得到:limWk→∞k=W
即:limAk=Ak→∞
是否在理论上有依据。
3.一般情况下,主观判断矩阵A在逼近于一致阵A的过程中,用与A接近的A*来代替A,即有A*≈A,这种近似的替代一致性矩阵A的作法,就导致了产生的偏差估计问题,即一致性检验问题,即要确定一种一致性检验判断指标,由此指标来确定在什么样的允许范围内,主观判断矩阵是可以接受的,否则,要两两比较构造主观判断矩阵。此问题即一致性检验问题的内容。
以上三个问题:前两个问题由数学严格比较可获得(见教材P325,定理1、定理2)。第3个问题:Satty给出一致性指标(TH1,TH2介绍如下:)
附:
Th1:(教材P326,perronTh比隆1970)对于正矩阵A(A的所有元素为正数)
(1)A的最大特征根是正单根λ;
(2)λ对应正特征向量W(W的所有分量为正数)
Ake(3)limTk=Wk→∞eAe?1????1?其中:e=??为半径向量,W是对应λ的归一化特征向量L???1???
证明:(3)可以通过将A化为标准形证明
Th2:n阶正互反阵A的最大特征根λ≥n;
当λ=n时,A是一致阵
五、一致性检验——一致性指标:
——C?I的定义:1.一致性检验指标的定义和确定.一致性检验指标的定义和确定——
18
数学建模基础 数学建模入门基础
当人们对复杂事件的各因素,采用两两比较时,所得到的主观判断矩阵A,一般不可直接保证正互反矩阵A就是一致正互反矩阵A,因而存在误差(及误差估计问题)。[www.61k.com]这种误差,必然导致特征值和特征向量之间的误差(λ?λ)及W-W。此时就导致问题
(上述问题中λmax是主观判断矩阵A的特征AW=λmaxW与问题AW=nW之间的差别。
值,W是带有偏差的相对权向量)。这是由判断矩阵不一致性所引起的。
因此,为了避免误差太大,就要衡量主观判断矩阵的一致性。
因为:
①当主观判断矩阵为一致阵A时就有:[)]
k=∑λk=∑akk=∑1=n∑knkk=1=1=1=1nnnnA为一致阵时有:aii=1
此时存在唯一的非λ=λmax=n
(由一致阵性质1:Rark(4)=1,A有唯一非O最大特征根且λmax=n)
②当主观判断矩阵A不是一致矩阵时,此时一般有:λmax≥n
此时,应有:(Th2)
λmax+
即:k≠λmax∑λh=∑aii=nλmax?n=?
k≠max∑λk
所以,可以取其平均值作为检验主观判断矩阵的准则,一致性的指标,即:
显然:
(1)当λmax=n时,有:C?I=0,为完全一致性
(2)λ?nC?I=max=n?1?k≠max∑λkn?1C?I值越大,主观判断矩阵A的完全一致性越差,即:A偏离A越远(用特征
向量作为权向量引起的误差越大)
(3)一般C?I≤0?1,认为主观判断矩阵A的一致性可以接受,否则应重新进行两
两比较,构造主观判断矩阵。
——R?I2.随机一致性检验指标.随机一致性检验指标——
问题:实际操作时发现:主观判断矩阵的维数越大,判断的一致性越差,故应放宽对高
19
数学建模基础 数学建模入门基础
维矩阵的一致性要求。(www.61k.com)于是引入修正值R?I来校正一致性检验指标:即定义R?I的修正值表为:
的维数R?I
10.00
20.00
30.58
40.96
51.12
61.24
71.32
81.41
91.45
并定义新的一致性检验指标为:C?R=
C?IR?I
随机一致性检验指标——R?I的解释:
为确定A的不一致程度的容许范围,需要确定衡量A的一致性指示C?I的标准。于是Satty又引入所谓随机一致性指标R?I,其定义和计算过程为:①
中随机取值,对固定的n,随机构造正互反阵A′,其元素a′ij(i<j)从1~9和1~
′且满足a′ij与a′ji的互反性,即:aij=
′ji
′=1.,且aii
②
③④
然后再计算A′的一致性指标C?I,因此A′是非常不一致的,此时,C?I值相当大.如此构造相当多的A′,再用它们的C?I平均值作为随机一致性指标。
Satty对于不同的n(n=1~11),用100~500个样本A′计算出上表所列出的随机一致性指标R?I作为修正值表。
——一致性比率C?R。3.一致性检验指标的定义一致性检验指标的定义————一致性比率
由随机性检验指标C?R可知:
当n=1, 2时,R?I=0,这是因为1,2阶正互反阵总是一致阵。
对于n≥3的成对比较阵A,将它的一致性指标C?I与同阶(指n相同)的随机一致性指标R?I之比称为一致性比率——简称一致性指标,即有:定义:C?R=
C?IC?I
:C?R=R?IR?I
C?I
当:C?R=<0?1时,认为主观判断矩阵的不一致程度在容许范围之
R?I
内,可用其特征向量作为权向量。否则,对主观判断矩阵A重新进行成对比较,构重新的主观判断矩阵A。注:上式C?R=
C?I
<0?1的选取是带有一定主观信度的。R?I
六、标度——比较尺度解:
在构造正互反矩阵时,当比较两个可能是有不同性质的因素Ci和Cj对于上层因素
20
数学建模基础 数学建模入门基础
O的影响时,採用什么样的相对刻度较好,即aij的元素的值在(1~9)或(1~)或更多的数字,Satty提出用1~9尺度最好,即aij取值为1~9或其互反数1~,心理学家也提出:人们区分信息等级的极限解能力为7±2。[www.61k.com)可见对n×n阶矩阵,只需作出n(n?1)个判断值即可2
标度aij定
因素与因素相同重要
因素i比因素j稍重要
因素i比因素j较重要
因素i比因素j非常重要
因素i比因素j绝对重要
因素i与因素j的重要性的比较值介于上述两
个相邻等级之间
因素j与因素i比较得到判断值为aij的互反
数,义135792,4,6,8,倒数1,11111111, , ,, , , , 23456789aji=1
aijaii=1
注:以上比较的标度Satty曾用过多种标度比较层,得到的结论认为:1~9尺度不仅在较简单的尺度中最好,而且比较的结果并不劣于较为复杂的尺度。Satty曾用的比较尺度为:
①1~3,1~5,1~6,…,1~11,以及
②(d+0.1)~(d+0.9),其中d=1, 2, 3, 4
③1p~9P,其中P=2, 3, 4, 5…
等共27种比较尺度,对放在不同距离处的光源亮度进行比较判断,并构造出成对比较矩阵,计算出权向量。同时把计算出来的这些权向量与按照物理学中光强度定律和其他物理知识得到的实际权向量进行对比。结果也发现1~9的比较标度不仅简单,而效果也较好(至少不比其他更复杂的尺度差)
因而用1~9的标度来构造成对比较矩阵的元素较合适。
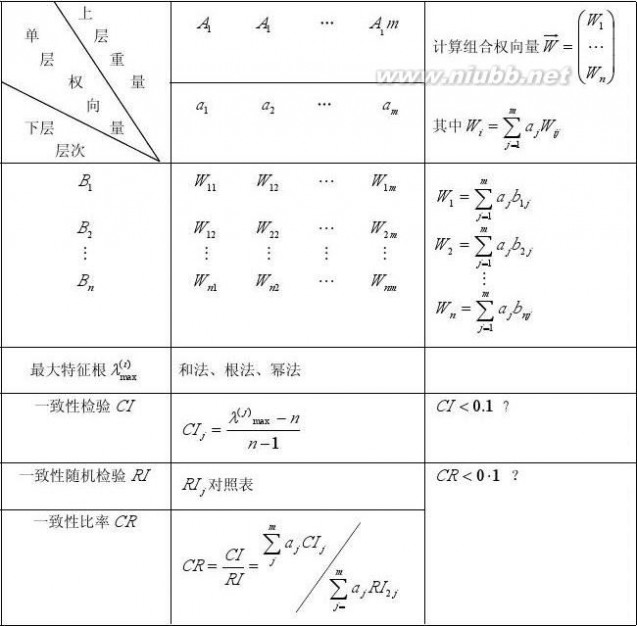
七、组合权向量的计算——层次总排序的权向量的计算
层次分析法的基本思想:
(1)计算出下一层每个元素对上一层每个元素的权向量W
def:层次总排序,计算同一层次所有元素对最高层相对重要性的排序权值。
当然要先:①构造下一层每个元素对上一次每个元素的成对比较矩阵
②计算出成对比较矩阵的特征向量(和法,根法,幂法)
③由特征向量求出最大特征根λmax(由和法,根法,幂法求得)
21
数学建模基础 数学建模入门基础
④用最大特征根λmax用方式
C?I=
λmax?nC?R
及C?R=对成对比较
n?1R?I
矩阵进行一致性检,并通过。(www.61k.com)
(2)并把下层每个元素对上层每个元素的权向量按列排成以下表格形式:例,假定:
上层A有m个元素,A1, A2, L, Am,且其层次总排序权向量为
a1, a2, L, am,下层B有n个元素B1, B2, L, Bn,则按Bj对
的单排序权向量的列向量为bij,即有:
Ai个元素
A1
层次
A1a2b12b22Mbn2
……
A1mamb1mb2mMbnm
B层总是排序权重(权向
量、列向量)
a1
B1B2
MBn
b11b12Mbn1
LLML
W1=∑ajb1jW2=∑ajb2j
j=1j=1m
m
M
Wn=∑ajbnj
j=1
m
λmaxC?
计算出最大特根(方法:和法、根法、幂法)
一致性检验
C?I=
λmax?nn?1
检验CR<0?1否?
C?
一致性检验比率
C?I∑C?R==jR?I
m
ajCI3
ajRIj∑j
=
m
注:①若下层元素Bk与上层元素Aj无关系时,取bkj=0
②总排序权向量各分量的计算公式:Wi=
∑ab
j=1
m
jij
(i=1,L,n)
(3)对层次总排序进行一致性检验:从高层到低层逐层进行,如果
如果B层次某些元素对Aj单的排序的一致性指标为CIj,相应的平均随机一致性指标
22
数学建模基础 数学建模入门基础
为RIj,则B层总排序随机一致性比率为:C?R=ajCIj∑
j
ajRIj∑
j=1=1mm
当CR<0?1时,认为层次总排序里有满意的一致性,否则应重新调整判断矩阵的元素取值。[www.61k.com)
八、层次分析法的基本步骤:
(S1将有关因素按照属性自上而下地分解成若干层次:
同一层各因素从属于上一层因素,或对上层因素有影响,同时又支配下一层的因素或受到下层因素的影响。
最上层为目标层(一般只有一个因素),最下层为方案层或对象层/决策层,中间可以有1个或几个层次,通常为准则层或指标层。
当准则层元素过多(例如多于9个)时,应进一步分解出子准则层。
(S2)构造成对比较矩阵,以层次结构模型的第2层开始,对于从属于(或影响及)上一层每个因素的同一层诸因素,用成对比较法和1~9比较尺度构造成对比较矩阵,直到最下层。
(S3)计算(每个成对比较矩阵的)权向量并作一致性检验
①对每一个成对比较矩阵计算最大特征根λmax及对应的特征向量(和法、根法、幂法
?W1???等)W=?M??W??n?
②利用一致性指标C?I,随机一致性指标C?R和一致性比率作一致性检验
C?I???CR=?R?I??
?W1???③若通过检验(即C?R<0.1,或C?I<0.1)则将上层出权向量W=?M?归一化
?W??n?
之后作为(Bj到Aj)的权向量(即单排序权向量)
④若C?R<0.1不成立,则需重新构造成对比较矩阵
(S4)计算组合权向量并作组合一致性检验——即层次总排序
?W1???①利用单层权向量的权值Wj=?M?j=1, L, m构组合权向量表:并计算出特征根,
?W??n?
组合特征向量,一致性
23
数学建模基础 数学建模入门基础
?W1???
②若通过一致性检验,则可按照组合权向量W=?L?的表示结果进行决策
?W??n?
?W1???T
(=?L?中Wi中最大者的最优),即:W*=maxW:i∈(W1,L,Wn)
?W??n?
{}
③若未能通过检验,则需重新考虑模型或重新构造那些一致性比率,CR较大的成对
比较矩阵
24
数学建模基础 数学建模入门基础
第四章数值计算:用matlab

最重要的是拟合和插值:
问题:给定一批数据点(输入变量与输出变量的数据),需确定满足特定要求的曲线或曲面。[www.61k.com]如果输入变量和输出变量都只有一个,则属于一元函数的拟合和插值;而若输入变量有多个,则为多元函数的拟合和插值(有点回归分析的意思)
解决方案:
(1)若要求所求曲线(面)通过所给所有数据点,就是插值问题;
(2)若不要求曲线(面)通过所有数据点,而是要求它反映对象整体的变化趋势,这就是数据拟合,又称曲线拟合或曲面拟合。
注意:函数插值与曲线拟合都是要根据一组数据构造一个函数作为近似,由于近似的要求不同,二者的数学方法上是完全不同的。
用matlab进行拟合:
用matlab作线性最小二乘拟合,作多项式f(x)=a1xm+...+amx+am+1拟合
a=polyfit(x,y,m)
用matlab进行插值:
一维插值函数:yi=interp1(x,y,xi,'method')method为插值方法;
二维插值函数:z=interp2(x0,y0,z0,x,y,’method’)
解线性方程组:
数值积分:
常微分方程数值解法:
25
数学建模基础 数学建模入门基础
第五章微分方程:
动态过程的变化规律一般要用微分方程建立的动态模型来描述。(www.61k.com]动态连续的。
对于某些实际问题,建模的主要目的并不是要寻求动态过程每个瞬时的性态,而是研究某种意义下稳定状态的特征,特别是当时间充分长以后动态的变化趋势。这就是微分方程稳定性问题。
微分方程稳定性理论:
一阶方程的平衡点及稳定性:
设有微分方程
&(t)=f(x)x
右端不含字变量t,称为自治方程.代数方程(1)
f(x)=0(2)
的实根x=x0称为方程(1)的平衡点(或奇点),它也是(1)的解(奇解)。
如果存在某个邻域,使方程(1)的解x(t)从这个邻域内的某个x(0)出发,满足
limx(t)=x0t→∞(3)
则称平衡点x0是稳定的(稳定性理论中称渐进稳定);;否则,称x0是不稳定的(不渐进稳定)。判断平衡点x0是否稳定通常有两种方法:利用定义即(3)式称间接法。不求方程(1)的解x(t),因而不利用(3)式的方法称直接法。下面介绍直接法:
将f(x)在x0点作Taylor展开,只取一次项,方程(1)近似为
&(t)=f′(x0)(x?x0)x
(4)称为(1)的近似线性方程,x0也是方程(4)的平衡点.(4)关于x0点稳定性有如下结论:
若f′(x0)<0,则x0对于方程(4)和(1)都是稳定的;
若f′(x0)>0,则x0对于方程(4)和(1)都是不稳定的。
注:x0点对方程(4)稳定性很容易由定义(3)证明:记f′(x0)=a,则(4)的一般解为
x(t)=ceat+x0
其中常数c由初始条件确定,显然,a<0时(3)式成立。
二阶方程的平衡点和稳定性:
二阶方程可用两个一阶方程表为(5)
26
数学建模基础 数学建模入门基础
&1(t)=f(x1,x2)??x?
&2(t)=g(x1,x2)??x
右端不显含t,是自治方程.
代数方程组
(6)
??f(x1,x2)=0???g(x1,x2)=0
(7)
的实根x1=x1,x2=x2称为方程(6)的平衡点,记作P0x1,x2
(
00
)
如果存在某个邻域,使方程(6)的解x1(t),x2(t)从这个邻域内的某个(x1(0),x2(0))出发,满足
limx1(t)=x10
t→∞t→∞
limx2(t)=x
2
(8)
则称平衡点P0是稳定的(渐进稳定);否则,称P0是不稳定的(不渐进稳定)。[www.61k.com)先看线性常系数方程
&1(t)=a1x1+a2x2??x?
&2(t)=b1x1+b2x2??x
(9)
(非齐次方程组,可用平移的方法(x1=u1+c1,x2=u2+c2)化为齐次方程组)系数矩阵记作
?a1A=?
?b1a2??b2?
(10)
为研究方程(9)的唯一平衡点P0(0,0)的稳定性,假定A的行列式
detA≠0
(11)
P0(0,0)的稳定性由(9)的特征方程
det(A?λI)=0
的根λ(特征根)决定。方程(12)可以写成更加明晰的形式
(12)
?λ2+pλ+q=0?
?p=?(a1+b2)?q=detA?
将特征根记作λ1,λ
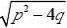
2,则
(13)
λ1,λ2=
1
?p±2
((14)
27
数学建模基础 数学建模入门基础
方程(9)的一般解具有形式
c1eλ1t+c2eλ2t(λ1≠λ2)
或
c1eλ1t+c2teλ1t(λ1=λ2)
c1,c2为任意常数.
按照稳定性的定义(8)式可知,当λ1,λ2均为负数或均有负实部时P0(0,0)是稳定平衡点;而当λ1,λ2有一个为正数或有正实部时P0(0,0)是不稳定平衡点。[www.61k.com]在条件(11)下λ1,
λ2均不为零.
按上述理论可得根据特征方程的系数p,q的正负来判断平衡点稳定性的准则:若p>0,q>0,则平衡点稳定;若p<0,q<0,则平衡点不稳定.
对一般的非线性方程(6),仍可在平衡点作一次Taylor展开,得常系数的近似线性方程来讨论。
第六章差分方程:
差分方程:差分方程反映的是关于离散变量的取值与变化规律。通过建立一个或几个离散变量取值所满足的平衡关系,从而建立差分方程。动态离散的建立差分方程。差分方程常用解法与差分方程稳定性:常系数线性差分方程的解:
方程a0xn+k+a1xn+k?1+...+akxn=b(n)
其中a0,a1,...,ak为常数,称方程(8)为常系数线性方程。
又称方程a0xn+k+a1xn+k?1+...+akxn=0
为方程(8)对应的齐次方程。
如果(9)有形如xn=λn的解,带入方程中可得:
(9)(8)
a0λk+a1λk?1+...+ak?1λ+ak=0
称方程(10)为方程(8)、(9)的特征方程。
显然,如果能求出(10)的根,则可以得到(9)的解。基本结果如下:
1、若(10)有k个不同的实根,则(9)有通解:
n
n
n
(10)
xn=c1λ1+c2λ2+...+ckλk,
28
数学建模基础 数学建模入门基础
2、若(10)有m重根λ,则通解中有构成项:
(c1+c2n+...+cmnm?1)λ
3、若(10)有一对单复根???nλ=α±iβ,令:λ=ρe±i?,ρ=2+β2,?=arctanβ则(9)的通解中有构成项:α
c1ρcos?n+c2ρnsin?n?n?
4、若有m重复根:λ=α±iβ,λ=ρe±iφ,则(9)的通项中有构成项:
????(c1+c2n+...+cmn
?m?1)ρcos?n+(cm+1+cm+2n+...+c2mnm?1)ρnsin?nn综上所述,由于方程(10)恰有k个根,从而构成方程(9)的通解中必有k个独立的任意
常数。[www.61k.com]通解可记为:xn。如果能得到方程(8)的一个特解:xn,则(8)必有通解:*
xn=xn+xn
(1)的特解可通过待定系数法来确定。
n?*(11)例如:如果b(n)=bpm(n),pm(n)为n的多项式,则当b不是特征根时,可设成形如
bnqm(n)形式的特解,其中qm(n)为m次多项式;如果b是r重根时,可设特解:bnnrqm(n),将其代入(8)中确定出系数即可。
差分方程的z变换解法:
对差分方程两边关于xn取Z变换,利用xn的Z变换F(z)来表示出xn+k的Z变换,然后通过解代数方程求出F(z),并把F(z)在z=0的解析圆环域中展开成洛朗级数,其系数就是所要求的xn
例1设差分方程xn+2+3xn+1+2xn=0,x0=0,x1=1,求xn
2解:解法1:特征方程为λ+3λ+2=0,有根:λ1=?1,λ2=?2
故:xn=c1(?1)n+c2(?2)n为方程的解。
由条件x0=0,x1=1得:xn=(?1)?(?2)
解法2:设F(z)=Z(xn),方程两边取变换可得:nn
29
数学建模基础 数学建模入门基础
1z2(F(z)?x0?x1.)+3z(F(z)?x0)+2F(z)=0z
z由条件x0=0,x1=1得F(z)=2z+3z+2
由F(z)在z>2中解析,有
∞∞∞11112kk1F(z)=z(?)=?=∑(?1)k?∑(?1)k=∑(?1)k(1?2k)z?kz+1z+21+11+2k=0zzk=0k=0
zz
所以,xn=(?1)n?(?2)n
二阶线性差分方程组:
设z(n)=(xnab),A=(),形成向量方程组yncd
z(n+1)=Az(n)
则
(13)即为(12)的解。[www.61k.com)(12)(13)z(n+1)=Anz(1)
为了具体求出解(13),需要求出A,这可以用高等代数的方法计算。常用的方法有:
(1)如果A为正规矩阵,则A必可相似于对角矩阵,对角线上的元素就是A的特征值,相似变换矩阵由A的特征向量构成:n
A=p?1Λp,An=p?1Λnp,∴z(n+1)=(p?1Λnp)z(1)。
(2)将A分解成A=ξη,ξ,η/,为列向量,则有
An=(ξ.η/)n=ξ.η/..ξ.η/...ξ.η=(ξ/η)n?1.
从而,z(n+1)=Az(1)=(ξη)n/n?1.Az(1)
n(3)或者将A相似于约旦标准形的形式,通过讨论A的特征值的性态,找出A的内
在构造规律,进而分析解z(n)的变化规律,获得它的基本性质。
关于差分方程稳定性的几个结果:
1、k阶常系数线性差分方程(8)的解稳定的充分必要条件是它对应的特征方程(10)所有的特征根λi,i=1,2...k满足λi<1
2、一阶非线性差分方程
30
数学建模基础 数学建模入门基础
xn+1=f(xn)
(14)的平衡点x由方程x=f(x)决定,
将f(xn)在点x处展开为泰勒形式:??(14)??
f(xn)=f(x)(xn?x)+f(x)
故有:f(x)<1时,(14)的解x是稳定的,/??/???(15)
f(x)>1时,方程(14)的平衡点x是不稳定的。[www.61k.com)/??
第七章图论
基本概念和名词:
1、图:由若干个不同的点(顶点或节点)与其中某些顶点的连线所组成的图形
图的表示:G=G(V,E),其中V=V(G)为顶点集,E=E(G)为边集,?e∈E,e联结V中的两个顶点。
2、权:图中的每条边都有一个具体的数与之对应,这些数为权,带权的图为赋权图或网络
3、边与弧:两点之间不带箭头的连线称为边,带箭头的连线称为弧
4、无向图:一个图G是由顶点和边构成的
5、有向图:一个图G是由顶点和弧构成的
设V和E分别是图的顶点的集合和边的集合,V={v1,...,vn},E={e1,...,em};弧的集合为A={a1,...,am}
6、链:在无向图中,点与边的交错序列(vi1,ei1,vi2,...,vik?1,vik)称为连结vi1和vik的链。(eit为连结vit和vit+1的边)
7、路径:(vi1,ei1,vi2,...,vik?1,vik)是有向图中一条链(ait为从vit指向vit+1的弧),称之为从vi1到vik的路径。
8、回路:闭合的路径称为回路。
9、圈:闭合的链称为圈。
10、连通图:图G中任何两个点之间至少有一条链,称G为连通图。
11、树:一个无圈的连通图称为树
31
数学建模基础 数学建模入门基础
12、生成树:若G1=(V1,E1)是连通图G2=(V2,E2)的生成子图(即V1=V2,E1?E2),且G1本身是树,则称G1为G2的生成树。[www.61k.com)
13、邻接矩阵:bij表示图G中从顶点vi到vj的弧(无向图只考虑vi与vj间的边)的数目,则矩阵B=bij称为图G的邻接矩阵。
14、带权邻接矩阵:以wij表示网络G中从顶点vi到vj的弧的权(无向网只考虑vi与vj间的边的权),当vi到vj无弧或边时,wij=∞,则矩阵W=wij称为图G的带权邻接矩阵。
图论中最常用的知识点:最短路问题、最小生成树问题、遍历性问题和图的匹配问题。这里仅简单介绍前两个问题的解决方法。
1、最短路问题
两个指定顶点之间的最短路径
问题如下:给出了一个连接若干个城镇的铁路网络,在这个网络的两个指定城镇间,找一条最短铁路线。
以各城镇为图G的顶点,两城镇间的直通铁路为图G相应两顶点间的边,得图G。对G的每一边e,赋以一个实数w(e)—直通铁路的长度,称为e的权,得到赋权图G。G的子图的权是指子图的各边的权和。问题就是求赋权图G中指定的两个顶点u0,v0间的具最小权的轨。这条轨叫做u0,v0间的最短路,它的权叫做u0,v0间的距离,亦记作d(u0,v0)。
求最短路已有成熟的算法:迪克斯特拉(Dijkstra)算法,其基本思想是按距u0从近到远为顺序,依次求得u0到G的各顶点的最短路和距离,直至v0(或直至G的所有顶点),算法结束。为避免重复并保留每一步的计算信息,采用了标号算法。下面是该算法。
(i)令l(u0)=0,对v≠u0,令l(v)=∞,S0={u0},i=0。
(ii)对每个v∈ii=V/Si,用minl(v),l(u)+w(uv)代替l(v)。计算u∈Si()()(){}
min{l(v)},把达到这个最小值的一个顶点记为ui+1,令Si+1=SiU{ui+1}。u∈Si
(iii)若i=V?1,停止;若i<?1,用i+1代替,转(ii)。i
算法结束时,从u0到各顶点v的距离由v的最后一次的标号l(v)给出。在v进入Si之前的标号l(v)叫T标号,v进入Si时的标号l(v)叫P标号。算法就是不断修改各项点的T标号,直至获得P标号。若在算法运行过程中,将每一顶点获得P标号所由来的边在图上
32
数学建模基础 数学建模入门基础
标明,则算法结束时,至各项点的最短路也在图上标示出来了。[www.61k.com]
每对顶点之间的最短路径
计算赋权图中各对顶点之间最短路径,显然可以调用Dijkstra算法。具体方法是:每次以不同的顶点作为起点,用Dijkstra算法求出从该起点到其余顶点的最短路径,反复执行次这样的操作,就可得到从每一个顶点到其它顶点的最短路径。这种算法的时间复杂度为。第二种解决这一问题的方法是由FloydRW提出的算法,称之为Floyd算法。Floyd算法的基本思想是:递推产生一个矩阵序列A0,A1,...,Ak,...,An,其中Ak(i,j)表
示从顶点vi到vj顶点的路径上所经过的顶点序号不大于k的最短路径长度。
计算时用迭代公式:
Ak(i,j)=min(Ak?1(i,j),Ak?1(i,k),Ak?1(k,j))
k是迭代次数,i,j,k=1,2,...,n。
最后,当k=n时,An即是各顶点之间的最短通路值。
2、最小生成树与Kruskal算法思想
最小生成树:在赋权图G中,求一棵生成树使其总权最小,称此为图G的最小生成树。Kruskal算法思想及步骤:每次添加权尽量小的边,使新的图无圈,直到生成一棵树为止,便得最小生成树。
算法步骤如下:
1)把赋权图G中的边按权的非减次序排列。
2)按1)排列的次序检查G中的每一条边,如果这条边与已得到的边不产生圈,则取这一条边为解的一部分。
3)若已取到n?1条边,算法终止。此时以V为顶点集,以取到的n?1条边为边集的图即为最小生成树。
Dijkstra的matlab实现代码
function[d,DD]=dijkstra(D,s)
%Dijkstra最短路算法Matlab程序用于求从起始点s到其它各点的最短路
%D为赋权邻接矩阵
%d为s到其它各点最短路径的长度
%DD记载了最短路径生成树
[m,n]=size(D);
d=inf.*ones(1,m);
d(1,s)=0;
dd=zeros(1,m);
dd(1,s)=1;
33
数学建模基础 数学建模入门基础
y=s;
DD=zeros(m,m);
DD(y,y)=1;
counter=1;
whilelength(find(dd==1))<M
fori=1:m
ifdd(i)==0
d(i)=min(d(i),d(y)+D(y,i));
end
end
ddd=inf;
fori=1:m
ifdd(i)==0&&d(i)<DDD
ddd=d(i);
end
end
yy=find(d==ddd);
counter=counter+1;
DD(y,yy(1,1))=counter;
DD(yy(1,1),y)=counter;
y=yy(1,1);
dd(1,y)=1;
end
第八章BP人工神经网络:
人工神经网络:指模拟人脑神经系统的结构和功能,运用大量的处理部件,由人工方式建立起来的网络系统。[www.61k.com]可以有多个输入,同时可以有多个输出。
用于一些高度非线性的数据,达到预测的效果;对于线性的数据,我们可以是使用线性回归的方法来计算。
M-P模型:
人工神经元是组成人工神经网络的基本处理单元,简称为神经元,就是一个M-P模型

:
34
数学建模基础 数学建模入门基础
?n?vi=f?∑wjivj??j=0?
其中w0i=?θ,v0=1
MP模型学习算法(Hebb学习规则):
对于人工神经网络而言,这种学习归结为神经元连接权的变化。[www.61k.com]调整wij的原则为:若第i和第j个神经元同时处于兴奋状态,则它们之间的连接应当加强,即:
?wij=αuivj
这一规则与“条件反射”学说一致,并已得到神经细胞学说的证实。α是表示学习速率的比例常数。
B-P模型:
(1)神经网络的定义简介
神经网络是由多个神经元组成的广泛互连的神经网络,能够模拟生物神经系统真实世界及物体之间所做出的交互反应。人工神经网络处理信息是通过信息样本对神经网络的训练,使其具有人的大脑的记忆,辨识能力,完成名种信息处理功能。它不需要任何先验公式,就能从已有数据中自动地归纳规则,获得这些数据的内在规律,具有良好的自学习,自适应,联想记忆,并行处理和非线性形转换的能力,特别适合于因果关系复杂的非确定性推理,判断,识别和分类等问题。对于任意一组随机的,正态的数据,都可以利用人工神经网络算法进行统计分析,做出拟合和预测。
人工神经网络是由神经元广泛互连构成的,不同的连接方式就构成了网络的不同连接模型。常用的有以下几种:前向网络、从输出层到输入层有反馈的网络、层内有互连的网络、互连网络。
B-P模型是一种用于前向多层神经网络的反传学习算法。B-P算法用于多层网络,网络中不仅有输入层节点及输出层节点,而且还有一层至多层隐层节点。
基于误差反向传播(Backpropagation)算法的多层前馈网络(Multiple-layerfeedforwardnetwork,简记为BP网络),是目前应用最成功和广泛的人工神经网络。
(2)BP模型的基本原理
学习过程中由信号的正向传播与误差的逆向传播两个过程组成。正向传播时,模式作用于输入层,经隐层处理后,传入误差的逆向传播阶段,将输出误差按某种子形式,通过隐层向输入层逐层返回,并“分摊”给各层的所有单元,从而获得各层单元的参考误差或称误差信号,以作为修改各单元权值的依据。权值不断修改的过程,也就是网络学习过程。此过程一直进行到网络输出的误差准逐渐减少到可接受的程度或达到设定的学习次数为止。BP网络模型包括其输入输出模型,作用函数模型,误差计算模型和自学习模型。
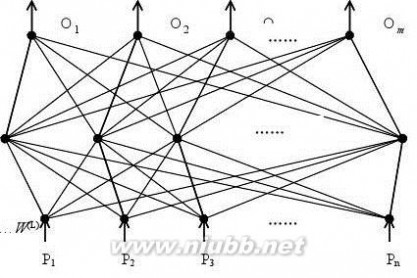
BP网络由输入层,输出层以及一个或多个隐层节点互连而成的一种多层网,这种结构使多层前馈网络可在输入和输出间建立合适的线性或非线性关系,又不致使网络输出限制在-1和1之间.见图(1)。
35
数学建模基础 数学建模入门基础
输出层隐含层输入层(大于等于一层)W1图1BP网络模型(3)BP神经网络的训练
BP算法通过“训练”这一事件来得到这种输入,输出间合适的线性或非线性关系。(www.61k.com)“训练”的过程可以分为向前传输和向后传输两个阶段:
[1]向前传输阶段:
①从样本集中取一个样本Pi,Qj,将Pi输入网络;
(1)②计算出误差测度E1和实际输出Oi=FL(...(F2(F1(PW)W(2))...)W(L));i
③对权重值W(1),W(2),...WL各做一次调整,重复这个循环,直到∑Ei<ε.
[2]向后传播阶段——误差传播阶段:
①计算实际输出Op与理想输出Qi的差;
②用输出层的误差调整输出层权矩阵;
1m
③Ei=∑(Qij?Oij)2;2j=1
④用此误差估计输出层的直接前导层的误差,再用输出层前导层误差估计更前一层的误差.如此获得所有其他各层的误差估计;
⑤并用这些估计实现对权矩阵的修改.形成将输出端表现出的误差沿着与输出信号相反的方向逐级向输出端传递的过程.
网络关于整个样本集的误差测度:
E=∑Ei
i
36
数学建模基础 数学建模入门基础
BP神经网络的matlab程序
p=p1';t=t1';
[pn,minp,maxp,tn,mint,maxt]=premnmx(p,t);%原始数据归一化
net=newff(minmax(pn),[5,1],{'tansig','purelin'},'traingdx');%设置网络,建立相应的BP网络net.trainParam.show=2000;
net.trainParam.lr=0.01;
net.trainParam.epochs=100000;
net.trainParam.goal=1e-5;
[net,tr]=train(net,pn,tn);
网络
pnew=pnew1';
pnewn=tramnmx(pnew,minp,maxp);
anewn=sim(net,pnewn);
anew=postmnmx(anewn,mint,maxt);
y=anew';%调用TRAINGDM算法训练BP%训练网络%对BP网络进行仿真%还原数据
第九章GM(1,1)灰色预测
灰色系统理论认为对既含有已知信息又含有未知或非确定信息的系统进行预测,就是对在一定方位内变化的、与时间有关的灰色过程的预测。[www.61k.com)尽管过程中所显示的现象是随机的、杂乱无章的,但毕竟是有序的、有界的,因此这一数据集合具备潜在的规律,灰色预测就是利用这种规律建立灰色模型对灰色系统进行预测。
GM(1,N)表示1阶的,N个变量的微分方程型模型。而GM(1,1)则是1阶的,1个变量的微分方程型模型。
GM(1,1)预测模型的基本原理
(1)GM(1,1)灰色系统
所谓灰色系统是指既含有已知信息,又含有未知信息的系统,是由邓聚龙教授在1986年提出的。灰色理论自诞生以来,发展很快,由于它所需因素少,模型简单,特别是对于因素空间难以穷尽,运行机制尚不明确,又缺乏建立确定关系的信息系统,灰色系统理论及方法为解决此类问题提供了新的思路和有益的尝试。
灰色预测方法是根据过去及现在已知的或非确知的信息,建立一个从过去引申到将来的GM模型,从而确定系统在未来发展变化的趋势,为规划决策提供依据。在灰色预测模型中,对时间序列进行数量大小的预测,随机性被弱化了,确定性增强了。此时在生成层次上求解得到生成函数,据此建立被求序列的数列预测,其预测模型为一阶微分方程,即只有一个变量的灰色模型,记为GM(1,1)模型。
灰色GM(1,1)预测模型在计算过程中主要是以矩阵为主,它和MATLAB的结合可以有效的解决了灰色系统理论在矩阵计算中的问题,为灰色系统理论的应用提供了一种新的方法。
(2)GM(1,1)预测模型的基本原理
GM(1,1)模型是灰色预测的核心,它是一个单个变量预测的一阶微分方程模型,其离散时间响应函数近似呈指数规律。建立GM(1,1)模型的方法是:
设X(0)={X(0)(1),X(0)(2),L,X(0)(n)}为原始非负时间序列,X(1)(t)为累加生成
37
数学建模基础 数学建模入门基础
序列,即
X(1)(t)=∑X(0)(m),t=1,2,L,n
m=1i(1)
GM(1,1)模型的白化微分方程为:
dX(1)
+aX(1)=udt
?a?
?u?(2)式(2)中,a为待辨识参数,亦称发展系数;u为待辨识内生变量,亦称灰作用量。[www.61k.com)设待辨?=??,按最小二乘法求得a识向量a?=(BTB)?1BTy式中
1X(1)(1)+X(1)(2)2
1?X(1)(2)+X(1)(3)2
LL?())
)11L
1B=?(1X(1)(n?1)+X(1)(n)2(X(0)(2)
X(0)(3)y=L
X(0)(n)
于是可得到灰色预测的离散时间响应函数为:u?u?X(1)(t+1)=?X(0)(1)??e?at+a?a?
X(1)(t+1)为所得的累加的预测值,将预测值还原即为:
?(0)(t+1)=X?(1)(t+1)?X?(1)(t),(t=1,2,3Ln)X(3)(4)
(3)GM(1,1)预测模型的MATLAB程序
根据上述GM(1,1)模型的数学思想,结合MATLAB语言的特点编制了一套可读性强,容易理解的预测程序.该程序操作简单灵活,稳定性好,直接面向用户.
GM(1,1)的matlab程序
gm.m
functionf=gm(x0,m)
n=length(x0);
x1=zeros(1,n);
x1(1)=x0(1);
fori=2:n%为文件名%定义为函数gm(x)%计算累加序列x1
38
数学建模基础 数学建模入门基础
x1(i)=x1(i-1)+x0(i);
end
i=2:n;%对原始数列平行移位并负值给yy(i-1)=x0(i);
y=y';
i=1:n-1;
c(i)=-0.5*(x1(i)+x1(i+1));
B=[c'ones(n-1,1)];
au=inv(B'*B)*B'*y;%计算参数a,u矩阵
i=1:m;%计算预测累加数列的值ago(i)=(x0(1)-au(2)/au(1))*exp(-au(1)*(i-1))+au(2)/au(1);
yc(1)=ago(1);
i=1:m-1;%还原数列的值
yc(i+1)=ago(i+1)-ago(i);
i=2:n;
error(i)=yc(i)-x0(i);%计算残差值
yc(1)=ago(1);
i=1:m-1;%修正还原数列的值
yc(i+1)=ago(i+1)-ago(i);
c=std(error)/std(x0);%计算后验差比
relerror=abs((error)-mean(error)*ones(size(error)));
[nrow,ncol]=size(relerror);
p=0;
fori=2:ncol
ifrelerror(1,i)<0.6745*std(x0)
p=p+1;
end
end
p=p/(n-1);
w1=min(abs(error));
w2=max(abs(error));
i=1:n;%计算关联度
w(i)=(w1+0.5*w2)./(abs(error(i))+0.5*w2);
w=sum(w)/(n-1);
au%输出参数a,u的值
ago;%输出累加数列ago的值x0;%输出原始序列值f=yc;%输出预测的值error;%输出残差的值
c;%输出后验差比的值p;%输出小误差概率的值w%输出关联度end
39
本文标题:数学建模基础-C4D人物头部建模基础篇61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1