一 : spss 多元线性回归和多元逐步回归一样么?
spss 多元线性回归和多元逐步回归一样么?
如题.
如果不一样,分别这么用SPSS做呢?
逐步回归只是回归过程采用的其中一种方法而已.
多元线性回归可以和非线性回归相区分,也就是解释变量和被解释变量之间建立的回归方程,如果是线性的,则是线性回归,否则是非线性回归.
多元逐步回归是回归分析建模的一种,举个例子来说,现在有一个因变量A,建模的时候可能的解释变量有5个,分别是B1,B2,B3,B4和B5,但是搞不清楚5个变量哪些是解释变量,哪些是干扰变量,所以就想到把变量采用不同的方法放到模型中去进行回归建模,放变量的方法具体有可分为Enter法、Forward前进法、Backward后退法、Stepwise逐步回归法等.当然你最终建立的模型可以是线性的,也可以是非线性的.
SPSS里线性回归过程,操作的菜单:Analyze——Regression——Linear,回归过程解释变量的方法默认的时候method是Enter法,如果是逐步回归则采用Stepwise,当然因为选的是线性回归过程,只能建立出线性回顾模型
二 : SPSS中多元回归分析实例(上)
在大多数的实际问题中,影响因变量的因素不是一个而是多个,我们称这类回问题为多元回归分析。可以建立因变量y与各自变量xj(j=1,2,3,…,n)之间的多元线性回归模型:
其中:b0是回归常数;bk(k=1,2,3,…,n)是回归参数;e是随机误差。
多元回归在病虫预报中的应用实例:
某地区病虫测报站用相关系数法选取了以下4个预报因子;x1为最多连续10天诱蛾量(头);x2为4月上、中旬百束小谷草把累计落卵量(块);x3为4月中旬降水量(毫米),x4为4月中旬雨日(天);预报一代粘虫幼虫发生量y(头/m2)。分级别数值列成表2-1。
预报量y:每平方米幼虫0~10头为1级,11~20头为2级,21~40头为3级,40头以上为4级。
预报因子:x1诱蛾量0~300头为l级,301~600头为2级,601~1000头为3级,1000头以上为4级;x2卵量0~150块为1级,15l~300块为2级,301~550块为3级,550块以上为4级;x3降水量0~10.0毫米为1级,10.1~13.2毫米为2级,13.3~17.0毫米为3级,17.0毫米以上为4级;x4雨日0~2天为1级,3~4天为2级,5天为3级,6天或6天以上为4级。
表2-1
x1 | x2 | x3 | x4 | y | ||||||
年 | 蛾量 | 级别 | 卵量 | 级别 | 降水量 | 级别 | 雨日 | 级别 | 幼虫密度 | 级别 |
1960 | 1022 | 4 | 112 | 1 | 4.3 | 1 | 2 | 1 | 10 | 1 |
1961 | 300 | 1 | 440 | 3 | 0.1 | 1 | 1 | 1 | 4 | 1 |
1962 | 699 | 3 | 67 | 1 | 7.5 | 1 | 1 | 1 | 9 | 1 |
1963 | 1876 | 4 | 675 | 4 | 17.1 | 4 | 7 | 4 | 55 | 4 |
1965 | 43 | 1 | 80 | 1 | 1.9 | 1 | 2 | 1 | 1 | 1 |
1966 | 422 | 2 | 20 | 1 | 0 | 1 | 0 | 1 | 3 | 1 |
1967 | 806 | 3 | 510 | 3 | 11.8 | 2 | 3 | 2 | 28 | 3 |
1976 | 115 | 1 | 240 | 2 | 0.6 | 1 | 2 | 1 | 7 | 1 |
1971 | 718 | 3 | 1460 | 4 | 18.4 | 4 | 4 | 2 | 45 | 4 |
1972 | 803 | 3 | 630 | 4 | 13.4 | 3 | 3 | 2 | 26 | 3 |
1973 | 572 | 2 | 280 | 2 | 13.2 | 2 | 4 | 2 | 16 | 2 |
1974 | 264 | 1 | 330 | 3 | 42.2 | 4 | 3 | 2 | 19 | 2 |
1975 | 198 | 1 | 165 | 2 | 71.8 | 4 | 5 | 3 | 23 | 3 |
1976 | 461 | 2 | 140 | 1 | 7.5 | 1 | 5 | 3 | 28 | 3 |
1977 | 769 | 3 | 640 | 4 | 44.7 | 4 | 3 | 2 | 44 | 4 |
1978 | 255 | 1 | 65 | 1 | 0 | 1 | 0 | 1 | 11 | 2 |
数据保存在“DATA6-5.SAV”文件中。
1)准备分析数据
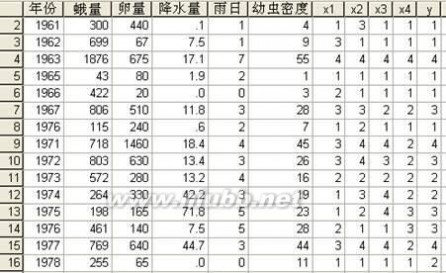
在SPSS数据编辑窗口中,创建“年份”、“蛾量”、“卵量”、“降水量”、“雨日”和“幼虫密度”变量,并输入数据。再创建蛾量、卵量、降水量、雨日和幼虫密度的分级变量“x1”、“x2”、“x3”、“x4”和“y”,它们对应的分级数值可以在SPSS数据编辑窗口中通过计算产生。编辑后的数据显示如图2-1。
图2-1
或者打开已存在的数据文件“DATA6-5.SAV”。
2)启动线性回归过程
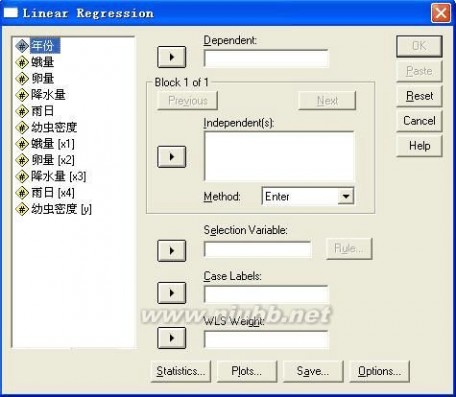
单击SPSS主菜单的“Analyze”下的“Regression”中“Linear”项,将打开如图2-2所示的线性回归过程窗口。
图2-2 线性回归对话窗口
3) 设置分析变量
设置因变量:用鼠标选中左边变量列表中的“幼虫密度[y]”变量,然后点击“Dependent”栏左边的向右拉按钮,该变量就移到“Dependent”因变量显示栏里。
设置自变量:将左边变量列表中的“蛾量[x1]”、“卵量[x2]”、“降水量[x3]”、“雨日[x4]”变量,选移到“Independent(S)”自变量显示栏里。
设置控制变量:本例子中不使用控制变量,所以不选择任何变量。
选择标签变量: 选择“年份”为标签变量。
选择加权变量:本例子没有加权变量,因此不作任何设置。
4)回归方式
本例子中的4个预报因子变量是经过相关系数法选取出来的,在回归分析时不做筛选。因此在“Method”框中选中“Enter”选项,建立全回归模型。
5)设置输出统计量
单击“Statistics”按钮,将打开如图2-3所示的对话框。该对话框用于设置相关参数。其中各项的意义分别为:
图2-3 “Statistics”对话框
①“RegressionCoefficients”回归系数选项:
“Estimates”输出回归系数和相关统计量。
“Confidence interval”回归系数的95%置信区间。
“Covariancematrix”回归系数的方差-协方差矩阵。
本例子选择“Estimates”输出回归系数和相关统计量。
②“Residuals”残差选项:
“Durbin-Watson”Durbin-Watson检验。
“Casewisediagnostic”输出满足选择条件的观测量的相关信息。选择该项,下面两项处于可选状态:
“Outliers outside standarddeviations”选择标准化残差的绝对值大于输入值的观测量;
“All cases”选择所有观测量。
本例子都不选。
③其它输入选项
“Model fit”输出相关系数、相关系数平方、调整系数、估计标准误、ANOVA表。
“R squaredchange”输出由于加入和剔除变量而引起的复相关系数平方的变化。
“Descriptives”输出变量矩阵、标准差和相关系数单侧显著性水平矩阵。
“Part and partialcorrelation”相关系数和偏相关系数。
“Collinearitydiagnostics”显示单个变量和共线性分析的公差。
本例子选择“Model fit”项。
6)绘图选项
在主对话框单击“Plots”按钮,将打开如图2-4所示的对话框窗口。该对话框用于设置要绘制的图形的参数。图中的“X”和“Y”框用于选择X轴和Y轴相应的变量。
图2-4“Plots”绘图对话框窗口
左上框中各项的意义分别为:
“Standardized ResidualPlots”设置各变量的标准化残差图形输出。其中共包含两个选项:
“Histogram”用直方图显示标准化残差。
“Normal probabilityplots”比较标准化残差与正态残差的分布示意图。
“Produce all partialplot”偏残差图。对每一个自变量生成其残差对因变量残差的散点图。
事务所业务:
1.为学生毕业论文、公司、高校课题提供spss、LISREL、Amos等数据分析服务。
2.为公司、高校和科研机构提供价格优惠的调查问卷数据录入服务。
3.为课题提供量化统计指导和咨询。
联系方式:
QQ:3098529344
电话:18375425162
公司地址:山东省青岛市平度市白沙河街道办事处256号
三 : SPSS中多元回归分析实例解析
SPSS中多元回归分析实例
在大多数的实际问题中,影响因变量的因素不是一个而是多个,我们称这类回问题为多元回归分析。[www.61k.com]可以建立因变量y与各自变量xj(j=1,2,3,…,n)之间的多元线性回归模型:
其中:b0是回归常数;bk(k=1,2,3,…,n)是回归参数;e是随机误差。 多元回归在病虫预报中的应用实例:
某地区病虫测报站用相关系数法选取了以下4个预报因子;x1为最多连续10天诱蛾量(头);x2为4月上、中旬百束小谷草把累计落卵量(块);x3为4月中旬降水量(毫米),x4为4月中旬雨日(天);预报一代粘虫幼虫发生量y(头/m2)。分级别数值列成表2-1。
预报量y:每平方米幼虫0~10头为1级,11~20头为2级,21~40头为3级,40头以上为4级。
预报因子:x1诱蛾量0~300头为l级,301~600头为2级,601~1000头为3级,1000头以上为4级;x2卵量0~150块为1级,15l~300块为2级,301~550块为3级,550块以上为4级;x3降水量0~10.0毫米为1级,10.1~13.2毫米为2级,13.3~17.0毫米为3级,17.0毫米以上为4级;x4雨日0~2天为1级,3~4天为2级,5天为3级,6天或6天以上为4级。
表2-1
x1
年 1960 1961 1962 1963 1965
x2 x3 x4 y
蛾量 级别 卵量 级别 10224 300 699
1 3
112 440 67 675 80
1 3 1 4 1
降水幼虫密
级别 级别雨日 级别
量 度 4.3 0.1 7.5 17.1 1.9
1 1 1 4 1
2 1 1 7 2
1 1 1 4 1
10 4 9 55 1
1 1 1 4 1
18764 43
1
多元回归分析 SPSS中多元回归分析实例解析
1966 1967 1976 1971 1972 1973 1974 1975 1976 1977 1978
422 806 115 718 803 572 264 198 461 769 255
2 3 1
20 510 240
1 3 2 4 4 2 3 2 1 4 1
0 11.8 0.6 18.4 13.4 13.2 42.2 71.8 7.5 44.7 0
1 2 1 4 3 2 4 4 1 4 1
0 3 2 4 3 4 3 5 5 3 0
1 2 1 2 2 2 2 3 3 2 1
3 28 7 45 26 16 19 23 28 44 11
1 3 1 4 3 2 2 3 3 4 2
3 1460 3 2 1 1 2 3 1
630 280 330 165 140 640 65
数据保存在“DATA6-5.SAV”文件中。(www.61k.com) 1)准备分析数据
在SPSS数据编辑窗口中,创建“年份”、“蛾量”、“卵量”、“降水量”、“雨日”和“幼虫密度”变量,并输入数据。再创建蛾量、卵量、降水量、雨日和幼虫密度的分级变量“x1”、“x2”、“x3”、“x4”和“y”,它们对应的分级数值可以在SPSS数据编辑窗口中通过计算产生。编辑后的数据显示如图2-1。
图2-1
多元回归分析 SPSS中多元回归分析实例解析
或者打开已存在的数据文件“DATA6-5.SAV”。(www.61k.com]
2)启动线性回归过程
单击SPSS主菜单的“Analyze”下的“Regression”中“Linear”项,将打开如图2-2所示的线性回归过程窗口。
图2-2 线性回归对话窗口
3) 设置分析变量
设置因变量:用鼠标选中左边变量列表中的“幼虫密度[y]”变量,然后点击
“Dependent”栏左边的向右拉按钮,该变量就移到“Dependent”因变量显示栏里。
设置自变量:将左边变量列表中的“蛾量[x1]”、“卵量[x2]”、“降水量[x3]”、“雨日[x4]”变量,选移到“Independent(S)”自变量显示栏里。
设置控制变量: 本例子中不使用控制变量,所以不选择任何变量。
选择标签变量: 选择“年份”为标签变量。
选择加权变量: 本例子没有加权变量,因此不作任何设置。
4)回归方式
多元回归分析 SPSS中多元回归分析实例解析








本例子中的4

个预报因子变量是经过相关系数法选取出来的,在回归分析时不做筛选。(www.61k.com]因此在“Method”框中选中“Enter”选项,建立全回归模型。
5)设置输出统计量
单击“Statistics”按钮,将打开如图2-3所示的对话框。该对话框用于设置相关参数。其中各项的意义分别为:
图2-3 “Statistics”对话框
①“Regression Coefficients”回归系数选项:
“Estimates”输出回归系数和相关统计量。
“Confidence interval”回归系数的95%置信区间。
“Covariance matrix”回归系数的方差-协方差矩阵。
本例子选择“Estimates”输出回归系数和相关统计量。
②“Residuals”残差选项:
“Durbin-Watson”Durbin-Watson检验。
“Casewise diagnostic”输出满足选择条件的观测量的相关信息。选择该项,下面两项处于可选状态:
扩展:spss多元线性回归 / spss多元线性回归分析 / 多元回归分析 spss
“Outliers outside standard deviations”选择标准化残差的绝对值大于输入值的观测量;
“All cases”选择所有观测量。
本例子都不选。
③ 其它输入选项
“Model fit”输出相关系数、相关系数平方、调整系数、估计标准误、ANOVA表。
“R squared change”输出由于加入和剔除变量而引起的复相关系数平方的
多元回归分析 SPSS中多元回归分析实例解析



变化。(www.61k.com]
“Descriptives”输出变量矩阵、标准差和相关系数单侧显著性水平矩阵。 “Part and partial correlation”相关系数和偏相关系数。
“Collinearity diagnostics”显示单个变量和共线性分析的公差。
本例子选择“Model fit”项。
6)绘图选项
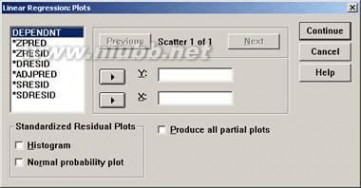
在主对话框单击“Plots”按钮,将打开如图2-4所示的对话框窗口。该对话框用于设置要绘制的图形

的参数。图中的“X”和“Y”框用于

选择X轴和Y轴相应的变量。
图2-4“Plots”绘图对话框窗口
左上框中各项的意义分别为: ?
?
?
?
?
?
? “DEPENDNT”因变量。 “ZPRED”标准化预测值。 “ZRESID”标准化残差。 “DRESID”删除残差。 “ADJPRED”调节预测值。 “SRESID”学生氏化残差。 “SDRESID”学生氏化删除残差。
“Standardized Residual Plots”设置各变量的标准化残差图形输出。其中共包含两个选项:
“Histogram”用直方图显示标准化残差。
“Normal probability plots”比较标准化残差与正态残差的分布示意图。 “Produce all partial plot”偏残差图。对每一个自变量生成其残差对因变量残差的散点图。
本例子不作绘图,不选择。
7) 保存分析数据的选项
在主对话框里单击“Save”按钮,将打开如图2-5所示的对话框。
多元回归分析 SPSS中多元回归分析实例解析
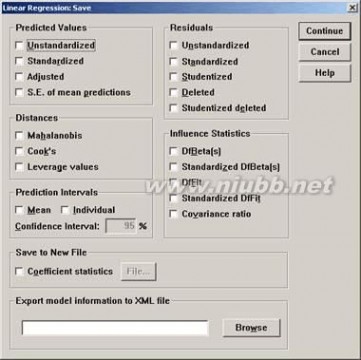









图2-5 “

Save”对话框
①“Predicted Values”预测值栏选项:
Unstandardized 非标准化预测值。(www.61k.com]就会在当前数据文件中新添加一个以字符“PRE_”开头命名的变量,存放根据回
归模型拟合的预测值。
Standardized 标准化预测值。
Adjusted 调整后预测值。
S.E. of mean predictions 预测值的标准误。
本例选中“Unstandardized”非标准化预测值。
②“Distances”距离栏选项:
Mahalanobis: 距离。
Cook’s”: Cook距离。
Leverage values: 杠杆值。
③“Prediction Intervals”预测区间选项:
Mean: 区间的中心位置。
Individual: 观测量上限和下限的预测区间。在当前数据文件中新添加一个以字符“LICI_”开头命名的变量,存放
预测区间下限值;以字符“UICI_”开头命名的变量,存放预测区间上限值。
Confidence Interval:置信度。
多元回归分析 SPSS中多元回归分析实例解析
本例不选。[www.61k.com]




扩展:spss多元线性回归 / spss多元线性回归分析 / 多元回归分析 spss






④“Save to New File”保存为新文件:
选中“Coefficient statistics”项将回归系数保存到指定的文件中。本例不选。 ⑤ “Export model information to XML file” 导出统计过程中的回归模型信息到指定文件。本例不选。
⑥“Residuals” 保存残差选项:
“Unstandardized”非标准化残差。
“Standardized”标准化残差。
“Studentized”学生氏化残差。
“Deleted”删除残差。
“Studentized deleted”学生氏化删除残差。
本例不选。
⑦“Influence Statistics” 统计量的影响。
“DfBeta(s)”删除一个特定的观测值所引起的回归系数的变化。
“Standardized DfBeta(s)”标准化的DfBeta值。
“DiFit” 删除一个特定的观测值所引起的预测值的变化。
“Standardized DiFit”标准化的DiFit值。
“Covariance ratio”删除一个观测值后的协方差矩隈的行列式和带有全部观测值的协方差矩阵的行列式的比率。
本例子不保存任何分析变量,不选择。
8)其它选项
在主对话框里单击“Options”按钮,将打开如图2-6所示的对话框。
多元回归分析 SPSS中多元回归分析实例解析
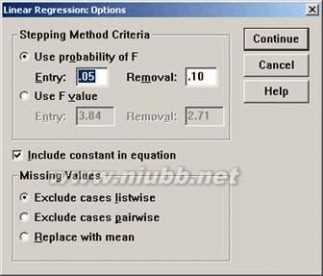



图2-6 “Options”设置对话框
①“Stepping Method Criteria”框用于进行逐步回归时内部数值的设定。(www.61k.com]其中各项为:
“Use probability of F”如果一个变量的F值的概率小于所设置的进入值(Entry),那么这个变量将被选入回归方程
中;当变量的F值的概率大于设置的剔除值(Removal),则该变量将从回归方程中被剔除。由此可见,设置
“Use probability of F”时,应使进入值小于剔除值。
“Ues F value”如果一个变量的F值大于所设置的进入值(Entry),那么这个变量将被选入回归方程中;当变量的
F值小于设置的剔除值(Removal),则该变量将从回归方程中被剔除。同时,设置“Use F value”时,应使进
入值大于剔除值。
本例是全回归不设置。
②“Include constant in equation”选择此项表示在回归方程中有常数项。 本例选中“Include constant in equation”选项在回归方程中保留常数项。 ③“Missing Values”框用于设置对缺失值的处理方法。其中各项为: “Exclude cases listwise”剔除所有含有缺失值的观测值。
“Exchude cases pairwise”仅剔除参与统计分析计算的变量中含有缺失值的观测量。
“Replace with mean”用变量的均值取代缺失值。
多元回归分析 SPSS中多元回归分析实例解析
本例选中“Exclude cases listwise”。[www.61k.com]

9)提交执行
在主对话框里单击“OK”,提交执行,结果将显示在输出窗口中。主要结果见表2-2至表2-4。
10) 结果分析
主要结果:
表2-2
表2-2 是回归模型统计量:R 是相关系数;R Square 相关系数的平方,又称判定系数,判定线性回归的拟合程度:用来说明用自变量解释因变量变异的程度(所占比例);Adjusted R Square 调整后的判定系数;Std. Error of the Estimate 估计标准误差。
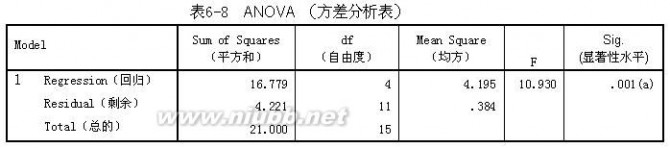
表2-3
表2-3 回归模型的方差分析表,F值为10.930,显著性概率是0.001,表明回归极显著。
注:Sig值是t统计量对应的概率值,所以t和Sig两者是等效的,看Sig就够了。Sig值要求小于给定的显著性水平,一般是0.05、0.01等,Sig越接近于0越好; R方衡量方程拟合优度,R方越大越好,一般地,大于0.8说明方程对样本点的拟合效果很好,0.5~0.8之间也可以接受。时间序列的话,R方很容易达到很大,如果是截面数据,R方的要求没那么严格。但要注意的是R方统计量不是检验的统计量,只衡量显著性; F是检验方程显著性的统计量,是平均的回归平方和与平均剩余平方和之比,越大越好。
“SIG”,SIG=significance,意为“显著性”,后面的值就是统计出的P值,如果P值0.01<P<0.05,则为差异显著,如果P<0.01,则差异极显著。
多元回归分析 SPSS中多元回归分析实例解析
表 2-4分析: 建立回归模型: 根据多元回归模型: 把表 6-9 中“非标准化回归系数”栏目中的“B”列系数代入上式得预报方程:预测值 的标准差可用剩余均方估计: 回归方程的显著性检验: 从表 6-8 方差分析表中得知:F 统计量为 10.93,系统自动检验的显著性水平为 0.001。[www.61k.com] F(0.05,4,11)值为 3.36,F(0.01,4,11) 值为 5.67,F(0.001,4,11) 值为 10.35。因 此回归方程相关非常显著。(F 值可在 Excel 中用 FINV( )函数获得)。 回代检验 需要作预报效果的验证时,在主对话框(图 6-8)里单击“Save”按钮,在打开如 图 3-6 所示对话框里,选中“Predicted Values”预测值选项栏中的 “Unstandardized”非标准化预测值选项。这样在过程运算时,就会在当前文件中 新添加一个“PRE_1”命名的变量,该变量存放根据回归模型拟合的预测值。 然后,在 SPSS 数据窗口计算“y”与“PRE_1”变量的差值(图 2-7),本例子把绝对 差值大于 0.8 视为不符合,反之则符合。结果符合的年数为 15 年,1 年不符合, 历史符合率为 93.75%。
扩展:spss多元线性回归 / spss多元线性回归分析 / 多元回归分析 spss
多元回归分析 SPSS中多元回归分析实例解析
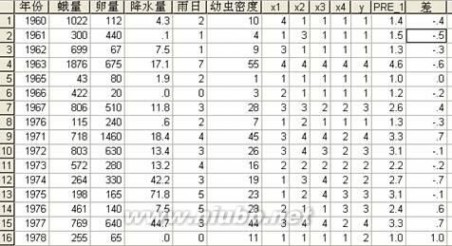
图2-7
多元回归分析法可综合多个预报因子的作用,作出预报,在统计预报中是一种应用较为普遍的方法。(www.61k.com)
在实际运用中,采取将预报因子和预报量按一定标准分为多级,用分级尺度代换较大的数字,更能揭示预报因子与预报量的关系,预报效果比采用数量值统计方法有明显的提高,在实际应用中具有一定的现实意义。
扩展:spss多元线性回归 / spss多元线性回归分析 / 多元回归分析 spss
本文标题:spss多元logistic回归-spss 多元线性回归和多元逐步回归一样么?61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1