一 : 河南省郑州市第五十一中学2014秋九年级数学上册 4.2 平行线分线段成比例

4.2平行线分线段成比例

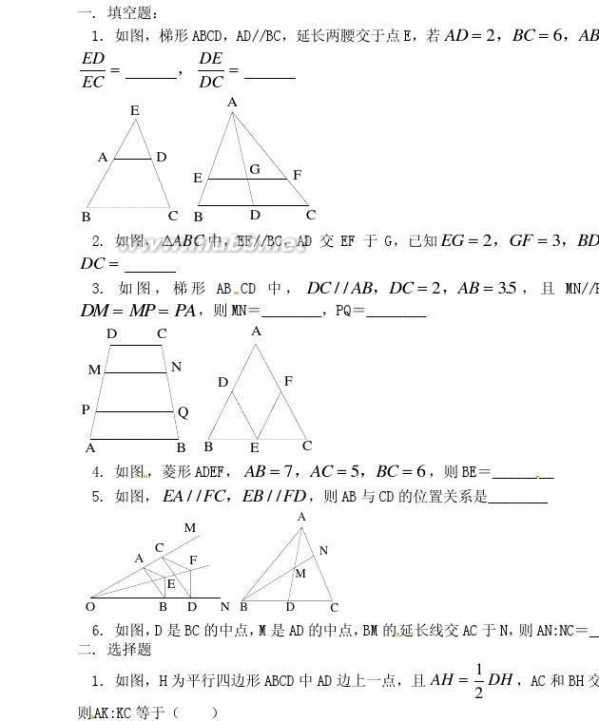
?4，则?5，则

，_。(www.61k.com］

A. 1:2 B. 1:1 C. 1:3 D. 2:3 K， 1

郑州平行线 河南省郑州市第五十一中学2014秋九年级数学上册 4.2 平行线分线段成比例练习题

A

2. 如图，?ABC中，D在AB上，E在AC上，下列条件中，能判定DE//BC的是（ ）

A. AD?AC?AE?AB B. AD?AE?EC?DB

C. AD?AB?AE?AC D. BD?AC?AE?AB

3. 如图，?ABC中，DE//BC，BE与CD交于点O，AO与DE、BC交于N、M，则下列式子

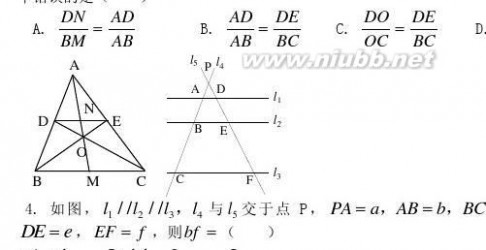
A H D B C B C AEAO? ECOM?c，PD?d，5. 如图，?ABC中，

A. 1 2ADAE1??，则OE:OB?（ ） DBEC2111B. C. D. 345

E

B C

三. 计算题：

1. 如图，已知菱形BEDF内接于?ABC，点E、D、F分别在AB、AC和BC上，若AB?15，BC?12，求菱形边长。(www.61k.com]

2

郑州平行线 河南省郑州市第五十一中学2014秋九年级数学上册 4.2 平行线分线段成比例练习题

B F C

2. 如图，已知?ABC中，DE//BC，AD?8，AC?6，BD?AE，求BD的长。(www.61k.com）

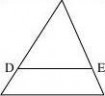
B C

3. 如图，?ABC中，AD是角平分线，DE//AC交

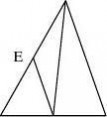
AB于E，已知AB?12，AC?8，求DE。

A

3

郑州平行线 河南省郑州市第五十一中学2014秋九年级数学上册 4.2 平行线分线段成比例练习题

4. 如图F为平行四边形ABCD的AD延长线上一点，BF分别交CD、AC于G、E，若

A B

4 EF?32，GE?8，求BE。[www.61k.com)

二 : 平行线的成就感

那年夏天

我不再飘流

我不再孤独

我不再追逐

你说我很傻

我知道自己只是不假( 文章阅读网：www.61k.com )

你说我可爱

我了解自己那是真实

你说羡慕我以后的女朋友

我想告诉你

其实我一直希望你能一直陪我走

平行线不会的交集

我想要打破

我想要一个唯一

不知道你是否知道我的心意

我终于鼓起勇气

对你说了：我喜欢你

可是你的表情里

写满了不尽的怀疑

我问你为什么喜欢和我在一起

你说：因为能够融化我这块坚冰

很有成就感

于是我的心碎了一地

我知道是自己骗了自己

我根本就活在自己的想象里

我不愿承认但也必须了解

平行线本没有交集

平行线的成就感

埋葬了我懵懂的笑脸

平行线的成就感

让我忘不了你

却只能望着你

三 : 线段比例尺

教学内容：教科书第16页上的，练习五的第4—9题。
教学目的：使学生理解的含义，会根据求图上距离或实际距离。
教具准备：教师准备一些的地图或平面图。
教学过程 ：
    —、导人新课
    教师：上节课我们学习了一些比例尺的知识，我们学过的比例尺都是用数值来标明的，如比例尺1：10000就表示图上距离是l厘米实际距离就是10000厘米，像这样的比例尺叫做数值比例尺。除了数值比例尺外，还有。什么是线段比例
尺呢：这就是我们这节课要学习的内容。(板书课题）
    二、新课
    教师：是在图上附有一条注有数量的线段。用来表示和地面上相对应的实际距离。同学们可以翻开教科书第16页．看右下角有一幅地图。地图的下面就 有一条。它上面有0、50和100几个数，还注明了长度单位“千米”。这些数和单位表示什么意思呢?大家量一量从0到50这段线段有多长。(1厘米。)从50到100呢?(也是1厘米。)从0到50就表示地图上1厘米的距离相当于地面上50千米的实际距离。从0到100就表示地图上2厘米的距离相当于地面上100千米的实际距 离。

    然后教师问：
    l“如果知道了两个城市之间的图上距离，你能不能计算出这两个城市之间的实际距离?”
    让学生在地图上找到沈阳和长春这两个城市，并量出它们的距离是多少厘米。再想一想：要求地面上这两个城市之间的实际距离大约是多少千米，该怎样计算?
    引导学生想：1厘米．的图上距离代表地面上多少千米的实际距离，(50千米。)我们量出沈阳到长春的图上距离是5．5厘米，就代表几个50千米的实际距离。(5.5个50千米。)怎么列式计算?
    让学生说怎样列式。教师板书：50×5．5＝275(千米)
    之后，进一步提出：
    “你能不能把这个地图上的改写成数值比例尺?怎样改写?”(因为图上1厘米相当于地面上50千米的实际距离，现在图上距离和实际距离的单位不同，根据图上距离：实际距离＝比例尺，要把图上距离和实际距离的单位化成同级单位，50
千米等于5000000厘米。所以这条改写成数值比例尺就是1：5000000。)
教师板书出数值比例尺。 
    三、课堂练习
    完成练习五的第4—9题：
    1．第5题，让学生独立填表：填表前，要提醒学生图上距离的单位应用什么，实际距离的单位应用什么。
    2．第8题，让学生独立计算。集体订正后，让学生按照东南西北的方位说说拖拉机站、电影院、汽车站和供销社离学校的距离。如，电影院在学校的南面，距学校200米；拖拉机站在学校的西北面，距学校2500米。
    3．第9题，让学生先求出试验田长和宽的图上距离，然后画出平面图，并且要注意在平面图上注明比例尺。

四 : 比例线段教案

教学建议
    知识结构
    重难点分析
    本节的重点是线段的比和比例线段的概念以及比例的性质.以前的平面几何主要研究线段的位置关系和相等关系,从本章开始研究线段及相关图形的比例关系――相似三角形,这些内容的研究都离不开线段的比和比例性质的应用.
    本节的难点是比例性质及应用,虽然小学时已经接触过比例性质的一些知识,但由于内容比较简单,而且间隔时间较长,学生印象并不深刻,而本节涉及到的比例基本性质变式较多,合分比性质以及等比性质学生又是初次接触,内容不但多,而且轻易混淆,作题不知应用哪条性质,不知如何应用是常有的.
    教法建议
    1.生活中比例的例子比比皆是,在新课引入时最好从生活实例引入,可使学生感觉轻松自然,轻易产生爱好,增加学生学习的主动性
    2.小学时曾学过数的比及相关概念,学习时也可以复习引入,从数的比过渡到线段的比,渗透类比思想
    3.这一节概念比较多,也比较轻易混淆,教学中可设计不同层次的题组来进行巩固,非凡是要举一些反例,同时要注重对相近概念的比较
    4.黄金分割的内容要求学生理解,主要体现数学美,可由学生从生活中寻找实例,激发学生的爱好和参与感
    5.比例性质由于变式多,理解和应用上轻易出现错误,教学时可利用等式性质和分式性质来处理
    教学设计示例1
    (第1课时)
    一、教学目标
    1.理解线段的比的概念.
    2.通过与小学知识到比较,初步培养学生“类比”的数学思想.
    3.通过线段的比的有关计算,培养学习的计算能力.
    4.通过“引言”及“例1”的教学,激发学生学习爱好,对学生进行热爱爱国主义教育.
    二、教学设计
    先学后做,启发引导
    三、重点及难点
    1.教学重点 两条线段比的概念.
    2.教学难点 正确理解两条线段的比及应用.
    四、课时安排
    1课时
    五、教具学具预备
    股影仪、胶片、常用画图工具
    六、教学步骤
    复习提问
    找学生回答小学学过的比、比的前项和后项的概念.
    (两个数相除又叫做两数的比,记作 或a:b,其中a叫比的前项,b叫比的后项)
    讲解新课
    把学生分成三组,分别以米、厘米、毫米作为长度单位,量一下几何教材的长与宽(令长为a,宽为b).再求出长与宽的比.然后找三名同学把结果写在黑板上.如:
    等.
    可以看出,在同一长度单位下,两条线段长度的比就是两条线段的比.
    一般地:若a、b的长度分别是m、n(单位相同),那么就说这两条线段的比是 ,或写成 ,和数的比一样,a叫比的前项,b叫比的后项.
    关于两条线段比的概念,教学中要揭示它的实质,即 表示a是b的k倍,这是学生已有的知识,较易理解,也轻易使学生注重到求比时,长度单位要一致.另外,可组织学生举例实际生活中两条线段的比的问题,充分调动学生联系实际和积极思维的能力,对活跃课堂气氛也很有利,但教师需注重尺度.
    就刚才三组学生做过的练习及问题回答,在教师启发和点拨下,让学生讨论或试述两条线段的比应注重的问题,归纳出:
    (l)两条线段的比就是它们的长度的比.
    (2)比与所选线段的长度单位无关,求比时,两条线段的长度单位要一致.
    (3)两条线段的比值总是正数.(并不都是正数)
    (4)除了a=b之外, . 与 互为倒数.
    例1 见教材p202.
    讲解完例1后:
    (l)提问学生ab是 的多少倍, 是ab的多少倍,以加深学生对线段比的逾义的理解.
    (2)给出:比例尺= ,就例1的图上,若图距是8cm的两地,实际距离是多少?
    另外,还可鼓励学生课后根据地图上的比例尺,测量并计算出你所在省会与首都北京的直线距离,从而丰富了知识,激发了学习爱好.
    例2 见教材p202.
    讲解完例2后:
    (l)可改变线段ab的长度,或给出ac、bc的长度,再求这些比,使学生熟悉这种三角形中边的比与长度无关.
    (2)常识1:有一锐角是30°的直角三角形中,三边(从小到大)的比为 .
    常识2:等腰直角三角形三边(从小到大)的比为1:1: .
    学生把握了这些常识可有两点好处:
    ①知道例2中“ ”以及习题5.l第2题(1)中“边长为4”.(2)中的“对角线ac=a”这些条件实际上都是多余的.
    ②这些题目若改成“填空题”,可避免一些不必要的计算.从而提高做题速度.这样不仅培养了能力,而且在考试中也受益匪浅.
    因此,今后如碰到和此常识有关的知识要反复渗透,反复给学生强调,让它扎根于学生的下意识中。
    小结
    1.两条线段比的概念以及应注重的问题.
    2.会求两条线段的比.
    七、布置作业
    教材p210中2、3.
    八、板书设计 本文标题：平行线分线段成比例-河南省郑州市第五十一中学2014秋九年级数学上册 4.2 平行线分线段成比例
本文地址： http://www.61k.com/1173140.html