一 : 2014年全国数学各省高考试卷及答案

2014年北京高考数学（理科）试题

一.选择题（共8小题，每小题5分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项）

1.已知集合A?{x|x2?2x?0},B?{0,1,2}，则AB?( )

C.{0,2 } D.{0,1, 2}A.{0} B.{0,1}

2.下列函数中，在区间(0,??)上为增函数的是（ ）

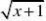
2 C.y?2?x D.y?lo0g.5x(? 1)?1)A.y? B.y?(x

?x??1?cos?3.曲线?（?为参数）的对称中心（ ）

?y?2?sin?

A.在直线y?2x上 B.在直线y??2x上

C.在直线y?x?1上 D.在直线y?x?1上

4.当m?7,n?3时，执行如图所示的程序框图，输出的S值为（ ）

A.7 B.42 C.210 D.840

5.设{an}是公比为q的等比数列，则"q?1"是"{an}"为递增数列的（ ）

A.充分且不必要条件 B.必要且不充分条件

C.充分必要条件 D.既不充分也不必要条件

?x?y?2?0?6.若x,y满足?kx?y?2?0且z?y?x的最小值为-4，则k的值为（ ）

?y?0?

11A.2 B.?2 C. D.? 22

7.在空间直角坐标系Oxyz中，已知A?2,0,0?，B?2,2,0?，C

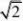
?0,2,0?，D，若 S1，S2，S3分别表示三棱锥D?ABC在xOy，yOz，zOx坐标平面上的正投影图形的 面积，则（ ）

（A）S1?S2?S3 （B）S1?S2且 S3?S1

（C）S1?S3且 S3?S2 （D）S2?S3且 S1?S3

8.有语文、数学两学科，成绩评定为“优秀”“合格”“不合格”三种.若A同学每科成绩不 低于B同学，且至少有一科成绩比B高，则称“A同学比B同学成绩好.”现有若干同学，

?

他们之间没有一个人比另一个成绩好，学科 网且没有任意两个人语文成绩一样，数学成绩也一样 的.问满足条件的最多有多少学生（ ）

（A）2 （B）3 （C）4 （D）5

二、填空题（共6小题，每小题5分，共30分）

?1?i?9.复数???________. 1?i??

10.已知向量a、b满足a?1，b??2,1?，且?a?b?0???R?，则??________.

y2

?x2?1具有相同渐近线，则C的方程为________； 11.设双曲线C经过点?2,2?，且与4

渐近线方程为________.

12.若等差数列?an?满足a7?a8?a9?0，a7?a10?0，则当n?________时?an?的前n 项和最大.

13. 把5件不同产品摆成一排，若产品A与产品C不相邻，则不同的摆法有_______种.

14. 设函数f(x)?sin(?x??)，A?0,??0，若f(x)在区间[

f?2??,]上具有单调性，且 62????2???????f????f??，则f(x)的最小正周期为________. ?2??3??6?

三．解答题（共6题，满分80分）

?B?15. （本小题13分）如图，在?ABC中，

（1）求sin?BAD

（2）求BD,AC的长 ?3,AB?8，点D在BC边上，且CD?2,cos?ADC?1 7

16. （本小题13分）.

李明在10场篮球比赛中的投篮情况如下（假设各场比赛互相独立）：

（1）从上述比赛中随机选择一场，求李明在该场比赛中投篮命中率超过0.6的概率.

（2）从上述比赛中选择一个主场和一个客场，学科 网求李明的投篮命中率一场超过0.6，一 场不超过0.6的概率.

（3）记x是表中10个命中次数的平均数，从上述比赛中随机选择一场，记X为李明 在这比赛中的命中次数，比较E(X)与x的大小（只需写出结论）

17.（本小题14分）

如图，正方形AMDE的边长为2，B,C分别为AM,MD的中点，在五棱锥P?ABCDE 中，F为棱PE的中点，平面ABF与棱PD,PC分别交于点G,H.

（1）求证：AB//FG；

（2）若PA?底面ABCDE，且AF?PE，求直线BC与平面ABF所成角的大小，并 求线段PH的长.

18.（本小题13分） f(x)?xcosx?sinx,x?[0,]， 2

（1）求证：f(x)?0；

sinx?（2）若a??b在(0,)上恒成立，求a的最大值与b的最小值. 2x已知函数

19.（本小题14分）

已知椭圆C:x2??2y2?4，

OB，求直线AB与圆（1）求椭圆C的离心率. （2）设O为原点，若点A在椭圆C上，点B在直线y?2上，且OA?

x2?y2?2的位置关系，并证明你的结论

.

20.（本小题13分）

对于数对序列P(a1,b1),(a2,b2),,(an,bn)，记T1(P)?a1?b1，

Tk(P)?bk?max{Tk?1(P),a1?a2??ak}(2?k?n)，其中

max{Tk?1(P),a1?a2??ak}表示Tk?1(P)和a1?a2??ak两个数中最大的数，

（1）对于数对序列P(2,5),P(4,1)，求T1(P),T2(P)的值.

（2）记m为a,b,c,d四个数中最小值，学科 网对于由两个数对(a,b),(c,d)组成的数对序列P(a,b),(c,d)和P'(a,b),(c,d)，试分别对m?a和m?d的两种情况比较T2(P)和T2(P')的大小.

（3）在由5个数对(11,8),(5,2),(16,11),(11,11),(4,6)组成的所有数对序列中，写出一个数对序列P使T5(P)最小，并写出T5(P)的值.（只需写出结论）.

2014年全国普通高等学校招生统一考试

上海 数学试卷(理工农医类)

考生注意：

1. 本试卷共4页，23道试题，满分150分. 考试时间120分钟.

2. 本考试分设试卷和答题纸. 试卷包括试题与答题要求. 作答必须涂（选择题）或写（非选择题）在答题纸上，在试卷上作答一律不得分.

3. 答卷前，务必用钢笔或圆珠笔在答题纸正面清楚地填写姓名、准考证号，并将核对后的条形码贴在指定位置上，在答题纸反面清楚地填写姓名.

一、填空题（本大题共有14题，满分56分）考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分.

1. 函数y?1?2cos(2x)的最小正周期是.

【解析】：原式＝?cos4x，T?22??? 42

2. 若复数z?1?2i，其中i是虚数单位，则?z?

【解析】：原式＝z?z?1?z?1?5?1?6 2??1???z?. z?

x2y2

??1的右焦点重合，则该抛物线的准线方程3. 若抛物线y?2px的焦点与椭圆952

为 .

【解析】：椭圆右焦点为(2,0)，即抛物线焦点，所以准线方程x??2

?x,x?(??,a),4. 设f(x)??2 若f(2)?4，则a的取值范围为. x,x?[a,??).?

【解析】：根据题意，2?[a,??)，∴a?2

5. 若实数x,y满足xy?1，则x?2y的最小值为.

【解析】

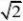
：x2?2y2?2?x?6. 若圆锥的侧面积是底面积的3倍，则其母线与底面夹角的大小为值表示）.

【解析】：设圆锥母线长为R，底面圆半径为r，∵S侧?3S底，∴??r?R?3??r2，即R?3r，∴22cos??11，即母线与底面夹角大小为arccos 33

7. 已知曲线C的极坐标方程为?(3cos??4sin?)?1，则C与极轴的交点到极点的距离是 .

【解析】：曲线C的直角坐标方程为3x?4y?1，与x轴的交点为(,0)，到原点距离为

8. 设无穷等比数列?an?的公比为q，若a1?lim?a3?a4?n??131 3?an?，则q?a3a1q2【解析】

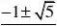
：a1?，∵0?q?

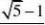
1，∴q? ??q2?q?1?0?q?1?q1?q9. 若f(x)?x?x2

3?1

2，则满足f(x)?0的x的取值范围是2

3?1

2【解析】：f(x)?0?x?x，结合幂函数图像，如下图，可得x的取值范围是(0,1)

10. 为强化安全意识，某商场拟在未来的连续10天中随机选择3天进行紧急疏散演练，则 选择的3天恰好为连续3天的概率是 （结果用最简分数表示）.

【解析】：P?81 ?3C1015

2211. 已知互异的复数a,b满足ab?0，集合?a,b??a,b，则a?b???

【解析】：第一种情况：a?a,b?b，∵ab?0，∴a?b?1，与已知条件矛盾，不符；

43222第二种情况：a?b,b?a，∴a?a?a?1，∴a?a?1?0，即a?b??1； 22

x12. 设常数a使方

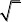
程sin

x1?x2?x3.

【解析】：化简得2sin(x?

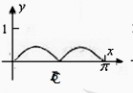
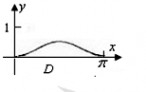
即x1?x2?x3?0?3cox?sa在闭区间[0,?2上]恰有三个解x1,x2,x3，则?3)?

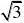
a，根据下图，当且仅当a? 7? 3?3?2??

13. 某游戏的得分为1,2,3,4,5，随机变量?表示小白玩该游戏的得分. 若E(?)?4.2，则小白得5分的概率至少为 .

【解析】：设得i分的概率为pi，∴p1?2p2?3p3?4p4?5p5?4.2，

且p1?p2?p3?p4?p5?1，∴4p1?4p2?4p3?4p4?4p5?4，与前式相减得：

?3p1?2p2?p3?p5?0.2，∵pi?0，∴?3p1?2p2?p3?p5?p5，即p5?0.2

14.

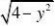
已知曲线C:x?，直线l:x?6. 若对于点A(m,0)，存在C上的点P和l 上的Q使

得AP?AQ?0，则m的取值范围为 .

【解析】：根据题意，A是PQ中点，即m?xP?xQ

2?xP?6，∵?2?xP?0，∴m?[2,3] 2

二、选择题（本大题共有4题，满分20分）每题有且只有一个正确答案，考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分.

15. 设a,b?R，则“a?b?4”是“a?2且b?2”的 （ ）

(A) 充分条件.

(B) 必要条件. (D) 既非充分又非必要条件. (C) 充分必要条件.

【解析】：B

16. 如图，四个棱长为1的正方体排成一个正四棱柱，AB是一条侧

P2

P5

P4

3

6

P7

P8

棱，

Pi(i?1,

2 ,是上底面上其余的八个点，则

P1

AB?AP, 2, i(i?1

(A) 1. (C) 4.

, 8)的不同值的个数为 B(B) 2. (D) 8.

A

（ ）

【解析】：根据向量数量积的几何意义，AB?APi等于AB乘以APi在AB方向上的投影，而APi在

1AB方向上的投影是定值，AB也是定值，∴AB?APi为定值，∴选A

k17. 已知P1(a1,b1)与P2(a2,b2)是直线y?kx?1（为常数）上两个不同的点，则关于x 和y的方

程组?

?a1x?b1y?1,

的解的情况是

?a2x?b2y?1

（ ）

(B) 无论k,P1,P2如何，总有唯一解. (D) 存在k,P1,P2，使之有无穷多解.

(A) 无论k,P1,P2如何，总是无解. (C) 存在k,P1,P2，使之恰有两解.

【解析】：由已知条件b1?ka1?1，b2?ka2?1，

D?

a1b1

a2b2

?a1b2?a2b1?a1(ka2?1)?a2(ka1?1)?a1?a2?0，∴有唯一解，选B

?(x?a)2,x?0,

?

18. 设f(x)?? 若f(0)是f(x)的最小值，则a的取值范围为（ ） 1

?x??a,x?0.

x?

(A) [?1,2].

(B) [?1,0].

(C) [1,2].

(D) [0,2].

【解析】：先分析x?0的情况，是一个对称轴为x?a的二次函数，当a?0时，

不符合题意，排除AB选项；当a?0时，根据图像f(

x)min?f(0)，即a?0f(x)min?f(a)?f(0)，符合题意，排除C选项；∴选D；

三、解答题（本大题共有5题，满分74分）解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.

19. (本题满分12分)

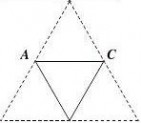
底面边长为2的正三棱锥P-ABC，其表面展开图是

三角形

P1

V. 如图PP. 求△PP2，12P3的各边长及此三棱锥的体积

【解析】：根据题意可得P1,B,P2共线，

P1

2

?ABC?60?， ∵?ABP1??BAP1??CBP2，

∴?ABP1??BAP1??CBP2?60?，∴?P1?60?，同理?P2??P3?60?，

P?ABC是正四面体，所以△PP ∴△PP12P3是等边三角形，12P3边长为4；

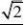
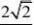
∴V?

20. (本题满分14分) 本题共有2个小题，第1小题满分6分，第2小题满分8分.

AB3?

2x?a

设常数a?0，函数f(x)?x.

2?a

?1

(1) 若a?4，求函数y?f(x)的反函数y?f(x)；

(2) 根据a的不同取值，讨论函数y?f(x)的奇偶性，并说明理由.

2x?44y?44y?4

?y，∴2x?【解析】：（1）∵a?4，∴f(x)?x，∴x?log2， 2?4y?1y?1

∴y?f

?1

(x)?log2

4x?4

，x?(??,?1)?(1,??) x?1

2x?a2?x?a

??x （2）若f(x)为偶函数，则f(x)?f(?x)，∴x，

2?a2?a

整理得a(2x?2?x)?0，∴a?0，此时为偶函数

2x?a2?x?a

???x 若f(x)为奇函数，则f(x)??f(?x)x， 2?a2?a

2

整理得a?1?0，∵a?0，∴a?1，此时为奇函数

当a?(0,1)?(1,??)时，此时f(x)既非奇函数也非偶函数

21. (本题满分14分) 本题共有2个小题，第1小题满分6分，第2小题满分8分.

如图，某公司要在A、B两地连线上的定点

D

C处建

长80米. 角分别

CB造广告牌CD，其中D为顶端，AC长35米，B在同一水平面上，从A和B看D的仰设点A、

为?和?.

(1) 设计中CD是铅垂方向. 若要求??2?，长至多为多少（结果精确到0.01米）？

A

C

?

B

问CD的

(2) 施工完成后，CD与铅垂方向有偏差．现在实测得??38.12?，??18.45?，求CD的长（结

果精确到0.01米）.

【解析】：（1）设CD的长为x米，则tan??xx?,tan?????2??0， 35802

x

2tan?x?160x， ∴tan??tan2?，∴tan??，∴?1?tan2?x2356400?x2

1?64002

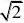
解得0?x??28.28，∴CD的长至多为28.28米

（2）设DB?a,DA?b,DC?m，?ADB?180??????123.43?，

则aAB115sin38.12???85.06， ，解得a?sin?sin?ADBsin123.43?

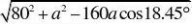
∴m??26.93，∴CD的长为26.93米

22. (本题满分16分) 本题共有3个小题，第1小题满分3分，第2小题满分5分，第3小题满分8分.

在平面直角坐标系xOy中，对于直线l:ax?by?c?0和点P)记1(x1,y1),P2(x2,y2，

lC与直线l没有公共. c若??0，则称点P??(axc(a2x?b?)1,P2被直线分割. 若曲线1?by1?)2y

llC的一条分割线. 点，且曲线C上存在点P1,P2被直线分割，则称直线为曲线

(1) 求证：点A(1,2),B(?1,0)被直线x?y?1?0分割；

(2) 若直线y?kx是曲线x2?4y2?1的分割线，求实数k的取值范围；

(3) 动点M到点Q(0,2)的距离与到y轴的距离之积为1，设点M的轨迹为曲线E. 求证：通过原点的直线中，有且仅有一条直线是E的分割线.

【解析】：（1）将A(1,2),B(?1,0)分别代入x?y?1，得(1?2?1)?(?1?1)??4?0

∴点A(1,2),B(?1,0)被直线x?y?1?0分割

?x2?4y2?1 （2）联立?，得(1?4k2)x2?1，依题意，方程无解， ?y?kx

2 ∴1?4k?0，∴k??11或k? 22

（3）设M(x,y

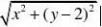
)?1，

∴曲线E的方程为[x?(y?2)]x?1 ①

当斜率不存在时，直线x?0，显然与方程①联立无解，

又P,2),P,2)为E上两点，且代入x?0，有???1?0， 1(12(?1

∴x?0是一条分割线；

当斜率存在时，设直线为y?kx，代入方程得：(k?1)x?4kx?4x?1?0， 2432222

令f(x)?(k2?1)x4?4kx3?4x2?1，则f(0)??1，

f(1)?k2?1?4k?3?(k?2)2，f(?1)?k2?1?4k?3?(k?2)2，

当k?2时，f(1)?0，∴f(0)f(1)?0，即f(x)?0在(0,1)之间存在实根，

∴y?kx与曲线E有公共点

当k?2时，f(0)f(?1)?0，即f(x)?0在(?1,0)之间存在实根，

∴y?kx与曲线E有公共点

∴直线y?kx与曲线E始终有公共点，∴不是分割线，

综上，所有通过原点的直线中，有且仅有一条直线x?0是E的分割线

23. (本题满分18分) 本题共有3个小题，第1小题满分3分，第2小题满分7分，第3小题满分8分. 已知数列?an?满足an?an?1?3an，n?N，a1?1. *1

3

(1) 若a2?2,a3?x,a4?9，求x的取值范围；

(2) 设?an?是公比为q的等比数列，Sn?a1?a2?值范围； 1*?an. 若Sn?Sn?1?3Sn，n?N，求q的取3

,ak成等差数列，且a1?a2??ak?1000，求正整数k的最大值，以及k取最大值

时相应数列a1,a2,,ak的公差.

121【解析】：（1）依题意，a2?a3?3a2?x?6，又a3?a4?3a3，∴3?x?27， 333

综上可得3?x?6；

11 （2）由已知得an?qn?1，又a1?a2?3a1?q?3 33

1n 当q?1时，Sn?n，Sn?Sn?1?3Sn，即?n?1?3n，成立 33

qn?111qn?1qn?1?1qn?1 当1?q?3时，Sn?，Sn?Sn?1?3Sn，即， ??3q?133q?1q?1q?1(3) 若a1,a2,

?3qn?1?qn?2?01qn?1?1 ?n，∵q?1， ?3，此不等式即?n?1n3q?1?q?3q?2?0

?qn?2?qn(3q?1)?2?2qn?2?0，

n?1n2 对于不等式q?3q?2?0，令n?1，得q?3q?2?0，解得1?q?2，

又当1?q?2时，q?3?0， ∴3q

∴q?3q?2?q(q?3)?2?q(q?3)?2?(q?1)(q?2)?0成立，

∴1?q?2 n?1nnn?1

1?qn111?qn1?qn?11?qn1??3当?q?1时，Sn?，Sn?Sn?1?3Sn，即， 331?q31?q1?q1?q

?3qn?1?qn?2?0即?n?1，3q?1?0,q?3?0 n?q?3q?2?0

∵3qn?1?qn?2?qn(3q?1)?2?2qn?2?0

qn?1?3qn?2?qn(q?3)?2?q(q?3)?2?(q?1)(q?2)?0 1?q?1时，不等式恒成立 3

1综上，q的取值范围为?q?2 3

（3）设公差为d，显然，当k?1000,d?0时，是一组符合题意的解，

1?(k?2)d?1?(k?1)d?3[1?(k?2)d]， ∴kmax?1000，则由已知得3

?(2k?1)d??222,d??∴?，当k?1000时，不等式即d??， 2k?12k?5(2k?5)d??2?

2k(k?1)d?1000， ∴d??，a1?a2?...?ak?k?2k?12

2000?2k2∴k?1000时，d?，

??k(k?1)2k?1

解得1000?k?1000k?1999，

2000?2k19981∴k的最大值为1999，此时公差d? ????k(k?1)1999?19981999

2014年普通高等学校招生全国统一考试全国课标I（河南、河北、山西）

理科数学

第Ⅰ卷 （选择题 共60分）

一．选择题：共12小题，每小题5分，共60分。在每个小题给出的四个选项中，只有一项是符合题

目要求的一项。

21.已知集合A={x|x?2x?3?0}，B={x|－2≤x＜2＝，则A?B=

A.[-2,-1] B.[-1,2） C.[-1,1] D.[1,2） (1?i)3

2.= (1?i)2

A.1?i B.1?i C.?1?i D.?1?i

3.设函数f(x)，g(x)的定义域都为R，且f(x)时奇函数，g(x)是偶函数，则下列结论正确的是

A.f(x)g(x)是偶函数 B.|f(x)|g(x)是奇函数

C.f(x)|g(x)|是奇函数 D.|f(x)g(x)|是奇函数

224.已知F是双曲线C：x?my?3m(m?0)的一个焦点，则点F到C的一条渐近线的距离为A

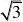
B.3 C

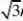
D.3m

5.4位同学各自在周六、周日两天中任选一天参加公益活动，则周六、周日

都有同学参加公益活动的概率

A.1357 B. C. D. 8888

6.如图，圆O的半径为1，A是圆上的定点，P是圆上的动点，角x

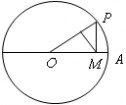
的始边

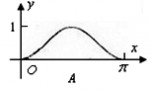
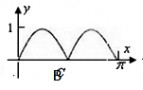
为射线OA，终边为射线OP，过点P作直线OA的垂线，垂足为M，将点M到直线OP的距离表示为x的函数f(x)，则y=f(x)在[0,?]上的图像大致为

7.执行下图的程序框图，若输入的a,b,k分别为1,2,3，则输出的M=

2016715 B. C. D. 3528

1?sin???8.设??(0,)，??(0,)，且tan??，则 22cos?A.

222

?x?y?19.不等式组?的解集记为D.有下面四个命题： x?2y?4?

p1：?(x,y)?D,x?2y??2， p2：?(x,y)?D,x?2y?2, A.3????? B.2????? C.3????? D.2?????2

P3：?(x,y)?D,x?2y?3， p4：?(x,y)?D,x?2y??1.

其中真命题是

A.p2，p3 B.p1，p4 C.p1，p2 D.p1，p3

10.已知抛物线C：y?8x的焦点为F，准线为l，P是l上一点，Q是直线PF与C的一个焦点，若FP?4FQ，则|QF|= 2

75 B. C.3 D.2 22

3211.已知函数f(x)=ax?3x?1，若f(x)存在唯一的零点x0，且x0＞0，则a的取值范围为

A.（2，+∞） B.（-∞，-2） C.（1，+∞） D.（-∞，-1） A.

12.如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的

三视图，则该多面体的个条棱中，最长的棱的长度为

A

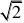
. B

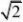
. C.6 D.4

第Ⅱ卷（非选择题 共90分）

本卷包括必考题和选考题两个部分。第（13）题-第（21）题为必

考题，每个考生都必须作答。第（22）题-第（24）题为选考题，考生

根据要求作答。

二．填空题：本大题共四小题，每小题5分。

13.(x?y)(x?y)8的展开式中x2y2的系数为用数字填写答案)

14.甲、乙、丙三位同学被问到是否去过A，B，C三个城市时，

甲说：我去过的城市比乙多，但没去过B城市； 乙说：我没去过C城市；

丙说：我们三人去过同一个城市. 由此可判断乙去过的城市为 .

1(AB?AC)，则AB与AC的夹角为. 2

16.已知a,b,c分别为?ABC的三个内角A,B,C的对边，a=2，且(2?b)(sinA?sinB)?(c?b)sinC，则15.已知A，B，C是圆O上的三点，若AO??ABC面积的最大值为三.解答题：解答应写出文字说明，证明过程或演算步骤。

17.(本小题满分12分)已知数列{an}的前n项和为Sn，a1=1，an?0，anan?1??Sn?1，其中?

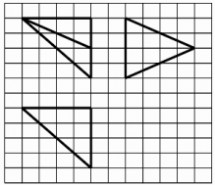
为

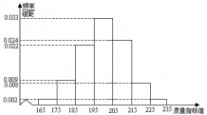
常数.

（I）证明：an?2?an??；

（Ⅱ）是否存在?，使得{an}为等差数列？并说明理由.

18. (本小题满分12分)从某企业的某种产品中抽取500件，测量这些产品的一项质量指标值，由测量结果得如下频率分布直方图：

（I）求这500件产品质量指标值的样本平均数x和样本方差s2（同一组数据用该区间的中点值作代表）；

（Ⅱ）由频率分布直方图可以认为，这种产品的质量指标值Z服从正态分布N(?,?2)，其中?近似为样本平均数x，?2近似为样本方差s2.

（i）利用该正态分布，求P(187.8?Z?212.2)；

（ii）某用户从该企业购买了100件这种产品，学科网记X表示这100件产品中质量指标值为于区间（187.8,212.2）的产品件数，利用（i）的结果，求EX.

若Z～N(?,?2)，则P(????Z????)=0.6826，P(??2??Z???2?)=0.9544.

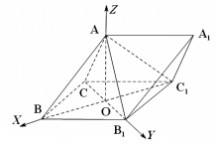
19. (本小题满分12分)如图三棱锥ABC?A1B1C1中，

侧面BB1C1C为菱形，AB?B1C.

（I）证明：AC?AB1；

（Ⅱ）若AC?AB1，?CBB1?60o，AB=Bc，求二面角

A?A1B1?C1的余弦值.

20. (本小题满分12分) 已知点A（0，-2），椭圆E：

x2y2??1(a?b?

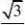
0)，Fa2b2圆的焦点，直线AF

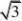
的斜率为，O为坐3

点.

（I）求E的方程；

（Ⅱ）设过点A的直线l与E相交于P,Q两是椭标原点，当?OPQ的面积最大时，求l的方程.

21. (本小题满分

x12分)设函数bex?1

f(x0?aelnx?，曲线y?f(x)在点（1，f(1)）处的切线为y?e(x?1)?2. （I）求a,b； x

（Ⅱ）证明：f(x)?1.

请考生从第（22）、（23）、（24）三题中任选一题作答。注意：只能做所选定的题目。如果多做，则按所做的第一个题目计分，作答时请用2B铅笔在答题卡上将所选题号后的 方框涂黑。

22.（本小题满分10分）选修4—1：几何证明选讲

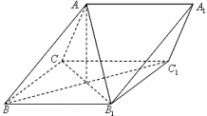
如图，四边形ABCD是⊙O的内接四边形，AB的延长线与DC的延长线交于点E，且CB=CE (Ⅰ)证明：∠D=∠E；

（Ⅱ）设AD不是⊙O的直径，AD的中点为M，且MB=MC，证明：△ADE为等边三角形.

23. （本小题满分10分）选修4—4：坐标系与参数方程

?x?2?tx2y2

??1，直线l：?已知曲线C：（t为参数）. 49?y?2?2t

（I）写出曲线C的参数方程，直线l的普通方程；

（Ⅱ）过曲线C上任一点P作与l夹角为30o的直线，交l于点A，求|PA|的最大值与最小值.

24. （本小题满分10分）选修4—5：不等式选讲

若a?0,b?

0，且11??. ab

（I） 求a3?b3的最小值；

（Ⅱ）是否存在a,b，使得2a?3b?6？并说明理由.

2014年普通高等学校招生全国统一考试全国课标I 答案

1—5ADCAD 6—12 CDCBBCB 13．－20 14．A 15．90° 16

17．【解析】：(Ⅰ)由题设anan?1??Sn?1，an?1an?2??Sn?1?1，两式相减

an?1?an?2?an???an?1，由于an?0，所以an?2?an?? …………6分 （Ⅱ）由题设a1=1，a1a2??S1?1，可得a2??1?1，由(Ⅰ)知a3???1

假设{an}为等差数列，则a1,a2,a3成等差数列，∴a1?a3?2a2，解得??4；

证明??4时，{an}为等差数列：由an?2?an?4知

数列奇数项构成的数列?a2m?1?是首项为1，公差为4的等差数列a2m?1?4m?3

n?1，∴an?2n?1(n?2m?1) 2

数列偶数项构成的数列?a2m?是首项为3，公差为4的等差数列a2m?4m?1 令n?2m?1,则m?

n，∴an?2n?1(n?2m) 2

∴an?2n?1（n?N*），an?1?an?2 令n?2m,则m?

因此，存在存在??4，使得{an}为等差数列. ………12分

18．【解析】：(Ⅰ) 抽取产品质量指标值的样本平均数和样本方差s2分别为

?170?0.02?180?0.09?190?0.22?200?0.33

?210?0.24?220?0.08?230?0.02

?200

222

222 s2???30??0.02???20??0.09???10??0.22?0?0.33??10??0.24??20??0.08??30??0.02

?150 …………6分

（Ⅱ）（ⅰ）由(Ⅰ)知Z～N(200,150)，从而

P(187.8?Z?212.2)?P(200?12.2?Z?200?12.2)?0.6826 ………………9分 （ⅱ）由（ⅰ）知，一件产品中质量指标值为于区间（187.8,212.2）的概率为0.6826 依题意知XB(100,0.6826)，所以EX?100?0.6826?68.26 ………12分

19．【解析】：(Ⅰ)连结BC1，交B1C于O，连结AO．因为侧面BB1C1C为菱形，所以B1C?BC1，且O为B1C与BC1的中点．又AB?B1C，所以B1C?平面ABO，故B1C?AO故AC?AB1 ………6分

（Ⅱ）因为AC?AB1且O为B1C的中点，所以

故OA⊥，从而OA，OB，OB1两两互相垂直． 又因为，所以?BOA??BOC 又 B1O?CO，

以O为坐标原点，OB的方向为x轴正方向，OB为单位长，

建立如图所示空间直角坐标系O-xyz． 因为?CBB1?600，

所以?CBB1为等边三角形．又，则

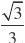
?????B

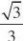
1,0,0，，， A?BC0,?????1???????

???

?

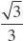
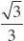
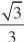
????， AB1??AB?AB?1,0,,BC?BC??1,???11??11???

?

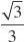
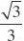
??设n??x,y,z?是平面的法向量，则

yz?0??nAB1?0，即

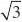
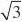
所以可取n? ???xz?0?

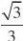
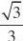
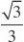
nA1B1?0

??

??mA1B1?0设m是平面的法向量，则?，同理可取m?1, ??

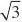
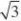
nB1C1?0

nm11则cosn,m??，所以二面角A?A1B1?C1的余弦值为. 7nm7??2c，得c?又?， ?c

ax2

222所以，b?a?c?1 ,故E的方程?y2?1. ……….6分 4

（Ⅱ）依题意当l?x轴不合题意，故设直线l：y?kx?2，设P?x1,y1?,Q?x2,y2? 20

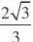
．【解析】(Ⅰ) 设F?c

,0?，由条件知

x2

将y?kx?2代入?y2?1，得?1?4k2?x2?16kx?12?0， 4

3

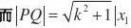
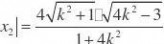
当??16(4k?3)?0

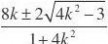
，即k?时，x1,2?

22

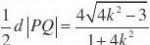
又点O到直线PQ的距离

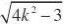
d?

?OPQ的面积S?OPQ? ，

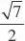
?t，则t?0，S?OPQ?4t4

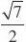
??1， t2?4t?

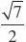
4

t

??0，所以当?OPQ的面积最大时，l的方程为：y??2 或y??2. …………………………12分 abb21．【解析】(Ⅰ) 函数f(x)的定义域为?0,???，f?(x)?aexlnx?ex?2ex?1?ex?1 xxx

由题意可得f(1)?2,f?(1)?e，故a?1,b?2 ……………6分 当且仅当t?2，k?2ex?12（Ⅱ）由(Ⅰ)知，f(x)?elnx?，从而f(x)?1等价于xlnx?xe?x? xex

设函数g(x)?xlnx，则g?(x)?x?lnx，所以当x??0,?时，g?(x)?0，当x??,???时，?

?1?e??1?e??

?1??1?g?(x)?0，故g(x)在?0,?单调递减，在?,???单调递增，从而g(x)在?0,???的最小值为?e??e?

11g()??. ……………8分 ee

2?x设函数h(x)?xe?x?，则h?(x)?e?1?x?，所以当x??0,1?时，h?(x)?0，当x??1,???时，e

h?(x)?0，故h(x)在?0,1?单调递增，在?1,???单调递减，从而h(x)g(x)在?0,???的最小值为

1h(1)??. 综上：当x?0时，g(x)?h(x)，即f(x)?1. ……12分 e

22．【解析】.(Ⅰ) 由题设知得A、B、C、D四点共圆，所以?D=?CBE，由已知得，?CBE=?E , 所以?D=?分

（Ⅱ）设BCN中点为，连接MN,则由知MN⊥所以O在MN上，又AD不是O的直径，M为AD中点，故OM⊥AD， 即MN⊥AD，所以AD//BC,故?A=?CBE， 又?CBE=?E，故?A=?由(Ⅰ)（1）知?D=?E， 所以△ADE为等边三角形． ……………10分

23．【解析】.(Ⅰ) 曲线C的参数方程为：??x?2cos? （?为参数）， ?y?3sin?

直线l的普通方程为：2x?y?6?0 ………5分

（Ⅱ）（2）在曲线C上任意取一点P (2cos?,3sin?)到l的距离为

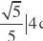
??3sin??6， d4?则|PA|?，其中为锐角．且. ?????6tan???

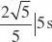
?0sin303

当sin???????1时，|PA

|； 当sin??????1时，|PA|

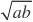
…………10分 1124．【解析】(Ⅰ)

???

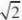
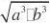
，得ab?2，且当a?b?时等号成立， abd?

故

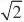
a?b??

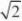
，且当a?b?33a3?

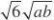
b3的最小值为.…5

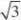
分 （Ⅱ）由(Ⅰ)

知：2a?3b??，

由于＞6，从而不存在a,b，使得2a?3b?6. ……………10分

2014年普通高等学校招生全国统一考试（湖南卷）

数 学（理工农医类）

一、选择题：本大题共10小题，每小题5分，共50分，在每小题的四个选项中，只有一项是符合题目要求的

z?1=i （i的虚数单位）的复数z= z

11111111A、?i B、?i C、??i D、??i 222222221、满足

2、对一个容量为N的总体抽取容量为n的样本，当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时，总体中每个个体被抽中的概率分别为p1、p2、p3，则

A、p1?p2?p3

B、p1?p2?p3

C、p1?p3?p2

D、p1?p3?p2

3、已知f（x），g（x）分别是定义在R上的偶函数和奇函数，且f（x）-g（x）= x?x?1，则f（1）+g（1）=

A、?3 B、?1 C、1 D、3 32

54、(x?2y)的展开式中x2y3的系数是 1

2

A、-20 B、-5 C、5 D、20

【答案】A

5?nn?1?【解析】第n?1项展开式为C5, x?2y????2??n

5?n3?1?n?1?则n?2时, C5x?2y?10x?2y??20x2y3,故选A. ?????????2??2?n2

【考点定位】二项式定理

5、已知命题p：若x>y，则-x<-y ：命题q：若x>y，在命题

①p?q ②p?q ③p?(?q) ④(?p)?q

中，真命题是

A、①③ B、①④ C、②③ D、②④

【答案】C

22【解析】当x?y时,两边乘以?1可得?x??

y,

所以命题

p为真命题,当x?1,y??2时,因为x?y,

所以命题q为假命题,所以②③为真命题,故选C.

【考点定位】命题真假 逻辑连接词

6、执行如图1所示的程序框图，如果输入的t?[?2,2]，则输出的S属于

A、[-6,-2] B、[-5,-1] C、[-4，5] D、[-3,6]

6.【答案】D

【解析】当t???2,0?时,运行程序如下,t?2t?1??1,9?,S?t?3???2,6?,当t??0,2?时 ,则2

S???2,6???3,?1????3,6?,故选D.

【考点定位】程序框图 二次函数

7、一块石材表示的几何体的三视图如图2所示，将该石材切削、打磨、加工成球，则能得到的最大球的半径等于

A、1 B、2 C、3 D、4

【答案】B

【解析】由图可得该几何体为三棱柱,所以最大球的半径为正视图直角三角形内切圆的半径r,

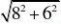
则8?r?6?r?r?2,故选B.

【考点定位】三视图 内切圆 球

8、某市生产总值连续两年持续增加，第一年的增长率为p，第二年的增长率为q，则该市这两年的生产总值的年平均增长率为

A、

C

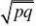
p?q(p?1)(q?1)?1 B、 22 D

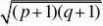
1

2【答案】D 【解析】设两年的平均增长率为x,则有?1?x???1?p??1?

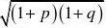
q??x?

【考点定位】实际应用题

9、已知函数发f（x）=sin(x??)，且

A、x=1,故选D. ?2x30f(x)dx?0，则函数f（x）的图象的一条对称轴是 5?7??? B、x= C、x= D、x= 61236

【答案】A

【解析】函数f?x?的对称轴为x???

2?

3?2?k??x????2?k?, ????2???sin??sinx??dx?0??cos???cos??0?????0, ????3??3?0

5?则x?是其中一条对称轴,故选A. 6因为

【考点定位】三角函数图像 辅助角公式

2x10、已知函数f（x）=x+e-12（x<0）与g（x）=x+In（x+a)的图象在存在关于y轴对称点，则2

a的取值范围是

（-?（A、

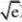
B、

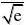
C

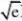
、（-?10.【答案】B

2【解析】由题可得存在x0????,0?满足x0?e0?x（

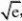
D

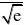
、 12???x0??ln??x0?a? 2

11?ex0?ln??x0?a???0,当x0取决于负无穷小时,ex0?ln??x0?a??趋近于??,因为函数22

1y?ex?ln??x?a??

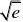
在定义域内是单调递增的,

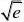
所以lna?a故选B. 2

【考点定位】指对数函数 方程

二、填空题，本大题共6小题，考生作答5小题，每小题5分，共25分

(一)选做题(请考生在第11，12，13三题中任选两题作答，如果全做，则按前两题记分）

?x?2?cosa?l11．在平面直角坐标系中，倾斜角为的直线 与曲线 C:?（a为参数） 4y?1?sina?

交于A，B两点，且 AB?2.以坐标原点O为极点，x轴正半轴为极轴建立极坐标

系，则直线l的极坐标方程是_________。

12.如图3，已知AB，BC

是

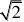
BC=

O的两条弦，AO?BC，

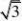
AB= O的半径等于________。

13．若关于x的不等式 ax?2?3的解集为 ?x|? a=________. ??51??x??，则 33?

(二)必做题(14-16题)

?y?x,?14若变量 x,y满足约束条件 ?x?y?4,且 z?2x?y的最小值为-6，则 k?_______。 ?y?k,?

15.如图4正方形ABCD和正方形DEFG的边长分别为a,b(a<b),

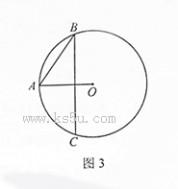
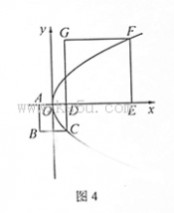
原点O为AD的中点，抛物线 y2?2px(p?0)经

过C、F两点，则

15.

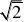
1 b?_________。 a

?a2?paa?a??a????1,

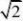
1. 【解析】由题可得C?,?a?,F??b,b?,则?2?a?b?2??2??b?2p??b??2?

?

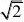
【考点定位】抛物线

16

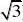
．在平面直角坐标系中，O为原点 A(?1

C(3 0)动点D满足 CD

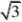
?1，则 OA?OB?OD的最

大值是__________。

16.【答案】s,s?i?n???【解析】动点D的轨迹为以C为圆心的单位圆,则设为?3?co??0

??,?2,则

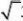
OA?OB?OD

?

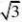
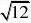
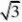
，因为cos?si?n的最大值为2,所以OA?OB?O?故填

【考点定位】参数方程 圆 三角函数

三、解答题：本大题共6小题．共75分，解答应写出文字说明、证明过程或演算步骤

17 .(本小题满分l2分)

某企事业有甲、乙两个研发小组，他们研发新产品成功的概率分别为 23和

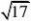
，现安排甲组研发新产35

品A，乙组研发新产品

B，设甲、乙两组的研发相互独立。

(1)求至少有一种新产品研发成功的概率；

(II)若新产品A研发成功，预计企业可获利润120万元；若新产品B研发成功，预计企业可获利润100万元，求该企业可获利润的分布列和数学期望

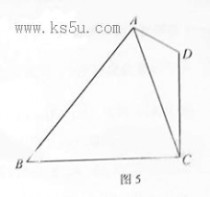
18． （本小题满分l2分）

如图5，在平面四边形ABCD中，AD?1,CD?2,AC? (I) 求cos?CAD的值

(II)若cos?BAD? ?CBA?146

求BC的长

19. （本小题满分l2分）

如图6，四棱柱ABCD?

ACBD?O,AC11

(I)证明：O1O?底面ABCD； 所有棱长都相等，A1B1

C的1DB1D1?O1，四边形ACC1A1和四边形BDD1B1均为矩形。 1

(II)若?CBA?60，求二面角C1?OB1?D的余弦值。

20. （本小题满分13分）

已知数列?an?满足a1?1,an?1?an?p,n?N. n? (I)若?an?是递增数列，且a1,2a2,3a3成等差数列，求p的值； (II)若p?

1，且?a2n?1?是递增数列，?a2n?是递减数列，求数列?an?的通项公式。 2

x2y2

21、如图7，O为坐标原点，椭圆C1:2+2=1（a>b>0）的左、右焦点分别为F1，F2，离心率为e1：ab

x2y2双曲线C22-2=1的左、右焦点分别为F3，F4，离心率为e2。已知e1e

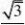
2，

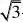
且F2F4。 ab（Ⅰ）求C1、C2的的方程；

求四边形APBQ面积的最小值 （Ⅱ）过F1做C1的不垂直于y轴的弦AB，M为AB的中点，当直线OM与C2交于P，Q两点时，

22、已知常数a>0，函数f（x）=In（1+ax）-2x。 x+2

（0，+?）（Ⅰ）讨论f（x）在区间上的单调性；

（Ⅱ）若f（x）存在两个极值点x1、x2，且f（x1）+f（x2）>0，求a的取值范围

一.选择题.

4.【答案】A

5?nn?1?【解析】第n?1项展开式为C5, x?2y????2??n

5?n3?1?n?1?则n?2时, C5

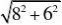
x?2y?10x?2y??20x2y3,故选A. 学科网 ?????????2??2?n2

【考点定位】二项式定理

5.【答案】C

【解析】当x?y时,两边乘以?1可得?x??y,所以命题p为真命题,当x?1,y??2时,因为x2?y2,所以命题q为假命题,所以②③为真命题,故选C.

【考点定位】命题真假 逻辑连接词

6.【答案】D [来源学科网]

【解析】当t???2,0?时,运行程序如下,t?2t?1??1,9?,S?t?3???2,6?,当t??0,2?时,2

S?t?3???3,?1?,则S???2,6???3,?1????3,6?,故选D. 学科网

【考点定位】程序框图 二次函数

7.【答案】B

【解析】由图可得该几何体为三棱柱,所以最大球的半径为正视图直角三角形内切圆的半径r,则8?r?6?r?r?2,故选B.

【考点定位】三视图 内切圆 球

【考点定位】指对数函数 方程

二.填空题

.

13.

【答案】?3

?5??3a?2?3??a??3,故填?3. 【解析】由题可得??1a?2?3??3

【考点定位】绝对值不等式

14.【答案】?2 [来源学*科*网]

【解析】求出约束条件中三条直线的交点为?k,k?,?4?k,k?,?2,2?,学科网

且y?x,x?y?4的可行域如图,所以k?2,则当?k,k?为最优解时,3k??6?k??2,当?4?k,k?为最优解时,2?4?k??k??6?k?14, 因为k?2,所以k??2,故填?2.[来源:Z.xx.k.Com]

【考点定位】线性规划

15.

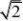
1 ?a2?paa?a??a????1,

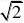
1. 【解析】由题可得C?,?a?,F??b,b?,则?2a??bb?2p?b22???????2??

?

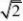
【学科网考点定位】抛物线

【解析】(1)解:设至少有一组研发成功的事件为事件A且事件B为事件A的对立事件,则事件B为一种新

产

则数学期望

E??0?2412

?120

??100??220??32?20?88?130. 151555

【考点定位】分布列 期望 独立试验的概率

18.如图5,在平面四边形ABCD中,AD?1,CD?2,AC.

(1)求cos?CAD的值;

(2)若cos?BAD?,sin?CBA?,求BC的长. 6

二 : 2016年河北高考数学试卷及答案

2016年河北高考数学考试于6月7日下午15:00-17:00举行，具体其它科目考试时间请查看全国各地2016年高考时间安排。

中学学科网会在6月7日数学考试结束后的第一时间公布2016年河北高考数学试卷及答案，并为广大师生提供名师点评试卷，在线估分，最及时的高考成绩查询、高考录取分数线、高考报志愿填报等信息。敬请期待！

中学学科网2016年高考全程跟踪，在线即时估分，点击进入2016年高考专题。

点击进入2016年河北高考|2016年河北高考数学试卷及答案|，|2016河北高考成绩查询|，|2016年河北高考分数线|，|2016年河北高考作文|。

2016年河北高考试卷及答案
2016河北高考语文试卷及答案	2016河北高考文数试卷及答案
2016河北高考理数试卷及答案	2016河北高考英语试卷及答案
2016河北高考文综试卷及答案	2016河北高考理综试卷及答案

距离2016年高考越来越近，为了帮助广大考生全力备战2016年高考，小编带你重新回顾一下2015年河北高考数学试卷：2015年河北卷仍然呈现了“起点低，坡度缓，试题难度呈阶梯式上升”的特点，但较2014年试题要难度有所增加，特别是选择题第12题与填空题第16题难点有所增加，其余选择题与填空题难度均有所降低，都很容易想到解题方向，体现了高中新课程标准的要求与理念，即注重基础知识，基本技能，基本思想方法…[查看详细]

中学学科网历年各地高考数学试题回顾，数学2015|数学2014|数学2013|数学2012|数学2011。

最后，中学学科网祝广大考生金榜提名，实现理想！

倾力推荐>>2016年高考 5月各学科复习指导
资讯专题>>各省市2016年高考考试志愿填报时间2016年全国各省市高考时间
备战2016年高考临考指南2016年高考志愿填报指南
倾力推荐>>2016年高考押题预测卷2016年高考考前最后一卷
资料专题>>各地历年高考试题各地历年高考模拟试题

三 : 上海市2011高考理科数学试卷及答案

2011年上海高考数学试卷（理）

-------------------------------------------------------------------------

word版本下载地址：

图片版本浏览地址：http://www.zxxk.com/Feature/2011gk/AInfo.aspx?InfoID=137565

解析答案下载地址：请关注此文章以待更新

本文标题：2011高考数学试卷及答案-2014年全国数学各省高考试卷及答案
本文地址： http://www.61k.com/1142450.html