一 : 2000—2012年考研数学(一)真题及答案解析 19

二 : 2012年深圳中考语文试题及答案

2012年广东省深圳中考语文试题及答案

第一部分 选择题（1—4题）

一、本大题共4小题，每题3分，共12分

1. 请选出下列词语中加点字读音正确的一项（ ）

A. zhě jí róng qì

B.piāo yìn zhù qù

C. 追溯sù 叱咤chà 箱箧qiè 瘦骨嶙峋xún

D. óu yīn chì lín

【答案】B

2.请选出下列句子中加点成语运用有误的一项（ ）

A顶着肋骨被撞断和肝脏破裂的剧痛，停稳汽车，保障了乘客的安全。[www.61k.com）

B.

C.

D.这篇小说，人物个性鲜明，情节抑扬顿挫，语言幽默诙谐，让人只想先睹为快

【答案】D

3.请选出下列选项中衔接排序正确的一项。（ ）

桂花象征着友好、吉祥和光荣。

①月桂树叶编织成的“桂冠”成了“光荣称号”的代名词

②《吕氏春秋》中以“物之美者，招摇之桂”称赞桂花是世界上最美好的东西 ③“蟾宫折桂”则成为人们对读书人金榜题名的美好祝愿

④某些少数民族地区青年男女也常以赠送桂花来表示爱慕之情

⑤战国时期，韩燕两国曾以相互馈赠桂花来表示亲善友好

A.⑤③②④① B.①⑤②④③ C.⑤④②③① D.②⑤①③④

【答案】C

4.请选出下列说法正确的一项( )

A.“那晚，妹妹的角色没有一句台词。”这个单句的主干是“妹妹没有台词”。

B．序是一种文体，有书序和赠序之分，《送东阳马生序》是一篇赠序。

C．“闭了眼，树上仿佛已经满是桃儿、杏儿、梨儿。”这句话运用了比喻的修辞手法。

D.“通过新闻传媒对深圳‘5.26’酒后飙车致人伤亡事件”的追踪报道，使我们深刻认识到醉驾的严重危害。“这个句子没有语病。

【答案】B

第二部分 非选择题（5—18）

二、本大题共1小题，没空1分，共15分

5.请在下面横线上填空相应的句子。

（1）锦江春色来天地，玉垒浮云变古今（杜甫《登楼》

（2） 绿树村边合，青山郭外斜（孟浩然《过故人庄》）

（3）不畏浮云遮望眼，自缘身在最高层（王安石《登飞来峰》）

（4）海日生残夜，江春入旧年（王湾《次北固山下》）

（5）月下飞天境，云生结海楼（李白《渡荆门送别》）

（6）春潮带雨晚来急，野渡无人舟自横（韦应物《滁州西涧》）

（7）鸡声茅店月，人迹板桥霜（温庭筠《商山早行》）

（8）忽如一夜春风来，千树万树梨花开。（《岑参《白雪歌送武判官归京》》

2012中考语文 2012年深圳中考语文试题及答案

（9）白头吊古风霜里，老木沧波无限悲（陈与义《登岳阳楼》） （10）水是眼波横，山是眉峰聚（王观《卜算子送鲍浩然之浙东》）

（11）谁道人生无再少？门前流水尚能西！休将白发唱黄鸡（苏轼《浣溪沙》） （12）采菊东篱下，悠然见南山（陶渊明《饮酒》）

（13）“穷则独善其身，达则兼济天下，”这是世世代代中国儒家知识分子的终身追求，是欧阳修“与民同乐”的大道践行，是才华被埋没时韩愈借千里马发出的“其真不知马也”的愤懑控诉，是孟子希望统治者施行仁政而提出的“天时不如地利，地利不如人和”的谆谆告诫，更是范仲淹“先天下之忧而忧，后天下之乐而乐”的千古吟诵----万千语言表达，一样赤子情怀。(www.61k.com]

三、本大题共三段阅读，计12小题，共33分

（一）阅读下面选文，完成6-8题（10分）

陈胜、吴广乃谋曰：“今亡亦死，举大计亦死；等死，死国可乎？”陈胜曰：“天下苦秦久矣。吾闻二世少子也，不当立，当立者乃公子扶苏。扶苏以数谏故，上使外将兵。今或闻无罪，二世杀之。百姓多闻其贤，未知其死也。项燕为楚将，数有功，爱士卒，楚人怜之。或以为死，或以为亡。今诚以吾众诈自称公子扶苏、项燕，为天下唱，宜多应者。”吴广以为然。乃行卜。卜者知其指意，曰：“足下事皆成，有功。然足下卜之鬼乎？”陈胜、吴广喜，念鬼，曰：“此教我先威众耳。”乃丹书帛曰“陈胜王”，置人所罾鱼腹中。卒买鱼烹食，得鱼腹中书，固以怪之矣。又间令吴广之次所旁丛祠中，夜篝火，狐鸣呼曰：“大楚兴，陈胜王”。卒皆夜惊恐。旦日，卒中往往语，皆指目陈胜。

吴广素爱人，士卒多为用者。将尉醉，广故数言欲亡，忿恚尉，令辱之，以激怒其众。尉果笞广。尉剑挺，广起，夺而杀尉。陈胜佐之，并杀两尉。召令徒属曰：“公等遇雨，皆已失期，失期当斩。藉第令毋斩，而戍死者固十六七。且壮士不死即已，死即举大名耳，王侯将相宁有种乎！”徒属皆曰：“敬受命。”（节选自司马迁《陈涉世家》）

6.解释下列加点的词

⑴为天下唱 通假字，同“倡”，首发。 ．

⑵楚人怜之 爱戴。 ．

⑶置人所罾鱼腹中 鱼网，这里是名词用为动词，用网捕。 ．

7.将下列句子翻译成现代汉语

⑴卒中往往语，皆指目陈胜

士卒中到处都在谈论，都指指点点着、互相用眼睛示意注意陈胜。

⑵藉第令毋斩，而戍死者固十六七

即使免于斩刑，但戍边而死的本来就有十分之六七。

8.选段再现了陈胜、吴广大泽乡揭竿而起的英雄壮举，上古神话《共工怒触不周山》则曲折反映了原始部落间的激烈斗争。请比较陈胜和共工这两个人物形象的异同。

【答案】都是不畏牺牲，不怕强权，勇敢反抗，威武不屈挑战旧制度旧秩序的英雄形象。但反抗的目的不同，共工是为了争夺帝位，而陈胜是为了求生存，是为了反抗暴政；共工形象暴烈鲁莽，而陈胜智慧沉着；共工孤独反抗，而陈胜带领被压迫的群众斗争。

（二）阅读下面文段，完成9-12题（9分）

中国人的“忍”

⑴“忍”字头上一把刀。每个耳聪目明的中国人或许都听过这句话。

⑵孔夫子说，“小不忍则乱大谋”；孟夫子说，“天将降大任于斯人也，必先苦其心志，劳其筋骨，饿其体肤”。圣人们强调，为人做事，万般皆需忍受、忍耐。

⑶中国人因忍字而得以百炼成钢的数不胜数，因逞强好胜而走麦城的也不少。唐代高宗时，张公艺不仅位九世同堂，人生如此圆满，引得皇帝也羡慕，遂问其秘诀，张公

2012中考语文 2012年深圳中考语文试题及答案

艺在纸上写下“一百个忍字”。（www.61k.com)高宗喟叹，原来如此。大家耳熟能详的韩信，他早年能忍胯下之辱，终成大业，真个是“无度不丈夫”；后来却张扬高调，浑然忘记了“忍”字，颇有些“庸人得志”，最后横死吕后之手也就不冤。

⑷“吃得苦中苦，方为人上人”。为了遥想中的绚烂未来，人们忍受着当下的种种不堪，人们夸赞着“忍”，绝口不想提心中暗暗怀想的他日之收获；若百忍后仍不能得道，自然也会有诸多温润的慰藉理由。

⑸英国哲学家罗素在其《论中国人的性格》一文中说，“中国人的性格的另一最大特点，是喜欢妥协，易屈服于公众舆论。”封建社会官场中的“见风使舵”，生活细节的“防患于未然”，平头百姓们普遍存在的谨小慎微、办事圆滑等特点，皆可在各怀心事的“忍”字上找到源头。罗素由是感叹，“没有什么能比中国人的忍耐性更令欧洲人吃惊的了”。

⑹一个忍字，两副面孔。一面是温和下的良善，一面是摇摆中的功利；有些人得道，有些人中毒。鲁迅笔下的冷漠看客，便是一“忍”成痴，浑浑噩噩，麻木不仁，无异于行尸走肉。忽然明白了鲁迅的可贵，只因他在崇尚忍耐的国度，居然可以从来不忍。

⑺“忍”字头上一把刀---“每临大事有静气”为了一个远大的目标，暂时的隐忍蛰伏自是上策，然刀为利器，久忍终恐伤人。

⑻忍该忍之事，说当说之话，为比为之事。(选自《青年文摘》2012年第12期)

9.本文的主要观点是什么？（2分）

【答案】忍该忍之事，说当说之话，为必为之事。

10.选文第三段除了举例论证外，还运用了什么论证方法？它有何作用？（3分）

【答案】还运用了对比手法，对比了忍的成功和不忍的失败，鲜明地证明了该忍时候要忍的道理。

11.第二段结尾处的“忍受”、“忍耐”两个词语是否重复累赘？为什么？（2分）

【答案】不重复。“忍受”是把痛苦磨难等勉强地承受下来。“忍耐”是把痛苦的感觉和想发作的情绪抑制下来。

12.“忍”是一柄双刃剑。请具体谈谈现实生活中你该如何把握“忍”的“度”（2分）

【答案】对伤到自己的一些无关原则的小事就忍下来，不必斤斤计较；对必须付出的磨难代价，如学习的艰辛，锻炼的艰苦，都要忍受下来。但是，对于坏人坏事，对于有损我们社会我们国家的思想行为，我们要敢于大声说“不”或者“no”，并且当出手时就出手哇，风风火火闯九州哇，嘿哟嘿！

（三）阅读下面文段，完成13-17题（14分）

夜的尽头是家的灯光

⑴父亲在河南开封长大。父亲一直在奋斗，考上了武汉，留武汉工作，结婚，生了我。他的奋斗，换来了理想的大学合适的职业和幸福的家庭。这也许就是别人眼中我平凡的父亲——离家游子。他的心也许一半是黄河，一半是长江。

⑵我仍记得，父亲接我放学后带我直奔前往开封的列车，夜色如墨，列车摇晃着我疲倦的神经，懵懂的我从未读懂过父亲那晚的表情，他一直看着窗外，眼里似乎闪烁着什么，但不是眼泪，是一种难于言说的情感??火车哀鸣着停止了摇晃，我从父亲的怀里惺忪醒来，又是一段颠簸的汽车行程后，父亲拽着我，高一脚、低一脚地赶往乡村，黄河的风凉湿了父亲的手心。

⑶沉沉夜色，静默村庄，木门一开，黑漆漆的夜色瞬间被老屋里的灯光穿透，我有些晕眩，模糊的视线里烟雾缭绕，纸钱的火苗摇摆在黑红的棺材前，父亲嚎啕着，跪地不起??

2012中考语文 2012年深圳中考语文试题及答案

⑷那时的我的确太小，奶奶去世，我竟没有一滴眼泪。[www.61k.com]长大了一点儿，我才明白，和自己深爱的人离别，心有多么痛。对于父亲也是，造就自己、牵着自己长大的人走了，并且是永远地走了??

⑸我一直单纯地认为这就是父亲全部的痛苦。

⑹现在我知道，其中还夹杂着一丝恐慌：他也许在奶奶身上已经看到了自己的影子。 ⑺奶奶是中秋节去世的。几年之后的一个中秋节，刚搬进新房不久，父亲在奶奶的照片前点了一炷香，慢慢的鞠了个躬，缓缓坐下，然后静静地注视着照片。良久，父亲看着我，轻轻地说：“今后别再让你妈生气了。”

⑻也许他在遗憾自己小的时候没有好好报答自己的母亲，现在没机会了。不知道天下有没有人不想出去闯一番事业然后衣锦还乡的？不知道最后的回家在终日等待面前是否显得渺小？不知道天下有多少父母再也等不到儿女回家的那一天？

⑼可是，谁又能改变这一切？也许最深的母子之情只能属于童年，因为那时，孩子一无所有。到现在，我也不知道我们这一代独生子女离家后，天下将会有多少老无所依的父母。 ⑽父亲那眼神中，也许还有责任。父亲的母亲已经将全部交给父亲，我懂得有一天，父亲也会将全部交给我，虽然我极不愿那一天的到来。但我知道，这个轮回终会由我接下去！ ⑾那晚，窗外的夜色似乎被满月稀释过一般，我和父亲静静地坐在一起，我能感受到，他害怕失去的，不只是他的母亲，还有他的孩子。他知道，有一天他的孩子也会离家的。 ⑿父亲一直在弥补，他总是一有时间就带我和母亲回开封看看，摇晃的火车不再让我疲倦，如墨的夜色早已被家的灯光照耀的温暖、明媚！父亲总是把手搭在我的肩膀上，我总是握着母亲还未衰老的手，渐渐意识到：该轮到我了！

（作者：马家越 选自《读者》2012第11期）

13.通读全文，你认为文中“我”所领悟到的父亲表情和眼神中的“难于言说”的情感包括哪些？（3分）

【答案】⑴造就自己、牵着自己长大的母亲永远的走了，父亲深深为深爱的母亲离别而心痛。⑵意识到有一天自己也像母亲一样，没有儿子在身边。⑶遗憾自己没来得及报答母亲。⑷意识到承当起母亲留下来的责任。

14.写出第11中的含义。（2分）

【答案】动词，这里是“冲淡”的意思，夜色因为有了满满的圆月亮照射，而不再黢黑，有了薄薄的光亮。

15.第7段划线句子运用何种人物描写方法？有什么表达效果？（3分）

【答案】动作描写，心理描写。表达了父亲对奶奶深深的思念、没有好好报答甚至曾经让奶奶生气的愧疚。

16.请品析第8段划线的句子（3分）

【答案】这一组句子，使用了反复的修辞，疑问的句式，议论抒情的表达方式，层层深入对父亲没机会报答奶奶这类现象进行了评价思考。表达了这样深刻的思想：人们都追求的出外闯荡干出大事业再衣锦还乡，但这样的抱负比起父母亲守侯盼望游子的亲情，简直微不足道；而且让人悲哀的是，很多父母是看不到孩子成功的那一天就离开了人间的。作者对我们在成功与亲情之间的选择进行了反思，表达了无奈的质疑。

17.春晚一曲《常回家看看》温暖了万千家庭；也有人说，父母、子女之间，身体与身体的距离不等于心灵与心灵的距离。读完上文，请结合你和父母的关系，谈谈你的看法。（3分）

【答案】儿行千里母担忧，古人云父母在不远游。父母子女之间虽然身体与身体的距离，不等于心灵的距离，甚至空间距离越发增加了心灵的贴近。但是，远离毕竟违背了父母希望儿女绕膝的亲情需要，毕竟牺牲了父母对天伦之乐的享受，毕竟造成了父母对远方游子的牵

2012中考语文 2012年深圳中考语文试题及答案

挂担忧。（www.61k.com）再说，做儿女的如果心灵没有距离，哪里会舍得让自己的父母思念儿女呢？如果能够身体无距离的生活在一起却拒绝了，那么这是心灵没有距离吗？

四、本大题共一小题，共40分

18.命题作文

你是挫折，为我的世界荡开圈圈涟漪；你是拼搏，为我的世界激起朵朵浪花；你是追梦，为我的世界犁出段段航程；你是呵护的春风，是关爱的雨露，是友善的阳光；你是思辨的春雨，是求索的夏风，是奉献的秋实，是感恩的冬雪??那些人，那些物，那些事，让我的世界变得如此亮丽。

(1) 请以“我的世界因你而亮丽”为题，写一篇不少于600字，不超过900字的文章。除诗歌外，文体不限。

(2) 文中不得出现真实的校名、人名，否则扣分，如无法避免，请以**代替。

【答案】略

贵州张宗明编辑整理

三 : 2012年全国高考理科数学试题及答案-新课标

绝密*启用前

2012年普通高等学校招生全国统一考试（新课标）

理科数学

注息事项:

1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题)两部分。(www.61k.com)答卷前，考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。

2.问答第Ⅰ卷时。选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动.用橡皮擦干净后，再选涂其它答案标号。写在本试卷上无效.

3.回答第Ⅱ卷时。将答案写在答题卡上.写在本试卷上无效·

4.考试结束后.将本试卷和答且卡一并交回。

第一卷

一． 选择题：本大题共12小题，每小题5分，在每小题给同的四个选项中，只有一项是符合

题目要求的。

（1）已知集合A?{1,2,3,4,5},B?{(x,y)x?A,y?A,x?y?A}；,则B中所含元素

的个数为（ ）

(A)3 (B)6 (C)? (D)??

（2）将2名教师，4名学生分成2个小组，分别安排到甲、乙两地参加社会实践活动，

每个小组由1名教师和2名学生组成，不同的安排方案共有（ ）

(A)12种 (B)10种 (C)?种 (D)?种

（3）下面是关于复数z?2的四个命题：其中的真命题为（ ） ?1?i

p1:z?2 p2:z2?2i p3:z的共轭复数为1?i p4:z的虚部为?1 (A)p2,p3 (B) p1,p2 (C)p?,p? (D)p?,p?

x2y23a（4）设F1F2是椭圆E:2?2?1(a?b?0)的左、右焦点，P为直线x?上一点， 2ab

E的离心率为（ ） ?F2PF1是底角为30的等腰三角形，则

(A)12? (B) (C) 23?(D)? ?

（5）已知?an为等比数列，a4?a7?2，a5a6??8，则a1?a10?（ ）

?(A)7 (B) 5 (C)?? (D)??

2012年数学高考 2012年全国高考理科数学试题及答案-新课标

（6）如果执行右边的程序框图，输入正整数N(N?2)和

实数a1,a2,...,an，输出A,B，则（ ）

(A)A?B为a1,a2,...,an的和

(B)A?B为a1,a2,...,an的算术平均数 2

(C)A和B分别是a1,a2,...,an中最大的数和最小的数

(D)A和B分别是a1,a2,...,an中最小的数和最大的数

（7）如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（ ）

(A)6 (B) 9 (C)?? (D)??

2（8）等轴双曲线C的中心在原点，焦点在x轴上，C与抛物线y?16x的准线交于A,B

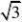
两点，AB?；则C的实轴长为（ ）

(A)

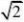
(B

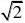
) (C)?

（9）已知??0，函数f(x)?sin(?x? ?)在(,?)上单调递减。[www.61k.com］则?的取值范围是（ ） 42?1513(A)[,] (B) [,] 2424

1 (C) (0,] (D)(0,2] 2

（10） 已知函数f(x)?1；则y?f(x)的图像大致为（ ）

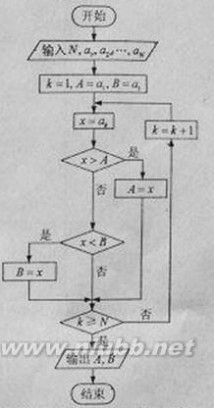
ln(x?1)?x

2012年数学高考 2012年全国高考理科数学试题及答案-新课标

（11）已知三棱锥S?ABC的所有顶点都在球O的求面上，?ABC是边长为1的正三角形，

SC为球O的直径，且SC?2；则此棱锥的体积为（ ）

(A)

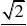
(B

) (C

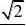
) (D)

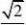
1xe上，点Q在曲线y?ln(2x)上，则PQ最小值为（ ） 2（12）设点P在曲线y?

(A)1?ln2 (B

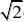
) ?ln2) (C) 1?ln2 (D)

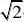
?ln2)

第Ⅱ卷

本卷包括必考题和选考题两部分。（www.61k.com)第13题~第21题为必考题，每个试题考生都必须作答，第22-第24题为选考题，考生根据要求做答。

二．填空题：本大题共4小题，每小题5分。

（13）已知向量a,b夹角为45

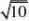
，且a?1,2a?b?；则b?_____ ?

?x,y?0? (14) 设x,y满足约束条件：?x?y??1；则z?x?2y的取值范围为

?x?y?3?

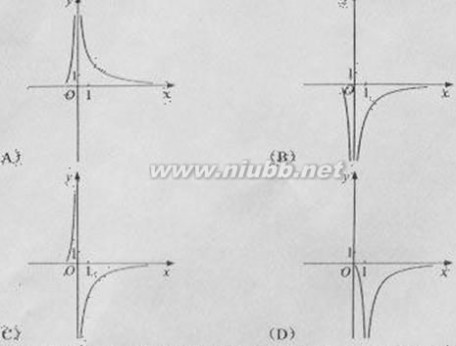
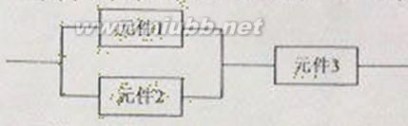
（15）某个部件由三个元件按下图方式连接而成，元件1或元件2正常工作，且元件3

正常工作，则部件正常工作，设三个电子元件的使用寿命（单位：小时）均服从

正态分布N(1000,50)，且各个元件能否正常相互独立，那么该部件的使用寿命

超过1000小时的概率为

2

2012年数学高考 2012年全国高考理科数学试题及答案-新课标

（16）数列{an}满足an?1?(?1)nan?2n?1，则{an}的前60项和为三、解答题：解答应写出文字说明，证明过程或演算步骤。[www.61k.com］

（17）（本小题满分12分）

已知a,b,c分别为?ABC三个内角A,B,C

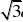
的对边，acosCsinC?b?c?0

（1）求A （2）若a?2，?ABC的面积为3；求b,c。

18.（本小题满分12分）

某花店每天以每枝5元的价格从农场购进若干枝玫瑰花，然后以每枝10元的价格出售， 如果当天卖不完，剩下的玫瑰花作垃圾处理。

（1）若花店一天购进16枝玫瑰花，求当天的利润y(单位：元)关于当天需求量n （单位：枝，n?N）的函数解析式。

（2）花店记录了100天玫瑰花的日需求量（单位：枝），整理得下表：

以100天记录的各需求量的频率作为各需求量发生的概率。

（i）若花店一天购进16枝玫瑰花，X表示当天的利润（单位：元），求X的分布列，

数学期望及方差；

（ii）若花店计划一天购进16枝或17枝玫瑰花，你认为应购进16枝还是17枝？

请说明理由。

2012年数学高考 2012年全国高考理科数学试题及答案-新课标

（19）（本小题满分12分） 如图，直三棱柱ABC?A1B1C1中，AC?BC?1AA1， 2D是棱AA1的中点，DC1?BD

（1）证明：DC1?BC

（2）求二面角A1?BD?C1的大小。［www.61k.com]

2012年数学高考 2012年全国高考理科数学试题及答案-新课标

（20）（本小题满分12分）

设抛物线C:x2?2py(p?0)的焦点为F，准线为l，A?C，已知以F为圆心， FA为半径的圆F交l于B,D两点；

0（1）若?BFD?90，?ABD的面积为42；求p的值及圆F的方程；

（2）若A,B,F三点在同一直线m上，直线n与m平行，且n与C只有一个公共点，

求坐标原点到m,n距离的比值。(www.61k.com］

（21）（本小题满分12分）

已知函数f(x)满足满足f(x)?f?(1)e

（1）求f(x)的解析式及单调区间；

（2）若f(x)?x?1?f(0)x?12x； 212x?ax?b，求(a?1)b的最大值。 2

2012年数学高考 2012年全国高考理科数学试题及答案-新课标

请考生在第22,23,24题中任选一题做答，如果多做，则按所做的第一题计分， 做答时请写清题号。（www.61k.com）

（22）（本小题满分10分）选修4-1：几何证明选讲

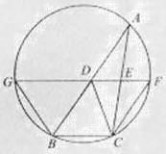
如图，D,E分别为?ABC边AB,AC的中点，直线DE交

?ABC的外接圆于F,G两点，若CF//AB，证明：

（1）CD?BC；

（2）?BCD?GBD

2012年数学高考 2012年全国高考理科数学试题及答案-新课标

（23）本小题满分10分)选修4—4；坐标系与参数方程 已知曲线C1的参数方程是??x?2cos?(?为参数)，以坐标原点为极点，x轴的正半轴

?y?3sin?

为极轴建立坐标系，曲线C2的坐标系方程是??2，正方形ABCD的顶点都在C2上， 且A,B,C,D依逆时针次序排列，点A的极坐标为(2,

（1）求点A,B,C,D的直角坐标；

（2）设P为C1上任意一点，求PA?PB?PC?PD的取值范围。［www.61k.com)

（24）（本小题满分10分）选修4?5：不等式选讲 已知函数f(x)?x?a?x?2

（1）当a??3时，求不等式f(x)?3的解集；

（2）若f(x)?x?4的解集包含[1,2]，求a的取值范围。

2222?3)

2012年数学高考 2012年全国高考理科数学试题及答案-新课标

2012年理科数学答案

一（1）【解析】选Dx?5,y?1,2,3,4，x?4,y?1,2,3，x?3,y?1,2，x?2,y?1共10个

（2）【解析】选A

12 甲地由1名教师和2名学生：C2C4?12种

（3）【解析】选C

z?22(?1?i)???1?i ?1?i(?1?i)(?1?i)

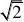
p1:z?

（4）【解析】选C p2:z2?2i，p3:z的共轭复数为?1?i，p4:z的虚部为?1

3

2c3? a4?PF2?F2F1?2(a?c)?2c?e? ?F2PF1是底角为30的等腰三角形

（5）【解析】选Da4?a7?2，a5a6?a4a7??8?a4?4,a7??2或a4??2,a7?4 a4?4,a7??2?a1??8,a10?1?a1?a10??7

a4??2,a7?4?a10??8,a1?1?a1?a10??7

（6）【解析】选C

（7）【解析】选B 该几何体是三棱锥，底面是俯视图，高为3

此几何体的体积为V?11??6?3?3?9 32

2222（8）【解析】选C 设C:x?y?a(a?0)交y?16x的准线l:x??

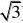
4于

A

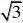
(?B(?4,?

得：a2?(?4)2?2?4?a?2?2a?4

（9【解析】选A ??2?(?x??

4)?[5?9?,] 不合题意 排除(D) 44

?3?5???1?(?x?)?[,] 合题意 排除(B)(C) 444

?????3?)?????2，(?x?)?[??,???]?[,] 2424422

????3?15???? 得：???,????2424224另：?(???

xg(x)?ln(?1x?)x??gx(?（10） 【解析】选B 1?x

?g?(x)?0???1x?0?g,x?()?0?x?0g?x()g?(0)0

2012年数学高考 2012年全国高考理科数学试题及答案-新课标

得：x?0或?1?x?0均有f(x)?0 排除A,C,D

（11）【解析】选A

?

ABC的外接圆的半径r?O到面ABC

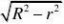
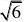
的距离d?? 33

SC为球O的直径?点S到面ABC

的距离为2d?

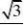
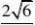
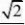
此棱锥的体积为V?11 S?ABC?2d??33

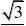
另：V?1排除B,C,D S?ABC?2R?31xe与函数y?ln(2x)互为反函数，图象关于y?x对称 2（12）【解析】选A 函数y?

1x1x 函数y?e上的点P(x,e)到直线y?

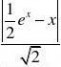
x的距离为d? 22

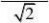
设函数g(x)?1x1e?x?g?(x)?ex?1?g(x)min?1?ln2?dmin? 22 由图象关于y?x对称得：PQ

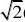
最小值为2dmin??ln2)

（13）【解析】b

?_____

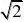
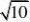
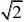
2a?b??(2a?b)?10?4?b?4bcos45??10?b?(14)【解析】z?x?2y的取值范围为[?3,3]

约束条件对应四边形OABC边际及内的区域：O(0,0),A(0,1),B(1,2),C(3,0)

则z?x?2y?[?3,3] 22（15）解析】使用寿命超过1000小时的概率为 3 8

2 三个电子元件的使用寿命均服从正态分布N(1000,50)

得：三个电子元件的使用寿命超过1000小时的概率为p?1 2

2012年数学高考 2012年全国高考理科数学试题及答案-新课标

超过1000小时时元件1或元件2正常工作的概率P1?1?(1?p)?

那么该部件的使用寿命超过1000小时的概率为p2?p1?p?

（16）【解析】{an}的前6023 43 8

可证明：bn?1?a4n?1?a4n?2?a4n?3?a4n?4?a4n?3?a4n?2?a4n?2?a4n?16?bn?16

?0 b1?a1?a2?a3?a4115?14?S151?01?21?6?1 830

三、解答题：解答应写出文字说明，证明过程或演算步骤。[www.61k.com)

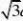
（17）【解析】（

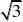
1）由正弦定理得：

acosCsinC?b?c?0?sinAcosCAsinC?sinB?sinC ?sinAcosC?AsinC?sin(a?C)?sinC

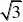
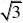
?A?cosA?1?sin(A?30?)?1

2

?A?30??30??A?60?

（2）S?

21bcsinA??bc?4 222 a?b?c?2bccosA?b?c?4

解得：b?c?2（l fx lby）

18. 【解析】（1）当n?16时，y?16?(10?5)?80

当n?15时，y?5n?5(16?n)?10n?80

得：y???10n?80(n?15)(n?N) (n?16)?80

（2）（i）X可取60，70，80

P(X?60)?0.1,P(X?70)?0.2,P(X?80)?0.7

X

DX?16?0.1?6?0.2?4?0.7?44

（ii）购进17枝时，当天的利润为 222

y?(14?5?3?5)?0.1?(15?5?2?5)?0.2?(16?5?1?5)?0.16?17?5?0.54?76.4

2012年数学高考 2012年全国高考理科数学试题及答案-新课标

76.4?76 得：应购进17枝

（19）【解析】（1）在Rt?DAC中，AD?AC

得：?ADC?45

?? 同理：?A1DC1?45??CDC1?90 ?

得：DC1?DC,DC1?BD?DC1?面BCD?DC1?BC

（2）DC1?BC,CC1?BC?BC?面ACC1A1?BC?AC

取A1B1的中点O，过点O作OH?BD于点H，连接C1O,C1H A?C1O?1C1?B1C1

OH?BD?1CH?，面ABA1B1C1?面A1BD?C1O?面A1BD 1H与点D重合 得：点BD

且?C1DO是二面角A1?BD?C1的平面角

设AC?

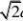
a，则C1O?

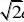
，C1D??2C1O??C1DO?30? 2

? 既二面角A1?BD?C1的大小为30

（20）（【解析】（1）由对称性知：?BFD是等腰直角?，斜边BD?2p 点A到准线l

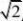
的距离d?FA?FB?

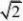
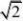
1 S?ABD???BD?d??p?2 2

圆F的方程为x2?(y?1)2?8

2px0 （2）由对称性设A(x0,)(x0?0)，则F(0,) 22p

22x0x0p2 点A,B关于点F对称得：B(?x0,p?)?p????x0?3p2 2p2p2

3pp?3px?p?x??0

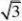
)，直线m:y?

得：A

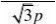
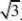
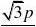
,22px2x,) x?2py?y??y????x?p?

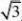
切点P362pp332

2012年数学高考 2012年全国高考理科数学试题及答案-新课标

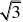
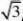
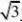
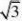
直线n:y?p?x?)?x??p?0 6336

:?3。[www.61k.com）（lfx lby） 26

?f(0)x?12x?f?(x)?f?(1)ex?1?f(0)?x 2坐标原点到m,n

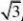
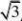
距离的比值为（21）【解析】（1）f(x)?f?(1)ex?1

令x?1得：f(0)?1 f(x)?f?(1)ex?1?x?12x?f(0)?f?(1)e?1?1?f?(1)?e 2

得：f(x)?e?x?x12x?g(x)?f?(x)?ex?1?x 2

g?(x)?ex?1?0?y?g(x)在x?R上单调递增

f?(x)?0?f?(0)?x?0,f?(x)?0?f?(0)?x?0

得：f(x)的解析式为f(x)?e?x?x12x 2

且单调递增区间为(0,??)，单调递减区间为(??,0)

（2）f(x)?12x?ax?b?h(x)?ex?(a?1)x?b?0得h?(x)?ex?(a?1) 2

①当a?1?0时，h?(x)?0?y?h(x)在x?R上单调递增

x???时，h(x)???与h(x)?0矛盾

②当a?1?0时，h?(x)?0?x?ln(a?1),h?(x)?0?x?ln(a?1) 得：当x?ln(a?1)时，h(x)min?(a?1)?(a?1)ln(a?1)?b?0 (a?1)b?(a?1)?(a?1)ln(a?1)(a?1?0)

令F(x)?x?xlnx(x?0)；则F?(x)?x(1?2lnx)

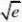
F?(x)?0?0?xF?(x)?0?x?

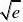
当x?2222F(x)max?e 2

e 2

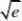
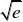
当a?1,b?(a?1)b的最大值为

请考生在第22,23,24题中任选一题做答，如果多做，则按所做的第一题计分， 做答时请写清题号。

2012年数学高考 2012年全国高考理科数学试题及答案-新课标

（22）（本小题满分10分）选修4-1：几何证明选讲

如图，D,E分别为?ABC边AB,AC的中点，直线DE交

?ABC的外接圆于F,G两点，若CF//AB，证明：

（1）CD?BC；

（2）?BCD?GBD

【解析】（1）CF//AB，DF//BC?CF//BD//AD?CD?BF CF//AB?AF?BC?BC?CD

（2）BC//GF?BG?FC?BD

BC//GF??GDE??BGD??DBC??BDC??BCD

（23）【解析】（1）点A,B,C,D的极坐标为(2,?GBD ?

3),(2,5?4?11?),(2,),(2,) 636

点A,B,C,D

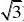
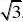
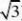
的直角坐标为(1?1,?1)

?x0?2cos?(?为参数) （2）设P(x0,y0)；则?y?3sin??0

22 t?PA?PB?PC?PD?4x?4y?40 2222

?56?20sin2??[56,76]（lfxlby）

（24）【解析】（1）当a??3时，f(x)?3?x?3?x?2?3

x?2x?3??2?x?3? ??或??或?? 3?x?2?x?33?x?x?2?3x?3?x?2?3???

?x?1或x?4

（2）原命题?f(x)?x?4在[1,2]上恒成立

?x?a?2?x?4?x在[1,2]上恒成立

??2?x?a?2?x在[1,2]上恒成立

??3?a?0

四 : 中国医科大学2016年1月考试《医学科研方法学》考查课试题参考答案

中国医科大学2016年1月考试《医学科研方法学》考查课试题

一、单选题（共 20 道试题，共 20 分。[www.61k.com））V

1. 下列不属于非参数统计优点的是

A. 不受总体分布的限定

B. 简便、易掌握

C. 适用于等级资料

D. 检验效能高于参数检验

E. 适用于未知分布型资料

正确答案：D

2. 直线回归与相关分析中，正确的是

A. r=0时，b=0

B. |r|＞0，b＞0

C. r＞0时，b＞0

D. |r|=1时，b=1

E. |r|＞0，b<0

正确答案：C

3. 某次研究进行随机抽样，测量得到该市120名健康成年男子的血红蛋白，则本次研究总体为：

A. 所有成年男子

B. 该市所有成年男子

C. 该市所有健康成年男子

D. 120名该市成年男子

E. 120名该市健康成年男子

正确答案：C

4. 实验设计和调查设计的根本区别是

A. 实验设计以动物为对象

B. 实验设计可随机分组

C. 实验设计可人为设置处理因素

D. 调查设计以人为对象

E. 调查设计可随机分组

正确答案：C

5. 下列文献类型属于一次文献的是

A. 期刊论文

B. 百科全书

C. 索引

D. 综述

E. 述评

正确答案：A

6. 直线回归分析中，直线回归方程为=0．3+2X ，代入两点描出回归直线。下面正确的是

A. 所有实测点都应在回归线上

B. 所绘回归直线必过点（x均数，y均数）

中国医学考试 中国医科大学2016年1月考试《医学科研方法学》考查课试题参考答案

抱歉，获取内容失败请稍后刷新尝试

中国医学考试 中国医科大学2016年1月考试《医学科研方法学》考查课试题参考答案

抱歉，获取内容失败请稍后刷新尝试

中国医学考试 中国医科大学2016年1月考试《医学科研方法学》考查课试题参考答案

抱歉，获取内容失败请稍后刷新尝试

中国医学考试 中国医科大学2016年1月考试《医学科研方法学》考查课试题参考答案

抱歉，获取内容失败请稍后刷新尝试

中国医学考试 中国医科大学2016年1月考试《医学科研方法学》考查课试题参考答案

抱歉，获取内容失败请稍后刷新尝试

中国医学考试 中国医科大学2016年1月考试《医学科研方法学》考查课试题参考答案

抱歉，获取内容失败请稍后刷新尝试

中国医学考试 中国医科大学2016年1月考试《医学科研方法学》考查课试题参考答案

抱歉，获取内容失败请稍后刷新尝试

中国医学考试 中国医科大学2016年1月考试《医学科研方法学》考查课试题参考答案

抱歉，获取内容失败请稍后刷新尝试

五 : 2012年导数高考题汇编(含答案)

高三第一轮单元复习强化训练

2012年导数高考题汇编

一、选择题：

12x?lnx的单调递减区间为 2

A.(?1,1] B.(0,1] C.[1,??) D.(0,??) 1.（2012年辽宁文）函数y?解：y??x??

为(0,1].

答案：B 1x(x?1)(x?1),x?0.当0?x?1时，y??0，函数单调递减；当x?1时，y??0，函数单调递增.故函数单调递减区间x

2.（2012福建理）如图所示，在边长为1的正方形OABC中任取一 点P，则点P恰好取自阴影部分的概率为

1111A. B. C. D. 4567

21211解：设阴影面积为S

，则S??x)dx?x2?x2|1??，又正方形面积S??1，∴由几何 0?03232613概型知，P恰好取自阴影部分的概率为

答案：C 1. 6

3.（2012年陕西理）设函数f(x)?xex，则

A.x?1为f(x)的极大值点 B.x?1为f(x)的极小值点

C.x??1为f(x)的极大值点 D.x??1为f(x)的极小值点 解：f?(x)?ex?xex?ex(x?1)，当x??1时，f?(x)?0，f(x)单调递减；当x??1时，f?(x)?0，f(x)单调递增.故当x??1时，函数f(x)有极小值.

答案：C

4.（2012年江西理）计算定积分??1(x2?sinx)dx? .

??解：∵?x3?cosx??x2?sinx，∴??1(x2?sinx)dx??x3?cosx??111?3???1?3???12. 3

答案：2. 3

25.（2012年江西文）设函数f(x)??lnx，则 x

11为f(x)的极大值点 B.x?为f(x)的极小值点 22

C.x?2为f(x)的极大值点 D.x?2为f(x)的极小值点 A.x?

6.已知函数y?x3?3x?c的图象与x轴恰有两个公共点，则c?

A.?2或2 B.?9或3 C.?1或1 D.?3或1

7.（2012重庆理）设函数f(x)在R上可导，其导函数为f?(x)，且函数y?(1?

x)f?(x)的图

1

2012高考题答案 2012年导数高考题汇编(含答案)

高三第一轮单元复习强化训练

象如图所示，则下列结论中一定成立的是

A.函数f(x)有极大值f(2)和极小值f(1)

B.函数f(x)有极大值f(?2)和极小值f(1)

C.函数f(x)有极大值f(2)和极小值f(?2)

D.函数f(x)有极大值f(?2)和极小值f(2)

8.（2012重庆文）设函数f(x)在R上可导，其导函数为f?(x)，且函数f(x)在x??2处取得极小值，则函数y?xf?(x)的图象可能是

B A C D 解：∵f(x)在x??2处取得极小值，∴当x??2时，f(x)单调递减，即f?(x)?0；当x??2时，f(x)单调递增，即f?(x)?0. ∴当x??2时，y?xf?(x)?0；当x??2时，y?xf?(x)?0；当?2?x?0时，y?xf?(x)?0；当x?0时，y?xf?(x)?0；当x?0时，y?xf?(x)?0.

答案：选C

19.（2012年新课标理）设点P在曲线y?ex上，点Q在曲线y?ln(2x)上，则|PQ|的最小2

值为

A.1?ln2 B

?ln2) C.1?ln2 D

?ln2) 解：函数y?ex与y?ln(2x)互为反函数，图象关于直线y?x对称，故|PQ|的最小值就应是点P（或点）到直线y?x的最小距1

2

离的2倍.设函数y?ex图象上点P(x0,y0)处的切线平行于直线y?x.则有k?y?|x?x?ex?1?x0?ln2?y0?1,因此，直线y?x与 曲0

01212

线y?

ex答案：选B 12?ln2)?2?ln2). ?

ln2)变式 设点P在曲线y?ex上，点Q在曲线y?1?

A

1上，则|PQ|的最小值为 x ?1) B

?1) C

D

11的公共点情况，即考查方程lnx?1?的解的个数，即考查xx解：函数y?ex的反函数为y?lnx，考查函数y?lnx与图象y?1?函数h(x)?lnx??1的零点个数. 1

x

h(x)?lnx?111x?1?1，h?(x)??2?2，当0?x?1时，h?(x)?0，h(x)递减；当x?1时，h?(x)?0，h(x)递增.故x?0时，xxxx

1，仅当x?1时，取等号.因此|PQ|最小值就是函数y?ex及其反函数y?

lnx图象上两点距离最小值，易知xh(x)?h(1)?0，即lnx?1?

2

2012高考题答案 2012年导数高考题汇编(含答案)

高三第一轮单元复习强化训练

此时P(0,1)，Q(1,0)，故|PQ

|.

答案：选C

10.（2012年湖南文）设定义在R上的函数f(x)是最小正周期为2?的偶函数，f?(x)是f(x)

0?f(x)?1；(,)?且x?的导数，当x?[0,?]时，当x?0

?

2

???

时，?x??f?(x)?0.则函数y?f(x)?sinx

?

2?

在[?2?,2?]上的零点个数为

A.2 B.4 C.5 D.8

解：根据函数f(x)的性质，将y?f(x)?sinx的零点个数转化为函数y1?f(x)与y2?sinx图象的交点的个数. ∵?x??f?(x)?0，当

2

???

π?

ππ?π??π?

?x?π时，f?(x)?0，∴f(x)在?,π?上是增函数；当0?x?时，f?(x)?0，∴f(x)在?0,?上是减函数.

?2?22?2?

设π?x?2π，则0?2π?x?π.由f(x)是以2π为最小正周期的偶函数知f(2π?x)?f(x).故π?x?2π时，0?f(x)?1. 依题意作出草图可知，y1?f(x)与y2?sinx在[?2π,2π]上有四个交点. 答案：选B

11.（2012年辽宁理）若x?[0,??)，则下列不等式恒成立的是 A.ex?1?x?x2 B

1111

?1?x?x2 C.cosx?1?x2 D.ln(1?x)?x?x2

2824解：对选项A，在区间[0,??)上，函数y?ex和y?1?x?x2的增长速度不在同一个“档次”上，随着x的增大，y?ex的增长速度越来越快，会超过并会远远大于y?1?x?x2的增长速度，故不等式ex?1?x?x2不能恒成立.

对选项B

：令t，则t?1，x?t2?1.于是，原不等式对x?[0,??)是否恒成立?t5?4t3?7t?4?0对t?[1,??)是否恒成立. 记f(t)?t5?4t3?7t?4?0,t?[1,??

)，则f?(t)?5t4?12t2?7?5??t??

?t(t?1)(t?1),t?[1,??)，易知f(t

)在?内递减.

当???53

t???时，f(t)?f(1)?0，故不等式t?4t?7t?4?0对t?[1,??)不恒成立，从而排除选项B. ?对选项C：记f(x)?cosx?21?,x[0?,)??

1

2

，f?(x)?x?sinx?0在[0,??)上恒成立，故f(x)在[0,??)上递增，所以f(x)?f(0)?0，

即当x?[0,??)时，不等式cosx??x2?1恒成立.

1

2

对选项D：取x?4，则左边?ln5?lne2?2?右边，此时ln(1?x)?x?x2，从而排除选项D. 答案：选C

18

12.（2012年福建文）已知f(x)?x3?6x2?9x?abc,a?b?c，且f(a)?f(b)?f(c)?0.现给出如下结论：

①f(0)f(1)?0；②f(0)f(1)?0；③f(0)f(3)?0；④f(0)f(3)?0.

其中正确结论的序号是

A.①③ B.①④ C.②③ D.②④

1

，g(x)??x2?bx，若y?f(x)的图象与y?g(x)的图象x

有且只有两个不同的公共点A(x1,y1)，B(x2,y2)，则下列判断正确的是

13.（2012山东文）设函数f(x)?

A.x1?x2?0，y1?y2?0 B.x1?x2?0，y1?y2?0 C.x1?x2?0，y1?y2?0 D.x1?x2?0，y1?y2?0

3

2012高考题答案 2012年导数高考题汇编(含答案)

高三第一轮单元复习强化训练

解：设F(x)?x3?bx2?1，则方程F(x)?0与f(x)?g(x)同解，故其有且仅有两个不同零点x1,x2.由F?(x)?0得x?0或x?b.这样，

??必须且只需F(0)?0或F?b??0. 2

?3?23

??因为F(0)?1，故必有F?b??0，

由此得b3??22则x2?b

所以F(x)?(x?x1)(x，

比较系数得?x1，

不妨设x1?x2，

3故x1?

11x?x2?0. x1?x20，由此知y1?y2???1x1x2x1x2答案：B

13.（2012全国大纲理）已知函数y?x3?3x?c的图象与x轴恰有两个公共点，则c?

A.?2或2 B.?9或3 C.?1或1 D.?3或1 解：∵y??3x2?3?3(x?1)(x?1)，∴当x??1时，y??0，函数单调递增；当?1?x?1时，y??0，函数单调递减；当x?1时，y??0，函数单调递增.

因此，当x??1时，函数取得极大值c?2；当x?1时，函数取得极小值c?2. 当函数图象与轴恰有两个公共点时，必有c?2?0或c?2?0，∴c??2或c?2. 答案：B

二、填空题：本大题共4小题，每小题5分，共20分.

13.（2012新课标文）曲线y?x(3lnx?1)在点(1,1)处的切线方程为 提示：y??3lnx?1?x??3lnx?4，故k?y?|x?1?4，所求切线方程为y?1?4(x?1)，即y?4x?3.

答案：y?4x?3. 3x

14.（2012年广东理）曲线y?x3?x?3在点(1,3)处的切线方程为 .

15.（2012年山东理）设a?

0，若曲线y?x?a，y?0所围成封闭图形的面积为a2，则a?提示

：S??4. 9224x?x2?a2?a2，故a?. 33933答案：

16.（2012年浙江理、文）定义：曲线C上的点到直线l的距离的最小值称为曲线C到直线l的距离.已知曲线C1:y?x2?a到直线l:y?x的距离等于曲线C2:x2?(y?4)2?2到直线l:y?x的距离，则实数a? .

曲线C2是圆心为(0,?4)，

半径r圆心到直线l:y?

x的距离d1所以曲线C2到直线l

的距离为d1?r.设曲线C1上的点(x0,y0)到直线l:y?x的距离最短为d，则过(x0,y0)的切线平行于直线y?x.

已知函数y?x2?a，则y?|x?x1?1?|???a?||1?a|11?2x0?1，即x0?，y0??a，点(x0,y0)到直线l:y?

x的距离d，由题意240

4

2012高考题答案 2012年导数高考题汇编(含答案)

高三第一轮单元复习强化训练

1|?a|977a??或a?.当a??时，直线l与曲线C1相交，不合题意，故舍去. 444答案：4. 9

116.（2012年江西理）计算定积分?(x2?sinx)dx? . ?1

解：??1(x2?sinx)dx???1x2dx???1sinxdx?x3

2. 311113?cosx1??12. 3答案：

三、解答题：本大题共6小题，共70分.

17.（2012年新课标文）设函数f(x)?ex?ax?2.

（1）求f(x)的单调区间；

（2）若a?1，k为整数，且当x?0时，(x?k)f?(x)?x?1?0，求k的最大值. 解：（1）f(x)的定义域为(??,??)，f?(x)?ex?a.

若a?0，则f?(x)?0，所以f(x)在(??,??)上单调递增.

若a?0，则当x?(??,lna)时，f?(x)?0；当x?(lna,??)时，f?(x)?0.所以，f(x)在(??,lna)上单调递减，在(lna,??)上单调递增.

故f(x)的递减区间为(??,lna)，递增区间为(lna,??).

（2）由于a?1，所以(x?k)f?(x)?x?1?(x?k)(ex?1)?x?1.

故当x?0时，(x?k)f?(x)?x?1?0等价于k?x?1?x(x?0).① ex?1

令g(x)??xex?1ex(ex?x?2)x?1?g(x)??1?，则. ?xx2(e?1)(ex?1)2e?1

由（1）知，函数h(x)?ex?x?2在(0,??)上单调递增.而h(1)?0，h(2)?0，所以h(x)在(0,??)上存在唯一的零点，故g?(x)在(0,??)上存在唯一的零点.

设此零点为?，则??(1,2).

当x?(0,?)时，g?(x)?0；当x?(?,??)时，g?(x)?0.所以g(x)在(0,??)上的最小值为g(?). 又由g?(?)?0，可得e????2，所以g(?)???1?(2,3).

由于①式等价于k?g(?)，故整数k的最大值为2.

118.（2012年新课标理）已知函数f(x)?f?(1)ex?1?f(0)x?x2. 2

（1）求f(x)的解析式及单调区间；

1（2）若f(x)?x2?ax?b，求(a?1)b的最大值. 2

解：（1）求导：f?(x)?f?(1)ex?1?f(0)?x，令x?1，则f?(1)?f?(1)e0?f(0)?1?f(0)?1. 在原函数中，令x?0，则f(0)?f?(1)e0?1?1?f?(1)?e，故f(x)?ex?x?x2. 由于f?(x)?ex?1?x，故当x?(??,0)时，f?(x)?0；当x?(0,??)时，f?(x)?0. 从而，f(x)的单调递减区间为(0,??)，单调增区间为(0,??). 12

5

2012高考题答案 2012年导数高考题汇编(含答案)

高三第一轮单元复习强化训练

（2）由已知条件得ex?(a?1)x?b.（*） ①若a?1?0，则对任意实数b，当x?0，且x?②若a?1?0，则(a?1)b?0.

③若a?1?0，设g(x)?ex?(a?1)x，则g?(x)?ex?(a?1).

当x?(??,ln(a?1))时，g?(x)?0；当x?(ln(a?1),??)时，g?(x)?0. 从而g(x)在(??,ln(a?1))上单调递减，在(ln(a?1),??)上单调递增. 故g(x)有最小值g(ln(a?1))?a?1?(a?1)ln(a?1).

所以f(x)?x2?ax?b等价于b?a?1?(a?1)ln(a?1).（**） 因此(a?1)b?(a?1)2?(a?1)2ln(a?1).

?()(?设h(a)?(a?1)2?(a?1)2ln(a?1)，则haa1[)1(n2l?])1?

a?

22

.所以h(a)在?在?故h(a)??1,e?1??上单调递增，?e?1,????上单调递减，

1?b

时，可得ex?(a?1)x?b，因此（*）式不成立. a?1

12

??

1

??

??

1

??

1

在a?e2?1处取得最大值.从而h(a)?，即(a?1)b?.

1

e2e2

e21

当a?e?1，b?时，（**）式成立，故f(x)?x2?ax?b.

22

1

2

综上，(a?1)b的最大值为

e. 2

19.（2012年江苏理）已知a,b是实数，1和?1是函数f(x)?x3?ax2?bx的两个极值点. （1）求a和b的值；（2）设函数g(x)的导数g?(x)?f(x)?2，求g(x)的极值点； （3）设h(x)?f(f(x))?c，其中c?[?2,2]，求函数y?h(x)的零点个数.

解：（1）由题设知f?(x)?3x2?2ax?b，且f?(?1)?3?2a?b?0，f?(1)?3?2a?b?0，解得a?0，b??3.

（2）由（1）知f(x)?x3?3x.因为f(x)?2?(x?1)2(x?2)，所以g?(x)?0的根为x1?x2?1，x3??2，于是函数g(x)的极值点只可能是1或?2.

当x??2时，g?(x)?0；当?2?x?1时，g?(x)?0，故?2是g(x)的极值点. 当?2?x?1或x?1时，g?(x)?0，故1不是g(x)的极值点. 所以的极值点为?2.

（3）令f(x)?t，则h(x)?f(t)?c.先讨论关于x的方程f(x)?d根的情况，d?[?2,2]. 当|d|?2时，由（2）可知，f(x)??2的两个不同的根为1和?2， 注意到f(x)是奇函数，所以f(x)?2的两个不同的根为?1和2.

当|d|?2时，因为f(?1)?d?f(2)?d?2?d?0，f(1)?d?f(?2)?d??2?d?0， 所以?2，?1，1，2都不是f(x)?d的根. 由（1）知f?(x)?3(x?1)(x?1).

①当x?(2,??)时，f?(x)?0，于是f(x)是单调递增函数，从而f(x)?f(2)?2， 此时f(x)?d无实根.同理，f(x)?d在(??,?2)上无实根.

②当x?(1,2)时，f?(x)?0，于是f(x)是单调递增函数.又f(1)?d?0，f(2)?d?0，y?f(x)?d的图象不间断，所以f(x)?d在(1,2)内有唯一实根.同理，f(x)?d在(?2,?1)内有唯一实根.

③当x?(?1,1)时，f?(x)?0，故f(x)是单调减函数.又f(?1)?d?0，f(1)?d?0，y?f(x)?d的图象不间断，所以f(x)?d在(?1,1)

6

2012高考题答案 2012年导数高考题汇编(含答案)

高三第一轮单元复习强化训练

内有唯一实根.

由上可知：当|d|?2时，f(x)?d有两个不同的实根x1，x2满足|x1|?1，|x2|?2；当|d|?2时，f(x)?d有三个不同的实根x3,x4,x5满足|xi|?2,i?3,4,5.

现考虑函数y?h(x)的零点.

（ⅰ）当|c|?2时，f(t)?c有两个根t1,t2满足|t1|?1，|t2|?2，而f(x)?t1有三个不同的根，f(x)?t2有两个不同的根，故y?h(x)有5个零点.

（ⅱ）当|c|?2时，f(t)?c有三个不同的根t3,t4,t5满足|ti|?2(i?3,4,5)，而f(x)?ti(i?3,4,5)有三个不同的根，故y?h(x)有9个零点.

综上可知，当|c|?2时，函数y?h(x)有5个零点；当|c|?2时，函数y?h(x)有9个零点.

lnx?k（k为常数，e?2.71828?是自然对数的底数），曲ex

线y?f(x)在点(1,f(1))处的切线与x轴平行. 20.（2012山东）已知函数f(x)?

（1）求k的值；（2）求f(x)的单调区间；

（3）（理）设g(x)?(x2?x)f?(x)，其中f?(x)为f(x)的导函数，证明：对任意x?0，g(x)?1?e?2.

（文）设g(x)?xf?(x)，其中f?(x)为f(x)的导函数，证明：对任意x?0，g(x)?1?e?2. 解：（1）由f(x)?lnx?k1?kx?xlnx，得f?(x)?,x?(0,??). exe因为曲线y?f(x)在(1,f(1))处的切线与x轴平行，

所以f?(1)?0，因此k?1.

（2）由（1）得f?(x)?1?x?xlnx,x?(0,??)， xex

当x?(0,1)时，1?x?0，?xln?0，f?(x)?0；当x?(1,??)时，1?x?0，?xlnx?0，f?(x)?0. 所以f(x)的单调增区间是(0,1)，单调递减区间是(1,??).

（3）（文）因为g(x)?xf?(x)，所以g(x)?1(1?x?xlnx),x?(0,??). e令h(x)?1?x?xlnx,x?(0,??)，则h?(x)??lnx?2??(lnx?lne?2),x?(0,??). 因此，当x?(0,e?2)时，h?(x)?0，h(x)单调递增；当x?(e?2,??)时，h?(x)?0，h(x)单调递减. 所以h(x)的最大值为h(e?2)?1?e?2，故h(x)?1?e?2.

又当x?(0,??)时，0?1?1， e1?2h(x)?1?e?2，即g(x)?1?e. ex?1(1?x?xlnx),x?(0,??). ex故当x?(0,??)时，所以（理）证明：因为g(x)?(x2?x)f?(x)，所以g(x)?

因此，对任意x?0，g(x)?1?e?2等价于1?x?xlnx?ex

(1?e?2). x?1

7

2012高考题答案 2012年导数高考题汇编(含答案)

抱歉，获取内容失败请稍后刷新尝试

2012高考题答案 2012年导数高考题汇编(含答案)

高三第一轮单元复习强化训练

22.（2012年浙江理）已知a?0，b?R，函数f(x)?4ax3?2bx?a?b.

（1）证明：当0?x?1时，①函数f(x)的最大值为|2a?b|?a；②f(x)?|2a?b|?a?0.

（2）若?1?f(x)?1对x?[0,1]恒成立，求a?b的取值范围.

?解：（1）①f?(x)?12ax2?2b?12a?x2??b??.当b?0时，有f?(x)?0，此时f(x)在[0,??)上单调递增； 6a?

当b?

0时，f?(x)?12a??x????，此时f(x

)在?上单调递增. x?上单调递减，在???

?

?3a?b,b?2a,?|2a?b|?a. ??a?b,b?2a所以当0?x?1时，f(x)max?max{f(0),f(1)}?max{?a?b,3a?b}??

②由于0?x?1，故当b?2a时，f(x)?|2a?b|?a?f(x)?3a?b?4ax3?2bx?2a?4ax3?2ax?2a?2a(2x3?2x?1). 当b?2a时，f(x)?|2a?b|?a?f(x)?a?b?4ax3?2b(1?x)?2a?4ax3?4a(1?x)?2a?4ax3?4a(1?x)?2a?2a(2x3?2x?1). 设g(x)?2x3?2x?1,0?x?

1，则g?(x)?6x2?2?6??x??x，于是g?(x)，g(x)随x的变化情况如下： ???

所以，g(x)min?g?10.所以当0?x?1时，2x3?2x?1?0.故f(x)?|2a?b|?a?2a(2x3?2x?1). （2）由①知，当0?x?1时，f(x)max?|2a?b|?a，所以|2a?b|?a?1.若|2a?b|?a?1，则由②知f(x)??(|2a?b|?a)??1.

?2a?b?0,?2a?b?0,?|2a?b|?a?1,??所以?1?f(x)?1对任意0?x?1恒成立的充要条件是?即?3a?b?1,或?b?a?1,（*） a?0,??a?0?a?0.??

在直角坐标系aOb中，（*）所表示的平面区域为如图所示的阴影部分，其中不包括线段BC. 做一组平行直线a?b?t(t?R)，得?1?a?b?3，所以a?b的取值范围是(?1,3].

23.（2012年浙江文）已知a?R，函数f(x)?4ax3?2ax?a.

（1）求f(x)的单调区间；

（2）证明：当0?x?1时，f(x)?|a?2|?0.

解：（1）依题意得f?(x)?12x2?2a.

当a?0时，f?(x)?0恒成立，此时f(x)的单调增区间为(??,??)；

当a?

0时，f?(x)?12a??x?????x??,?，此时f(x

)的单调增区间为?和，递减区间为????.

??

?（2）证明：由于当0?x?1时，故当a?2时，f(x)?|2?a|?4x3?2ax?2?4x3?4x?2； 当a?2时，f(x)?|2?a|?4x3?2a(1?x)?2?4x3?4(1?x)?2?4x3?4x?2.

设g(x)?2x3?2x?1,0?x?

1，则g?(x)?6x2?2?6??x??x，于是g?(x)，g(x)随x的变化情况如下：

???

9

2012高考题答案 2012年导数高考题汇编(含答案)

所以，g(x)min?g?10.所以当0?x?1时，2x3?2x?1?0.故f(x)?|2?a|?4x3?4x?2?0.

24.（2012年辽宁理）设f(x)?ln(x?1)ax?b（a,b?R，a,b为常数），曲线y?f(x)与直线y?

3

x在点(0,0)相切. 2

（1）求a,b的值；（2）证明：当0?x?2时，f(x)?

解：（1）由y?f(x)过点(0,0)，得b??1. 由y?f(x)在(0,0)点的切线斜率为

9x

. x?6

3?13

，又y?|x?0??|x?0??a，得a?0. 22?x?1（2）证法一：由均值不等式，当x?0时，x?1?1?x?2?1.

1

2?(x?1)

54(x?6)3?216(x?1)2. ??

2(x?1)(x?6)4(x?1)(x?6)x

2

9x15454

记h(x)?f(x)?，则h?(x)??x?6x?1(x?6)(x?6)令g(x)?(x?6)3?216(x?1)，则当0?x?2时，g?(x)?3(x?6)2?216?0. 因此g(x)在(0,2)内是递减函数.又g(0)?0，得g(x)?0，所以h?(x)?0. 因此h(x)在(0,2)内是递减函数.又h(0)?0，得h(x)?0. 于是当0?x?2时，f(x)?

9x

. x?6

（2）证法二：由（1）知f(x)?ln(x?1)1.

由均值不等式，当x?0时，x?1?1?x?2?1.①

x2

记k(x)?ln(x?1)?x，则k(0)?0，k?(x)?

1?x?1??0，故k(x)?0，即ln(x?1)?x.② x?1x?1

由①②得，当x?0时，f(x)?x. 记h(x)?(x?6)f(x)?9x，则当0?x?2时，

311

h?(x)?f(x)?(x?6)f?(x)?9?x?(x?6)(?9?[3x(x?1)?(x?6)(2?18(x?1)]

2x?12(x?1)?

1xx

[3x(x?1)?(x?6)(3?)?18(x?1)]?(7x?18)?0. 2(x?1)24(x?1)

9x

. x?6

32

因此h(x)在(0,2)内是递减函数.又h(0)?0，得h(x)?0.即f(x)?

25.（2012年辽宁文）设f(x)?lnx1.证明：

10

2012高考题答案 2012年导数高考题汇编(含答案)

高三第一轮单元复习强化训练

3（1）当x?1时，f(x)?(x?1)； 2

（2）当1?x?3时，f(x)?9(x?1). x?5

. 3313解：（1）证法一：

记g(x)?lnx1?(x?1)，则当x?

1时，g?(x)?所以有g(x)?0，即f(x)?1)??0.又g(1)?0，22x2

证法二：当x?

1时，x?

1?x

21.① 2

令k(x)?lnx?x?1，则k(1)?0，k?(x)??1?0，故k(x)?0，即lnx?x?1.② 1

x

由①②得，当x?1时，f(x)?(x?1). 3

2

（2）证法一：记h(x)?f(x)?9(x?1)，由（1）得

x?5

112?(x?)322?54?x?5?54?(x?5)?216x. 2x(x?5)4x(x?5)4(x?1)(x?5)15454h?(x)??x(x?5)(x?5)令G(x)?(x?5)3?216x，则当1?x?3时，G?(x)?3(x?5)2?216?0，因此G(x)在(1,3)上是减函数.

又由G(1)?0，得G(x)?0，所以h?(x)?0.

因此h(x)在(1,3)内是递减函数.又h(1)?0，得h(x)?0.

于是当1?x?3时，f(x)?9(x?1). x?5

（2）证法二：记h(x)?(x?5)f(x)?9(x?1)，则当1?x?3时，由（1）得

311x11h?(x)?f(x)?(x?5)f?(x)?9?(x?1)?(x?5)(?9?[3x(x?1)?(x?5)(2???18x]?(7x2?32x?55)?0. 2x2x224x

因此h(x)在(1,3)内是递减函数.又h(1)?0，得h(x)?0.即f(x)?9(x?1). x?5

26.（2012年福建理）已知函数f(x)?ex?ax2?ex(a?R).

（1）若曲线y?f(x)在点(1,f(1))处的切线平行于x轴，求函数f(x)的单调区间；

（2）试确定a的取值范围，使得曲线y?f(x)上存在唯一的点P，曲线在该点处的切线与曲线只有一个公共点P.

解：（1）由于f?(x)?ex?2ax?e，曲线y?f(x)在点(1,f(1))处的切线斜率k?2a?0，所以a?0，即f(x)?ex?ex. 此时f?(x)?ex?e.当x?(??,1)时，f?(x)?0，当x?(1,??)时，f?(x)?0.

故f(x)的单调递减区间为(??,1)，单调递增区间为(1,??).

（2）设点P(x0,f(x0))，曲线y?f(x)在点P处的切线方程为y?f?(x0)(x?x0)?f(x0)，令g(x)?f(x)?f?(x，故曲线0)(x?x0)?f(x0)y?f(x)在点P处的切线与曲线只有一个公共点P等价于函数g(x)有唯一零点.

因为g(x0)?0，且g?(x)?f?(x)?f?(x0)?ex?ex?2a(x?x0). 0

①若a?0，当x?x0时，g?(x)?0，则g(x)?g(x0)?0；当x?x0时，g?(x)?0，则g(x)?g(x0)?0.

故g(x)只有唯一零点x?x0.由P的任意性知，a?0不合题意.

②若a?0，令h(x)?ex?ex?2a(x?x0)，则h(x0)?0，h?(x)?ex?2a. 0

当x?(??,ln(?2a))时，h?(x)?0，从而h(x)在(??,ln(?2a))内单调递减；当x?(ln(?2a),??)时，h?(x)?0，从而h(x)在(ln(?2a),??)内

11

2012高考题答案 2012年导数高考题汇编(含答案)

高三第一轮单元复习强化训练

单调递增.

（ⅰ）若x0?ln(?2a)，当x?(??,ln(?2a))时，g?(x)?h(x)?h(x0)?0；当x?(ln(?2a),??)时，g?(x)?h(x)?h(x0)?0.所以g(x)在R上单调递增.所以函数g(x)在R上有且只有一个零点x?ln(?2a).

（ⅱ）若x0?ln(?2a)，由于h(x)在(ln(?2a),??)内单调递增，且h(x0)?0，则当x?(ln(?2a),??)时有g?(x)?h(x)?h(x0)?0，g(x)?g(x0)?0；任取x1?(ln(?2a),x0)有g(x1)?0.

xx222又当x?(??,x1)时，易知g(x)?e?ax?(e?f?(x0))x?f(x0)?x0f?(x0)?e?ax?(e?f?(x0))x?f(x0)?x0f?(x0)?ax?bx?c，其中

1

，c?ex?f(x0)?x0f?(x0). b??(e?f?(0x))

1

2

?bx2?c?0. 由于a?0，则必存在x2?x1，使得ax2

所以g(x2)?0，故g(x)在(x2,x1)内存在零点，即g(x)在R上至少有两个零点. （ⅲ）若x0?ln(?2a)，仿（ⅱ）并利用ex?

x3

，可证函数g(x)在上R至少有两个零点. 6

综上，当a?0时，曲线y?f(x)上存在唯一的点P(ln(?2a),f(ln(?2a)))，曲线在该点处的切线与曲线有且只有一个公共点P.

3π?3?π?

27.（2012福建文）已知函数f(x)?axsinx?(a?R)，且在?0,?上的最大值为.

22?2?

（1）函数f(x)的解析式；

（2）判断函数f(x)在(0,π)内的零点个数，并加以证明.

28.（2012天津理）已知函数f(x)?x?ln(x?a)的最小值为0，其中a?0.

（1）求a的值；（2）若对任意的x?[0,??)，有f(x)?kx2成立，求实数k的最小值； （3）证明：?

2

?ln(2n?1)?2(n?N?).

i?12i?1

1x?(1?a)

，显然导函数零点x?1?a?(?a,??). ?

x?ax?a

n

解：(1)f(x)的定义域为(?a,??). 由f(x)?x?ln(x?a)，得f?(x)?1?

当?a?x?1?a时，f?(x)?0，f(x)递减；当x?1?a时，f?(x)?0，f(x)递增.

故x?1?a时，f(x)有极小值f(1?a)?1?a，因为f(x)是单峰函数，故f(x)min?f(1?a)?1?a?0，得a?1. （2）设g(x)?kx2?f(x)?kx2?x?ln(x?1)(x?0)，则

g(x)?0对x?[0,??)恒成立当且仅当g(x)min?0?g(0)，取x?1，则应有g(1)?k?1?ln2?0，从而k?0. g?(x)?2kx?1?

1x[x?(1?2k)]. ?

x?12k(x?1)

1

，则当x?(0,??)时，g?(x)?0，g(x)递增. 2

1

适合题意. 2

①若1?2k?0，即k?

这时有g(x)min?0?g(0)，故k?

②若1?2k?0，即k?

1

，则当x?(0,1?2k)时，g?(x)?0，g(x)递减；当x?(1?2k,??)时，g?(x)?0，g(x)递增. 2

1

不合题意. 2

22?f(x0)?0，即f(x0)?kx0取x0?(0,1?2k)，有g(x0)?g(0)?0?kx0不成立.故0?k?

12

2012高考题答案 2012年导数高考题汇编(含答案)

高三第一轮单元复习强化训练

③若k?

1x2，则g?(x)??0在[0,??)上恒成立，仅当x?0时取等号，故g(x)递增. 2x?1

综上，k的最小值为

1

. 2

（3）当n?1时，不等式左边?2?ln3?2?右边，所以不等式成立. 当n?2时，?f?

i?1n

nn

2??n22?2?n?2?

??ln1???[ln(2i?1)?ln(2i?1)]??ln(2n?1). ?????????2i?1??i?12i?1i?1?2i?1?i?1?2i?1?i?12i?1

在（2）中取k?

n

2211?2?

?(i?N?,i?2)， ，得f(x)?x2(x?0)，从而f???(2i?3)(2i?1)?2i?1?(2i?1)22

所以有?

i?1n

nnn

221?2??2?

?ln(2n?1)??f??2?ln3?1??2. ??f(2)??f???2?ln3??2i?12n?1?2i?1??2i?1?i?1i?2i?2(2i?3)(2i?1)

综上，?

i?1

2

?ln(2n?1)?2(n?N?). 2i?1

11?a2

29.（2012天津文）已知函数f(x)?x3?x?ax?a,x?R，其中a?0.

32

（1）求函数f(x)的单调区间；

（2）若函数f(x)在区间(?2,0)内恰有两个零点，求a的取值范围；

（3）当a?1时，设函数f(x)在区间[t,t?3]上的最大值为M(t)，最小值为m(t)，记g(t)?M(t)?m(t，求函数)g(t)在区间[?3,?1]上的最小值.

30.（2012陕西理）设函数fn(x)?xn?bx?c(n?N?,b,c?R)

?1?

（1）设n?2，b?1，c??1，证明：fn(x)在区间?,1?内存在唯一零点；

?2?

（2）设n?2，若对任意x1,x2?[?1,1]，有|f2(x1)?f2(x2)|?4，求b的取值范围；

?1?

（3）在（1）的条件下，设xn是fn(x)在?,1?内的零点，判断数列x2,x3,?,xn,?的增减性.

?2?

30.（2012陕西文）设函数f(x)?xn?bx?c(n?N?,b,c?R)

?1?

（1）设n?2，b?1，c??1，证明：fn(x)在区间?,1?内存在唯一零点；

?2?

（2）设n为偶数，|f(?1)|?1，|f(1)|?1，求b?3c的最小值和最大值；

（3）设n?2，若对任意x1,x2?[?1,1]，有|f(x1)?f(x2)|?4，求b的取值范围.

31.（2012湖南理）已知函数f(x)?eax?x，其中a?0.

（1）对一切x?R，f(x)?1恒成立，求a的取值范围；

B(x2,f(x2))(x1?x2)，（2）在函数f(x)的图象上取定两点A(x1,f(x1))，记直线AB的斜率为k.

问：是否存在x0?(x1,x2)，使f?(x0)?k成立？若存在，求x0的取值范围；若不存在，请说明理由.

13

2012高考题答案 2012年导数高考题汇编(含答案)

高三第一轮单元复习强化训练

32.（2012湖南文）已知函数f(x)?ex?ax，其中a?0.

（1）对一切x?R，f(x)?1恒成立，求a的取值集合；

B(x2,f(x2))(x1?x2)，（2）在函数f(x)的图象上取定两点A(x1,f(x1))，记直线AB的斜率为k.

证明：存在x0?(x1,x2)，使f?(x0)?k成立.

33.（2012北京理）已知函数f(x)?ax2?1(a?0)，g(x)?x3?bx.

（1）若曲线y?f(x)与曲线y?g(x)在它们的交点(1,c)处具有公共切线，求a,b的值；

（2）当a2?4b时，求函数f(x)?g(x)的单调区间，并求其在区间(??,?1]上的最大值.

34.（2012北京文）已知函数f(x)?ax2?1(a?0)，g(x)?x3?bx.

（1）若曲线y?f(x)与曲线y?g(x)在它们的交点(1,c)处具有公共切线，求a,b的值；

（2）当a?3，b??9时，求函数f(x)?g(x)在区间[k,2]上的最大值为28，求k的取值范围.

35.（2012江西理）若函数h(x)满足①h(0)?1，h(1)?0；②对任意a?[0,1]，有h(h(a))?a；③在(0,1)上单调递减.

?1?x?则称h(x)为补函数.已知函数h(x)??(λ??1,p?0). p?1?λx??p1p

（1）判断函数h(x)是否为补函数，并证明你的结论；

1（2）若存在m?[0,1]，使h(m)?m，称m是函数h(x)的中介元.记p?(n?N?)时h(x)的中n

介元为xn，且Sn??xi对任意的n?N?，都有Sn?

i?1n1，求λ的取值范围； 2

（3）当λ?0，x?(0,1)时，函数y?h(x)的图象总在直线y?1?x的上方，求p的取值范围.

36.（2012江西文）已知函数f(x)?(ax2?bx?c)ex在[0,1]上单调递减且满足f(0)?1，f(1)?0.

（1）求a的取值范围；

（2）设g(x)?f(x)?f?(x)，求g(x)在[0,1]上的最大值和最小值.

37.（2012湖北理）（1）已知函数f(x)?rx?xr?(1?r)(x?0)，其中r为有理数，且0?r?1.f(x)求的最小值；

（2）试用（1）的结果证明如下命题：

b?a1b1?a2b2； 设a1?0，a2?0，b1,b2为正有理数. 若b1?b2?1，则a1ba212

（3）请将（2）中的命题推广到一般形式，并用数学归纳法证明你所推广的命题. ．．．．．

14

2012高考题答案 2012年导数高考题汇编(含答案)

高三第一轮单元复习强化训练

注：当α为正有理数时，有求导公式(xα)??αxα?1. 解：（1）f?(x)?r?rxr?1?r(1?xr?1).

当0?x?1时，f?(x)?0，故f(x)单调递减；当x?1时，f?(x)?0，故f(x)单调递增. 故函数f(x)在x?1处取得最小值f(1)?0.

（2）由（1）知，当x?(0,??)时，有f(x)?f(1)?0，即xr?rx?(1?r). ①

b

?a1b1?a2b2成立. 若a1,a2中有一个为0，则a1ba2

1

2

?a?aa?b1

?a1b1?a2(1?b1)，若a1,a2均不为0，由b1?b2?1，可得b2?1?b1，于是在①中令x?1，r?b1，可得?1??b1?1?(1?b1)，即a1b1a12

a2aa?2?2

?b

?a1b1?a2b2. 亦即a1ba12

1

1

b1

?b

?a1b1?a2b2. ② 综上，对a1?0，a2?0，b1,b2为正有理数，且b1?b2?1，总有a1ba12

1

1

（3）（2）中的命题推广形式为：设a1,a2,?,an为非负实数，b1,b2,?,bn为正有理数，若b1?b2???bn?1，则

bnb2

a1b1a2?an?a1b1?a2b2???anbn.③

用数学归纳法证明如下：

（ⅰ）当n?1时，b1?1，有a1?a1，③成立.

（ⅱ）假设当n?k时，③成立，即若a1,a2,?,ak为非负实数，b1,b2,?,bk为正有理数，且b1?b2???bk?1，

bb

?ak?a1b1?a2b2???akbk.当n?k?1时，已知a1,a2?则a1ba2,a,kak,?1为非负实数，b1,b2?,b,kbk,?1为正有理数，且

1

2

k

， b1?b2???bk?bk??11

b1

1

2

k

k?1

1

2

k

k?1

k?1

b2

k?1

bk

k?1

k?1

k?1

bbbb1?b1?b1?bbbbb

此时0?bk?1?1，即1?bk?1?0，于是a1ba2. ?akak?1?(a1a2?ak)aka2?ak)1?b?ak?1?(a1?1

因为

b1

1?bk?11

bkb1b2

?????1，由归纳假设可得 1?bk?11?bk?11?bk?1

b21?bk?12

bk1?bk?1k

aa?a

?a1?

bkab?a2b2???akbkb1b2

?a2????ak??11. 1?bk?11?bk?11?bk?11?bk?1

1?bk?1

bk?1

?ak?1.

bbb

?akak?1??从而a1ba2

1

2

k

k?1

?a1b1?a2b2???akbk?

?

1?bk?1??

又因为(1?bk?1)?bk?1?1，由②得

?a1b1?a2b2???akbk?

??

1?bk?1??

1

2

k

k?1

1?bk?1

bk?1

?ak?1?

a1b1?a2b2???akbk

?(1?bk?1)?ak?1bk?1?a1b1?a2b2???akbk?ak?1bk?1，

1?bk?1

bbb

?akak从而a1ba2?1?a1b1?a2b2???akbk?ak?1bk?1.

故当n?k?1时，③成立.由（ⅰ）、（ⅱ）可知，对一切正整数n，所推广的命题成立.

38.（2012湖北文）设函数f(x)?axn(1?x)?b(x?0)，n为正整数，a,b为常数，曲线y?f(x)在(1,f(1))处的切线方程为x?y?1.

（1）求a,b的值； （2）求函数f(x)的最大值； （3）证明：f(x)?

（1）解：因为f(1)?b，由点(1,b)在直线x?y?1上，可得1?b?1，即b?0. 因为f?(x)?anxn?1?a(n?1)xn，所以f?(1)??a.

又因为切线x?y?1的斜率为?1，所以?a??1，即a?1.故a?1，b?0.

?

（2）解：有（1）知f(x)?xn(1?x)?xn?xn?1，f?(x)?(n?1)xn?1?

n??x?. ?n?1?

1

. ne

15

2012高考题答案 2012年导数高考题汇编(含答案)

高三第一轮单元复习强化训练

当x??0,

??

n??n?

,???时，f?(x)?0，故f(x)单调递减. ?时，f?(x)?0，故f(x)单调递增；当x??

n?1??n?1?

????

故f(x)在(0,??)上的最大值为f?????

?n?1??n?1?

nn

n

n?nn???1??. ?

n?1?(n?1)?

（3）证明：令φ(t)?lnt?1?(t?0)，则φ?(t)??

1

t11t?1

?2(t?0). tt2t

当t?(0,1)时，φ?(t)?0，故φ(x)单调递减；当t?(1,??)时，φ?(t)?0，故φ(t)单调递增. 故在(0,??)上φ(t)的最小值为φ(1)?0，所以φ(t)?0(t?1)，即lnt?1?(t?1).

n?1

n?1

1

t

令t?1?

1n?11?n?1?，得ln，两边取对数得ln???nnn?1?n?

nn1

?.

(n?1)n?1ne

?n?1?

?lne，所以??

?n?

?e，即

nn1

?. n?1

(n?1)ne

由（2）知f(x)?

39.（2012大纲理）设函数f(x)?ax?cosx,x?[0,π].

（1）讨论f(x)的单调性；

（2）设f(x)?1?sinx，求a的取值范围.

解：（1）f?(x)?a?sinx.

①当a?1时，f?(x)?0，且仅当a?1，x?

?

2

时，f?(x)?0，所以f(x)在[0,?]上是增函数；

②当a?0时，f?(x)?0，且仅当a?0，x?0，或x??时，f?(x)?0，所以f(x)在[0,?]上是减函数； 当0?a?1时，方程f?(x)?0有两实根x1，x2. 当x?[0,x1)时，sinx?a，f?(x)?0，f(x)是增函数； 当x?(x1,x2)时，sinx?a，f?(x)?0，f(x)是减函数； 当x?(x2,?]时，sinx?a，f?(x)?0，f(x)是增函数. （2）.

1

40.（2012全国大纲文）已知函数f(x)?x3?x2?ax.

3

（1）讨论f(x)的单调性；

（2）设f(x)有两个极值点x1,x2，若过两点(x1,f(x1))，(x2,f(x2))的直线l与x轴的交点在曲线y?f(x)上，求a的值.

an

41.（2012四川理）已知a为正实数，n为自然数，抛物线y??x?与x轴正半轴相交于

2

点A.设f(n)为该抛物线在点A处的切线在y轴上的截距.

（1）用a和n表示f(n)；

2

f(n)?1n3

?（2）求对所有n都有成立的a的最小值；

f(n)?1n3?1

（3）当0?a?1时，比较?

k?1

n

127f(1)?f(n)

与?的大小，并说明理由.

f(k)?f(2k)4f(0)?f(1)

n

解：（1）由已知得，交点A

的坐标为?12

对y??，?x??2?

求导得y???2x，则抛物线在A

处的切线方程为y?x， 16

2012高考题答案 2012年导数高考题汇编(含答案)

高三第一轮单元复习强化训练

即y??an，则f(n)?an.

（2）由（1）知f(n)?an，则f(n)?1n3

?3成立的充要条件是an?2n3?1. f(n)?1n?1

即知an?2n3?1对所有n成立.特别地，取n?

2，得到a

2233122333当an?3时，an?4n?(1?3)n?1?C1n[5(n?2)2?(2n?5)]?2n3?1. n?3?Cn?3?Cn?3???1?Cn?3?Cn?3?Cn?3?1?2n?1

2

当n?

0,1,2时，显然n?2n3?1.

故当af(n)?1n3

?对所有自然数n都成立. f(n)?1n?1

所以满足条件的a

.

（3）由（1）知f(k)?ak，则?k?1

nnn11f(1)?f(n)a?an??k?，. 2kf(k)?f(2k)k?1a?af(0)?f(1)1?a下面证明：?k?1127f(1)?f(n)??. f(k)?f(2k)4f(0)?f(1)

首先证明：当0?x?1时，127?x. 2x?x4

设函数g(x)?81?2?27x(x2?x)?1,0?x?1，则g?(x)?x?x??. 4?3?4

当0?x?22时，g?(x)?0；当?x?1时，g?(x)?0. 33

2??故g(x)在区间(0,1)上的最小值g(x)min?g???0. ?3?

所以，当0?x?1时，g(x)?0，即得127?x. 2x?x4

由0?a?1知0?ak?1(k?N?)，因此127?ak，从而 2ka?a4k

?k?1nn1127nk27a?an?127a?an27f(1)?f(n)??k??a?4?1?a?4?1?a?4?f(0)?f(1). f(k)?f(2k)k?1a?a2k4k?1

an

42.（2012四川文）已知a为正实数，n为自然数，抛物线y??x?与x轴正半轴相交于2点A.设f(n)为该抛物线在点A处的切线在y轴上的截距. 2

（1）用a和n表示f(n)；

（2）求对所有n都有f(n)?1n?成立的a的最小值； f(n)?1n?1

111f(1)?f(n?1)????与6?的大f(1)?f(2)f(2)?f(4)f(n)?f(2n)f(0)?f(1)

，

（3）当0?a?1时，比较小，并说明理由. 解：（1）由已知得，交点A

的坐标为即y??an，则f(n)?an. ?12对y??，?x??2?n求导得y???2x，则抛物线在A

处的切线方程为y?x 17

2012高考题答案 2012年导数高考题汇编(含答案)

高三第一轮单元复习强化训练

f(n)?1n（2）由（1）知f(n)?an，则成立的充要条件是an?2n?1. ?f(n)?1n?1

即知an?2n?1对所有n成立.特别地，取n?1，得到a?3.

当a?3，n?1时，an?3n?(1?2)n?1?C1

n?2???2n?1.

当n?0时，显然an?2n?1.

故当a?3时，f(n)?1n对所有自然数n都成立. ?f(n)?1n?1

所以满足条件的a的最小值为3.

（3）由（1）知f(k)?ak. 下面证明：111f(1)?f(n?1). ?????6?f(1)?f(2)f(2)?f(4)f(n)?f(2n)f(0)?f(1)

1?6x. x?x2首先证明：当0?x?1时，

2??设函数g(x)?6x(x2?x)?1,0?x?1，则g?(x)?18x?x??. ?3?

当0?x?22时，g?(x)?0；当?x?1时，g?(x)?0. 33

21??故g(x)在区间(0,1)上的最小值g(x)min?g????0. ?3?9

所以，当0?x?1时，g(x)?0，即得1?6x. x?x2

由0?a?1知0?ak?1(k?N?)，因此1?6ak，从而 a?a2kk

111111?????????nf(1)?f(2)f(2)?f(4)f(n)?f(2n)a?a2a2?a4a?a4?ak?1nk1a?an?1f(1)?f(n?1)?6(a?a2???an)?6??6?. 2n?a1?af(0)?f(1)

43.（2012重庆理）设f(x)?alnx?

线垂直于y轴.

（1）求a的值；

（2）求函数f(x)的极值.

解：（1）因为f(x)?alnx?13?x?1，其中a?R，曲线y?f(x)在点(1,f(1))处的切2x213a13?x?1，故f?(x)???. 2x2x2x2

1

232由于曲线y?f(x)在点(1,f(1))处的切线垂直于y轴，故该切线斜率为0，即f?(1)?0，从而a???0，解得a??1.

（2）由（1）知f(x)??lnx?13113(3x?1)(x?1). ?x?1(x?0)，f?(x)???2??2x2x2x22x2当x?(0,1)时，f?(x)?0，故f(x)单调递减；当x?(1,??)时，f?(x)?0，故f(x)单调递增. 所以f(x)在x?1处取得极小值f(1)?3.

44.（2012重庆文）已知函数f(x)?ax3?bx?c在x?2处取得极值c?16.

（1）求a,b的值；

18

2012高考题答案 2012年导数高考题汇编(含答案)

高三第一轮单元复习强化训练

（2）若f(x)有极大值28，求f(x)在[?3,3]上的最小值. 解：（1）因为f(x)?ax3?bx?c，故f?(x)?3ax2?b.

由于f(x)在x?2处取得极值c?16，故有?f?(2)?0,12a?b?0,??a?1,即?解得? f(2)?c?16,8a?2b?c?c?16,???b??12.?

（2）由（1）知f(x)?x3?12x?c，f?(x)?3x2?12?3(x?2)(x?2). 当x?(??,?2)时，f?(x)?0，故f(x)在(??,?2)上为增函数；当x?(?2,2)时，f?(x)?0，故f(x)在(?2,2)上为减函数；当x?(2,??)时，f?(x)?0，故f(x)在(2,??)上为增函数.

由此可知f(x)在x??2处取得极大值f(?2)?16?c，f(x)在x?2处取得极小值f(2)?c?16. 由题设条件知16?c?28，解得c?12.

此时f(?3)?9?c?21，f(3)??9?c?3，f(2)??16?c??4， 因此f(x)在[?3,3]上的最小值为f(2)??4.

19

本文标题：2012年中考数学试题及答案-2000—2012年考研数学(一)真题及答案解析 19
本文地址： http://www.61k.com/1091029.html