一 : 北京市海淀区2013届高三一模数学理试题

2013年北京市海淀区高考数学一模试卷（理科）

参考答案与试题解析

一、选择题：本大题共8小题，每小题5分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.

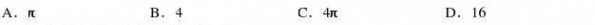
2

3．（5分）（2013?海淀区一模）某程序的框图如图所示，执行该程序，若输入的x值为5，则输出的y值（ ）

2013海淀一模数学 北京市海淀区2013届高三一模数学理试题

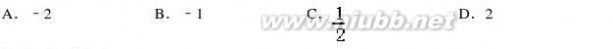
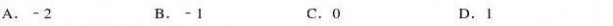
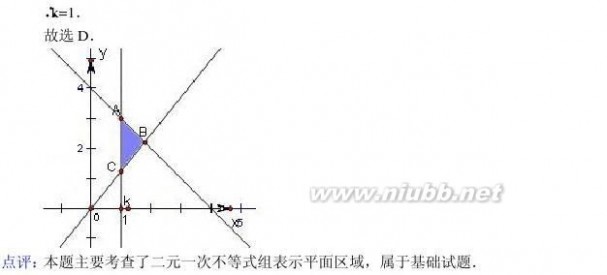
4．（5分）（2013?海淀区一模）不等式组表示面积为1的直角三角形区域，则

2013海淀一模数学 北京市海淀区2013届高三一模数学理试题

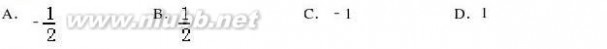
5．（5分）（2013?甘肃三模）若向量，满足||=||=|+|=1，则?的值为（ ） 6．（5分）（2013?海淀区一模）一个盒子里有3个分别标有号码为1，2，3的小球，每次取

2013海淀一模数学 北京市海淀区2013届高三一模数学理试题

27．（5分）（2013?海淀区一模）抛物线y=4x的焦点为F，点P（x，y）为该抛物线上的动

点，又点A（﹣1，0），则

的最小值是（ ）

8．（5分）（2013?海淀区一模）设l1，l2，l3为空间中三条互相平行且两两间的距离分别为4，5，6的直线．给出下列三个结论：

①?Ai∈li（i=1，2，3），使得△A1A2A3是直角三角形；

2013海淀一模数学 北京市海淀区2013届高三一模数学理试题

②①?Ai∈li（i=1，2，3），使得△A1A2A3是等边三角形；

③三条直线上存在四点Ai（i=1，2，3，4），使得四面体A1A2A3A4为在一个顶点处的三条棱两两互相垂直的四面体．

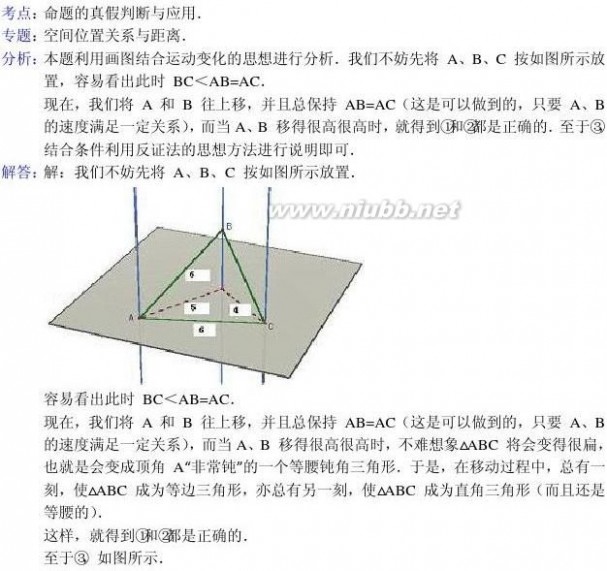
2013海淀一模数学 北京市海淀区2013届高三一模数学理试题

二、填空题：本大题共6小题，每小题5分，共30分.

9．（5分）（2013?海淀区一模）在复平面上，若复数a+bi（a，b∈R）对应的点恰好在实轴上，则b= 0 ．

10．（5分）（2013?海淀区一模）等差数列{an}中，a3+a4=9，a2a5=18，则a1a6=

2013海淀一模数学 北京市海淀区2013届高三一模数学理试题

11．（5分）（2013?海淀区一模）如图，AP⊙O切于点A，交弦DB的延长线于点P，过点B作圆O的切线交AP于点C．若∠ACB=90°，BC=3，CP=4，则弦DB的长为 ．

12．（5分）（2013?海淀区一模）在△ABC中，若a=4，b=2，cosA=﹣，则c= 3 ，sinC=

．

2013海淀一模数学 北京市海淀区2013届高三一模数学理试题

13．（5分）（2013?海淀区一模）已知函数f（x）=有三个不同的零点，则实数a的取值范围是 ＜a≤1 ．

2013海淀一模数学 北京市海淀区2013届高三一模数学理试题

14．（5分）（2013?海淀区一模）已知函数f（x）=sinx，任取t∈R，定义集合：At={y|y=f（x），点P（t，f（t）），Q（x，f（x））满足|PQ|≤}．设Mt，mt分别表示集合At中元素的最大值和最小值，记h（t）=Mt﹣mt．则

（1）函数h（t）的最大值是 2 ；

（2）函数h（t）的单调递增区间为 （2k﹣1，2k），k∈Z ．

2013海淀一模数学 北京市海淀区2013届高三一模数学理试题

三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程.

215．（13分）（2013?海淀区一模）已知函数f（x）=2﹣（sinx﹣cosx）．

（Ⅰ）求f（）的值和f（x）的最小正周期；

，]上的最大值和最小值． （Ⅱ）求函数f（x）在区间[﹣

2013海淀一模数学 北京市海淀区2013届高三一模数学理试题

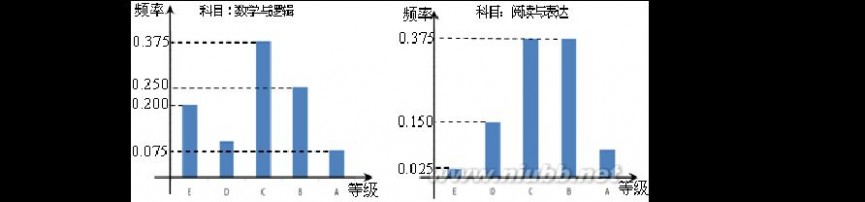
16．（13分）（2013?海淀区一模）在某大学自主招生考试中，所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试，成绩分为A，B，C，D，E五个等级．某考场考生两科的考试成绩的数据统计如下图所示，其中“数学与逻辑”科目的成绩为B的考生有10人．

（I）求该考场考生中“阅读与表达”科目中成绩为A的人数；

（II）若等级A，B，C，D，E分别对应5分，4分，3分，2分，1分．

（i）求该考场考生“数学与逻辑”科目的平均分；

（ii）若该考场共有10人得分大于7分，其中有2人10分，2人9分，6人8分．从这10人中随机抽取两人，求两人成绩之和的分布列和数学期望．

2013海淀一模数学 北京市海淀区2013届高三一模数学理试题

17．（14分）（2013?海淀区一模）在四棱锥P﹣ABCD中，PA⊥平面ABCD，△ABC是正三角形，AC与BD的交点M恰好是AC中点，又PA=AB=4，∠CDA=120°，点N在线段PB上，且PN=．

（Ⅰ）求证：BD⊥PC；

（Ⅱ）求证：MN∥平面PDC；

（Ⅲ）求二面角A﹣PC﹣B的余弦值．

2013海淀一模数学 北京市海淀区2013届高三一模数学理试题

2013海淀一模数学 北京市海淀区2013届高三一模数学理试题

18．（13分）（2013?海淀区一模）已知函数f（x）=lnx+ax+bx（其中a，b）为常数且a≠0）在x=1处取得极值．

（I）当a=1时，求f（x）的单调区间；

（II）若f（x）在（0，e]上的最大值为1，求a的值．

2

2013海淀一模数学 北京市海淀区2013届高三一模数学理试题

2013海淀一模数学 北京市海淀区2013届高三一模数学理试题

19．（14分）（2013?海淀区一模）已知圆M：（x﹣）+y=r=r（r＞0）．若椭圆C：2222+=1（a＞b＞0）的右顶点为圆M的圆心，离心率为．

（I）求椭圆C的方程；

（II）若存在直线l：y=kx，使得直线l与椭圆C分别交于A，B两点，与圆M分别交于G，H两点，点G在线段AB上，且|AG|=|BH|，求圆M半径r的取值范围．

2013海淀一模数学 北京市海淀区2013届高三一模数学理试题

20．（13分）（2013?海淀区一模）设A（xA，yA），B=（xB，yB）为平面直角坐标系上的两点，其中xA，yA，xB，yB∈Z．令△x=xB﹣xA，△y=yB﹣yA，若|△x|?|△y|≠0，则x|+|△Y|=3，且|△

称点B为点A的“相关点”，记作：B=i（A）．已知0（x0，y0）（x0y0∈Z）为平面上一个定点，平面上点列{Pi}满足：Pi=i（Pi﹣1），且点Pi的坐标为（xiyi），其中i=1，2，3，…n． （Ⅰ）请问：点p0的“相关点”有几个？判断这些“相关点”是否在同一个圆上，若在同一个圆上，写出圆的方程；若不在同一个圆上，说明理由；

（Ⅱ）求证：若P0与Pn重合，n一定为偶数；

（Ⅲ）若p0（1，0），且yn=100，记T=，求T的最大值．

2013海淀一模数学 北京市海淀区2013届高三一模数学理试题

2013海淀一模数学 北京市海淀区2013届高三一模数学理试题

二 : 2013海淀中考一模数学答案

2013海淀中考一模数学参考答案

数学试卷答案及评分参考

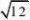
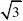
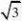
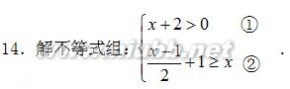
三、解答题（本题共30分，每小题5分） 13?2cos30??1)0?()?1 ．

81

解：原式?2?

2

?1?8 ………………………4分

??7．………………………5分

解：由①得 x??2．………………………2分 由②得 x?1．………………………4分

则不等式组的解集为?2?x?1．………………………5分

1?x?1?

15．先化简，再求值：?1?，其中x?3． ??

x?22x?4??

2

解：原式? ?

?

x?2?12x?4

?2 ………………………2分

x?2x?1

x?1x?2

?

2(x?2)(x?1)(x?1)

………………………3分

2x?1

. ………………………4分

2x?1

?12

当x?3时，原式=.………………………5分

16.证明：?AB∥EC，

∴?A??DCE. ………………………1分 在△ABC和△CDE中， ??B??EDC,?

??A??DCE, ?AC?CE,?

E

A

B

D

C

∴△ABC≌△CDE.………………………4分 ∴BC?DE. ………………………5分

1

2013海淀一模数学 2013海淀中考一模数学答案

17.解：（1）∵ 点A(?1,n)在反比例函数y??2

x的图象上，

∴ n?2. ………………………1分

∴ 点A的坐标为（?1，2）.

∵ 点A在一次函数y?kx?k的图象上，

∴2??k?k.

∴k??1.………………………2分

∴ 一次函数的解析式为y??x?1．………………………3分

（2）点P的坐标为（-3,0）或（1,0）．………………………5分 （写对一个给1分）

18.解：设原计划每天加工x顶帐篷. ………………………1分

1500?300

x?1500?300

2x?4.………………………3分

解得 x?150. ………………………4分

经检验，x?150是原方程的解，且符合题意.

答：原计划每天加工150顶帐篷. ………………………5分

四、解答题（本题共20分，每小题5分）

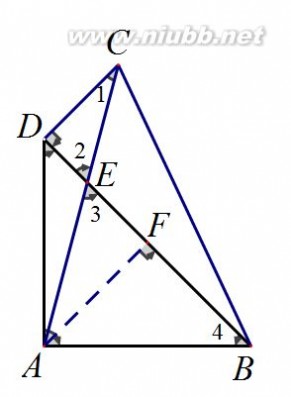
19. 解：过点A作AF⊥BD于F.

∵∠CDB=90°,∠1=30°,

∴∠2=∠3=60°. ………………………1分

在△AFB中，∠AFB=90°.

∵∠4=45

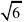
°，AB?,

∴AF=BF

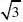
………………………2分

在△AFE中，∠AFE=90°.

∴EF?1,AE?2.………………………3分

在△ABD中，∠DAB=90°.

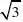
∴DB?

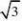
∴DE?DB?BF?EF?1.………………………4分

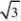
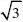
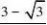
∴S11

?ADE?2DE?AF?2?1)??2.………………………5分

20.(1)证明：连接OD. ………………………1分 ∵AB=AC,

∴?B??C.

又∵OB?OD,

∴?B??

1.

2

2013海淀一模数学 2013海淀中考一模数学答案

∴?C??1.

∴OD∥AC.

∵DE⊥AC于E,

∴DE⊥OD.

∵点D在⊙O上，

∴DE与⊙O相切. ………………………2分

(2)解：连接AD.

∵AB为⊙O的直径，

∴∠ADB=90°.

∵AB=6，sinB=5

5，

∴AD?AB?sinB=65

5.………………3分

∵?1??2??3??2?90?，

∴?1??3.

∴?B??3.

在△AED中，∠AED=90°.

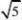
∵sin?3?AE

AD

5?5，

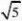
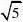
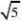
∴AE?AD?5?5?6

5. ………………………4分

又∵OD∥AE，

∴△FAE∽△FOD. ∴FA

FOOD

∵AB?6,

FA2?AE. ∴OD?AO?3. ∴FA?35

∴AF?2. ………………………5分 ?.

21.（1）1

3.………………………1分

（2）∵(3?3?18)?80%?30，

∴被小博同学抽取的监测点个数为30个. ………………………2分

………………………3分

3

2013海淀一模数学 2013海淀中考一模数学答案

（3）设去年同期销售x万箱烟花爆竹.

(1?35%)x?37. 解得x?56

∴5612

131213.………………………4分 1213?20. ?37?19

答：今年比去年同期少销售约20万箱烟花爆竹. ……………………… 5分

22.（1

………………………2分

（2）①如图：

(答案不唯一) ………………………4分

………………………5分

五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）

23．解：（1）依题意，可得抛物线的对称轴为x???2m

2m?1.………………………1分

∵抛物线与x轴交于A、B两点，点A的坐标为(?2,0)，

∴点B的坐标为 (4,0)．………………………2分

（2）∵点B在直线y= 1x+4m+n上， 2

∴0?2?4m?n①.

∵点A在二次函数y?mx-2mx?n的图象上，

∴0?4m?4m?n②. ………………………3分 由①、②可得m?1

2，n??4. ………………………4分

112∴ 抛物线的解析式为y＝x2?x?4，直线的解析式为y＝x?2． ……………5分 22

（3）?5

2?d?0． ………………………7分

24．（1）AE?2.………………………1分

（2）线段AE、CD之间的数量关系为AE?2CD.………………………2分 证明：如图1，延长AC与直线l交于点G．

4

2013海淀一模数学 2013海淀中考一模数学答案

依题意，可得∠1＝∠2． ∵∠ACB＝90?， ∴∠3=∠4.

∴BA?BG.

∴CA＝CG．………………………3分 ∵AE⊥l，CD⊥l， ∴CD∥AE． ∴△GCD∽△GAE． ∴ CD

AE＝GC

GA?1

2．

∴AE?2CD．………………………4分

（3）解：当点F在线段AB上时，如图2， 过点C作CG∥l交AB于点H，交AE于点G．∴∠2＝∠HCB． ∵∠1=∠2，

∴∠1＝∠HCB． ∴CH?BH． ∵∠ACB＝90?，

∴∠3+∠1＝∠HCB+∠4 =90?． ∴∠3＝∠4．

∴CH?AH?BH． ∵CG∥l，

∴△FCH∽△FEB． ∴ CFCH5

EF＝EB?6．

设CH?5x,BE?6x，则AB?10x． ∴在△AEB中，∠AEB＝90?，AE?8x． 由（2）得，AE?2CD． ∵CD?4,

∴AE?8.

∴x?1.

∴AB?10,BE?6,CH?5． ∵CG∥l，

∴△AGH∽△AEB． ∴HG

BE?AH

AB?1

2．

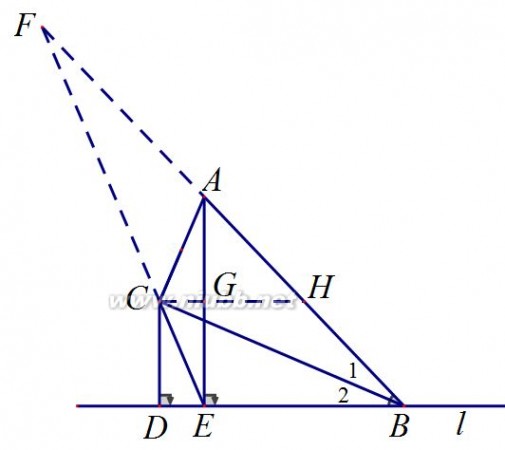
图

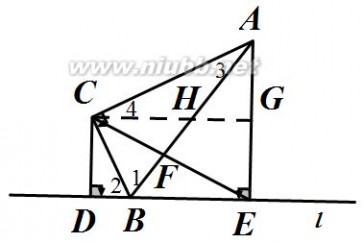
2 图

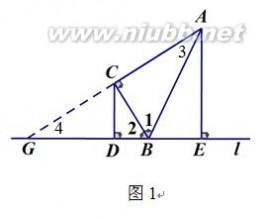
3

5

2013海淀一模数学 2013海淀中考一模数学答案

∴HG?3．………………………5分

∴CG?CH?HG?8．

∵CG∥l，CD∥AE,

∴四边形CDEG为平行四边形.

∴DE?CG?8.

∴BD?DE?BE?2．……………………6分

当点F在线段BA的延长线上时，如图3，

同理可得CH?5,GH?3,BE?6.

∴DE=CG?CH?HG?2．

∴ BD?DE?BE?8．

∴BD?2或8．……………………7分

25.解：（1）?y?x2?2mx?m2?m??x?m?2?m，……………………1分 ∴顶点坐标为C(m,m).……………………2分

（2）①?y?x?2与抛物线y?x2?2mx?m2?m交于A、B两点， ∴x?2?x2?2mx?m2?m.

解方程，得x1?m?1,x2?m?2.……………………4分

?点A在点B的左侧，

∴A(m?1,m?1),B(m?2,m?4).

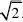
∴AB?……………………5分

?直线OC的解析式为y?x，直线AB的解析式为y?x?2， ∴AB∥OC，两直线AB、OC之间距离h=

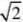
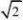
∴S1

?APB?2AB?h?1

2??3.………………………6分

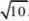
……………………8分

(注：本卷中许多问题解法不唯一,请老师根据评分标准酌情给分)

6

本文标题：2013海淀一模数学-北京市海淀区2013届高三一模数学理试题
本文地址： http://www.61k.com/1132063.html