一 : 等比数列的前n项和(第一课时)优质课比赛课件

图片展示

等比数列前n项和ppt 等比数列的前n项和(第一课时)优质课比赛课件

图片展示

等比数列前n项和ppt 等比数列的前n项和(第一课时)优质课比赛课件

图片展示

等比数列前n项和ppt 等比数列的前n项和(第一课时)优质课比赛课件

图片展示

等比数列前n项和ppt 等比数列的前n项和(第一课时)优质课比赛课件

图片展示

等比数列前n项和ppt 等比数列的前n项和(第一课时)优质课比赛课件

图片展示

等比数列前n项和ppt 等比数列的前n项和(第一课时)优质课比赛课件

图片展示

等比数列前n项和ppt 等比数列的前n项和(第一课时)优质课比赛课件

图片展示

等比数列前n项和ppt 等比数列的前n项和(第一课时)优质课比赛课件

图片展示

等比数列前n项和ppt 等比数列的前n项和(第一课时)优质课比赛课件

图片展示

等比数列前n项和ppt 等比数列的前n项和(第一课时)优质课比赛课件

图片展示

等比数列前n项和ppt 等比数列的前n项和(第一课时)优质课比赛课件

图片展示

等比数列前n项和ppt 等比数列的前n项和(第一课时)优质课比赛课件

图片展示

等比数列前n项和ppt 等比数列的前n项和(第一课时)优质课比赛课件

图片展示

等比数列前n项和ppt 等比数列的前n项和(第一课时)优质课比赛课件

图片展示

等比数列前n项和ppt 等比数列的前n项和(第一课时)优质课比赛课件

图片展示

等比数列前n项和ppt 等比数列的前n项和(第一课时)优质课比赛课件

图片展示

等比数列前n项和ppt 等比数列的前n项和(第一课时)优质课比赛课件

图片展示

等比数列前n项和ppt 等比数列的前n项和(第一课时)优质课比赛课件

图片展示

等比数列前n项和ppt 等比数列的前n项和(第一课时)优质课比赛课件

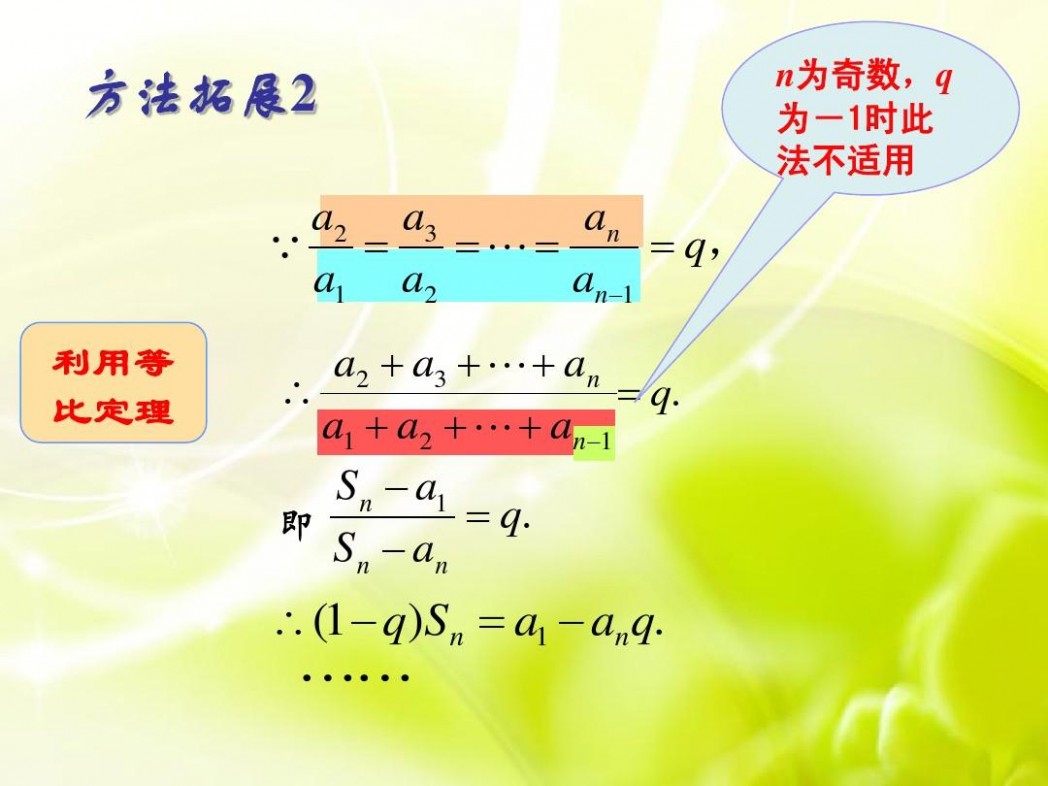
图片展示

等比数列前n项和ppt 等比数列的前n项和(第一课时)优质课比赛课件

图片展示

等比数列前n项和ppt 等比数列的前n项和(第一课时)优质课比赛课件

图片展示

二 : 等比数列的前n项和

教学目标
    1.把握等比数列前 项和公式,并能运用公式解决简单的问题.
    (1)理解公式的推导过程,体会转化的思想;
    (2)用方程的思想熟悉等比数列前 项和公式,利用公式知三求一;与通项公式结合知三求二;
    2.通过公式的灵活运用,进一步渗透方程的思想、分类讨论的思想、等价转化的思想.
    3.通过公式推导的教学,对学生进行思维的严谨性的练习,培养他们实事求是的科学态度.
    教学建议
    教材分析
    (1)知识结构
    先用错位相减法推出等比数列前 项和公式,而后运用公式解决一些问题,并将通项公式与前 项和公式结合解决问题,还要用错位相减法求一些数列的前 项和.
    (2)重点、难点分析
    教学重点、难点是等比数列前 项和公式的推导与应用.公式的推导中蕴含了丰富的数学思想、方法(如分类讨论思想,错位相减法等),这些思想方法在其他数列求和问题中多有涉及,所以对等比数列前 项和公式的要求,不单是要记住公式,更重要的是把握推导公式的方法. 等比数列前 项和公式是分情况讨论的,在运用中要非凡注重 和 两种情况.
    教学建议
    (1)本节内容分为两课时,一节为等比数列前 项和公式的推导与应用,一节为通项公式与前 项和公式的综合运用,另外应补充一节数列求和问题.
    (2)等比数列前 项和公式的推导是重点内容,引导学生观察实例,发现规律,归纳总结,证实结论.
    (3)等比数列前 项和公式的推导的其他方法可以给出,提高学生学习的爱好.
    (4)编拟例题时要全面,不要忽略 的情况.
    (5)通项公式与前 项和公式的综合运用涉及五个量,已知其中三个量可求另两个量,但解指数方程难度大.
    (6)补充可以化为等差数列、等比数列的数列求和问题.
    教学设计示例
    课题:等比数列前 项和的公式
    教学目标
    (1)通过教学使学生把握等比数列前 项和公式的推导过程,并能初步运用这一方法求一些数列的前 项和.
    (2)通过公式的推导过程,培养学生猜想、分析、综合能力,提高学生的数学素质.
    (3)通过教学进一步渗透从非凡到一般,再从一般到非凡的辩证观点,培养学生严谨的学习态度.
    教学重点,难点
    教学重点是公式的推导及运用,难点是公式推导的思路.
    教学用具
    幻灯片,课件,电脑.
    教学方法
    引导发现法.
    教学过程
    一、新课引入:
    (问题见教材第129页)提出问题: (幻灯片)
    二、新课讲解:
    记 ,式中有64项,后项与前项的比为公比2,当每一项都乘以2后,中间有62项是对应相等的,作差可以相互抵消.
    (板书)即 , ①
    , ②
    ②-①得 即 .
    由此对于一般的等比数列,其前 项和 ,如何化简?
    (板书)等比数列前 项和公式
    仿照公比为2的等比数列求和方法,等式两边应同乘以等比数列的公比 ,即
    (板书) ③两端同乘以 ,得
    ④,
    ③-④得 ⑤,(提问学生如何处理,适时提醒学生注重 的取值)
    当 时,由③可得 (不必导出④,但当时设想不到)
    当 时,由⑤得 .
    于是
    反思推导求和公式的方法——错位相减法,可以求形如 的数列的和,其中 为等差数列, 为等比数列.
    (板书)例题:求和: .
    设 ,其中 为等差数列, 为等比数列,公比为 ,利用错位相减法求和.
    解: ,
    两端同乘以 ,得
    ,
    两式相减得
    于是 .
    说明:错位相减法实际上是把一个数列求和问题转化为等比数列求和的问题.
    公式其它应用问题注重对公比的分类讨论即可.
    三、小结:
    1.等比数列前 项和公式推导中蕴含的思想方法以及公式的应用;
    2.用错位相减法求一些数列的前 项和.
    四、作业:略 .
    五、板书设计:
    等比数列前 项和公式例题

三 : 3.5 等比数列的前n项和（第一课时）

教学目的：1．掌握等比数列的前n项和公式及公式证明思路．2．会用等比数列的前n项和公式解决有关等比数列的一些简单问题。教学重点：等比数列的前n项和公式推导教学难点：灵活应用公式解决有关问题教学过程：一、复习等比数列的通项公式，有关性质，及等比中项等概念。二、引进课题，采用印度国际象棋发明者的故事，即求           ①用错项相消法推导结果，两边同乘以公比：           ②②－①： 这是一个庞大的数字>1．84× ，以小麦千粒重为40 计算，则麦粒总质量达7000亿吨——国王是拿不出来的。三、一般公式推导：设     ①乘以公比 ，       ②①-②： ， 时：                            时： 公式的推导方法二：有等比数列的定义， 根据等比的性质，有 即 （结论同上）围绕基本概念，从等比数列的定义出发，运用等比定理，导出了公式．公式的推导方法三：  ＝     ＝ ＝ （结论同上）注意：（1） 和 各已知三个可求第四个，     （2）注意求和公式中是 ，通项公式中是 不要混淆，     （3）应用求和公式时 ，必要时应讨论 的情况。四、例1、求等比数列 的前8项和.（p127，例一）——直接应用公式。    例2、某商场第1年销售计算机5000台，如果平均每年的销售量比上一年增加10%，那么从第1年起，约几年内可使总销售量达到30000台（保留到个位）（p127，例二）——应用题，且是公式逆用（求 ），要用对数算。    例3、求和：（x+ （其中x≠0，x≠1，y≠1）（p127，例三）——简单的“分项法”。    例4、设数列 为 求此数列前 项的和。     ——用错项相消法，注意分 两种情况讨论例5、  已知{ }为等比数列，且 =a， =b，（ab≠0），求 ．——注意这是一道多级分类讨论题. 一级分类：分 两种情况讨论； 时 ，要分  四、练习：是等比数列， 是其前n项和，数列  （ ）是否仍成等比数列？提示：应注意等比数列中的公比q的各种取值情况的讨论，还易忽视等比数列的各项应全不为0的前提条件.五、小结  1. 等比数列求和公式：当q=1时， 当 时，   或    ； 2． 是等比数列 的前n项和，①当q=－1且k为偶数时， 不是等比数列.②当q≠－1或k为奇数时，  仍成等比数列。3．这节课我们从已有的知识出发，用多种方法（迭加法、运用等比性质、错位相减法、方程法）推导出了等比数列的前n项和公式，并在应用中加深了对公式的认识．

六、作业：p129.  习题3．5  1，2，3，4，5，6，7.

四 : 上学期 3.5等比数列的前n项和

教学设计示例 课题：等比数列前 项和的公式 教学目标  （1）通过教学使学生掌握等比数列前 项和公式的推导过程，并能初步运用这一方法求一些数列的前 项和. （2）通过公式的推导过程，培养学生猜想、分析、综合能力，提高学生的数学素质. （3）通过教学进一步渗透从特殊到一般，再从一般到特殊的辩证观点，培养学生严谨的学习态度. 教学重点，难点 教学重点是公式的推导及运用，难点是公式推导的思路. 教学用具 幻灯片，课件，电脑. 教学方法 引导发现法. 教学过程  一、新课引入： （问题见教材第129页）提出问题： （幻灯片） 二、新课讲解： 记 ，式中有64项，后项与前项的比为公比2，当每一项都乘以2后，中间有62项是对应相等的，作差可以相互抵消. （板书）即 ，       ① ，      ② ②－①得 即 . 由此对于一般的等比数列，其前 项和 ，如何化简？ （板书）等比数列前 项和公式 仿照公比为2的等比数列求和方法，等式两边应同乘以等比数列的公比 ，即 （板书） ③两端同乘以 ，得 ④， ③－④得 ⑤，（提问学生如何处理，适时提醒学生注意 的取值） 当 时，由③可得 （不必导出④，但当时设想不到） 当 时，由⑤得 . 于是 反思推导求和公式的方法——错位相减法，可以求形如 的数列的和，其中 为等差数列， 为等比数列. （板书）例题：求和： . 设 ，其中 为等差数列， 为等比数列，公比为 ，利用错位相减法求和. 解： ， 两端同乘以 ，得 ， 两式相减得 于是 . 说明：错位相减法实际上是把一个数列求和问题转化为等比数列求和的问题. 公式其它应用问题注意对公比的分类讨论即可. 三、小结： 1.等比数列前 项和公式推导中蕴含的思想方法以及公式的应用； 2.用错位相减法求一些数列的前 项和. 四、作业 ：略. 五、板书设计 ： 等比数列前 项和公式 例题

本文标题：等比数列的前n项和-等比数列的前n项和(第一课时)优质课比赛课件
本文地址： http://www.61k.com/1066388.html