一 : 4.9函数y=Asin(ωx+φ) 的图象（5）

教学目的：三角函数图象和性质的综合应用 教学重点、难点：三角函数图象和性质的综合应用.一、例题：  例1 （1）已知 ，且 是第一象限角，则 的集合为（    ）   a．      b．     c．     d． （2）函数 的最大值与最小值依次分别为   a．    b．    c．    d． （3）在锐角 中，下列结论一定成立的是（     ） a．     b．     c．      d． 例2奇函数f(x)在其定义域( , )上是减函数，且f(1-sinα)+f(1-sin2α)<0求角α的取值范围。

例3知 )且函数

的最小值为0，求 的值.

例4已知函数  的图像过a(0，1)，b( ，1)两点，当函数的定义域为[0, ]时，恒有  成立，试确定实数a的范围.

例5 的周期为 ,且有最大值 .(1)求 .

(2) 若 为方程 的两根,( 的终边不共线),求 的值.

例6设定义域为一切实数的奇函数 是减函数,若当 时， 的取值范围.

二、作业：《绿色通道》五十.

二 : 函数y=cos(x

函数y=cos(x- π 8 )(x∈[ π 6 ， 2 3 π])的最小值是______．

题型：填空题难度：偏易来源：不详

∵ π 6 ≤x≤ 2π 3 ，∴ π 24 ≤x- π 8 ≤ 13π 24 ，∴y=cos（x- π 8 ）的最小值等于 cos 13π 24 ， 故答案为：cos 13π 24 ．

考点：

考点名称：正弦、余弦函数的图象与性质（定义域、值域、单调性、奇偶性等）

正弦函数和余弦函数的图象：正弦函数y=sinx（x∈R）和余弦函数y=cosx（x∈R）的图象分别叫做正弦曲线和余弦曲线，

1．正弦函数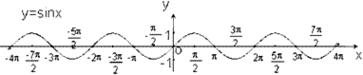

2．余弦函数

函数图像的性质
正弦、余弦函数图象的性质：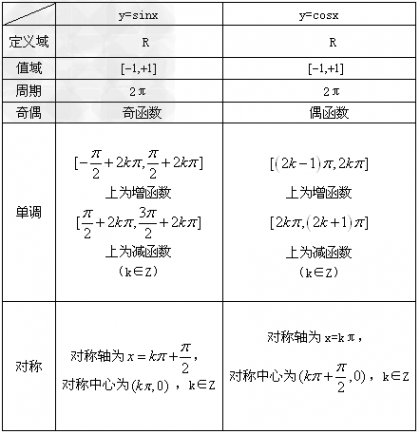

由上表知，正弦与余弦函数的定义域都是R，值域都是[-1，1]，对y=sinx，当时，y取最大值1，
当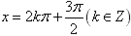时，y取最小值-1；对y=cosx，当x=2kπ（k∈Z）时，y取最大值1，当x=2kπ+π（k∈Z）时，y取最小值-1。

正弦、余弦函数图象的性质：

由上表知，正弦与余弦函数的定义域都是R，值域都是[-1，1]，对y=sinx，当时，y取最大值1，
当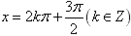时，y取最小值-1；对y=cosx，当x=2kπ（k∈Z）时，y取最大值1，当x=2kπ+π（k∈Z）时，y取最小值-1。

三 : 函数y=tan(π4x

函数y=tan( π 4 x- π 2 )的部分图象如图所示，则( OA + OB )? AB =______．

题型：填空题难度：中档来源：不详

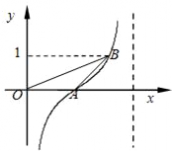由图象得，令y=tan( π 4 x- π 2 )=0，即 π 4 x- π 2 =kπ，k=0时解得x=2， 令y=tan( π 4 x- π 2 )=1，即 π 4 x- π 2 = π 4 ，解得x=3， ∴A（2，0），B（3，1）， ∴ OA =（2，0）， OB =（3，1）， AB =（1，1）， ∴( OA + OB )? AB =（5，1）?（1，1）=5+1=6． 故答案为：6．

考点：

考点名称：正切、余切函数的图象与性质（定义域、值域、单调性、奇偶性等）

正切函数的图像：

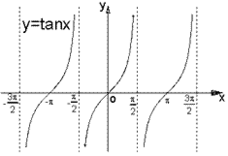
余切函数的图像：

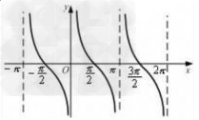
正切函数的性质：

（1）定义域：；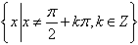
（2）值域是R，在上面定义域上无最大值也无最小值；
（3）周期性：是周期函数且周期是π，它与直线y=a的两个相邻交点之间的距离是一个周期π；
（4）奇偶性：是奇函数，对称中心是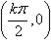（k∈Z），无对称轴；
（5）单调性：正切函数在开区间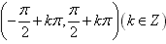内都是增函数。但要注意在整个定义域上不具有单调性。

余切函数的性质:

（1）定义域：{x|x≠kπ，k∈Z}
（2）值域：实数集R；
（3）周期性：是周期函数，周期为kπ（k∈Z且k≠0），最小正周期T=π
（4）奇偶性：奇函数，图像关于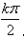（，0）（k∈z）对称，实际上所有的零点都是它的对称中心
（5）单调性：在每一个开区间（kπ，（k+1）π），（k∈Z）上都是减函数，在整个定义域上不具有单调性

四 : 求函数y=x+2x

求函数y=x+ 2x-1 的值域______．

题型：填空题难度：中档来源：不详

令t= 2x-1 ，（t≥0）， 则x= t2+1 2 ，问题转化为求函数f（t）= t2+1 2 +t= (t+1)2 2 在t≥0上的值域问题， 因为t≥0时，函数f（t）有最小值f（0）= 1 2 ．无最大值，故其值域为[ 1 2 ，+∞）． 即原函数的值域为[ 1 2 ，+∞）． 故答案为：[ 1 2 ，+∞）

考点：

考点名称：函数的定义域、值域

定义域、值域的概念：

自变量取值范围叫做函数的定义域，函数值的集合叫做函数的值域。

1、求函数定义域的常用方法有：

（1）根据解析式要求如偶次根式的被开方大于零，分母不能为零等；
（2）根据实际问题的要求确定自变量的范围；
（3）根据相关解析式的定义域来确定所求函数自变量的范围；
（4）复合函数的定义域：如果y是u的函数，而u是x的函数，即y=f（u），u=g（x），那么y=f[g（x）]叫做函数f与g的复合函数，u叫做中间变量，设f（x）的定义域是x∈M，g（x）的定义域是x∈N，求y=f[g（x）]的定义域时，则只需求满足的x的集合。设y=f[g（x）]的定义域为P，则 。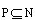

3、求函数值域的方法：

（1）利用一些常见函数的单调性和值域，如一次函数，二次函数，反比例函数，指数函数，对数函数，三角函数，形如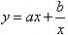（a，b为非零常数）的函数；
（2）利用函数的图象即数形结合的方法；
（3）利用均值不等式；
（4）利用判别式；
（5）利用换元法（如三角换元）；
（6）分离法：分离常数与分离参数两种形式；
（7）利用复合函数的单调性。（注：二次函数在闭区间上的值域要特别注意对称轴与闭区间的位置关系，含字母时要注意讨论）

五 : 函数y=1

函数y= 1-x2 1+x2 的值域是______．

题型：填空题难度：中档来源：不详

∵y= 1-x2 1+x2 ∴y（1+x2）=1-x2即（y+1）x2=1-y 当y=-1时，等式不成立 当y≠-1时，x2= 1-y 1+y ≥0解得y∈（-1，1] 故函数的定义域为：（-1，1] 故答案为：（-1，1]

考点：

考点名称：函数的定义域、值域

定义域、值域的概念：

自变量取值范围叫做函数的定义域，函数值的集合叫做函数的值域。

1、求函数定义域的常用方法有：

（1）根据解析式要求如偶次根式的被开方大于零，分母不能为零等；
（2）根据实际问题的要求确定自变量的范围；
（3）根据相关解析式的定义域来确定所求函数自变量的范围；
（4）复合函数的定义域：如果y是u的函数，而u是x的函数，即y=f（u），u=g（x），那么y=f[g（x）]叫做函数f与g的复合函数，u叫做中间变量，设f（x）的定义域是x∈M，g（x）的定义域是x∈N，求y=f[g（x）]的定义域时，则只需求满足的x的集合。设y=f[g（x）]的定义域为P，则 。

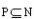3、求函数值域的方法：

（1）利用一些常见函数的单调性和值域，如一次函数，二次函数，反比例函数，指数函数，对数函数，三角函数，形如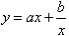（a，b为非零常数）的函数；
（2）利用函数的图象即数形结合的方法；
（3）利用均值不等式；
（4）利用判别式；
（5）利用换元法（如三角换元）；
（6）分离法：分离常数与分离参数两种形式；
（7）利用复合函数的单调性。（注：二次函数在闭区间上的值域要特别注意对称轴与闭区间的位置关系，含字母时要注意讨论）

本文标题：函数y=Asin-4.9函数y=Asin(ωx+φ) 的图象（5）
本文地址： http://www.61k.com/1111162.html