一 : 反三角函数：反三角函数-概述，反三角函数-相关介绍

反三角函数（Inverse of the trigonometric functions）就是三角函数的反函数。反三角函数是一种数学术语，是一种基本初等函数。反三角函数并不能狭义的理解为三角函数的反函数，是个多值函数。它是反正弦Arcsin x，反余弦Arccos x，反正切Arctan x，反余切Arccot x这些函数的统称，各自表示其正弦、余弦、正切、余切为x的角。为限制反三角函数为单值函数，将反正弦函数的值y限在-π/2≤y≤π/2，将y作为反正弦函数的主值，记为y=arcsin x；相应地，反余弦函数y=arccos x的主值限在0≤y≤π；反正切函数y=arctan x的主值限在-π/2。

反三角函数_反三角函数 -概述

三角函数的反函数，是多值函数。它们是反正弦arcsinx，反余弦arccosx，反正切Arctan x，反余切arccotx，反正割arcsecx，反余割Arccsc x等，各自表示其正弦、余弦、正切、余切、正割、余割为x的角。

反三角函数_反三角函数 -相关介绍

为限制反三角函数为单值函数，将反正弦函数的值y限在y=-π/2≤y≤π/2，将y为反正弦函数的主值，记为y=arcsin x；相应地，反余弦函数y=arccos x的主值限在0≤y≤π；反正切函数y=arctan x的主值限在-π/2

反三角函数_反三角函数 -分类

三角函数的反函数不是单值函数，因为它并不满足1个自变量对应1个函数值的要求，其图像与其原函数关于函数y=x对称。欧拉提出反三角函数的概念，并且首先使用了“arc+函数名”的形式表示反三角函数，而不是。
为限制反三角函数为单值函数，将反正弦函数的值y限在-π/2≤y≤π/2，将y作为反正弦函数的主值，记为y=arcsinx；相应地，反余弦函数y=arccosx的主值限在0≤y≤π；反正切函数y=arctanx的主值限在-π/2<y<π/2；反余切函数y=arccotx的主值限在0<y<π。

反正弦函数

y=sinx在[-π/2，π/2]上的反函数，叫做反正弦函数。记作arcsinx，表示1个正弦值为x的角，该角的范围在[-π/2，π/2]区间内。定义域[-1，1]，值域[-π/2，π/2]。

反余弦函数

y=cosx在[0，π]上的反函数，叫做反余弦函数。记作arccosx，表示1个余弦值为x的角，该角的范围在[0，π]区间内。定义域[-1，1]，值域[0，π]。
绿的为y=arccos(x)红的为y=arcsin(x)
绿的为y=arccos(x)红的为y=arcsin(x)

反正切函数

y=tanx在(-π/2，π/2）上的反函数，叫做反正切函数。记作arctanx，表示1个正切值为x的角，该角的范围在（-π/2，π/2）区间内。定义域R，值域（-π/2，π/2）。

反余切函数

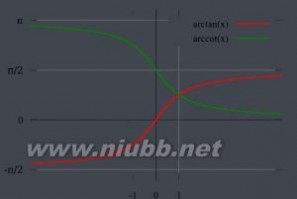绿的为y=arccot(x) 红的为y=arctan(x)y=cotx在[0，π）上的反函数，叫做反余切函数。记作arccotx，表示1个余切值为x的角，该角的范围在（0，π）区间内。定义域R，值域（0，π）。
绿的为y=arccot(x)红的为y=arctan(x)
绿的为y=arccot(x)红的为y=arctan(x)

反正割函数

y=secx在[0,π/2)U(π/2,π]上的反函数，叫做反正割函数。记作arcsecx，表示1个正割值为x的角，该角的范围在[0,π/2)U(π/2,π]区间内。定义域（-∞,-1]U[1,+∞),值域[0,π/2)U(π/2,π]。

反余割函数

y=cscx在[-π/2,0)U(0,π/2]上的反函数，叫做反余割函数。记作arccscx，表示1个余割值为x的角，该角的范围在[-π/2,0)U(0,π/2]区间内。定义域（-∞,-1]U[1,+∞),值域[-π/2,0)U(0,π/2]。

反三角函数_反三角函数 -数学公式

基本

secant（正割）Sec(X)=1/Cos(X)
cosecant（余割）Cosec(X)=1/Sin(X)
cotangent（余切）Cotan(X)=1/Tan(X)
InverseSine（反正弦）Arcsin(X)=Atn(X/Sqr(-X*X+1))
InverseSecant（反正割）Arcsec(X)=Atn(X/Sqr(X*X-1))+Sgn((X)-1)*(2*Atn(1))
InverseCosecant（反余割）Arccosec(X)=Atn(X/Sqr(X*X-1))+(Sgn(X)-1)*(2*Atn(1))
InverseCotangent（反余切）Arccotan(X)=Atn(X)+2*Atn(1)

其他公式

cos(arcsinx)=(1-x^2)^0.5
arcsin(-x)=-arcsinx
arccos(-x)=π-arccosx
arctan(-x)=-arctanx
arccot(-x)=π-arccotx
arcsinx+arccosx=π/2=arctanx+arccotx
sin(arcsinx)=cos(arccosx)=tan(arctanx)=cot(arccotx)=x
arcsinx=x+x^3/(2*3)+(1*3)x^5/(2*4*5)+1*3*5(x^7)/(2*4*6*7）……+(2k+1)!!*x^(2k-1)/(2k!!*(2k+1))+……（|x|<1)!！表示双阶乘
arccosx=π-(x+x^3/(2*3)+(1*3)x^5/(2*4*5)+1*3*5(x^7)/(2*4*6*7）……）（|x|<1)
arctanx=x-x^3/3+x^5/5-……
举例
当x∈[-π/2，π/2]有arcsin(sinx)=x
x∈[0，π]，arccos(cosx)=x
x∈（-π/2，π/2），arctan(tanx)=x
x∈（0，π），arccot(cotx)=x
x>0，arctanx=π/2-arctan1/x，arccotx类似
若(arctanx+arctany）∈（-π/2，π/2），则arctanx+arctany=arctan((x+y)/(1-xy))
例如，arcsinχ表示角α，满足α∈[-π/2，π/2]且sinα=χ;arccos(-4/5)表示角β，满足β∈[0，π]且cosβ=-4/5;arctan2表示角φ，满足φ∈（-π/2，π/2)且tanφ=2

反三角函数_反三角函数 -数学术语

为限制反三角函数为单值函数，将反正弦函数的值y限在y=-π/2≤y≤π/2，将y为反正弦函数的主值，记为y=arcsinx；相应地，反余弦函数y=arccosx的主值限在0≤y≤π；反正切函数y=arctanx的主值限在-π/2<y<π/2；反余切函数y=arccotx的主值限在0<y<π。
反三角函数实际上并不能叫做函数，因为它并不满足1个自变量对应1个函数值的要求，其图像与其原函数关于函数y=x对称。其概念首先由欧拉提出，并且首先使用了arc+函数名的形式表示反三角函数，而不是f-1(x).
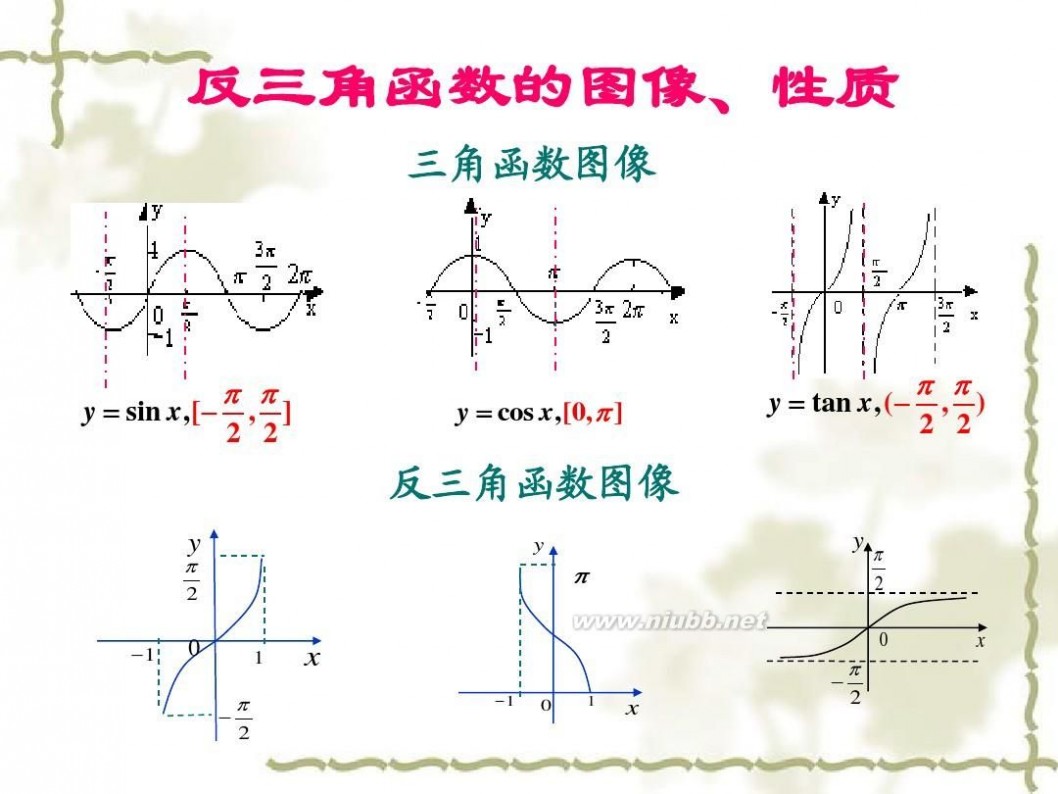
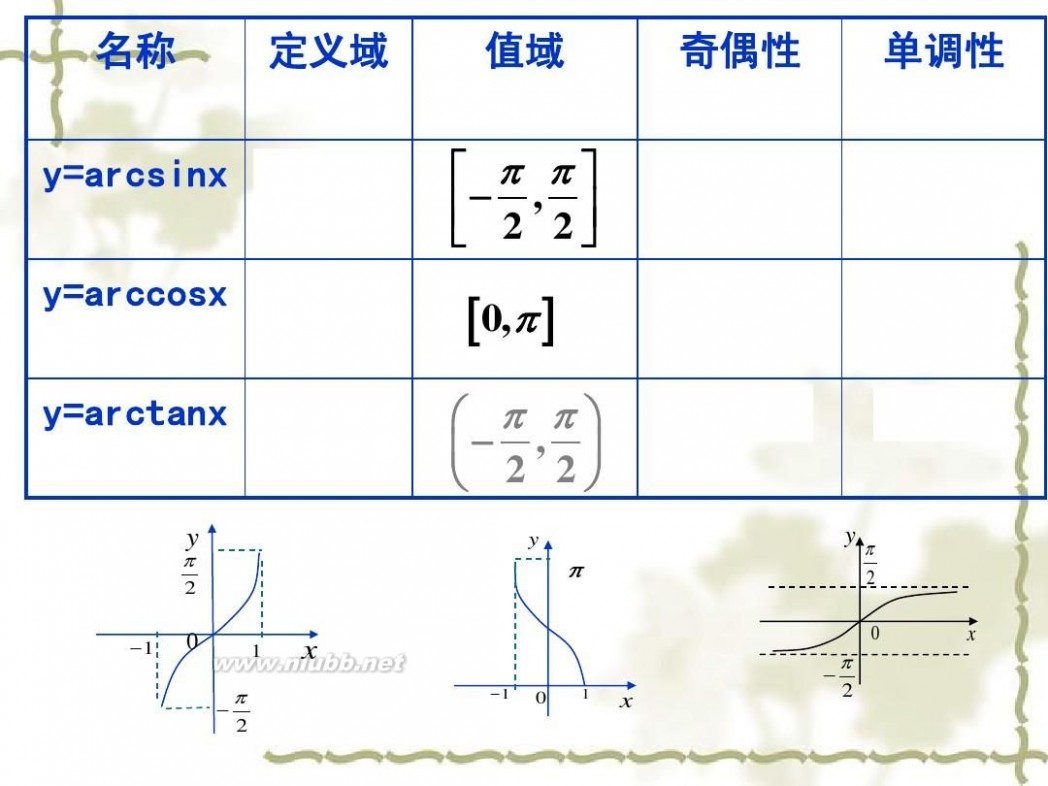
（1）正弦函数y=sinx在[-π/2,π/2]上的反函数，叫做反正弦函数。arcsinx表示1个正弦值为x的角，该角的范围在[-π/2,π/2]区间内。
（2）余弦函数y=cosx在[0,π]上的反函数，叫做反余弦函数。arccosx表示1个余弦值为x的角，该角的范围在[0,π]区间内。
（3）正切函数y=tanx在(-π/2,π/2)上的反函数，叫做反正切函数。arctanx表示1个正切值为x的角，该角的范围在(-π/2,π/2)区间内。
反三角函数主要是3个：
y＝arcsin(x)，定义域[-1,1]，值域[-π/2,π/2]图象用红色线条；
y=arccos(x)，定义域[-1,1]，值域[0,π]，图象用蓝色线条；
y=arctan(x)，定义域(-∞,+∞)，值域(-π/2,π/2)，图象用绿色线条；
y=arccot(x)，定义域(-∞,+∞)，值域(0,π)，图象用绿色线条；
sin(arcsinx)=x,定义域[-1,1],值域[-1,1]arcsin(-x)=-arcsinx
证明方法如下：设arcsin(x)=y,则sin(y)=x,将这2个式子代入上式就可以得
其他几个用类似方法可得
cos(arccosx)=x,arccos(-x)=π-arccosx
tan(arctanx)=x,arctan(-x)=-arctanx

二 : 反三角函数

反三角函数 反三角函数

反三角函数 反三角函数

反三角函数 反三角函数

反三角函数 反三角函数

反三角函数 反三角函数

反三角函数 反三角函数

反三角函数 反三角函数

反三角函数 反三角函数

三 : 2.4反函数（三课时）

教学目的：1.掌握反函数的概念和表示法，会求一个函数的反函数          2.互为反函数的图象间的关系.           3.反函数性质的应用.教学重点：反函数的定义和求法，互为反函数的图象间的关系.教学难点：反函数的定义，反函数性质的应用.教学过程：

第一课时教学目的：1.掌握反函数的概念和表示法，会求一个函数的反函数          2.互为反函数的图象间的关系. 教学重点：反函数的定义和求法，互为反函数的图象间的关系.教学难点：反函数的定义和求法。教学过程：一、复习引入：由物体作匀速直线运动的位移公式s=vt,（其中速度v是常量）s是时间t的函数；可以变形为： ，这时，位移s是自变量，时间t是位移s的函数.又如，在函数 中，x是自变量，y是x的函数. 由 中解出x，得到式子 . 这样，对于y在r中任何一个值，通过式子 ，x在r中都有唯一的值和它对应. 因此，它也确定了一个函数：y为自变量，x为y的函数，定义域是y r，值域是x r.上述两例中，由函数s=vt得出了函数 ；由函数 得出了函数 ，不难看出，这两对函数中，每一对中两函数之间都存在着必然的联系：①它们的对应法则是互逆的；②它们的定义域和值域相反：即前者的值域是后者的定义域，而前者的定义域是后者的值域. 我们称这样的每一对函数是互为反函数.二、讲解新课：反函数的定义设函数 的值域是c，根据这个函数中x,y 的关系，用y把x表示出，得到x= (y). 若对于y在c中的任何一个值，通过x= (y)，x在a中都有唯一的值和它对应，那么，x= (y)就表示y是自变量，x是自变量y的函数，这样的函数x= (y) (y c)叫做函数 的反函数，记作 ,习惯上改写成 开始的两个例子：s=vt记为 ，则它的反函数就可以写为 ，同样 记为 ，则它的反函数为： .从映射的角度看，若确定函数y=f(x)的映射是定义域a到值域c的一一映射，则它的逆映射f -1:  (x=f -1(y)) c→a 确定的函数x=f -1(y)(习惯上记为y=f -1(x))叫做函数y=f(x)的的反函数.即，函数 是定义域a到值域c的映射，而它的反函数 是集合c到集合a的映射，由此可知：1.      只有“一一映射”确定的函数才有反函数.如 （x∊r）没有反函数,而 , 有反函数是 2.互为反函数的定义域和值域互换.即函数 的定义域正好是它的反函数 的值域；函数 的值域正好是它的反函数 的定义域.且 （如下表）：

函数

反函数 定义域

a

c值 域

c

a3. 函数 与 互为反函数。即若函数 有反函数 ，那么函数 的反函数就是 . 三、例题：例1．求下列函数的反函数：① ；           ② ；③ ；           ④ .小结：⑴求反函数的一般步骤分三步，一解、二换、三注明⑵反函数的定义域由原来函数的值域得到，而不能由反函数的解析式得到。⑶求反函数前先判断一下决定这个函数是否有反函数，即判断映射是否是一一映射。例2．求函数 （ ）的反函数，并画出原来的函数和它的反函数的图像。解：（略） 它们的图像为：   由图象看出，函数（ ）和它的反函数 的图象关于直线y=x对称.一般地，函数  的图象和它的反函数 的图象关于直线y=x对称..例3求函数  （-1<x<0）的反函数。例4 已知 = -2x(x≥2),求 .解法1：⑴令y= -2x，解此关于x的方程得 ，∵x≥2，∴ ，即x=1+ --①, ⑵∵x≥2，由①式知 ≥1，∴y≥0--②,⑶由①②得 =1+ （x≥0，x∈r）；解法2：⑴令y= -2x= -1，∴ =1+y，∵x≥2，∴x-1≥1，∴x-1= --①,即x=1+ , ⑵∵x≥2，由①式知 ≥1，∴y≥0,⑶∴函数 = -2x(x≥2)的反函数是 =1+ （x≥0）；说明：二次函数在指定区间上的反函数可以用求根公式反求x，也可以用配方法求x，但开方时必须注意原来函数的定义域.四、课堂练习：课本p63练习：1—4五、课后作业：课本第64习题2.4：1（2）（3）（4）（6）（7）（8）；2.

本文标题：反三角函数-反三角函数：反三角函数-概述，反三角函数-相关介绍
本文地址： http://www.61k.com/1055607.html