一 : 复数的有关概念
教学目标
(1)掌握,如虚数、纯虚数、复数的实部与虚部、两复数相等、复平面、实轴、虚轴、共轭复数、共轭虚数的概念。
(2)正确对复数进行分类,掌握数集之间的从属关系;
(3)理解复数的几何意义,初步掌握复数集C和复平面内所有的点所成的集合之间的一一对应关系。
(4)培养学生数形结合的数学思想,训练学生条理的逻辑思维能力.
教学建议
(一)教材分析
1、知识结构
本节首先介绍了,然后指出复数相等的充要条件,接着介绍了有关复数的几何表示,最后指出了有关共轭复数的概念.
2、重点、难点分析
(1)正确复数的实部与虚部
对于复数 ,实部是 ,虚部是 .注意在说复数 时,一定有 ,否则,不能说实部是 ,虚部是 ,复数的实部和虚部都是实数。
说明:对于复数的定义,特别要抓住 这一标准形式以及 是实数这一概念,这对于解有关复数的问题将有很大的帮助。
(2)正确地对复数进行分类,弄清数集之间的关系
分类要求不重复、不遗漏,同一级分类标准要统一。根据上述原则,复数集的分类如下:
注意分清复数分类中的界限:
①设 ,则 为实数
② 为虚数
③ 且 。
④ 为纯虚数 且
(3)不能乱用复数相等的条件解题.用复数相等的条件要注意:
①化为复数的标准形式
②实部、虚部中的字母为实数,即
(4)在讲复数集与复平面内所有点所成的集合一一对应时,要注意:
①任何一个复数 都可以由一个有序实数对( )唯一确定.这就是说,复数的实质是有序实数对.一些书上就是把实数对( )叫做复数的.
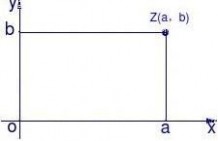
②复数 用复平面内的点Z( )表示.复平面内的点Z的坐标是( ),而不是( ),也就是说,复平面内的纵坐标轴上的单位长度是1,而不是 .由于 =0+1· ,所以用复平面内的点(0,1)表示 时,这点与原点的距离是1,等于纵轴上的单位长度.这就是说,当我们把纵轴上的点(0,1)标上虚数 时,不能以为这一点到原点的距离就是虚数单位 ,或者 就是纵轴的单位长度.
③当 时,对任何 , 是纯虚数,所以纵轴上的点( )( )都是表示纯虚数.但当 时, 是实数.所以,纵轴去掉原点后称为虚轴.
由此可见,复平面(也叫高斯平面)与一般的坐标平面(也叫笛卡儿平面)的区别就是复平面的虚轴不包括原点,而一般坐标平面的原点是横、纵坐标轴的公共点.
④复数z=a+bi中的z,书写时小写,复平面内点Z(a,b)中的Z,书写时大写.要学生注意.
(5)关于共轭复数的概念
设 ,则 ,即 与 的实部相等,虚部互为相反数(不能认为 与 或 是共轭复数).
教师可以提一下当 时的特殊情况,即实轴上的点关于实轴本身对称,例如:5和-5也是互为共轭复数.当 时, 与 互为共轭虚数.可见,共轭虚数是共轭复数的特殊情行.
(6)复数能否比较大小
教材最后指出:“两个复数,如果不全是实数,就不能比较它们的大小”,要注意:
①根据两个复数相等地定义,可知在 两式中,只要有一个不成立,那么 .两个复数,如果不全是实数,只有相等与不等关系,而不能比较它们的大小.
②命题中的“不能比较它们的大小”的确切含义是指:“不论怎样定义两个复数间的一个关系‘<’,都不能使这关系同时满足实数集中大小关系地四条性质”:
(i)对于任意两个实数a, b来说,a<b, a=b, b<a这三种情形有且仅有一种成立;
(ii)如果a<b,b<c,那么a<c;
(iii)如果a<b,那么a+c<b+c;
(iv)如果a<b,c>0,那么ac<bc.(不必向学生讲解)
(二)教法建议
1.要注意知识的连续性:复数 是二维数,其几何意义是一个点 ,因而注意与平面解析几何的联系.
2.注意数形结合的数形思想:由于复数集与复平面上的点的集合建立了一一对应关系,所以用“形”来解决“数”就成为可能,在本节要注意复数的几何意义的讲解,培养学生数形结合的数学思想.
3.注意分层次的教学:教材中最后对于“两个复数,如果不全是实数就不能本节它们的大小”没有证明,如果有学生提出来了,在课堂上不要给全体学生证明,可以在课下给学有余力的学生进行解答.
教学目标 1.了解复数的实部,虚部; 2.掌握复数相等的意义; 3.了解并掌握共轭复数,及在复平面内表示复数. 教学重点 复数的概念,复数相等的充要条件. 教学难点 用复平面内的点表示复数M. 教学用具:直尺 课时安排:1课时 教学过程 : 一、复习提问: 1.复数的定义。 2.虚数单位。 二、讲授新课 1.复数的实部和虚部: 复数 中的a与b分别叫做复数的实部和虚部。 2.复数相等 如果两个复数 与 的实部与虚部分别相等,就说这两个复数相等。 即: 的充要条件是 且 。 例如: 的充要条件是 且 。 例1: 已知 其中 ,求x与y. 解:根据复数相等的意义,得方程组: ∴ 例2:m是什么实数时,复数 , (1) 是实数,(2)是虚数,(3)是纯虚数. 解: (1) ∵ 时,z是实数, ∴ ,或 . (2) ∵ 时,z是虚数, ∴ ,且 (3) ∵ 且 时, z是纯虚数. ∴ 3.用复平面(高斯平面)内的点表示复数 复平面的定义 建立了直角坐标系表示复数的平面,叫做复平面. 复数 可用点 来表示.(如图)其中x轴叫实轴,y轴 除去原点的部分叫虚轴,表示实数的点都在实轴上,表示纯虚数的点都在虚轴上。原点只在实轴x上,不在虚轴上. 4.复数的几何意义: 复数集c和复平面所有的点的集合是一一对应的. 5.共轭复数 (1)当两个复数实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数。(虚部不为零也叫做互为共轭复数) (2)复数z的共轭复数用 表示.若 ,则: ; (3)实数a的共轭复数仍是a本身,纯虚数的共轭复数是它的相反数. (4)复平面内表示两个共轭复数的点z与 关于实轴对称. 三、练习 1,2,3,4. 四、小结: 1.在理解时应注意: (1)明确什么是复数的实部与虚部; (2)弄清实数、虚数、纯虚数分别对实部与虚部的要求; (3)弄清复平面与复数的几何意义; (4)两个复数不全是实数就不能比较大小。 2.复数集与复平面上的点注意事项: (1)复数 中的z,书写时小写,复平面内点Z(a,b)中的Z,书写时大写。 (2)复平面内的点Z的坐标是(a,b),而不是(a,bi),也就是说,复平面内的纵坐标轴上的单位长度是1,而不是i。 (3)表示实数的点都在实轴上,表示纯虚数的点都在虚轴上。 (4)复数集C和复平面内所有的点组成的集合一一对应: 五、作业 1,2,3,4, 六、板书设计 : §8,2 1定义: 例1 3定义: 4几何意义: …… …… …… …… 2定义: 例2 5共轭复数: …… …… …… ……
二 : 什么是复数复数的概念
什么是复数
复数的概念
我学的时候好像是这样说的~~
实数和虚数统称复数~~~
三 : 复数的概念
高中数学教案 第三册(选修Ⅱ)第4章复数(第1课时)
课 题: 4.1复数的概念
教学目的:
1.了解引进复数的必要性;理解并掌握虚数的单位2.3.理解并掌握复数的有关概念(复数集、代数形式、虚数、纯虚数、实部、虚部4.教学重点:复数的概念,虚数单位i,复数的分类(实数、虚数、纯虚数)和复数相等等概念是本节课的教学重点.复数在现代科学技术中以及在数学学科中的地教学难点:虚数单位i的引进及复数的概念是本节课的教学难点.复数的概念是在引入虚数单位i并同时规定了它的两条性质之后,自然地得出的.在规定i的第授课类型:新授课课时安排:1课时 教 具:多媒体、实物投影仪 内容分析:
?复数的概念如果单纯地讲解或介绍会显得较为枯燥无味,学生不易接受,教学时,我们采用讲解或体验已学过的数集的扩充的历史,让学生体会到数集的扩充是生产实践的需要,也是数学学科自身发展的需要;介绍数的概念的发展过程,使学生对数的形成、发展的历史和规律,各种数集中之间的关系有着比较清晰、完整的认识.从而让学生积极主动地建构虚数的概念、复数的概念、复教学过程:
一、复习引入:
数的概念是从实践中产生和发展起来的.早在人类社会初期,人们在狩猎、采集果实等劳动中,由于计数的需要,就产生了1,2,3,4等数以及表示“没有”的数0.自然数的全体构成自然数集为了解决测量、分配中遇到的将某些量进行等分的问题,人们引进了分数;为了表示各种具有相反意义的量以及满足记数的需要,人们又引进了负数.这样就把数集扩充到有理数集Q.显然NQ.如果把自然数集(含正整数和0)与负整数集合并在一起,构成整数集Z,则有ZQ、NZ.如果把整数看作分母为1的分有些量与量之间的比值,例如用正方形的边长去度量它的对角线所得的结果,无法用有理数表示,为了解决这个矛 盾,人们又引进了无理数.所谓无理数,就是无限不循环小数.有理数集与无理数集合并在一起,构成实数集R.因为有理 第 1页(共6页)
高中数学教案 第三册(选修Ⅱ)第4章复数(第1课时)
数都可看作循环小数(包括整数、有限小数),无理数都是无限不循环小数,所以因生产和科学发展的需要而逐步扩充,数集的每一次扩充,对数学学科本身来说,也解决了在原有数集中某种运算不是永远可以实施的矛盾,分数解决了在整数集中不能整除的矛盾,负数解决了在正有理数集中不够减的矛盾,无理数解决了开方开不尽的矛盾.但是,数集扩到实数集R以后,像x2=-1这样的方程还是无解的,因为没有一个实数的平方等于-1.由于解方程的需要,人们引入了一个新数i,叫做虚数单位.二、讲解新课:
1.虚数单位i:
(1)它的平方等于-1,即 i??1;
(2)实数可以与它进行四则运算,进行四则运算时,原有加、乘运算律仍然成立.
2. i与-1的关系: i就是-1的一个平方根,即方程x2=-1的一个根,方程x2=-1的另一个根是-i!
3. i的周期性:i4n+1=i, i4n+2=-1, i4n+3=-i, i4n2
4.复数的定义:形如a?bi(a,b?R)的数叫复数,a叫复数的实部,b叫复C表示
3. 复数的代数形式: 复数通常用字母z表示,即z?a?bi(a,b?R),把复数表示成a+bi4. 复数与实数、虚数、纯虚数及0的关系:对于复数a?bi(a,b?R),当且仅当b=0时,复数a+bi(a、b∈R)是实数a;当b≠0时,复数z=a+bi叫做虚数;当a=0且b≠0时,z=bi叫做纯虚数;当且仅当a=b=0时,z就是实数0.

5.复数集与其它数集之间的关系:NZQRC.
第 2页(共6页)
高中数学教案 第三册(选修Ⅱ)第4章复数(第1课时)
6. 两个复数相等的定义:如果两个复数的实部和虚部分别相等,那么我们这就是说,如果a,b,c,d∈R,那么a+bi=c+di?a=c,b= 一般地,两个复数只能说相等或不相等,而不能比较大小.如3+5i与4+3i不能比较大小.
现有一个命题:“任何两个复数都不能比较大小”如果两个复
7. 复平面、实轴、虚轴:复数z=a+bi(a、b∈R)与有序实数对(a,b)是一一z=a+bi(a、b∈R),由复数相等的定义可知,可以由一个有序实数对(a,b)惟一确定,如z=3+2i可以由有序实数对(3,2)确定,又如z=-2+i可以由有序实数对(-2,1)来确定;又因为有序实数对(a,b)与平面直角坐标系中的点是一一对应的,如有序实数对(3,2)它与平面直角坐标系
中的点A,横坐标为3,纵坐标为2,建立了一一对由此可知,复数集与平面直角坐标系中
的点集之间可以建立一一对应的关系.
点Z的横坐标是a,纵坐标是b,复数z=a+bi(a、b∈R)可用点Z(a,b)表示,这个建立了直角坐标系
来表示复数的平面叫做复平面,也叫高斯平面,x轴叫做实轴,y轴叫做实轴上的点都表示
对于虚轴上的点要除原点外,因为原点对应的有序实数对为(0,0), 它所确定的复数是z=0+0i=0表示是实数.故除了原点外,虚轴上的点都表示在复平面内的原点(0,0)表示实数0,实轴上的点(2,0)表示实数2,虚轴上的点(0,-1)表示纯虚数-i,虚轴上的点(0,5)表示纯虚数5非纯虚数对应的点在四个象限,例如点(-2,3)表示的复数是-2+3i,z=-5-3i对应的点(-5,-3)在第三象限等等.
复数集C和复平面内所有的点所成的集合是一一对应关系,即

这是因为,每一个复数有复平面内惟一的一个点和它对应;反过来,复平面内的每一个点,有惟一的一个复数和它对应.
这就是复数的一种几何意义.也就是复数的另一种表示方法,即几何表示方法.
三、讲解范例: 112?3i,?3?i,?i,?3?i的实部和虚部,有没有例1请说出复数23
纯虚数?
第 3页(共6页)
高中数学教案 第三册(选修Ⅱ)第4章复数(第1课时) 答:它们都是虚数,它们的实部分别是2,-3,0,-;虚部分别是3,
111,-,-;-——www.61k.com——i是纯虚数. 332
例2 复数-2i+3.14的实部和虚部是什么?
答:实部是3.14,虚部是-2.
易错为:实部是-2,虚部是3.14!
例3实数m取什么数值时,复数z=m+1+(m-1)i是:
(1)实数? (2)虚数? (3)纯虚数?
[分析]因为m∈R,所以m+1,m-1都是实数,由复数z=a+bi是实数、虚数和纯虚数的条件可以确定m的值.
解:(1)当m-1=0,即m=1时,复数z是实数;
(2)当m-1≠0,即m≠1时,复数z是虚数;
(3)当m+1=0,且m-1≠0时,即m=-1时,复数z 是纯虚数.
例4 已知(2x-1)+i=y-(3-y)i,其中x,y∈R,求x与y.
解:根据复数相等的定义,得方程组??2x?1?y,5,所以x=,y2?1??(3?y)
四、课堂练习:
1.设集合C={复数},A={实数},B={纯虚数},若全集S=C,则下列结论正确的是( )
A.A∪B=C B. CSA=B C.A∩CSB=? D.B∪CSB=C
2.复数(2x2+5x+2)+(x2+x-2)i为虚数,则实数x满足( )
A.x=-11 B.x=-2或- C.x≠-2 D.x≠1且x≠-2 22
3.已知集合M={1,2,(m2-3m-1)+(m2-5m-6)i},集合P={-1,3}.M∩P={3},则实数m的值为( )
A.-1 B.-1或4 C.6 D.6或-1
4.满足方程x2-2x-3+(9y2-6y+1)i=0的实数对(x,y)表示的点的个数是______.
5.复数z1=a+|b|i,z2=c+|d|i(a、b、c、d∈R),则z1=z2的充要条件是______.
6.设复数z=log2(m2-3m-3)+ilog2(3-m)(m∈R),如果z是纯虚数,求m的值.
7.若方程x2+(m+2i)x+(2+mi)=0至少有一个实数根,试求实数m的值. 第 4页(共6页)
高中数学教案 第三册(选修Ⅱ)第4章复数(第1课时)
8.已知m∈R,复数z=m(m?2)+(m2+2m-3)i,当m为何值时, m?1
1+4i. 2(1)z∈R; (2)z是虚数;(3)z是纯虚数;(4)z=
答案:1.-http://www.61k.com-D 2.D 3. 解析:由题设知3∈M,∴m2-3m-1+(m2-5m-6)i=3
?m2?3m?1?3?m?4或m??1∴?,∴?∴m=-1,故选A. 2?m?6或m??1?m?5m?6?0
?x?3或x??1?x2?2x?3?0,?4. 解析:由题意知?∴? 12y??9y?6y?1?0,?3?
∴点对有(3,11),(-1,)共有2个.答案:2 33
?a?c?a=c且b2=d2.答案:a=c且b2=d2
?|b|?|d|5. 解析:z1=z2??
2?m?3m?3?12?log2(m?3m?3)?0,?6.解:由题意知?∴?3?m?1
?log2(3?m)?0,?3?m?0?
?m2?3m?4?0?m?4或m??1∴?∴?,∴m=-1.
?m?3且m?2?m?2且m?3
2?x?mx?2?027. 解:方程化为(x+mx+2)+(2x+m)i=0.∴?,
?2x?m?0
m2mm??2?0,∴m2=8,∴m=±22. ∴x=-,∴422
?m2?2m?3?0,8. 解:(1)m须满足?解之得:m=-3. m?1?1.?
(2)m须满足m2+2m-3≠0且m-1≠0,解之得:m≠1且m≠-3. 第 5页(共6页)
高中数学教案 第三册(选修Ⅱ)第4章复数(第1课时)
?m(m?2)?0,?(3)m须满足?m?1解之得:m=0或m=-2.
?m2?2m?3?0.?
?m(m?2)1??(4)m须满足?m?12解之得:m∈? ?m2?2m?3?4.?
五、小结 :这节课我们学习了虚数单位i及它的两条性质,复数的定义、实部、虚部及有关分类问题,复数相等的充要条件,复平面等等.基本思想是:利用复数的概念,联系以前学过的实数的性质,对复数的知识有较完整的认识,以及
六、课后作业:
七、板书设计
第 6页(共6页)
四 : 复苏的念头
雪漫舞飘零
飞往希望与温暖
却在梦中消融
化为一片冰凉
溶有无限心酸
梦的种子
降临在一片片雪茫中
终被这冷的
化为了冰晶
可心却从未落下
梦想依守护着她
他也记恋着她
从未放下
就等这冷,这寒,这忘却的希望
冒起复苏的念头
她就一崛起而起
再不放弃
初三:曹炳霞
五 : 复数的有关概念
教学目标61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1