一 : 不定积分习题集89
第四章 不定积分 练习题
1、dx11x=(artanxarctan+C. ?∫(x2+1)(x2+4)322
2131x2+1?12132、求 ∫xarctanxdx.解: 原式=xarctanx?∫x=xarctanx 236x+13
1x2+1?121311=xarctanx?x2+ln(1+x2)+C. ?∫26x+1366
3、求不定积分 ∫ln(x+1)
x.解:
=t,则x=t2,dx=2tdt. ln(t2+1)原式=∫
2tdt=2∫ln(t2+1)dt=x+1)?+C. t
4、求
2.解: 令x=sint,则dx=costdt
sin2tcostdt(1?cos2t)costdt故∫=∫=∫=∫(1?cost)costdt 1+cost1+cost=∫(cost?5
、21+cos2ttsintcostarcsinx1+
C=x??C. )dt=sint??22222∫=+x2+C.
6、求x∫1+cos2xdx.
x解: ∫dx=∫xsec2xdx=∫xdtanx=xtanx+ln|cosx|+C. 1+cos2x
7、dx12=ln||ln(1)+C. x?+x∫x(x2+1)2
x2x2x218、求∫xln(x?1)dx.解:∫xln(x?1)dx=∫ln(x?1)d(=ln(x?1)?∫?dx 222x?1
x211x2?11x=ln(x?1)?∫(x+1+)dx=ln(x?1)?x2?+C. 22x?1242
9、dx1?=∫xln2xlnx+C.
10、求
t2?1.
解:令t=x=,dx=tdt 2t2?13+63919原式=∫?tdt=∫(t2+dt=t3+t+C. t2222
11、求xdx.解:令u=tan (?π<x<π),则 ∫3+cosx+2sinx2
2u1?u22sinx=,cos,x=dx=du, 原式=∫2221+u1+u1+u11?u24u+3+1+u21+u2?2du 21+u
=∫12、11x==arctan(1+u)+C=arctan(1+tan)+C. 22∫2u+2u+2(u+1)+1∫2x+32ln|x+3x?10|+C. dx2x+3x?10
dx=arctan(x+1)+C. x2+2x+213、∫
14
、求∫dx.解:令x=sint,则dx=costdt,故原式 2x
cost2?arcsinx+C. =∫2costdt=∫(csct?1)dt=?cott?
t+C=sintx
15、已知xlnx为f(x
)的一个原函数,则∫f′dx=
C.
16
、求
t=x=t3?2,dx=
3t2dt, 3t2t21=dt=3∫(t?1+故)dt=3(?t+ln|1+t|)+
C 21+t∫1+t
=?3ln|1++C. 17、求∫e2xcosxdx.解:∫e2xcosxdx=∫e2xdsinx=e2xsinx?2∫e2xsinxdx
=e2xsinx+2∫e2xdcosx=e2xsinx+2e2xcosx?4∫e2xcosxdx
1=(e2xsinx+2e2xcosx)+C. 5
18、求∫sin(lnx)dx..解:令t=lnx,则x=et,dx=etdt原式=∫etsintdt
=esint?ecostdt=esint?ecost?esintdt=t∫ttt∫t1t(esint?etcost)+C. 2
19、设∫xf(x)dx=arcsinx+C,则∫11dx=?(1?x2)3/2+C. f(x)3
xearctanxarctanx
dx20、求 ∫
+C) 23/2(1+x)21、设f(x)=ln(1+x)?xxx,计算∫f(x)dx.(?eln(1+e)+x?ln(1+e)+C) x
sinxxcos2x?sin2x22、已知f(x)的一个原函数为,求∫xf′(2x)dx. (+C) 4xx
23
、求
x2
xdxx?+C) 4
二 : 不定积分经典习题 92
第六次习题课
通过这一章的学习,我们认为应达到如下要求: 1、理解原函数、不定积分的概念。
2、掌握不定积分的基本性质,牢记基本积分公式,了解并能灵活应用若干常用积分公式。 3、理解不定积分的换元积分法和分部积分法的基本思想并能熟练运用于不定积分的计算。
4、掌握有理函数、三角函数有理式和简单无理函数的不定积分的计算方法和技巧。
一、知识网络图
??原函数
??基本概念1.?不定积分?
?不定积分的几何意义?
??
??不定积分的性质不?2.性质与公式?
?基本积分公式?
?
?直接积分法定?
????换元积分法?第一换元积分法(凑微分法)
???
积?3.计算方法??第二换元积分法
??
?分部积分法?
?分??查表法
?
?有理函数积分?
?4.特殊函数的积分??三角函数有理式积分??某些无理函数积分???
一、求不定积分:
2arctanex
. 例1. 计算?2x
e
dex2arctanex?2x?2xxx
] =??arctanede??[earctane??2x提示: ?2x2x
e(1?e)e
=?[e
?2x
dexdex
arctane??2x??] 2x
e(1?e)
x
=?e?2xarctanex?
例2.计算?
1x?e?C arctanxe
1x(1?x)
dx
[解一]
?
1x(1?x)
dx =?
111(x?)2?()2
22
1111
d(x??ln(x??(x?)2?()2?C
2222
=lnx?
1
?x(x?1)?C 21
dx =?
1x(1?x)
dx??
2dx?(x)
2
[解二]
?
x(1?x)
?2ln(x??x)?C1
=lnx?
其中C?C1?ln2
1
?x(x?1)?C 2
[方法小结]当被积函数含有根式时,通过巧妙的凑微分化成常用积分公式。
xex
dx 例3.计算?x
2
(e?1) [解一] 令e
x
?t,则
xexlnttlnt11lnt11
ln(dtdx=??td????? ?(ex?1)2?(t?1)2t?(t?1)2?t?11?t?t?1t =?
lnt11lnt
??[??lnt?ln(t?1)?C ]dt??t?1tt?1t?1
xex
=x?ln(ex?1)?C
e?1
xd(ex?1)xxex11
( [解二] ?xxd dx=??????(ex?1)2?ex?1ex?1?ex?1(e?1)2xexxdex
??x =?x ??xx??xx
e?1e(e?1)e?1e(e?1) =?
x11xxxx
?(?)de???lne?ln(e?1)?C ?xxxx
e?1ee?1e?1
xex
=x?ln(ex?1)?C
e?1
可令e[方法小结] 被积函数中含有e的不定积分,
x
x
?t, 从而将积分化为其它易积的积分。
另一方面,当用分部积分法,其中u,dv难以一步得到时,可以先将其中一部分凑成
f?(?(x))d?(x)的形式,从而dv?df(?(x))。
例4.计算?
arctanx
. 22
x(1?x)
[解一] 令arctanx?t,即x?tgt,则dx?sec
2
tdt
arctanxt222
sectdt?tcottdt?t(csct?1)dt =2222?x(1?x)?tant?sect??
t2
=??tdcott??tdt??tcott??cottdt?
2t2
=?tcott?ln|sint|??C
2
arctgx(arctgx)2x
?ln||??C =?
2x2?x
[解二] ?
arctanx11arctanx
()arctan??xdx=?x21?x2?x2??arctanxdarctanx x2(1?x2)
arctanx(arctanx)21(arctanx)2
????arctanxd?=? 2
x22x
arctanx1(arctanx)2
????dx? 2
xx(1?x)2
11t1112x?dx????(t?1)??ln(t2?1)?C 令,则???222
t22t?1x(1?x)t?1
=ln|
x?x
2
|?C
arctanx(arctanx)2
?ln||??C。 从而原式
=?
x2[方法小结]当被积函数含有难积的反三角函数时,通常的做法是将这一部分作变量替换。另若分母为相差一个常数的两个因式的乘积,则可以将分式拆项,分别积分。 例5. 计算?
1?sinx
dx
1?cosx
[分析一]本题属于三角函数有理式的积分, 可以利用万能公式作变量替换。
2t1?t22dtx
??x?xdxsin,cos,t?tan,则 [解一] 令
21?t21?t21?t2
2t
21?sinxt2?2t?12t22?t1dx???????dtttdt)ln(1)?C (1?1?cosx?1?t21?t2?1?t2?1?t2
1?
1?t2
1?
=tan
xx
?ln(1?tan2)?C 22
[分析二] 本题被积函数含有三角函数, 若适当利用三角函数恒等式(如倍角、半角公式、和差化积、积化和差等公式),往往能简化计算。
[解二]
xxx
1?2sincossin1?sinx1x?dx?tanx?2ln|cosx|?C dx2???1?cosx??2x2?x2222x2coscoscos
222
[方法小结] 一般地,被积函数含有三角函数时,常利用万能公式作变量替换或利用三角函数恒等式进行化简。前者虽然是通用的方法,但往往不是最简便的。另须注意,本题两种解法给出的结果虽然不一致,但求导后都等于被积函数,所以都是正确的。 例6.计算?
1x?a)(b?x)
dx
[分析一]注意到被积函数中含有两个根式,可以先将其中一个根式有理化,再将余下的根式作变量替换。
[解一]
1(x?a)(b?x)
?
x?ax?a?x
?
1
x?ax?a
b?x
2(b?a)ta?bt2x?a
?t, 即x?令,?dt, dx222
b?x1?t(1?t)
?
1?t22(b?a)t1dx=?????C tdt2dt2arctantC2arctan2222?(b?a)t(1?t)1?t(x?a)(b?x)
1
[分析二]本题也可以用凑微分法,计算过程更为简便。 [解二]
?
1(x?a)(b?x)
dx=?
2b?x
dx?a?2?
dx?a(b?a)?(x?a)2
?2arcsin
x?a
?C b?x
[方法小结] 当被积函数含有根式时,常常需要对根式进行处理,通常作变量替换,也可以用凑微分法。 例7. 计算?
1
dx 2
3?sinx
[分析一] 被积函数分子、分母同除以sin2x,可化为csc2x的函数,利用?csc2x?dcotx,
csc2x?cot2x?1可以将积分化简。
dcotxdcotx1
csc2x1????dx= [解一] ?dx?(3csc2x?1)?3cot2x?43?223?sin2xcotx?
=?
1cotx
arctg?C。
32
[分析二] 被积函数分子、分母同除以cos2x,可化为sec2x,tan2x的函数,而利用sec2x?dtanx,可以将积分化简。 [解二]
1sec2xdtanx1
??dx ?
=dx?(3sec2x?tg2x)?
4tan2x?34?3?sin2x
2
?C 2
[方法小结] 当被积函数含有sinx或cosx的齐次函数时,常从各项中提取sin2x或cos2x,凑成dtanx或dcotx。 例8. 计算?
1x
4
?x
2
dx
[分析一] 注意到被积函数中根式内外都有x的幂次,可尝试用倒代换。 1
[解一]令x?,则
t
?x
1
4
?x
2
dx=??
1t2dt21udu1u?1?1
?t2?? ??????22222?u?u?t?t
3
1
t3dt
1111
=???udu????(1?u)2?(1?u)2?C
22?u3
31
(1?x2)31?x22222
??C =?(1?t)?(1?t)?C=?3
3x3x
[分析二]本题也可以用三角代换,令x?tant,则根式下可化为sec2x。从而 被积函数可化为sinx、cosx的函数。
[解二] 令x?tant,
?x
4
dsintdsintcos3t1?sin2t11?3
dt?t????t??C sin(sin)dx=????444223sintsintsintsintsint?x
1
(1?x2)31sect3sect?x2
=?(??C????C 3
3tanttantx3x
[方法小结] 被积函数中含有x的幂次,可尝试用倒代换,如果出现(x2?a2),(a2?x2)或
(x2?a2),(a2?x2)则可以采用三角代换,然后利用三角函数恒等式将被积表达式化简。 例9. 计算?
?x1
?dx 1?xx
不定积分经典习题 92_不定积分习题
[分析一]被积函数中含有复杂的根式
?x
,因此可以先将此根式作变量替换。 1?x
?4t1?t2?x
dx?dt,从而 [解一]令,?t,则x?222
1?x1?t(1?t)
?
1?t2?4tt2?x1
?dx??t? ?dt??4?22222
1?xx1?t(1?t)(1?t)(1?t)dt
11t?1
=?2?(?dt?ln?2arctant?C
1?t21?t2t?1=?2arctanC
?x21
?dx,然后令x?sint,即可将根式化去。 1?xx
[分析二]本题可以先根式有理化为?[解二]
?
?x21?x1
?dx ?dx=?
1?xx1?xx
令x?tant,则 原式=?
?x21cos2t1cost1
?dx=??dt ?dsint=?
1?sintsint1?sintsint1?xx
=lncsct?cott?t?C=?csctdt?t?C=?csctdt?t?C=lncsct?cott?t?C
1?x2
=ln??arcsinx?C
xx
[方法小结] 被积函数中含有复杂的根式,可以先将根式作变量替换。可以先根式有理化,然后通过三角代换将根式化去。
sin2x例10. 计算?dx 3
cosx
sin2x1?cos2x
[分析一] ?dx????sec3xdx??secxdx,而前一个积分可以用分部积分法,33
cosxcosx后一个积分可以利用常用积分公式。
sin2x1?cos2x3
[解一] ?dx??secxdx??secxdx ??33
cosxcosx
由于?sec3xdx??secxdtanx?secx?tanx??tan2xsecxdx?secx?tanx??sec3xdx??secxdx
11
故?sec3xdx?secx?tanx??secxdx
22
11
从而原式=?sec3xdx??secxdx?secx?tanx??secxdx
22
11
=secx?tanx?lnsecx?tanx?C 22
sin2xsin2x
dx??tanx??tanxsinxdtanx,本题也可以用凑微分法。 [分析二]注意到?3
cosxcosxsin2xsin2x12dx?x?xxdx?xdxtantansintansin(tan) [解二] ??cosx?cos3x2?
1111
=sinx(tanx)2??sinxtanxdx?sinx(tanx)2??tanxdcosx 2222111
=sinx(tanx)2?tanxcosx??cosxsec2xdx 222111
=sinx(tanx)2?tanxcosx??secxdx 22211
=tanx(sinxtanx?cosx)?lnsecx?tanx?C 22
[方法小结]在用分部积分法的过程中,常会出现所求积分在等式右端再现的情况,从中即可求出所求积分。
x?x
例11.(2004年高数一)已知f?(e)?xe,且f(1)?0,则f(x)? [分析] 已知条件与f(x)的导数有关, 所求的是f(x)的表达式, 若能求出f(x)的导数, 则其导数的不定积分即为f(x).
[解答] 设e
x
?t, 则x?lnt, 从而f?(t)?
lnt. t
因?f?(x)dx?f(x)?C. 所以有?故f(x)?
lnx1
dx??lnxdlnx?ln2x?C1?f(x)?C2. x2
12
lnx?C1?C2.由于f(1)?0,故取C1?C2?0,所以f(x)?1ln2x. 22
练习:设f?(tan2x)?sec2x,且f(0)?1,求f(x)
解: 令u?tan2x,则f?(u)?u?1,于是f(u)??f?(u)du?
12
u?u?1 2
?f(0)?1,?c?1,f(x)?
12
x?x?1。 2
例12.(1992年高数二) 求
?
x3dx?x
2
2
[分析一] 本题中难积的部分是?x.如果将1?x2视作整体,则分子部分可设法凑成
d(1?x2). [解一]
?
x3dx?x2
???
x22?x2
d(1?x)??
2
1?x2?12?x2
d(1?x2)
1122
(?x?)d(1?x)?22?x
3
1
1
?(1?x2)2?(1?x2)2?C3
[分析二] 注意到被积函数中含有a2?x2的形式,故可考虑用三角代换法. [解二] 令x?tant
(?
?
2
?t?
?
2
, 则dx?
sec2tdt
tan3t2??sectdt??tan2tdsect??(sec2t?1)dsect
sect1
?sec3t?sect?C 3
31
12222
?(1?x)?(1?x)?C3
3例13.(1997年高数二)
?
dxx(4?x)
?
dxx
?2dx.而分母中余下的部分可化为
[分析一] 本题分母中分离出x. 与分子可结合为
4?(x)2.
1
[解一]
?
dxx(4?x)
??
2dxxx
???2arcsin?C.
224?x4?(x)
dx
[分析二] 本题分母中根号下部分可配成完全平方形式:
4?(x?2)2.而分子可凑成
d(x?2).
[解二]
?
dxx(4?x)
??
x?2?arcsin?C. 224?(x?2)
d(x?2)
例14.(1993年高数一) 求
?
xexe?1
x
.
xx
[分析] 本题中难积的部分是e?1. 如果将e?1视作整体,则分子部分须设法凑成x
d(ex?1)?exdx的形式,但本题分子部分是xexdx,故须将e?1视作整体,作变量替换。
2
[解答] 令u?ex?1, 则x?ln(1?u).dx?
2u
du. 2
1?u
?
(1?u2)ln(1?u2)2u2
??duu2ln(1)du????2xu1?ue?1
2u4
du?2uln(1?u2)??2 1?u
?2uln(1?u2)?4u?4arctgu?C
?2xex?1?4ex?1?4arctgex?1?C
xex
例15 (2003年高数二) 计算不定积分
?
xearctanx(1?x)
322
.
[分析] 本题中含有难积的反三角函数,遇到这种情形,通常的做法是将反三角部分作变量替换。
[解答] 令arctanx?t,则x?tant.dx?sec2tdt.
?
xearctanx
(1?x2)2
??3
ettant(1?tan2t)
3
2
sec2tdt??etsintdt??sintdet?etsint??etcostdt
?etsint?etcost??etsintdt
1tarctanx
??esintdt?e(sint?cost)?C??C. 故?32(1?x2)2
t
xearctanx
arcsinx1?x2
练习: ? ?
2x2?x
解: 令x?sinu,则dx?cosudu
12u1?sin2uu
udu 原式???cos?????duuduudcotuu ?sin2u??cosu2sin2u
12?x21
??ucotu?lnsinu?u?c??arcsinx?lnx?(arcsinx)2?c。
2x2
xex
例16. (1999年高数四) 设F(x)是f(x)的原函数,且当x?0时,f(x)F(x)?2
2(1?x)已知F(0)?1,F(x)?0,试求f(x).
[分析] 已知条件与f(x)的原函数F(x),若能求出F(x),求导后即得f(x). xex
[解答] 由F?(x)?f(x), 有2F(x)F?(x)?,两边积分得: 2
(1?x)
F(x)??2F(x)F?(x)dx??
x
2
exxex
?C dx?2
1?x(1?x)
xe
x
2
32
由F(0)?1,F(x)?0,得F(x)?
e
. 求导后即得f(x)?F?(x)?1?x
.
2(1?x)
2
练习:设F(x)是f(x)的一个原函数,当x?0时有f(x)F(x)?sin2x,且F(0)=1,F(x)?0,求f(x)
解: 因为f(x)?F?(x),所以F?(x)F(x)?sin2x ,F?(x)F(x)dx?sin2xdx
2
??
2
?F?(x)F(x)dx?
2
12
F(x), 2
2sin?2xdx?
111
(1?cos4x)dx?x?sin4x?c ?228
1
2
故F(x)?x?
11??
sin4x?c,由F(0)?1?c?1,于是有F(x)??x?sin4x?1?
44??
1?cos4x
?f(x)?F?(x)?
1
2x?sin4x?1
4
例17. (1999年高数二)
x?5
?x2?6x?13? [分析] 本题属于有理分式的积分,一般来说,可以将真分式化为若干部分分式之和,然后分项积分。但这样做,有时显得很繁杂,本题可以将分母的一部分凑成完全平方。
[解答]
t?8x?5x?5
??3?xt令?x2?6x?13?(x?3)2?22?t2?22
1t1x?3
?C. ?ln(t2?4)?4arctan?C=ln(x2?6x?13)?4arctan
2222
?1?1
ln?1??arctan
x?x? ② 2?x(x?1)1?x
例18 求 ①
?
不定积分经典习题 92_不定积分习题
arctan
解: ① 原式??
?
1x
1?
1x2
112?1?1
????arctandarctan???arctan??c
xxx?3?x
3
2
?1??1?ln?1??ln?1??2
??111xx??????????1?② 原式???????ln?1????c。 ?11x??2??x????1?x2?1??
xx??
lntanx
?sin2xdx lntanxlntanx1lntanx112
解:???dtanx??lntanxdlntanx??lntanx??C。 dx=?sinxsin2x2tanx242cos2x
cosx
11
例19. 求 ① ?dx ② ?3dx
sin2x?2sinxsinxcosx
xd
dxdx1解: ① 原式?? ????xxxxx2sinx(cosx?1)4
4sincos?2cos2sin?cos3
22222
xx
1?tan2dtan
11tanx?1lntanx?1tan2x?c ????xx4x424282
tantan?cos2
222
练习:
sin2x?cos2xdxcosxsinxcosx1
??dxdx ②原式??dx???332????sinxcosxcosxsinxsinxcosxsinx2sinx
??lncosx?lnsinx?
1
?c
2sin2x
x2ex
dx 练习1:求 ?2
(x?2)
?1x2ex1x2ex2xx
????xe?2xedx????xexdx(再分部积分) 解:原式??xed
x?2x?2x?2x?2
2
x
?
x2exx2exxx
???xe??edx???xex?ex?c
x?2x?2
3
xexsinxxcosx?sinx练习2: 求 ① ?dx ②?edx 22(x?1)cosx
(x?1)ex?exex1exexx
解: ① 原式????dxdx?dx?ed dx22????x?1x?1x?1(x?1)(x?1)
11
?ex
?x?1
dx?
exx?1??exx?1dx?exx?1?c ② 原式??
e
sinx
xcosxdx??esinx?sinxsinxsin1cos2x
dx??xde??ex
dcosx ?xe
sinx
??e
sinx
dx?
esinxsinxsinx
esinxcosx??edx?xe?cosx
?c。 x2
例20.(1)设f(x2
?1)?lnx2?2
,且f[?(x)]?lnx,求??(x)dx;
(2)设f(lnx)?
ln(1?x)
x
,计算?f(x)dx. 提示:(1)令x2
?1?t?f(t)?ln
t?1?(t?1,f(?(x))?lnx)?1x?1
?(x)?1?lnx??(x)?
x?1
,于是 ??(x)dx?2lnx?1?x?C.
(2)令lnx?t,x?et
?f(t)?ln(1?et)ln(1?ex)x?x
et
,于是?f(x)dx=?ex???ln(1?e)de=?e
?x
ln(1?ex)??
1
1?e
x
dx??e?xln(1?ex)?ln(1?ex)?C. 练习:设f(sin2
x)?
xsinx,求f(x)dx.
提示:令sin2
x?u,x??f(x),于是原式
=??2?=??C.
二、补充练习
1、 求 ① ?exdxsinxcosx
e2x?1 ② ?1?sin4
xdx
(
①
arctanex?c
1
2
arctan(sin2x)?c ) 2、 求
?1?lnx(xlnx)2
dx ?
???1xlnx?c??? 3、 求
?xcosx?sinxx2dx ??1
??x
sinx?c?? 12
②
4、 若f(x)可积,求e1、 求e
??f(x)?f?(x)?dx ?e
x
x
f(x)?c
?
?
?2x
?e?2x?
?sin3xdx ? ???(3cos3x2sin3x)c??3??
2???1?x??c? dx ln
??x??
6、 求
?1?x2
xlnx
7、 求
1
?dx
11??
arctanx???c? ?x4x2?18、 求
?1?tanx
sin2xdx 9、 求
?x?sinx
1?cosxdx 10、求?1?sinx1?cosx
ex
dx
13
?
x3x3
?
??1
?2
tanx?1?2lntanx?c??
?xtanx?c? ?extan?c?
三 : 高中数学定积分习题
(1)定积分的值是一个常数,可正、可负、可为零;
(2)用定义求定积分的四个基本步骤:①分割;②近似代替;③求和;④取极限. 如果F?(x)?f(x),且f(x)在[a,b]上可积,则
?
baf(x)dx?F(x)a?F(b)?F(a), b【其中F(x)叫做f(x)的一个原函数,因为?F(x)?C???F?(x)?f(x)】
x??1
?c(???1) ⑴?0dx?c(c为常数) ⑵?1dx?x?c ⑶?xdx???1?
ax1xxx?c(a?0,a?1) ⑷?dx?lnx?c ⑸?edx?e?c ⑹?adx?xlna
⑺?sinxdx??cosx?c ⑻?cosxdx?sinx?c
11⑼?sinaxdx??cosax?c(a?0) ⑽?cosaxdx?sinax?c(a?0) aa⑴?kf(x)dx?k?f(x)dx(k为常数); ⑵?f(x)?g(x)dx??f(x)dx??g(x)dx; aaaaabbbbb⑶?f(x)dx??f(x)dx??f(x)dx(其中a?c?b); aac
⑷利用函数的奇偶性求定积分:若f(x)是[?a,a]上的奇函数,则?f(x)dx?0;若f(x)是[?a,a]上的?a
偶函数,则?f(x)dx?2?f(x)dx. ?a0aaabcb
定积分?f(x)dx表示在区间[a,b]上的曲线y?f(x)与直线x?a、x?b以及x轴所围成的平面ab
图形(曲边梯形)的面积的代数和,即?f(x)dx?Sx轴上方-Sx轴下方.(在x轴上方的面积取正号,在ab
x轴下方的面积取负号)
⑵借助图形确定出被积函数,求出交点坐标,确定积分的上、下限;
⑶写出定积分表达式;
⑷求出曲边梯形的面积和,即各积分的绝对值的和.
1
不定积分习题 高中数学定积分习题
高中数学高考总复习定积分与微积分基本定理习题
班级:__________ 姓名:__________ 学号:__________
一、选择题
1.(2010·山东日照模考)a=?2xdx,b=?2exdx,c=?2sinxdx,则a、b、c的大小关系是( ) ?0?0?0
A.a<c<b B.a<b<c C.c<b<a D.c<a<b
2.(2010·山东理,7)由曲线y=x2,y=x3围成的封闭图形面积为( )
1A.12 1B.4 1C.3 7D.12 同类题;(2010·湖南师大附中)设点P在曲线y=x2上从原点到A(2,4)移动,如果把由直线OP,直线y=x2及直线x=2所围成的面积分别记作S1,S2.如图所示,当S1=S2时,点P的坐标是( )
?416?A.?3,9? ?? ?416?415?B.?5,9 C.?3,7? ???? ?413D.?57 ??
3.由三条直线x=0、x=2、y=0和曲线y=x3所围成的图形的面积为( )
A.4 4B.3 18C.5 D.6
4.(2010·湖南省考试院调研)?1-1(sinx+1)dx的值为( ) ?
A.0 B.2 C.2+2cos1 D.2-2cos1
5.曲线y=cosx(0≤x≤2π)与直线y=1所围成的图形面积是( )
A.2π 3π B.3π C.2 D.π
6.函数F(x)=?xt(t-4)dt在[-1,5]上( ) ?0
32A.有最大值0,无最小值 B.有最大值0和最小值-332C.有最小值-3 D.既无最大值也无最小值
17.已知等差数列{an}的前n项和Sn=2n2+n,函数f(x)=?xtt,若f(x)<a3,则x的取值范围是?1
( )
?3?A.?,+∞? ?6? B.(0,e21) C.(e-11,e) D.(0,e11)
8.(2010·福建厦门一中)如图所示,在一个长为π,宽为2的矩形OABC内,曲线y=sinx(0≤x≤π)与x轴围成如图所示的阴影部分,向矩形OABC内随机投一点(该点落在矩形OABC内任何一 2
不定积分习题 高中数学定积分习题
点是等可能的),则所投的点落在阴影部分的概率是(
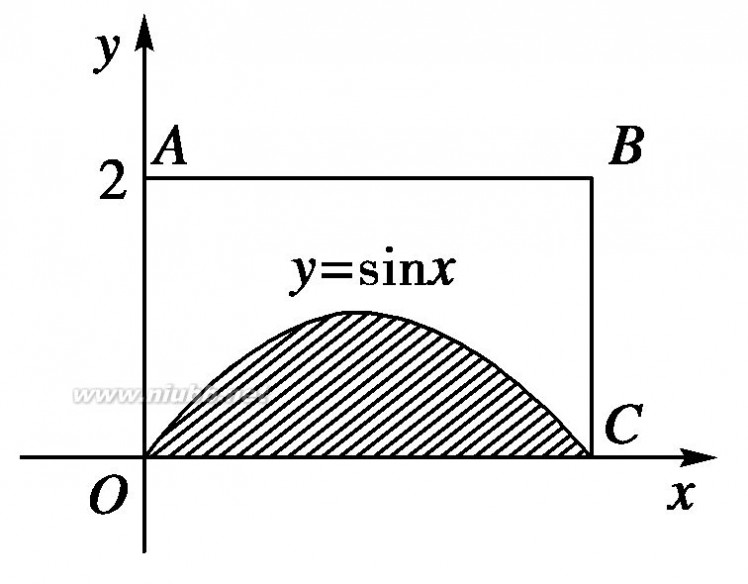
)
1A.π 2B.π 3C.π πD.4
x+2?-2≤x<0???9.(2010·吉林质检)函数f(x)=?π2cosx?0≤x≤?2?
3A.2 B.1 C.4 1D.2 的图象与x轴所围成的图形面积S为( )
10.(2010·沈阳二十中)设函数f(x)=x-[x],其中[x]表示不超过x的最大整数,如[-1.2]=-2,
x[1.2]=1,[1]=1.又函数g(x)=-3,f(x)在区间(0,2)上零点的个数记为m,f(x)与g(x)的图象
交点的个数记为n,则?ng(x)dx的值是( ) ?m
5A.-2 45 B.-3 C.-4 7D.-6
11.(2010·江苏盐城调研)甲、乙两人进行一项游戏比赛,比赛规则如下:甲从区间[0,1]上随机等可能地抽取一个实数记为b,乙从区间[0,1]上随机等可能地抽取一个实数记为c(b、c可以相等),若关于x的方程x2+2bx+c=0有实根,则甲获胜,否则乙获胜,则在一场比赛中甲获胜的概率为( )
1A.3 2 B.3 1 C.2 3D.412.(2010·吉林省调研)已知正方形四个顶点分别为O(0,0),A(1,0),B(1,1),C(0,1),曲线y=x2(x≥0)与x轴,直线x=1构成区域M,现将一个质点随机地投入正方形中,则质点落在区域M内的概率是( )
1A.2 11B.4 C.3 2D.5
二、填空题
13.(2010·芜湖十二中)已知函数f(x)=3x2+2x+1,若?1-1f(x)dx=2f(a) ?
成立,则a=________.
π114.已知a=∫20(sinx+cosx)dx,则二项式(ax-6的展开式中含x2项的系数是________. x
15.抛物线y2=2x与直线y=4-
x围成的平面图形的面积为________.
3
不定积分习题 高中数学定积分习题
416.(2010·安徽合肥质检)抛物线y=ax(a>0)与直线x=1围成的封闭图形的面积为3l2
与抛物线相切且平行于直线2x-y+6=0,则l的方程为______.
17.(2010·福建福州市)已知函数f(x)=-x3+ax2+bx(a,b∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围成区域(图中阴影部分)的面积为
112,则a的值为________.
三、解答题
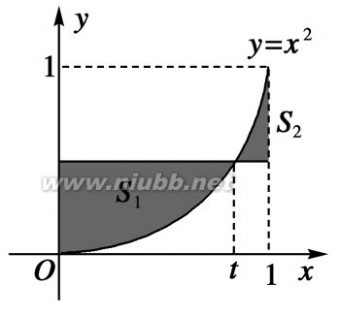
18.如图所示,在区间[0,1]上给定曲线y=x2,试在此区间内确定t的值,使图中阴影部分的面
积S1+S2最小.
61阅读提醒您本文地址:
4
61阅读提醒您本文地址:
四 : 不定积分经典习题

不定积分习题 不定积分经典习题

不定积分习题 不定积分经典习题

不定积分习题 不定积分经典习题

不定积分习题 不定积分经典习题

不定积分习题 不定积分经典习题

不定积分习题 不定积分经典习题

不定积分习题 不定积分经典习题

不定积分习题 不定积分经典习题

不定积分习题 不定积分经典习题

不定积分习题 不定积分经典习题

不定积分习题 不定积分经典习题

不定积分习题 不定积分经典习题

61阅读提醒您本文地址:
五 : 定积分练习题
题型
1.定积分与极限的计算
2.计算下列定积分
3.计算下列广义积分
内容
一.定积分的概念与性质
1.定积分的定义
2.定积分的性质
3.变上限函数及其导数
4.牛顿—莱布尼茨公式
5.换元积分公式与分部积分公式
6.广义积分
题型
题型I 利用定积分定义求极限
题型II比较定积分的大小
题型III利用积分估值定理解题
题型IV关于积分上限函数以及牛顿—莱布尼茨公式问题
题型V定积分的计算
题型VI积分等式证明 题型VII积分不等式证明 题型VIII广义积分的计算
自测题五
1.根据极限计算定积分 2.根据定积分求导 3.求极限
4.求下列定积分 5.证明题
4月21日定积分练习题
基础题:
一.选择题、填空题 p1.将和式的极限lim
1?2
p
?3p?.......?np
n??
n
P?1
(p?0)表示成定积分
(
A.?
1
1B.?1
xp
dx
C.1
p
1
p
x
?(1
x
)dx
D.?(x
n
)dx
2.将和式lim(
11n??
n?1
?
n?2
?.........?
12n
)表示为定积分 .3.下列等于1的积分是
(
A.?1
1
xdx B.?0
(x?1)dx
C.?10
1dx D.?1
10
2
4.?1
|x20
?4|dx=
(
A.
21 B.
22 C.
23 D.253
3
3
3
5.曲线y?cosx,x?[0,32
?]与坐标周围成的面积
(
A.4 B.2
C.52
D.3 6.?1
x
?x
(e?e
)dx=
(
)))))
A.e?
1e
x
B.2e C.
2e
D.e?
1e
7.若m?
?
1
edx,n?
?
e
1x
1
dx,则m与n的大小关系是( )
A.m?n B.m?n C.m?n D.无法确定
,k为常数,m1,m2为两质点的质量,
8. 按万有引力定律,两质点间的吸引力F?k
m1m2r
2
r为两点间距离,若两质点起始距离为a,质点m1沿直线移动至离m2的距离为b处,试求所作之功(b>a) .
9.由曲线y?x2?1和x轴围成图形的面积等于S.给出下列结果: ①?(x?1)dx;②?(1?x)dx;③2?(x?1)dx;④2?(1?x2)dx.
?1
?1
?1
1
2
1
2
1
2
则S等于( ) A.①③ 10.y?A.1
B.③④
C.②③
D.②④
x
?
(sint?costsint)dt,则y的最大值是( )
B.2 C.?
1
72
D.0
1
11. 若f(x)是一次函数,且?f(x)dx?5,?xf(x)dx?
176
,那么?
2
f(x)x
1
dx的值是
.
?x
?tf(t)dt??0
12.F(x)??,2
?x?,?c
x?0x?0
,其中f(x)在x?0处连续,且f(0)?0若F(x)在
x?0处连续,则c?( )。
(A).c?0; (B).c?1; (C).c不存在; (D).c??1.
?x
?tf(t)dt??0
13.F(x)??,2
?x?,?c
x?0x?0
,其中f(x)在x?0处连续,且f(0)?0若F(x)在
x?0处连续,则c?( )。
(A).c?0;
(B).c?1;
(C).c不存在;
(D).c??1.
14.设?f(x)dx?0且f(x)在[a,b]连续,则( )。 b
a
(A).f(x)?0;
(B).必存在x使f(x)?0;
(C).存在唯一的一点x使f(x)?0 ;
(D).不一定存在点x使 f(x)?0。
???
15.设f(x)??sinx3?x??,则
???0f(x)cos2xdx?( )
?0其余
(A)33
4 (B)?4 (C)1 (D)-1 ?
16.d2
dx?0sinx2dx=________
17. 定积分 ??sinx?sin3xdx等于_______ 0
18. 定积分 ??
0cosx?cos3xdx 等于( )
(A) 0 (B) 3
2
(C) 44
3 (D) ?3
?
19. 定积分?2
0|sinx?cosx|dx 等于( )
(A) 0 (B) 1
(C) 2?1 (D) 2(2?1)
20.定积分?2max{x3,x2
?2,1}dx等于( )
(A) 0 (B) 4
(C) 16
3 (D)97
12
x
2
x
2
21.设f(x)?
?ln(1?
t)dt,g(x)?
?arcsin
t2
,则当x?0时,f(x)是g(x)的( )
(A) 同阶无穷小,但不等价 (B) 等价无穷小 (C) 低价无穷小 (D) 高价无穷小
x
22. F(x)?
?
2
?e
?t
costdt,则F(x)在[0,?]上有( )
(A) F((B) F((C) F((D) F(综合题:

)为极大值,F(0)为最小值 )为极大值,但无最小值 )为极小值,但无极大值 )为最小值,F(0)为最大值
?
2
?
2
?
2
(1)?
10
2
x?2x?x?2
dx
(2)?ln(1?x)dx
1
(3)?
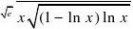


(x
?2
2
xcosx)dx
5
(4)e2
2
(5)?
20
dx
3
(3?2x?x)2dx
2
20
?
(6)?
2?
?2
tanx[sin2x?ln(x?
(7)?
(8)已知函数f(x)在[0,2]上二阶可导,且:f(2)?1,f'(2)?0及
?
20
f(x)dx?4,求:
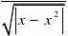
?xf''(2x)dx
1
2
(9)?
??
arctanxx
2
1
dx
(10)?
??
dxe
x?1
3
3?x
1
?e
(11)?12
2
(12)?(1?x)
?1
1
210
?dx
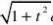
(13)求极限lim(
x?0
x0
x
2
??
n
x0
sintdtx
2
)
(14)用定积分定义计算极限:lim(
n??
nn?1
2
?
nn?2
2
?...?
n?n
22
)
(15)设隐函数y?y(x)由方程x?
3
?
x0
e
?t
2
dt?y?ln4?0所确定,求:
3
dydx
?2x(et2?1)dt??0
2(16)设f(x)??
x
?
?Ax?0处可导,并求出f'(0).
?
4
x?0,问当A为何值时,f(x)在x?0点
(17)设f(x)?cosx?2?
20
f(x)dx,其中f(x)为连续函数,试求:f(x)
(18)设正整数a,且满足关系lim(
x?0
a?xa?x
2
)?
x
?
??1a
xe
?4x
dx,试求a的值。
4月22日定积分练习题
基础题:
1.积分中值定理?af(x)dx?f(?)(b?a),其中( )。 (A) ?是[a,b]内任一点;
(B). ?是[a,b]内必定存在的某一点; (C). ?是[a,b]内唯一的某一点; (D). ?是[a,b]的中点。 2. ?(1?x)?x2dx?( )
?11
b
(A)? (B)
?
2
1
(C)2? (D)
?
20
?
4
3. 设f?C[0,1],且?f(x)dx?2,则?
f(cos
2
x)sin2xdx?( )
(A)2 (B)3 (C)4
ba
(D)1
4. 设f(x)在[a,b]上连续,且?f(x)dx?0,则( )。
(A)在[a,b]的某个子区间上,f(x)?0; (B)在[a,b]上,f(x)?0;
(C)在[a,b]内至少有一点c,f(c)?0; (D)在[a,b]内不一定有x,使f(x)?0。
2
5. ?x3?2x2?xdx=( )
(A) 4
15(2?2)
(B) ?4
15(2?2)
(C) 4282
3?5 (D)?42
3?82
5
dlnx
6.dx?ln(1?t)dt=( )
2x
(A) 1
xln(1?lnx)?2ln(1?2x)
(B) 1
xln(1?lnx)?ln(1?2x)
(C) ln(1?lnx)?ln(1?2x)
(D)ln(1?lnx)?2ln(1?2x) ?
?2
2(1?cosx)x?0
f(x)???x
7. ?1x?0,则f(x)在x?0点( )
?
?1x
?x?0?x?cost2dt
(A) 连续,但不可导
(B) 可导,但导函数不连续
(C) 不连续
(D) 导函数连续
?1ex
?11?exdx?( )
(A) ?1 (B) 1?e
1?e (C) 1?e
1?e
(D) ?1
填空、选择题
??
8(1)?2sinxdx?_______,0?

20cosxdx?_______,7
?(2)limx?0
2
?1x0tsintdt?______;ln(1?x)(3)?x?2xdx?_______;2
(4)曲线y?
(5)?0
???x1t(1?t)dt的上凸区间是_______; ?_______;
(6)设f(x)是连续函数,且f(x)?sinx?
(7)?x(1?x?112005??0f(x)dx,则
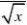

:f(x)?______;)(e?e
1
x?x)dx?______;(8)lim1
x????x1ln(1?
x
02dt?_______;t2(9)设函数y??(t?1)edt的极大值点为_______;
(10)设正值函数f(x)在[a,b]上连续,则函数F(x)?在(a,b)上至少有___个根
(A)0
x?xaf(t)dt??xb1f(t)dt (B)1(C)2(D)34(11)?f(t)dt?0x24,则
:?
(C)40fdx?______;(A)16
(12)?2
?1(B)8(D)21x2dx?_______
(B)
12(C)?12(D)不存在 (A)?
(13)??32
1?________(B)(A)?0
?2(C)?4(D)发散
4月23日定积分练习题
一.计算下列定积分的值
(1)?(4x?x)dx;(2)?(x?1)dx; (3)?2(x?sinx)dx;(4)?2?cos
?1
1
?2
3
2
2
?
5
?
2
xdx;
π
(5)?cos
20
2
?
dx
d? (6)?(2x?3)dx; (7)?dx2; (8)?exlnx; 0021?x
1
1
e
2
1?x
2
(9)?0 (13)?1
ee
1
e?e
2
x?x?
dx; (10)?0
3
tanxdx
2
(11)?4
9
(x?
1x
)dx;(12)?
4
dx1?
x
;
1
dx
cosxsin2xdx;esinxdx;(15) (16)(lnx)dx ?0?0(x2?x?1)3/2; (14)?0
x
2
2
5
2
x
??
1
?
2
(17)?01?sin2x
二.求下列极限:
1
x
2
cosx
dx; (18)?
1
x
dxe?e
?x
;
(1)lim
x?0?x
costdt; (2)lim
x??
(?edt)
x
t
2
2
?
x
e
2t
2
.
dt
三.利用定积分求极限
(1)lim
n??
?111n?????222
(n?2)(n?n)?(n?1)?
?; ?
(2)lim
n??
n(
1n?1
2
?
1(n?2)
2
???
12n
2
);
四.证明题
d
(1)设f'(x在)??(??,上)连续,证明dx
?
xa
(x?(tf)t'(d?t))f?x()。f a()
?
(2)证明:?
20sinxsinx?cosx3?dx??20cosxsinx?cosx3dx,并求出积分值。
(3)设函数f(x)在[0,?]上连续,且?
x
0?0f(x)dx?0,??0f(x)cosxdx?0试证明在(0,?)内至少存在两个不同的点?1,?2,使f(?1)?f(?2)?0(作辅助函数F(x)??f(t)dt,x?(0,?),再使用积分中值定理和Rolle定理)
1
(4)设f(x)在[0,1]上可导,且满足f(1)?2?2xf(x)dx,证明:必存在点??(0,1),
使得f'(?)??f(?)
?(利用积分中值定理和Rolle定理证明)
4月24日定积分练习题
一、填空题:
1. 如果在区间[a,b]上, f(x)?1,则?f(x)dx? . ab2. ?1
0(2x?3)dx?3. 设f(x)?
4. 设f(x)?
5. ??x012sintdt,则f?(x)?cosxe?t2dt,则f?(x)? . ?
?
?2?0cosxsinxdx? 5?6. 2??2sin1
x32n?1xdx?7. ??1?.
8. 比较大小, ?3
1xdx2?31xdx. 3
9. 由曲线y?sinx与x轴,在区间[0,?]上所围成的曲边梯形的面积为 .
10. 曲线y?x在区间[0,1]上的弧长为.
二、选择题:
1. 设函数 f(x)仅在区间[0,4]上可积,则必有?f(x)dx=[ ] 032
A.?f(x)dx?02?
?
2
1323f(x)dx B.??10f(x)dx??3?1f(x)dx C.?f(x)dx?055f(x)dx D.?100f(x)dx??310f(x)dx 2.设I1=?xdx,I2=?x2dx,则[ ] 01
A. I1?I2 B.I1?I2 C.I1?I2 D.I1?I2 3
3. y??x
0(t?1)(t?2)dt则dydxx?0???
A.2 B.-2 C.0 D.1
4. ?a
0x(2?3x)dx?2,则a???
A.2 B.-1 C.0 D.1
5. 设f(x)=?
?x2(x?0)则0)?1f(x)dx=[ ]
?x(x??1
A.2?0xdx B.2?1x2
0dx ?1
C.?1x2dx+?0xdx D.?12
0?10xdx??0?1xdx x
6. t2dt
lim?0sin
x?0x2???
A.11
2 B.3 C.0 D.1
x
7. F(x)??e?tcostdt,则F(x)在[0,?]上有( )
(E) F(?
2)为极大值,F(0)为最小值
(F) F(?
2)为极大值,但无最小值
(G) F(?
2)为极小值,但无极大值
(H) F(?
2)为最小值,F(0)为最大值
?x?8. 设方程组???x0sintdt确定了y是x的函数,则dy
??y??tdx?(
0costdt
(A)cott (B)tant
(C)sint (D)cost
)
9. 设f(x)是区间?a,b?上的连续函数,且?x?22
f(t)dt?x?3,则f(2)?( )
1
(A) 2
(B) -2 (C) 1
4 (D)?1
4
10. 定积分 ?1ln(1?x)( )
01?x2dx =
(A) 1 (B) ?
2
(C) ln2 (D) ?
8ln2
?
11. 定积分 ?4tan2x =( )
??
41?e?x(A) 11
2 (B) 4??
2
(C) 1??
2 (D) 1??
4
12.下述结论错误的是 ( ) (A ) ???x
0 发散 ( B ) 1?x???201?x2收敛
(C ) ???xx
??1?x2?0 ( D ) ???
??发散 1?x2
?
13. 设函数 f?R[a,b], 则极限 limn????f(x)|sinnx|dx 等于( ) 0
??
(A) 2?f(x)dx (B) 2)dx
0??f(x0
(C) 1?
??f(x)dx (D) 不存在
14. 设f(x)为连续函数,且满足?xf(t?x)dt?x2
0?2?e?x?1,则f(x)?(
(A)?x?e?x
(B)x?ex
)。
(C)?x?e?x (D)x?ex
15. 设正定函数f?C[a,b),F(x)??x
af(t)dt??xb1f(x)dt,则F(x)?0在
(a,b)内根的个数为 ( )
(A)0
(C)2 (B)1 (D)3
b n
f(?i)?xi,以下哪些任意性是错误的?( ) 16.定积分的定义为?f(x)dx?lima??0?i?1
(A) 随然要求当??max?xi?0时,?f(?i)?xi的极限存在且有限,但极限值仍是ii
任意的。
(B) 积分区间[a,b]所分成的分数n是任意的。
(C) 对给定的份数n,如何将[a,b]分成n份的分法也是任意的,即除区间端点
a?x0,b?xn外,各个分点x1?x2???xn?1的取法是任意的。
(D) 对指定的一组分点,各个?i?[xi?1,xi]的取法也是任意的。
17. d
dxlnx?ln(1?t)dt=( )
2x
(D)
(E) 1x1
xln(1?lnx)?2ln(1?2x) ln(1?lnx)?ln(1?2x)
(F) ln(1?lnx)?ln(1?2x)
(D)ln(1?lnx)?2ln(1?2x)
2x2d18. (?1t?tdt)?( ) dx
(A ) x
(C ) x2?x (B ) x?x22?x?52 24 ( D ) 2x?x
三.计算题:

1.
ddx
1?
x0
2
2.
?
x0
2?0
sinxdx
2
3.
?
4. lim
(?edt)
t2
x?0
?
4x0
te
2t
2
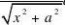
dt
5.
?a(a?0)
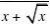
6.
?
2
7. ?
1?t
te
2
dt
1
8.
?
10

61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1