一 : 已知一个数的几分之几是多少求这个数的应用题(用算术方法解)
教学内容教科书第34~35页的例1、例2及其“做一做”的题目,练习九的第6~10题.教学目的使学生能够用算术方法解答已知一个数的几分之几是多少求这个数的应用题.教具准备教师准备大、小齿轮的教具各一个.有条件的学校可以借用自然课的教具──齿轮模型.教学过程一、复习1.口算下列各题.× × × ×÷ ÷ ÷7 ÷做完后集体订正.2.下面各题中应该把哪个量看作单位“1”?(1)黄花的朵数相当于红花朵数的.(红花朵数是单位“1”.)(2)黄花朵数的是红花的朵数.(黄花朵数是单位“1”.)二、新课1.教学例1.教师出示例1.教师:这道题中应该把哪个数量看作单位“1”?(题目中说:水分占体重的,所以应该把体重看作单位“1”.)教师:根据题意,题目中数量间的相等关系式应该怎样写?(数量间相等关系式是:体重×=体内水分的重量.)在这个关系式中哪个量是已知的?哪个量是未知的?如果不用列方程解,还可以怎样计算?(水分的重量和45是已知的,体重是未知的.根据分数除法的意义,已知积和一个因数,求另一个因数可以直接用除法计算.)教师要求学生用算术方法来解答例1.做完后教师让学生对算术解法和方程解法进行比较.(它们都是根据数量间的相等关系来列式的.算术解法是按照除法的意义直接列出除法算式来解答的;方程解法是先设未知数,然后按照数量间的相等关系列方程来解答的.)2.做教科书第49页“做一做”的题目.要求学生用算术方法解答.做完后集体订正.3.教学例2.教师出示例2:一条裤子75元,是一件上衣价钱的.一件上衣多少钱?教师:这道题中把哪个数量看作单位“1”?数量间的相等关系式怎样写?(裤子是上衣价钱的,应该把上衣的单价看作单位“1”.相等关系式是:上衣的单价×=裤子的单价.)教师:根据除法的意义“已知两个因数的积与其中一个因数,求另一个因数”,要求学生直接列出除法算式.学生列式解答后,指名回答解题思路.4.做教科书第50页“做一做”的题目.让学生用算术方法解答,独立完成.做完后集体订正.5.小结用算术方法解分数除法应用题的解题思路.教师:大家想一想,利用算术方法解答分数除法应用题的解题思路是怎样的?指名回答后,明确解题思路:(1)根据题意确定把哪个数量看作单位“1”.(2)按照题目中数量间的相等关系式,根据除法的意义直接列出除法算式.三、巩固练习1.做练习九的第6题.让学生将答案直接写在题后.做完后集体订正.2.做练习十四的第7题.教师要求学生读题、分析数量关系,找出把哪个数量看作单位“1”,再写出数量间的相等关系式.解题后教师提问:这两题之间有什么联系和区别?(题里所包含的数量关系是一样的,都把果园的总面积看作单位“1”,数量间的相等关系式都是:果园总面积×=苹果树占地面积.不同的是第(1)小题的单位“1”是已知的,用乘法计算;第(2)小题的单位“1”是未知的,要列方程或用除法计算.)3.做练习九的第8题.让学生观察大、小齿轮咬合后转动的情况,并提问:小齿轮齿数少,大齿轮齿数多;小齿轮转一圈时,大齿轮能不能转一圈?(不能.)然后,再让大家做题.4.做练习九的第9题.先让学生读题,再引导学生分析题里的数量关系,画线段图.(1)应该把哪个数量看作单位“1”?怎样用线段表示?(要把小兰的画片数看作单位“1”,画一条线段表示小兰的画片数.)(2)怎样用线段图表示小丽的画片数?(先画出一条跟小兰的画片数同样长的线段.因为小丽比小兰多的画片数正好相当于小兰画片数的310,所以这条线段还要加长,加长的一段相当于小兰的,画出线段图如下:)(3)怎样求小兰有多少张画片?(由于小丽比小兰多的12张画片正好相当于小兰画片数的,所以小兰的画片数为:)12÷==40(张)(4)怎样求小丽有多少张画片?(小丽比小兰多12张画片,所以小丽的画片张数为:40+12=52张.)四、作业练习九的第10题.二 : 高等应用数学问题的MATLAB求解_习题参考解答
高等应用数学问题MATLAB求解
习题参考解答
薛定宇
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
目录
第1章计算机数学语言概述第2章MATLAB语言程序设计基础第3章微积分问题的计算机求解第4章线性代数问题的计算机求解
第5章积分变换与复变函数问题的计算机求解第6章代数方程与最优化问题的计算机求解第7章微分方程问题的计算机求解
第8章数据插值、函数逼近问题的计算机求解第9章概率论与数理统计问题的计算机求解第10章数学问题的非传统解法第A章自由数学语言Scilab简介参考文献
25172943537193114127136142
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第1章计算机数学语言概述
1在你的机器上安装MATLAB语言环境,并键入demo命令,由给出的菜单系统和对话框原型演示程序,领略MATLAB语言在求解数学问题方面的能力与方法。[www.61k.com)
图1-1MATLAB演示程序界面
例如,用户选择MATLAB→Graphics→VolumeVlsulization演示,则将得出如图1-2所示的演示说明,单击其中的Runthisdemo栏目,则将得出如图1-3所示的演示界面。用户可以在该界面下按按钮,逐步演示相关内容,而实现这样演示的语句将在该程序界面的下部窗口中给出。
2作者用MATLAB语言编写了给出例子的源程序,读者可以自己用type语句阅读一下源程序,对照数学问题初步理解语句的含义,编写的源程序说明由下表列出。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第1

章计算机数学语言概述3
图1-2MATLAB演示程序界面举例序号
例1.1
例1.2文件名c1ex1.mc1ex2.m程序说明利用MATLAB的符号运算工具箱求解微分问题分别利用MATLAB的符号运算工具箱和数值运算功能求解多项式方程,其中用数值方法得出
的结果有误差
例1.3c1ex3.m分别利用MATLAB的符号运算工具箱和数值运算功能计算Hilbert矩阵的行列式,其中用数值
方法得出的结果有很大误差
例1.4c1ex4.m令x1=y,x2=y˙,则可以将原来的二阶微分方程转换成一阶微分方程组,然后就可以求解微分
方程的数值解了,原方程是非线性微分方程,故不存在解析解。[www.61k.com)ode45()函数可以求解常微分方
程组,而dde23()可以求解延迟微分方程,或更直观地采用Simulink绘制求解框图。
例1.5c1ex5.m线性规划问题调用最优化工具箱中的linprog()函数可以立即得出结果,若想求解整数规划问
题,则需要首先安装整数规划程序ipslv。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
4第1章

计算机数学语言概述
图1-3MATLAB体视化演示程序界面
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第2章MATLAB语言程序设计基础
1启动MATLAB环境,并给出语句tic,A=rand(500);B=inv(A);norm(A*B-eye(500)),toc,试运行该语句,观察得出的结果,并利用help命令对你不熟悉的语句进行帮助信息查询,逐条给出上述程序段与结果的解释。[www.61k.com)
【求解】在MATLAB环境中感触如下语句,则可以看出,求解500×500随机矩阵的逆,并求出得出的逆矩阵与原矩阵的乘积,得出和单位矩阵的差,得出范数。一般来说,这样得出的逆矩阵精度可以达到10?12。
>>tic,A=rand(500);B=inv(A);norm(A*B-eye(500)),tocans=
1.2333e-012
Elapsedtimeis1.301000seconds.
2试用符号元素工具箱支持的方式表达多项式f(x)=x5+3x4+4x3+2x2+3x+6,并令
s?1x=,将f(x)替换成s的函数。
s+1
【求解】可以先定义出f函数,则由subs()函数将x替换成s的函数
>>symssx
f=x^5+3*x^4+4*x^3+2*x^2+3*x+6;F=subs(f,x,(s-1)/(s+1))F=
(s-1)^5/(s+1)^5+3*(s-1)^4/(s+1)^4+4*(s-1)^3/(s+1)^3+2*(s-1)^2/(s+1)^2+3*(s-1)/(s+1)+6
3用MATLAB语句输入矩阵A和B矩阵
???
1+4j1234
??4321?
?,②B=?4+1j①A=??2+3j?2341?
3+2j3241
2+3j
3+2j3+2j2+3j3+2j2+3j4+1j4+1j
?4+1j1+4j??1+4j?1+4j
前面给出的是4×4矩阵,如果给出A(5,6)=5命令将得出什么结果?【求解】用课程介绍的方法可以直接输入这两个矩阵
>>A=[1234;4321;2341;3241]A=
1
2
3
4
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
6
423
332
244
111
第2章MATLAB语言程序设计基础
若给出A(5,6)=5命令,虽然这时的行和列数均大于B矩阵当前的维数,但仍然可以执行该语句,得出
>>A(5,6)=5A=
14230
23320
32440
41110
00000
00005
复数矩阵也可以用直观的语句输入
>>B=[1+4i2+3i3+2i4+1i;B=
1.0000+4.0000i4.0000+1.0000i2.0000+3.0000i3.0000+2.0000i
2.0000+3.0000i3.0000+2.0000i3.0000+2.0000i2.0000+3.0000i
3.0000+2.0000i2.0000+3.0000i4.0000+1.0000i4.0000+1.0000i
4.0000+1.0000i1.0000+4.0000i1.0000+4.0000i1.0000+4.0000i
4+1i3+2i2+3i1+4i;
1+4i];
2+3i3+2i4+1i1+4i;3+2i2+3i4+1i
4假设已知矩阵A,试给出相应的MATLAB命令,将其全部偶数行提取出来,赋给B矩阵,用A=magic(8)命令生成A矩阵,用上述的命令检验一下结果是不是正确。[www.61k.com]【求解】魔方矩阵可以采用magic()生成,子矩阵也可以提取出来
>>A=magic(8),B=A(2:2:end,:)A=
64917403241498B=
9
55
54
12
13
51
50
16
255472634231558
354462735221459
611220372944525
601321362845534
651433038191162
750423139181063
571624332548561
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第2章MATLAB语言程序设计基础
40
41
82623582722593744536454301962311833487631
?x>D?h,
h/Dx,|x|??D。(www.61k.com)5用MATLAB语言实现下面的分段函数y=f(x)=??h,x<?D
【求解】两种方法,其一,巧用比较表达式解决
>>y=h*(x>D)+h/D*x.*(abs(x)<=D)-h*(x<-D);
另外一种方法,用循环语句和条件转移语句
>>fori=1:length(x)
ifx(i)>D,y(i)=h;
elseifabs(x(i))<=D,y(i)=h/D*x(i);
else,y(i)=-h;end
end
其中,前者语句结构简单,但适用范围更广,允许使用矩阵型x,后者只能使用向量型的x,但不能处理矩阵问题。
6用数值方法可以求出S=63??
i=02i=1+2+4+8+···+262+263,试不采用循环的形式求出和式的数值解。由于数值方法采用double形式进行计算的,难以保证有效位数字,所以结果
不一定精确。试采用符号运算的方法求该和式的精确值。
【求解】用符号运算的方式可以采用下面语句
>>sum(sym(2).^[1:63])
ans=
18446744073709551614
由于结果有19位数值,所以用double型不能精确表示结果,该数据类型最多表示16位有效数字。其实用符号运算方式可以任意保留有效数字,例如可以求200项的和或1000项的和可以由下面语句立即得出。
>>sum(sym(2).^[1:200])
ans=
3213876088517980551083924184682325205044405987565585670602750
>>sum(sym(2).^[1:1000])
ans=
214301721437253464189685009812000362112280962341106721488750077674070210224987224498639675763139171625518934583510629365037429057138462808
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
8第2章MATLAB语言程序设计基础
719691551493971496078691355496484619708421492101247422837559083643060
929499671638825347975351183310878921541258291423929553730843353208596
63305248773674411336138750
7编写一个矩阵相加函数matadd(),使其具体的调用格式为A=matA1,A2,A3,···),要求该函数能接受任意多个矩阵进行解法运算。(www.61k.com]
【求解】可以编写下面的函数,用varargin变量来表示可变输入变量
functionA=mat_add(varargin)
A=0;
fori=1:length(varargin),A=A+varargin{i};end
如果想得到合适的错误显示,则可以试用try,catch结构。
functionA=mat_add(varargin)
try
A=0;
fori=1:length(varargin),A=A+varargin{i};end
catch,error(lasterr);end
8自己编写一个MATLAB函数,使它能自动生成一个m×m的Hankel矩阵,并使其调用格式为v=[h1,h2,hm,hm+1,···,h2m?1];H=myhankel(v)。
【求解】解决这样的问题可以有多种方法:
①最直接的方法,Hi,j=hi+j?1,利用双重循环
functionH=myhankel(v)
m=(length(v)+1)/2;
fori=1:m,forj=1:m
H(i,j)=v(i+j-1);
end,end
②考虑某一行(或列),ai=[hi,hi+1,···,hi+m?1],就可以用单重循环生成Hankel矩阵了functionH=myhankel(v)
m=(length(v)+1)/2;%严格说来还应该判定给定输入向量长度奇偶性
fori=1:m,H(i,:)=v(i:i+m-1);end
③利用现有的hankel()函数,则
functionH=myhankel(v)
m=(length(v)+1)/2;%严格说来还应该判定给定输入向量长度奇偶性
H=hankel(v(1:m),v(m:end));%严格说来还应该判定给定输入向量长度奇偶性
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第2章MATLAB语言程序设计基础99已知Fibonacci数列由式ak=ak?1+ak?2,k=3,4,···可以生成,其中初值为a1=a2=1,试编写出生成某项Fibonacci数值的MATLAB函数,要求
①函数格式为y=fib(k),给出k即能求出第k项ak并赋给y向量;
②编写适当语句,对输入输出变量进行检验,确保函数能正确调用;
③利用递归调用的方式编写此函数。(www.61k.com)
【求解】假设fib(n)可以求出Fibonacci数列的第n项,所以对n??3则可以用k=fib(n?
1)+fib(n?2)可以求出数列的n+1项,这可以使用递归调用的功能,而递归调用的出口为
1。综上,可以编写出M-函数。
functiony=fib(n)
ifround(n)==n&n>=1
ifn>=3
y=fib(n-1)+fib(n-2);
else,y=1;end
else
error(’nmustbepositiveinteger.’)
end
例如,n=10可以求出相应的项为
>>fib(10)
ans=
55
现在需要比较一下递归实现的速度和循环实现的速度
>>tic,fib(20),toc
ans=
832040
elapsed_time=
62.0490
>>
ans=
832040
elapsed_time=
0.0100
应该指出,递归的调用方式速度较慢,比循环语句慢很多,所以不是特别需要,解这样问题没有必要用递归调用的方式。tic,a=[11];fori=3:30,a(i)=a(i-1)+a(i-2);end,a(30),toc
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
10第2章MATLAB语言程序设计基础
10由矩阵理论可知,如果一个矩阵M可以写成M=A+BCBT,并且其中A,B,C为相应
阶数的矩阵,则M矩阵的逆矩阵可以由下面的算法求出
?????1?????1
?1T?1?1?1T?1M=A+BCB=A?ABC+BABBTA?1
试根据上面的算法用MATLAB语句编写一个函数对矩阵M进行求逆,并通过一个小例子来检验该程序,并和直接求逆方法进行精度上的比较。[www.61k.com)【求解】编写这个函数
functionMinv=part_inv(A,B,C)
Minv=inv(A)-inv(A)*B*inv(inv(C)+B’*inv(A)*B)*B’*inv(A);假设矩阵为
?
51?50M=??36
16??
10
?0??,B=?2?30?
44
?
1632??48?68??
44
?0??,C=?0?00?
00
?
00??0?1
5077603236608748
且已知该矩阵可以分解成
?10?02A=??00
00对这个例子。可以
00302340340003000020
>>M=[51503616;50776032;36608748;16324868];
iM=inv(M);%数值逆,直接解法iM=
0.0553-0.03890.00170.0041
-0.03890.0555-0.0210-0.0021
0.0017-0.02100.0328-0.0137
0.0041-0.0021-0.01370.0244
>>A=diag([1234]);B=hankel([1234]);C=diag([4321]);
iM1=part_inv(A,B,C)iM1=
0.0553-0.03890.00170.0041
-0.03890.0555-0.0210-0.0021
0.0017-0.02100.0328-0.0137
0.0041-0.0021-0.01370.0244
%分块矩阵的求解方法
乍看结果,似乎二者完全一致,实际上数值算法是有区别的。我们这里用解析方法得出矩阵的逆,然后用下面的语句比较两个结果的精度
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第2章MATLAB语言程序设计基础
>>M1=sym(M);
iM0=
[10713/193751,-7546/193751,
[
[
ans=
2.7990e-017
>>norm(double(iM0)-iM1)%间接求解的误差范数
ans=
3.6583e-016332/193751,796/193751]-416/193751][-7546/193751,10759/193751,-4068/193751,796/193751,iM0=inv(M1)11332/193751,-4068/193751,19075/581253,-2652/193751]-416/193751,-2652/193751,18919/775004]>>norm(double(iM0)-iM)%直接求解的误差范数
可见,用间接方法得出的逆矩阵误差更大,因为在这里新编写的函数中inv()函数使用了多次,由此产生很大的传递误差。(www.61k.com)由此可以得出结论:如果某问题存在直接解,则尽量别使用间接方法,以加大传递误差。
11下面给出了一个迭代模型??xk+1=1+yk?1.4x2k
yk+1=0.3xk
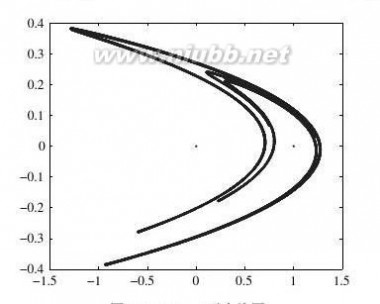
写出求解该模型的M-函数,如果取迭代初值为x0=0,y0=0,那么请进行30000次迭代求出一组x和y向量,然后在所有的xk和yk坐标处点亮一个点(注意不要连线),最后绘制出所需的图形。提示这样绘制出的图形又称为Henon引力线图,它将迭代出来的随机点吸引到一起,最后得出貌似连贯的引力线图。
【求解】用循环形式解决此问题,可以得出如图2-1所示的Henon引力线图。
>>x=0;y=0;
fori=1:29999
x(i+1)=1+y(i)-1.4*x(i)^2;
y(i+1)=0.3*x(i);
end
plot(x,y,’.’)
上述的算法由于动态定义x和y,所以每循环一步需要重新定维,这样做是很消耗时间的,所以为加快速度,可以考虑预先定义这两个变量,如给出x=zeros(1,30000)。
12用MATLAB语言的基本语句显然可以立即绘制一个正三角形,试结合循环结构,编写一个小程序,在同一个坐标系下绘制出该正三角形绕其中心旋转后得出的一系列三角形,还可以调整旋转步距观察效果。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
12
第2章MATLAB语言程序设计基础
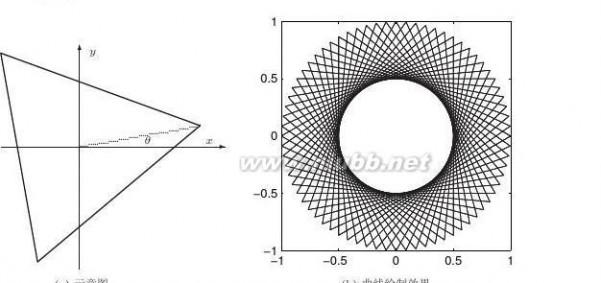
【求解】假设正三角形逆时针旋转θ度,则可以得出如图2-2a所示的示意图,三角形的三个顶点为(cosθ,sinθ),(cos(θ+120?),sin(θ+120?)),(cos(θ+240?),sin(θ+240?)),可以绘制出其曲线,如图2-2b所示,试减小步距,如选择?θ=2,1,0.1,观察效果。(www.61k.com)
图2-2曲线绘制
>>t=[0,120,240,0]*pi/180;
xxx=[];yyy=[];
fori=0:5:360
tt=i*pi/180;
xxx=[xxx;cos(tt+t)];yyy=[yyy;sin(tt+t)];
end%变换成弧度
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第2章MATLAB语言程序设计基础
plot(xxx’,yyy’,’r’),axis(’square’)
????113选择合适的步距绘制出下面的图形sin,其中t∈(?1,1)。(www.61k.com)t13
【求解】
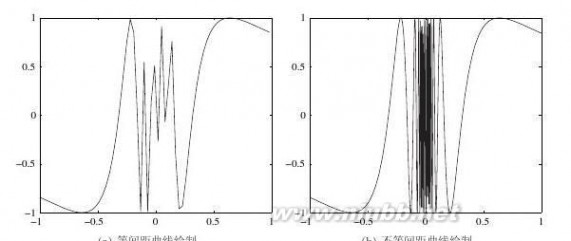
用普通的绘图形式,选择等间距,得出如图2-3a所示的曲线,其中x=0左右显得粗糙。
>>t=-1:0.03:1;y=sin(1./t);plot(t,y)
选择不等间距方法,可以得出如图2-3b所示的曲线。
>>t=[-1:0.03:-0.25,-0.248:0.001:0.248,0.25:.03:1];y=sin(1./t);plot(t,y)图2-3不同自变量选取下的sin(1/t)曲线
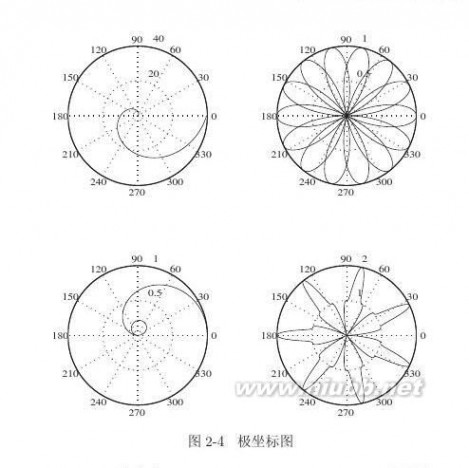
14对合适的θ范围选取分别绘制出下列极坐标图形
①ρ=1.0013θ2,②ρ=cos(7θ/2),③ρ=sin(θ)/θ,④ρ=1?cos3(7θ)
【求解】绘制极坐标曲线的方法很简单,用polar(θ,ρ)即可以绘制出极坐标图,如图2-4所示。注意绘制图形时的点运算:
>>t=0:0.01:2*pi;subplot(221),polar(t,1.0013*t.^2),%(a)
subplot(222),t1=0:0.01:4*pi;polar(t1,cos(7*t1/2))
subplot(223),polar(t,sin(t)./t)%(c)
subplot(224),polar(t,1-(cos(7*t)).^3)
15用图解的方式找到下面两个方程构成的联立方程的近似解。
x2+y2=3xy2,x3?x2=y2?y
【求解】这两个方程应该用隐式方程绘制函数ezplot()来绘制,交点即方程的解,如图2-5a所示。%(b)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
14
>>ezplot(’x^2+y^2-3*x*y^2’);
holdon
ezplot(’x^3-x^2=y^2-y’)
可用局部放大的方法求出更精确的值,如图

2-5b所示。(www.61k.com]从图上可以精确读出两个交点,(0.4012,?0.8916),(1.5894,0.8185)。试将这两个点分别代入原始方程进行验证。
(a)两个方程的曲线,交点为解(b)局部放大区域
图2-5二元联立方程的图解法
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第2章MATLAB语言程序设计基础
16请分别绘制出xy和sin(xy)的三维图和等高线。[www.61k.com]
【求解】(a)
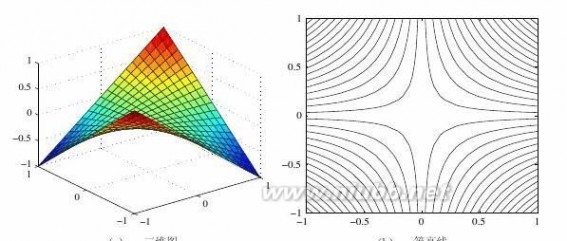
给出下面命令即可,得出的图形如图2-6a、b所示。
>>[x,y]=meshgrid(-1:.1:1);
surf(x,y,x.*y),figure;contour(x,y,x.*y,30)15
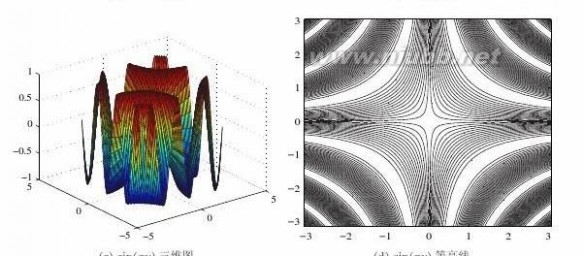
(b)给出下面命令即可,得出的图形如图2-6c、d所示。
>>[x,y]=meshgrid(-pi:.1:pi);
surf(x,y,sin(x.*y)),figure;contour(x,y,sin(x.*y),30)
图2-6三维图与等高线
17在图形绘制语句中,若函数值为不定式NaN,则相应的部分不绘制出来,试利用该规律绘制z=sinxy的表面图,并剪切下x2+y2??0.52的部分。
【求解】给出下面命令可以得出矩形区域的函数值,再找出x2+y2??0.52区域的坐标,将其函数值设置成NaN,最终得出如图2-7所示的曲面。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
16
>>[x,y]=meshgrid(-1:.1:1);z=sin(x.*y);第2章MATLAB语言程序设计基础
ii=find(x.^2+y.^2<=0.5^2);z(ii)=NaN;surf(x,y,z)

高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第3章
1试求出如下极限。(www.61k.com]微积分问题的计算机求解
(x+2)x+2(x+3)x+3
①lim(3+9),②limx→∞x→∞(x+5)xx1【求解】极限问题由下面的语句可以直接求出。
>>symsx;f=(3^x+9^x)^(1/x);limit(f,x,inf)ans=
9
>>symsx;f=(x+2)^(x+2)*(x+3)^(x+3)/(x+5)^(2*x+5);limit(f,x,inf)
ans=
exp(-5)
2试求下面的双重极限。
①lim
x→?1y→2x2y+xy3(x+y),xy②lim,?1x→0y→0????1?cosx2+y2③limx+y。22x→0x+yey→0
【求解】双重极限问题可以由下面语句直接求解。>>symsxy
fa=(x^2*y+x*y^3)/(x+y)^3;limit(limit(fa,x,-1),y,2)ans=
-6
>>fb=x*y/(sqrt(x*y+1)-1);limit(limit(fb,x,0),y,0)ans=
2
>>fc=(1-cos(x^2+y^2))*exp(x^2+y^2)/(x^2+y^2);limit(limit(fc,x,0),y,0)
ans=
3求出下面函数的导数。??①y(x)=xsinx,②y=√1?x(1?cos)
y1xn+a22,n>0③atan=ln(x+y),④y(x)=?lnxnaxn
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
18第3章微积分问题的计算机求解
【求解】由求导函数diff()可以直接得出如下结果,其中③为隐函数,故需要用隐函数求导公式得出导数。(www.61k.com)
>>symsx;
f=sqrt(x*sin(x)*sqrt(1-exp(x)));simple(diff(f))
ans=
1/2/(x*sin(x)*(1-exp(x))^(1/2))^(1/2)*(sin(x)*(1-exp(x))^(1/2)+
x*cos(x)*(1-exp(x))^(1/2)-1/2*x*sin(x)/(1-exp(x))^(1/2)*exp(x))
>>symsax
y=(1-sqrt(cos(a*x)))/(x*(1-cos(sqrt(a*x))))
simple(diff(y))
ans=
1/2/cos(a*x)^(1/2)*sin(a*x)*a/x/(1-cos((a*x)^(1/2)))-
(1-cos(a*x)^(1/2))/x^2/(1-cos((a*x)^(1/2)))-1/2*(1-cos(a*x)^(1/2))
/x/(1-cos((a*x)^(1/2)))^2*sin((a*x)^(1/2))/(a*x)^(1/2)*a
>>f=atan(y/x)-log(x^2+y^2);
f1=simple(-diff(f,x)/diff(f,y))
f1=
(y+2*x)/(x-2*y)
>>symsnpositive;symsa;f=-log((x^n+a)/x^n)/(n*a);diff(f,x)
ans=
-(n/x-(x^n+a)/(x^n)*n/x)/(x^n+a)*x^n/n/a
A用LTEX表示上面的结果,则????x√√xsin(x)e1①1/2sin(x)+xcos(x)?1/2xsin(x)??????√??1?sin()a1?sin(ax)a②1/2?1/2?x(1?cos(x(1?cos(x(1?cos(y+2xx?2y????n(xn+a)n?1④??xn(xn+a)n?1a?1
xxx
??
(x?1)(x?2)4试求出y(t)=函数的4阶导数。(x?3)(x?4)③
【求解】高阶导数可以由下面语句直接得出
>>symsax
f=sqrt((x-1)*(x-2)/(x-3)/(x-4));simple(diff(f,x,4))
ans=
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第3章微积分问题的计算机求解
3*(16*x^11-392*x^10+4312*x^9-28140*x^8+121344*x^7-
364560*x^6+783552*x^5-1214604*x^4+1342560*x^3-1015348*x^2+
474596*x-103741)/((x-1)*(x-2)/(x-3)/(x-4))^(7/2)/(x-3)^8/(x-4)^8
????16x11?392x10+4312x9?28140x8+121344x7?3364560x6+783552x5?1214604x4+1342560x3?1015348x2+474596x?1037417/2(x?1)(x?2)88(x?3)(x?4)(x?3)(x?4)19
5在高等数学中,求解分子和分母均同时为0或∞时,分式极限时可使用L’H?opital法则,即
ln(1+x)ln(1?x)?ln(1?x2)对分子分母分别求导数,再由比值得出,试用该法则lim,x→0x4
并和直接求出的极限结果相比较。(www.61k.com)
【求解】从给出的分母看,若想使之在x=0处的值不为0,则应该对其求4阶导数,同样,还应该对分子求4阶导数,将x=0代入结果,这样就可以使用L’H?opital法则求出极限了。>>symsx;n=log(1+x)*log(1-x)-log(1-x^2);d=x^4;
n4=diff(n,x,4);d4=diff(d,x,4);n4=subs(n4,x,0);
L=n4/d4
L=
1/12
现在直接求极限可以验证上述结果是正确的。
>>limit(n/d,x,0)
ans=
1/12
??
6已知参数方程??dyd2y??x=lncost??,试求出和。y=cost?tsintdxdx??t=p/3
【求解】参数方程的导数可以由下面语句直接求出。
>>symst;x=log(cos(t));y=cos(t)-t*sin(t);
diff(y,t)/diff(x,t)
ans=
-(-2*sin(t)-t*cos(t))/sin(t)*cos(t)
>>f=diff(y,t,2)/diff(x,t,2);subs(f,t,sym(pi)/3)
ans=
3/8-1/24*pi*3^(1/2)
??7假设u=cos?1?2u?2u,试验证=。y?x?y?y?x
【求解】证明二者相等亦可以由二者之差为零来证明,故由下面的语句直接证明。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
20
>>symsxy;u=acos(x/y);
diff(diff(u,x),y)-diff(diff(u,y),x)
ans=
??
8设?2u,试求解。(www.61k.com]?x?yyu+xv=1xu+yv=0第3章微积分问题的计算机求解
【求解】用下面的语句可以直接得出如下结果。
>>symsxyuv
[u,v]=solve(’x*u+y*v=0’,’y*u+x*v=1’,’u,v’);diff(diff(u,x),y)
ans=
2/(x^2-y^2)^2*x+8*y^2/(x^2-y^2)^3*x
??xy?2f?2fx?2f?t29假设f(x,y)=edt,试求?2+。y?x?x?y?y0
【求解】由下面的命令可以得出所需结果。
>>symsxyt
f=int(exp(-t^2),t,0,x*y);
x/y*diff(f,x,2)-2*diff(diff(f,x),y)+diff(f,y,2)simple(ans)
ans=
-2*exp(-x^2*y^2)*(-x^2*y^2+1+x^3*y)
????3x+eyz10假设已知函数矩阵f(x,y,z)=3,试求出其Jacobi矩阵。x+y2sinz
【求解】Jacobi矩阵可以由下面的语句直接得出。
>>symsxyz
F=[3*x+exp(y)*z;x^3+y^2*sin(z)];
jacobian(F,[x,y,z])
ans=
[
[3,exp(y)*z,exp(y)]3*x^2,2*y*sin(z),y^2*cos(z)]
11试求解下面的不定积分问题。??????3x2+adx①I(x)=?dx,②I(x)=+x2(x2+a)????
③I(x)=xeaxcosbxdx,④I(t)=eaxsinbxsincxdx
【求解】①该不定积分可以由下面的命令直接求出
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第3章微积分问题的计算机求解
>>symsxa
f=(3*x^2+a)/(x^2+(x^2+a)^2);int(f,x)
ans=
12/(4+16*a)/(2+4*a+2*(1+4*a)^(1/2))^(1/2)*
atan(2*x/(2+4*a+2*(1+4*a)^(1/2))^(1/2))+
48/(4+16*a)/(2+4*a+2*(1+4*a)^(1/2))^(1/2)*
atan(2*x/(2+4*a+2*(1+4*a)^(1/2))^(1/2))*a+
12/(4+16*a)/(2+4*a+2*(1+4*a)^(1/2))^(1/2)*
atan(2*x/(2+4*a+2*(1+4*a)^(1/2))^(1/2))*(1+4*a)^(1/2)+16/(4+16*a)/(2+4*a+2*(1+4*a)^(1/2))^(1/2)*
atan(2*x/(2+4*a+2*(1+4*a)^(1/2))^(1/2))*(1+4*a)^(1/2)*a+12/(4+16*a)/(2+4*a-2*(1+4*a)^(1/2))^(1/2)*
atan(2*x/(2+4*a-2*(1+4*a)^(1/2))^(1/2))+
48/(4+16*a)/(2+4*a-2*(1+4*a)^(1/2))^(1/2)*
atan(2*x/(2+4*a-2*(1+4*a)^(1/2))^(1/2))*a-
12/(4+16*a)/(2+4*a-2*(1+4*a)^(1/2))^(1/2)*
atan(2*x/(2+4*a-2*(1+4*a)^(1/2))^(1/2))*(1+4*a)^(1/2)-16/(4+16*a)/(2+4*a-2*(1+4*a)^(1/2))^(1/2)*
atan(2*x/(2+4*a-2*(1+4*a)^(1/2))^(1/2))*(1+4*a)^(1/2)*a②可以用下面的语句求出问题的解
>>symsx;f=sqrt(x*(x+1))/(sqrt(x)+sqrt(x+1));int(f,x);latex(ans)
并将其显示如下????x(3x+5)(x+1)(?2+3x)?2/152/15③可以求出下面的结果
>>symsabx
f=x*exp(a*x)*cos(b*x);int(f,x);latex(ans)
其数学显示为????????22a?babaxbxax?+2ecos(bx)??eaxsin(bx)2222a+ba+b(a2+b2)(a2+b2)④用下面的语句求解,得
>>symsxabc;f=exp(a*x)*sin(b*x)*sin(c*x);
latex(int(f,x))21
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
22第3章微积分问题的计算机求解
亦即
aeaxcos((b?c)x)(?b+c)eaxsin((b?c)x)1/2?1/2a2+(b?c)a2+(b?c)
(?b?c)eaxsin((b+c)x)aeaxcos((b+c)x)?1/2+1/2a2+(b+c)a2+(b+c)
12试求出下面的定积分或无穷积分。(www.61k.com]??1??∞1+x2cosxdx,②I=①I=dx1+x00
【求解】①可以直接求解
>>symsx;int(cos(x)/sqrt(x),x,0,inf)
ans=
1/2*2^(1/2)*pi^(1/2)
②可以得出
>>symsx;int((1+x^2)/(1+x^4),x,0,1)
ans=
1/4*2^(1/2)*pi
??
13假设f(x)=e?5xtsin(3x+p/3),试求出积分函数R(t)=
0f(x)f(t+x)dx。
【求解】定义了x的函数,则可以由subs()函数定义出t+x的函数,这样由下面的语句可以直接得出R函数。
>>symsxt;f=exp(-5*x)*sin(3*x+sym(pi)/3);
R=int(f*subs(f,x,t+x),x,0,t);simple(R)
ans=
1/1360*(15*exp(t)^10*3^(1/2)*cos(3*t)-25*cos(9*t)+
25*exp(t)^10*3^(1/2)*sin(3*t)-68*cos(3*t)-15*3^(1/2)*cos(9*t)-
25*3^(1/2)*sin(9*t)-15*exp(t)^10*sin(3*t)+15*sin(9*t)+
93*exp(t)^10*cos(3*t))/exp(t)^15
该结果可以写成
√√√t10t10t10cos(3t)?68cos(3t)?15(e)sin(3t)?25sin(9t)+25(e)sin(3t)15(e)√t10+15sin(9t)?25cos(9t)?15cos(9t)+93(e)cos(3t)1
1360(et)
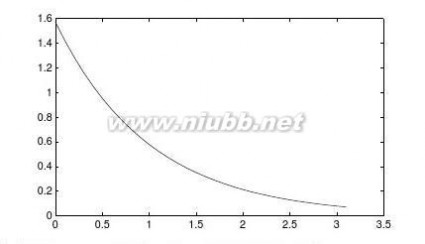
14对a的不同取值试求出I=cosaxdx。1+x0
【求解】由下面的循环结构可以得出不同a值下的无穷积分值,并可以绘制出它们之间关系的曲线,如图3-1所示。??∞
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第3章微积分问题的计算机求解
>>symsxa;f=cos(a*x)/(1+x^2);aa=[0:0.1:pi];y=[];
forn=aa
b=int(subs(f,a,n),x,0,inf);y=[y,double(b)];
end
plot(aa,y)
23
15试对下面函数进行Fourier幂级数展开。(www.61k.com)
①f(x)=(p?|x|)sinx,?p??x<p②f(x)=e|x|,?p??x<p??2x/l,0<x<l/2,且l=p。③f(x)=2(l?x)/l,l/2<x<l
【求解】①可以立即由下面的语句求出。
>>symsx;f=(sym(pi)-abs(x))*sin(x);
[A,B,F]=fseries(f,x,10,-pi,pi);FF=
1/2*pi*sin(x)+16/9/pi*sin(2*x)+32/225/pi*sin(4*x)+
48/1225/pi*sin(6*x)+64/3969/pi*sin(8*x)+80/9801/pi*sin(10*x)A该结果在LTEX下可以显示为
116sin2x32sin4x48sin6x64sin8x80sin10xpsinx+++++29225122539699801②可以由下面语句求解,并得出数学公式为
>>symsx;f=exp(abs(x));
[A,B,F]=fseries(f,x,10,-pi,pi);F
得出的解析解为
2ep?2(?ep?1)cos(x)(2/5ep?2/5)cos(2x)(?1/5ep?1/5)cos(3x)1/2+++
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
24第3章微积分问题的计算机求解
??2p??2e?(2/17ep?2/17)cos(4x)(?1/13ep?1/13)cos(5x)cos(6x)+++??2p??2(?1/41ep?1/41)cos(9x)(?1/25ep?1/25)cos(7x)e?cos(8x)+++??2p??2e?cos(10x)+进一步观察结果可见,该式子可以手工化简,例如提取系数(ep?(?1)n)/p。[www.61k.com)或对各项系数逐项求值(保留10位有效数字)
>>vpa(F,10)
ans=
7.047601355-7.684221126*cos(x)+2.819040541*cos(2.*x)-1.536844225*cos(3.*x)+.8291295709*cos(4.*x)-.5910939328*cos(5.*x)+.3809514246*cos(6.*x)
-.3073688450*cos(7.*x)+.2168492724*cos(8.*x)-.1874200274*cos(9.*x)
+.1395564625*cos(10.*x)
③似乎求解起来更困难,巧妙利用符号运算工具箱中的heaviside()函数,则可以将原函数表示成
p??2|x?p/2|f(x)=2?heavisidex??x2x?p/2??
这样就可以用下面的语句求出函数的Fourier级数。
>>symsx;pi1=sym(pi);
f=2*heaviside(x-pi1/2)-2/pi1*x*abs(x-pi1/2)/(x-pi1/2);
[a,b,F]=fseries(f,x,10,-pi,pi);F
F=
-1/4+4/pi^2*cos(x)+(4/pi+2)/pi*sin(x)-2/pi^2*cos(2*x)-1/pi*sin(2*x)+
4/9/pi^2*cos(3*x)+(-4/9/pi+2/3)/pi*sin(3*x)-1/2/pi*sin(4*x)+
4/25/pi^2*cos(5*x)+(4/25/pi+2/5)/pi*sin(5*x)-2/9/pi^2*cos(6*x)-
1/3/pi*sin(6*x)+4/49/pi^2*cos(7*x)+(-4/49/pi+2/7)/pi*sin(7*x)-
1/4/pi*sin(8*x)+4/81/pi^2*cos(9*x)+(4/81/pi+2/9)/pi*sin(9*x)-
2/25/pi^2*cos(10*x)-1/5/pi*sin(10*x)
???1??4p+2sin(x)cos(x)cos(2x)sin(2x)cos(3x)+??1/4+4?2+4/9????????4?1p+2/5sin(5x)?4/9p?1+2/3sin(3x)sin(4x)4cos(5x)++?1/2+25??4?1???p+2/7sin(7x)sin(6x)cos(6x)4cos(7x)sin(8x)?1/3+?2/9+?1/449??4?1??+2/9sin(9x)4cos(9x)2cos(10x)sin(10x)p++?1/5?812516试求出下面函数的Taylor幂级数展开。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第3章微积分问题的计算机求解
??????????1+xsint2①dt②ln③lnx+1+x④(1+4.2x2)0.2
t1?x0
⑤e?5xsin(3x+p/3)分别关于x=0、x=a的幂级数展开????1?cosx2+y2⑥对f(x,y)=22关于x=1,y=0进行二维Taylor幂级数展开。(www.61k.com]x2+y2ex+y??x25
【求解】由下面的语句可以分别求出各个函数的幂级数展开,由latex(ans)函数可以得出下面的数学表示形式。
>>symstx;f=int(sin(t)/t,t,0,x);
taylor(f,x,15)
>>symsx;f=log((1+x)/(1-x)),taylor(f,x,15)
>>symsx;f=log(x+sqrt(1+x^2));taylor(f,x,15)
>>symsx;f=(1+4.2*x^2)^0.2;taylor(f,x,13)
151111x?x7+x9?x11+x13
6003528032659204390848008095127040035791113②2x+2/3x+2/5x+2/7x+2/9x+2/11x+2/13x
357359631123113③x?1/6x3+x5?x+x?x+x4011211522816133128824555666408410181629556299101368827291161221x+x?x+x?x④1+x2?2562515625390625488281251220703125
⑤该函数的前4项展开为①x?1/18x3+>>symsxa;f=exp(-5*x)*sin(3*x+sym(pi)/3);
taylor(f,x,4,a)
??????p?????5ap??p?????5a?5aesin3a++3ecos3a+?5esin3a+(x?a)333??????p??p????2?5a?5a+8esin3a+?15ecos3a+(x?a)3????????3p????p3+33e?5acos3a++5/3e?5asin3a+(x?a)33
⑥该函数需要使用Maple的展开函数。
>>symsxy;f=(1-cos(x^2+y^2))/((x^2+y^2)*exp(x^2+y^2));
F=maple(’mtaylor’,f,’[x=1,y]’,4)
1?cos(1)(2sin(1)?4+4cos(1))(x?1)(?6cos(1)?7sin(1)+8)(x?1)++e1e1e1??3432??3?+sin(1)+16/3cos(1)(x?1)(sin(1)?2+2cos(1))y2
++ee??83??4342?6cos(1)?sin(1)(x?1)(?8cos(1)+10?8sin(1))y(x?1)++1ee1
2(24sin(1)+16cos(1)?27)y2(x?1)(?2cos(1)+5/2?2sin(1))y4
++ee????134????253194244164140cos(1)+sin(1)??28cos(1)?sin(1)(x?1)y(x?1)++e1e12
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
26
(14sin(1)?16+10cos(1))y4(x?1)+e1
17试求下面级数的前n项及无穷项的和。(www.61k.com)
111①++···++···1×66×11(5n?4)(5n+1)????????????111111②+++2+···++n+···232232n3
【求解】下面的语句可以直接求解级数的和。
>>symsnk;symsum(1/(5*k-4)/(5*k+1),k,1,n)ans=
-1/5/(5*n+1)+1/5
>>symsum(1/(5*k-4)/(5*k+1),k,1,inf)ans=
1/5
>>symsnk;symsum(1/2^k+1/3^k,k,1,n)ans=
-2*(1/2)^(n+1)-3/2*(1/3)^(n+1)+3/2
>>symsum(1/2^k+1/3^k,k,1,inf)
ans=
3/2
当然,无穷级数的和还可以通过极限的方式求出。第3章微积分问题的计算机求解18试求出下面的极限。????1111①lim+2++···+n→∞22?14?162?1(2n)2?1????1111②limn+++···+n→∞n+pn+2pn+3pn+np
【求解】①可以用下面两种方法求解。
>>symskn;symsum(1/((2*k)^2-1),k,1,inf)ans=
1/2
>>limit(symsum(1/((2*k)^2-1),k,1,n),n,inf)ans=
1/2
②可以由下面的语句直接求解。
>>symskn
limit(n*symsum(1/(n^2+k*pi),k,1,n),n,inf)ans=
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第3章微积分问题的计算机求解
1
19试对下面数值描述的函数求取各阶数值微分,并用梯形法求取定积分。(www.61k.com]xi
yi00.10.20.30.40.50.60.70.80.911.11.22702.20773.20583.44353.2412.81642.3111.81011.36020.981720.679070.44730.27684
【求解】
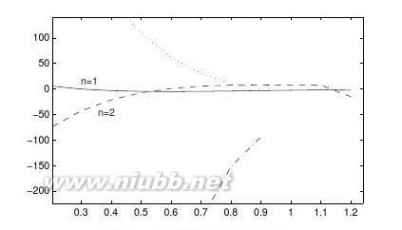
可以由下面的语句得出函数的各阶导数,得出的曲线如图3-2所示。
>>x=[0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1,1.1,1.2];
y=[0,2.2077,3.2058,3.4435,3.241,2.8164,2.311,1.8101,...
1.3602,0.9817,0.6791,0.4473,0.2768];
[dy1,dx1]=diff_ctr(y,x(2)-x(1),1);
[dy2,dx2]=diff_ctr(y,x(2)-x(1),2);
[dy3,dx3]=diff_ctr(y,x(2)-x(1),3);
[dy4,dx4]=diff_ctr(y,x(2)-x(1),4);
plot(dx1+x(1),dy1,’-’,dx2+x(1),dy2,’--’,dx3+x(1),dy3,’:’,dx4+x(1),dy4,’-.’)
20试求出以下的曲线积分。??
①(x2+y2)ds,l为曲线x=a(cost+tsint),y=a(sint?tcost),(0??t??2p)。
l??
②(yx3+ey)dx+(xy3+xey?2y)dy,其中l为a2x2+b2y2=c2正向上半椭圆。
l??
③ydx?xdy+(x2+y2)dz,l为曲线x=et,y=e?t,z=at,0??t??1,a>0。
l??
④(exsiny?my)dx+(excosy?m)dy,其中l为由(a,0)点到(0,0)再经x2+y2=ax上正向半圆周构成的曲线。
【求解】套用书中给出的第一类和第二类曲线积分公式,则可以直接得出曲线积分的结果。l
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
28第3章微积分问题的计算机求解
>>symsat;x=a*(cos(t)+t*sin(t));y=a*(sin(t)-t*cos(t));
f=x^2+y^2;I=int(f*sqrt(diff(x,t)^2+diff(y,t)^2),t,0,2*pi)
I=
2*a^3*pi^2+4*a^3*pi^4
>>symsxyabct;x=c*cos(t)/a;y=c*sin(t)/b;
P=y*x^3+exp(y);Q=x*y^3+x*exp(y)-2*y;
ds=[diff(x,t);diff(y,t)];I=int([PQ]*ds,t,0,pi)
I=
2/15*c*(2*c^4-15*b^4)/a/b^4
>>symst;symsapositive;x=exp(t);y=exp(-t);z=a*t;
F=[y,-x,(x^2+y^2)];
ds=[diff(x,t);diff(y,t);diff(z,t)];I=int(F*ds,t,0,1)
I=
2+1/2*a*exp(1)^2-1/2*a*exp(-1)^2
>>symstm;symsapositive;
x1=t;y1=0;
F1=[exp(x1)*sin(y1)-m*y1,exp(x1)*cos(y1)-m];
x2=a/2+a/2*cos(t);y2=a/2*sin(t);
F2=[exp(x2)*sin(y2)-m*y2,exp(x2)*cos(y2)-m];
I1=int(F1*[diff(x1,t);diff(y1,t)],t,0,a)
I2=int(F2*[diff(x2,t);diff(y2,t)],t,0,pi);I=I1+I2
I2=
1/8*a^2*m*pi
21试求出下面的曲面积分。[www.61k.com]??????4yxyz+zds,S为平面++=1与x=?1,y=?2,z=?3围成的表面。①2x+3234??S??②x2y2zdxdy,其中S为半球面z=R?x?y的下侧。
S
【求解】
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第4章线性代数问题的计算机求解
1Jordan矩阵是矩阵分析中一类很实用的矩阵,其一般形式为
?????51000?α10···0?0?5100??0?α1···?0??????00?510J=?.,例如J=?...1..??...?.?.....?000?51?
000···?α0000?5
试利用diag()函数给出构造J1的语句。[www.61k.com]
【求解】利用diag()能够构造对角矩阵和次对角矩阵的性质,可以由下面语句建立起所需的矩阵。
>>J1=diag([-5-5-5-5-5])+diag([1111],1)
J1=
-5
01-500001-500001-500001-5
2幂零矩阵是一类特殊的矩阵,其基本形式为
?0?0??.Hn=?.
?.?0
010...000···1···......0···0···?00???...??1?0
i亦即,矩阵的次主对角线元素为1,其余均为0,试验证对指定阶次的幂零矩阵,有Hn=0
对所有的i??n成立。
【求解】可以用循环的方式构造出各阶幂零矩阵,并对其求出i+1次方,判定得出矩阵的范数,若发现范数大于0的阶次,则显示其阶次,若为零矩阵则不显示任何内容。通过运行下面的语句,可见不显示任何内容,故i<100的幂零矩阵满足上述性质。
>>fori=1:100
A=diag(ones(1,i),1);
ifnorm(A^(1+i))>0,disp(i);end
end
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
30第4章线性代数问题的计算机求解3试从矩阵的显示格式区分符号矩阵和数值矩阵,明确它们的含义和应用场合。[www.61k.com]若A矩阵为数值矩阵,B为符号矩阵,C=A*B运算得出的C矩阵是符号矩阵还是数值矩阵?
【求解】得出的结果当然是符号矩阵,见下例。
>>A=ones(5);B=sym(A);A*B
ans=
[5,5,5,5,5]
[5,5,5,5,5]
[5,5,5,5,5]
[5,5,5,5,5]
[5,5,5,5,5]
4请将下面给出的矩阵A和B输入到MATLAB环境中,并将它们转换成符号矩阵。
????35501235765165?3?2310014?254625??????6420644???1211346??????,B=?35152123963662A=???????4?10760077?101201??????3?4?737812??7244077?
1?107?68154867217
【求解】矩阵的输入与转换是很直接的。
>>A=[5,7,6,5,1,6,5;2,3,1,0,0,1,4;6,4,2,0,6,4,4;3,9,6,3,6,6,2;
10,7,6,0,0,7,7;7,2,4,4,0,7,7;4,8,6,7,2,1,7];A=sym(A)
A=
[
[
[
[
[
[5,2,6,3,7,4,7,3,4,9,7,2,8,6,1,2,6,6,4,6,5,0,0,3,0,4,7,1,0,6,6,0,0,2,6,1,4,6,7,7,1,5]4]4]2]7]7]7][10,
>>B=[3,5,5,0,1,2,3;3,2,5,4,6,2,5;1,2,1,1,3,4,6;3,5,1,5,2,1,2;
4,1,0,1,2,0,1;-3,-4,-7,3,7,8,12;1,-10,7,-6,8,1,5];B=sym(B)
B=
[
[
[
[
[3,3,1,3,4,5,2,2,5,1,5,5,1,1,0,0,4,1,5,1,1,6,3,2,2,2,2,4,1,0,3]5]6]2]1]
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第4章线性代数问题的计算机求解
[
[-3,-4,-7,7,3,-6,7,8,
a3
b3
c3
d3
e38,1,a2b2c2d2e212]5]abcde311,-10,?4a?b4?45试求出Vandermonde矩阵A=??c4?de4?11??1??的行列式,并以最简的形式显示结果。(www.61k.com)1?1
【求解】利用书中编写的面向符号矩阵的vander()函数,可以构造出Vandermonde矩阵并可以求出该矩阵的行列式。
>>symsabcde;A=vander([abcde])
A=
[a^4,a^3,a^2,
[b^4,b^3,b^2,
[c^4,c^3,c^2,
[d^4,d^3,d^2,
[e^4,e^3,e^2,
ans=
(c-d)*(b-d)*(b-c)*(a-d)*(a-c)*(a-b)*(-d+e)*(e-c)*(e-b)*(e-a)
6利用MATLAB语言提供的现成函数对习题4中给出的两个矩阵进行分析,判定它们是否为奇异矩阵,得出矩阵的秩、行列式、迹和逆矩阵,检验得出的逆矩阵是否正确。
【求解】以A矩阵为例,可以对其进行如下分析。
>>A=[5,7,6,5,1,6,5;2,3,1,0,0,1,4;6,4,2,0,6,4,4;3,9,6,3,6,6,2;
10,7,6,0,0,7,7;7,2,4,4,0,7,7;4,8,6,7,2,1,7];A=sym(A);
rank(A)
ans=
7
>>det(A)
ans=
-35432
>>trace(A)
ans=
27
>>B=inv(A);latex(B)a,b,c,d,e,1]1]1]1]1]>>det(A),simple(ans)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
32
??6465?
??24047??
??5515=???
??6163??3781?
?9225?2297第4章线性代数问题的计算机求解
?115715374651?977?887?2565495927714151?1709?13326091173469?3079794?127?921?9??1278?17584827842?12714292601?2064141854632196663?A?1
?142416131892137?1467????6439?
?
?491????1567?
?
?3353???
1785
178??
>>A*Bans=
[1,0,0,0,0,0,0][0,1,0,0,0,0,0][0,0,1,0,0,0,0][0,0,0,1,0,0,0][0,0,0,0,1,0,0][0,0,0,0,0,1,0][0,0,0,0,0,0,1]
7试求出习题4中给出的A和B矩阵的特征多项式、特征值与特征向量,并验证Hamilton-Caylay定理,解释并验证如何运算能消除误差。(www.61k.com)【求解】仍以A矩阵为例。
>>A=[5,7,6,5,1,6,5;2,3,1,0,0,1,4;6,4,2,0,6,4,4;3,9,6,3,6,6,2;
10,7,6,0,0,7,7;7,2,4,4,0,7,7;4,8,6,7,2,1,7];A=sym(A);eig(A)ans=
5.009396680079366526215873006955228.679593193974410579078264020229
.27480714110743938760483528351799e-1+1.1755376247101009492093136044131*i-1.6336795424500642956747726147329+6.9740721596526560301948635104611*i
-3.4765922173751363914655588544224
-1.6336795424500642956747726147329-6.9740721596526560301948635104611*i.27480714110743938760483528351799e-1-1.1755376247101009492093136044131*i>>p=poly(A)p=
x^7-27*x^6-18*x^5-1000*x^4+3018*x^3+24129*x^2+2731*x+35432>>p=sym2poly(p)p=
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第4章线性代数问题的计算机求解
1ans=
[0,0,0,0,0,0,0][0,0,0,0,0,0,0][0,0,0,0,0,0,0][0,0,0,0,0,0,0][0,0,0,0,0,0,0][0,0,0,0,0,0,0][0,0,0,0,0,0,0]
8试对习题4中给出的A和B矩阵进行奇异值分解、LU分解及正交分解矩阵。[www.61k.com)【求解】仍以A矩阵为例,这里只考虑数值解。
>>A=[5,7,6,5,1,6,5;2,3,1,0,0,1,4;6,4,2,0,6,4,4;3,9,6,3,6,6,2;
10,7,6,0,0,7,7;7,2,4,4,0,7,7;4,8,6,7,2,1,7];[s,v,d]=svd(A)s=
-0.4239-0.1481-0.2974-0.3982-0.4894-0.3790-0.4101v=
32.4615
000000
d=
-0.4492-0.4821-0.3878-0.2372-0.1669
0.5090-0.4781-0.1693-0.3550-0.4500
-0.1602-0.07020.12480.5985-0.6026
0.22810.1634-0.2472-0.26010.2746
0.0328-0.5653-0.24680.50350.5497
-0.60710.1976-0.3642-0.1915-0.0438
0.30280.3857-0.74210.3188-0.1643
09.3091
00000
007.8637
0000
0004.8206
000
00004.4123
00
000001.6953
0000000.4135
-0.10610.08940.0356-0.57600.49700.4736-0.4200
0.20300.0836-0.5776-0.4427-0.15640.22210.5902
-0.40910.40270.4840-0.34450.0971-0.32760.4480
-0.0746-0.20520.4829-0.0925-0.60670.57990.0790
0.05760.8703-0.12220.1884-0.30100.1683-0.2644
0.76910.03780.3069-0.3884-0.1447-0.3328-0.1739
-27
-18
-1000
3018
24129
2731
35432
33
>>polyvalm(p,A)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
34
-0.3931-0.4204L=
0.50000.20000.60000.30001.00000.70000.4000U=
10.0000
000000
>>orth(A)ans=
-0.4239-0.1481-0.2974-0.3982-0.4894-0.3790-0.4101
-0.10610.08940.0356-0.57600.49700.4736-0.4200
0.20300.0836-0.5776-0.4427-0.15640.22210.5902
-0.40910.40270.4840-0.34450.0971-0.32760.4480
7.00006.9000
00000
6.00004.20001.5652
0000
03.00005.26095.0556
000
0.50720.2319-0.02901.0000
-0.42030.7536
0.5556-0.7500-0.9444
001.00000.2778
0.10990.64291.0000
0000.6484
0.27000.2869
-0.33250.3491
-0.69470.4842
第4章线性代数问题的计算机求解
0.13940.2081
0.39170.5173
0.0807-0.2714
>>[LU]=lu(A)
0.50000.5702
00001.0000
06.00002.52178.5556-8.7692
00
0.53761.0000
000007.00003.90003.73913.4444-8.01103.8534
1.0000
0000007.0000-0.10002.05801.74072.57511.5794-1.9204
-0.0746-0.20520.4829-0.0925-0.60670.57990.0790
0.05760.8703-0.12220.1884-0.30100.1683-0.2644
0.76910.03780.3069-0.3884-0.1447-0.3328-0.1739
9试求出下面矩阵的特征值、特征向量、奇异值。[www.61k.com]
???
70327577
?547?74933?
???
?,B=?44539838A=????
?695?59636?
62126854【求解】A矩阵的分析如下。
795
95752388017398027125287673713712894199299
?661284??469??65?988
>>A=[2,7,5,7,7;7,4,9,3,3;3,9,8,3,8;5,9,6,3,6;2,6,8,5,4]
B=[703,795,980,137,661;547,957,271,12,284;445,523,252,894,469;
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第4章线性代数问题的计算机求解
695,880,876,199,65;621,173,737,299,988][e,f]=eig(A)e=
0.44520.42560.49330.46070.4062f=27.8629
0000
>>svd(A)ans=
28.78196.58304.23452.69491.4393
10试判定下面矩阵是否为正定矩阵,如是,则得出其Cholesky分解矩阵。(www.61k.com)
????
16179121292122
?171212218??24333?
????
?,B=?91218713?13734A=?????
?12271812??23354?
121813121023445【求解】A矩阵能进行Cholesky分解,故为正定矩阵。
>>A=[9,2,1,2,2;2,4,3,3,3;1,3,7,3,4;2,3,3,5,4;2,3,4,4,5];
chol(A)ans=
3.0000
0000
0.66671.8856
000
0.33331.47312.1723
00
0.66671.35530.35961.6092
0.66671.35530.82000.88481.1240
02.6062
000
00
-2.2306+1.8926i
00
000
-2.2306-1.8926i
0000
-5.0078
0.57560.1987-0.56290.5010-0.2478
0.3203-0.3633i-0.5697
-0.0168+0.0797i-0.0594+0.3503i0.5457-0.1010i
0.3203+0.3633i-0.5697
-0.0168-0.0797i-0.0594-0.3503i0.5457+0.1010i
-0.07060.6063-0.4901-0.52290.3373
35
B矩阵进行Cholesky分解失败,故为非正定矩阵。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
36第4章线性代数问题的计算机求解
>>B=[16,17,9,12,12;17,12,12,2,18;9,12,18,7,13;
12,2,7,18,12;12,18,13,12,10];
chol(B)
???Errorusing==>chol
Matrixmustbe
??2?011试对矩阵A=??2
2positivedefinite.?0.5?0.50.5?1.50.5?0.5??进行Jordan变换,并得出变换矩阵。[www.61k.com)0.5?4.50.5?1?2?2
【求解】将A输入,并转换成符号矩阵,这样就能得出Jordan变换矩阵与Jordan矩阵。
>>A=[-2,0.5,-0.5,0.5;0,-1.5,0.5,-0.5;2,0.5,-4.5,0.5;2,1,-2,-2];
[VJ]=jordan(sym(A))
V=
[
[
[
[
J=
[-4,
[
[
[0,0,0,0,1,0]0]1]0,-2,0,0,0,1/4,1/4,1/2,0,1/2,1/2,1/2,-1/4]1/2,1]1/2,-1/4]1,-1/4]0,-2,0,-2]
12试求下面齐次方程的基础解系。
?6x1+x2+4x3?7x4?3x5=0??????2x1?7x2?8x3+6x4=0
?4x1+5x2+x3?6x4+8x5=0???34x1+36x2+9x3?21x4+49x5=0????26x1?12x2?27x3+27x4+17x5=0
【求解】可以将方程写成矩阵形式,得出的两列向量为方程的基础解系。
>>A=[6,1,4,-7,-3;-2,-7,-8,6,0;-4,5,1,-6,8;
-34,36,9,-21,49;-26,-12,-27,27,17];A=sym(A);
rank(A)
ans=
3
>>null(A)
ans=
[191/34,95/17]
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第4章线性代数问题的计算机求解
[
[0,1,1]0]37
[109/34,103/34]
[173/34,151/34]
13试求下面线性代数方程的解析解与数值解,并检验解的正确性。(www.61k.com)
????2?93?2?1?1?40?10?110??50???X=??3?8?4??8?2?4?63??033?
?5?6?6?8?49?53
【求解】求出A,[A,B]两个矩阵的秩,可见二者相同,所以方程不是矛盾方程,应该有无穷多解。
>>A=[2,-9,3,-2,-1;10,-1,10,5,0;8,-2,-4,-6,3;-5,-6,-6,-8,-4];
B=[-1,-4,0;-3,-8,-4;0,3,3;9,-5,3];
[rank(A),rank([AB])]
ans=
44
用下面的语句可以求出方程的解析解,并可以验证该解没有误差。
>>x0=null(sym(A));
x_analytical=sym(A)\B;symsa;
x=a*[x0x0x0]+x_analytical
x=
[
[
[
[
ans=
[0,0,0]
[0,0,0]
[0,0,0]
[0,0,0]
用数值解方法也可以求出方程的解,但会存在误差,且与任意常数a的值有关。
>>x0=null(A);x_numerical=A\B;symsa;
x=a*[x0x0x0]+x_numerical;vpa(x,10)a+967/1535,-1535/1524*a,1321/508*a+759/1535,-170/127*a-694/307,a-943/1535,-1535/1524*a,1321/508*a-56/1535,-170/127*a+719/307,a-159/1535]-1535/1524*a]1321/508*a-628/1535]-170/127*a+103/307][-3659/1524*a-1807/1535,-3659/1524*a-257/1535,-3659/1524*a-141/1535]>>A*x-B
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
38
ans=
[.2474402553*a+.1396556436,
[
[-.5940839201*a,.6434420813*a-.7805411315,
>>A*x-B
ans=
[
[
[1/18014398509481984*a,-5/4503599627370496*a,13/18014398509481984*a,第4章线性代数问题的计算机求解.2474402553*a-.6840666849,.2474402553*a-.1418420333]-.5940839201*a,-.5940839201*a][-.2492262414*a+.4938507789,-.2492262414*a+.7023776988e-1,-.2492262414*a+.3853511888e-1].6434420813*a-.2178190763,.6434420813*a-.5086089095]-.3312192394*a+2.435364854,-.3312192394*a+.3867176824][-.3312192394*a-1.604263460,1/18014398509481984*a,-5/4503599627370496*a,13/18014398509481984*a,1/18014398509481984*a]-5/4503599627370496*a]13/18014398509481984*a][-25/18014398509481984*a,-25/18014398509481984*a,-25/18014398509481984*a]14试判定下面的线性代数方程是否有解。(www.61k.com)
?162?511??97
414310615???131??8??X=?3??4?12?17
【求解】由秩判定矩阵可以得出如下结果。
>>A=[16,2,3,13;5,11,10,8;9,7,6,12;4,14,15,1];
B=[1;3;4;7];
[rank(A),rank([AB])]
ans=
34
由得出的结果看,A,[A,B]两个矩阵的秩不同,故方程是矛盾方程,没有解。15试求出线性代数方程的解析解,并验证解的正确性。
?2941258?1228733??303575??3116699??1121468??5?181?911?1
26?27?10?15?13???196?512?7??????41210??????1091?X=?????057?????1018?18??20218
【求解】先判定方程解的存在性,得出结论,方程有无穷多解。
>>A=[2,9,4,12,5,8,6;12,2,8,7,3,3,7;3,0,3,5,7,5,10;3,11,6,6,9,9,1;
11,2,1,4,6,8,7;5,-18,1,-9,11,-1,18;26,-27,-1,0,-15,-13,18];
X=[1,9;5,12;4,12;10,9;0,5;10,18;-20,2];
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第4章线性代数问题的计算机求解
[rank(A),rank([AX])]
ans=
5539
这样就能解出方程的解析解,并验证方程解是这正确的。(www.61k.com]
>>x0=null(sym(A));symsa1a2;
x1=sym(A)\X;
x=a1*[x0(:,1)x0(:,1)]+a2*[x0(:,2)x0(:,2)]+x1
x=
[
[
[
[
[
[
>>A*x-X
ans=
[0,0]
[0,0]
[0,0]
[0,0]
[0,0]
[0,0]
[0,0]
16试用数值方法和解析方法求取下面的Sylvester方程,并验证得出的结果。
?????21?13?6?405???4?1?12?3?2142?24??????6?X+X??2?92?=?5?61?3?673?????6?4?4???1310?2?190?110?
?66?304034
【求解】用下面的语句可以直接求出其数值解,并可以判定该解的精度。
>>A=[3,-6,-4,0,5;1,4,2,-2,4;-6,3,-6,7,3;-13,10,0,-11,0;0,4,0,3,4];B=[3,-2,1;-2,-9,2;-2,-1,9];
C=[-2,1,-1;4,1,2;5,-6,1;6,-4,-4;-6,6,-3];
X=lyap(A,B,C)
X=6386/9453*a1-7118/9453*a2-10519/37810,a1+17927/18905,6437/9453*a1-15716/9453*a2-54143/37810,16855/9453*a1-24190/9453*a2,-25198/9453*a1+25561/9453*a2,a2+29837/37810,6386/9453*a1-7118/9453*a2-2159/7562]a1+1397/3781]6437/9453*a1-15716/9453*a2-3527/7562]16855/9453*a1-24190/9453*a2]-25198/9453*a1+25561/9453*a2]a2+8671/7562][-14446/9453*a1+15643/9453*a2+25857/18905,-14446/9453*a1+15643/9453*a2+4691/3781]
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
40
-4.0569
0.0356
9.4886
2.6969
7.7229
ans=
2.7917e-013-14.512825.074325.932321.645031.91001.5653-2.7408-4.4177-2.8851-3.7634第4章线性代数问题的计算机求解>>norm(A*X+X*B+C)
利用书中给出的解析解方法,可以求出该方程的解析解。(www.61k.com)
>>X=lyap(sym(A),B,C)
X=
[-434641749950/107136516451,-4664546747350/321409549353,
[503105815912/321409549353]3809507498/107136516451,8059112319373/321409549353,-880921527508/321409549353]
[1016580400173/107136516451,8334897743767/321409549353,-1419901706449/321409549353]
[288938859984/107136516451,6956912657222/321409549353,-927293592476/321409549353]
[827401644798/107136516451,10256166034813/321409549353,-1209595497577/321409549353]>>A*X+X*B+C
ans=
[0,0,0]
[0,0,0]
[0,0,0]
[0,0,0]
[0,0,0]
17假设某Riccati方程的数学表达式为PA+ATP
???0?276?39??2?6?2?6??,B=?16A=???7??50?5?2?
1034?119?PBR?1BTP??365?4??,Q=?56?334?644+Q=0,且已知?34????34?41?,R=62?1526
试求解该方程,得出P矩阵,并检验得出解的精度。
【求解】可以容易地得出该Riccati方程的数值解,并可见精度可以达到10?13级。
>>A=[-27,6,-3,9;2,-6,-2,-6;-5,0,-5,-2;10,3,4,-11];
B=[0,3;16,4;-7,4;9,6];
Q=[6,5,3,4;5,6,3,4;3,3,6,2;4,4,2,6];
R=[4,1;1,5];
C=Q;
B=B*inv(R)*B’;
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第4章线性代数问题的计算机求解
X=are(A,B,C)X=
0.122635827115470.108846082445780.027265604293760.11845697768205ans=
3.142051364911015e-014
18假设已知某Jordan块矩阵A及其组成部分为
0.108846082445780.281274170245520.165874155595240.06370964357824
0.027265604293760.165874155595240.402299389560820.01389200165902
41
0.118456977682050.063709643578240.013892001659020.22086908688248
>>norm(A’*X+X*A-X*B*X+C)
??
???1100?????310?0?11?510???,A1=?0?31?,A2=A2,A3=??00?50?11?
A300?3
000?1
??p??A2t2At
试用解析解运算的方式得出e,sin2At+,eA+sin(A3t)At+esinAt。[www.61k.com)
3
【求解】用下面的语句可以求出矩阵问题的解析解。?A1
A=?
?
>>A1=diag([-3-3-3])+diag([11],1);
A2=[-51;0-5];
A3=diag([-1-1-1-1])+diag([111],1);A=sym(diagm(A1,A2,A3));>>symst;expm(A*t)
A可以用LTEX将其显示成??3t
ete?3t1/2t2e?3t??0e?3tte?3t???00e?3t???000???000???000???000???000?
000
000e?5t00000
000te?5te?5t0000
00000e?t000
00000te?te?t00
000001/2t2e?t
te?te?t0
000001/6t3e?t1/2t2e?t
te?te?t
??
????????????????????
其他矩阵函数可以由下面的语句求出,限于篇幅,不列出具体结果。
>>symsxt;funm(A,’sin(2*x*t+sym(pi)/3)’,x)
funm(A,’exp(x^2*t)*x^2+sin(x^3*t)*x*t+exp(sin(x*t))’,x)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
42
例如可以求出上述结果的第一行第二列元素为
第4章线性代数问题的计算机求解
?54te9t?6e9t?81cos(27t)t2?sin(27t)t+cos(3t)te?sin(3t)
????
19假设已知矩阵A如下给出,试求出eAt,sinAt,eAtsinA2eAtt。(www.61k.com)
???4.500.5?1.5??0.5?40.5?0.5?
?A=??1.51?2.51.5?
0?1?1?3【求解】用下面的语句可以直接得出矩阵指数解析解。
>>A=[-4.5,0,0.5,-1.5;-0.5,-4,0.5,-0.5;1.5,1,-2.5,1.5;0,-1,-1,-3];
A=sym(A);symst;expm(A*t)??
1???2??
e?3t(1?t+t2)+e?5t(t?1)e?3t+e?5t(t+1)e?3t?e?5t
?t2e?3t
可以得出其他矩阵函数。
>>symsxt;funm(A,’sin(x*t)’,x)
symsxt;funm(A,’exp(x*t)*sin(x^2*exp(x*t)*t)’,x)
e?5t+(?1+2t)e?3t
e?3t+e?5t?e?5t+e?3t
?te?3t
(t+t2)e?3t
te?3t(1+t)e?3t?(t+t2)e?3t
e?5t?(1+t?t2)e?3t(t?1)e?3t+e?5t(t+1)e?3t?e?5t
(2?t2)e?3t
???????
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第5章积分变换与复变函数问题的计算机求解1对下列的函数f(t)进行Laplace变换
sinαt①fa(t)=,②fb(t)=t5sinαt,③fc(t)=t8cosαt④fd(t)=t6eαt
t
?at⑤fe(t)=5e+t4e?at+8e?2t,⑥ff(t)=eβtsin(αt+θ),⑦fg(t)=e?12t+6e9t
【求解】给定函数的Laplace变换可以用下面的语句直接得出
>>symsat;f=sin(a*t)/t;laplace(f)
ans=
atan(a/s)
>>symsta;f=t^5*sin(a*t);laplace(f)
ans=
120/(s^2+a^2)^3*sin(6*atan(a/s))
>>symsta;f=t^8*cos(a*t);laplace(f)
ans=
40320/(s^2+a^2)^(9/2)*cos(9*atan(a/s))
>>symsta;f=t^6*exp(a*t);laplace(f)
ans=
720/(s-a)^7
>>symsat;f=5*exp(-a*t)+t^4*exp(-a*t)+8*exp(-2*t);laplace(f)ans=
5/(s+a)+24/(s+a)^5+8/(s+2)
>>symsabct;f=exp(b*t)*sin(a*t+c);laplace(f)
ans=
cos(c)*a/((s-b)^2+a^2)+sin(c)*(s-b)/((s-b)^2+a^2)
>>symst;f=exp(-12*t)+6*exp(9*t);laplace(f)
ans=
1/(s+12)+6/(s-9)
2对下面的F(s)式进行Laplace反变换√√1s?a①Fa(s)=,②Fb(s)=?③Fc(s)=lns?bs2?a2)(s+b)
3a2(s?1)81,⑤Fe(s)=,⑥F(s)=④Fd(s)=fs+ass+a)
s2+a2s2+3s+81s+α,⑧F(s)=⑦Fg(s)=ln2,⑨F(s)=his+b22s?αi=1(s+i)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
44第5章积分变换与复变函数问题的计算机求解
【求解】Laplace变换可以用下面语句直接求得。(www.61k.com]
>>symssab;F=1/(s^2*(s^2-a^2)*(s+b));ilaplace(F)
teat1e?ate?bt
?2+3+?22+ab2a(a+b)b2a2b(a?b2)2a3(a?b)
>>symssab;F=sqrt(s-a)-sqrt(s-b);ilaplace(F)
ans=
1/2/t/(pi*t)^(1/2)*(exp(b*t)-exp(a*t))
>>symsabs;F=log((s-a)/(s-b));ilaplace(F)
ans=
(exp(b*t)-exp(a*t))/t
>>symsas;F=1/sqrt(s)/(s+a);ilaplace(F)
ans=
1/(-a)^(1/2)*exp(-a*t)*erf((-a*t)^(1/2))
>>symsas;F=3*a^2/(s^3+a^3);ilaplace(F)
ans=
exp(-a*t)+exp(1/2*a*t)*(-cos(1/2*3^(1/2)*a*t)+3^(1/2)*sin(1/2*3^(1/2)*a*t))>>symss;F=(s-1)^8/s^7;ilaplace(F)
ans=
dirac(1,t)-8*dirac(t)+28+7/6*t^4-56*t+1/720*t^6-1/15*t^5-28/3*t^3+35*t^2>>symssab;F=log((s^2+a^2)/(s^2+b^2));ilaplace(F)
ans=
2/t*(cos((b^2)^(1/2)*t)-cos((a^2)^(1/2)*t))
>>symss;F=s^2+3*s+8;fori=1:8,F=F/(s+i);end;ilaplace(F)
ans=
1/30*exp(-3*t)-1/12*exp(-4*t)-1/105*exp(-8*t)-1/120*exp(-2*t)-
13/120*exp(-6*t)+1/8*exp(-5*t)+1/20*exp(-7*t)+1/840*exp(-t)
>>symsas;F=(s+a)/(s-a)/2;ilaplace(F)
ans=
1/2*dirac(t)+a*exp(a*t)
3Laplace变换的一个重要应用是求解常系数线性微分方程,可以利用当函数具有零初始值和各阶导数的零初始值下L[dnf(t)/dtn]=snL[f(t)]这一性质对微分方程进行Laplace变换的方法其求解微分方程,试使用这样的方法求解下面的微分方程。
y????(t)+3y??(t)+2y(t)=e?t,y(0)=y??(0)=0
【求解】将微分方程两侧进行Laplace变换则(s2+3s+2)Y(s)=L[e?t],这样微分方程????的解可以由下面的式子求出y(t)=L?1L[e?t]/(s2+3s+2),这些式子可以用下面的MATLAB语句求解,得出微分方程的解析解。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第5章积分变换与复变函数问题的计算机求解
>>symsst;y=ilaplace(laplace(exp(-t))/(s^2+3*s+2))
y=
(-1+t)*exp(-t)+exp(-2*t)45
4试求出下面函数的Fourier变换,对得出的结果再进行Fourier反变换,观察是否能得出原来函数。[www.61k.com)
①f(x)=x2(3p?2|x|),0??x??2p,②f(t)=t2(t?2p)2,0??t??2p
③f(t)=e?t,?l??t??l,④f(t)=te?|t|,?p??t??p
【求解】用下面的语句可以立即得出①的Fourier变换,对得出的结果进行Fourier反变换,则可以还原出原始的函数,这是-4*x*heaviside(x)+2*x实际上就是?2|x|。
>>symsx;f=x^2*(3*sym(pi)-2*abs(x));F=fourier(f)
F=
-6*(4+pi^2*dirac(2,w)*w^4)/w^4
>>ifourier(F)
ans=
x^2*(-4*x*heaviside(x)+3*pi+2*x)
利用现成的Fourier变换及反变换函数可以直接得出如下结果,并可见,结果反变换能得出和原函数完全等效的结果。
>>symst;f=t^2*(t-2*sym(pi))^2;F=fourier(f)
F=
2*pi*(4*i*pi*dirac(3,w)-4*pi^2*dirac(2,w)+dirac(4,w))
>>ifourier(F)
ans=
x^2*(-2*pi+x)^2
>>symst;f=exp(-t^2);F=fourier(f)
F=
pi^(1/2)*exp(-1/4*w^2)
>>ifourier(F)
ans=
exp(-x^2)
>>symst;f=t*exp(-abs(t));F=fourier(f)
F=
-4*i/(1+w^2)^2*w
>>ifourier(F)
ans=
x*(exp(-x)*heaviside(x)+exp(x)*heaviside(-x))2
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
46
5试证明cosθ+cos2θ+···+cosnθ=第5章积分变换与复变函数问题的计算机求解sin(nθ/2)cos[(n+1)θ/2]。(www.61k.com)sinθ/2
【求解】用下面的语句可以直接证明题中的等式。
>>symsknt
F=symsum(cos(k*t),k,1,n)
F=
1/2*(cos(t)+1)/sin(t)*sin((n+1)*t)-1/2*cos((n+1)*t)-1/2
>>simple(F-sin(n*t/2)*cos((n+1)*t/2)/sin(t/2))
ans=
6试求出下面函数的Fourier正弦和余弦变换,并用Fourier正弦、余弦反变换对得出的结果进行处理,观察是否能还原成原始函数。
cosx2
①f(t)=e?tlnt,②f(x)=,③f(x)=sin(1+x)x
【求解】从下面的语句可以求出Fourier正弦、余弦变换,但由于算法的原因,很多函数的反变换是不能正确得出的。
>>symstw;f=exp(-t)*log(t);
F=maple(’fouriersin’,f,t,w)
F=
2^(1/2)/pi^(1/2)/(1+w^2)*(atan(w)-eulergamma*w-1/2*w*log(1+w^2))
>>f1=maple(’invfouriersin’,F,w,t)
f1=
invfouriersin(2^(1/2)/pi^(1/2)/(1+w^2)*
(atan(w)-eulergamma*w-1/2*w*log(1+w^2)),w,t)
>>F=maple(’fouriercos’,f,t,w)
F=
-2^(1/2)/pi^(1/2)/(1+w^2)*(eulergamma+1/2*log(1+w^2)+w*atan(w))
>>f1=maple(’invfouriercos’,F,w,t)
f1=
invfouriercos(-2^(1/2)/pi^(1/2)/(1+w^2)*
(eulergamma+1/2*log(1+w^2)+w*atan(w)),w,t)
>>symsxw;f=cos(x^2)/x;F=maple(’fouriersin’,f,x,w)
F=
1/2*2^(1/2)*pi^(1/2)*(2^(1/2)/pi^(1/2)*FresnelC(1/8*2^(1/2)*pi^(1/2)*w^2)+2^(1/2)/pi^(1/2)*FresnelS(1/8*2^(1/2)*pi^(1/2)*w^2))
>>f1=maple(’invfouriersin’,F,w,t)
f1=
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第5章积分变换与复变函数问题的计算机求解
invfouriersin(1/2*2^(1/2)*pi^(1/2)*(2^(1/2)/pi^(1/2)*
FresnelC(1/8*2^(1/2)*pi^(1/2)*w^2)+
2^(1/2)/pi^(1/2)*FresnelS(1/8*2^(1/2)*pi^(1/2)*w^2)),w,t)
>>symsxw;f=sin(1+x^2);F=maple(’fouriersin’,f,x,w)
F=
FresnelC(1/2*2^(1/2)/pi^(1/2)*w)*cos(1/4*w^2)*cos(1)+
FresnelC(1/2*2^(1/2)/pi^(1/2)*w)*sin(1/4*w^2)*sin(1)+
FresnelS(1/2*2^(1/2)/pi^(1/2)*w)*sin(1/4*w^2)*cos(1)-
FresnelS(1/2*2^(1/2)/pi^(1/2)*w)*cos(1/4*w^2)*sin(1)
>>f1=maple(’invfouriersin’,F,w,t)
7试求下面函数的离散Fourier正弦、余弦变换。(www.61k.com)
①f(x)=ekx②f(x)=x347
【求解】零散Fourier正弦、余弦变换可以由下面的积分表达式直接求出
??a??akptkptFs(k)=f(t)sindt,Fc(k)=f(t)cosdtaa00
利用MATLAB语言的符号运算工具箱,则可以给出下面的语句。
>>symskx;symsapositive;f=exp(k*x);
Fs=int(f*sin(k*sym(pi)*x/a),x,0,a)
Fs=
-a*(exp(a*k)*pi*cos(k*pi)-exp(a*k)*a*sin(k*pi)-pi)/k/(a^2+pi^2)
>>Fc=int(f*cos(k*sym(pi)*x/a),x,0,a)
Fc=
a*(exp(a*k)*a*cos(k*pi)+exp(a*k)*pi*sin(k*pi)-a)/k/(a^2+pi^2)
>>symsxk;symsapositive;f=x^3;
Fs=int(f*sin(k*sym(pi)*x/a),x,0,a)
Fs=
-a^4*(-6*cos(k*pi)*k*pi+6*sin(k*pi)+k^3*pi^3*cos(k*pi)-
3*k^2*pi^2*sin(k*pi))/k^4/pi^4
>>Fc=int(f*cos(k*sym(pi)*x/a),x,0,a)
Fc=
a^4*(-6*k*pi*sin(k*pi)-6*cos(k*pi)+k^3*pi^3*sin(k*pi)+
3*k^2*pi^2*cos(k*pi)+6)/k^4/pi^4
8试对下面的函数进行Mellin变换。??sin(alnx),x??1f(x)=0,其他x
【求解】对给定的分段函数利用heaviside()函数描述,则可以立即求解出该函数的Mellin变换,然而,Maple提供的Mellin反变换不能求出。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
48第5章积分变换与复变函数问题的计算机求解
>>symsxz;f=sin(a*log(x))*heaviside(1-x);
F=maple(’mellin’,f,x,z)
F=
-a/(a^2+z^2)
9请将下述时域序列函数f(kT)进行Z变换,并对结果进行反变换检验。[www.61k.com)
1①fa(kT)=cos(kaT),②fb(kT)=(kT)2e?akT,③fc(kT)=(akT?1+e?akT)a
?akT?bkT④fd(kT)=e?e,⑤fe(kT)=sin(αkT),⑥ff(kT)=1?e?akT(1+akT)
【求解】用ztrans()和iztrans()函数,可以立即得出下面各个函数的变换结果,通过反变换得出的结果完全可以还原出原函数。
>>symskaT;f=cos(k*a*T);F=ztrans(f)
F=
(z-cos(a*T))*z/(z^2-2*z*cos(a*T)+1)
>>f1=iztrans(F)
f1=
cos(a*T*n)
>>symskTa;f=(k*T)^2*exp(-a*k*T);F=ztrans(f)
F=
T^2*z*exp(-a*T)*(z+exp(-a*T))/(z-exp(-a*T))^3
>>f1=iztrans(F)
f1=
T^2*(1/exp(a*T))^n*n^2
>>symsakT;f=(a*k*T-1+exp(-a*k*T))/a;F=ztrans(f)
F=
1/a*(a*T*z/(z-1)^2-z/(z-1)+z/exp(-a*T)/(z/exp(-a*T)-1))
>>iztrans(F)
ans=
(a*T*n+(1/exp(a*T))^n-1)/a
>>symsabkT;f=exp(-a*k*T)-exp(-b*k*T);F=ztrans(f)
F=
z/exp(-a*T)/(z/exp(-a*T)-1)-z/exp(-b*T)/(z/exp(-b*T)-1)
>>iztrans(F)
ans=
(1/exp(a*T))^n-(1/exp(b*T))^n
>>symsakT;f=1-exp(-a*k*T)*(1+a*k*T);F=ztrans(f)
F=
z/(z-1)-z/exp(-a*T)/(z/exp(-a*T)-1)-a*T*z/exp(-a*T)/(z/exp(-a*T)-1)^2
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第5章积分变换与复变函数问题的计算机求解
>>iztrans(F)
ans=
1-(1/exp(a*T))^n-a*T*(1/exp(a*T))^n*n
10已知下述各个Z变换表达式F(z),试对它们分别进行Z反变换
10zz2z①Fa(z)=,②Fb(z)=,③Fc(z)=(z?1)(z?2)(z?0.8)(z?0.1)(z?a)(z?1)Az[zcosβ?cos(αT?β)]z?1(1?e?aT),⑤F(z)=④Fd(z)=e(1?z?1)(1?z?1e?aT)z2?2zcos(αT)+1
【求解】函数的Z变换及反变换可以由下面的语句直接求出。(www.61k.com]
>>symsz;F=10*z/((z-1)*(z-2));iztrans(F)
ans=
10*2^n-10
>>symsz;F=z^2/((z-0.8)*(z-0.1));iztrans(F)
ans=
8/7*(4/5)^n-1/7*(1/10)^n
>>symsza;F=z/((z-a)*(z-1)^2);iztrans(F)
ans=
(-n*a-1+n+a^n)/(-2*a+a^2+1)
>>symsaTz;F=z^(-1)*(1-exp(-a*T))/((1-z^(-1))*(1-z^(-1)*exp(-a*T)));iztrans(F)
ans=
1-(1/exp(a*T))^n
>>symsAzbaT;
F=A*z*(z*cos(b)-cos(a*T-b))/(z^2-2*z*cos(a*T)+1);
iztrans(F)
ans=
cos(b)*A*cos(a*T*n)-A*sin(a*T*n)*sin(b)
11已知某信号的Laplace变换为b,试求其Z变换,并验证结果。s2(s+a)
【求解】应该先对其进行Laplace反变换,再对结果进行Z变换。
>>symssab;F=b/(s^2*(s+a));
f=simple(ztrans(ilaplace(F)))
f=49
(a*z*exp(a)+z-z*exp(a)+exp(a)-a-1)*z*b/(z^2*exp(a)-z-z*exp(a)+1)/(z-1)/a^2其结果的数学形式为
???1??(azea+z?zea+ea?a?1)zbZL[F(s)]=b2a(ze?z?zea+1)(z?1)a2
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
50第5章积分变换与复变函数问题的计算机求解
若想对得出的结果进行检验,则可以对结果进行Z反变换,再对结果进行Laplace变换,观察是否能还原成原给出的函数,经过验证,可以看出得出的结果完全正确。[www.61k.com)
>>f1=simple(laplace(iztrans(f)))
f1=
b/s^2/(s+a)
????????az(Az+B)?akT12用计算机证明Z1?ecos(bkT)+sin(bkT)=,b(z?1)(z2?2e?aTcos(bT)z+e?2aT)
aa式中A=1?e?aTcos(bT)?e?aTsin(bT),B=e?2aT+e?aTsin(bT)?e?aTcos(bT)。bb
【求解】证明等号两边的差为零则可以证明等式,故可以用下面的语句证明该等式。
>>symsabkT;
f=1-exp(-a*k*T)*(cos(b*k*T)+a/b*sin(b*k*T));
F=ztrans(f)
F=
z/(z-1)-(z/exp(-a*T)-cos(b*T))*z/exp(-a*T)/(z^2/exp(-a*T)^2-
2*z/exp(-a*T)*cos(b*T)+1)-a/b*z/exp(-a*T)*sin(b*T)/(z^2/exp(-a*T)^2-
2*z/exp(-a*T)*cos(b*T)+1)
>>A=1-exp(-a*T)*cos(b*T)-a/b*exp(-a*T)*sin(b*T);
B=exp(-2*a*T)+a/b*exp(-a*T)*sin(b*T)-exp(-a*T)*cos(b*T);
R=(z*(A*z+B))/((z-1)*(z^2-2*exp(-a*T)*cos(b*T)*z+exp(-2*a*T)));
simple(F-R)
ans=
x2+4x+313试求出f(x)=e?5x的奇点、奇点重数及各个奇点处的留数。x+4x+3x+2x+5x+2
【求解】可以通过部分分式展开的方法得出不含有e?5x的函数为
>>symsx;F=(x^2+4*x+3)/(x^5+4*x^4+3*x^3+2*x^2+5*x+2);
F1=residue(F,x)
F1=
.36884528691474116546123212343386/(x+.45724164080327398113522153431736)+(-.22945647070219925912151734772687+.25494104062724336140044336717309*i)/(x-.42435341429491731455583339444997+.95306503142068537993544636676469*i)-(.22945647070219925912151734772687+.25494104062724336140044336717309*i)/(x-.42435341429491731455583339444997-.95306503142068537993544636676469*i)+.87010455388092257243752819445340e-1/(x+1.2999198059930349140607395655546)+.30571991015650955380497525745543e-2/(x+3.0915453817935257339157056890279)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第5章积分变换与复变函数问题的计算机求解51
可以得出该函数可以写成a/(x+b),这样b为奇点,ae?5b则为相应的留数,这样可以得出函数的奇点和留数在下表中给出。[www.61k.com]奇点
-.45724164080327398113522153431736
0.42435341429492±j0.95306503142069
-1.29991980599303
-3.09154538179353
14试求出下面有理函数的部分分式展开
G(s)=s+5
s+21s+181s+839s+2330s+4108s+4620s+3100s+1000留数0.03749355589649-0.03195888822474?j0.0258386112737657.851075189953751.579534887213670e+004
A并用LTEX的形式比较好地显示得出的结果。【求解】下面的语句可以直接求解本习题中的问题,并得出数学显示如下。
>>symss
F=(s+5)/(s^8+21*s^7+181*s^6+839*s^5+2330*s^4+4108*s^3+4620*s^2+3100*s+1000);f=residue(F,s)
f=
(-7/2312-23/2312*i)/(s+1+i)^2+(-517/39304+143/9826*i)/(s+1+i)+(-7/2312+23/2312*i)/(s+1-i)^2-(517/39304+143/9826*i)/(s+1-i)+1/36/(s+2)-1/867/(s+5)^2-65/44217/(s+5)
?235171437235171437?j?j?j+j???s+1+js+1?j(s+1+j)(s+1??)
1165+??36(s+2)867(s+5)44217(s+5)
15求下面的封闭环路积分。??z15
①dz,其中Γ为|z|=3正向圆周Γ(z?1)(z?2)??z31/z②edz,其中Γ为|z|=2正向圆周1+zΓ
【求解】
>>symsz;F=z^(15)/((z^2-1)^2*(z^4-2)^3);
residue(F,z);vpa(ans,10)
ans=
-.2500000000/(z-1.)^2-6.500000000/(z-1.)+.2500000000/(z+1.)^2-
6.500000000/(z+1.)-.7582521470e-2/(z+1.189207115*sqrt(-1))^3-
.5200904179e-1*sqrt(-1)/(z+1.189207115*sqrt(-1))^2+
.1412427894/(z+1.189207115*sqrt(-1))+.2575825204/(z-1.189207115)^3-
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
52第5章积分变换与复变函数问题的计算机求解
.6837753459/(z-1.189207115)^2+6.858756405/(z-1.189207115)-
.7582521470e-2/(z-1.189207115*sqrt(-1))^3+
.5200904179e-1*sqrt(-1)/(z-1.189207115*sqrt(-1))^2+
.1412427894/(z-1.189207115*sqrt(-1))+.2575825204/(z+1.189207115)^3+
.6837753459/(z+1.189207115)^2+6.858756405/(z+1.189207115)
>>symsz;F=z^3/(1+z)*exp(1/z);
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第6章代数方程与最优化问题的计算机求解1求解能转换成多项式方程的联立方程,并检验得出的高精度数值解的精度。[www.61k.com)????x2y2?zxy?4x2yz2=xz2??2x1?x2?1=0,②①xy3?2yz2=3x3z2+4xzy2
22?(x1?2)+(x2?0.5)?1=0??y2x?7xy2+3xz2=x4zy
【求解】①中给出的方程可以由下面的语句直接求解,经检验可见,精度是相当高的,达1030级。
>>[x1,x2]=solve(’x1^2-x2-1=0’,’(x1-2)^2+(x2-0.5)^2-1=0’,’x1,x2’)x1=
-1.3068444845633173592407431426632-1.2136904451605911320167045558746*sqrt(-1)-1.3068444845633173592407431426632+1.2136904451605911320167045558746*sqrt(-1)
1.0673460858066897134085973128070
1.5463428833199450050728889725194
x2=
-.76520198984055124633885565606586+3.1722093284506318231178646481143*sqrt(-1)-.76520198984055124633885565606586-3.1722093284506318231178646481143*sqrt(-1)
.13922766688686144048362498805141
1.3911763127942410521940863240803
>>norm(double([x1.^2-x2-1(x1-2).^2+(x2-0.5).^2-1]))
ans=
6.058152713871457e-031
现在考虑②中的方程,可以由下面的语句求解并检验精度。
>>[x,y,z]=solve(’x^2*y^2-z*x*y-4*x^2*y*z^2=x*z^2’,...
’x*y^3-2*y*z^2=3*x^3*z^2+4*x*z*y^2’,...
’y^2*x-7*x*y^2+3*x*z^2=x^4*z*y’,’x,y,z’)
x=
x
.31763330066708094899226744383315
-.57342208805666904699955413755046
-3.0414669315515393342891214860256
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
54第6章代数方程与最优化问题的计算机求解
1.2406494592172202024946761755143+2.6726341184257446950051342796237*sqrt(-1)
1.9395779085729820052691770221678-1.8460302354285923475099876321714*sqrt(-1)-.12175724403625789114277654158125+.76608643264311922968528253940276*sqrt(-1)-2.2119059377823750236571580666120-1.3098483298501442852199024916922*sqrt(-1).18091793647835958266865409918250-.43514167087309843831595260429068*sqrt(-1)-.55869174189107447600021216575845+2.3297622385407573613585339888001*sqrt(-1)
-.68680307411564099103394996937251
2.2449864792628313778324119367846
.80149155267622824623322517103811
-.55869174189107447600021216575845-2.3297622385407573613585339888001*sqrt(-1).18091793647835958266865409918250+.43514167087309843831595260429068*sqrt(-1)-2.2119059377823750236571580666120+1.3098483298501442852199024916922*sqrt(-1)-.12175724403625789114277654158125-.76608643264311922968528253940276*sqrt(-1)
1.9395779085729820052691770221678+1.8460302354285923475099876321714*sqrt(-1)
1.2406494592172202024946761755143-2.6726341184257446950051342796237*sqrt(-1)y=
y
-.10247418659393300993582067594235
.88186908582844666977541315922472
6.2206205278493911181266569143240
3.8883892104923440119866877297435+2.6775872796906346863164643745055*sqrt(-1)-.19521984362257729205542902543230+2.1755659889967168917621095367660*sqrt(-1).19300043308429639136627772430949+.55085821682149293523314538512818*sqrt(-1)-1.5345777137990494704652954417309+.42952982009383733582600047744276e-1*sqrt(-1).59285406023469299432404383306933e-1-.14560032849820344999561561093140*sqrt(-1)-.13504742647411551604956518296040-1.3353390289175827351921401819303*sqrt(-1)
.23206681025858886578639216095379
1.2500352093099975887186243233388
-.40877757806122608090142625675228
-.13504742647411551604956518296040+1.3353390289175827351921401819303*sqrt(-1).59285406023469299432404383306933e-1+.14560032849820344999561561093140*sqrt(-1)-1.5345777137990494704652954417309-.42952982009383733582600047744276e-1*sqrt(-1)
.19300043308429639136627772430949-.55085821682149293523314538512818*sqrt(-1)-.19521984362257729205542902543230-2.1755659889967168917621095367660*sqrt(-1)
3.8883892104923440119866877297435-2.6775872796906346863164643745055*sqrt(-1)z=
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第6章代数方程与最优化问题的计算机求解55
z
.14437409800864935567667171646044
1.2197465522537746902599296344473
1.2977198721910510602444950254432
1.0166830329716235095778013718903+.37011032131730244971789188681237*sqrt(-1).45233167057904744299654223927744+.51464117109451634939209195854989*sqrt(-1).31864673037377358785409663022781+.78415604801861425880017838557048*sqrt(-1).38457694363000428639271157033224e-1+.57967291207543468143911103709180*sqrt(-1)-.83830187383058822380943737709146e-1+.20866770020547056525334588752981*sqrt(-1)-.36349211548848392020797588683844+.46022200523351838974797619203293*sqrt(-1)
-.34096135567852262861343237947182
-.58923295037333858669309875602950
-.61423986723341834383214878861209
-.36349211548848392020797588683844-.46022200523351838974797619203293*sqrt(-1)-.83830187383058822380943737709146e-1-.20866770020547056525334588752981*sqrt(-1).38457694363000428639271157033224e-1-.57967291207543468143911103709180*sqrt(-1).31864673037377358785409663022781-.78415604801861425880017838557048*sqrt(-1).45233167057904744299654223927744-.51464117109451634939209195854989*sqrt(-1)1.0166830329716235095778013718903-.37011032131730244971789188681237*sqrt(-1)>>norm(double([x.^2.*y.^2-z.*x.*y-4*x.^2.*y.*z.^2-x.*z.^2,...
x.*y.^3-2*y.*z.^2-3*x.^3.*z.^2-4*x.*z.*y.^2,...
y.^2.*x-7*x.*y.^2+3*x.*z.^2-x.^4.*z.*y]))
ans=
3.493005633414428e-024
可见,除了前三组解之外,其余的解均是单个的,这样的解共有18组,另外(x,0,0)、(0,y,0)和(0,0,z)对任意的x,y,z均满足原始方程,故方程有无数根。(www.61k.com)
2试用图解法求解下面一元和二元方程,并验证得出的结果。
①f(x)=e?(x+1)2+p/2sin(5x+2),②f(x,y)=(x2+y2+xy)e?x2?y2?xy
【求解】①中给出的一元方程可以用曲线表示出来,这些曲线和y=0线的交点即为方程的解,可以用图形局部放大的方法读出这些交点的x值,如图6-1所示。在本图中,xi均为方程的解,若放大x轴区域,则可能得出更多的解。
>>ezplot(’exp(-(x+1)^2+pi/2)*sin(5*x+2)’)
②中的二元方程可以由下面的命令用图形的方式显示出来,如图6-2a所示。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
56第6章代数方程与最优化问题的计算机求解
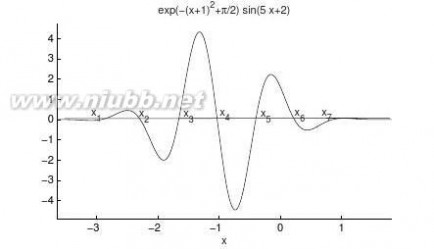
图6-1一元方程的图解法
>>ezsurf(’(x^2+y^2+x*y)*exp(-x^2-y^2-x*y)’)
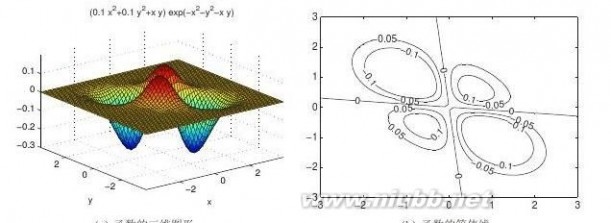
图6-2函数图形及方程求解
用下面的语句可以得出等高线,如图6-2b所示。(www.61k.com]为了比较起见,还绘制出其他值下的等高线。等高线值为0的两条斜线为方程的解。
>>[x,y]=meshgrid(-3:0.1:3);
z=(0.1*x.^2+0.1*y.^2+x.*y).*exp(-x.^2-y.^2-x.*y);[C,h]=contour(x,y,z,[-0.1:0.05:0.1]);set(h,’ShowText’,’on’)
3用数值求解函数求解上述的方程的根,并对得出的结果进行检验。
【求解】求解方程求解问题可以采用fsolve()和solve()函数直接求解,这里采用这两个函数分别求取这两个方程的根。
①可以用下面方法求出一元函数的根,经检验结果较精确。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第6章代数方程与最优化问题的计算机求解
>>symsx;x1=solve(’exp(-(x+1)^2+pi/2)*sin(5*x+2)’)
x1=
-2/5
>>subs(’exp(-(x+1)^2+pi/2)*sin(5*x+2)’,x,x1)
ans=
>>f=inline(’exp(-(x+1).^2+pi/2).*sin(5*x+2)’,’x’);
x2=fsolve(f,0)
x2=
0.22831852178755
>>subs(’exp(-(x+1)^2+pi/2)*sin(5*x+2)’,x,x2)
ans=
4.750949292642762e-008
>>x3=fsolve(f,-1)
x3=
-1.02831853071796
>>subs(’exp(-(x+1)^2+pi/2)*sin(5*x+2)’,x,x3)
ans=
-5.886413288211306e-016%选择不同的初值可以得出其他的解57
采用解析解函数solve()能求出精确的解,但只能求出其一个根,如果采用fsolve()函数则可以让用户自己选择初值,选择不同的初值可能得出不同的结果。[www.61k.com]在实际应用时这样的方法也有其问题,例如由图6-2a可见,若x大于1,则函数值本身就很小,很容易满足数值解的收敛条件,例如选择x0=4,则由数值解的程序能得出方程解为x0,事实上这样的解不是数学意义下的方程解,但确实能使得该函数的值趋于0。
>>x4=fsolve(f,4)
x4=
>>subs(’exp(-(x+1)^2+pi/2)*sin(5*x+2)’,x,x4)
ans=
-5.913350831018913e-013
②可以用下面的语句求解该函数,则可以得出方程的解,代入原方程则可以得出误差,可见误差为0,这样说明得出的解确实满足原方程。
>>symsx;y1=solve(’(x^2+y^2+x*y)*exp(-x^2-y^2-x*y)=0’,’y’)
y1=
(-1/2+1/2*i*3^(1/2))*x
(-1/2-1/2*i*3^(1/2))*x
>>y2=simple(subs(’(x^2+y^2+x*y)*exp(-x^2-y^2-x*y)’,’y’,y1))%选择大的初值得出的解不是严格意义下方程的根
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
58
y2=
4试求出使得
0第6章代数方程与最优化问题的计算机求解??1(ex?cx)dx取得极小值的c值。(www.61k.com]2
【求解】给定的函数可以积分,由MATLAB语句可以求出积分为
>>symsxc;y=int((exp(x)-c*x)^2,x,0,1)
y=
1/2*exp(1)^2+1/3*c^2-1/2-2*c
这样可以立即写出目标函数的MATLAB表示为
functiony=exc6ff(c)
y=1/2*exp(1)^2+1/3*c^2-1/2-2*c;
由下面的语句可以求解出使得积分值为最小时的c值,由下面的语句还可以绘制出不同c值
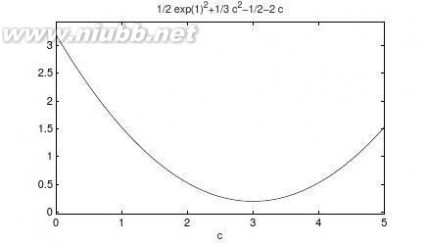
下的函数曲线,如图6-3所示,由此验证得出解的正确性。
>>x=fminsearch(’exc6ff’,0)
x=
3.00000000000000
>>ezplot(y,[0,5])
图6-3不同c值下的的积分值曲线
5试求解下面的无约束最优化问题。
22222100(x2?x21)+(1?x1)+90(x4?x3)+(1?x3)+min????x10.1(x2?1)2+(x4?1)2+19.8(x2?1)(x4?1)
【求解】无约束最优化问题可以由下面的语句直接求解,并得出所需结果。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第6章代数方程与最优化问题的计算机求解
>>f=inline([’100*(x(2)-x(1)^2)^2+(1-x(1))^2+’,...
’90*(x(4)-x(3)^2)+(1-x(3)^2)^2+’,...
’10.1*((x(2)-1)^2+(x(4)-1)^2)+’,...
’19.8*(x(2)-1)*(x(4)-1)’],’x’);
x=fminunc(f,ones(7,1))
x=
1.0e+002*
0.10546446798713
1.11232066767234
0.06782323911149
-1.11504746457726
0.01000000000000
0.01000000000000
0.0100000000000059
26考虑Rastrigin函数[25]f(x1,x2)=20+x21+x2?10(cospx1+cospx2),试用三维曲面绘制
该函数的函数值,选择初值求取该函数的最小值,并理解全局最优解和局部最优解的概念,及最优解对初值的依赖关系。(www.61k.com]
【求解】使用不同的处初值,本目标函数可能有不同的解,且对应的目标函数值可能有很大差异,其中大部分均为局部最优值。
>>y=inline(’20+x(1)^2+x(2)^2-10*(cos(pi*x(1))+cos(pi*x(2)))’,’x’);
x1=fminunc(y,[1;0])
x1=
1.0e-008*
-0.35249693804338
0.44265808885143
>>y(x1)
ans=
3.552713678800501e-015
>>x2=fminunc(y,[0;2])
x2=
-0.00000000596857
1.96017472106964
>>y(x2)
ans=
3.92045146143746
由下面的语句可以绘制出目标函数的三维曲面,如图6-4a所示,还可以得出该函数的等高线,如图6-4b所示。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
60
>>[x1,x2]=meshgrid(-3:0.1:3);第6章代数方程与最优化问题的计算机求解
z=20+x1.^2+x2.^2-10*(cos(pi*x1)+cos(pi*x2));
surf(x1,x2,z)
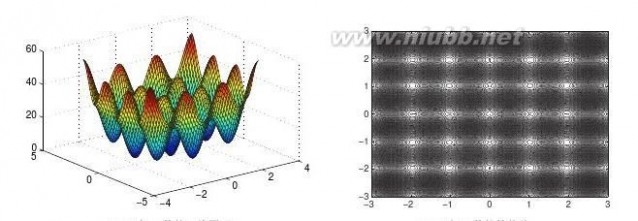
图6-4目标函数的图形表示
7试用图解法求解下面的非线性规划问题,并用数值求解算法验证结果。[www.61k.com)
min?2(x31+x2?4x1+4)
???x1?x2+2??0
xs.t.?x21+x2?1??0???x1??0,x2??0
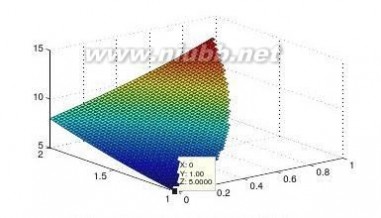
【求解】通过选择适当的区域(当然,这需要在较大范围内先观察一下最优点或可行区域,然后再较确切地选择合适的区域),这样就可以可以绘制出如图6-5所示的曲面表示,在曲面绘制中先选择整个矩形区域,然后将不满足约束条件的区域剪切掉。从得出的目标函数曲面看,x=0,y=1处为全局最小点。
>>[x1,x2]=meshgrid(0:0.02:1,1:0.02:2);
z=x1.^3+x2.^2+4*x1+4;
ii=find(x1-x2+2<0);z(ii)=NaN;
ii=find(-x1.^2+x2-1<0);z(ii)=NaN;
ii=find(x1<0);
surf(x1,x2,z)
下面的语句可以用数值方法求解
function[c,ce]=exc6f4(x)
ce=[];
c=[x(1)^2-x(2)+1];z(ii)=NaN;ii=find(x2<0);z(ii)=NaN;
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第6章代数方程与最优化问题的计算机求解61
>>f_opt=inline(’x(1)^3+x(2)^2+4*x(1)+4’,’x’);
A=[-11];B=2;Aeq=[];Beq=[];xm=[0;0];
x=fmincon(f_opt,[0;1],A,B,Aeq,Beq,xm,[],’exc6f4’);
8试求解下面的线性规划问题。(www.61k.com]
①?3x1+4x2min??4x1?x2+2x3?x4=?2?????x+x?x+2x??141234xs.t.?2x1?3x2?x3?x4???2?????x1,2,3???1,x4无约束
max??2x3+5x4②x6+x7?min?x1+x2+x3+x4=4??????2x+x?x?x+x=112367xs.t.?3x2+x3+x5+x7=9?????x1,2,···,7??0③2800(x11+x21+x31+x41)
?x11+x12+x13+x14??15????????x12+x13+x14+x21+x22+x23??10
xs.t.x13+x14+x22+x23+x31+x32??20?????x14+x23+x32+x41??12????x??0,(i=1,2,3,4,j=1,2,3,4)ij+4500(x12+x22+x32)+6000(x13+x23)+7300x14
【求解】①先将不等式约束统一变换成??关系,这样原问题的解可以由下面的语句直接得出原线性规划问题的解为
>>f=[-34-25];
Aeq=[4-12-1];Beq=-2;
A=[11-12;-2311];B=[14;2];xm=[-1;-1;-1;-inf];
x=linprog(f,A,B,Aeq,Beq,xm)
Optimizationterminatedsuccessfully.
x=
-0.99999999999422
2.49999999985070
-0.99999999999055
-6.49999999980869
②用下面的语句可以求解出线性规划问题
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
62
>>f=[0,0,0,0,0,1,1];第6章代数方程与最优化问题的计算机求解
Aeq=[1111000;-21-100-11;0310101];Beq=[4;1;9];xm=[0;0;0;0;0;0;0];A=[];B=[];x=linprog(f,A,B,Aeq,Beq,xm)
Optimizationterminatedsuccessfully.
x=
0.39517811869632
2.32126957607183
0.53091333867908
0.75263896655277
1.50527793310533
0.00000000000020
0.00000000000008
③应该重新选定变量,令x1=x11,x2=x12,x3=x13,x4=x14,x5=x21,x6=x22,x7=x23,x8=x31,x9=x32,x10=x41,这样可以将原问题改写成
2800(x1+x5+x8+x10)
??(x1+x2+x3+x4)???15?????????(x2+x3+x4+x5+x6+x7)???10
xs.t.?(x3+x4+x6+x7+x8+x9)???20?????(x4+x7+x9+x10)???12?????x??0,(i=1,2,3,4,j=1,2,3,4)min?ij+4500(x2+x6+x9)+6000(x3+x7)+7300x4
这样就可以用下面的语句解出问题的最优解。(www.61k.com)
>>f=2800*[1000100101]+...
4500*[0100010010]+...
6000*[0010001000]+...
7300*[0001000000];
A=-[1111000000;
0111111000;
0011011110;
0001001011];
B=-[15;10;20;12];
xm=[0000000000];Aeq=[];Beq=[];
x=linprog(f,A,B,Aeq,Beq,xm)
x=
4.20692336952143
0.00000005346043
0.00000022615003
10.79307638057559
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第6章代数方程与最优化问题的计算机求解
0.00000003042569
0.00000005085698
0.00000005499777
7.99999980262819
1.20692351450631
0.00000010137137
9试求解下面的二次型规划问题,并用图示的形式解释结果。(www.61k.com)①
???x1+x2??3
xs.t.4x1+x2??9???x1,2??063min?22x21?4x1x2+4x2?6x1?3x2②????x1+x2=1xs.t.x1+x2??2???x1,2??0min?(x1?1)2+(x2?2)2
【求解】①可以由目标函数写出二次型规划的H和f矩阵为
????4?4H=,f=[?6,?3]?48
这样由二次型规划求解函数可以直接解出该最优化问题的解。>>H=[4-4;-48];f=[-6-3];
Aeq=[];Beq=[];A=[11;41];B=[3;9];xm=[0;0];x=quadprog(H,f,A,B,Aeq,Beq,xm)
x=
1.95000000000000
1.05000000000000
②展开目标函数,则可以得出
????20H=,f=[?2,?4]02
这样则可以由下面的语句得出最优化问题的解。
>>H=diag([22]);f=[-2-4];
Aeq=[-11];Beq=1;A=[11];B=2;xm=[0;0];x=quadprog(H,f,A,B,Aeq,Beq,xm)
x=
0.50000000000000
1.50000000000000
10试求解下面的非线性规划问题。
①ex1(4x21?min
?x+x??0?12?????xx+x+x??1.51212xs.t.??x1x2???10?????10??x1,x2??10+2x22+4x1x2+2x2+1)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
64
②max第6章代数方程与最优化问题的计算机求解????????31.51x1x2(1+x5)+x3x41+2cosx6x5?33?0.003079x31x2x5?cosx6??0????323?0.1017x3?3x4?x5cosx6??0???232????0.09939(1+x5)x1x2?cosx6??0
222xs.t.0.1076(31.5+x5)x33x4?x5cosx6??0????x3x4(x5+31.5)?x5[2(x1+5)cosx6+x1x2x5]??0??????0.2??x1??0.5,14<??x2??22,0.35??x3??0.6,????16??x4??22,5.8??x5??6.5,0.14??x6??0.2618【求解】①可以用下面的语句描述目标函数
functiony=exc6fun6(x)
y=exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1);
也可以写出约束函数
function[c,ce]=exc6fun6a(x)
ce=[];
c=[x(1)+x(2);x(1)*x(2)-x(1)-x(2)+1.5;-10-x(1)*x(2)];
这时调用非线性最优化问题求解函数可以得出如下结果。(www.61k.com]
>>A=[];B=[];Aeq=[];Beq=[];xm=[-10;-10];xM=[10;10];
x0=(xm+xM)/2;
ff=optimset;ff.TolX=1e-10;ff.TolFun=1e-20;
x=fmincon(’exc6fun6’,x0,A,B,Aeq,Beq,xm,xM,’exc6fun6a’,ff)
Maximumnumberoffunctionevaluationsexceeded;
increaseOPTIONS.MaxFunEvals
x=
0.41947326053910
0.41947326053910
从得出的提示看,该结果并非原问题的解,所以考虑用得出的最优解代入作为初值再求解,如此可以利用循环,则可以得出原问题的最优解。
>>i=1;x=x0;
while(1)
[x,a,b]=fmincon(’exc6fun6’,x,A,B,Aeq,Beq,xm,xM,’exc6fun6a’,ff);
ifb>0,break;end
i=i+1;
end
x,i
x=
1.18249727581645%循环次数为5
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第6章代数方程与最优化问题的计算机求解
-1.73976692398900
i=
5
②可以写出约束函数为
function[c,ce]=exc6fun5a(x)
ce=[];
c=[-0.003079*x(1)^3*x(2)^3*x(5)+cos(x(6))^3;
-0.1017*x(3)^3*x(4)^3+x(5)^2*cos(x(6)))^3;
-0.09939*(1+x(5))*x(1)^3*x(2)^2+cos(x(6))^2;
-0.1076*(31.5+x(5))*x(3)^3*x(4)^2+x(5)^2*cos(x(6))^2;
-x(3)*x(4)*(x(5)+31.5)+x(5)*(2*(x(1)+5)*cos(x(6))+x(1)*x(2)*x(5))];目标函数可以写成
functiony=exc6fun5(x)
y=1/(2*cos(x(6)))*(x(1)*x(2)*(1+x(5))+x(3)*x(4)*(1+31.5/x(5)));这样,由下面的语句可以得出最优化问题的解为
>>xm=[0.2;14;0.35;16;5.8;0.14];
xM=[0.5;22;0.6;22;6.5;0.2618];
A=[];B=[];Aeq=[];Beq=[];x0=(xm+xM)/2;
ff=optimset;ff.TolX=1e-10;ff.TolFun=1e-20;
x=fmincon(’exc6fun5’,x0,A,B,Aeq,Beq,xm,xM,’exc6fun5a’,ff)x=
0.20124417463214
18.36290007737820
0.35957532400838
18.57799951563967
5.80000000000000
0.26179905972118
其实设x?6=cosx6,则可能简化原最优化问题的求解。(www.61k.com)
11求解下面的整数线性规划问题。
①
xs.t.65max??x??0(592x1+381x2+273x3+55x4+48x5+37x6+23x7)
?3534x1+2356x2+1767x3+589x4+528x5+451x6+304x7??119567
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
66
②?x1+x2+x3=30??????x4+x5+x6=18?????x+x=1014xs.t.??x2+x5??18?????x3+x6??30????x1,···,6??0第6章代数方程与最优化问题的计算机求解max(120x1+66x2+72x3+58x4+132x5+104x6)
【求解】①整数规划问题用下面两种方法可以得出相同的结果。(www.61k.com]
>>f=-[59238127355483723];
A=[353423561767589528451304];B=119567;
intlist=[1;1;1;1;1;1;1];ctype=-1;
xm=zeros(7,1);xM=inf*ones(7,1);
[res,b]=ipslv_mex(f,A,B,intlist,xM,xm,ctype)
res=
32
2
1
b=
>>A=[3534,2356,1767,589,528,451,304];B=119567;
intlist=ones(7,1);Aeq=[];Beq=[];
xm=zeros(7,1);xM=20000*ones(7,1);x0=xM;
[errmsg,f,x]=bnb20(’exc6fun2’,x0,intlist,xm,xM,A,B,Aeq,Beq);iflength(errmsg)==0,x=round(x),end
x=
32
2
1
其中目标函数为
functiony=exc6fun2(x)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第6章代数方程与最优化问题的计算机求解
y=-(592*x(1)+381*x(2)+273*x(3)+55*x(4)+48*x(5)+37*x(6)+23*x(7));②此题中整数规划的解可以通过以下两种方法得出
>>f=[120667258132104];
A=[111000;000111;100100;010010;001001];B=[30;18;10;18;30];intlist=[1;1;1;1;1];
ctype=[0;0;0;-1;1];xm=zeros(5,1);xM=inf*ones(5,1);
[res,b]=ipslv_mex(f,A,B,intlist,xM,xm,ctype);res
res=
8
22
10
8
>>Aeq=[111000;000111;100100];Beq=[30;18;10];A=[010010;00-100-1];B=[18;-30];
intlist=ones(6,1);xm=zeros(6,1);xM=20000*ones(6,1);x0=xm;
[errmsg,f,x]=bnb20(’exc6fun3’,x0,intlist,xm,xM,A,B,Aeq,Beq);iflength(errmsg)==0,x=round(x),end
x=
8
22
10
8
其中目标函数可以描述为
functiony=exc6fun3(x)
y=[120667258132104]*x;
12试求解下面的0-1线性规划问题,并对①、②题用穷举方法检验得出的结果。(www.61k.com]①x1?x2+5x3+x4?4x5??2??????2x+6x?3x?2x+2x??012345xs.t.???2x2+2x3?x4?x5??1????0??xi??167min??(5x1+7x2+10x3+3x4+x5)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
68
②min??第6章代数方程与最优化问题的计算机求解(?3x1?4x2?5x3+4x4+4x5+2x6)
xs.t.?4975110?x③10500??????????600?45085150659530017004025200025002501650850000100?x??6003020125580253573121515405101012109020604050364940191502250727014148310042255101188047924355288511748455046504407503080061549033037201950???0??xi??1x1?x6??0?????x1?x5??0????????x2?x4??0xs.t.x2?x5??0????x3?x4??0??????x1+x2+x3??2????0??xi??1?1898440?1160max560
③说明,目标函数中的系数实际上是行向量,由于排版原因只能这样表示。(www.61k.com)
【求解】①中的问题可以由下面语句直接求解
>>f=[571035];B=[2;0;1];ctype=[1;1;-1];
A=[1-151-4;-26-3-22;0-22-1-1];
intlist=[1;1;1;1;1];xM=intlist;xm=zeros(5,1);
[res,b]=ipslv_mex(f,A,B,intlist,xM,xm,ctype);res’
ans=
01100
用下面的语句利用MATLAB7.0提供的新函数可以得出如下结果,该结果与前面方法得出的结果是完全一致的。
>>f=[571035];B=[-2;0;1];
A=[-11-5-14;2-632-2;0-22-1-1];
x=bintprog(f,A,B,[],[])’
x=
01100
利用穷举法可以验证上面的结果是正确的。
>>[x1,x2,x3,x4,x5]=ndgrid([0,1]);
i=find((x1-x2+5*x3+x4-4*x5>=2)&(-2*x1+6*x2-3*x3-2*x4+2*x5>=0)&...
(-2*x2+2*x3-x4-x5<=1));
f=5*x1(i)+7*x2(i)+10*x3(i)+3*x4(i)+x5(i);[fmin,ii]=sort(f);fmin’
ans=
17202226
>>index=i(ii(1));
x=[x1(index),x2(index),x3(index),x4(index),x5(index)]
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第6章代数方程与最优化问题的计算机求解
x=
0110069
②中的的最优化问题由下面的函数可以直接求解
>>A=[10000-1;1000-10;010-100;
0100-10;001-100;111000];
B=[0;0;0;0;0;2];c=[-3-4-5442];
intlist=ones(1,6);xM=intlist;xm=zeros(1,28);ctype=[-1;-1;-1;-1;-1];
[res,b]=ipslv_mex(c,A,B,intlist,xM,xm,ctype);res’
ans=
011110
用MATLAB7.0提供的0-1整数规划求解函数可以得出如下结果。[www.61k.com)
>>A=[10000-1;1000-10;010-100;
0100-10;001-100;111000];
B=[0;0;0;0;0;2];c=[-3-4-5442];
x=bintprog(c,A,B,[],[])’
x=
001100
比较两种方法得出的结果可见,二者是不相同的,可以用下面的语句分别求出二者的函数值>>[c*x’,c*res]
ans=
-1-1
可见二者都将得出?1,故两种方法得出的结果都是原函数的最优解。该问题是否还有其他的解析解呢?对简单的问题可以采用穷举法进行求解,并可以得出如下结果
>>[x1,x2,x3,x4,x5,x6]=ndgrid([0,1]);
i=find((x1-x6<=0)&(x1-x5<=0)&(x2-x4<=0)&(x2-x5<=0)&...
(x3-x4<=0)&(x1+x2+x3<=2));
f=-3*x1(i)-4*x2(i)-5*x3(i)+4*x4(i)+4*x5(i)+2*x6(i);[fmin,ii]=sort(f);fmin(1:5)’
ans=
-1-1011
可见,前两个函数值为?1,故该问题只有两个最优值,该两个最优值即用前面两种方法分别得出的解。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
70
>>index=i(ii(1:2));第6章代数方程与最优化问题的计算机求解
x=[x1(index),x2(index),x3(index),x4(index),x5(index),x6(index)]x=
00111110100
③由线性整数规划求解函数ipslvmex()可以求出问题的解为
>>A=[45,0,85,150,65,95,30,0,170,0,40,25,20,...
0,0,25,0,0,25,0,165,0,85,0,0,0,0,100;
30,20,125,5,80,25,35,73,12,15,15,40,5,...
10,10,12,10,9,0,20,60,40,50,36,49,40,19,150];
B=[600;600];
c=-[1898,440,22507,270,14148,3100,4650,30800,615,4975,1160,4225,510,...
11880,479,440,490,330,110,560,24355,2885,11748,4550,750,...
3720,1950,10500];
intlist=ones(1,28);xM=intlist;xm=zeros(1,28);ctype=[-1;-1];
[res,b]=ipslv_mex(c,A,B,intlist,xM,xm,ctype);res’
ans=
0010111101011100001010110100
若采用MATLAB7.0提供的bintprog()函数也可以得出相同的结果。(www.61k.com]
>>x=bintprog(c,A,B);x’
ans=
0010111101011100001010110100
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第7章微分方程问题的计算机求解
1试求出下面线性微分方程的通解。(www.61k.com)
??????d5y(t)d4y(t)d3y(t)d2y(t)dy(t)p???2t+13+64+152+176+80y(t)=esin2t++cos(3t)dt5dt4dt3dt2dt3
假设上述微分方程满足已知条件y(0)=1,y(1)=3,y(p)=2,y˙(0)=1,y˙(1)=2,试求出满足该条件的微分方程解析解。
【求解】先定义t为符号变量,求出等号右侧的函数,则可以由下面命令求出方程的解析解,解的规模较大,经常能占数页。
>>symst
exp(-2*t)*(sin(2*t+sym(pi)/3)+cos(3*t))
ans=
exp(-2*t)*(sin(2*t+1/3*pi)+cos(3*t))
>>y=dsolve([’D5y+13*D4y+64*D3y+152*D2y+176*Dy+80*y=’,...
’exp(-2*t)*(sin(2*t+1/3*pi)+cos(3*t))’],’y(0)=1’,’y(1)=3’,’y(pi)=2’,...’Dy(0)=1’,’Dy(1)=2’)
y=
1/486*exp(-2*t)*cos(3*t)+(3/416*exp(-2*t)+1/208*3^(1/2)*exp(-2*t))*sin(2*t)+(-1/208*exp(-2*t)+3/416*3^(1/2)*exp(-2*t))*cos(2*t)+1/72*exp(-2*t)*t^2+
5/432*exp(-2*t)*t+1/72*exp(-2*t)*t*3^(1/2)-1/72*exp(-2*t)*t^3-5/1296*exp(-2*t)-1/48*exp(-2*t)*t^2*3^(1/2)+5/864*3^(1/2)*exp(-2*t)+1/486*exp(-2*t)*sin(3*t)-1/50544*(-101088*pi^3*exp(3*pi+5)+604407*pi^2*exp(3*pi+3)-303225*pi*exp(3*pi+3)+101088*exp(5*pi+3)-50878*exp(3)+2916*pi^2*sin(1)^2*exp(3*pi+3)-
2496*pi^2*sin(1)^3*exp(3*pi+3)+1872*pi^2*sin(1)*exp(3*pi+3)+
2080*pi^3*sin(1)^3*exp(3*pi+3)-1560*pi^3*sin(1)*exp(3*pi+3)-
2430*pi^3*sin(1)^2*exp(3*pi+3)+104*pi^3*cos(1)*exp(3*pi+3)+
305268*pi^2*exp(3*pi)+542*exp(3*pi+3)-301620*pi^3*exp(3*pi+3)-
50544*pi^2*exp(3*pi+5)-254390*pi^3*exp(3*pi)+
2916*pi^2*sin(1)*cos(1)*3^(1/2)*exp(3*pi+3)-3942*pi^2*3^(1/2)*exp(3*pi)+1215*pi^2*sin(1)*cos(1)*exp(3*pi+3)-1215*pi^2*3^(1/2)*sin(1)^2*exp(3*pi+3)+486*pi^3*3^(1/2)*sin(1)^2*exp(3*pi+3)-486*pi^3*sin(1)*cos(1)*exp(3*pi+3)-
416*pi^3*cos(1)*sin(1)^2*exp(3*pi+3)+657*3^(1/2)*exp(3)-657*3^(1/2)*exp(3*pi+3)+2457*pi*3^(1/2)*exp(3*pi+3)-2430*pi^3*sin(1)*cos(1)*3^(1/2)*exp(3*pi+3)+3285*pi^3*exp(3*pi)*3^(1/2)-3429*pi^2*3^(1/2)*exp(3*pi+3)+
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
72第7章微分方程问题的计算机求解
1629*pi^3*3^(1/2)*exp(3*pi+3))/(3*pi*exp(3*pi+3)+pi^3*exp(3*pi+3)+
5*pi^3*exp(3*pi)+exp(3)-3*pi^2*exp(3*pi+3)-6*pi^2*exp(3*pi)-
exp(3*pi+3))*exp(-2*t)-1/50544*(-1215*pi^2*sin(1)*cos(1)*exp(3*pi+3)+
1215*pi^2*3^(1/2)*sin(1)^2*exp(3*pi+3)-486*pi*3^(1/2)*exp(3*pi+3)+
1458*pi^2*3^(1/2)*exp(3*pi+3)-486*pi^3*3^(1/2)*sin(1)^2*exp(3*pi+3)+
486*pi^3*sin(1)*cos(1)*exp(3*pi+3)+416*pi^3*cos(1)*sin(1)^2*exp(3*pi+3)-
2080*pi^3*sin(1)^3*exp(3*pi+3)+1560*pi^3*sin(1)*exp(3*pi+3)+
2430*pi^3*sin(1)^2*exp(3*pi+3)-104*pi^3*cos(1)*exp(3*pi+3)-
101088*exp(5*pi+3)+101088*pi^3*exp(3*pi+5)+50336*exp(3*pi+3)-
451773*pi^2*exp(3*pi+3)+150591*pi*exp(3*pi+3)+250742*pi^3*exp(3*pi+3)+
50544*pi^2*exp(3*pi+5)+2430*pi^3*sin(1)*cos(1)*3^(1/2)*exp(3*pi+3)-
972*pi^3*3^(1/2)*exp(3*pi+3)-2916*pi^2*sin(1)*cos(1)*3^(1/2)*exp(3*pi+3)-2916*pi^2*sin(1)^2*exp(3*pi+3)+2496*pi^2*sin(1)^3*exp(3*pi+3)-
1872*pi^2*sin(1)*exp(3*pi+3))/(3*pi*exp(3*pi+3)+pi^3*exp(3*pi+3)+
5*pi^3*exp(3*pi)+exp(3)-3*pi^2*exp(3*pi+3)-6*pi^2*exp(3*pi)-exp(3*pi+3))*exp(-5*t)+1/50544*(-302559*pi^2*exp(3*pi+3)+603741*pi*exp(3*pi+3)-101088*exp(3*pi+5)+
101088*exp(5*pi+3)+251444*exp(3)-251680*exp(3*pi)-4374*pi^2*sin(1)^2*exp(3*pi+3)-6240*sin(1)^3*pi*exp(3*pi+3)+312*cos(1)*pi^2*exp(3*pi+3)-
416*cos(1)*sin(1)^2*exp(3*pi+3)+486*sin(1)*cos(1)*exp(3)+
416*cos(1)*sin(1)^2*exp(3)+3744*pi^2*sin(1)^3*exp(3*pi+3)-
486*sin(1)*cos(1)*exp(3*pi+3)-2808*pi^2*sin(1)*exp(3*pi+3)-
312*cos(1)*pi*exp(3*pi+3)+4680*sin(1)*pi*exp(3*pi+3)+
7290*sin(1)^2*pi*exp(3*pi+3)-486*3^(1/2)*sin(1)^2*exp(3)+
486*3^(1/2)*sin(1)^2*exp(3*pi+3)+750201*pi^2*exp(3*pi)-
301780*exp(3*pi+3)+702*pi^3*exp(3*pi+3)-353808*pi^2*exp(3*pi+5)-
1560*sin(1)*exp(3*pi+3)-2430*sin(1)^2*exp(3*pi+3)+2430*sin(1)^2*exp(3)+
3510*pi^3*exp(3*pi)-859248*pi^2*exp(3*pi+2)+2080*sin(1)^3*exp(3*pi+3)-
4374*pi^2*sin(1)*cos(1)*3^(1/2)*exp(3*pi+3)-1458*pi^2*3^(1/2)*exp(3*pi)-
243*pi^2*sin(1)*cos(1)*exp(3*pi+3)+243*pi^2*3^(1/2)*sin(1)^2*exp(3*pi+3)+
303264*pi*exp(3*pi+5)+505440*exp(5*pi)-972*3^(1/2)*exp(3)+972*3^(1/2)*exp(3*pi+3)+2430*pi*3^(1/2)*exp(3*pi)+624*cos(1)*pi^2*exp(3*pi)-2430*pi*3^(1/2)*exp(3*pi+3)-2080*sin(1)^3*exp(3)-752955*pi*exp(3*pi)-104*cos(1)*exp(3)+
7290*sin(1)*cos(1)*3^(1/2)*pi*exp(3*pi+3)+1560*sin(1)*exp(3)+
1458*sin(1)*cos(1)*pi*exp(3*pi+3)+2430*sin(1)*cos(1)*3^(1/2)*exp(3)-
2430*sin(1)*cos(1)*3^(1/2)*exp(3*pi+3)-1458*3^(1/2)*sin(1)^2*pi*exp(3*pi+3)-3159*pi^2*exp(3*pi)*3^(1/2)*sin(1)^2+1248*cos(1)*sin(1)^2*pi*exp(3*pi+3)+3159*pi^2*exp(3*pi)*sin(1)*cos(1)-2496*cos(1)*sin(1)^2*pi^2*exp(3*pi)-
1248*cos(1)*sin(1)^2*pi^2*exp(3*pi+3)+101088*exp(5)+1458*pi^2*3^(1/2)*exp(3*pi+3)+
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第7章微分方程问题的计算机求解73
104*cos(1)*exp(3*pi+3))/(3*pi*exp(3*pi+3)+pi^3*exp(3*pi+3)+5*pi^3*exp(3*pi)+exp(3)-3*pi^2*exp(3*pi+3)-6*pi^2*exp(3*pi)-exp(3*pi+3))*exp(-2*t)*t^3+
1/16848*(117936*pi^3*exp(3*pi+5)+702*pi^2*exp(3*pi+3)-301884*pi*exp(3*pi+3)-
16848*exp(3*pi+5)-101088*exp(5*pi+3)-150825*exp(3)+100672*exp(3*pi)+
2496*sin(1)^3*pi*exp(3*pi+3)-405*sin(1)*cos(1)*exp(3)+405*sin(1)*cos(1)*exp(3*pi+3)-1872*sin(1)*pi*exp(3*pi+3)-2916*sin(1)^2*pi*exp(3*pi+3)+405*3^(1/2)*sin(1)^2*exp(3)-405*3^(1/2)*sin(1)^2*exp(3*pi+3)-1248*pi^3*sin(1)^3*exp(3*pi+3)+
936*pi^3*sin(1)*exp(3*pi+3)+1458*pi^3*sin(1)^2*exp(3*pi+3)-104*pi^3*cos(1)*exp(3*pi+3)-208*pi^3*exp(3*pi)*cos(1)+1404*pi^2*exp(3*pi)+201161*exp(3*pi+3)+99917*pi^3*exp(3*pi+3)+624*sin(1)*exp(3*pi+3)+972*sin(1)^2*exp(3*pi+3)-972*sin(1)^2*exp(3)+
286416*pi^3*exp(3*pi+2)-252641*pi^3*exp(3*pi)-832*sin(1)^3*exp(3*pi+3)-
2106*pi^2*3^(1/2)*exp(3*pi)-81*pi^3*3^(1/2)*sin(1)^2*exp(3*pi+3)+
81*pi^3*sin(1)*cos(1)*exp(3*pi+3)+416*pi^3*cos(1)*sin(1)^2*exp(3*pi+3)+
1053*pi^3*exp(3*pi)*3^(1/2)*sin(1)^2+832*pi^3*exp(3*pi)*cos(1)*sin(1)^2-
1053*pi^3*exp(3*pi)*sin(1)*cos(1)+50544*pi*exp(3*pi+5)-202176*exp(5*pi)+
837*3^(1/2)*exp(3)-837*3^(1/2)*exp(3*pi+3)-972*pi*3^(1/2)*exp(3*pi)+
2025*pi*3^(1/2)*exp(3*pi+3)+832*sin(1)^3*exp(3)+301182*pi*exp(3*pi)-
2916*sin(1)*cos(1)*3^(1/2)*pi*exp(3*pi+3)+1458*pi^3*sin(1)*cos(1)*3^(1/2)*exp(3*pi+3)-624*sin(1)*exp(3)-1215*sin(1)*cos(1)*pi*exp(3*pi+3)-972*sin(1)*cos(1)*3^(1/2)*exp(3)+972*sin(1)*cos(1)*3^(1/2)*exp(3*pi+3)+1215*3^(1/2)*sin(1)^2*pi*exp(3*pi+3)+16848*exp(5)+2241*pi^3*exp(3*pi)*3^(1/2)-1053*pi^2*3^(1/2)*exp(3*pi+3)-
135*pi^3*3^(1/2)*exp(3*pi+3))/(3*pi*exp(3*pi+3)+pi^3*exp(3*pi+3)+
5*pi^3*exp(3*pi)+exp(3)-3*pi^2*exp(3*pi+3)-6*pi^2*exp(3*pi)-exp(3*pi+3))*exp(-2*t)*t^2-1/16848*(101088*pi^3*exp(3*pi+5)-301767*pi^2*exp(3*pi+3)+585*pi*exp(3*pi+3)-
101088*exp(5*pi+3)-50002*exp(3)-
2916*pi^2*sin(1)^2*exp(3*pi+3)+2496*pi^2*sin(1)^3*exp(3*pi+3)-
1872*pi^2*sin(1)*exp(3*pi+3)-2080*pi^3*sin(1)^3*exp(3*pi+3)+
1560*pi^3*sin(1)*exp(3*pi+3)+2430*pi^3*sin(1)^2*exp(3*pi+3)-
104*pi^3*cos(1)*exp(3*pi+3)+300012*pi^2*exp(3*pi)+100338*exp(3*pi+3)+
200740*pi^3*exp(3*pi+3)+50544*pi^2*exp(3*pi+5)-250010*pi^3*exp(3*pi)-
2916*pi^2*sin(1)*cos(1)*3^(1/2)*exp(3*pi+3)-2376*pi^2*3^(1/2)*exp(3*pi)-
1215*pi^2*sin(1)*cos(1)*exp(3*pi+3)+1215*pi^2*3^(1/2)*sin(1)^2*exp(3*pi+3)-
486*pi^3*3^(1/2)*sin(1)^2*exp(3*pi+3)+486*pi^3*sin(1)*cos(1)*exp(3*pi+3)+
416*pi^3*cos(1)*sin(1)^2*exp(3*pi+3)+396*3^(1/2)*exp(3)-396*3^(1/2)*exp(3*pi+3)+702*pi*3^(1/2)*exp(3*pi+3)+2430*pi^3*sin(1)*cos(1)*3^(1/2)*exp(3*pi+3)+
1980*pi^3*exp(3*pi)*3^(1/2)+270*pi^2*3^(1/2)*exp(3*pi+3)-
576*pi^3*3^(1/2)*exp(3*pi+3))/(3*pi*exp(3*pi+3)+pi^3*exp(3*pi+3)+
5*pi^3*exp(3*pi)+exp(3)-3*pi^2*exp(3*pi+3)-6*pi^2*exp(3*pi)-exp(3*pi+3))*exp(-2*t)*t
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
74第7章微分方程问题的计算机求解
事实上,仔细阅读求出的解析解就会发现,其中大部分表达式是关于系数的,所以如果能对系数进行近似则将大大减小解的复杂度。[www.61k.com)
>>vpa(y)
ans=
.20576131687242798353909465020576e-2*exp(-2.*t)*cos(3.*t)+
.15538705805619602372728107411086e-1*exp(-2.*t)*sin(2.*t)+
.76830587084294035590921611166287e-2*exp(-2.*t)*cos(2.*t)-
106.24422608844727797303237726774*exp(-2.*t)*t^2+
98.159206062620455331994871615083*exp(-2.*t)*t+
59.405044899367325888329709780356*exp(-2.*t)*t^3-
30.741892776456442808809983330755*exp(-2.*t)+
.20576131687242798353909465020576e-2*exp(-2.*t)*sin(3.*t)+
31.732152104579289125415500223136*exp(-5.*t)
2试求解下面微分方程的通解及满足x(0)=1,x(p)=2,y(0)=0条件下的解析解。
??x¨(t)+5x˙(t)+4x(t)+3y(t)=e?6tsin(4t)
2y˙(t)+y(t)+4x˙(t)+6x(t)=e?6tcos(4t)
【求解】可以用下面的语句得出微分方程组的通解。
>>symst
[x,y]=dsolve(’D2x+5*Dx+4*x+3*y=exp(-6*t)*sin(4*t)’,...
’2*Dy+y+4*Dx+6*x=exp(-6*t)*cos(4*t)’)
A该结果可以用LT√11013?6t681?6tt?tt?13cos(4t)?esin(4t)+C1e+C2e+EX表示成x(t)=40820e40820
C3e√?13t+1/4t√433?6t279?6tt?13t?1/4ty(t)=?ecos(4t)+esin(4t)?10/3C1e?5/8C2e?40824082√√√√√1313131/8C2e?t?1/4t57?5/8C3e?t+1/4t+1/8C3e?t+1/4t57
将已知初始条件代入,则可以得出下面的特解。
>>symst
[x,y]=dsolve(’D2x+5*Dx+4*x+3*y=exp(-6*t)*sin(4*t)’,...
’2*Dy+y+4*Dx+6*x=exp(-6*t)*cos(4*t)’,’x(0)=1’,’x(pi)=2’,’y(0)=0’)
>>vpa(x),vpa(y)
可以得出下面的准解析解表达式为
x(t)=0.024816266536011758941695247427732e?6tcos(4t)?
0.016682998530132288094071533561979e?6tsin(4t)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第7章微分方程问题的计算机求解
+0.085861668591377882798659931739391et?
0.057658489325155296991205006467701e?5.1374586088176874243091712017365t
+0.94698055419776565525084982730045e?1.3625413911823125756908287982635t
y(t)=?0.10607545320921117099461048505634e?6tcos(4t)+
0.068348848603625673689367956883880e?6tsin(4t)?
0.28620556197125960932886643913130et+
0.090450561852315609553848362733226e?5.1374586088176874243091712017365t+
0.30183045332815517076962856144409e?1.3625413911823125756908287982635t
3试求出下面的时变线性微分方程解析解。(www.61k.com)
2dx2dx+n(n+1)x=0①Legendre微分方程(1?t)2?2tdtdt
2dx2dx②Bessel微分方程t+t+(t2?n2)x=02dtdt
【求解】①Legendre微分方程的解包括Legendre函数,方程的解为
>>symstn
x=dsolve(’(1-t^2)*D2x-2*t*Dx+n*(n+1)*x=0’,’x’)
x=
C1*LegendreP(n,t)+C2*LegendreQ(n,t)75
结果中的LegendreP()和LegendreQ()为特殊函数,其内容可以由mhelp命令可以得出如下的信息
>>mhelpLegendreP
LegendreP,LegendreQ-LegendrefunctionsandassociatedLegendrefunctionsofthefirstandsecondkinds
...............
②Bessel微分方程的解包括Bessel函数,方程的解为
>>symstn
x=dsolve(’t^2*D2x+t*Dx+(t^2-n^2)*x=0’)
x=
C1*besselj(n,t)+C2*bessely(n,t)
????????114试求出微分方程y¨(x)?2?y˙(x)+1?y(x)=x2e?5x的解析解通解,并求出满足xx
边界条件y(1)=p,y(p)=1的解析解。
【求解】微分方程的通解可以由下面的函数直接求出
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
76
>>symsx第7章微分方程问题的计算机求解
y=dsolve(’D2y-(2-1/x)*Dy+(1-1/x)*y=x^2*exp(-5*x)’,’x’)
y=
exp(x)*C2+exp(x)*log(x)*C1+1/1296*(6*exp(6*x)*Ei(1,6*x)+11+30*x+36*x^2)*exp(-5*x)若需要求取满足边界条件的特解,需要在求解时代入边界条件,这样就可以由下面的语句得出微分方程的特解。(www.61k.com)
>>symsx
y=dsolve(’D2y-(2-1/x)*Dy+(1-1/x)*y=x^2*exp(-5*x)’,...
’y(1)=sym(pi)’,’y(sym(pi))=1’,’x’)
y=
-1/1296*exp(x)*(6*exp(1)*Ei(1,6)+77*exp(-5)-1296*sym(pi))/exp(1)+
1/1296*exp(x)*log(x)*(6*Ei(1,6)*exp(6*sym(pi)+6)+77*exp(6*sym(pi))-
1296*sym(pi)*exp(6*sym(pi)+5)+3*sqrt(-1)*pi*csgn(sym(pi))*exp(6*sym(pi)+6)-6*Ei(1,6*sym(pi))*exp(6*sym(pi)+6)-3*sqrt(-1)*pi*exp(6*sym(pi)+6)-
3*sqrt(-1)*pi*csgn(6*sqrt(-1)*sym(pi))*exp(6*sym(pi)+6)-30*sym(pi)*exp(6)+3*sqrt(-1)*pi*csgn(sym(pi))*csgn(6*sqrt(-1)*sym(pi))*exp(6*sym(pi)+6)-
36*sym(pi)^2*exp(6)-11*exp(6)+1296*exp(5*sym(pi)+6))/log(sym(pi))*exp(-6*sym(pi)-6)+1/1296*(6*exp(6*x)*Ei(1,6*x)+11+30*x+36*x^2)*exp(-5*x)
由于使用了sym(pi)这样精确的表示,其实还可以用数值解的方法对各个系数进行近似,这样可以得出如下结果。
>>vpa(y,10)
ans=
1.155578411*exp(x)-.9717266142*exp(x)*log(x)+
.7716049383e-3*(6.*exp(6.*x)*Ei(1,6.*x)+11.+30.*x+36.*x^2)*exp(-5.*x)还可以对该结果进行图形显示,得出如图7-1所示的解曲线,可见,该曲线通过两个给定点。
>>x1=0.5:0.01:4;y1=subs(y,x,x1);
plot(x1,y1,1,pi,’o’,pi,1,’o’)
5试用Laplace变换求解下面微分方程组的解析解,并和其他方法比较。
??x????(t)+y????(t)+x(t)+y(t)=0,x(0)=2,y(0)=1
2x????(t)?y????(t)?x(t)+y(t)=sint,x??(0)=y??(0)=?1
【求解】假设y(t)的Laplace变换为Y(s),则L[y????(t)]=s2Y(s)?sy(0)?y??(0),这样可以
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第7章微分方程问题的计算机求解
77
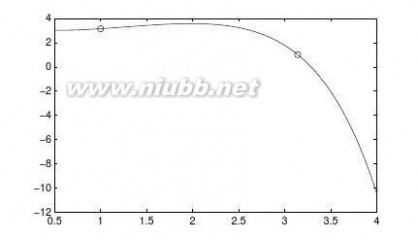
将前面的微分方程组变换成
??s2X(s)?sx(0)?x??(0)+s2Y(s)?sy(0)?y??(0)+X(s)+Y(s)=0
?2s2X(s)?2sx(0)?2x??(0)?s2Y(s)+sy(0)+y??(0)?X(s)+Y(s)=1
s2+1
这样由下面的语句可以得出X(s)和Y(s),再通过Laplace反变换则可以得出方程的解。(www.61k.com)>>symssXY;
[X,Y]=solve(’s^2*X-s*2-(-1)+s^2*Y-s*1-(-1)+X+Y=0’,...
’2*(s^2*X-s*2-(-1))-(s^2*Y-s*1-(-1))-X+Y=1/(s^2+1)’,’X,Y’)
X=
(6*s^3-3*s^2+2)/(3*s^4-2+s^2)
Y=
(3*s^3-6*s-3*s^2+2)/(3*s^4-2+s^2)
>>x0=ilaplace(X)
x0=
6/5*cos(t)-sin(t)+4/5*cosh(1/3*6^(1/2)*t)
>>y0=ilaplace(Y)
y0=
9/5*cos(t)-sin(t)-4/5*cosh(1/3*6^(1/2)*t)
直接采用微分方程组求解的函数可以得出如下的结果
>>symst
[x,y]=dsolve(’D2x+D2y+x+y=0’,’2*D2x-D2y-x+y=sin(t)’)
x=
C1*sin(t)+C2*cos(t)+C3*exp(1/3*6^(1/2)*t)+C4*exp(-1/3*6^(1/2)*t)y=
3/2*C1*sin(t)+3/2*C2*cos(t)-C3*exp(1/3*6^(1/2)*t)-C4*exp(-1/3*6^(1/2)*t)+1/2*sin(t)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
78第7章微分方程问题的计算机求解
这样的方程可以写成
??√√1/3?1/3tx(t)=C1sint+C2cost+C3e+C4e
y(t)=3/2C1sint+3/2C2cost?C3e1/3考虑初始条件,则可以得出方程的解为
>>symst
[x,y]=dsolve(’D2x+D2y+x+y=0’,’2*D2x-D2y-x+y=sin(t)’,’x(0)=2’,’y(0)=1’,...’Dx(0)=-1’,’Dy(0)=-1’)
x=
-sin(t)+6/5*cos(t)+2/5*exp(1/3*6^(1/2)*t)+2/5*exp(-1/3*6^(1/2)*t)
y=
-sin(t)+9/5*cos(t)-2/5*exp(1/3*6^(1/2)*t)-2/5*exp(-1/3*6^(1/2)*t)√?C4e?1/3√t+1/2sint
6试求出下面微分方程的通解。[www.61k.com)
①x¨(t)+2tx˙(t)+t2x(t)=t+1②y˙(x)+2xy(x)=xe?x③y??????+3y????+3y??+y=e?tsint
【求解】求解线性微分方程解析解是很直观的,调用标准函数dsolve()函数就可以直接求解,得出各个方程的通解。
>>symst;~
x=dsolve(’D2x+2*t*Dx+t^2*x=t+1’)
x=
exp(-1/2*t*(-2+t))*C2+exp(-1/2*t*(2+t))*C1-
1/2*i*pi^(1/2)*2^(1/2)*erf(1/2*i*2^(1/2)*t-
1/2*i*2^(1/2))*exp(-1/2*(-1+t)^2)
>>symsx
y=dsolve(’Dy+2*x*y=x*exp(-x^2)’,’x’)
y=
(1/2*x^2+C1)*exp(-x^2)
>>symst;y=dsolve(’D3y+3*D2y+3*Dy+y=exp(-t)*sin(t)’)
y=
exp(-t)*cos(t)+C1*exp(-t)+C2*exp(-t)*t+C3*exp(-t)*t^2
应该注意的是如何处理自变量,MATLAB符号运算默认的自变量是t,所以若选择t为自变量,故①、③的求解不存在问题,在②微分方程求解时,若不指出x为自变量,则可以尝试下面的MATLAB语句,得出解析解。
>>symsx
y=dsolve(’Dy+2*x*y=x*exp(-x^2)’,’x’)
y=
(1/2*exp(-x*(x-2*t))+C1)*exp(-2*t*x)2
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第7章微分方程问题的计算机求解79
这样看似的出了问题的解析解,但实际上这样的解错误的,因为在求解微分方程时是将x作为常数时问题的方程的解析解,所以在解中既含有t,也含有x,故解是错误的。(www.61k.com)
7极限环是二阶非线性常微分方程中一种常见的现象,对某些非线性微分方程来说,不论初始状态为何值,微分方程的相轨迹都将稳定在一条封闭的曲线上,该曲线称为微分方程的极限??x˙=y+x(1?x2?y2)的极限环,并对不同初值验证微分方程环。试绘制出微分方程y˙=?x+y(1?x2?y2)
的相平面曲线确实收敛于极限环。
【求解】由于微分方程是非线性微分方程,所以只能求解其数值解,而一般解析解是不存在的。令x1=x,x2=y,则可以用下面的语句求解该微分方程,这样在不同的初值下,可以绘

制出解的相平面曲线,如图7-2所示,可见,对不同的初值,微分方程解的相空间轨迹将收敛于封闭的曲线,以及极限环。
>>f=inline(’[x(2)+x(1)*(1-x(1)^2-x(2)^2);-x(1)+x(2)*(1-x(1)^2-x(2)^2)]’,’t’,’x’);
[t,x]=ode45(f,[0,10],[1;2]);plot(x(:,1),x(:,2));holdon
[t,x]=ode45(f,[0,10],[0.1;0.2]);plot(x(:,1),x(:,2));
??˙=?y?z??x
8考虑著名的R¨ossler化学反应方程组,选定a=b=0.2,c=5.7,且y˙=x+ay???z˙=b+(x?c)z
x1(0)=x2(0)=x3(0),绘制仿真结果的三维相轨迹,并得出其在x-y平面上的投影。在实际求解中建议将a,b,c作为附加参数,同样的方程若设a=0.2,b=0.5,c=10时,绘制出状态变量的二维图和三维图。
【求解】令x1=x,x2=y,x3=z,这样可以求解出该微分方程数值解,并绘制出解的三维相空间曲线,如图7-3a所示。
>>f=inline(’[-x(2)-x(3);x(1)+a*x(2);b+(x(1)-c)*x(3)]’,...
’t’,’x’,’flag’,’a’,’b’,’c’);
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
80第7章微分方程问题的计算机求解
[t,x]=ode45(f,[0,100],[0;0;0],[],0.2,0.2,5.7);
plot3(x(:,1),x(:,2),x(:,3));grid

图7-3R¨ossler方程的相空间轨迹
修改a,b,c参数,则可以用下面的语句绘制出相空间轨迹,如图7-3b所示。[www.61k.com]
>>[t,x]=ode45(f,[0,100],[0;0;0],[],0.2,0.5,10);
plot3(x(:,1),x(:,2),x(:,3));grid
??˙=α[y?x?f(x)]??x
,其中f(x)为y˙=x?y+z???z˙=?βy?γz9Chua电路方程是混沌理论中经常提到的微分方程[54]
1Chua电路的二极管分段线性特性,f(x)=bx+(a?b)(|x+1|?|x?1|),且a<b<0,试编写2
出MATLAB函数描述该微分方程,并绘制出α=15,β=20,γ=0.5,a=?120/7,b=?75/7,且初始条件为x(0)=?2.121304,y(0)=?0.066170,z(0)=2.881090时的相空间曲线。
【求解】令x1=x,x2=y,x3=z,则可以用下面的语句描述微分方程组
functiondx=c7chua(t,x,flag,a,b,alpha,beta,gamma)
dx=[alpha*(x(2)-x(1)-nlfun(x(1),a,b));
x(1)-x(2)+x(3);-beta*x(2)-gamma*x(3)];
functionf0=nlfun(x,a,b)
f0=b*x+(a-b)*(abs(x+1)-abs(x-1))/2;
这样用下面的语句可以求解微分方程,并绘制出相空间轨迹,如图7-15所示。
>>a=-120/7;b=-75/7;alpha=15;beta=20;gamma=0.5;
f=odeset;f.RelTol=1e-6;
[t,x]=ode15s(’c7chua’,[0,10],[-2.121304;-0.06617;2.88109],f,...
a,b,alpha,beta,gamma);
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第7章微分方程问题的计算机求解
??
10Lotka-Volterra扑食模型方程为x˙(t)=4x(t)?2x(t)y(t)81
y˙(t)=x(t)y(t)?3y(t)
试求解该微分方程,并绘制相应的曲线。(www.61k.com]
线,分别如图7-4a、b所示。,且初值为x(0)=2,y(0)=3,【求解】用下面命令可以立即解出微分方程的模型,并绘制出解的时间响应曲线和相平面曲
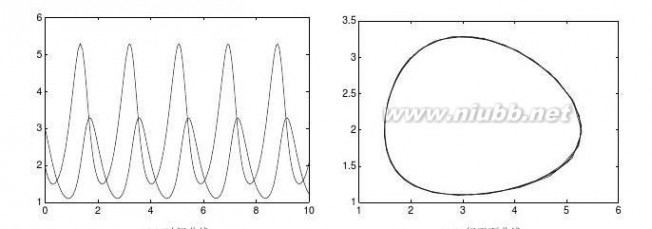
>>f=inline(’[4*x(1)-2*x(1)*x(2);x(1)*x(2)-3*x(2)]’,’t’,’x’);
[t,x]=ode45(f,[0,10],[2;3]);
图7-4Lotka-Volterra扑食模型的解
11请给出求解下面微分方程的MATLAB命令
y(3)+tyy¨+t2yy˙2=e?ty,y(0)=2,y˙(0)=y¨(0)=0
并绘制出y(t)曲线,试问该方程存在解析解吗?选择四阶定步长Runge-Kutta算法求解该方程时,步长选择多少可以得出较好的精度,试与MATLAB语言给出的现成函数在速度、精度上进行比较。
【求解】因为该方程为含有非线性项的微分方程,所以一般来说该方程不能有解析解,只能求解其数值解。要求解该方程。,则需要引入状态变量x1=y,x2=y,˙x3=y¨,这样可以写出一阶微分方程组为
??˙1=x2??x
x˙2=x3???x?tx1˙3=?tx1x2?t2x2x21+ex1(0)=2,x2(0)=x3(0)0
这样就可以用下面的语句求解微分方程,并绘制出状态变量的时域响应曲线,如图7-15所示,可见,时变微分方程也可以容易地求解。
>>f=inline(’[x(2);x(3);-t^2*x(1)*x(2)-t^2*x(2)*x(1)^2+exp(-t*x(1))]’,’t’,’x’);
[t,x]=ode45(f,[0,10],[2;0;0]);
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
82
第7章微分方程问题的计算机求解
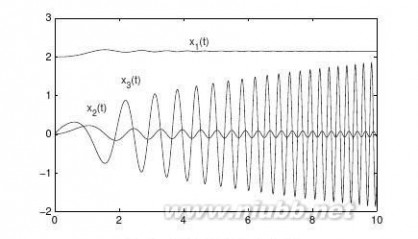
12试选择状态变量,将下面的非线性微分方程组转换成一阶显式微分方程组,并用MATLAB对其求解,绘制出解的相平面或相空间曲线。(www.61k.com]
??x????=?x?y?(3x??)2+(y??)3+6y????+2t????y??????=?y?????x???e?x?t①?x(1)=2,x??(1)=?4????y(1)=?2,y??(1)=7,y????(1)=6??x?????2xzx??=3x2yt2????????y??2???y?ey=4xtz②z?????2tz??=2texy????z??(1)=x??(1)=y??(1)=2????z??(1)=x(1)=y(1)=3
【求解】①选择x1=x,x2=x??,x3=y,x4=y??,x5=y????,则可以将原来的微分方程组转换成下面的一阶微分方程组
??x˙1=x2?????˙2=?x1?x3?(3x2)2+(x4)3+6x5+2t??x
x˙3=x4????x˙4=x5????x˙=?x?x?e?x1?t552
且x(1)=[2,?4,?2,7,6]T,
>>f=inline([’[x(2);-x(1)-x(3)-(3*x(2))^2+(x(4))^3+6*x(5)+2*t;’,...
’x(4);x(5);-x(5)-x(2)-exp(-x(1))-t]’],’t’,’x’);
[t1,x1]=ode45(f,[1,0],[2,-4,-2,7,6]’);
[t2,x2]=ode45(f,[1,2],[2,-4,-2,7,6]’);
t=[t1(end:-1:1);t2];x=[x1(end:-1:1,:);x2];
plot(t,x)
figure;plot(x(:,1),x(:,3))
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第7章微分方程问题的计算机求解
83
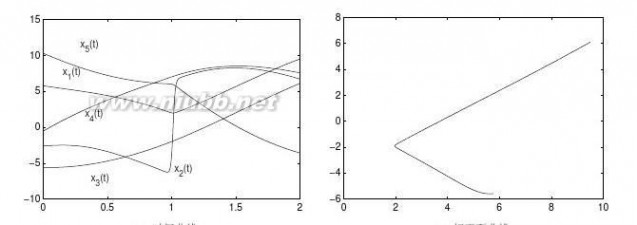
图7-6微分方程的解
②选择状态变量x1=x,x2=x??,x3=y,x4=y??,x5=z,x6=z??,
??x˙1=x2????2?x˙2=2x1x2x5+3x2?1x3t???x˙3=x4
?x˙4=e?x3x4+4x1t2x5?????x˙5=x6????x˙6=2tx6+2te?x1x3
x(1)=[3,2,3,2,2,3]T
>>f=inline([’[x(2);2*x(1)*x(2)*x(5)+3*x(1)^2*x(3)*t^2;’,...
’x(4);exp(-x(3))*x(4)+4*x(1)*t^2*x(5);’,...
’x(6);2*t*x(6)+2*t*exp(-x(1)*x(3))]’],’t’,’x’);
[t,x]=ode15s(f,[10],[3,2,3,2,2,3]’);
13试用解析解和数值解的方法求解下面的微分方程组。(www.61k.com]??x????(t)=?2x(t)?3x??(t)+e?5t,x(0)=1,x??(0)=2
y????(t)=2x(t)?3y(t)?4x??(t)?4y??(t)?sint,y(0)=3,y??(0)=4
【求解】该方程的解析解可以由下面的语句直接得出
>>symst
[x,y]=dsolve(’D2x=-2*x-3*Dx+exp(-5*t)’,’D2y=2*x-3*y-4*Dx-4*Dy-sin(t)’,...’x(0)=1’,’Dx(0)=2’,’y(0)=3’,’Dy(0)=4’)
x=
1/12*exp(-5*t)-10/3*exp(-2*t)+17/4*exp(-t)
y=
-71/5*exp(-3*t)-265/16*exp(-t)+11/48*exp(-5*t)+100/3*exp(-2*t)+
1/5*cos(t)-1/10*sin(t)+51/4*exp(-t)*t
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
84第7章微分方程问题的计算机求解
还可以令x1=x(t),x2=x??(t),x3=y(t),x4=y??(t),这时可以将微分方程组改写成
??x˙1=x2????x˙2=?2x1?3x2+e?5t
?x˙3=x4????x˙4=2x1?3x3?4x2?4x4?sint,x˙T(0)=[1,2,3,4]
可以写出描述微分方程组的MATLAB函数为
>>f=inline(...
’[x(2);-2*x(1)-3*x(2)+exp(-5*t);x(4);2*x(1)-3*x(3)-4*x(2)-4*x(4)-sin(t)]’,...’t’,’x’);
[t1,x1]=ode45(f,[0,10],[1;2;3;4]);
ezplot(x,[0,10]),line(t1,x1(:,1))
figure;ezplot(y,[0,10]),line(t1,x1(:,3))
得出的x(t)和y(t)
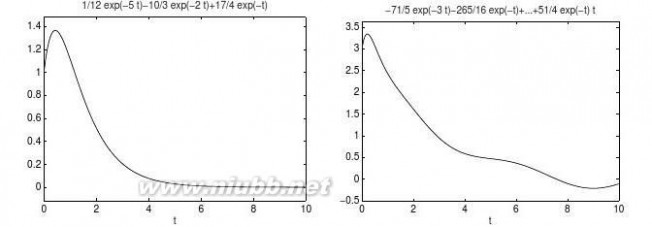
曲线的数值解与解析解分别如图7-7a、b所示,可见,得出的数值解精度还是很高的,在曲线上无法区分出解析解和数值解。(www.61k.com)
(a)x(t)(b)y(t)
图7-7微分方程的解析解与数值解比较
??
14给定微分方程组u¨(t)=?u(t)/r3(t)
v¨(t)=?v(t)/r3(t),其中r(t)=??u2(t)+v2(t),且u(0)=1,u˙(0)=
2,v˙(0)=2,v(0)=1,试选择一组状态变量,将其变换成MATLAB语言能直接求解的微分方程组形式,并绘制出u(t),v(t)的轨迹曲线。
【求解】令x1=u,x2=u,˙x3=v,x4=v˙,这样可以将原微分方程组转换成关于xi的一阶微分方程组??x˙1=x2????x˙2=?x1/r3
?x˙3=x4????x˙4=?x3/r3
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第7章微分方程问题的计算机求解
其中r=??85T13,x(0)=[1,2,2,1]。[www.61k.com)由于有中间变量r,所以原问题不大适合用inline()函数描述,
functiondx=exc7eqa(t,x)
r=sqrt(x(1)^2+x(3)^2);
dx=[x(2);-x(1)/r^3;x(4);-x(3)/r^3];
这样用下面的语句就可以求解该方程,绘制出v(t)和u(t)

关系曲线,如图7-8所示。>>[t,x]=ode45(’exc7eqa’,[0,10],[1221]’);
plot(x(:,1),x(:,3))
??u˙1=u3????u˙2=u4[30],其中15已知微分方程可以表示为2?2u˙+cos(u?u)u˙=?gsinu?sin(u?u)u?31241124???cos(u1?u2)u˙3+u˙4=?gsinu2+sin(u1?u2)u23
u1(0)=45,u2(0)=30,u3(0)=u4(0)=0,g=9.81,试求解此微分方程并绘制出各个状态变量的时间曲线。
【求解】显然这是一个微分代数方程的标准形,可以由给出的方程写出M(t,u)矩阵
??1000?01?00?M(t,u)=??002cos(u1?u2)?
00cos(u1?u2)1
这样可以编写MATLAB文件来描述M矩阵
functionM=exc7eqm(t,u)
M=[1000;0100;002cos(u(1)-u(2));00cos(u(1)-u(2))1];还可以立即写出状态方程文件为
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
86
functiondu=exc7eqb(t,u)
du=[u(3);
u(4);
9.81*sin(u(1))-sin(u(1)-u(2))*u(4)^2;
9.81*sin(u(2))+sin(u(1)-u(2))*u(3)^2];
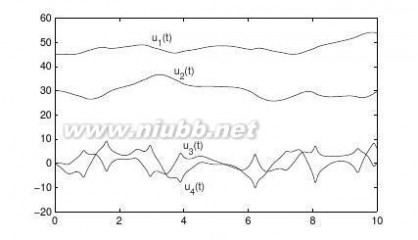
第7章微分方程问题的计算机求解
从而可以用下面的语句求解该微分代数方程,得出的状态变量曲线如图7-9所示。[www.61k.com)
>>ff=odeset;ff.Mass=@exc7eqm;
[t,x]=ode45(@exc7eqb,[0,10],[45;30;0;0],ff);plot(t,x)
??
16试求出隐式微分方程22?x2x˙1x¨2sin(x1x2)+5¨x1x˙2cos(x21)+tx1x2=e2
x¨1x2+x¨2x˙1sin(x2x2x2)=sint1)+cos(¨
1,x˙1(0)=1,x2(0)=2,x˙2(0)=2,并绘制出轨迹曲线。的数值解,x1(0)=
【求解】引入u1=x1,u2=x˙1,u3=x2,u4=x˙2,这样可以写出如下的隐式微分方程标准形为??u˙1?u2=0????uu22?u23=0˙2u4cos(u2)+tuu?e2˙4sin(u1u3)+5u113
?u˙3?u4=0????u˙2u3+u˙4u2sin(u2˙4u3)?sint=01)+cos(u
这样可以编写出下面的隐式微分方程的MATLAB表达
functionfun=exc7eqc(t,u,ud)
fun=[ud(1)-u(2);
-u(2)*ud(4)*sin(u(1)*u(3))-5*ud(2)*u(4)*cos(u(1)^2)-t*u(1)*u(3)^2+exp(-u(3)^2);ud(3)-u(4);
-ud(2)*u(3)-ud(4)*u(2)*sin(u(1)^2)-cos(ud(4)*u(3))-sin(t)];
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第7章微分方程问题的计算机求解87
˙(0)和u(0)共需要8个初值信息,而直接由习题提供的只有4个值,为产生不矛盾的由于u
初值,应该采用decic()函数求解初值方程,这里需要确保给定的4个初值量,用该函数可以解出其余4个量
>>u0=[1;0;2;0];ud0=[0;1;0;2];
[y0,yp0]=decic(@exc7eqc,0,u0,[1010],ud0,[0101])
y0=
1.00000000000000
-0.80000166579942
2.00000000000000
0.54532232612148
yp0=
-0.80000166579942
1.00000000000000
0.54532232612148
2.00000000000000
利用MATLAB7.0引入的隐式微分方程求解函数ode15i(),可以用下面的语句求出微分方
程的数值解,并绘制出状态曲线,如图7-10所示。(www.61k.com]
>>r=ode15i(@exc7eqc,[0,1.2],y0,yp0);plot(r.x,r.y)
17下面的方程在传统微分方程教程中经常被认为是刚性微分方程,试用常规微分方程解法和刚性微分方程解法分别求解这两个微分方程的数值解,并求出解析解,用状态变量曲线比较数值求解的精度。?11??y˙1=9y1+24y2+5cost?sint,y1(0)=33①12??y˙2=?24y1?51y2?9cost+sint,y2(0)=33??˙1=?0.1y1?49.9y2,y1(0)=1??y②y˙2=?50y2,y2(0)=2???y˙3=70y2?120y3,y3(0)=1
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
88第7章微分方程问题的计算机求解
??˙1=?0.04y1+104y2y3??y
2,其初值18考虑下面的化学反应系统的反应速度方程组y˙2=0.04y1?104y2y3?3×107y2???y2˙3=3×107y2
为y1(0)=1,y2(0)=y3(0)=0,该方程往往被认为是刚性方程,试采用ode45()对之求解,观察是否能正确求解,如果不能求解应该如何解决问题?
【求解】用下面的语句可以分别用两种方法,即RKF四阶五级算法及刚性方程的求解方法,求解该方程,则可以分别测出计算的点数有极大的差异,求解这样的方程用刚性方程求解方
法比较合适。[www.61k.com)得出的解还可以用曲线表示出来,如图7-11所示。
>>f=inline([’[-0.04*y(1)+10^4*y(2)*y(3);0.04*y(1)-10^4*y(2)*y(3)-3e7*y(2)^2;’,...
’3e7*y(2)^2]’],’t’,’y’);
[t,y]=ode45(f,[0,10],[1;0;0]);size(t)
ans=
29109
ans=
411
1>>[t,y]=ode15s(f,[0,10],[1;0;0]);size(t),plot(t,y)19试求出习题4中给出的微分方程边值问题数值解,绘制出y(t)曲线,并和该习题得出的解析解比较精度。
【求解】微分方程的解析解可以由下面的函数直接求出
>>symsx
y=dsolve(’D2y-(2-1/x)*Dy+(1-1/x)*y=x^2*exp(-5*x)’,...
’y(1)=sym(pi)’,’y(sym(pi))=1’,’x’)
ezplot(y,[0,10])
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第7章微分方程问题的计算机求解8920考虑VanderPol方程y¨+μ(y2?1)y˙+y=0,试求解μ=1,且边值y(0)=1,y(5)=3时方程的数值解。[www.61k.com)如果假设μ为自由参数,试求出满足边值条件,且满足y˙(5)=2时方程的数值解及μ的值,并绘图验证之。
【求解】用下面的语句可以写出原方程的MATLAB表示,其中μ的值用变量m表示,该变量可以看成是附加参数。
functiondx=exc7ffo1(t,x,flag,m)
dx=[x(2);-m*(x(1)^2-1)*x(2)-x(1)];
这样可以将原问题转换成方程y˙(5)=2求解的问题,该方程由下面的语句即可描述。
functiony=exc7ffo(x)
[t,y1]=ode45(’exc7ffo1’,[0,5],[1;3],[],x);
y=abs(y1(end,2)-2);
求解,且绘制出该μ
值下的状态变量曲线,如图7-12所示。
>>x=fsolve(’exc7ffo’,0)
[t,y]=ode45(’exc7ffo1’,[0,5],[1;3],[],x);plot(t,y);
x=
-0.03459759451208
?2?u?2u??+2=0???y??x2
,并绘制出u函数曲面。21试用数值方法求解偏微分方程u|=1,u|=0?x=0,y>0y=0,x??0????x>0,y>0
【求解】可以看出,该方程为椭圆型偏微分方程,且c=1,f=0,用pdetool函数提供的界面求解该方程,选择并设置椭圆微分方程,再选择矩形区域,可以设置出横轴和纵轴的边界条件,求解微分方程则可以得出如图7-13所示的解曲面。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
90Color: u Height: u第 7 章 微分方程问题的计算机求解0.9 1 0.8 0.7 0.5 0.6 0.5 0.4 0 1.5 1 0.5 0 0 0.5 1 0.3 1.5 0.2 0.1图 7-13 偏微分方程解曲面 22 考虑简单的线性微分方程 y (4) + 3y (3) + 3¨ + 4y + 5y = e?3t + e?5t sin(4t + p/3),且方程 y ˙ 的初值为 y(0) = 1, y(0) = y (0) = 1/2, y (3) (0) = 0.2,试用 Simulink 搭建起系统的仿真模 ˙ ¨ 型,并绘制出仿真结果曲线。(www.61k.com)考虑上面的模型,假设给定的微分方程变化成时变线性微分 方程 y (4) + 3ty (3) + 3t2 y + 4y + 5y = e?3t + e?5t sin(4t + p/3),而方程的初值仍为 y(0) = 1, ¨ ˙ y(0) = y (0) = 1/2, y (3) (0) = 0.2,试用 Simulink 搭建起系统的仿真模型,并绘制出仿真结果 ˙ ¨ 曲线。 【求解】 可见该方程含有 y(t) 的四阶导数,所以需要四个积分器,这样可以容易地搭建出如 图 7-14 所示的 Simulink 仿真模型。exp(?3*u) Clock exp(?5*u)*sin(4*u+pi/3) 1 s Integrator 3Dy31 s Integrator1Dy21 s Integrator2Dyy 1 s Integrator3 1 Out1exc7m5.mdl3 4 5图 7-14 Simulink 模型 将各个积分器的初值按照给定的方式设置一下,则将由下面的语句 >> [t,x,y]=sim(’exc7m5’,[0,10]); plot(t,x) figure; plot(t,y) 可以得出得出如图 7-15a、b 所示的状态变量曲线和输出信号曲线。 考虑本例给出的时变微分方程,可以用 Simulink 绘制出该系统的仿真模型,如图 ?? 所示。 用下面的语句可以绘制出系统的状态变量曲线和输出曲线,分别如图 7-17a、b 所示。 >> [t,x,y]=sim(’exc7m5’,[0,10]); plot(t,x) figure; plot(t,y)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第7章微分方程问题的计算机求解
91

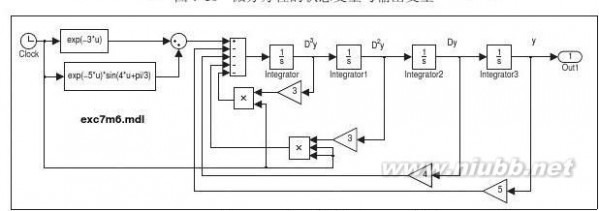

图7-17微分方程的状态变量与输出变量
23考虑延迟微分方程y(4)(t)+4y(3)(t?0.2)+6y????(t?0.1)+6y????(t)+4y??(t?0.2)+y(t?0.5)=e?t,
且在t??0时该方程具有零初始条件,试分别用Simulink建模与dde23()函数求解的方式直接求解该微分方程,并绘制出y(t)曲线。[www.61k.com)
【求解】可以按图7-18中所示的方式建立起该方程的Simulink仿真模型,对其进行仿真则可以得出如图7-19所示的输出曲线。
2
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
92第7章微分方程问题的计算机求解
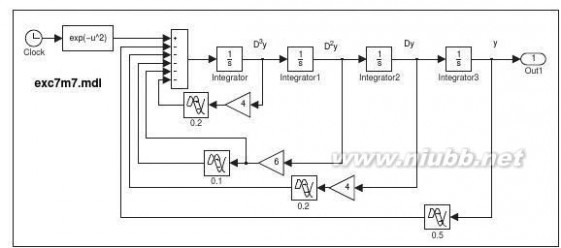
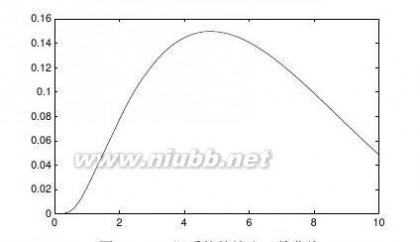
下面考虑用dde23()函数求解该方程。(www.61k.com]从给出的方程看,有三个延迟时间常数τ1=0.2,τ2=0.1,τ3=0.5,则可以写出该延迟微分方程的MATLAB表示为
functiondx=exc7ffo2(t,x,z)
xlag1=z(:,1);xlag2=z(:,2);xlag3=z(:,3);
dx=[x(2);x(3);x(4);
exp(-t.^2)-4*xlag1(4)-6*xlag2(3)-6*x(3)-4*xlag1(2)-xlag3(1)];
这样可以由下面的语句求取微分方程的数值解,其结论与图7-19中给出的完全一致。该方法求解所需的时间明显高于Simulink模型。
>>lags=[0.2,0.1,0.5];tx=dde23(’exc7ffo2’,lags,zeros(4,1),[0,10]);
plot(tx.x,tx.y(2,:))
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第8章数据插值、函数逼近问题的计算机求解1用y(t)=t2e?5tsint生成一组较稀疏的数据,并用一维数据插值的方法对给出的数据进行曲线拟合,并将结果与理论曲线相比较。[www.61k.com]
【求解】

由下面的语句可以立即得出一组数据,这些数据分布情况如图8-1a所示。>>t=0:0.2:2;
y=t.^2.*exp(-5*t).*sin(t);plot(t,y,’o’)
(a)已知样本数据分布(b)样条插值拟合效果
图8-1曲线的样条插值拟合
由这些数据作出发点,就可以用各种插值算法对其进行插值,这里只给出效果最好的样条插值,其插值结果和理论曲线一起在图8-1b中给出,可见,拟合效果相当理想,几乎看不出和理论曲线之间的区别。
>>ezplot(’t.^2.*exp(-5*t).*sin(t)’,[0,2]);holdon
x1=0:0.01:2;y1=interp1(t,y,x1,’spline’);
plot(x1,y1)
2用y(t)=sin(10t2+3)在(0,3)区间内生成一组较稀疏的数据,并用一维数据插值的方法对给出的数据进行曲线拟合,并将结果与理论曲线相比较。
【求解】类似于上面的例子,可以用几乎一致的语句得出样本数据和插值效果,如图8-2a、b所示。
>>t=0:0.2:3;
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
94第8章数据插值、函数逼近问题的计算机求解
y=sin(10*t.^2+3);plot(t,y,’o’)
ezplot(’sin(10*t^2+3)’,[0,3]);holdon
x1=0:0.001:3;y1=interp1(t,y,x1,’spline’);
plot(x1,y1)
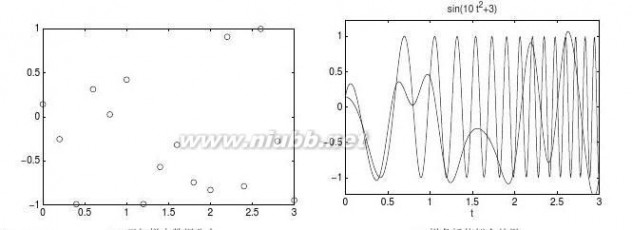
图8-2曲线的样条插值拟合
由于曲线本身变换太大,所以在目前选定的样本点下是不可能得出理想插值效果的,因为样本数据提供的信息量不够。(www.61k.com)为了得到好的插值效果,必须增大样本数据的信息量,对本例来说,必须在快变化区域减小样本点的步长。
>>holdoff
t=[0:0.1:1,1.1:0.04:3];y=sin(10*t.^2+3);plot(t,y,’o’)
ezplot(’sin(10*t^2+3)’,[0,3]);holdon
x1=0:0.001:3;y1=interp1(t,y,x1,’spline’);
plot(x1,y1)
3用f(x,y)=1?x2?y4esin(xy2+x2y)原型函数生成一组网格数据或随机数据,分别拟3x+y
合出曲面,并和原曲面进行比较。
是三维表面图,如图8-4a所示。
>>[x,y]=meshgrid(0.2:0.2:2);
z=exp(-x.^2-y.^4).*sin(x.*y.^2+x.^2.*y)./(3*x.^3+y);
surf(x,y,z)
选择新的密集网格,则可以通过二元插值得出插值曲面,如图8-4b所示。对比插值结果和新网格下的函数值精确解,则可以绘制出绝对插值误差曲面,如图8-5所示。由插值结果可见精度是令人满意的。【求解】由下面的语句可以直接生成一组网格数据,用下面语句还可以还绘制出给定样本点
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第8章数据插值、函数逼近问题的计算机求解95
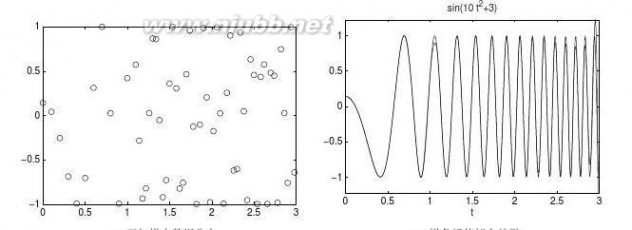
图8-3加密样本点后曲线的样条插值拟合
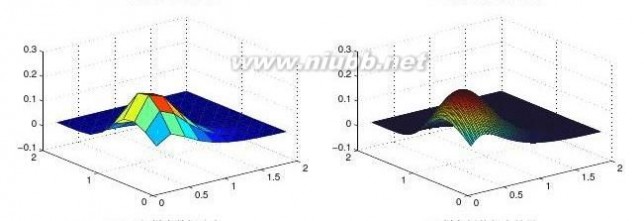
图8-4曲面的样条插值拟合
>>[x1,y1]=meshgrid(0.2:0.02:2);
z1=interp2(x,y,z,x1,y1,’spline’);
surf(x1,y1,z1)
>>z0=exp(-x1.^2-y1.^4).*sin(x1.*y1.^2+x1.^2.*y1)./(3*x1.^3+y1);
surf(x1,y1,abs(z1-z0))
现在假设已知的样本点不是网格形式分布的,而是随机分布的,则可以用下面语句生成样本点,得出分布的二维、三维示意图如图8-6a、b所示。[www.61k.com]
>>x=0.2+1.8*rand(400,1);y=0.2+1.8*rand(400,1);
%仍生成(0.2,2)区间的均匀分布随机数
z=exp(-x.^2-y.^4).*sin(x.*y.^2+x.^2.*y)./(3*x.^3+y);
plot(x,y,’x’)
figure,plot3(x,y,z,’x’)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
96
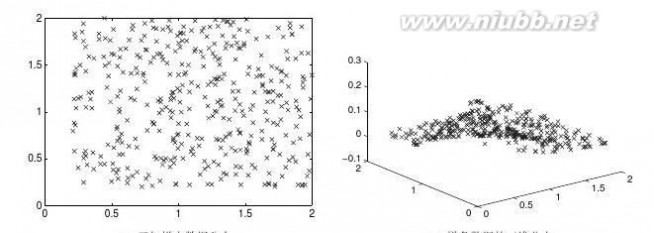
第8章数据插值、函数逼近问题的计算机求解
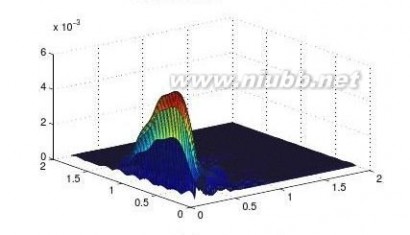
图8-6非网格样本点分布
利用下面的语句可以得出三维插值结果,如图8-7a所示,同时可以绘制出插值的绝对误差曲面,如图8-7b所示,可见插值结果还是很好的,但由于边界样本点信息不能保证,所以不能像网格数据那样对(0.2,2)区域,而只能选择(0.3,1.9)区域进行插值。[www.61k.com]
>>[x1,y1]=meshgrid(0.3:0.02:1.9);
z1=griddata(x,y,z,x1,y1,’v4’);surf(x1,y1,z1)
>>z0=exp(-x1.^2-y1.^4).*sin(x1.*y1.^2+x1.^2.*y1)./(3*x1.^3+y1);
surf(x1,y1,abs(z1-z0))
4假设已知一组数据,试用插值方法绘制出x∈(?2,4.9)区间内的光滑函数曲线,比较各种插值算法的优劣。
xixi
-21.6
-1.71.9
-1.42.2
-1.12.5
-0.82.8
-0.53.1
-0.23.4
0.13.7
0.44
0.74.3
14.6
1.34.9
yi0.102890.117410.131580.144830.156560.166220.173320.17750.178530.176350.171090.16302yi0.152550.14020.126550.112190.097680.083530.070150.057860.046870.037290.029140.02236
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第8章数据插值、函数逼近问题的计算机求解97
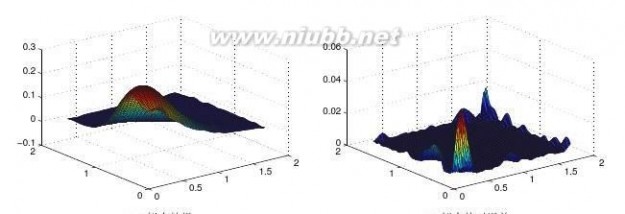

图8-7非网格样本点的样条插值结果
【求解】用下面的语句可以立即得出给定样本点数据的三次插值与样条插值,得出的结果如图8-8所示,可见,用两种插值方法对此例得出的结果几乎一致,效果均很理想。(www.61k.com)
>>x=[-2,-1.7,-1.4,-1.1,-0.8,-0.5,-0.2,0.1,0.4,0.7,1,1.3,...
1.6,1.9,2.2,2.5,2.8,3.1,3.4,3.7,4,4.3,4.6,4.9];
y=[0.10289,0.11741,0.13158,0.14483,0.15656,0.16622,0.17332,...
0.1775,0.17853,0.17635,0.17109,0.16302,0.15255,0.1402,...
0.12655,0.11219,0.09768,0.08353,0.07019,0.05786,0.04687,...
0.03729,0.02914,0.02236];
x0=-2:0.02:4.9;
y1=interp1(x,y,x0,’cubic’);
y2=interp1(x,y,x0,’spline’);
plot(x0,y1,’:’,x0,y2,x,y,’o’)
5假设已知实测数据由下表给出,试对(x,y)在(0.1,0.1)~(1.1,1.1)区域内的点进行插值,并
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
98
用三维曲面的方式绘制出插值结果。[www.61k.com]
yi0
x10.1
x20.2
x30.3
x40.4
x50.5
第8章数据插值、函数逼近问题的计算机求解
x60.60.81610.92841.00861.10191.20461.3111.41381.50341.56841.5964
x70.7
x80.8
x90.9
x101
x111.10.98011.15291.32221.46051.53351.50521.3461.04540.62477
0.10.830410.827270.824060.820980.818240.30.835870.843450.856310.874660.898670.40.842860.860130.885370.918650.959850.50.852680.882510.922860.973460.60.865320.910490.968470.70.880780.943960.80.899040.982760.90.920061
0.943811.10.97023
1.02661.07521.1279
1.02171.0821.14821.21911.2929
1.03831.11181.19221.27681.36241.4448
1.03361.1181.21021.30611.40051.48661.5564
0.814810.814630.815790.818530.823040.963771.06421.17641.29371.40631.50211.56611.58211.5341
1.00451.12531.2541.37931.48591.55551.56781.50321.3473
1.05021.19041.33081.45391.53771.55731.48891.3151.0321
1.11.2571.40171.50861.54841.49151.31561.0155
0.20.831720.832490.835840.842010.851250.863760.879750.899350.922630.94959
0.612680.14763
【求解】直接采用插值方法可以解决该问题,得出的插值曲面如图8-9a所示。
>>[x,y]=meshgrid(0.1:0.1:1.1);
z=[0.83041,0.82727,0.82406,0.82098,0.81824,0.8161,0.81481,0.81463,0.81579,0.81853,0.82304;0.83172,0.83249,0.83584,0.84201,0.85125,0.86376,0.87975,0.89935,0.92263,0.94959,0.9801;0.83587,0.84345,0.85631,0.87466,0.89867,0.9284,0.96377,1.0045,1.0502,1.1,1.1529;0.84286,0.86013,0.88537,0.91865,0.95985,1.0086,1.0642,1.1253,1.1904,1.257,1.3222;0.85268,0.88251,0.92286,0.97346,1.0336,1.1019,1.1764,1.254,1.3308,1.4017,1.4605;0.86532,0.91049,0.96847,1.0383,1.118,1.2046,1.2937,1.3793,1.4539,1.5086,1.5335;0.88078,0.94396,1.0217,1.1118,1.2102,1.311,1.4063,1.4859,1.5377,1.5484,1.5052;0.89904,0.98276,1.082,1.1922,1.3061,1.4138,1.5021,1.5555,1.5573,1.4915,1.346;0.92006,1.0266,1.1482,1.2768,1.4005,1.5034,1.5661,1.5678,1.4889,1.3156,1.0454;0.94381,1.0752,1.2191,1.3624,1.4866,1.5684,1.5821,1.5032,1.315,1.0155,0.62477;0.97023,1.1279,1.2929,1.4448,1.5564,1.5964,1.5341,1.3473,1.0321,0.61268,0.14763];[x1,y1]=meshgrid(0.1:0.02:1.1);z1=interp2(x,y,z,x1,y1,’spline’);surf(x1,y1,z1)
axis([0.1,1.1,0.1,1.1,min(z1(:)),max(z1(:))])
其实,若光需要插值曲面而不追求插值数值的话,完全可以直接采用MATLAB下的shadinginterp命令来实现,得出的效果如图8-9b所示。可见,这样的插值方法更好,得出的插值曲面更光滑。
>>surf(x,y,z);shadinginterp
6假设已知一组实测数据在文件c8pdat.dat中给出,试通过插值的方法绘制出三维曲面。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第8章数据插值、函数逼近问题的计算机求解99
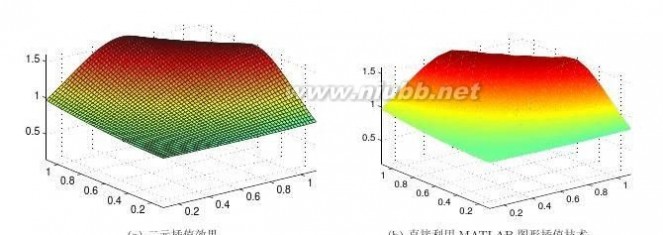
图8-9给定数据的插值结果
【求解】由该文件可见,给定的数据是非网格型的x,y,z向量,故提取这些向量并按非网格
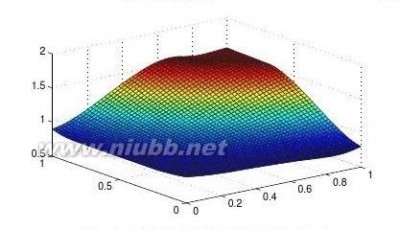
数据进行插值,则将得出如图8-10所示的插值结果。[www.61k.com)
>>loadc8pdat.dat
x=c8pdat(:,1);y=c8pdat(:,2);z=c8pdat(:,3);
[max(x),min(x)max(y),min(y)]
ans=
0.99430.01290.99940.0056
>>[x1,y1]=meshgrid(0:0.02:1);
z1=griddata(x,y,z,x1,y1,’v4’);
surf(x1,y1,z1)%找出插值区域
7假设已知数据由文件c8pdat3.dat给出,其中数据的第1-3列分别为x,y,z坐标,第4列为测出的V(x,y,z)函数值,试用三维插值方法对其进行插值。
【求解】四维插值问题可以由下面的语句直接求解,并可以考虑用切片的方式在三维空间内表示出来,如图8-11所示。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
100
>>loadc8pdat3.mat第8章数据插值、函数逼近问题的计算机求解
x=c8pdat3(:,1);y=c8pdat3(:,2);z=c8pdat3(:,3);V=c8pdat3(:,4);
[x1,y1,z1]=meshgrid(0.1:0.05:0.9);
V1=griddata3(x,y,z,V,x1,y1,z1);
xs=[0.1,0.6];ys=[0.20.5];zs=[0.20.6];
slice(x1,y1,z1,V1,xs,ys,zs)
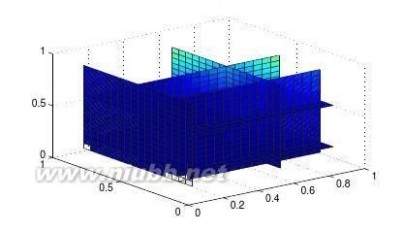
√√?8考虑函数f(x)=,试在x=3:0.4:8处生成一组样本点,采用分段三次样+条和B样条分别对数据进行拟合,并由数据结果求取二阶导数,将得出的结果与理论曲线进行比较。(www.61k.com)
【求解】先考虑分段三次样条插值模型,可以显示出拟合模型的参数,并可以得出如图8-12a所示的函数拟合效果。可见,函数拟合效果还是令人满意的。
>>x=3:0.4:8;
y=(sqrt(1+x)-sqrt(x-1))./(sqrt(2+x)+sqrt(x-1));
S=csapi(x,y)
S=
form:’pp’
breaks:[33.40003.80004.20004.600055.40005.8000...
6.20006.60007.00007.40007.8000]
coefs:[12x4double]
pieces:12
order:4
dim:1
>>S.coefs
ans=
-0.003437033991930.01686329459568-0.053381633364410.16047705669500
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第8章数据插值、函数逼近问题的计算机求解
-0.00343703399193-0.00181418461263-0.00132512662530-0.00089566193169-0.00065333026034-0.00048093934582-0.00036443767449-0.00028009094835-0.00022184675863-0.00016763585508-0.00016763585508holdon;fnplt(S)
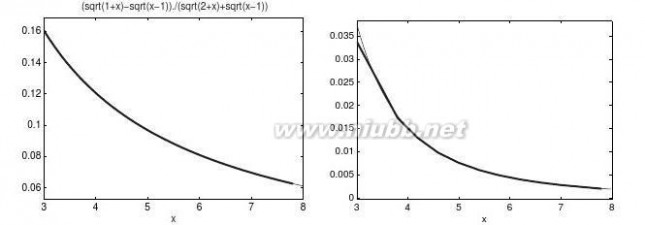
0.012738853805360.008614413015040.006437391479890.004847239529520.003772445211490.002988448899090.002411321684110.001973996474720.001637887336700.001371671226340.00117050820024
-0.04154077400400-0.03299946727584-0.02697874547786-0.02246489307410-0.01901701917770-0.01631266153346-0.01415275330019-0.01239862603666-0.01095387251209-0.00975004908687-0.00873317731623
101
0.141602560309060.126804497140840.114866908497700.105020584839320.096752863570770.089707833996870.083630141089210.078331527227420.073669990428020.069536305204510.06584502427125
>>ezplot(’(sqrt(1+x)-sqrt(x-1))./(sqrt(2+x)+sqrt(x-1))’,[3,8]);
(a)函数拟合(b)函数二阶导数
图8-12分段三次样条插值拟合效果
对函数的二阶导数进行插值运算,则可以得出如图8-12b所示的曲线,该曲线还绘制了导数的理论值,可以看出当x较小时拟合效果不太理想,这是因为原来的三次多项式经求导变成线性表达式,所以拟合效果明显降低。[www.61k.com)
>>symsx;y=(sqrt(1+x)-sqrt(x-1))/(sqrt(2+x)+sqrt(x-1));
y2=diff(y,x,2);ezplot(y2,[3,8]);holdonS2=fnder(S,2);fnplt(S2)
现在考虑B-样条插值,用下面的语句可以得出如图8-12所示的函数插值与导数插值效果,可见,函数拟合与二阶导数拟合效果明显改善。这里选择的B-样条为6阶的,若选择5阶的,则二阶导数效果会降低,但也远优于三次样条插值。
>>x=3:0.4:8;
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
102第8章数据插值、函数逼近问题的计算机求解
y=(sqrt(1+x)-sqrt(x-1))./(sqrt(2+x)+sqrt(x-1));
S=spapi(6,x,y)
S=
form:’B-’
knots:[1x19double]
coefs:[1x13double]
number:13
order:6
dim:1
>>ezplot(’(sqrt(1+x)-sqrt(x-1))./(sqrt(2+x)+sqrt(x-1))’,[3,8]);
holdon;fnplt(S)

(a)函数拟合(b)函数二阶导数
图8-13B-样条插值拟合效果
>>symsx;y=(sqrt(1+x)-sqrt(x-1))/(sqrt(2+x)+sqrt(x-1));
y2=diff(y,x,2);ezplot(y2,[3,8]);holdon
S2=fnder(S,2);fnplt(S2)
9已知如下的样本点(xi,yi)数据,试对其进行分段三次多项式样条插值。(www.61k.com)
xi
yi1244.02221.03208.04208.05211.56216.07219.08221.09221.510220.0
【求解】用下面的语句可以得出样本的三次样条插值,相应的插值曲线如图8-14所示。
>>x=1:10;
y=[244.0,221.0,208.0,208.0,211.5,216.0,219.0,221.0,221.5,220.0];
S=csapi(x,y)
S=
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第8章数据插值、函数逼近问题的计算机求解
form:’pp’
breaks:[12345678910]coefs:[9x4double]pieces:9order:4dim:1
>>S.coefsans=1.0e+002*0.011447956028860.01144795602886-0.027239780144280.00251116454827-0.007804878048780.00370834764686-0.00202851253865-0.00059429749227-0.00059429749227
0.015656131913430.050000000000000.084343868086570.002624527653730.01015802129852-0.01325661284782-0.00213156990725-0.00821710752319-0.01000000000000
-0.25710408794229-0.19144795602886-0.057104087942290.029864307798010.042646856750260.039548265200960.024160082445890.01381140501546-0.00440570250773
103
2.440000000000002.210000000000002.080000000000002.080000000000002.115000000000002.160000000000002.190000000000002.210000000000002.21500000000000
>>fnplt(S);holdon;plot(x,y,’o’)
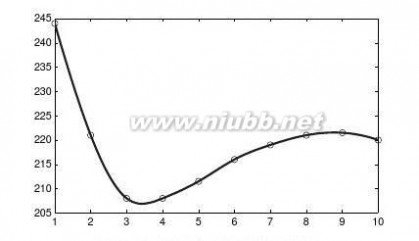
10习题4和5中给出的数据分别为一元数据和二元数据,试用分段三次样条函数和B样条函数
对其进行拟合,并求出它们相应函数的数值导数。(www.61k.com)
【求解】先考虑习题4,相应的三次样条插值和B-样条插值原函数与导数函数分别如图8-15a、b所示。
>>x=[-2,-1.7,-1.4,-1.1,-0.8,-0.5,-0.2,0.1,0.4,0.7,1,1.3,...
1.6,1.9,2.2,2.5,2.8,3.1,3.4,3.7,4,4.3,4.6,4.9];
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
104第8章数据插值、函数逼近问题的计算机求解
y=[0.10289,0.11741,0.13158,0.14483,0.15656,0.16622,0.17332,...
0.1775,0.17853,0.17635,0.17109,0.16302,0.15255,0.1402,...
0.12655,0.11219,0.09768,0.08353,0.07019,0.05786,0.04687,...
0.03729,0.02914,0.02236];
S=csapi(x,y);S1=spapi(6,x,y);
fnplt(S);holdon;fnplt(S1)
>>Sd=fnder(S);Sd1=fnder(S1);
fnplt(Sd),holdon;fnplt(Sd1)
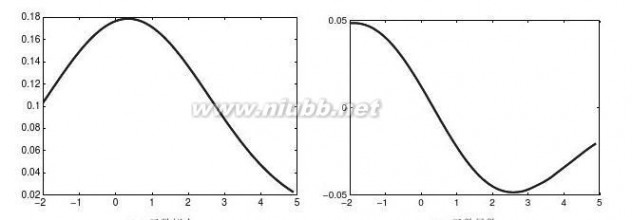
图8-15三次样条插值和B-样条插值拟合效果
再考虑习题5中的数据,原始数据不能直接用于样条处理,因为meshgrid()函数产生的数据
格式与要求的ndgrid()函数不一致,所以需要对数据进行处理,其中需要的x和y均应该
是向量,而z是原来z矩阵的转置,所以用下面的语句可以建立起三次样条和B-样条的插值
模型,函数的表面图分别如图8-16a、b所示,可见二者得出的结果很接近。(www.61k.com]
>>[x,y]=meshgrid(0:0.1:1.1);
z=[0.83041,0.82727,0.82406,0.82098,0.81824,0.8161,0.81481,0.81463,0.81579,0.81853,0.82304;0.83172,0.83249,0.83584,0.84201,0.85125,0.86376,0.87975,0.89935,0.92263,0.94959,0.9801;0.83587,0.84345,0.85631,0.87466,0.89867,0.9284,0.96377,1.0045,1.0502,1.1,1.1529;0.84286,0.86013,0.88537,0.91865,0.95985,1.0086,1.0642,1.1253,1.1904,1.257,1.3222;0.85268,0.88251,0.92286,0.97346,1.0336,1.1019,1.1764,1.254,1.3308,1.4017,1.4605;0.86532,0.91049,0.96847,1.0383,1.118,1.2046,1.2937,1.3793,1.4539,1.5086,1.5335;
0.88078,0.94396,1.0217,1.1118,1.2102,1.311,1.4063,1.4859,1.5377,1.5484,1.5052;
0.89904,0.98276,1.082,1.1922,1.3061,1.4138,1.5021,1.5555,1.5573,1.4915,1.346;
0.92006,1.0266,1.1482,1.2768,1.4005,1.5034,1.5661,1.5678,1.4889,1.3156,1.0454;
0.94381,1.0752,1.2191,1.3624,1.4866,1.5684,1.5821,1.5032,1.315,1.0155,0.62477;
0.97023,1.1279,1.2929,1.4448,1.5564,1.5964,1.5341,1.3473,1.0321,0.61268,0.14763];>>x0=[0.0:0.1:1];y0=x0;z=z’;
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第8章数据插值、函数逼近问题的计算机求解
S=csapi({x0,y0},z);fnplt(S)
figure;S1=spapi({5,5},{x0,y0},z);fnplt(S1)
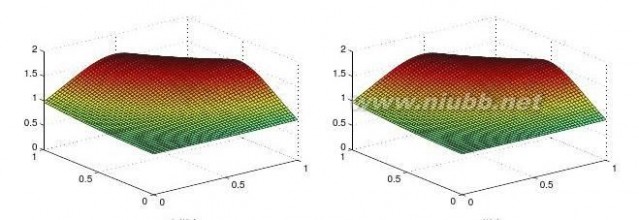
105
图8-16三次样条插值和B-样条插值拟合效果

用下面的语句还可以得出函数偏导数的曲面,分别如图8-17a、b所示。[www.61k.com]
>>S1x=fnder(S1,[0,1]);fnplt(S1x)
figure;S1y=fnder(S1,[0,1]);fnplt(S1y)
图8-17B-样条插值拟合的偏导数
11重新考虑习题4中给出的数据,试考虑用多项式插值的方法对其数据进行逼近,并选择一个能较好拟合原数据的多项式阶次。
【求解】可以选择不同的多项式阶次,例如选择3,5,7,9,11,则可以对其进行多项式拟合,并绘制出曲线,如图8-18所示。
>>x=[-2,-1.7,-1.4,-1.1,-0.8,-0.5,-0.2,0.1,0.4,0.7,1,1.3,...
1.6,1.9,2.2,2.5,2.8,3.1,3.4,3.7,4,4.3,4.6,4.9];
y=[0.10289,0.11741,0.13158,0.14483,0.15656,0.16622,0.17332,...
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
106第8章数据插值、函数逼近问题的计算机求解
0.1775,0.17853,0.17635,0.17109,0.16302,0.15255,0.1402,...
0.12655,0.11219,0.09768,0.08353,0.07019,0.05786,0.04687,...
0.03729,0.02914,0.02236];
x0=-2:0.02:4.9;
p3=polyfit(x,y,3);y3=polyval(p3,x0);
p5=polyfit(x,y,5);y5=polyval(p5,x0);
p7=polyfit(x,y,7);y7=polyval(p7,x0);
p9=polyfit(x,y,9);y9=polyval(p9,x0);
p11=polyfit(x,y,11);y11=polyval(p11,x0);
plot(x0,[y3;y5;y7;y9;y11])
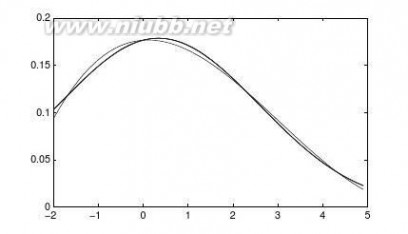
从拟合的结果可以发现,选择5次多项式就能较好地拟合原始数据。[www.61k.com]这样可以得出多项式模型为
>>latex(poly2sym(p5))
29864261567365158119899405842371448546642314722293x5+x?x?36893488147419103232922337203685477580892233720368547758085131514101203257266241610245927793184123074273009x+x+28823037615171174457646075230342348818014398509481984
?(x?μ)2/2σ2112假设习题4中给出的数据满足原型y(x)=e,试用最小二乘法求出μ,σ的σ
值,并用得出的函数将函数曲线绘制出来,观察拟合效果。p5(x)=?
【求解】令a1=μ,a2=σ,则可以将原型函数写成
?(x?a1)2/2a212ey(x)=a2
这时可以写出原型函数为
>>f=inline(’exp(-(x-a(1)).^2/2/a(2)^2)/(sqrt(2*pi)*a(2))’,’a’,’x’);
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第8章数据插值、函数逼近问题的计算机求解107
由原型函数则可以用下面的语句拟合出待定参数a1,a2
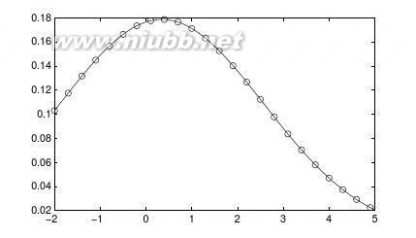
。(www.61k.com)这样,拟合曲线如图8-19所示,可见这样得出的拟合效果是例如满意的。
>>x=[-2,-1.7,-1.4,-1.1,-0.8,-0.5,-0.2,0.1,0.4,0.7,1,1.3,...
1.6,1.9,2.2,2.5,2.8,3.1,3.4,3.7,4,4.3,4.6,4.9];
y=[0.10289,0.11741,0.13158,0.14483,0.15656,0.16622,0.17332,...
0.1775,0.17853,0.17635,0.17109,0.16302,0.15255,0.1402,...
0.12655,0.11219,0.09768,0.08353,0.07019,0.05786,0.04687,...
0.03729,0.02914,0.02236];
a=lsqcurvefit(f,[1,1],x,y)
a=
0.34605753554886
plot(x0,y0,x,y,’o’)
2.23400202798747>>x0=-2:0.02:5;y0=f(a,x0);
13试将常数e用连分式形式表示,并找出能较精确近似其值的项数。
【求解】一个常数的连分式可以用下面的语句直接得出
>>maple(’with(numtheory):’);f=maple([’cfe:=cfrac(exp(1),20)’])
f=
cfe:=2+1/(1+1/(2+1/(1+1/(1+1/(4+1/(1+1/(1+1/(6+1/(1+1/(1+1/(8+
1/(1+1/(1+1/(10+1/(1+1/(1+1/(12+1/(1+1/(1+1/(14+‘...‘))))))))))))))))))))>>n=maple(’nthnumer’,’cfe’,8);d=maple(’nthdenom’,’cfe’,8);[vpa(n),vpa(d)]ans=
[1264.,
ans=
2.2586e-006465.]>>abs(exp(1)-1264/465)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
108第8章数据插值、函数逼近问题的计算机求解
保留前8项连分式展开则可以用1264/465近似e的值,得出的误差为10?6级。(www.61k.com)从部分分式展开的结果容易得出其连分式形式e??2+
1+
2+
1+
1+
4+
1+
1+
6+
1+
1+
8+
1+
1+
10+
1+
1+
12+
1+
1+
1111111111111111111114+
14试用连分式展开和Pad′e近似方法分别求出下面函数的有理式近似表达式,绘制图形观察拟合
效果,并求出具有较好拟合效果的有理式阶次。①f(x)=e
?2x
sin5x
x3+7x2+24x+24
e?3x②f(x)=4
32x+10x+35x+50x+24
【求解】①根据要求,可以用下面的语句立即得出前10级连分式表达式
>>symsx;fun=’sin(5*x)*exp(-2*x)’;
maple(’with(numtheory):’);f=maple([’cfe:=cfrac(’fun’,x,10)’])f=
cfe:=5*x/(1+2*x/(1-37*x/(12+673*x/(37+15983*x/(673+76954709*x/(79915-8067507978993*x/(58235996+37499813958898841*x/(3995793947-43179475772595131902309*x/(63348243564429-3321320335975994080588556805203*x/(20760790656566837+‘...‘))))))))))
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第8章数据插值、函数逼近问题的计算机求解
这样可以得出连分式表达式为
f(x)??5x
2x1+37x1?673x12+15983x37+76954709x673+8067507978993x79915?37499813958898841x58235996+···109
由下面的语句可以得出的分式表达式为
>>n=collect(maple(’nthnumer’,’cfe’,4),x);
d=collect(maple(’nthdenom’,’cfe’,4),x);[n,d]=numden(n/d);G1=n/d;latex(G1)
n=collect(maple(’nthnumer’,’cfe’,6),x);d=collect(maple(’nthdenom’,’cfe’,6),x);
[n,d]=numden(n/d);G2=n/d;latex(G2)
n=collect(maple(’nthnumer’,’cfe’,8),x);d=collect(maple(’nthdenom’,’cfe’,8),x);
[n,d]=numden(n/d);G3=n/d;latex(G3)
n=collect(maple(’nthnumer’,’cfe’,10),x);d=collect(maple(’nthdenom’,’cfe’,10),x);
[n,d]=numden(n/d);G4=n/d;latex(G4)
x(58x?37)
673x+96x+222?30
????x4048829x2?484416x?958980?54159714x+2833713x+2402376x+958980
76413836368455826880688951760x4?70457302668018382345794908200x3?29650677086927142000164
3884269666444572870871194074x+4245936723281196701697102592x+8314899324526819564757508720x+518336用图形可以表示拟合效果,可见n=5时近似的效果还比较理想,如图8-20所示。[www.61k.com)
>>symsx;ezplot(sin(5*x)*exp(-2*x),[0,1]);holdon
ezplot(G1,[0,1]);ezplot(G2,[0,1]);ezplot(G3,[0,1]);ezplot(G4,[0,1]);
用Pad′e近似也可以得出同样恶结果。
>>f=taylor(sin(5*x)*exp(-2*x),x,12)
f=
5*x-10*x^2-65/6*x^3+35*x^4-295/24*x^5-923/36*x^6+23323/1008*x^7+
41/24*x^8-731471/72576*x^9+126319/36288*x^10+11107139/7983360*x^11
>>symsx;ezplot(sin(5*x)*exp(-2*x),[0,1]);holdon
c=sym2poly(f);
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
110
第8章数据插值、函数逼近问题的计算机求解
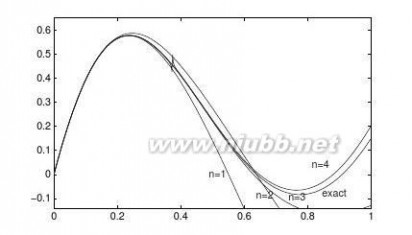
[n,d]=padefcn(c,5,6);
G=poly2sym(n)/poly2sym(d);ezplot(G,[0,1])
[n,d]=padefcn(c,3,4);
G=poly2sym(n)/poly2sym(d);ezplot(G,[0,1])
15假设习题5中数据的原型函数为z(x,y)=asin(x2y)+bcos(y2x)+cx2+dxy+e,试用最小二乘方法识别出a,b,c,d,e的数值。[www.61k.com)
【求解】用下面的语句可以用最小二乘的得出
>>[x,y]=meshgrid(0.1:0.1:1.1);
z=[0.83041,0.82727,0.82406,0.82098,0.81824,0.8161,0.81481,0.81463,0.81579,0.81853,0.82304;0.83172,0.83249,0.83584,0.84201,0.85125,0.86376,0.87975,0.89935,0.92263,0.94959,0.9801;0.83587,0.84345,0.85631,0.87466,0.89867,0.9284,0.96377,1.0045,1.0502,1.1,1.1529;0.84286,0.86013,0.88537,0.91865,0.95985,1.0086,1.0642,1.1253,1.1904,1.257,1.3222;0.85268,0.88251,0.92286,0.97346,1.0336,1.1019,1.1764,1.254,1.3308,1.4017,1.4605;0.86532,0.91049,0.96847,1.0383,1.118,1.2046,1.2937,1.3793,1.4539,1.5086,1.5335;
0.88078,0.94396,1.0217,1.1118,1.2102,1.311,1.4063,1.4859,1.5377,1.5484,1.5052;
0.89904,0.98276,1.082,1.1922,1.3061,1.4138,1.5021,1.5555,1.5573,1.4915,1.346;
0.92006,1.0266,1.1482,1.2768,1.4005,1.5034,1.5661,1.5678,1.4889,1.3156,1.0454;
0.94381,1.0752,1.2191,1.3624,1.4866,1.5684,1.5821,1.5032,1.315,1.0155,0.62477;
0.97023,1.1279,1.2929,1.4448,1.5564,1.5964,1.5341,1.3473,1.0321,0.61268,0.14763];x1=x(:);y1=y(:);z1=z(:);
A=[sin(x1.^2.*y1)cos(y1.^2.*x1)x1.^2x1.*y1ones(size(x1))];
theta=A\z1
theta=
-0.89204693251635
3.09378647090361
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第8章数据插值、函数逼近问题的计算机求解
-0.12203277931186
2.70828089435211
-2.42507028220675
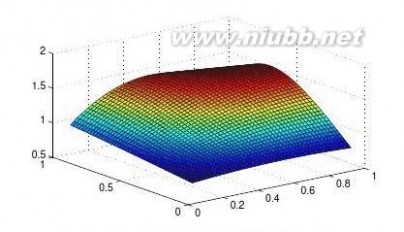
用下面的语句可以绘制出拟合结果,如图8-21所示。[www.61k.com]
>>[x,y]=meshgrid(0.1:0.02:1.1);
z=theta(1)*sin(x.^2.*y)+theta(2)*cos(y.^2.*x)+theta(3)*x.^2+...
theta(4)*x.*y+theta(5);
surf(x,y,z)111
16假设已知函数f(t)=e?3tcos(2t+p/3)+e?2tcos(t+p/4),试计算其自相关函数。
【求解】用下面的语句可以计算出自相关函数
>>symsTttau;
f=exp(-3*t)*cos(2*t+pi/3)+exp(-2*t)*cos(t+pi/4);
R=int(f*subs(f,t,t+tau),t,0,inf);latex(simple(R))
??√√τ1A其LTEX表示为?270cos(τ)+1445cos(2τ)?2652sin(τ)eτ+1989cos(τ)eτ?26520(eτ)√√√√√τ√τ510cos(2τ)+960cos(2τ)?765sin(2τ)+570sin(τ)+960cos(τ)+??√τ√√√√510sin(2τ)?1290sin(τ)?960sin(2τ)?270sin(2τ)?270cos(2τ)
t1?3e17试求出Gauss分布函数f(t)=的自相关函数,并用MATLAB函数生成一组满足3
Gauss分布的伪随机数,用这些数据检验其自相关函数是否和理论值很接近。2
【求解】用下面的语句可以计算出自相关函数
>>symsTttau;
f=exp(-t^2/2/3^2)/sqrt(2*pi)/3;
R=int(f*subs(f,t,t+tau),t,0,inf);latex(simple(R))
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
112
解出自相关函数为第8章数据插值、函数逼近问题的计算机求解
2535301200456458802993406410752√?1/36τ2Rtt(τ)=?e9557860351189671683947187847636318假设由下面的语句可以生成噪声污染的信号???1+erf??1τ6????
>>t=0:0.005:5;y=15*exp(-t).*sin(2*t);r=0.3*randn(size(y));y1=y+r;
试求出该信号的Nyquist频率,并选择滤波频率,设计出8阶Butterworth滤波器,使其能有效滤除噪声,又有较小的延迟。[www.61k.com)
【求解】Nyquist频率为250000Hz

,并可以得出被噪声污染的信号,如图8-22a所示。
>>h=0.005;t=0:0.005:5;y=15*exp(-t).*sin(2*t);
r=0.3*randn(size(y));y1=y+r;
f=t/h;Nf=floor(length(f)/2)/h
Nf=
250000
>>plot(t,y1)
图8-22滤波后信号
设计出8阶的Butterworth滤波器,这时的滤波效果如图8-22b所示,可见,对噪声信号有较好的过滤效果,但同时也带来了信号的滞后。
>>[b,a]=butter(8,0.1);y2=filter(b,a,y1);
plot(t,y2,’:’,t,y,’r-’)
选择不同的滤波频率,可以得出不同的滤波效果,比较好的滤波器为N=0.1,得出的结果仍如图8-22b所示。
19高通滤波器可以滤去低频的部分,而保留高频的部分,试为上面的数据设计一个高通滤波器,提取出噪声信号,并和叠加上的实际噪声信号r相比较。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第8章数据插值、函数逼近问题的计算机求解113
【求解】从滤波器本身性质看,高通滤波器实际上等于1减去低通滤波器,所以用相应的高
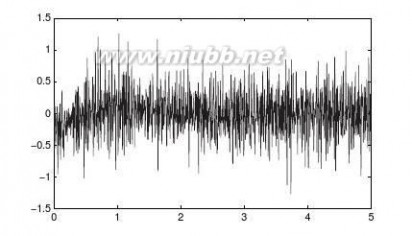
通滤波器可以得出如下的滤波效果,得出的噪声曲线如图8-23所示。[www.61k.com]
>>h=0.005;t=0:0.005:5;y=15*exp(-t).*sin(2*t);
r=0.3*randn(size(y));y1=y+r;
[b,a]=butter(8,0.6);b1=b-a;y2=filter(b1,a,y1);plot(t,y2)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第9章概率论与数理统计问题的计算机求解
x??0
x<0,试用解析推导的方?x2?x?2be1假设已知Rayleigh分布的概率密度函数为pr(x)=b2?0
随机数,用数值方法检验得出的解析结果是否正确。[www.61k.com]法求出该分布的分布函数、均值、方差、中心矩和原点矩。生成一组满足Rayleigh分布的伪
【求解】工具相应的数学定义的公式,所需的分布函数、均值、方差、中心矩和原点矩等可以由下面的语句推导出来。
>>symsx;symsbpositive
p=x*exp(-x^2/2/b^2)/b^2*heaviside(x);
>>symstau;F=int(subs(p,x,tau),tau,-inf,x)
F=
-exp(-1/2*x^2/b^2)+1
>>Emean=int(x*p,x,-inf,inf)
Emean=
1/2/b^2*2^(1/2)/(1/b^2)^(3/2)*pi^(1/2)
>>Evar=int((x-Emean)^2*p,x,-inf,inf)
Evar=
-1/2*b^2*pi+2*b^2
>>Ev=int(x^r*p,x,0,inf)
Ev=
2^(1/2*r)*b^r*gamma(1/2*r+1)
>>Evm=int((x-Emean)^r*p,x,0,inf)%不能得出解析解
MATLAB6.*版本不支持heaviside()函数,因为x<0时p=0,所以实际求解可以由下面的语句实现,得出的结果和前面一致。
>>symsx;symsbpositive
p=x*exp(-x^2/2/b^2)/b^2;
>>symstau;F=int(subs(p,x,tau),tau,0,x)
F=
-exp(-1/2*x^2/b^2)+1
>>Emean=int(x*p,x,0,inf)
Emean=
1/2/b^2*2^(1/2)/(1/b^2)^(3/2)*pi^(1/2)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第9章概率论与数理统计问题的计算机求解
>>Evar=int((x-Emean)^2*p,x,0,inf)
Evar=
-1/2*b^2*pi+2*b^2
假设b=1,则可以由下面语句
>>R=raylrnd(1,10000,1);mean(R)
>>vpa(subs(Emean,b,1))
ans=
1.26374494951941
ans=
1.2533141373155003428507825447014
>>vpa(subs(Evar,b,1))
ans=
.42920367320510344200101826572791
>>cov(R-mean(R))
ans=
0.43460979618693115
2假设某两地A、B间有6个交通岗,在各个交通岗处遇到红灯的概率均相同,为p=1/3,且中途遇到红灯的次数满足二项分布B(6,p)[56],试求出某人从A出发到达B处至少遇到一次红灯的概率。(www.61k.com)若选择不同的p值,试再绘制出至少遇到一次红灯的概率曲线。
【求解】
3某次外语考试抽样调查结果表明,学生外语考试成绩近似服从正态分布,且其均值为72分,并已知超过96分的人数占总数的2.3%,试求出考生外语成绩介于60,80之间的概率。
【求解】
4试生成满足正态分布N(0.5,1.42)的30000个伪随机数,对其均值和方差进行验证,并用直方图的方式观察其分布与理论值是否吻合,若改变直方图区间的宽度会得出什么结论。
【求解】用下面的语句可以生成随机数,并计算均值和方差,可见,其结果接近给定的数值。
>>x=normrnd(0.5,1.4,30000,1);
m=mean(x),s=std(x)
m=
0.49974242123102
s=
1.40033494141044
>>xx=-5:0.3:5;yy=hist(x,xx);bar(xx,yy/length(x)/0.3);holdon
x0=-5:0.1:5;y0=normpdf(x0,0.5,1.5);plot(x0,y0)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
116第9章概率论与数理统计问题的计算机求解
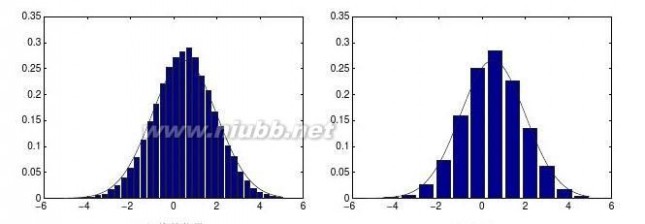
图9-1滤波后信号
>>xx=-5:0.8:5;yy=hist(x,xx);bar(xx,yy/length(x)/0.8);
holdon;plot(x0,y0)
5假设通过实验测出某组数据,试用MATLAB对这些数据进行检验。[www.61k.com]
①若认为该数据满足正态分布,且标准差为1.5,请检验该均值为0.5的假设是否成立。②若未知其方差,试再检验其均值为0.5的假设是否成立。③试对给出数据的正态性进行检验。
-1.7908
1.58031.59242.7278-0.71772-1.8152
2.8943
0.47035-1.51610.74033
2.3831-1.1251
2.32581.93183.4477
0.0903162.00330.488740.99252-2.50043.92230.32378-0.121491.08870.413512.50063.2618-1.0665
3.372
3.2303-0.118
2.9135
1.047-0.052119-0.805590.804144.6585-2.3273
-2.9145
5.3067
0.18716-0.11899-1.1234
-1.1022-0.281160.5219-0.079639-2.11760.47461-1.61810.66059
1.21221.6246
-2.67144.48271.2325-2.0178
3.1634
5.47820.0473431.2363.8942
0.45396-1.01421.12750.164012.8812
-5.01031.5649
5.69594.6927
1.6804-0.675760.200450.49816-2.14280.46528-3.87641.7065
-3.2812
0.516930.473480.73271-2.3586-0.061232-1.7976-1.2615
2.5546-1.3172-3.2431
1.3923-0.403753.3757-1.112-0.790451.8988
1.82060.625872.031-0.065217-1.9909-4.8203
-1.083-0.094030.89075-0.732591.132
-3.244
0.23873
1.0868
1.8958-0.975010.081913-3.43890.763133.357
1.2073
0.5201
2.069
-0.82998
【求解】①引入两个命题
??
H0:μ=μ0
H1:拒绝H0假设
这样
>>x=[-1.7908;0.090316;3.9223;0.41351;3.2618;-1.0665;0.51693;-1.2615;1.8206;...
-0.065217;1.5803;2.0033;0.32378;2.5006;5.6959;1.6804;0.47348;2.5546;...
μ满足要求
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第9章概率论与数理统计问题的计算机求解117
0.62587;-1.9909;1.5924;0.48874;-0.12149;3.372;4.6927;-0.67576;0.73271;
-1.3172;2.031;-4.8203;2.7278;0.99252;1.0887;3.2303;-0.118;0.20045;-2.3586;-3.2431;-1.083;1.132;-0.71772;-2.5004;2.9135;-1.1022;0.47461;0.49816;
-0.061232;1.3923;-0.09403;-3.244;-1.8152;1.047;-2.3273;-0.28116;-1.6181;-2.1428;-1.7976;-0.40375;0.89075;0.23873;2.8943;-0.052119;-2.9145;0.5219;
0.66059;1.2122;1.6246;3.3757;-0.73259;1.0868;0.47035;-0.80559;5.3067;-0.079639;-2.6714;4.4827;1.2325;-2.0178;1.8958;3.357;-1.5161;0.80414;0.18716;-2.1176;
3.1634;0.46528;1.7065;-1.112;-0.97501;1.2073;0.74033;4.6585;-0.11899;5.4782;
3.8942;-3.8764;-3.2812;-0.79045;0.081913;0.5201;2.3831;-1.1251;-1.1234;0.047343;0.45396;1.1275;2.8812;1.8988;-3.4389;2.069;2.3258;1.9318;3.4477;1.236;-1.0142;0.16401;-5.0103;1.5649;0.76313;-0.82998];
u=sqrt(length(x))*(mean(x)-0.5)/1.5
u=
-0.18857874651686
因为|u|<1.96,所以可以接受其假设。(www.61k.com]
②方差未知,则应该引入T检验
>>[H,p,ci]=ttest(x,0.5,0.02)
H=
p=
0.89494112815610
ci=
0.014056373289240.93429921004409
因为H=0,所以应该不能拒绝该检验,这时还可以得出置信区间为[0.014,0.9343]。
③采用Jarque-Bera假设检验,则可见该分布为正态分布。
>>[h,s]=jbtest(x,0.05)
h=
s=
0.99075654463354
6某研究者对随机抽取的一组保险丝进行了实验,测出使保险丝烧断的电流值为10.4,10.2,12.0,11.3,10.7,10.6,10.9,10.8,10.2,12.1A,假设这些值满足正态分布,试在置信水平
α??0.05的条件下求出这些保险丝的溶断电流及其置信区间。
【求解】方法①由normfit()函数可以直接求出置信区间,亦即溶断电流的均值为10.92
A,其置信区间为(10.43,11.41)A。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
118第9章概率论与数理统计问题的计算机求解
>>x=[10.4,10.2,12,11.3,10.7,10.6,10.9,10.8,10.2,12.1];
[m1,s1,ma,sa]=normfit(x,0.05);m1,ma
m1=
10.92000000000000
ma=
10.4327164343476811.40728356565233
方法②采用T检验函数即可判定是否接受均值为mean(x)的检验,也能求出同样的均值与置信区间
>>x=[10.4,10.2,12,11.3,10.7,10.6,10.9,10.8,10.2,12.1];
mean(x)
ans=
10.92000000000000
>>[H,p,ci]=ttest(x,mean(x),0.05)
H=
p=
1
ci=
10.4327164343476811.40728356565233
7假设在某固定气压下对水的沸点进行多次测试,得出一组数据113.53,120.25,106.02,101.05,116.46,110.33,103.95,109.29,93.93,118.67?C,并假设它们满足正态分布,试求出置信水平α??0.05的条件下,该气压下水沸点的总体方差的置信区间。[www.61k.com)
【求解】采用normfit()可以直接得出结果
>>x=[113.53,120.25,106.02,101.05,116.46,110.33,103.95,109.29,93.93,118.67];
[m1,s1,ma,sa]=normfit(x,0.05);s1,sa
s1=
8.31047638693341
sa=
5.71623824378902
15.17169031357411
8甲、乙两位化验员独立地对某种聚合物的含氮量用相同的方法各取了10次测定,其测定值的
?2?222修正样本方差S1,S2依次为0.5419和0.6050,求总体方差比σ1/σ2置信度为0.90的置信区
间.假定测定值总体服从正态分布。
【求解】
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第9章概率论与数理统计问题的计算机求解119
9假设测出某随机变量的12个样本为9.78,9.17,10.06,10.14,9.43,10.60,10.59,9.98,10.16,10.09,9.91,10.36,试求其方差及方差的置信区间。[www.61k.com)
【求解】先假设该随机变量满足状态分布,则可以用下面的语句进行检验
>>x=[9.78,9.17,10.06,10.14,9.43,10.6,10.59,9.98,10.16,10.09,9.91,10.36];
[H,p,c,d]=jbtest(x,0.05);HH=
经确认满足正态分布,所以用normfit()函数即可以求出方差及方差的置信区间
>>[m1,s1,ma,sa]=normfit(x,0.05);s1,sas1=
0.42203242012476sa=
0.298965719923050.71655956889670
1010个失眠者服用A、B两种药后,延长睡眠时间由下表给出,试判定两种药物对失眠的疗效
有无显著差异。
AB
1.90.7
0.8-1.6
1.1-0.2
0.1-1.2
-0.1-0.1
4.43.4
5.53.7
1.60.8
4.60
3.42
【求解】可以用下面语句输入两组数据,并求出均值的置信区间
>>x=[1.9,0.8,1.1,0.1,-0.1,4.4,5.5,1.6,4.6,3.4];
y=[0.7,-1.6,-0.2,-1.2,-0.1,3.4,3.7,0.8,0,2];
11假设两个随机变量A,B的样本点如下,试判定二者是否有显著差异。
AB
10.4212.94
10.4812.68
7.9811.01
8.5211.68
12.1610.57
9.749.36
10.7813.18
10.1811.38
8.7312.39
8.8812.28
10.8912.03
8.110.8
【求解】
>>A=[10.42,10.48,7.98,8.52,12.16,9.74,10.78,10.18,8.73,8.88,10.89,8.1];
B=[12.94,12.68,11.01,11.68,10.57,9.36,13.18,11.38,12.39,12.28,12.03,10.8];
12假设测出一组输入值x1,x2,x3,x4,x5和输出值y,且已知y=a1x1+a2x2+a3x3+a4x4+a5x5,
试用线性回归方法估计出ai的值及其置信区间。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
120
x1x2x3x4x5y
8.112.13-3.98-6.555.9227.676
9.252.660.68-6.857.5438.774
7.630.83-1.42-6.255.3923.314
7.891.540.96-5.344.6523.828
12.941.740.28-6.856.4735.154
第9章概率论与数理统计问题的计算机求解
10.110.79-3.37-7.25.121.779
7.570.68-4.58-6.126.0425.516
9.922.93-2.15-6.075.3729.845
7.742.01-2.66-5.516.5432.642
7.31.35-3.69-6.66.5528.443
9.482.81-1-6.155.831.5
11.912.230.98-6.433.9523.554
【求解】用下面的语句可以直接得出ai参数的值为
>>X=[8.11,9.25,7.63,7.89,12.94,10.11,7.57,9.92,7.74,7.3,9.48,11.91;
2.13,2.66,0.83,1.54,1.74,0.79,0.68,2.93,2.01,1.35,2.81,2.23;-3.98,0.68,-1.42,0.96,0.28,-3.37,-4.58,-2.15,-2.66,-3.69,-1,0.98;-6.55,-6.85,-6.25,-5.34,-6.85,-7.2,-6.12,-6.07,-5.51,-6.6,-6.15,-6.43;5.92,7.54,5.39,4.65,6.47,5.1,6.04,5.37,6.54,6.55,5.8,3.95];Y=[27.676,38.774,23.314,23.828,35.154,21.779,25.516,29.845,...
32.642,28.443,31.5,23.554];a=X’\Y’a=
1.000000000000002.000000000000000.300000000000002.000000000000005.00000000000000
拟合误差的最大值为
>>norm(X’*a-Y’)ans=
2.060573933704291e-013
13假设测出一组输入值xi和输出值yi,且已知原型函数为f(x)=a1e?a2xcos(a3x+p/3)+
a4e?a5xcos(a6x+p/4),试估计出ai的值及其置信区间。(www.61k.com)
x
1.027
1.319
1.204
0.684
0.984
0.864
0.795
0.753
1.058
0.914
1.011
0.926
y-8.8797-5.9644-7.1057-8.6905-9.2509-9.9224-9.8899-9.6364-8.5883-9.7277-9.023-9.6605
【求解】最小二乘拟合问题可以轻易由下面语句解出,拟合的效果如图9-2所示。值得指出的是,拟合结果是不唯一的,可以验证,方程y=120e?3xcos(2x+p/3)+110e?2xcos(x+p/4)也满足该数据。
>>x=[1.027,1.319,1.204,0.684,0.984,0.864,0.795,0.753,1.058,0.914,1.011,0.926];
y=[-8.8797,-5.9644,-7.1057,-8.6905,-9.2509,-9.9224,-9.8899,-9.6364,-8.5883,...
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第9章概率论与数理统计问题的计算机求解
-9.7277,-9.023,-9.6605];
121
f=inline(’a(1)*exp(-a(2)*x).*cos(a(3)*x+pi/3)+a(4)*exp(-a(5)*x).*cos(a(6)*x+pi/4)’,...
’a’,’x’);
[c,ci]=nlinfit(x,y,f,[1;2;3;4;5;6])c=
0.00040711158509-5.06015593813225-13.0843247559217496.074987216406232.144718846602081.74002018682341ci=
-0.00863222677865-0.016579920378020.008673805953680.035727120817980.016346333746850.00721778662337-0.03696112284095-0.04648093944159-0.027385586451550.027903939587940.001415029573540.02935899564930
>>[x1,ii]=sort(x);y1=y(ii);
y2=f(c,x1);plot(x1,y1,x1,y2)
14假设测出一组输入值x1,x2,x3,x4,x5和输出值y,且已知y=e?a1x1sin(a2x2+a3)+
x24cos(a4x5),试估计出ai的值及其置信区间。(www.61k.com]
x1x2x3x4x5y
8.112.13-3.98-6.555.92
9.252.660.68-6.857.54
7.630.83-1.42-6.255.39
7.891.540.96-5.344.65
12.941.740.28-6.856.47
10.110.79-3.37-7.25.1
7.570.68-4.58-6.126.04
9.922.93-2.15-6.075.37
7.742.01-2.66-5.516.54
7.31.35-3.69-6.66.55
9.482.81-1-6.155.8
11.912.230.98-6.433.95
22.126250.16-144.11-152.07234.09-318.0454.401-136.8132.03229.26-19.048-145.83
【求解】可以用下面的语句得出待定参数ai
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
122
第9章概率论与数理统计问题的计算机求解

>>X=[8.11,9.25,7.63,7.89,12.94,10.11,7.57,9.92,7.74,7.3,9.48,11.91;
2.13,2.66,0.83,1.54,1.74,0.79,0.68,2.93,2.01,1.35,2.81,2.23;
-3.98,0.68,-1.42,0.96,0.28,-3.37,-4.58,-2.15,-2.66,-3.69,-1,0.98;
-6.55,-6.85,-6.25,-5.34,-6.85,-7.2,-6.12,-6.07,-5.51,-6.6,-6.15,-6.43;
5.92,7.54,5.39,4.65,6.47,5.1,6.04,5.37,6.54,6.55,5.8,3.95];
Y=[22.1259,250.1646,-144.1066,-152.066,234.0853,-318.044,54.4014,...
-136.8012,132.0323,229.257,-19.0483,-145.8268];
f=inline(’exp(-a(1)*X(1,:)).*sin(a(2)*X(2,:)+X(3,:))+X(4,:).^3.*cos(a(3)*X(5,:))’,...’a’,’X’);
c=lsqcurvefit(f,[1;2;3],X,Y)
Optimizationterminatedsuccessfully:
RelativefunctionvaluechangingbylessthanOPTIONS.TolFun
c=
3.08179659583053
11.78076836387161
3.54384055825696
当然也可以由nlinfit()函数就可以识别其参数
>>X=[8.11,9.25,7.63,7.89,12.94,10.11,7.57,9.92,7.74,7.3,9.48,11.91;
2.13,2.66,0.83,1.54,1.74,0.79,0.68,2.93,2.01,1.35,2.81,2.23;
-3.98,0.68,-1.42,0.96,0.28,-3.37,-4.58,-2.15,-2.66,-3.69,-1,0.98;
-6.55,-6.85,-6.25,-5.34,-6.85,-7.2,-6.12,-6.07,-5.51,-6.6,-6.15,-6.43;
5.92,7.54,5.39,4.65,6.47,5.1,6.04,5.37,6.54,6.55,5.8,3.95]’;
Y=[22.1259,250.1646,-144.1066,-152.066,234.0853,-318.044,54.4014,...
-136.8012,132.0323,229.257,-19.0483,-145.8268]’;
f=inline(’exp(-a(1)*X(:,1)).*sin(a(2)*X(:,2)+X(:,3))+X(:,4).^3.*cos(a(3)*X(:,5))’,...
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第9章概率论与数理统计问题的计算机求解
’a’,’X’);
[c,ci]=nlinfit(X,Y,f,[1;2;3])c=
1.0e+003*1.426080442849962.457606957982770.00354363113884ci=
1.0e+002*-1.266536614380562.452016901491770.92407037128426-2.613929475891510.43516910883431-0.51920358880931-1.363710194755820.832442796117300.689596527561771.30361787474512-0.49826846521209-1.08775930008078
123
15设从两个不同的地区各取得某种植物的样品12个,测得植物中铁元素含量(μg/g)的数据如
下,假定已经知道这种植物中铁元素含量分布为正态,且分布的方差是不受地区影响的,检验这两个地区该种植物中铁元素含量的分布是否相同?
地区A地区B
11.516.2
18.615.2
7.612.3
18.29.7
11.410.2
16.519.5
19.217
10.112
11.218
99
1419
15.310
【求解】用下面参数可以
>>x=[11.5,18.6,7.6,18.2,11.4,16.5,19.2,10.1,11.2,9,14,15.3];
y=[16.2,15.2,12.3,9.7,10.2,19.5,17,12,18,9,19,10];
16假设可以通过实验测出如下的数据,且假设这些数据满足y(t)=c1e?5tsin(c2t)+(c3t2+
c4t3)e?3t,是根据下面的数据求出ci参数的估计值与置信区间。[www.61k.com)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
124
-0.216280.120121.87876.41157.12516.86593.66023.45562.31941.95911.7978
8.01067.02867.84167.97015.5421
6.005
2.73937.29886.46695.80744.69942.25022.20311.3541
2.72387.89036.45534.95434.53253.31672.32062.2263
第9章概率论与数理统计问题的计算机求解
4.52197.47427.36575.75555.01363.46822.36181.5807
5.08337.45946.77794.96964.35413.3062.8711.80391.73270.370770.12812
4.96997.13087.21486.0773.63013.15181.92031.61660.95505
5.59477.71327.16474.83934.03792.80772.35571.21971.3536
5.90736.06636.89817.90656.99587.16455.37995.10033.24143.053
3.6372.928
6.81668.32896.73034.40623.52582.4471.4025
4.59614.00263.20483.82182.29551.64331.928
1.2625
2.39352.4159
1.22361.69220.963351.28321.15380.61867
1.66160.937091.18680.698240.16428
1.7534
1.0259
0.625230.890350.463940.50880.940670.379410.251670.778911.36971.2397
0.766270.42491.13740.83772
1.3317
0.941261.18950.261980.600590.685010.195310.214631.36710.830171.41320.304320.1444
0.435
1.2313
0.3089
-0.0060570.592590.453080.186090.8465
0.880240.11233-0.0703640.461370.479810.746410.197450.411940.26110.102870.677130.678780.29351-0.63869
0.430651.22990.15113-0.227090.67362-0.0204060.44189
0.447981.17150.87767-0.42820.31630.0085371-0.16908-0.280060.475530.110580.347330.129780.0756030.488030.661241.3478-0.3922-0.23006
0.795040.076187-0.424510.419021.03310.60566
【求解】
>>y1=[-0.21628,0.12012,1.8787,2.7393,2.7238,4.5219,5.0833,4.9699,5.5947,5.9073,6.0663,6.8166,
6.4115,8.0106,7.0286,7.2988,7.8903,7.4742,7.4594,7.1308,7.7132,6.8981,7.9065,8.3289,7.1251,7.8416,7.9701,6.4669,6.4553,7.3657,6.7779,7.2148,7.1647,6.9958,7.1645,6.7303,6.8659,5.5421,6.005,5.8074,4.9543,5.7555,4.9696,6.077,4.8393,5.3799,5.1003,4.4062,3.6602,4.5961,4.0026,4.6994,4.5325,5.0136,4.3541,3.6301,4.0379,3.2414,3.637,3.5258,3.4556,3.2048,3.8218,2.2502,3.3167,3.4682,3.306,3.1518,2.8077,3.053,2.928,2.447,2.3194,2.2955,1.6433,2.2031,2.3206,2.3618,2.871,1.9203,2.3557,2.3935,2.4159,1.4025,1.9591,1.928,1.2625,1.3541,2.2263,1.5807,1.8039,1.6166,1.2197,1.2236,1.6922,0.96335,1.7978,1.6616,0.93709,1.1868,0.69824,0.16428,1.7327,0.95505,1.3536,1.2832,1.1538,0.61867,0.62523,0.89035,0.46394,0.5088,1.7534,1.0259,0.37077,0.94067,0.37941,0.25167,0.77891,1.3697,0.94126,1.1895,0.26198,0.60059,0.68501,
0.19531,0.12812,1.2397,0.76627,0.4249,1.1374,0.83772,0.21463,1.3671,0.83017,1.4132,1.2313,0.3089,-0.006057,0.59259,0.45308,0.18609,0.8465,1.3317,0.30432,0.1444,0.435,0.88024,0.11233,-0.070364,0.46137,0.47981,0.74641,0.19745,0.41194,0.2611,0.43065,1.2299,0.15113,-0.22709,0.67362,-0.020406,0.44189,0.10287,0.67713,0.67878,0.29351,-0.63869,0.44798,1.1715,0.87767,-0.4282,0.3163,0.0085371,-0.16908,-0.28006,0.47553,0.11058,0.34733,0.12978,0.075603,0.48803,0.66124,1.3478,-0.3922,-0.23006,0.79504,0.076187,-0.42451,0.41902,1.0331,0.60566]
17一批由同种原料织成的布,用不同的染整工艺处理,每台进行缩水串试验,目的是考察不同
的工艺对布的缩水率是否有显著影响.现采用5种不同的染整工艺,每种工艺处理4块布样,测得缩水率的百分数见表9-1。[www.61k.com]
【求解】可以得出如下的方差检验结果,得出的盒式图如图9-3所示。
>>A=[4.3,6.1,6.5,9.3,9.5;7.8,7.3,8.3,8.7,8.8;3.2,4.2,8.6,7.2,11.4;
6.5,4.2,8.2,10.1,7.8];[p,tbl,stats]=anova1(A);p,tbl
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第9章概率论与数理统计问题的计算机求解
表9-1不同工艺下的缩水率
布样1234
4.37.83.26.5
染整工艺数据
学校
6.17.34.24.2
6.58.38.68.2
9.38.77.210.1
9.58.811.47.8
123
128.1150.3140.6
134.1147.9143.1
实测身高数据133.1136.8144.5
138.9126143.7
140.8150.7148.5
127.4155.8146.4
125
表9-2不同学校实测身高数据表
p=
0.00414899690752tbl=
’Source’’Columns’’Error’’Total’
’SS’[55.1450][34.1150][89.2600]
’df’[4][15][19]
’MS’[13.7863][2.2743]
[]
’F’[6.0617]
[][]
’Prob>F’[0.0041]
[][]

图9-3缩水率的盒式图
图9-4身高的盒式图
18抽查某地区3所小学五年级男学生的身高由表9-2给出,问该地区这3所小学五年级男学生
的平均身高是否有显著差别(α=0.05)?
【求解】可以得出如下的方差检验结果,得出的盒式图如图9-4所示。(www.61k.com)
>>A=[128.1,134.1,133.1,138.9,140.8,127.4;150.3,147.9,136.8,126,150.7,155.8;
140.6,143.1,144.5,143.7,148.5,146.4];[p,tbl,stats]=anova1(A);p,tblp=
0.78379156988812tbl=
’Source’’Columns’
’SS’[
211.3361]
’df’[5]
’MS’[42.2672]
’F’[0.4813]
’Prob>F’[0.7838]
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
126
’Error’’Total’
[1.0538e+003][1.2651e+003]
第9章概率论与数理统计问题的计算机求解
[12][17]
[87.8167]
[]
[][]
[][]
19下表记录了3位操作工分别在4台不同机器上操作的日产量,试检验
①操作工之间的差异是否显著?②机器之间的差异是否显著?③交互作用是否显著(α=0.05)?
机器M1M2
1517
11517
1717
1915
操作工
21915
1615
1619
31822
2122
机器M3M4
1518
11720
1622
1815
操作工
21716
1617
1817
31817
1817
【求解】
>>A=[15,15,17,19,19,16,16,18,21;17,17,17,15,15,15,19,22,22;
15,17,16,18,17,16,18,18,18;18,20,22,15,16,17,17,17,17];[p,tbl]=anova2(X)p=
0.2887tbl=
’Source’’Columns’’Rows’’Error’’Total’
’SS’[[
43]2.7500]
’df’[8][3][24][35]
’MS’[5.3750][0.9167][4.1250]
[]
’F’[1.3030][0.2222]
[][]
’Prob>F’[0.2887][0.8800]
[][]
0.8800
[99.0000][144.7500]
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第10章数学问题的非传统解法
1考虑一个餐馆小费付费问题[24],假设平均小费为15%消费,试根据服务水平(例如可以分为好、中、差或更详细的分段)和食物质量(也可以根据实际情况分成若干段)建立起小费确定的模糊推理系统。[www.61k.com)【求解】(略)
2已知如下的样本点(xi,yi)数据,试利用神经网络理论在x∈(1,10)求解绘制出样本对应的函数曲线。还可以尝试不同的神经网络结构和训练算法,将基于神经网络的曲线拟合结果和前面介绍的分段三次多项式插值的算法进行比较。
xiyi
1244.0
2221.0
3208.0
4208.0
5211.5
6216.0
7219.0
8221.0
9221.5
10220.0
【求解】可以选择6个隐层节点,每层的传输函数均选为tansig(),这样就可以构造并训练出所需的神经网络了。
>>x=1:10;
y=[244.0,221.0,208.0,208.0,211.5,216.0,219.0,221.0,221.5,220.0];net=newff([0,10],[5,1],{’tansig’,’purelin’});net.trainParam.epochs=100;net=train(net,x,y)
3假设已知实测数据由下表给出,试利用神经网络对(x,y)在(0.1,0.1)~(1.1,1.1)区域内的点进行插值,并用三维曲面的方式绘制出基于神经网络的插值结果。
yi0
x10.1
x20.2
x30.3
x40.4
x50.5
x60.60.81610.92841.00861.10191.20461.3111.41381.50341.56841.5964
x70.7
x80.8
x90.9
x101
x111.10.98011.15291.32221.46051.53351.50521.3461.04540.62477
%设置最大步数
0.10.830410.827270.824060.820980.818240.30.835870.843450.856310.874660.898670.40.842860.860130.885370.918650.959850.50.852680.882510.922860.973460.60.865320.910490.968470.70.880780.943960.80.899040.982760.90.920061
0.943811.10.97023
1.02661.07521.1279
1.02171.0821.14821.21911.2929
1.03831.11181.19221.27681.36241.4448
1.03361.1181.21021.30611.40051.48661.5564
0.814810.814630.815790.818530.823040.963771.06421.17641.29371.40631.50211.56611.58211.5341
1.00451.12531.2541.37931.48591.55551.56781.50321.3473
1.05021.19041.33081.45391.53771.55731.48891.3151.0321
1.11.2571.40171.50861.54841.49151.31561.0155
0.20.831720.832490.835840.842010.851250.863760.879750.899350.922630.94959
0.612680.14763
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
128第10章数学问题的非传统解法
4DeJong最优化问题[5]是一个富有挑战性的最优化基准测试问题,其目标函数为
22
J=minxTx=min(x21+x2+···+x20)
x
x
若?512??xi??512,i=1,2,···,20,试用遗传算法得出其最优化问题的解,并用普通的无约束最优化算法函数fminunc()求解同样的问题,比较两种方法所需的时间和精度。(www.61k.com)显然,该问题的全局最优解为x1=x2=···=x20=0。【求解】可以写出最优化的目标函数
function[sol,y]=c10dejong(sol,opts)x=sol(1:20);y=-(x(:).’)*x(:);这样就可以用遗传算法直接求解
>>[abc]=gaopt(512*[-ones(20,1)ones(20,1)],’c10dejong’);aa=
1.0e+003*-0.0015-0.00680.0104
-0.01380.00320.0100
-0.0146-0.0116-5.2321
-0.0057-0.0281
-0.0530-0.0029
-0.01230.0060
0.0164-0.0057
0.0131-0.0098
0.00100.0057
显然,该解是错误的,这说明选择的代数偏小,若将代数设置成1500,则可以用下面的语句来搜索最优化问题的解,最终得出接近0的解。可见这样得出的解的精度是令人满意的。
>>[abc]=gaopt(512*[-ones(20,1)ones(20,1)],’c10dejong’,...
[],[],[],’maxGenTerm’,1500);a
a=
-0.0001-0.0007-0.0007
-0.0003-0.0002-0.0026
-0.0002-0.0010-0.0000
0.0007-0.0009
-0.00050.0001
-0.0011-0.0003
0.0012-0.0005
-0.00040.0006
0.0001-0.0007
利用MATLAB7.0中提供的遗传算法与直接搜索工具箱可以在100代内得出如下的结果。
>>f=@(x)x(:).’*x(:);
x=ga(f,20)x=
-0.06410.02950.0913
-0.0343-0.04590.0999
-0.0876-0.0078
0.0424-0.0023
0.0977-0.0197
-0.1673-0.0017
0.03920.0522
0.06980.0866
-0.0665-0.0070
5假设由下面的语句可以生成噪声污染的信号t=0:0.005:5;y=15*exp(-t).*sin(2*t);r=0.3*randn(size(y));y1=y+r;试利用小波分解与小波重建方法对该信号进行滤波处理,并和第8章习题中采用的方法进行比较。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第10章数学问题的非传统解法129
【求解】
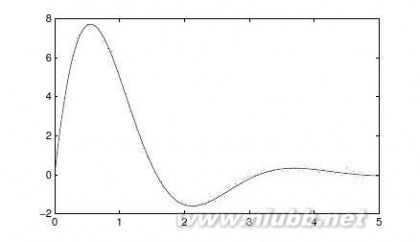
可以用三级小波分解的分式可以立即得出滤波后的效果曲线,如图10-1所示。[www.61k.com)从得出的曲线看,这样得出的曲线能够很好地完成滤波任务。
>>t=0:0.005:5;y=15*exp(-t).*sin(2*t);r=0.3*randn(size(y));y1=y+r;
[c,L]=wavedec(y1,3,’db4’);
y2=wrcoef(’a’,c,L,’db4’,3);
plot(t,y,t,y2,’:’)
6试利用遗传算法求解下面的有约束最优化问题,并和传统数值方法进行比较。????????131.5maxx1x2(1+x5)+x3x41+?2cosxx53336?0.003079xxx5?cosx6??012????3323?0.1017xx?34?x5cosx6??0???322????0.09939(1+x5)x1x2?cosx6??0
222xs.t.0.1076(31.5+x5)x33x4?x5cosx6??0????x3x4(x5+31.5)?x5[2(x1+5)cosx6+x1x2x5]??0??????0.2??x1??0.5,14<??x2??22,0.35??x3??0.6,????16??x4??22,5.8??x5??6.5,0.14??x6??0.2618
【求解】可以写出如下的目标函数
functiony=exc10f1(x)
y=1/(2*cos(x(6)))*(x(1)*x(2)*(1+x(5))+x(3)*x(4)*(1+31.5/x(5)));
if(-0.003079*x(1)^3*x(2)^3*x(5)+cos(x(6))^3>=0|...
-0.1017*x(3)^3*x(4)^3+x(5)^2*cos(x(6)))^3>=0|...
-0.09939*(1+x(5))*x(1)^3*x(2)^2+cos(x(6))^2>=0|...
-0.1076*(31.5+x(5))*x(3)^3*x(4)^2+x(5)^2*cos(x(6))^2>=0|...
-x(3)*x(4)*(x(5)+31.5)+x(5)*(2*(x(1)+5)*cos(x(6))+x(1)*x(2)*x(5))>=0)
y=1e100;
end
这样用遗传算法可以得出如下的结果。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
130
>>xm=[0.2;14;0.35;16;5.8;0.14];
xM=[0.5;22;0.6;
ans=
0.20867038931128
17.90896848486194
0.39158907718346
17.97144522871530
6.04207245703139
0.14000000014558
>>exc6fun5(x)
ans=
35.3677106402546922;6.5;0.2618];第10章数学问题的非传统解法[a,b,c]=gaopt([xmxM],’exc10f2’,[],[],[],’maxGenTerm’,1000);x=a(1:6)’
遗传算法再运行一次,可能得出这样的结果,其目标函数值更优
>>[a,b,c]=gaopt([xmxM],’exc10f2’,[],[],[],’maxGenTerm’,1000);x=a(1:6)’x=
0.22011024113285
16.59786719986876
0.37680249400478
19.54238347314203
6.46699491298085
0.14000000000000
>>exc6fun5(x)
ans=
35.60364473155970
考虑前面第6章的习题,得出如下的最优结果,其函数值不如遗传算法得出的结果。(www.61k.com]>>xm=[0.2;14;0.35;16;5.8;0.14];
xM=[0.5;22;0.6;22;6.5;0.2618];
A=[];B=[];Aeq=[];Beq=[];x0=(xm+xM)/2;
ff=optimset;ff.TolX=1e-10;ff.TolFun=1e-20;
x=fmincon(’exc6fun5’,x0,A,B,Aeq,Beq,xm,xM,’exc6fun5a’,ff)
x=
0.20124417463214
18.36290007737820
0.35957532400838
18.57799951563967
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第10章数学问题的非传统解法
5.80000000000000
0.26179905972118
>>exc6fun5(x)
ans=
35.24568192186342131
7假设通过实验测出一系列数据,可以列出一个60×13的表格,由文件c10rsdat.txt给出,其中每行为一个样本,前12列每列对应一个条件,最后一列表示某事件是否发生的标志,试用粗糙集的方法找出前12个条件中哪些条件对事件的发生起着重要的作用。(www.61k.com)
【求解】由粗糙集工具箱中函数可以立即判定出第3458910列数据对事件发生其作用,其余条件是没有作用的,可以约去。
>>loadc10rsdat.txt
c=1:12;d=13;
a=redu(c,d,c10rsdat)
a=
3458910
8给定信号f(t)=e?3tsin(t+p/3)+t2+3t+2,试利用定义计算出该函数的0.2阶微分信号及0.7阶积分信号,并将结果信号用曲线表示出来。
【求解】

该信号的分数阶微积分曲线可以用下面语句直接绘制出来,如图10-2所示。
>>t=0:0.01:5;
y=exp(-3*t).*sin(t+pi/3)+t.^2+3*t+2;
dy=glfdiff(y,t,0.2);
iy=glfdiff(y,t,-0.7);
plot(t,dy,t,iy,t,y)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
132第10章数学问题的非传统解法9分别为上面给出的信号设计出连续和离散滤波器,并对该信号进行分数阶微积分运算,和前面介绍出的较精确的数值结果相比较,研究所用方法的精度。(www.61k.com)
【求解】连续滤波器可以由下面的语句设计,从而可以用两种方法得出函数的0.2阶微分信
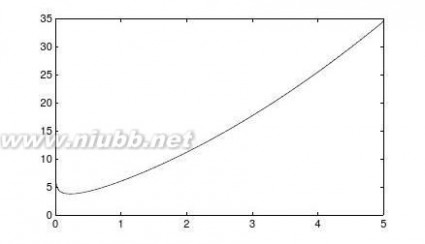
号,这样二者在图10-3中给出,可见,二者很接近。
>>G=ousta_fod(0.2,2,0.01,100),
2.512s^5+98.83s^4+531.7s^3+442.3s^2+56.87s+1
-----------------------------------------------------------
s^5+56.87s^4+442.3s^3+531.7s^2+98.83s+2.512
>>t=0:0.01:5;
y=exp(-3*t).*sin(t+pi/3)+t.^2+3*t+2;
dy=glfdiff(y,t,0.2);
dy1=lsim(G,y,t);plot(t,dy,’-’,t,dy1,’:’)
10考虑第10.6节中介绍的IIR滤波器,该滤波器可以很好地拟合Bode图中的相位特性,但在高频下放大倍数迅速增高,所以对高频噪声有放大作用,这显然是实际应用中不希望的,试研究在其后设计低通滤波器的方法改善这样的滤波器效果。
【求解】FIR滤波器可以由下面的语句得出,得出的滤波效果如图10-4所示。可见,即使选择滤波器的阶次为1000,得出的效果和精确值仍有很大的差异。
>>t=0:0.001:5;
y=exp(-3*t).*sin(t+pi/3)+t.^2+3*t+2;
dy=glfdiff(y,t,0.2);
G1=dfod2(50,0.001,0.2);y1=filter(G1.num{1},G1.den{1},y);
G1=dfod2(800,0.001,0.2);y2=filter(G1.num{1},G1.den{1},y);
G1=dfod2(1000,0.001,0.2);y3=filter(G1.num{1},G1.den{1},y);
plot(t,dy,t,y1,t,y2,t,y3)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第10章数学问题的非传统解法
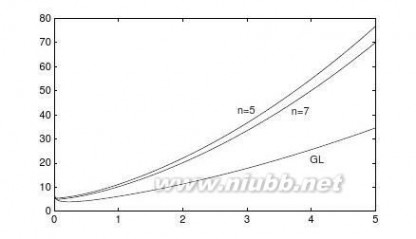
133
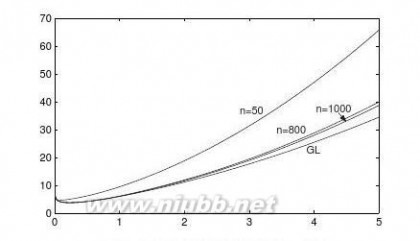
利用IIR滤波器,可见7阶以上的滤波器趋于不稳定,故可以得出如图10-5所示的滤波效果,然而这样的滤波器与GL定义的值相差甚远。[www.61k.com)
>>H1=iir_frac(0.2,0,5,0.001);H2=iir_pade(0.2,0.5,7,0.001);
y1=filter(H1.num{1},H1.den{1},y);
y2=filter(H2.num{1},H2.den{1},y);
plot(t,dy,t,y1,t,y2)
11假设已知分数阶线性微分方程为[38]
2.20.90.8Dty(t)+0.5Dty(t)+y(t)=1,y(0)=y??(0)=y????(0)=0
试求该微分方程的数值解。若将微分阶次2.2近似成2,0.9阶近似成1阶,则可以将该微分方程近似为整数阶微分方程,试比较整数阶近似的计算精度。
【求解】用下面的语句可以直接求解给出的分数阶微分方程,并用整数阶近似原微分方程,得出近似解,由图10-6给出,可见二者有一定的相似性。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
134
>>a=[0.8,0.5,1];n=[2.20.90];第10章数学问题的非传统解法
t=0:0.002:10;u=ones(size(t));y=glfode(u,t,a,n);
symsst1;
Y=1/(0.8*s^2+0.5*s+1)/s;y1=ilaplace(Y,s,t1);
y1=subs(y1,t1,t);
plot(t,y,t,y1,’:’)
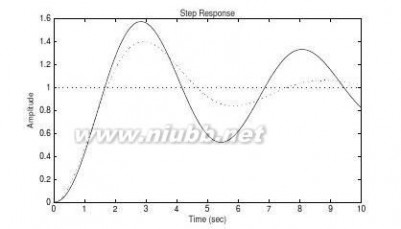
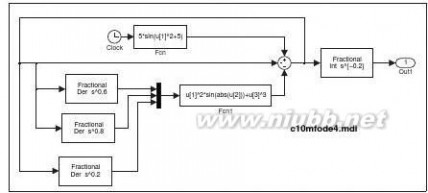
图10-6线性分数阶微分方程的解及整数阶近似曲线
12设分数阶非线性微分方程由图10-7中的Simulink模型描述,试写出该微分方程的数学表达式,并绘制出输出信号y(t)。(www.61k.com]
图10-7非线性分数阶微分方程的Simulink描述
【求解】可以由给出的Simulink仿真模型为
????2????3D0.2y(t)=5sin(2t+5)?D0.2y(t)?D0.8y(t)sinD1y(t)?D0.4y(t)
这样就可以得出如图10-8所示的仿真结果。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
第10章数学问题的非传统解法135
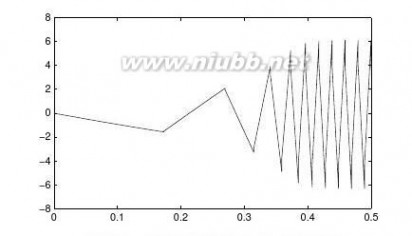
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
附录自由数学语言Scilab简介
1用Scilab语句绘制出y(x)=sin(1/t)在t∈[?p,p]区间内的曲线。[www.61k.com]
【求解】和MATLAB一样,Scilab也支持不等间距图形绘制功能。仿照MATLAB语句,可

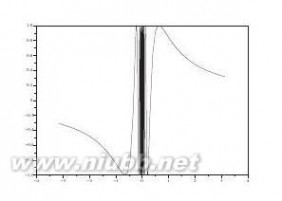
以尝试下面的语句来绘制图形,得出如图A-1a所示的结果。
-->x=[-%pi:0.1:-0.3,-0.29:0.001:0.29,0.3:0.1:%pi,%pi];
plot(x,sin(1./x))
(a)错误结果(b)正确结果
图A-1sin(1/t)曲线绘制
不幸的是,这样的结果显然是错误的,因为1./x得出的结果和MATLAB是不同的,这在编程时应该格外注意。例如,
-->xx=[1234];1./xx
ans
!
!
!
!=.0333333!.0666667!.1!.1333333!
要想解决这样的问题,需要将分子也做成和分母同阶的矩阵,亦即给出下面的指令(亦有错)-->y=sin(ones(x)./x);
!--error
divisionbyzero...27
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
附录自由数学语言Scilab简介137
产生错误的原因是x向量含有0值。(www.61k.com]从错误信息上看,得出的结果出现了“除0”的错误,使得程序终止,这显然和MATLAB是不一致的,MATLAB下给出的是警告信息,相应的点为Inf,不影响实际程序运行。解决该问题可以用下面语句,最终绘制出如图A-1b所示的正确曲线。
-->i=find(x==0);x(i)=[];//剔除x=0点
y=sin(ones(x)./x);plot(x,y)
通过这个例子可以看出,处理同样的问题,用MATLAB语言比用Scilab语言要简明得多。2对下面给出的各个矩阵求取各种参数,如矩阵的行列式、迹、秩、特征多项式、范数、逆矩阵、特征值与特征向量等,并求出eA、eB。
???7.53.50057?8??334.10??710A=?,B=?0?689103?1.5?
57003.719.3
【求解】(a)A矩阵的分析
-->A=[7.53.500;8334.10;09103-1.5;003.719.3]
A
!
!
!
!
ans=7.58.0.0.=
432221.
-->trace(A)
ans=
162.8
-->rank(A)
ans=
4.
-->poly(A,’x’)
ans=
2
-->norm(A)
ans=
103.7228534432221-106590.65x+7129.2x-162.8x+x3.533.9.0.0.4.1103.3.70.0.-1.5!!!?57??9?106810919.3!-->det(A)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
138
-->inv(A)ans!!-!!-d!!!!v!!-!!-ans!!!!
=
6.4308386000=
.9559930.2920317.0270956.0077902=.0193592.53077469.0837728.3993582
.23221396.3666368108.959784.7902982
1.810446449.637233849.5006237.347371
-----.1320356.9823820.1280082.0332583
----.0021255.0582753.9973349.0438467
--0
33.54098200
00
103.459930
000
=.1505519.0368969.0032150.0006164
--.0161424.0345908.0030141.0005778
--.0006408.0013731.0098014.0018790
-
附录自由数学语言Scilab简介
.0000498!.0001067!.0007618!.0516674!
-->[v,d]=spec(A)
!!!
19.368245!.0013944!.0047283!.0184413!.9998178!
-->expm(A)
1.0E+42*
.0322680!.8846947!.6656500!
-15.140826!
(b)B矩阵分析
-->B=[5765;71087;68109;57910]B=!!!!ans
5.7.6.5.=1.-->rank(B)ans
=4.
7.10.8.7.
6.8.10.9.
5.7.9.
!!!
10.!
-->det(B)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
附录自由数学语言Scilab简介
-->trace(B)ans
=35.-->poly(B,’x’)ans
=
2
-->inv(B)ans!
=68.
-41.25.10.-6.
-17.10.5.-3.
10.!-6.-3.2.
!!!3
4
1-100x+146x-35x+x
139
!-41.!-17.!d!!!!v!!-!-!ans!!!
==10.
-->[v,d]=spec(B)
.01015000.0.0..8304438.5015651.2085536.1236975=3408.39043506.74912373.082
4262.52714395.87922967.6478
3990.3859!4101.3149!2778.5753!
?21?1
--0..84310710.0..0933050.3016523.7603184.5676407
--0.0.3.85805750..3963056.6148613.2716010.6253962
0.0.0.
!!!
30.288685!.3802621!.5285678!.5519548!.5209248!
-->expm(B)
3求解下面的Sylvester方程,并检验所得解的精度。(www.61k.com)
?????1232361?456?X+X?352?=?37803225
3
42
【求解】Scilab下用sylv()函数可以求解该方程,注意和MATLAB的lyap()函数在C矩阵上符号是有差别的。
-->A=[123;456;780];
B=[236;352;322];
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
140
C=[132;341;521];
X=sylv(A,B,C,’c’)
X
!
!
!-
ans=.4058824.1936652.1183258=
4.555E-15-.1434641.0980895.5237808--.2267974!.3416792!.2417295!附录自由数学语言Scilab简介-->norm(A*X+X*B-C)
4用数值方法求解下面的常微分方程
?????2119?201???˙=19?2120y,y0=0?y
40?40?40?1
【求解】可以用Scilab的deff()函数动态定义系统的状态方程模型,然后选择t向量,解出
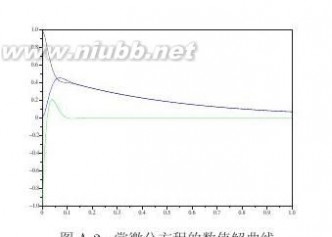
系统的状态方程解,如图A-2所示。[www.61k.com)
-->deff(’dx=myeq(t,x)’,’dx=[-2119-20;19-2120;40-40-40]*x’);
t=10;x0=[1;0;-1];t=0:.01:10;
x=ode(x0,0,t,myeq);plot2d(t’,x)
5求解下面的有约束最优化问题
??
min?222???x1+x2+x3?25=0
xs.t.8x1+14x2+7x3?56=0???x1,x2,x3??01000?x21?2x22?x23???x1x2?x1x3
【求解】用下面的语句可以直接求解最优化问题。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
附录自由数学语言Scilab简介
-->deff(’y=f1(x)’,’y=1000-x(1)^2-2*x(2)^2-x(3)^2-x(1)*x(2)-x(1)*x(3)’);deff(’[y,yeq]=fc(x)’,...
[’y=[-x(1);x(2);x(3)];’,...
’yeq=[x(1)^2+x(2)^2+x(3)^2-25;8*x(1)+14*x(2)+7*x(3)-56]’]);
x=optim(f1,fc,[1;1;1])141
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
参考文献
[1]AthertonDP,Xue,D.TheanalysisoffeedbacksystemswithpiecewiselinearnonlinearitieswhensubjectedtoGaussianinputs.In:KozinF,OnoT(eds.).Controlsystems,topicsontheoryandapplication,pp23-38.Tokyo:MitaPress,1991
[2]BosleyMJ,KrophellerHW,andLeesFP.Ontherelationbetweenthecontinuedfractionexpansionandmomentsmatchingmethodsofmodelreduction.InternationalJournalofControl,18:461-474,1973
[3]陈传璋,金福临,朱学炎等.数学分析.北京:人民教育出版社,1979
[4]ChenYQ,VinagreBM.AnewIIR-typedigitalfractionalorderdi?erentiator.SignalProcessing,83:2359-2365,2003
[5]Chipper?eldA,FlemingP,etal.Geneticalgorithmtoolboxuser’sguide.DepartmentofAutomaticControlandSystemsEngineering,UniversityofShe?eld,1994
[6]ConoverWJ.Practicalnonparametricstatistics.NewYork:Wiley,1980
[7]DongarraJJ,BunshJR,MolorCB.LINPACKuser’sguide.Philadelphia:SocietyofIndustrialandAppliedMathematics(SIAM),1979
[8]ForsytheGE,MalcolmMA,MolerCB.Computermethodsformathematicalcomputations.EnglewoodCli?s:Prentice-Hall,1977
[9]FrankG.TheMapleBook,Chapman&Hall/CRC,2001
[10]GarbowBS,BoyleJM,DongarraJJ,MolerCB.Matrixeigensystemroutines—EISPACKguideextension,Lecturenotesincomputersciences.Vol.51,NewYork:Springer-Verlag,1977
[11]GongzalezRC,WoodsRE.Digitalimageprocessing(2nded).EnglewoodCli?s:Prentice-Hall,2002(电子工业出版社有影印版)。[www.61k.com)
[12]HaganMT,DemuthHBandBealeMH.Neuralnetworkdesign.PWSPublishingCompany,1995,中译本:戴葵等译.神经网络设计.机械工业出版社,2002
[13]何文章,桂占吉,贾敬.大学数学实验.哈尔滨:哈尔滨工程大学出版社,1999
[14]HilferR.Applicationsoffractionalcalculusinphysics.Singapore:WorldScienti?c,2000
[15]Holmstr¨omK,G¨oranAandEdvallMM.User’sguideforTomLAB4.1.0,电子版,2000
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
参考文献143
[16]HouckCR,JoinesJA,KayMG.Ageneticalgorithmforfunctionoptimization:a
MATLABimplementation.GAOT工具箱手册电子版,1995
[17]胡包钢,赵星,康孟珍.科学计算自由软件SCILAB教程.北京:清华大学出版
社,2003
[18]胡运权主编.运筹学教程.北京:清华大学出版社,1998
[19]黄琳.系统与控制理论中的线性代数.北京:科学出版社,1984
[20]KnuthDE.TheTEXbook:VolumnAofcomputersandtypesetting.ReadingMA:
Addison-WesleyPublishingCompany,1986
A[21]LamportL.LTEX:adocumentpreparationsystem—user’sguideandreference
manual.ReadingMA:Addision-WesleyPublishingCompany,2ndedition,1994
[22]李岳生,黄友谦.数值逼近.北京:人民教育出版社,1978
[23]陆璇.应用统计.北京:清华大学出版社,1999
[24]MathWorks.Fuzzylogictoolboxuser’smanual,2004
[25]MathWorks.Geneticalgorithmanddirectsearchtoolboxuser’smanual,2004
[26]MathWorks.Signalprocessingtoolboxuser’smanual,2004
[27]MathWorks.UsingMATLAB(MATLAB用户手册),2004
[28]MathWorks.Simulinkuser’smanual.2004
[29]MolerCB.MATLAB—AnInteractiveMatrixLaboratory.TechnicalReport369,
DepartmentofMathematicsandStatistics,UniversityofNewMexico,1980.
[30]MolorCB.NumericalComputingwithMATLAB.MathWorksInc,2004
[31]MolerCB,StewarGW.Analgorithmforgeneralizedmatrixeigenvalueproblems.
SIAMJournalofNumericalAnalysis.10:241-256,1973
[32]MolerCB,VanLoanCF.Nineteendubiouswaystocomputetheexponentialofa
matrix.SIAMReview,20:801-836,1979
[33]NelderJA,MeadR.Asimplexmethodforfunctionminimization.ComputerJournal,
7:308-313,1965
[34]NumericalAlgorithmGroup.NAGFORTRANlibrarymanual.1982
[35]OustaloupA,LevronF,MathieuB,NanotFM.Frequency-bandcomplexnoninteger
di?erentiator:characterizationandsynthesis.IEEETransactiononCircuitandSystems-I:FundamentalTheoryandApplications,47(1):25-39,2000
[36]PawlakZ.Roughsets—theoreticalaspectsofreasoningaboutdata.Boston:Kluwer
AcademicPub.,1991
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答
144参考文献
[37]Petr′aˇsI,PodlubnyI,O’LearyPetal.Analoguerealizationoffractionalorder
controllers.FakultaBERG,TUKoˇsice,2002
[38]PodlubnyI.Fractionaldi?erentialequations.SanDiago:AcademicPress,1999
[39]PressWH,FlanneryBP,TeukolskySA,andVitterlingWT.Numericalrecipes,
theartofscienti?ccomputing.Cambridge:CambridgeUniversityPress,1986
[40]邵军力,张景,魏长华.人工智能基础.北京:电子工业出版社,2000
[41]《数学手册》编写组.数学手册.北京:人民教育出版社,1979
[42]SmithBT,BoyleJM,DongarraJJetal.Matrixeigensystemroutines–EISPACK
guide,Lecturenotesincomputersciences.Vol.6(Secondedition).NewYork:Springer-Verlag,1976
[43]TsengC-C,PeiS-C,HsiaS-C.ComputationoffractionalderivativesusingFourier
transformanddigitalFIRdi?erentiator.SignalProcessing,80:151-159,2000
[44]汪培庄.模糊集合论及其应用.上海:上海科学技术出版社,1983
[45]王小平,曹立明.遗传算法——理论、应用与软件实现.西安:西安交通大学出版
社,1998
[46]王珏.Roughset约简与数据浓缩.高技术通讯,11:40-45,1997
[47]VinagreBMandYangQuanChen.Fractionalcalculusapplicationsinautomatic
controlandrobotics.41stIEEECDC,Tutorialworkshop2,LasVegas,2002.
[48]WolframS.TheMathematicabook.CambridgeUniversityPress,1988
[49]武汉大学,山东大学.计算方法.北京:人民教育出版社,1979
[50]西安交通大学高等数学教研室编.复变函数(第二版).北京:人民教育出版社,1981
[51]XueD.Modelreductionapproachesforcontrolsystems.东北大学讲义,1994
[52]薛定宇,陈阳泉.基于MATLAB/Simulink的系统仿真技术与应用.北京:清华大学
出版社,2002
[53]ZadehLA.Fuzzysets.InformationandControl,8:338-353,1965
[54]张化光,王智良,黄伟.混沌系统的控制理论.沈阳:东北大学出版社,2003
[55]张雪峰.粗糙集数据分析系统应用平台的研究与程序开发.沈阳:东北大学硕士学位
论文,2004
[56]赵选民,师义民.概率论与数理统计典型题分析解集.西安:西北工业大学出版
社,1999
[57]中山大学数学力学系.概率论与数理统计.北京:人民教育出版社,1980
三 : 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
50第5章积分变换与复变函数问题的计算机求解
若想对得出的结果进行检验,则可以对结果进行Z反变换,再对结果进行Laplace变换,观察是否能还原成原给出的函数,经过验证,可以看出得出的结果完全正确。(www.61k.com]
>>f1=simple(laplace(iztrans(f)))
f1=
b/s^2/(s+a)
????????az(Az+B)?akT12用计算机证明Z1?ecos(bkT)+sin(bkT)=,b(z?1)(z2?2e?aTcos(bT)z+e?2aT)
aa式中A=1?e?aTcos(bT)?e?aTsin(bT),B=e?2aT+e?aTsin(bT)?e?aTcos(bT)。bb
【求解】证明等号两边的差为零则可以证明等式,故可以用下面的语句证明该等式。
>>symsabkT;
f=1-exp(-a*k*T)*(cos(b*k*T)+a/b*sin(b*k*T));
F=ztrans(f)
F=
z/(z-1)-(z/exp(-a*T)-cos(b*T))*z/exp(-a*T)/(z^2/exp(-a*T)^2-
2*z/exp(-a*T)*cos(b*T)+1)-a/b*z/exp(-a*T)*sin(b*T)/(z^2/exp(-a*T)^2-
2*z/exp(-a*T)*cos(b*T)+1)
>>A=1-exp(-a*T)*cos(b*T)-a/b*exp(-a*T)*sin(b*T);
B=exp(-2*a*T)+a/b*exp(-a*T)*sin(b*T)-exp(-a*T)*cos(b*T);
R=(z*(A*z+B))/((z-1)*(z^2-2*exp(-a*T)*cos(b*T)*z+exp(-2*a*T)));
simple(F-R)
ans=
x2+4x+313试求出f(x)=e?5x的奇点、奇点重数及各个奇点处的留数。x+4x+3x+2x+5x+2
【求解】可以通过部分分式展开的方法得出不含有e?5x的函数为
>>symsx;F=(x^2+4*x+3)/(x^5+4*x^4+3*x^3+2*x^2+5*x+2);
F1=residue(F,x)
F1=
.36884528691474116546123212343386/(x+.45724164080327398113522153431736)+(-.22945647070219925912151734772687+.25494104062724336140044336717309*i)/(x-.42435341429491731455583339444997+.95306503142068537993544636676469*i)-(.22945647070219925912151734772687+.25494104062724336140044336717309*i)/(x-.42435341429491731455583339444997-.95306503142068537993544636676469*i)+.87010455388092257243752819445340e-1/(x+1.2999198059930349140607395655546)+.30571991015650955380497525745543e-2/(x+3.0915453817935257339157056890279)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
第5章积分变换与复变函数问题的计算机求解51
可以得出该函数可以写成a/(x+b),这样b为奇点,ae?5b则为相应的留数,这样可以得出函数的奇点和留数在下表中给出。[www.61k.com)奇点
-.45724164080327398113522153431736
0.42435341429492±j0.95306503142069
-1.29991980599303
-3.09154538179353
14试求出下面有理函数的部分分式展开
G(s)=s+5
s+21s+181s+839s+2330s+4108s+4620s+3100s+1000留数0.03749355589649-0.03195888822474?j0.0258386112737657.851075189953751.579534887213670e+004
A并用LTEX的形式比较好地显示得出的结果。【求解】下面的语句可以直接求解本习题中的问题,并得出数学显示如下。
>>symss
F=(s+5)/(s^8+21*s^7+181*s^6+839*s^5+2330*s^4+4108*s^3+4620*s^2+3100*s+1000);f=residue(F,s)
f=
(-7/2312-23/2312*i)/(s+1+i)^2+(-517/39304+143/9826*i)/(s+1+i)+(-7/2312+23/2312*i)/(s+1-i)^2-(517/39304+143/9826*i)/(s+1-i)+1/36/(s+2)-1/867/(s+5)^2-65/44217/(s+5)
?235171437235171437?j?j?j+j???s+1+js+1?j(s+1+j)(s+1??)
1165+??36(s+2)867(s+5)44217(s+5)
15求下面的封闭环路积分。??z15
①dz,其中Γ为|z|=3正向圆周Γ(z?1)(z?2)??z31/z②edz,其中Γ为|z|=2正向圆周1+zΓ
【求解】
>>symsz;F=z^(15)/((z^2-1)^2*(z^4-2)^3);
residue(F,z);vpa(ans,10)
ans=
-.2500000000/(z-1.)^2-6.500000000/(z-1.)+.2500000000/(z+1.)^2-
6.500000000/(z+1.)-.7582521470e-2/(z+1.189207115*sqrt(-1))^3-
.5200904179e-1*sqrt(-1)/(z+1.189207115*sqrt(-1))^2+
.1412427894/(z+1.189207115*sqrt(-1))+.2575825204/(z-1.189207115)^3-
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
52第5章积分变换与复变函数问题的计算机求解
.6837753459/(z-1.189207115)^2+6.858756405/(z-1.189207115)-
.7582521470e-2/(z-1.189207115*sqrt(-1))^3+
.5200904179e-1*sqrt(-1)/(z-1.189207115*sqrt(-1))^2+
.1412427894/(z-1.189207115*sqrt(-1))+.2575825204/(z+1.189207115)^3+
.6837753459/(z+1.189207115)^2+6.858756405/(z+1.189207115)
>>symsz;F=z^3/(1+z)*exp(1/z);
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
第6章代数方程与最优化问题的计算机求解1求解能转换成多项式方程的联立方程,并检验得出的高精度数值解的精度。[www.61k.com]????x2y2?zxy?4x2yz2=xz2??2x1?x2?1=0,②①xy3?2yz2=3x3z2+4xzy2
22?(x1?2)+(x2?0.5)?1=0??y2x?7xy2+3xz2=x4zy
【求解】①中给出的方程可以由下面的语句直接求解,经检验可见,精度是相当高的,达1030级。
>>[x1,x2]=solve(’x1^2-x2-1=0’,’(x1-2)^2+(x2-0.5)^2-1=0’,’x1,x2’)x1=
-1.3068444845633173592407431426632-1.2136904451605911320167045558746*sqrt(-1)-1.3068444845633173592407431426632+1.2136904451605911320167045558746*sqrt(-1)
1.0673460858066897134085973128070
1.5463428833199450050728889725194
x2=
-.76520198984055124633885565606586+3.1722093284506318231178646481143*sqrt(-1)-.76520198984055124633885565606586-3.1722093284506318231178646481143*sqrt(-1)
.13922766688686144048362498805141
1.3911763127942410521940863240803
>>norm(double([x1.^2-x2-1(x1-2).^2+(x2-0.5).^2-1]))
ans=
6.058152713871457e-031
现在考虑②中的方程,可以由下面的语句求解并检验精度。
>>[x,y,z]=solve(’x^2*y^2-z*x*y-4*x^2*y*z^2=x*z^2’,...
’x*y^3-2*y*z^2=3*x^3*z^2+4*x*z*y^2’,...
’y^2*x-7*x*y^2+3*x*z^2=x^4*z*y’,’x,y,z’)
x=
x
.31763330066708094899226744383315
-.57342208805666904699955413755046
-3.0414669315515393342891214860256
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
54第6章代数方程与最优化问题的计算机求解
1.2406494592172202024946761755143+2.6726341184257446950051342796237*sqrt(-1)
1.9395779085729820052691770221678-1.8460302354285923475099876321714*sqrt(-1)-.12175724403625789114277654158125+.76608643264311922968528253940276*sqrt(-1)-2.2119059377823750236571580666120-1.3098483298501442852199024916922*sqrt(-1).18091793647835958266865409918250-.43514167087309843831595260429068*sqrt(-1)-.55869174189107447600021216575845+2.3297622385407573613585339888001*sqrt(-1)
-.68680307411564099103394996937251
2.2449864792628313778324119367846
.80149155267622824623322517103811
-.55869174189107447600021216575845-2.3297622385407573613585339888001*sqrt(-1).18091793647835958266865409918250+.43514167087309843831595260429068*sqrt(-1)-2.2119059377823750236571580666120+1.3098483298501442852199024916922*sqrt(-1)-.12175724403625789114277654158125-.76608643264311922968528253940276*sqrt(-1)
1.9395779085729820052691770221678+1.8460302354285923475099876321714*sqrt(-1)
1.2406494592172202024946761755143-2.6726341184257446950051342796237*sqrt(-1)y=
y
-.10247418659393300993582067594235
.88186908582844666977541315922472
6.2206205278493911181266569143240
3.8883892104923440119866877297435+2.6775872796906346863164643745055*sqrt(-1)-.19521984362257729205542902543230+2.1755659889967168917621095367660*sqrt(-1).19300043308429639136627772430949+.55085821682149293523314538512818*sqrt(-1)-1.5345777137990494704652954417309+.42952982009383733582600047744276e-1*sqrt(-1).59285406023469299432404383306933e-1-.14560032849820344999561561093140*sqrt(-1)-.13504742647411551604956518296040-1.3353390289175827351921401819303*sqrt(-1)
.23206681025858886578639216095379
1.2500352093099975887186243233388
-.40877757806122608090142625675228
-.13504742647411551604956518296040+1.3353390289175827351921401819303*sqrt(-1).59285406023469299432404383306933e-1+.14560032849820344999561561093140*sqrt(-1)-1.5345777137990494704652954417309-.42952982009383733582600047744276e-1*sqrt(-1)
.19300043308429639136627772430949-.55085821682149293523314538512818*sqrt(-1)-.19521984362257729205542902543230-2.1755659889967168917621095367660*sqrt(-1)
3.8883892104923440119866877297435-2.6775872796906346863164643745055*sqrt(-1)z=
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
第6章代数方程与最优化问题的计算机求解55
z
.14437409800864935567667171646044
1.2197465522537746902599296344473
1.2977198721910510602444950254432
1.0166830329716235095778013718903+.37011032131730244971789188681237*sqrt(-1).45233167057904744299654223927744+.51464117109451634939209195854989*sqrt(-1).31864673037377358785409663022781+.78415604801861425880017838557048*sqrt(-1).38457694363000428639271157033224e-1+.57967291207543468143911103709180*sqrt(-1)-.83830187383058822380943737709146e-1+.20866770020547056525334588752981*sqrt(-1)-.36349211548848392020797588683844+.46022200523351838974797619203293*sqrt(-1)
-.34096135567852262861343237947182
-.58923295037333858669309875602950
-.61423986723341834383214878861209
-.36349211548848392020797588683844-.46022200523351838974797619203293*sqrt(-1)-.83830187383058822380943737709146e-1-.20866770020547056525334588752981*sqrt(-1).38457694363000428639271157033224e-1-.57967291207543468143911103709180*sqrt(-1).31864673037377358785409663022781-.78415604801861425880017838557048*sqrt(-1).45233167057904744299654223927744-.51464117109451634939209195854989*sqrt(-1)1.0166830329716235095778013718903-.37011032131730244971789188681237*sqrt(-1)>>norm(double([x.^2.*y.^2-z.*x.*y-4*x.^2.*y.*z.^2-x.*z.^2,...
x.*y.^3-2*y.*z.^2-3*x.^3.*z.^2-4*x.*z.*y.^2,...
y.^2.*x-7*x.*y.^2+3*x.*z.^2-x.^4.*z.*y]))
ans=
3.493005633414428e-024
可见,除了前三组解之外,其余的解均是单个的,这样的解共有18组,另外(x,0,0)、(0,y,0)和(0,0,z)对任意的x,y,z均满足原始方程,故方程有无数根。[www.61k.com]
2试用图解法求解下面一元和二元方程,并验证得出的结果。
①f(x)=e?(x+1)2+p/2sin(5x+2),②f(x,y)=(x2+y2+xy)e?x2?y2?xy
【求解】①中给出的一元方程可以用曲线表示出来,这些曲线和y=0线的交点即为方程的解,可以用图形局部放大的方法读出这些交点的x值,如图6-1所示。在本图中,xi均为方程的解,若放大x轴区域,则可能得出更多的解。
>>ezplot(’exp(-(x+1)^2+pi/2)*sin(5*x+2)’)
②中的二元方程可以由下面的命令用图形的方式显示出来,如图6-2a所示。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
56第6章代数方程与最优化问题的计算机求解
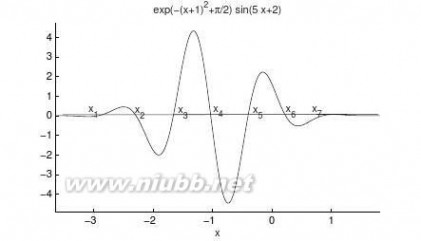
图6-1一元方程的图解法
>>ezsurf(’(x^2+y^2+x*y)*exp(-x^2-y^2-x*y)’)
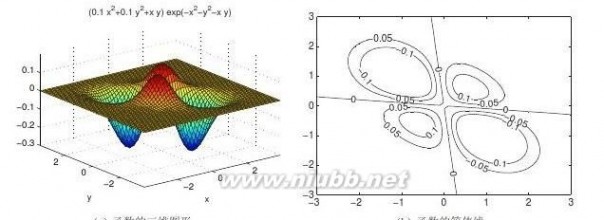
图6-2函数图形及方程求解
用下面的语句可以得出等高线,如图6-2b所示。[www.61k.com]为了比较起见,还绘制出其他值下的等高线。等高线值为0的两条斜线为方程的解。
>>[x,y]=meshgrid(-3:0.1:3);
z=(0.1*x.^2+0.1*y.^2+x.*y).*exp(-x.^2-y.^2-x.*y);[C,h]=contour(x,y,z,[-0.1:0.05:0.1]);set(h,’ShowText’,’on’)
3用数值求解函数求解上述的方程的根,并对得出的结果进行检验。
【求解】求解方程求解问题可以采用fsolve()和solve()函数直接求解,这里采用这两个函数分别求取这两个方程的根。
①可以用下面方法求出一元函数的根,经检验结果较精确。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
第6章代数方程与最优化问题的计算机求解
>>symsx;x1=solve(’exp(-(x+1)^2+pi/2)*sin(5*x+2)’)
x1=
-2/5
>>subs(’exp(-(x+1)^2+pi/2)*sin(5*x+2)’,x,x1)
ans=
>>f=inline(’exp(-(x+1).^2+pi/2).*sin(5*x+2)’,’x’);
x2=fsolve(f,0)
x2=
0.22831852178755
>>subs(’exp(-(x+1)^2+pi/2)*sin(5*x+2)’,x,x2)
ans=
4.750949292642762e-008
>>x3=fsolve(f,-1)
x3=
-1.02831853071796
>>subs(’exp(-(x+1)^2+pi/2)*sin(5*x+2)’,x,x3)
ans=
-5.886413288211306e-016%选择不同的初值可以得出其他的解57
采用解析解函数solve()能求出精确的解,但只能求出其一个根,如果采用fsolve()函数则可以让用户自己选择初值,选择不同的初值可能得出不同的结果。[www.61k.com]在实际应用时这样的方法也有其问题,例如由图6-2a可见,若x大于1,则函数值本身就很小,很容易满足数值解的收敛条件,例如选择x0=4,则由数值解的程序能得出方程解为x0,事实上这样的解不是数学意义下的方程解,但确实能使得该函数的值趋于0。
>>x4=fsolve(f,4)
x4=
>>subs(’exp(-(x+1)^2+pi/2)*sin(5*x+2)’,x,x4)
ans=
-5.913350831018913e-013
②可以用下面的语句求解该函数,则可以得出方程的解,代入原方程则可以得出误差,可见误差为0,这样说明得出的解确实满足原方程。
>>symsx;y1=solve(’(x^2+y^2+x*y)*exp(-x^2-y^2-x*y)=0’,’y’)
y1=
(-1/2+1/2*i*3^(1/2))*x
(-1/2-1/2*i*3^(1/2))*x
>>y2=simple(subs(’(x^2+y^2+x*y)*exp(-x^2-y^2-x*y)’,’y’,y1))%选择大的初值得出的解不是严格意义下方程的根
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
58
y2=
4试求出使得
0第6章代数方程与最优化问题的计算机求解??1(ex?cx)dx取得极小值的c值。[www.61k.com]2
【求解】给定的函数可以积分,由MATLAB语句可以求出积分为
>>symsxc;y=int((exp(x)-c*x)^2,x,0,1)
y=
1/2*exp(1)^2+1/3*c^2-1/2-2*c
这样可以立即写出目标函数的MATLAB表示为
functiony=exc6ff(c)
y=1/2*exp(1)^2+1/3*c^2-1/2-2*c;
由下面的语句可以求解出使得积分值为最小时的c值,由下面的语句还可以绘制出不同c值
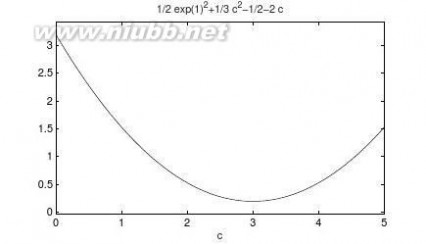
下的函数曲线,如图6-3所示,由此验证得出解的正确性。
>>x=fminsearch(’exc6ff’,0)
x=
3.00000000000000
>>ezplot(y,[0,5])
图6-3不同c值下的的积分值曲线
5试求解下面的无约束最优化问题。
22222100(x2?x21)+(1?x1)+90(x4?x3)+(1?x3)+min????x10.1(x2?1)2+(x4?1)2+19.8(x2?1)(x4?1)
【求解】无约束最优化问题可以由下面的语句直接求解,并得出所需结果。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
第6章代数方程与最优化问题的计算机求解
>>f=inline([’100*(x(2)-x(1)^2)^2+(1-x(1))^2+’,...
’90*(x(4)-x(3)^2)+(1-x(3)^2)^2+’,...
’10.1*((x(2)-1)^2+(x(4)-1)^2)+’,...
’19.8*(x(2)-1)*(x(4)-1)’],’x’);
x=fminunc(f,ones(7,1))
x=
1.0e+002*
0.10546446798713
1.11232066767234
0.06782323911149
-1.11504746457726
0.01000000000000
0.01000000000000
0.0100000000000059
26考虑Rastrigin函数[25]f(x1,x2)=20+x21+x2?10(cospx1+cospx2),试用三维曲面绘制
该函数的函数值,选择初值求取该函数的最小值,并理解全局最优解和局部最优解的概念,及最优解对初值的依赖关系。(www.61k.com]
【求解】使用不同的处初值,本目标函数可能有不同的解,且对应的目标函数值可能有很大差异,其中大部分均为局部最优值。
>>y=inline(’20+x(1)^2+x(2)^2-10*(cos(pi*x(1))+cos(pi*x(2)))’,’x’);
x1=fminunc(y,[1;0])
x1=
1.0e-008*
-0.35249693804338
0.44265808885143
>>y(x1)
ans=
3.552713678800501e-015
>>x2=fminunc(y,[0;2])
x2=
-0.00000000596857
1.96017472106964
>>y(x2)
ans=
3.92045146143746
由下面的语句可以绘制出目标函数的三维曲面,如图6-4a所示,还可以得出该函数的等高线,如图6-4b所示。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
60
>>[x1,x2]=meshgrid(-3:0.1:3);第6章代数方程与最优化问题的计算机求解
z=20+x1.^2+x2.^2-10*(cos(pi*x1)+cos(pi*x2));
surf(x1,x2,z)
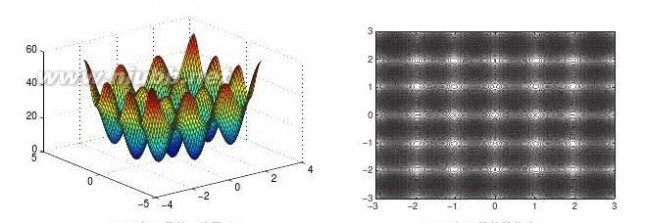
图6-4目标函数的图形表示
7试用图解法求解下面的非线性规划问题,并用数值求解算法验证结果。(www.61k.com)
min?2(x31+x2?4x1+4)
???x1?x2+2??0
xs.t.?x21+x2?1??0???x1??0,x2??0
【求解】通过选择适当的区域(当然,这需要在较大范围内先观察一下最优点或可行区域,然后再较确切地选择合适的区域),这样就可以可以绘制出如图6-5所示的曲面表示,在曲面绘制中先选择整个矩形区域,然后将不满足约束条件的区域剪切掉。从得出的目标函数曲面看,x=0,y=1处为全局最小点。
>>[x1,x2]=meshgrid(0:0.02:1,1:0.02:2);
z=x1.^3+x2.^2+4*x1+4;
ii=find(x1-x2+2<0);z(ii)=NaN;
ii=find(-x1.^2+x2-1<0);z(ii)=NaN;
ii=find(x1<0);
surf(x1,x2,z)
下面的语句可以用数值方法求解
function[c,ce]=exc6f4(x)
ce=[];
c=[x(1)^2-x(2)+1];z(ii)=NaN;ii=find(x2<0);z(ii)=NaN;
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
第6章代数方程与最优化问题的计算机求解61
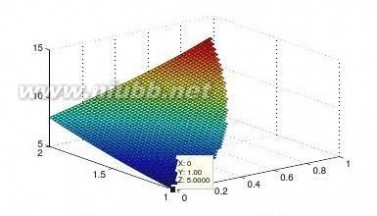
>>f_opt=inline(’x(1)^3+x(2)^2+4*x(1)+4’,’x’);
A=[-11];B=2;Aeq=[];Beq=[];xm=[0;0];
x=fmincon(f_opt,[0;1],A,B,Aeq,Beq,xm,[],’exc6f4’);
8试求解下面的线性规划问题。(www.61k.com]
①?3x1+4x2min??4x1?x2+2x3?x4=?2?????x+x?x+2x??141234xs.t.?2x1?3x2?x3?x4???2?????x1,2,3???1,x4无约束
max??2x3+5x4②x6+x7?min?x1+x2+x3+x4=4??????2x+x?x?x+x=112367xs.t.?3x2+x3+x5+x7=9?????x1,2,···,7??0③2800(x11+x21+x31+x41)
?x11+x12+x13+x14??15????????x12+x13+x14+x21+x22+x23??10
xs.t.x13+x14+x22+x23+x31+x32??20?????x14+x23+x32+x41??12????x??0,(i=1,2,3,4,j=1,2,3,4)ij+4500(x12+x22+x32)+6000(x13+x23)+7300x14
【求解】①先将不等式约束统一变换成??关系,这样原问题的解可以由下面的语句直接得出原线性规划问题的解为
>>f=[-34-25];
Aeq=[4-12-1];Beq=-2;
A=[11-12;-2311];B=[14;2];xm=[-1;-1;-1;-inf];
x=linprog(f,A,B,Aeq,Beq,xm)
Optimizationterminatedsuccessfully.
x=
-0.99999999999422
2.49999999985070
-0.99999999999055
-6.49999999980869
②用下面的语句可以求解出线性规划问题
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
62
>>f=[0,0,0,0,0,1,1];第6章代数方程与最优化问题的计算机求解
Aeq=[1111000;-21-100-11;0310101];Beq=[4;1;9];xm=[0;0;0;0;0;0;0];A=[];B=[];x=linprog(f,A,B,Aeq,Beq,xm)
Optimizationterminatedsuccessfully.
x=
0.39517811869632
2.32126957607183
0.53091333867908
0.75263896655277
1.50527793310533
0.00000000000020
0.00000000000008
③应该重新选定变量,令x1=x11,x2=x12,x3=x13,x4=x14,x5=x21,x6=x22,x7=x23,x8=x31,x9=x32,x10=x41,这样可以将原问题改写成
2800(x1+x5+x8+x10)
??(x1+x2+x3+x4)???15?????????(x2+x3+x4+x5+x6+x7)???10
xs.t.?(x3+x4+x6+x7+x8+x9)???20?????(x4+x7+x9+x10)???12?????x??0,(i=1,2,3,4,j=1,2,3,4)min?ij+4500(x2+x6+x9)+6000(x3+x7)+7300x4
这样就可以用下面的语句解出问题的最优解。[www.61k.com]
>>f=2800*[1000100101]+...
4500*[0100010010]+...
6000*[0010001000]+...
7300*[0001000000];
A=-[1111000000;
0111111000;
0011011110;
0001001011];
B=-[15;10;20;12];
xm=[0000000000];Aeq=[];Beq=[];
x=linprog(f,A,B,Aeq,Beq,xm)
x=
4.20692336952143
0.00000005346043
0.00000022615003
10.79307638057559
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
第6章代数方程与最优化问题的计算机求解
0.00000003042569
0.00000005085698
0.00000005499777
7.99999980262819
1.20692351450631
0.00000010137137
9试求解下面的二次型规划问题,并用图示的形式解释结果。[www.61k.com]①
???x1+x2??3
xs.t.4x1+x2??9???x1,2??063min?22x21?4x1x2+4x2?6x1?3x2②????x1+x2=1xs.t.x1+x2??2???x1,2??0min?(x1?1)2+(x2?2)2
【求解】①可以由目标函数写出二次型规划的H和f矩阵为
????4?4H=,f=[?6,?3]?48
这样由二次型规划求解函数可以直接解出该最优化问题的解。>>H=[4-4;-48];f=[-6-3];
Aeq=[];Beq=[];A=[11;41];B=[3;9];xm=[0;0];x=quadprog(H,f,A,B,Aeq,Beq,xm)
x=
1.95000000000000
1.05000000000000
②展开目标函数,则可以得出
????20H=,f=[?2,?4]02
这样则可以由下面的语句得出最优化问题的解。
>>H=diag([22]);f=[-2-4];
Aeq=[-11];Beq=1;A=[11];B=2;xm=[0;0];x=quadprog(H,f,A,B,Aeq,Beq,xm)
x=
0.50000000000000
1.50000000000000
10试求解下面的非线性规划问题。
①ex1(4x21?min
?x+x??0?12?????xx+x+x??1.51212xs.t.??x1x2???10?????10??x1,x2??10+2x22+4x1x2+2x2+1)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
64
②max第6章代数方程与最优化问题的计算机求解????????31.51x1x2(1+x5)+x3x41+2cosx6x5?33?0.003079x31x2x5?cosx6??0????323?0.1017x3?3x4?x5cosx6??0???232????0.09939(1+x5)x1x2?cosx6??0
222xs.t.0.1076(31.5+x5)x33x4?x5cosx6??0????x3x4(x5+31.5)?x5[2(x1+5)cosx6+x1x2x5]??0??????0.2??x1??0.5,14<??x2??22,0.35??x3??0.6,????16??x4??22,5.8??x5??6.5,0.14??x6??0.2618【求解】①可以用下面的语句描述目标函数
functiony=exc6fun6(x)
y=exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1);
也可以写出约束函数
function[c,ce]=exc6fun6a(x)
ce=[];
c=[x(1)+x(2);x(1)*x(2)-x(1)-x(2)+1.5;-10-x(1)*x(2)];
这时调用非线性最优化问题求解函数可以得出如下结果。[www.61k.com)
>>A=[];B=[];Aeq=[];Beq=[];xm=[-10;-10];xM=[10;10];
x0=(xm+xM)/2;
ff=optimset;ff.TolX=1e-10;ff.TolFun=1e-20;
x=fmincon(’exc6fun6’,x0,A,B,Aeq,Beq,xm,xM,’exc6fun6a’,ff)
Maximumnumberoffunctionevaluationsexceeded;
increaseOPTIONS.MaxFunEvals
x=
0.41947326053910
0.41947326053910
从得出的提示看,该结果并非原问题的解,所以考虑用得出的最优解代入作为初值再求解,如此可以利用循环,则可以得出原问题的最优解。
>>i=1;x=x0;
while(1)
[x,a,b]=fmincon(’exc6fun6’,x,A,B,Aeq,Beq,xm,xM,’exc6fun6a’,ff);
ifb>0,break;end
i=i+1;
end
x,i
x=
1.18249727581645%循环次数为5
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
第6章代数方程与最优化问题的计算机求解
-1.73976692398900
i=
5
②可以写出约束函数为
function[c,ce]=exc6fun5a(x)
ce=[];
c=[-0.003079*x(1)^3*x(2)^3*x(5)+cos(x(6))^3;
-0.1017*x(3)^3*x(4)^3+x(5)^2*cos(x(6)))^3;
-0.09939*(1+x(5))*x(1)^3*x(2)^2+cos(x(6))^2;
-0.1076*(31.5+x(5))*x(3)^3*x(4)^2+x(5)^2*cos(x(6))^2;
-x(3)*x(4)*(x(5)+31.5)+x(5)*(2*(x(1)+5)*cos(x(6))+x(1)*x(2)*x(5))];目标函数可以写成
functiony=exc6fun5(x)
y=1/(2*cos(x(6)))*(x(1)*x(2)*(1+x(5))+x(3)*x(4)*(1+31.5/x(5)));这样,由下面的语句可以得出最优化问题的解为
>>xm=[0.2;14;0.35;16;5.8;0.14];
xM=[0.5;22;0.6;22;6.5;0.2618];
A=[];B=[];Aeq=[];Beq=[];x0=(xm+xM)/2;
ff=optimset;ff.TolX=1e-10;ff.TolFun=1e-20;
x=fmincon(’exc6fun5’,x0,A,B,Aeq,Beq,xm,xM,’exc6fun5a’,ff)x=
0.20124417463214
18.36290007737820
0.35957532400838
18.57799951563967
5.80000000000000
0.26179905972118
其实设x?6=cosx6,则可能简化原最优化问题的求解。(www.61k.com]
11求解下面的整数线性规划问题。
①
xs.t.65max??x??0(592x1+381x2+273x3+55x4+48x5+37x6+23x7)
?3534x1+2356x2+1767x3+589x4+528x5+451x6+304x7??119567
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
66
②?x1+x2+x3=30??????x4+x5+x6=18?????x+x=1014xs.t.??x2+x5??18?????x3+x6??30????x1,···,6??0第6章代数方程与最优化问题的计算机求解max(120x1+66x2+72x3+58x4+132x5+104x6)
【求解】①整数规划问题用下面两种方法可以得出相同的结果。[www.61k.com]
>>f=-[59238127355483723];
A=[353423561767589528451304];B=119567;
intlist=[1;1;1;1;1;1;1];ctype=-1;
xm=zeros(7,1);xM=inf*ones(7,1);
[res,b]=ipslv_mex(f,A,B,intlist,xM,xm,ctype)
res=
32
2
1
b=
>>A=[3534,2356,1767,589,528,451,304];B=119567;
intlist=ones(7,1);Aeq=[];Beq=[];
xm=zeros(7,1);xM=20000*ones(7,1);x0=xM;
[errmsg,f,x]=bnb20(’exc6fun2’,x0,intlist,xm,xM,A,B,Aeq,Beq);iflength(errmsg)==0,x=round(x),end
x=
32
2
1
其中目标函数为
functiony=exc6fun2(x)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
第6章代数方程与最优化问题的计算机求解
y=-(592*x(1)+381*x(2)+273*x(3)+55*x(4)+48*x(5)+37*x(6)+23*x(7));②此题中整数规划的解可以通过以下两种方法得出
>>f=[120667258132104];
A=[111000;000111;100100;010010;001001];B=[30;18;10;18;30];intlist=[1;1;1;1;1];
ctype=[0;0;0;-1;1];xm=zeros(5,1);xM=inf*ones(5,1);
[res,b]=ipslv_mex(f,A,B,intlist,xM,xm,ctype);res
res=
8
22
10
8
>>Aeq=[111000;000111;100100];Beq=[30;18;10];A=[010010;00-100-1];B=[18;-30];
intlist=ones(6,1);xm=zeros(6,1);xM=20000*ones(6,1);x0=xm;
[errmsg,f,x]=bnb20(’exc6fun3’,x0,intlist,xm,xM,A,B,Aeq,Beq);iflength(errmsg)==0,x=round(x),end
x=
8
22
10
8
其中目标函数可以描述为
functiony=exc6fun3(x)
y=[120667258132104]*x;
12试求解下面的0-1线性规划问题,并对①、②题用穷举方法检验得出的结果。[www.61k.com]①x1?x2+5x3+x4?4x5??2??????2x+6x?3x?2x+2x??012345xs.t.???2x2+2x3?x4?x5??1????0??xi??167min??(5x1+7x2+10x3+3x4+x5)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
68
②min??第6章代数方程与最优化问题的计算机求解(?3x1?4x2?5x3+4x4+4x5+2x6)
xs.t.?4975110?x③10500??????????600?45085150659530017004025200025002501650850000100?x??6003020125580253573121515405101012109020604050364940191502250727014148310042255101188047924355288511748455046504407503080061549033037201950???0??xi??1x1?x6??0?????x1?x5??0????????x2?x4??0xs.t.x2?x5??0????x3?x4??0??????x1+x2+x3??2????0??xi??1?1898440?1160max560
③说明,目标函数中的系数实际上是行向量,由于排版原因只能这样表示。[www.61k.com]
【求解】①中的问题可以由下面语句直接求解
>>f=[571035];B=[2;0;1];ctype=[1;1;-1];
A=[1-151-4;-26-3-22;0-22-1-1];
intlist=[1;1;1;1;1];xM=intlist;xm=zeros(5,1);
[res,b]=ipslv_mex(f,A,B,intlist,xM,xm,ctype);res’
ans=
01100
用下面的语句利用MATLAB7.0提供的新函数可以得出如下结果,该结果与前面方法得出的结果是完全一致的。
>>f=[571035];B=[-2;0;1];
A=[-11-5-14;2-632-2;0-22-1-1];
x=bintprog(f,A,B,[],[])’
x=
01100
利用穷举法可以验证上面的结果是正确的。
>>[x1,x2,x3,x4,x5]=ndgrid([0,1]);
i=find((x1-x2+5*x3+x4-4*x5>=2)&(-2*x1+6*x2-3*x3-2*x4+2*x5>=0)&...
(-2*x2+2*x3-x4-x5<=1));
f=5*x1(i)+7*x2(i)+10*x3(i)+3*x4(i)+x5(i);[fmin,ii]=sort(f);fmin’
ans=
17202226
>>index=i(ii(1));
x=[x1(index),x2(index),x3(index),x4(index),x5(index)]
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
第6章代数方程与最优化问题的计算机求解
x=
0110069
②中的的最优化问题由下面的函数可以直接求解
>>A=[10000-1;1000-10;010-100;
0100-10;001-100;111000];
B=[0;0;0;0;0;2];c=[-3-4-5442];
intlist=ones(1,6);xM=intlist;xm=zeros(1,28);ctype=[-1;-1;-1;-1;-1];
[res,b]=ipslv_mex(c,A,B,intlist,xM,xm,ctype);res’
ans=
011110
用MATLAB7.0提供的0-1整数规划求解函数可以得出如下结果。[www.61k.com]
>>A=[10000-1;1000-10;010-100;
0100-10;001-100;111000];
B=[0;0;0;0;0;2];c=[-3-4-5442];
x=bintprog(c,A,B,[],[])’
x=
001100
比较两种方法得出的结果可见,二者是不相同的,可以用下面的语句分别求出二者的函数值>>[c*x’,c*res]
ans=
-1-1
可见二者都将得出?1,故两种方法得出的结果都是原函数的最优解。该问题是否还有其他的解析解呢?对简单的问题可以采用穷举法进行求解,并可以得出如下结果
>>[x1,x2,x3,x4,x5,x6]=ndgrid([0,1]);
i=find((x1-x6<=0)&(x1-x5<=0)&(x2-x4<=0)&(x2-x5<=0)&...
(x3-x4<=0)&(x1+x2+x3<=2));
f=-3*x1(i)-4*x2(i)-5*x3(i)+4*x4(i)+4*x5(i)+2*x6(i);[fmin,ii]=sort(f);fmin(1:5)’
ans=
-1-1011
可见,前两个函数值为?1,故该问题只有两个最优值,该两个最优值即用前面两种方法分别得出的解。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
70
>>index=i(ii(1:2));第6章代数方程与最优化问题的计算机求解
x=[x1(index),x2(index),x3(index),x4(index),x5(index),x6(index)]x=
00111110100
③由线性整数规划求解函数ipslvmex()可以求出问题的解为
>>A=[45,0,85,150,65,95,30,0,170,0,40,25,20,...
0,0,25,0,0,25,0,165,0,85,0,0,0,0,100;
30,20,125,5,80,25,35,73,12,15,15,40,5,...
10,10,12,10,9,0,20,60,40,50,36,49,40,19,150];
B=[600;600];
c=-[1898,440,22507,270,14148,3100,4650,30800,615,4975,1160,4225,510,...
11880,479,440,490,330,110,560,24355,2885,11748,4550,750,...
3720,1950,10500];
intlist=ones(1,28);xM=intlist;xm=zeros(1,28);ctype=[-1;-1];
[res,b]=ipslv_mex(c,A,B,intlist,xM,xm,ctype);res’
ans=
0010111101011100001010110100
若采用MATLAB7.0提供的bintprog()函数也可以得出相同的结果。[www.61k.com]
>>x=bintprog(c,A,B);x’
ans=
0010111101011100001010110100
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
第7章微分方程问题的计算机求解
1试求出下面线性微分方程的通解。[www.61k.com)
??????d5y(t)d4y(t)d3y(t)d2y(t)dy(t)p???2t+13+64+152+176+80y(t)=esin2t++cos(3t)dt5dt4dt3dt2dt3
假设上述微分方程满足已知条件y(0)=1,y(1)=3,y(p)=2,y˙(0)=1,y˙(1)=2,试求出满足该条件的微分方程解析解。
【求解】先定义t为符号变量,求出等号右侧的函数,则可以由下面命令求出方程的解析解,解的规模较大,经常能占数页。
>>symst
exp(-2*t)*(sin(2*t+sym(pi)/3)+cos(3*t))
ans=
exp(-2*t)*(sin(2*t+1/3*pi)+cos(3*t))
>>y=dsolve([’D5y+13*D4y+64*D3y+152*D2y+176*Dy+80*y=’,...
’exp(-2*t)*(sin(2*t+1/3*pi)+cos(3*t))’],’y(0)=1’,’y(1)=3’,’y(pi)=2’,...’Dy(0)=1’,’Dy(1)=2’)
y=
1/486*exp(-2*t)*cos(3*t)+(3/416*exp(-2*t)+1/208*3^(1/2)*exp(-2*t))*sin(2*t)+(-1/208*exp(-2*t)+3/416*3^(1/2)*exp(-2*t))*cos(2*t)+1/72*exp(-2*t)*t^2+
5/432*exp(-2*t)*t+1/72*exp(-2*t)*t*3^(1/2)-1/72*exp(-2*t)*t^3-5/1296*exp(-2*t)-1/48*exp(-2*t)*t^2*3^(1/2)+5/864*3^(1/2)*exp(-2*t)+1/486*exp(-2*t)*sin(3*t)-1/50544*(-101088*pi^3*exp(3*pi+5)+604407*pi^2*exp(3*pi+3)-303225*pi*exp(3*pi+3)+101088*exp(5*pi+3)-50878*exp(3)+2916*pi^2*sin(1)^2*exp(3*pi+3)-
2496*pi^2*sin(1)^3*exp(3*pi+3)+1872*pi^2*sin(1)*exp(3*pi+3)+
2080*pi^3*sin(1)^3*exp(3*pi+3)-1560*pi^3*sin(1)*exp(3*pi+3)-
2430*pi^3*sin(1)^2*exp(3*pi+3)+104*pi^3*cos(1)*exp(3*pi+3)+
305268*pi^2*exp(3*pi)+542*exp(3*pi+3)-301620*pi^3*exp(3*pi+3)-
50544*pi^2*exp(3*pi+5)-254390*pi^3*exp(3*pi)+
2916*pi^2*sin(1)*cos(1)*3^(1/2)*exp(3*pi+3)-3942*pi^2*3^(1/2)*exp(3*pi)+1215*pi^2*sin(1)*cos(1)*exp(3*pi+3)-1215*pi^2*3^(1/2)*sin(1)^2*exp(3*pi+3)+486*pi^3*3^(1/2)*sin(1)^2*exp(3*pi+3)-486*pi^3*sin(1)*cos(1)*exp(3*pi+3)-
416*pi^3*cos(1)*sin(1)^2*exp(3*pi+3)+657*3^(1/2)*exp(3)-657*3^(1/2)*exp(3*pi+3)+2457*pi*3^(1/2)*exp(3*pi+3)-2430*pi^3*sin(1)*cos(1)*3^(1/2)*exp(3*pi+3)+3285*pi^3*exp(3*pi)*3^(1/2)-3429*pi^2*3^(1/2)*exp(3*pi+3)+
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
72第7章微分方程问题的计算机求解
1629*pi^3*3^(1/2)*exp(3*pi+3))/(3*pi*exp(3*pi+3)+pi^3*exp(3*pi+3)+
5*pi^3*exp(3*pi)+exp(3)-3*pi^2*exp(3*pi+3)-6*pi^2*exp(3*pi)-
exp(3*pi+3))*exp(-2*t)-1/50544*(-1215*pi^2*sin(1)*cos(1)*exp(3*pi+3)+
1215*pi^2*3^(1/2)*sin(1)^2*exp(3*pi+3)-486*pi*3^(1/2)*exp(3*pi+3)+
1458*pi^2*3^(1/2)*exp(3*pi+3)-486*pi^3*3^(1/2)*sin(1)^2*exp(3*pi+3)+
486*pi^3*sin(1)*cos(1)*exp(3*pi+3)+416*pi^3*cos(1)*sin(1)^2*exp(3*pi+3)-
2080*pi^3*sin(1)^3*exp(3*pi+3)+1560*pi^3*sin(1)*exp(3*pi+3)+
2430*pi^3*sin(1)^2*exp(3*pi+3)-104*pi^3*cos(1)*exp(3*pi+3)-
101088*exp(5*pi+3)+101088*pi^3*exp(3*pi+5)+50336*exp(3*pi+3)-
451773*pi^2*exp(3*pi+3)+150591*pi*exp(3*pi+3)+250742*pi^3*exp(3*pi+3)+
50544*pi^2*exp(3*pi+5)+2430*pi^3*sin(1)*cos(1)*3^(1/2)*exp(3*pi+3)-
972*pi^3*3^(1/2)*exp(3*pi+3)-2916*pi^2*sin(1)*cos(1)*3^(1/2)*exp(3*pi+3)-2916*pi^2*sin(1)^2*exp(3*pi+3)+2496*pi^2*sin(1)^3*exp(3*pi+3)-
1872*pi^2*sin(1)*exp(3*pi+3))/(3*pi*exp(3*pi+3)+pi^3*exp(3*pi+3)+
5*pi^3*exp(3*pi)+exp(3)-3*pi^2*exp(3*pi+3)-6*pi^2*exp(3*pi)-exp(3*pi+3))*exp(-5*t)+1/50544*(-302559*pi^2*exp(3*pi+3)+603741*pi*exp(3*pi+3)-101088*exp(3*pi+5)+
101088*exp(5*pi+3)+251444*exp(3)-251680*exp(3*pi)-4374*pi^2*sin(1)^2*exp(3*pi+3)-6240*sin(1)^3*pi*exp(3*pi+3)+312*cos(1)*pi^2*exp(3*pi+3)-
416*cos(1)*sin(1)^2*exp(3*pi+3)+486*sin(1)*cos(1)*exp(3)+
416*cos(1)*sin(1)^2*exp(3)+3744*pi^2*sin(1)^3*exp(3*pi+3)-
486*sin(1)*cos(1)*exp(3*pi+3)-2808*pi^2*sin(1)*exp(3*pi+3)-
312*cos(1)*pi*exp(3*pi+3)+4680*sin(1)*pi*exp(3*pi+3)+
7290*sin(1)^2*pi*exp(3*pi+3)-486*3^(1/2)*sin(1)^2*exp(3)+
486*3^(1/2)*sin(1)^2*exp(3*pi+3)+750201*pi^2*exp(3*pi)-
301780*exp(3*pi+3)+702*pi^3*exp(3*pi+3)-353808*pi^2*exp(3*pi+5)-
1560*sin(1)*exp(3*pi+3)-2430*sin(1)^2*exp(3*pi+3)+2430*sin(1)^2*exp(3)+
3510*pi^3*exp(3*pi)-859248*pi^2*exp(3*pi+2)+2080*sin(1)^3*exp(3*pi+3)-
4374*pi^2*sin(1)*cos(1)*3^(1/2)*exp(3*pi+3)-1458*pi^2*3^(1/2)*exp(3*pi)-
243*pi^2*sin(1)*cos(1)*exp(3*pi+3)+243*pi^2*3^(1/2)*sin(1)^2*exp(3*pi+3)+
303264*pi*exp(3*pi+5)+505440*exp(5*pi)-972*3^(1/2)*exp(3)+972*3^(1/2)*exp(3*pi+3)+2430*pi*3^(1/2)*exp(3*pi)+624*cos(1)*pi^2*exp(3*pi)-2430*pi*3^(1/2)*exp(3*pi+3)-2080*sin(1)^3*exp(3)-752955*pi*exp(3*pi)-104*cos(1)*exp(3)+
7290*sin(1)*cos(1)*3^(1/2)*pi*exp(3*pi+3)+1560*sin(1)*exp(3)+
1458*sin(1)*cos(1)*pi*exp(3*pi+3)+2430*sin(1)*cos(1)*3^(1/2)*exp(3)-
2430*sin(1)*cos(1)*3^(1/2)*exp(3*pi+3)-1458*3^(1/2)*sin(1)^2*pi*exp(3*pi+3)-3159*pi^2*exp(3*pi)*3^(1/2)*sin(1)^2+1248*cos(1)*sin(1)^2*pi*exp(3*pi+3)+3159*pi^2*exp(3*pi)*sin(1)*cos(1)-2496*cos(1)*sin(1)^2*pi^2*exp(3*pi)-
1248*cos(1)*sin(1)^2*pi^2*exp(3*pi+3)+101088*exp(5)+1458*pi^2*3^(1/2)*exp(3*pi+3)+
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
第7章微分方程问题的计算机求解73
104*cos(1)*exp(3*pi+3))/(3*pi*exp(3*pi+3)+pi^3*exp(3*pi+3)+5*pi^3*exp(3*pi)+exp(3)-3*pi^2*exp(3*pi+3)-6*pi^2*exp(3*pi)-exp(3*pi+3))*exp(-2*t)*t^3+
1/16848*(117936*pi^3*exp(3*pi+5)+702*pi^2*exp(3*pi+3)-301884*pi*exp(3*pi+3)-
16848*exp(3*pi+5)-101088*exp(5*pi+3)-150825*exp(3)+100672*exp(3*pi)+
2496*sin(1)^3*pi*exp(3*pi+3)-405*sin(1)*cos(1)*exp(3)+405*sin(1)*cos(1)*exp(3*pi+3)-1872*sin(1)*pi*exp(3*pi+3)-2916*sin(1)^2*pi*exp(3*pi+3)+405*3^(1/2)*sin(1)^2*exp(3)-405*3^(1/2)*sin(1)^2*exp(3*pi+3)-1248*pi^3*sin(1)^3*exp(3*pi+3)+
936*pi^3*sin(1)*exp(3*pi+3)+1458*pi^3*sin(1)^2*exp(3*pi+3)-104*pi^3*cos(1)*exp(3*pi+3)-208*pi^3*exp(3*pi)*cos(1)+1404*pi^2*exp(3*pi)+201161*exp(3*pi+3)+99917*pi^3*exp(3*pi+3)+624*sin(1)*exp(3*pi+3)+972*sin(1)^2*exp(3*pi+3)-972*sin(1)^2*exp(3)+
286416*pi^3*exp(3*pi+2)-252641*pi^3*exp(3*pi)-832*sin(1)^3*exp(3*pi+3)-
2106*pi^2*3^(1/2)*exp(3*pi)-81*pi^3*3^(1/2)*sin(1)^2*exp(3*pi+3)+
81*pi^3*sin(1)*cos(1)*exp(3*pi+3)+416*pi^3*cos(1)*sin(1)^2*exp(3*pi+3)+
1053*pi^3*exp(3*pi)*3^(1/2)*sin(1)^2+832*pi^3*exp(3*pi)*cos(1)*sin(1)^2-
1053*pi^3*exp(3*pi)*sin(1)*cos(1)+50544*pi*exp(3*pi+5)-202176*exp(5*pi)+
837*3^(1/2)*exp(3)-837*3^(1/2)*exp(3*pi+3)-972*pi*3^(1/2)*exp(3*pi)+
2025*pi*3^(1/2)*exp(3*pi+3)+832*sin(1)^3*exp(3)+301182*pi*exp(3*pi)-
2916*sin(1)*cos(1)*3^(1/2)*pi*exp(3*pi+3)+1458*pi^3*sin(1)*cos(1)*3^(1/2)*exp(3*pi+3)-624*sin(1)*exp(3)-1215*sin(1)*cos(1)*pi*exp(3*pi+3)-972*sin(1)*cos(1)*3^(1/2)*exp(3)+972*sin(1)*cos(1)*3^(1/2)*exp(3*pi+3)+1215*3^(1/2)*sin(1)^2*pi*exp(3*pi+3)+16848*exp(5)+2241*pi^3*exp(3*pi)*3^(1/2)-1053*pi^2*3^(1/2)*exp(3*pi+3)-
135*pi^3*3^(1/2)*exp(3*pi+3))/(3*pi*exp(3*pi+3)+pi^3*exp(3*pi+3)+
5*pi^3*exp(3*pi)+exp(3)-3*pi^2*exp(3*pi+3)-6*pi^2*exp(3*pi)-exp(3*pi+3))*exp(-2*t)*t^2-1/16848*(101088*pi^3*exp(3*pi+5)-301767*pi^2*exp(3*pi+3)+585*pi*exp(3*pi+3)-
101088*exp(5*pi+3)-50002*exp(3)-
2916*pi^2*sin(1)^2*exp(3*pi+3)+2496*pi^2*sin(1)^3*exp(3*pi+3)-
1872*pi^2*sin(1)*exp(3*pi+3)-2080*pi^3*sin(1)^3*exp(3*pi+3)+
1560*pi^3*sin(1)*exp(3*pi+3)+2430*pi^3*sin(1)^2*exp(3*pi+3)-
104*pi^3*cos(1)*exp(3*pi+3)+300012*pi^2*exp(3*pi)+100338*exp(3*pi+3)+
200740*pi^3*exp(3*pi+3)+50544*pi^2*exp(3*pi+5)-250010*pi^3*exp(3*pi)-
2916*pi^2*sin(1)*cos(1)*3^(1/2)*exp(3*pi+3)-2376*pi^2*3^(1/2)*exp(3*pi)-
1215*pi^2*sin(1)*cos(1)*exp(3*pi+3)+1215*pi^2*3^(1/2)*sin(1)^2*exp(3*pi+3)-
486*pi^3*3^(1/2)*sin(1)^2*exp(3*pi+3)+486*pi^3*sin(1)*cos(1)*exp(3*pi+3)+
416*pi^3*cos(1)*sin(1)^2*exp(3*pi+3)+396*3^(1/2)*exp(3)-396*3^(1/2)*exp(3*pi+3)+702*pi*3^(1/2)*exp(3*pi+3)+2430*pi^3*sin(1)*cos(1)*3^(1/2)*exp(3*pi+3)+
1980*pi^3*exp(3*pi)*3^(1/2)+270*pi^2*3^(1/2)*exp(3*pi+3)-
576*pi^3*3^(1/2)*exp(3*pi+3))/(3*pi*exp(3*pi+3)+pi^3*exp(3*pi+3)+
5*pi^3*exp(3*pi)+exp(3)-3*pi^2*exp(3*pi+3)-6*pi^2*exp(3*pi)-exp(3*pi+3))*exp(-2*t)*t
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
74第7章微分方程问题的计算机求解
事实上,仔细阅读求出的解析解就会发现,其中大部分表达式是关于系数的,所以如果能对系数进行近似则将大大减小解的复杂度。(www.61k.com]
>>vpa(y)
ans=
.20576131687242798353909465020576e-2*exp(-2.*t)*cos(3.*t)+
.15538705805619602372728107411086e-1*exp(-2.*t)*sin(2.*t)+
.76830587084294035590921611166287e-2*exp(-2.*t)*cos(2.*t)-
106.24422608844727797303237726774*exp(-2.*t)*t^2+
98.159206062620455331994871615083*exp(-2.*t)*t+
59.405044899367325888329709780356*exp(-2.*t)*t^3-
30.741892776456442808809983330755*exp(-2.*t)+
.20576131687242798353909465020576e-2*exp(-2.*t)*sin(3.*t)+
31.732152104579289125415500223136*exp(-5.*t)
2试求解下面微分方程的通解及满足x(0)=1,x(p)=2,y(0)=0条件下的解析解。
??x¨(t)+5x˙(t)+4x(t)+3y(t)=e?6tsin(4t)
2y˙(t)+y(t)+4x˙(t)+6x(t)=e?6tcos(4t)
【求解】可以用下面的语句得出微分方程组的通解。
>>symst
[x,y]=dsolve(’D2x+5*Dx+4*x+3*y=exp(-6*t)*sin(4*t)’,...
’2*Dy+y+4*Dx+6*x=exp(-6*t)*cos(4*t)’)
A该结果可以用LT√11013?6t681?6tt?tt?13cos(4t)?esin(4t)+C1e+C2e+EX表示成x(t)=40820e40820
C3e√?13t+1/4t√433?6t279?6tt?13t?1/4ty(t)=?ecos(4t)+esin(4t)?10/3C1e?5/8C2e?40824082√√√√√1313131/8C2e?t?1/4t57?5/8C3e?t+1/4t+1/8C3e?t+1/4t57
将已知初始条件代入,则可以得出下面的特解。
>>symst
[x,y]=dsolve(’D2x+5*Dx+4*x+3*y=exp(-6*t)*sin(4*t)’,...
’2*Dy+y+4*Dx+6*x=exp(-6*t)*cos(4*t)’,’x(0)=1’,’x(pi)=2’,’y(0)=0’)
>>vpa(x),vpa(y)
可以得出下面的准解析解表达式为
x(t)=0.024816266536011758941695247427732e?6tcos(4t)?
0.016682998530132288094071533561979e?6tsin(4t)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
第7章微分方程问题的计算机求解
+0.085861668591377882798659931739391et?
0.057658489325155296991205006467701e?5.1374586088176874243091712017365t
+0.94698055419776565525084982730045e?1.3625413911823125756908287982635t
y(t)=?0.10607545320921117099461048505634e?6tcos(4t)+
0.068348848603625673689367956883880e?6tsin(4t)?
0.28620556197125960932886643913130et+
0.090450561852315609553848362733226e?5.1374586088176874243091712017365t+
0.30183045332815517076962856144409e?1.3625413911823125756908287982635t
3试求出下面的时变线性微分方程解析解。[www.61k.com]
2dx2dx+n(n+1)x=0①Legendre微分方程(1?t)2?2tdtdt
2dx2dx②Bessel微分方程t+t+(t2?n2)x=02dtdt
【求解】①Legendre微分方程的解包括Legendre函数,方程的解为
>>symstn
x=dsolve(’(1-t^2)*D2x-2*t*Dx+n*(n+1)*x=0’,’x’)
x=
C1*LegendreP(n,t)+C2*LegendreQ(n,t)75
结果中的LegendreP()和LegendreQ()为特殊函数,其内容可以由mhelp命令可以得出如下的信息
>>mhelpLegendreP
LegendreP,LegendreQ-LegendrefunctionsandassociatedLegendrefunctionsofthefirstandsecondkinds
...............
②Bessel微分方程的解包括Bessel函数,方程的解为
>>symstn
x=dsolve(’t^2*D2x+t*Dx+(t^2-n^2)*x=0’)
x=
C1*besselj(n,t)+C2*bessely(n,t)
????????114试求出微分方程y¨(x)?2?y˙(x)+1?y(x)=x2e?5x的解析解通解,并求出满足xx
边界条件y(1)=p,y(p)=1的解析解。
【求解】微分方程的通解可以由下面的函数直接求出
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
76
>>symsx第7章微分方程问题的计算机求解
y=dsolve(’D2y-(2-1/x)*Dy+(1-1/x)*y=x^2*exp(-5*x)’,’x’)
y=
exp(x)*C2+exp(x)*log(x)*C1+1/1296*(6*exp(6*x)*Ei(1,6*x)+11+30*x+36*x^2)*exp(-5*x)若需要求取满足边界条件的特解,需要在求解时代入边界条件,这样就可以由下面的语句得出微分方程的特解。(www.61k.com]
>>symsx
y=dsolve(’D2y-(2-1/x)*Dy+(1-1/x)*y=x^2*exp(-5*x)’,...
’y(1)=sym(pi)’,’y(sym(pi))=1’,’x’)
y=
-1/1296*exp(x)*(6*exp(1)*Ei(1,6)+77*exp(-5)-1296*sym(pi))/exp(1)+
1/1296*exp(x)*log(x)*(6*Ei(1,6)*exp(6*sym(pi)+6)+77*exp(6*sym(pi))-
1296*sym(pi)*exp(6*sym(pi)+5)+3*sqrt(-1)*pi*csgn(sym(pi))*exp(6*sym(pi)+6)-6*Ei(1,6*sym(pi))*exp(6*sym(pi)+6)-3*sqrt(-1)*pi*exp(6*sym(pi)+6)-
3*sqrt(-1)*pi*csgn(6*sqrt(-1)*sym(pi))*exp(6*sym(pi)+6)-30*sym(pi)*exp(6)+3*sqrt(-1)*pi*csgn(sym(pi))*csgn(6*sqrt(-1)*sym(pi))*exp(6*sym(pi)+6)-
36*sym(pi)^2*exp(6)-11*exp(6)+1296*exp(5*sym(pi)+6))/log(sym(pi))*exp(-6*sym(pi)-6)+1/1296*(6*exp(6*x)*Ei(1,6*x)+11+30*x+36*x^2)*exp(-5*x)
由于使用了sym(pi)这样精确的表示,其实还可以用数值解的方法对各个系数进行近似,这样可以得出如下结果。
>>vpa(y,10)
ans=
1.155578411*exp(x)-.9717266142*exp(x)*log(x)+
.7716049383e-3*(6.*exp(6.*x)*Ei(1,6.*x)+11.+30.*x+36.*x^2)*exp(-5.*x)还可以对该结果进行图形显示,得出如图7-1所示的解曲线,可见,该曲线通过两个给定点。
>>x1=0.5:0.01:4;y1=subs(y,x,x1);
plot(x1,y1,1,pi,’o’,pi,1,’o’)
5试用Laplace变换求解下面微分方程组的解析解,并和其他方法比较。
??x????(t)+y????(t)+x(t)+y(t)=0,x(0)=2,y(0)=1
2x????(t)?y????(t)?x(t)+y(t)=sint,x??(0)=y??(0)=?1
【求解】假设y(t)的Laplace变换为Y(s),则L[y????(t)]=s2Y(s)?sy(0)?y??(0),这样可以
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
第7章微分方程问题的计算机求解
77
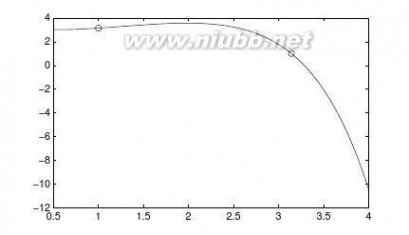
将前面的微分方程组变换成
??s2X(s)?sx(0)?x??(0)+s2Y(s)?sy(0)?y??(0)+X(s)+Y(s)=0
?2s2X(s)?2sx(0)?2x??(0)?s2Y(s)+sy(0)+y??(0)?X(s)+Y(s)=1
s2+1
这样由下面的语句可以得出X(s)和Y(s),再通过Laplace反变换则可以得出方程的解。(www.61k.com]>>symssXY;
[X,Y]=solve(’s^2*X-s*2-(-1)+s^2*Y-s*1-(-1)+X+Y=0’,...
’2*(s^2*X-s*2-(-1))-(s^2*Y-s*1-(-1))-X+Y=1/(s^2+1)’,’X,Y’)
X=
(6*s^3-3*s^2+2)/(3*s^4-2+s^2)
Y=
(3*s^3-6*s-3*s^2+2)/(3*s^4-2+s^2)
>>x0=ilaplace(X)
x0=
6/5*cos(t)-sin(t)+4/5*cosh(1/3*6^(1/2)*t)
>>y0=ilaplace(Y)
y0=
9/5*cos(t)-sin(t)-4/5*cosh(1/3*6^(1/2)*t)
直接采用微分方程组求解的函数可以得出如下的结果
>>symst
[x,y]=dsolve(’D2x+D2y+x+y=0’,’2*D2x-D2y-x+y=sin(t)’)
x=
C1*sin(t)+C2*cos(t)+C3*exp(1/3*6^(1/2)*t)+C4*exp(-1/3*6^(1/2)*t)y=
3/2*C1*sin(t)+3/2*C2*cos(t)-C3*exp(1/3*6^(1/2)*t)-C4*exp(-1/3*6^(1/2)*t)+1/2*sin(t)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
78第7章微分方程问题的计算机求解
这样的方程可以写成
??√√1/3?1/3tx(t)=C1sint+C2cost+C3e+C4e
y(t)=3/2C1sint+3/2C2cost?C3e1/3考虑初始条件,则可以得出方程的解为
>>symst
[x,y]=dsolve(’D2x+D2y+x+y=0’,’2*D2x-D2y-x+y=sin(t)’,’x(0)=2’,’y(0)=1’,...’Dx(0)=-1’,’Dy(0)=-1’)
x=
-sin(t)+6/5*cos(t)+2/5*exp(1/3*6^(1/2)*t)+2/5*exp(-1/3*6^(1/2)*t)
y=
-sin(t)+9/5*cos(t)-2/5*exp(1/3*6^(1/2)*t)-2/5*exp(-1/3*6^(1/2)*t)√?C4e?1/3√t+1/2sint
6试求出下面微分方程的通解。(www.61k.com)
①x¨(t)+2tx˙(t)+t2x(t)=t+1②y˙(x)+2xy(x)=xe?x③y??????+3y????+3y??+y=e?tsint
【求解】求解线性微分方程解析解是很直观的,调用标准函数dsolve()函数就可以直接求解,得出各个方程的通解。
>>symst;~
x=dsolve(’D2x+2*t*Dx+t^2*x=t+1’)
x=
exp(-1/2*t*(-2+t))*C2+exp(-1/2*t*(2+t))*C1-
1/2*i*pi^(1/2)*2^(1/2)*erf(1/2*i*2^(1/2)*t-
1/2*i*2^(1/2))*exp(-1/2*(-1+t)^2)
>>symsx
y=dsolve(’Dy+2*x*y=x*exp(-x^2)’,’x’)
y=
(1/2*x^2+C1)*exp(-x^2)
>>symst;y=dsolve(’D3y+3*D2y+3*Dy+y=exp(-t)*sin(t)’)
y=
exp(-t)*cos(t)+C1*exp(-t)+C2*exp(-t)*t+C3*exp(-t)*t^2
应该注意的是如何处理自变量,MATLAB符号运算默认的自变量是t,所以若选择t为自变量,故①、③的求解不存在问题,在②微分方程求解时,若不指出x为自变量,则可以尝试下面的MATLAB语句,得出解析解。
>>symsx
y=dsolve(’Dy+2*x*y=x*exp(-x^2)’,’x’)
y=
(1/2*exp(-x*(x-2*t))+C1)*exp(-2*t*x)2
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
第7章微分方程问题的计算机求解79
这样看似的出了问题的解析解,但实际上这样的解错误的,因为在求解微分方程时是将x作为常数时问题的方程的解析解,所以在解中既含有t,也含有x,故解是错误的。(www.61k.com)
7极限环是二阶非线性常微分方程中一种常见的现象,对某些非线性微分方程来说,不论初始状态为何值,微分方程的相轨迹都将稳定在一条封闭的曲线上,该曲线称为微分方程的极限??x˙=y+x(1?x2?y2)的极限环,并对不同初值验证微分方程环。试绘制出微分方程y˙=?x+y(1?x2?y2)
的相平面曲线确实收敛于极限环。
【求解】由于微分方程是非线性微分方程,所以只能求解其数值解,而一般解析解是不存在的。令x1=x,x2=y,则可以用下面的语句求解该微分方程,这样在不同的初值下,可以绘
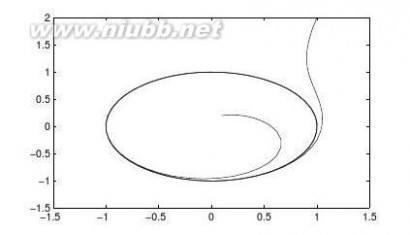
制出解的相平面曲线,如图7-2所示,可见,对不同的初值,微分方程解的相空间轨迹将收敛于封闭的曲线,以及极限环。
>>f=inline(’[x(2)+x(1)*(1-x(1)^2-x(2)^2);-x(1)+x(2)*(1-x(1)^2-x(2)^2)]’,’t’,’x’);
[t,x]=ode45(f,[0,10],[1;2]);plot(x(:,1),x(:,2));holdon
[t,x]=ode45(f,[0,10],[0.1;0.2]);plot(x(:,1),x(:,2));
??˙=?y?z??x
8考虑著名的R¨ossler化学反应方程组,选定a=b=0.2,c=5.7,且y˙=x+ay???z˙=b+(x?c)z
x1(0)=x2(0)=x3(0),绘制仿真结果的三维相轨迹,并得出其在x-y平面上的投影。在实际求解中建议将a,b,c作为附加参数,同样的方程若设a=0.2,b=0.5,c=10时,绘制出状态变量的二维图和三维图。
【求解】令x1=x,x2=y,x3=z,这样可以求解出该微分方程数值解,并绘制出解的三维相空间曲线,如图7-3a所示。
>>f=inline(’[-x(2)-x(3);x(1)+a*x(2);b+(x(1)-c)*x(3)]’,...
’t’,’x’,’flag’,’a’,’b’,’c’);
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
80第7章微分方程问题的计算机求解
[t,x]=ode45(f,[0,100],[0;0;0],[],0.2,0.2,5.7);
plot3(x(:,1),x(:,2),x(:,3));grid
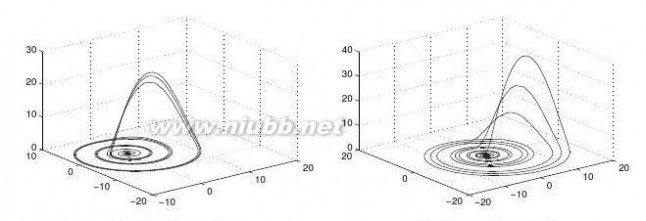
图7-3R¨ossler方程的相空间轨迹
修改a,b,c参数,则可以用下面的语句绘制出相空间轨迹,如图7-3b所示。[www.61k.com)
>>[t,x]=ode45(f,[0,100],[0;0;0],[],0.2,0.5,10);
plot3(x(:,1),x(:,2),x(:,3));grid
??˙=α[y?x?f(x)]??x
,其中f(x)为y˙=x?y+z???z˙=?βy?γz9Chua电路方程是混沌理论中经常提到的微分方程[54]
1Chua电路的二极管分段线性特性,f(x)=bx+(a?b)(|x+1|?|x?1|),且a<b<0,试编写2
出MATLAB函数描述该微分方程,并绘制出α=15,β=20,γ=0.5,a=?120/7,b=?75/7,且初始条件为x(0)=?2.121304,y(0)=?0.066170,z(0)=2.881090时的相空间曲线。
【求解】令x1=x,x2=y,x3=z,则可以用下面的语句描述微分方程组
functiondx=c7chua(t,x,flag,a,b,alpha,beta,gamma)
dx=[alpha*(x(2)-x(1)-nlfun(x(1),a,b));
x(1)-x(2)+x(3);-beta*x(2)-gamma*x(3)];
functionf0=nlfun(x,a,b)
f0=b*x+(a-b)*(abs(x+1)-abs(x-1))/2;
这样用下面的语句可以求解微分方程,并绘制出相空间轨迹,如图7-15所示。
>>a=-120/7;b=-75/7;alpha=15;beta=20;gamma=0.5;
f=odeset;f.RelTol=1e-6;
[t,x]=ode15s(’c7chua’,[0,10],[-2.121304;-0.06617;2.88109],f,...
a,b,alpha,beta,gamma);
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
第7章微分方程问题的计算机求解
??
10Lotka-Volterra扑食模型方程为x˙(t)=4x(t)?2x(t)y(t)81
y˙(t)=x(t)y(t)?3y(t)
试求解该微分方程,并绘制相应的曲线。(www.61k.com)
线,分别如图7-4a、b所示。,且初值为x(0)=2,y(0)=3,【求解】用下面命令可以立即解出微分方程的模型,并绘制出解的时间响应曲线和相平面曲

>>f=inline(’[4*x(1)-2*x(1)*x(2);x(1)*x(2)-3*x(2)]’,’t’,’x’);
[t,x]=ode45(f,[0,10],[2;3]);
图7-4Lotka-Volterra扑食模型的解
11请给出求解下面微分方程的MATLAB命令
y(3)+tyy¨+t2yy˙2=e?ty,y(0)=2,y˙(0)=y¨(0)=0
并绘制出y(t)曲线,试问该方程存在解析解吗?选择四阶定步长Runge-Kutta算法求解该方程时,步长选择多少可以得出较好的精度,试与MATLAB语言给出的现成函数在速度、精度上进行比较。
【求解】因为该方程为含有非线性项的微分方程,所以一般来说该方程不能有解析解,只能求解其数值解。要求解该方程。,则需要引入状态变量x1=y,x2=y,˙x3=y¨,这样可以写出一阶微分方程组为
??˙1=x2??x
x˙2=x3???x?tx1˙3=?tx1x2?t2x2x21+ex1(0)=2,x2(0)=x3(0)0
这样就可以用下面的语句求解微分方程,并绘制出状态变量的时域响应曲线,如图7-15所示,可见,时变微分方程也可以容易地求解。
>>f=inline(’[x(2);x(3);-t^2*x(1)*x(2)-t^2*x(2)*x(1)^2+exp(-t*x(1))]’,’t’,’x’);
[t,x]=ode45(f,[0,10],[2;0;0]);
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
82
第7章微分方程问题的计算机求解
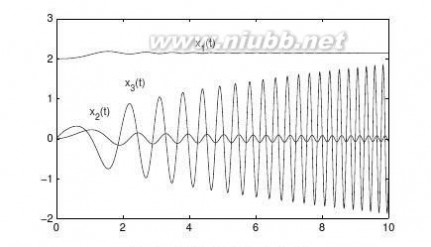
12试选择状态变量,将下面的非线性微分方程组转换成一阶显式微分方程组,并用MATLAB对其求解,绘制出解的相平面或相空间曲线。(www.61k.com)
??x????=?x?y?(3x??)2+(y??)3+6y????+2t????y??????=?y?????x???e?x?t①?x(1)=2,x??(1)=?4????y(1)=?2,y??(1)=7,y????(1)=6??x?????2xzx??=3x2yt2????????y??2???y?ey=4xtz②z?????2tz??=2texy????z??(1)=x??(1)=y??(1)=2????z??(1)=x(1)=y(1)=3
【求解】①选择x1=x,x2=x??,x3=y,x4=y??,x5=y????,则可以将原来的微分方程组转换成下面的一阶微分方程组
??x˙1=x2?????˙2=?x1?x3?(3x2)2+(x4)3+6x5+2t??x
x˙3=x4????x˙4=x5????x˙=?x?x?e?x1?t552
且x(1)=[2,?4,?2,7,6]T,
>>f=inline([’[x(2);-x(1)-x(3)-(3*x(2))^2+(x(4))^3+6*x(5)+2*t;’,...
’x(4);x(5);-x(5)-x(2)-exp(-x(1))-t]’],’t’,’x’);
[t1,x1]=ode45(f,[1,0],[2,-4,-2,7,6]’);
[t2,x2]=ode45(f,[1,2],[2,-4,-2,7,6]’);
t=[t1(end:-1:1);t2];x=[x1(end:-1:1,:);x2];
plot(t,x)
figure;plot(x(:,1),x(:,3))
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
第7章微分方程问题的计算机求解
83
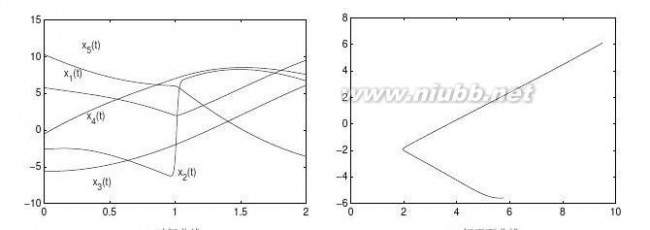
图7-6微分方程的解
②选择状态变量x1=x,x2=x??,x3=y,x4=y??,x5=z,x6=z??,
??x˙1=x2????2?x˙2=2x1x2x5+3x2?1x3t???x˙3=x4
?x˙4=e?x3x4+4x1t2x5?????x˙5=x6????x˙6=2tx6+2te?x1x3
x(1)=[3,2,3,2,2,3]T
>>f=inline([’[x(2);2*x(1)*x(2)*x(5)+3*x(1)^2*x(3)*t^2;’,...
’x(4);exp(-x(3))*x(4)+4*x(1)*t^2*x(5);’,...
’x(6);2*t*x(6)+2*t*exp(-x(1)*x(3))]’],’t’,’x’);
[t,x]=ode15s(f,[10],[3,2,3,2,2,3]’);
13试用解析解和数值解的方法求解下面的微分方程组。(www.61k.com]??x????(t)=?2x(t)?3x??(t)+e?5t,x(0)=1,x??(0)=2
y????(t)=2x(t)?3y(t)?4x??(t)?4y??(t)?sint,y(0)=3,y??(0)=4
【求解】该方程的解析解可以由下面的语句直接得出
>>symst
[x,y]=dsolve(’D2x=-2*x-3*Dx+exp(-5*t)’,’D2y=2*x-3*y-4*Dx-4*Dy-sin(t)’,...’x(0)=1’,’Dx(0)=2’,’y(0)=3’,’Dy(0)=4’)
x=
1/12*exp(-5*t)-10/3*exp(-2*t)+17/4*exp(-t)
y=
-71/5*exp(-3*t)-265/16*exp(-t)+11/48*exp(-5*t)+100/3*exp(-2*t)+
1/5*cos(t)-1/10*sin(t)+51/4*exp(-t)*t
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
84第7章微分方程问题的计算机求解
还可以令x1=x(t),x2=x??(t),x3=y(t),x4=y??(t),这时可以将微分方程组改写成
??x˙1=x2????x˙2=?2x1?3x2+e?5t
?x˙3=x4????x˙4=2x1?3x3?4x2?4x4?sint,x˙T(0)=[1,2,3,4]
可以写出描述微分方程组的MATLAB函数为
>>f=inline(...
’[x(2);-2*x(1)-3*x(2)+exp(-5*t);x(4);2*x(1)-3*x(3)-4*x(2)-4*x(4)-sin(t)]’,...’t’,’x’);
[t1,x1]=ode45(f,[0,10],[1;2;3;4]);
ezplot(x,[0,10]),line(t1,x1(:,1))
figure;ezplot(y,[0,10]),line(t1,x1(:,3))
得出的x(t)和y(t)

曲线的数值解与解析解分别如图7-7a、b所示,可见,得出的数值解精度还是很高的,在曲线上无法区分出解析解和数值解。(www.61k.com]
(a)x(t)(b)y(t)
图7-7微分方程的解析解与数值解比较
??
14给定微分方程组u¨(t)=?u(t)/r3(t)
v¨(t)=?v(t)/r3(t),其中r(t)=??u2(t)+v2(t),且u(0)=1,u˙(0)=
2,v˙(0)=2,v(0)=1,试选择一组状态变量,将其变换成MATLAB语言能直接求解的微分方程组形式,并绘制出u(t),v(t)的轨迹曲线。
【求解】令x1=u,x2=u,˙x3=v,x4=v˙,这样可以将原微分方程组转换成关于xi的一阶微分方程组??x˙1=x2????x˙2=?x1/r3
?x˙3=x4????x˙4=?x3/r3
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
第7章微分方程问题的计算机求解
其中r=??85T13,x(0)=[1,2,2,1]。(www.61k.com]由于有中间变量r,所以原问题不大适合用inline()函数描述,
functiondx=exc7eqa(t,x)
r=sqrt(x(1)^2+x(3)^2);
dx=[x(2);-x(1)/r^3;x(4);-x(3)/r^3];
这样用下面的语句就可以求解该方程,绘制出v(t)和u(t)
关系曲线,如图7-8所示。>>[t,x]=ode45(’exc7eqa’,[0,10],[1221]’);
plot(x(:,1),x(:,3))
??u˙1=u3????u˙2=u4[30],其中15已知微分方程可以表示为2?2u˙+cos(u?u)u˙=?gsinu?sin(u?u)u?31241124???cos(u1?u2)u˙3+u˙4=?gsinu2+sin(u1?u2)u23
u1(0)=45,u2(0)=30,u3(0)=u4(0)=0,g=9.81,试求解此微分方程并绘制出各个状态变量的时间曲线。
【求解】显然这是一个微分代数方程的标准形,可以由给出的方程写出M(t,u)矩阵
??1000?01?00?M(t,u)=??002cos(u1?u2)?
00cos(u1?u2)1
这样可以编写MATLAB文件来描述M矩阵
functionM=exc7eqm(t,u)
M=[1000;0100;002cos(u(1)-u(2));00cos(u(1)-u(2))1];还可以立即写出状态方程文件为
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
86
functiondu=exc7eqb(t,u)
du=[u(3);
u(4);
9.81*sin(u(1))-sin(u(1)-u(2))*u(4)^2;
9.81*sin(u(2))+sin(u(1)-u(2))*u(3)^2];
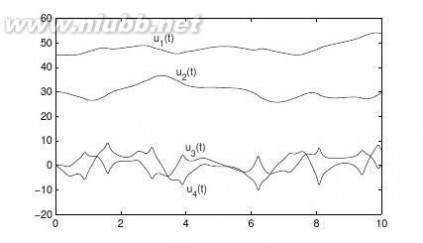
第7章微分方程问题的计算机求解
从而可以用下面的语句求解该微分代数方程,得出的状态变量曲线如图7-9所示。[www.61k.com)
>>ff=odeset;ff.Mass=@exc7eqm;
[t,x]=ode45(@exc7eqb,[0,10],[45;30;0;0],ff);plot(t,x)
??
16试求出隐式微分方程22?x2x˙1x¨2sin(x1x2)+5¨x1x˙2cos(x21)+tx1x2=e2
x¨1x2+x¨2x˙1sin(x2x2x2)=sint1)+cos(¨
1,x˙1(0)=1,x2(0)=2,x˙2(0)=2,并绘制出轨迹曲线。的数值解,x1(0)=
【求解】引入u1=x1,u2=x˙1,u3=x2,u4=x˙2,这样可以写出如下的隐式微分方程标准形为??u˙1?u2=0????uu22?u23=0˙2u4cos(u2)+tuu?e2˙4sin(u1u3)+5u113
?u˙3?u4=0????u˙2u3+u˙4u2sin(u2˙4u3)?sint=01)+cos(u
这样可以编写出下面的隐式微分方程的MATLAB表达
functionfun=exc7eqc(t,u,ud)
fun=[ud(1)-u(2);
-u(2)*ud(4)*sin(u(1)*u(3))-5*ud(2)*u(4)*cos(u(1)^2)-t*u(1)*u(3)^2+exp(-u(3)^2);ud(3)-u(4);
-ud(2)*u(3)-ud(4)*u(2)*sin(u(1)^2)-cos(ud(4)*u(3))-sin(t)];
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
第7章微分方程问题的计算机求解87
˙(0)和u(0)共需要8个初值信息,而直接由习题提供的只有4个值,为产生不矛盾的由于u
初值,应该采用decic()函数求解初值方程,这里需要确保给定的4个初值量,用该函数可以解出其余4个量
>>u0=[1;0;2;0];ud0=[0;1;0;2];
[y0,yp0]=decic(@exc7eqc,0,u0,[1010],ud0,[0101])
y0=
1.00000000000000
-0.80000166579942
2.00000000000000
0.54532232612148
yp0=
-0.80000166579942
1.00000000000000
0.54532232612148
2.00000000000000
利用MATLAB7.0引入的隐式微分方程求解函数ode15i(),可以用下面的语句求出微分方

程的数值解,并绘制出状态曲线,如图7-10所示。(www.61k.com)
>>r=ode15i(@exc7eqc,[0,1.2],y0,yp0);plot(r.x,r.y)
17下面的方程在传统微分方程教程中经常被认为是刚性微分方程,试用常规微分方程解法和刚性微分方程解法分别求解这两个微分方程的数值解,并求出解析解,用状态变量曲线比较数值求解的精度。?11??y˙1=9y1+24y2+5cost?sint,y1(0)=33①12??y˙2=?24y1?51y2?9cost+sint,y2(0)=33??˙1=?0.1y1?49.9y2,y1(0)=1??y②y˙2=?50y2,y2(0)=2???y˙3=70y2?120y3,y3(0)=1
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
88第7章微分方程问题的计算机求解
??˙1=?0.04y1+104y2y3??y
2,其初值18考虑下面的化学反应系统的反应速度方程组y˙2=0.04y1?104y2y3?3×107y2???y2˙3=3×107y2
为y1(0)=1,y2(0)=y3(0)=0,该方程往往被认为是刚性方程,试采用ode45()对之求解,观察是否能正确求解,如果不能求解应该如何解决问题?
【求解】用下面的语句可以分别用两种方法,即RKF四阶五级算法及刚性方程的求解方法,求解该方程,则可以分别测出计算的点数有极大的差异,求解这样的方程用刚性方程求解方
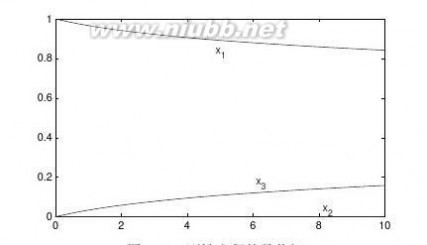
法比较合适。(www.61k.com]得出的解还可以用曲线表示出来,如图7-11所示。
>>f=inline([’[-0.04*y(1)+10^4*y(2)*y(3);0.04*y(1)-10^4*y(2)*y(3)-3e7*y(2)^2;’,...
’3e7*y(2)^2]’],’t’,’y’);
[t,y]=ode45(f,[0,10],[1;0;0]);size(t)
ans=
29109
ans=
411
1>>[t,y]=ode15s(f,[0,10],[1;0;0]);size(t),plot(t,y)19试求出习题4中给出的微分方程边值问题数值解,绘制出y(t)曲线,并和该习题得出的解析解比较精度。
【求解】微分方程的解析解可以由下面的函数直接求出
>>symsx
y=dsolve(’D2y-(2-1/x)*Dy+(1-1/x)*y=x^2*exp(-5*x)’,...
’y(1)=sym(pi)’,’y(sym(pi))=1’,’x’)
ezplot(y,[0,10])
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
第7章微分方程问题的计算机求解8920考虑VanderPol方程y¨+μ(y2?1)y˙+y=0,试求解μ=1,且边值y(0)=1,y(5)=3时方程的数值解。(www.61k.com)如果假设μ为自由参数,试求出满足边值条件,且满足y˙(5)=2时方程的数值解及μ的值,并绘图验证之。
【求解】用下面的语句可以写出原方程的MATLAB表示,其中μ的值用变量m表示,该变量可以看成是附加参数。
functiondx=exc7ffo1(t,x,flag,m)
dx=[x(2);-m*(x(1)^2-1)*x(2)-x(1)];
这样可以将原问题转换成方程y˙(5)=2求解的问题,该方程由下面的语句即可描述。
functiony=exc7ffo(x)
[t,y1]=ode45(’exc7ffo1’,[0,5],[1;3],[],x);
y=abs(y1(end,2)-2);
求解,且绘制出该μ

值下的状态变量曲线,如图7-12所示。
>>x=fsolve(’exc7ffo’,0)
[t,y]=ode45(’exc7ffo1’,[0,5],[1;3],[],x);plot(t,y);
x=
-0.03459759451208
?2?u?2u??+2=0???y??x2
,并绘制出u函数曲面。21试用数值方法求解偏微分方程u|=1,u|=0?x=0,y>0y=0,x??0????x>0,y>0
【求解】可以看出,该方程为椭圆型偏微分方程,且c=1,f=0,用pdetool函数提供的界面求解该方程,选择并设置椭圆微分方程,再选择矩形区域,可以设置出横轴和纵轴的边界条件,求解微分方程则可以得出如图7-13所示的解曲面。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
90Color: u Height: u第 7 章 微分方程问题的计算机求解0.9 1 0.8 0.7 0.5 0.6 0.5 0.4 0 1.5 1 0.5 0 0 0.5 1 0.3 1.5 0.2 0.1图 7-13 偏微分方程解曲面 22 考虑简单的线性微分方程 y (4) + 3y (3) + 3¨ + 4y + 5y = e?3t + e?5t sin(4t + p/3),且方程 y ˙ 的初值为 y(0) = 1, y(0) = y (0) = 1/2, y (3) (0) = 0.2,试用 Simulink 搭建起系统的仿真模 ˙ ¨ 型,并绘制出仿真结果曲线。(www.61k.com)考虑上面的模型,假设给定的微分方程变化成时变线性微分 方程 y (4) + 3ty (3) + 3t2 y + 4y + 5y = e?3t + e?5t sin(4t + p/3),而方程的初值仍为 y(0) = 1, ¨ ˙ y(0) = y (0) = 1/2, y (3) (0) = 0.2,试用 Simulink 搭建起系统的仿真模型,并绘制出仿真结果 ˙ ¨ 曲线。 【求解】 可见该方程含有 y(t) 的四阶导数,所以需要四个积分器,这样可以容易地搭建出如 图 7-14 所示的 Simulink 仿真模型。exp(?3*u) Clock exp(?5*u)*sin(4*u+pi/3) 1 s Integrator 3Dy31 s Integrator1Dy21 s Integrator2Dyy 1 s Integrator3 1 Out1exc7m5.mdl3 4 5图 7-14 Simulink 模型 将各个积分器的初值按照给定的方式设置一下,则将由下面的语句 >> [t,x,y]=sim(’exc7m5’,[0,10]); plot(t,x) figure; plot(t,y) 可以得出得出如图 7-15a、b 所示的状态变量曲线和输出信号曲线。 考虑本例给出的时变微分方程,可以用 Simulink 绘制出该系统的仿真模型,如图 ?? 所示。 用下面的语句可以绘制出系统的状态变量曲线和输出曲线,分别如图 7-17a、b 所示。 >> [t,x,y]=sim(’exc7m5’,[0,10]); plot(t,x) figure; plot(t,y)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
第7章微分方程问题的计算机求解
91
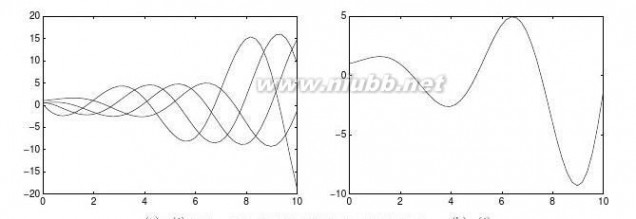

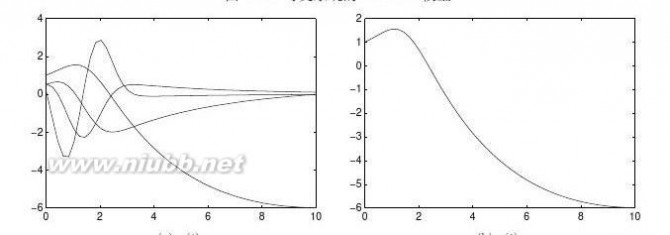
图7-17微分方程的状态变量与输出变量
23考虑延迟微分方程y(4)(t)+4y(3)(t?0.2)+6y????(t?0.1)+6y????(t)+4y??(t?0.2)+y(t?0.5)=e?t,
且在t??0时该方程具有零初始条件,试分别用Simulink建模与dde23()函数求解的方式直接求解该微分方程,并绘制出y(t)曲线。(www.61k.com)
【求解】可以按图7-18中所示的方式建立起该方程的Simulink仿真模型,对其进行仿真则可以得出如图7-19所示的输出曲线。
2
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
92第7章微分方程问题的计算机求解
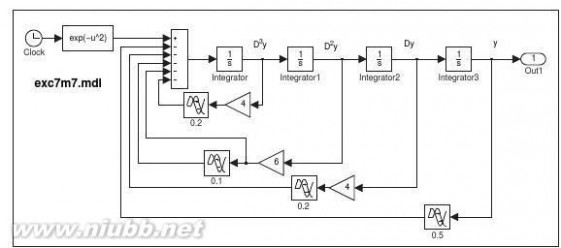

下面考虑用dde23()函数求解该方程。(www.61k.com)从给出的方程看,有三个延迟时间常数τ1=0.2,τ2=0.1,τ3=0.5,则可以写出该延迟微分方程的MATLAB表示为
functiondx=exc7ffo2(t,x,z)
xlag1=z(:,1);xlag2=z(:,2);xlag3=z(:,3);
dx=[x(2);x(3);x(4);
exp(-t.^2)-4*xlag1(4)-6*xlag2(3)-6*x(3)-4*xlag1(2)-xlag3(1)];
这样可以由下面的语句求取微分方程的数值解,其结论与图7-19中给出的完全一致。该方法求解所需的时间明显高于Simulink模型。
>>lags=[0.2,0.1,0.5];tx=dde23(’exc7ffo2’,lags,zeros(4,1),[0,10]);
plot(tx.x,tx.y(2,:))
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
第8章数据插值、函数逼近问题的计算机求解1用y(t)=t2e?5tsint生成一组较稀疏的数据,并用一维数据插值的方法对给出的数据进行曲线拟合,并将结果与理论曲线相比较。(www.61k.com)
【求解】
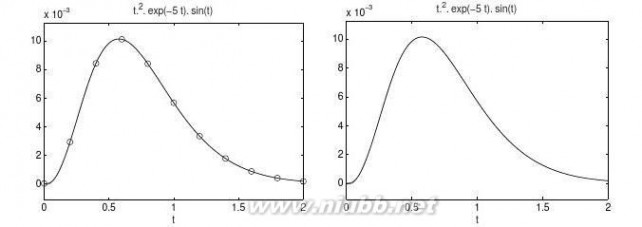
由下面的语句可以立即得出一组数据,这些数据分布情况如图8-1a所示。>>t=0:0.2:2;
y=t.^2.*exp(-5*t).*sin(t);plot(t,y,’o’)
(a)已知样本数据分布(b)样条插值拟合效果
图8-1曲线的样条插值拟合
由这些数据作出发点,就可以用各种插值算法对其进行插值,这里只给出效果最好的样条插值,其插值结果和理论曲线一起在图8-1b中给出,可见,拟合效果相当理想,几乎看不出和理论曲线之间的区别。
>>ezplot(’t.^2.*exp(-5*t).*sin(t)’,[0,2]);holdon
x1=0:0.01:2;y1=interp1(t,y,x1,’spline’);
plot(x1,y1)
2用y(t)=sin(10t2+3)在(0,3)区间内生成一组较稀疏的数据,并用一维数据插值的方法对给出的数据进行曲线拟合,并将结果与理论曲线相比较。
【求解】类似于上面的例子,可以用几乎一致的语句得出样本数据和插值效果,如图8-2a、b所示。
>>t=0:0.2:3;
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
94第8章数据插值、函数逼近问题的计算机求解
y=sin(10*t.^2+3);plot(t,y,’o’)
ezplot(’sin(10*t^2+3)’,[0,3]);holdon
x1=0:0.001:3;y1=interp1(t,y,x1,’spline’);
plot(x1,y1)

图8-2曲线的样条插值拟合
由于曲线本身变换太大,所以在目前选定的样本点下是不可能得出理想插值效果的,因为样本数据提供的信息量不够。[www.61k.com)为了得到好的插值效果,必须增大样本数据的信息量,对本例来说,必须在快变化区域减小样本点的步长。
>>holdoff
t=[0:0.1:1,1.1:0.04:3];y=sin(10*t.^2+3);plot(t,y,’o’)
ezplot(’sin(10*t^2+3)’,[0,3]);holdon
x1=0:0.001:3;y1=interp1(t,y,x1,’spline’);
plot(x1,y1)
3用f(x,y)=1?x2?y4esin(xy2+x2y)原型函数生成一组网格数据或随机数据,分别拟3x+y
合出曲面,并和原曲面进行比较。
是三维表面图,如图8-4a所示。
>>[x,y]=meshgrid(0.2:0.2:2);
z=exp(-x.^2-y.^4).*sin(x.*y.^2+x.^2.*y)./(3*x.^3+y);
surf(x,y,z)
选择新的密集网格,则可以通过二元插值得出插值曲面,如图8-4b所示。对比插值结果和新网格下的函数值精确解,则可以绘制出绝对插值误差曲面,如图8-5所示。由插值结果可见精度是令人满意的。【求解】由下面的语句可以直接生成一组网格数据,用下面语句还可以还绘制出给定样本点
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
第8章数据插值、函数逼近问题的计算机求解95
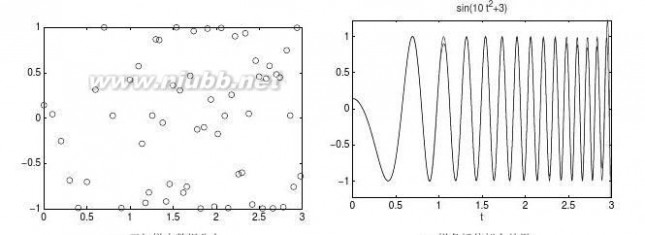
图8-3加密样本点后曲线的样条插值拟合
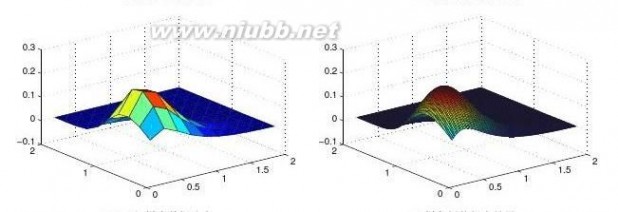
图8-4曲面的样条插值拟合
>>[x1,y1]=meshgrid(0.2:0.02:2);
z1=interp2(x,y,z,x1,y1,’spline’);
surf(x1,y1,z1)
>>z0=exp(-x1.^2-y1.^4).*sin(x1.*y1.^2+x1.^2.*y1)./(3*x1.^3+y1);
surf(x1,y1,abs(z1-z0))
现在假设已知的样本点不是网格形式分布的,而是随机分布的,则可以用下面语句生成样本点,得出分布的二维、三维示意图如图8-6a、b所示。[www.61k.com)
>>x=0.2+1.8*rand(400,1);y=0.2+1.8*rand(400,1);
%仍生成(0.2,2)区间的均匀分布随机数
z=exp(-x.^2-y.^4).*sin(x.*y.^2+x.^2.*y)./(3*x.^3+y);
plot(x,y,’x’)
figure,plot3(x,y,z,’x’)
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
96
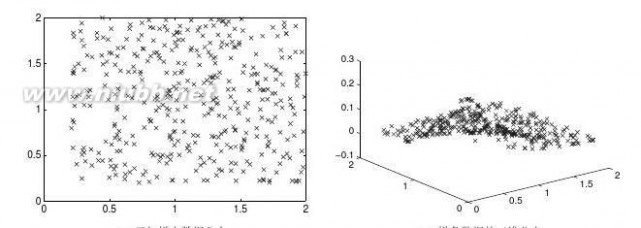
第8章数据插值、函数逼近问题的计算机求解
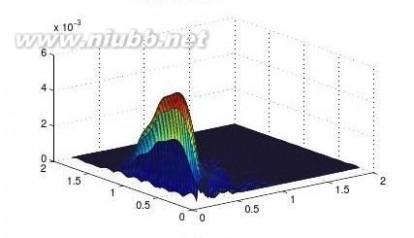
图8-6非网格样本点分布
利用下面的语句可以得出三维插值结果,如图8-7a所示,同时可以绘制出插值的绝对误差曲面,如图8-7b所示,可见插值结果还是很好的,但由于边界样本点信息不能保证,所以不能像网格数据那样对(0.2,2)区域,而只能选择(0.3,1.9)区域进行插值。(www.61k.com)
>>[x1,y1]=meshgrid(0.3:0.02:1.9);
z1=griddata(x,y,z,x1,y1,’v4’);surf(x1,y1,z1)
>>z0=exp(-x1.^2-y1.^4).*sin(x1.*y1.^2+x1.^2.*y1)./(3*x1.^3+y1);
surf(x1,y1,abs(z1-z0))
4假设已知一组数据,试用插值方法绘制出x∈(?2,4.9)区间内的光滑函数曲线,比较各种插值算法的优劣。
xixi
-21.6
-1.71.9
-1.42.2
-1.12.5
-0.82.8
-0.53.1
-0.23.4
0.13.7
0.44
0.74.3
14.6
1.34.9
yi0.102890.117410.131580.144830.156560.166220.173320.17750.178530.176350.171090.16302yi0.152550.14020.126550.112190.097680.083530.070150.057860.046870.037290.029140.02236
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
第8章数据插值、函数逼近问题的计算机求解97

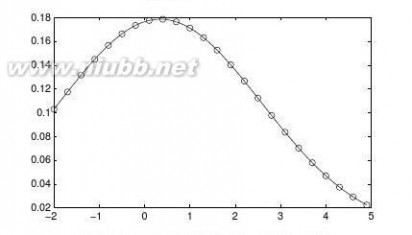
图8-7非网格样本点的样条插值结果
【求解】用下面的语句可以立即得出给定样本点数据的三次插值与样条插值,得出的结果如图8-8所示,可见,用两种插值方法对此例得出的结果几乎一致,效果均很理想。[www.61k.com]
>>x=[-2,-1.7,-1.4,-1.1,-0.8,-0.5,-0.2,0.1,0.4,0.7,1,1.3,...
1.6,1.9,2.2,2.5,2.8,3.1,3.4,3.7,4,4.3,4.6,4.9];
y=[0.10289,0.11741,0.13158,0.14483,0.15656,0.16622,0.17332,...
0.1775,0.17853,0.17635,0.17109,0.16302,0.15255,0.1402,...
0.12655,0.11219,0.09768,0.08353,0.07019,0.05786,0.04687,...
0.03729,0.02914,0.02236];
x0=-2:0.02:4.9;
y1=interp1(x,y,x0,’cubic’);
y2=interp1(x,y,x0,’spline’);
plot(x0,y1,’:’,x0,y2,x,y,’o’)
5假设已知实测数据由下表给出,试对(x,y)在(0.1,0.1)~(1.1,1.1)区域内的点进行插值,并
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
98
用三维曲面的方式绘制出插值结果。(www.61k.com)
yi0
x10.1
x20.2
x30.3
x40.4
x50.5
第8章数据插值、函数逼近问题的计算机求解
x60.60.81610.92841.00861.10191.20461.3111.41381.50341.56841.5964
x70.7
x80.8
x90.9
x101
x111.10.98011.15291.32221.46051.53351.50521.3461.04540.62477
0.10.830410.827270.824060.820980.818240.30.835870.843450.856310.874660.898670.40.842860.860130.885370.918650.959850.50.852680.882510.922860.973460.60.865320.910490.968470.70.880780.943960.80.899040.982760.90.920061
0.943811.10.97023
1.02661.07521.1279
1.02171.0821.14821.21911.2929
1.03831.11181.19221.27681.36241.4448
1.03361.1181.21021.30611.40051.48661.5564
0.814810.814630.815790.818530.823040.963771.06421.17641.29371.40631.50211.56611.58211.5341
1.00451.12531.2541.37931.48591.55551.56781.50321.3473
1.05021.19041.33081.45391.53771.55731.48891.3151.0321
1.11.2571.40171.50861.54841.49151.31561.0155
0.20.831720.832490.835840.842010.851250.863760.879750.899350.922630.94959
0.612680.14763
【求解】直接采用插值方法可以解决该问题,得出的插值曲面如图8-9a所示。
>>[x,y]=meshgrid(0.1:0.1:1.1);
z=[0.83041,0.82727,0.82406,0.82098,0.81824,0.8161,0.81481,0.81463,0.81579,0.81853,0.82304;0.83172,0.83249,0.83584,0.84201,0.85125,0.86376,0.87975,0.89935,0.92263,0.94959,0.9801;0.83587,0.84345,0.85631,0.87466,0.89867,0.9284,0.96377,1.0045,1.0502,1.1,1.1529;0.84286,0.86013,0.88537,0.91865,0.95985,1.0086,1.0642,1.1253,1.1904,1.257,1.3222;0.85268,0.88251,0.92286,0.97346,1.0336,1.1019,1.1764,1.254,1.3308,1.4017,1.4605;0.86532,0.91049,0.96847,1.0383,1.118,1.2046,1.2937,1.3793,1.4539,1.5086,1.5335;0.88078,0.94396,1.0217,1.1118,1.2102,1.311,1.4063,1.4859,1.5377,1.5484,1.5052;0.89904,0.98276,1.082,1.1922,1.3061,1.4138,1.5021,1.5555,1.5573,1.4915,1.346;0.92006,1.0266,1.1482,1.2768,1.4005,1.5034,1.5661,1.5678,1.4889,1.3156,1.0454;0.94381,1.0752,1.2191,1.3624,1.4866,1.5684,1.5821,1.5032,1.315,1.0155,0.62477;0.97023,1.1279,1.2929,1.4448,1.5564,1.5964,1.5341,1.3473,1.0321,0.61268,0.14763];[x1,y1]=meshgrid(0.1:0.02:1.1);z1=interp2(x,y,z,x1,y1,’spline’);surf(x1,y1,z1)
axis([0.1,1.1,0.1,1.1,min(z1(:)),max(z1(:))])
其实,若光需要插值曲面而不追求插值数值的话,完全可以直接采用MATLAB下的shadinginterp命令来实现,得出的效果如图8-9b所示。可见,这样的插值方法更好,得出的插值曲面更光滑。
>>surf(x,y,z);shadinginterp
6假设已知一组实测数据在文件c8pdat.dat中给出,试通过插值的方法绘制出三维曲面。
高等应用数学问题的MATLAB求解 高等应用数学问题的MATLAB求解_习题参考解答_薛定宇00002
第8章数据插值、函数逼近问题的计算机求解99
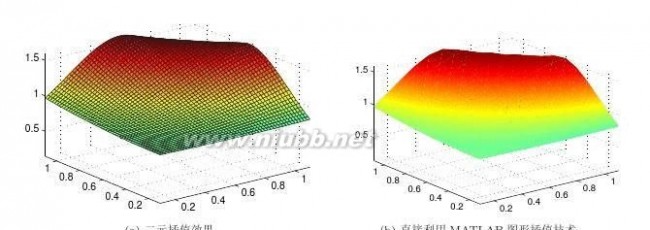
图8-9给定数据的插值结果
【求解】由该文件可见,给定的数据是非网格型的x,y,z向量,故提取这些向量并按非网格
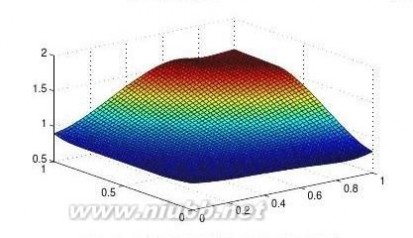
数据进行插值,则将得出如图8-10所示的插值结果。[www.61k.com]
>>loadc8pdat.dat
x=c8pdat(:,1);y=c8pdat(:,2);z=c8pdat(:,3);
[max(x),min(x)max(y),min(y)]
ans=
0.99430.01290.99940.0056
>>[x1,y1]=meshgrid(0:0.02:1);
z1=griddata(x,y,z,x1,y1,’v4’);
surf(x1,y1,z1)%找出插值区域
7假设已知数据由文件c8pdat3.dat给出,其中数据的第1-3列分别为x,y,z坐标,第4列为测出的V(x,y,z)函数值,试用三维插值方法对其进行插值。
【求解】四维插值问题可以由下面的语句直接求解,并可以考虑用切片的方式在三维空间内表示出来,如图8-11所示。
四 : yalmip + lpsolve + matlab 求解混合整数线性规划问题(MIP/MILP)
最近建立了一个网络流模型,是一个混合整数线性规划问题(模型中既有连续变量,又有整型变量)。(www.61k.com]当要求解此模型的时候,发现matlab优化工具箱竟没有自带的可以求解这类问题的算法(只有bintprog求解器,但是只能求解不含连续变量的二值线性规划问题)。于是在网上找了一些解决问题的途径,下面说说我试过的几种可能的解决方案,包括cplex、GLPK、lpsolve 和 yalmip。
cplex
首先想到的是IBM公司大名鼎鼎的cplex。cplex是IBM公司一款高性能的数学规划问题求解器,可以快速、稳定地求解线性规划、混合整数规划、二次规划等一系列规划问题。CPLEX 的速度非常快,可以解决现实世界中许多大规模的问题,它能够处理有数百万个约束 (constraint) 和变量 (variable) 的问题,而且一直刷新数学规划的最高性能记录。他的标准版本是一个windows下的IDE应用软件,但是开发人员能通过组件库从其他程序语言调用 CPLEX 算法。随标准版本一起发布的文件中包含一个名为matlab文件夹,将此文件夹添加到matlab的搜索路径下就可以在matlab下调用cplex高效地求解数学规划问题。
CPLEX Optimizer中文介绍:http://www.sstc.org.cn/components/detailview.aspx?id=ce16c50e-0059-417b-9806-c8b1d3224084
官方网址:http://www.sstc.org.cn/components/detailview.aspx?id=ce16c50e-0059-417b-9806-c8b1d3224084
遗憾的是,cplex是一款商业软件,可以从以上官方网址上下载免费试用版,使用时限是90天,而且试用版对问题规模有限制(我的问题有300个变量,370个约束,结果因为问题规模限制无法用试用版求解)。如果你要用cplex解决问题的话,可能还需要学习特定于cplex的建模语言。
值得一提的是,IBM公司一直对学术界有或多或少的支持,要想使用完整版的cplex,你可以参与IBM的学院计划,前提条件是你是大学/研究机构的老师/研究员,或者IBM公式的职员,通过这个网址:http://www-03.ibm.com/ibm/university/academic/pub/page/ban_ilog_programming? ,填写一个申请表格,通过审核之后你就有权限使用cplex的完整版,没有任何限制,和商业版完全一样的功能。
由于没钱买软件,试用版有规模限制,又是个学生不能参与学院计划,只好放弃这一途径==。
GLPK
在放弃了cplex之后搜寻其他解决方案的时候,我想起了GLPK。GLPK (GNU Linear Programming Kit,GNU线性编程工具)是GNU下的一个项目,用于建立大规模线性规划LP和混合型整数规划MIP问题,并对模型进行最优化求解。由于是GNU下的项目,因此没有商业非商业的版本限制,可以自由使用。
GLPK实现了对windows的支持,但是为此,你同样需要学习它的建模语言,并且所有的操作都在 glpsol.exe 提共的命令行下完成,比较不方便,且耗时长。如果要在matlab下使用,还需要下载额外的驱动文件。
GLPK英文介绍:http://www.gnu.org/software/glpk/
GLPK for windows:http://winglpk.sourceforge.net/
lpsolve(详细介绍,最好结合后面介绍的“yalmip”工具箱一起看)
在弄了一阵GLPK无果之后,我又转投lpsolve了。lpsolve是sourceforge下的一个开源项目,它的介绍如下:
Mixed Integer Linear Programming (MILP) solver lp_solve solves pure linear, (mixed) integer/binary, semi-cont and special ordered sets (SOS) models.lp_solve is written in ANSI C and can be compiled on many different platforms like Linux and WINDOWS
它是一个混合整数线性规划求解器,可以求解纯线性、(混合)整数/二值、半连续和特殊有序集模型。并且经过实际验证,有极高的求解效率。
sourceforge主页:http://sourceforge.net/projects/lpsolve/?source=directory
从以上主页上可以下载lpsolve的IDE版本,界面比较简陋,类似于如下的样子:
以上是用IDE工具建模求解,如果要在matlab下使用lpsolve,需要在网址http://sourceforge.net/projects/lpsolve/files/lpsolve/5.5.2.0/ 提供的文件列表中下载类似lp_solve_5.5.2.0_MATLAB_exe_win32(只针对windows 32位操作系统,其他操作系统请选择对应版本下载)的zip文件。
由于我的问题就是用的lpsolve解决的,在这里详细介绍一下,以lp_solve_5.5.2.0_MATLAB_exe_win32为例,过程如下:
1. 下载。将下载的zip解压后,得到以下文件结构:
bin目录下有matlab插件所必须的.mexw32文件和函数库API(.dll)。ex开头的一系列文件是自带的一些demo,教你如何在matlab下建模和求解。mxlpsove.m 是建模的核心函数,一个线性规划模型的所有配置和求解都是通过这个函数完成的。lp_maker.m 和 lp_solve.m 是对mxlpsolve.m的高层包装,简化了模型建立和求解的过程(后面会详细介绍)。
2. 准备驱动文件。在解压的bin目录下找到mxlpsolve.mexw32和mxlpsolve.dll两个文件,拷贝到解压根目录下(这两个文件就是matlab调用lpsolve的驱动文件),然后将此根目录添加到matlab搜索路径下(试试 pathtool 命令)。
3. 准备dll库文件。到这里不够,还需要lpsolve55.dll文件,真正求解问题的算法在这个函数库中。在lpsolve项目sourceforge首页下载安装一个IDE版本的程序,在安装目录下可以找到此dll文件,然后将此文件放到系统文件夹C:\Windows\System32下。也可以从我分享的这个链接下载到:http://vdisk.weibo.com/s/z4URgeDRTzBPd
4. 代码、求解。至此就可以在matlab下进尽情使用lpsolve了。以一个具体的例子说明用lpsolve求解数学规划问题的方法。
假设我们要用matlab解决如下线性规划问题:
付费,试用版有规模限制,需要学习特定建模语言。
GLPK
GNU
开源,免费;适合linux用户。
windows下繁琐,需要学习特定建模语言。
lpsolve
sourceforge
开源,免费。
需要学习特定建模语言;建模语言较繁琐。
yalmip
开放网络
网络开放获取,建模语言简单、统一,自带基本求解算法,并支持集成几乎所有其他求解器。推荐使用。
暂无。
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1