一 : 10大言过其实的数码产品:WebOS和WinME在列
苹果前CEO史蒂夫·乔布斯是极具魅力的产品演示大师,在发布会上标志性的“还有一件事”(one more thing)通常都会迎来一系列的尖叫和掌声,但是并非是所有产品都会获得如此待遇。事实上,在科技产品领域,一些投入了大量营销、看上去很美的产品,最终都被用户贴上“言过其实”、“噱头”的标签,并惨遭市场淘汰,最终沦为一个经典的失败案例,以下便是十大言过其实并最终失败的科技数码产品汇总:
1.Silverlight

微软曾经在Mix 07大会上发布了Silverlight技术,并宣称它将是一个最有趣的Web应用平台。,会让Flash看起来像“玩具”一样。不幸的是,该技术并没有获得软件开发商及用户的亲睐,尽管Netflix等厂商给予了支持,但仍回天乏术。目前,微软似乎也放弃了Silverlight的开发,基本上不会谈到它的未来,虽然最新版本可以支持到2021年。而诸如Netflix这样寥寥的支持者,也宣布将抛弃Silverlight转而使用更流行的HTML 5技术。
2. PowerMac G4 Cube

史蒂夫·乔布斯曾在2000年的Macworld大会上展示了拥有“苹果最美设计” PowerMac G4 Cube一体机,它拥有8英寸屏幕和内置式的DVD播放器,滑出式硬件设计以及各种强大的规格,产品体积却十分小巧,让各大科技媒体为之倾倒。但是,在一年后,这款缺乏扩展性的产品便宣告停产,尽管大幅降价但仍无法获得良好的销售成绩。当然,具有里程碑式意义的设计让它出现在纽约现代艺术博物馆中。
3. Palm Pre和WebOS

在2009年的CES大展上,Palm公司发布了全新的Web OS以及Palm Pre手机,拥有华丽的界面、出色的多任务处理系统以及整合Facebook等其他竞争对手所缺乏的功能,被媒体盛赞为“某些部分相比iPhone更具革命性”。但遗憾的是,由于市场推广不力,这款产品几乎没有在市场中形成影响,即使惠普公司后来花费12亿美元收购了Palm,也回天乏力。
4. 黑莓Storm
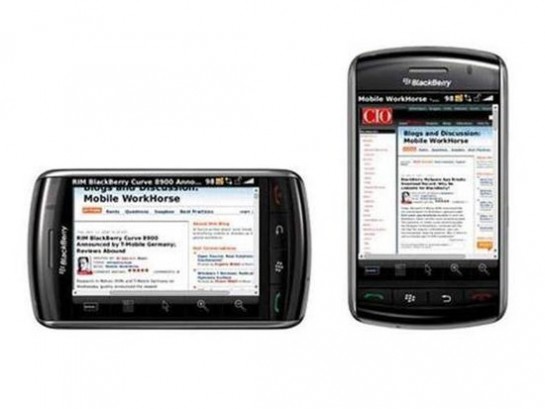
黑莓Storm是旗下首款采用全触控设计的机型,但毫无疑问是十分失败的。虽然它在当时拥有视频拍摄和GPS等先进功能,但较差的触控体验和令人失望的浏览器导致整个产品的失败,即使后续机型有所改进,但也给消费者造成了一种印象:黑莓不会做触控手机。
5. Onlive云游戏平台

与目前流游戏的概念相似,Onlive服务在2009年描绘了一个相当理想的游戏体验:不需要主机以及光盘或是下载游戏,只需要高带宽的互联网连接、远程服务器以及图形渲染,用户就可以在高清电视或是PC显示器上进行大型游戏。三年后,Onlive服务每况愈下,甚至还连累了诸如HTC等投资厂商,潜在的服务问题以及与微软授权的纠纷,让Onlive难以逃脱失败的命运。
6. NeXT Cube

这是乔布斯自立门户后推出的第二款电脑,于1989年推出,在当时拥有十分先进的硬件,比如采用了光存储、100万像素的显示器,以及非乔布斯风格的精美设计,诸如用户也表现出极大的兴趣。但是,当乔布斯透露该机的售价或许为10000美元(当时汇率折合人民币约为37600元)的天价时,基本上就决定了它失败的命运。
7. Windows ME系统

毫无疑问,Windows ME是微软迄今为止最失败的操作系统,虽然其数字媒体、网络和方便的还原选项是极大的卖点,但是极易发生的硬件和程序错误,使人难以忍受,即使狂打补丁也无法改善其较差的用户体验。
8. 黑莓Playbook

又一款黑莓的失败产品。虽然硬件规格出色,并以高安全性为卖点,但却极度“脑残”地没有内置本地的电子邮件和日历程序,需要与黑莓手机配合使用才能实现。时隔两年后,由于销量萎靡不振,黑莓无奈停产了部分型号的Playbook。
9. 思科Cius平板电脑

这是思科针对企业用户在2010年推出的Android平板电脑,拥有英特尔Atom 1.6GHz 处理器、7 英寸 WSVGA分辨率屏幕以及1GB RAM+32GB ROM的主流配置,功能卖点则为视频会议、良好的安全性以及思科的系统通信应用。但是,过高的售价相比苹果iPad显然没有丝毫竞争力,惨遭企业用户抛弃。
10. 苹果lisa

苹果lisa以乔布斯的爱女命名,是全球首款将图形用户界面(GUI)和鼠标结合起来的个人电脑。但是,华而不实的定位最终导致该机在市场中落败,事实上乔布斯也从来没有支持过这款产品,他在个人传记中将lisa研发团队中归类为“B级水准”。
来源:computerworld
二 : 一个数的约数和倍数的求法
课题二:
教学要求 ①通过直观教学,使学生进一步认识约数和倍数的意义。②使学生学会求一个数的约数和倍数的方法,知道一个数的约数的个数是有限的,一个数的倍数是无限的。③培养学生观察、探索、抽象、概括的能力。
教学重点 学会求一个数的约数和倍数的方法。
教学难点 弄清为什么一个数的约数的个数是有限的,一个数的倍数的个数是无限的。
教学用具 教师和学生都准备一套教学用的奎逊耐彩条。
教学过程
一、创设情境
1.说出约数和倍数的意义。
2.下面的数中,哪些是12的约数,哪些是2的倍数?1、2、3、4、5、6、7、8、9、10、11、12、13、……
12的约数有: 。
2的倍数有: 。
师:上面我们找出了12的约数和2的倍数,如果不给你这些数你能求出12的约数和2的倍数吗?下面我们来学习。(板书课题)
二、探索研究
1.小组合作,研究例2。
(1)思考并回答:求“12 的约数有哪几个”就是求什么。
(2)从摆彩条的规律中找方法。
①从小往大找,看哪些相同的彩条正好摆出12。
②一对一对找,看这些相同的彩条是否正好摆出12。
③得出12的约数有:1、2、3、4、6、12。
并用图表示: 12的约数
1、2、3、4、6、
12
④比较:哪几种方法好?
(3)尝试练习。
做教材51页下面的“做一做”。
让学生独立做,教师巡视,个别辅导,做完后点几名学生说一说是怎样做的。
(4)观察并回答:(观察例子和练习)
一个数的约数中最小的是几?最大的是几?一个数的约数的个数是多少?
2.小组合作,学习例3。
(1)思考:求2的倍数有哪些,该怎样想?
(2)从摆彩条的规律中找方法。
①从最小的倍数摆起,边摆边列算式。
②你发现规律了吗?
③2的倍数有多少个?为什么?
④得出2的倍数有:2、4、6、8、10……
用图表示为:
2 的倍数
2、4、6、
8、10……
(3)尝试练习。
做教材第52页的“做一做”,学生独立圈、写,集体订正。
(4)观察并回答:怎样求一个数的倍数?一个数的倍数有多少个?最小的是多少?
三、课堂实践
1、做练习十一的第5题,让学生独立写,教师辅导有困难的学生。
2、做练习十一的第6题。要使学生明确:40以内7的倍数为什么不打省略号。
四、课堂小结
学生小结今天的学习内容。
求一个数的约数 =求能整除这个数的所有整数(或者说是求这个数能被哪些数整除)
求一个数的倍数 =求能被这个数整除的所有整数(或者说是求哪些数能被这个数整除)
一个数的约数是有限的,最大的约数是它本身,最小的约数是1。
一个数的倍数是无限的,最小的倍数是它本身,没有最大的。
三 : 阅读下列材料材料一:祖冲之的科技才能是多方面的,尤其数学和天文学,他根据自己的观察与计算测定一年的实
| 阅读下列材料 材料一:祖冲之的科技才能是多方面的,尤其数学和天文学,他根据自己的观察与计算测定一年的实际天数是365.242814811天,和近代天文学测得的结果几乎完全吻合。 材料二:贾思勰对古书中的农业知识加以总结,走访收集观察实验,写成《齐民要术》。 材料三:郦道元通过收集文献资料和进行实地考察,在前人《水经》基础上写成《水经注》。 |
| 请回答: (1)他们三人都是什么时期的科学家? (2)依据他们的行动总结获取知识的方法。 (3)祖冲之还有其他哪些成就? (4)他们的成就有何历史影响? (5)我们今天可以学习他们什么精神? |
| ①南北朝时期的科学家; ②观察法,查阅资料法,访问法,实验法,实地考察法; ③计算出圆周率,千里船,指南车等; ④祖冲之是世界上第一个把圆周率的数值计算到小数点后七位数的人,比欧洲早约1000年,《齐民要术》是我国现存的第一部完整的农学著作,《水经注》是一部优秀的地理学著作,很高的文学和史学价值; ⑤刻苦钻研、注重实践、坚强毅力和决心的精神。 |
考点:
考点名称:郦道元和《水经注》《水经注》:《水经注》:
祖冲之:
南朝宋、齐时期我国伟大的科学家,在数学、天文历法、机械制造等方面都有突出成就。其中尤其是数学,我国自古就有”周三径一的说法,他在前人的基础上,求出了圆周率在3.1415926和3.1415926之间,是世界上第一个把圆周率准确数值推算到小数点后第七位的人,比欧洲早1100年,他的著作是《缀数》。

“祖率”:
祖冲之还是两个分数来表示圆周率,一个是335/113,叫密率;一个是22/7,叫约率。密率是分子分母在1000以内的分数形式的圆周率最佳近似值,是当时的最高成就。为了纪念他的贡献,人们把密率成为“祖率”。
 《齐民要术》简介:
《齐民要术》简介:四 : 数列求和的常用方法:
| 数列求和的常用方法: |
| (1)公式求和法: ①等差数列、等比数列求和公式 ②重要公式:1+2+…+n=
12+22+…+n2=
13+23+…+n3=(1+2+…+n)2=
(2)裂项求和法:将数列的通项分成两个式子的代数和,即an=f(n+1)-f(n),然后累加抵消掉中间的许多项,这种先裂后消的求和法叫裂项求和法.用裂项法求和,需要掌握一些常见的裂项,如:an=
(3)错位相减法:对一个由等差数列及等比数列对应项之积组成的数列的前n项和,常用错位相减法.an=bncn,其中{bn}是等差数列,{cn}是等比数列 (4)倒序相加法:Sn表示从第一项依次到第n项的和,然后又将Sn表示成第n项依次反序到第一项的和,将所得两式相加,由此得到Sn的一种求和方法. (5)通项分解法(分组求和法):有一类数列,既不是等差数列,也不是等比数列,若将这类数列适当拆开,可分为几个等差、等比或常见的数列,然后分别求和,再将其合并即可.an=bn±cn (6)并项求和法:把数列的某些项放在一起先求和,然后再求Sn.如:1002-992+982-972+…+22-12的和. (7)利用通项求和法:先求出数列的通项,然后进行求和 |
考点:
考点名称:数列求和的其他方法(倒序相加,错位相减,裂项相加等)数列求和的常用方法:
1.裂项相加法:数列中的项形如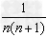 的形式,可以把
的形式,可以把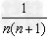 表示为
表示为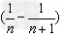 ,累加时抵消中间的许多项,从而求得数列的和;
,累加时抵消中间的许多项,从而求得数列的和;
2、错位相减法:源于等比数列前n项和公式的推导,对于形如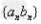 的数列,其中
的数列,其中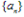 为等差数列,
为等差数列,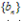 为等比数列,均可用此法;
为等比数列,均可用此法;
3、倒序相加法:此方法源于等差数列前n项和公式的推导,目的在于利用与首末两项等距离的两项相加有公因式可提取,以便化简后求和。
4、分组转化法:把数列的每一项分成两项,或把数列的项“集”在一块重新组合,或把整个数列分成两个部分,使其转化为等差或等比数列,这一求和方法称为分组转化法。
5、公式法求和:所给数列的通项是关于n的多项式,此时求和可采用公式求和,常用的公式有: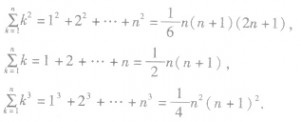
数列求和的方法多种多样,要视具体情形选用合适方法。
数列求和特别提醒:
(1)对通项公式含有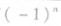 的一类数列,在求
的一类数列,在求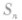 时,要注意讨论n的奇偶性;
时,要注意讨论n的奇偶性;
(2)在用等比数列前n项和公式时,一定要分q=1和q≠1两种情况来讨论。
五 : 数列求和的常用方法:
| 数列求和的常用方法: |
| (1)公式求和法: ①等差数列、等比数列求和公式 ②重要公式:1+2+…+n=
12+22+…+n2=
13+23+…+n3=(1+2+…+n)2=
(2)裂项求和法:将数列的通项分成两个式子的代数和,即an=f(n+1)-f(n),然后累加抵消掉中间的许多项,这种先裂后消的求和法叫裂项求和法.用裂项法求和,需要掌握一些常见的裂项,如:an=
(3)错位相减法:对一个由等差数列及等比数列对应项之积组成的数列的前n项和,常用错位相减法.an=bncn,其中{bn}是等差数列,{cn}是等比数列 (4)倒序相加法:Sn表示从第一项依次到第n项的和,然后又将Sn表示成第n项依次反序到第一项的和,将所得两式相加,由此得到Sn的一种求和方法. (5)通项分解法(分组求和法):有一类数列,既不是等差数列,也不是等比数列,若将这类数列适当拆开,可分为几个等差、等比或常见的数列,然后分别求和,再将其合并即可.an=bn±cn (6)并项求和法:把数列的某些项放在一起先求和,然后再求Sn.如:1002-992+982-972+…+22-12的和. (7)利用通项求和法:先求出数列的通项,然后进行求和 |
考点:
考点名称:数列求和的其他方法(倒序相加,错位相减,裂项相加等)数列求和的常用方法:
1.裂项相加法:数列中的项形如 的形式,可以把
的形式,可以把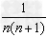 表示为
表示为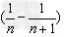 ,累加时抵消中间的许多项,从而求得数列的和;
,累加时抵消中间的许多项,从而求得数列的和;
2、错位相减法:源于等比数列前n项和公式的推导,对于形如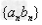 的数列,其中
的数列,其中 为等差数列,
为等差数列,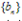 为等比数列,均可用此法;
为等比数列,均可用此法;
3、倒序相加法:此方法源于等差数列前n项和公式的推导,目的在于利用与首末两项等距离的两项相加有公因式可提取,以便化简后求和。
4、分组转化法:把数列的每一项分成两项,或把数列的项“集”在一块重新组合,或把整个数列分成两个部分,使其转化为等差或等比数列,这一求和方法称为分组转化法。
5、公式法求和:所给数列的通项是关于n的多项式,此时求和可采用公式求和,常用的公式有: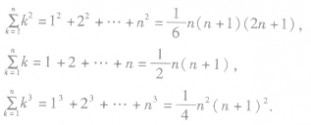
数列求和的方法多种多样,要视具体情形选用合适方法。
数列求和特别提醒:
(1)对通项公式含有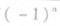 的一类数列,在求
的一类数列,在求 时,要注意讨论n的奇偶性;
时,要注意讨论n的奇偶性;
(2)在用等比数列前n项和公式时,一定要分q=1和q≠1两种情况来讨论。
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1