一 : 列含有未知数X等式解应用题（一）

教学目标 

1．使学生初步学会列含有未知数 的等式，解答需要逆思考的加、减法一步应用题．

2．培养学生分析推理能力．

教学重点

分析数量关系．

教学难点 

准确迅速地找出等量关系．

教学过程 

一、复习引入

1．求未知数 （要求口述口算过程，并说出根据）

18＋ ＝37      54－ ＝23       ＋67＝83

－26＝13      ＋47＝79       35－ ＝7

2．板演（与口算同步进行）   

学校买来70盒粉笔，用去28盒，还剩下多少盒？

（订正板演，同时把条件和问题对调，变成例7）

二、讲授新课

教师谈话：今天我们继续学习解答应用题．（板书课题：解应用题）

1．教学例7

学校买来一些粉笔，用去28盒，还剩42盒．学校买来多少盒粉笔？

（1）指名读题，分析题意，明确已知条件和所求问题．

（2）板书线段图，学生根据线段图列式解答．

28＋42＝70（盒）   

（3）引导学生理解算理

提问：怎样进行检验呢？

A： 用买来的70盒粉笔作为已知条件，减去用去的28盒，如果等于剩下的42盒说明解答正确．

B： 用买来的70盒粉笔作为已知条件，减去剩下的42盒，如果等于用去的28盒说明解答正确．

教师板书：

A：买来的盒数－用去的盒数＝剩下的盒数   

B：买来的盒数－剩下的盒数＝用去的盒数

提问：（a）买来的盒数知道吗？

教师说明：可以设买来粉笔 盒．    

（b）买来的盒数为 ，用去的知道吗？剩下的知道吗？谁能列出一个等式 ？

引导学生列式： －28＝42  －42＝28

（补充课题：列含有未知数 的等式）

（c）结合题意说一说等式的意思．

（d）解答等式   －28＝42 －42＝28

＝42＋28 ＝42＋28

＝70 ＝70

教师说明：因为设未知数 时，已经说明单位名称是盒，所以计算结果就不用再写单位名称．

（e）指导学生检验．    

2．引导学生小结

提问：今天我们学习的列含有未知数 的等式来解答应用题，它有哪些步骤呢？结合例7说一说．

第一步：读题弄清题意，分清已知条件，求的是什么？设未知数为 （板书：设）

第二步：按照题意，找出哪些数量与哪些数量有相等的关系，列出含有未知数 的等式．（板书：列）

第三步：求出未知数 是多少（板书：求）

注意： 代表的数量不写单位名称．

第四步：检验并写出答话．（板书：验、答）

三、巩固练习

1．食堂原来有27袋大米，又买来一些，现在共有43袋．食堂又买来多少袋大米？（列含有未知数 的等式，再解答出来）

订正时要让学生说一说根据什么列出含有未知数 的等式，并注意计算和书写格式有没有错误．

2．小林原来有一些邮票，同学又送给他14张，现在一共有70张．小林原来有多少张邮票？

3．小强读一本童话书，已经读了49页，还有36页没有读．这本童话书有多少页？

四、课堂小结

今天我们学习了什么知识？谁能说一说列含有未知数 的等式解应用题的步骤？

五、课后作业 

1．山坡上栽满了松树和柏树．松树有250棵，比柏树多120棵．柏树有多少棵？

2．小明有连环画38本，比小林少13本。小林有多少本？

板书设计 

探究活动

大家来找茬

活动目的

使学生进一步熟悉求未知数x的过程．

活动准备

教师将下列题目制成幻灯片或写在小黑板上．

（1） －467＝267

＝467＋267

＝200

（2）520－ ＝180

520＋180＝

340＝

活动过程 

1．教师出示错题（幻灯片或小黑板）．

2．学生分组挑出题目中的错误．

3．挑得越多越快的小组获胜．

二 : 用公式法解下列方程0.09y2-0.21y+0.1=0过程

用公式法解下列方程0.09y2-0.21y+0.1=0

过程

---

0.09y^2-0.21y+0.1=0

→9y^2-21y+10=0.

△=(-21)^2-4×9×10

=81，

∴y=(21±√△)/18，

即y1=5/3，y2=2/3。

三 : 用公式法解下列方程：（1）2x2

用公式法解下列方程： （1）2x2-4x-1=0； （2）5x+2=3x2； （3）4x2-3x+1=0。

题型：计算题难度：中档来源：同步题

解：（1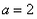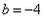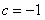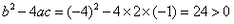），， ∴ ∴x= 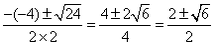∴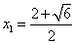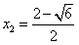，； （2）将方程化为一般形式 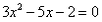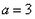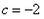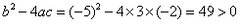，， ∴ ∴x= 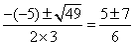∴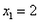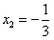，； （3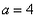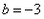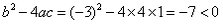），， ∴ ∵在实数范围内，负数不能开平方 ∴此方程无实数根。

考点：

考点名称：一元二次方程的解法一元二次方程的解：
能够使方程左右两边相等的未知数的值叫做方程的解。
解一元二次方程方程：
求一元二次方程解的过程叫做解一元二次方程方程。

韦达定理：
一元二次方程根与系数的关系（以下两个公式很重要，经常在考试中运用到）
一般式：ax2+bx+c=0的两个根x₁和x₂关系：
x₁+x₂= -b/a
x₁·x₂=c/a

一元二次方程的解法：
1、直接开平方法
利用平方根的定义直接开平方求一元二次方程的解的方法叫做直接开平方法。
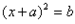直接开平方法适用于解形如的一元二次方程，根据平方根的定义可知，x+a 是b的平方根，当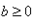时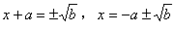，；当b<0时，方程没有实数根。
用直接开平方法求一元二次方程的根，一定要正确运用平方根的性质，即正数的平方根有两个，它们互为相反数，零的平方根是零，负数没有平方根。

2、配方法
配方法是一种重要的数学方法，它不仅在解一元二次方程上有所应用，而且在数学的其他领域也有着广泛的应用。
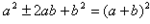配方法的理论根据是完全平方公式，把公式中的a看做未知数x，并用x代替，则有 。

3、公式法
公式法是用求根公式解一元二次方程的解的方法，它是解一元二次方程的一般方法。
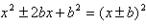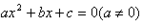一元二次方程 的求根公式：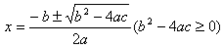
求根公式是专门用来解一元二次方程的，故首先要求a≠0；有因为开平方运算时，被开方数必须是非负数，所以第二个条件是b²-4ac≥0。即求根公式使用的前提条件是a≠0且b²-4ac≥0。

4、因式分解法
因式分解法就是利用因式分解的手段，求出方程的解的方法，这种方法简单易行，是解一元二次方程最常用的方法。

四 : 列方程（组）或不等式（组）解应用题：（1）某校的

列方程（组）或不等式（组）解应用题： （1）某校的一间阶梯教室，第1排的座位数为a，从第2排开始，每一排都比前一排增加b个座位． 1、请你在下表的空格里填写一个适当的代数式： 第1排的座位数 第2排的座位数 第3排的座位数 第4排的座位数 … a a+b a+2b … 2、已知第4排有18个座位，第15排座位数是第5排座位数的2倍，求第1排有多少个座位？ （2）某校初一、初二两年段学生参加社会实践活动，原计划租用48座客车若干辆，但还有24人无座位坐． ①设原计划租用48座客车x辆，试用含x的代数式表示这两个年段学生的总人数； ②现决定租用60座客车，则可比原计划租48座客车少2辆，且所租60座客车中有一辆没有坐满，但这辆车已坐的座位超过36位．请你求出该校这两个年段学生的总人数．

题型：解答题难度：中档来源：不详

解；（1）1、填表如下： 第1排的座位数 第2排的座位数 第3排的座位数 第4排的座位数 … a a+b a+2b a+3b … 2、设第1排有x个座位，根据题意得； x+3b=18 x+14b=2(x+4b) ， 解得： x=12 b=2 ， 答：第一排有12个座位； （2）①设原计划租用48座客车x辆，则这两个年段学生的总人数是48x+24； ②根据题意得： 48x+24-60(x-2)＜60 48x+24-60(x-2)＞36 ， 解得：7＜x＜9， ∵x只能取整数， ∴x=8， ∴该校这两个年段学生的总人数是48×8+24=408（人）．

考点：

考点名称：二元一次方程组的应用二元一次方程组应用中常见的相等关系：
1． 行程问题（匀速运动）
基本关系：s=vt
①相遇问题（同时出发）：
确定行程过程中的位置路程
相遇路程÷速度和=相遇时间
相遇路程÷相遇时间= 速度和
相遇问题（直线）
甲的路程+乙的路程=总路程
相遇问题（环形）
甲的路程 +乙的路程=环形周长
②追及问题（同时出发）：
追及时间＝路程差÷速度差
速度差＝路程差÷追及时间
追及时间×速度差＝路程差
追及问题（直线）
距离差=追者路程-被追者路程=速度差X追及时间
追及问题（环形）
快的路程-慢的路程=曲线的周长
③水中航行
顺水行程＝（船速＋水速）×顺水时间
逆水行程＝（船速－水速）×逆水时间
顺水速度=船速＋水速
逆水速度＝船速－水速
静水速度=（顺水速度＋逆水速度）÷2
水速：（顺水速度－逆水速度）÷2

2．配料问题：溶质=溶液×浓度
溶液=溶质+溶剂

3．增长率问题

4．工程问题
基本关系：工作量=工作效率×工作时间（常把工作量看成单位“1”）。

5．几何问题
①常用勾股定理，几何体的面积、体积公式，相似形及有关比例性质等。
②注意语言与解析式的互化:
如，“多”、“少”、“增加了”、“增加为（到）”、“同时”、“扩大为（到）”、“扩大了”、……
又如，一个三位数，百位数字为a，十位数字为b，个位数字为c，则这个三位数为：100a+10b+c，而不是abc。
③注意从语言叙述中写出相等关系：
如，x比y大3，则x-y=3或x=y+3或x-3=y。又如，x与y的差为3，则x-y=3。
④注意单位换算:
如，“小时”“分钟”的换算；s、v、t单位的一致等。

二元一次方程组的应用：
列方程（组）解应用题是中学数学联系实际的一个重要方面。
其具体步骤是：
⑴审题。理解题意。弄清问题中已知量是什么，未知量是什么，问题给出和涉及的相等关系是什么。
⑵设元（未知数）。①直接未知数②间接未知数（往往二者兼用）。一般来说，未知数越多，方程越易列，但越难解。
⑶用含未知数的代数式表示相关的量。
⑷寻找相等关系（有的由题目给出，有的由该问题所涉及的等量关系给出），列方程。一般地，未知数个数与方程个数是相同的。
⑸解方程及检验。
⑹答案。
综上所述，列方程（组）解应用题实质是先把实际问题转化为数学问题（设元、列方程），在由数学问题的解决而导致实际问题的解决（列方程、写出答案）。在这个过程中，列方程起着承前启后的作用。因此，列方程是解应用题的关键。

考点名称：一元一次不等式组的应用应用：列一元一次不等式组解决实际问题。

一元一次不等式的应用主要涉及问题：
1.分配问题：
例：一堆玩具分给若干个小朋友，若每人分3件，则剩余4件，若前面每人分4件，则最后一人得到的玩具最多3件，问小朋友的人数至少有多少人？。

2.积分问题：
例：某次数学测验共20道题（满分100分）。评分办法是：答对1道给5分，答错1道扣2分，不答不给分。某学生有1道未答。那么他至少答对几道题才能及格？

3.比较问题:
例：某校校长暑假将带领该校“三好学生”去三峡旅游，甲旅行社说：如果校长买全票一张，则其余学生可享受半价优惠；乙旅行社说：包括校长在内全部按全票的6折优惠。已知两家旅行社的全票价都是240元，至少要多少名学生选甲旅行社比较好？

4.行程问题:
例：抗洪抢险，向险段运送物资，共有120公里原路程，需要1小时送到，前半小时已经走了50公里后，后半小时速度多大才能保证及时送到？

5.车费问题:
例：出租汽车起价是10元(即行驶路程在5km以内需付10元车费),达到或超过5km后,每增加1km加价1.2元(不足1km部分按1km计),现在某人乘这种出租 汽车从甲地到乙地支付车费17.2元,从甲地到乙地的路程超过多少km?

6.浓度问题:
例：在1千克含有40克食盐的海水中，在加入食盐，使他成为浓度不底于20%的食盐水，问：至少加入多少食盐？

7.增减问题:
例：一根长20cm的弹簧，一端固定，另一端挂物体。在弹簧伸长后的长度不超过30cm的限度内，每挂1㎏质量的物体，弹簧伸长0.5cm.求弹簧所挂物体的最大质量是多少？

8.销售问题:
例：商场购进某种商品m件，每件按进价加价30元售出全部商品的65%，然后再降价10%，这样每件仍可获利18元，又售出全部商品的25%。
(1)试求该商品的进价和第一次的售价；
(2)为了确保这批商品总的利润率不低于25%，剩余商品的售价应不低于多少元？

一元一次不等式组解应用题的一般步骤为：
列不等式组解决实际问题的步骤与列一元一次不等式解应用题的步骤相类似,所不同的是,前者需寻求的不等关系往往不止一个,而后者只需找出一个不等关系即可。
（1）审：认真审题，分清已知量、未知量及其关系，找出题中的不等关系，要抓住题中的关键词语，如“大于”、“小于”、“不大于”、“至少”、“不超过”、“超过”等；
（2）设：设出适当的未知数；
（3）列：根据题中的不等关系列出不等式组；
（4）解：解出所列不等式组的解集；
（5）答：写出答案，从不等式组的解集中找出符合题意的答案，并检验是否符合题意。 本文标题：列分式方程解应用题-列含有未知数X等式解应用题（一）
本文地址： http://www.61k.com/1056898.html