一 : 《三角形三条边的关系》教学实录

　　　　　　《三角形三条边的关系》教学实录

开课时间： 2012年4月24日

授课班级：郊尾中心小学四年（3）班

执教老师：郑雪梅

参与人员：“先学后教　高效课堂”课题组全体成员

记录人员：蔡寿坚

课堂实录：

一、创设情境，导入新课：

师：同学们，几只可爱的的小朋友给我们带来了6条长短不一的小棒，请看！

（多媒体出示）

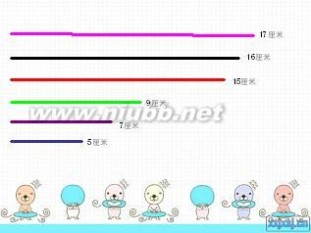
师：这些小棒的长度分别是5厘米、7厘米、9厘米、15厘米、16厘米和17厘米，大家猜猜，哪三条小棒可以围成三角形？哪些不能？

生：选择17厘米、16厘米和15厘米的小棒可以围成1个三角形。

生：选择16厘米、15厘米和9厘米的小棒可以围成1个三角形。

师：为什么6根小棒中，有的可以围成三角形，有的不能呢？这节课我们就来学习这其中的奥秘――《三角形三边的关系》。

二、出示导学提纲：

师：为了更好地达到今天的学习目标，请同学们读一读导学提纲。

生（齐读）：1.自学课本P82页,并通过实验完成实验表。

2.想一想：三角形三条边长度存在着什么关系？

3.什么情况下三角形任意两条边大于第三边。

4.通过自学你发现了什么规律？你还有哪些不懂的地方？

三、学一学（先学）：

师：请大家按导学提纲，开始认真自学，看谁学得最好。

（生自学）

四、议一议（后教）：

1、学生质疑问答。

2、出示：

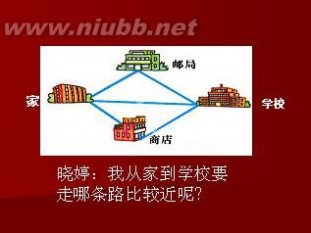
师：请大家仔细观察，想一想，晓婷从家到学校要走哪条路比较近呢？为什么？

生：走中间那条路最近，因为两点间的距离，线段最短。

生：从家到邮局再到学校形成1个三角形，这两条边加起来比第三条边长，所以走中间那条路最近。

师：是不是所有的三角形的两条边的和都大于第三条边呢？我们以小组为单位动手实验来验证。请大家齐读小组合作活动要求。

生（齐读）：小组合作活动要求

①.摆一摆：

小组同学合作，任意取出三条线段，动手摆一摆，看能否围成1个三角形；

②.记一记：

小组长根据操作结果，记录好实验记录单：能围成三角形的就将三条线段的数据记录在“能围成”这一栏，不能围成的则记录在“不能围成”这一栏。注意：实验一次记录一次,并且每一组的数据不能出现重复；

③.议一议：

根据实验结果，小组讨论：三角形的三条边存在着怎样的关系。

3、生以小组为单位，用不同的小棒摆一摆进行验证。

附：实验记录表。

三角形三条边的关系实验记录表

单位：厘米

试验次数	小棒的长度			围的结果	我的发现
	1	2	3
1				能围成
2
3
4
5				不能围成
6
7
8

4、反馈：

师：谁上台来演示你的实验，并说一说。

（生边上台演示，边说。）

生：我用了9厘米、7厘米和6厘米的三根小棒可以围成三角形。

生：我用了3厘米、7厘米和9厘米的三根小棒可以围成三角形。

生：我用了7厘米、5厘米和9厘米的三根小棒可以围成三角形。

生：我用了6厘米、3厘米和5厘米的三根小棒可以围成三角形。

生：我用了3厘米、6厘米和9厘米的三根小棒不能围成三角形。

生：我用了3厘米、5厘米和9厘米的三根小棒不能围成三角形。

生：我用了3厘米、3厘米和6厘米的三根小棒不能围成三角形。

生：我用了3厘米、3厘米和9厘米的三根小棒不能围成三角形。

师：通过这些实验，你们有什么发现？

生：我发现了任意两条边之和大于第三边能围成三角形。

生：我发现了任意两条边之和小于或等于第三边的不能围成三角形。

（师结合学生的回答，相机课件演示。）

师：那谁能用一句话来概括三角形三条边的关系吗？

生：三角形任意两边的和大于第三边。

师：通过学习和反馈，同学们还有什么不明白的地方吗？

生：三角形任意两边的差是否小于第三边？

生：这里的“任意两边”是什么意思？

师：请同学们围绕这2个问题小组讨论。

（生小组内讨论）

生：“任意两边”就是任随其意，随便两条边。

生：三角形任意两边的差小于第三边。

五、做一做（当堂检测）：

1、

2.用长度为2cm、2cm、6cm、6cm、6cm这五条线段中的任意三条线段拼成1个三角形，你能拼成几种不同的形状？拼成的三角形有什么特点？

3.用15根等长的火柴棒摆成的三角形中，最长边最多可以由几根火柴棒组成？

六、课堂小结：

师：同学们，通过这节课的学习，你有什么收获？

生：我明白了三角形任意两边的和大于第三边。

生：我学会了判断三条线段是否可以围成三角形。

（下课）

二 : 数学教案－三角形三条边的关系

1、教材分析

(1)知识结构

 

(2)重点、难点分析

本节内容的重点是三角形三边关系定理及推论.这个定理与推论不仅给出了三角形的三边之间的大小关系，更重要的是提供了判断三条线段能否组成三角形的标准；熟练灵活地运用三角形的两边之和大于第三边，是数学严谨性的一个体现；同时也有助于提高学生全面思考数学问题的能力；它还将在以后的学习中起着重要作用.

本节内容的难点一是三角形按边分类，很多学生常常把等腰三角形与等边三角形看成独立的两类，而在解题中产生错误.二是利用三角形三边之间的关系解题，在学习和应用这个定理时，“两边之和大于第三边”指的是“任何两边的和”都“大于第三边”而学生的错误就在于以偏概全；分类讨论在解题中也是学生感到困难的一个地方.

2、教法建议

没有学生参与的教学是不成功的教学，教师为了充分调动主体参与，必须在为学生提供必要的背景知识的前提下，与学生一道探索定理在结构上、应用上留给我们的启示.具体说明如下：

(1)强化能力

新课引入，先让学生阅读教材第一部分，然后通过回答教师设计的几个问题，使学生明确对三角形按边分类，做到不重不漏，其中等腰三角形包括等边三角形，反过来等边三角形是等腰三角形的一种特例.

通过阅读，使学生初步认识数学概念的含义，发现疑难；理解领会数学语言（文字语言、符号语言、图形语言），促进数学语言内化，从而提高学生的数学语言水平、自学能力及交流能力

(2)主动获取

在得出三角形三条边关系定理过程中，针对基础比较好的学生，让学生考虑回忆第

一册第一章中学过的这条公理并给出证明，在这个基础上，让学生把定理的内容叙述出来.（3）激荡思维

由定理获得了：判断三条线段构成一个三角形的一种方法，除了这一种方法外，是否还有其它的判断方法呢？从而激荡起学生思维浪花：方法是什么呢？学生最初可能很快得到“推论”，此时瓜熟蒂落，顺理成章地引出教材中的推论.在此基础上，让学生通过讨论，简化上述两种方法，由此得到下面两种方法.这里，学生若感到困难，教师可适当做提示.方法3：已知线段 ， （ ）,若第三条线段c满足 - <c<a+ ，则线段 , ,c可组成一个三角形.方法4：已知线段 , ,c且 ,若 + >c则线段 , ,c可组成一个三角形.教学中采用这种教学方法可培养学生分析问题探索问题的能力，提高学生对数学知识结构完整性的认识.

（4）加深理解

进行必要的例题讲解和适当的解题练习，以达到熟练地运用定理及推论.从过程中让学生体味到数学造化之神奇.也可适当指出，此定理及推论不仅提供了判定三条线段是否构成三角形的根据，也为今后解决字母取值范围问题提供了有利的依据.

整个教学过程 ，是学生主动参与，教师及时点拨，学生积极探索的过程，教学过程 跌宕起伏，问题逐步深化，学生思维逐步扩展，使学生在愉快、主动中得到发展.
教学目标 ：

(1)掌握三角形三边关系定理及其推论，会根据三条线段的长度判断他们能否构成三角形；

(2)弄清三角形按边的相等关系的分类；

(3)通过三角形的分类学习，使学生知道分类的基本思想，提高学生归纳概括的能力；

(4)通过三角形三边关系定理的学习，培养学生转化的能力；

(5)通过等边三角形是等腰三角形的特例，渗透一般与特殊的辩证关系.

教学重点：三角形三边关系定理及推论

教学难点 ：三角形按边分类及利用三角形三边关系解题

教学用具：直尺、微机

教学方法：谈话、探究式

教学过程 ：

1、阅读新课，回答问题

先让学生阅读教材的第一部分，然后回答下列问题：

(1)这一部分教材中的数学概念有哪些？（指出来并给予解释）

(2)等腰三角形与等边三角形有什么关系？

估计有的学生可能把等腰三角形和等边三角形看成独立的两类.

(3)写出三角形按边的相等关系分类的情况.

教师最后板书给出.

(要求学生之间可互相补充，从一开始就鼓励双边交流与多边交流)

2、发现并推导出三边关系定理

问题1：用长度为4cm、 10cm 、16cm的线绳（课前准备好的）能否搭建一个三角形？（让学生动手操作）

问题2：你能解释上述结果的原因吗？

问题3：任何三条线段都能组成一个三角形吗？满足什么条件时，三条线段可组成一个三角形？

定理：三角形两边的和大于第三边

（发现过程采用小步子原则，让学生在不知不觉中发现数学中的真理）

3、导出三边关系定理的推论及其它两种方法

由前面得到了判断所给三条线段能否组成三角形的一个依据.那么是否还有其它方法呢？请同学们在定理的基础上来找：

估计学生很容易得到推论，让学生用自己的语言叙述，教师稍加整理后给出规范叙述.

推论：三角形两边的差小于第三边

（给每一个学生表现个人数学语言表达才能的机会）

能否简化上面定理及推论？从而得到如下两种判定方法：

(1)、已知线段 ， （ ）,若第三条线段c满足 - <c<a+ ，则线段 , ,c可组成一个三角形.（2）、已知线段 , ,c且 ,若 + >c则线段 , ,c可组成一个三角形.

4、三角形三边关系定理及推论的应用

例1 判断题：（出示投影）

(1)等边三角形是等腰三角形

(2)三角形可分为不等边三角形、等腰三角形和等边三角形

(3)已知三线段 满足 ,那么 为边可构成三角形

(4)等腰三角形的腰比底长

（本例主要考察学生对概念、定理及推论的理解程度，不要求做在本上，只需口答即可）

（本例要求学生说出解题思路，教师点到为止）

例3 一个等腰三角形的周长为18 .

(1) 已知腰长是底边长的2倍，求各边长.

(2) 其中一边长4 ，求其他两边长.

这是一道有课堂练习性质的例题，允许学生有3分钟左右的独立思考，允许想出来的同学表达自己的想法，其它同学补充完善.

（数学教师的课堂教学应该是敢于放手，尽可能多地给学生创造展示自己的思维空间和时间）

例4 草原上有4口油井，位于四边形abcd的4个顶点，

如图1现在要建一个维修站h，试问h建在何处，

才能使它到4口油井的距离ha+hb+hc+hd为最小，

说明理由.

 

本例有一定的难度，给出的方法是解决此类型问题常见的极为简捷的方法，略微构造就可以使用三角形三边关系定理得出答案.

5、小结

本节课我们学习了三角形三边关系的定理和推论，还知道了定理和推论的一系列灵活运用：

(1)判断三条已知线段能否组成三角形

采用一种较为简便的判法：若最短边与较长边的和大于最长边，则可构成三角形，否则不能.

(2)确定三角形第三边的取值范围

两边之差＜第三边＜两边之和

若时间宽裕，让学生经讨论后自由表述，其他同学补充，自己将知识系统化，以自己的方式进行建构.

6、布置作业 

a. 书面作业 p41＃8、9

b. 思考题：1、在四边形abcd中，ac与bd相交于p，求证：

（ab+bc+cd+ad）＜ac+bd＜ab+bc+cd+ad

2、用15根等长的火柴棒摆成的三角形中，最长边最多可以由几根火柴棒组成？（提示：由上面方法2，a+b+c>2a 又a+b+c<3a得出a的范围，所以可知最多可以由7根火柴棒组成）

板书设计 ：

三 : 三角形三条边的关系

1、教材分析

(1)知识结构

(2)重点、难点分析

本节内容的重点是三角形三边关系定理及推论.这个定理与推论不仅给出了三角形的三边之间的大小关系，更重要的是提供了判断三条线段能否组成三角形的标准；熟练灵活地运用三角形的两边之和大于第三边，是数学严谨性的一个体现；同时也有助于提高学生全面思考数学问题的能力；它还将在以后的学习中起着重要作用.

本节内容的难点一是三角形按边分类，很多学生常常把等腰三角形与等边三角形看成独立的两类，而在解题中产生错误.二是利用三角形三边之间的关系解题，在学习和应用这个定理时，“两边之和大于第三边”指的是“任何两边的和”都“大于第三边”而学生的错误就在于以偏概全；分类讨论在解题中也是学生感到困难的一个地方.

2、教法建议

没有学生参与的教学是不成功的教学，教师为了充分调动主体参与，必须在为学生提供必要的背景知识的前提下，与学生一道探索定理在结构上、应用上留给我们的启示.具体说明如下：

(1)强化能力

新课引入，先让学生阅读教材第一部分，然后通过回答教师设计的几个问题，使学生明确对三角形按边分类，做到不重不漏，其中等腰三角形包括等边三角形，反过来等边三角形是等腰三角形的一种特例.

通过阅读，使学生初步认识数学概念的含义，发现疑难；理解领会数学语言（文字语言、符号语言、图形语言），促进数学语言内化，从而提高学生的数学语言水平、自学能力及交流能力

(2)主动获取

在得出三角形三条边关系定理过程中，针对基础比较好的学生，让学生考虑回忆第

一册第一章中学过的这条公理并给出证明，在这个基础上，让学生把定理的内容叙述出来.（3）激荡思维

由定理获得了：判断三条线段构成一个三角形的一种方法，除了这一种方法外，是否还有其它的判断方法呢？从而激荡起学生思维浪花：方法是什么呢？学生最初可能很快得到“推论”，此时瓜熟蒂落，顺理成章地引出教材中的推论.在此基础上，让学生通过讨论，简化上述两种方法，由此得到下面两种方法.这里，学生若感到困难，教师可适当做提示.方法3：已知线段 ， （ ）,若第三条线段c满足 - <c<a+ ，则线段 , ,c可组成一个三角形.方法4：已知线段 , ,c且 ,若 + >c则线段 , ,c可组成一个三角形.教学中采用这种教学方法可培养学生分析问题探索问题的能力，提高学生对数学知识结构完整性的认识.

（4）加深理解

进行必要的例题讲解和适当的解题练习，以达到熟练地运用定理及推论.从过程中让学生体味到数学造化之神奇.也可适当指出，此定理及推论不仅提供了判定三条线段是否构成三角形的根据，也为今后解决字母取值范围问题提供了有利的依据.

整个教学过程，是学生主动参与，教师及时点拨，学生积极探索的过程，教学过程跌宕起伏，问题逐步深化，学生思维逐步扩展，使学生在愉快、主动中得到发展.
  第 1 2 页  

四 : 三角形三条边的关系

1、教材分析

(1)知识结构

(2)重点、难点分析

本节内容的重点是三角形三边关系定理及推论.这个定理与推论不仅给出了三角形的三边之间的大小关系，更重要的是提供了判断三条线段能否组成三角形的标准；熟练灵活地运用三角形的两边之和大于第三边，是数学严谨性的一个体现；同时也有助于提高学生全面思考数学问题的能力；它还将在以后的学习中起着重要作用.

本节内容的难点一是三角形按边分类，很多学生常常把等腰三角形与等边三角形看成独立的两类，而在解题中产生错误.二是利用三角形三边之间的关系解题，在学习和应用这个定理时，“两边之和大于第三边”指的是“任何两边的和”都“大于第三边”而学生的错误就在于以偏概全；分类讨论在解题中也是学生感到困难的一个地方.

2、教法建议

没有学生参与的教学是不成功的教学，教师为了充分调动主体参与，必须在为学生提供必要的背景知识的前提下，与学生一道探索定理在结构上、应用上留给我们的启示.具体说明如下：

(1)强化能力

新课引入，先让学生阅读教材第一部分，然后通过回答教师设计的几个问题，使学生明确对三角形按边分类，做到不重不漏，其中等腰三角形包括等边三角形，反过来等边三角形是等腰三角形的一种特例.

通过阅读，使学生初步认识数学概念的含义，发现疑难；理解领会数学语言（文字语言、符号语言、图形语言），促进数学语言内化，从而提高学生的数学语言水平、自学能力及交流能力

(2)主动获取

在得出三角形三条边关系定理过程中，针对基础比较好的学生，让学生考虑回忆第

一册第一章中学过的这条公理并给出证明，在这个基础上，让学生把定理的内容叙述出来.（3）激荡思维

由定理获得了：判断三条线段构成一个三角形的一种方法，除了这一种方法外，是否还有其它的判断方法呢？从而激荡起学生思维浪花：方法是什么呢？学生最初可能很快得到“推论”，此时瓜熟蒂落，顺理成章地引出教材中的推论.在此基础上，让学生通过讨论，简化上述两种方法，由此得到下面两种方法.这里，学生若感到困难，教师可适当做提示.方法3：已知线段 ， （ ）,若第三条线段c满足 - <c<a+ ，则线段 , ,c可组成一个三角形.方法4：已知线段 , ,c且 ,若 + >c则线段 , ,c可组成一个三角形.教学中采用这种教学方法可培养学生分析问题探索问题的能力，提高学生对数学知识结构完整性的认识.

（4）加深理解

进行必要的例题讲解和适当的解题练习，以达到熟练地运用定理及推论.从过程中让学生体味到数学造化之神奇.也可适当指出，此定理及推论不仅提供了判定三条线段是否构成三角形的根据，也为今后解决字母取值范围问题提供了有利的依据.

整个教学过程，是学生主动参与，教师及时点拨，学生积极探索的过程，教学过程跌宕起伏，问题逐步深化，学生思维逐步扩展，使学生在愉快、主动中得到发展.

教学目标：

(1)掌握三角形三边关系定理及其推论，会根据三条线段的长度判断他们能否构成三角形；

(2)弄清三角形按边的相等关系的分类；

(3)通过三角形的分类学习，使学生知道分类的基本思想，提高学生归纳概括的能力；

(4)通过三角形三边关系定理的学习，培养学生转化的能力；

(5)通过等边三角形是等腰三角形的特例，渗透一般与特殊的辩证关系.

教学重点：三角形三边关系定理及推论

教学难点：三角形按边分类及利用三角形三边关系解题

教学用具：直尺、微机

教学方法：谈话、探究式

教学过程：

1、阅读新课，回答问题

先让学生阅读教材的第一部分，然后回答下列问题：

(1)这一部分教材中的数学概念有哪些？（指出来并给予解释）

(2)等腰三角形与等边三角形有什么关系？

估计有的学生可能把等腰三角形和等边三角形看成独立的两类.

(3)写出三角形按边的相等关系分类的情况.

教师最后板书给出.

(要求学生之间可互相补充，从一开始就鼓励双边交流与多边交流)

2、发现并推导出三边关系定理

问题1：用长度为4cm、 10cm 、16cm的线绳（课前准备好的）能否搭建一个三角形？（让学生动手操作）

问题2：你能解释上述结果的原因吗？

问题3：任何三条线段都能组成一个三角形吗？满足什么条件时，三条线段可组成一个三角形？

定理：三角形两边的和大于第三边

（发现过程采用小步子原则，让学生在不知不觉中发现数学中的真理）

3、导出三边关系定理的推论及其它两种方法

由前面得到了判断所给三条线段能否组成三角形的一个依据.那么是否还有其它方法呢？请同学们在定理的基础上来找：

估计学生很容易得到推论，让学生用自己的语言叙述，教师稍加整理后给出规范叙述.

推论：三角形两边的差小于第三边

（给每一个学生表现个人数学语言表达才能的机会）

能否简化上面定理及推论？从而得到如下两种判定方法：

(1)、已知线段 ， （ ）,若第三条线段c满足 - <c<a+ ，则线段 , ,c可组成一个三角形.（2）、已知线段 , ,c且 ,若 + >c则线段 , ,c可组成一个三角形.

4、三角形三边关系定理及推论的应用

例1 判断题：（出示投影）

(1)等边三角形是等腰三角形

(2)三角形可分为不等边三角形、等腰三角形和等边三角形

(3)已知三线段 满足 ,那么 为边可构成三角形

(4)等腰三角形的腰比底长

（本例主要考察学生对概念、定理及推论的理解程度，不要求做在本上，只需口答即可）

（本例要求学生说出解题思路，教师点到为止）

例3 一个等腰三角形的周长为18 .

(1) 已知腰长是底边长的2倍，求各边长.

(2) 其中一边长4 ，求其他两边长.

这是一道有课堂练习性质的例题，允许学生有3分钟左右的独立思考，允许想出来的同学表达自己的想法，其它同学补充完善.

（数学教师的课堂教学应该是敢于放手，尽可能多地给学生创造展示自己的思维空间和时间）

例4 草原上有4口油井，位于四边形abcd的4个顶点，

如图1现在要建一个维修站h，试问h建在何处，

才能使它到4口油井的距离ha+hb+hc+hd为最小，

说明理由.

本例有一定的难度，给出的方法是解决此类型问题常见的极为简捷的方法，略微构造就可以使用三角形三边关系定理得出答案.

5、小结

本节课我们学习了三角形三边关系的定理和推论，还知道了定理和推论的一系列灵活运用：

(1)判断三条已知线段能否组成三角形

采用一种较为简便的判法：若最短边与较长边的和大于最长边，则可构成三角形，否则不能.

(2)确定三角形第三边的取值范围

两边之差＜第三边＜两边之和

若时间宽裕，让学生经讨论后自由表述，其他同学补充，自己将知识系统化，以自己的方式进行建构.

6、布置作业 

a. 书面作业 p41＃8、9

b. 思考题：1、在四边形abcd中，ac与bd相交于p，求证：

（ab+bc+cd+ad）＜ac+bd＜ab+bc+cd+ad

2、用15根等长的火柴棒摆成的三角形中，最长边最多可以由几根火柴棒组成？（提示：由上面方法2，a+b+c>2a 又a+b+c<3a得出a的范围，所以可知最多可以由7根火柴棒组成）

板书设计：

本文标题：三角形三条边的关系-《三角形三条边的关系》教学实录
本文地址： http://www.61k.com/1188027.html