一 : 电势和电势能的关系，大小比较

电势和电势能的关系

电势和电势能的关系，大小比较

---

电势能=电势乘以电荷量。

注意上式中，电势，电荷量均有正负之分。

按照上面计算出电势能，即可比较。

二 : 几种典型带电体的场强和电势公式

几种电荷分布所产生的场强和电势

1、均匀分布的球面电荷（球面半径为R，带电量为q） ?1qr??, （球面外，即r?R）? E(r)?3电场强度矢量：? 4? ?r0?? E(r)?0 。［www.61k.com） （球面内，即r?R）?

1q??? Ur?， （球外）?4? ? 0r?电势分布为：? 1q? U?r?? 。 （球内）?4? ?R 0?

2、均匀分布的球体电荷（球体的半径为R,带电量为q） ??1qr? E(r)? ， （球体内，即r?R）3?4? ?0R??电场强度矢量：?? 1qr? E(r)? 。 （球体外，即r?R）3?4? ?r0?

1q??? Ur?， （r?R 即球外）?4? ? 0r?电势分布为：? 221q3R?r? U?r??。 （r?R 即球内）3?8? ? 0R???

3、均匀分布的无限大平面电荷（电荷面密度为σ） ???电场强度矢量：E(x)? (? i)（平板两侧的场强与距 离无关。）2?0

电势分布为：

U?r????r0?r? 其中假设r0处为零电势参考点。若选取原点（即带2? 0

电平面）为零电势参考点。即U0?0。那么其余处的电势表达式为：

???? Ux??x x?0?2?0? ??? U?x??x x?0?2?0?

4、均匀分布的无限长圆柱柱面电荷（圆柱面的半径为R，单位长度的带电量为λ。）

??? r? ，（ r?R,即在柱面外）? E(r)?2电场强度矢量 ? 2? ?0r?? E(r)?0 。 （r?R，即在柱面内）?

电势公式 几种典型带电体的场强和电势公式

ra???? Ur?ln, （r?R 即柱体外）?2? ?0r?电势分布为：? ra?? U?r??ln 。［www.61k.com） （r?R 即柱体内）?2? ?R0?

其中假设ra处为零电势参考点。且ra处位于圆柱柱面外部。（即ra>R）。若选取带电圆柱柱面处为零电势参考点。（即U?R??0）。那么，其余各处的电势表达式为：

?U?r??0 0?r?R ?即在圆柱面内? ??r ? U?r???ln r?R ?即在圆柱面外??2? ?0R?

5、均匀分布的无限长带电圆柱体（体电荷密度为ρ、半径为R。）

?? E?r????电场强度矢量： ??? E?r??????r 0?r?R ?圆柱体内?2?0 ? R2?r r?R ?圆柱体外?2?0r2

?? r2?圆柱体内?U?r??? 0?r?R ? 4?0?电势： ? 其中假22? R? RR? ?圆柱体外?U?r????ln r?R ?4?02?0r?

设圆柱体轴线处为零电势参考点。即U?r?0??0。

6、均匀分布的带电圆环（带电量为q；圆环的半径为R。）在其轴线上x处的电场强度和电势

?电场强度矢量： E?x??1

4? ?0qxx2?R2??x0。其中x0为轴线方向的单位

矢量。

?q i讨论： （a）当 x??R 或 x??时 Ep(x)?4? ?0x2。此时带电圆

环可视为点电荷进行处理。 （b）当x??R 或 x?0 时 Ep(0)?0 。即，带电圆环在其圆心处的电场强度为零。

电势： U?x??1q

4? ?0x2?R2 。其中电势的零参考点位于无穷远处。

电势公式 几种典型带电体的场强和电势公式

带电圆环在其圆心处的电势为： U(x)x?0?q4??0R 。［www.61k.com］

7、均匀分布的带电直线（其中，线电荷密度λ，直线长为l）

（1）在直线的延长线上，与直线的端点距离为d的P点处：

电场强度矢量： Ep?d??

Up?d????l??11??i????i 。 4? ?0dl?d4? ?0?dl?d??l?d 。 ln4? ?0d

（2）在直线的中垂线上，与直线的距离为d的Q点处：

电场强度矢量为：

???l?2lEQ?d??j?j 。 2224? ?04? ?0d?4dl?2d???d?2?

电势：

?UQ?d??ln4? ?0l?l?????d22?2?l?l??????d2

2?2?22?l?l2?4d2 。 ?ln224? ?0?l?l?4d

（3）在直线外的空间中任意点处：

?? 电场强度矢量： ?r??Exi?Eyj 。

其中：

???Sin?2?Sin?1? E?x?4? ?0? 。 ??? Ey??Cos?1?Cos?2??4? ?0?

或者改写为另一种表示式:

?即: Ep(r,z)?Err?Ezk 。 0

其中：

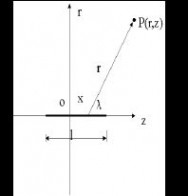
电势公式 几种典型带电体的场强和电势公式

??????11? Er?? r????4? ?0?ll2l2ll2l2?2222(z?)r?(z?)?r?(z?)(z?)r?(z?)?r?(z?)???222222??? ????????11?? Ez???4? ?ll?2222?0?r?(z?)r?(z?)??22????

ll?r2?(z?)2

?22 。［www.61k.com） 电势： Up?ln4? ?0llz??r2?(z?)2

22z?

（4）若带电直线为无限长时，那么，与无限长带电直线的距离为d的P点处： 电场强度矢量： Ep?d??

电势： Up?d????? 。 d0 或 Ep?r??r22? ?0d2? ?0rdr??ln0或 Up?r??ln0 。其中假设d0或（r0）2? ?0d2? ?0r

为电势的零参考点。

（5）半无限长带电直线在其端点处：（端点与带电直线的垂直距离为d）

??? 电场强度矢量：E?Exi?Eyj 。 其中Ex?Ey?

?8、电偶极子P的电场强度和电势 ? 。 4? ?0d

（1）在电偶极子的延长线上x处：其中（X >>l）

????12P12P 电场强度矢量：E?x?? 。 或 E?r??334? ?0x4? ?0r

电势： U?x??1P1P?? 。 或 Ur?224? ?0x4? ?0r

（2）在电偶极子的中垂线上y处：其中（Y >>l）

??1P 电场强度矢量： E?y??? 。 34? ?0y

电势： U?y??1?q?q?????0 。 4? ?0?rr?

（3）在空间中任意点r处：其中（r >>l）

电场强度矢量：（采用平面极坐标系）

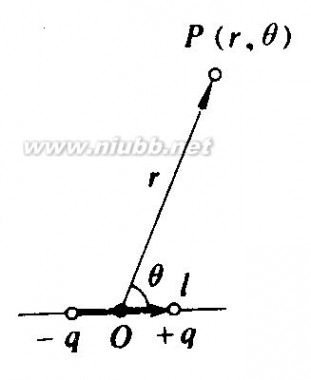
电势公式 几种典型带电体的场强和电势公式

?E?r??

14? ?0P?2pCos?0PSin?0?2

r?? 其大小为 E?3Cos??1 ， ??332

r4? ?0r?r?

?E?E

方向为??arctg??tg?1??EEr?r

????1?10

??。（www.61k.com]其中为与之间的夹角。 E?tgtg?r???

?2??

??

1P Cos?1P?r

电势：U?r?? 。 ?

61阅读请您转载分享：

4? ?or24? ?0r3

电场强度矢量的另一种表达式为：

?1???0??????E??p?3r?pr ee?式中：r?r为矢径r方向的单位矢量。4??0r3

???

上式电场强度矢量的表达式就是将电场强度E矢量分解在电偶极矩Pe和矢径r的方向上。可以证明：该表达式与电场强度的平面极坐标表达式是相等的。

若采用二维笛卡尔坐标系（平面直角坐标系）：

因为各物理量之间的关系为：r2?x2?y2 ， Cos??

所以电势的表达式为： U?r??

1Px

4? ?0x2?y2

x?r

xx?y

2

2

。

。

???

而电场强度的表达式为： E?Exi?Eyj 。 其中：

?U1P2x2?y2?U13PxyEx???， E???y

?x4? ?0x2?y2?y4? ?0x2?y2

??

。

22

1P4x?y

其大小为：E?E?E? 。 2224? ?0x?y

2

x

2y

若采用三维笛卡尔坐标系（即三维直角坐标系）则有如下关系式：

r2?x2?y2?z2 ， Cos??那么，电势的表达式为： U?r??

z

?r

zx?y?z

2

2

2

。

1P z

4? ?0x2?y2?z2

????

而电场强度的表达式为： E?Exi?Eyj?Ezk 。

。

其中：

Ex??

?UP3 x z

?

?x4? ?0x2?y2?z2

??

； Ey??

?UP3 y z

?

?y4? ?0x2?y2?z2

? ;

电势公式 几种典型带电体的场强和电势公式

?UP2z2?x2?y2

Ez???。（www.61k.com］ ?z4? ?0x2?y2?z2????

9、带电圆盘在其轴线上距离圆心为x点处：

? 电场强度矢量： Ep(x)?2?0

对上式结果进行讨论： ??1??????i 。 22?x?R?x

?qq（a）当 x??R 或 x?? 时 Ep(x)?i 或 E(r)?r0 p224? ?0x4? ?0r

此时带电圆盘可视为点电荷进行处理。 （b）当x??R 或 x?0 时 ， 则 Ep(x)?

大带电平板进行处理。

电势： Up(x)???即此时带电圆盘可视为无限i 。2?0?2?0R?x?x? 。 22

带电圆盘在其圆心处附近处的电势为：U(x)x?0??R　 　。2?0

10、均匀分布的带电半球面在其球心处：（球面的面电荷密度为σ，球面的半径为R。）

电场强度矢量： E0???i 。 4?0

电势： Up(x)?? RQ ?。2?04? ?0R

???此时电势并不是Up(x)??Eo?dr，因为E(x)?Eo(x)?。 04?0

本文标题：场强和电势的关系-电势和电势能的关系，大小比较
本文地址： http://www.61k.com/1151232.html