一 : 直线和圆的位置关系
1.知识结构
2.重点、难点分析
重点:的性质和判定.因为它是本单元的基础(如:“切线的判断和性质定理”是在它的基础上研究的),也是高中解析几何中研究“”的基础.
难点:在对性质和判定的研究中,既要有归纳概括能力,又要有转换思想和能力,所以是本节的难点;另外对“相切”要分清直线与圆有唯一公共点是指有一个并且只有一个公共点,与有一个公共点含义不同(这一点到直线和曲线相切时很重要),学生较难理解.
3.教法建议
本节内容需要一个课时.
(1)教师通过电脑演示,组织学生自主观察、分析,并引导学生把“点和圆的位置关系”研究的方法迁移过来,指导学生归纳、概括;
(2)在教学中,以“形”归纳“数”, 以“数”判断“形”为主线,开展在教师组织下,以学生为主体,活动式教学.
教学目标 :
1、使学生理解直线和圆的三种位置关系,掌握其判定方法和性质;
2、通过的探究,向学生渗透分类、数形结合的思想,培养学生
观察、分析和概括的能力;
3、使学生从运动的观点来观察直线和圆相交、相切、相离的关系、培养学生的辩证唯物主义观点.
教学重点:的判定方法和性质.
教学难点 :直线和圆的三种位置关系的研究及运用.
教学设计:
(一)基本概念
1、观察:(组织学生,使学生从感性认识到理性认识)
2、归纳:(引导学生完成)
(1)直线与圆有两个公共点;(2)直线和圆有唯一公共点(3)直线和圆没有公共点
3、概念:(指导学生完成)
由直线与圆的公共点的个数,得出以下直线和圆的三种位置关系:
(1)相交:直线与圆有两个公共点时,叫做直线和圆相交.这时直线叫做圆的割线.
(2)相切:直线和圆有唯一公共点时,叫做直线和圆相切.这时直线叫做圆的切线,唯一的公共点叫做切点.
(3)相离:直线和圆没有公共点时,叫做直线和圆相离.
研究与理解:
①直线与圆有唯一公共点的含义是“有且仅有”,这与直线与圆有一个公共点的含义不同.
②直线和圆除了上述三种位置关系外,有第四种关系吗?即一条直线和圆的公共点能否多于两个?为什么?
(二)直线与圆的位置关系的数量特征
1、迁移:点与圆的位置关系
(1)点P在⊙O内 d<r;
(2)点P在⊙O上 d=r;
(3)点P在⊙O外 d>r.
2、归纳概括:
如果⊙O的半径为r ,圆心O到直线l的距离为d,那么
(1)直线l和⊙O相交 d<r;
(2)直线l和⊙O相切 d=r;
(3)直线l和⊙O相离 d>r.
(三)应用
例1、在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有何种位置关系?为什么?
(1)r=2cm; (2)r=2.4cm; (3)r=3cm.
学生自主完成,老师指导学生规范解题过程.
解:(图形略)过C点作CD⊥AB于D,
在Rt△ABC中,∠C=90°,
AB= ,
∵ ,∴AB·CD=AC·BC,
∴ (cm),
(1)当r =2cm时 CD>r,∴圆C与AB相离;
(2)当r=2.4cm时,CD=r,∴圆C与AB相切;
(3)当r=3cm时,CD<r,∴圆C与AB相交.
练习P105,1、2.
(四)小结:
1、知识:(指导学生归纳)
2、能力:观察、归纳、概括能力,知识迁移能力,知识应用能力.
(五)作业 :教材P115,1(1)、2、3.
探究活动
问题:如图,正三角形ABC的边长为6 厘米,⊙O的半径为r厘米,当圆心O从点A出发,沿着线路AB一BC一CA运动,回到点A时,⊙O随着点O的运动而移动.在⊙O移动过程中,从切点的个数来考虑,相切有几种不同的情况?写出不同情况下,r的取值范围及相应的切点个数.
略解:由正三角形的边长为6 厘米,可得它一边上的高为9厘米.
①∴当⊙O的半径r=9厘米时,⊙O在移动中与△ABC的边共相切三次,即切点个数为3.
②当0<r<9时,⊙O在移动中与△ABC的边共相切六次,即
二 : 直线与圆的位置关系的题目圆x^2+y^2-2x=0和圆x^2+y
直线与圆的位置关系的题目
圆x^2+y^2-2x=0和圆x^2+y^2+4y=0的位置关系是
A。相切
B。外切
。内切
D。相交
最好有解题过程
(1)对x^2+y^2-2x=0变形,有:x^2-2x+1+y^2=1即
(x-1)^2+y^2=1
(2)对x^2+y^2+4y=0变形,有:x^2+y^2+4y+4=4即
x^2+(y+2)^2=4
(3)由坐标平移,知(1)为x^2+y^2=1向右平移一个单位所得
(2)为x^2+y^2=4向下平移两个单位所得
(4)由图知两圆相交选D
三 : 直线与圆的位置关系
(1) 点到直线距离公式:
|Ax0+By0+C| d= √A2+B2
(2)圆的标准方程:
(x-a)2+(y-b)2=r2
(3)圆的一般方程:
x2+ y2+Dx+Ey+F=0(D2+E2-4F>0)
D 圆心坐标 : ( , 2
-
-
1 E 2 2 D ? E ? 4F ) ,半径: 2 2
2 P x , y ? ? 点 0 0 和圆 ? x ? a ? ? ? y ? b ? ? r 的位置 关系有几种? 2 2
点P到圆心C的距离为d,圆的半径为r,则:
点在圆外
d ?r d ?r d?r
? x ? x0 ? ? ? y ? y0 ?
2
2
2
2
?r ;
2
2
点在圆上
点在圆内
? x ? x0 ? ? ? y ? y0 ?
?r ;
? x ? x0 ? ? ? y ? y0 ?
2
2
?r ;
2
数形结合: 位置关系
数量关系
直线和圆的位置关系
(一) 直线与圆的位置关系的判定
思考1:在平面几何中,直线与圆的位置关系 有几种?
思考2:在平面几何中,我们怎样判断直线与 圆的位置关系?
d d r r d
r
d<r
d=r
d>r
(一) 直线与圆的位置关系的判定 思考3:如何根据直线与圆的公共点个数判断 直线与圆的位置关系?
两个公共点 相交
一个公共点 相切
没有公共点 相离
(一) 直线与圆的位置关系的判定 思考4:在平面直角坐标系中,我们用方程表 示直线和圆,如何根据直线与圆的方程判断 它们之间的位置关系?
方法一:根据直线与圆的联立方程组 的公共解个数判断; 代数法
方法二:根据圆心到直线的距离与圆 半径的大小关系判断. 几何法
(一) 直线与圆的位置关系的判定
代数法:操作步骤
1.将直线方程与圆方程联立成方程组;
2.通过消元,得到一个一元二次方程; 3.求出其判别式△的值;
4.比较△与0的大小关系: 若△>0,则直线与圆相交; 若△=0,则直线与圆相切; 若△<0,则直线与圆相离.
(一) 直线与圆的位置关系的判定
几何法:操作步骤
1.把直线方程化为一般式,并求出圆 心坐标和半径r; 2.利用点到直线的距离公式求圆心到直 线的距离d; 3.比较d与r的大小关系: 若d>r,则直线与圆相离; 若d=r,则直线与圆相切; 若d<r,则直线与圆相交.
例1:已知直线l:3x+y-6=0和圆C:x2+y2-2y-4=0, 判断直线l与圆的位置关系;如果相交,求它们 交点的坐标.
例 2:已知圆的方程是 x +y =2,直线 y=x+b,当 b 为何值 时,圆与直线相交、相切、相离?
法二 = 2 .
|b| 圆心O(0,0)到y=x+b的距离d= ,半径r 2
2
2
①当d<r,即-2<b<2时,直线与圆相交; ②当d=r,即b=2或b=-2时,直线与圆相切; ③当d>r,即b>2或b<-2时,直线与圆相离.
(二)直线与圆相切
只要有相切;就要考虑圆心到切点的直线!
A
O
|OA|=r(即:d=r) kl· kOA=-1
l
相切问题中列方程的基本依据!
(二)直线与圆相切---圆的切线方程
思考1:设点M(x0,y0)为圆 x2+y2=r2上一点,则过 M点可以作几条圆
的切线?如何求过点M的圆的 y0 切线方程? 解:设x0 ? 0, y0 ? 0, 则kOM ? x0 y x0 ? 切线方程为 y ? y ? ? ( x ? x ) 0 0 M(x0,y0) y0 2 2 即xx0 ? yy0 ? x0 ? y0 ? r2 o x 易验证x0 ? 0或y0 ? 0时方程也成立
x0x+y0y=r2
(二)直线与圆相切---圆的切线方程
思考2:设点M(x0,y0)为圆 x2+y2=r2外一点,则过M 点可以作几条圆的切线?如何求过点M的圆的切线 方程? M(x0,y0) y P o x
(二)直线与圆相切---圆的切线方程
例3.过点A(4, ?3)作圆C : ( x ? 3) ? ( y ? 1) ? 1的切线,
2 2
求切线方程. 解:(1)若斜率存在,设切线为y ? 3 ? k ( x ? 4)
即kx ? y ? 4k ? 3 ? 0
15 |3k ? 1 ? 4k ? 3 | ? ?1 ?k ? ? 8 1? k 2 15 ? 切线为y ? 3 ? ? ( x ? 4) 即 15x ? 8 y ? 36 ? 0 8 (2)若斜率不存在,直线x ? 4与圆相切
综上,圆的切线方程为 15x ? 8 y ? 36 ? 0或x ? 4
注意: 在求过一定点的圆的切线方程时, 应首先判断这点与圆的位置关系, 若点在圆上,则该点为切点,切线 只有一条; 若点在圆外,切线应有两条; 若点在圆内,无切线.
(三)直线与圆相切---圆的切线长度
思考3:设点M(x0,y0)为圆 x2+y2=r2外一点,如何求 过点M的圆的切线长度? y P o x M(x0,y0)
(三)直线与圆相切---圆的切线长度
推广:设点M(x0,y0)为圆 (x-a)2+(y-b)2=r2外一点, 过点M的圆的切线长度是多少? y M(x0,y0) P
o
C(a,b) x
推广:设点M(x0,y0)为圆 x2+y2+Dx+Ey+F=0外一 点,过点M的圆的切线长度是多少?
(四)直线与圆相交
OC称为弦心距且 相交
C为弦AB的中点
注:只要有相交;就要考虑 弦心距及弦心距三角形.
A
C B
O
OA2=AC2+OC2
l
1 2 2 r ? ( AB) ? d 2
2
(四)直线与圆相交---求弦长 例 4: 已知直线 y=x+1 与圆 x2+y2=4 相交于 A,B 两点,求弦长|AB|的值
解法一:(求出交点利用两点间距离公式)
? ?y ? x ? 1 2 由? 2 , 消 去 y 得 2 x ? 2x ? 3 ? 0 2 ? ?x ? y ? 4 ?1? 7 ?1? 7 ? x1 ? , x2 ? 2 2 1? 7 1? 7 ? y1 ? ,y2 ? 2 2 ?1? 7 1? 7 ?1? 7 1? 7 ? A( , ), B( , ) 2 2 2 2 ?| AB |? 14
y B x
A
O
(四)直线与圆相交---求弦长 例 4: 已知直线 y=x+1 与圆 x2+y2=4 相交于 A,B
两点,求弦长|AB|的值.
解法二:(弦长公式)
? ?y ? x ? 1 由? 2 消 去y 2 ? ?x ? y ? 4 得 2x 2 ? 2x ? 3 ? 0 3 ? x1 ? x 2 ? ?1, x1 x 2 ? ? 2
y B x
A
O
?| AB |? 1 ? k 2 | x1 ? x 2 |? 1 ? k 2 [(x1 ? x 2 ) 2 ? 4x1 x 2 ] ? 1?1
2
3 [(?1) ? 4 ? ( ? )] ? 14 2
2
弦长公式: | AB |? 1 ? k 2 | x1 ? x2 |
(四)直线与圆相交---求弦长 例 4: 已知直线 y=x+1 与圆 x2+y2=4 相交于 A,B 两点,求弦长|AB|的值.
解法三:(解弦心距,半弦及半径构成的直角三角形)
设圆心O(
0,0)到直线的距离为d,则 y
d? 2 ? 2 2 1 ? ( ?1)
2 2
1
B
r d O
?| AB |? 2 r ? d ? 14
A
x
(四)直线与圆相交---求弦长 求圆的弦长方法 (1)几何法:用弦心距,半径及半 弦构成直角三角形的三边
(2)代数法:用弦长公式
| AB |? 1 ? k | x1 ? x2 |? (1 ? k )[( x1 ? x2 ) ? 4 x1 x2 ]
2 2 2
(四)直线与圆相交---求弦长
例5:已知过点 M (?3,?3) 的直线被圆
x ? y ? 4 y ? 21 ? 0 所截得的弦长为 4 5 ,
2 2
求直线的方程.
(五)有关圆的最值问题
例6:求过点A(2,1)的直线中, 被圆 x2+y22x+4y=0 截得弦长最大的直线方程.
y .A x
. C
有关圆的最值问题
问题1.已知点A(1,3), P为圆: (x-2)2+(y+1)2=4上 一点,求|PA|的最大值和最小值. Key: 最大值是:d+r,最小值是:|d-r|.
问题2.已知直线3x-2y+6=0, P为圆: (x-2)2 +(y+1)2=4 上一点,求点P到直线的距离的最大值和最小值. Key: 若相离,最大值是:d+r,最小值是:d-r. 若相交,最大值为:d+r, 最小值为:0.
(五)有关圆的最值问题
例7:求过圆: (x+2)2+(y-2)2=9内一点A(-1,3) 的最长弦和最短弦所在的直线方程。
解: ?圆 心 为 C( ?2,2), ? k AC 3?2 ? ?1 ?1? 2
最长弦所在的直线方程为: x-y+4=0 最短弦所在的直线方程为: x+y-2=0
?C
?A
(五)有关圆的最值问题
例7: 已知x,y满足方程 x2+y2-6x-2y+6=0,
求: (1)x2+y2的最大值;
解:(1) 如图? | O C|? 9 ? 1 ? 10 2 2 ? ( x ? y )max
?| O A |
2
?
A
C
O
2
? ( 10 ? 2) ? 14 ? 4 10
(五)有关圆的最值问题
例7: 已知x,y满足方程 x2+y2-6x-2y+6=0,
3k ? 1 ? k ? 3 y?3 ?2 设 ? k , 则 :kx? y ? k ? 3 ? 0 ? 2 x?1 k ?1
y?3 求: (2) 的最大值和最小值. x ?1
4? 7 ? 3k ? 8k ? 3 ? 0 ? k ? 3 y?3 4? 7 ?( )min ? ; x?1 3 O y?3 4? 7 ( )max ? x?1 3 P ?
2
A
?
C
(五)有关圆的最值问题
例7: 已知x,y满足方程 x2+y2-6x-2y+6=0,
求:?3? y-x的最小值.
练习:
1.由点P(1,3)引圆x2+y2=9的切线的长是( ). A.2 B. C.1 D.4 2.过原点且倾斜角为60°的直线被圆x2+y2-4y =0所截得的弦长为________. 3.若直线x-y=2被圆(x-a)2+y2=4所截得的弦 长为2,则实数a的值为( ). A.-1或 3 B.1或3 C.-2或6 D.0或4 4.直线x+y+2=0与圆x2+(y+1)2=a2有公共点, 则a的取值范围是________.
四 : 我们知道,判断直线与圆的位置关系可以用圆心到直
| 我们知道,判断直线与圆的位置关系可以用圆心到直线的距离进行判别,那么直线与椭圆的位置关系有类似的判别方法吗?请同学们进行研究并完成下面问题. (1)设F1、F2是椭圆M:
(2)设F1、F2是椭圆M:
(3)试写出一个能判断直线与椭圆的位置关系的充要条件,并证明. (4)将(3)中得出的结论类比到其它曲线,请同学们给出自己研究的有关结论(不必证明). |
(1)d1?d2=
联立方程
∴△=(50
(2)联立方程组
∴△=(2a2mp)2-4a2(a2m2+b2n2)(p2-b2n2)=4a2b2n2(a2m2+b2n2-p2)=0 ∴p2=a2m2+b2n2…(8分) ∵椭圆的焦点为:F1(-c,0),F2(c,0),其中c2=a2-b2 ∴d1?d2=
=
(3)设F1、F2是椭圆M:
点F1、F2到直线L:mx+ny+p=0(m、n不同时为零)的距离分别为d1、d2,且F1、F2在直线L的同侧. 那么直线L与椭圆相交的充要条件为:d1d2<b2; 直线L与椭圆M相切的充要条件为:d1d2=b2; 直线L与椭圆M相离的充要条件为:d1d2>b2…(14分) 证明:由(2)得,直线L与椭圆M相交?(*)中△>0?p2<a2m2+b2n2 ?d1?d2=
同理可证:直线L与椭圆M相离?d1d2>b2;直线与椭圆相切?d1d2=b2…(16分).命题得证. (写出其他的充要条件仅得(2分),未指出“F1、F2在直线L的同侧”得3分) (4)可以类比到双曲线:设F1、F2是双曲线M:
点F1、F2到直线L:mx+ny+p=0(m、n不同时为零)距离分别为d1、d2,且F1、F2在直线L的同侧. 那么直线L与双曲线相交的充要条件为:d1d2<b2; 直线L与双曲线M相切的充要条件为:d1d2=b2; 直线L与双曲线M相离的充要条件为:d1d2>b2.…(20分) |
考点:
考点名称:圆锥曲线综合圆锥曲线的综合问题:
1、圆锥曲线的范围问题有两种常用方法:
(1)寻找合理的不等式,常见有△>0和弦的中点在曲线内部;
(2)所求量可表示为另一变量的函数,求函数的值域。
2、圆锥曲线的最值、定值及过定点等难点问题。
直线与圆锥曲线的位置关系:
(1)从几何角度来看,直线和圆锥曲线有三种位置关系:相离、相切和相交,相离是直线和圆锥曲线没有公共点,相切是直线和圆锥曲线有唯一公共点,相交是直线与圆锥曲线有两个不同的公共点,并特别注意直线与双曲线、抛物线有唯一公共点时,并不一定是相切,如直线与双曲线的渐近线平行时,与双曲线有唯一公共点,但这时直线与双曲线相交;直线平行(重合)于抛物线的对称轴时,与抛物线有唯一公共点,但这时直线与抛物线相交,故直线与双曲线、抛物线有唯一公共点时可能是相切,也可能是相交,直线与这两种曲线相交,可能有两个交点,也可能有一个交点,从而不要以公共点的个数来判断直线与曲线的位置关系,但由位置关系可以确定公共点的个数.
(2)从代数角度来看,可以根据直线方程和圆锥曲线方程组成的方程组解的个数确定位置关系.设直线l的方程与圆锥曲线方程联立得到ax2+bx+c=0.
①若a=0,当圆锥曲线是双曲线时,直线l与双曲线的渐近线平行或重合;当圆锥曲线是抛物线时,直线l与抛物线的对称轴平行或重合.
②若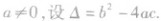
当Δ>0时,直线和圆锥曲线相交于不同两点,相交.
当Δ=0时,直线和圆锥曲线相切于一点,相切.
当Δ<0时,直线和圆锥曲线没有公共点,相离.
直线与圆锥曲线相交的弦长公式:
若直线l与圆锥曲线F(x,y)=0相交于A,B两点,求弦AB的长可用下列两种方法:
(1)求交点法:把直线的方程与圆锥曲线的方程联立,解得点A,B的坐标,然后用两点间距离公式,便得到弦AB的长,一般来说,这种方法较为麻烦.
(2)韦达定理法:
不求交点坐标,可用韦达定理求解.若直线l的方程用y=kx+m或x=n表示.


61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1