一 : 《多边形的内角和》公开课

    《多边形的内角和》公开课教案     北京市第五中学 曹自由      
    教学任务分析
    教学目标
    知识与技能
    掌握多边形内角和公式及外角和定理,并能应用.
    过程与方法
    1.经历把多边形内角和问题转化为三角形内角和问题的过程,体会转化思想在几何中的应用,同时体会从特殊到一般的认识问题的方法;
    2.经历探索多边形内角和公式的过程,尝试从不同角度寻求解决问题的方法.训练学生的发散性思维,培养学生的创新精神.
    情感态度价值观
    通过猜想、推理等数学活动,感受数学充满着探索以及数学结论的确定性,提高学生学习数学的热情.
    重点
    多种方法探索多边形内角和公式
    难点
    多边形内角和公式的推导
    教学流程安排
    活动流程
    活动内容和目的
    活动1学生自主探索四边形内角和
    活动2教师引导学生探索总结把四边形转化为三角形添加辅助线的基本方法
    活动3探索n边形内角和公式
    活动4师生共同研究递推法确定n边形内角和公式
    活动5多边形内角和公式的应用
    活动6小结
    作业
    从对三角形及特殊四边形(正方形、长方形)内角和的认识出发,使学生积极参加到探索四边形内角和的活动中.
    加深对转化思想方法的理解, 训练发散思维、培养创新能力.
    通过把多边形转化为三角形体会转化思想,感受从特殊到一般的数学思考方法.
    学生提高动手实操能力、突破“添”的思维局限
    综合运用新旧知识解决问题.
    回顾本节内容,培养学生的归纳概括能力.
    反思总结,巩固提高.
    课前准备
    教具
    学具
    补充材料
    教师用三角尺
    课件
    剪刀
    复印材料
    三角形纸片
    教学过程设计
    问题与情景
    师生行为
    设计意图
    [活动1、2]
    问题1.三角形的内角和是多少?
    与形状有关吗?
    问题2.正方形、长方形的内角和是多少?
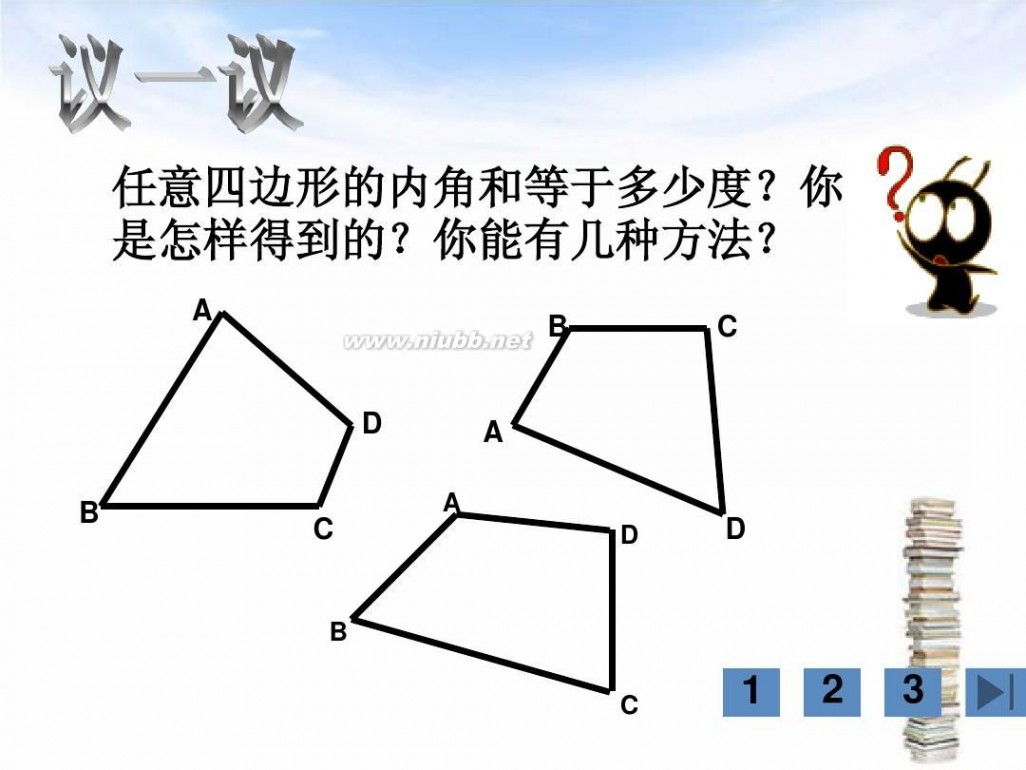
    由此你能猜想任意凸四边形内角和吗?
    动脑筋、想办法,说明你的猜想是正确的.
    问题3添加辅助线的目的是什么,方法有没有什么规律呢?
    学生回答:
    三角形内角和是180°,与形状无关;正方形、长方形内角和是360°(4×90°),由此猜想任意凸四边形内角和是360°.
    学生先独立探究,再小组交流讨论.
    教师深入小组指导,倾听学生交流.对于通过测量、拼图说明的,可以引导学生利用添加辅助线的方法把四边形转化为三角形.
    学生汇报结果.
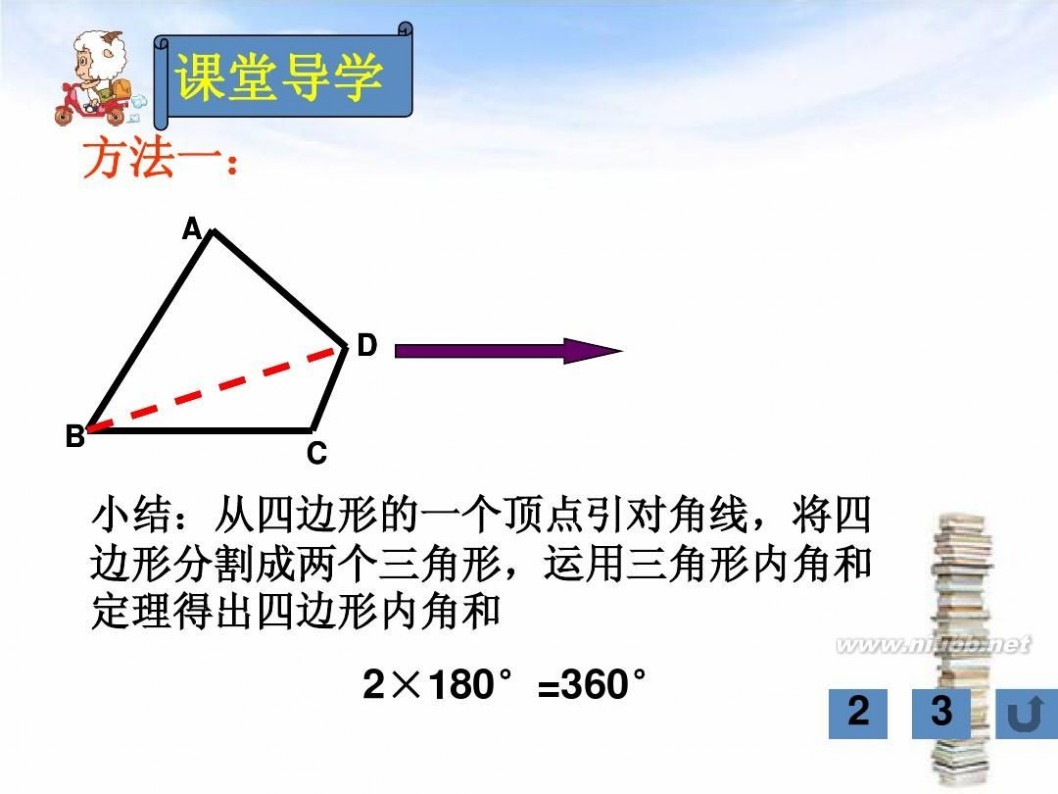
    ①过一个顶点画对角线1条,得到2个三角
    形,内角和为2×180°;
    ②画2条对角线,在四边形内部交于一点,得到4个三角形,内角和为4×180°-360°;
    ③若在四边形内部任取一点,如图,也可以得到相应的结论;
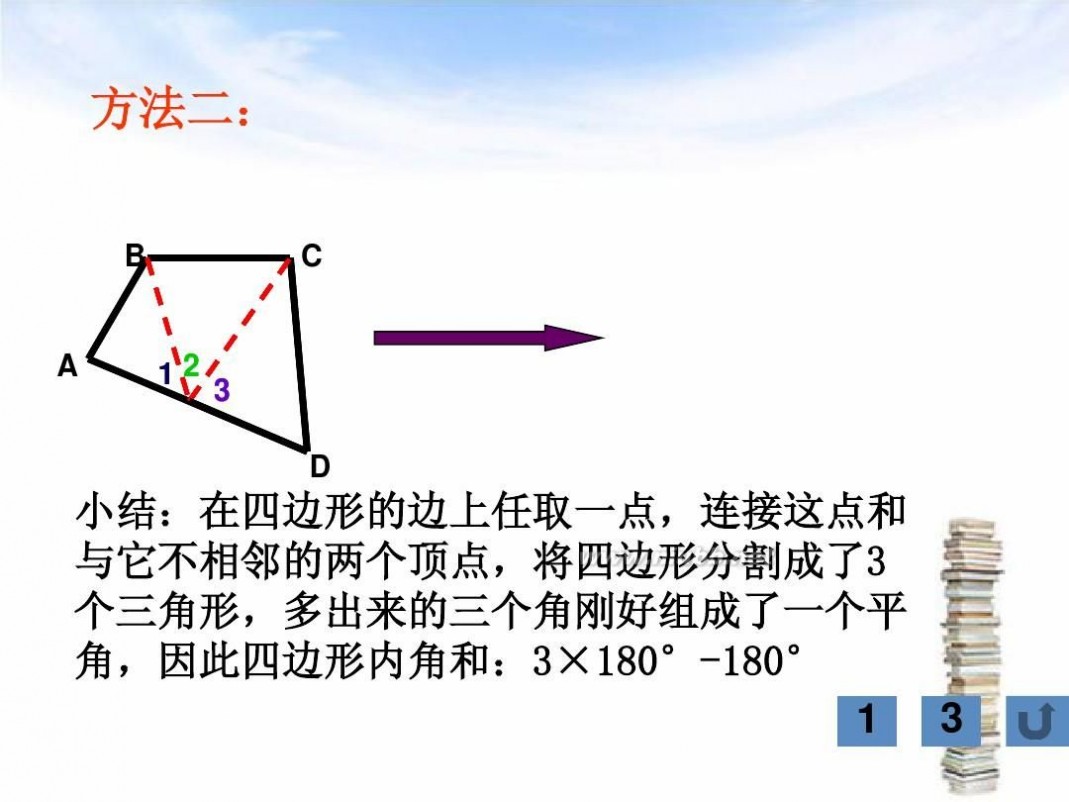
    ④这个点还可以取在边上(若与顶点重合,转化为第一种情况——连接对角线;否则如图4)
    内角和为3×180°-180°;
    ⑤点还可以取在外部,如图5、6.由图5,内角和为3×180°-180°;由图6,内角和为2×180°;
    教师重点关注:①学生能否借助辅助线把四边形分割成几个三角形;②能否借助辅助线找到不同的分割方法.
    教师总结:利用辅助线把四边形的内角和转化为三角形的内角和,体现了化未知为已知的转化思想. .以上这些方法同样适用于探究任意凸多边形的内角和.为方便起见,下面我们可以选用最简单的方法——过一点画多边形的对角线,来探究五边形、六边形,甚至任意n边形的内角和.
    通过回忆三角形的内角和,有助于后续问题的解决.
    从四边形入手,有利于学生探求它与三角形的关系,从而有利于发现转化的思想方法.
    通过动手操作寻找结论,让他们积极参加数学活动、主动思考、合作交流,体验解决问题策略的多样性.
    通过寻求多种方法解决问题,训练学生发散思维能力、培养创新意识.
    [活动3]
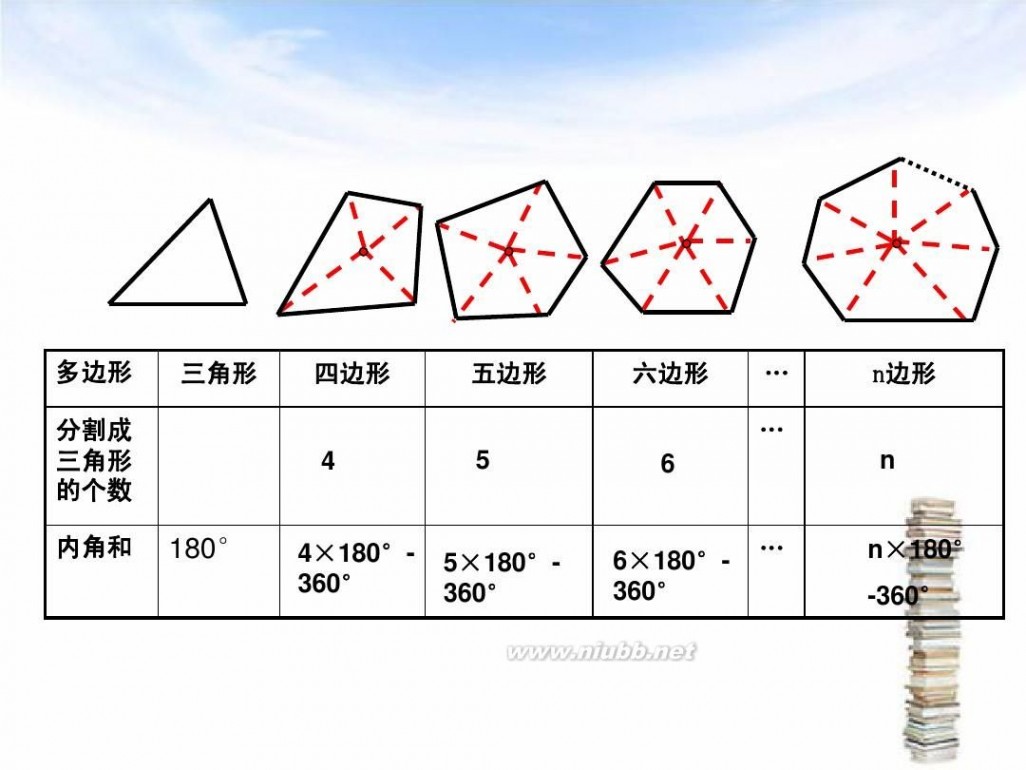
    问题4怎样求n边形的内角和?(n是大于等于3的整数)
    学生归纳得出结论:从n边形的一个顶点出发可以引(n-3)条对角线,它们将n边形分割成(n-2)个三角形,(凸)n边形的内角和等于(n-2)×180°.
    特点:内角和都是180°的整数倍.
    通过归纳概括得出任意凸多边形的内角和与边数关系的表达式,体会数形之间的联系,感受从特殊到一般的数学推理过程和数学思想方法.   
    [活动4]
    每名同学发一张三角形纸片
    问题5一张三角形纸片只剪一刀,能不能得到一个四边形,在这一过程中内角发

《多边形的内角和》公开课生了怎样的变化
    问题6由四边形得到五边形呢?
    依此类推能否猜想n边形内角和公式
    将三角形去掉一个角可以得到四边形,如图7,四边形内角和为
    180°+2×180°-180°=2×180°.
    每个图形都是前一个图形剪去一个三角形,每次操作内角和增加180°,n边形是三角形经过(n-3)次操作得到的,所以n边形内角和公式为(n-2)×180°
    (严谨的证明应在学习数学归纳法后)
    学生突破常规,学会逆向思维,变以往的“把多边形转化成三角形”为“把三角形转化成多边形”同样使问题得到解决
    [活动5]
    知道了凸多边形的内角和,它可以解决哪些问题呢?
    问题6:六边形的外角和等于多少?
    n边形外角和是多少?
    学生自己画图、思考.叙述理由:六边形的六个外角与六个内角构成6个平角,结合内角和公式,因此得到
    6×180°-(6-2)×180°=360°
    学生思考,回答.
    n边形中,每个顶点处的内角与一个外角组成一个平角,它们的和,即n边形内角和与外角和的和为n×180°,而内角和为(n-2)×180°,因此外角和为360°.
    利用内角和求外角和,巩固了内角和公式.  
    如时间允许,此时还可补充利用“转角”求多边形外角和的方法,这样就变成了可以利用外角和来推导内角和,这又是一种逆向思维
    练习
    一个多边形各内角都相等,都等于150°,它的边数是      ,内角和是     .
    练习.解:(n-2)180=150n,n=12;
    或360÷(180-150)=12(利用外角和)
    150°×12=1800°.
    巩固内角和公式,外角和定理.
    [活动5]
    小结
    下面请同学们总结一下这节课你有哪些收获.
    学生自己小结,老师再总结.
    1.       多边形内角和公式(n-2)180°,外角和是360°;
    2.       由特殊到一般的数学方法、转化思想.
    学会总结,培养归纳概括能力.
    作业:
    课后思考题.
    一同学在进行多边形的内角和计算时,求得内角和为1125°,可能吗?
    当他发现错了之后,重新检查,发现少算了一个内角,你能求出这个内角是多少度?他求的是几边形的内角和吗?
    多边形内角和与不等式的综合应用题,一题多解,提高学生的综合应用能力.
    作业:
    解法1.设这是n边形,这个内角为x°,依题意:(n-2)180=1125+x
    x=(n-2)180-1125
    ∵0<x<180
    ∴0<(n-2)180-1125<180
    解得:<n<
    ∵n是整数,
    ∴n=9.
    x=(9-2)180-1125=135
    注:方程(n-2)180=1125+x中有两个未知数,解法1用n表示x,根据x的取值范围解不等式组求出了n;如果用x表示n,你能解出来吗?
    解法2.设这是n边形,这个内角为x°,依题意:(n-2)180=1125+x
    ∵n是整数,
    ∴45+x是180的倍数.
    又∵0<x<180
    ∴45+x=180,x=135,n=9
    还可以根据内角和的特点,先求出内角和.
    解法3.设此多边形的内角和为x°,依题意:1125<x<1125+180
    即:180×6+45<x<180×7+45
    ∵x是多边形内角和的度数
    ∴x是180的倍数
    ∴x=180×7=1260     边数=7+2=9,
    这个内角=1260°-1125°=135°
    解法4(极值法).设这是n边形,这个内角为x°,则0<x<180,依题意:(n-2)180=1125+x
    令x=0,得:n=,令x=180,得:n=
    ∴<n<   其余同解法1.    
    此作品为天津市人教版初中数学课标实验教材研讨会公开课教学设计

二 : 多边形内角和公式课件

多边形内角和 多边形内角和公式课件

多边形内角和 多边形内角和公式课件

多边形内角和 多边形内角和公式课件

多边形内角和 多边形内角和公式课件

多边形内角和 多边形内角和公式课件

多边形内角和 多边形内角和公式课件

多边形内角和 多边形内角和公式课件

多边形内角和 多边形内角和公式课件

多边形内角和 多边形内角和公式课件

多边形内角和 多边形内角和公式课件

多边形内角和 多边形内角和公式课件

多边形内角和 多边形内角和公式课件

多边形内角和 多边形内角和公式课件

多边形内角和 多边形内角和公式课件

多边形内角和 多边形内角和公式课件

多边形内角和 多边形内角和公式课件

多边形内角和 多边形内角和公式课件

多边形内角和 多边形内角和公式课件

多边形内角和 多边形内角和公式课件

多边形内角和 多边形内角和公式课件

三 : 多边形内角和公式的几种推导方法

多边形内角和公式的几种推导方法

云南省西双版纳州勐海县勐阿中学 赵艳

学生在学习探索多边形的内角和的时候，已学习了三角形内角和定理、三角形相关知识，在前面特殊四边形性质的探索过程中，也体会了转化思想在解题中的应用，所以具备了进一步学习的基础。（www.61k.com]随着几何知识学习的逐步深入，学生具备了一定的解决几何问题的方法，本节课需要用到图形转化，多边形内角和定理的探索，需要学生结合图形发现规律。所以在教学中教师引导学生推导多边形内角和公式的方法是将多边形分割为多个三角形，将多边形的内角和转化为我们所熟知的三角形内角和来解决。下面介绍几种推导多边形内角和公式常用的方法。

A方法（一）：如（图七）所示，取多边形上任意一个

顶点，连接除相邻的两点，则多边形的内角和可转化为

FB三角形内角和之间的关系，即六边形ABCDEF的内角和

等于4个三角形内角和之和：4×1800 ，从而边数为6C

D

(图七)E的多边形内角和为（6-2）×1800 =4×1800 ，再列举

其它多边形可以归纳总结出n边形内角和为（n-2）×

AH

G1800 。

FB方法（二）：如（图八）所示，在多边形内任意找一

点O，连接各个点，则多边形的内角和可转化为三角形O

C

D(图八）E内角和之间的关系，即八边形ABCDEFGH的内角和等于

8个三角形内角和减去一个周角的度数：8×1800

AF

-3600=8×1800 -2×1800 =（8-2）×1800 ，再列举其它

BE多边形可以归纳总结出n边形内角和为（n-2）×1800 。

方法（三）：如（图九）所示，在多边形的一条边上

C

AP（图九）FD任意取一点P，连接这点与各顶点的线段，把六边形

ABCDEF分成了五个三角形，所以此六边形的内角和等

BE于五个三角形的内角和减去一个平角的度数，即：5×

1800 -1800=4×1800 ，归纳之后得到n边形的内角和为

C

P

（图十）D（n-2）×1800 。

方法（四）：如（图十）所示，在多边形外取一点

第1页，共2页

多边形内角和 多边形内角和公式的几种推导方法

P（点P不在n边形任一边的延长线上），连接此点与各顶点，得到五个三角形（不含△CPD），所以此六边形的内角和等于五个三角形的内角和减去△CPD的内角和，即5×1800 -1800=4×1800，归纳之后得到n边形的内角和为（n-2）×1800 。(www.61k.com]

综述以上几种方法，不难发现，推导多边形的内角和公式，都是利用转化思想而得，即把多边形分成若干个三角形，从而将多边形问题转化为三角形问题来解决，这种思想对于学好数学是极为重要的，而且对学生理解及掌握知识有一定的帮助，有利于教师的教学和学生的学习。

第2页，共2页

四 : 多边形内外角和的问题（公式）多边形的内角和公式：多边形外角和公式

多边形内外角和的问题（公式）

多边形的内角和公式：多边形外角和公式：多边形每个内角公式：多边形每个外角公式：握手问题：一个多边形从一个定点可以分为多少个三角型，和多少条对角线?(用带N的字母表示）一个多边形从它的内部定点可以分为多少个三角型，和多少条对角线?(用带N的字母表示）

---

多边形的内角和公式：Sn=(n-2)180°

多边形外角和公式：360°（常数，与边数无关）

正多边形每个内角公式：(n-2)180°/n

正多边形每个外角公式： 360°/n

1个多边形从1个顶点可以分为多少个三角形，和多少条对角线?

（n-2)个三角形，(n-3)条对角线

1个多边形从它的内部顶点可以分为多少个三角形，和多少条对角线?

n(n-2)个三角形，n(n-3)/2条对角线。

本文标题：多边形内角和公式-《多边形的内角和》公开课
本文地址： http://www.61k.com/1127876.html