一 : 定义新运算“*”,规则:a*b=a(a≥b)b(a<b),如1*2=2,(
定义新运算“*”,规则:a*b=
|
| 在x2+x-1=0中, a=1,b=1,c=-1, ∴b2-4ac=5>0, 所以x1=
∴x1*x2=
|
考点:
考点名称:一元二次方程根与系数的关系一元二次方程根与系数的关系: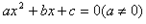 的两个实数根是
的两个实数根是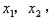 那么
那么 ,
, 。
。一元二次方程根与系数关系的推论:
1.如果方程x2+px+q=0的两个根是x1、x2,那么x1+x2=-p, x1`x2=q
2.以两个数x1、x2为根的一元二次方程(二次项系数为1)是x2-(x1+x2)x+x1x2=0
提示:
①运用根与系数的关系和运用根的判别式一样,都必须先把方程化为一般形式,以便正确确定a、b、c的值。
②有推论1可知,对于二次项系数为1的一元二次方程,他的两根之和等于一次项系数的相反数,两根之积等于常数项。
③推论2可以看作推论1的逆定理,利用推论2可以直接求出以两个数x1、x2为根的一元二次方程(二次项系数是1)是x2-(x1+x2)x+x1x2=0
二 : 定义新运算(含答案)-
七年级奥赛练习题:定义新运算
班级 姓名
规定新的代数运算是一类较新颖的数学问题,它是以近世代数为背景的。[www.61k.com]近年来,多次出现在国内外的数学竞赛题中。解这类问题的关键在于认识新运算的含义。在计算时严格遵照规定的法则代入数值。值得注意的是,这样规定的新运算未必满足通常的结合律及交换律。
一、填空题:
1.对任意有理数A、B,规定A*B=
2.A~B=A?B
A?B?1A?B2,则1*9= 。 ,则2002~2003= 。
2a?b
2ab3.“*”表示一个运算符号,它的一个意思是:a*b=
4.对于正有理数,运算“*”定义为a*b=
2,则5* (3*2)= 。 aba?b,则4* (4*4)= 。 5.规定f(a)=a+2a+3, 则f(2)= 。
6.定义a△b=ba+ab,则4△50= 。
7.若规定运算a*b=2(a+b),则(a*b)*2= 。
8.若规定A△B=3A+4B,则(4△5)△6= ,若7△B=45,则B= 。
9.对有理数a、b,规定a*b=ab-a-b+1,如果(x*x)*2=0,则 。
10.如果定义运算“*”,使得3*2=32+42=25,4*3=42+52+62=77,则6*5= 。
二、解答题:
11.“*”表示一种运算符号,它的含义是:x*y=
1
31xy+1(x?1)(y?A)。 已知2*3=
,求2002*2003。 1
定义新运算 定义新运算(含答案)-
12. a、b为有理数,当a≥b时,a*b=b,当a<b时,a*b=b-a。(www.61k.com)若2*x=36,求x的值。
13.x是实数,﹤x﹥表示不超过x的素数的个数,如﹤5﹥=3,即不超过5的素数有2,3,5三个。求﹤﹤19﹥×﹤9﹥+﹤1﹥﹥的值。
14.对于有理数x、y定义一种运算“*”,规定x*y=ax+by-cxy,其中a,b,c为已知数,等式右边是加、减、乘法运算,又知道1*2=3,2*3=4,x*m=x(m≠0)。试求m的值。
2 a
定义新运算 定义新运算(含答案)-
答案
一、填空题:
1.5 2.1001 3.29
10
2 4.432 5.11 6.6250200 7.4a+4b+4 8.120,6 9.0或2 10.6+7+8+9+10=330
二、解答题:
11.由2*3=1
2?3222+1
3?(3?A)=1
3,得A=-1,所以2002*2003=1
2005003
12.分情况讨论,当x≥2时,由2*x=x2=36,得到x=6;当x<2时,由x*x=x-2=36,得到x=38(舍去)。(www.61k.com)所以x的值为6。
13.﹤19﹥=8, ﹤9﹥=4, ﹤1﹥=0,﹤19﹥×﹤9﹥+﹤1﹥=8×4+0=32, ﹤32﹥=11。
14.由已知x*m=x(m≠0),可令x=0,所以有0*m=bm=0。
∵m≠0,∴b=0。所以x*y=ax+-cxy。
再由1*2=3,2*3=4,得到a-2c=3,2a-6b=4,解得a=5,c=1。
所以x*y=5x-xy。
再令x=1,得1*m=1,得5-m=1,于是m=4。
3
61阅读提醒您本文地址:
三 : 数学f1初中数学新定义运算1
知识决定命运 百度提升自我
本文为自本人珍藏 版权所有 仅供参考
新定义运算
定义新运算是用某些特殊的符号,表示特定的意义,从而解答某些特殊算式的运算。(www.61k.com]在定义新运算中的※,〇,△……与+、-、×、÷是有严格区别的。解答定义新运算问题,必须先理解新定义的含义,遵循新定义的关系式把问题转化为一般的+、-、×、÷运算问题。
典型例题
例【1】 若A*B表示(A+3B)×(A+B),求5*7的值.
分析 A*B是这样结果这样计算出来:先计算A+3B的结果,再计算A+B的结果,最后两个结果求乘积。
解 由A*B=(A+3B)×(A+B)
可知:5*7=(5+3×7)×(5+7)
=(5+21)×12
=26×12
=312
例【2】 定义新运算为a△b=(a+1)÷b,求的值。6△(3△4)
分析 所求算式是两重运算,先计算括号,所得结果再计算。
解 由a△b=(a+1)÷b得,3△4=(3+1)÷4=4÷4=1;
6△(3△4)
=6△1
=(6+1)÷1
=7
例【3】 对于数a、b、c、d,规定,< a、b、c、d >=2ab-c+d,已知< 1、3、5、x >=7,求x的值。
分析 根据新定义的算式,列出关于x的等式,解出x即可。
解 将1、3、5、x代入新定义的运算得:2×1×3-5+x=1+x,又根据已知< 1、3、5、x >=7,故1+x=7,x=6。
例【4】 规定:符号“&”为选择两数中较大数的运算,“◎”为选择两数中较小数的运算。计算下式:[(7◎6)& 5]×[ 5◎(3 & 9)]
分析 新定义运算进行计算时如果遇到有括号的,要先计算小括号里的,再计算中括号里的。
解 [(7◎6)& 5]×[ 5◎(3 & 9)]
=[ 6 & 5] ×[ 5◎9 ]
=6×5
=30
1
定义新运算 数学f1初中数学新定义运算1
知识决定命运 百度提升自我
例【5】 如果1※2=1+11
2※3=2+22+222
3※4=3+33+333+333+3333
计算:(5※3)×5。[www.61k.com)
分析 通过观察发现:a※b中的b表示加数的个数,每个加数数位上的数字都由a组成,都由一个数位,依次增加到b个数位。
解 (5※3)×5。
=(5+55+555)×5
=3075
例【6】(2006?嘉兴).定义一种对正整数n的“F”运算:①当n为奇数时,结
果为3n+5;②当n为偶数时,结果为n(其中k是使n为奇数的正整数),2k2k
并且运算重复进行.例如,取n=26,则:
26 F② 第一次 13 F① 第二次 44 F② 第三次 11 ?
若n=449,则第449次“F运算”的结果是__________.
分析:本题提供的“F运算”,需要对正整数n分情况(奇数、偶数)循环计算,由于n=449为奇数应先进行F①运算,即3×449+5=1352(偶数),
需再进行F②运算,即1352÷23=169(奇数),
再进行F①运算,得到3×169+5=512(偶数),
再进行F②运算,即512÷29=1(奇数),
再进行F①运算,得到3×1+5=8(偶数),
再进行F②运算,即8÷23=1,
再进行F①运算,得到3×1+5=8(偶数),?,
即第1次运算结果为1352,?,
第4次运算结果为1,第5次运算结果为8,?,
可以发现第6次运算结果为1,第7次运算结果为8,
从第6次运算结果开始循环,且奇数次运算的结果为8,偶数次为1,而第499次是奇数,这样循环计算一直到第449次“F运算”,得到的结果为8. 故本题答案为:8.
练习题:
1. 设a,b表示两个不同的数,规定a?b?4?a?3?b.求(4?3)?2.
2. 定义运算“?”为x?y?2xy?(x?y).求12?(3?4).
3. 设a,b表示两个不同的数,规定a?b?3?a?2?b,如果已知4?b?2.求b. 2
定义新运算 数学f1初中数学新定义运算1
知识决定命运 百度提升自我
4. 定义新的运算a?b?a?b?a?b.求(1?2)?3.
5. 有一个数学运算符号“?”,使下列算式成立:2?4=10,5?3=18,3?5=14, 9?7=34.求7?3=?
6. 定义新运算为a?b?
a?1.求2?(3?4)的值. b
7. 对于数x,y规定运算“○”为x○y?(a?4)?(b?3).求7○(8○9)的值.
8. 设a?b表示a的3倍减去b的2倍,即a?b=3a?2b,已知x?(4?1)=7.求x.
9. 定义两种运算“?”、“?”,对于任意两个整数a,b,a?b?a?b?1,
a?b?a?b?1.计算4?[(6?8)?(3?5)]的值.
10. 对于数a,b规定运算“?”为a?b?(a?1)?(1?b),若等式(a?a)?(a?1) ?(a?1)?(a?a)成立,求a的值.
11. x,y表示两个数,规定新运算“※”及“○”如下:x※y?5x?4y,x○y?6xy.求(3※4)○5的值.
12. 设a,b分别表示两个数,如果a?b表示
5)]的结果是什么?
a?b,照这样的规则,3?[6?(8? 3
13. 规定x?y?
Ax?y,且5?6=6?5,求(3?2)×(1?10)的值. xy3
定义新运算 数学f1初中数学新定义运算1
知识决定命运 百度提升自我
14. 有一个数学运算符号“○”,使下列算式成立:12347115○?,○?,○236594561634?.求○的值. 742115
小结 解决新定义运算问题,首先理
解新定义符号的含义,严格按新的规则操作,在操作过程中,不能按原来+、-、×、÷运算法则合并使用,但可以根据不同的定义归纳出相对应的运算规律,因此解决新定义问题的关键是同学们对问题的理解及适应能力。[www.61k.com)
4
四 : 新定义运算
定 义 新 运 算
导言:
加、减、乘、除这四种运算的意义和运算法则,我们都很熟悉,在近年来竞赛中,出现了一种由一些新定义的运算符号导出的运算。即定义一些别的运算,如◎表示一种的运算,它是这样定义的:a◎b=a×b-(a+b),这种新运算的意义就是:a◎b是两个数的积减去两个数的和所得到的差。这就是定义新运算问题。这里所说的“定义”,就是按照规定的运算法则进行计算。解答这类问题的关键是理解新运算所表示的意义,严格按规定的计算法则代入计数,把定义新符号运算转化为熟悉的四则运算。这类题目目的是培养学生的数学阅读理解能力
例1.规定a★b=5a-3b,其中a、b是自然数,求
(1)6★8的值(2)8★6的值 (3)(3★2)★4(4)x★7=19
解析:此题规定了一种新运算符号(★),我们要理解它的意思,a★b表示a的5倍减去b的3倍,把表示a、b的数代入等式右边的(5a-3b)中,并算出结果来。
(1)此时,a=6,b=8,那么a★b=6★8=5×6-3×8=6
(2)此时,a=8,b=6,那么a★b=8★6=5×8-3×6=22
(3)在计算(3★2)★4时,运算的顺序是先算括号内的,再算括号外
(3★2)★4=(5×3-3×2)★4 =9★4=5×9-3×4=33
(4)x★7=19 即5x-3×7=195x-21=19 5x=40 x=8
例2.如果2♀3=2+3+4,5♀4=5+6+7+8,
求(1)9♀6的值(2)解方程:x♀3=15
解析:♀表示求连续自然数的和,♀前的数表示连续自然数的第一个数,♀后面的数表示连续自然数的个数
(1)9♀6=9+10+11+12+13+14=69
(2)x♀3=15 即x+(x+1)+(x+2)=15 解得x=4
例3.规定□的运算法则如下,对于任何整数a,b,有
(1)当a+b≥10时,a□b=2×a+b-1
(2)当a+b<10时,a□b=2×a×b
求(1□2)+(2□3)+(3□4)+(4□5)+(5□6)+(6□7)的值
解析:这道题实际上定义了两种运算,必须根据a、b两数的和的大小,来确定对它们施行哪种新运算。1□2、2□3、3□4、4□5这几个中,a、b的和都会小于10,运用(2)中的新运算,即a□b=2×a×b;而5□6、6□7这两个中,a、b的和大于10,运用(1)中的新运算,即a□b=2×a+b-1
所以,(1□2)+(2□3)+(3□4)+(4□5)+(5□6)+(6□7)
=2×1×2+2×2×3+2×3×4+2×4×5+(2×5+6-1)+(2×6+7-1)
=4+12+24+40+15+22=117
例4.有一个数字符号“※”使下列算式成立:6※2=12,4※3=13,3※4=15,5※1=8,按此规律计算:8※4的值
解析:仔细观察和分析这几个算式,可以发现:6※2=12=6+2×3,4※3=13=4+3×3,3※4=15=3+4×3,5※1=8=5+1×3,即符号※前面的数加上符号※后面数的三倍,a※b=a+3b。所以8※4=8+4×3=20
例5.小明来到红毛族探险,看到下面向个红毛族的算式:
8×8=8,9×9×9=5,9×3=3,(93+8)×7=837
老师告诉他,红毛族算术中所用的符号“+、-、×、÷、()、=”与我们算术中的意义相同,进位也是十进制,只是每个数字虽然与我们的写法相同,但代表的数却不同。
请你按红毛族的算术规则,完成下面算式:89×57=()
解析:对红毛族算式“8×8=8”的理解是:两个相同的数相乘,积还是这个数,说明算式中的“8”相当于我们的数字“1”或“0”;对红毛族算式“9×3=3”的理解是:一个数乘以另一个数,积还是另一个数,可推出红毛族算式中的“3”相当于我们的数字“0”,那么“8”相当于我们的数字“1”。对红毛族算式“9×9×9=5”的理解是:三个相同的数相乘,积还是一位数,说明算式中的“9”相当于我们的数字“2”算式中的“5”相当于我们的数字“8”。根据红毛族算式“(93+8)×7=837”我们很容易推出算式中的“7”相当于我们的数字“5”。
所以,红毛族的“89×57”换成我们的算式就是“12×85=1020”,再把我们的数字“1020”换成红毛族的数字就是“8393”,即89×57=8393
例6.有A、B、C、D四种计算装置,装置A:将输入的数乘以5;装置B:将输入的数加3;装置C:将输入的数除以4;装置D:将输入的数减6。这些装置可以连接,如装置A后面连连接装置B,写成A∮B,输入4,结果是24;装置B后面连接装置A,就写成B∮A,输入4,结果是35;
(1)装置A∮C∮D连接,输入19,结果是多少?
(2)装置D∮C∮B∮A连接,输入什么数字,可得结果96
解析:由“装置A后面连连接装置B,写成A∮B,输入4,结果是24”,我们可清楚24是怎么算出来的,24=4×5+3。即,输入一个数后,先进行前面装置的运算,运算结果再进行后一装置的运算。
(1)(19×5)÷4-6=17.75
(2)倒推法。(96÷5-3)×4+6=70.8
小结:正确理解新运算所表示的意义,严格按照规定的法则进行运算.这是正确解答这类问题最关键的思维
五 : 定义新运算:我们定义=ad-bc,例如=2×5-3×4=-2.则(填最后的结果).
定义新运算:我们定义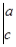 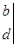 =ad-bc,例如 =ad-bc,例如 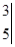 =2×5-3×4=-2. =2×5-3×4=-2.则 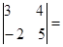 (填最后的结果). (填最后的结果). |
| 23 |
解:由题意得,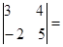 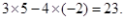 |
考点:
考点名称:有理数定义及分类有理数的定义:正数:
就是大于0的(实数)
负数:
就是小于0的(实数)
0既不是正数也不是负数。
非负数:正数与零的统称。
非正数:负数与零的统称。
正负数的认识:
1.对于正数和负数的概念,不能简单的理解为:带“+”号的数是正数,带“-”号的数是负数。
例如:-a一定是负数吗?
答案是不一定,因为字母a可以表示任意的数。
若a表示正数时,-a是负数;
当a表示0时,-a就是在0的前面加一个负号,仍是0,0不分正负;
当a表示负数时,-a就不是负数了,它是一个正数。
2.引入负数后,数的范围扩大为有理数,奇数和偶数的外延也由自然数扩大为整数,整数也可以分为奇数和偶数两类,能被2整除的数是偶数,
如…-6,-4,-2,0,2,4,6…,不能被2整除的数是奇数,如…-5,-4,-2,1,3,5…
3.数细分有五类:正整数、正分数、0、负整数、负分数;
但研究问题时,通常把有理数分为三类:正数、0、负数,进行讨论。
4.通常把正数和0统称为非负数,负数和0统称为非正数,正整数和0称为非负整数;
负整数和0统称为非正整数。
数轴的应用范畴:
符号相反的两个数互为相反数,零的相反数是零。(如2的相反—2)
在数轴上离开原点的距离就叫做这个数的绝对值。一个正数的绝对值是它本身,一个负数的相反数是它的正数,0的绝对值是0。
相反数的定义:
像2和-2,5和-5这样,只有符号不同的两个数叫做互为相反数。
相反数的几何意义:在数轴上到原点距离相等的两个点表示的两个数叫做互为相反数。
相反数的代数意义:如果两个数的和为零,其中一个数是另一个数的相反数,这两个数称为互为相反数。
相反数的特性:
1、若a,b互为相反数,则a+b=0; 反之,若a+b=0,则a,b互为相反数;
2、在数轴上,互为相反数(0除外)的两个点位于原点的两旁,并且关于原点对称;
3、此时,b的相反数为﹣b=﹣(﹣a)=a,那么我们就说“相反数具有互称性”。
4、相反数的规律:正数的相反数是负数,负数的相反数是正数,0的相反数是0。
5、相反数的表示方法:a的相反数是-a,-a的相反数是a;a-b的相反数是b-a,b-a的相反数是a-b;a+b的相反数是-(a+b),即-a-b。
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1