一 : 2.2数轴的三要素

2.2

学习目标： 数轴的三要素

1.进一步掌握数轴的三个要素，并正确画出数轴.

2.能利用数轴比较两个有理数的大小.

3.掌握在数轴上有理数是按照一定的顺序排列的，由数轴上两个数的位置关系，就可以判断 这两个数的大小关系。

4.深化对数轴的理解，体会数形结合的思想.

学习重点：

数轴上的已 知点说出它所表示的数，能将有理数用数轴上的点表示出来.

学习难点：

会利用数轴比较有理数的大小.

学习过程：

一、课前预习

1.自学课本17页到18页，有哪些疑惑？

2.数轴上离原点43.从数轴上观察，不小于－3而且不超过有( ) ．．．．．．4的正整数．．．

A.5个 B.6个 C.7个 D.8个

4.下面的说法错误的是（ ）

A.数轴上的点表示一个数 B.数轴上表示＋3的点只有一个

C.数轴上到原点的距离等于2个单位长度的点表示的数是2.

D.－5是可以用数轴上原点左边离原点5个单位长度的点表示.

5.设○,△,□表示三种不同的物体.用天平比较它们质量的大小，两次情况如图所示，那么○、△、□这三种物体按质量从大到小的顺序排列应为（ ）

第1页 二、自学、合作探究

（一）自学探究

1.课本17页议一议.

2.①数轴上，右边的点所表示的数总是大于左边的点所表示的数.

②正数大于零，零大于负数，正数大于一切负数.

3.课本18页例3.

4.课本18页例4.

（二）自学、相信自己

1.课本18页：练一练

2.课本19页：习题2.2 3、5、6.

(三）应用探究

1.在数轴上表示下列各数，并把它们按照从小到大的顺序排列： ．．．．

2，?

2.如图，数轴上一点，把点A向左移动3个单位长度到点B，把点A向右移动5个单位长度到点C.

⑴用“<”连结A、B、C三点表示的数；

⑵点B表示的数比点C表示的数大多少？

94，－1.5，0，?312

3.观察数轴，回答下列问题

（1）有没有最大或最小的整数？有没有最小的自然数？

（2）不小于－3的负整数有哪些？

（3）比－2小4的数是什么数？

（4）－3比－9大多少？

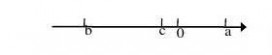
4.如图，根据有理数a,b,c在数轴上的位置，下列关系正确的是（ ）

A.b>c>0>a B.a>0>c>b C.b>a>c>0 D.c<0<a<b

2页

1.在数轴上表示的两个数，右边的数总比左边的大；

2.正数都大于零，负数都小于零，正数大于负数．

四、自我练习

A组

1.下列说法正确的是（ ）

A.0是最小的有理数

B.若有理数m>n，则数轴上表示m的点一 定在表示n的点的左边

C.一个有理数在数轴上表示的点离原点越远，这个有理数就越大

D.既没有最小的正数，也没有最大的负数

2.数a、b在数轴上的如下图所示，则下列判断中，正确的是( )

A.a>－1

B.b>1 C.a<－1 D.b<0 3.大于－2.6而又不大于3的整数有（ ）

A.7个 B.6个 C.5个 D.4个

4.用“＞”或“＜”填空：

(1)?3 (2)1

1011100 (3)0 ?10 (4) ?3.14.

5.观察数轴，能否找出符合下列要求的数：

(1)最大的正整数和最小的正整数；

(2)最大的负整数和最小的负整数；

(3)最大的整数和最小的整数；

(4)最小的正分数和最大的负分数．

B组

6.观察数轴，回答下列问题

（1）不超过3的自然数有哪些？

（2）比－3小5的数是什么？比－3大5的数是什么？

（3）－2和6的正中间的数是什么？

（4）－2比－8大多少？

第3页

7.如图，有三点，A、B、C，请回答：

（1）将点A向右移动4个单位长度后，三个点所表示的数谁最小？是多少？

（2）将点B向左移动3个单位长度后，三个点所表示的数谁最小？是多少？

（3）将点C向左移动5个单位长度后，这时点B表示的数比点C表示的数大还是小？

8.数轴上离开原点的距离小于3的整数点的个数为x，不大于3的整数点的个数为y，等于3的整数点的个数为z，求x+y+z的值.

9.数轴上的一个点表示一个数，当这个点 表示的是整数时，我们称它为整数点，如果有一条 数轴的单位长度是1cm时，有一条长2m的线段放在数轴上，它可以盖住整数点.

(1) 若2m.

（2）若2m的线段的两端点不与两个整数点重合，则它可盖住的整数点有 个.

五、学习札记

第4页

二 : 数轴的三要素为（）、（）、（）．

数轴的三要素为（）、（）、（）．

题型：填空题难度：偏易来源：月考题

原点；单位长度；正方向

考点：

考点名称：数轴数轴定义：
规定了唯一的原点，正方向和单位长度的一条直线叫做数轴。
数轴具有三要素：
原点、正方向和单位长度，三者缺一不可。
数轴是直线，可以向两方无限延伸，因此所有的有理数都可用数轴上的点来表示。用数轴上的点表示有理数：
每一个有理数都可用数轴上的点来表示，表示正数的点在数轴原点的右边，表示负数的点在数轴原点的左边，原点表示数0。
1.数轴上的点表示的数不一定都是有理数，还可能是无理数，但有理数都可用数轴上的点来表示。
2.表示正数的点都在原点右边，表示负数的点都在原点左边。
3.数轴上的点表示的数，右边的点表示的数总比左边的点表示的数大，因此，可借助数轴比较有理数的大小。
数轴的画法：
1.画一条直线（一般画成水平的直线）；
2.在直线上根据需要选取一点为原点（在原点下面标上“0”）；
3.确定正方向（一般规定向右为正，并用箭头表示出来）；
4.选取适当的长度为单位长度，
从原点向右，每隔一个单位长度取一点，依次表示1，2，3，…；
从原点向左，用类似的方法依次表示-1，-2，-3，…。

数轴的应用范畴:
符号相反的两个数互为相反数，零的相反数是零。（如2的相反—2）
在数轴上离开原点的距离就叫做这个数的绝对值。一个正数的绝对值是它本身，一个负数的相反数是它的正数，0的绝对值是0。

三 : 2.2数轴的三要素

2.2

学习目标： 数轴的三要素

1.进一步掌握数轴的三个要素，并正确画出数轴.

2.能利用数轴比较两个有理数的大小.

3.掌握在数轴上有理数是按照一定的顺序排列的，由数轴上两个数的位置关系，就可以判断 这两个数的大小关系。[www.61k.com]

4.深化对数轴的理解，体会数形结合的思想.

学习重点：

数轴上的已知点说出它所表示的数，能将有理数用数轴上的点表示出来.

学习难点：

会利用数轴比较有理数的大小.

学习过程：

一、课前预习

1.自学课本17页到18页，有哪些疑惑？

2.数轴上离原点43.从数轴上观察，不小于－3而且不超过有( ) ．．．．．．4的正整数．．．

A.5个 B.6个 C.7个 D.8个

4.下面的说法错误的是（ ）

A.数轴上的点表示一个数 B.数轴上表示＋3的点只有一个

C.数轴上到原点的距离等于2个单位长度的点表示的数是2.

D.－5是可以用数轴上原点左边离原点5个单位长度的点表示.

5.设○,△,□表示三种不同的物体.用天平比较它们质量的大小，两次情况如图所示，那么○、△、□这三种物体按质量从大到小的顺序排列应为（ ）

第1页 二、自学、合作探究

数轴三要素 2.2数轴的三要素

（一）自学探究

1.课本17页议一议.

2.①数轴上，右边的点所表示的数总是大于左边的点所表示的数.

②正数大于零，零大于负数，正数大于一切负数.

3.课本18页例3.

4.课本18页例4.

（二）自学、相信自己

1.课本18页：练一练

2.课本19页：习题2.2 3、5、6.

(三）应用探究

1.在数轴上表示下列各数，并把它们按照从小到大的顺序排列： ．．．．

2，?

2.如图，数轴上一点，把点A向左移动3个单位长度到点B，把点A向右移动5个单位长度到点C.

⑴用“<”连结A、B、C三点表示的数；

⑵点B表示的数比点C表示的数大多少？

94，－1.5，0，?312

3.观察数轴，回答下列问题

（1）有没有最大或最小的整数？有没有最小的自然数？

（2）不小于－3的负整数有哪些？

（3）比－2小4的数是什么数？

（4）－3比－9大多少？

4.如图，根据有理数a,b,c在数轴上的位置，下列关系正确的是（ ）

A.b>c>0>a B.a>0>c>b C.b>a>c>0 D.c<0<a<b

2页

数轴三要素 2.2数轴的三要素

1.在数轴上表示的两个数，右边的数总比左边的大；

2.正数都大于零，负数都小于零，正数大于负数．

四、自我练习

A组

1.下列说法正确的是（ ）

A.0是最小的有理数

B.若有理数m>n，则数轴上表示m的点一定在表示n的点的左边

C.一个有理数在数轴上表示的点离原点越远，这个有理数就越大

D.既没有最小的正数，也没有最大的负数

2.数a、b在数轴上的如下图所示，则下列判断中，正确的是( )

A.a>－1

B.b>1 C.a<－1 D.b<0 3.大于－2.6而又不大于3的整数有（ ）

A.7个 B.6个 C.5个 D.4个

4.用“＞”或“＜”填空：

(1)?3 (2)1

1011100 (3)0 ?10 (4) ?3.14.

5.观察数轴，能否找出符合下列要求的数：

(1)最大的正整数和最小的正整数；

(2)最大的负整数和最小的负整数；

(3)最大的整数和最小的整数；

(4)最小的正分数和最大的负分数．

B组

6.观察数轴，回答下列问题

（1）不超过3的自然数有哪些？

（2）比－3小5的数是什么？比－3大5的数是什么？

（3）－2和6的正中间的数是什么？

（4）－2比－8大多少？

第3页

数轴三要素 2.2数轴的三要素

7.如图，有三点，A、B、C，请回答：

（1）将点A向右移动4个单位长度后，三个点所表示的数谁最小？是多少？

（2）将点B向左移动3个单位长度后，三个点所表示的数谁最小？是多少？

（3）将点C向左移动5个单位长度后，这时点B表示的数比点C表示的数大还是小？

8.数轴上离开原点的距离小于3的整数点的个数为x，不大于3的整数点的个数为y，等于3的整数点的个数为z，求x+y+z的值.

9.数轴上的一个点表示一个数，当这个点表示的是整数时，我们称它为整数点，如果有一条 数轴的单位长度是1cm时，有一条长2m的线段放在数轴上，它可以盖住整数点.

(1) 若2m.

（2）若2m的线段的两端点不与两个整数点重合，则它可盖住的整数点有 个.

五、学习札记

第4页

四 : 数轴的三要素为（）、（）、（）．

数轴的三要素为（）、（）、（）．

题型：填空题难度：偏易来源：月考题

原点；单位长度；正方向

考点：

考点名称：数轴数轴定义：
规定了唯一的原点，正方向和单位长度的一条直线叫做数轴。
数轴具有三要素：
原点、正方向和单位长度，三者缺一不可。
数轴是直线，可以向两方无限延伸，因此所有的有理数都可用数轴上的点来表示。用数轴上的点表示有理数：
每一个有理数都可用数轴上的点来表示，表示正数的点在数轴原点的右边，表示负数的点在数轴原点的左边，原点表示数0。
1.数轴上的点表示的数不一定都是有理数，还可能是无理数，但有理数都可用数轴上的点来表示。
2.表示正数的点都在原点右边，表示负数的点都在原点左边。
3.数轴上的点表示的数，右边的点表示的数总比左边的点表示的数大，因此，可借助数轴比较有理数的大小。
数轴的画法：
1.画一条直线（一般画成水平的直线）；
2.在直线上根据需要选取一点为原点（在原点下面标上“0”）；
3.确定正方向（一般规定向右为正，并用箭头表示出来）；
4.选取适当的长度为单位长度，
从原点向右，每隔一个单位长度取一点，依次表示1，2，3，…；
从原点向左，用类似的方法依次表示-1，-2，-3，…。

数轴的应用范畴:
符号相反的两个数互为相反数，零的相反数是零。（如2的相反—2）
在数轴上离开原点的距离就叫做这个数的绝对值。一个正数的绝对值是它本身，一个负数的相反数是它的正数，0的绝对值是0。

五 : 数轴的三要素为（）、（）、（）．

数轴的三要素为（）、（）、（）．

题型：填空题难度：偏易来源：月考题

原点；单位长度；正方向

考点：

考点名称：数轴数轴定义：
规定了唯一的原点，正方向和单位长度的一条直线叫做数轴。
数轴具有三要素：
原点、正方向和单位长度，三者缺一不可。
数轴是直线，可以向两方无限延伸，因此所有的有理数都可用数轴上的点来表示。用数轴上的点表示有理数：
每一个有理数都可用数轴上的点来表示，表示正数的点在数轴原点的右边，表示负数的点在数轴原点的左边，原点表示数0。
1.数轴上的点表示的数不一定都是有理数，还可能是无理数，但有理数都可用数轴上的点来表示。
2.表示正数的点都在原点右边，表示负数的点都在原点左边。
3.数轴上的点表示的数，右边的点表示的数总比左边的点表示的数大，因此，可借助数轴比较有理数的大小。
数轴的画法：
1.画一条直线（一般画成水平的直线）；
2.在直线上根据需要选取一点为原点（在原点下面标上“0”）；
3.确定正方向（一般规定向右为正，并用箭头表示出来）；
4.选取适当的长度为单位长度，
从原点向右，每隔一个单位长度取一点，依次表示1，2，3，…；
从原点向左，用类似的方法依次表示-1，-2，-3，…。

数轴的应用范畴:
符号相反的两个数互为相反数，零的相反数是零。（如2的相反—2）
在数轴上离开原点的距离就叫做这个数的绝对值。一个正数的绝对值是它本身，一个负数的相反数是它的正数，0的绝对值是0。

本文标题：数轴的三要素-2.2数轴的三要素
本文地址： http://www.61k.com/1146876.html