一 : 有理数的混合运算习题精选

有理数的混合运算典型例题

例1 计算： ．

,

, 分析：此算式以加、减分段, 应分为三段：．这三段可以同时进行计算，先算乘方，再算乘除．式中－0.2

化为 参加计算较为方便．

解：原式

说明：做有理数混合运算时，如果算式中不含有中括号、大括号，那么计算时一般用“加”、“减”号分段，使每段只含二、三级运算，这样各段可同时进行计算，有利于提高计算的速度和正确率．

例2 计算： ．

分析：此题运算顺序是：第一步计算

三步做乘方运算；第四步做除法． 和

；第二步做乘法；第

解：原式

1

说明：由此例题可以看出，括号在确定运算顺序上的作用，所以计算题也需认真审题．

例3 计算：

分析：要求 、 、 的值，用笔算在短时间内是不可能的，必须

，逆用乘法分配律，另辟途径．观察题目发现，，

前三项可以凑成含有0的乘法运算，此题即可求出．

解：原式

说明：“0”乘以任何数等于0．因为运用这一结论必能简化数的计算，所以运算中，能够凑成含“0”因数时，一般都凑成含有0的因数进行计算．当算式中的数字很大或很繁杂时，要注意使用这种“凑0法”．

例4 计算

分析：

是 的倒数，应当先把它化成分数后再求倒数；右边两项含绝对值号，应当先计算出绝对值的算式的结果再求绝对值．

解：原式

2

说明：对于有理数的混合运算，一定要按运算顺序进行运算，注意不要跳步，每一步的运算结果都应在算式中体现出来，此题(1)要注意区别小括号与绝对值的运算；(2)要熟练掌握乘方运算，注意(-0.1)3，-0.22，(-2)3，-32在意义上的不同．

例5 计算：

．

分析：含有括号的混合运算，一般按小、中、大括号的顺序进行运算，括号里面仍然是先进行第三级运算，再进行第二级运算，最后进行第一级运算． 解：原式

例6 计算

解法一：原式

解法二：原式

说明：加减混合运算时，带分数可以化为假分数，也可把带分数的整数部分与分数部分分别加减，这是因为带分数是一个整数和一个分数的和.

例如：

3

有理数的混合运算习题精选

一、选择题

1．若

A．

2．已知

是( ) ．

A． ， B． ，则有( ) ． C． ，当 D． 时， ，当 时， 的值 B．44C．28 D．17

，那么 的值为( ) ． 3．如果

A．0B．4C．－4D．2

4．代数式

A． B． 取最小值时， 值为( ) ． C． D．无法确定

，

互不相等，则 5．六个整数的积

( ) ．

A．0 B．4C．6D．8

6．计算

A．2B．

二、填空题 C． 所得结果为( ) ． D．

1．有理数混合运算的顺序是__________________________．

2．已知 为有理数，则 _________0，

_______0．（填“＞”、“＜”或“≥”＝） _________0，

3．平方得16的有理数是_________，_________的立方等于－8．

4． __________.

4

5．一个负数减去它的相反数后，再除以这个负数的绝对值，所得商为__________．

三、判断题

1．若 为任意有理数，则

2．

.( ) ．( )

3． ．( )

4． ．()

5．

．( )

四、解答题

1．计算下列各题：

（1） ；

（2） ；

（3） ；

（4） ；

（5） ；

（6）

；

（7） ；

5

（8） ．

2．若有理数 、 、 满足等式

的值．

3．当 ， 时，求代数式

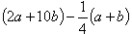
的值．

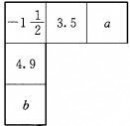
4．已知如图2-11-1，横行和竖列的和相等，试求

5．求 的值．

6．计算 ．

计算：

6 ，试求 的值．

有理数的混合运算参考答案：

一、1．C 2．C 3．C 4．B 5．A 6．B

二、1．略；2．≥，＞，＜；3． ， ；4．1；5． ． 三、1．× 2．× 3．√ 4．× 5．√

四、1．（1）

（8）

3． ; （2） （3） ； 2．∵ ， （4） ， （5）30（6） ∴ （7

） ；

4．

5．设 ， ，则 ， ; ， ;

6．原式

.

7

二 : 有理数的混合运算经典习题

有理数混合运算的方法技巧

一、理解运算顺序

有理数混合运算的运算顺序：

①从高级到低级：先算乘方，再算乘除，最后算加减；

有理数的混合运算涉及多种运算，确定合理的运算顺序是正确解题的关键

例1：计算：3＋50÷22×(?)－1

②从内向外：如果有括号，就先算小括号里的，再算中括号里的，最后算大括号里的.

1?2例2：计算：?1????1?0.5?????2???3? ??3????15??

③从左向右：同级运算，按照从左至右的顺序进行；

37例3：计算：??1????487??7??8?????????????? 12???8??3?

二、应用四个原则：

1、整体性原则： 乘除混合运算统一化乘，统一进行约分；加减混合运算按正负数分类，分别统一计算，或把带分数的整数、分数部分拆开，分别统一计算。

2、简明性原则：计算时尽量使步骤简明，能够一步计算出来的就同时算出来；运算中尽量运用简便方法，如五个运算律的运用。

3、口算原则：在每一步的计算中，都尽量运用口算，口算是提高运算率的重要方法之一，习惯于口算，有助于培养反应能力和自信心。

4、分段同时性原则： 对一个算式，一般可以将它分成若干小段，同时分别进行运算。如何分段呢?主要有：(1)运算符号分段法。有理数的基本运算有五种：加、减、乘、除和乘方，其中加减为第一级运算，乘除为第二级运算，乘方为第三级运算。在运算中，低级运算把高级运算分成若干段。 一般以加号、减号把整个算式分成若干段，然后把每一段中的乘方、乘除的结果先计算出来，最后再算出这几个加数的和．

把算式进行分段，关键是在计算前要认真审题，妥用整体观察的办法，分清运算符号，确定整个式子中有几个加号、减号，再以加减号为界进行分段，这是进行有理数混合运算行之有效的方法．

(2)括号分段法，有括号的应先算括号里面的。在实施时可同时分别对括号内外的算式进行运算。

(3)绝对值符号分段法。绝对值符号除了本身的作用外，还具有括号的作用，从运算顺序的角度来说，先计算绝对值符号里面的，因此绝对值符号也可以把算式分成几段，同时进行计算．

(4)分数线分段法，分数线可以把算式分成分子和分母两部分并同时分别运算。

14210122例2计算：-0.25÷(－ )-(-1)＋(-2)×(-3) 2

说明：本题以加号、减号为界把整个算式分成三段，这三段分别计算出来的结果再相加。

三、掌握运算技巧

（1）、归类组合：将不同类数(如分母相同或易于通分的数)分别组合；将同类数(如正数或负数)归类计算。

（2）、凑整：将相加可得整数的数凑整，将相加得零的数（如互为相反数）相消。

（3）、分解：将一个数分解成几个数和的形式,或分解为它的因数相乘的形式。

（4）、约简：将互为倒数的数或有倍数关系的数约简。

（5）、倒序相加：利用运算律，改变运算顺序,简化计算。

例 计算2+4+6+?+2000

（6）、正逆用运算律：正难则反, 逆用运算定律以简化计算。

乘法分配律a(b+c)=ab+ac在运算中可简化计算．而反过来，ab+ac=a(b+c)同样成立，有时逆用也可使运算简便.

例3计算：

16123112(1) -32 ÷(-8×4)+2.5+(－－ )×24 2523412

311313314 (2)(－)×(－－×(－ )＋×(215215215

四、理解转化的思想方法

有理数运算的实质是确定符号和绝对值的问题。

因此在运算时应把握“遇减化加．遇除变乘，乘方化乘”，这样可避免因记忆量太大带来的一些混乱，同时也有助于学生抓住数学内在的本质问题。

把我们所学的有理数运算概括起来。可归纳为三个转化：

一个是通过绝对值将加法、乘法在先确定符号的前提下，转化为小学里学的算术数的加法、乘法；

二是通过相反数和倒数分别将减法、除法转化为加法、乘法；

三是将乘方运算转化为积的形式．

若掌握了有理数的符号法则和转化手段，有理数的运算就能准确、快速地解决了． 例计算：

（1） (-6)-(+5)+(-9)+(-4)-(-9)

11(2) (-2 )÷1×(-4) 24

122(3)2+(2-5)× ×[1-(-5)] 3

六、会用三个概念的性质

如果a．b互为相反数，那么a+b=O，a= -b；

如果c，d互为倒数，那么cd=l，c=1/d；

如果|x|=a(a＞0)，那么x=a或-a.

例6 已知a、b互为相反数，c、d互为倒数，x的绝对值等于2，试求x2-(a+b+cd)x+(a+b)2000+(-cd)2001的值

有理数的混合运算习题

一．选择题

1. 计算(?2?5)?（ ）

A.1000 B.－1000 C.30

2. 计算?2?3?(?2?3)?( )

A.0 B.－54 C.－72

3. 计算?(?5)?(?)?5?

A.1 B.25 C.－5

4. 下列式子中正确的是（ ）

A.?2?(?2)?(?2)

C. ?2?(?2)?(?2)

42432423223D.－30 D.－18 1515D.35 342B. (?2)??2?(?2) D. (?2)?(?3)??2

D.－2 2345. ?2?(?2)的结果是（ ） A.4 B.－4 C.2

26. 如果a?1?0,(b?3)?0，那么

A.－2

三.计算题

2b?1的值是（ ） aB.－3 C.－4 D.4 1. ?(?3)?2 2.

3. (?1.5)?4

12411?(?)??(?)?(?) 2352311?2.75?(?5) 4. ?8?(?5)?63 42

5. 4?5?(?) 6. (?)?(?)?(?4.9)?0.6

7. (?10)?5?(?) 8. (?5)?(?)

21232556253352

9. 5?(?6)?(?4)?(?8) 10. 2?(?)?(?2)

11.(?16?50?3)?(?2) 12. (?6)?8?(?2)?(?4)?5

13. (?)?

15. ??[?3?(?)?2] 16. (?)?(?

17. ?14?(1?0.5)??[2?(?3)2] 18. (?81)?(?2.25)?(?)?16

?5?[?4?(1?0.2?)?(?2)] 20. (?5)?(?3)?(?7)?(?3)?12?(?3)

(?)?(?4)?0.25?(?5)?(?4) 22. (?3)?(1)?

2

2

146712

25

32

12

2

1221?(??2) 14. ?11997?(1?0.5)? 2333

32

2

23

2

34

2

2

?1)?0 3

1349

15676767

58

232

12

3

22?6?? 93

三 : 有理数的混合运算习题精选

有理数的混合运算典型例题

例1 计算： ．

,

, 分析：此算式以加、减分段, 应分为三段：．这三段可以同时进行计算，先算乘方，再算乘除．式中－0.2

化为 参加计算较为方便．

解：原式

说明：做有理数混合运算时，如果算式中不含有中括号、大括号，那么计算时一般用“加”、“减”号分段，使每段只含二、三级运算，这样各段可同时进行计算，有利于提高计算的速度和正确率．

例2 计算： ．

分析：此题运算顺序是：第一步计算

三步做乘方运算；第四步做除法． 和

；第二步做乘法；第

解：原式

1

有理数的混合运算习题 有理数的混合运算习题精选

说明：由此例题可以看出，括号在确定运算顺序上的作用，所以计算题也需认真审题．

例3 计算：

分析：要求 、 、 的值，用笔算在短时间内是不可能的，必须

，逆用乘法分配律，另辟途径．观察题目发现，，

前三项可以凑成含有0的乘法运算，此题即可求出．

解：原式

说明：“0”乘以任何数等于0．因为运用这一结论必能简化数的计算，所以运算中，能够凑成含“0”因数时，一般都凑成含有0的因数进行计算．当算式中的数字很大或很繁杂时，要注意使用这种“凑0法”．

例4 计算

分析：

是 的倒数，应当先把它化成分数后再求倒数；右边两项含绝对值号，应当先计算出绝对值的算式的结果再求绝对值．

解：原式

2

有理数的混合运算习题 有理数的混合运算习题精选

说明：对于有理数的混合运算，一定要按运算顺序进行运算，注意不要跳步，每一步的运算结果都应在算式中体现出来，此题(1)要注意区别小括号与绝对值的运算；(2)要熟练掌握乘方运算，注意(-0.1)3，-0.22，(-2)3，-32在意义上的不同．

例5 计算：

．

分析：含有括号的混合运算，一般按小、中、大括号的顺序进行运算，括号里面仍然是先进行第三级运算，再进行第二级运算，最后进行第一级运算． 解：原式

例6 计算

解法一：原式

解法二：原式

说明：加减混合运算时，带分数可以化为假分数，也可把带分数的整数部分与分数部分分别加减，这是因为带分数是一个整数和一个分数的和.

例如：

3

有理数的混合运算习题 有理数的混合运算习题精选

有理数的混合运算习题精选

一、选择题

1．若

A．

2．已知

是( ) ．

A． ， B． ，则有( ) ． C． ，当 D． 时， ，当 时， 的值 B．44C．28 D．17

，那么 的值为( ) ． 3．如果

A．0B．4C．－4D．2

4．代数式

A． B． 取最小值时， 值为( ) ． C． D．无法确定

，

互不相等，则 5．六个整数的积

( ) ．

A．0 B．4C．6D．8

6．计算

A．2B．

二、填空题 C． 所得结果为( ) ． D．

1．有理数混合运算的顺序是__________________________．

2．已知 为有理数，则 _________0，

_______0．（填“＞”、“＜”或“≥”＝） _________0，

3．平方得16的有理数是_________，_________的立方等于－8．

4． __________.

4

有理数的混合运算习题 有理数的混合运算习题精选

5．一个负数减去它的相反数后，再除以这个负数的绝对值，所得商为__________．

三、判断题

1．若 为任意有理数，则

2．

.( ) ．( )

3． ．( )

4． ．()

5．

．( )

四、解答题

1．计算下列各题：

（1） ；

（2） ；

（3） ；

（4） ；

（5） ；

（6）

；

（7） ；

5

有理数的混合运算习题 有理数的混合运算习题精选

（8） ．

2．若有理数 、 、 满足等式

的值．

3．当 ， 时，求代数式

的值．

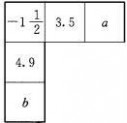
4．已知如图2-11-1，横行和竖列的和相等，试求

5．求 的值．

6．计算 ．

计算：

6 ，试求 的值．

有理数的混合运算习题 有理数的混合运算习题精选

有理数的混合运算参考答案：

一、1．C 2．C 3．C 4．B 5．A 6．B

二、1．略；2．≥，＞，＜；3． ， ；4．1；5． ． 三、1．× 2．× 3．√ 4．× 5．√

四、1．（1）

（8）

3． ; （2） （3） ； 2．∵ ， （4） ， （5）30（6） ∴ （7

） ；

4．

5．设 ， ，则 ， ; ， ;

6．原式

.

7

本文标题：有理数的混合运算习题-有理数的混合运算习题精选
本文地址： http://www.61k.com/1114076.html