一 : 第一册等腰三角形
(一)、温故知新,激发情趣:
1、轴对称图形的有关概念,什么样的三角形叫做等腰三角形?
2、指出等腰三角形的腰、底边、顶角、底角。
(首先教师提问了解前置知识掌握情况,学生动脑思考、口答。)
(二) 、构设悬念,创设情境:
3、一般三角形有哪些特征? (三条边、三个内角、高、中线、角平分线)
4、等腰三角形除具有一般三角形的特征外,还有那些特殊特征?
(把问题3作为教学的出发点,激发学生的学习兴趣。问题4给学生留下悬念。)
(三)、目标导向,自然引入:
本节课我们一起研究——9.3 等腰三角形
(板书课题) 9.3 等腰三角形(了解本节课的学习内容)
(四)、设问质疑,探究尝试:
结合问题4请同学们拿出准备好的不同规格的等腰三角形,与教师一起演示(模型)等腰三角形是轴对称图形的实验,引导学生观察实验现象。
[问题]通过观察,你发现了什么结论?
(让学生由实验或演示指出各自的发现,并加以引导,用规范的数学语言进行逐条归纳,最后得出等腰三角形的特征)
[结论]等腰三角形的两个底角相等。
(板书学生发现的结论)
等腰三角形特征1:等腰三角形的两个底角相等
在△ ABC中,∵AB=AC( )
∴∠B=∠C( )
[方法]可由学生从多种途径思考,纵横联想所学知识方法,为命题的证明打下基础。
例1:已知:在△ABC中,AB=AC,∠B=80°,求∠C和∠A的度数。
〔学生思考,教师分析,板书〕
练习思考:课本P84 练习2(等腰三角形的底角可以是直角或钝角吗?为什么?)
〔继续观察实验纸片图形〕(以下内容学生可能在前面实验中就会提出)
[问题]纸片中的等腰三角形的对称轴可能是我们以前学习过的什么线?
(通过设问、质疑、小组讨论,归纳总结,培养学生概括数学问题的能力)
[引导学生观察]折痕AD是等腰三角形的对称轴,AD可能还是等腰三角形的什么线?
[学生发现]AD是等腰三角形的顶角平分线、底边中线、底边上的高.
[结论]等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合.简称为:“三线合一”。
等腰三角形特征2:
等腰三角形的顶角平分线、底边上的中线和高线互相重合(三线合一)
(出示小黑板)
[填空]根据等腰三角形特征的推论,在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠_=∠_,_=_;
(2)∵AB=AC,AD是中线,
∴∠_=∠_,_⊥_;
(3)∵AB=AC,AD是角平分线,
∴_⊥_,_=_
通过直观模具演示,引出推论2,并出示小黑板[填空]、强调“三线合一”的运用方法。使学生留下深刻印象,并通过[填空]了解三线合一的运用方法。
强调“三线合一”特征中的三线段前的定语的重要性,可让学生实际画图验证。
(五)、启发诱导,初步运用:
例2:如图,在△ABC中,AB=AC,D是BC边上的中点,
∠B=30°,求∠1和∠ADC的度数。
课堂练习:
(1)P85练习3
(2)例3已知:如图,房屋的顶角∠BAC=100°,过屋顶A的立柱AD⊥BC、屋椽AB=AC.求顶架上∠B、∠C、∠BAD、∠CAD的度数.
(这是一道几何计算题,要使学生加深对本课内容的应用,引导学生写出解题过程)
(六)、归纳小结,强化思想:
(1)叙述等腰三角形的特征及其应用;
(2)利用等腰三角形的特征可证明:两角相等,两线段相等,两直线互相垂直。
(3) 联想方法要经常运用,对今后解题大有裨益。
(七)、布置作业 ,引导预习:
P86 习题9.3 1、3、4 预习课本:P85 等腰三角形
课后思考题:等腰三角形两腰上的中线(高线)是否相等?为什么?
二 : 2014等腰三角形三线合一专项综合练习
北师大版七下数学等腰三角形相关练习
1、已知?ABC的周长为36cm,且AB?AC,又AD?BC,D为垂足,?ABD的周长为30cm,那么AD的长为( )
A.6cm B. 8cm C. 12cm D. 20cm
02.如图2,在△ABC中,AB=AC,∠BAD=30,AD=AE,则∠EDC=( )
0000A.10 B. 12.5 C.15 D.20
C 第3题图
第4题图 F D C 第2题图
3、如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB于E,DF⊥AC于F,则图中全等三角形
共有( )
A. 2对 B、3对 C、4对 D、5对
4 、如图,在等腰直角△ABC中,AD为斜边上的高,以D为端点任作两条互相垂直的射线与两腰相
交于E、F,连结EF与AD相交于G,则∠AED与∠AGF的关系为( )
A.∠AED>∠AGF B.∠AED=∠AGF C.∠AED<∠AGF D.不能确定
5、如图,在△ABC中,AB=AC,BD平分∠ABC,且BD=BE,∠A=84°,则∠DEC=
6、如图,CE平分∠ACB,且CE⊥BD,DA=DB,又知AC=18,△CDB的周长为28,那么BE的长为 。[www.61k.com] C 第5题图 B 第7题图 F C 第6题图
7、如图,在等腰△ABC中,∠ABC=90°,D为AC边上中点,过D点作DE⊥DF,交AB于E,交
BC于F,若AE=4,FC=3,则△ABC的面积为
8、、如图,四边形ABCD中,对角线AC与BD相交于E点,若AC平分∠DAB,且AB=AE,AC=AD,有如下四个结论:①AC⊥BD;②BC=DE;③∠DBC=1∠DAB; 2
④△ABE是等边三角形.请写出正确结论的序号 .
9、已知:如图2,△ABC中,AB=AC,CE⊥AE于E,CE?
E在△ABC外,求证:∠ACE=∠B。
10
、如图△ABC中,AB=AC D为AC上任意一点,延长BA到E,使得AE=AD
1
A1BC, 2题8 E
A B D
等腰三角形三线合一 2014等腰三角形三线合一专项综合练习
连接DE,求证DE⊥BC
11、已知:如图1,△ABC中,AB=AC,D是BC上一点,E、F分别为AB、AC上的点,且BD=CF,CD=BE,G为EF的中点,求证:DG⊥EF.
12、如图,以△ABC的边AB,AC为边分别向形外作正方形ABDE和ACFG,DM、FN分别垂直直线BC于M、N.若∠BDM=∠CFN,求证: ∠ABC=∠ACB
2 EADGFMBCN
等腰三角形三线合一 2014等腰三角形三线合一专项综合练习
13.. 已知,如图1,AD是?ABC的角平分线,DE、DF分别是?ABD和?ACD的高。[www.61k.com) 求证:AD垂直平分EF
A
E
F
B D C
图1 14.已知AB=AC,BD=DC,AE平分∠FAB,问:AE与AD是否垂直?为什么?
15.如图,已知:△ABC中,BC<AC,AB边上的垂直平分线DE交AB于D,交AC于E,AC=9 cm,
△
BCE的周长为15 cm,求BC的长.
C
D
B
F
E
16.如图所示,在等边三角形ABC中,∠B、∠C的平分线交于点O,OB和OC的垂直平分线交BC
于E、F,试用你所学的知识说明BE=EF=FC的道理.
3
B
C
等腰三角形三线合一 2014等腰三角形三线合一专项综合练习
17.已知AB=AC,D是AB上一点,DE⊥BC于E,ED的延长线交CA的延长线于F,试说明△ADF是等腰三角形的理由.
18.等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试说明你的结论.
C E B D F
19. 如图,Rt△ABC中,∠ACB=90°,D是AB上一点,且BD=BC。(www.61k.com]DE⊥AB交AC于E。
求证:CD⊥BE。
O
4
等腰三角形三线合一 2014等腰三角形三线合一专项综合练习
20.如图,已知∠A=300,∠B=400,∠1=950,求∠D的度数。[www.61k.com)
D
A B E
21. 已知a、b、c是三角形的三边,且满足a2+b2+c2-ab-bc-ca=0.试判断三角形的形状.
22.如图所示,在ABC△中,已知∠ABC=660,∠ACB=540,BE是AC边上的高,CF是AB边上的高,H是BE和CF的交点.求∠ABE,∠ACF和∠
BHC.
5
三 : 怎么证明 等腰三角形三线合一
怎么证明 等腰三角形三线合一
等腰三角形"三线合一"是指等腰三角形底边的高,底边的中线和顶角的平分线互相重合.
【利用三角形全等的知识可以证明这个结论.】
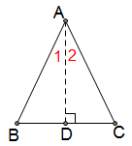
已知:如图,⊿ABC中,AB=AC.
求证:BC边的中线,高,以及∠BAC的平分线互相重合.
证明:作AD⊥BC于D.
∵AB=AC(已知);
AD=AD(公共边相等).
∴Rt⊿BAD≌Rt⊿CAD(HL).
∴BD=CD;∠1=∠2.
故:BC边的高AD也是底边的中线,也是顶角∠BAC的平分线.
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1