一 : 模糊数学分析方法

模糊数学分析方法
本章学习要点 在教育技术研究中具有许多不确定因素, 在教育技术研究中具有许多不确定因素,通常是指随机性和模糊性，其中模糊性 表现为客观事物在类属、性态方面定义的不精确和不明晰，它与精确性相对。要描述 对象的模糊性特征，就需要运用模糊数学，通过模糊数学分析，实现由模糊向精确的 转化。本章中介绍了模糊数学分析的基本概念；具体论述了在模糊数学分析中隶属函 数的确定以及模糊关系与模糊矩阵的确定；详细说明了模糊综合评判方法和模糊聚类 分析方法。 通过本章的学习，应了解模糊数学分析的基本概念，明确隶属函数的分布统计求 法、对比平均求法和模糊统计法，掌握模糊关系矩阵的运算、模糊关系的合成以及模 糊关系合成图解法的使用，能够熟练的运用模糊综合评判方法和模糊聚类分析方法分 析解决教育技术研究中的具体问题。 本章内容结构
模糊数学分 析的基概念 教育技术研究中的不确定性 普通集合及其特征函数 模糊集合及其隶属函数 隶属函数的分布统计求法 【文章窝】对比平均法求隶属函数 模糊统计法求隶属函灵敏 模糊关系与 模糊矩阵 模糊关系 模糊矩阵 模糊关系矩阵的运算 模糊关系的合成 模糊关系合成图解法 模糊变换 模糊综合评判的原理 模糊综合评判应用实例模糊综合评判应用实例-网络课程评价 模糊聚类分析基本原理 模糊等价矩阵聚类法 最大树法

隶属函数 的确定

模糊综合 评判方法

模糊聚类 分析方法

第一节 模糊数学分析的基本概念
在自然科学或社会科学研究中, 在自然科学或社会科学研究中,存在着许多定义不很严格或者说具有模糊性的概念。这里 所谓的模糊性，主要是指客观事物的差异在中间过渡中的不分明性，如某一生态条件对某种害虫、 某种作物的存活或适应性可以评价为“有利、比较有利、不那么有利、不利”；灾害性霜冻气候 对农业产量的影响程度为“较重、严重、很严重”，等等。这些通常是本来就属于模糊的概

念，为处理分析这些“模糊” 念，为处理分析这些“模糊”概念的数据，便产生了模糊集合论。
根据集合论的要求，一个对象对应于一个集合，要么属于，要么不属于，二者必居其一， 且仅居其一。这样的集合论本身并无法处理具体的模糊概念。为处理这些模糊概念而进行的种种 努力，催生了模糊数学。模糊数学的理论基础是模糊集。模糊集的理论是1965年美国自动控制专 努力，催生了模糊数学。模糊数学的理论基础是模糊集。模糊集的理论是1965年美国自动控制专 家查德(L. 家查德(L. A. Zadeh)教授首先提出来的，近10多年来发展很快。 Zadeh)

教授首先提出来的，近10多年来发展很快。 模糊集合论的提出虽然较晚，但目前在各个领域的应用十分广泛。实践证明，模糊数学 在农业中主要用于病虫测报、种植区划、品种选育等方面，在图像识别、天气预报、地质地震、 交通运输、医疗诊断、信息控制、人工智能等诸多领域的应用也已初见成效。从该学科的发展趋 势来看，它具有极其强大的生命力和渗透力。

一、教育技术研究中的不确定性 （一） 教育技术研究中具有许多不确定性因素，这些不确定性因素来源主要有如下
几个方面： 1、研究对象活动出现条件的不确定性，具有概率的特征。 2、研究对象类属的边界具有不清晰和性态不确定的特征。 3、研究对象信息显示的不充分及其无序性所导致的不清晰特征。 4、研究中使用的某些概念、命题在语言语义上的多义与歧义导致的不确定性。 5、某些数学运算、逻辑推理误差所导致的不确定性。 6、描述对象的内涵和外延与对象称谓之间的不贴切，词不达意所导致的不确定。

（二）各种不确定因素可分为两类：
1、随机性。特征：关于对象在类属和性态方面的定义是完全确定的，但对象出 现的条件方面是概率的、不确定的。和必然性相对。 2、模糊性。特征：表征对象在认识中的分辨界限是不确定的，即对象在类属、 性态方面的定义是不精确的、不明晰的。和精确性相对。
客观事物 以事物出现的 条件为依据 数理统计

确 定 性

必 然 性

随 机 性

精 确 性

模糊数学

不 确 定 性

以事物性态、类 属边界为判据

模 糊 性

随机性与模糊性的关系

二、普通集合及其特征函数 1、集合的基本概念
论域，被讨论对象的全体叫做论域，对称全域，通常用大写字母U 论域，被讨论对象的全体叫做论域，对称全域，通常用大写字母U、E、X、Y等 来表示。 元素 ，组成某一集合的单个对象就称为该集合的一个元素，通常用小写字母表 元素，组成某一集合的单个对象就称为该集合的一个元素，通常用小写字母表 示。 子集，由同一集合中的部分元素组成一个新集合，称为原集合的一个子集，通 子集，由同一集合中的部分元素组成一个新集合，称为原集合的一个子集，通 常用大写字母表示。 集合的表示方法，把集合中的全部元素列出，并用括事情把它们括起来表示集 集合的表示方法，把集合中的全部元素列出，并用括事情把它们括起来表示集 合的全域。

2、集合的基本运算 并集、交集、差集、补集。 三、模糊集合及其隶属函数 1、模糊集合：无明确边界的集合。 2、模糊集合的特点：把原来普通集合对类属、性态的非此即彼的绝对属于 或

不属于的判定，转化为对类属、性态做从0 或不属于的判定，转化为对类属、性态做从0互1不同程度的相对判定。 3、隶属函数：为了将普通集合与模糊集合加以区别，把模糊集合的特征函 数称为隶属函数。

第二节 隶属函数的确定
一、隶属函数的分布统计求法 利用统计试验计算隶属函数或隶属度的步骤： 1、确定集合的因素 2、选择部分学生进行试验 3、找出各因素数据中的最大值和最小值算出分组组距、计算数据落在各 组中的数，根据次数分布情况确定较为适合的隶属度。 二、对比平均法求隶属函数
设论域U={x 设论域U={x1，x2， x3，… ，xn} 论域中各因素之间按照某一种性为标准，以每两个因素为一组，判定它们各自们归 属这一标准的程度，并用符号g(x 属这一标准的程度，并用符号g(xi,xj)表示(i,j=1，2，…，n)。 表示(i,j=1， n)。 三、模糊统计法求隶属函数 模糊统计法的步骤： （1）确定论域与因素集。 （2）要求参与实验者就论域中各给出的点是否属于因素集的各元素进行投票。 （3）统计投票结果，求出隶属函数。

例14-4 设论域U年龄={20，35，50，65}，因素A={年青人，老年人}，20 14- 设论域U ={20，35，50，65}，因素A={年青人，老年人}
个人参与投票，结果如表14.7所示 个人参与投票，结果如表14.7所示：
表14.7投票结果表
U∈A的次数

u

20 20 0

35 16 0

50 2 18

65 0 19

A 年表人 老年人

则有u20对“年青人”这一概念的隶属度： μ20=20/20=1 u20对“老年人”这一概念的隶属度： μ20=0/20=0 所以，μ20={1，0}。同理可求出年龄论域中各点对于因素集的隶属度 μ35={0.8，0} μ50={0.1，0.9} μ65={0，0.95}

第三节 模糊关系与模糊矩阵
一、模糊关系 1、关系，描写事物之间联系的数学模型之一就是关系，常用符号“X”来表 、关系，描写事物之间联系的数学模型之一就是关系，常用符号“ 示。 2、模糊关系，是普遍关系的推广，普通关系只能描述元素间关系的有无， 而模糊关系则描述元素之间关系的多少。 例14-6 在医学上常用公式：体重B（公斤）=身高A（厘米）－100来表示 14- 在医学上常用公式：体重B（公斤）=身高A（厘米）－100来表示 标准体重，这就给出了身高（A）与体重（B）的普通关系。 标准体重，这就给出了身高（A）与体重（B 若A={140，150，160，170，180} A={140，150，160，170， B={40，50，60，70， B={40，50，60，70，80} 身高与体重 的普通关系如表14.8所示： 身高与体重的普通关系如表14.8所示：
表14.8身高与体重的普通关系 R(A,B) Ai 140 150 160 170 180 Bi 40 1 0 0 0 0 50 0 1 0 0 0 60 0 0 1 0 0 70 0 0 0 1 0 80 0 0 0 0 1

但人的胖瘦不同，对于非标准的情况，身高与体重的关系应该以接

近标准的程 度来描述，这就导致产生如表14.9所示的模糊关系。它能更深刻、更完整地给 出身高与体重的对应关系。 表14.9 身高与体重的模糊关系 R(A,B) Ai 140 150 160 170 180 Bi 40 1 0.8 0 0 0 50 0.8 1 0 0 0.1 60 0.2 0.8 1 0.8 0.2 70 0.1 0.2 0.8 1 0.8 80 0 0.1 0.2 0.8 1

例14-7 设有一组同学（徐X，张X，王X），他们选修英，日，俄，法四种外语中 14- 设有一组同学（徐X，张X，王X 的任几门，他们选修和结业成绩如下： 徐X 英语 85 徐X 日语 70 徐X 俄语 75 张X 英语 90 王X 英语 70 王X 法语 80

用A表示学生集合：A={徐X，张X，王X}， 用B表示语种集合：B={英，日，俄，法}。 若用成绩除以100折合成隶属度来描述掌握外语的程度，则由如表14.10可以构 造出一个在A×B直积空间中存在的模糊关系 R ，用它来表示小组成员“掌握外 ~ 语程度”的模糊关系。 表14.10 掌握外语的程度 英语 徐X 张X 王X 0.85 0.90 0.70 俄语 0.75 0 0 日语 0.70 0 0 法语 0 0 0.8

二、模糊矩阵
1、矩阵 矩阵可以用来表现关系，如果集合A 矩阵可以用来表现关系，如果集合A有m 个元素，集合B有n个元素、我 个元素，集合B 们可以用矩阵R来表示由集合A到集合B 们可以用矩阵R来表示由集合A到集合B的关系
r11 R= r21 rm1 r12 … r1n r22 … r2n rm2 …rmn

其中rij=0或1，1≤i≤m，1≤j≤n。

2、模糊矩阵 当论域A 当论域A×B为有限集时，模糊关系可以用矩阵形式 来表示，该矩阵元素r 仅在闭区间[0，1]中取值，即0 来表示，该矩阵元素rij 仅在闭区间[0，1]中取值，即0 ≤rij ≤1，此矩阵称为模糊矩阵。 ≤1，此矩阵称为模糊矩阵。

R=
~

r11 r21 rm1

r12 … r1n r22 … r2n rm2 … rmn

其中0≤rij≤1，1≤i≤m，1≤j≤n。 模糊矩阵是研究模糊关系的重要工具，当它用来表示模糊关系时，其中 rij表示集合A中第i个元素和集合B中第个j元素之间的关联程度，例14-7中小组 表示集合A中第i个元素和集合B中第个j元素之间的关联程度，例14成员外语成员与外语学科的关联程度可以用如下矩阵形式表示它们之间的模糊 关系。

R=
~

0.85 0.90 0.70

0.70 0 0

0.70 0 0

0 0 0.80

三、模糊关系矩阵的运算 设 和 S 是A×B中模糊关系。 ~ ~

R

（1）

R和 S
~

的并。

~

R∪ S
~
~

=(rij∨sij)

（2） （3） ）

R和 S
~ ~

的交。 的补。

~ ~

R∨ S
~
~

=(rij∩sij)

R和 S

R=(1－ R=(1－Rij) S=(1－ S=(1－Sij)

其中，“ 其中，“∧”表示rij与sij相比较后取较小者 表示r “∨”表示rij与sij相比较后取较大者 表示r

五、模糊关系合成图解法 图解法计算模糊关系的合成的步骤： 1、画出关系合成图 2、在图中找出xi到zj的各种可能途径； 3、在同一路径中相比较取隶属度最小者作为该路径 的隶属度； 4、把路径所取得隶属度中

最大者作为qij的元素值； 5、画出模糊关系合成矩阵。

第四节 模糊综合评判方法 一、模糊变换 1、模糊向量 对于一个有限模糊集合X可以表为： X = {x ，x ，x ，…，x } 1 2 3 n ~ xi是各元素相应的隶属度 μ R (xi)，其中0≤xi≤1 ~ （i=1，2，…，n）对于只有一行的模糊矩阵又可以 看成模糊向量，如： X = {x1，x2，x3，…. ，xn}是一个模糊向量 ~ 2、模糊变换 现有一个模糊矩阵： R ={ rij}，其中0≤rij≤1, ~ X × R =Y称为模糊变换。
~

~

模糊变换的结果为：

Y={y1，y2，…，ym}
~

式中的各分量： Yi=
k =1

∨ (xk∧rkj)(k=1,2,…,m)

m

[ 14-10] [例14-10]给出

X =（0.2，0.5，0.3）， = 0.2 0.5 0.3
~
0.2 0 0.2 0.7 0.4 0.2 0.1 0.5 0.4 0 0.1 0.1

R=
~

模糊变换：

Y= X × R ~ ~
~

0.2 = (0.2，0.5，0.3) × 0 (0.2，0.5， 0.2 =（0.2，0.4，0.5，0.1） 0.2，0.4，0.5，0.1）

0.7 0.4 0.3

0.1 0.5 0.4

0 0.1 0.1

式中Y 各分量的计算如下： ~
Y1=(0.2∧0.2)∨(0.5∧0)∨(0.3∧0.2) =0.2∨0∨0.2 =0.2 y2=(0.2∧0.7)∨(0.5∧0.4)∨(0.3∧0.3) =0.2∨0.4∨0.3 =0.4 y3=(0.2∧0.1)∨(0.5∧0.5)∨(0.3∧0.4) =0.1∨0.5∨0.3 =0.5 y4=(0.2∧0)∨(0.5∧0.1)∨(0.3∧0.1) =0∨0.1∨0.1 =0.1

3、归一化处理 由于 Y 中各元素之和，即
~
m i 1 m i 1

∑ y =1，为了保证处理后 ∑ y ≠1，需
yi
n

要进行归一化处理，其方法是取Y’i=

∑y
1

，故有：

i

Y’i=0.2/1.2=0.167 Y’i=0.4/1.2=0.333 Y’i=0.5/1.2=0.417 Y’i=0.1/1.2=0.083 经归一化后的模糊变换结果为：

Y= X ~
~

×

R
~

= （0.167，0.333，0.417，0.083）

二、模糊综合评判的原理 （1）确定评价指标集合论域U：
U={u1，u2，…，um}（m为指标项目数）

（2）确定评语集合论域V：
V={v1，v2，…，vn}（n为评语等级数）

（3）确定权重分配模糊向量 A ： ~ A ={a1，a2，…，am}（m为指标项目数） ~ （4）进行实际评判，形成评判模糊矩阵R：

R
~

=

r11 r21 ： rm1

r12 … r1n r22 … r2n ： ： rm2 … rmn ,其中 其中 ， B ={b ，b ，…，b
1 2 m}

（5）进行模糊变换：

R = A ×R
~ ~ ~
1 2

~

（6）得到归一化后的模糊变换结果：
， B ’={b ，b ，…，b
m}

~

（7）根据最大隶属度法，对

B ’做出评价判断。
~

三、模糊综合评判应用实例——网络课程评价 三、模糊综合评判应用实例——网络课程评价 例14-11 我们对于某学校的校园网络一期建设情况进行评判， 14设包括三个因素，即硬件建设，软件建设、人员培训，用论域U 设包括三个因素，即硬件建设，软件建设、人员培[61阅读]训，用论域U 表示为：
U={硬件建设（u ），软件建设（u ），人员培训（u U={硬件建设（u1），软件建设（u2），人员培训（u3）}

而评语论域V 而评语论域V表示为：
V={很好（v ），较好（v ），可以（v ），不好（v V={很好（v1），较好

（v2），可以（v3），不好（v4）}

亦即分为四个等级，并用百分比或小数表示。现邀请一些专门 人员进行评价，若用人数的百分比来表示评价结果如表14.13所 人员进行评价，若用人数的百分比来表示评价结果如表14.13所 示；
表14.13评价结果 评价结果
评语 指标

很好 50% 40% 0%

较好 40% 30% 10%

可以 10% 20% 30%

不好 0 10% 60%

硬件指标 软件指标 人员指标

表14.13就构成模糊矩 14.13就构成模糊矩

R
~

0.2 = 0 0.2

0.7 0.4 0.2

0.1 0.5 0.4

0 0.1 0.1

现在假定根据实际需要，在对校园网络一期建设做出要求时， 现在假定根据实际需要，在对校园网络一期建设做出要求时，主要是硬件建设 （0.5）,其次是人员培训（0.3），对软件建设要求稍低（0.2）。这就构成 ） 一个由三个权数分配构成的一行模糊向量 A ； ~ A=（0.5，0.2，0.3） ~ 现要做出综合评判，必须进行模糊变换 B = A × R

B = A×R
~

~

~

~

~

0.5 0.4 =（0.5，0.2，0.3） 0.4 0.3 0 0.1 =(0.5，0.4，0.3，0.3)

~

0.1 0.2 0.3

0 0.1 0.6

为了明确地显示综合评判的结果，还需做归一化处理。 归一化后的模糊变换结果为： B ’=（0.33，0.27，0.20，0.20）
~

此结果表示，对该学校的校园网一期建设情况而言，将硬件建设、软件建设、 人员培训同时考虑的结果，根据最大隶属度法，该校园网建设仍然是“很好”占 最大比重（0.33）

第五节 模糊聚类分析方法
聚类分析是指根据事物本身的特性，将事物性质上的亲疏程度进行分类的 方法。 一、模糊聚类分析基本原理 （一）聚类分析步骤如下： 1、确定样本统计指标与数据标准化 2、标定距离，建立相似关系矩阵 3、进行聚类 （二）模糊等价矩阵聚类 1、模糊等价关系 通过标定距离，可以建立样本之间的相似关系矩阵，但模糊关系 必须是模糊等价关系才能聚类。模糊等价关系的条件是模糊关系必须同时具 有： （1）自反性 （2）对称性 （3）传递性 2、模糊等价矩阵聚类的步骤： （1）标定距离，建立相似关系矩阵。 （2）求传递闭仓。 （3）动态聚类

（4）画出动态聚类图 三、最大树方法 1、最大树方法的画法 最大树方法，就是构造一个特殊的图，它有N个顶点，N 最大树方法，就是构造一个特殊的图，它有N个顶点，N-1条边，顶点之 间通过边连通，但不包任何回路。 具体画法，先画出顶点集中的某一个i，然后按r 具体画法，先画出顶点集中的某一个i，然后按rij从大到小的顺序依次连 接成边，并要求不产生回路，直到所有顶点都被连通为止，这样就得到一棵 最大树。

二 : 从AdventureWorks学习数据库建模——实体分析

最近打算写写数据库建模的文章，所以打算分析微软官方提供的SQL Server示例数据库AdventureWorks，看看这个数据库中有哪些值得学习的地方。(www.61k.com）

首先我们需要下载安装一个SQL Server数据库引擎，然后下载示例数据库，这里笔者用的是SQL2008R2，所以下载的是AdventureWorks2008R2，下载地址：

http://msftdbprodsamples.codeplex.com/

下载数据库后附加到SQL Server中即可看到这个数据库。

这是一个自行车制造和销售公司的数据库，该公司建立自己的销售网站，提供在线销售。首先看看这个数据库的结构，其建立了多个Schema，通过Schema来划分表所在的模块，比如HumanResources，Person，Production，Purchasing和Sales。如果是非常通用的表，比如日志表，那么就不属于任何模块，使用系统默认的Schema：dbo。

对于这么一个复杂的模型，我们可以按照：主要实体、附属实体、事务实体关联关系的顺序进行分析。

主要实体

对于整个系统来说，BusinessEntity是最核心的实体，用于表示一个“人”，这里的人是打引号的，因为它既可以表示真实的自然人，也可以表示：公司、组织甚至一个商店，可以认为是一个法人。对于这个数据库模型来说，有3个实体继承自BusinessEntity，那就是Person，Store，Vendor。

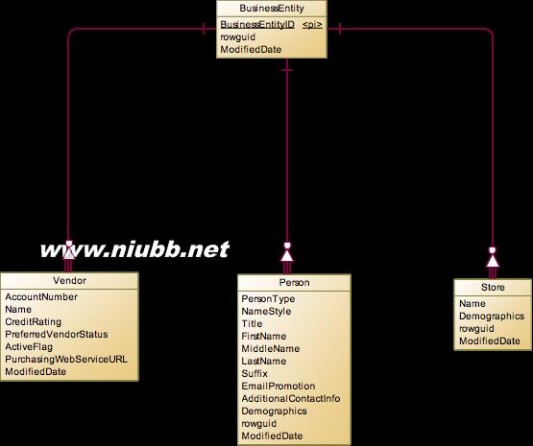
对于Person自然人来说，他可能是公司的员工，也可能是客户，所以我们又关联出了两个实体Employee和Customer。这里需要注意的是，在这个模型中，他并不把一个自然人标识为一个客户，而是对不同的Store，会形成不同的客户。也就是说对于公司来说，他并没有客户主数据，同一个人在不同的店消费，那么就会在不同的店中记为一个客户。为什么要这么设计，确实很奇怪，可能是业务上的需求吧。

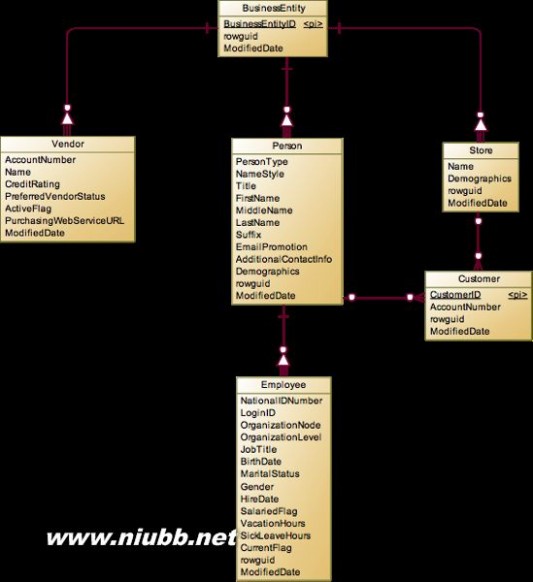
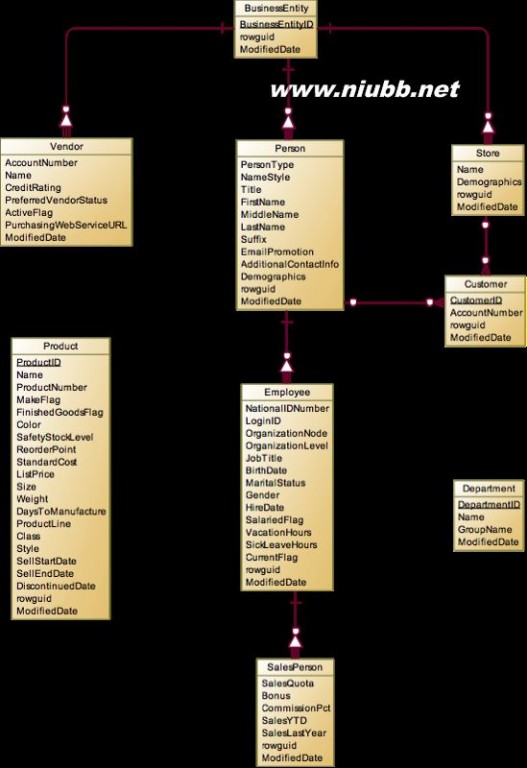
这里延伸到Employee，就可以把HumanResources下面的实体分析一下，很显然Department是主要实体，至于Employee和Department之间的关系，我们接下来再分析，这里我们只找主要实体。Employee如果在销售部门，那么就是一个SalesPerson，所以这个实体是继承自Employee。另外在Production中还有一个很重要的实体Product，用于表示生产和销售的产品。

附属实体

所谓附属实体，就是依附于主要实体而存在，对主实体的属性进行补充的实体，如果主要实体不存在，那么附属实体里面的数据就没有意义。对于前面找的主要实体，我们一个一个的分析：

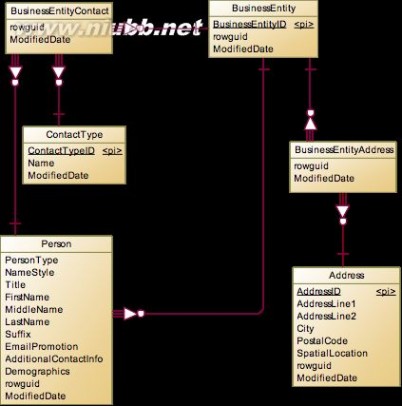
BusinessEntity

BusinessEntity有两个附属实体：BusinessEntityContact和BusinessEntityAddress，对于联系人实体，是和Person形成多对多关系，所以BusinessEntityContact是多对多产生的中间表，另外再加上ContactType说明联系人的类型。而对于业务实体的地址，系统也抽象出了一个Address表，使得BusinessEntity和Address之间形成多对多关系。

Person

对于Person表，关联的表分为两类，一类是一对多或多对多的普通关联表，比如一个人有多个PersonPhone，一个人有多个EmailAddress，或者一个人持有多张信用卡PersonCreditCard。这里把CreditCard和Person设置成多对多的关系，我想应该这里的CreditCard包含公司商务卡的情况，这种卡的真正持有人是公司，但是公司会派发给Sales用，如果Sales离职了，那么这张卡会收回，派发给其他的员工用，所以这就形成了多对多关系。另外一类是一对一的拆分或继承关系，比如Password表。如果是简单的设计，我们完全可以把Password相关字段放在Person表中，而这里却独立出来形成一对一关系，主要可能是以下几方面的原因：

安全考虑：Password的内容很机密，独立成表后可以单独对这个表进行加密，权限分配等。

性能考虑：Password的内容只用于登录系统时验证，以后接下来的所有查询都用不到这些字段，所以不放在Person表中，系统在查询Person表时就不需要连带着把不需要的字段查出来。

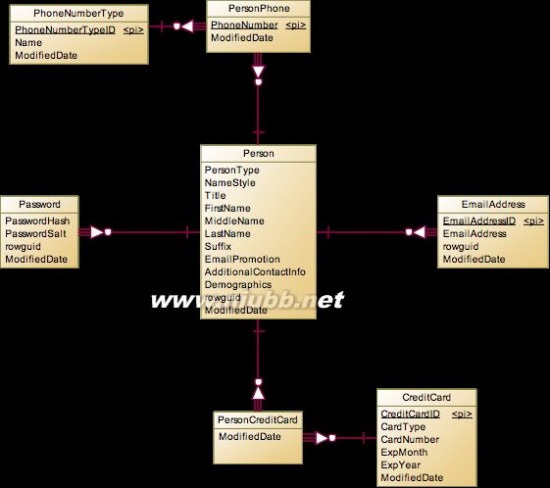
Employee

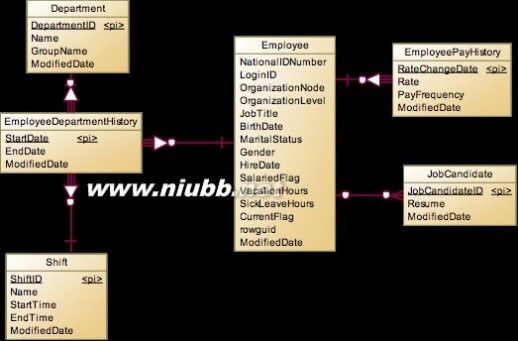
这里主要涉及到的是HumanResources下的表，除了员工的基本信息外还记录了员工的履历，工资变动，部门变动情况。一个Employee对应多个JobCandidate，为什么是一对多关系呢？因为应聘者可以制作个人简历的多个版本，然后投公司的不同部门，最后如果应聘者被录取了，那么就可以把JobCandidate中的BusinessEntityID设置为Employee的ID，如果应聘失败，那么BusinessEntityID就是NULL。EmployeePayHistory是员工的工资表，但是不是发工资的记录表，只是记录员工的工资基本信息，如果工资变动就创建一条新的记录。Employee和Department是多对多的关系，并不是因为一个员工身兼数职，在多个部门同时干活，而是因为要记录员工的部门调动情况，所以保留了所有历史记录，形成了多对多关系。另外比普通公司的部门员工表不同，这个系统还有一个轮班表Shift，那是因为这是个制造业公司也有门店进行销售，所以会分为早班，中班和晚班，一个员工的轮班是固定的，如果发生变化，比如以前是上夜班，现在改为上早班，那么EmployeeDepartmentHistory中也会对应生成一条新的记录。

Sales

销售继承至Employee，主要有销售区域，销售配额等附加的属性。本身销售区域和销售配额可以看做是Sales表的属性，但是为了记录历史，所以独立出来了一对多的表：SalesTerritoryHistory和SalesPersonQuotaHistory。

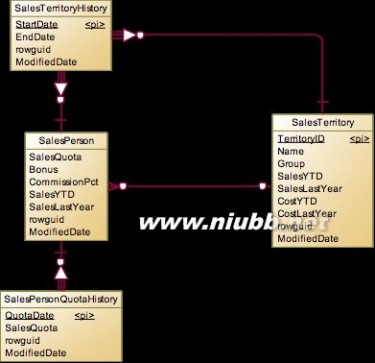
这里需要说明一下SalesTerritory表并不是Sales的附属表，他本身是一个独立的实体。

Product

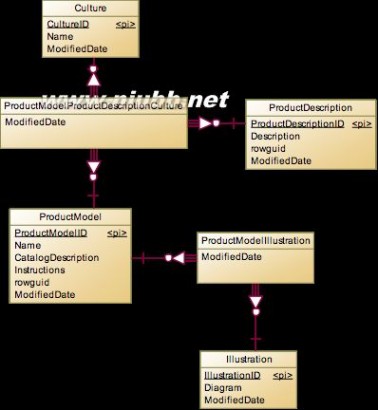
这个实体应该是各个主实体中属性最复杂的实体了。主要分为ProductModel和Product两块。

先说ProductModel，可以理解为样品，样机或者是模型，在进行量产前需要先生产ProductModel。对于ProductModel，主要有产品的部件关系图Illustration和描述ProductDescription。ProductModel和Illustration是普通的多对多关系，一个模型有多个部件关系图，一个部件关系图也可以用于多个样机中。而对于描述，除了普通的多对多关系外，还增加了一个多语言的关系。于是增加了Culture表，形成了三个表的多对多关系。实际上这种多语言模型并不好，很容易产生错误，对于多语言的处理，可以建立更好的模型。

接下来就是Product实体，可以将相关的表分为三类：

多对一：产品的分类Category和前面提到的ProductModel。

一对多：产品成本历史ProductCostHistory，产品的组成BillOfMaterials，产品的库存ProductInventory，产品价格历史ProductListPriceHistory，产品的复查ProductReview。

多对多：产品文档ProductDocument和产品照片ProductPhoto。

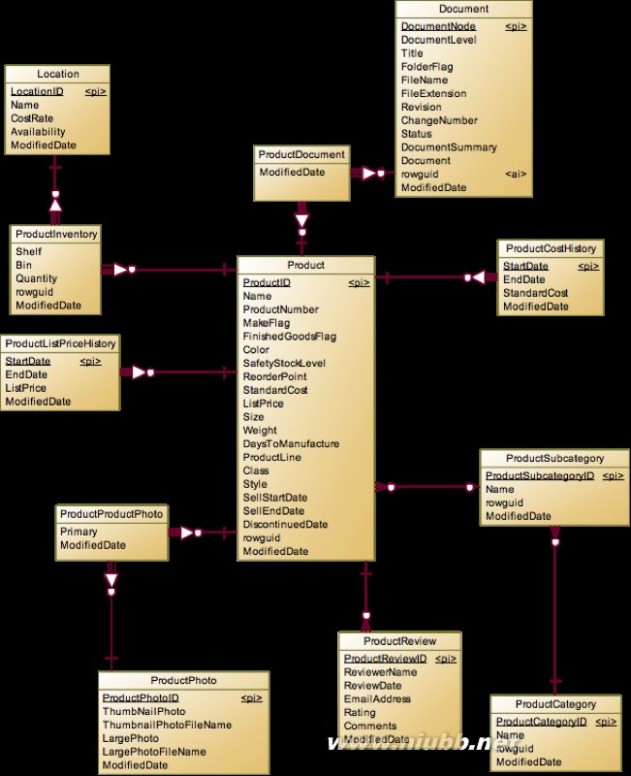
产品分类没啥好说的，就是普通的二级分类法，一级大分类在ProductCategory，二级小分类在ProductSubcategory，然后所有产品都必须归属到二级小分类上。ProductCostHistory和ProductListPriceHistory都是因为要记录基于时间段的历史而形成的一对多关系，其中必有StartDate和EndDate来划分时间区间。【历史数据记录】

关于产品文档和产品照片，由于存在复用的情况（比如产品的外观是一模一样的，只是某些内部参数不一样，那么产品照片就可以复用。）所以就形成了多对多关系，有多对多关系就会有中间表。产品图片由于会有细节照片，各个角度的照片，所以在多对多关系表中另外定义了一个Primary字段用于说明当前选用的照片是不是主体照片。

事务实体

前面分析的实体都是在主谓宾语句中当主语的对象，接下来我们要分析这些主语之间发生关联，进行事务操作后产生的宾语对象。

对于SalesPerson、Product、Customer在一起时，联想到的就是销售订单：

SalesOrder

只要是涉及表单的东西（销售订单、报销单、采购订单、发货单等）大部分情况都会分为Header和ItemDetail两个表，在销售订单中Header用于记录单据的销售的人员，客户，总金额等信息，而ItemDetail中记录了具体销售的产品，数量等信息。

下面先分析Header：

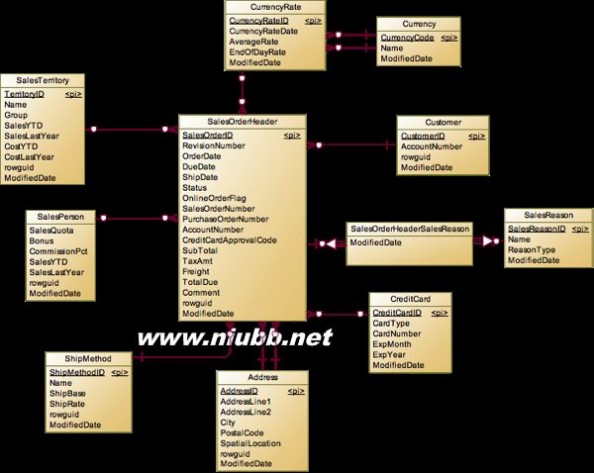
Header建立了SalesPerson与Customer的联系，另外还有范式化的一些字段，比如ShipToAddress，BillToAddress，ShipMethod等。除了这几个实体外，我们需要单独分析一下以下几个实体：

Territory，这是在前面介绍Sales的时候说到，这个销售区域和SalesPerson是有关联的，按理来说，Header表已经关联了SalesPerson表，我们就可以通过SalesPerson获得其下单时对应的Territory，为什么还需要额外添加这个Header到Territory的直接关系呢？这是出于性能的考虑而增加的冗余，对于有时效性的对象，最好是直接关联，而不是通过中间对象jion多个表去关联。让我们看看如果没有直接关联Territory，那么我们的查询到底有多复杂：

select h.*,st.*

from Sales.SalesOrderHeader h

left join Sales.SalesPerson sp

on h.SalesPersonID=sp.BusinessEntityID

left join Sales.SalesTerritoryHistory sth

on sp.BusinessEntityID=sth.BusinessEntityID and h.OrderDate between sth.StartDate and sth.EndDate

left join Sales.SalesTerritory st

on sth.TerritoryID=st.TerritoryID

下面再来看看币种和汇率的相关表Currency。在这个系统中，Header并没有直接说明用什么币种付款，什么币种结算，汇率是多少，而是把这几个字段放在CurrencyRate表中，通过引用CurrencyRate来表示。虽然说独立出来后没有直接放在Header表中直观，不过减少了冗余，只需要做一次Join就能拿到结果，所以性能上还是能接受的。【虽然从关系上需要Join了CurrencyRate后再JoinCurrency表才能完整，但是一般来说Currency表只用于CurrencyRate的限定，而不需要在查询时使用Currency表，因为CurrencyCode是国际标准编码，只需要显示Code就够了。】

Header和SalesReason是多对多关系，在客户下单的时候让用户复选购买原因，是因为促销，还是看了杂志广告之类的，简单多对多关系，这个没啥好说的。

SalesOrderDetail

Header和OrderDetail是一对多关系，Detail记录了具体购买了啥产品，购买单价，数量等，所以关联的是Product，但是在这个系统中，他并不是直接关联Product对象，而是在之间建立了SpecialOfferProduct，该表是Product和SpecialOffer的多对多中间表。

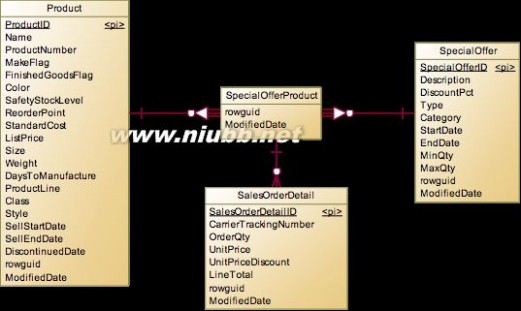
为什么会这么做呢？这主要是跟具体的业务相关。产品在生产出来以后有一个标价Product.ListPrice，但是在实际销售中，商家会有各种促销活动（比如买10个以上9.8折，25个以上9折等），所以会形成Product和SpecialOffer的多对多关系，维护了哪些产品能够有哪些折扣。为了统一模型，如果产品不做任何打折促销，也会在SpecialOffer中维护一条记录“No Discount”。

这里有一个特别的技巧，SpecialOfferProduct是没有自己独立的主键的，而是使用ProductId和SpecialOfferId作为联合主键，然后在OrderDetail引用具体的SpecialOfferProduct时，就会将ProductId和SpecialOfferId引用到其列中。所以在模型上来说，是OrderDetail关联SpecialOfferProduct，然后再关联Product，但是我们在实际查询中，完全可以忽略SpecialOfferProduct表，直接用OrderDetail去Join Product即可，所以性能上没有任何影响，这是一个漂亮的设计。

而当Employee、Product和Vendor在一起时，联想到的就是采购订单：

PurchaseOrder

和销售订单类似，采购订单也 分为PurchaseOrderHeader和PurchaseOrderDetail。

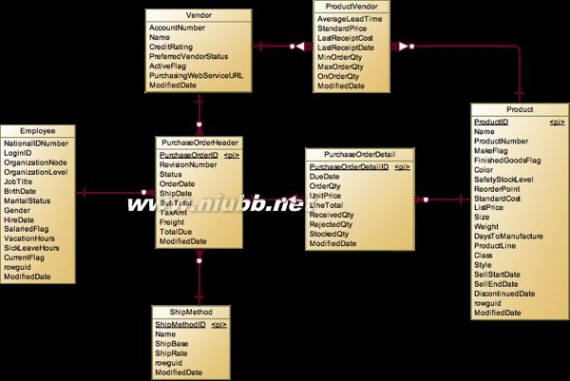
系统中先使用ProductVendor定义了哪些Vendor能供应哪些产品，在生成采购订单时会基于这里面的内容来生成，但是在模型上并不直接反应，因为Product属于Detail表，而Vendor是属于Header表，不能像前面说到的SpecialOfferProduct一样通过引用来传递这种限制。

Header记录的是采购人员Employee与供应商Vendor的关系。一个采购订单Header中会包含多个明细Detail，里面记录了采购哪些Product。采购订单比销售订单简单很多，最为买方，不会去记录促销，购买原因之类的信息。另外采购中没有涉及到币种汇率问题，我估计这是因为产品都在国内采购和结算，所以只有一种币种，而销售是面向世界各地，所以涉及到币种汇率。

WorkOrder

除了前面说到的销售订单和采购订单外，在生产过程中还有生产订单，用于表示产品的生产情况。主要有WorkOrder和WorkOrderRouting两个实体。

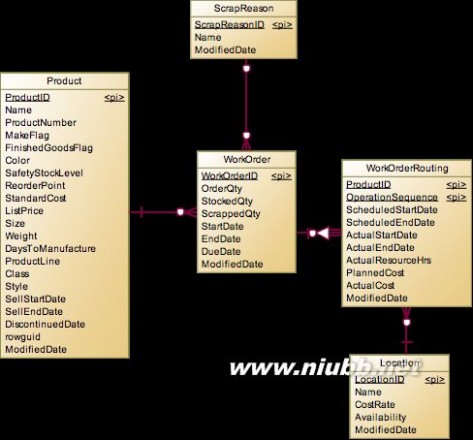
WorkOrder记录了生产某个产品的数量、报废和时间情况，而WorkOrderRouting记录的是在某个产品的具体生产过程中有哪些工序，每个工序的时间、成本等情况。总的来说，这是一个非常非常简化的生产工作订单模型。

其他实体

除了前面说到的实体外，还有其他几个独立出来的实体需要说明一下：

TransactionHistory

另外还有一个其归档表TransactionHistoryArchive，其结构和TransactionHistory一模一样，这里面记录的是生产工作订单或者采购订单或者销售订单这3个事务的产品、日期，数量等公共信息。这个表可以认为是一个事务的日志表，平时并不参与各个实体的查询，只有在审计或者跟踪数据变化时才用到。

TransactionHistory表中的数据是在各个Order表上建立Trigger自动插入进去的，而不是由外部程序代码去控制。由于本身事务表的数据量就比较大，而这个表却存了三个事务表中的数据，所以增长特别快，必须进行归档操作，把老数据搬移到另一个归档表中，这样才能保证查询新TransactionHistory表的速度。

AWBuildVersion

这是一个记录当前数据库定义创建时数据库的版本也可以定义当前数据库定义脚本的版本。对于通用的产品来说，这个表比较重要，因为产品可能需要升级，升级程序在升级前读取这个表，知道了当前数据库定义是什么个版本，然后就可以查询到将当前版本的数据库升级到新版的数据库所需要修改的SQL，然后执行这些SQL。

而应用程序在运行时第一件事就是检查这个表中的版本信息，保证数据库定义的版本与程序要求的版本匹配，这样程序才能正常运行。

对于企业内部系统，一般只有一个实例，而且由企业内部的IT人员开发维护，所以这个表没有也没什么问题。

DatabaseLog

这是记录数据库DDL（数据定义语言，比如CREATE， ALTER， DROP等）操作的日志表。这个表是由Database Trigger自动维护，当在这个数据库中执行了DDL的时候，系统会触发Trigger，往这个表中记录一条数据。这是一个好东西！

另外还有一些因为范式化抽象出来的码表，我在前面的模型中没有提到，比如CountryRegion，StateProvince等这些都比较简单，就不一一累述了。

这篇文章我只是简单分析了下实体和实体关系，下面一篇文章会进一步分析其中的细节，有哪些优缺点。

三 : 《除法》教材分析与教学建议

单元教学目标
1．结合提出并解决除法问题的过程，进一步体会除法的意义，并掌握用6~9的乘法口诀求商的方法。
2．熟练用乘法口诀进行表内乘除法的口算。
教材分析与教学建议
本节教材结合解决实际问题的过程，学习用6－9的乘法口诀求商。对实际问题的理解包括两方面：一是已知什么（42只小鸟，6只小鸟住一间房子），二是求什么（要为小鸟准备几间房子）。进而从这个实际问题中出抽象数学模型：42可以分成几个6？或者42是6的几倍？于是知道要列除法算式42÷6解决这个问题。从而引出用什么方法求商的讨论，体会用乘法口诀求商的简便性。根据“六七四十二”得42÷6=7，再回到实际问题的情境中，解释这个7的实际意义，并写出问题的答案：要为小鸟准备7间房子。这个过程就是从实际问题抽象出数学模型并进行解释与应用的过程，而且同时也发现了问题所涉及的数量。关系：小鸟总数=每间房子住的小鸟只数×房子间数。
　　教学时，教师要让学生认真看图，说一说图意，明确问题。然后让学生独立列式计算，解决问题，并在小组内说一说用哪一句乘法口诀求商，进一步体会除法与乘法的内在联系。
教师在指导时，要强调从实际问题中抽象出来的数学问题（数学模型）是什么，这一点容易被忽视，因为学生往往从实际问题字面上的意义直接就列出除法算式计算；其次，要强调计算的结果要回到实际问题的情境中，去检验和解释它的意义，并写出答案。这才是解决实际问题的一个比较完整的思维过程。
单元编写意图
本单元是本册教材“数与代数”部分的最后一个单元，是在学生已经对除法意义有初步的体会，会用2~9的乘法口诀口算表内乘法和用2~5的乘法口诀口算表内除法的基础上进行教学的。本单元包括“长颈鹿和小鸟”“小兔安家”和“游乐场”三节。本单元的标题是“除法”，除法与乘法之间具有密切的联系，除法关联着“倍”的意义，除法又以乘法口诀为最基本的口算工具。这个单元综合了除法的这些特征与联系，所以，本单元也是本册教材在“数与计算”领域的一次复习与提高。 “长颈鹿和小鸟”复习除法的意义，学习用6~9的乘法口诀求商；“小兔安家”复习除法的两类问题；“运动场”强调乘除法在生活中的实际应用，理解乘除法的内在联系，在发展解决实际问题能力的同时，进一步熟练用乘法口诀进行表内乘除法的口算，为今后进一步学习乘除法打好基础。
长颈鹿与小鸟教学目标
1．结合提出并解决除法问题的过程，进一步体会除法的意义，并掌握用6~9的乘法口诀求商的方法。
2．熟练用乘法口诀进行表内乘除法的口算。
教材分析与教学建议
　　本节教材结合解决实际问题的过程，学习用6－9的乘法口诀求商。对实际问题的理解包括两方面：一是已知什么（42只小鸟，6只小鸟住一间房子），二是求什么（要为小鸟准备几间房子）。进而从这个实际问题中出抽象数学模型：42可以分成几个6？或者42是6的几倍？于是知道要列除法算式42÷6解决这个问题。从而引出用什么方法求商的讨论，体会用乘法口诀求商的简便性。根据“六七四十二”得42÷6=7，再回到实际问题的情境中，解释这个7的实际意义，并写出问题的答案：要为小鸟准备7间房子。这个过程就是从实际问题抽象出数学模型并进行解释与应用的过程，而且同时也发现了问题所涉及的数量。关系：小鸟总数=每间房子住的小鸟只数×房子间数。
　　教学时，教师要让学生认真看图，说一说图意，明确问题。然后让学生独立列式计算，解决问题，并在小组内说一说用哪一句乘法口诀求商，进一步体会除法与乘法的内在联系。
教师在指导时，要强调从实际问题中抽象出来的数学问题（数学模型）是什么，这一点容易被忽视，因为学生往往从实际问题字面上的意义直接就列出除法算式计算；其次，要强调计算的结果要回到实际问题的情境中，去检验和解释它的意义，并写出答案。这才是解决实际问题的一个比较完整的思维过程。
小兔安家教学目标
1．结合提出并解决除法问题的过程，进一步体会除法的意义，并掌握用6~9的乘法口诀求商的方法。
2．熟练用乘法口诀进行表内乘除法的口算。
教材分析与教学建议
　“小兔安家”的情境图中没有提出数学问题。从图中发现并利用有关的数学信息（小兔只数，房子间数）提出数学问题，培养问题意识，是本节课要引导学生去做的第一件事情。针对具体情境，教材中提出两个问题，代表除法问题的两种基本类型，目的是引导学生提出类似的问题，一类是求“每间房子住几只小兔”，另一类是求“需要几间房子”。会根据具体情境提出这两类数学问题，是以理解情境中蕴涵的数量关系为前提的。因此，提出数学问题这个教学环节本身也为后续解决问题奠定了基础。
　　教学时，教师应以“小兔安家”为主题，鼓励学生结合具体情境提出问题，并简单地记录提出的问题。然后启发学生把所提的问题进行整理，分成两类，再回到教材中提出的两个问题，让学生独立列式解答。最后组织学生比较这两个问题及其算式的区别与联系。
　　事实上，上述两类除法问题包含了相同的数量关系，即小兔的总数=每间房子住的小兔的只数×房子的间数。体会到这一层联系，有助于理解除法与乘法的内在联系，以及除法的意义。
游乐场教学目标
1．结合提出并解决除法问题的过程，进一步体会除法的意义，并掌握用6~9的乘法口诀求商的方法。
2．熟练用乘法口诀进行表内乘除法的口算。
教材分析与教学建议
　“游乐场”是学生熟悉的生活情境，其中包含很多数学信息。如，小火车有9节车厢，每节车厢可乘4人；碰碰车有4辆，每辆可乘2人；每张小火车票3 元，每张碰碰车票5元等，是显而易见的。让学生提出数学问题，实际上是要他们去发现能够联系其中有关信息的数量关系。例如，“小火车有9节车厢，每节车厢能乘4人，这列小火车一共能乘多少人？”如果能提出这个问题，那么他一定意识到：小火车满载的人数=每节车厢可乘的人数×车厢的数量。能够提出“每张小火车票3元，买7张应付多少元”也意味着他懂得：应付的钱=每张小火车票的价格×车票的张数。教材采用“你问我答”的方式，互相提出问题，解决问题，实际上对问答双方，都提出了理解情境中数量关系的要求。生活中处处有数学，也可以说生活中处处有数量关系。
　　教学时，教师要发现学生提出的好问题，让大家借鉴，开阔数学的视野，提高提出数学问题的能力。什么是好的数学问题呢？就是尽可能充分地利用情境中的数学信息，提高问题的综合性。如果学生还提不出好问题，教师要加以启发引导。如：“能坐满一节小火车车厢的乘客，去玩碰碰车时，需要几辆碰碰车？”这个数学问题就用上了情境中两个没有必然联系的信息。又如：“买6张小火车车票的钱，能买几张碰碰车的车票”这个问题涉及两步运算。对学生提出的比较复杂的问题应给予肯定和鼓励，可以不要求他们列式，但可以让他们交流想法。

四 : 北师大第九册《分数加减法》教材分析与教学建议

单元教学目标
1．在操作活动中，理解异分母分数加减法的算理，并能正确计算。
2．理解分数加减混合运算的顺序，并能正确计算。
3．能把分数化成有限小数，也能把有限小数化成分数。
4．能结合实际情境，解决简单分数加减法的实际问题。单元学习内容的前后联系单元
单元编写意图
　在三年级下学期时，学生已经学习了简单的同分母分数加减法，在本册教材中，学生又学习了倍数与因数以及分数的再认识等，这些知识为本单元的学习打下了很好的基础。为进一步加强学习的探索性，本单元的内容分为3个情境呈现：在 “折纸”中，主要学习异分母分数的加减法；在“星期日的安排”中，则重点学习分数加减法的混合运算；在“看课外书时间”中，通过解决不同形式的数的比较，引出分数与小数的相互转化的方法。与整数的加减法相比，分数加减法是一种较为抽象的运算，学生在理解运算的意义、掌握运算的方法等过程中会遇到不少困难。
折纸教学目标
1．通过直观的操作活动，理解异分母分数加减法的算理。
2．能正确计算异分母分数的加减法。
教材分析与教学建议
在三年级时，学生已经学习了简单的同分母分数的加减法，本课时的分数加减法主要是异分母分数的加减法。为了让学生直观地认识异分母分数加减法的必要性，教材安排了折纸活动，感受计算异分母分数加法的必要性。接着，又提出了估一估与算一算的要求，并用两种提示性的算法，说明学生在探索中可能出现的思考方法。对于异分母分数的减法，教材则直接呈现了计算的方法，主要是让学生运用知识迁移的方法，能直接进行减法的计算。在“试一试”的练习后，教材安排了对异分母分数加减计算方法的归纳，以便学生能用简单的算理直接进行计算。
在开展教学时，首先，教师应让学生明白异分母分数加减计算的必要性。教材中通过计算两个小朋友折纸所用纸的数量提出异分母分数的加法，目的是说明在实际生活中存在着这样的需求。当然，教师们在设计教学时，也可以根据当地的实际情况进行设计。其次，帮助学生理解异分母分数加法的算理。教材中安排折纸活动是为了学生能直观地理解两个不同分数相加在图形上所呈现的特点，从而使学生知道这两部分的相加并不是分母与分母、分子与分子简单的相加。因此，如何相加应成为计算的重点。当学生初步理解先通分、后相加的算理后，教师仍应结合直观图形，请学生说明为什么要先通分的道理，以进一步加深学生对算理的理解。最后，在独立探索中掌握异分母分数的减法。在学生掌握异分母分数的加法后，教师可以直接出示相应的减法，供学生进行独立探索。教师可以请学生在尝试后开展交流，也可以请学生用直观的图形来说明自己的思考过程，以帮助一些有困难的学生能形象地理解异分母分数的减法。
根据《标准》的要求，异分母分数的加减法不要出现过分烦琐的分数，以减轻学生不必要的负担。
星期日的安排教学目标
1．通过直观的操作活动，理解异分母分数加减法的算理。
2．能正确计算异分母分数的加减法。
教材分析与教学建议
在三年级时，学生已经学习了简单的同分母分数的加减法，本课时的分数加减法主要是异分母分数的加减法。为了让学生直观地认识异分母分数加减法的必要性，教材安排了折纸活动，感受计算异分母分数加法的必要性。接着，又提出了估一估与算一算的要求，并用两种提示性的算法，说明学生在探索中可能出现的思考方法。对于异分母分数的减法，教材则直接呈现了计算的方法，主要是让学生运用知识迁移的方法，能直接进行减法的计算。在“试一试”的练习后，教材安排了对异分母分数加减计算方法的归纳，以便学生能用简单的算理直接进行计算。
在开展教学时，首先，教师应让学生明白异分母分数加减计算的必要性。教材中通过计算两个小朋友折纸所用纸的数量提出异分母分数的加法，目的是说明在实际生活中存在着这样的需求。当然，教师们在设计教学时，也可以根据当地的实际情况进行设计。其次，帮助学生理解异分母分数加法的算理。教材中安排折纸活动是为了学生能直观地理解两个不同分数相加在图形上所呈现的特点，从而使学生知道这两部分的相加并不是分母与分母、分子与分子简单的相加。因此，如何相加应成为计算的重点。当学生初步理解先通分、后相加的算理后，教师仍应结合直观图形，请学生说明为什么要先通分的道理，以进一步加深学生对算理的理解。最后，在独立探索中掌握异分母分数的减法。在学生掌握异分母分数的加法后，教师可以直接出示相应的减法，供学生进行独立探索。教师可以请学生在尝试后开展交流，也可以请学生用直观的图形来说明自己的思考过程，以帮助一些有困难的学生能形象地理解异分母分数的减法。
根据《标准》的要求，异分母分数的加减法不要出现过分烦琐的分数，以减轻学生不必要的负担。
星期日的安排教学目标
1．理解分数加减混合运算的顺序。
2．能正确计算分数加减混合运算。
教材分析与教学建议
日常生活中，经常会遇到一些需要运用分数计算的方法来解决的问题。本课时提出的“留在家中的同学占全班同学的几分之几？” 就是这样的问题。教材在安排分数加减混合运算时，继承了本套教材的特点，在解决具体的问题中引出分数加减混合运算，从而使学生体会到这一知识的来源与学习的必要性。在学生列出算式后，教材安排了两种解决的方法，但这并不代表所有的解法，学生在实际解题时，可能还有不同的算法，只要学生说得合理，教师就应该给予鼓励。
根据教材呈现的内容，在开展教学活动时可以从下面几个方面思考：
一是适当地开展一些调查活动，为引出具体问题作好铺垫。教材中安排的调查活动是“星期日的安排”，通过星期日三种形式的安排，引出了问题。当然，在实际教学时，也可以根据当地学生星期日安排的习惯，来开展教学。
二是讨论怎样列出算式。虽然提出的问题是求剩余，学生在中低年级已大量接触这一类
数量关系，但是本题涉及的是分数中的剩余问题，其理解比整数要困难得多，特别是把全体学生看作整体“1”，并作为总数进入运算，这对学生来说是十分抽象的。对此，提出问题后，可以让学生独立尝试列式，随后再组织讨论，以充分发挥学生的积极性。在讨论时，重点要讨论总数“1”的问题，只有每个学生理解 “1”可以代表全班的学生数量后，才能进行后面的具体运算。
三是讨论具体的运算过程。教材中已经呈现了两种具体的运算过程，学生在解答时将会
出现丰富多彩、各种各样的方法，主要有：先全部通分，再进行计算；先从“1”中减去部分，再用剩余的减去另外部分；先计算两个部分的和，再从“1”中减去“和”；等等。对于学生的每种具体运算，不要过早地比较运算的简便与烦琐，相信高年级的学生在交流中，自己会吸取其他同学的好方法。
四是适当地安排一些练习活动。
看课外书时间教学目标
1．理解分数、小数相互转化的必要性。
2．能正确地将简单的分数化为有限小数。
3．能正确地将有限小数化为分数。
教材分析与教学建议
在学习本课时的知识前，学生分别认识了分数与小数，也会比较分数的大小与小数的大小，而本课的内容则是在这一基础上的发展。为了提高学生学习的挑战性，教材出示了两个小朋友课外看书的时间，但呈现的方式一个是用分数，一个则是用小数，然后请学生比一比“谁用的时间多一些？”为解决这个问题，教材呈现了四种思考的方法：第一种用画图的方法，直观地比较两个小朋友看书的时间；第二种通过简单推理的方法，得出谁用的时间多一些；第三种是将分数表示的时间转化为小数，然后再比较时间的多少；第四种则是将小数化为分数，然后再比较。在探索问题的过程中，教材将分数与小数的相互转化方法渗透在其中。一般地说，分数化为小数是运用分数与除法的关系， 即用分子除以分母；而小数化为分数则是先把小数化为十进分数，然后再进行通分。这也是本课时教学的重点。
在开展教学时，建议注意以下几个方面：
一是问题的引入。教材在比较看书的时间中，提出了需要解决的问题。这一点在教学设计时需要有明确的指导思想，并让学生知道学习这部分知识的必要性，以引起他们学习的需求与兴趣。
二是解决问题的探索。比较两个用不同形式表示的数，这是一个新知识，也是学生认知上的新冲突。如何解决这种冲突则需要学生自己进行探索。为此，教师不要过早地将解决问题的方式告诉学生，可以为学生准备一些材料，以供他们进行探索。可能学生的探索并没有书上所呈现的那么完整，但这并不影响他们的探索。教师不需要千方百计地去引导，如果学生确实没有思考到，教师也可以从一个参与者的角度，提供一些自己的思路，以供学生进行讨论。
三是分数与小数相互转化的讨论。分数与小数的相互转化是本课时的重点，学生在上述的探索中，可能会出现这些实例，对于学生的这些实例教师不要过早地加以概括，可以再出示一些类似的题目供学生练习，在一定量的练习后再组织学生进行概括。如分数化小数，在探索中学生可能会解决14转化为小数的问题，接着可以继续安排15，12等分数怎样转化。

五 : 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

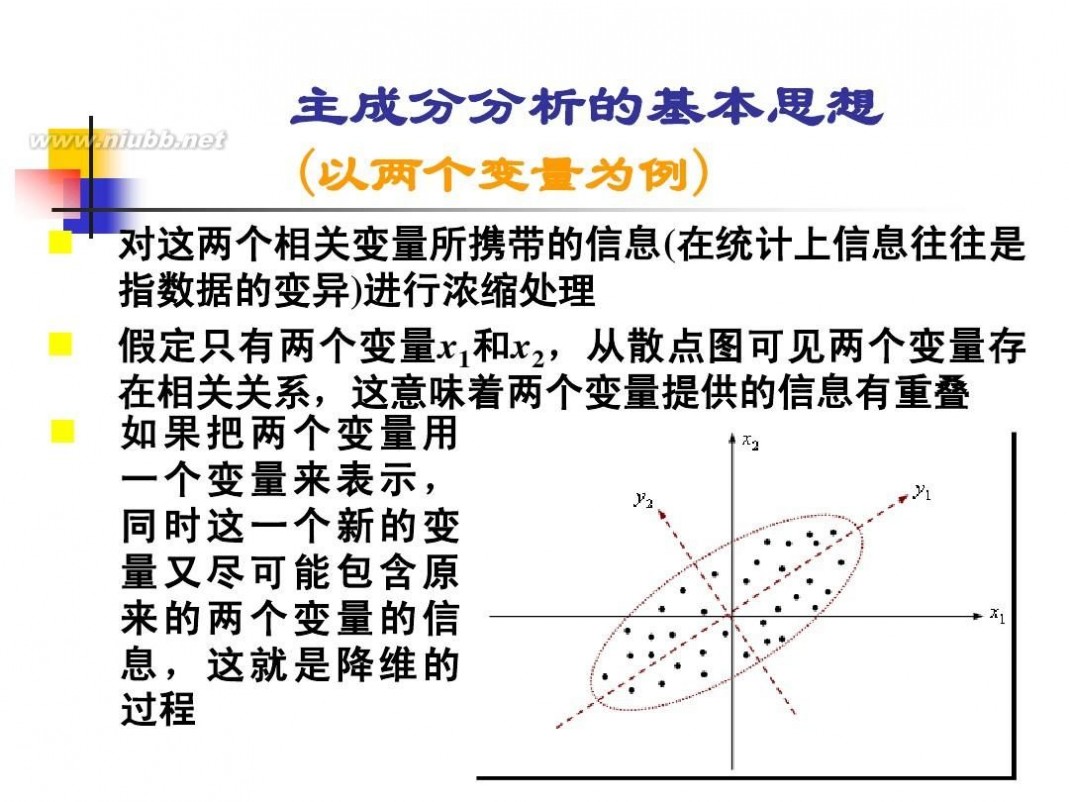
因子分析模型 数学建模因子分析

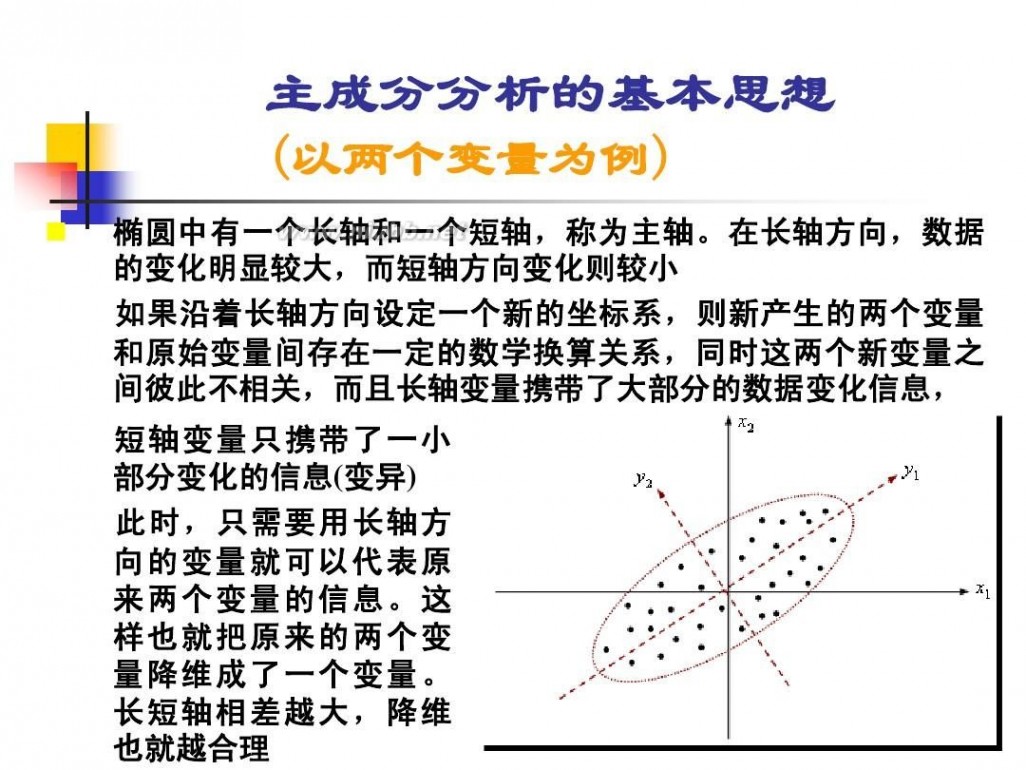
因子分析模型 数学建模因子分析

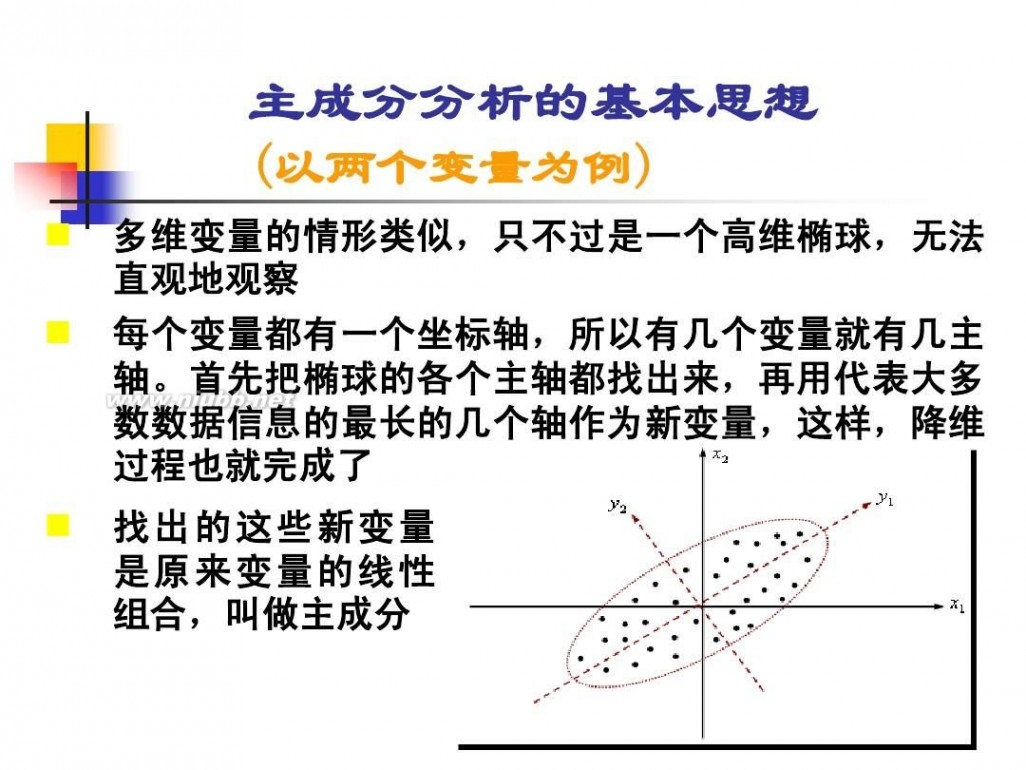
因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

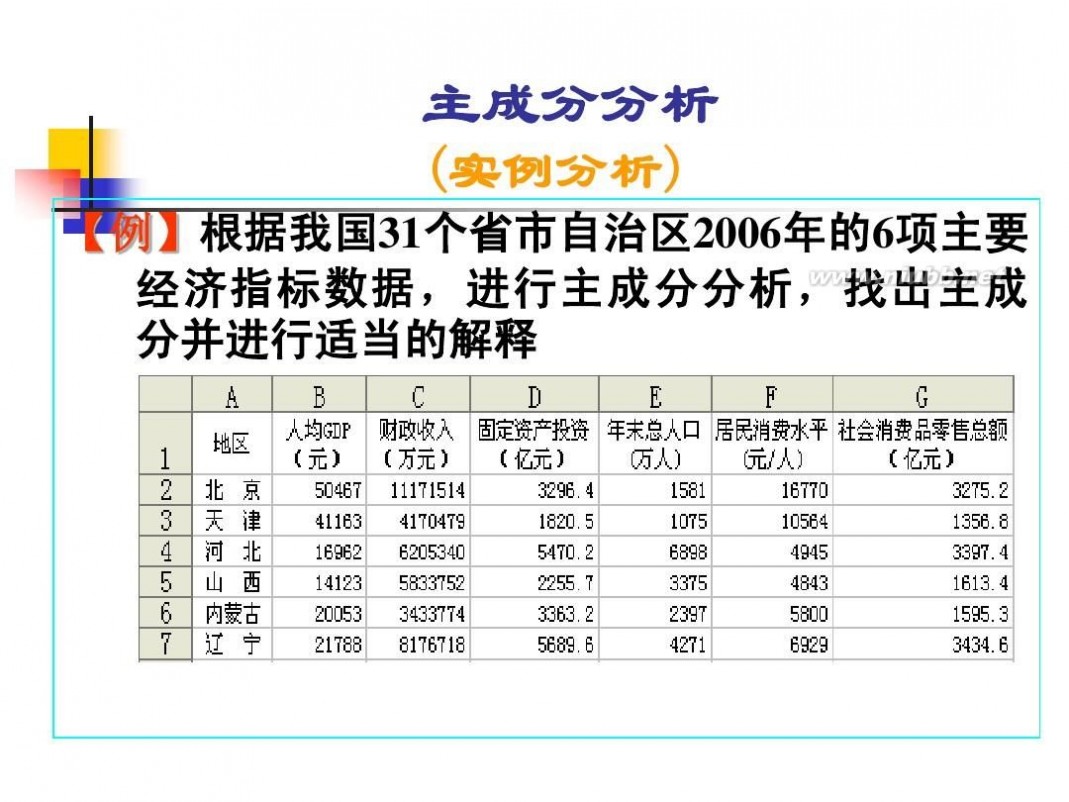
因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

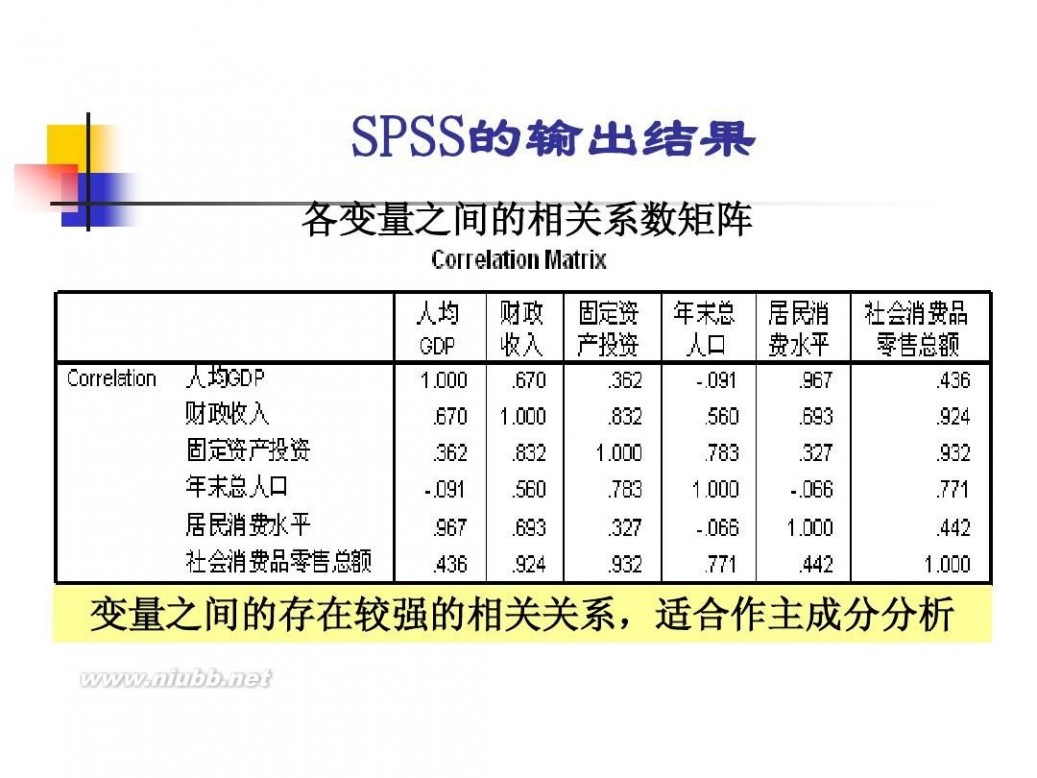
因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

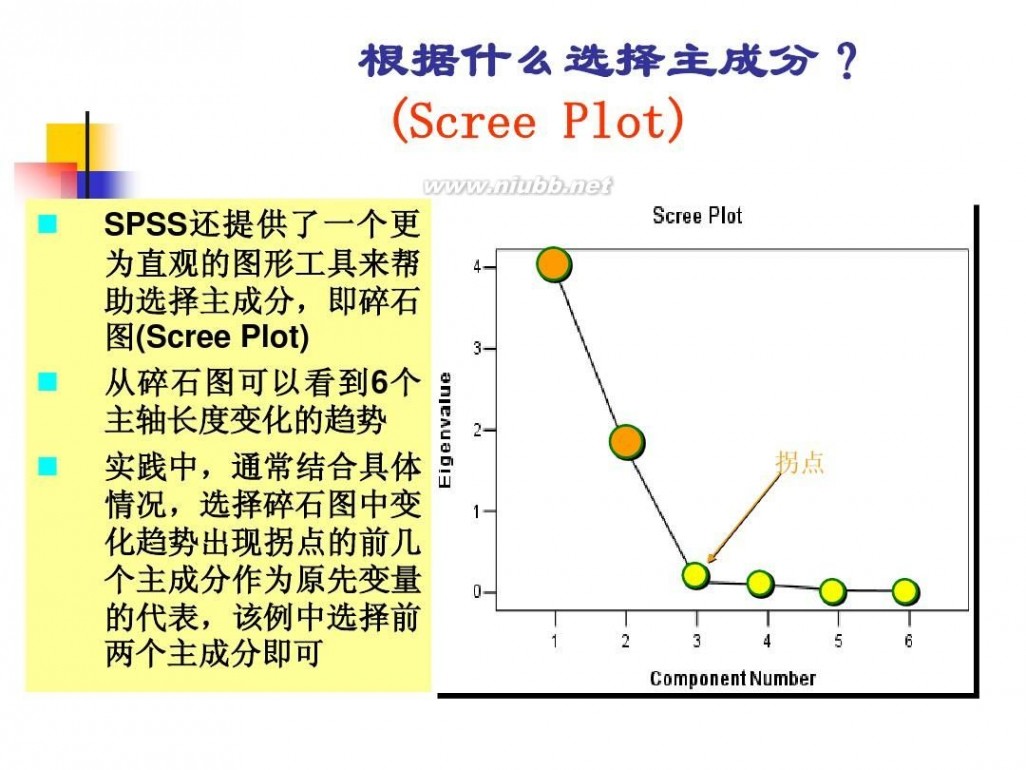
因子分析模型 数学建模因子分析

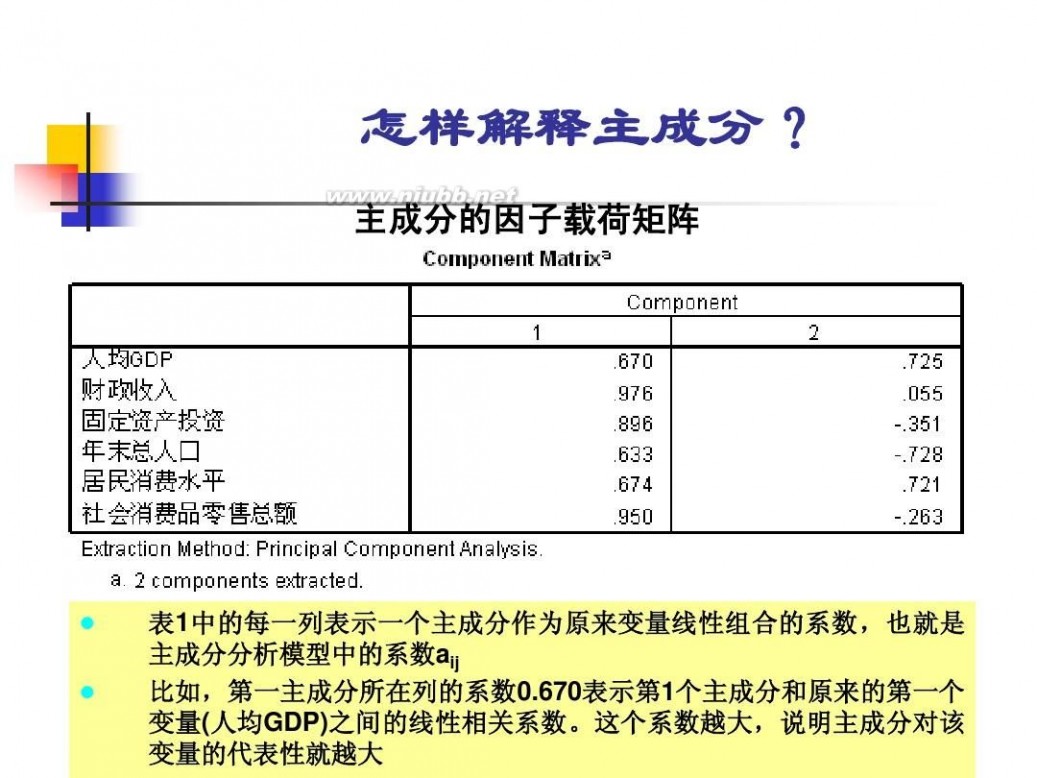
因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

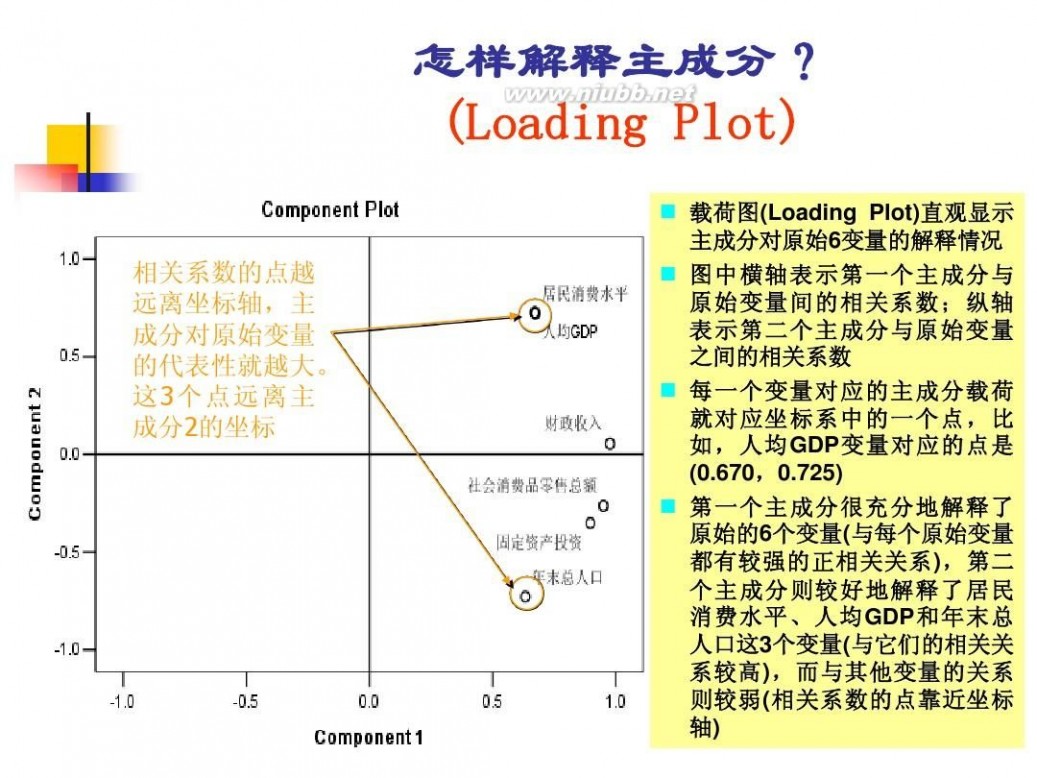
因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

61阅读提醒您本文地址：

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

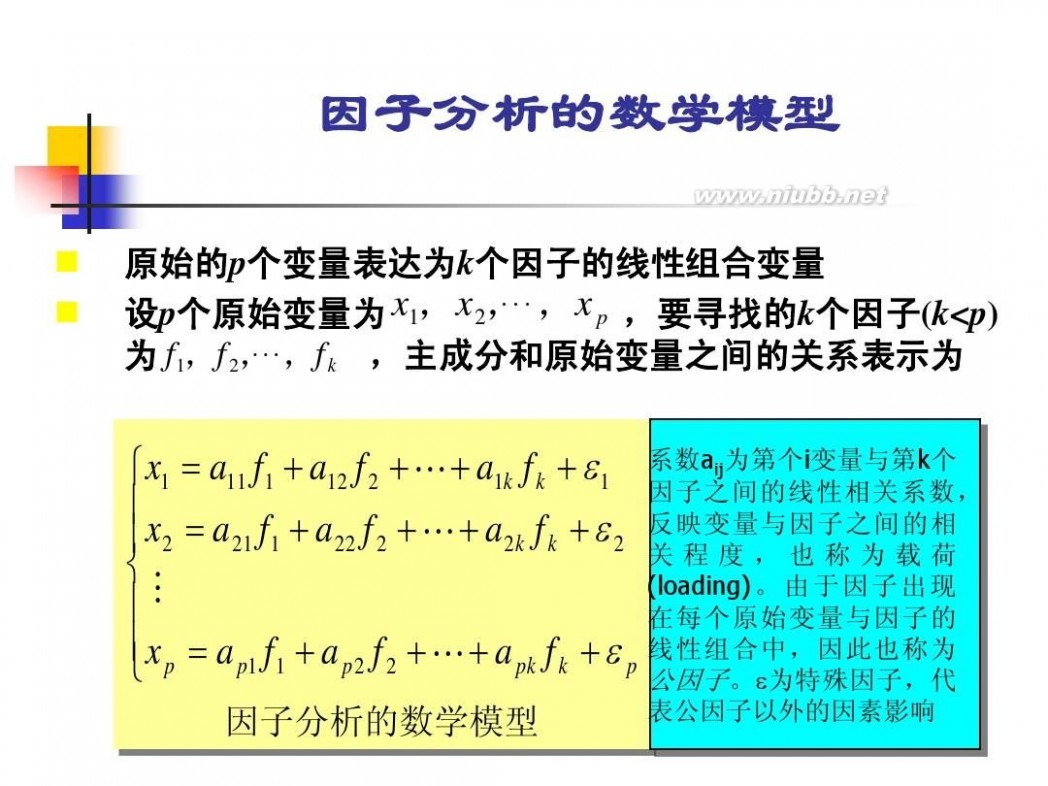
因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

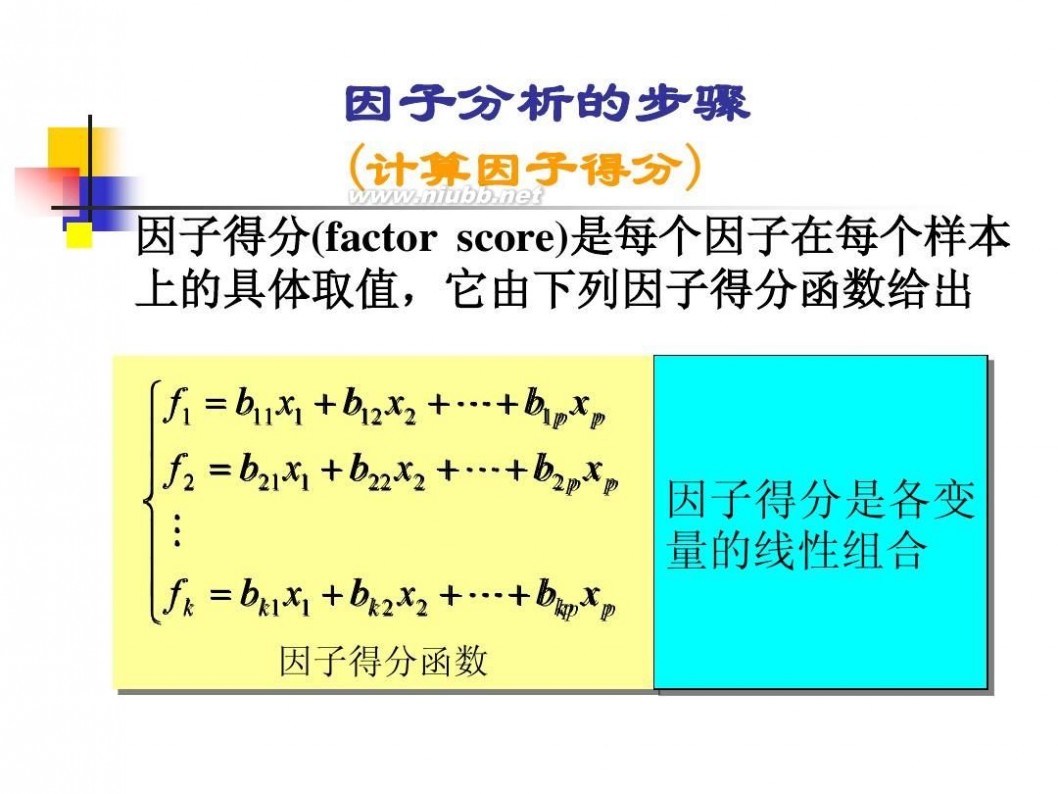
因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

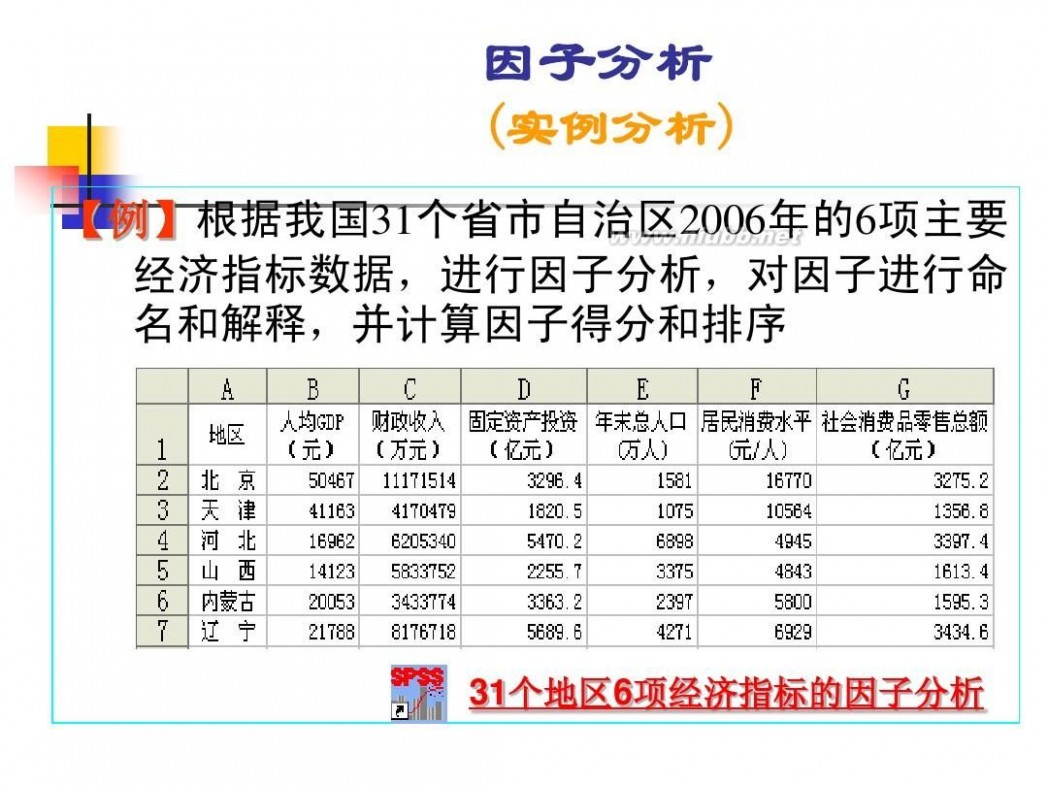
因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

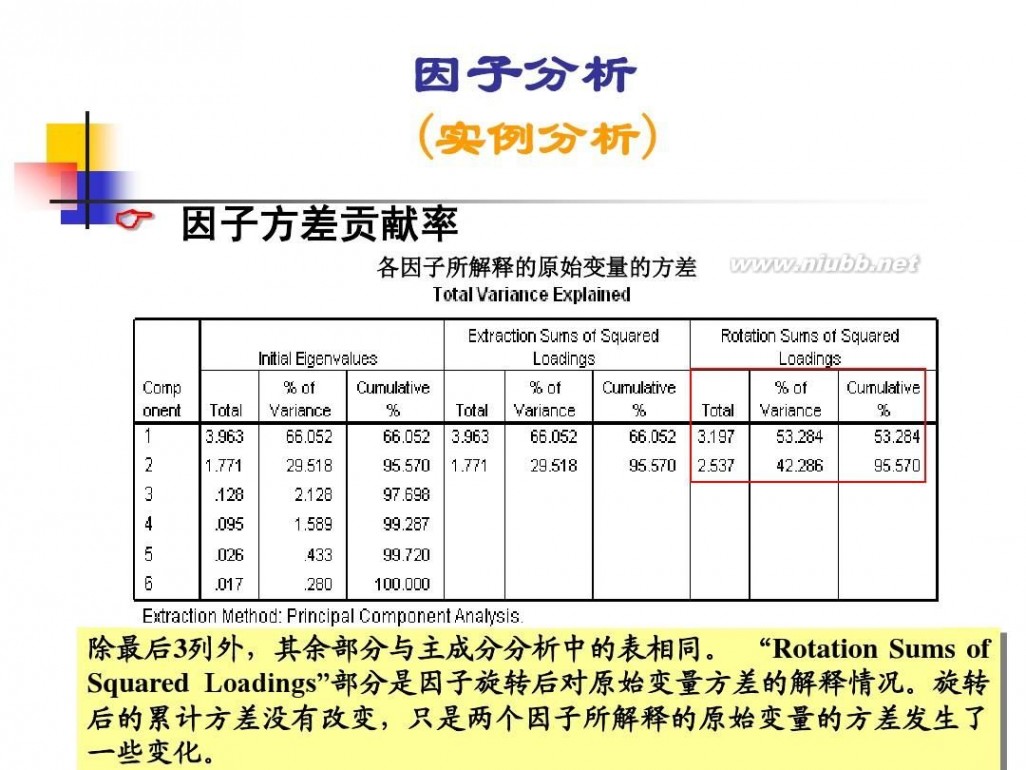
因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

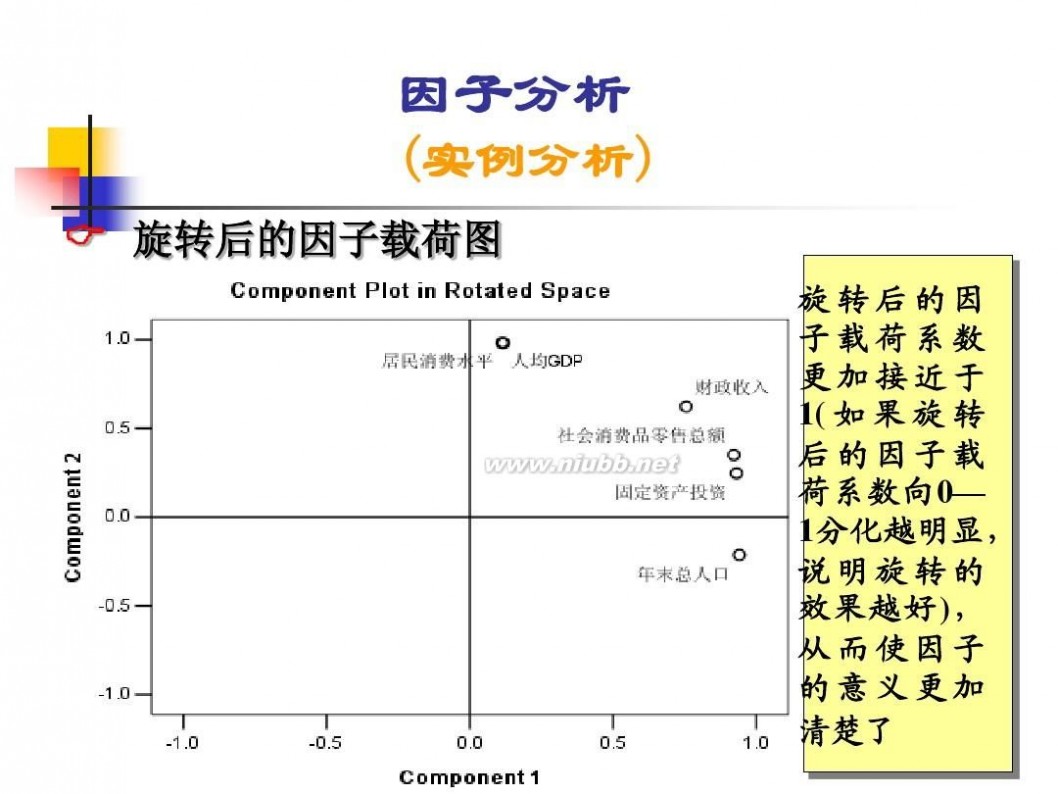
因子分析模型 数学建模因子分析

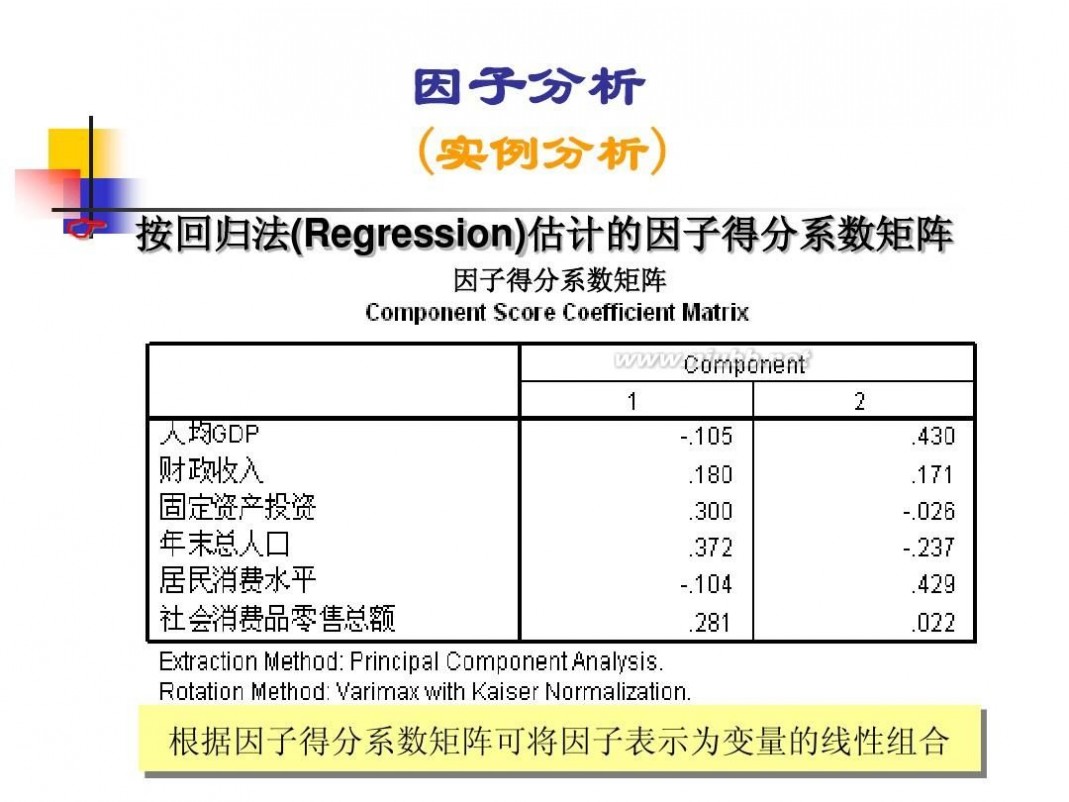
因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

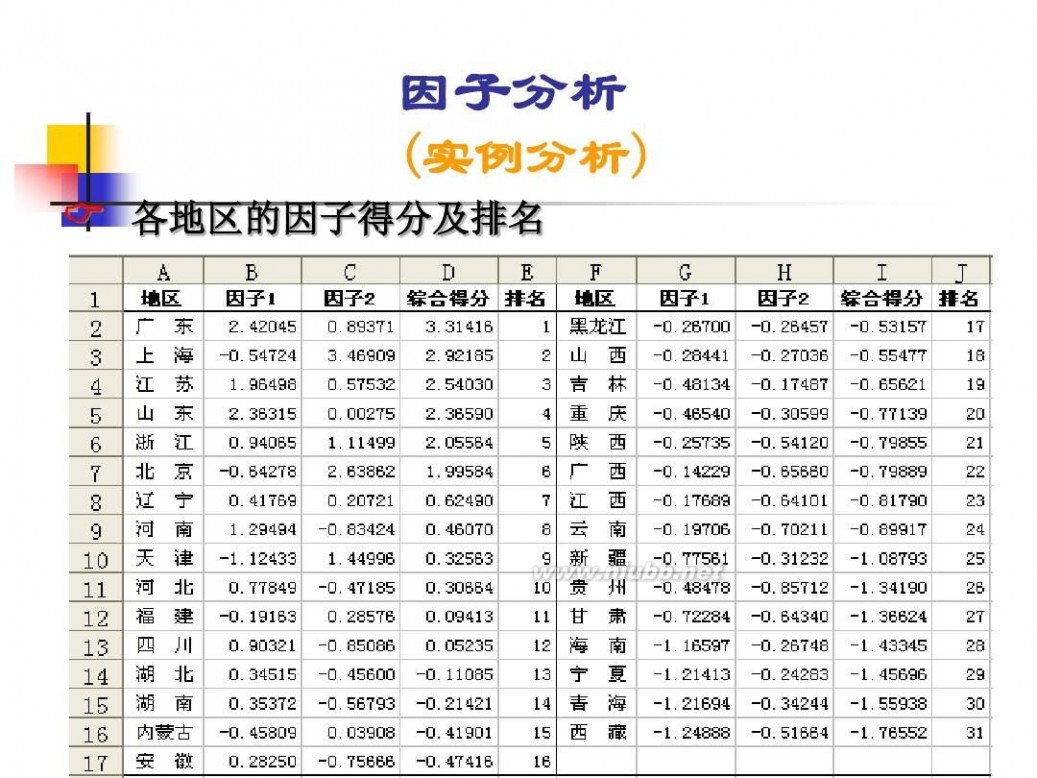
因子分析模型 数学建模因子分析

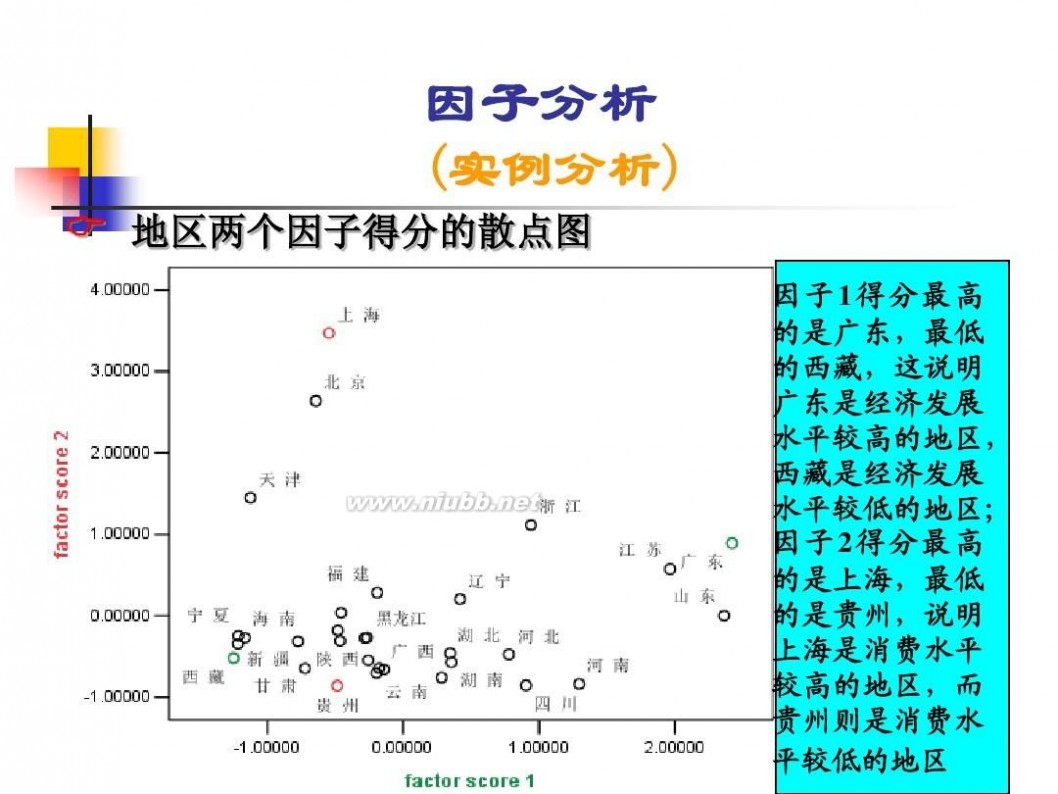
因子分析模型 数学建模因子分析

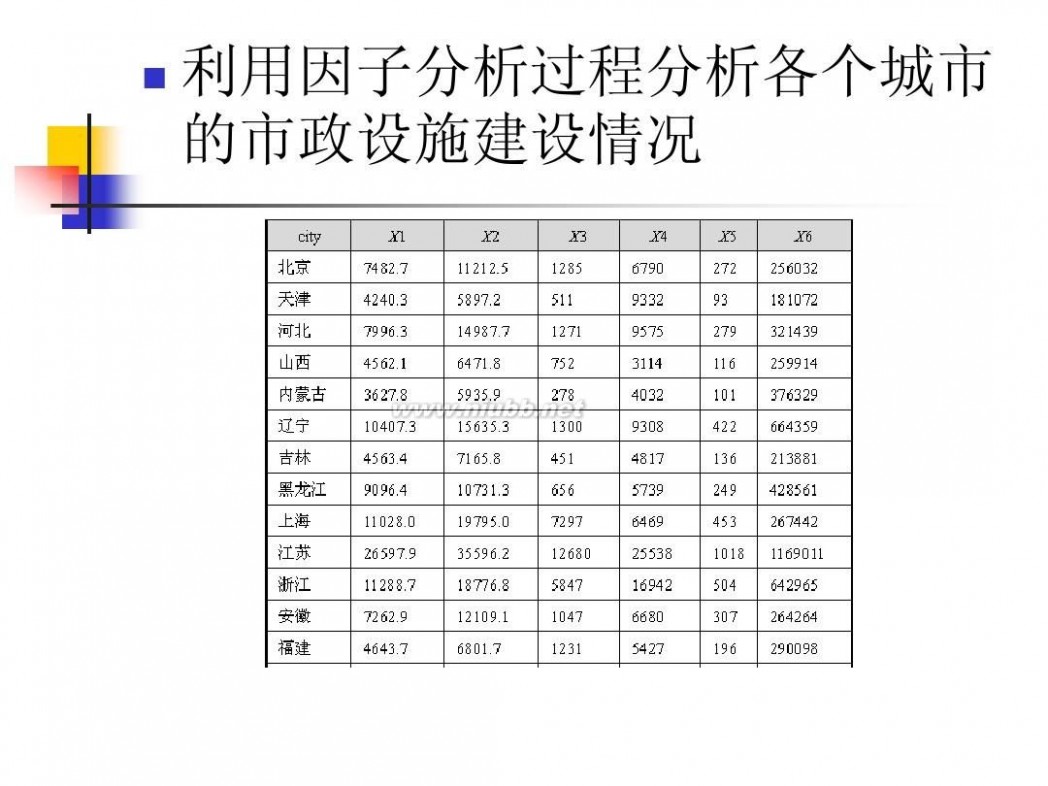
因子分析模型 数学建模因子分析

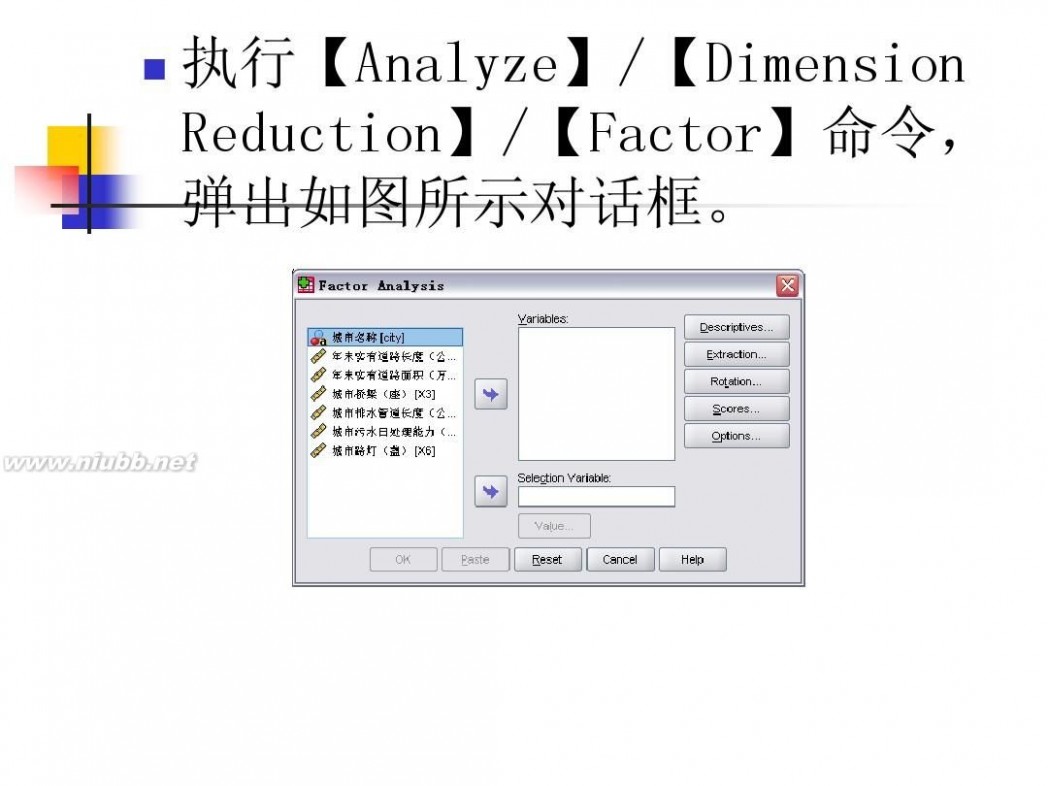
因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

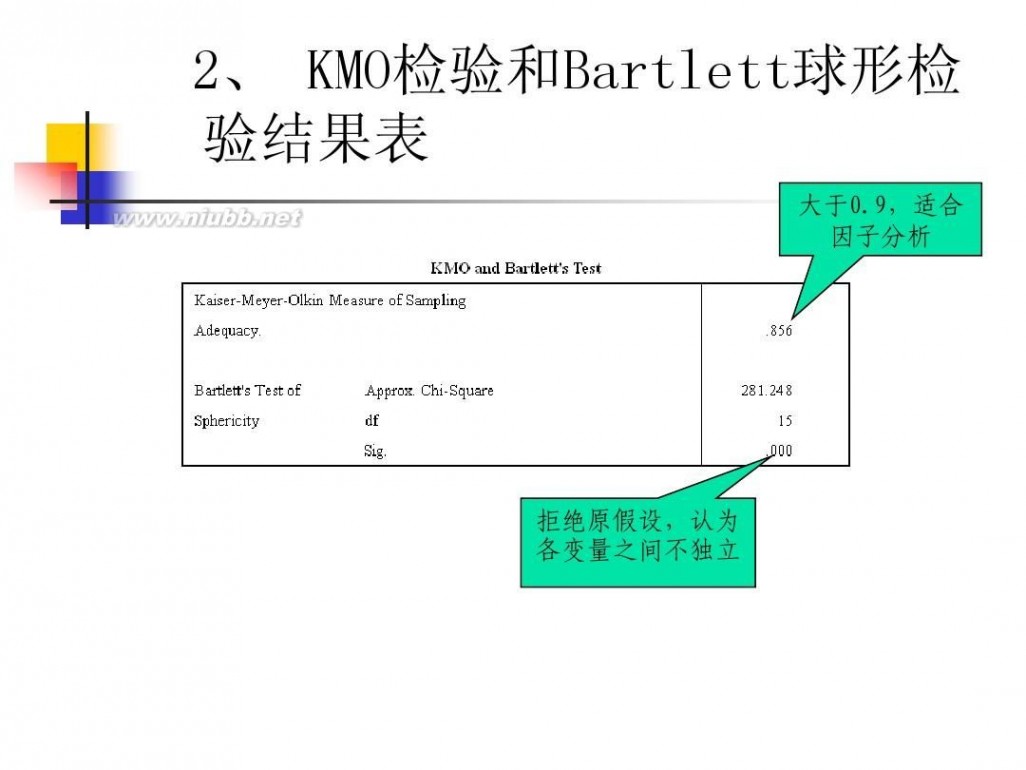
61阅读提醒您本文地址：

因子分析模型 数学建模因子分析

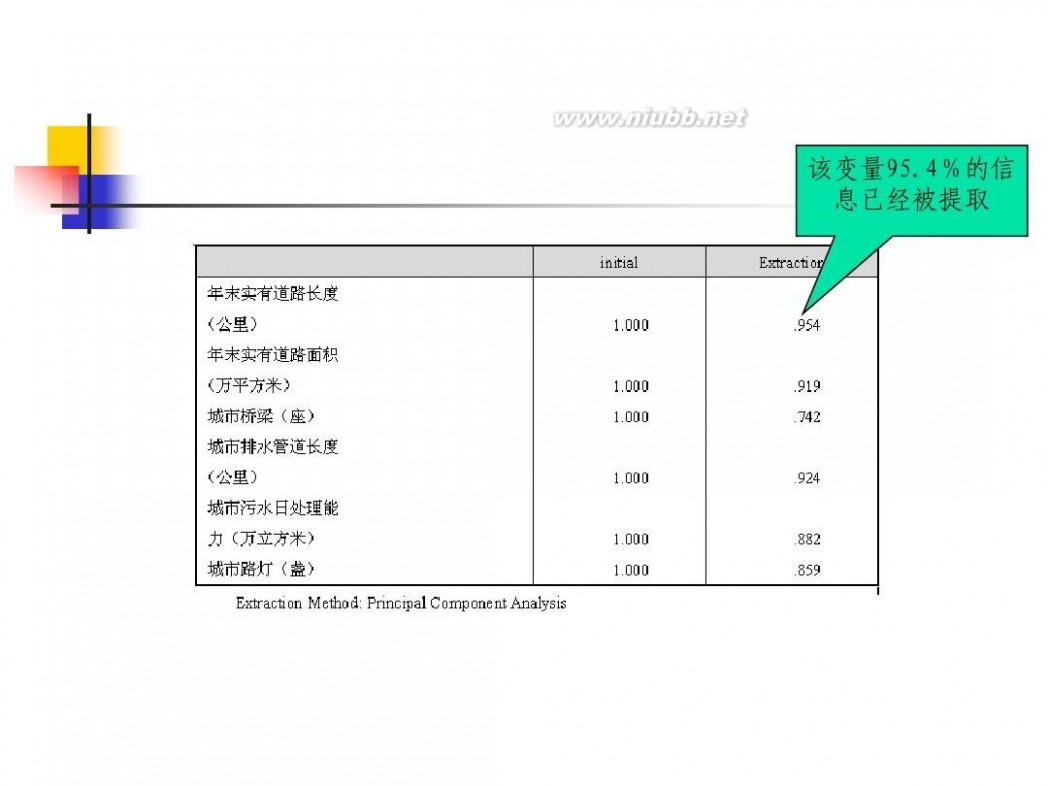
因子分析模型 数学建模因子分析

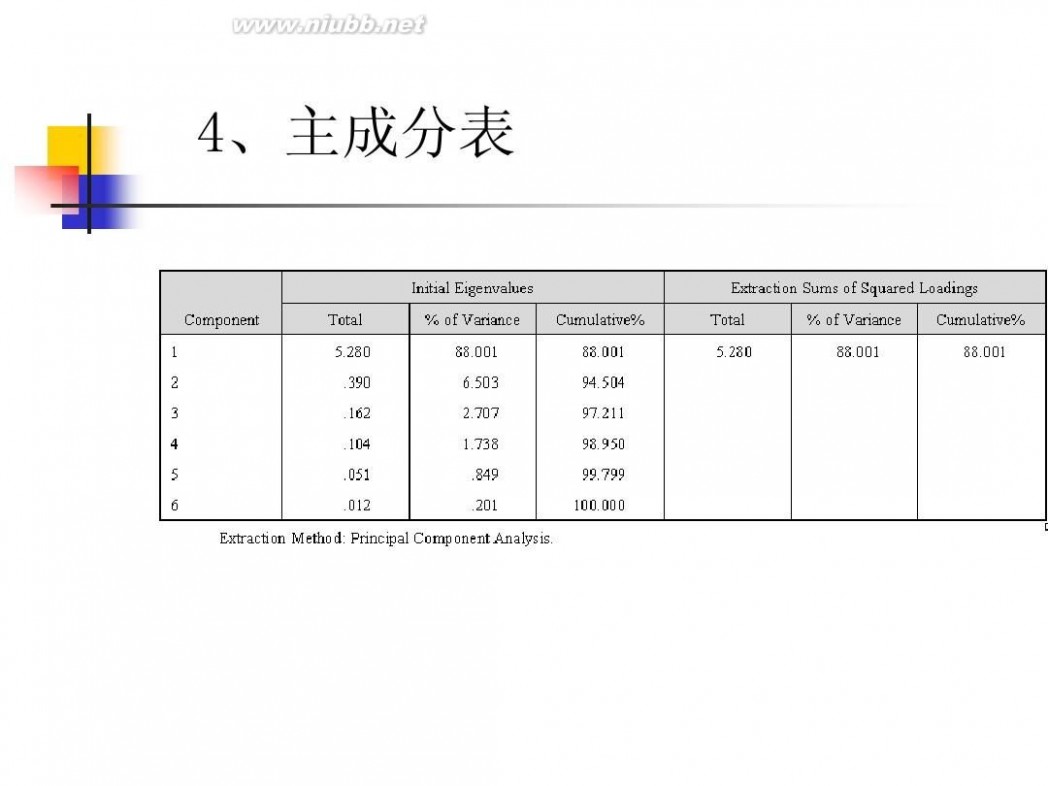
因子分析模型 数学建模因子分析

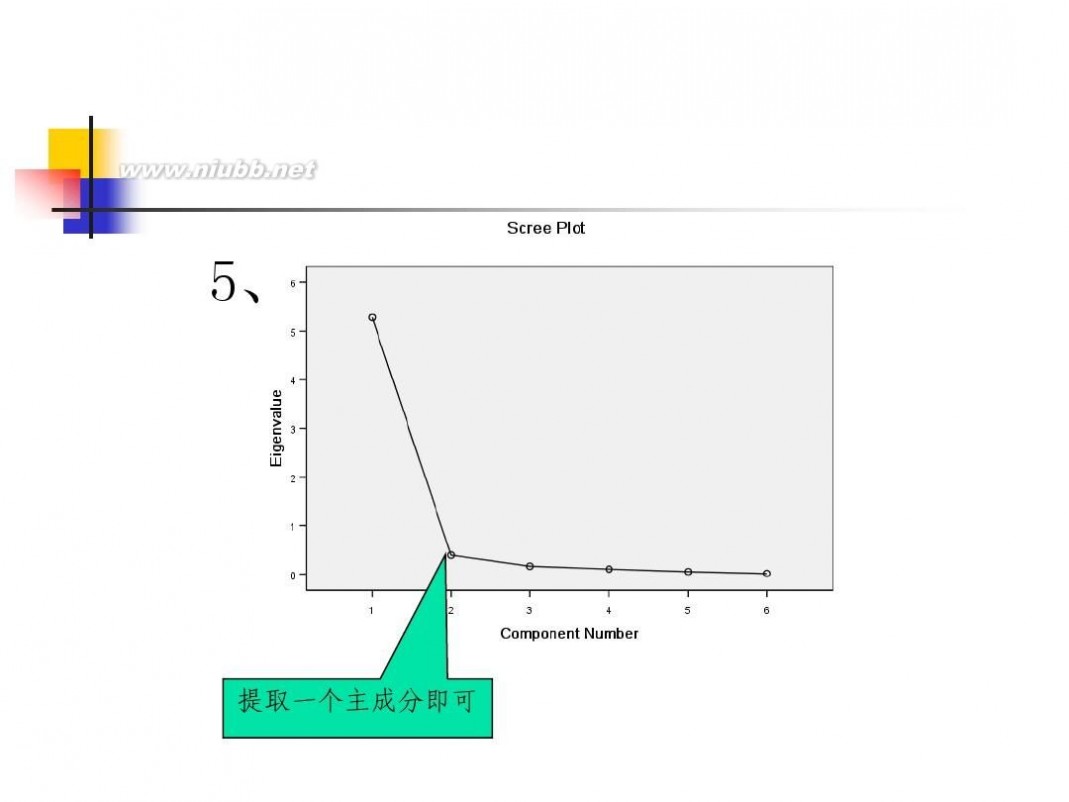
因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

因子分析模型 数学建模因子分析

61阅读提醒您本文地址：

本文标题：数学建模方法与分析-模糊数学分析方法
本文地址： http://www.61k.com/1124896.html