一 : 五一旅游防晕车妙招大全
晕车是怎么回事?
晕车这种感觉源自于感觉平衡的神经器官——前庭。前庭是我们的平衡器官,位于耳朵深处。它的里面生长着很多小毛毛,在充满液体的空腔里,像水草一样在摇动。“水草”的下面通过神经连着大脑。我们头一动,这些“水草”就跟着晃,大脑就知道了。
如果把我们蒙上眼睛捆在椅子上,固定在一个封闭的小空间里往死里摇——就像游乐园里一些机器做的一样,虽然我们得不到任何视觉、听觉、触觉上的提示,但也能大致感觉到现在是大头朝下还是朝上。这就是前庭的功能。
哪些方法可以解决晕车问题或者减轻晕车症状呢?
睡眠法:您准备出游前,应保证足够的睡眠,以提高人体对旅途中颠簸刺激的适应能力。
饮食法:出游前应尽量避免摄入高脂、高蛋白食品,以防胃负担过重,加上旅途颠簸而使胃“翻江倒海”。在旅途中也要注意适度进食,每顿以吃七八分饱为宜。
心理调适法:放松、愉悦的心情对消除晕车具有十分重要的作用。在旅游途中,不要总担心自己会晕车,而应通过与别人聊天、唱歌、做些小游戏的方式分散自己的注意力。
远视法:首先,入座时要与汽车行驶方向保持一致。其次,在车辆行进过程中,不要在车上读书看报或看窗外一闪而过的东西,而应将视点集中于远方。
口含法:在上车前即含两片鲜姜,途中可以含话梅、陈皮等。
鼻吸入法:将两片鲜姜或薄荷精存于口罩或手帕上,并置于鼻孔下,在途中吸入。也可将新鲜橘皮对准两个鼻孔后用力挤压,使皮中汁液喷射到鼻孔中,反复吸入。
穴位疗法:乘车前,滴两滴风油精或取一片鲜姜或鲜橘皮敷于神阕穴(肚脐)上,用伤风止痛膏敷盖。也可将风油精或清凉油涂擦于太阳穴、风池穴、内关穴处。
药物疗法:在乘车前半小时至一小时服用胃复安、安定等药物,以便在乘车后产生药效。在长途旅行过程中,还要根据药品说明规定,每间隔几小时重复服用药物。要注意有些抗晕车药在服用后会出现口干、头晕等副作用。
其他疗法:保证车内通风,稍微束紧腰带。
只要乘车前注意采取上述措施,就会减小您晕车的机率或减轻晕车的程度。
相关阅读:5月旅游景点大推荐,适合五一旅游的地方 适合情侣五一节去旅游的十大景点 2012年五一上海旅游大攻略
二 : 绝对要收藏!史上最实用的防治过敏大全
过敏性疾病如过敏性鼻炎、哮喘和湿疹、荨麻疹等已经成为当今影响健康的全球性疾病。(www.61k.com)相信有过过敏的人都知道,过敏的滋味很不好受!
健康时报记者综合多位专家观点,为您奉上一份防治过敏大全,让您以后生活无忧!
鼻子痒、打喷嚏

过敏性鼻炎是鼻腔粘膜的变应性疾病,主要表现为鼻痒、喷嚏频频、流清鼻涕、鼻塞等症状,这些症状可自行或经治疗后消失,常伴有过敏性结膜炎的症状如眼痒、流泪等。
过敏性鼻炎的核心过敏原,如尘螨、霉菌、猫毛狗毛等一年四季都存在,以尘螨为主要过敏原的过敏性鼻炎发作几率很大。
治疗招
1、鼻喷或口服抗过敏药物
对于一年累计发作小于一个月,对生活影响不大的患者来说,主要以药物治疗为主,鼻喷或口服抗过敏药物。对于症状较重,一年累计发作大于三个月,出现哮喘的倾向,如胸闷、咳嗽、喘息的患者,要进行脱敏治疗,疗程通常为2~3年。
2、名医的中药方:“过敏煎”
已故著名中医肝病专家关幼波,有一个治疗过敏性鼻炎的验方,叫做“过敏煎”,分享给大家:柴胡10克、白芍20克、蝉衣6克、鸟梅10克、甘草10克,一日一服,水煎服。
3、吃乌梅
乌梅养阴,有很好的收敛补益效果,同时可以抗过敏。此外,过敏性鼻炎大都与气虚、肺脾虚有关,可以适当吃些玉屏风制剂,同时吃些山药薏米粥,补肺健脾。中国中医科学院西苑医院的院内制剂玉蝉卫肺丸是著名老专家经验的总结,对过敏性鼻炎有很好的疗效。
预防招
以往我们认为勤换洗家居用品、使用防螨床罩就能起到很好的阻隔效果,其实不然。调查发现,和螨虫含量关系最密切的是使用年限。被子、棉絮、枕头使用年限越长,螨虫越多。如果家里有过敏性鼻炎发作厉害的人,使用超过三年的就应该换新。
长时间待在空调房间里,很多人会频繁打喷嚏,这是因为受冷空气刺激所致。预防很简单,调高温度多活动。将室温调高,并定时开窗,每隔一小时走出空调房活动一下。
皮肤肿、起疱疹

吃了口海鲜、被蚊子叮了下、多吹了空调、免疫力下降等都可能诱发。被蚊虫叮咬后会皮肤瘙痒,出现红斑、风团,这是皮肤对蚊虫体液的过敏反应,一般很快就会消除;还有人可能会出现皮炎或者丘疹性荨麻疹,表现为皮肤增厚或出现丘疱疹、水疱,难以速愈。
治疗招
1、不要挠和热敷
荨麻疹“不能挠,不能热”,即使是寒冷型的,也别想当然地认为热敷下会好。荨麻疹都是皮肤毛细血管扩张导致的,一热敷反而会加速毛细血管扩张,使症状加重。
2、试试擦韭菜
取新鲜韭菜一把(约250克),洗净,用宽带扎紧,在韭菜根部切掉一小段,令其露出横切面,以此横切面对准患部擦摩。擦完韭菜汁后再用刀切出新鲜横切面,继续擦摩患处。擦完一遍后,休息5~10分钟,同法再擦第二遍,每日擦2~3遍。
预防招
远离水草多的地方
老年人晨练晚练时最容易被叮咬,因此应避免在水边及花草多的地方。傍晚时蚊子出没最频繁,应避免在树荫、草丛等处长时间逗留。
如果被蚊虫叮咬,一旦感染上荨麻疹,千万不能抓挠,以防继发感染;出现比较严重的过敏反应时,应尽快去医院皮肤科进行治疗,有针对性地采用比较强效的抗炎药物,以免引起伤口感染和损伤。
皮肤发红发痒

夏季引起皮肤过敏的原因很多,但主要由于紫外线晒伤、饮食不当或蚊虫叮咬、防晒霜等护肤品使用不当等引起。
治疗招
脸上过敏用点软膏
对于面部皮肤过敏者,可以选择非激素类止痒抗炎药物,或短期弱中效的软性糖皮质激素。这类药物较为便宜,而且性价比高。对于病程长、反复发作的面部皮肤过敏,可以选用0.1%的吡美莫司软膏等,比激素类药物副作用小,相对安全一些。
如果用药过程中出现病情加重、外用药物过敏等现象,要马上停药并去医院就诊。
预防招
1、防晒
暴晒后出现皮肤红肿、瘙痒等表现,就是因紫外线引发过敏的典型症状。
尽量避免在午后阳光炽烈时外出。其他时段外出选择戴帽子、遮阳伞防晒。选择防晒品时先在耳后或手腕处局部试用。
对于5、6岁以下年龄较小的孩子,皮肤更娇嫩,可采用戴宽边遮阳帽、遮阳伞、穿长袖衣裤等物理防晒方式。
2、衣服消毒+硫磺膏
外出住宿,难免接触到一些不干净的被褥,再加上消毒不彻底,一些疥疮病毒很容易在被褥中残留。
疥疮能够通过密切接触传播,而且传染性很强。即使个人很干净,也有传染上疥虫的可能。
防止疥虫传播,避免沾染其他的携带病菌,最好在外出归来后将衣物进行消毒。可以用开水对衣物进行热烫,也可以用适量的消毒液浸泡。
一旦感染了疥疮,也不必惊慌,在用药上,每天使用硫磺膏涂抹一次,连用三天就能有效缓解病情。
哮喘

夏季湿热多雨,而这种潮湿气候正是室内各种螨类、霉菌类物质大行其道的时机,霉菌常年漂浮于空气中,一般在6~7月达到高峰。而这,正是引发呼吸道疾病的罪魁祸首。居住在有霉菌的室内,患支气管炎和咽峡炎的风险更大。
治疗招 61阅读请您转载分享:
1、用电吹风吹穴位
用电吹风的热气反复吹以三阴交穴(此穴位于小腿内侧,内踝高点上4 横指,胫骨内侧面后缘处)为中心的小腿内侧,使穴位受刺激发热,3~5分钟后,再按摩上述穴位,可反复多次。“按摩+电吹风吹穴位”具有预防呼吸道感染,缓解因气管、膈肌痉挛引起的过敏性哮喘。
2、试试食疗法
食物疗法对过敏性疾病尤其是哮喘很有效。
寒喘:手足冷,鼻塞流涕,痰白稀,舌淡。取北瓜一只,去籽洗净,切成小块状,煮透去渣留汁,浓缩后加入饴糖500克,再熬汁10分钟,最后倒入姜汁,再拌蜂蜜500克而成,每次1匙,每日两次,有散寒平喘作用。
热喘:咳喘,痰色黄,口渴,舌红。取豆腐500克,麦芽糖500克,生萝卜汁100克,混合煮开,每日两次,有清热化痰平喘的功效。
虚喘:面色苍白,气喘,乏力。取山药100克,枸杞子30克,冰糖15克,加水煮烂,做点心服用,有健脾补肾防喘作用。
预防招
清除雨天室内过敏原的主要方法是常通风,保持空气流通和房间干燥,居室要经常吸尘,以消灭尘螨。
对花粉过敏的哮喘患者,要最大限度地减少花粉吸入。中午日晒最强,花粉的释放量最多,此时哮喘患者最好不要外出,如果外出一定要戴口罩。
眼痒、流眼泪

过敏性结膜炎,隐形眼镜族最易中招。一旦风沙、花粉、尘螨等被吹入眼,会附着在隐形眼镜上,加之人们本能地揉眼睛,对眼球造成机械性摩擦,就易因眼部感染而导致过敏性结膜炎。
发作时常感眼部奇痒,常伴鼻子痒,打喷嚏等症状。此外还常伴有结膜充血、水肿,有粘性分泌物等。
治疗招
首先,冷敷
治疗不要着急用眼药水,可先用冷敷来缓解症状,比如包个湿毛巾放眼睛上冷敷约15~20分钟,每天多次,同时用生理盐水冲洗结膜囊。
其次,眼药膏
如果症状很重,冷敷不好用的时候,可以适当点色甘酸钠滴眼液、皮质炎固醇眼药等,每天3~4次;如果病情严重或使用常规药物治疗无效的过敏性结膜炎患者,在医生指导下可短期内使用激素类药水。
预防招
游泳后点几滴眼药水
游泳时应当注意眼部卫生,以免患上急性结膜炎。
最好的预防方法是佩戴密闭性较好的游泳镜,尽量避免眼睛接触到池水。如果眼睛接触到池水,可以在游泳后点几滴抗菌素眼药水,防止细菌病毒的侵袭,同时还可以起到清洁眼结膜的作用,对预防红眼病有一定的作用。
小贴士
药箱备点抗过敏药
常用的抗过敏药有扑尔敏、苯海拉明、氯雷他定、西替利嗪等,小孩可喝氯雷他定糖浆。需要提醒的是,有的抗过敏药有嗜睡作用,不建议司机朋友使用。
因为每个人各自的过敏原不一样,这是需要由医生进行检查诊断的,查出过敏原后,再进行针对性治疗。
常过敏喝喝五味子茶
中药五味子对于抗过敏的效果较突出,过敏性哮喘、过敏性鼻炎、过敏性肠炎,还有湿疹,可以在医生的指导下,用五味子10~15克,每日一剂,水煎服,以一周为一个疗程来防治。
61阅读请您转载分享:
三 : 史上最齐全高数公式
高等数学复习公式
高等数学公式
·平方关系:
sin^2(α)+cos^2(α)=1
tan^2(α)+1=sec^2(α)
cot^2(α)+1=csc^2(α)
·积的关系:
sinα=tanα*cosα
cosα=cotα*sinα
tanα=sinα*secα
cotα=cosα*cscα
secα=tanα*cscα
cscα=secα*cotα
·倒数关系:
tanα·cotα=1
sinα·cscα=1
cosα·secα=1
直角三角形ABC中,
角A的正弦值就等于角A的对边比斜边,
余弦等于角A的邻边比斜边
正切等于对边比邻边,
·三角函数恒等变形公式
·两角和与差的三角函数:
cos(α+β)=cosα·cosβ-sinα·sinβ
cos(α-β)=cosα·cosβ+sinα·sinβ
sin(α±β)=sinα·cosβ±cosα·sinβ
tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)
tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)
·三角和的三角函数:
sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγ cos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγ tan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)
·辅助角公式:
Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t),其中
sint=B/(A^2+B^2)^(1/2)
cost=A/(A^2+B^2)^(1/2)
第 1 页 共 19 页
高等数学复习公式
tant=B/A
Asinα+Bcosα=(A^2+B^2)^(1/2)cos(α-t),tant=A/B ·倍角公式:
sin(2α)=2sinα·cosα=2/(tanα+cotα)
cos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α) tan(2α)=2tanα/[1-tan^2(α)]
·三倍角公式:
sin(3α)=3sinα-4sin^3(α)
cos(3α)=4cos^3(α)-3cosα
·半角公式:
sin(α/2)=±√((1-cosα)/2)
cos(α/2)=±√((1+cosα)/2)
tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα
·降幂公式
sin^2(α)=(1-cos(2α))/2=versin(2α)/2
cos^2(α)=(1+cos(2α))/2=covers(2α)/2
tan^2(α)=(1-cos(2α))/(1+cos(2α))
·万能公式:
sinα=2tan(α/2)/[1+tan^2(α/2)]
cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]
tanα=2tan(α/2)/[1-tan^2(α/2)]
·积化和差公式:
sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]
cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]
cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]
sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]
·和差化积公式:
sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]
sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]
cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]
cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]
·推导公式
tanα+cotα=2/sin2α
tanα-cotα=-2cot2α
1+cos2α=2cos^2α
1-cos2α=2sin^2α
1+sinα=(sinα/2+cosα/2)^2
第 2 页 共 19 页
高等数学复习公式
·其他:
sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0
cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0 以及 sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2
tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0
三角函数的角度换算
[编辑本段]
公式一:
设α为任意角,终边相同的角的同一三角函数的值相等:
sin(2kπ+α)=sinα
cos(2kπ+α)=cosα
tan(2kπ+α)=tanα
cot(2kπ+α)=cotα
公式二:
设α为任意角,π+α的三角函数值与α的三角函数值之间的关系: sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
cot(π+α)=cotα
公式三:
任意角α与 -α的三角函数值之间的关系:
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
cot(-α)=-cotα
公式四:
利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
cot(π-α)=-cotα
公式五:
利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系: sin(2π-α)=-sinα
cos(2π-α)=cosα
tan(2π-α)=-tanα
cot(2π-α)=-cotα
公式六:
第 3 页 共 19 页
高等数学复习公式
π/2±α及3π/2±α与α的三角函数值之间的关系:
sin(π/2+α)=cosα
cos(π/2+α)=-sinα
tan(π/2+α)=-cotα
cot(π/2+α)=-tanα
sin(π/2-α)=cosα
cos(π/2-α)=sinα
tan(π/2-α)=cotα
cot(π/2-α)=tanα
sin(3π/2+α)=-cosα
cos(3π/2+α)=sinα
tan(3π/2+α)=-cotα
cot(3π/2+α)=-tanα
sin(3π/2-α)=-cosα
cos(3π/2-α)=-sinα
tan(3π/2-α)=cotα
cot(3π/2-α)=tanα
(以上k∈Z)
部分高等内容
[编辑本段]
·高等代数中三角函数的指数表示(由泰勒级数易得):
sinx=[e^(ix)-e^(-ix)]/(2i) cosx=[e^(ix)+e^(-ix)]/2 tanx=[e^(ix)-e^(-ix)]/[ie^(ix)+ie^(-ix)]
泰勒展开有无穷级数,e^z=exp(z)=1+z/1!+z^2/2!+z^3/3!+z^4/4!+…+z^n/n!+…
此时三角函数定义域已推广至整个复数集。
·三角函数作为微分方程的解:
对于微分方程组 y=-y'';y=y'''',有通解Q,可证明
Q=Asinx+Bcosx,因此也可以从此出发定义三角函数。
补充:由相应的指数表示我们可以定义一种类似的函数——双曲函数,其拥有很多与三角函数的类似的性质,二者相映成趣。 特殊三角函数值
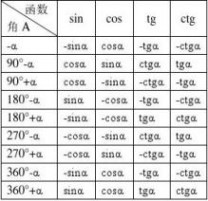
a 0` 30` 45` 60` 90`
sina 0 1/2 √2/2 √3/2 1
cosa 1 √3/2 √2/2 1/2 0
tana 0 √3/3 1 √3 None
cota None √3 1 √3/3 0
第 4 页 共 19 页
高等数学复习公式
导数公式:
(tgx)??sec2x
(ctgx)???csc2x
(secx)??secx?tgx
(cscx)???cscx?ctgx
(ax)??axlna
(logax)??
基本积分表: (arcsinx)??11xlna?x21(arccosx)????x21(arctgx)??1?x21(arcctgx)???1?x2
?tgxdx??lncosx?C
?ctgxdx?lnsinx?C
?secxdx?lnsecx?tgx?C
?cscxdx?lncscx??C
dx1x?arctg?C?a2?x2aa
dx1x?a?ln?x2?a22ax?a?C
dx1a?x??a2?x22alna?x?C
dxx?arcsin?C?a2?x2a
?
2ndx2?cos2x??secxdx?tgx?Cdx2?csc2?sinx?xdx??ctgx?C?secx?tgxdx?secx?C?cscx?ctgxdx??cscx?Cax?adx?lna?Cx?shxdx?chx?C?chxdx?shx?C?dxx2?a2?ln(x?x2?a2)?C?2
In??sinxdx??cosnxdx?
00n?1In?2n
?
?
?x2a22x?adx?x?a?ln(x?x2?a2)?C22x2a2222x?adx?x?a?lnx?x2?a2?C22xa2x2222a?xdx?a?x?arcsin?C22a22
三角函数的有理式积分:
2u1?u2x2dusinx?, cosx?, u?tg, dx? 22221?u1?u1?u
第 5 页 共 19 页
高等数学复习公式
一些初等函数: 两个重要极限:
ex?e?x
双曲正弦:shx?
2ex?e?x
双曲余弦:chx?
2
shxex?e?x
双曲正切:thx??
chxex?e?xarshx?ln(x?x2?1)archx??ln(x?x2?1)11?x
arthx?ln
21?x
三角函数公式: ·诱导公式:
sinx lim?1x?0 x
1
lim(1?)x?e?2.718281828459045...x?? x
·和差角公式: ·和差化积公式:
sin(???)?sin?cos??cos?sin?cos(???)?cos?cos??sin?sin?tg(???)?
tg??tg?
1?tg??tg?ctg??ctg??1
ctg(???)?
ctg??ctg?
sin??sin??2sin
???
22??????
sin??sin??2cossin
22??????
cos??cos??2coscos
22??????
cos??cos??2sinsin
22
cos
???
第 6 页 共 19 页
高等数学复习公式
·倍角公式:
sin2??2sin?cos?
cos2??2cos2??1?1?2sin2??cos2??sin2?
ctg2??1ctg2??2ctg?
2tg?tg2??1?tg2?
·半角公式: sin3??3sin??4sin3?cos3??4cos3??3cos?3tg??tg3?tg3??1?3tg2?
sin
tg?2?????cos???cos? cos??222?cos?1?cos?sin??1?cos?1?cos?sin??? ctg????1?cos?sin?1?cos?21?cos?sin?1?cos??2 ·正弦定理:
abc???2R ·余弦定理:c2?a2?b2?2abcosC sinAsinBsinC
·反三角函数性质:arcsinx??
2?arccosx arctgx??
2?arcctgx
高阶导数公式——莱布尼兹(Leibniz)公式:
(uv)(n)k(n?k)(k)??Cnuv
k?0n
?u(n)v?nu(n?1)v??n(n?1)(n?2)n(n?1)?(n?k?1)(n?k)(k)uv?????uv???uv(n)
2!k!
中值定理与导数应用:
拉格朗日中值定理:f(b)?f(a)?f?(?)(b?a)
f(b)?f(a)f?(?)?F(b)?F(a)F?(?)
曲率: 当F(x)?x时,柯西中值定理就是拉格朗日中值定理。
第 7 页 共 19 页
高等数学复习公式
弧微分公式:ds??y?2dx,其中y??tg?
平均曲率:K?????:从M点到M?点,切线斜率的倾角变化量;?s:MM?弧长。?s
y????d?M点的曲率:K?lim??. 23?s?0?sds(1?y?)
直线:K?0;
1半径为a的圆:K?.a
定积分的近似计算:
b
矩形法:?f(x)?
a
bb?a(y0?y1???yn?1)nb?a1[(y0?yn)?y1???yn?1]n2
b?a[(y0?yn)?2(y2?y4???yn?2)?4(y1?y3???yn?1)]3n 梯形法:?f(x)?ab抛物线法:?f(x)?
a
定积分应用相关公式:
功:W?F?s
水压力:F?p?A
m1m2,k为引力系数 r2
b1函数的平均值:y?f(x)dxb?a?a引力:F?k
12f(t)dt?b?aa
空间解析几何和向量代数: b
第 8 页 共 19 页
高等数学复习公式
空间2点的距离:d?M1M2?(x2?x1)2?(y2?y1)2?(z2?z1)2向量在轴上的投影:Prju??cos?,?是u轴的夹角。
????Prju(a1?a2)?Prja1?Prja2????a?b?a?bcos??axbx?ayby?azbz,是一个数量,
两向量之间的夹角:cos??
i???c?a?b?ax
bxjaybykaxbx?ayby?azbzax?ay?az?bx?by?bz222222??????az,c?a?bsin?.例:线速度:v?w?r.bz
ay
by
cyazcz???bz?a?b?ccos?,?为锐角时, ax??????向量的混合积:[abc]?(a?b)?c?bxcx
代表平行六面体的体积。
平面的方程:
?1、点法式:A(x?x0)?B(y?y0)?C(z?z0)?0,其中n?{A,B,C},M0(x0,y0,z0)
2、一般方程:Ax?By?Cz?D?0
xyz3???1abc
平面外任意一点到该平面的距离:d?Ax0?By0?Cz0?D
A2?B2?C2
?x?x0?mtx?xy?y0z?z0??0???t,其中s?{m,n,p};参数方程:?y?y0?ntmnp?z?z?pt0?
二次曲面:
x2y2z2
12?2?2?1abc
x2y2
2??z(,p,q同号)2p2q
3、双曲面:
x2y2z2
2?2?2?1abc
x2y2z2
2?2?2?(马鞍面)1abc
多元函数微分法及应用
第 9 页 共 19 页
高等数学复习公式
全微分:dz?
?z?z?u?u?udx?dy du?dx?dy?dz?x?y?x?y?z
全微分的近似计算:?z?dz?fx(x,y)?x?fy(x,y)?y多元复合函数的求导法:
dz?z?u?z?v
z?f[u(t),v(t)]????
dt?u?t?v?t
?z?z?u?z?v
z?f[u(x,y),v(x,y)]????
?x?u?x?v?x
当u?u(x,y),v?v(x,y)时,du?
?u?u?v?v
dx?dy dv?dx?dy ?x?y?x?y
隐函数的求导公式:
FxFFdydyd2y??
隐函数F(x,y)?0??2?(?x)+(?x)?
dxFy?xFy?yFydxdxFyF?z?z
隐函数F(x,y,z)?0??x??
?xFz?yFz
?F?F(x,y,u,v)?0?(F,G)?u
隐函数方程组: J????GG(x,y,u,v)?0?(u,v)?
?u
?u1?(F,G)?v1?(F,G)???????xJ?(x,v)?xJ?(u,x)?u1?(F,G)?v1?(F,G)???????yJ?(y,v)?yJ?(u,y)
微分法在几何上的应用:
?F
?v?Fu?GGu?v
FvGv
?x??(t)
x?xy?y0z?z0?
空间曲线?y??(t)在点M(x0,y0,z0)0??
???(t)?(t)??(t0)00?z??(t)
?
在点M处的法平面方程:??(t0)(x?x0)???(t0)(y?y0)???(t0)(z?z0)?0??FyFzFzFxFx?F(x,y,z)?0
若空间曲线方程为:,则切向量T?{,,?
GGGxGx?yzGz?G(x,y,z)?0
曲面F(x,y,z)?0上一点M(x0,y0,z0),则:
?
1、过此点的法向量:n?{Fx(x0,y0,z0),Fy(x0,y0,z0),Fz(x0,y0,z0)}x?x0y?y0z?z0
3??
Fx(x0,y0,z0)Fy(x0,y0,z0)Fz(x0,y0,z0)
方向导数与梯度:
FyGy
2、过此点的切平面方程:Fx(x0,y0,z0)(x?x0)?Fy(x0,y0,z0)(y?y0)?Fz(x0,y0,z0)(z?z0)?0
第 10 页 共 19 页
高等数学复习公式
?f?f?f
函数z?f(x,y)在一点p(x,y)沿任一方向l?cos??sin?
?l?x?y其中?为x轴到方向l的转角。
?f??f?
函数z?f(x,y)在一点p(x,y)的梯度:gradf(x,y)?i?j
?x?y
???f??
它与方向导数的关系是?gradf(x,y)?e,其中e?cos??i?sin??j,为l方向上的
?l
单位向量。?
?f
是gradf(x,y)在l上的投影。?l
多元函数的极值及其求法:
设fx(x0,y0)?fy(x0,y0)?0,令:fxx(x0,y0)?A, fxy(x0,y0)?B, fyy(x0,y0)?C??A?0,(x0,y0)为极大值2AC?B?0时,??
?A?0,(x0,y0)为极小值??2
则:?AC?B?0时, 无极值?AC?B2?0时, 不确定???
重积分及其应用:
??f(x,y)dxdy???f(rcos?,rsin?)rdrd?
D
D?
曲面z?f(x,y)的面积A???
D
??z???z?
1???????y??dxdy?x????
2
2
?
Mx?M
??x?(x,y)d?
D
???(x,y)d?
D
D
, ?
MyM
?
??y?(x,y)d?
D
???(x,y)d?
D
D
平面薄片的转动惯量:对于x轴Ix???y2?(x,y)d?, 对于y轴Iy???x2?(x,y)d?平面薄片(位于xoy平面)对z轴上质点M(0,0,a),(a?0)的引力:F?{Fx,Fy,Fz},其中:Fx?f??
D
?(x,y)xd?
(x?y?a)
2
2
22
Fy?f??3
D
?(x,y)yd?
(x?y?a)
2
2
22
Fz??fa??3
D
?(x,y)xd?
(x?y?a)
2
2
3
22
柱面坐标和球面坐标:
第 11 页 共 19 页
高等数学复习公式
?x?rcos??柱面坐标:f(x,y,z)dxdydz????F(r,?,z)rdrd?dz,?y?rsin?, ??????z?z?
其中:F(r,?,z)?f(rcos?,rsin?,z)
?x?rsin?cos??2球面坐标:?y?rsin?sin?, dv?rd??rsin??d??dr?rsin?drd?d??z?rcos??
2?
2 ?r(?,?)2F(r,?,?)rsin?dr?0???f(x,y,z)dxdydz????F(r,?,?)rsin?drd?d???d??d???00
重心:?1
M???x?dv, ?
?
?1M???y?dv, ???1M???z?dv, 其中M??????dv???转动惯量:Ix????(y2?z2)?dv, Iy????(x2?z2)?dv, Iz????(x2?y2)?dv
曲线积分:
第一类曲线积分(对弧长的曲线积分):
?x??(t)设f(x,y)在L上连续,L的参数方程为:, (??t??),则:?y??(t)?
?L?x?tf(x,y)ds??f[?(t),?(t)]?2(t)???2(t)dt (???) 特殊情况:??y??(t)??
第 12 页 共 19 页
高等数学复习公式
第二类曲线积分(对坐标的曲线积分):
?x??(t)设L的参数方程为?,则:y??(t)?
?
?P(x,y)dx?Q(x,y)dy?
??{P[?(t),?(t)]??(t)?Q[?(t),?(t)]??(t)}dtL
两类曲线积分之间的关系:?Pdx?Qdy??(Pcos??Qcos?)ds,其中?和?分别为
LL
L上积分起止点处切向量的方向角。
格林公式:??(
D?Q?P?Q?P?)dxdy?Pdx?Qdy格林公式:(?)dxdy?Pdx?Qdy???x?y?x?yLDL
?Q?P1当P??y,Q?x??2时,得到D的面积:A???dxdy?xdy?ydx?x?y2LD
·平面上曲线积分与路径无关的条件:
1、G是一个单连通区域;
2、P(x,y),Q(x,y)在G内具有一阶连续偏导数,且
减去对此奇点的积分,注意方向相反!
·二元函数的全微分求积:
?Q?P在=时,Pdx?Qdy才是二元函数u(x,y)的全微分,其中:?x?y
(x,y)?Q?P。注意奇点,如(0,0),应?x?y
u(x,y)?
(x0,y0)?P(x,y)dx?Q(x,y)dy,通常设x0?y0?0。
曲面积分:
22对面积的曲面积分:f(x,y,z)ds?f[x,y,z(x,y)]?z(x,y)?z(x,y)dxdyxy????
?Dxy
对坐标的曲面积分:??P(x,y,z)dydz?Q(x,y,z)dzdx?R(x,y,z)dxdy,其中:
?
??R(x,y,z)dxdy????R[x,y,z(x,y)]dxdy,取曲面的上侧时取正号;
?Dxy
??P(x,y,z)dydz????P[x(y,z),y,z]dydz,取曲面的前侧时取正号;
?Dyz
??Q(x,y,z)dzdx????Q[x,y(z,x),z]dzdx,取曲面的右侧时取正号。
?Dzx
两类曲面积分之间的关系:??Pdydz?Qdzdx?Rdxdy???(Pcos??Qcos??Rcos?)ds
??
高斯公式:
第 13 页 共 19 页
高等数学复习公式
???(
??P?Q?R??)dv?Pdydz?Qdzdx?Rdxdy?(Pcos??Qcos??Rcos?)ds?x?y?z??
高斯公式的物理意义——通量与散度:
??P?Q?R?散度:div????,即:单位体积内所产生的流体质量,若div??0,则为消失...?x?y?z??通量:??A?nds???Ands???(Pcos??Qcos??Rcos?)ds,
?因此,高斯公式又可写成:???divAdv?Ands
?????
斯托克斯公式——曲线积分与曲面积分的关系:
??(
??R?Q?P?R?Q?P?)dydz?(?)dzdx?(?)dxdy?Pdx?Qdy?Rdz?y?z?z?x?x?y?
cos?
?
?y
Qcos???zR
dydzdzdxdxdycos?????上式左端又可写成:??????x?y?z?x??PQRP?R?Q?P?R?Q?P空间曲线积分与路径无????y?z?z?x?x?y
ijk????旋度:rotA??x?y?z
PQR???向量场A沿有向闭曲线?Pdx?Qdy?Rdz?A?tds
??
常数项级数:
1?qn
等比数列:1?q?q???q?1?q
(n?1)n等差数列:1?2?3???n? 2
111调和级数:1?????是发散的23n2n?1
级数审敛法:
第 14 页 共 19 页
高等数学复习公式
1、正项级数的审敛法——根植审敛法(柯西判别法):
???1时,级数收敛?设:??limun,则???1时,级数发散n?????1时,不确定?
2、比值审敛法:
???1时,级数收敛U?设:??limn?1,则???1时,级数发散n??Un???1时,不确定?
3、定义法:
sn?u1?u2???un;limsn存在,则收敛;否则发散。n??
交错级数u1?u2?u3?u4??(或?u1?u2?u3??,un?0)的审敛法——莱布尼兹定理:
? ?un?un?1如果交错级数满足?,那么级数收敛且其和s?u1,其余项rn的绝对值rn?un?1。limu?0??n??n
绝对收敛与条件收敛:
(1)u1?u2???un??,其中un为任意实数;
(2)u1?u2?u3???un??
如果(2)收敛,则(1)肯定收敛,且称为绝对收敛级数;如果(2)发散,而(1)收敛,则称(1)为条件收敛级数。
1(?1)n
调和级数:?n发散,而?n1 级数:?n2收敛;
?1时发散1 p级数:?npp?1时收敛
幂级数:
第 15 页 共 19 页
高等数学复习公式
1x?1时,收敛于1?x1?x?x2?x3???xn??x?1时,发散
对于级数(3)a0?a1x ?a2x2???anxn??,如果它不是仅在原点收敛,也不是在全
x?R时收敛
数轴上都收敛,则必存在R,使x?R时发散,其中R称为收敛半径。
x?R时不定
1 ??0时,R?
求收敛半径的方法:设liman?1??,其中an,an?1是(3)??0时,R???n??an????时,R?0?函数展开成幂级数:
f??(x0)f(n)(x0)2函数展开成泰勒级数:f(x)?f(x0)(x?x0)?(x?x0)???(x?x0)n??2!n!
f(n?1)(?)余项:Rn?(x?x0)n?1,f(x)可以展开成泰勒级数的充要条件是:limRn?0 n??(n?1)!
f??(0)2f(n)(0)nx0?0时即为麦克劳林公式:f(x)?f(0)?f?(0)x?x???x??2!n!
一些函数展开成幂级数:
m(m?1)2m(m?1)?(m?n?1)nx???x?? (?1?x?1)2!n! 2n?1x3x5xsinx?x?????(?1)n?1?? (???x???)3!5!(2n?1)!(1?x)m?1?mx?
欧拉公式:
?eix?e?ix
cosx???2eix?cosx?isinx 或? ix?ix?sinx?e?e
?2?
三角级数:
a0?
f(t)?A0??Ansin(n?t??n)???(ancosnx?bnsinnx)2n?1n?1
其中,a0?aA0,an?Ansin?n,bn?Ancos?n,?t?x。
正交性:1,sinx,cosx,sin2x,cos2x?sinnx,cosnx?任意两个不同项的乘积在[??,?]上的积分=0。
傅立叶级数: ?
第 16 页 共 19 页
高等数学复习公式
a0?
f(x)???(ancosnx?bnsinnx),周期?2?2n?1
??1(n?0,1,2?)?an??f(x)cosnxdx ????其中???b?1f(x)sinnxdx (n?1,2,3?)?n?????
11?2
1?2?2???835 111?2?2?2???224246
正弦级数:an?0,bn?余弦级数:bn?0,an?111?21?2?2?2???6234111?21?2?2?2???12234f(x)sinnxdx n?1,2,3? f(x)??b??0 2?nsinnx是奇函数2?
??0f(x)cosnxdx n?0,1,2? f(x)?a0??ancosnx是偶函数2
周期为2l的周期函数的傅立叶级数:
第 17 页 共 19 页
高等数学复习公式
a0?n?xn?xf(x)???(ancos?bnsin),周期?2l2n?1ll
l?1n?xdx (n?0,1,2?)?an??f(x)cosl?ll?其中?l?b?1f(x)sinn?xdx (n?1,2,3?)?nl?l?l?
微分方程的相关概念:
一阶微分方程:y??f(x,y) 或 P(x,y)dx?Q(x,y)dy?0
可分离变量的微分方程:一阶微分方程可以化为g(y)dy?f(x)dx的形式,解法:?g(y)dy??f(x)dx 得:G(y)?F(x)?C称为隐式通解。
dyy?f(x,y)??(x,y),即写成的函数,解法:
dxx
ydydududxduy设u?,则?u?x,u???(u),??代替u,xdxdxdxx?(u)?ux齐次方程:一阶微分方程可以写成
即得齐次方程通解。
一阶线性微分方程:
dy1?P(x)y?Q(x)dx
?P(x)dx当Q(x)?0时,为齐次方程,y?Ce?
P(x)dx?P(x)dx当Q(x)?0时,为非齐次方程,y?(?Q(x)e?dx?C)e?
dy2?P(x)y?Q(x)yn,(n?0,1)dx
全微分方程:
如果P(x,y)dx?Q(x,y)dy?0中左端是某函数的全微分方程,即:
?u?udu(x,y)?P(x,y)dx?Q(x,y)dy?0?P(x,y)?Q(x,y) ?x?y
?u(x,y)?C应该是该全微分方程的通解。
二阶微分方程:
f(x)?0时为齐次d2ydy?P(x)?Q(x)y?f(x) dxdx2f(x)?0时为非齐次
二阶常系数齐次线性微分方程及其解法:
(*)y???py??qy?0,其中p,q为常数;
求解步骤:
1、写出特征方程:(?)r2?pr?q?0,其中r2,r的系数及常数项恰好是(*)式中y??,y?,y的系数;
2、求出(?)式的两个根r1,r2
第 18 页 共 19 页
高等数学复习公式

3、根据r1,r2的不同情况,按下表写出(*)式的通解:
y???py??qy?f(x),p,q为常数f(x)?e?xPm(x)型,?为常数;f(x)?e?x[Pl(x)cos?x?Pn(x)sin?x]型
第 19 页 共 19 页
四 : 史上最齐全高数公式
高等数学复习公式
高等数学公式
·平方关系:
sin^2(α)+cos^2(α)=1
tan^2(α)+1=sec^2(α)
cot^2(α)+1=csc^2(α)
·积的关系:
sinα=tanα*cosα
cosα=cotα*sinα
tanα=sinα*secα
cotα=cosα*cscα
secα=tanα*cscα
cscα=secα*cotα
·倒数关系:
tanα·cotα=1
sinα·cscα=1
cosα·secα=1
直角三角形ABC中,
角A的正弦值就等于角A的对边比斜边,
余弦等于角A的邻边比斜边
正切等于对边比邻边,
·三角函数恒等变形公式
·两角和与差的三角函数:
cos(α+β)=cosα·cosβ-sinα·sinβ
cos(α-β)=cosα·cosβ+sinα·sinβ
sin(α±β)=sinα·cosβ±cosα·sinβ
tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)
tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)
·三角和的三角函数:
sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγ cos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγ tan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)
·辅助角公式:
Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t),其中
sint=B/(A^2+B^2)^(1/2)
cost=A/(A^2+B^2)^(1/2)
第 1 页 共 19 页
高数公式 史上最齐全高数公式
高等数学复习公式
tant=B/A
Asinα+Bcosα=(A^2+B^2)^(1/2)cos(α-t),tant=A/B ·倍角公式:
sin(2α)=2sinα·cosα=2/(tanα+cotα)
cos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α) tan(2α)=2tanα/[1-tan^2(α)]
·三倍角公式:
sin(3α)=3sinα-4sin^3(α)
cos(3α)=4cos^3(α)-3cosα
·半角公式:
sin(α/2)=±√((1-cosα)/2)
cos(α/2)=±√((1+cosα)/2)
tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα
·降幂公式
sin^2(α)=(1-cos(2α))/2=versin(2α)/2
cos^2(α)=(1+cos(2α))/2=covers(2α)/2
tan^2(α)=(1-cos(2α))/(1+cos(2α))
·万能公式:
sinα=2tan(α/2)/[1+tan^2(α/2)]
cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]
tanα=2tan(α/2)/[1-tan^2(α/2)]
·积化和差公式:
sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]
cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]
cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]
sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]
·和差化积公式:
sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]
sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]
cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]
cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]
·推导公式
tanα+cotα=2/sin2α
tanα-cotα=-2cot2α
1+cos2α=2cos^2α
1-cos2α=2sin^2α
1+sinα=(sinα/2+cosα/2)^2
第 2 页 共 19 页
高数公式 史上最齐全高数公式
高等数学复习公式
·其他:
sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0
cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0 以及 sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2
tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0
三角函数的角度换算
[编辑本段]
公式一:
设α为任意角,终边相同的角的同一三角函数的值相等:
sin(2kπ+α)=sinα
cos(2kπ+α)=cosα
tan(2kπ+α)=tanα
cot(2kπ+α)=cotα
公式二:
设α为任意角,π+α的三角函数值与α的三角函数值之间的关系: sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
cot(π+α)=cotα
公式三:
任意角α与 -α的三角函数值之间的关系:
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
cot(-α)=-cotα
公式四:
利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
cot(π-α)=-cotα
公式五:
利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系: sin(2π-α)=-sinα
cos(2π-α)=cosα
tan(2π-α)=-tanα
cot(2π-α)=-cotα
公式六:
第 3 页 共 19 页
高数公式 史上最齐全高数公式
高等数学复习公式
π/2±α及3π/2±α与α的三角函数值之间的关系:
sin(π/2+α)=cosα
cos(π/2+α)=-sinα
tan(π/2+α)=-cotα
cot(π/2+α)=-tanα
sin(π/2-α)=cosα
cos(π/2-α)=sinα
tan(π/2-α)=cotα
cot(π/2-α)=tanα
sin(3π/2+α)=-cosα
cos(3π/2+α)=sinα
tan(3π/2+α)=-cotα
cot(3π/2+α)=-tanα
sin(3π/2-α)=-cosα
cos(3π/2-α)=-sinα
tan(3π/2-α)=cotα
cot(3π/2-α)=tanα
(以上k∈Z)
部分高等内容
[编辑本段]
·高等代数中三角函数的指数表示(由泰勒级数易得):
sinx=[e^(ix)-e^(-ix)]/(2i) cosx=[e^(ix)+e^(-ix)]/2 tanx=[e^(ix)-e^(-ix)]/[ie^(ix)+ie^(-ix)]
泰勒展开有无穷级数,e^z=exp(z)=1+z/1!+z^2/2!+z^3/3!+z^4/4!+…+z^n/n!+…
此时三角函数定义域已推广至整个复数集。(www.61k.com]
·三角函数作为微分方程的解:
对于微分方程组 y=-y'';y=y'''',有通解Q,可证明
Q=Asinx+Bcosx,因此也可以从此出发定义三角函数。
补充:由相应的指数表示我们可以定义一种类似的函数——双曲函数,其拥有很多与三角函数的类似的性质,二者相映成趣。 特殊三角函数值
a 0` 30` 45` 60` 90`
sina 0 1/2 √2/2 √3/2 1
cosa 1 √3/2 √2/2 1/2 0
tana 0 √3/3 1 √3 None
cota None √3 1 √3/3 0
第 4 页 共 19 页
高数公式 史上最齐全高数公式
高等数学复习公式
导数公式:
(tgx)??sec2x
(ctgx)???csc2x
(secx)??secx?tgx
(cscx)???cscx?ctgx
(ax)??axlna
(logax)??
基本积分表: (arcsinx)??11xlna?x21(arccosx)????x21(arctgx)??1?x21(arcctgx)???1?x2
?tgxdx??lncosx?C
?ctgxdx?lnsinx?C
?secxdx?lnsecx?tgx?C
?cscxdx?lncscx??C
dx1x?arctg?C?a2?x2aa
dx1x?a?ln?x2?a22ax?a?C
dx1a?x??a2?x22alna?x?C
dxx?arcsin?C?a2?x2a
?
2ndx2?cos2x??secxdx?tgx?Cdx2?csc2?sinx?xdx??ctgx?C?secx?tgxdx?secx?C?cscx?ctgxdx??cscx?Cax?adx?lna?Cx?shxdx?chx?C?chxdx?shx?C?dxx2?a2?ln(x?x2?a2)?C?2
In??sinxdx??cosnxdx?
00n?1In?2n
?
?
?x2a22x?adx?x?a?ln(x?x2?a2)?C22x2a2222x?adx?x?a?lnx?x2?a2?C22xa2x2222a?xdx?a?x?arcsin?C22a22
三角函数的有理式积分:
2u1?u2x2dusinx?, cosx?, u?tg, dx? 22221?u1?u1?u
第 5 页 共 19 页
高数公式 史上最齐全高数公式
高等数学复习公式
一些初等函数: 两个重要极限:
ex?e?x
双曲正弦:shx?
2ex?e?x
双曲余弦:chx?
2
shxex?e?x
双曲正切:thx??
chxex?e?xarshx?ln(x?x2?1)archx??ln(x?x2?1)11?x
arthx?ln
21?x
三角函数公式: ·诱导公式:

sinx lim?1x?0 x
1
lim(1?)x?e?2.718281828459045...x?? x
·和差角公式: ·和差化积公式:
sin(???)?sin?cos??cos?sin?cos(???)?cos?cos??sin?sin?tg(???)?
tg??tg?
1?tg??tg?ctg??ctg??1
ctg(???)?
ctg??ctg?
sin??sin??2sin
???
22??????
sin??sin??2cossin
22??????
cos??cos??2coscos
22??????
cos??cos??2sinsin
22
cos
???
第 6 页 共 19 页
高数公式 史上最齐全高数公式
高等数学复习公式
·倍角公式:
sin2??2sin?cos?
cos2??2cos2??1?1?2sin2??cos2??sin2?
ctg2??1ctg2??2ctg?
2tg?tg2??1?tg2?
·半角公式: sin3??3sin??4sin3?cos3??4cos3??3cos?3tg??tg3?tg3??1?3tg2?
sin
tg?2?????cos???cos? cos??222?cos?1?cos?sin??1?cos?1?cos?sin??? ctg????1?cos?sin?1?cos?21?cos?sin?1?cos??2 ·正弦定理:
abc???2R ·余弦定理:c2?a2?b2?2abcosC sinAsinBsinC
·反三角函数性质:arcsinx??
2?arccosx arctgx??
2?arcctgx
高阶导数公式——莱布尼兹(Leibniz)公式:
(uv)(n)k(n?k)(k)??Cnuv
k?0n
?u(n)v?nu(n?1)v??n(n?1)(n?2)n(n?1)?(n?k?1)(n?k)(k)uv?????uv???uv(n)
2!k!
中值定理与导数应用:
拉格朗日中值定理:f(b)?f(a)?f?(?)(b?a)
f(b)?f(a)f?(?)?F(b)?F(a)F?(?)
曲率: 当F(x)?x时,柯西中值定理就是拉格朗日中值定理。(www.61k.com]
第 7 页 共 19 页
高数公式 史上最齐全高数公式
高等数学复习公式
弧微分公式:ds??y?2dx,其中y??tg?
平均曲率:K?????:从M点到M?点,切线斜率的倾角变化量;?s:MM?弧长。[www.61k.com]?s
y????d?M点的曲率:K?lim??. 23?s?0?sds(1?y?)
直线:K?0;
1半径为a的圆:K?.a
定积分的近似计算:
b
矩形法:?f(x)?
a
bb?a(y0?y1???yn?1)nb?a1[(y0?yn)?y1???yn?1]n2
b?a[(y0?yn)?2(y2?y4???yn?2)?4(y1?y3???yn?1)]3n 梯形法:?f(x)?ab抛物线法:?f(x)?
a
定积分应用相关公式:
功:W?F?s
水压力:F?p?A
m1m2,k为引力系数 r2
b1函数的平均值:y?f(x)dxb?a?a引力:F?k
12f(t)dt?b?aa
空间解析几何和向量代数: b
第 8 页 共 19 页
高数公式 史上最齐全高数公式
高等数学复习公式
空间2点的距离:d?M1M2?(x2?x1)2?(y2?y1)2?(z2?z1)2向量在轴上的投影:Prju??cos?,?是u轴的夹角。(www.61k.com]
????Prju(a1?a2)?Prja1?Prja2????a?b?a?bcos??axbx?ayby?azbz,是一个数量,
两向量之间的夹角:cos??
i???c?a?b?ax
bxjaybykaxbx?ayby?azbzax?ay?az?bx?by?bz222222??????az,c?a?bsin?.例:线速度:v?w?r.bz
ay
by
cyazcz???bz?a?b?ccos?,?为锐角时, ax??????向量的混合积:[abc]?(a?b)?c?bxcx
代表平行六面体的体积。
平面的方程:
?1、点法式:A(x?x0)?B(y?y0)?C(z?z0)?0,其中n?{A,B,C},M0(x0,y0,z0)
2、一般方程:Ax?By?Cz?D?0
xyz3???1abc
平面外任意一点到该平面的距离:d?Ax0?By0?Cz0?D
A2?B2?C2
?x?x0?mtx?xy?y0z?z0??0???t,其中s?{m,n,p};参数方程:?y?y0?ntmnp?z?z?pt0?
二次曲面:
x2y2z2
12?2?2?1abc
x2y2
2??z(,p,q同号)2p2q
3、双曲面:
x2y2z2
2?2?2?1abc
x2y2z2
2?2?2?(马鞍面)1abc
多元函数微分法及应用
第 9 页 共 19 页
高数公式 史上最齐全高数公式
高等数学复习公式
全微分:dz?
?z?z?u?u?udx?dy du?dx?dy?dz?x?y?x?y?z
全微分的近似计算:?z?dz?fx(x,y)?x?fy(x,y)?y多元复合函数的求导法:
dz?z?u?z?v
z?f[u(t),v(t)]????
dt?u?t?v?t
?z?z?u?z?v
z?f[u(x,y),v(x,y)]????
?x?u?x?v?x
当u?u(x,y),v?v(x,y)时,du?
?u?u?v?v
dx?dy dv?dx?dy ?x?y?x?y
隐函数的求导公式:
FxFFdydyd2y??
隐函数F(x,y)?0??2?(?x)+(?x)?
dxFy?xFy?yFydxdxFyF?z?z
隐函数F(x,y,z)?0??x??
?xFz?yFz
?F?F(x,y,u,v)?0?(F,G)?u
隐函数方程组: J????GG(x,y,u,v)?0?(u,v)?
?u
?u1?(F,G)?v1?(F,G)???????xJ?(x,v)?xJ?(u,x)?u1?(F,G)?v1?(F,G)???????yJ?(y,v)?yJ?(u,y)
微分法在几何上的应用:
?F
?v?Fu?GGu?v
FvGv
?x??(t)
x?xy?y0z?z0?
空间曲线?y??(t)在点M(x0,y0,z0)0??
???(t)?(t)??(t0)00?z??(t)
?
在点M处的法平面方程:??(t0)(x?x0)???(t0)(y?y0)???(t0)(z?z0)?0??FyFzFzFxFx?F(x,y,z)?0
若空间曲线方程为:,则切向量T?{,,?
GGGxGx?yzGz?G(x,y,z)?0
曲面F(x,y,z)?0上一点M(x0,y0,z0),则:
?
1、过此点的法向量:n?{Fx(x0,y0,z0),Fy(x0,y0,z0),Fz(x0,y0,z0)}x?x0y?y0z?z0
3??
Fx(x0,y0,z0)Fy(x0,y0,z0)Fz(x0,y0,z0)
方向导数与梯度:
FyGy
2、过此点的切平面方程:Fx(x0,y0,z0)(x?x0)?Fy(x0,y0,z0)(y?y0)?Fz(x0,y0,z0)(z?z0)?0
第 10 页 共 19 页
高数公式 史上最齐全高数公式
高等数学复习公式
?f?f?f
函数z?f(x,y)在一点p(x,y)沿任一方向l?cos??sin?
?l?x?y其中?为x轴到方向l的转角。[www.61k.com]
?f??f?
函数z?f(x,y)在一点p(x,y)的梯度:gradf(x,y)?i?j
?x?y
???f??
它与方向导数的关系是?gradf(x,y)?e,其中e?cos??i?sin??j,为l方向上的
?l
单位向量。?
?f
是gradf(x,y)在l上的投影。?l
多元函数的极值及其求法:
设fx(x0,y0)?fy(x0,y0)?0,令:fxx(x0,y0)?A, fxy(x0,y0)?B, fyy(x0,y0)?C??A?0,(x0,y0)为极大值2AC?B?0时,??
?A?0,(x0,y0)为极小值??2
则:?AC?B?0时, 无极值?AC?B2?0时, 不确定???
重积分及其应用:
??f(x,y)dxdy???f(rcos?,rsin?)rdrd?
D
D?
曲面z?f(x,y)的面积A???
D
??z???z?
1???????y??dxdy?x????
2
2
?
Mx?M
??x?(x,y)d?
D
???(x,y)d?
D
D
, ?
MyM
?
??y?(x,y)d?
D
???(x,y)d?
D
D
平面薄片的转动惯量:对于x轴Ix???y2?(x,y)d?, 对于y轴Iy???x2?(x,y)d?平面薄片(位于xoy平面)对z轴上质点M(0,0,a),(a?0)的引力:F?{Fx,Fy,Fz},其中:Fx?f??
D
?(x,y)xd?
(x?y?a)
2
2
22
Fy?f??3
D
?(x,y)yd?
(x?y?a)
2
2
22
Fz??fa??3
D
?(x,y)xd?
(x?y?a)
2
2
3
22
柱面坐标和球面坐标:
第 11 页 共 19 页
高数公式 史上最齐全高数公式
高等数学复习公式
?x?rcos??柱面坐标:f(x,y,z)dxdydz????F(r,?,z)rdrd?dz,?y?rsin?, ??????z?z?
其中:F(r,?,z)?f(rcos?,rsin?,z)
?x?rsin?cos??2球面坐标:?y?rsin?sin?, dv?rd??rsin??d??dr?rsin?drd?d??z?rcos??
2?
2 ?r(?,?)2F(r,?,?)rsin?dr?0???f(x,y,z)dxdydz????F(r,?,?)rsin?drd?d???d??d???00
重心:?1
M???x?dv, ?
?
?1M???y?dv, ???1M???z?dv, 其中M??????dv???转动惯量:Ix????(y2?z2)?dv, Iy????(x2?z2)?dv, Iz????(x2?y2)?dv
曲线积分:
第一类曲线积分(对弧长的曲线积分):
?x??(t)设f(x,y)在L上连续,L的参数方程为:, (??t??),则:?y??(t)?
?L?x?tf(x,y)ds??f[?(t),?(t)]?2(t)???2(t)dt (???) 特殊情况:??y??(t)??
第 12 页 共 19 页
高数公式 史上最齐全高数公式
高等数学复习公式
第二类曲线积分(对坐标的曲线积分):
?x??(t)设L的参数方程为?,则:y??(t)?
?
?P(x,y)dx?Q(x,y)dy?
??{P[?(t),?(t)]??(t)?Q[?(t),?(t)]??(t)}dtL
两类曲线积分之间的关系:?Pdx?Qdy??(Pcos??Qcos?)ds,其中?和?分别为
LL
L上积分起止点处切向量的方向角。[www.61k.com)
格林公式:??(
D?Q?P?Q?P?)dxdy?Pdx?Qdy格林公式:(?)dxdy?Pdx?Qdy???x?y?x?yLDL
?Q?P1当P??y,Q?x??2时,得到D的面积:A???dxdy?xdy?ydx?x?y2LD
·平面上曲线积分与路径无关的条件:
1、G是一个单连通区域;
2、P(x,y),Q(x,y)在G内具有一阶连续偏导数,且
减去对此奇点的积分,注意方向相反!
·二元函数的全微分求积:
?Q?P在=时,Pdx?Qdy才是二元函数u(x,y)的全微分,其中:?x?y
(x,y)?Q?P。注意奇点,如(0,0),应?x?y
u(x,y)?
(x0,y0)?P(x,y)dx?Q(x,y)dy,通常设x0?y0?0。
曲面积分:
22对面积的曲面积分:f(x,y,z)ds?f[x,y,z(x,y)]?z(x,y)?z(x,y)dxdyxy????
?Dxy
对坐标的曲面积分:??P(x,y,z)dydz?Q(x,y,z)dzdx?R(x,y,z)dxdy,其中:
?
??R(x,y,z)dxdy????R[x,y,z(x,y)]dxdy,取曲面的上侧时取正号;
?Dxy
??P(x,y,z)dydz????P[x(y,z),y,z]dydz,取曲面的前侧时取正号;
?Dyz
??Q(x,y,z)dzdx????Q[x,y(z,x),z]dzdx,取曲面的右侧时取正号。
?Dzx
两类曲面积分之间的关系:??Pdydz?Qdzdx?Rdxdy???(Pcos??Qcos??Rcos?)ds
??
高斯公式:
第 13 页 共 19 页
高数公式 史上最齐全高数公式
高等数学复习公式
???(
??P?Q?R??)dv?Pdydz?Qdzdx?Rdxdy?(Pcos??Qcos??Rcos?)ds?x?y?z??
高斯公式的物理意义——通量与散度:
??P?Q?R?散度:div????,即:单位体积内所产生的流体质量,若div??0,则为消失...?x?y?z??通量:??A?nds???Ands???(Pcos??Qcos??Rcos?)ds,
?因此,高斯公式又可写成:???divAdv?Ands
?????
斯托克斯公式——曲线积分与曲面积分的关系:
??(
??R?Q?P?R?Q?P?)dydz?(?)dzdx?(?)dxdy?Pdx?Qdy?Rdz?y?z?z?x?x?y?
cos?
?
?y
Qcos???zR
dydzdzdxdxdycos?????上式左端又可写成:??????x?y?z?x??PQRP?R?Q?P?R?Q?P空间曲线积分与路径无????y?z?z?x?x?y
ijk????旋度:rotA??x?y?z
PQR???向量场A沿有向闭曲线?Pdx?Qdy?Rdz?A?tds
??
常数项级数:
1?qn
等比数列:1?q?q???q?1?q
(n?1)n等差数列:1?2?3???n? 2
111调和级数:1?????是发散的23n2n?1
级数审敛法:
第 14 页 共 19 页
高数公式 史上最齐全高数公式
高等数学复习公式
1、正项级数的审敛法——根植审敛法(柯西判别法):
???1时,级数收敛?设:??limun,则???1时,级数发散n?????1时,不确定?
2、比值审敛法:
???1时,级数收敛U?设:??limn?1,则???1时,级数发散n??Un???1时,不确定?
3、定义法:
sn?u1?u2???un;limsn存在,则收敛;否则发散。(www.61k.com)n??
交错级数u1?u2?u3?u4??(或?u1?u2?u3??,un?0)的审敛法——莱布尼兹定理:
? ?un?un?1如果交错级数满足?,那么级数收敛且其和s?u1,其余项rn的绝对值rn?un?1。limu?0??n??n
绝对收敛与条件收敛:
(1)u1?u2???un??,其中un为任意实数;
(2)u1?u2?u3???un??
如果(2)收敛,则(1)肯定收敛,且称为绝对收敛级数;如果(2)发散,而(1)收敛,则称(1)为条件收敛级数。
1(?1)n
调和级数:?n发散,而?n1 级数:?n2收敛;
?1时发散1 p级数:?npp?1时收敛
幂级数:
第 15 页 共 19 页
高数公式 史上最齐全高数公式
高等数学复习公式
1x?1时,收敛于1?x1?x?x2?x3???xn??x?1时,发散
对于级数(3)a0?a1x ?a2x2???anxn??,如果它不是仅在原点收敛,也不是在全
x?R时收敛
数轴上都收敛,则必存在R,使x?R时发散,其中R称为收敛半径。(www.61k.com]
x?R时不定
1 ??0时,R?
求收敛半径的方法:设liman?1??,其中an,an?1是(3)??0时,R???n??an????时,R?0?函数展开成幂级数:
f??(x0)f(n)(x0)2函数展开成泰勒级数:f(x)?f(x0)(x?x0)?(x?x0)???(x?x0)n??2!n!
f(n?1)(?)余项:Rn?(x?x0)n?1,f(x)可以展开成泰勒级数的充要条件是:limRn?0 n??(n?1)!
f??(0)2f(n)(0)nx0?0时即为麦克劳林公式:f(x)?f(0)?f?(0)x?x???x??2!n!
一些函数展开成幂级数:
m(m?1)2m(m?1)?(m?n?1)nx???x?? (?1?x?1)2!n! 2n?1x3x5xsinx?x?????(?1)n?1?? (???x???)3!5!(2n?1)!(1?x)m?1?mx?
欧拉公式:
?eix?e?ix
cosx???2eix?cosx?isinx 或? ix?ix?sinx?e?e
?2?
三角级数:
a0?
f(t)?A0??Ansin(n?t??n)???(ancosnx?bnsinnx)2n?1n?1
其中,a0?aA0,an?Ansin?n,bn?Ancos?n,?t?x。
正交性:1,sinx,cosx,sin2x,cos2x?sinnx,cosnx?任意两个不同项的乘积在[??,?]上的积分=0。
傅立叶级数: ?
第 16 页 共 19 页
高数公式 史上最齐全高数公式
高等数学复习公式
a0?
f(x)???(ancosnx?bnsinnx),周期?2?2n?1
??1(n?0,1,2?)?an??f(x)cosnxdx ????其中???b?1f(x)sinnxdx (n?1,2,3?)?n?????
11?2
1?2?2???835 111?2?2?2???224246
正弦级数:an?0,bn?余弦级数:bn?0,an?111?21?2?2?2???6234111?21?2?2?2???12234f(x)sinnxdx n?1,2,3? f(x)??b??0 2?nsinnx是奇函数2?
??0f(x)cosnxdx n?0,1,2? f(x)?a0??ancosnx是偶函数2
周期为2l的周期函数的傅立叶级数:
第 17 页 共 19 页
高数公式 史上最齐全高数公式
高等数学复习公式
a0?n?xn?xf(x)???(ancos?bnsin),周期?2l2n?1ll
l?1n?xdx (n?0,1,2?)?an??f(x)cosl?ll?其中?l?b?1f(x)sinn?xdx (n?1,2,3?)?nl?l?l?
微分方程的相关概念:
一阶微分方程:y??f(x,y) 或 P(x,y)dx?Q(x,y)dy?0
可分离变量的微分方程:一阶微分方程可以化为g(y)dy?f(x)dx的形式,解法:?g(y)dy??f(x)dx 得:G(y)?F(x)?C称为隐式通解。[www.61k.com]
dyy?f(x,y)??(x,y),即写成的函数,解法:
dxx
ydydududxduy设u?,则?u?x,u???(u),??代替u,xdxdxdxx?(u)?ux齐次方程:一阶微分方程可以写成
即得齐次方程通解。
一阶线性微分方程:
dy1?P(x)y?Q(x)dx
?P(x)dx当Q(x)?0时,为齐次方程,y?Ce?
P(x)dx?P(x)dx当Q(x)?0时,为非齐次方程,y?(?Q(x)e?dx?C)e?
dy2?P(x)y?Q(x)yn,(n?0,1)dx
全微分方程:
如果P(x,y)dx?Q(x,y)dy?0中左端是某函数的全微分方程,即:
?u?udu(x,y)?P(x,y)dx?Q(x,y)dy?0?P(x,y)?Q(x,y) ?x?y
?u(x,y)?C应该是该全微分方程的通解。
二阶微分方程:
f(x)?0时为齐次d2ydy?P(x)?Q(x)y?f(x) dxdx2f(x)?0时为非齐次
二阶常系数齐次线性微分方程及其解法:
(*)y???py??qy?0,其中p,q为常数;
求解步骤:
1、写出特征方程:(?)r2?pr?q?0,其中r2,r的系数及常数项恰好是(*)式中y??,y?,y的系数;
2、求出(?)式的两个根r1,r2
第 18 页 共 19 页
高数公式 史上最齐全高数公式
高等数学复习公式
3、根据r1,r2的不同情况,按下表写出(*)式的通解:
y???py??qy?f(x),p,q为常数f(x)?e?xPm(x)型,?为常数;f(x)?e?x[Pl(x)cos?x?Pn(x)sin?x]型
第 19 页 共 19 页
本文标题:史上最全防治晕车招数大全-五一旅游防晕车妙招大全61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1