一 : 一阶微分方程解法

解微分方程 一阶微分方程解法

解微分方程 一阶微分方程解法

解微分方程 一阶微分方程解法

解微分方程 一阶微分方程解法

解微分方程 一阶微分方程解法

解微分方程 一阶微分方程解法

解微分方程 一阶微分方程解法

解微分方程 一阶微分方程解法

解微分方程 一阶微分方程解法

解微分方程 一阶微分方程解法

解微分方程 一阶微分方程解法

解微分方程 一阶微分方程解法

解微分方程 一阶微分方程解法

解微分方程 一阶微分方程解法

解微分方程 一阶微分方程解法

解微分方程 一阶微分方程解法

解微分方程 一阶微分方程解法

解微分方程 一阶微分方程解法

二 : 怎样通过微分方程的特解,确定它的通解并求微分方程方程为二阶常系数
怎样通过微分方程的特解,确定它的通解并求微分方程
方程为二阶常系数非齐次线性方程,并有两个特解
y1=cos2x-1/4(xsin2x),y2=sin2x-1/4(xsin2x),求满足条件的微分方程。
答案,上来就直接说“根据方程解的结构知,方程的通解为”
y=c1cos2x+c2sin2x-1/4(xsin2x),其中-1/4(xsin2x)
符号不好打,这里1/4是四分之一,后面的括号内的是它的分子
方程中解中有cos2x,sin2x, 特征方程中有两根 即 +/-2i;
所以齐次方程是 y''+4y =0;观察到解中有xsin2x 项;
所以非齐次解右边为 sin2x,和cos2x;
所以设 y''+4y = c1sin2x+c2 cos2x;
代入y1特解可得 :
y1' = -2sin2x -1/4sin2x -1/2xcos2x;
y1'' = -5cos2x + xsin2x;
y1''+4y1 = cos2x;
所以解为y''+4y = cos2x
三 : (1)一阶微分方程的通解里含有一个任意常数,这个“任意常数”是指?
微分方程
(1)一阶微分方程的通解里含有一个任意常数,这个“任意常数”是指他的范围在(-∞,+∞)还是指他仅仅表示一部分或某个未确定的数呢?
(2)上一道题是这样的:(题目不写了)他解到了这一步:lny=(+/-)C1x=cx 然后得出了y=e^cx 而没有写成y=cx,c>0 这样是不是表示c的范围在(-∞,+∞),如果加上了c>0的范围就不表示任意常数从而不满足通解的定义了?
(3)图中的题:答案中貌似C>0?是否满足任意常数呢?
(1)微分方程通解中的“任意常数”并不是一定可以取遍实数的,也不要求它一定要取遍实数。例如通解是:y=√(Cx),当x≥0时,C只能取非负实数,当x≤0时,C只能取非正实数,这个C仍然是我们所谓的“任意常数”。需要注意的是,当C取遍它可以取的数,一定是得到了微分方程的全部解,不可以少掉一个或几个解的!
(2)问题你没有描述清楚,我只讲后半段,通解:y=(e^C)x是不可以写成y=Cx(C为任意正数)的,没有这种写法的!你写通解y=Cx,人家当然认为C<0时,y=Cx也是方程的解。
(3)图片中方程的通解10^x+10^(-y)=C是正确的,不必去注明C>0的,因为当C≤0时,方程10^x+10^(-y)=C没有解,不确定任何函数,只要C的取值使10^x+10^(-y)=C确定函数,这个函数一定是原来微分方程的解就可以了。
四 : 求解一个四阶行列式,要过程第一行四个1,第二行分别是abcd,第
求解一个四阶行列式,要过程
第一行四个1,第二行分别是ab,第三行分别是abcd的平方,第四行分别是abcd四次方
图片实在太大了,所以显示的文字很小,需要用鼠标点击以后才可能看得清:
五 : EES:EES-一、方程求解器,EES-二、学校简称
ees_EES -一、方程求解器
EES(engineering equation solver)
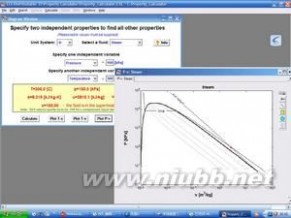
Engineering Equation Solver
EES (pronounced 'ease') is anacronymfor Engineering Equation Solver. The basic function provided by EES is the solution of a set of algebraic equations. EES can efficiently solve hundreds of coupled non-linear algebraic equations. EES can also be used to solve initial value differential equations.
A major difference between EES and existing equation solving programs is the many built-in mathematical and thermophysical property functions which EES provides. For example, the steam tables are implemented such that any thermodynamic property can be obtained from a built-in function call in terms of any two other properties. Similar capability is provided many other fluids, e.g., ammonia, nitrogen, methane, propane, all common CFC refrigerants, R-134a and others. Air tables are built-in, as are psychrometric functions and JANAF table data for many common gases. Transport property functions are also provided. Thermophysical property functions operate in either SI and English units. Additional property data may be added by the user.
EES provides the capability to do parametric studies. Selected variables can be included in a spreadsheet-like table. The user determines which variables are independent by entering their values in the table cells. EES will solve the table to determine the values of all dependent variables. A plotting option is provided to display the relationship between any two variables in the table. Multiple plots can be overlayed. Publication quality plots can be output on Postscript - compatible printers.
EES offers the advantages of a simple set of intuitive commands with which a novice can quickly learn to use for solving numerical problems. The large data bank of thermodynamic and transport properties built into EES are helpful in solving problems in thermodynamics, fluid mechanics, and heat transfer. Additional data can be added by the user as functions (written in Pascal, C, or EES) or in atabularform, which EES will automatically interpolate. As a result, EES is can be used to solve problems in any engineering application.
EES是1款(工程用)方程(公式)求解器的英文简称。它主要用于求解一系列的代数方程。例如:数百个非线性的方程构成的代数方程组
它和现在一般的方程求解器的1个主要不同在于,它内置了大量数学和热力学方面的函数。例如精确实现了水蒸气的焓熵表(H,V,S;P;T),使得由任何2个通过函数调用时传入的参数就能获得水蒸气的第3个参数值。(P,T>>H)对于象氨,氮,甲烷,丙烷,所有普通氟氯化碳制冷剂,R-134A(1种环保型制冷剂不含氯)这1类的流体EES也提供了相似的便利。空气性质表也通过内置的湿度函数得以实现而且还同时实现了许多(如果包括不同物相有3千多组)常见气体的JANAF热力表。它还包括一些流质传递相关的函数。其中热力学相关的函数同时支持国际标准单位和英制单位。EES还支持用户自定义数据库补充属性数据。
EES能够自动判别参数的独立性。所选变量均被包含在一张可扩展的电子数据表格中。用户只需要把相互独立的变量的值填入表中对应单元中,它就能自动计算出相关变量的值并能自动生成表格中任意2个被选变量的关系图象。并且多张图纸可以覆盖生成,结果图可以根据需要通过与程序兼容的打印机输出到一般出版物的附录中。
初学者通过EES只需要使用一些简单直观的命令就能解决许多复杂的数学问题。EES内嵌的大量热力学和流体力学方面的数据使得它在解决工程热力学,流体力学,传热学的许多问题上都显得相当的快捷和便利。用户还可以通过自定义函数(用PASCAL,C,EES写成)或者表单来加入自己的数据,而这些数据将会被EES自动插入它自己内置的数据库中。因为这些原因,EES被广泛用于解决各个工程领域中的问题。
EES 轻松省节能技术
技嘉研发的 主板 EES轻松省节能技术(Easy EnergySaver),
ees_EES -二、学校简称
Guancheng English Experimental School——莞城英文实验学校的简称:EES

ees_EES -三、环境雌激素简称
环境雌激素,指进入人体后可产生具有模拟雌激素作用的环境毒素。常见的环境雌激素来源包括如二手烟、农药、杀虫剂、废气、食品添加剂等。
英国伦敦国王学院生殖生物学教授弗拉瑟领导的研究团队,曾以老鼠实验证实,环境雌激素会使男性精子让女性卵子受精的能力受损。这项发现有助于解释男性不育症的起[www.61k.com)因。
本文标题:
二阶常微分方程求解-一阶微分方程解法 本文地址:
http://www.61k.com/1055905.html 


















 Engineering Equation Solver
Engineering Equation Solver