一 : 最小的一位数是几
最小的一位数是几
1.最小的一位数是1还是0?要回答这个问题须从“位数”和“数位”说起。(www.61k.com]位数是指一个整数所占有数位的个数。把占有一个数位的数叫一位数,占有两个数位的数叫两位数??例如,48076是五位数,因为它占有五个数位,这里“0”占有数位。
0能不能称为一位数呢?不能。因为记数法里有个规定:一个数的最高位不能是0。为什么要这样规定呢?因为若没有这样的规定,0就是一位数,由此可以得出最小的两位数是00,最小的三位数是000,这样的结论显然是不对的。不仅这样,若没有这样的规定,对一个数也就无法确定它是几位数了。例如,15是两位数,“015”就变成了三位数,“0015”就变成了四位数。这样,同一个数我们可以随意称它为几位数,“位数”这一概念的存在也就没有必要了。因此,一个数的最高位不能“0”。也就是说,最小的一位数是1,而不是0。 至于日常生活中、生产工作中遇到的数,如004785、043等,它是在特定条件下用来表示特定意义的。例如,电话号码0074816,它表示当地的电话容量不足一千万,最大号码是七个数字组成的,但不能说0074816是一个七位数。
最小的一位数是几 最小的一位数是几
2.目前,国外的数学界大部分都规定0是自然数。[www.61k.com]为了国际交流的方便,1993年颁布的《中华人民共和国国家标准》(GB
3100~3102-93)《量和单位》(11-2.9)第311页,规定自然数包括0。所以在近几年进行的中小学数学教材修订中,我们的教材研究编写人员根据上述国家标准进行了修改。即一个物体也没有,用0表示。0也是自然数。
但是,在小学阶段的“整除”部分,仍然不考虑自然数0,因而在约数、倍数等概念中都不包括0。另外,一般情况下我们不说数0是几位数,所以最小的一位数是1
《九年义务教育六年制小学数学第八册教师教学用书》第98页“关于几位数”是这样叙述的:“通常在自然数里,含有几个数位的数,叫做几位数。例如,2,含有一个数位的数,叫做一位数;30含有两个数位的数,叫做两位数;405含有三个数位的数,叫做三位数??但是要注意:一般不说0是几位数。
所谓最大的几位数,最小的几位数,通常也是在非零自然数有范围来说。所以,最大一位数是9,最小一位数是1;最大两位数是99,最小两位数是10;最大三位数是999,最小三位数是100??”
最小的一位数是几 最小的一位数是几
综上所述,“0”虽然是最小的自然数,但仍然不能称为“一位数”,更不能称为最小的一位数。[www.61k.com)
3. 自然数的计数单位还是“1”吗?
大家都知道,0是自然数中最小的一个。0加1得1,1加1得2 ,2加1得3,??这样继续下去可以得到任意一个自然数。而从自然数的排列顺序可知,后面一个自然数比前面一个自然数多1。因此,任何一个自然数都是由若干个1合并而成,所以1是自然数的单位。0可以看成是由0个1组成的自然数。
4. 0是其它非零自然数的倍数吗?
《九年义务教育六年制小学数学》第十册中,关于“数的整除”及“约数和倍数”的定义并未做任何改变,教材第54页就有这样的叙述:“因为0也能被2整除,所以0也是偶数”。以此类推,0能被所有非零自然数整除,根据约数倍数的定义,0是任何非零自然数的倍数,任何非零自然数都是0的约数。但考虑到研究分解质因数、最大公约数、最小公倍数时,一般限于非零自然数范围内,如讲最小公倍数时,是把0排除在外的。为此,《九年义务教育六年制小学数学》第十册
最小的一位数是几 最小的一位数是几
50页明确指出:“为了方便,以后在研究约数和倍数时,我们所说的数一般不包括0”。[www.61k.com)这样就避免了一些不必要的麻烦。
5. 0是不是合数?
过去,在教学中,关于自然数的组成,有两种情况:一是所有奇数和所有的偶数组成自然数集合;二是所有的质数与所有的合数及1也组成自然数集合。现在0也成为了自然数集合的一员,因而有许多教师提出这样的问题:0是不是合数?
前面已经谈过了,以后“在研究约数和倍数时,我们所说的数一般不包括0”,但作为一种学术研究,进行探讨也未尝不可。笔者以为,0的约数有无数个,根据《九年义务教育六年制小学数学》第十册中关于合数的定义:“一个数,如果除了1和它本身还有别的约数,这样的数叫做合数。”似乎应该把0划归为合数范围,但仔细一想0是个特殊的自然数,因为所有非零自然数都有“本身”这个约数,如,1是1的约数,2也是2的约数??,而0这个自然数恰恰少了“本身”这个约数,因此,也不能归为合数。试想:假设如果0是合数,那么它能用质因数相乘的形式表现出来吗?这就与“每个合数都可以写成几个质数相乘的形式”产生了矛盾。所以,我主张把0划归为“既不质数,也不是合数”范围。当然了,这需要权威机构和专家们的认定。但我认为,目前在没有明确0是不是合数的情况下,还是以回避
最小的一位数是几 最小的一位数是几
为好。[www.61k.com)
6.“任何相邻的两个自然数是互质数”对吗?
0没有成为自然数时,这一结论毫无疑问是正确的。现在0也是自然数,我们只要研究“0和1”这两个相邻的自然数是不是质数,就行了。根据《九年义务教育六年制小学数学》第十册中关于互质数的定义:“公约数只有1的两个数,叫做互质数。”笔者认为,0的约数有无数个,而1的约数只有一个,那就是它本身。综上所述,0和1的公约数只有“1”,因此,0和1是互质数。自然,“任何相邻的两个自然数是互质数”这个结论也是正确的。
二 : 最大的三位数加最小的一位数,得数是(C)A.999B.1100C?
0是不是个数?
最大的三位数加最小的一位数,得数是()
A.999 B.1100 C.1000 D.1001
0是不是个数?
楼主你理解错了吧
"最大的三位数加最小的一位数,得数是1000"
明显就是:999+1=1000
这里与0无关的.
三 : 小学四年级的数学问题一个数的最高位是百万位,它是几位数,一个数的
小学四年级的数学问题
一个数的最高位是百万位,它是几位数,一个数的最高位是十亿位,它是几位数? 是几位数?
一个数的最高位是百万位,它是7位数,一个数的最高位是十亿位,它是10位数
43006700是8位数
四 : 十几加减一位数
教学目标:
1、通过学习,让学生掌握十几加减一位数的计算方法,并能够正确地进行计算。
2、鼓励学生能够用多种算法进行计算,培养学生的求异思维能力。
教学重点:能够熟练掌握自己喜欢的计算方法,并能够运用这种方法进行计算
教学难点:能用多种方法进行计算, 并在实际数学问题中运用该方法解决问题。
教学准备:小棒 计数器 课件
教学思路:
一:复习旧知
1)我们学过了11到20各数的认识。现在,老师来考你们几个问题。
听好题目,再举手回答。
(1)11里面有()个十和()个一
(2)13里面有( )个十和( )个一
(学生回答好后)看来,这些问题你们都已经会了。
2)听音乐找朋友(连一连)
课件
师:(1)讲讲算法。
二:新知探索
1.师:里面哪个算式是我们以前没学过的,而且特别特殊?
学:¨¨¨11+2=13 (板书)
师:你是怎么算出来的呢?(引导学生用多种方法计算)
学:(两个人讨论下,说说自己的想法)并汇报
学:预设用小棒摆摆。11是由一个十和一个一组成,加上二个一就是13。用计数器计算¨¨
师:你们明白了吗?懂吗?
引入课题 :十几加减一位数
2.体验,11+2=13的由来
1)摆小棒
2)计数器计算
3)用语言讲方法
师:总结
3.你们好棒哦,能想出那么多的方法
我奖赏你们一个故事,
仔细听,听好后我们要提出并解决一些相关的数学问题。
在一个美丽的大森林里,一天早上,二只松鼠提着一个篮子上山采松果,松鼠妈妈采了13个,松鼠宝宝采了2个,然后就一起高高兴兴地回家去了。
先解决第一个问题:一共有多少个松果?
(1)师:列出算式
学:13+2= (板书)
(2)学生说一说算法。
再解决第2个问题:松鼠妈妈比松鼠宝宝多采了几个松果?
(1)师:列出算式
学:13-2= (板书)
师你是怎么知道?讲讲自己的方法
(2)用小棒摆一摆,并说一说:13里面有1个十和3个一,一个十和三个一去掉2个一就是一个十和1个一,也就是11。 (教师领说,学生跟说)
(3)再用计数器来演示计算过程。
(4)学生说一说,有没有自己的算法。
4、介绍算式中各部分的名称(给他们取个响亮的名字)
加数加加数等于和
被减数减去减数等于差(一起读一读)
三:巩固新知
(1)智力大过关
12+2= 13+2= 16+3= 15-5= 14-3= 17-2=
它们的名称:
(2) 谁学的最棒
加数
10
12
3
加数
5
6
和
13
被减数
16
18
17
减数
5
6
差
10
四:今天你学了什么知识? 讲讲你的收获
作业设计:书上练习p89—p90
板书设计: 十几加减一位数
11+2=13
13 + 2 =15 13 - 2 = 11
加数 加数 和 被减数 减数 差
五 : 最大的三位数乘最小的一位数,积是()。
| 最大的三位数乘最小的一位数,积是()。 |
| 999 |
考点:
考点名称:两位数(多位数)乘一位数学习目标: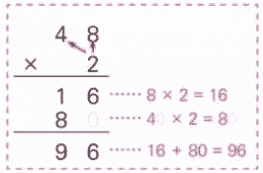 方法点拨:
方法点拨:61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1