一 : 美团网重大组织调整 平台竞争或陷入补贴怪圈
◎每经记者 张斯
昨日(7月1日),国内本地生活服务平台美团网发布内部公告,宣布进行重大组织调整,即日起新设外卖配送事业群和酒店旅游事业群,王慧文和陈亮分别出任两事业群的总裁。
显然,美团网此次组织调整,突出了外卖配送平台和出行度假平台的建设,以及与产业上下游广泛合作。
值得注意的是,百度董事长兼CEO李彦宏6月30日表示,打算3年内对糯米业务追加投资200亿元。而不久前,阿里则刚刚宣布60亿组建新口碑。对此,互联网分析人士王利阳对《每日经济新闻》记者表示,BAT三巨头在O2O领域发起猛攻已是不可逆的趋势,新一轮的竞争即将爆发。
据了解,目前,饿了么与腾讯等深度合作,开始在一些高端业务上做自配物流尝试。此外,百度外卖、阿里巴巴淘点点也已介入该市场。
王利阳表示,从美团网的策略来看,将来还会分拆更多强势业务更明确的抢市场,也是从团购转型的标志,多品牌运营是去团购化的一种手段。
值得注意的是,从团购转型到本地生活服务较成功的便是窝窝(原窝窝团)。其成为国内首家O2O上市公司后,还与众美联(香港)投资有限公司签订合并协议成立“众美窝窝”。
王利阳认为,窝窝的本次合并一反行业惯例,向产业链上游并购,在当前O2O领域横向并购热潮中具有标杆意义。合并后“众美窝窝”已形成餐饮行业全产业链互联网平台。而在窝窝的平台上,还有如美业、汽车服务、家政等众多生活服务细分行业的商家,未来窝窝如果将这一模式复制到其他细分行业,潜在价值巨大。
今年4月,美团也正式推出开放平台,增加了“上门”入口,接入美业、家政、汽车洗护等多种品类的上门服务提供商。而百度糯米同样也在瞄着这块市场,李彦宏追加200亿投资糯米正是为了让其实现突破性增长。
有业内人士认为,目前在生态关系上,传统的团购模式已陷入低价竞争的恶性循环,商家和平台互相羁绊、争利博弈,平台已进入补贴怪圈。
二 : 九(3)班学生参加学校组织的"绿色奥运"知识竞赛,老师将
| 九(3)班学生参加学校组织的"绿色奥运"知识竞赛,老师将学生的成绩按10分的组距分段,统计每个分数段出现的频数,填入频数分布表,并绘制频数分布直方图。 | ||||||||||||||||||||||||
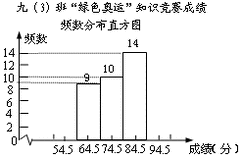 | ||||||||||||||||||||||||
(2)把频数分布直方图补充完整; (3)学校设定成绩在69.5分以上的学生将获得一等奖或二等奖,一等奖奖励作业本15本及奖金50元,二等奖奖励作业本10本及奖金30元。已知这部分学生共获得作业本335本,请你求出他们共获得的奖金。 |
| (1)a=2,b=12.5%; (2) 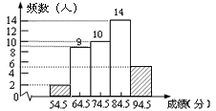 ; ;(3)设一等奖x人,二等奖y人,依题意得 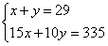 解得 解得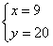 所以他们共获奖金=50×9+30×20=1050元。 |
考点:
考点名称:直方图频数分布直方图的定义:频数分布直方图的特点:
①能够显示各组频数分布的情况;
②易于显示各组之间频数的差别。
作直方图的目的有:
作直方图的目的就是通过观察图的形状,判断生产过程是否稳定,预测生产过程的质量。
1判断一批已加工完毕的产品;
搜集有关数据。
直方图将数据根据差异进行分类,特点是明察秋毫地掌握差异。
2在公路工程质量管理中,作直方图的目的有:
①估算可能出现的不合格率;
②考察工序能力估算法
③判断质量分布状态;
④判断施工能力;
制作频数分布直方图的方法:
①集中和记录数据,求出其最大值和最小值。数据的数量应在100个以上,在数量不多的情况下,至少也应在50个以上。 我们把分成组的个数称为组数,每一个组的两个端点的差称为组距。
②将数据分成若干组,并做好记号。分组的数量在5-12之间较为适宜。
③计算组距的宽度。用最大值和最小值之差去除组数,求出组距的宽度。
④计算各组的界限位。各组的界限位可以从第一组开始依次计算,第一组的下界为最小值减去最小测定单位的一半,第一组的上界为其下界值加上组距。第二组的下界限位为第一组的上界限值,第二组的下界限值加上组距,就是第二组的上界限位,依此类推。
⑤统计各组数据出现频数,作频数分布表。
⑥作直方图。以组距为底长,以频数为高,作各组的矩形图。
应用步骤:
(1)收集数据。作直方图的数据一般应大于50个。
(2)确定数据的极差(R)。用数据的最大值减去最小值 求得。
(3)确定组距(h)。先确定直方图的组数,然后以此组数去除极差,可得直方图每组的宽度,即组距。组数的确定要适当。组数太少,会引起较大计算误差;组数太多,会影响数据分组规律的明显性,且计算工作量加大。
(4)确定各组的界限值。为避免出现数据值与组界限值重合而造成频数据计算困难,组的界限值单位应取最小测量单位的1/2。分组时应把数据表中最大值和最小值包括在内。
第一组下限值为:最小值-0.5;
第一组上限值为:第一组下限值加组距;
第二组下限值就是第一组的上限值;
第二组上限值就是第二组的下限值加组距;
第三组以后,依此类推定出各组的组界。
(5)编制频数分布表。把多个组上下界限值分别填入频数分布表内,并把数据表中的各个数据列入相应的组,统计各组频数据(f )。
(6)按数据值比例画出横坐标。
(7)按频数值比例画纵坐标。以观测值数目或百分数表示。
(8)画直方图。按纵坐标画出每个长方形的高度,它代表取落在此长方形中的数据数。(注意:每个长方形的宽度都是相等的。)在直方图上应标注出公差范围(T)、样本容量(n)、样本平均值(x)、样本标准偏差值(s)和x的位置等。
一元一次方程应用题型及技巧:
列方程解应用题的几种常见类型及解题技巧:
(1)和差倍分问题:
①倍数关系:通过关键词语“是几倍,增加几倍,增加到几倍,增加百分之几,增长率……”来体现。
②多少关系:通过关键词语“多、少、和、差、不足、剩余……”来体现。
③基本数量关系:增长量=原有量×增长率,现在量=原有量+增长量。
(2)行程问题:
基本数量关系:路程=速度×时间,时间=路程÷速度,速度=路程÷时间,
路程=速度×时间。
①相遇问题:快行距+慢行距=原距;
②追及问题:快行距-慢行距=原距;
③航行问题:
顺水(风)速度=静水(风)速度+水流(风)速度,
逆水(风)速度=静水(风)速度-水流(风)速度
例:甲、乙两站相距480公里,一列慢车从甲站开出,每小时行90公里,一列快车从乙站开出,每小时行140公里。
慢车先开出1小时,快车再开。两车相向而行。问快车开出多少小时后两车相遇?
两车同时开出,相背而行多少小时后两车相距600公里?
两车同时开出,慢车在快车后面同向而行,多少小时后快车与慢车相距600公里?
两车同时开出同向而行,快车在慢车的后面,多少小时后快车追上慢车?
慢车开出1小时后两车同向而行,快车在慢车后面,快车开出后多少小时追上慢车? (此题关键是要理解清楚相向、相背、同向等的含义,弄清行驶过程。)
例:一艘船在两个码头之间航行,水流速度是3千米每小时,顺水航行需要2小时,逆水航行需要3小时,求两码头的之间的距离?
(3)劳力分配问题:抓住劳力调配后,从甲处人数与乙处人数之间的关系来考虑。 这类问题要搞清人数的变化。
例.某厂一车间有64人,二车间有56人。现因工作需要,要求第一车间人数是第二车间人数的一半。问需从第一车间调多少人到第二车间?
(4)工程问题:
三个基本量:工作量、工作时间、工作效率;
其基本关系为:工作量=工作效率×工作时间;相关关系:各部分工作量之和为1。
例:一件工程,甲独做需15天完成,乙独做需12天完成,现先由甲、乙合作3天后,甲有其他任务,剩下工程由乙单独完成,问乙还要几天才能完成全部工程?
(5)利润问题:
基本关系:
①商品利润=商品售价-商品进价;
②商品利润率=商品利润/商品进价×100%;
③商品销售额=商品销售价×商品销售量;
④商品的销售利润=(销售价-成本价)×销售量。
⑤商品售价=商品标价×折扣率例.
例:一家商店将某种服装按进价提高40%后标价,又以8折优惠卖出,结果每件仍获利15元,这种服装每件的进价是多少?
(6)数字问题:一般可设个位数字为a,十位数字为b,百位数字为c,十位数可表示为10b+a, 百位数可表示为100c+10b+a,然后抓住数字间或新数、原数之间的关系找等量关系列方程。
数字问题中一些表示:两个连续整数之间的关系,较大的比较小的大1;
偶数用2n表示,连续的偶数用2n+2或2n—2表示;奇数用2n+1或2n—1表示。
例:有一个三位数,个位数字为百位数字的2倍,十位数字比百位数字大1,若将此数个位与百位顺序对调(个位变百位)所得的新数比原数的2倍少49,求原数。
(7)盈亏问题:“盈”表示分配中的多余情况;“亏”表示不足或缺少部分。
(8)储蓄问题:
其数量关系是:
利息=本金×利率×存期;:(注意:利息税)。
本息=本金+利息,利息税=利息×利息税率。
注意利率有日利率、月利率和年利率,年利率=月利率×12=日利率×365。
(9)溶液配制问题:
其基本数量关系是:溶液质量=溶质质量+溶剂质量;
溶质质量=溶液中所含溶质的质量分数。
这类问题常根据配制前后的溶质质量或溶剂质量找等量关系,分析时可采用列表的方法来帮助理解题意。
(10)比例分配问题:
这类问题的一般思路为:设其中一份为x,利用已知的比,写出相应的代数式。
常用等量关系:各部分之和=总量。
还有劳力调配问题、配套问题、年龄问题、比赛积分问题、增长率问题等都会有涉及。
频数:
在一组依大小顺序排列的测量值中,当按一定的组距将其分组时出现在各组内的测量值的数目。
如有一组测量数据,数据的总个数N=148最小的测量值xmin=0.03,最大的测量值xmax=31.67,按组距为△x=3.000将148个数据分为11组,其中分布在15.05~18.05范围内的数据有26个,则称该数据组的频数为26。
频率:
如在314159265358979324中,‘9’出现的频数是3,出现的频率是3/18=16.7%
频数也称“次数”,对总数据按某种标准进行分组,统计出各个组内含个体的个数。而频率则每个小组的频数与数据总数的比值。
在变量分配数列中,频数(频率)表明对应组标志值的作用程度。
频数(频率)数值越大表明该组标志值对于总体水平所起的作用也越大,反之,频数(频率)数值越小,表明该组标志值对于总体水平所起的作用越小。
三 : 某电视台组织知识竞赛,共设20道选择题,各题分值相同,每题必答.下表记录的是5名参赛者的得分情况.参
某电视台组织知识竞赛,共设20道选择题,各题分值相同,每题必答.下表记录的是5名参赛者的得分情况.
(2)参赛者的76分,他答对了几道题?(请用方程作答) (3)参赛者说他得80分,你认为可能吗?为什么? |
| (1)由题意,得, 答对一题的得分是:100÷20=5分, 答错一题的扣分为:19×5-94=1分, 故答案为:5,1; (2)设参赛者答对了x道题,答错了(20-x)道题,由题意,得, 5x-(20-x)=76, 解得:x=16. 答:参赛者得76分,他答对了16道题; (3)假设他得80分可能,设答对了y道题,答错了(20-y)道题,由题意,得, 5y-(20-y)=80, 解得:y=
∵y为整数, ∴参赛者说他得80分,是不可能的. |
考点:
考点名称:一元一次方程的应用许多实际问题都归结为解一种方程或方程组,所以列出方程或方程组解应用题是数学联系实际,解决实际问题的一个重要方面;一元一次方程应用题型及技巧:
列方程解应用题的几种常见类型及解题技巧:
(1)和差倍分问题:
①倍数关系:通过关键词语“是几倍,增加几倍,增加到几倍,增加百分之几,增长率……”来体现。
②多少关系:通过关键词语“多、少、和、差、不足、剩余……”来体现。
③基本数量关系:增长量=原有量×增长率,现在量=原有量+增长量。
(2)行程问题:
基本数量关系:路程=速度×时间,时间=路程÷速度,速度=路程÷时间,
路程=速度×时间。
①相遇问题:快行距+慢行距=原距;
②追及问题:快行距-慢行距=原距;
③航行问题:
顺水(风)速度=静水(风)速度+水流(风)速度,
逆水(风)速度=静水(风)速度-水流(风)速度
例:甲、乙两站相距480公里,一列慢车从甲站开出,每小时行90公里,一列快车从乙站开出,每小时行140公里。
慢车先开出1小时,快车再开。两车相向而行。问快车开出多少小时后两车相遇?
两车同时开出,相背而行多少小时后两车相距600公里?
两车同时开出,慢车在快车后面同向而行,多少小时后快车与慢车相距600公里?
两车同时开出同向而行,快车在慢车的后面,多少小时后快车追上慢车?
慢车开出1小时后两车同向而行,快车在慢车后面,快车开出后多少小时追上慢车? (此题关键是要理解清楚相向、相背、同向等的含义,弄清行驶过程。)
例:一艘船在两个码头之间航行,水流速度是3千米每小时,顺水航行需要2小时,逆水航行需要3小时,求两码头的之间的距离?
(3)劳力分配问题:抓住劳力调配后,从甲处人数与乙处人数之间的关系来考虑。 这类问题要搞清人数的变化。
例.某厂一车间有64人,二车间有56人。现因工作需要,要求第一车间人数是第二车间人数的一半。问需从第一车间调多少人到第二车间?
(4)工程问题:
三个基本量:工作量、工作时间、工作效率;
其基本关系为:工作量=工作效率×工作时间;相关关系:各部分工作量之和为1。
例:一件工程,甲独做需15天完成,乙独做需12天完成,现先由甲、乙合作3天后,甲有其他任务,剩下工程由乙单独完成,问乙还要几天才能完成全部工程?
(5)利润问题:
基本关系:
①商品利润=商品售价-商品进价;
②商品利润率=商品利润/商品进价×100%;
③商品销售额=商品销售价×商品销售量;
④商品的销售利润=(销售价-成本价)×销售量。
⑤商品售价=商品标价×折扣率例.
例:一家商店将某种服装按进价提高40%后标价,又以8折优惠卖出,结果每件仍获利15元,这种服装每件的进价是多少?
(6)数字问题:一般可设个位数字为a,十位数字为b,百位数字为c,十位数可表示为10b+a, 百位数可表示为100c+10b+a,然后抓住数字间或新数、原数之间的关系找等量关系列方程。
数字问题中一些表示:两个连续整数之间的关系,较大的比较小的大1;
偶数用2n表示,连续的偶数用2n+2或2n—2表示;奇数用2n+1或2n—1表示。
例:有一个三位数,个位数字为百位数字的2倍,十位数字比百位数字大1,若将此数个位与百位顺序对调(个位变百位)所得的新数比原数的2倍少49,求原数。
(7)盈亏问题:“盈”表示分配中的多余情况;“亏”表示不足或缺少部分。
(8)储蓄问题:
其数量关系是:
利息=本金×利率×存期;:(注意:利息税)。
本息=本金+利息,利息税=利息×利息税率。
注意利率有日利率、月利率和年利率,年利率=月利率×12=日利率×365。
(9)溶液配制问题:
其基本数量关系是:溶液质量=溶质质量+溶剂质量;
溶质质量=溶液中所含溶质的质量分数。
这类问题常根据配制前后的溶质质量或溶剂质量找等量关系,分析时可采用列表的方法来帮助理解题意。
(10)比例分配问题:
这类问题的一般思路为:设其中一份为x,利用已知的比,写出相应的代数式。
常用等量关系:各部分之和=总量。
还有劳力调配问题、配套问题、年龄问题、比赛积分问题、增长率问题等都会有涉及。
四 : 光明小学组织一次知识竞赛,下表是三位选手的参赛证号码及所代表的信息.参赛证号参赛选手信息340105
光明小学组织一次知识竞赛,下表是三位选手的参赛证号码及所代表的信息.
(2)写出六(2)班在第4考场第9个座位学生的编号. |
| (1)参赛证号码是530726学生的信息是: 五(3)班,第7考场,第26个座位. (2)六(2)班在第4考场第9个座位学生的编号是640409. |
考点:
考点名称:数字和编码数字和编码:身份证号码的编码含义:
数字编码实际应用于很多领域,比如:身份证号码、学号、车牌号、邮政编码、电话区号、银行帐号等等。
身份证号码共18位:AAAAAABBBBBBCCCD
1、号码的结构
公民身份号码是特征组合码,由十七位数字本体码和一位校验码组成。排列顺序从左至右依次为:六位数字地址码,八位数字出生日期码,三位数字顺序码和一位数字校验码。
2、地址码(前六位数)
表示编码对象常住户口所在县(市、旗、区)的行政区划代码,按GB/T2260的规定执行。
3、出生日期码(第七位至十四位)
表示编码对象出生的年、月、日,按GB/T7408的规定执行,年、月、日代码之间不用分隔符。
4、顺序码(第十五位至十七位)
表示在同一地址码所标识的区域范围内,对同年、同月、同日出生的人编定的顺序号,顺序码的奇数分配给男性,偶数分配给女性。
5、校验码(第十八位数)
作为尾号的校验码,是由号码编制单位按统一的公式计算出来的,如果某人的尾号是0-9,都不会出现X,但如果尾号是10,那么就得用X来代替,因为如果用10做尾号,那么此人的身份证就变成了19位。X是罗马数字的10,用X来代替10,可以保证公民的身份证符合国家标准。
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1