一 : 平面图形的周长和面积的整理与复习
教学内容:二 : 平面图形的周长和面积教学设计
《平面图形的周长和面积》教学设计
蒋艳红
教学内容:人教版小学数学第十二册第134页内容及练习练习三十3、4、8、9题
教材分析:本节内容是九年义务教育六年制小学数学教材第十二册第五单元“整理和复习”的第五小节的教学内容。[www.61k.com)本内容复习前学生已经系统复习和整理了各种平面图形的特征,掌握了它们之间的联系和区别,为本节课整理和复习平面图形的周长和面积打好基础。本节教材在安排上分了四个层次。第一个层次,让学生举例说明什么是平面图形的周长和面积,让学生主动回顾所学知识,为本课学习提供感性材料;第二层次,由学生的举例分归纳概括出周长和面积的概念;第三层次,比较周长和面积的区别,通过网格两组图形的比较,学生从直观上和理性上认识面积相等的两个图形,周长不相等;周长相等的两个图形,面积不相等。第四层次,用图形构建了平面图形面积和周长推导公式系统图,提示内在的联系,重温了割、补、化圆为方等数学思维方法,由学生根据图形得出周长和面积的计算公式。
教学目标:
1、 进一步理解周长和面积的含义,弄清和理解平面图形的周长和面积公式的推导过程,以及它们之间的内在联系。
2、 通过教学使学生能熟练掌握公式和运用公式进行解题,提高学生
运用知识的能力和解决问题的灵活性。
平面图形的周长和面积 平面图形的周长和面积教学设计
3、 教学中进上一步渗透割、补、化圆为方等数学转化的思维方法,
提高学生提示事物之间内在联系的能力,并使学生学会整理知识的方法。(www.61k.com]
教学重点:周长和面积的公式推导和运用。
教学难点:周长和面积的区分
教法:1、发挥学生自主能动性,主动构建知识网络。
2、整理和提高相结合,培养思维能力。
3、强化辨析对比,加强联系沟通。
学法:通过自己举例、观察、回顾,在教师的引导下概括出周长和面积的概念。通过数一数、比一比、算一算区别两种概念,充分发挥自己的主观能动性。
课前准备:教师制作课件,学生课前了解一些平面图形的知识。 教学过程:
一、 导入
1、 师:同学们,我们学过的平面图形有哪些?(电脑显示学生所说的六种平面图形)
2、 师:前面我们已经复习了“平面图形的认识”,今天我们来学习平面图形的周长和面积。(板书:平面图形的周长和面积) 3、 师:同学们,围绕着这个课题,你觉得我们该复习哪些相关的内容呢?(学生自由说)
4、 师:今天我们要进一步理解它们的含义,熟练掌握它们的计
平面图形的周长和面积 平面图形的周长和面积教学设计
算公式,并能灵活运用所学的知识来解决实际问题。[www.61k.com)
含义
板书: 进一步 公式
运用
二、 复习整理知识
(一)、周长和面积的概念
1、周长
(1) 师:什么是平面图形的周长?(学生分别说出这六种平面图
形的周长指的是什么。电脑并演示平面图形周长的含义。)那么我们能不能用一句话来概括什么叫周长?(学生回答后,电脑显示周长的定义:围成平面图形的所有边长的总和叫做周长。)
(2) 练习:判断题——平面图形里所有边长的总和就是这个
平面图形的周长。( )
2、面积
(1) 师:什么是平面图形的面积?(学生个别说,电脑演示面积
的含义,老师引导学生概括出面积的定义:物体表面或围成的平面图形的大小叫做面积。)
(2) 练习:判断题:物体表面或围成的平面图形的大小叫做面积。
平面图形的周长和面积 平面图形的周长和面积教学设计
( )
3、 齐读周长和面积的定义。[www.61k.com)
(说明:这一层次通过学生举例、回忆、借助计算机演示给学生强烈的色彩刺激,形成和概括出周长和面积的概念。)
(二)、周长和面积的区别。
1、 师:下面请同学们看这两组图,在每一组图形中两个图形的周长相等吗?面积相等吗?(计算机出示课本第134页中间的两幅图,教师说明小方格是边长1厘米的方格。学生四人小组讨论,并在练习纸上填写结果。)
2、 学生讨论完后,请个别学生汇报本小组的学习情况,并用电脑演示来验证学生说的是否正确。第一组图是面积相等、周长不等,第二组图是面积不等,周长相等。
3、 师:通过刚才的学习,你们看看这道判断题是对的还是错的:如果两个平面图形的周长相等,则它们的面积一定相等。( ) 4、 把正确答案的编号填入括号内。
(1)从下图的大正方形中去掉一个小正方形后,面积( ),周长
( )
A、 增加 B、减少 C、不变
平面图形的周长和面积 平面图形的周长和面积教学设计
(3) 观察下图甲乙两个部分的面积和周长,下面哪个说法是
正确的。(www.61k.com)( )
A、C甲=C乙 S甲=S乙 B、C甲=C乙 S甲>S乙
(说明:这一层次学生比较网格上两组图形的周长和面积,通过数一数,算一算,计算机上的图形变一变,让学生直观感知第一幅网格面积相等,周长不等,第二幅周长相等,面积不等,从而认识到周长和面积没有必然的联系。)
(三)、周长和面积公式推导教学。
1、 师:刚才我们理解了周长和面积的含义,那么它们的周长和面积的计算公式是怎样呢?请同学们打开数学书134页,分别写出它们的公式,在写的过程中并回忆一下它们是怎样推导出来的?
2、 填化工说推导方法。学生说电脑显示公式,并简单说出公式的推导方法。长方形是数方格的方法,正方形是特殊的长方形,
平面图形的周长和面积 平面图形的周长和面积教学设计
平行四边形、三角形梯形用教具演示。(www.61k.com)圆用电脑演示。(板书:数、割、平移、补、重合、旋转、实验、转化。读一次板书) 3、 沟通面积化工之间的关系:
(1) 师:同学们看一看老师这六种平面图形的摆放,跟课本上的
摆放一样吗?
(2) 师:那么课本为什么要这样摆呢?(4个同学一个小组进行
讨论)
(3) 师:同学们真聪明,课本这样摆可使我们清楚地看出长方形
的面积计算公式是平面图形面积计算公式的基础,其它平面图形都是转化为长方形来计算的。同学们以后在息的时候,都可以利用知识之间的联系来整理我们所学过的知识,这样既方便我们理解知识,又有利于我们记忆。
4、 练习:根据表中条件计算下面各图形的周长和面积。(印在练习纸上)
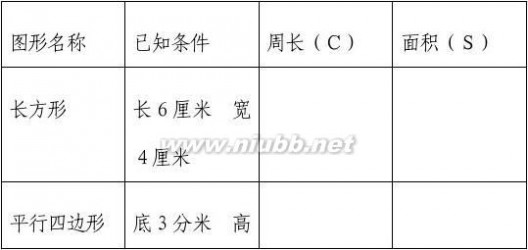
平面图形的周长和面积 平面图形的周长和面积教学设计
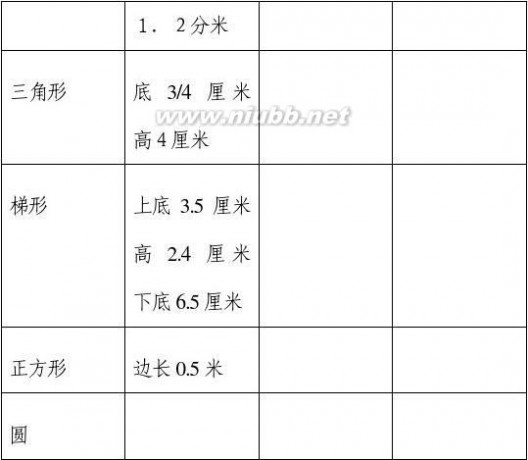
三、 练习
1、 判断题
(1) 三角形的面积是平行四边形面积的一半。[www.61k.com)( )
(2) 圆的周长和直径的比值叫做圆周率,用字母π来表示。( ) 2、 选择题
(1)一个平行四边形和一个三角形等底等高,已知平行四边形的面积是25平方厘米,三角形的面积是( )。
A 、12.5 B 、25 C 、50
(2)求右图的面积,列式正确的是( )。
平面图形的周长和面积 平面图形的周长和面积教学设计
A 、3.14×8÷2 B 、3.14×(8÷2)÷2 C 、3.14×8÷2+8 3、 应用题
(1) 从一块长18分米,宽10分米的长方形木板上切下一个最大的圆,切下的圆的面积是多少平方分米?剩下木板的面积是多少平方分米?
(2) 小明家装修一间长4米,宽3.2米,高3米的房子。[www.61k.com]在地面
上铺的是边长0.4米的方砖,请你算一算装修时至少要用多少块方砖?
(3) 市政府拍卖如下图形的一块土地,底价是每平方米200元,
如果有一位开发商准备50万元买这块地,你认为他有没有可能买到?
(4) 阿凡提的故事:阿凡提到一个地主家里干活,狡猾的地主总
是想找借口克扣阿凡提的工钱。有一次地主叫阿凡提把一群羊赶进一个用栅栏围成的长是9米,宽是6.7米的长方形的羊圈里,但阿凡提发现这个羊圈根本无法容纳这群羊,因为这群羊至少需要70平方米的羊圈才够大。同学们你能够帮助阿凡提解脱困境吗?
(师总结:生活中到处都充满着数学知识,我们要从生活中学习数学知识,又要把数学知识运用到生活中去,解决生活中遇到
平面图形的周长和面积 平面图形的周长和面积教学设计
的问题。[www.61k.com))
四、 课堂总结
同学们,通过今天的复习,你有什么收获?(学生自由发言) 教师进行归纳总结:
(1) 平面图形的周长和面积的概念。
(2) 平面图形的周长和面积的计算公式,并用转化的方法推
导出公式。
(3) 用所学的知识解决生活中的实际问题。
三 : 平面几何图形周长与面积
教学目标1、通过复习平面图形的周长和面积公式,使学生形成知识网络.
2、通过复习培养学生归纳、总结、比较、分析的逻辑思维能力.
3、通过复习,使学生了解知识的内在联系,渗透数学转化思想以及辩证唯物主义思想.
教学重点
1、系统整理平面图形的周长、面积公式的推导,区分平面图形周长,面积的不同点.
2、熟练运用公式进行计算.
教学难点
使学生掌握平面图形的面积和周长公式的推导过程,并形成知识网络.
教学过程
一、复习平面图形“周长”和“面积”的概念
出示图:
1、请你观察:从图中你发现了什么?
面积不相等,周长相等
2、互相交流
(1)什么叫做平面图形的周长?周长指的是哪部分?
(2)什么叫做平面图形的面积?面积指的是哪部分?
3、学生汇报并且请学生到前面指出图形的周长和面积.
4、引导学生从直观到抽象理解概念.
判断:
(1)周长相等的2个平面图形,他们的面积一定相等.( )
(2)面积相等的2个平面图形,他们的周长一定相等.( )
(3)周长相等的2个组和平面图形,他们的面积一定不相等.( )
(4)周长的单位有:米、分米、平方厘米.( )
(5)面积单位有:平方米、平方分米、平方厘米.( )
二、复习平面图形的周长
1、回忆平面图形周长公式的学习顺序.
我们都学习了哪些平面图形的周长,你能够按照学习的先后顺序说说吗?
2、小组共同回忆探讨
(1)这3个平面图形的周长公式分别是什么?
(2)他们的周长公式是怎样推导得来的?
3、学生汇报:
长方形:因为长方形两组对边分别相等,所以:c=a×2+b×2或者 c=(a+b)×2
正方形:因为正方形4条边相等,所以:c=a×4
圆形:通过实验可以知道圆形的周长总是圆的直径的π倍,所以:c=πd或者c=2πr
4、如果已知长方形的周长和长,怎样求宽?
如果已知长方形的周长和宽,怎样求长?
如果已知正方形的周长,怎样求边长?
如果想求圆形的半径,需要已知什么,怎样求?
如果想求圆形的直径,需要已知什么,怎样求?
5、完善平面图形的周长知识结构:
三、复习平面图形的面积
(一)复习长方形、正方形和圆形的面积
1、长方形的面积公式是什么?
正方形的面积公式是什么?
圆形的面积公式是什么?
2、请同学以小组为单位共同回忆探讨:
(1)这3个平面图形的面积公式分别是什么?
(2)他们的面积公式是怎样推导得来的?
3、教师提问:
(1)如果想求圆的面积,需知道什么条件?
(2)知道半径如何求圆的面积?知道直径呢?知道周长呢?
4、完善长方形、正方形和圆形面积公式及知识结构.
(二)复习平行四边形、三角形和梯形面积公式及公式推导
观察图形:
1、请同学以小组为单位共同回忆探讨:
(1)这3个平面图形的面积公式分别是什么?
(2)他们的面积公式是怎样推导得来的?
2、小组汇报
3、这3个平面图形的面积公式有什么关系?
4、教师完善平面图形面积公式及知识结构
四、课堂练习
1、计算.(单位:厘米)
2、判断
(1)四边相等的四边形都是正方形. ( )
(2)半径的长短决定圆的大小. ( )
(3)有一组对边平行的四边形叫做梯形. ( )
3、一块长1米20厘米,宽90厘米的铝皮,剪成直径是30厘米的圆片,最多可以剪多少块?
五、课堂小结
通过本节课的学习,你有了哪些收获?
六、板书设计
四 : 平面图形的周长和面积教学设计
《平面图形的周长和面积》教学设计
蒋艳红
教学内容:人教版小学数学第十二册第134页内容及练习练习三十3、4、8、9题
教材分析:本节内容是九年义务教育六年制小学数学教材第十二册第五单元“整理和复习”的第五小节的教学内容。本内容复习前学生已经系统复习和整理了各种平面图形的特征,掌握了它们之间的联系和区别,为本节课整理和复习平面图形的周长和面积打好基础。本节教材在安排上分了四个层次。第一个层次,让学生举例说明什么是平面图形的周长和面积,让学生主动回顾所学知识,为本课学习提供感性材料;第二层次,由学生的举例分归纳概括出周长和面积的概念;第三层次,比较周长和面积的区别,通过网格两组图形的比较,学生从直观上和理性上认识面积相等的两个图形,周长不相等;周长相等的两个图形,面积不相等。第四层次,用图形构建了平面图形面积和周长推导公式系统图,提示内在的联系,重温了割、补、化圆为方等数学思维方法,由学生根据图形得出周长和面积的计算公式。
教学 目标:
1、 进一步理解周长和面积的含义,弄清和理解平面图形的周长和面积公式的推导过程,以及它们之间的内在联系。
2、 通过教学使学生能熟练掌握公式和运用公式进行解题,提高学生
运用知识的能力和解决问题的灵活性。
3、 教学中进上一步渗透割、补、化圆为方等数学转化的思维方法,
提高学生提示事物之间内在联系的能力,并使学生学会整理知识的方法。
教学重点:周长和面积的公式推导和运用。
教学难点:周长和面积的区分
教法:1、发挥学生自主能动性,主动构建知识网络。
2、整理和提高相结合,培养思维能力。
3、强化辨析对比,加强联系沟通。
学法:通过自己举例、观察、回顾,在教师的引导下概括出周长和面积的概念。通过数一数、比一比、算一算区别两种概念,充分发挥自己的主观能动性。
课前准备:教师制作课件,学生课前了解一些平面图形的知识。 教学过程:
一、 导入
1、 师:同学们,我们学过的平面图形有哪些?(电脑显示学生所说的六种平面图形)
2、 师:前面我们已经复习了“平面图 形的认识”,今天我们来学习平面图形的周长和面积。(板书:平面图形的周长和面积) 3、 师:同学们,围绕着这个课题,你觉得我们该复习哪些相关的内容呢?(学生自由说)
4、 师:今天我们要进一步理解它们的含义,熟练掌握它们的计
算公式,并能灵活运用所学的知识来解决实际问题。
含义
板书: 进一步 公式
运用
二、 复习整理知识
(一)、周长和文章窝面积的概念
1、周长
(1) 师:什么是平面图形的周长?(学生分别说出这六种平面图
形的周长指的是什么。电脑并演示平面图形周长的含义。)那么我们能不能用一句话来概括什么叫周长?(学生回答后,电脑显示周长的定义:围成平面图形的所有边长的总和叫做周长。)
(2) 练习:判断题——平面图形里所有边长的总和就是这个
平面图形的周长。( )
2、面积
(1) 师:什么是平面图形的面积?(学生个别说,电脑演示面积
的含义,老师引导学生概括出面积的定义:物体表面或围成的平面图形的大小叫做面积。)
(2) 练习:判断题:物体表面或围成的平面图形的大小叫做面积。
( )
3、 齐读周长和面积的定义。
(说明:这一层次通过学生举例、回忆、借助计算机演示给学生强烈的色彩刺激,形成和概括出周长和面积的概念。)
(二)、周长和面积的区别。
1、 师:下面请同学们看这两组图,在每一组图形中两个图形的周长相等吗?面积相等吗?(计算机出示课本第134页中间的两幅图,教师说明小方格是边长1厘米的方格。学生四人小组讨论,并在练习纸上填写结果。)
2、 学生讨论完后,请个别学生汇报本小组的学习情况,并用电脑演示来验证学生说的[www.61k.com是否正确。第一组图是面积相等、周长不等,第二组图是面积不等,周长相等。
3、 师:通过刚才的学习,你们看看这道判断题是对的还是错的:如果两个平面图形的周长相等,则它们的面积一定相等。( ) 4、 把正确答案的编号填入括号内。
(1)从下图的大正方形中去掉一个小正方形后,面积( ),周长
( )
A、 增加 B、减少 C、不变

(3) 观察下图甲乙两个部分的面积和周长,下面哪个说法是
正确的。( )
A、C甲=C乙 S甲=S乙 B、C甲=C乙 S甲>S乙
(说明:这一层次学生比较网格上两组图形的周长和面积,通过数一数,算一算,计算机上的图形变一变,让学生直观感知第一幅网格面积相等,周长不等,第二幅周长相等,面积不等,从而认识到周长和面积没有必然的联系。)
(三 )、周长和面积公式推导教学。
1、 师:刚才我们理解了周长和面积的含义,那么它们的周长和面积的计算公式是怎样呢?请同学们打开数学书134页,分别写出它们的公式,在写的过程中并回忆一下它们是怎样推导出来的?
2、 填化工说推导方法。学生说电脑显示公式,并简单说出公式的推导方法。长方形是数方格的方法,正方形是特殊的长方形,
平行四边形、三角形梯形用教具演示。圆用电脑演示。(板书:数、割、平移、补、重合、旋转、实验、转化。读一次板书) 3、 沟通面积化工之间的关系:
(1) 师:同学们看一看老师这六种平面图形的摆放,跟课本上的
摆放一样吗?
(2) 师:那么课本为什么要这样摆呢?(4个同学一个小组进行
讨论)
(3) 师:同学们真聪明,课本这样摆可使我们清楚地看出长方形
的面积计算公式是平面图形面积计算公式的基础,其它平面图形都是转化为长方形来计算的。同学们以后在息的时候,都可以利用知识之间的联系来整理我们所学过的知识,这样既方便我们理解知识,又有利于我们记 忆。
4、 练习:根据表中条件计算下面各图形的周长和面积。(印在练习纸上)

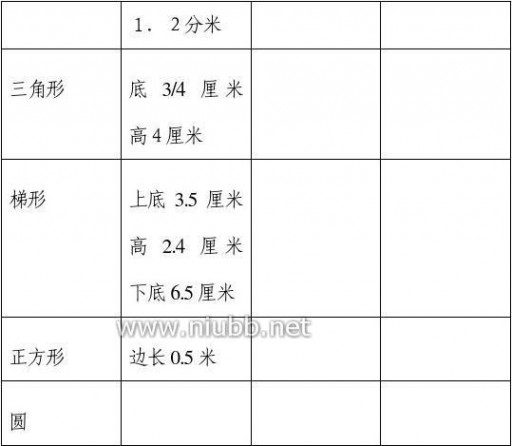
三、 练习
1、 判断题
(1) 三角形的面积是平行四边形面积的一半。( )
(2) 圆的周长和直径的比值叫做圆周率-网络日记-,用字母π来表示。( ) 2、 选择题
(1)一个平行四边形和一个三角形等底等高,已知平行四边形的面积是25平方厘米,三角形的面积是( )。
A 、12.5 B 、25 C 、50
(2)求右图的面积,列式正确的是( )。
A 、3.14×8÷2 B 、3.14×(8÷2)÷2 C 、3.14×8÷2+8 3、 应用题
(1) 从一块长18分米,宽10分米的长方形木板上切下一个最大的圆,切下的圆的面积是多少平方分米?剩下木板的面积是多少平方分米?
(2) 小明家装修一间长4米,宽3.2米,高3米的房子。在地面
上铺的是边长0.4米的方砖,请你算一算装修时至少要用多少块方砖?
(3) 市政府拍卖如下图形的一块土地,底价是每平方米200元,
如果有一位 开发商准备50万元买这块地,你认为他有没有可能买到?
(4) 阿凡提的故事:阿凡提到一个地主家里干活,狡猾的地主总
是想找借口克扣阿凡提的工钱。有一次地主叫阿凡提把一群羊赶进一个用栅栏围成的长是9米,宽是6.7米的长方形的羊圈里,但阿凡提发现这个羊圈根本无法容纳这群羊,因为这群羊至少需要70平方米的羊圈才够大。同学们你能够帮助阿凡提解脱困境吗?
(师总结:生活中到处都充满着数学知识,我们要从生活中学习数学知识,又要把数学知识运用到生活中去,解决生活中遇到
的问题。)
四、 课堂总结
同学们,通过今天的复习,你有什么收获?(学生自由发言) 教师进行归纳总结:
(1) 平面图形的周长和面积的概念。
(2) 平面图形的周长和面积的计算公式,并用转化的方法推
导出 公式。
(3) 用所学的知识解决生活中的实际问题。
五 : 平面图形的周长和面积(总复习)
人教版六年级数学下册第六单元
小学数学总复 习
图形的认识与测量
李垠火 2014年5月
你学过哪些平面图形
复习提纲: 1、平面图形的周长和面积的 意义各是什么?
2、这些周长和面积公式各是 怎样的?它们是怎样推导出来的?
围成一个图形的所 有边长的总和叫做这 个图形的周长。
计量周长的常用单位有哪些? 米;分米;厘米
1平方厘米
5 厘米
小正方形的个数 = 每排个数 × 排数 长方形的面积 = 长
× 宽
3厘米
1平方厘米
3厘米
小正方形的个数 =
正方形面积 =
每排个数 × 排数 边长 × 边长
平行四边形的面积=底×高
三角形面积=底 ×高÷2
梯形面积=(上底+下底)×高÷2
圆的面积=∏r 2
物体的表面或围成的 平面图形的大小,叫 做它们的面积。
常用的面积单位有哪些? 平方米;平方分米;平方厘米
平面图形的周长和面积公式推导:
a
C= 4a S=
a2
a S = ah÷2 h
b
a
C = (a+b)×2 S = ab
a S = ah
h
b S = (a+b)h÷2
h
a
r
C = 2πr S=
πr2
面积相等,周长不相等。
周长相等,面积不相等。
周长与面积的关系: 小学阶段你学习过哪些平面图形?
面积相等的图形,周 长不一定相等。
周长相等的图形,面 积不一定相等。
面积相等的图形: 圆的周长 < 正方形的周长 < 长方形的周长
周长相等的图形: 圆的面积 > 正方形的面积 > 长方形的面积
练一练
一、口算下面各图形的周长和面积。(单位:米)
2
2
2 3
2
周长: (3+2)×2=10(米)
周长: 2 ×4=8(米)
周长: 2 ×3.14 ×2=12.56(米)
面积:3 ×2=6(平方米)
面积: 2 ×2=4(平方米) 面积: 3.14 ×22=12.56(平方米)
二、计算图形的周长和面积。(单位:米)
6 4 20 10.5 3.14×4÷2+4 16+12+20=48(米) 6+6+10.5+7.5=30(米) =6.28+4 =10.28(米) 16×12÷2=96(平方米) (6+10.5)×6÷2 2 3.14 ×(4 ÷2) ÷2 =16.5×6÷2 =3.14×4÷2 答:它的周长是48米, =49.5(平方米) =6.28(平方米) 面积是96平方米。
答:它的周长是30 米,面积是49.5平 方米。 答:它的周长10.28米, 面积是6.28平方米。
6
判 断
1、面积相等的两个梯形一定可以拼成一个平行四 边形。 ( × ) ) ) 2、面积相等的两个三角形形状也相同。( ×
3、同底等高的两个三角形的面积一定相等。( √
4、周长相等的长方形和平行四边形,他们的面积一
× 定相等。 (
)
5、底和高都是0.2厘米的三角形的面积是0.2平方 × 厘米。 ( ) 6、平行四边形的底越长,它的面积就越大。( × ) 7、三角形的面积是平行四边形面积的一半。( × ) 8两个三角形的高相等,它们的面积就相等。( × )
解决问题
1、 一个镜框的长是4.5分米,宽是3分米,做这 个镜框要用线条多少米?要用玻璃多少平方米?
周长:(4.5+3)×2=15(分 =1.5
(米) 米) 面积:4.5×3=13.5(平方分米) =0.135(平方米) 答:做这个镜框要用线条1.5米。要用玻璃0.135平方米。
解决问题
2、求右面图形的面积。 (单位:厘米)
8 10
15
25 9
S﹦ah÷2+ (a+b)h÷2 + ah 15×8÷2 +(15+25)×10÷2 + 25×9 ﹦60+200+225 ﹦485(平方厘米) 答:它的面积是485平方厘米。
解决问题
3、一块周长为120米的正方形地与一块三角形地的 面积相等,三角形地的底为60,求三角形地的高是 多少?
【解题思路导引】找出正方形的面积→S正方形=S三角形 →三角形的高
正方形的边长为:120÷4=30(m)
三角形面积为:30×30=900 (m2) 三角形的高为:900×2÷60=30(m) 答:三角形地的高为30米。
解决问题
4、把一个圆分割拼成一个近似的长方形,长方形 的周长比圆的周长多10厘米,求圆的面积。 3.14×(10÷2)2
=3.14×52 =3.14×25 =78.5(cm2) πr r r
解决问题
5、一块长方形的铁板,长15米,宽是长的 , 要在这块铁板上截一个最大的圆,这个圆的面积 是多少平方米?
2 长方形的宽为: - =10(m) 15× 3
2 3
圆的半径为:10÷2=5(m)
圆的面积为:52×3.14=78.5(m2)
答:圆的面积是78.5平方米。
?
知识拓展 1、你能计算出这个图形 中绿色 部分的周长、面积吗?
20厘米
20厘米
通过这节课的复习,
我们复习了什么? 你有哪些收获?
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1