一 : 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

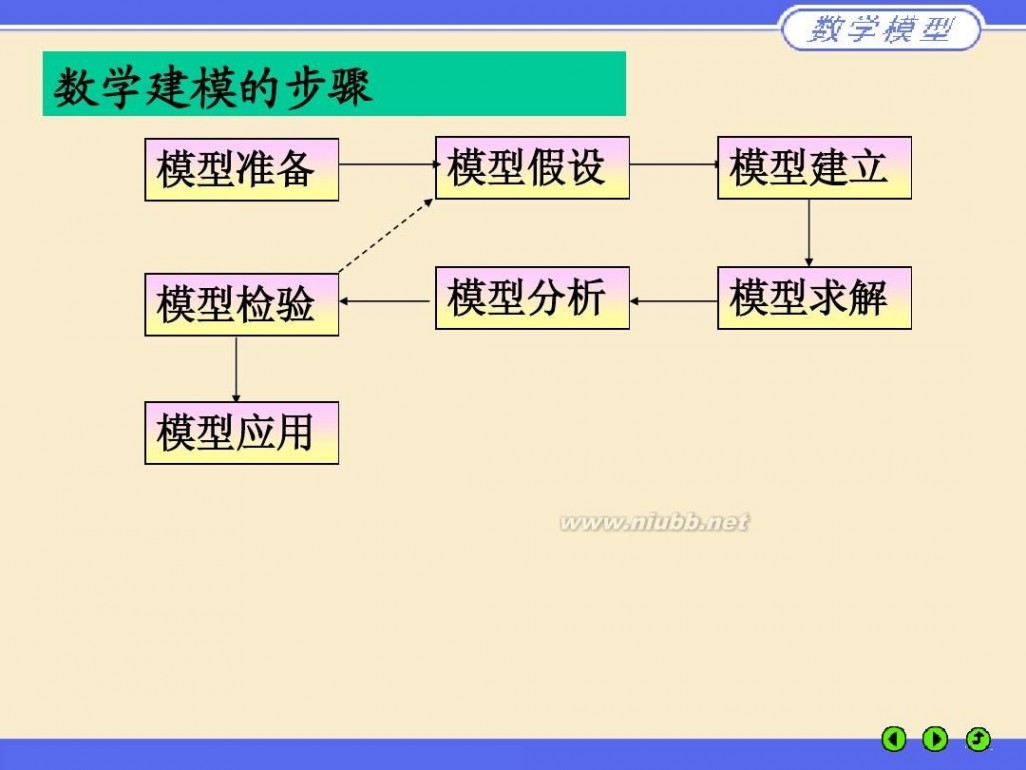
牛刀简历 第一章 数学建模简介

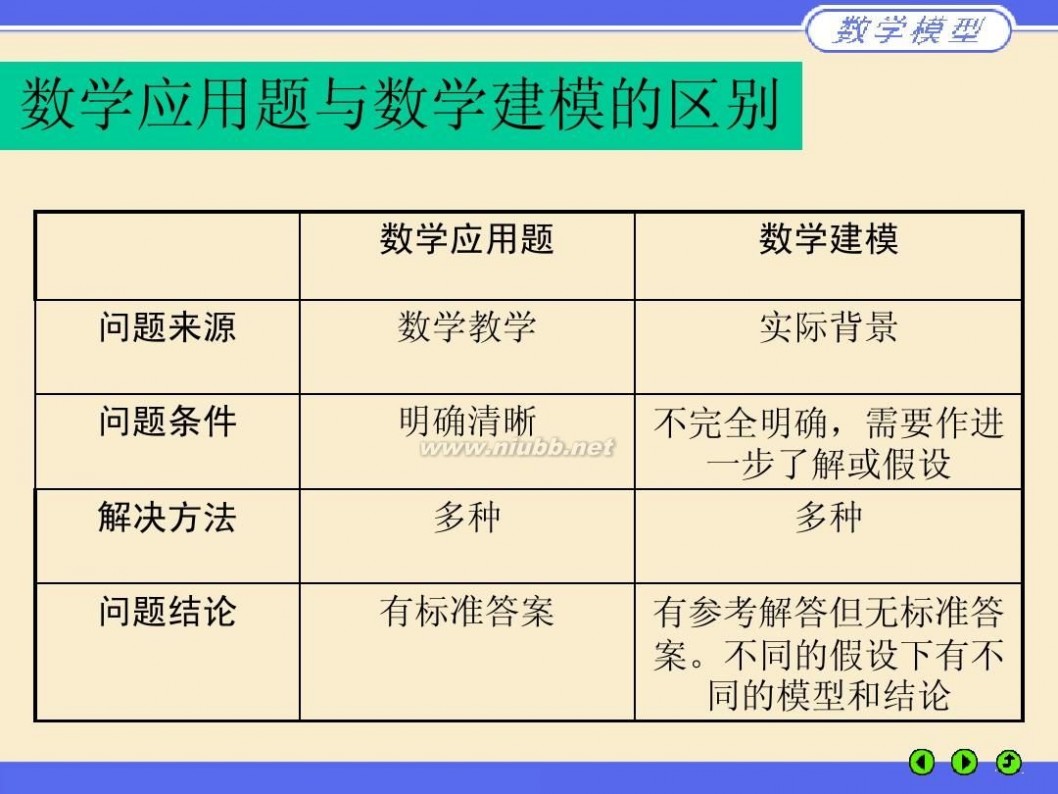
牛刀简历 第一章 数学建模简介

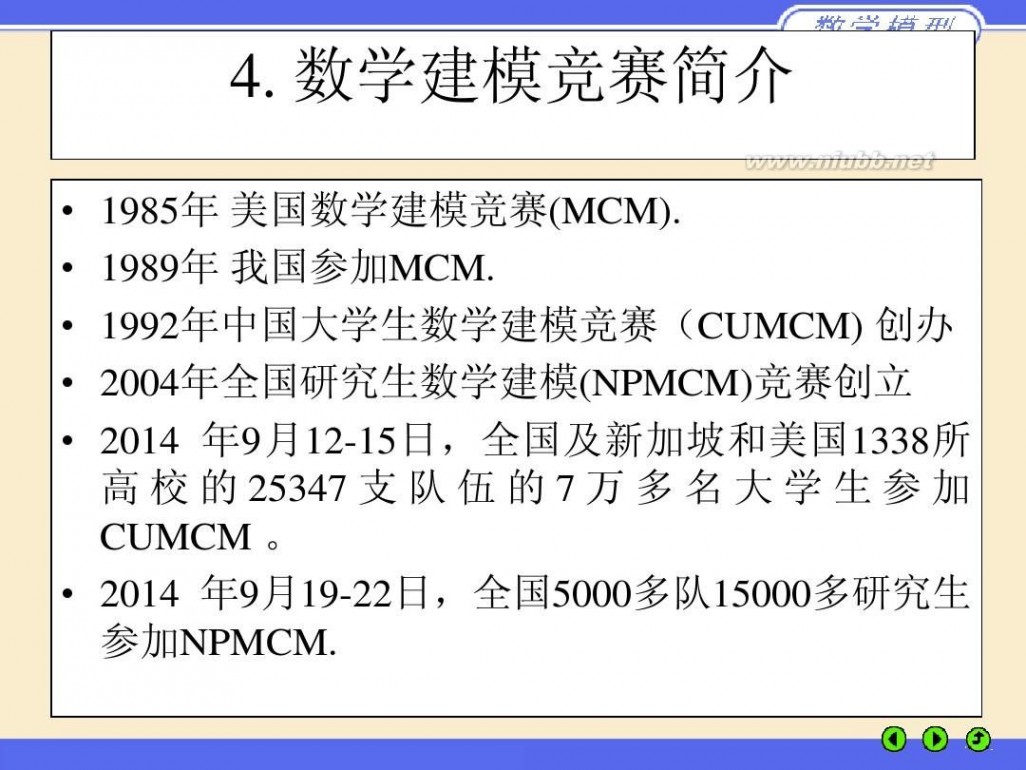
牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

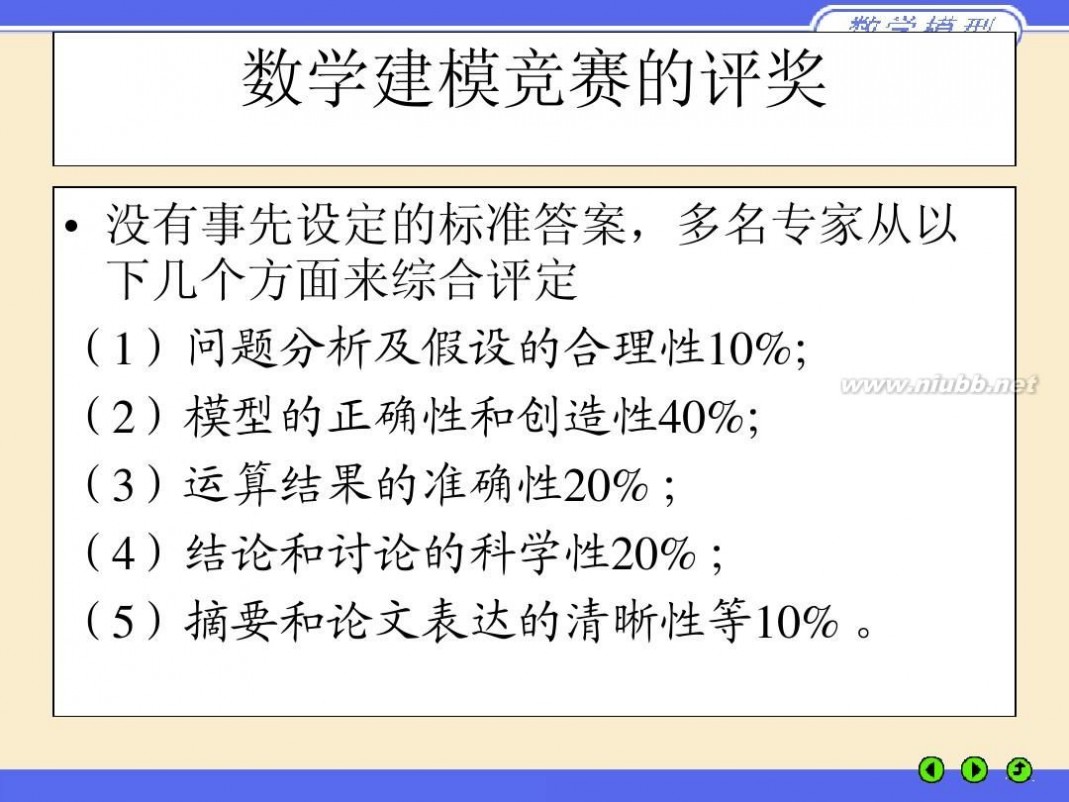
61阅读提醒您本文地址：

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

牛刀简历 第一章 数学建模简介

61阅读提醒您本文地址：

二 : 单摆运动的数学建模78

单摆在不同摆角下运动的数学模型

报告人：曾云霖

专业学号：微电子92 09053057

关键词：单摆、简谐运动、空气阻力，摆角大小

摘要：

单摆是生活中常见的模型，也是常用的简单模型。物理学中所讨论的单摆是一种理想化的模型,也称数学摆。它由一根不可伸缩的细线(质量不计),一端固定,另一端悬挂一质量为M的小球(视为质点)而构成的振动系统。

对于理想单摆，我们总是尽可能的简化它的一般分析，认为它只受到重力和拉力的作用。因为拉力与小球的运动总是相互垂直的，对小球的运动没什么影响

但生活中的单摆往往是非理想的，非理想单摆还考虑到绳的重力、空气阻力等，且单摆的运动还与单摆的摆角有关，研究单摆在不同摆角下的运动是有现实和理论意义的

模型建立：

考虑在摆角很小的范围内（小于5度），sinθ≈θ

由牛顿第二定律可知

mgsin???m?

??l? ??l?

??d?

dt

?2?mg??ml2?0?t

化简可得

?2?g???02l ?t

这是一个二阶常系数的奇次线性微分方程,设定初值条件： ??0??0,?(0)?a

利用高等数学知识可以解得：

?(t)?c1sint?c2cost

代入初值条件：

?(t)?acos?t ??结论：理想单摆在小摆角下（小于5度）的运动是简谐运动 周期

T?2?

??2问题扩展：

实际生活中的单摆是非理想的，总要收到其它力的作用，如绳的重力，空气阻力等

现在我们忽略绳的重力，考虑在空气阻力环境下单摆的运动。 查阅知识可知：空气粘滞阻力与小球速度成正比，即f?kv

所以单摆的受力方程变换为

mgsin??kv??m?

v?l??ld?

dt

化简可得：

d2?kd?g????02dtmdtl

可令

kg?2n,???ml

d2?d??2n??^2??02dtdt

22n??0当时

??asin?t?bcos?t

22n??0当时

?t??(a?bt)e

22n??0当时

?t?t ??ae?be 12

深化扩展：

以上讨论都是在摆角较小的前提下讨论出来的，若是大摆角的摆动，则sin???不再成立了，此时可以sin?考虑泰勒式展开。

sin?????3?5

3!?5! ?........

因为后面的级数对结果影响不大，所以近似可取

sin?????3

3!代入理想方程中

d2?mg(??)?ml2?03!dt ?3

这个微分方程比较难解，可以考虑用Matlab去求其解析解或数值解。

本文标题：简单数学建模论文-第一章 数学建模简介
本文地址： http://www.61k.com/1119460.html