一 : PHP使用数组实现矩阵数学运算的方法示例
本文实例讲述了PHP使用数组实现矩阵数学运算的方法。分享给大家供大家参考,具体如下:
矩阵运算就是对两个数据表进行某种数学运算,并得到另一个数据表.
下面的例子中我们创建了一个基本完整的矩阵运算函数库,以便用于矩阵操作的程序中.
来自 PHP5 in Practice (U.S.)Elliott III & Jonathan D.Eisenhamer
<?php // A Library of Matrix Math functions. // All assume a Matrix defined by a 2 dimensional array, where the first // index (array[x]) are the rows and the second index (array[x][y]) // are the columns // First create a few helper functions // A function to determine if a matrix is well formed. That is to say that // it is perfectly rectangular with no missing values: function _matrix_well_formed($matrix) { // If this is not an array, it is badly formed, return false. if (!(is_array($matrix))) { return false; } else { // Count the number of rows. $rows = count($matrix); // Now loop through each row: for ($r = 0; $r < $rows; $r++) { // Make sure that this row is set, and an array. Checking to // see if it is set is ensuring that this is a 0 based // numerically indexed array. if (!(isset($matrix[$r]) && is_array($matrix[$r]))) { return false; } else { // If this is row 0, calculate the columns in it: if ($r == 0) { $cols = count($matrix[$r]); // Ensure that the number of columns is identical else exit } elseif (count($matrix[$r]) != $cols) { return false; } // Now, loop through all the columns for this row for ($c = 0; $c < $cols; $c++) { // Ensure this entry is set, and a number if (!(isset($matrix[$r][$c]) && is_numeric($matrix[$r][$c]))) { return false; } } } } } // Ok, if we actually made it this far, then we have not found // anything wrong with the matrix. return true; } // A function to return the rows in a matrix - // Does not check for validity, it assumes the matrix is well formed. function _matrix_rows($matrix) { return count($matrix); } // A function to return the columns in a matrix - // Does not check for validity, it assumes the matrix is well formed. function _matrix_columns($matrix) { return count($matrix[0]); } // This function performs operations on matrix elements, such as addition // or subtraction. To use it, pass it 2 matrices, and the operation you // wish to perform, as a string: '+', '-' function matrix_element_operation($a, $b, $operation) { // Verify both matrices are well formed $valid = false; if (_matrix_well_formed($a) && _matrix_well_formed($b)) { // Make sure they have the same number of columns & rows $rows = _matrix_rows($a); $columns = _matrix_columns($a); if (($rows == _matrix_rows($b)) && ($columns == _matrix_columns($b))) { // We have a valid setup for continuing with element math $valid = true; } } // If invalid, return false if (!($valid)) { return false; } // For each element in the matrices perform the operatoin on the // corresponding element in the other array to it: for ($r = 0; $r < $rows; $r++) { for ($c = 0; $c < $columns; $c++) { eval('$a[$r][$c] '.$operation.'= $b[$r][$c];'); } } // Return the finished matrix: return $a; } // This function performs full matrix operations, such as matrix addition // or matrix multiplication. As above, pass it to matrices and the // operation: '*', '-', '+' function matrix_operation($a, $b, $operation) { // Verify both matrices are well formed $valid = false; if (_matrix_well_formed($a) && _matrix_well_formed($b)) { // Make sure they have complementary numbers of rows and columns. // The number of rows in A should be the number of columns in B $rows = _matrix_rows($a); $columns = _matrix_columns($a); if (($columns == _matrix_rows($b)) && ($rows == _matrix_columns($b))) { // We have a valid setup for continuing $valid = true; } } // If invalid, return false if (!($valid)) { return false; } // Create a blank matrix the appropriate size, initialized to 0 $new = array_fill(0, $rows, array_fill(0, $rows, 0)); // For each row in a ... for ($r = 0; $r < $rows; $r++) { // For each column in b ... for ($c = 0; $c < $rows; $c++) { // Take each member of column b, with each member of row a // and add the results, storing this in the new table: // Loop over each column in A ... for ($ac = 0; $ac < $columns; $ac++) { // Evaluate the operation eval('$new[$r][$c] += $a[$r][$ac] '. $operation.' $b[$ac][$c];'); } } } // Return the finished matrix: return $new; } // A function to perform scalar operations. This means that you take the scalar value, // and the operation provided, and apply it to every element. function matrix_scalar_operation($matrix, $scalar, $operation) { // Verify it is well formed if (_matrix_well_formed($matrix)) { $rows = _matrix_rows($matrix); $columns = _matrix_columns($matrix); // For each element in the matrix, multiply by the scalar for ($r = 0; $r < $rows; $r++) { for ($c = 0; $c < $columns; $c++) { eval('$matrix[$r][$c] '.$operation.'= $scalar;'); } } // Return the finished matrix: return $matrix; } else { // It wasn't well formed: return false; } } // A handy function for printing matrices (As an HTML table) function matrix_print($matrix) { // Verify it is well formed if (_matrix_well_formed($matrix)) { $rows = _matrix_rows($matrix); $columns = _matrix_columns($matrix); // Start the table echo '<table>'; // For each row in the matrix: for ($r = 0; $r < $rows; $r++) { // Begin the row: echo '<tr>'; // For each column in this row for ($c = 0; $c < $columns; $c++) { // Echo the element: echo "<td>{$matrix[$r][$c]}</td>"; } // End the row. echo '</tr>'; } // End the table. echo "</table>/n"; } else { // It wasn't well formed: return false; } } // Let's do some testing. First prepare some formatting: echo "<mce:style><!-- table { border: 1px solid black; margin: 20px; } td { text-align: center; } --></mce:style><style mce_bogus="1">table { border: 1px solid black; margin: 20px; } td { text-align: center; }</style>/n"; // Now let's test element operations. We need identical sized matrices: $m1 = array( array(5, 3, 2), array(3, 0, 4), array(1, 5, 2), ); $m2 = array( array(4, 9, 5), array(7, 5, 0), array(2, 2, 8), ); // Element addition should give us: 9 12 7 // 10 5 4 // 3 7 10 matrix_print(matrix_element_operation($m1, $m2, '+')); // Element subtraction should give us: 1 -6 -3 // -4 -5 4 // -1 3 -6 matrix_print(matrix_element_operation($m1, $m2, '-')); // Do a scalar multiplication on the 2nd matrix: 8 18 10 // 14 10 0 // 4 4 16 matrix_print(matrix_scalar_operation($m2, 2, '*')); // Define some matrices for full matrix operations. // Need to be complements of each other: $m3 = array( array(1, 3, 5), array(-2, 5, 1), ); $m4 = array( array(1, 2), array(-2, 8), array(1, 1), ); // Matrix multiplication gives: 0 31 // -11 37 matrix_print(matrix_operation($m3, $m4, '*')); // Matrix addition gives: 9 20 // 4 15 matrix_print(matrix_operation($m3, $m4, '+')); ?> PS:这里再为大家推荐几款在线计算工具供大家参考使用:
在线一元函数(方程)求解计算工具:
http://tools.61k.com/jisuanqi/equ_jisuanqi
科学计算器在线使用_高级计算器在线计算:
http://tools.61k.com/jisuanqi/jsqkexue
在线计算器_标准计算器:
http://tools.61k.com/jisuanqi/jsq
更多关于PHP相关内容感兴趣的读者可查看本站专题:《PHP数学运算技巧总结》、《PHP运算与运算符用法总结》、《php字符串(string)用法总结》、《PHP数组(Array)操作技巧大全》、《PHP常用遍历算法与技巧总结》、《PHP数据结构与算法教程》、《php程序设计算法总结》、《php正则表达式用法总结》及《php常见数据库操作技巧汇总》
希望本文所述对大家PHP程序设计有所帮助。
二 : 实例讲解木马的分析方法
三 : 超实用:PS修图磨皮技法实例解析
开始前,咱们先分析下中性灰修图手法的原理依据,这样可以让大家更简洁明了的理解它。
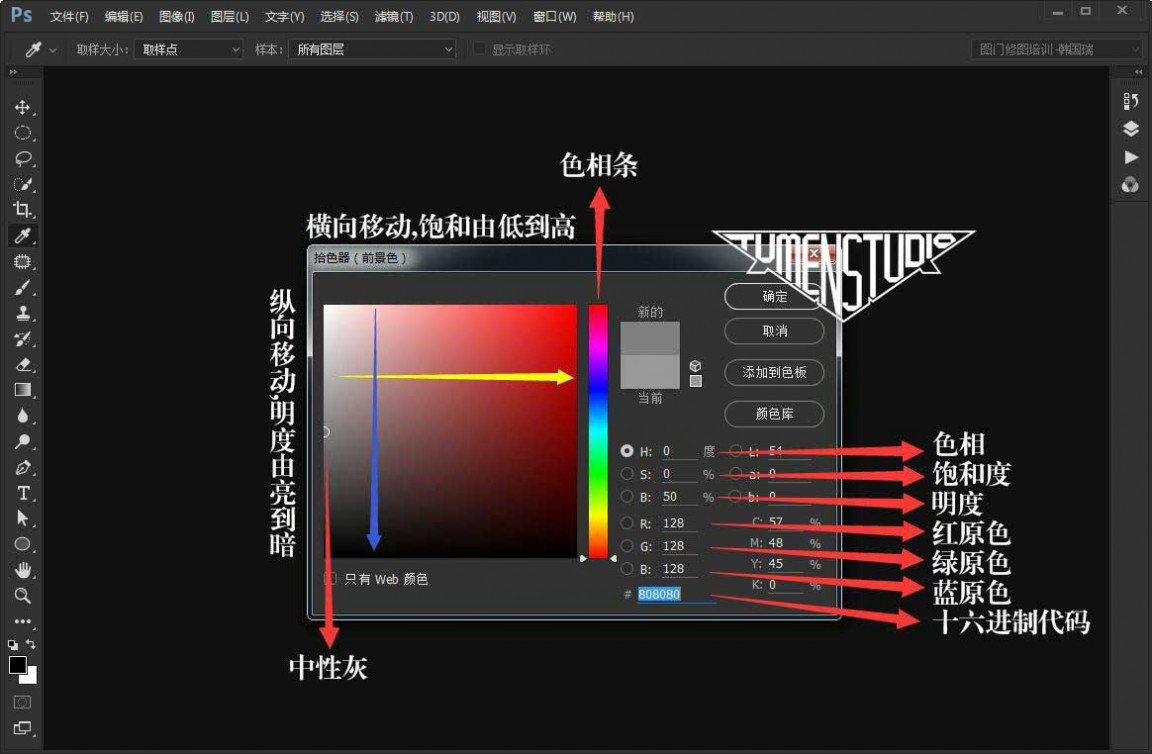
首先,咱们要弄明白什么样子的灰度才是咱们所讲的中性灰。
大家应该都清楚图片是由R、G、B三原色组成,每个颜色满阶都是255阶,加上0一共是256阶,
所以也就有了1600万色或千万色的说法(256×256×256=16777216)。
当R、G、B值都为255时为白色,当R、G、B值都为0时为黑色, 因为黑与白只是明度的改变,所以当R、G、B值相等且不是0或255时为灰色。
当R、G、B值相等且不是0或255时,均等值越大那么这个灰色也就越亮,越小也就越暗。
那么,我们这里所提到的中性灰R、G、B值应该均为128,因为256÷2=128。
但网络上见到有朋友在自己翻录的中性灰教程里介绍说中性灰的R、G、B值都为125, 如果这类朋友的小学算术没问题的话,
肯定就是把R、G、B的满值错解成250了。
接下来再说一下中性灰修图过程当中一个必不可少的环节-将中性灰图层模式修改为柔光。
大家都清楚的一点是,中性灰图层需要配合柔光图层模式才好进行图片的光影与质感修饰, 那么要想更通俗易懂的了解中性灰手法,
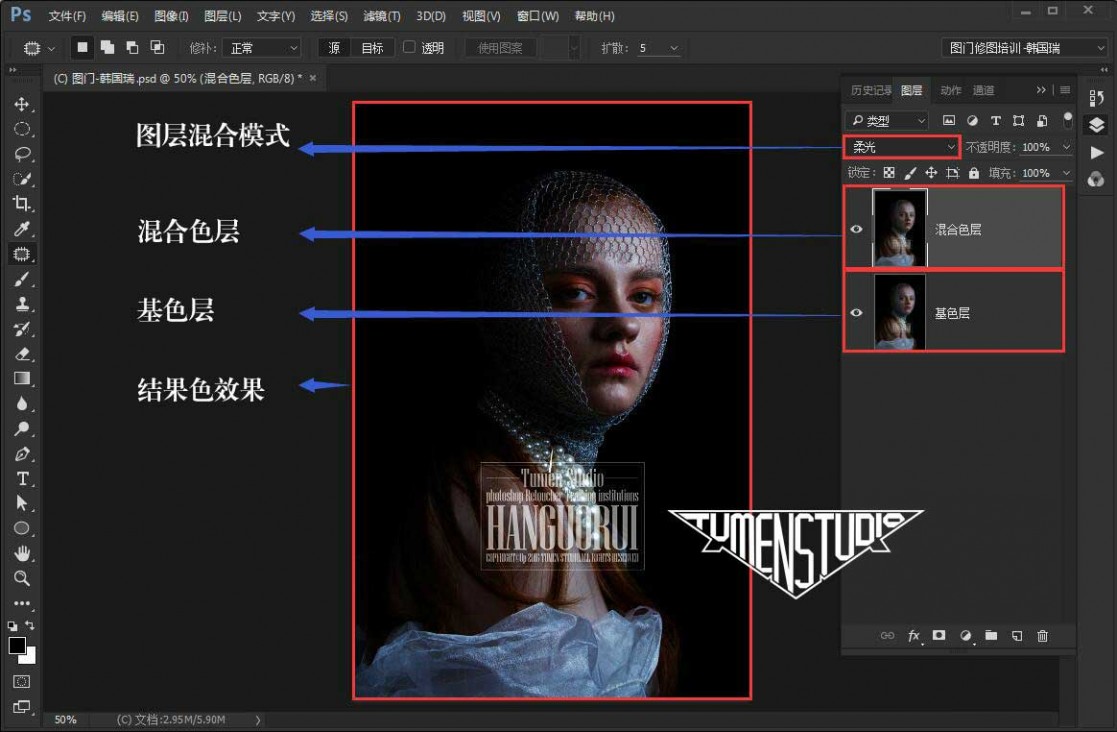
咱们就必须先理解柔光混合图层模式的具体作用。 在讲柔光混合模式之前,咱们先要明白三个概念,即基色、混合色、结果色。
比如咱们在PS里打开了一张图片,然后新建或复制一层,亦或者置入了一个新的图像, 那么,咱们这里称下面的背景图层为基色层,
其每个像素的颜色咱们这里称之为基色; 称上面的图层为混合色层,其每个像素的颜色咱们这里称之为混合色;
修改混合色图层的混合模式后显示出的最终效果色,咱们这里称之为结果色。
接下来咱们就介绍下柔光模式的特点,柔光混合模式的效果与发散的聚光灯照在图像上相似。
该模式根据混合色的明暗来决定图像的最终效果是变亮还是变暗,继而改变基色的饱和程度。 使用该模式让颜色变亮或变暗,
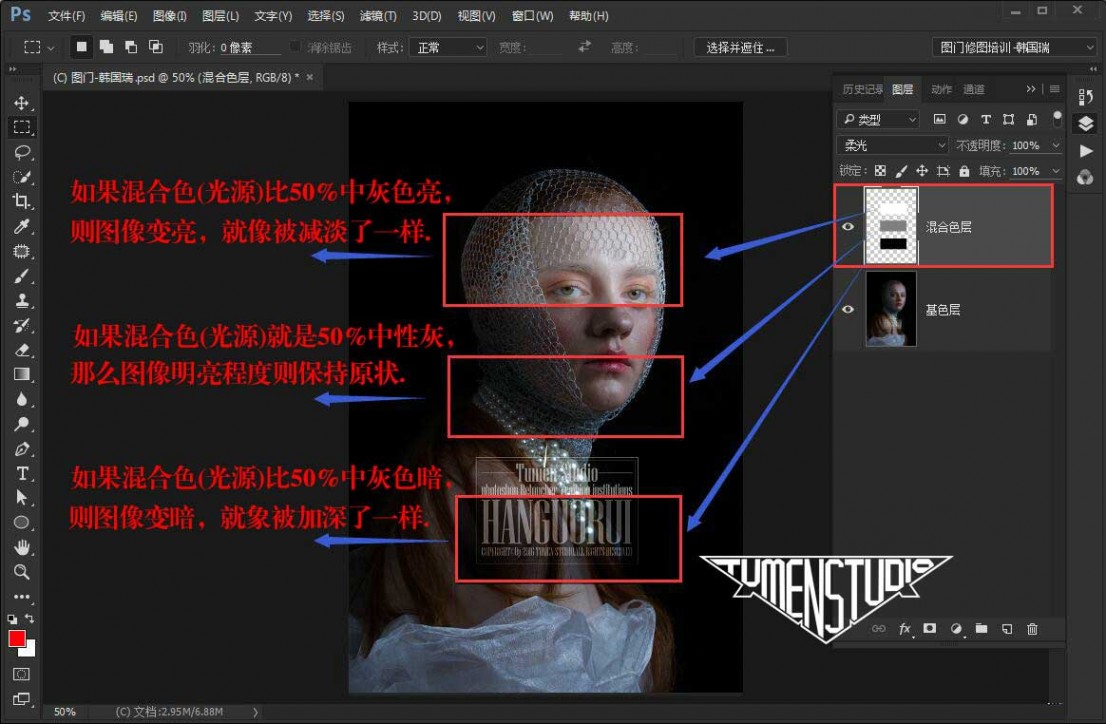
可产生比叠加模式或强光模式更为精细柔和的效果。 如果混合色(光源)比50%中灰色亮,则图像变亮,就像被减淡了一样;
如果混合色(光源)比50%中灰色暗,则图像变暗,就象被加深了一样; 如果混合色(光源)就是50%中性灰,那么图像明亮程度则保持原状。
用纯黑色或纯白色绘画会产生明显较暗或较亮的区域,但不会产生纯黑色或纯白色,
这是由柔光混合模式在前期设计编程时所依据的计算公式来决定的。
混合色<=128:结果色 = 基色 + (2 * 混合色 - 255) * (基色 - 基色 * 基色 / 255) / 255; 混合色 >128:
结果色 = 基色 + (2 * 混合色 - 255) * (Sqrt(基色/255)*255 - 基色)/255。 当然,咱们只需要了解相应图层模式的特点即可,没必要去深度研究其计算公式。
这就如同咱们在平时做菜时只需了解盐有多咸、糖有多甜,并能做出美味菜肴即可, 没必要非要打破沙锅问到底的去研究盐和糖的化学成分或具体构造,
有个学无止境、精益求精的心态是极好的,但切忌轻重倒置、舍本逐末,从而枉费了光阴。
大家可能会问,既然"如果混合色(光源)就是50%中性灰,那么图像明亮程度则保持原状。
那么咱们又为何非要给混合层填充中性灰呢?为什么不直接用混合模式为柔光的空白层?
这是因为填充了中性灰以后,即可用黑白画笔在中灰层上涂抹以完成图像效果的加深减淡, 也可以直接用减淡加深工具在中性灰图层上涂抹
以达到异曲同工的减淡加深效果。 当然,你如果觉得填充中性灰这一步太麻烦,直接用混合模式为柔光的空白层也是可以的,
不过,这样一来你就只有黑白画笔一种选择了,因为空白层是没有任何像素可供加深减淡的。
由于减淡的英文翻译是Dodge,加深的英文翻译是Burn,所以也有人称这类修图方法为D&B。 ------------------------------------------------------------------------
网络上还见到有朋友在自己翻录的中性灰教程里介绍说中性灰图层既可以用柔光,也可以用叠加,
这个理解也是大错特错的,因为柔光混合模式与叠加混合模式有着本质上的显著差异。
下面咱们就再大致介绍一下叠加图层混合模式的特点,以解释为什么说这类理解的错误的。
叠加混合模式的特点是在为底层图像(基色层)添加颜色的同时,可保持底层图像的高光和暗调。
该模式是将混合色与基色相互叠加,也就是说底层图像控制着上面的图层,可以使之变亮或变暗。
比50%暗的区域将采用正片叠底模式变暗,比50%亮的区域则采用滤色模式变亮。 一般来说,发生变化的都是中间色调,高色和暗色区域基本保持不变。
颜色会被混合,但基色层颜色的高光与阴影部分的亮度细节会被保留。 所以说,中性灰修图法中的中性灰图层混合模式只能为柔光,而不能是叠加。
可能是因为这些朋友在擦中灰层的时候画笔力度偏低,所以很难肉眼分辨出叠加与柔光下的差异, 从而才有了中灰层既可以用叠加模式
也可以用柔光模式、叠加等于柔光的荒谬歪解。

网络上还见到有朋友介绍说自己发明创造了一种新的修图手法,叫空白层(柔光混合模式)修图法,
个人觉得这样的"创造发明"真的是有点穿凿附会、生拉硬扯了。
想必大家多少了解或听说过双曲线修图法,即建立一亮一暗两个曲线调整层,将蒙版反相为黑色, 然后设置前景色为白色,
图像需要提亮的区域就用画笔在做了提亮调整的曲线调整层蒙版上轻擦, 图像需要压暗的区域就用画笔在做了压暗调整的曲线调整层蒙版上轻擦,
从而完成光影质感修饰。 双曲线与中性灰两种修图手法利用的都是加深减淡原理,相对来说各有利弊,这里就不多作说明了。
那么,假如咱们用两个色阶取代双曲线,咱们就能寡廉鲜耻的说自己发明创造了双色阶修图法吗?
咱们大家都习惯用筷子吃饭,假如换用两根树枝吃饭就能说自己发明创造了新的吃饭方法?
也有在网络上见到一种叫做"明度修图法"的修图技巧,也是用上面所述的"空白层修图法"操作,
不同的是这种修图方法所使用的图层混合模式是明度模式。个人对这种修图方法也是不敢苟同。
下面咱们再来大致介绍一下明度图层混合模式的特点,以解释为什么说这种方法也是不可取的。
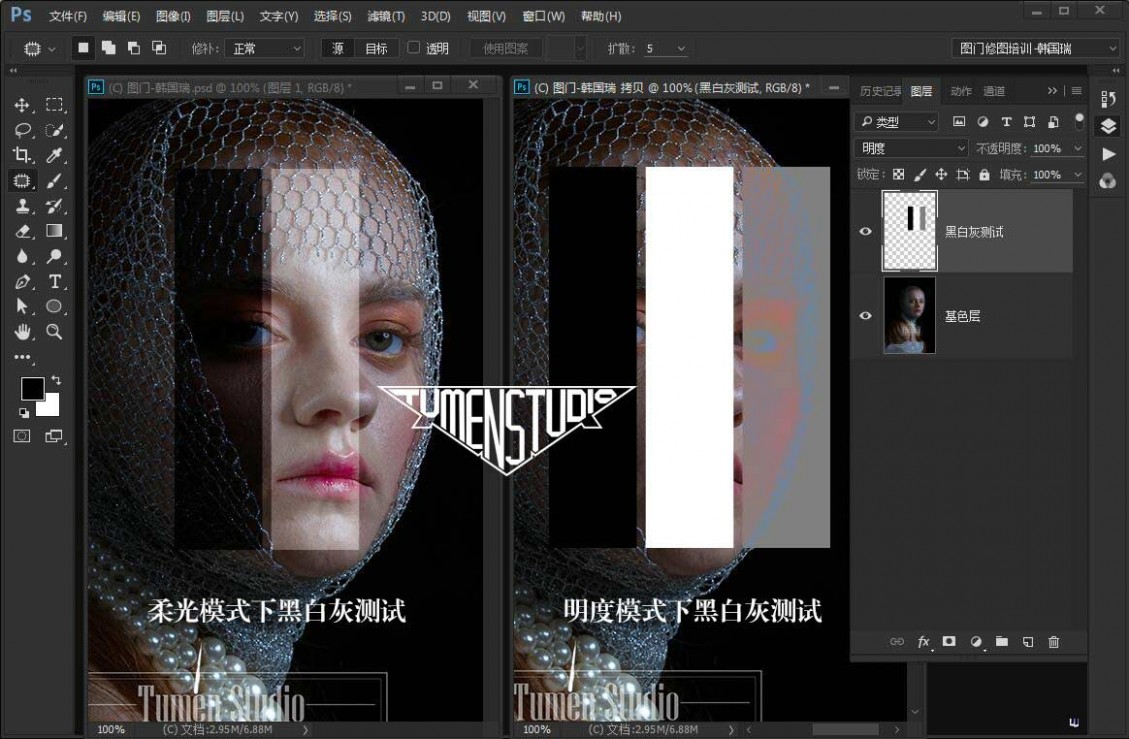
明度混合模式的特点是可将当前图像的亮度应用于底层图像中,并保持底层图像的色相与饱和度。
此模式下所创建的效果与颜色图层混合模式相反。 因此混合色图片只能影响图片的明暗度,不能对基色的颜色产生影响。
但请切记,黑、白、灰除外。 明度模式下,纯黑色与基色混合得到的仍是纯黑色,因为纯黑色的明度是最低的;
纯白色与基色混合得到的仍是纯白色,因为纯白色的明度是最高的; 不同程度的灰色与基色混合得到的是不同程度的灰色。
个人猜想,造成这样错误理解的原因,同样是因为在用明度混合模式修图时画笔的整体力度很小,
以致修图者在修图时肉眼很难觉察到明度改变的同时,色相及饱和度其实也已经悄然发生了改变。
可能有朋友会说,利用中性灰修图手法修饰图片后,明度改变的同时饱和度也发生了改变啊?
这是因为柔光混合模式的特点是通过明暗对比度的增加继而完成饱和度的增加或降低。
但需要注意的是,中性灰修图手法是不会改变基色色相的,从而为后面的颜色统一减轻了负担。
只要是正确的引导教程,是没有所谓的"高级"与"基础"之分的,具体要看不同的受众群。
一篇大家所谓的高级教程,在基础还不扎实的新手朋友看来就是无字天书,因为根本看不懂;
反之,你给他一篇大家所谓的基础教程,他会如获至宝,因为这才是解决他当前瓶颈的法宝。
一篇大家所谓的基础教程,在基本功相对比较扎实的朋友看来就是垃圾,因为他早已驾轻就熟;
反之,你给他一篇大家所谓的高级教程,他会欣喜若狂,因为这其中有他朝思暮想的法门所在。
同样的道理,工具之间也没有高低贵*之分,对于不同的修饰调整,只纯在工具选择正确于否。
如果选择用液化滤镜做调色肯定无从下手,那么咱们就能以此断言液化滤镜是个低端工具吗?
如果选择用色阶或曲线工具轻松实现了明暗调整,咱们就能妄言置评说它们比液化滤镜高级了?
咱们所崇拜的高手们也是在用和咱们一样的看似基础的工具,但为什么他们就能做到出神入化?
那是因为人家把恰当的工具用在了正确的地方,那是因为人家把所谓基础的工具用的炉火纯青。
学习如同逆水行舟一般,不进则退,简单举例,就像我们平时逆向乘坐电梯一样, 想要在逆行的状态下到达终点,一般的努力只能是原地踏步,
唯有拼命狂奔才能修成正果; 但是,如果选择了正确的方向(顺向乘坐电梯)就能事半功倍,从而轻松得到咱们渴望的美好。 --------------------------
图片显"脏",大致以下三个方面的原因:色相、饱和度、明亮度的不统一,即H、S、B。
咱们这里要讲的中性灰修图手法即是通过对局部明亮度的调整从而让图片光影变得干净顺畅。
唠叨了这么久,在正式介绍中性灰修图手法之前,还得再说一个事情,即明度观察组的建立。
建立明度观察组的目的是为了屏蔽颜色对咱们修饰光影时的影响及增加明暗对比以辅助观察。
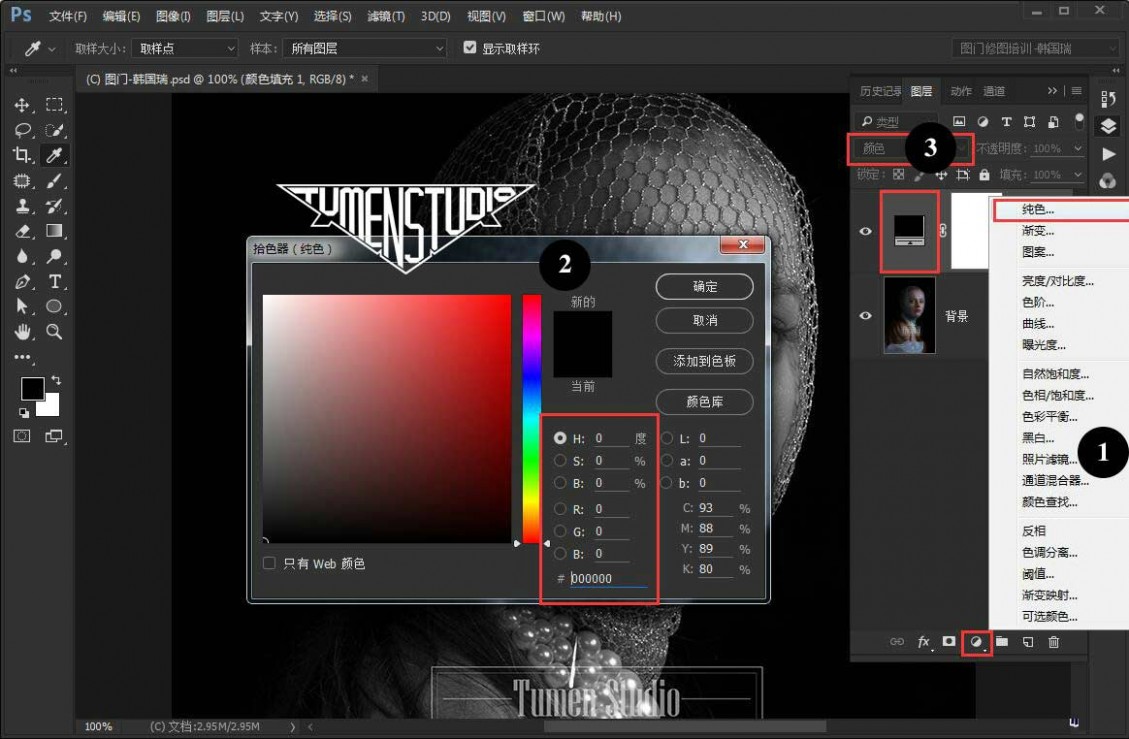
打开图像,建立一个纯黑色调整层,修改图层模式为颜色,这样做的目的是为了屏蔽颜色。
方式方法是多种多样的,不是说必须用我说的这种方法,只要达到了去色的目的即可。
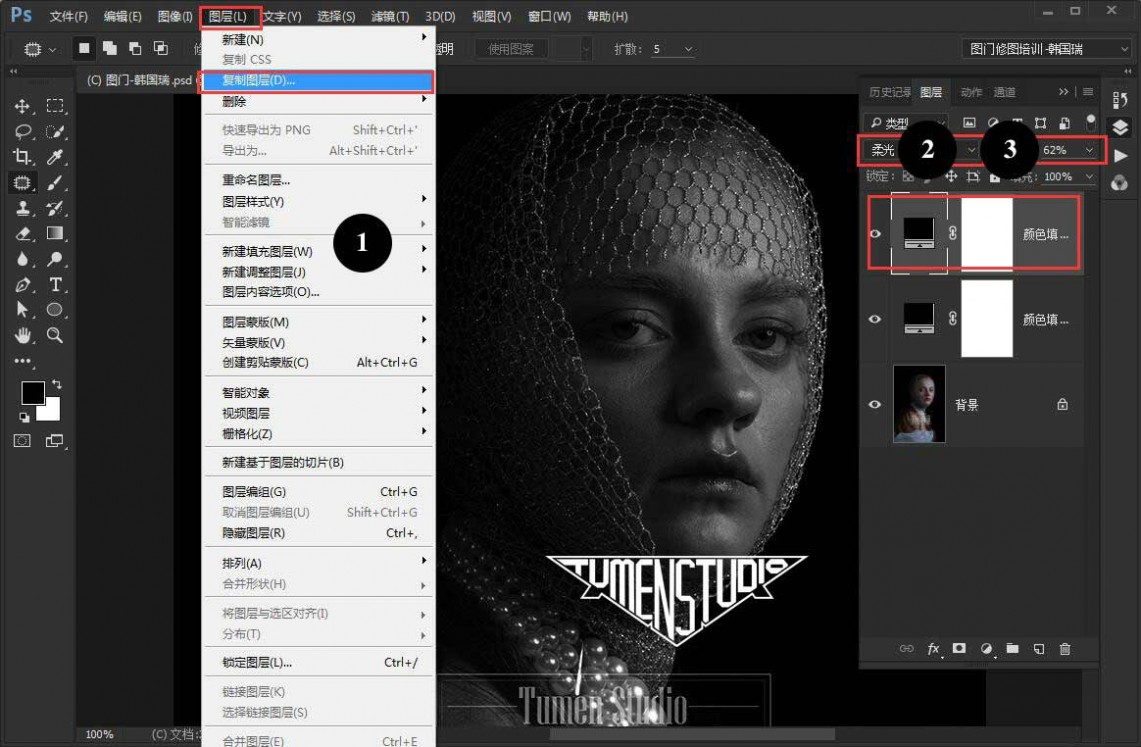
然后就是增加明暗对比了,我习惯用的方式是复制刚刚建立的纯黑色调整层,改模式为柔光。
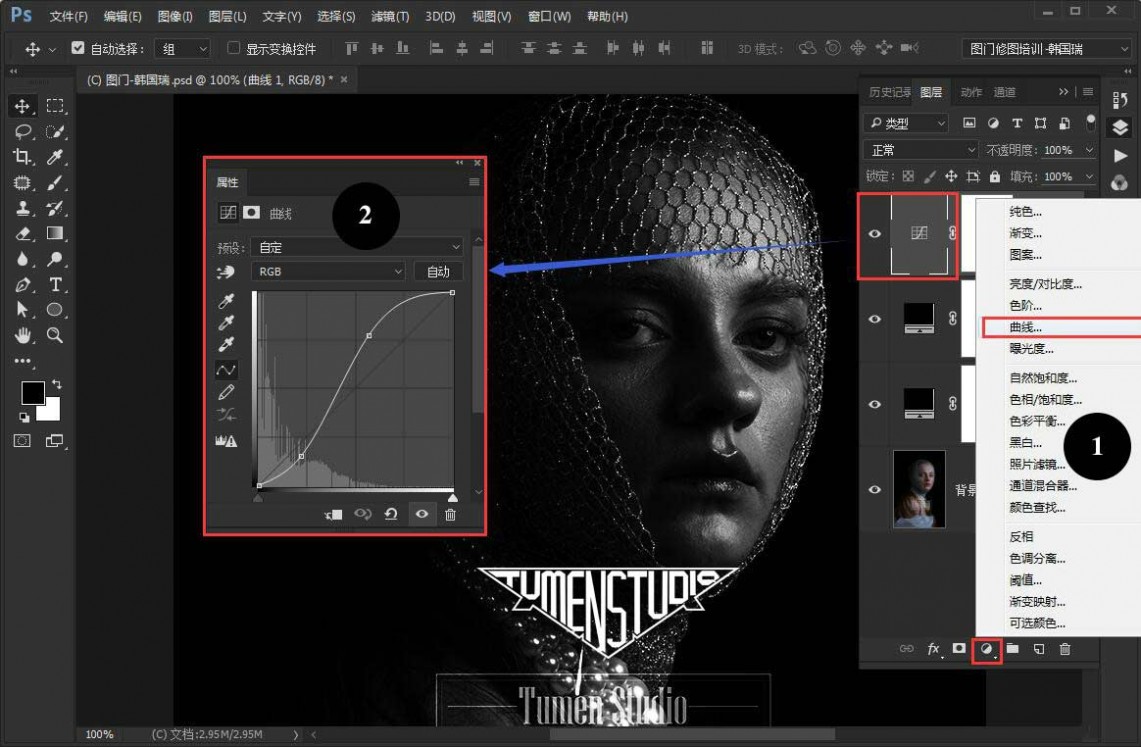
如果觉得明暗对比还不够强的话,可以修改图层模式为叠加或者再添加一个曲线调整层, 在曲线调整层里做提亮高光并压暗阴影参数调整,
同样,只要达到增加明暗对比的目的就可以。 为了方便管理及操作,选中两个纯色及曲线调整层,按快捷键Ctrl+G建组并命名为明度观察组。
我早期的教程内这一步介绍的是"复制第一步建立的纯黑色调整层,改模式为叠加。"
有好心的朋友就跑出来纠错了,我按照你的方法并没有得到和你一样的观察组效果,你说的不对。
我在教程内早已经说明了的,建立明度观察组的方法有很多种,不见得非要按照我说的方法走,
而且在要具体结合所修图片本身的明暗关系及修图过程中的需要,继而随时调整明暗对比的。
学习,切忌死搬硬套,学习的是思路方法及思维方式,这样才能举一反三、真正融魂贯通。

明度观察组建立完毕,下面咱们就进入到中性灰图层的擦拭阶段的讲解。
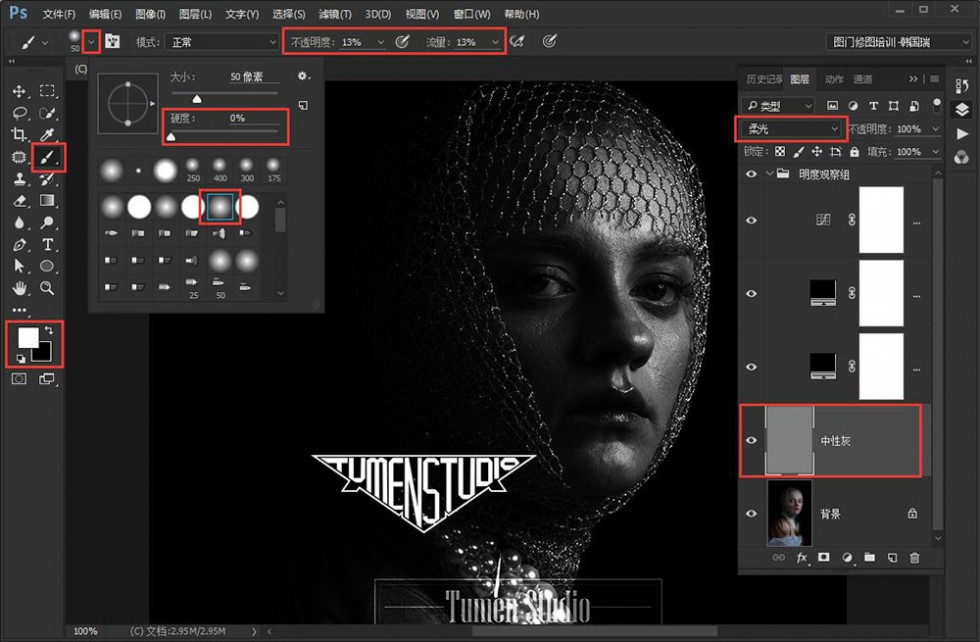
在观察组下方新建图层,填充50%的中性灰,修改图层混合模式为"柔光"。 也可以按快捷键Ctrl+Shift+N,在弹出的窗口选择设置模式为柔光
并勾选"填充柔光中性色"。 按快捷键D将默认前景色设置为黑色、背景色为白色,按快捷键X切换前景色与背景色位置。
按快捷键B选择画笔工具,并设置画笔为柔角笔刷,硬度选择默认的0度即可。 画笔的大小可以先随意设置,
具体的大小参数要根据具体所修饰的区域大小来随时调整的。 将画笔的不透明度及流量设置在10-15之间。
当然,也可以根据个人喜好及具体情况适当调整。 很多朋友不晓得"不透明度"与"流量"的区别,这里咱们大致讲一下。
不透明度想必大家都了解,因为只看字面意思就明白它的作用和特点了,流量的理解可能是盲区。
流量可以看做不透明度的二级控制,实际绘画的不透明度是二者的乘积。 如果这样说大家还不能够简单明了的理解,
那么就大白话介绍以解开这个困扰大家很久的问题。 如果你喜欢用点的形式使用画笔,那么就把不透明度的参数设置小一些,流量参数设置大一些;
如果你喜欢用拖的形式使用画笔,那么就把不透明度的参数设置大一些,流量参数设置小一些。
具体修图的时候到底是用"点"还是用"拖"的形式去使用,这要根据你所修饰的具体区域来定。
如果你修饰的区域是一个小点或者小线条,那么肯定用点的形式比较轻松方便;
如果你修饰的区域是一个面或者说比较大的区域,那么肯定用拖的形式比较简洁省事。
还是那句话,具体的方式方法还要参考你所修饰的具体区域来定,切勿照葫芦画瓢而事倍功半。
说到这里在多句嘴,再捎带介绍下图层"不透明度"与"填充"的区别。
降低图层的不透明度参数,会使图层整体不透明度降低(包含样式的不透明度,如描边、投影等), 降低图层的填充参数,
该图层图像的不透明度会降低,但图层样式的不透明度不会发生任何改变。

所有前期准备工作已就绪,接下来就是耐心的擦拭中灰层了,但只有耐心还是远远不够的, 在擦拭的时候要先处理大光影(图片自身光影分布),
然后才是放大画布进行细节的具体修饰。 自身需要了解面部五官的高低起伏,因为突起的地方即为高光区,凹陷的地方即为阴影区。
当然,这仅仅是在平光状态下的理解,具体还要结合图片自身拍摄时的光源方向来做光影分布判断。
咱们今天主要是解析中性灰修图手法,所以具体的光影及纹理分布这里就不一一赘述了, 感兴趣的小伙伴可以自行网络搜索或者去书店
翻阅一下有关素描类的书籍资料。 很多朋友咨询为什么要先修饰大光影,而后才是局部细节的精雕细琢?下面咱们就举例说明一下,
假如咱们是商店买衣服,是不是脑海中前期就有了自己想要的大致款式?
如果没有也没关系, 那么逛街的时候是不是要先在街面上观察每家店橱窗内的风格展示?如果没有这样做也没关系, 进到店内以后是不是就要先看款式?
款式喜欢了再看具体做工或者试穿,检查有没有线头等等, 相信大家再逛街买衣服时不会是一进门直接拿着一件衣服先看有没有做工质量问题,
觉得质量没问题后再一看衣服款式,才发现自己根本不喜欢这款,然后在换旁边的衣服继续看细节?
任何事情都是先把大致做好,然后才是局部细节的分区处理,根基打不好是很难百尺高楼平地起的。
有热心的朋友质疑说,你早期的教程介绍里不是说要把画布放大到500%并以单位像素做具体修饰吗?
那是因为我那篇教程中所用到的图片大光影本身问题不大,所以直接跳过大光影环节去修饰的细节。
也有热心的朋友批判说,你早期教程内的图片细节修饰的太失真了,细节过于细腻了,看起来很假。
那是为了凸显中性灰功能特性而特意做的教程,具体制作的时候根据自己的需要确定细腻程度即可, 还是那句话,切忌循规蹈矩。
具体的修图力度及参数要根据自己所修图片的具体情况和需求来定。 吸取别人的精华并摒弃糟粕,结合自己的个人偏好并加以创新,
就有了自己独有的风格特点。 市场里买了块肉回家下酒,但发现肉中有肥有瘦,就因为自己不喜欢吃肥肉就把整块肉都丢垃圾桶?
咱们这里的分享就如同教你做一道地道的川菜佳肴,假如你不太喜欢吃辣或者不太喜欢吃麻, 那么自己做的时候少放点辣椒花椒就是了,
变通一下就好了,为什么非要逼着自己照抄别人的呢?
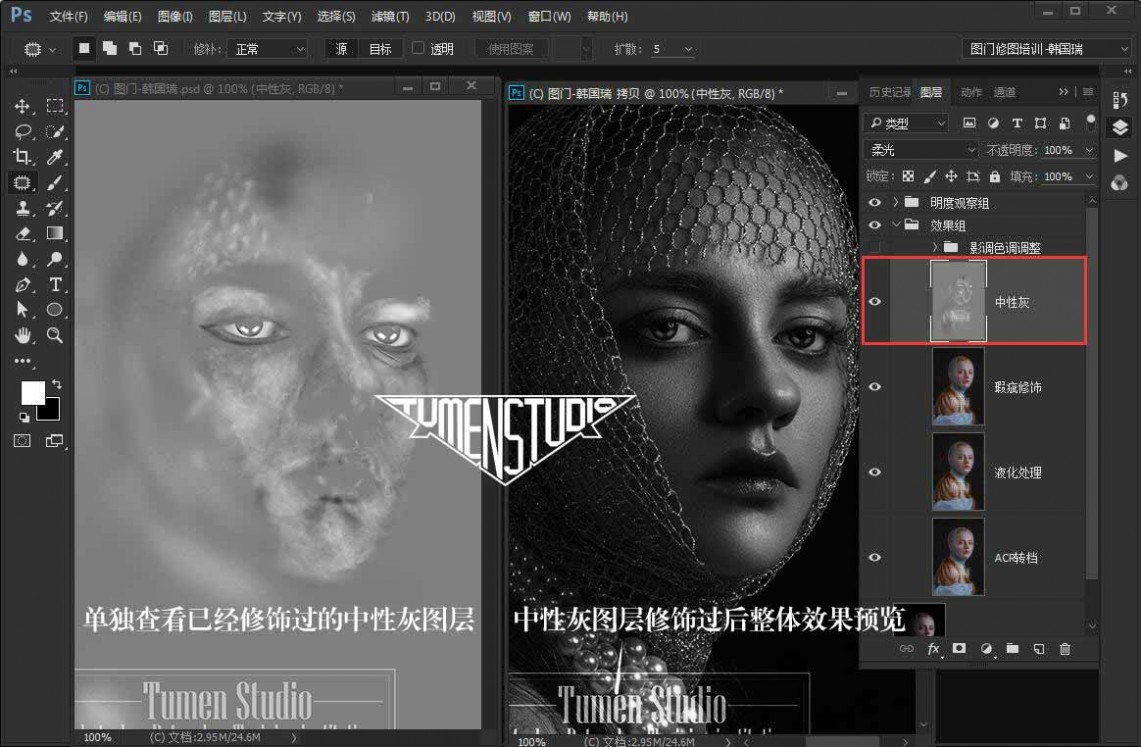
因为柔光混合模式具有"通过明暗对比度的增加继而完成基色饱和度的增加或降低"特点,
所以,在中性灰修饰完成以后,会出现局部颜色与整体肤色不统一的现象,后面再做肤色统一即可。
明度不统一,我们可以建议明度观察组配合D&B修图手法进行修饰, 其实色相及饱和度不统一,
也可以建立色相观察组及饱和度观察组配合具体修饰方法进行统一。 但这种方法过于繁琐,
下面咱们就介绍一种相对简便的色彩统一方法,即"颜色混合模式统一法"。
操作方法很简单,新建一层空白层,将图层混合模式修改为颜色,吸取前景色为偏色旁边的颜色,
用柔角画笔工具在偏色的地方轻轻擦拭直到颜色基本统一即可。 这个方法虽然不是十分精确,但对于绝大多数片子来说其实已经够用了。
下面再介绍下颜色混合模式的特点,以便大家更好的理解这种颜色统一的方法。 颜色混合模式引用基色的明度和混合色的色相与饱和度创建结果色。
它能够使用混合色的饱和度和色相同时进行着色, 这样可以保护图像的灰色色调(明暗程度),但结果色的颜色(色相饱和度)由混合色决定。
颜色模式可以看作是饱和度模式和色相模式的综合效果,一般用于为图像添加单色效果。

可能大家会觉得说,明明的说好的中性灰修图手法解析,为什么中性灰没讲多少,反而废话一大推?
因为中性灰就是一个加深减淡的工作原理,只要大家掌握好画笔的力度控制及光影纹理具体分布,
勤加练习后就可以轻松驾驭D&B修图手法,从而得到自己梦寐以求的光影质感很棒的图片效果。
咱们这里虽然没有用很大的篇幅去介绍中性灰修图的具体操作(因为它本身也没有什么好讲的),
但用了大量时间去讲解中性灰修图手法错误的理解,摒弃了错误的理解,不就只剩下正确方法了?
少犯错,争取不犯错,那么整体方向就不会偏太远,再加上自己刻苦努力的练习,成功,舍我其谁?
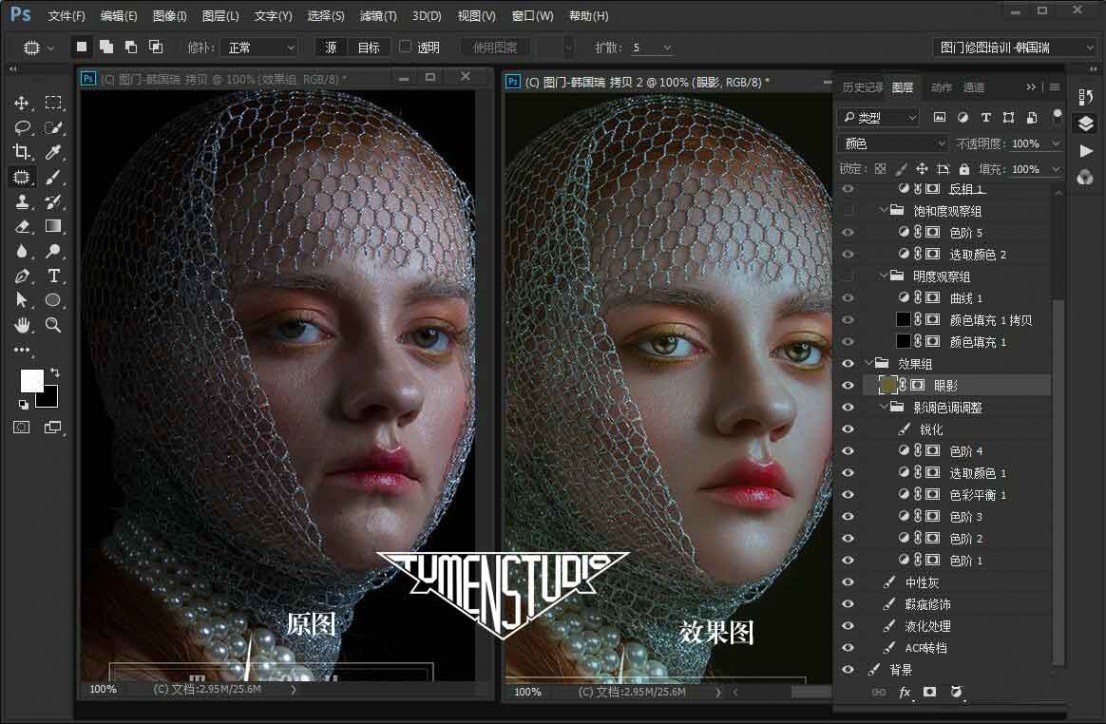
说一个番外话题,有不少新手朋友问我,是不是用数位板修出来的图像会比鼠标修的好很多?
这里我不多作解释了,就用一个小例子来给大家简要的说明一下吧。 一个不会玩飘移的新手司机,难道咱们给了他一辆跑车他就突然会了?
一个会玩飘移的车手,给他辆小烂车他也一样得意的飘儿,只是他"飘"起来没那么顺手罢了。
我一直用的是鼠标,但不否认如果用惯了数位板肯定是要比鼠标轻松快捷很多。 只是我平时太忙,一直没这么多的时间去适应它而已。
修图靠的是基本功,硬件起到的是辅助作用。
希望大家可以花更多的心思在技术及审美能力的提升上,因为这才是成功的不二捷径。 ------------------------------------------------------------------------
最后送给大家十个字,"多看,多练,多总结,循环之。"。 多看,提高自己的整体审美能力;多练,提高自己的基本功;
多总结,去繁求简,摒弃糟粕;循环之,精益求精,更上层楼。 好的,今天的分享就先到这里了,欢迎有机会大家再多多交流。
四 : PS实例解析选区减法运用
今天为大家分享PS解析选区减法运用方法,教程很基础,适合新手来学习,希望能对大家有所帮助!
步骤:
1、选择“矩形选框工具”,在文档中绘制一个矩形;


2、选择“单行选框工具”;

3、按住“alt键”,这是选区减法的快捷键,绘制单行选区;

4、最终效果:

五 : 实例讲解矩形造字法
矩形造字法的方法和过程介绍!





61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1