一 : 弧度制和弧度制与角度制的换算
弧度制和弧度制与角度制的换算
1、1o的角是怎样规定的? 规定周角的1/360叫做1度的角。 2、什么叫角度制? 用度作单位来度量角的单位制叫做 角度制。 3、角度制的单位是什么? “度”(即“ o ”) 不能省略
B O? 1o A
一、弧度制
1、1弧度的角: 长度等于半径的弧所对的圆心角 叫作1弧度的角,记作1 rad。
弧 AB 的长等于半径 1弧度的角 .
C
B r o 1 rad r A
r ,则弧 AB 所对的圆心角是
请问:周角、平角、直角的弧度数分别是多少?
B r
B’
r’
o
r
A
o’
r’
A’
2、弧度制的定义: 正角的弧度数是一个正数,负角的弧度数是一 个负数,零角的弧度数是0;
角 ? 的弧度数的绝对值 作为圆心角时所对弧的 以弧度作为单位来度量 | ? |? l r 长, r 是圆的半径,这种 角的单位制,叫做弧度 制 ,其中 l 是以角 ?
二、角度与弧度的换算:
1、把角度换成弧度:
360 ? ? 2? rad
[总结]
(1)仅出现度的,可以直 ? 接乘以 rad , 180 约简即可;出现分秒的应 先化为度,然后再换算。
180 ? ? ? rad ? rad ? 0 . 01745 rad 1? ?
180
(2)用弧度作单位时,
常常把弧度数写成多少 个 ? 的形式,如不作特
例1、把 90o , 67o30? 化成弧度。
解:
90 ? ?
?
180
rad ? 90 ?
1 2 )? ?
?
2
rad
1 2 ) ?
殊说明不必将? 写成小
数。
67 ? 3 0 ? ? ( 67
?
180
rad ? ( 67
3 8
? rad
2、把弧度换成角度:
2? rad ? 360 ?
[总结]
带 ? 者常可用来 180o 代 换; 不 带 ? 者 可用 其 弧 度 数 乘 以57.30o 来 求近似 值。
? rad ? 180 ?
1 rad ? ? 180 ? ? 57 . 30 ? ? 57 ? 1 8 ? ? ? ? ? ?
?
例2、把
解:
3 5
?
rad ,-2.1 rad 化成度。
3 5 ? 180 ? ? 108 ?
3 5
? rad ?
? 2 . 1rad ? ? 2 . 1 ? 57 . 30 ? ? ? 120 . 33 ?
注意:
1、用弧度制表示角时,“弧度”二字或“rad” 可省略,而只写这个角所对应的弧度数;但用 角度制表示角时,“度”或“0”不能省去。 2、用“弧度”为单位度量角时,常把弧度数写 成多少 ? 的形式,如无特别要求不必把 ? 写 成小数。
3、终边相同的角的表示方法,可用角度制表示, 也可以用弧度制表示,但要注意前后两项所采 用的单位制必须一致。
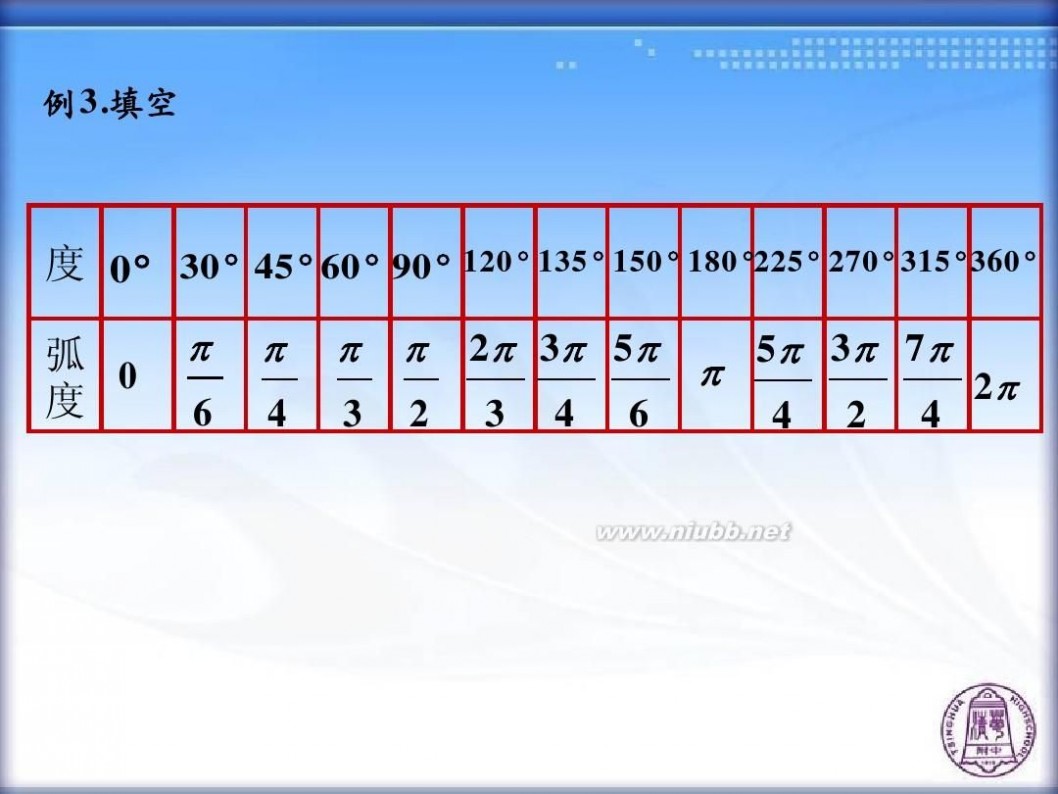
例 3 .填空
度 0 ? 30 ? 45 ? 60 ? 90 ? 弧 0 度
?
6
120 ? 135 ? 150 ? 180 ? 225 ? 270 ? 315 ? 360 ?
?
4
?
3
?
2
2? 3? 5? 3 4 6
?
5? 3? 7? 4 2 4
2?
例 4 .利用弧度制推导扇形面 S ? 1 2 lr
积公式
其中 l 是扇形弧长, r 是扇形的半径
.
课堂练习
1 .若 ? ? ? 3,则 ? 的终边在第( A .一 B.二 C. 三 D.四
)象限
2 .圆弧长度等于其内接正 则该圆弧所对圆心角的 A.
三角形的边长, 弧度数为( D .2 )
?
3
B.
2? 3
C. 3
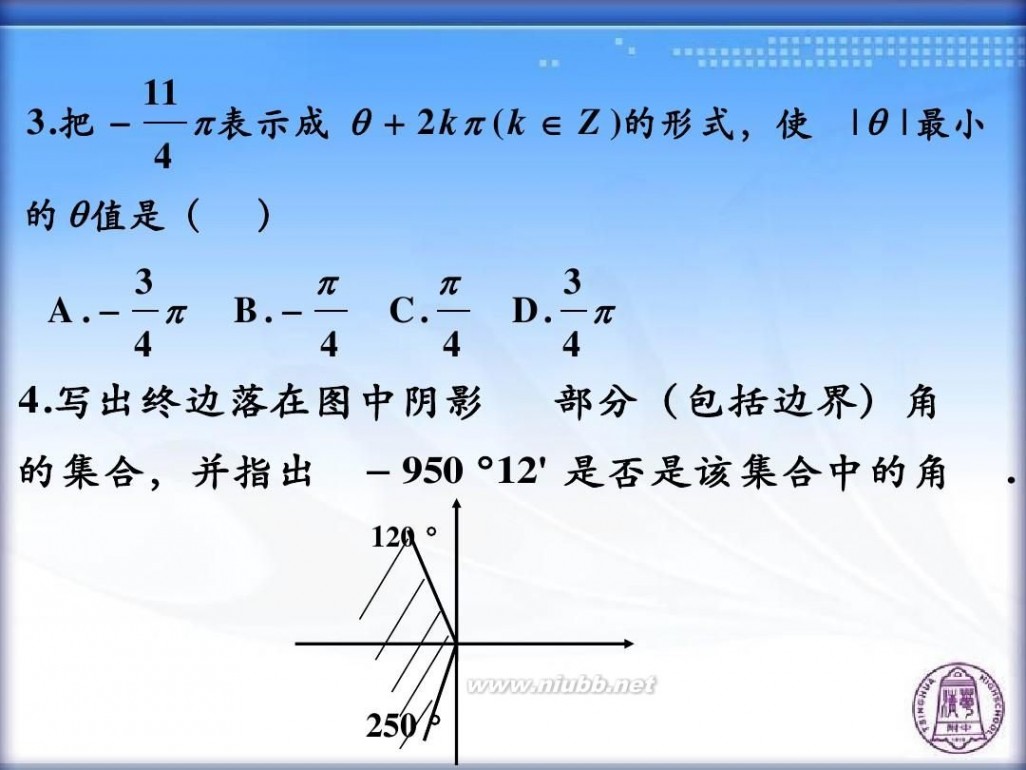
3 .把 ?
11 4
? 表示成 ? ? 2 k ? ( k ? Z )的形式,使
) B. ?
| ? | 最小
的 ? 值是( A .? 3
?
?
C.
?
D.
3
?
4 4 4 4 .写出终边落在图中阴影
4 部分(包括边界)角
的集合,并指出
? 950 ? 12' 是否是该集合中的角
120 ?
.
250 ?
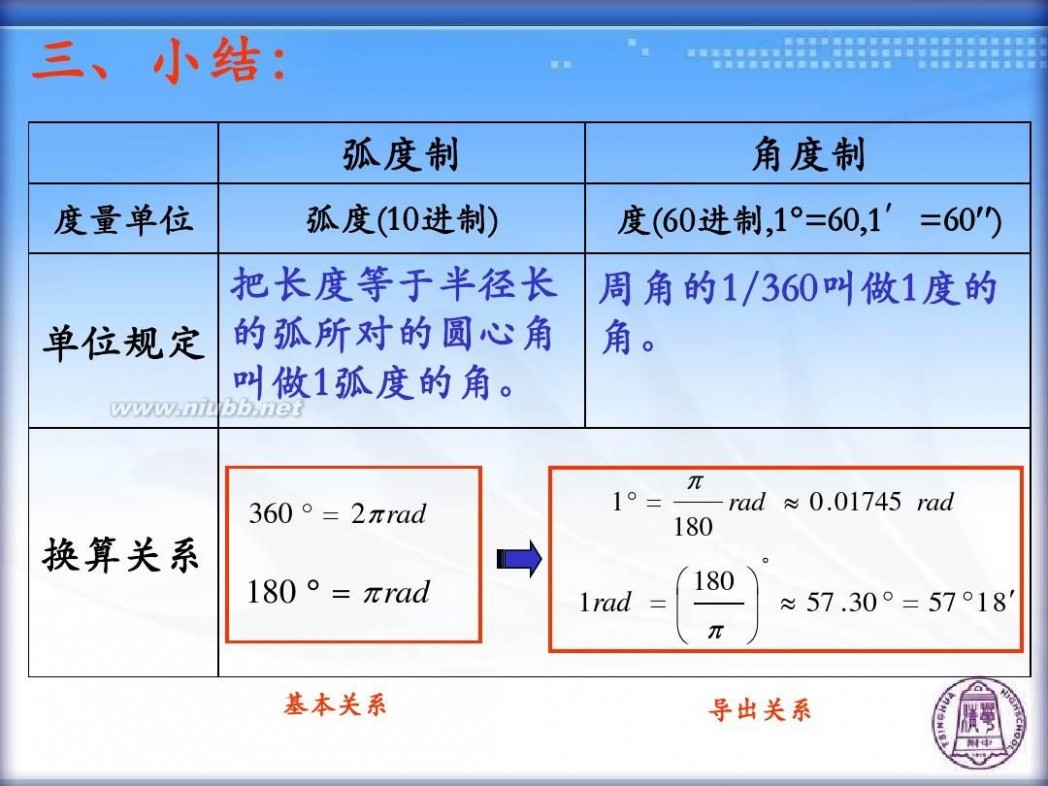
三、小结:
弧度制
度量单位 弧度(10进制)
角度制
度(60进制,1?=60,1′=60??)
把长度等于半径长 周角的1/360叫做1度的 单位规定 的弧所对的圆心角 角。 叫做1弧度的角。
360 ? ? 2? rad
1? ?
?
180
rad ? 0 . 01745 rad
?
换算关系
180 ? ? ? rad
基本关系
? 180 ? 1 rad ? ? ? ? 57 . 30 ? ? 57 ? 1 8 ? ? ? ?
导出关系
二 : 弧度制和弧度制与角度制的换算

弧度制 弧度制和弧度制与角度制的换算

弧度制 弧度制和弧度制与角度制的换算

弧度制 弧度制和弧度制与角度制的换算
弧度制 弧度制和弧度制与角度制的换算

弧度制 弧度制和弧度制与角度制的换算

弧度制 弧度制和弧度制与角度制的换算

弧度制 弧度制和弧度制与角度制的换算

弧度制 弧度制和弧度制与角度制的换算
弧度制 弧度制和弧度制与角度制的换算

弧度制 弧度制和弧度制与角度制的换算

弧度制 弧度制和弧度制与角度制的换算
弧度制 弧度制和弧度制与角度制的换算
三 : 数学:1.1.2《弧度制和弧度制与角度制的换算》课件

1度等于多少弧度 数学:1.1.2《弧度制和弧度制与角度制的换算》课件
1度等于多少弧度 数学:1.1.2《弧度制和弧度制与角度制的换算》课件

1度等于多少弧度 数学:1.1.2《弧度制和弧度制与角度制的换算》课件

1度等于多少弧度 数学:1.1.2《弧度制和弧度制与角度制的换算》课件

1度等于多少弧度 数学:1.1.2《弧度制和弧度制与角度制的换算》课件

1度等于多少弧度 数学:1.1.2《弧度制和弧度制与角度制的换算》课件

1度等于多少弧度 数学:1.1.2《弧度制和弧度制与角度制的换算》课件
1度等于多少弧度 数学:1.1.2《弧度制和弧度制与角度制的换算》课件

1度等于多少弧度 数学:1.1.2《弧度制和弧度制与角度制的换算》课件
1度等于多少弧度 数学:1.1.2《弧度制和弧度制与角度制的换算》课件

1度等于多少弧度 数学:1.1.2《弧度制和弧度制与角度制的换算》课件
1度等于多少弧度 数学:1.1.2《弧度制和弧度制与角度制的换算》课件

四 : 数学:1.1.2《弧度制和弧度制与角度制的换算》课件
1.1.2 弧度制和 弧度制与角度制的换算
问题一:
度量长度有哪些单位? 度量长度有哪些单位? 长度有哪些单位 度量重量又有哪些单位? 重量又有哪些单位 度量重量又有哪些单位?
问题二:
1 什么叫1度角 度角? 什么叫 度角?1o为圆周的 360 。
这种用度为单位来度量角的制度叫做角度制。 这种用度为单位来度量角的制度叫做角度制。
1.定义: 定义: 定义 长度等于半径长的圆弧所对的圆心角叫做 弧 长度等于半径长的圆弧所对的圆心角叫做1弧 所对的圆心角叫做 度的角,弧度记作 度的角,弧度记作rad。这种以弧度为单位来 。 度量角的制度叫做弧度制。 度量角的制度叫做弧度制。 弧度制
r r
注:今后在用弧度制表示角的时候,弧度二字 今后在用弧度制表示角的时候, 或rad可以略去不写。 可以略去不写。 可以略去不写
3. 弧度制与角度制相比: 弧度制与角度制相比: (1) 弧度制是以“弧度”为单位的度量角的单 弧度制是以“弧度” 单位的度量角的单 位制,角度制是以“ 位制,角度制是以“度”为单位来度量角的 单位制; 弧度 弧度≠1o 单位制;1弧度 o; 弧度是弧长等于半径长的圆弧所对的圆 (2)1弧度是弧长等于半径长的圆弧所对的圆 ) 弧度 1 心角的大小, 心角的大小,而1度是圆周 度是圆周 的所对的圆心 360 角的大小; 角的大小;
(3)弧度制是十进制,它的表示是用一个实 )弧度制是十进制, 数表示,而角度制是六十进制; 数表示,而角度制是六十进制; (4)以弧度和度为单位的角,都是一个与 )以弧度和度为单位的角, 半径无关的定值。 半径无关的定值。 负角的弧度数是负数, (5)正角的弧度数是正数, 正角的弧度数是正数, 正角的弧度数是正数 负角的弧度数是负数, 零角的弧度数零。 -http://www.61k.com-零角的弧度数零。
l 4.公式: α = 公式: 公式 r
表示的是在半径为r的圆中,弧长为l的 表示的是在半径为 的圆中,弧长为 的 的圆中 。 弧所对的圆心角是αrad。
α的正负由旋转方向确定
5. 弧度制与角度制的换算 思考 1度角等于多少弧度? 度角等于多少弧度? 度角等于多少弧度
1 =
o
π
180
rad ≈ 0.01745rad
度 ≈ 57.30
o
1弧度角等于多少度? 弧度角等于多少度? 弧度角等于多少度
1rad =
180
π
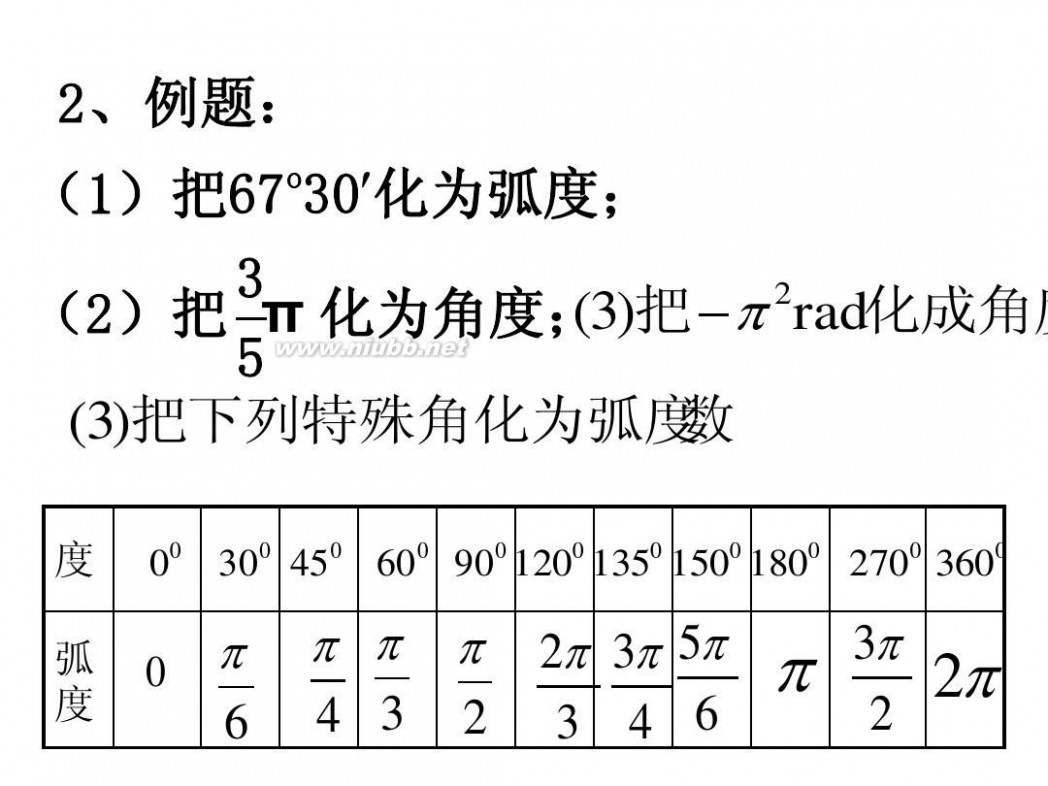
2 、例题: (1)把67 30′化为弧度; 3 2 (3 (2)把 π化为角度; )把 ? π rad化成角度 5 (3)把下列特殊角化为弧度数
o
度 弧 度
00 300 450 600 900 1200 1350 1500 1800 2700 3600
0 π
π π
4 3
π
6
2π 3π 5π 2 3 4 6
π
3π 2
2π
于扇形的公式: 例3.利用弧度制证明下列关 于扇形的公式: 1 2 1 (1)l = αr ; ( 2) S = αr ; ( 3) S = lr ; 2 2 r为半径, l为
弧长, α (0 < α < 2π )为圆心角, 为半径, 为弧长, 为圆心角, S为扇形的面积 .
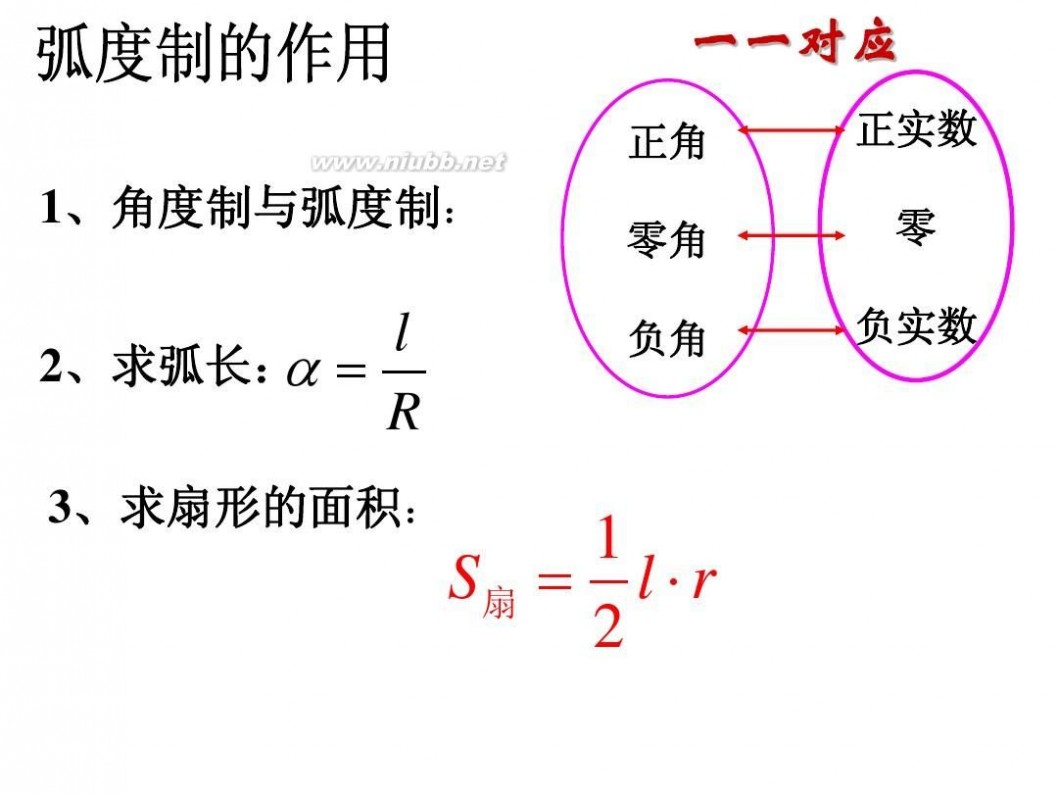
一一对应
正角 正实数 零 负实数
1、角度制与弧度制: 、
零角 负角
l 2、求弧长: = 、求弧长: α R
3、求扇形的面积: 、
1 S扇 = l ? r 2
例4,若扇形OAB的面积是1平 若扇形OAB的面积是1 OAB的面积是
方厘米,它的周长是4厘米, 方厘米,它的周长是4厘米, 求扇形的圆心角的弧度数。 求扇形的圆心角的弧度数。
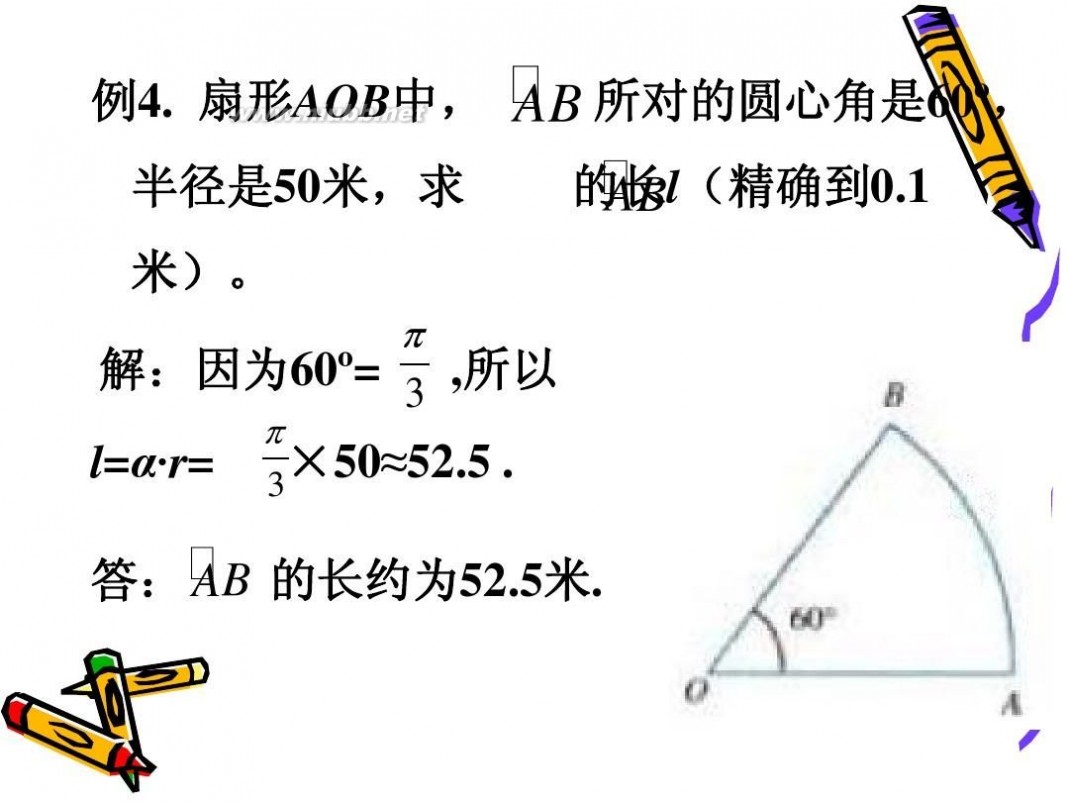
扇形AOB中, AB 所对的圆心角是 , 所对的圆心角是60o, 例4. 扇形 中 半径是50米,求 半径是 米 米)。 解:因为60o= 3 ,所以 因为 所以 π l=α·r= 3×50≈52.5 . 的长约为52.5米. 答: AB 的长约为 米
π
的长l(精确到0.1 的长 (精确到 AB
已知一半径为R的扇形 的扇形, 例5. 已知一半径为 的扇形,它的周长等于 所在圆的周长, 所在圆的周长,那么扇形的中心角是多少弧 度?合多少度?扇形的面积是多少? 合多少度?扇形的面积是多少? 解:周长=2πR=2R+l,所以l=2(π-1)R. 周长=2πR=2R+l,所以l=2(π- 所以扇形的中心角是2(π- 所以扇形的中心角是 -1) rad. 合(
360(π ? 1)
π
)o
2
扇形面积是 (π ? 1)R
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1