一 : 数据结构复习题及参考答案
网络教育课程考试复习题及参考答案
数据结构(专科)
一、判断题:
1.数组是一种复杂的数据结构,数组元素之间的关系既不是线性的也不是树形的。(www.61k.com] [ ]
2.链式存储在插人和删除时需要保持物理存储空间的顺序分配,不需要保持数据元素之间的逻辑
顺序。 [ ]
3.在只有度为0和度为k的结点的k叉树中,设度为0的结点有n0个,度为k的结点有nk个,
则有n0=nk+1。 [ ]
4.折半搜索只适用于有序表,包括有序的顺序表和有序的链表。 [ ]
5.如果两个串含有相同的字符,则这两个串相等。 [ ]
6.数组可以看成线性结构的一种推广,因此可以对它进行插入、删除等运算。 [ ]
7.在用循环单链表表示的链式队列中,可以不设队头指针,仅在链尾设置队尾指针。 [ ]
8.通常递归的算法简单、易懂、容易编写,而且执行的效率也高。 [ ]
9.一个广义表的表尾总是一个广义表。 [ ]
10.当从一个小根堆(最小堆)中删除一个元素时,需要把堆尾元素填补到堆顶位置,然后再按条
件把它逐层向下调整,直到调整到合适位置为止。 [ ]
11.对于一棵具有n 个结点,其高度为h的二叉树,进行任一种次序遍历的时间复杂度为O(h)。 [ ]
12.存储图的邻接矩阵中,邻接矩阵的大小不但与图的顶点个数有关,而且与图的边数也有关。 [ ]
13.直接选择排序是一种稳定的排序方法。 [ ]
14.闭散列法通常比开散列法时间效率更高。 [ ]
15.有n个结点的不同的二叉树有n!棵。 [ ]
16.直接选择排序是一种不稳定的排序方法 。 [ ]
17.在2048个互不相同的关键码中选择最小的5个关键码,用堆排序比用锦标赛排序更快。 [ ]
18.当3阶B_树中有255个关键码时,其最大高度(包括失败结点层)不超过8。 [ ]
19.一棵3阶B_树是平衡的3路搜索树,反之,一棵平衡的3路搜索树是3阶非B_树。 [ ]
20.在用散列表存储关键码集合时,可以用双散列法寻找下一个空桶。在设计再散列函数时,要求
计算出的值与表的大小m互质。 [ ]
21.在索引顺序表上实现分块查找,在等概率查找情况下,其平均查找长度不仅与表中元素个数有
关,而且与每一块中元素个数有关。 [ ]
22.在顺序表中取出第i个元素所花费的时间与i成正比。 [ ]
23.在栈满情况下不能作进栈运算,否则产生“上溢”。 [ ]
24.二路归并排序的核心操作是将两个有序序列归并为一个有序序列。 [ ]
25.对任意一个图,从它的某个顶点出发,进行一次深度优先或广度优先搜索,即可访问图的每个
顶点。 [ ]
26.二叉排序树或者是一棵空二叉树,或者不是具有下列性质的二叉树:若它的左子树非空,则根
结点的值大于其左孩子的值;若它的右子树非空,则根结点的值小于其右孩子的值。 [ ]
27.在执行某个排序算法过程中,出现了排序码朝着最终排序序列位置相反方向移动,则该算法是
不稳定的。 [ ]
28.一个有向图的邻接表和逆邻接表中表结点的个数一定相等。 [ ]
二、选择题:
1.在一个长度为n的顺序表的任一位置插入一个新元素的渐进时间复杂度为 [ ]
A.O(n) B.O(n/2) C.O(1) D.O(n2)
2.带头结点的单链表first为空的判定条件是 [ ]
A.first==NULL
B.first一>1ink==NULL
C.first一>link==first
第1页共7页
数据结构试题及答案 数据结构复习题及参考答案
D.first!=NUlL
3.当利用大小为n的数组顺序存储一个队列时,该队列的最大长度为 [ ]
A. n-2 B. n-l C. n D. n+1
4.在系统实现递归调用时需利用递归工作记录保存实际参数的值。[www.61k.com)在传值参数情形,需为对应 形式参数分配空间,以存放实际参数的副本;在引用参数情形,需保存实际参数的( ),在
被调用程序中可直接操纵实际参数。 [ ]
A.空间 B.副本 C.返回地址 D.地址
5.在一棵树中,( )没有前驱结点。 [ ]
A.分支结点 D.叶结点 C.树根结点 D.空结点
6.在一棵二叉树的二叉链表中,空指针域数等于非空指针域数加 [ ]
A. 2 B. 1 C. 0 D. -1
7.对于长度为9的有序顺序表,若采用折半搜索,在等概率情况下搜索成功的平均搜索长度为
( )的值除以9。 [ ]
61阅读提醒您本文地址:
A. 20 B. 18 C. 25 D. 22
8.在有向图中每个顶点的度等于该顶点的 [ ]
A.入度 B.出度
C.入度与出度之和 D.入度与出度之差
9.在基于排序码比较的排序算法中,( )算法的最坏情况下的时间复杂度不高于O(n10g2n)。 [ ]
A.起泡排序 B.希尔排序 C.归并排序 D.快速排序
10.当α的值较小时,散列存储通常比其他存储方式具有( )的查找速度。 [ ]
A.较慢 B.较快 C.相同 D.不清楚
11.设有一个含200个表项的散列表,用线性探查法解决冲突,按关键码查询时找到一个表项的
平均探查次数不超过 1.5,则散列表项应能够至少容纳( )个表项。 [ ] (设搜索成功的平均搜索长度为Snl={1+l/(1一α)}/2,其中α为装填因子)
A. 400 B. 526 C. 624 D. 676
12.堆是一个键值序列{k1,k2,?..kn},对I=1,2,?.|_n/2_|,满足 [ ]
A.ki≤k2i≤k2i+1 B.ki<k2i+1<k2i
C.ki≤k2i且ki≤k2i+1(2i+1≤n) D.ki≤k2i 或ki≤k2i+1(2i+1≤n)
13.若将数据结构形式定义为二元组(K,R),其中K是数据元素的有限集合,则R是K上 [ ]
A.操作的有限集合 B.映象的有限集合
C.类型的有限集合 D.关系的有限集合
14.在长度为n的顺序表中删除第i个元素(1≤i≤n)时,元素移动的次数为 [ ]
A. n-i+1 B. I C. i+1 D. n-i
15.若不带头结点的单链表的头指针为head,则该链表为空的判定条件是( )
A. head==NULL B. head->next==NULL
C. head!=NULL D. head->next==head
16.引起循环队列队头位置发生变化的操作是 [ ]
A.出队 B.入队 C.取队头元素 D.取队尾元素
17.若进栈序列为1,2,3,4,5,6,且进栈和出栈可以穿插进行,则不可能出现的出栈序列是 [ ]
A. 2,4,3,1,5,6 B. 3,2,4,1,6,5
C. 4,3,2,1,5,6 D. 2,3,5,1,6,4
18.字符串通常采用的两种存储方式是 [ ]
A.散列存储和索引存储 B.索引存储和链式存储
C.顺序存储和链式存储 D.散列存储和顺序存储
19.设主串长为n,模式串长为m(m≤n),则在匹配失败情况下,朴素匹配算法进行的无效位移次数为[ ]
A. m B. n-m C. n-m+1 D. n
20.二维数组A[12][18]采用列优先的存储方法,若每个元素各占3个存储单元,且第1个元素
的地址为150,则元素A[9][7]的地址为 [ ]
A.429 B.432 C.435 D.438
21.对广义表L=((a,b),(c,d),(e,f))执行操作tail(tail(L))的结果是 [ ]
第2页共7页
数据结构试题及答案 数据结构复习题及参考答案
A.(e,f) B.((e,f)) C.(f) D.( )
22.下列图示的顺序存储结构表示的二叉树是
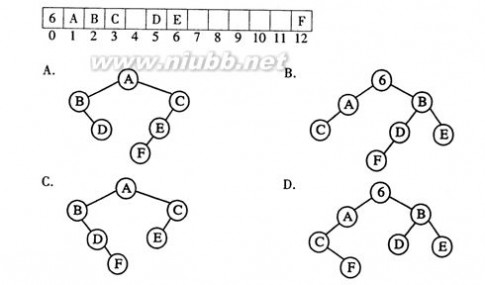
( )
23.n个顶点的强连通图中至少含有 [ ]
A.n-1条有向边 B.n条有向边
C.n(n-1)/2条有向边 D.n(n-1)条有向边
24.对关键字序列(56,23,78,92,88,67,19,34)进行增量为3的一趟希尔排序的结果为
A. (19,23,56,34,78,67,88,92)
B. (23,56,78,66,88,92,19,34)
C. (19,23,34,56,67,78,88,92)
D. (19,23,67,56,34,78,92,88)
25.若在9阶B-树中插入关键字引起结点分裂,则该结点在插入前含有的关键字个数为 [ ]
A. 4 B. 5 C. 8 D. 9
26.由同一关键字集合构造的各棵二叉排序树 [ ]
A.其形态不一定相同,但平均查找长度相同
B.其形态不一定相同,平均查找长度也不一定相同
C.其形态均相同,但平均查找长度不一定相同
D.其形态均相同,平均查找长度也都相同
27.ISAM文件和VSAM文件的区别之一是 [ ]
A.前者是索引顺序文件,后者是索引非顺序文件
B.前者只能进行顺序存取,后者只能进行随机存取
C.前者建立静态索引结构,后者建立动态索引结构
D.前者的存储介质是磁盘,后者的存储介质不是磁盘
28.下列描述中正确的是 [ ]
A.线性表的逻辑顺序与存储顺序总是一致的
B.每种数据结构都具备三个基本运算:插入、删除和查找
C.数据结构实质上包括逻辑结构和存储结构两方面的内容
D.选择合适的数据结构是解决应用问题的关键步骤
29.下面程序段的时间复杂度是 [ ] i=s=0
while(s<n)
{i++;
s+=i;
}
A.O(1) B.O(n) C.O(log2
2n) D.O(n)
第3页共7页 [ ]
数据结构试题及答案 数据结构复习题及参考答案
30.对于顺序表来说,访问任一节点的时间复杂度是 [ ]
61阅读提醒您本文地址:
2A.O(1) B.O(n) C.O(log2n) D.O(n)
31.在具有n个节点的双链表中做插入、删除运算,平均时间复杂度为 [ ]
2A.O(1) B.O(n) C.O(log2n) D.O(n)
32.经过下列运算后,QueueFront(Q)的值是 [ ] InitQueue(Q);EnQueue(Q,a);EnQueue(Q,a);DeQueue(Q,x);
A.a B.b C.1 D.2
33.一个栈的入栈序列是a,b,c,则栈的不可能输出序列是 [ ]
A. acb B.abc C.bca D.cab
34.循环队列是空队列的条件是 [ ]
A.Q->rear==Q->front B.(Q->rear+1)%maxsize==Q->front
C.Q->rear==0 D.Q->front==0
35.设s3="I AM",s4="A TERCHER".则strcmp(s3,s4)= [ ]
A.0 B.小于0 C.大于0 D.不确定
36.一维数组的元素起始地址loc[6]=1000,元素长度为4,则loc[8]为 [ ]
A.1000 B.1004 C.1008 D.8
37.广义表((a,b),c,d)的表尾是 [ ]
A.a B.b C.(a,b) D.(c,d)
38.对于二叉树来说,第I层上至多有____个节点 [ ]
A.2i B.2i -1 C.2i-1 D.2i-1-1
39.某二叉树的前序遍历序列为ABDGCEFH,中序遍历序列为DGBAECHF,则后序遍历序列为 [ ]
A.BDGCEFHA B.GDBECFHA C.BDGAECHF D.GDBEHFCA
40.M叉树中,度为0的节点数称为 [ ]
A.根 B.叶 C.祖先 D.子孙
41.已知一个图如下所示,若从顶点a出发按宽度搜索法进行遍历,则可能得到的一种顶 点序列为

[ ]
42.堆的形状是一棵 [ ]
A.二叉排序树 B.满二叉树 C.完全二义树 D.平衡二叉树
43.排序方法中,从未排序序列中挑选元素,并将其依次放入已排序序列(初始时为空)的一端的
方法,称为 [ ]
A.希尔排序 B.归并排序 C.插入排序 D.选择排序
44.采用顺序查找方法查找长度为n的线性表时,每个元素的平均查找长度为 [ ]
A.n B.n/2 C.(n+1)/2 D.(n-1)/2
45.散列查找是由键值( )确定散列表中的位置,进行存储或查找 [ ]
A.散列函数值 B.本身 C.平方 D.相反数
46.顺序文件的缺点是 [ ]
A.不利于修改 B.读取速度慢 C.只能写不能读 D.写文件慢
47.索引文件的检索方式是直接存取或按_____存取 [ ]
A.随机存取 B.关键字 C.间接 D.散列
48.堆是一个键值序列{k1,k2,?..kn},对i=1,2,?.|_n/2_|,满足 [ ]
A. ki≤k2i≤k2i+1 B. ki<k2i+1<k2i
第4页共7页
数据结构试题及答案 数据结构复习题及参考答案
C. ki≤k2i且ki≤k2i+1(2i+1≤n) D. ki≤k2i 或ki≤k2i+1(2i+1≤n)
三、 计算与算法应用题:
1.给定表(119,14,22,1,66,21,83,27,56,13,10)
请按表中元素的顺序构造一棵平衡二叉树,并求其在等概率情况下查找成功的平均长度。(www.61k.com](9分)
2.已知一个有向图的顶点集V和边集G分别为:
V={a,b,c,d,e,f,g,h}
E={<a,b>,<a,c>,<b,f>,<c,d>,<c,e>,<d,a>,<d,f>,<d,g>,<e,g>,<f,h>};
假定该图采用邻接矩阵表示,则分别写出从顶点a出发进行深度优先搜索遍历和广度优先搜索遍历得到
的顶点序列。(9分)
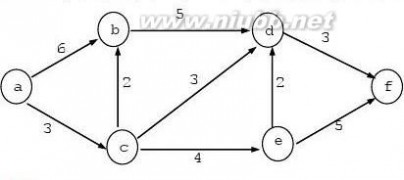
3.设散列表的长度为13,散列函数为H(h)= k%13,给定的关键码序列为19,14,23,01,68,20,84,
27。试画出用线性探查法解决冲突时所构成的散列表。(8分)


4.对(1)假设关键字集合为{1,2,3,4,5,6,7},试举出能达到上述结果的初始关键字序列;
(2)对所举序列进行快速排序,写出排序过程。(9分)
5.如图所示二叉树,回答下列问题。(9分)
6.画出在一个初始为空的AVL树中依次插入3,1,4,6,9,8,5,7时每一插入后AVL树的形态。若做了某种旋转,说明旋转的类型。然后,给出在这棵插入后得到的AVL树中删去根结点后的结果。 7.已知一组记录的排序码为( 46 , 79 , 56 , 38 , 40 , 80 , 95 , 24 ),写出对其进行快速排序的每一次划分结果。
8.一个线性表为 B= ( 12 , 23 , 45 , 57 , 20 , 03 , 78 , 31 , 15 , 36 ),设散列表为 HT[0..12] ,散列函数为 H ( key ) = key % 13 并用线性探查法解决冲突,请画出散列表,并计算等概率情况下查找成功的平均查找长度。
61阅读提醒您本文地址:
9.已知一棵二叉树的前序遍历的结果序列是 ABECKFGHIJ ,中序遍历的结果是 EBCDAFHIGJ ,试写出这棵二叉树的后序遍历结果。
10.假定对线性表(38,25,74,52,48,65,36)进行散列存储,采用H(K)=K%9作为散列函数,若分别采用线性探查法和链接法处理冲突,则对应的平均查找长度分别为 和 。
11.假定一组记录的排序码为(46,79,56,38,40,80,25,34,57,21),则对其进行快速排序的第一次划分后又对左、右两个子区间分别进行一次划分,得到的结果为: 。
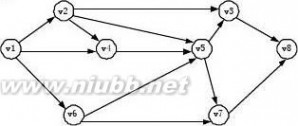
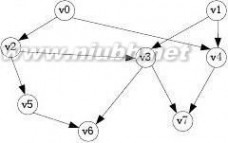
12.下图是带权的有向图G的邻接表表示法。从结点V1出发,深度遍历图G所得结点序列为( A ),广度
遍历图G所得结点序列为( B );G的一个拓扑序列是( C );从结点V1到结点V8的最短路径为( D );从结点V1到结点V8的关键路径为( E )。
其中A、B、C的选择有:
V1,V2,V3,V4,V5,V6,V7,V8
V1,V2,V4,V6,V5,V3,V7,V8
V1,V2,V4,V6,V3,V5,V7,V8
V1,V2,V4,V6,V7,V3,V5,V8
V1,V2,V3,V8,V4,V5,V6,V7
V1,V2,V3,V8,V4,V5,V7,V6
第5页共7页
数据结构试题及答案 数据结构复习题及参考答案
V1,V2,V3,V8,V5,V7,V4,V6
D、E的选择有:
① V1,V2,V4,V5,V3,V8
② V1,V6,V5,V3,V8
③ V1,V6,V7,V8
④ V1,V2,V5,V7,V8

13.画出对长度为10的有序表进行折半查找的判定树,并求其等概率时查找成功的平均查找长度。(www.61k.com]
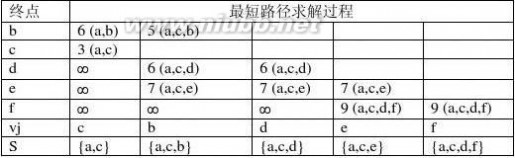
14.已知如图所示的有向网,试利用Dijkstra算法求顶点1到其余顶点的最短路径,并给出算法执行过程
中各步的状态。

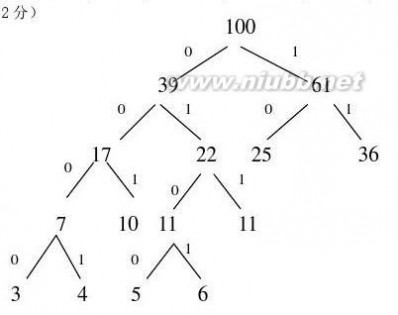
15.假定用于通信的电文由8个字母a,b,c,d,e,f,g,h组成,各字母在电文中出现的频率分别为5,25,3,6,10,11,36,4。试为这8个字母设计不等长Huffman编码,并给出该电文的总码数。
16.已知一棵二叉树的中序和前序序列如下,试画出该二叉树并求该二叉树的后序序列。(9分) 中序序列:c,b,d,e,a,g,i,h,j,f
前序序列:a,b,c,d,e,f,g,h,i,j
17.假设用于通信的电文仅由8个字母组成,字母在电文中出现的频率分别为0.07,0.19,0.02,0.06,
第6页共7页
数据结构试题及答案 数据结构复习题及参考答案
0.32,0.03,0.21,0.10。(www.61k.com)试为这8个字母设计哈夫曼编码。使用0~7的二进制表示形式是另一种编码方案。对于上述实例,比较两种方案的优缺点。
四、算法设计题:
h1.已知深度为h的二叉树以一维数组BT(1:2-1)作为其存储结构。请写一算法,求该二叉树中叶结点的个
数。
2.编写在以BST为树根指针的二叉搜索树上进行查找值为item的结点的非递归算法,若查找item带回整个结点的值并返回ture,否则返回false。
bool Find(BtreeNode*BST,ElemType&item)
3.编写算法,将一个结点类型为 Lnode 的单链表按逆序链接,即若原单链表中存储元素的次序为 a 1 ,?? a n-1 , a n ,则逆序链接后变为 , a n , a n-1 ,?? a 1 。
4.根据下面函数原型,编写一个递归算法,统计并返回以BT为树根指针的二叉树中所有
叶子结点的个数。
int Count(BTreeNode * BT);
5.设A=(a1,...,am)和B=(b1,...,bn)均为顺序表,A'和B'分别为A和B中除去最大共同前缀后的子表。若A'=B'=空表,则A=B;若A'=空表,而B'≠空表,或者两者均不为空表,且A'的首元小于B'的首元,则A<B;否则A>B。试写一个比较A,B大小的算法。
6.已知单链表a和b的元素按值递增有序排列, 编写算法归并a和b得到新的单链表c,c的元素按值递减有序。
7.编写递归算法,对于二叉树中每一个元素值为x的结点,删去以它为根的子树,并释放相应的空间。
8.编写算法判别T是否为二叉排序树.
9.试写一算法,判断以邻接表方式存储的有向图中是否存在由顶点Vi到顶点Vj的路径(i<>j)。注意:算法中涉及的图的基本操作必须在存储结构上实现。
第7页共7页
数据结构试题及答案 数据结构复习题及参考答案
参考答案
一、判断题:
1.√ 2.× 3.√ 4.× 5.√ 6.√ 7.× 8.× 9.× 10.×
11.× 12.√ 13.× 14.√ 15.× 16.√ 17.× 18.× 19.× 20.×
21.√ 22.× 23.√ 24.√ 25.× 26.× 27.× 28.√
二、单项选择题:
1.A 2.B 3.B 4.D 5.C 6.A 7.C 8.C 9.C 10.B
11.A 12 C 13.B 14.D 15.A 16.A 17.D 18.C 19.C 20.A
21.B 22.A 23.B 24.D 25.C 26.B 27.C 28.D 29.B 30.A
31.A 32.B 33.D 34.A 35.C 36.C 37.D 38.C 39.D 40.A
41.B 42.C 43.D 44.C 45.A 46.A 47.B 48.C
三、计算与算法应用题:
1.解答:

平均长度为4.
2.解:画图(略)
深度优先搜索序列:a,b,f,h,c,d,g,e
广度优先搜索序列:a,b,c,f,d,e,h,g
3.


4.对也就是基准和其他n-1个关键字比较。(www.61k.com]
这里要求10次,而7 - 1 + 2 * ( 3 - 1 ) = 10,这就要求2趟快速排序后,算法结束。 所以,列举出来的序列,要求在做partition的时候,正好将序列平分
61阅读提醒您本文地址:
(1)4 1 3 2 6 5 7
或 4 1 3 7 6 5 2
或 4 5 3 7 6 1 2
或 4 1 3 5 6 2 7 .......
(2)按自己序列完成
第1页共6页
数据结构试题及答案 数据结构复习题及参考答案
5.答案:(1)djbaechif (2)abdjcefhi (3)jdbeihfca
6.在这个AVL树中删除根结点时有两种方案:
【方案1】在根的左子树中沿右链走到底,用5递补根结点中原来的6,再删除5所在的结点.
【方案2】在根的右子树中沿左链走到底,用7递补根结点中原来的6,再删除7所在的结点. 7.
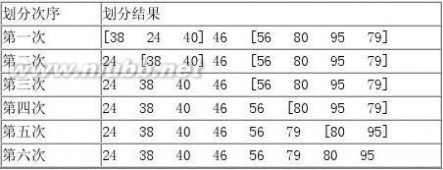

9.此二叉树的后序遍历结果是: EDCBIHJGFA
10.13/7 1l/7
11.2l 25 [34 38 40]46[79 56 57]80 12.
12.(A)深度遍历:1,2,3,8,4,5,7,6或1,2,3,8,5,7,4,
(B) 广度遍历:1,2,4,6,3,5,7,8
(C) 拓扑序列:1,2,4,6,5,3,7,8
(D) 最短路径:1,2,5,7,8
(E) 关键路径:1,6,5,3,8
13.
ASLsucc=(1+2X2+3X4+4X3)/10=2.9
14.源点 终点 最短路径 路径长度
1 2 1,3,2 19
3 1,3 15
4 1,3,2,4 29
5 1,3,5 29
6 1,3,2,4,6 44
15.已知字母集{a, b, c, d, e, f, g, h}
次数{5,25,3,6,10,11,36,4}
第2页共6页

数据结构试题及答案 数据结构复习题及参考答案
则Huffman 编码为(5分)
a b c d e f g h
16.树(略)后序序列:c,e,d,b,i,j,h,g,f,a (5+4分)
17.方案1;哈夫曼编码 先将概率放大100倍,以方便构造哈夫曼树。[www.61k.com] w={7,19,2,6,32,3,21,10},按哈夫曼规则:【[(2,3),6], (7,10)】, ??
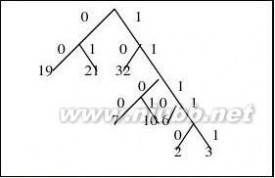
19, 21, 32
(100 (40 60)
19 21 32 17 7 10 6 2 3
方案比较:


第3页共6页 电文总码数为(2分)

数据结构试题及答案 数据结构复习题及参考答案
四、算法设计题:
1.二叉树采取顺序结构存储,是按完全二叉树格式存储的。[www.61k.com)对非完全二叉树要补上“虚结点”。由于不是完全二叉树,在顺序结构存储中对叶子结点的判定是根据其左右子女为0。叶子和双亲结点下标间的关系满足完全二叉树的性质。
int Leaves(int h) //求深度为h以顺序结构存储的二叉树的叶子结点数
hh{int BT[]; int len=2-1, count=0; //BT是二叉树结点值一维数组,容量为2
for (i=1;i<=len;i++) //数组元素从下标1开始存放
if (BT[i]!=0) //假定二叉树结点值是整数,“虚结点”用0填充
if(i*2)>len) count++; //第i个结点没子女,肯定是叶子
else if(BT[2*i]==0 && 2*i+1<=len && BT[2*i+1]==0)
count++; //无左右子女的结点是叶子
return (count)
} //结束Leaves
2.
bool Find(BtreeNode*BST,ElernType&item)
{
while(BST!=NULL)
{
if(item= =BST一>data){item=BST一>data; return true;}
else if(item<BST一>data=BST=BST一>left;
else BST=BST一>right;
}
return false;
}
3.Lnode *P=HL;
HL=NULL;
While (p!=null)
{
Lnode*q=p;
P=p → next;
q → next=HL;
HL=q;
}
}
4.int Count(BTreeNode* BT) //统计出二叉树中所有叶子结点数 { if(BT==NULL)return O; else if(BT->left==NULL&&BT->right==NULL)return 1;
else return Count(BT->left)+Count(BT->right); }
5.int Compare-List(SqList a, SqList b){
//a,b为顺序表,若a<b时,返回-1;a=b时,返回0;a>b时,返回1
i=0;
while (i<=a.length-1) && (i<=b.length-1) && (a.elem[i]=b.elem[i]) ++i;
switch {
case i=a.length && i=b.length : return 0; break;
case (i=a.length && i<=b.length-1)
||(i<=a.length-1 && i<=b.length-1 && a.elem[i]<b.elem[i]) : return -1;break;
default : return 1;
}
}//Compare-List
第4页共6页
数据结构试题及答案 数据结构复习题及参考答案 61阅读提醒您本文地址:
6.void MergeList(LinkList &a, LinkList &b, LinkList &c) {
//已知单链表a和b的元素按值递增有序排列
//归并a和b得到新的单链表c,c的元素按值递减有序
c=a; p=a->next; q=b->next; c->next=NULL;
while (p && q)
if (p->data<q->data) {
pn=p->next; p->next=c->next;
c->next=p; p=pn;
}
else {
qn=q->next; q->next=c->next;
c->next=q; q=qn;
}
while (p) {pn=p->next; p->next=c->next; c->next=p; p=pn;}
while (q) {qn=q->next; q->next=c->next; c->next=q; q=qn;}
free(b);
}//MergeList
7.Status Del-subtree(Bitree bt){
//删除bt所指二叉树,并释放相应的空间
if (bt) {
Del-subtree(bt->lchild);
Del-subtree(bt->rchild);
free(bt);
}
return OK;
}//Del-subtree
Status Search-del(Bitree bt, TelemType x){
//在bt所指的二叉树中,查找所有元素值为x的结点,并删除以它为根的子树 if (bt){
if (bt->data=x) Del-subtree(bt);
else {
Search-Del(bt->lchild, x);
Search-Del(bt->rchild, x);
}
}
return OK;
}//Search-Del
8.TelemType Maxv(Bitree T){
//返回二叉排序树T中所有结点的最大值
for (p=T; p->rchild; p=p->rchild);
return p->data;
}//Maxv
TelemType Minv(Bitree T){
//返回二叉排序树T中所有结点的最小值
for (p=T; p->lchild; p=p->lchild);
return p->data;
}//Minv
Status IsBST(Bitree T){
第5页共6页
数据结构试题及答案 数据结构复习题及参考答案
//判别T是否为二叉排序树
if (!T) return OK;
else if ((!T->lchild)||((T->lchild)&&(IsBST(T->lchild)&&(Maxv(T->lchild)<T->data)))
&&((!T->rchild)||((T->rchild)&&(IsBST(T->rchild)&&(Minv(T->rchild)>T->data)))
return OK
else return ERROR;
}//IsBST
9.评分标准:请根据编程情况酌情给分。[www.61k.com]
解答:
在有向图中,判断顶点Vi和顶点Vj间是否有路径,可采用遍历的方法,从顶点Vi出发,不论是深度优先遍历(dfs)还是宽度优先遍历(bfs),在未退出dfs或bfs前,若访问到Vj,则说明有通路,否则无通路。设一全程变量flag。初始化为0,若有通路,则flag=1。
算法 int visited[]=0; //全局变量,访问数组初始化
int dfs(AdjList g , vi)
//以邻接表为存储结构的有向图g,判断顶点Vi到Vj是否有通路,返回1或0表示有或无 { visited[vi]=1; //visited是访问数组,设顶点的信息就是顶点编号。
p=g[vi].firstarc; //第一个邻接点。
while ( p!=null)
{ j=p->adjvex;
if (vj==j) { flag=1; return(1);} //vi 和 vj 有通路。
if (visited[j]==0) dfs(g,j);
p=p->next; }//while
if (!flag) return(0);
}//结束
第6页共6页
61阅读提醒您本文地址:
二 : 数据结构试题库集及答案
数据结构试题库及答案
第一章 概论
一、选择题
1、研究数据结构就是研究( D)。[www.61k.com]
A.数据的逻辑结构 B.数据的存储结构
C.数据的逻辑结构和存储结构 D.数据的逻辑结构、存储结构及其基本操作
2、算法分析的两个主要方面是(A)。
A. 空间复杂度和时间复杂度 B. 正确性和简单性 C. 可读性和文档性 D. 数据复杂性和程序复杂性
3、具有线性结构的数据结构是(D)。
A.图 B.树 C.广义表 D.栈
4、计算机中的算法指的是解决某一个问题的有限运算序列,它必须具备输入、输出、(B)等5个特性。
A. 可执行性、可移植性和可扩充性 B. 可执行性、有穷性和确定性
C. 确定性、有穷性和稳定性 D. 易读性、稳定性和确定性
5、下面程序段的时间复杂度是( C)。
for(i=0;i<m;i++)
for(j=0;j<n;j++)
a[i][j]=i*j; 2 A. O(m) B. O(n2) C. O(m*n) D. O(m+n)
6、算法是( D)。
A.计算机程序 B.解决问题的计算方法 C.排序算法 D.解决问题的有限运算序列
7、某算法的语句执行频度为(3n+nlog2n+n2+8),其时间复杂度表示(C)。 2A. O(n) B. O(nlog2n) C. O(n) D. O(log2n)
8、下面程序段的时间复杂度为(C)。
i=1;
while(i<=n)
i=i*3;
A. O(n) B. O(3n) C. O(log3n) D. O(n3)
9、数据结构是一门研究非数值计算的程序设计问题中计算机的数据元素以及它们之间的()和运算等的学科。
A. 结构 B. 关系 C.运算 D. 算法
10、下面程序段的时间复杂度是()。
i=s=0;
while(s<n){
i++;s+=i;
}
A. O(n) B. O(n2) C. O(log2n) D. O(n3)
11、抽象数据类型的三个组成部分分别为()。
A. 数据对象、数据关系和基本操作 B.数据元素、逻辑结构和存储结构
C. 数据项、数据元素和数据类型 D. 数据元素、数据结构和数据类型
12、通常从正确性、易读性、健壮性、高效性等4个方面评价算法的质量,以下解释错误的是()。
A. 正确性算法应能正确地实现预定的功能
B.易读性算法应易于阅读和理解,以便调试、修改和扩充
C.健壮性当环境发生变化时,算法能适当地做出反应或进行处理,不会产生不需要的运行结果
D. 高效性即达到所需要的时间性能
13、下列程序段的时间复杂度为()。
x=n;y=0;
while(x>=(y+1)*(y+1))
y=y+1;
A.O(n) B.O(n) C. O(1) D.O(n2)
二、填空题
1、程序段“i=1;while(i<=n) i=i*2;”的时间复杂度为。
2、数据结构的四种基本类型中,树形结构的元素是一对多关系。
三、综合题
1、将数量级O(1),O(N),O(N2),O(N3),O(NLOG2N),O(LOG2N),O(2N)按增长率由小到大排序。
数据结构试卷 数据结构试题库集及答案
答案: O(1) O(log2N) O(N) O(Nlog2N) O(N) O(N) O(2N) 23
一、填空题
1. 数据结构被形式地定义为(D, R),其中D是的有限集合,R是D上的有限集合。[www.61k.com]
2. 数据结构包括数据的、数据的和数据的这三个方面的内容。
3. 数据结构按逻辑结构可分为两大类,它们分别是和。
4. 线性结构中元素之间存在关系,树形结构中元素之间存在关系,图形结构中元素之间存在多对多关系。
5.在线性结构中,第一个结点前驱结点,其余每个结点有且只有个前驱结点;最后一个结
点没有后续结点,其余每个结点有且只有1个后续结点。
6. 个前驱结点;叶子结点没有结点,其余每个结点的后续结点数可以任意多个。
7. 在图形结构中,每个结点的前驱结点数和后续结点数可以。
8.数据的存储结构可用四种基本的存储方法表示,它们分别是。
9. 数据的运算最常用的有5种,它们分别是。
10. 一个算法的效率可分为效率和效率。
11.任何一个C程序都由和若干个被调用的其它函数组成。
二、单项选择题
(B)1. 非线性结构是数据元素之间存在一种:
A)一对多关系 B)多对多关系 C)多对一关系 D)一对一关系
(C)2. 数据结构中,与所使用的计算机无关的是数据的结构;
A)存储 B)物理 C)逻辑 D)物理和存储
(C)3. 算法分析的目的是:
A)找出数据结构的合理性 B)研究算法中的输入和输出的关系
C) 分析算法的效率以求改进 D)分析算法的易懂性和文档性
(A)4. 算法分析的两个主要方面是:
A)空间复杂性和时间复杂性 B)正确性和简明性
C)可读性和文档性 D)数据复杂性和程序复杂性
(C)5. 计算机算法指的是:
A)计算方法 B) 排序方法 C)解决问题的有限运算序列 D)调度方法
(B)6. 计算机算法必须具备输入、输出和等5个特性。
A)可行性、可移植性和可扩充性 B)可行性、确定性和有穷性
C)确定性、有穷性和稳定性 D)易读性、稳定性和安全性
数据结构试卷 数据结构试题库集及答案
三、简答题
1.数据结构和数据类型两个概念之间有区别吗?
答:简单地说,数据结构定义了一组按某些关系结合在一起的数组元素。(www.61k.com)数据类型不仅定义了一组带结构的数据元素,而且还在其上定义了一组操作。
2. 简述线性结构与非线性结构的不同点。
答:线性结构反映结点间的逻辑关系是一对一的,非线性结构反映结点间的逻辑关系是多对多的。
四、分析下面各程序段的时间复杂度
1. for (i=0; i<n; i++) for (j=0; j<m; j++) A[i][j]=0;
3. x=0;
for(i=1; i<n; i++)
for (j=1; j<=n-i; j++)
x++;
2. s=0;
for (i=0; i<n; i++)
for(j=0; j<n; j++) s+=B[i][j]; sum=s;
4. i=1;
while(i<=n) i=i*3;
五、设有数据逻辑结构S=(D,R),试按各小题所给条件画出这些逻辑结构的图示,并确定其是哪种逻辑结构。
1. D={d1,d2,d3,d4} R={(d1,d2),(d2,d3),(d3,d4) }
2. D={d1,d2,?,d9}
R={(d1,d2),(d1,d3),(d3,d4),(d3,d6),(d6,d8),(d4,d5), (d6,d7),(d8,d9) }
3.D={d1,d2,?,d9}
R={(d1,d3),(d1,d8),(d2,d3),(d2,d4),(d2,d5),(d3,d9), (d5,d6),(d8,d9),(d9,d7), (d4,d7),(d4,d6)}
第二章 线性表
一、选择题
1、若长度为n的线性表采用顺序存储结构,在其第i个位置插入一个新元素算法的时间复杂度()。
A. O(log2n) B.O(1) C. O(n) D.O(n2)
2、若一个线性表中最常用的操作是取第i个元素和找第i个元素的前趋元素,则采用()存储方式最节省时间。 A. 顺序表 B. 单链表 C. 双链表 D. 单循环链表 3、具有线性结构的数据结构是()。
A.图 B.树 C.广义表 D.栈
4、在一个长度为n的顺序表中,在第i个元素之前插入一个新元素时,需向后移动()个元素。
A. n-i B. n-i+1 C. n-i-1 D. i 5、非空的循环单链表head的尾结点p满足()。
A. p->next==head B. p->next==NULL C. p==NULL D. p==head 6、链表不具有的特点是()。
A. 可随机访问任一元素 B. 插入删除不需要移动元素 C. 不必事先估计存储空间 D. 所需空间与线性表长度成正比
7、在双向循环链表中,在p指针所指的结点后插入一个指针q所指向的新结点,修改指针的操作是()。 A. p->next=q;q->prior=p;p->next->prior=q;q->next=q;
数据结构试卷 数据结构试题库集及答案
B. p->next=q;p->next->prior=q;q->prior=p;q->next=p->next;
C. q->prior=p;q->next=p->next;p->next->prior=q;p->next=q;
D. q->next=p->next;q->prior=p;p->next=q;p->next=q;
8、线性表采用链式存储时,结点的存储地址()。[www.61k.com]
A. 必须是连续的 B. 必须是不连续的
C. 连续与否均可 D. 和头结点的存储地址相连续
9、在一个长度为n的顺序表中删除第i个元素,需要向前移动()个元素。
A. n-i B. n-i+1 C. n-i-1 D. i+1
10、线性表是n个()的有限序列。
A. 表元素 B. 字符 C. 数据元素 D. 数据项
11、从表中任一结点出发,都能扫描整个表的是()。
A. 单链表 B.顺序表 C. 循环链表 D.静态链表
12、在具有n个结点的单链表上查找值为x的元素时,其时间复杂度为()。 2A. O(n) B. O(1) C. O(n) D. O(n-1)
13、线性表L=(a1,a2,……,an),下列说法正确的是()。
A. 每个元素都有一个直接前驱和一个直接后继
B.线性表中至少要有一个元素
C.表中诸元素的排列顺序必须是由小到大或由大到小
D.除第一个和最后一个元素外,其余每个元素都由一个且仅有一个直接前驱和直接后继
14、一个顺序表的第一个元素的存储地址是90,每个元素的长度为2,则第6个元素的存储地址是()。
A. 98 B.100 C. 102 D.106
15、在线性表的下列存储结构中,读取元素花费的时间最少的是()。
A. 单链表 B. 双链表 C. 循环链表 D. 顺序表
16、在一个单链表中,若删除p所指向结点的后续结点,则执行()。
A. p->next=p->next->next;
B. p=p->next;p->next=p->next->next;
C. p =p->next;
D. p=p->next->next;
17、将长度为n的单链表连接在长度为m的单链表之后的算法的时间复杂度为()。
A. O(1) B. O(n) C. O(m) D. O(m+n)
18、线性表的顺序存储结构是一种()存储结构。
A. 随机存取 B. 顺序存取 C. 索引存取 D. 散列存取
19、顺序表中,插入一个元素所需移动的元素平均数是()。
A. (n-1)/2 B. n C. n+1 D. (n+1)/2
10、循环链表的主要优点是()。
A. 不再需要头指针 B. 已知某结点位置后能容易找到其直接前驱
C. 在进行插入、删除运算时能保证链表不断开
D. 在表中任一结点出发都能扫描整个链表
11、不带头结点的单链表head为空的判定条件是()。
A. head==NULL B. head->next==NULL
C. head->next==head D. head!=NULL
12、在下列对顺序表进行的操作中,算法时间复杂度为O(1)的是()。
A. 访问第i个元素的前驱(1<i?n) B. 在第i个元素之后插入一个新元素(1?i?n)
C.删除第i个元素(1?i?n) D. 对顺序表中元素进行排序
13、已知指针p和q分别指向某单链表中第一个结点和最后一个结点。假设指针s指向另一个单链表中某个结点,则在s所指结点之后插入上述链表应执行的语句为()。
A. q->next=s->next;s->next=p;
B. s->next=p;q->next=s->next;
C. p->next=s->next;s->next=q;
D. s->next=q;p->next=s->next;
14、在以下的叙述中,正确的是()。
A.线性表的顺序存储结构优于链表存储结构
B. 线性表的顺序存储结构适用于频繁插入/删除数据元素的情况
C.线性表的链表存储结构适用于频繁插入/删除数据元素的情况
D.线性表的链表存储结构优于顺序存储结构
15、在表长为n的顺序表中,当在任何位置删除一个元素的概率相同时,删除一个元素所需移动的平均个数为()。
A. (n-1)/2 B. n/2 C. (n+1)/2 D. n
数据结构试卷 数据结构试题库集及答案
16、在一个单链表中,已知q所指结点是p所指结点的前驱结点,若在q和p之间插入一个结点s,则执行()。(www.61k.com]
A. s->next=p->next; p->next=s;
B. p->next=s->next;s->next=p;
C. q->next=s;s->next=p;
D. p->next=s;s->next=q;
17、在单链表中,指针p指向元素为x的结点,实现删除x的后继的语句是()。
A. p=p->next; B. p->next=p->next->next;
C. p->next=p; D.p=p->next->next;
18、在头指针为head且表长大于1的单循环链表中,指针p指向表中某个结点,若p->next->next==head,则()。
A. p指向头结点 B. p指向尾结点 C.p的直接后继是头结点
D.p的直接后继是尾结点
二、填空题
1、设单链表的结点结构为(data,next)。已知指针p指向单链表中的结点,q指向新结点,欲将q插入到p结点之后,则需要执行的语句:;。
答案:q->next=p->next p->next=q
2、线性表的逻辑结构是,其所含元素的个数称为线性表的。
答案:线性结构 长度
3、写出带头结点的双向循环链表L为空表的条件。
答案:L->prior==L->next==L
4、带头结点的单链表head为空的条件是。
答案:head->next==NULL
5、在一个单链表中删除p所指结点的后继结点时,应执行以下操作:
q= p->next; p->next= _ ___;
三、判断题
1、单链表不是一种随机存储结构。?
2、在具有头结点的单链表中,头指针指向链表的第一个数据结点。?
3、用循环单链表表示的链队列中,可以不设队头指针,仅在队尾设置队尾指针。?
4、顺序存储方式只能用于存储线性结构。?
5、在线性表的顺序存储结构中,逻辑上相邻的两个元素但是在物理位置上不一定是相邻的。?
6、链式存储的线性表可以随机存取。
四、程序分析填空题
1、函数GetElem实现返回单链表的第i个元素,请在空格处将算法补充完整。
int GetElem(LinkList L,int i,Elemtype *e){
LinkList p;int j;
p=L->next;j=1;
while(p&&j<i){
(1) ;++j;
}
if(!p||j>i) return ERROR; *e= (2) ;
}
答案:(1)p=p->next (2)p->data
2、函数实现单链表的插入算法,请在空格处将算法补充完整。
int ListInsert(LinkList L,int i,ElemType e){
LNode *p,*s;int j;
p=L;j=0;
while((p!=NULL)&&(j<i-1)){ p=p->next;j++;
}
if(p==NULL||j>i-1) return ERROR;
s=(LNode *)malloc(sizeof(LNode));
s->data=e;
数据结构试卷 数据结构试题库集及答案
(1) ;
return OK;
}/*ListInsert*/
答案:(1)s->next=p->next (2)p->next=s
3、函数ListDelete_sq实现顺序表删除算法,请在空格处将算法补充完整。[www.61k.com]
int ListDelete_sq(Sqlist *L,int i){
int k;
if(i<1||i>L->length) return ERROR;
for(k=i-1;k<L->length-1;k++)
L->slist[k]=(1);
(2);
return OK;
}
答案:(1)L->slist[k+1] (2) --L->Length
4、函数实现单链表的删除算法,请在空格处将算法补充完整。
int ListDelete(LinkList L,int i,ElemType *s){
LNode *p,*q;
int j;
p=L;j=0;
while(((1))&&(j<i-1)){
p=p->next;j++;
}
if(p->next==NULL||j>i-1) return ERROR;
q=p->next;
(2);
*s=q->data;
free(q);
return OK;
}/*listDelete*/
答案:(1)p->next!=NULL (2)p->next=q->next
5、写出算法的功能。
int L(head){
node * head;
int n=0;
node *p;
p=head;
while(p!=NULL)
{ p=p->next;
n++;
}
return(n);
}
答案:求单链表head的长度
五、综合题
1、编写算法,实现带头结点单链表的逆置算法。
答案:void invent(Lnode *head)
{Lnode *p,*q;
if(!head->next) return ERROR;
p=head->next; q=p->next; p->next =NULL;
while(q)
{p=q; q=q->next; p->next=head->next; head->next=p;}
}
2、有两个循环链表,链头指针分别为L1和L2,要求写出算法将L2链表链到L1链表之后,且连接后仍保持循环链表形式。
答案:void merge(Lnode *L1, Lnode *L2)
{Lnode *p,*q ;
while(p->next!=L1)
数据结构试卷 数据结构试题库集及答案
p=p->next;
while(q->next!=L2)
q=q->next;
q->next=L1; p->next =L2;
}
3、设一个带头结点的单向链表的头指针为head,设计算法,将链表的记录,按照data域的值递增排序。(www.61k.com)
答案:void assending(Lnode *head)
{Lnode *p,*q , *r, *s;
p=head->next; q=p->next; p->next=NULL;
while(q)
{r=q; q=q->next;
if(r->data<=p->data)
{r->next=p; head->next=r; p=r; }
else
{while(!p && r->data>p->data)
{s=p; p=p->next; }
r->next=p; s->next=r;}
p=head->next; }
}
4、编写算法,将一个头指针为head不带头结点的单链表改造为一个单向循环链表,并分析算法的时间复杂度。 答案:
void linklist_c(Lnode *head)
{Lnode *p; p=head;
if(!p) return ERROR;
while(p->next!=NULL)
p=p->next;
p->next=head;
}
设单链表的长度(数据结点数)为N,则该算法的时间主要花费在查找链表最后一个结点上(算法中的while循环),所以该算法的时间复杂度为O(N)。
5、已知head为带头结点的单循环链表的头指针,链表中的数据元素依次为(a1,a2,a3,a4,?,an),A为指向空的顺序表的指针。阅读以下程序段,并回答问题:
(1)写出执行下列程序段后的顺序表A中的数据元素;
(2)简要叙述该程序段的功能。
if(head->next!=head)
{
p=head->next;
A->length=0;
while(p->next!=head)
{
p=p->next;
A->data[A->length ++]=p->data;
if(p->next!=head)p=p->next;
}
}
答案:
(1) (a2, a4, ?, ) (2)将循环单链表中偶数结点位置的元素值写入顺序表A
6、设顺序表va中的数据元数递增有序。试写一算法,将x插入到顺序表的适当位置上,以保持该表的有序性。 答案:
void Insert_sq(Sqlist va[], ElemType x)
{int i, j, n;
n=length(va[]);
if(x>=va[i])
va[n]=x;
else
{i=0;
while(x>va[i]) i++;
for(j=n-1;j>=I;j--)
va[j+1]=va[j];
va[i]=x; }
n++;
数据结构试卷 数据结构试题库集及答案
}
7、假设线性表采用顺序存储结构,表中元素值为整型。[www.61k.com)阅读算法f2,设顺序表L=(3,7,3,2,1,1,8,7,3),写出执行算法f2后的线性表L的数据元素,并描述该算法的功能。
void f2(SeqList *L){
int i,j,k;
k=0;
for(i=0;i<L->length;i++){
for(j=0;j<k && L->data[i]!=L->data[j];j++);
if(j==k){
if(k!=i)L->data[k]=L->data[i];
k++;
}
}
L->length=k;
}
答案:
(3,7,2,1,8) 删除顺序表中重复的元素
8、已知线性表中的元素以值递增有序排列,并以单链表作存储结构。试写一算法,删除表中所有大于x且小于y的元素(若表中存在这样的元素)同时释放被删除结点空间。
答案:
void Delete_list(Lnode *head, ElemType x, ElemType y)
{Lnode *p, *q;
if(!head) return ERROR;
p=head; q=p;
while(!p)
{if(p->data>x) && (p->data<y)}i++;
if(p==head)
{head=p->next; free(p);
p=head; q=p; }
else
{q->next=p->next; free(p);
p=q->next; }
else
{q=p; p=p->next; }
}
}
9、在带头结点的循环链表L中,结点的数据元素为整型,且按值递增有序存放。给定两个整数a和b,且a<b,编写算法删除链表L中元素值大于a且小于b的所有结点。
第三章 栈和队列
一、选择题
1、一个栈的输入序列为:a,b,c,d,e,则栈的不可能输出的序列是()。
A. a,b,c,d,e B. d,e,c,b,a
C. d,c,e,a,b D. e,d,c,b,a
2、判断一个循环队列Q(最多n个元素)为满的条件是()。
A. Q->rear==Q->front B. Q->rear==Q->front+1
C. Q->front==(Q->rear+1)%n D. Q->front==(Q->rear-1)%n
3、设计一个判别表达式中括号是否配对的算法,采用()数据结构最佳。
A. 顺序表 B. 链表 C. 队列 D. 栈
4、带头结点的单链表head为空的判定条件是()。
A. head==NULL B. head->next==NULL
C. head->next!=NULL D. head!=NULL
5、一个栈的输入序列为:1,2,3,4,则栈的不可能输出的序列是()。
A. 1243 B. 2134 C. 1432 D. 4312 E. 3214
数据结构试卷 数据结构试题库集及答案
6、若用一个大小为6的数组来实现循环队列,且当rear和front的值分别为0,3。[www.61k.com)当从队列中删除一个元素,再加入两个元素后,rear和front的值分别为()。
A. 1和5 B. 2和4 C. 4和2 D. 5和1
7、队列的插入操作是在()。
A. 队尾 B.队头 C. 队列任意位置 D. 队头元素后
8、循环队列的队头和队尾指针分别为front和rear,则判断循环队列为空的条件是()。
A. front==rear B. front==0
C. rear==0 D. front=rear+1
9、一个顺序栈S,其栈顶指针为top,则将元素e入栈的操作是()。
A. *S->top=e;S->top++; B. S->top++;*S->top=e;
C. *S->top=e D. S->top=e;
10、表达式a*(b+c)-d的后缀表达式是()。
A. abcd+- B. abc+*d- C. abc*+d- D. -+*abcd
11、将递归算法转换成对应的非递归算法时,通常需要使用()来保存中间结果。
A.队列 B.栈 C.链表 D.树
12、栈的插入和删除操作在()。
A. 栈底 B. 栈顶 C. 任意位置 D. 指定位置
13、五节车厢以编号1,2,3,4,5顺序进入铁路调度站(栈),可以得到()的编组。
A. 3,4,5,1,2 B. 2,4,1,3,5
C. 3,5,4,2,1 D. 1,3,5,2,4
14、判定一个顺序栈S(栈空间大小为n)为空的条件是()。
A. S->top==0 B. S->top!=0
C. S->top==n D. S->top!=n
15、在一个链队列中,front和rear分别为头指针和尾指针,则插入一个结点s的操作为()。
A. front=front->next B.s->next=rear;rear=s
C. rear->next=s;rear=s; D. s->next=front;front=s;
16、一个队列的入队序列是1,2,3,4,则队列的出队序列是()。
A. 1,2,3,4 B. 4,3,2,1
C. 1,4,3,2 D. 3,4,1,2
17、依次在初始为空的队列中插入元素a,b,c,d以后,紧接着做了两次删除操作,此时的队头元素是()。
A. a B. b C. c D. d
18、正常情况下,删除非空的顺序存储结构的堆栈的栈顶元素,栈顶指针top的变化是()。
A. top不变 B. top=0 C. top=top+1 D. top=top-1
19、判断一个循环队列Q(空间大小为M)为空的条件是()。
A. Q->front==Q->rear B. Q->rear-Q->front-1==M
C. Q->front+1=Q->rear D. Q->rear+1=Q->front
20、设计一个判别表达式中左右括号是否配对出现的算法,采用()数据结构最佳。
A.线性表的顺序存储结构 B. 队列 C. 栈 D. 线性表的链式存储结构
21、当用大小为N的数组存储顺序循环队列时,该队列的最大长度为()。
A. N B. N+1 C. N-1 D. N-2
22、队列的删除操作是在()。
A. 队首 B. 队尾 C.队前 D. 队后
23、若让元素1,2,3依次进栈,则出栈次序不可能是()。
A. 3,2,1 B. 2,1,3 C. 3,1,2 D. 1,3,2
24、循环队列用数组A[0,m-1]存放其元素值,已知其头尾指针分别是front和rear,则当前队列中的元素个数是()。
A. (rear-front+m)%m B. rear-front+1
C. rear-front-1 D. rear-front
25、在解决计算机主机和打印机之间速度不匹配问题时,通常设置一个打印数据缓冲区,主机将要输出的数据依次写入该缓冲区,而打印机则从该缓冲区中取走数据打印。该缓冲区应该是一个()结构。
A. 堆栈 B. 队列 C. 数组 D. 线性表
26、栈和队列都是()。
A. 链式存储的线性结构 B. 链式存储的非线性结构
C. 限制存取点的线性结构 D. 限制存取点的非线性结构
27、在一个链队列中,假定front和rear分别为队头指针和队尾指针,删除一个结点的操作是()。
A. front=front->next B. rear= rear->next
C. rear->next=front D. front->next=rear
数据结构试卷 数据结构试题库集及答案
28、队和栈的主要区别是()。[www.61k.com]
A. 逻辑结构不同 B.存储结构不同
C. 所包含的运算个数不同 D. 限定插入和删除的位置不同
二、填空题
1、设栈S和队列Q的初始状态为空,元素e1,e2,e3,e4,e5,e6依次通过栈S,一个元素出栈后即进入队列Q,若6个元素出队的序列是e2,e4,e3,e6,e5,e1,则栈的容量至少应该是。
答案:3
2、一个循环队列Q的存储空间大小为M,其队头和队尾指针分别为front和rear,则循环队列中元素的个数为:。 答案:(rear-front+M)%M
3、在具有n个元素的循环队列中,队满时具有个元素。
答案:n-1
4、设循环队列的容量为70,现经过一系列的入队和出队操作后,front为20,rear为11,则队列中元素的个数为。 答案:61
5、已知循环队列的存储空间大小为20,且当前队列的头指针和尾指针的值分别为8和3,且该队列的当前的长度为_______。
三、判断题
1、栈和队列都是受限的线性结构。?
2、在单链表中,要访问某个结点,只要知道该结点的地址即可;因此,单链表是一种随机存取结构。?
3、以链表作为栈的存储结构,出栈操作必须判别栈空的情况。?
四、程序分析填空题
1、已知栈的基本操作函数:
int InitStack(SqStack *S); //构造空栈
int StackEmpty(SqStack *S);//判断栈空
int Push(SqStack *S,ElemType e);//入栈
int Pop(SqStack *S,ElemType *e);//出栈
函数conversion实现十进制数转换为八进制数,请将函数补充完整。
void conversion(){
InitStack(S);
scanf(“%d”,&N);
while(N){
(1);
N=N/8;
}
while((2)){
Pop(S,&e);
printf(“%d”,e);
}
}//conversion
答案:(1)Push(S,N%8) (2)!StackEmpty(S)
2、写出算法的功能。
int function(SqQueue *Q,ElemType *e){
if(Q->front==Q->rear)
return ERROR;
*e=Q->base[Q->front];
Q->front=(Q->front+1)%MAXSIZE;
return OK;
}
3、阅读算法f2,并回答下列问题:
(1)设队列Q=(1,3,5,2,4,6)。写出执行算法f2后的队列Q;
(2)简述算法f2的功能。
void f2(Queue *Q){
DataType e;
if (!QueueEmpty(Q)){
e=DeQueue(Q);
f2(Q);
EnQueue(Q,e);
数据结构试卷 数据结构试题库集及答案
}
}
答案:(1)6,4,2,5,3,1 (2)将队列倒置
五、综合题
1、假设以带头结点的循环链表表示队列,并且只设一个指针指向队尾结点,但不设头指针,请写出相应的入队列算法(用函数实现)。(www.61k.com]

答案:void EnQueue(Lnode *rear, ElemType e)
{Lnode *new;
New=(Lnode *)malloc(sizeof(Lnode));
If(!new) return ERROR;
new->data=e; new->next=rear->next;
rear->next=new; rear =new;
}
2、已知Q是一个非空队列,S是一个空栈。编写算法,仅用队列和栈的ADT函数和少量工作变量,将队列Q的所有元素逆置。
栈的ADT函数有:
void makeEmpty(SqStack s); 置空栈
void push(SqStack s,ElemType e); 元素e入栈
ElemType pop(SqStack s); 出栈,返回栈顶元素
int isEmpty(SqStack s); 判断栈空
队列的ADT函数有:
void enQueue(Queue q,ElemType e); 元素e入队
ElemType deQueue(Queue q); 出队,返回队头元素
int isEmpty(Queue q); 判断队空
答案:void QueueInvent(Queue q)
{ElemType x;
makeEmpty(SqStack s);
while(!isEmpty(Queue q))
{x=deQueue(Queue q);
push(SqStack s, ElemTypex);}
while(!isEmpty(SqStack s))
{x=pop(SqStack s);
enQueue(Queue q, ElemType x);}
}
3、对于一个栈,给出输入项A,B,C,D,如果输入项序列为A,B,C,D,试给出全部可能的输出序列。
答案:出栈的可能序列:
ABCD ABDC ACDB ACBD ADCB BACD BADC BCAD BCDA
CBDA CBAD CDBA DCBA
第四章 串
一、选择题
1、设有两个串S1和S2,求串S2在S1中首次出现位置的运算称作( C )。
A.连接 B.求子串 C.模式匹配 D.判断子串
2、已知串S=?aaab?,则next数组值为(A)。
A. 0123 B. 1123 C. 1231 D. 1211
3、串与普通的线性表相比较,它的特殊性体现在(C)。
A. 顺序的存储结构 B. 链式存储结构
个字符 D. 数据元素任意
4、设串长为n,模式串长为m,则KMP算法所需的附加空间为( A)。
A. O(m) B. O(n) C. O(m*n) D. O(nlog2m)
5、空串和空格串(B)。
A. 相同 B. 不相同 C. 可能相同 D. 无法确定 C. 数据元素是一
数据结构试卷 数据结构试题库集及答案
6、与线性表相比,串的插入和删除操作的特点是()。(www.61k.com)
A. 通常以串整体作为操作对象 B. 需要更多的辅助空间
C. 算法的时间复杂度较高 D. 涉及移动的元素更多
7、设SUBSTR(S,i,k)是求S中从第i个字符开始的连续k个字符组成的子串的操作,则对于S=’Beijing&Nanjing’,SUBSTR(S,4,5)=(B)。
A. ?ijing? B. ?jing&? C.?ingNa? D. ?ing&N?
二、判断题
()1、造成简单模式匹配算法BF算法执行效率低的原因是有回溯存在。
(√)2、KMP算法的最大特点是指示主串的指针不需要回溯。
(√ )3、完全二叉树某结点有右子树,则必然有左子树。
三、填空题
1、求子串在主串中首次出现的位置的运算称为模式匹配。
2、设s=?I︺AM︺A︺TEACHER?,其长度是____。
3、两个串相等的充分必要条件是两个串的长度相等且对应位置字符相同。
四、程序填空题
1、函数kmp实现串的模式匹配,请在空格处将算法补充完整。
intkmp(sqstring *s,sqstring *t,int start,int next[]){
int i=start-1,j=0;
while(i<s->len&&j<t->len)
if(j==-1||s->data[i]==t->data[j]){
i++;j++;
}
else j=;
if(j>=t->len)
return();
else
return(-1);
}
2、函数实现串的模式匹配算法,请在空格处将算法补充完整。
intindex_bf(sqstring*s,sqstring *t,int start){
int i=start-1,j=0;
while(i<s->len&&j<t->len)
if(s->data[i]==t->data[j]){
i++;j++;
}else{
i=i-j+1;j=0;
}
if(j>=t->len)
return else
return -1;
}}/*listDelete*/
3、写出下面算法的功能。
int function(SqString *s1,SqString *s2){
int i;
for(i=0;i<s1->length&&i<s1->length;i++)
if(s->data[i]!=s2->data[i])
return s1->data[i]-s2->data[i];
return s1->length-s2->length;
}
答案:.串比较算法
4、写出算法的功能。
int fun(sqstring*s,sqstring *t,int start){
int i=start-1,j=0;
while(i<s->len&&j<t->len)
if(s->data[i]==t->data[j]){
i++;j++;
}else{
i=i-j+1;j=0;
}
数据结构试卷 数据结构试题库集及答案
if(j>=t->len)
return i-t->len+1;
else
return -1;
}
答案:串的模式匹配算法
第五章 数组和广义表
一、选择题
1、设广义表L=((a,b,c)),则L的长度和深度分别为(C )。[www.61k.com]
A. 1和1 B. 1和3 C. 1和2 D. 2和3
2、广义表((a),a)的表尾是(B)。
A. a B. (a) C. () D. ((a))
3、稀疏矩阵的常见压缩存储方法有( C )两种。
A.二维数组和三维数组 B.三元组和散列表 C.三元组和十字链表 D.散列表和十字链表
4、一个非空广义表的表头(D)。
A. 不可能是子表 B.只能是子表 C. 只能是原子 D.可以是子表或原子
5、数组A[0..5,0..6]的每个元素占5个字节,将其按列优先次序存储在起始地址为1000的内存单元中,则元素A[5][5]的地址是()。
A. 1175 B. 1180 C. 1205 D. 1210
6、广义表G=(a,b(c,d,(e,f)),g)的长度是(A)。
A. 3 B. 4 C. 7 D. 8
7、采用稀疏矩阵的三元组表形式进行压缩存储,若要完成对三元组表进行转置,只要将行和列对换,这种说法(B)。
A. 正确 B. 错误 C. 无法确定 D. 以上均不对
8、广义表(a,b,c)的表尾是(B)。
A. b,c B. (b,c) C. c D. (c)
9、常对数组进行两种基本操作是()。
A. 建立和删除 B. 索引和修改 C. 查找和修改 D. 查找与索引
10、对一些特殊矩阵采用压缩存储的目的主要是为了(D)。
A. 表达变得简单 B.对矩阵元素的存取变得简单
C. 去掉矩阵中的多余元素 D. 减少不必要的存储空间的开销
11、设有一个10阶的对称矩阵A,采用压缩存储方式,以行序为主存储,a11为第一个元素,其存储地址为1,每元素占1个地址空间,则a85的地址为()。
A. 13 B. 33 C. 18 D. 40
12、设矩阵A是一个对称矩阵,为了节省存储,将其下三角部分按行序存放在一维数组B[1,n(n-1)/2]中,对下三角部分中任一元素ai,j(i>=j),在一维数组B的下标位置k的值是(B)。
A. i(i-1)/2+j-1 B. i(i-1)/2+j C. i(i+1)/2+j-1 D. i(i+1)/2+j
13、广义表A=((a),a)的表头是(B)。
A. a B. (a) C. b D. ((a))
14、稀疏矩阵一般的压缩存储方法有两种,即(C)。
A. 二维数组和三维数组 B.三元组和散列 C.三元组和十字链表 D.散列和十字链表
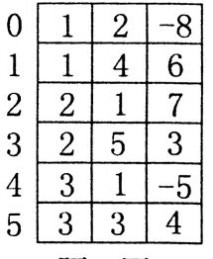
15、假设以三元组表表示稀疏矩阵,则与如图所示三元组表对应的4×5的稀疏矩阵是(注:矩阵的行列下标均从1开始)(B)。
?0?8060??0?8060?????7000070003????A. ? B. ??50400? 00000???????50400??00000?????
?0?8060??0?8???0003?0?0?7C. ? D.??5070000??????50400??00???
16、以下有关广义表的表述中,正确的是()。
060??000? 403??000??
数据结构试卷 数据结构试题库集及答案
A. 由0个或多个原子或子表构成的有限序列 B. 至少有一个元素是子表
C. 不能递归定义 D. 不能为空表
17、对广义表L=((a,b),((c,d),(e,f)))执行head(tail(head(tail(L))))操作的结果是()。[www.61k.com)
A. 的 B. e C. (e) D.(e,f)
二、判断题
()1、广义表中原子个数即为广义表的长度。
()2、一个稀疏矩阵采用三元组表示,若把三元组中有关行下标与列下标的值互换,并把mu和nu的值进行互换,则完成了矩阵转置。
(√)3、稀疏矩阵压缩存储后,必会失去随机存取功能。
()4、广义表的长度是指广义表中括号嵌套的层数。
(√)5、广义表是一种多层次的数据结构,其元素可以是单原子也可以是子表。
三、填空题
1、已知二维数组A[m][n]采用行序为主方式存储,每个元素占k个存储单元,并且第一个元素的存储地址是LOC(A[0][0]),则A[i][j]的地址是___Loc(A[0][0])+(i*N+j)*k。
2、广义表运算式HEAD(TAIL((a,b,c),(x,y,z)))的结果是:(x,y,z)。
3、二维数组,可以按照两种不同的存储方式。
4、稀疏矩阵的压缩存储方式有:和。
四、综合题
1、现有一个稀疏矩阵,请给出它的三元组表。
?0?1??0??0
i
1
1
2
3
3
40?000?? 210??0?20?j231233v31121-231答案:
第六章 树
一、选择题
1、二叉树的深度为k,则二叉树最多有( C )个结点。
A. 2k B. 2k-1 C. 2k-1 D. 2k-1
2、用顺序存储的方法,将完全二叉树中所有结点按层逐个从左到右的顺序存放在一维数组R[1..N]中,若结点R[i]有右孩子,则其右孩子是( B )。
A. R[2i-1] B. R[2i+1] C. R[2i] D. R[2/i]
3、设a,b为一棵二叉树上的两个结点,在中序遍历时,a在b前面的条件是( B)。
A. a在b的右方 B. a在b的左方 C. a是b的祖先 D. a是b的子孙
4、设一棵二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树先序遍历序列为()。
A. adbce B. decab C. debac D. abcde
5、在一棵具有5层的满二叉树中结点总数为()。
A. 31 B. 32 C. 33 D. 16
6、由二叉树的前序和后序遍历序列( B )惟一确定这棵二叉树。
A. 能 B. 不能
7、某二叉树的中序序列为ABCDEFG,后序序列为BDCAFGE,则其左子树中结点数目为( C )。
A. 3 B.2 C. 4 D. 5
8、若以{4,5,6,7,8}作为权值构造哈夫曼树,则该树的带权路径长度为(C)。
A. 67 B. 68 C. 69 D. 70
数据结构试卷 数据结构试题库集及答案
9、将一棵有100个结点的完全二叉树从根这一层开始,每一层上从左到右依次对结点进行编号,根结点的编号为1,则编号为49的结点的左孩子编号为( A )。(www.61k.com]
A. 98 B.99 C. 50 D. 48
10、表达式a*(b+c)-d的后缀表达式是( B )。
A. abcd+- B. abc+*d- C. abc*+d- D. -+*abcd
11、对某二叉树进行先序遍历的结果为ABDEFC,中序遍历的结果为DBFEAC,则后序遍历的结果是(B )。
A. DBFEAC B. DFEBCA C. BDFECA D. BDEFAC
12、树最适合用来表示( C )。
A. 有序数据元素 B. 无序数据元素 C. 元素之间具有分支层次关系的数据 D. 元素之间无联系的数据
13、表达式A*(B+C)/(D-E+F)的后缀表达式是(C)。
A. A*B+C/D-E+F B. AB*C+D/E-F+ C. ABC+*DE-F+/ D. ABCDED*+/-+
14、在线索二叉树中,t所指结点没有左子树的充要条件是()。
A. t->left==NULL B.t->ltag==1 C. t->ltag==1&&t->left==NULL
D.以上都不对
15、任何一棵二叉树的叶结点在先序、中序和后序遍历序列中的相对次序()。
A. 不发生改变 B. 发生改变 C. 不能确定 D. 以上都不对
16、假定在一棵二叉树中,度为2的结点数为15,度为1的结点数为30,则叶子结点数为()个。
A. 15 B. 16 C. 17 D. 47
17、在下列情况中,可称为二叉树的是(B)。
A.每个结点至多有两棵子树的树 B. 哈夫曼树
C. 每个结点至多有两棵子树的有序树 D. 每个结点只有一棵子树
18、用顺序存储的方法,将完全二叉树中所有结点按层逐个从左到右的顺序存放在一维数组R[1..n]中,若结点R[i]有左孩子,则其左孩子是()。
A. R[2i-1] B. R[2i+1] C. R[2i] D. R[2/i]
19、下面说法中正确的是()。
A. 度为2的树是二叉树 B. 度为2的有序树是二叉树
C. 子树有严格左右之分的树是二叉树 D.子树有严格左右之分,且度不超过2的树是二叉树
20、树的先根序列等同于与该树对应的二叉树的()。
A. 先序序列 B. 中序序列 C. 后序序列D. 层序序列
21、按照二叉树的定义,具有3个结点的二叉树有(C)种。
A. 3 B.4 C.5 D.6
22、由权值为3,6,7,2,5的叶子结点生成一棵哈夫曼树,它的带权路径长度为(A)。
A.51 B. 23 C. 53 D. 74
二、判断题
()1、存在这样的二叉树,对它采用任何次序的遍历,结果相同。
()2、中序遍历一棵二叉排序树的结点,可得到排好序的结点序列。
()3、对于任意非空二叉树,要设计其后序遍历的非递归算法而不使用堆栈结构,最适合的方法是对该二叉树采用三叉链表。
()4、在哈夫曼编码中,当两个字符出现的频率相同时,其编码也相同,对于这种情况应做特殊处理。
(√)5、一个含有n个结点的完全二叉树,它的高度是?log2n?+1。
(√)6、完全二叉树的某结点若无左孩子,则它必是叶结点。
三、填空题
1、具有n个结点的完全二叉树的深度是2。
2、哈夫曼树是其树的带权路径长度最小的二叉树。
3、在一棵二叉树中,度为0的结点的个数是n0,度为2的结点的个数为n2,则有n0=N2+1。
4、树内各结点度的最大值
四、代码填空题
1、函数InOrderTraverse(Bitree bt)实现二叉树的中序遍历,请在空格处将算法补充完整。
void InOrderTraverse(BiTree bt){
if(){
InOrderTraverse(bt->lchild);
printf(“%c”,bt->data);
;
}
数据结构试卷 数据结构试题库集及答案
}
2、函数depth实现返回二叉树的高度,请在空格处将算法补充完整。(www.61k.com)
int depth(Bitree *t){
if(t==NULL)
return 0;
else{
hl=depth(t->lchild);
hr=depth(t->rchild);
if(hl>hr)
return hl+1;
else
return hr+1;
}
}
3、写出下面算法的功能。
Bitree *function(Bitree *bt){
Bitree *t,*t1,*t2;
if(bt==NULL)
t=NULL;
else{
t=(Bitree *)malloc(sizeof(Bitree));
t->data=bt->data;
t1=function(bt->left);
t2=function(bt->right);
t->left=t2;
t->right=t1;
}
return(t);
}
答案:交换二叉树结点左右子树的递归算法
4、写出下面算法的功能。
void function(Bitree *t){
if(p!=NULL){
function(p->lchild);
function(p->rchild);
printf(“%d”,p->data);
}
}
答案:二叉树后序遍历递归算法
五、综合题
1、假设以有序对<p,c>表示从双亲结点到孩子结点的一条边,若已知树中边的集合为
{<a,b>,<a,d>,<a,c>,<c,e>,<c,f>,<c,g>,<c,h>,<e,i>,<e,j>,<g,k>},请回答下列问题:
(1)哪个结点是根结点?
(2)哪些结点是叶子结点?
(3)哪些结点是k的祖先?
(4)哪些结点是j的兄弟?
(5)树的深度是多少?。
2、假设一棵二叉树的先序序列为EBADCFHGIKJ,中序序列为ABCDEFGHIJK,请画出该二叉树。
3、假设用于通讯的电文仅由8个字母A、B、C、D、E、F、G、H组成,字母在电文中出现的频率分别为:0.07,0.19,0.02,0.06,0.32,0.03,0.21,0.10。请为这8个字母设计哈夫曼编码。
数据结构试卷 数据结构试题库集及答案
100
01
B 101A 000
38
062
1C 10000
121G0321ED 1001
E 11
F 10001
G 01
H 0017A10H0116D19B5023
CF答案:
4、已知二叉树的先序遍历序列为ABCDEFGH,中序遍历序列为CBEDFAGH,画出二叉树。(www.61k.com)
答案:二叉树形态
A
B
C
EDFGH
5、试用权集合{12,4,5,6,1,2}构造哈夫曼树,并计算哈夫曼树的带权路径长度。 答案:
30
1218
7
4
3
125116 WPL=12*1+(4+5+6)*3+(1+2)*4=12+45+12=69
6、已知权值集合为{5,7,2,3,6,9},要求给出哈夫曼树,并计算带权路径长度WPL。 答案:(1)树形态:
32
6791955
23 (2)带权路径长度:WPL=(6+7+9)*2+5*3+(2+3)*4=44+15+20=79
7、已知一棵二叉树的先序序列:ABDGJEHCFIKL;中序序列:DJGBEHACKILF。画出二叉树的形态。
数据结构试卷 数据结构试题库集及答案
A
B
D
G
JEHKILCF答案:
8、一份电文中有6种字符:A,B,C,D,E,F,它们的出现频率依次为16,5,9,3,30,1,完成问题:
(1)设计一棵哈夫曼树;(画出其树结构)
(2)计算其带权路径长度WPL;
答案:(1)树形态:
64
3034
1618
99
54
13 (2)带权路径长度:WPL=30*1+16*2+9*3+5*4+(1+3)*5=30+32+27+20+20=129
答案:
A
BCDE
GFH
10、有一分电文共使用5个字符;a,b,c,d,e,它们的出现频率依次为4、7、5、2、9,试构造哈夫曼树,并给出每个字符的哈夫曼编码。(www.61k.com)
11、画出与下图所示的森林相对应的二叉树,并指出森林中的叶子结点在二叉树中具有什么特点。
数据结构试卷 数据结构试题库集及答案
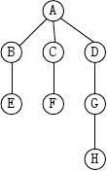
答案:先序:FDBACEGIHJ
中序:ABCDEFGHIJ
后序:ACBEDHJIGF
六、编程题
1、编写求一棵二叉树中结点总数的算法。[www.61k.com)
答案: (以先序遍历的方法为例)
void count_preorder(Bitree *t, int *n)
{
if(t!=NULL)
{*n++;
count_preorder(t->lchild);
count_preorder(t->lchild); }
}
第七章 图
一、选择题
1、12、对于具有n个顶点的图,若采用邻接矩阵表示,则该矩阵的大小为()。 2A. n B. n C. n-1 D. (n-1)2
2、如果从无向图的任一顶点出发进行一次深度优先搜索即可访问所有顶点,则该图一定是()。
A. 完全图 B. 连通图 C. 有回路 D. 一棵树
3、关键路径是事件结点网络中()。
A. 从源点到汇点的最长路径 B.从源点到汇点的最短路径
C.最长的回路 D.最短的回路
4、下面()可以判断出一个有向图中是否有环(回路)。
A. 广度优先遍历 B. 拓扑排序
C. 求最短路径 D. 求关键路径
5、带权有向图G用邻接矩阵A存储,则顶点i的入度等于A中()。
A. 第i行非无穷的元素之和 B. 第i列非无穷的元素个数之和
C. 第i行非无穷且非0的元素个数 D. 第i行与第i列非无穷且非0的元素之和
6、采用邻接表存储的图,其深度优先遍历类似于二叉树的()。
A. 中序遍历 B. 先序遍历 C. 后序遍历 D. 按层次遍历
7、无向图的邻接矩阵是一个()。
A. 对称矩阵 B. 零矩阵 C. 上三角矩阵 D. 对角矩阵
8、当利用大小为N的数组存储循环队列时,该队列的最大长度是()。
数据结构试卷 数据结构试题库集及答案
A. N-2 B. N-1 C. N
9、邻接表是图的一种()。(www.61k.com]
A. 顺序存储结构B.链式存储结构 C. 索引存储结构 D. 散列存储结构
10、下面有向图所示的拓扑排序的结果序列是()。
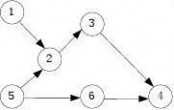
B. 516234 C. 123456 D. 521643
D. N+1 11、在无向图中定义顶点vi与vj之间的路径为从vi到vj的一个()。
A. 顶点序列 B. 边序列 C. 权值总和 D. 边的条数
12、在有向图的逆邻接表中,每个顶点邻接表链接着该顶点所有()邻接点。
A. 入边 B. 出边 C. 入边和出边 D. 不是出边也不是入边
13、设G1=(V1,E1)和G2=(V2,E2)为两个图,如果V1?V2,E1?E2则称()。
A. G1是G2的子图 B. G2是G1的子图 C. G1是G2的连通分量 D. G2是G1的连通分量
14、已知一个有向图的邻接矩阵表示,要删除所有从第i个结点发出的边,应()。
A. 将邻接矩阵的第i行删除 B. 将邻接矩阵的第i行元素全部置为0 C. 将邻接矩阵的第i列删除 D. 将邻接矩阵的第i列元素全部置为0
15、任一个有向图的拓扑序列()。
A.不存在 B. 有一个 C. 一定有多个 D. 有一个或多个
16、在一个有向图中,所有顶点的入度之和等于所有顶点的出度之和的()倍。
A. 1/2 B. 1 C. 2 D. 4
17、下列关于图遍历的说法不正确的是()。
A. 连通图的深度优先搜索是一个递归过程
B. 图的广度优先搜索中邻接点的寻找具有“先进先出”的特征
C. 非连通图不能用深度优先搜索法
D. 图的遍历要求每一顶点仅被访问一次
18、带权有向图G用邻接矩阵A存储,则顶点i的入度为A中:()。
A. 第i行非?的元素之和 B. 第i列非?的元素之和
C. 第i行非?且非0的元素个数 D. 第i列非?且非0的元素个数
19、采用邻接表存储的图的广度优先遍历算法类似于二叉树的()。
A. 先序遍历 B.中序遍历 C. 后序遍历 D. 按层次遍历
20、一个具有n个顶点的有向图最多有()条边。
A. n×(n-1)/2 B. n×(n-1) C. n×(n+1)/2 D.n2
21
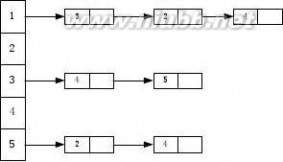
v1出发,所得到的顶点序列是()。
A. v1,v2,v3,v5,v4
C. v1,v3,v4,v5,v2
22、关键路径是事件结点网络中()。
A. 从源点到汇点的最长路径 B. 从源点到汇点的最短路径
C. 最长的回路 D. 最短的回路
23、以下说法正确的是()。
A. 连通分量是无向图中的极小连通子图
B. 强连通分量是有向图中的极大强连通子图
C.在一个有向图的拓扑序列中若顶点a在顶点b之前,则图中必有一条弧<a,b>
D. 对有向图G,如果以任一顶点出发进行一次深度优先或广度优先搜索能访问到每个顶点,则该图一定是完全图 B.v1,v2,v3,v4,v5 D. v1,v4,v3,v5,v2
数据结构试卷 数据结构试题库集及答案
24、假设有向图含n个顶点及e条弧,则表示该图的邻接表中包含的弧结点个数为()。[www.61k.com]
A. n B. e C. 2e
?011???25、设图的邻接矩阵为?001?,则该图为()。
?010???D. n*e
A. 有向图 B. 无向图 C.强连通图 D. 完全图
26、为便于判别有向图中是否存在回路,可借助于()。
A. 广度优先搜索算法 B. 最小生成树算法
C. 最短路径算法 D. 拓扑排序算法
27、任何一个无向连通图的最小生成树()种。
A. 只有一棵 B.有一棵或多棵 C.一定有多棵 D.可能不存在
28、已知一有向图的邻接表存储结构如图所示,根据有向图的广度优先遍历算法,从顶点v1出发,所得到的顶点序列是()。
A.
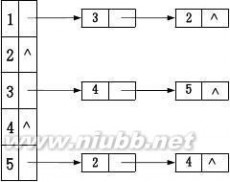
C. v1,v2,v3,v5,v4 D. v1,v4,v3,v5,v2
29、对于一个有向图,若一个顶点的入度为k1,、出度为k2,则对应邻接表中该顶点单链表中的结点数为()。
A. k1 B. k2 C. k1+k2 D. k1-k2
30、一个具有8个顶点的有向图中,所有顶点的入度之和与所有顶点的出度之和的差等于()。
A. 16 B. 4 C. 0 D. 2
31、无向图中一个顶点的度是指图中()。
A.通过该顶点的简单路径数 B. 与该顶点相邻接的顶点数
C. 与该顶点连通的顶点数 D. 通过该顶点的回路数
二、填空题
1、n个顶点的连通图至少有边。
答案:n-1条
2、一个连通图的生成树是一个,它包含图中所有顶点,但只有足以构成一棵树的n-1条边。
答案:极小连通子图
3、一个图的表示法是惟一的。
答案:邻接矩阵
4、遍历图的基本方法有深度优先搜索和广度优先搜索,其中是一个递归过程。
答案:深度优先搜索
5、在无向图G的邻接矩阵A中,若A[i][j]等于1,则A[j][i]等于。
答案:1
6、判定一个有向图是否存在回路,可以利用。
答案:拓扑排序
7、已知一个图的邻接矩阵表示,计算第i个结点的入度的方法是。
8、n个顶点的无向图最多有边。
9、已知一个图的邻接矩阵表示,删除所有从第i个结点出发的边的方法是。
10、若以邻接矩阵表示有向图,则邻接矩阵上第i行中非零元素的个数即为顶点vi的。
三、判断题
1、图的连通分量是无向图的极小连通子图。?
2、一个图的广度优先搜索树是惟一的。?
3、图的深度优先搜索序列和广度优先搜索序列不是惟一的。?
4、邻接表只能用于存储有向图,而邻接矩阵则可存储有向图和无向图。?
5、存储图的邻接矩阵中,邻接矩阵的大小不但与图的顶点个数有关,而且与图的边数也有关。?
6、AOV网是一个带权的有向图。?
数据结构试卷 数据结构试题库集及答案
7、从源点到终点的最短路径是唯一的。[www.61k.com]?
8、邻接表只能用于存储有向图,而邻接矩阵则可存储有向图和无向图。?
9、图的生成树是惟一的。?
四、程序分析题
1、写出下面算法的功能。
typedef struct{
int vexnum,arcnum;
char vexs[N];
int arcs[N][N];
}graph;
void funtion(int i,graph *g){
int j;
printf("node:%c\n",g->vexs[i]);
visited[i]=TRUE;
for(j=0;j<g->vexnum;j++) if((g->arcs[i][j]==1)&&(!visited[j]))
function(j,g);
}
答案:实现图的深度优先遍历算法
五、综合题
1、已知图G的邻接矩阵如下所示:
(1)求从顶点1出发的广度优先搜索序列;
(2)根据prim算法,求图G从顶点1出发的最小生成树,要求表示出其每一步生成过程。(用图或者表的方式均可)。 ??615????6?5?3??????15?564????
?5?5??2???36??6???????426???
答案:(1)广度优先遍历序列:1; 2, 3, 4; 5; 6 (2)最小生成树(prim算法)
1
111111112
5125333
43434345
6426426426
2、设一个无向图的邻接矩阵如下图所示:
(1)画出该图;
(2)画出从顶点0出发的深度优先生成树;
?0?1??1??1
?0???011100?01000??10110?? 01011?01101??00110??
答案:(1)图形态 (2)深度优先搜索树
数据结构试卷 数据结构试题库集及答案
1
1
3232
5454
3、写出下图中全部可能的拓扑排序序列。(www.61k.com]
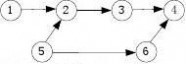
答案:1,5,2,3,6,4 1,5,6,2,3,4 5,1,2,3,6,4
5,1,6,2,3,4 5,6,1,2,3,4 4、AOE网G如下所示,求关键路径。(要求标明每个顶点的最早发生时间和最迟发生时间,并画出关键路径)
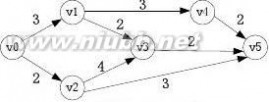
答案:(1)最早发生时间和最迟发生时间: (2)关键路径:
顶点v0v1v2v3
v4v5
ve032668
vl032668
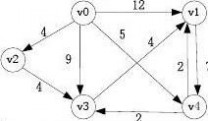
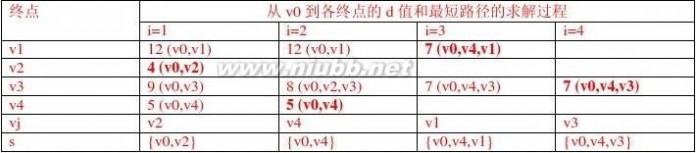
5、已知有向图G如下所示,根据迪杰斯特拉算法求顶点v0到其他顶点的最短距离。(给出求解过程)
6、已知图G如下所示,根据Prim算法,构造最小生成树。(要求给出生成过程)
数据结构试卷 数据结构试题库集及答案
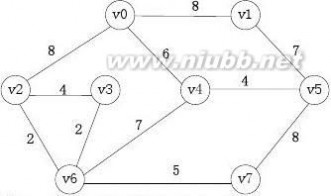
答案:prim算法求最小生成树如下:
v06v4
4
v5
7v6
v2
2
v06v4
4v5
7v6
v2
2
v06v4
4v5
v3
2
v06v47v6
v2
2
4
v5
v3
2v67
v06v4
5v7
v2
2
4
v5
v3
2
7v6
v06v4
5v74
v17v5
6
答案:拓扑排序如下:
v1, v2, v4, v6, v5, v3, v7, v8 v1, v2, v4, v6, v5, v7, v3, v8 v1, v2, v6, v4, v5, v3, v7, v8 v1, v2, v6, v4, v5, v7, v3, v8 v1, v6, v2, v4, v5, v3, v7, v8 v1, v6, v2, v4, v5, v7, v3, v8 8、如下图所示的AOE网,求:
(1
vl;
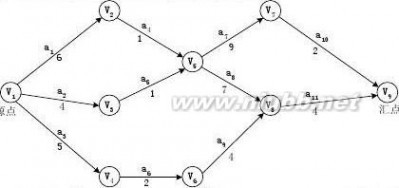
(2

答案:(1)求ve和vl (2)关键路径
事件vevl
100*
266*
346
458
577*
6710
71616*
81414*
91818*
如下所示的有向
图,回答下面问题:
数据结构试卷 数据结构试题库集及答案
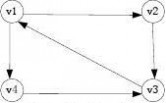
(1)该图是强连通的吗?若不是,给出强连通分量。(www.61k.com) (2)请给出图的邻接矩阵和邻接表表示。
答案:(1) 是强连通图 (2) 邻接矩阵和邻接表为:
0010
1000
0101

1000
v1v2v3v4
??112610??1?89????
9、已知图G的邻接矩阵A=?128??2?,试画出它所表示的图G,并根据Prim算法求出图的的最小生成树(给
??69??4????10?24???
出生成过程)。 答案:
(1)图形态: (2)prim算法求最小生成树:
v1
10
2v5
4v31
8
9v4
v1
1
8v3
v5
v2
2
v5
v3
2
4
v4
v2
v1
1
v2
v1
1
8
v3
v2
v1
1
8
v2
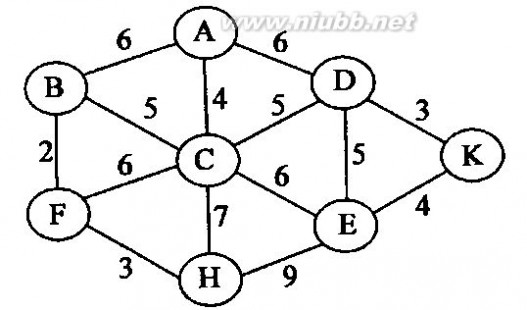
11、已知图G如下,根据克鲁斯卡尔算法求图G的一棵最小生成树。(要求给出构造过程)
答案:kruskal算法的最小生成树
数据结构试卷 数据结构试题库集及答案
B
2
B
2
D
3
B
2
D
3
B
2
A
4
D
3
FFK
F
3
KF
3
CK
HH
B
2
A
4
D
3
B
2
A
4
D
3
B
2
A
4
5
D
3
F
3
C
4
KF
3
C
4
KF
3
C
4
K
HEHEHE
(给出求解过程)
第九章 查找
一、选择题
1、已知一个有序表为(11,22,33,44,55,66,77,88,99),则折半查找55需要比较( A )次。(www.61k.com]
A. 1 B. 2 C. 3 D. 4
2、有一组关键字序列{13,16,6,34,32,98,73,1,27},哈希表的表长为13,哈希函数为H(key)=key MOD 13,冲突解决的办法为链地址法,请构造哈希表(用图表示)。 3、解决哈希冲突的主要方法有()。 A. 数字分析法、除余法、平方取中法 B. 数字分析法、除余法、线性探测法 C. 数字分析法、线性探测法、再哈希法 D. 线性探测法、再哈希法、链地址法 4、在一棵深度为h的具有n个元素的二叉排序树中,查找所有元素的最长查找长度为()。
A. n B. log2n C. (h+1)/2 D. h
5、已知表长为25的哈希表,用除留取余法,按公式H(key)=key MOD p 建立哈希表,则p应取()为宜。
A. 23 B.24 C. 25 D. 26
6、设哈希表长m=14,哈希函数H(key)=key MOD 11。表中已有4个结点:
addr(15)=4,addr(38)=5,addr(61)=6,addr(84)=7 其余地址为空,如用二次探测再散列处理冲突,则关键字为49的地址为(A)。
A.8 B. 3 C. 5 D. 9 7、在散列查找中,平均查找长度主要与(C)有关。
数据结构试卷 数据结构试题库集及答案
A. 散列表长度 B.散列元素个数 C. 装填因子 D. 处理冲突方法
8、根据一组记录(56,42,50,64,48)依次插入结点生成一棵AVL树,当插入到值为的结点时需要进行旋转调整。(www.61k.com)
9、m阶B-树中的m是指()。
A. 每个结点至少具有m棵子树 B. 每个结点最多具有m棵子树
C. 分支结点中包含的关键字的个数 D. m阶B-树的深度
10、一个待散列的线性表为k={18,25,63,50,42,32,9},散列函数为H(k)=k MOD 9,与18发生冲突的元素有()个。
A. 1 B. 2 C. 3 D. 4
11、在对查找表的查找过程中,若被查找的数据元素不存在,则把该数据元素插到集合中,这种方式主要适合于()。
A.静态查找表 B. 动态查找表 C. 静态查找表和动态查找表
D. 两种表都不适合
12、有一个有序表为{1,3,9,12,32,41,45,62,75,77,82,95,100},当折半查找值为82的结点时,(B)次比较后查找成功。
A. 1 B. 4 C. 2 D. 8
13、在各种查找方法中,平均查找承担与结点个数n无关的查找方法是(C)。
A. 顺序查找 B. 折半查找 C. 哈希查找 D. 分块查找
14、下列二叉树中,不平衡的二叉树是(C)。

.
15、对一棵二叉排序树按( B)遍历,可得到结点值从小到大的排列序列。
A. 先序 B.中序 C.后序 D.层次
16、解决散列法中出现的冲突问题常采用的方法是(D)。
A. 数字分析法、除余法、平方取中法 B.数字分析法、除余法、线性探测法
C. 数字分析法、线性探测法、多重散列法 D. 线性探测法、多重散列法、链地址法
17、对线性表进行折半查找时,要求线性表必须( C )。
A. 以顺序方式存储 B. 以链接方式存储
C. 以顺序方式存储,且结点按关键字有序排序 D. 以链接方式存储,且结点按关键字有序排序
二、填空题
1、在散列函数H(key)=key%p中,p应取。
2、已知有序表为(12,18,24,35,47,50,62,83,90,115,134),当用折半查找90时,需进行 2 次查找可确定成功。
3、具有相同函数值的关键字对哈希函数来说称为。
4、在一棵二叉排序树上实施遍历后,其关键字序列是一个有序表。
5、在散列存储中,装填因子α的值越大,则存取元素时发生冲突的可能性就越大;α值越小,则存取元素发生冲突的可能性就越小。
三、判断题
(×)1、折半查找只适用于有序表,包括有序的顺序表和链表。
()2、二叉排序树的任意一棵子树中,关键字最小的结点必无左孩子,关键字最大的结点必无右孩子。
()3、哈希表的查找效率主要取决于哈希表造表时所选取的哈希函数和处理冲突的方法。
()4、平衡二叉树是指左右子树的高度差的绝对值不大于1的二叉树。
(√)5、AVL是一棵二叉树,其树上任一结点的平衡因子的绝对值不大于1。
四、综合题
1、选取哈希函数H(k)=(k)MOD 11。用二次探测再散列处理冲突,试在0-10的散列地址空间中对关键字序列(22,41,53,46,30,13,01,67)造哈希表,并求等概率情况下查找成功时的平均查找长度。
答案:(1)表形态: 0
22
110112461313245673038411953110
(2)ASL:ASL(7)=(1*5+2*1+3*1)/7=(5+2+3)/7=10/7
数据结构试卷 数据结构试题库集及答案
2、设哈希表HT表长m为13,哈希函数为H(k)=k MOD m,给定的关键值序列为{19,14,23,10,68,20,84,27,55,11}。(www.61k.com)试求出用线性探测法解决冲突时所构造的哈希表,并求出在等概率的情况下查找成功的平均查找长度ASL。 答案:(1)表形态:
1141
2272
3681
4552
5
6191
7201
8843
9
10231
11102
12112
(2)平均查找长度:ASL(10)=(1*5+2*4+3*1)/10=1.6
3、设散列表容量为7(散列地址空间0..6),给定表(30,36,47,52,34),散列函数H(K)=K mod 6,采用线性探测法解决冲突,要求: (1)构造散列表;
(2)求查找数34需要比较的次数。 答案:(1)表形态:
0301
1262
2
3
4521
5471
6343
(2)查找34 的比较次数:3

1-9,请标出各结点的值。
答案:
5
19
616
27
5、若依次输入序列{62,68,30,61,25,14,53,47,90,84}中的元素,生成一棵二叉排序树。画出生成后的二叉排序树(不需画出生成过程)。
6、设有一组关键字{19,1,23,14,55,20,84,27,68,11,10,77},采用哈希函数H(key)=key MOD 13,采用开放地址法的二次探测再散列方法解决冲突,试在0-18的散列空间中对关键字序列构造哈希表,画出哈希表,并求其查找成功时的平均查找长度。
7、已知关键字序列{11,2,13,26,5,18,4,9},设哈希表表长为16,哈希函数H(key)=key MOD 13,处理冲突的方法为线性探测法,请给出哈希表,并计算在等概率的条件下的平均查找长度。
8、设散列表的长度为m=13,散列函数为H(k)=k MOD m,给定的关键码序列为19,14,23,1,68,20,84,27,55,11,13,7,试写出用线性探查法解决冲突时所构造的散列表。 答案:表形态:
38
数据结构试卷 数据结构试题库集及答案
0131
1141
212
3681
4274
5553
6191
7201
8843
973
10231
11111
12
9、依次读入给定的整数序列{7,16,4,8,20,9,6,18,5},构造一棵二叉排序树,并计算在等概率情况下该二叉排序树的平均查找长度ASL。(www.61k.com)(要求给出构造过程)
10、设有一组关键字(19,1,23,14,55,20,84,27,68,11,10,77),采用哈希函数H(key)=key%13,采用二次探测再散列的方法解决冲突,试在0-18的散列地址空间中对该关键字序列构造哈希表。 答案:
0273
111
2142
3551
4682
5843
6191
7201
8
9103
10231
11111
12771
13
14
15
16
17
18
第十章 内部排序
一、选择题
1、若需要在O(nlog2n)的时间内完成对数组的排序,且要求排序是稳定的,则可选择的排序方法是()。
A. 快速排序 B. 堆排序 C. 归并排序 D. 直接插入排序 2、下列排序方法中()方法是不稳定的。
A. 冒泡排序 B.选择排序 C. 堆排序 D. 直接插入排序
3、一个序列中有10000个元素,若只想得到其中前10个最小元素,则最好采用()方法。
A. 快速排序 B.堆排序 C.插入排序 D.归并排序 4、一组待排序序列为(46,79,56,38,40,84),则利用堆排序的方法建立的初始堆为()。
A. 79,46,56,38,40,80 B. 84,79,56,38,40,46 C. 84,79,56,46,40,38 D. 84,56,79,40,46,38 5、快速排序方法在()情况下最不利于发挥其长处。
A. 要排序的数据量太大 B.要排序的数据中有多个相同值 C. 要排序的数据已基本有序 D. 要排序的数据个数为奇数
6、排序时扫描待排序记录序列,顺次比较相邻的两个元素的大小,逆序时就交换位置,这是()排序的基本思想。
A. 堆排序 B. 直接插入排序 C. 快速排序 D. 冒泡排序 7、在任何情况下,时间复杂度均为O(nlogn)的不稳定的排序方法是()。 A.直接插入 B. 快速排序 C. 堆排序 D. 归并排序 8、如果将所有中国人按照生日来排序,则使用()算法最快。
A. 归并排序 B.希尔排序 C.快速排序 D.基数排序 9、在对n个元素的序列进行排序时,堆排序所需要的附加存储空间是()。
A. O(log2n) B. O(1) C. O(n) D. O(nlog2n)
10、排序方法中,从未排序序列中依次取出元素与已排序序列中的元素进行比较,将其放入已排序序列的正确位置上的方法,称为()。
A. 希尔排序 B. 冒泡排序 C. 插入排序 D.选择排序 11、一组记录的的序列未(46,79,56,38,40,84),则利用堆排序的方法建立的初始堆为()。
A. 79,46,56,38,40,80 B. 84,79,56,38,40,46 C. 84,79,56,46,40,38 D. 84,56,79,40,46,38
12、用某种排序方法对线性表( 25,84,21,47,15,27,68,35,20)进行排序时,元素序列的变化情况如下:
? 25,84,21,47,15,27,68,35,20 ? 20,15,21,25,47,27,68,35,84 ? 15,20,21,25,35,27,47,68,84 ? 15,20,21,25,27,35,47,68,84 则所采用的排序方法是()。 A. 选择排序 B. 希尔排序 C. 归并排序 D. 快速排序 13、设有1024个无序的元素,希望用最快的速度挑选出其中前5个最大的元素,最好选用()。 A.冒泡排序 B. 选择排序 C.快速排序 D.堆排序
数据结构试卷 数据结构试题库集及答案
14、下列排序方法中,平均时间性能为O(nlogn)且空间性能最好的是()。[www.61k.com]
A. 快速排序 B.堆排序 C. 归并排序
15、希尔排序的增量序列必须是()。
A.递增的 B. 递减的 C.随机的 D.非递减的
二、填空题
1、在插入和选择排序中,若初始数据基本正序,则选用,若初始数据基本反序,则选用。
答案:递增排列 递减排列 D. 基数排序
2、在插入排序、希尔排序、选择排序、快速排序、堆排序、归并排序和基数排序中,排序是不稳定的有。
三、判断题
1、直接选择排序是一种稳定的排序方法。?
2、快速排序在所有排序方法中最快,而且所需附加空间也最少。?
3、直接插入排序是不稳定的排序方法。?
4、选择排序是一种不稳定的排序方法。
四、程序分析题
五、综合题
1、写出用直接插入排序将关键字序列{54,23,89,48,64,50,25,90,34}排序过程的每一趟结果。
答案:初始: 54,23,89,48,64,50,25,90,34
1:(23,54),89,48,64,50,25,90,34
2:(23,54,89),48,64,50,25,90,34
3:(23,48,54,89),64,50,25,90,34
4:(23,48,54,64,89),50,25,90,34
5:(23,48,50,54,64,89),25,90,34
6:(23,25,48,50,54,64,89),90,34
7:(23,25,48,50,54,64,89,90),34
8:(23,25,48,50,54,64,89,90,34)
2、设待排序序列为{10,18,4,3,6,12,1,9,15,8}请写出希尔排序每一趟的结果。增量序列为5,3,2,1。 答案:初始: 10,18,4,3,6,12,1,9,15,8
d=5: 10,1,4,3,6,12,18,9,15,8
d=3: 3,1,4,8,6,12,10,9,15,18
d=2: 3,1,4,8,6,9,10,12,15,18
d=1: 1,3,4,6,8,9,10,12,15,18
3、已知关键字序列{418,347,289,110,505,333,984,693,177},按递增排序,求初始堆(画出初始堆的状态)。
答案:418,347,289,110,505,333,984,693,177

4、有一关键字序列(265,301,751,129,937,863,742,694,076,438),写出希尔排序的每趟排序结果。(取增量为5,3,1)
答案:
初始: 265,301,751,129,937,863,742,694,076,438
d=5: 265,301,694,076,438,863,742,751,129,937
d=3: 076,301,129,265,438,694,742,751,863,937
d=1: 076,129,265,301,438,694,742,751,863,937
数据结构试卷 数据结构试题库集及答案
5、对于直接插入排序,希尔排序,冒泡排序,快速排序,直接选择排序,堆排序和归并排序等排序方法,分别写出: (1)平均时间复杂度低于O(n2)的排序方法; (2)所需辅助空间最多的排序方法;
答案:(1) 希尔、快速、堆、归并 (2) 归并
6、对关键子序列(72,87,61,23,94,16,05,58)进行堆排序,使之按关键字递减次序排列(最小堆),请写出排序过程中得到的初始堆和前三趟的序列状态。[www.61k.com) 答案:

05

05
23
94
72
16
61
87
第2趟
87235905
94
61
16
05
87
59
94
23
61
16
05
87
59
94
72
61
16
第3趟
59728705
94
2361
16
第一章概论自测题答案
一、填空题
1. 数据结构被形式地定义为(D, R),其中D是数据元素的有限集合,R是D上的关系有限集合。 2. 数据结构包括数据的、数据的和数据的这三个方面的内容。 3. 数据结构按逻辑结构可分为两大类,它们分别是线性结构和非线性结构。
4. 线性结构中元素之间存在关系,树形结构中元素之间存在关系,图形结构中元素之间存在关系。 5.在线性结构中,第一个结点前驱结点,其余每个结点有且只有 1个前驱结点;最后一个结点后续结点,其余每个结点有且只有1个后续结点。
6. 在树形结构中,树根结点没有前驱结点,其余每个结点有且只有个前驱结点;叶子结点没有后续结点,其余每个结点的后续结点数可以任意多个。
7. 在图形结构中,每个结点的前驱结点数和后续结点数可以任意多个。
8.数据的存储结构可用四种基本的存储方法表示,它们分别是顺序、链式、索引和散列。 9. 数据的运算最常用的有5种,它们分别是。 10. 一个算法的效率可分为时间效率和空间效率。
11.任何一个C程序都由和若干个被调用的其它函数组成。
二、单项选择题
(B)1. 非线性结构是数据元素之间存在一种:
A)一对多关系 B)多对多关系 C)多对一关系 D)一对一关系
( C )2. 数据结构中,与所使用的计算机无关的是数据的结构;
A)存储 B)物理 C)逻辑 D)物理和存储
(C)3. 算法分析的目的是:
A)找出数据结构的合理性 B)研究算法中的输入和输出的关系 C) 分析算法的效率以求改进 D)分析算法的易懂性和文档性
(A)4. 算法分析的两个主要方面是:
A)空间复杂性和时间复杂性 B)正确性和简明性
C)可读性和文档性 D)数据复杂性和程序复杂性
(C )5. 计算机算法指的是:
A)计算方法 B) 排序方法 C)解决问题的有限运算序列 D)调度方法
(B)6. 计算机算法必须具备输入、输出和等5个特性。
A)可行性、可移植性和可扩充性 B)可行性、确定性和有穷性 C)确定性、有穷性和稳定性 D)易读性、稳定性和安全性
三、简答题
数据结构试卷 数据结构试题库集及答案
1.数据结构和数据类型两个概念之间有区别吗?
答:简单地说,数据结构定义了一组按某些关系结合在一起的数组元素。[www.61k.com)数据类型不仅定义了一组带结构的数据元素,而且还在其上定义了一组操作。
2. 简述线性结构与非线性结构的不同点。
答:线性结构反映结点间的逻辑关系是一对一的,非线性结构反映结点间的逻辑关系是多对多的。
四、分析下面各程序段的时间复杂度
1. for (i=0; i<n; i++)
for (j=0; j<m; j++)
A[i][j]=0;
答:O(m*n)
3. x=0;
for(i=1; i<n; i++)
for (j=1; j<=n-i; j++) x++;
解:因为x++共执行了n-1+n-2+??+1=
2
n(n-1)/2 ,所以执行时间为)
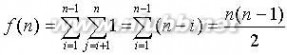
2. s=0;
for i=0; i<n; i++)
for(j=0; j<n; j++) s+=B[i][j]; sum=s;
答:O(n2)
4. i=1;
while(i<=n) i=i*3; 答:O(log3n)
第2章自测卷答案
一、填空
1.在顺序表中插入或删除一个元素,需要平均移动表中一半元素,具体移动的元素个数与表长和该元素在表中的位置有关。
2. 线性表中结点的集合是有限的,结点间的关系是一对一的。
3. 向一个长度为n的向量的第i个元素(1≤i≤n+1)之前插入一个元素时,需向后移动个元素。 4. 向一个长度为n的向量中删除第i个元素(1≤i≤n)时,需向前移动个元素。
5. 在顺序表中访问任意一结点的时间复杂度均为,因此,顺序表也称为的数据结构。
6.顺序表中逻辑上相邻的元素的物理位置相邻。单链表中逻辑上相邻的元素的物理位置相邻。 7.在单链表中,除了首元结点外,任一结点的存储位置由指示。
8.在n个结点的单链表中要删除已知结点*p,需找到它的,其时间复杂度为。
二、判断正误
(×)1. 链表的每个结点中都恰好包含一个指针。
答:错误。链表中的结点可含多个指针域,分别存放多个指针。例如,双向链表中的结点可以含有两个指针域,分别存放指向
其直接前趋和直接后继结点的指针。
(×)2.链表的物理存储结构具有同链表一样的顺序。错,链表的存储结构特点是无序,而链表的示意图有序。
(×)3.链表的删除算法很简单,因为当删除链中某个结点后,计算机会自动地将后续的各个单元向前移动。错,链表的
结点不会移动,只是指针内容改变。
(×)4.线性表的每个结点只能是一个简单类型,而链表的每个结点可以是一个复杂类型。
错,混淆了逻辑结构与物理结构,链表也是线性表!且即使是顺序表,也能存放记录型数据。
(×)5. 顺序表结构适宜于进行顺序存取,而链表适宜于进行随机存取。
错,正好说反了。顺序表才适合随机存取,链表恰恰适于“顺藤摸瓜”
(×)6. 顺序存储方式的优点是存储密度大,且插入、删除运算效率高。
错,前一半正确,但后一半说法错误,那是链式存储的优点。顺序存储方式插入、删除运算效率较低,在表长为n的顺序表中,插入和删除一个数据元素,平均需移动表长一半个数的数据元素。
(×)7. 线性表在物理存储空间中也一定是连续的。
错,线性表有两种存储方式,顺序存储和链式存储。后者不要求连续存放。
(×)8. 线性表在顺序存储时,逻辑上相邻的元素未必在存储的物理位置次序上相邻。
错误。线性表有两种存储方式,在顺序存储时,逻辑上相邻的元素在存储的物理位置次序上也相邻。
(×)9. 顺序存储方式只能用于存储线性结构。
错误。顺序存储方式不仅能用于存储线性结构,还可以用来存放非线性结构,例如完全二叉树是属于非线性结构,但其最佳存储方式是顺序存储方式。(后一节介绍)
(×)10. 线性表的逻辑顺序与存储顺序总是一致的。
数据结构试卷 数据结构试题库集及答案
错,理由同7。[www.61k.com]链式存储就无需一致。
三、单项选择题
( C)1.数据在计算机存储器内表示时,物理地址与逻辑地址相同并且是连续的,称之为:
(A)存储结构(B)逻辑结构(C)顺序存储结构(D)链式存储结构
(B )2.一个向量第一个元素的存储地址是100,每个元素的长度为2,则第5个元素的地址是
(A)110 (B)108 (C)100 (D)120
(A )3. 在n个结点的顺序表中,算法的时间复杂度是O(1)的操作是:
(A) 访问第i个结点(1≤i≤n)和求第i个结点的直接前驱(2≤i≤n)
(B) 在第i个结点后插入一个新结点(1≤i≤n)
(C) 删除第i个结点(1≤i≤n)
(D) 将n个结点从小到大排序
(B )4. 向一个有127个元素的顺序表中插入一个新元素并保持原来顺序不变,平均要移动个元素
(A)8 (B)63.5 (C)63 (D)7
( A )5. 链接存储的存储结构所占存储空间:
(A) 分两部分,一部分存放结点值,另一部分存放表示结点间关系的指针
(B) 只有一部分,存放结点值
(C)只有一部分,存储表示结点间关系的指针
(D)分两部分,一部分存放结点值,另一部分存放结点所占单元数
(B )6. 链表是一种采用存储结构存储的线性表;
(A)顺序(B)链式(C)星式(D)网状
(D)7. 线性表若采用链式存储结构时,要求内存中可用存储单元的地址:
(A)必须是连续的(B)部分地址必须是连续的
(C)一定是不连续的(D)连续或不连续都可以
(B)8.线性表L在情况下适用于使用链式结构实现。
(A)需经常修改L中的结点值(B)需不断对L进行删除插入
(C)L中含有大量的结点(D)L中结点结构复杂
(C)9.单链表的存储密度
(A)大于1;(B)等于1;(C)小于1;(D)不能确定
(B )10.设a1、a2、a3为3个结点,整数P0,3,4代表地址,则如下的链式存储结构称为
3 4
P
P0 ?

?

?

(A)循环链表(B)单链表(C)双向循环链表(D)双向链表
四、简答题
1.试比较顺序存储结构和链式存储结构的优缺点。在什么情况下用顺序表比链表好?
答:①顺序存储时,相邻数据元素的存放地址也相邻(逻辑与物理统一);要求内存中可用存储单元的地址必须是连续的。
优点:存储密度大(=1?),存储空间利用率高。缺点:插入或删除元素时不方便。
②链式存储时,相邻数据元素可随意存放,但所占存储空间分两部分,一部分存放结点值,另一部分存放表示结点间关系的指针 优点:插入或删除元素时很方便,使用灵活。缺点:存储密度小(<1)

,存储空间利用率低。
顺序表适宜于做查找这样的静态操作;链表宜于做插入、删除这样的动态操作。
若线性表的长度变化不大,且其主要操作是查找,则采用顺序表;
若线性表的长度变化较大,且其主要操作是插入、删除操作,则采用链表。

2 .描述以下三个概念的区别:头指针、头结点、首元结点(第一个元素结点)。在单链表中设置头结点的作用是什么?
答:首元结点是指链表中存储线性表中第一个数据元素a1的结点。为了操作方便,通常在链表的首元结点之前附设一个结点,称为头结点,该结点的数据域中不存储线性表的数据元素,其作用是为了对链表进行操作时,可以对空表、非空表的情况以及对首元结点进行统一处理。头指针是指向链表中第一个结点(或为头结点或为首元结点)的指针。若链表中附设头结点,则不管线性表是否为空表,头指针均不为空。否则表示空表的链表的头指针为空。这三个概念对单链表、双向链表和循环链表均适用。是否设置头结点,是不同的存储结构表示同一逻辑结构的问题。
? 简而言之,
数据结构试卷 数据结构试题库集及答案
头指针是指向链表中第一个结点(或为头结点或为首元结点)的指针; 头结点是在链表的首元结点之前附设的一个结点;数据域内只放空表标志和表长等信息(内放头指针?那还得另配一个头指针!!!) 首元素结点是指链表中存储线性表中第一个数据元素a1的结点。[www.61k.com)
五、线性表具有两种存储方式,即顺序方式和链接方式。现有一个具有五个元素的线性表L={23,17,47,05,31},若它以链接方式存储在下列100~119号地址空间中,每个结点由数据(占2个字节)和指针(占2个字节)组成,如下所示:
p->data=i; /* input data is saved */
p->link=(test*)malloc(m); /*m=sizeof(test));*/
q=p;
p=p->link;
}
q->link=NULL; /*原先用p->link=NULL似乎太晚!*/
p=head; i=0; /*统计链表结点的个数并打印出来*/
while (p->link!=NULL)
{printf("%d",p->data);
p=p->link;
i++;
}
printf("\n node number=%d\n", i-1);/*结点的个数不包括-9999*/
数据结构试卷 数据结构试题库集及答案

}
第3章栈和队列自测卷答案
一、填空题 1.向量、栈和队列都是结构,可以在向量的位置插入和删除元素;对于栈只能在插入和删除元素;对于队列只能在队尾插入和队首删除元素。[www.61k.com) 2. 栈是一种特殊的线性表,允许插入和删除运算的一端称为。不允许插入和删除运算的一端称为。
3. 队列是被限定为只能在表的一端进行插入运算,在表的另一端进行删除运算的线性表。
4. 在一个循环队列中,队首指针指向队首元素的位置。
5. 在具有n个单元的循环队列中,队满时共有个元素。
6. 向栈中压入元素的操作是先,后。
7. 从循环队列中删除一个元素时,其操作是先。
8.带表头结点的空循环双向链表的长度等于。
解:
head (×)1.
错,线性表是逻辑结构概念,可以顺序存储或链式存储,与元素数据类型无关。
(×)2.在表结构中最常用的是线性表,栈和队列不太常用。
错,不一定吧?调用子程序或函数常用,CPU中也用队列。
(√)3. 栈是一种对所有插入、删除操作限于在表的一端进行的线性表,是一种后进先出型结构。
(√)4.对于不同的使用者,一个表结构既可以是栈,也可以是队列,也可以是线性表。
正确,都是线性逻辑结构,栈和队列其实是特殊的线性表,对运算的定义略有不同而已。
(×)5.栈和链表是两种不同的数据结构。
错,栈是逻辑结构的概念,是特殊殊线性表,而链表是存储结构概念,二者不是同类项。
(×)6.栈和队列是一种非线性数据结构。
错,他们都是线性逻辑结构,栈和队列其实是特殊的线性表,对运算的定义略有不同而已。
(√)7. 栈和队列的存储方式既可是顺序方式,也可是链接方式。
(√)8. 两个栈共享一片连续内存空间时,为提高内存利用率,减少溢出机会,应把两个栈的栈底分别设在这片内存空
间的两端。
(×)9. 队是一种插入与删除操作分别在表的两端进行的线性表,是一种先进后出型结构。
错,后半句不对。
(×)10. 一个栈的输入序列是12345,则栈的输出序列不可能是12345。
错,有可能。
三、单项选择题
( B)1.栈中元素的进出原则是
A.先进先出B.后进先出C.栈空则进D.栈满则出
(C)2.若已知一个栈的入栈序列是1,2,3,?,n,其输出序列为p1,p2,p3,?,pn,若p1=n,则pi为
A.iB.n=iC.n-i+1D.不确定
解释:当p1=n,即n是最先出栈的,根据栈的原理,n必定是最后入栈的(事实上题目已经表明了),那么输入顺序必定是1,2,3,?,n,则出栈的序列是n,?,3,2,1。
(若不要求顺序出栈,则输出序列不确定)
(B)3.判定一个栈ST(最多元素为m0)为空的条件是
A.ST->top<>0B.ST->top=0C.ST->top<>m0D.ST->top=m0
( A)4.判定一个队列QU(最多元素为m0)为满队列的条件是
A.QU->rear - QU->front = = m0B.QU->rear - QU->front -1= = m0
C.QU->front = = QU->rearD.QU->front = = QU->rear+1
解:队满条件是元素个数为m0。由于约定满队时队首指针与队尾指针相差1,所以不必再减1了,应当选A。当然,更正确的答案应该取模,即:QU->front = = (QU->rear+1)% m0
(D)5.数组Q[n]用来表示一个循环队列,f为当前队列头元素的前一位置,r为队尾元素的位置,假定队列中元
素的个数小于n,计算队列中元素的公式为
(A)r-f;(B)(n+f-r)%n; (C)n+r-f;(D)(n+r-f)%n
6. 从供选择的答案中,选出应填入下面叙述?内的最确切的解答,把相应编号写在答卷的对应栏内。
设有4个数据元素a1、a2、a3和a4,对他们分别进行栈操作或队操作。在进栈或进队操作时,按a1、a2、a3、a4次序每次进入一个元素。假设栈或队的初始状态都是空。
数据结构试卷 数据结构试题库集及答案
现要进行的栈操作是进栈两次,出栈一次,再进栈两次,出栈一次;这时,第一次出栈得到的元素是 A ,第二次出栈得到的元素是 B 是;类似地,考虑对这四个数据元素进行的队操作是进队两次,出队一次,再进队两次,出队一次;这时,第一次出队得到的元素是 C ,第二次出队得到的元素是 D 。[www.61k.com]经操作后,最后在栈中或队中的元素还有 E个。
供选择的答案:
A~D:①a1②a2③a3④a4
E:①1 ②2 ③3 ④0
答:ABCDE=2, 4, 1, 2, 2
7.
栈是一种线性表,它的特点是 A 。设用一维数组A[1,…,n]来表示一个栈,A[n]为栈底,用整型变量T指示当前栈顶位置,A[T]为栈顶元素。往栈中推入(PUSH)一个新元素时,变量T的值 B ;从栈中弹出(POP)一个元素时,变量T的值 C 。设栈空时,有输入序列a,b,c,经过PUSH,POP,PUSH,PUSH,POP操作后,从栈中弹出的元素的序列是 D ,变量T的值是 E 。
供选择的答案:
A:①先进先出②后进先出 ③进优于出 ④出优于进 ⑤随机进出
B,C: ①加1 ②减1 ③不变 ④清0 ⑤加2 ⑥减2
D:①a,b②b,c ③c,a ④b,a ⑤ c,b ⑥ a,c
E:① n+1 ②n+2 ③ n ④ n-1 ⑤ n-2
答案:ABCDE=2,2,1,6,4
注意,向地址的高端生长,称为向上生成堆栈;向地址低端生长叫向下生成堆栈,本题中底部为n,向地址的低端递减生成,称为向下生成堆栈。
8.
在做进栈运算时,应先判别栈是否 A ;在做退栈运算时,应先判别栈是否 B 。当栈中元素为n个,做进栈运算时发生上溢,则说明该栈的最大容量为 C 。
为了增加内存空间的利用率和减少溢出的可能性,由两个栈共享一片连续的内存空间时,应将两栈的 D 分别设在这片内存空间的两端,这样,只有当 E 时,才产生上溢。
供选择的答案:
A,B:①空②满③上溢④下溢
C: ①n-1②n③n+1④n/2
D:①长度②深度③栈顶④栈底
E:①两个栈的栈顶同时到达栈空间的中心点②其中一个栈的栈顶到达栈空间的中心点
③两个栈的栈顶在达栈空间的某一位置相遇④两个栈均不空,且一个栈的栈顶到达另一个栈的栈底
答案:ABCDE=2, 1, 2, 4, 3
四、简答题
1.说明线性表、栈与队的异同点。
刘答:相同点:都是线性结构,都是逻辑结构的概念。都可以用顺序存储或链表存储;栈和队列是两种特殊的线性表,即受限的线性表,只是对插入、删除运算加以限制。
不同点:①运算规则不同,线性表为随机存取,而栈是只允许在一端进行插入、删除运算,因而是后进先出表LIFO;队列是只允许在一端进行插入、另一端进行删除运算,因而是先进先出表FIFO。
②用途不同,堆栈用于子程调用和保护现场,队列用于多道作业处理、指令寄存及其他运算等等。
2.设有编号为1,2,3,4的四辆列车,顺序进入一个栈式结构的车站,具体写出这四辆列车开出车站的所有可能的顺序。
刘答:至少有14种。
①全进之后再出情况,只有1种:4,3,2,1
②进3个之后再出的情况,有3种,3,4,2,1 3,2,4,1 3,2,1,4
③进2个之后再出的情况,有5种,2,4,3,1 2,3,4,1 2,1, 3,4 2,1,4,3 2,1,3,4
④进1个之后再出的情况,有5种,1,4,3,2 1,3,2,4 1,3,4,2 1, 2,3,4 1,2,4,3
3.顺序队的“假溢出”是怎样产生的?如何知道循环队列是空还是满?
答:一般的一维数组队列的尾指针已经到了数组的上界,不能再有入队操作,但其实数组中还有空位置,这就叫“假溢出”。
采用循环队列是解决假溢出的途径。
另外,解决队满队空的办法有三:
① 设置一个布尔变量以区别队满还是队空;
② 浪费一个元素的空间,用于区别队满还是队空。
③ 使用一个计数器记录队列中元素个数(即队列长度)。
我们常采用法②,即队头指针、队尾指针中有一个指向实元素,而另一个指向空闲元素。
判断循环队列队空标志是: f=rear 队满标志是:f=(r+1)%N
数据结构试卷 数据结构试题库集及答案
4.设循环队列的容量为40(序号从0到39),现经过一系列的入队和出队运算后,有
① front=11,rear=19; ② front=19,rear=11;问在这两种情况下,循环队列中各有元素多少个?
答:用队列长度计算公式: (N+r-f)% N
① L=(40+19-11)% 40=8 ② L=(40+11-19)% 40=32
第4~5章串和数组自测卷答案
一、填空题(每空1分,共20分)
1. 称为空串;称为空白串。(www.61k.com]
(对应严题集4.1①,简答题:简述空串和空格串的区别)
2. 设S=“A;/document/Mary.doc”,则strlen(s)=, “/”的字符定位的位置为。
4. 子串的定位运算称为串的模式匹配;被匹配的主串称为目标串,子串称为模式。
5. 设目标T=”abccdcdccbaa”,模式P=“cdcc”,则第次匹配成功。
6. 若n为主串长,m为子串长,则串的古典(朴素)匹配算法最坏的情况下需要比较字符的总次数为。
7. 假设有二维数组A6×8,每个元素用相邻的6个字节存储,存储器按字节编址。已知A的起始存储位置(基地址)为1000,则数组A的体积(存储量)为;末尾元素A57的第一个字节地址为1282 ;若按行存储时,元素A14的第一个字节地址为(8+4)×6+1000=1072;若按列存储时,元素A47的第一个字节地址为(6×7+4)×6+1000)=。
(注:数组是从0行0列还是从1行1列计算起呢?由末单元为A57可知,是从0行0列开始!)
8.设数组a[1?60, 1?70]的基地址为2048,每个元素占2个存储单元,若以列序为主序顺序存储,则元素a[32,58]的存储地址为8950。
答:不考虑0行0列,利用列优先公式:LOC(aij)=LOC(ac1,c2)+[(j-c2)*(d1-c1+1)+i-c1)]*L
得:LOC(a32,58)=2048+[(58-1)*(60-1+1)+32-1]]*2=8950
9. 三元素组表中的每个结点对应于稀疏矩阵的一个非零元素,它包含有三个数据项,分别表示该元素
的行下标、列下标和元素值。
10.求下列广义表操作的结果:
(1)GetHead【((a,b),(c,d))】===(a, b); //头元素不必加括号
(2)GetHead【GetTail【((a,b),(c,d))】】===(c,d);
(3)GetHead【GetTail【GetHead【((a,b),(c,d))】】】===b;
(4)GetTail【GetHead【GetTail【((a,b),(c,d))】】】===(d);
二、单选题(每小题1分,共15分)
(B)1.串是一种特殊的线性表,其特殊性体现在:
A.可以顺序存储B.数据元素是一个字符
C.可以链式存储D.数据元素可以是多个字符
(B)2.设有两个串p和q,求q在p中首次出现的位置的运算称作:
A.连接B.模式匹配C.求子串D.求串长
(D )3.设串s1=?ABCDEFG?,s2=?PQRST?,函数con(x,y)返回x和y串的连接串,subs(s,i,j)返回串s的从序号i开始的j个字符组成的子串,len(s)返回串s的长度,则con(subs(s1,2,len(s2)),subs(s1,len(s2),2))的结果串是:
A.BCDEF B.BCDEFG C.BCPQRST D.BCDEFEF
解:con(x,y)返回x和y串的连接串,即con(x,y)=‘ABCDEFGPQRST’;
subs(s,i,j)返回串s的从序号i开始的j个字符组成的子串,则
subs(s1,2,len(s2))=subs(s1,2, 5)=? BCDEF?; subs(s1,len(s2),2)=subs(s1,5, 2)=? EF?;
所以con(subs(s1,2,len(s2)),subs(s1,len(s2),2))=con(? BCDEF?, ? EF?)之连接,即BCDEFEF
(A )4.假设有60行70列的二维数组a[1?60, 1?70]以列序为主序顺序存储,其基地址为10000,每个元素占2个存储单元,那么第32行第58列的元素a[32,58]的存储地址为。(无第0行第0列元素)
数据结构试卷 数据结构试题库集及答案
A.16902 B.16904 C.14454 D.答案A, B, C均不对
答:此题与填空题第8小题相似。(www.61k.com)(57列×60行+31行)×2字节+10000=16902
( B )5. 设矩阵A是一个对称矩阵,为了节省存储,将其下三角部分(如下图所示)按行序存放在一维数组B[ 1, n(n-
1)/2 ]中,对下三角部分中任一元素ai,j(i≤j),在一维数组B中下标k的值是:
A.i(i-1)/2+j-1B.i(i-1)/2+jC.i(i+1)/2+j-1D.i(i+1)/2+j

?a1,1?a2,1A???????an,1a2,2an,2??????an,n??
6.
有一个二维数组A,行下标的范围是0到8,列下标的范围是1到5,每个数组元素用相邻的4个字节存储。存储器按字节编址。假设存储数组元素A[0,1]的第一个字节的地址是0。
存储数组A的最后一个元素的第一个字节的地址是 A 。若按行存储,则A[3,5]和A[5,3]的第一个字节的地址分别是
和。若按列存储,则A[7,1]和A[2,4]的第一个字节的地址分别是。
供选择的答案:
A~E:①28 ② 44 ③ 76 ④ 92 ⑤ 108
⑥ 116 ⑦ 132 ⑧ 176 ⑨ 184 ⑩ 188
答案:ABCDE=8, 3, 5, 1, 6
7. 有一个二维数组A,行下标的范围是1到6,列下标的范围是0到7,每个数组元素用相邻的6个字节存储,存储器按字节编址。那么,这个数组的体积是 A 个字节。假设存储数组元素A[1,0]的第一个字节的地址是0,则存储数组A的最后一个元素的第一个字节的地址是 B 。若按行存储,则A[2,4]的第一个字节的地址是 C 。若按列存储,则A[5,7]的第一个字节的地址是
供选择的答案
A~D:①12 ② 66 ③ 72 ④ 96 ⑤ 114 ⑥ 120
⑦ 156 ⑧ 234 ⑨ 276 ⑩ 282 (11)283 (12)288
答案:ABCD=12, 10, 3, 9
第6章树和二叉树自测卷解答
一、下面是有关二叉树的叙述,请判断正误(每小题1分,共10分)
(√)1. 若二叉树用二叉链表作存贮结构,则在n个结点的二叉树链表中只有n—1个非空指针域。
(×)2.二叉树中每个结点的两棵子树的高度差等于1。
(√)3.二叉树中每个结点的两棵子树是有序的。
(×)4.二叉树中每个结点有两棵非空子树或有两棵空子树。
(×)5.二叉树中每个结点的关键字值大于其左非空子树(若存在的话)所有结点的关键字值,且小于其右非空子树
(若存在的话)所有结点的关键字值。(应当是二叉排序树的特点)
k-1(×)6.二叉树中所有结点个数是2-1,其中k是树的深度。(应2i-1)
(×)7.二叉树中所有结点,如果不存在非空左子树,则不存在非空右子树。
(×)8.对于一棵非空二叉树,它的根结点作为第一层,则它的第i层上最多能有2i—1个结点。(应2i-1)
(√)9.用二叉链表法(link-rlink)存储包含n个结点的二叉树,结点的2n个指针区域中有n+1个为空指针。
(正确。用二叉链表存储包含n个结点的二叉树,结点共有2n个链域。由于二叉树中,除根结点外,每一个结点有且仅有一个双亲,所以只有n-1个结点的链域存放指向非空子女结点的指针,还有n+1个空指针。)即有后继链接的指针仅n-1个。
(√)10.具有12个结点的完全二叉树有5个度为2的结点。
最快方法:用叶子数=[n/2]=6,再求n2=n0-1=5
二、填空(每空1分,共15分)
1.由3个结点所构成的二叉树有种形态。
2. 一棵深度为6的满二叉树有6-1个叶子。
注:满二叉树没有度为1
3.一棵具有257个结点的完全二叉树,它的深度为。
数据结构试卷 数据结构试题库集及答案
(注:用? log2(n) ?+1= ? 8.xx ?+1=9
4. 设一棵完全二叉树有700个结点,则共有个叶子结点。[www.61k.com)
答:最快方法:用叶子数=[n/2]=350
5. 设一棵完全二叉树具有1000个结点,则此完全二叉树有个叶子结点,有个度为2的结点,有个结点只有非空左子树,有0个结点只有非空右子树。
答:最快方法:用叶子数=[n/2]=500,n2=n0-1=499。另外,最后一结点为2i属于左叶子,右叶子是空的,所以有1个非空左子树。完全二叉树的特点决定不可能有左空右不空的情况,所以非空右子树数=0.
6.一棵含有n个结点的k叉树,可能达到的最大深度为,最小深度为。
答:当k=1(单叉树)时应该最深,深度=n(层);当k=n-1(n-1叉树)时应该最浅,深度=2(层),但不包括n=0或1时的特例情况。教材答案是“完全k叉树”,未定量。)
7.二叉树的基本组成部分是:根(D)、左子树(L)和右子树(R)。因而二叉树的遍历次序有六种。最常用的是三种:前序法(即按N L R次序),后序法(即按L R D次序)和中序法(也称对称序法,即按L N R次序)。这三种方法相互之间有关联。若已知一棵二叉树的前序序列是BEFCGDH,中序序列是FEBGCHD,则它的后序序列必是F E G H D C 。解:法1:先由已知条件画图,再后序遍历得到结果;
法2:不画图也能快速得出后序序列,只要找到根的位置特征。由
前序先确定root,由中序先确定左子树。例如,前序遍历BEFCGDH
中,根结点在最前面,是B;则后序遍历中B一定在最后面。
法3:递归计算。如B在前序序列中第一,中序中在中间(可知左
右子树上有哪些元素),则在后序中必为最后。如法对B的左右子树同
样处理,则问题得解。
8.中序遍历的递归算法平均空间复杂度为O(n)。
答:即递归最大嵌套层数,即栈的占用单元数。精确值应为树的深度
k+1,包括叶子的空域也递归了一次。
9.用5个权值{3, 2, 4, 5, 1}构造的哈夫曼(Huffman)树的带权路径长度是。
解:先构造哈夫曼树,得到各叶子的路径长度之后便可求出WPL=(4+5+3)×2+(1+2)×3=33
(注:两个合并值先后不同会导致编码不同,即哈夫曼编码不唯一)
3 (注:合并值应排在叶子值之后)
1 2
(注:原题为选择题:A.32 B.33 C.34 D.15)
三、单项选择题(每小题1分,共11分)
(C)1.不含任何结点的空树。
(A)是一棵树;(B)是一棵二叉树;
(C)是一棵树也是一棵二叉树;(D)既不是树也不是二叉树
答:以前的标答是B,因为那时树的定义是n≥1
(C)2.二叉树是非线性数据结构,所以。
(A)它不能用顺序存储结构存储;(B)它不能用链式存储结构存储;
(C)顺序存储结构和链式存储结构都能存储;(D)顺序存储结构和链式存储结构都不能使用
( C)3. 具有n(n>0)个结点的完全二叉树的深度为。
(A) ?log2(n)?(B) ? log2(n)?(C) ? log2(n) ?+1(D) ?log2(n)+1?
注1:?x?表示不小于x的最小整数;?x?表示不大于x的最大整数,它们与[ ]含义不同!
注2:选(A)是错误的。例如当n为2的整数幂时就会少算一层。似乎? log2(n) +1?是对的?
(A)4.把一棵树转换为二叉树后,这棵二叉树的形态是。
(A)唯一的(B)有多种
(C)有多种,但根结点都没有左孩子(D)有多种,但根结点都没有右孩子
数据结构试卷 数据结构试题库集及答案
5.
树是结点的有限集合,它A 根结点,记为T。[www.61k.com)其余的结点分成为m(m≥0)个 B
的集合T1,T2,?,Tm,每个集合又都是树,此时结点T称为Ti的父结点,Ti称为T的子结点(1≤i≤m)。一个结点的子结点个数为该结点的 C 。
供选择的答案
A:①有0个或1个②有0个或多个③有且只有1个④有1个或1个以上
B: ①互不相交 ②允许相交③允许叶结点相交④允许树枝结点相交
C:①权 ②维数③次数(或度)④序
答案:ABC=1,1,3
6.
二叉树 A 。在完全的二叉树中,若一个结点没有 B ,则它必定是叶结点。每棵树都能惟一地转换成与它对应的二叉树。由树转换成的二叉树里,一个结点N的左子女是N在原树里对应结点的 C ,而N的右子女是它在原树里对应结点的 D 。
供选择的答案
A:①是特殊的树②不是树的特殊形式③是两棵树的总称④有是只有二个根结点的树形结构
B: ①左子结点②右子结点③左子结点或者没有右子结点④兄弟
C~D:①最左子结点②最右子结点③最邻近的右兄弟④最邻近的左兄弟
⑤最左的兄弟⑥最右的兄弟
答案:A= B= C= D=
答案:ABCDE=2,1,1,3
四、简答题(每小题4分,共20分)
1. 一棵度为2的树与一棵二叉树有何区别?
答:度为2的树从形式上看与二叉树很相似,但它的子树是无序的,而二叉树是有序的。即,在一般树中若某结点只有一个孩子,就无需区分其左右次序,而在二叉树中即使是一个孩子也有左右之分。
2.给定二叉树的两种遍历序列,分别是:
前序遍历序列:D,A,C,E,B,H,F,G,I;中序遍历序列:D,C,B,E,H,A,G,I,F,
试画出二叉树B,并简述由任意二叉树B的前序遍历序列和中序遍历序列求二叉树B的思想方法。
解:方法是:由前序先确定root,由中序可确定root的左、右子树。然后由其左子树的元素集合和右子树的集合对应前序遍历序列中的元素集合,可继续确定root的左右孩子。将他们分别作为新的root,不断递归,则所有元素都将被唯一确定,问题得解。
D A
F
G
B H I
下面是按先序遍历的思路建立二叉树的两种方法
#include <stdio.h>
#include <stdlib.h>
#define MAX 100
typedef struct node {
char data;
struct node *lchild, *rchild;
} Bitree;
void creatree1( Bitree *&bt)
{ char ch;
if (ch==??) bt=NULL
else
{ bt=(Bitree*)malloc(sizeof(Bitree));
bt-data=ch;
数据结构试卷 数据结构试题库集及答案
creatree1(bt->lchild);
creatree2(bt->rhcild);
}
}
Bitree *creatree2()
{ char ch; Bitree *&bt
if (ch==??) bt=NULL
else
{ bt=(Bitree*)malloc(sizeof(Bitree));
bt-data=ch;
bt->lchild= creatree2();
bt->rhcild= creatree2();
}
return bt;
}
第6章树和二叉树自测卷解答
一、下面是有关二叉树的叙述,请判断正误(每小题1分,共10分)
(√)1. 若二叉树用二叉链表作存贮结构,则在n个结点的二叉树链表中只有n—1个非空指针域。(www.61k.com]
(×)2.二叉树中每个结点的两棵子树的高度差等于1。
(√)3.二叉树中每个结点的两棵子树是有序的。
(×)4.二叉树中每个结点有两棵非空子树或有两棵空子树。
(×)5.二叉树中每个结点的关键字值大于其左非空子树(若存在的话)所有结点的关键字值,且小于其右非空子树
(若存在的话)所有结点的关键字值。(应当是二叉排序树的特点)
k-1(×)6.二叉树中所有结点个数是2-1,其中k是树的深度。(应2i-1)
(×)7.二叉树中所有结点,如果不存在非空左子树,则不存在非空右子树。
(×)8.对于一棵非空二叉树,它的根结点作为第一层,则它的第i层上最多能有2i—1个结点。(应2i-1)
(√)9.用二叉链表法(link-rlink)存储包含n个结点的二叉树,结点的2n个指针区域中有n+1个为空指针。
(正确。用二叉链表存储包含n个结点的二叉树,结点共有2n个链域。由于二叉树中,除根结点外,每一个结点有且仅有一个双亲,所以只有n-1个结点的链域存放指向非空子女结点的指针,还有n+1个空指针。)即有后继链接的指针仅n-1个。
(√)10.具有12个结点的完全二叉树有5个度为2的结点。
最快方法:用叶子数=[n/2]=6,再求n2=n0-1=5
二、填空(每空1分,共15分)
1.由3个结点所构成的二叉树有种形态。
2. 一棵深度为6的满二叉树有1220个分支结点和6-1个叶子。
注:满二叉树没有度为1的结点,所以分支结点数就是二度结点数。
3.一棵具有257个结点的完全二叉树,它的深度为。
(注:用? log2(n) ?+1= ? 8.xx ?+1=9
4. 设一棵完全二叉树有700个结点,则共有个叶子结点。
答:最快方法:用叶子数=[n/2]=350
5. 设一棵完全二叉树具有1000个结点,则此完全二叉树有个叶子结点,有个度为2的结点,有个结点只有非空左子树,有0个结点只有非空右子树。
答:最快方法:用叶子数=[n/2]=500,n2=n0-1=499。另外,最后一结点为2i属于左叶子,右叶子是空的,所以有1个非空左子树。完全二叉树的特点决定不可能有左空右不空的情况,所以非空右子树数=0.
6.一棵含有n个结点的k叉树,可能达到的最大深度为,最小深度为。
答:当k=1(单叉树)时应该最深,深度=n(层);当k=n-1(n-1叉树)时应该最浅,深度=2(层),但不包括n=0或1时的特例情况。教材答案是“完全k叉树”,未定量。)
数据结构试卷 数据结构试题库集及答案
7.二叉树的基本组成部分是:根(N)、左子树(L)和右子树(R)。[www.61k.com)因而二叉树的遍历次序有六种。最常用的是三种:前序法(即按N L R次序),后序法(即按L R N次序)和中序法(也称对称序法,即按L N R次序)。这三种方法相互之间有关联。若已知一棵二叉树的前序序列是BEFCGDH,中序序列是FEBGCHD,则它的后序序列必是F E G H D C 。解:法1:先由已知条件画图,再后序遍历得到结果;
法2:不画图也能快速得出后序序列,只要找到根的位置特征。由
前序先确定root,由中序先确定左子树。例如,前序遍历BEFCGDH
中,根结点在最前面,是B;则后序遍历中B一定在最后面。
法3:递归计算。如B在前序序列中第一,中序中在中间(可知左
右子树上有哪些元素),则在后序中必为最后。如法对B的左右子树同
样处理,则问题得解。
8.中序遍历的递归算法平均空间复杂度为O(n)。
答:即递归最大嵌套层数,即栈的占用单元数。精确值应为树的深度
k+1,包括叶子的空域也递归了一次。
9.用5个权值{3, 2, 4, 5, 1}构造的哈夫曼(Huffman)树的带权路径长度是。
解:先构造哈夫曼树,得到各叶子的路径长度之后便可求出WPL=(4+5+3)×2+(1+2)×3=33
(注:两个合并值先后不同会导致编码不同,即哈夫曼编码不唯一)
3 (注:合并值应排在叶子值之后)
1 2
(注:原题为选择题:A.32 B.33 C.34 D.15)
1.深度为k的完全二叉树至少有( 2k-1 )个结点,至多有(2k -1)个结点,若按自上而下,从左到右次序给结点编号(从1开始),则编号最小的叶子结点的编号是(2k-1 -1+1= 2k-1)
log(n+1)-12.一棵二叉树的第i(i>=1)层最多有(2i-1 )个结点,一棵有n(n>0)个结点的满二叉树共有( 22 )个叶子结点
和(22 -1 )个非叶子结点。
3.现有按中序遍历二叉树的结果是abc,问有( 5 )种不同形态的二叉树可以得到这一遍历结果,这些二叉树分别是( )。
4.以数据集{4,5,6,7,10,12,18}为结点权值所构造的哈夫曼树为( ),其带权路径长度为( )。
5.具有10个叶子结点的哈夫曼树,最大高度为( 10 ),最小高度为( 5)。
n个叶子结点的哈夫曼树,最大高度为n,(除最上一层和最下一层每层一个叶子点),最小高度为log2n +1 log(n+1)-1
三、单项选择题(每小题1分,共11分)
1.某二叉树的先序遍历序列和后序遍历序列正好相反,则该二叉树一定是(D )
A.空或只有一个结点 B、完全二叉树 C、二叉排序树 D、高度等于其结点数
2.设高度为h的二叉树上只有度为0和度为2的结点,则此类二叉树中所包含的结点数至少为( B )
A.2h B.2h-1 C.2h+1 D.h+1
除根结点层只有1个结点外,其余h-1层均有两个结点,结点总数=2(h-1)+1=2h-1.
3.对一个满二叉树,m个树叶,n个结点,深度为h,则( D)
A.n=h+m B.h+m=2n C.m=h-1 D.n=2h-1
4.根据使用频率为5的字符设计的哈夫曼编码不可能是( C )
A.111,110,10,01,00 B、000,001,010,011,1
C.100,11,10,1,0 D、001,000,01,11,10
C中,100和10冲突,即一个结点既是叶子结点又是内部结点,哈夫曼树中不可能出现这种情况。
5.根据使用频率为5的字符设计的哈夫曼编码不可能是( D )
A、000,001,010,011,1 B、0000,0001,001,01,1
C.000,001,01,10,11 D、00,100,101,110,111
哈夫曼树中只有度为0或度为2的结点,D不满足这种条件。
(C)1.不含任何结点的空树。
数据结构试卷 数据结构试题库集及答案
(A)是一棵树;(B)是一棵二叉树;
(C)是一棵树也是一棵二叉树;(D)既不是树也不是二叉树
答:以前的标答是B,因为那时树的定义是n≥1
(C)2.二叉树是非线性数据结构,所以。(www.61k.com]
(A)它不能用顺序存储结构存储;(B)它不能用链式存储结构存储;
(C)顺序存储结构和链式存储结构都能存储;(D)顺序存储结构和链式存储结构都不能使用
( C)3. 具有n(n>0)个结点的完全二叉树的深度为。
(A) ?log2(n)?(B) ? log2(n)?(C) ? log2(n) ?+1(D) ?log2(n)+1?
注1:?x?表示不小于x的最小整数;?x?表示不大于x的最大整数,它们与[ ]含义不同!
注2:选(A)是错误的。例如当n为2的整数幂时就会少算一层。似乎? log2(n) +1?是对的?
(A)4.把一棵树转换为二叉树后,这棵二叉树的形态是。
(A)唯一的(B)有多种
(C)有多种,但根结点都没有左孩子(D)有多种,但根结点都没有右孩子
5.从供选择的答案中,选出应填入下面叙述?内的最确切的解答,把相应编号写在答卷的对应栏内。
树是结点的有限集合,它A 根结点,记为T。其余的结点分成为m(m≥0)个 B
的集合T1,T2,?,Tm,每个集合又都是树,此时结点T称为Ti的父结点,Ti称为T的子结点(1≤i≤m)。一个结点的子结点个数为该结点的 C 。
供选择的答案
A:①有0个或1个②有0个或多个③有且只有1个④有1个或1个以上
B: ①互不相交 ②允许相交③允许叶结点相交④允许树枝结点相交
C:①权 ②维数③次数(或度)④序
答案:ABC=1,1,3
6.从供选择的答案中,选出应填入下面叙述?内的最确切的解答,把相应编号写在答卷的对应栏内。
二叉树 A 。在完全的二叉树中,若一个结点没有 B ,则它必定是叶结点。每棵树都能惟一地转换成与它对应的二叉树。由树转换成的二叉树里,一个结点N的左子女是N在原树里对应结点的 C ,而N的右子女是它在原树里对应结点的 D 。
供选择的答案
A:①是特殊的树②不是树的特殊形式③是两棵树的总称④有是只有二个根结点的树形结构
B: ①左子结点②右子结点③左子结点或者没有右子结点④兄弟
C~D:①最左子结点②最右子结点③最邻近的右兄弟④最邻近的左兄弟
⑤最左的兄弟⑥最右的兄弟
答案:A= B= C= D=
答案:ABCDE=2,1,1,3
四、简答题(每小题4分,共20分)
1. 一棵度为2的树与一棵二叉树有何区别?
答:度为2的树从形式上看与二叉树很相似,但它的子树是无序的,而二叉树是有序的。即,在一般树中若某结点只有一个孩子,就无需区分其左右次序,而在二叉树中即使是一个孩子也有左右之分。 2.〖01年计算机研题〗设如下图所示的二叉树B的存储结构为二叉链表,
root为根指针,结点结构为:(lchild,data,rchild)。其中lchild,rchild分别为指向左右孩子的指针,data为字符型,root为根指针,试回答下列问题: 1. 对下列二叉树B,执行下列算法traversal(root),试指出其输出结果; 2. 假定二叉树B共有n个结点,试分析算法traversal(root)的时间复杂度。(共8分)

数据结构试卷 数据结构试题库集及答案
二叉树B
解:这是“先根再左再根再右”,比前序遍历多打印各结点一次,输出结果为:A BC C E E B A D F F D G G
特点:①每个结点肯定都会被打印两次;②但出现的顺序不同,其规律是:凡是有左子树的结点,必间隔左子树的全部结点后再重复出现;如A,B,D等结点。[www.61k.com)反之马上就会重复出现。如C,E,F,G等结点。
时间复杂度以访问结点的次数为主,精确值为2*n,时间渐近度为O(n).
3. 〖01年计算机研题〗【严题集6.27③】给定二叉树的两种遍历序列,分别是:
前序遍历序列:D,A,C,E,B,H,F,G,I;中序遍历序列:D,C,B,E,H,A,G,I,F,
试画出二叉树B,并简述由任意二叉树B的前序遍历序列和中序遍历序列求二叉树B的思想方法。
解:方法是:由前序先确定root,由中序可确定root的左、右子树。然后由其左子树的元素集合和右子树的集合对应前序遍历序列中的元素集合,可继续确定root的左右孩子。将他们分别作为新的root,不断递归,则所有元素都将被唯一确定,问题得解。
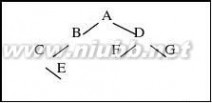
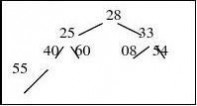
D A



F



G
B H I
4.【计算机研2000】给定如图所示二叉树T解:要遵循中序遍历的轨迹来画出每个前驱和后继。 中序遍历序列:55 40 25 60 28 08 33 54 33
五、阅读分析题(每题5分,共20分)
1. (P60 4-26)试写出如图所示的二叉树分别按先序、中序、后序遍历时得到的结点序列。
答:DLR:ABDFJGKCEHILM
LDR: BFJDGKACHELIM
LRD:JFKGDBHLMIECA
数据结构试卷 数据结构试题库集及答案
2. (P60 4-27)把如图所示的树转化成二叉树。[www.61k.com)
答:注意全部兄弟之间都要连线(包括度为2的兄弟),并注意原有连线结点一律归入左子树,新添连线结点一律归入右
子树。 A B
数据结构试卷 数据结构试题库集及答案
法二:
int LeafCount_BiTree(Bitree T)//求二叉树中叶子结点的数目
{
if(!T) return 0; //空树没有叶子
else if(!T->lchild&&!T->rchild) return 1; //叶子结点
else return Leaf_Count(T->lchild)+Leaf_Count(T->rchild);//左子树的叶子数加
上右子树的叶子数
}//LeafCount_BiTree
注:上机时要先建树!例如实验二的方案一。[www.61k.com)
① 打印叶子结点值(并求总数)
思路:先建树,再从遍历过程中打印结点值并统计。
步骤1 键盘输入序列12,8,17,11,16,2,13,9,21,4,构成一棵二叉排序树。叶子结点值应该是4,9, 13, 21, 总数应该是4.
12 7 17
11 21
编程:生成二叉树排序树之后,再中序遍历排序查找结点的完整程序如下:
说明部分为:
#include <stdio.h>
#include <stdlib.h>
typedef struct liuyu{int data;struct liuyu *lchild,*rchild;}test;
liuyu *root;
int sum=0;int m=sizeof(test);
void insert_data(int x) /*如何生成二叉排序树?参见教材P43C程序*/
{ liuyu *p,*q,*s;
s=(test*)malloc(m);
s->data=x;
s->lchild=NULL;
s->rchild=NULL;
if(!root){root=s; return;}
p=root;
while(p) /*如何接入二叉排序树的适当位置*/
{q=p;
if(p->data==x){printf("data already exist! \n");return;}
else if(x<p->data)p=p->lchild; else p=p->rchild;
}
if(x<q->data)q->lchild=s;
else q->rchild=s;
}
DLR(liuyu *root) /*中序遍历递归函数*/
{if(root!=NULL)
{if((root->lchild==NULL)&&(root->rchild==NULL)){sum++; printf("%d\n",root->data);}
DLR(root->lchild);
DLR(root->rchild); }
return(0);
}
main() /*先生成二叉排序树,再调用中序遍历递归函数进行排序输出*/
{int i,x;
i=1;
root=NULL; /*千万别忘了赋初值给root!*/
do{printf("please input data%d:",i);
i++;
scanf("%d",&x); /*从键盘采集数据,以-9999表示输入结束*/
if(x==-9999){
数据结构试卷 数据结构试题库集及答案
DLR(root);
printf("\nNow output count value:%d\n",sum);
return(0); }
else insert_data(x);} /*调用插入数据元素的函数*/
while(x!=-9999);
return(0);}
执行结果:
若一开始运行就输入-9999,则无叶子输出,sum=0。[www.61k.com)
2.【全国专升本统考题】写出求二叉树深度的算法,先定义二叉树的抽象数据类型。(10分) 或【严题集6.44④】编写递归算法,求二叉树中以元素值为x的结点为根的子树的深度。
答;设计思路:只查后继链表指针,若左或右孩子的左或右指针非空,则层次数加1;否则函数返回。 但注意,递归时应当从叶子开始向上计数,否则不易确定层数。
int depth(liuyu*root) /*统计层数*/
{int d,p; /*注意每一层的局部变量d,p都是各自独立的*/
p=0;
if(root==NULL)return(p); /*找到叶子之后才开始统计*/
else{
d=depth(root->lchild);
if(d>p) p=d; /*向上回朔时,要挑出左右子树中的相对大的那个深度值*/
d=depth(root->rchild);
if(d>p)p=d;
}
p=p+1;
return(p);
}
法二:
int Get_Sub_Depth(Bitree T,int x)//求二叉树中以值为x的结点为根的子树深度
{
if(T->data==x)
{
printf("%d\n",Get_Depth(T)); //找到了值为x的结点,求其深度
exit 1;
}
}
else
{
if(T->lchild) Get_Sub_Depth(T->lchild,x);
if(T->rchild) Get_Sub_Depth(T->rchild,x); //在左右子树中继续寻找
}
}//Get_Sub_Depth
int Get_Depth(Bitree T)//求子树深度的递归算法
{

数据结构试卷 数据结构试题库集及答案
if(!T) return 0;
else
{
m=Get_Depth(T->lchild);
n=Get_Depth(T->rchild);
return (m>n?m:n)+1;
}
}//Get_Depth
附:上机调试过程
步骤1 键盘输入序列12,8,17,11,16,2,13,9,21,4,构成一棵二叉排序树。(www.61k.com)层数应当为4
步骤2:执行求深度的函数,并打印统计出来的深度值。
完整程序如下:
#include <stdio.h>
#include <stdlib.h>
typedef struct liuyu{int data;struct liuyu *lchild,*rchild;}test;
liuyu *root;
int sum=0;int m=sizeof(test);
void insert_data(int x) /*如何生成二叉排序树?参见教材P43C程序*/
{ liuyu *p,*q,*s;
s=(test*)malloc(m);
s->data=x;
s->lchild=NULL;
s->rchild=NULL;
if(!root){root=s; return;}
p=root;
while(p) /*如何接入二叉排序树的适当位置*/
{q=p;
if(p->data==x){printf("data already exist! \n");return;}
else if(x<p->data)p=p->lchild; else p=p->rchild;
}
if(x<q->data)q->lchild=s;
else q->rchild=s;
}
int depth(liuyu*root) /*统计层数*/
{int d,p; /*注意每一层的局部变量d,p都是各自独立的*/
p=0;
if(root==NULL)return(p); /*找到叶子之后才开始统计*/
else{
d=depth(root->lchild);
if(d>p) p=d; /*向上回朔时,要挑出左右子树中的相对大的那个深度值*/
d=depth(root->rchild);
if(d>p)p=d;
}
p=p+1;
return(p);
}
void main() /*先生成二叉排序树,再调用深度遍历递归函数进行统计并输出*/ {int i,x;
i=1;

数据结构试卷 数据结构试题库集及答案
root=NULL; /*千万别忘了赋初值给root!*/
do{printf("please input data%d:",i);
i++;
scanf("%d",&x); /*从键盘采集数据,以-9999表示输入结束*/
if(x==-9999){
printf("\nNow output depth value=%d\n", depth (root)); return; }
else insert_data(x);} /*调用插入数据元素的函数*/
while(x!=-9999);
return;}
执行结果:

3. 【严题集6.47④】编写按层次顺序(同一层自左至右)遍历二叉树的算法。(www.61k.com)
或:按层次输出二叉树中所有结点;
解:思路:既然要求从上到下,从左到右,则利用队列存放各子树结点的指针是个好办法。
这是一个循环算法,用while语句不断循环,直到队空之后自然退出该函数。
技巧之处:当根结点入队后,会自然使得左、右孩子结点入队,而左孩子出队时又会立即使得它的左右孩子结点入队,??以此产生了按层次输出的效果。
level(liuyu*T)
/* liuyu *T,*p,*q[100]; 假设max已知*/
{int f,r;
f=0; r=0; /*置空队*/
r=(r+1)%max;
q[r]=T; /*根结点进队*/
while(f!=r) /*队列不空*/
{f=(f+1%max);
p=q[f]; /*出队*/
printf("%d",p->data); /*打印根结点*/
if(p->lchild){r=(r+1)%max; q[r]=p->lchild;} /*若左子树不空,则左子树进队*/
if(p->rchild){r=(r+1)%max; q[r]=p->rchild;} /*若右子树不空,则右子树进队*/
}
return(0);
}
法二:
void LayerOrder(Bitree T)//层序遍历二叉树
{
InitQueue(Q); //建立工作队列
EnQueue(Q,T);
while(!QueueEmpty(Q))
{
DeQueue(Q,p);
visit(p);
if(p->lchild) EnQueue(Q,p->lchild);
if(p->rchild) EnQueue(Q,p->rchild);
}
}//LayerOrder
数据结构试卷 数据结构试题库集及答案
可以用前面的函数建树,然后调用这个函数来输出。(www.61k.com]
完整程序如下(已上机通过)
#include <stdio.h>
#include <stdlib.h>
#define max 50
typedef struct liuyu{int data;struct liuyu *lchild,*rchild;}test;
liuyu *root,*p,*q[max];
int sum=0;int m=sizeof(test);
void insert_data(int x) /*如何生成二叉排序树?参见教材P43C程序*/
{ liuyu *p,*q,*s;
s=(test*)malloc(m);
s->data=x;
s->lchild=NULL;
s->rchild=NULL;
if(!root){root=s; return;}
p=root;
while(p) /*如何接入二叉排序树的适当位置*/
{q=p;
if(p->data==x){printf("data already exist! \n");return;}
else if(x<p->data)p=p->lchild; else p=p->rchild;
}
if(x<q->data)q->lchild=s;
else q->rchild=s;
}
level(liuyu*T)
/* liuyu *T,*p,*q[100]; 假设max已知*/
{int f,r;
f=0; r=0; /*置空队*/
r=(r+1)%max;
q[r]=T; /*根结点进队*/
while(f!=r) /*队列不空*/
{f=(f+1%max);
p=q[f]; /*出队*/
printf("%d",p->data); /*打印根结点*/
if(p->lchild){r=(r+1)%max; q[r]=p->lchild;} /*若左子树不空,则左子树进队*/
if(p->rchild){r=(r+1)%max; q[r]=p->rchild;} /*若右子树不空,则右子树进队*/
}
return(0);
}
void main() /*先生成二叉排序树,再调用深度遍历递归函数进行统计并输出*/
{int i,x;
i=1;
root=NULL; /*千万别忘了赋初值给root!*/
do{printf("please input data%d:",i);
i++;
scanf("%d",&x); /*从键盘采集数据,以-9999表示输入结束*/
if(x==-9999){
printf("\nNow output data value:\n", level(root)); return; }
else insert_data(x);} /*调用插入数据元素的函数*/
while(x!=-9999);
return;}
4.已知一棵具有n个结点的完全二叉树被顺序存储于一维数组A中,试编写一个算法打印出编号为i的结点的双亲和所有的孩子。
数据结构试卷 数据结构试题库集及答案
答:首先,由于是完全二叉树,不必担心中途会出现孩子为null的情况。(www.61k.com)
其次分析:结点i的左孩子为2i,右孩子为2i+1;直接打印即可。
Printf(“Left_child=”, %d, v[2*i].data; “Right_child=”, %d, v[2*i+1].data;);
但其双亲是i/2,需先判断i为奇数还是偶数。若i为奇数,则应当先i--,然后再除以2。
If(i/2!=0)i--;
Printf(“Parents=”, %d, v[i/2].data;);
5.【严题集6.49④】编写算法判别给定二叉树是否为完全二叉树。
答:int IsFull_Bitree(Bitree T)//判断二叉树是否完全二叉树,是则返回1,否则返回0
{
InitQueue(Q);
flag=0;
EnQueue(Q,T); //建立工作队列
while(!QueueEmpty(Q))
{
{
DeQueue(Q,p);
if(!p) flag=1;
else if(flag) return 0;
else
{
EnQueue(Q,p->lchild);
EnQueue(Q,p->rchild); //不管孩子是否为空,都入队列
}
}//while
return 1;
}//IsFull_Bitree
分析:该问题可以通过层序遍历的方法来解决.与6.47相比,作了一个修改,不管当前结点
是否有左右孩子,都入队列.这样当树为完全二叉树时,遍历时得到是一个连续的不包含空
指针的序列.反之,则序列中会含有空指针.
6. 【严题集6.26③】假设用于通信的电文仅由8个字母组成,字母在电文中出现的频率分别为0.07,0.19,0.02,0.06,
0.32,0.03,0.21,0.10。试为这8个字母设计哈夫曼编码。使用0~7的二进制表示形式是另一种编码方案。对于上述实例,比较两种方案的优缺点。
解:方案1;哈夫曼编码
先将概率放大100倍,以方便构造哈夫曼树。
w={7,19,2,6,32,3,21,10},按哈夫曼规则:【[(2,3),6], (7,10)】,??19,21,32
(100) (40)(60)
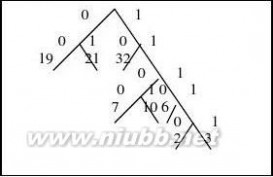
28) (1711) 5) 3
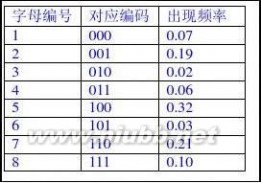
方案比较:
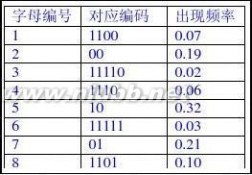
方案1的WPL=2(0.19+0.32+0.21)+4(0.07+0.06+0.10)+5(0.02+0.03)=1.44+0.92+0.25=2.61
方案2的WPL=3(0.19+0.32+0.21+0.07+0.06+0.10+0.02+0.03)=3
数据结构试卷 数据结构试题库集及答案
结论:哈夫曼编码优于等长二进制编码
1. 二叉树采用链接存储结构,设计算法计算一棵给定二叉树的度为2的结点数.
方法1:
int f(bitree T)
{ int num1,num2;
if (T==NULL) return 0;
else
{ num1=f(T->lchild); nmu2=f(T->rchild);
If (T->lchild && T->rchild) return (num1+num2+1);
Else return(num1+num2);
}
}
方法2:
void f(bitree T, int &n)
{ if (T)
{ If (T->lchild && T->rchild) n++;
f(T->lchild,n);
f(T->rchild,n);
}
}
2. 采用二叉链表的形式存储二叉树,编写一个算法判定两棵二叉树是否相似.
int like(bitree S, bitree T )
{ if (S==NULL && T=NULL) return (1);
else if (S && T)
return (like(S->lchild,T->lchild) && like(S->rchild,T->rchild));
else return 0;
}
3. 给定一棵用链表表示的二叉树,编写算法判定一棵二叉树T是否是完全二叉树.
采用层次遍历的思想解决这一问题.设置一个标志flag一旦某结点的左或右分支为空,则将flag置1.若此后遍历的结点的左、右分支都为空,则二叉树是完全二叉树,否则不是完全二叉树。(www.61k.com)
Int iscompletebit(bitree T)
{ queue Q[maxsize];
Int Flag=0;
Bitree p=T;
If (T==NULL) return 1;
Initqueue(Q);
Enqueue(Q,p);
While (!queueempty(Q))
{ dequeue(Q,p);
If (p->lchild && !flag) enqueue(Q,p->lchild);
Else
{ if (p->lchild ) return 0;
Else flag=1; }
If (T->rchild && !flag) enqueue(Q,p->rchild);
Else
{ if (p->rchild ) return 0;
Else flag=1; }
} Return 1;
}
4.已知一棵二叉树的中序遍历序列为CDBAEGF,前序遍历序列为ABCDEFG,试问能不能惟一确定一棵二叉树,若能请画出该二叉树。
第7章图自测卷解答
一、单选题(每题1分,共16分)
(C)1. 在一个图中,所有顶点的度数之和等于图的边数的倍。
数据结构试卷 数据结构试题库集及答案
A.1/2 B. 1 C. 2 D. 4
(B)2. 在一个有向图中,所有顶点的入度之和等于所有顶点的出度之和的倍。[www.61k.com)
A.1/2 B. 1 C. 2 D. 4
(B)3. 有8个结点的无向图最多有条边。
A.14 B. 28 C. 56 D. 112
(C)4. 有8个结点的无向连通图最少有条边。
A.5 B. 6 C. 7 D. 8
(C)5. 有8个结点的有向完全图有条边。
A.14 B. 28 C. 56 D. 112
(B)6. 用邻接表表示图进行广度优先遍历时,通常是采用来实现算法的。
A.栈 B. 队列 C. 树 D. 图
(A)7. 用邻接表表示图进行深度优先遍历时,通常是采用来实现算法的。
A.栈 B. 队列 C. 树 D. 图

8. 已知图的邻接矩阵,根据算法思想,则从顶点0出发按深度优先遍历的结点序列是
?0?1??1??1?1??0
??1111101?001001??000100??100110?011010??001101?100010??A.0 2 4 3 1 5 6 B. 0 1 3 6 5 4 2 C. 0 4 2 3 1 6 5 D. 0 3 6 1 5 4 2 建议:0 1 3 4 2 5 6
(D)9. 已知图的邻接矩阵同上题8,根据算法,则从顶点0出发,按深度优先遍历的结点序列是
A. 0 2 4 3 1 5 6 B. 0 1 3 5 6 4 2 C. 0 4 2 3 1 6 5 D. 0 1 3 4 2 5 6

10.已知图的邻接矩阵同上题8,根据算法,则从顶点0出发,按广度优先遍历的结点序列是
A. 0 2 4 3 6 5 1 B. 0 1 3 6 4 2 5 C. 0 4 2 3 1 5 6 D. 0 1 3 4 2 5 6
(建议:0 1 2 3 4 5 6)
(C)11. 已知图的邻接矩阵同上题8,根据算法,则从顶点0出发,按广度优先遍历的结点序列是
A. 0 2 4 3 1 6 5 B.

0 1 3 5 6 4 2 C. 0 1 2 3 4 6 5 D.
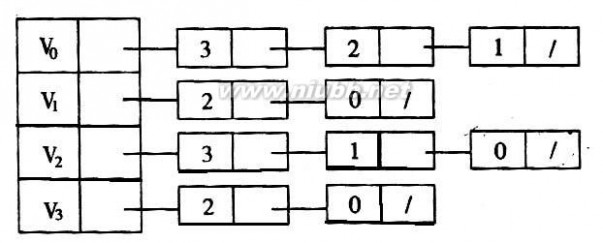
0 1 2 3 4 5 6
(D)12. 已知图的邻接表如下所示,根据算法,则从顶点0出发按深度优先遍历的结点序列是
A.0 1 3 2 B. 0 2 3 1
C. 0 3 2 1 D. 0 1 2 3
(A)13. 已知图的邻接表如下所示,根据算法,则从顶点0出发按广度优先遍历的结点序列是
A.0 3 2 1 B. 0 1 2 3
C. 0 1 3 2 D. 0 3 1 2
(A)14. 深度优先遍历类似于二叉树的
A.先序遍历B.中序遍历 C. 后序遍历D. 层次遍历
(D)15. 广度优先遍历类似于二叉树的
数据结构试卷 数据结构试题库集及答案
A.先序遍历B.中序遍历 C. 后序遍历D. 层次遍历
(A)16. 任何一个无向连通图的最小生成树
A.只有一棵B.一棵或多棵 C. 一定有多棵D. 可能不存在
(注,生成树不唯一,但最小生成树唯一,即边权之和或树权最小的情况唯一)
17、下面关于AOE网的叙述中,不正确的是()B
A.关键活动不按期完成就会影响整个工程的完成时间
B.任何一个关键活动提前完成,那么整个工程将会提前完成
C.所有的关键活动提前完成,那么整个工程将会提前完成
D.某个关键活动提前完成,那么整个工程将会提前完成
18、若邻接表中有奇数个表结点,则一定()D
A.图中有奇数个顶点 B、图中有偶数个顶点 C、图为无向图 D、图为有向图
19.在一个无向图中,所有顶点的度数之和等于所有边数的(B)倍,在一个有向图中,所有顶点的入度之和等于所有顶点出度之和的(C)。[www.61k.com)
A.1/2 B。2 C。1 D。4
20.若邻接表中的有奇数个表结点,则一定( D )
A.图中有奇数个顶点 B。图中有偶数个顶点 C。图为无向图 D。图为有向图
21.下面关于AOE网的叙述中,不正确的是( B )
A.关键活动不按期完成就会影响整个工程的完成时间
B.任何一个关键活动提前完成,那么整个工程将会提前完成
C.所有的关键活动提前完成,那么整个工程将会提前完成
D.某个关键活动提前完成,那么整个工程将会提前完成
二、填空题
1、29条边的无向连通图,至少有( 9 )个顶点,至多有( 30 )个顶点,有29条边的无向非连通图,至少有( 10 )个顶点。
2、n个顶点的强连通有向图G,最多有(n(n-1) ) 条边,最少有(n)边。
强连通图即是任何两个顶点之间有路径相通,当所有结点在一个环上时,必定是强连通图。
3、29条边的有向连通图,至少有(6 )个顶点,至多有(29 )个顶点,有29条边的有向非连通图,至少有( 7 )个顶点。
4、已知一个图的邻接矩阵表示,删除所有从第i个结点出发的边的方法是(将矩阵第i行全部置为0)
1. 图有、等存储结构,遍历图有、等方法。
2. 有向图G用邻接表矩阵存储,其第i行的所有元素之和等于顶点i的出度。
3. 如果n个顶点的图是一个环,则它有棵生成树。(以任意一顶点为起点,得到n-1条边)
4. n个顶点e条边的图,若采用邻接矩阵存储,则空间复杂度为2。
5. n个顶点e条边的图,若采用邻接表存储,则空间复杂度为。
6. 设有一稀疏图G,则G采用存储较省空间。
7. 设有一稠密图G,则G采用存储较省空间。
8. 图的逆邻接表存储结构只适用于图。
9. 已知一个有向图的邻接矩阵表示,删除所有从第i

10. 图的深度优先遍历序列惟一的。
11. n个顶点e条边的图采用邻接矩阵存储,深度优先遍历算法的时间复杂度为2;若采用邻接表存储时,该算法的
时间复杂度为O(n+e)。
12. n个顶点e条边的图采用邻接矩阵存储,广度优先遍历算法的时间复杂度为2;若采用邻接表存储,该算法的时
间复杂度为O(n+e)。
数据结构试卷 数据结构试题库集及答案
13. 若要求一个稀疏图G的最小生成树,最好用算法来求解。[www.61k.com]
14. 若要求一个稠密图G的最小生成树,最好用算法来求解。
15. 用Dijkstra算法求某一顶点到其余各顶点间的最短路径是按路径长度递增的次序来得到最短路径的。
16. 拓扑排序算法是通过重复选择具有个前驱顶点的过程来完成的。
三、简答题(每题6分,共24分)
1.请对下图的无向带权图:
(1) 写出它的邻接矩阵,并按普里姆算法求其最小生成树;
(2) 写出它的邻接表,并按克鲁斯卡尔算法求其最小生成树。
解:设起点为a。
?043??????
?40559???? ?3505???5?
??5507654?
??9?703??? ????6302?? ????5?206?
算法是将顶点归并:???54??60?PRIM??a, 依次归并的顶点集为:
{a},{a,c},{a,c,b},{a,c,b,d},{a,c,b,d,h},
{a,c,b,d,h,g},{a,c,b,d,h,g,f}, {a,c,b,d,h,g,f,e}。所得最小生成树如上。

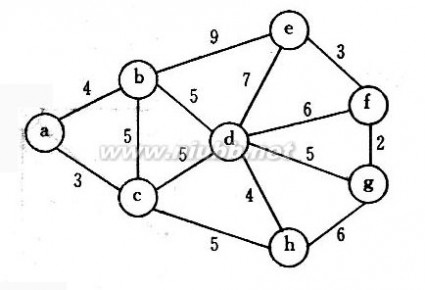
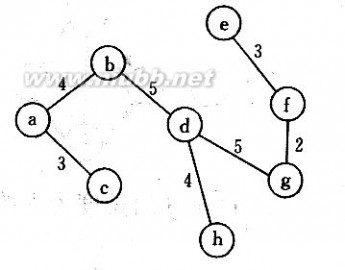

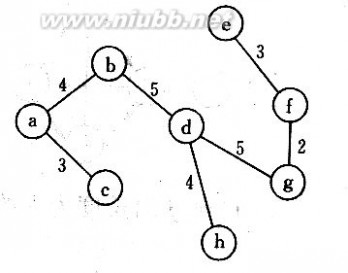
设初始顶点为克鲁斯卡尔算法是将连归并:依次归并的边集为:
{(f,g)}
{(f,g),(e,f)},
{ (f,g),(e,f) ,(a,c)},
{ (f,g),(e,f) ,(a,c) ,(a,b)},
{ (f,g),(e,f) ,(a,c) ,(a,b) ,(d,h)},
{ (f,g),(e,f) ,(a,c) ,(a,b) ,(d,h), (d,g)},
{ (f,g),(e,f) ,(a,c) ,(a,b) ,(d,h), (d,g),(b,d)},
{ (f,g),(e,f) ,(a,c) ,(a,b) ,(d,h), (d,g),(b,d), }, 所有的顶点同在一个连通分量上。
所得最小生成树如下。
数据结构试卷 数据结构试题库集及答案
第一章绪论
1.下面是几种数据的逻辑结构S=(D,R),分别画出对应的数据逻辑结构,并指出它们分别属于何种结构。(www.61k.com) D={a,b,c,d,e,f} R={r}
(a) r={<a,b>,<b,c>,<c,d>,<d,e>,<e,f>}
(b) r={<a,b>,<b,c>,<b,d>,<d,e>,<d,f>}
(c) r={<a,b>,<b,c>,<d,a>,<d,b>,<d,e>}
2.分析下列程序段的时间复杂度
(a) for(i=0;i<m;i++)
for(j=0;j<n;j++)
b[i][j]=0;
(b) s=0
for(i=0;i<n;i++)
for(j=0;j<n;j++)
s+=b[i][j];
(c) i=1
While(i<n)
i*=2;
3.在数据结构中,与所使用的计算机无关的是。
A.存储结构 B.物理结构 C.物理和存储结构 D.逻辑结构
4.非线性结构中每个结点。
A.无直接前驱结点 B.只有一个直接前驱和直接后继结点
C.无直接后继结点 D.可能有多个直接前驱和多个直接后继结点
5.可以把数据的逻辑结构划分成。
A.内部结构和外部结构 B.动态结构和静态结构
C.紧凑结构和非紧凑结构 D.线性结构和非线性结构
第二章线性表
一、单项选择题
1.下面关于线性表叙述中,错误的 是_(1)_。
(1):A.顺序表必须占用一片地址连续的存储单元
B.链表不必占用一片地址连续的存储单元
C.顺序表可以随机存取任一元素
D.链表可以随机存取任一元素
2.在表长为n的单链表中,算法时间复杂度为O(n)的操作是 (2)。
(2):A.查找单链表中第i个结点 B.在p结点之后插入一个结点
C.删除表中第一个结点 D.删除p结点的直接后继结点
3.单链表的存储密度 (3) 。
(3):A.大于1 B.等于1 C.小于1 D.不能确定
4.在表长为n的顺序表中,算法的时间复杂度为O(1)的操作是(4)。
(4):A.在第n个结点之后插入一个结点 B.在第i个结点前插入一个新结点
C.删除第i个结点 D.求表长
5.在下列链表中不能从当前结点出发访问到其余各结点的是(5)。
(5):A.单链表 B.单循环链表 C.双向链表 D.双向循环链表
6.在设头、尾指针的单链表中,与长度n有关的操作是(6)。
(6):A.删除第一个结点 B.删除最后一个结点
C.在第一个结点之前插入一个结点 D.在表尾结点后插入一个结点
7.设p结点是带表头结点的双循环链表中的结点,则
数据结构试卷 数据结构试题库集及答案
(1)在p结点后插入s结点的语句序列中正确的是 (7)。(www.61k.com]
(7):A.s->next=p->next;p->next->prior=s;
p->next=s;s->next=p->next;
B.p—>next=s;S—>next=p—>next;
p—>next—>prior=s;s—>next=p;
C.p->next=s;p—>next—>prior=s;
s->next=p—>next;S—>next=p;
D.p->next->prior=s;p->next=s;
s->next=p->next;s->next=p;
(2)在p结点之前插入s结点的语句序列中正确的是(8)。
(8):A.s->prior=p->prior;p->prior->next p->prior=s;s->next=p;
B.p->prior=s;p->prior->next=s;
s->prior=p->prior;s->next=p;
C.p->prior->next=s;p->prior=s;
s->prior=p->prior;s->next=p;
D.p->prior=s;s->next=p;
p->prior->next=s;s->prior=p->prior;
8.下列关于链表说法错误的是 (9) 。
(9):A.静态链表中存取每一个元素的时间相同
B.动态链表中存取每一个元素的时间不同
C.静态链表上插入或删除一个元素不必移动其他元素
D.动态链表上插入或删除一个元素不必移动其他元素
9.在链表中最常用的操作是在最后一个数据元素之后插入一个数据元素和删除第一个数据元素,则最节省运算时间的存储方式是 (10) 。
(10):A.仅有头指针的单链表B.仅有头指针的单循环链表
C.仅有头指针的双向链表 D.仅有尾指针的单循环链表
二、填空题
1.单链表中每个结点需要两个域,一个是数据域,另一个是 (1) 。
2.链表相对于顺序表的优点是 (2) 和 (3) 操作方便。
3.表长为n的顺序表中,若在第j个数据元素(1≤i≤n+1)之前插入一个数据元素,需要向后移动 (4) 个数据元素;删除第j个数据元素需要向前移动 (5) 个数据元素;在等概率的情况下,插入一个数据元素平均需要移动 (6) 个数据元素,删除一个数据元素平均需要移动 (7) 个数据元素。
4.单链表h为空表的条件是 (8) 。
5.带表头结点的单链表h为空表的条件是 (9) 。
6.在非空的单循环链表h中,某个p结点为尾结点的条件是 (10)。
7.在非空的双循环链表中,已知p结点是表中任一结点,则
(1)在p结点后插入s结点的语句序列是:
s->next=p->next;s->prior=p; (11) ; (12)
(2)在p结点前插入s结点的语句序列是:
s->prior=p->prior;s->next=p; (13) ; (14)
(3)删除p结点的直接后继结点的语句序列是:
q=p->next;p->next=q->next; (15) ;free(q);
(4)删除p结点的直接前驱结点的语句序列是:
q=p->prior;p->prior=q->prior; (16) ;free(q);
(5)删除p结点的语句序列是:
p->prior->next=p->next; (17) ;free(q);
8.在带有尾指针r的单循环链表中,在尾结点后插入p结点的语句序列是 (18) ; (19);删除第一个结点的语句序列是q=r->next; (20) ;free(q)。
三、应用题
1.简述顺序表和链表各自的优点。
2.简述头指针和头结点的作用。 .
四、算法设计题
1.请编写一个算法,实现将x插入到已按数据域值从小到大排列的有序表中。
2.设计一个算法,计算单链表中数据域值为x的结点个数。
3.设计一个用前插法建立带表头结点的单链表的算法。
数据结构试卷 数据结构试题库集及答案
4.请编写一个建立单循环链表的算法。(www.61k.com)
5.设计一个算法,实现将带头结点的单链表进行逆置。
6.编写一个算法,实现以较高的效率从有序顺序表A中删除其值在x和y之间(x≤A[i] ≤y)的所有元素。
第三章 栈和队列
一、选择题
1.插入和删除只能在表的一端进行的线性表,称为 (1) 。
(1):A.队列 B.循环队列 C.栈 D.双栈
2.队列操作应遵循的原则是 (2) 。
(2):A.先进先出 B.后进先出 C.先进后出 D.随意进出
3.栈操作应遵循的原则是 (3) 。
(3):A.先进先出 B.后进后出 C.后进先出 D.随意进出
4.设队长为n的队列用单循环链表表示且仅设头指针,则进队操作的时间复杂度为 (4) 。
2 (4):A.O(1) B.O(log2n) C.O(n) D.O(n)
5.设栈s和队列q均为空,先将a,b,c,d依次进队列q,再将队列q中顺次出队的元素进栈s,直至队空。再将栈s中的元素逐个出栈,并将出栈元素顺次进队列q,则队列q的状态是 (5) 。
(5):A.abcd B.dcba C.bcad D.dbca
6.若用一个大小为6的数组来实现循环队列,且当前front和rear的值分别为3和0,当从队列中删除一个元素,再加入两个元素后,front和rear的值分别为 (6) 。
(6):A.5和1 B.4和2 C.2和4 D.1和5
7.一个栈的入栈序列是a,b,c,d,e,。
(7):A.edcba B.decba C.dceab D.abcde
二、填空题
1.在栈结构中,允许插入、删除的一端称为 (1) ,另一端称为 (2) 。
2.在队列结构中,允许插入的一端称为 (3) ,允许删除的一端称为 (4) 。
3.设长度为n的链队列用单循环链表表示,若只设头指针,则进队和出队操作的时间复杂度分别是 (5) 和 (6) ;若只设尾指针,则进队和出队操作的时间复杂度分别为 (7) 和 (8) 。
4.设用少用一个元素空间的数组A[m]存放循环队列,front指向实际队首,rear指向新元素应存放的位置,则判断队空的条件是 (9) ,判断队满的条件是 (10) ,当队未满时,循环队列的长度是 (11) 。
5.两个栈共享一个向量空间时,可将两个栈底分别设在 (12) 。
三、应用题 .
1.简述线性表、栈和队列有什么异同?
2.循环队列的优点是什么?设用数组A[m]来存放循环队列,如何判断队满和队空。
3.若进栈序列为abcd,请给出全部可能的出栈序列和不可能的出栈序列。
4.设栈s和队列q初始状态为空,元素a,b,c,d,e和f,依次通过栈s,一个元素出栈后即进人队列,若6个元素出队的序列是bdcfea,则栈s的容量至少应该存多少个元素?
5.已知一个中缀算术表达式为 3 + 4 / (25- (6+15))*8 写出对应的后缀算术表达式(逆波兰表达式)。
四、算法设计题
1.已知q是一个非空顺序队列,s是一个顺序栈,请设计一个算法,实现将队列q中所有元素逆置。
2.已知递归函数: 1 当n=0时
F(n)=
n·F(n/2) 当n>0时
(1)写出求F(n)递归算法;
(2)写出求F(n)的非递归算法。
3.假设以带头结点的循环链表表示队列,并且仅设一个指针指向队尾元素结点(注意不设头指针),试编写相应的队列初始化、入队列和出队列的算法。
第四章 串、数组和广义表
数据结构试卷 数据结构试题库集及答案
一、选择题
1.串的模式匹配是指 (1) 。[www.61k.com]
(1):A.判断两个串是否相等
B.对两个串进行大小比较
C.找某字符在主串中第一次出现的位置
D.找某子串在主串中第一次出现的第一个字符位置
2.设二维数组A[m][n],每个数组元素占用d个存储单元,第一个数组元素的存储地址是如Loc(a[0][0]),求按行优先顺序存放的数组元素a[j][j](0≤i≤m-1,0≤j≤n-1)的存储地址 (2) 。
(2):A.Loc(a[0][0]+[(i-1)*n+j-1]*d
B.Loc(a[0][0])+[i*n+j]*d
C.Loc(a[0][0]+[j*m+i]*d
D.Loc(a[0][0])+[(j-1)*m+i-1]*d
3.设二维数组A[m][n],每个数组元素占d个存储单元,第1个数组元素的存储地址是Loc(a[0][0]),求按列优先顺序存放的数组元素a[j][j](0≤i≤m-1,0≤j≤n-1)的存储地址 (3) 。
(3):A.Loc(a[0][0]+[(i-1)*n+j-1]*d
B.Loc(a[0][0])+[i*n+j]*d
C.Loc(a[0][0]+[(j-1)*m+i]*d
D.Loc(a[0][0])+[j*m+i]*d
4.已知二维数组A[6][10],每个数组元素占4个存储单元,若按行优先顺序存放数组元素a[3][5]的存储地址是1000,则a[0][0]的存储地址是 (4) 。
(4):A.872 B.860 C.868 D.864
5.若将n阶上三角矩阵A,按列优先顺序压缩存放在一维数组F[n(n+1)/2]中,第1个非零元素a11存于F[0]中,则应存放到F[K]中的非零元素aij(1≤i≤n,1≤j≤i的下标i,j与K的对应关系是 (5) 。
(5):A.i(i+1)/2+j B.i(i-1)/2+j-1
C.j(j+1)/2+j D.j(j-1)/2+i—1
6.若将n阶下三角矩阵A,按列优先顺序压缩存放在一维数组F[n(n+1)/2]中,第一个非零元素a11,存于F[0]中,则应存放到F[K]中的非零元素aij(1≤j≤n,1≤j≤i)的下标i,i与K的对应关系是 (6) 。
(6):A.(2n-j+1)j/2+I-j B.(2n-j+2)(j-1)/2+i-j
C.(2n-i+1)i/2+j-I D.(2n-i+2)i/2+j-i
7.设有10阶矩阵A,其对角线以上的元素aij(1≤j≤10,1<i<j)均取值为-3,其他矩阵元素为正整数,现将矩阵A压缩存放在一维数组F[m]中,则m为 (7) 。
(7):A.45 B.46 C.55 D.56
8.设广义表L=(a,b,L)其深度是 (8) 。
(8):A.3 B.? C.2 D.都不对
9.广义表B:(d),则其表尾是 (9) ,表头是 (10) 。
(9)—(10):A.d B.() C.(d) D.(())
10.下列广义表是线性表的有 (11) 。
(11):A.Ls=(a,(b,c)) B.Ls=(a,Ls)
C.Ls=(a,b) D.Ls=(a,(()))
11.一个非空广义表的表尾 (12) 。
(12):A.只能是子表 B.不能是子表
C.只能是原子元素 D.可以是原子元素或子表
12.已知广义表A=((a,(b,c)),(a,(b,c),d)),则运算head
(head(tail(A)))的结果是 (13) 。
(13):A.a B.(b,c) C.(a,(b,c)) D.d
二、填空题
1.两个串相等的充分必要条件是 (1) 。
2.空串是 (2) ,其长度等于 (3) 。
3.设有串S=”good”,T=”morning”,求:
(1)concat(S,T)= (4) ;
(2)substr(T,4,3)= (5) ;
(3)index(T,”n”)= (6) ;
(4)replace(S,3,2,”to”)= (7) 。
4.若n为主串长,m为子串长,则用简单模式匹配算法最好情况下,需要比较字符总数是 (8) ,最坏情况下,需要比较字符总数是 (9) 。
数据结构试卷 数据结构试题库集及答案
5.设二维数组A[8][10]中,每个数组元素占4个存储单元,数组元素a[2][2]按行优先顺序存放的存储地址是1000,则数组元素a[0][0]的存储地址是 (10) 。(www.61k.com)
6.设有矩阵
A=

-3应存放到F[k1]中,k1为(12),元素aij(1≤i≤4,1≤j≤i)按行优先顺序存放到F[k3]中,k3为 (14) 。
7.广义表Ls=(a,(b),((c,(d))))的长度是 (15) ,深度是 (16) ,表头是 (17) ,表尾是 (18) 。
8.稀疏矩阵的压缩存储方法通常有两种,分别是 (19) 和 (20) 。
9.任意一个非空广义表的表头可以是原子元素,也可以是 (21) ,而表尾必定是 (22) 。
三、应用题
1.已知S=”(xyz)+*”试利用联接(concat(S,T)),取子串(substr(S,i,j))和置换(replace(S,i,j,T))基本操作将S转化为T=”(x+2)*y”。
2.设串S的长度为n,其中的字符各不相同,求S中互异的非平凡子串(非空且不同于S本身)的个数。
3.设模式串T=”abcaaccbaca”,请给出它的next函数及next函数的修正值nextval之值。
4.特殊矩阵和稀疏矩阵哪一种压缩存储会失去随机存储功能?
5.设n阶对称矩阵A压缩存储于一维数组F[m]中,矩阵元素aij(1≤i≤n,1≤j≤n),存于F[k](0≤k<m)中,当用行优先顺序转换时的对应关系是什么?用列优先顺序转换时的对应关系是什么?
第五章 树和二叉树
一、单项选择题
1.关于二叉树的下列说法正确的是 (1)。
(1):A.二叉树的度为2 B.二叉树的度可以小于2
C.每一个结点的度都为2 D.至少有一个结点的度为
2.设深度为h(h>0)的二叉树中只有度为0和度为2的结点,则此二叉树中所含的结点总数至少为 (2)。
(2)A.2h B.2h-1 C.2h+1 D.h+1
3.在树中,若结点A有4个兄弟,而且B是A的双亲,则B的度为 (3) 。
(3):A.3 B.4 C.5 D.6
4.若一棵完全二叉树中某结点无左孩子,则该结点一定是 (4) 。
(4):A.度为1的结点 B.度为2的结点 C.分支结点 D.叶子结点
5.深度为k的完全二叉树至多有 (5) 个结点,至少有 (6) 个结点。
k-1k-1 kk (5)-(6):A.2-1 B.2 C.2-1 D.2
6.前序序列为ABC的不同二叉树有 (7) 种不同形态。
(7):A.3 B.4 C.5 D.6
7.若二叉树的前序序列为DABCEFG,中序序列为BACDFGE,则其后序序列为 (8) ,层次序列为 (9) 。
(8)-(9):A.BCAGFED B.DAEBCFG C.ABCDEFG D.BCAEFGD
8.在具有200个结点的完全二叉树中,设根结点的层次编号为1,则层次编号为60的结点,其左孩子结点的层次编号为 (10) ,右孩子结点的层次编号为 (11) ,双亲结点的层次编号为 (12)。
(10)-(12):A.30 B.60 C.120 D.121
9.遍历一棵具有n个结点的二叉树,在前序序列、中序序列和后序序列中所有叶子结点的相对次序 (13) 。
(13):A.都不相同 B.完全相同 C.前序和中序相同 D.中序与后序相同
10.在由4棵树组成的森林中,第一、第二、第三和第四棵树组成的结点个数分别为30,10,20,5,当把森林转换成二叉树后,对应的二叉树中根结点的左子树中结点个数为 (14) ,根结点的右子树中结点个数为 (15) 。
(14)—(15):A.20 B.29 C.30 D.35
11.具有n个结点(n>1)的二叉树的前序序列和后序序列正好相反,则该二叉树中除叶子结点外每个结点 (16) 。
(16):A.仅有左孩子 B.仅有右孩子 C.仅有一个孩子 D.都有左、右孩子
12.判断线索二叉树中p结点有右孩子的条件是 (17) 。
(17):A.p!=NULL B.p->rchild!=NULL C.p->rtag=0 D.p->rtag=1
13.将一棵树转换成二叉树,树的前根序列与其对应的二叉树的 (18) 相等。树的后根序列与其对应的二叉树的
(19)相同。
(18)—(19):A.前序序列 B.中序序列 C.后序序列 D.层次序列
14.设数据结构(D,R),D={dl,d2,d3,d4,d5,d6},R={<d4,d2>,<d2,d1>,<d2,d3>,<d4,d6>,<d6,d5>},这个结构的图形是 (20) ;用 (21) 遍历方法可以得到序列{d1,d2,d3,d4,d5,d6}。
(20):A.线性表 B.二叉树C.队列 D.栈
数据结构试卷 数据结构试题库集及答案
(21):人前序 B.中序 C.后序 D.层次
15.对于树中任一结点x,在前根序列中序号为pre(x),在后根序列中序号为post(x),若树中结点x是结点y的祖先,下列 (22) 条件是正确的。[www.61k.com)
(22):A.pre(x)<pre(y)且post(x)<post(y)
B.pre(x)<pre(y)且post(x)>post(y)
C. pre(x)>pre(y)且post(x)<post(y)
D.pre(x)>pre(y)且post(x)>post(y)
16.每棵树都能惟一地转换成对应的二叉树,由树转换的二叉树中,一个结点N的左孩子是它在原树对应结点的 (23) ,而结点N的右孩子是它在原树里对应结点的 (24) 。
(23)—(24):A.最左孩子 B.最右孩子 C.右邻兄弟 D.左邻兄弟
17.二叉树在线索化后,仍不能有效求解的问题是 (25) 。
(25):A.前序线索树中求前序直接后继结点
B.中序线索树中求中序直接前驱结点
C.中序线索树中求中序直接后继结点
D.后序线索树中求后序直接后继结点
18.一棵具有124个叶子结点的完全二叉树,最多有 (26)个结点。
(26):A.247 B.248 C.249 D.250 。
19.实现任意二叉树的后序遍历的非递归算法而不使用栈结构,最有效的存储结构是采用 (27) 。 (27):A. 二叉链表 B.孩子链表 C.三叉链表 D.顺序表
二、填空题
1.树中任意结点允许有 (1)孩子结点,除根结点外,其余结点 (2) 双亲结点。
2.若一棵树的广义表表示为A(B(E,F),C(C(H,I,J,K),L),D(M(N)))。则该树的度为 (3) ,树的深度为 (4) ,树中叶子结点个数为 (5) 。
3.若树T中度为1、2、3、4的结点个数分别为4、3、2、2,则T中叶子结点的个数是 (6) 。
4.一棵具有n个结点的二叉树,若它有m个叶子结点,则该二叉树中度为1的结点个数是 (7) 。
5.深度为k(k>0)的二叉树至多有 (8) 个结点,第i层上至多有 (9) 个结点。
6.已知二叉树有52个叶子结点,度为1的结点个数为30则总结点个数为 (10) 。
7.已知二叉树中有30个叶子结点,则二叉树的总结点个数至少是 (11) 。
8.高度为6的完全二叉树至少有 (12) 个结点。
9.一个含有68个结点的完全二叉树,它的高度是 (13) 。
10.已知一棵完全二叉树的第6层上有6个结点(根结点的层数为1),则总的结点个数至少是 (14) ,其中叶子结点个数是 (15) 。
11.已知完全二叉树第6层上有10个叶子结点,则这棵二叉树的结点总数最多是 (16) 。
12.一棵树转换成二叉树后,这棵二叉树的根结点一定没有 (17) 孩子,若树中有m个分支结点,则与其对应的二叉树中无右孩子的结点个数为 (18) 。
13.若用二叉链表示具有n个结点的二叉树,则有 (19) 个空链域。
14.具有m个叶子结点的哈夫曼树,共有 (20)个结点。
15.树的后根遍历序列与其对应的二叉树的 (21) 遍历序列相同。
16.线索二叉树的左线索指向其 (22) ,右线索指向其 (23) 。
三、应用题
1.具有n个结点的满二叉树的叶子结点个数是多少?
2.列出前序遍历序列是ABC的所有不同的二叉树。
3.已知二叉树的层次遍历序列为ABCDEFGHIJK,中序序列为DBGEHJACIKF,请构造一棵二叉树。
4.已知二叉树的中序遍历序列是ACBDGHFE,后序遍历序列是ABDCFHEG,请构造一棵二叉树。
5.已知二叉树的前序、中序和后序遍历序列如下,其中有一些看不清的字母用*表示,请先填写*处的字母,再构造一棵符合条件的二叉树,最后画出带头结点的中序线索链表。
(1)前序遍历序列是:*BC***G*
(2)中序遍历序列是:CB*EAGH*
(3)后序遍历序列是:*EDB**FA
6.将下图所示的森林转换成一棵二叉树,并画出这棵二叉树的顺序存储结构。
数据结构试卷 数据结构试题库集及答案
7.将下图所示的二叉树还原成森林。(www.61k.com]

8.对于给定的一组权值{3,5,6,7,9},请构造相应的哈夫曼树,并计算其带权路径长度。
四、算法设计题
1.请设计一个算法,求以孩子兄弟链表表示的树中叶子结点个数。
2.请编写一个算法,实现将以二叉链表存储的二叉树中所有结点的左、右孩子进行交换。
3.请编写一个算法,将以二叉链表存储的二叉树输出其广义表表示形式。
4.请编写一个算法,判断以二叉链表存储的二叉树是否为完全二叉树。
5.假设二叉树采用链接存储方式存储,编写一个二叉树先序遍历和后序遍历的非递归算法。..
6.已知一棵二叉树用二叉链表存储,t指向根结点,p指向树中任一结点。请编写一个非递归算法,实现求从根结点t到结点p之间的路径。
第六章 图
一、单项选择题
1.下面关于图的存储结构的叙述中正确的是 (1) 。
(1):A.用邻接矩阵存储图占用空间大小只与图中顶点有关,与边数无关
B.用邻接矩阵存储图占用空间大小只与图中边数有关,而与顶点数无关
C.用邻接表存储图占用空间大小只与图中顶点数有关,而与边数无关
D.用邻接表存储图占用空大小只与图中边数有关,而与顶点数无关
2.下面关于对图的操作的说法不正确的是 (2) 。
(2):A:寻找关键路径是关于带权有向图的操作
B.寻找关键路径是关于带权无向图的操作
C.连通图的生成树不一定是惟一的
D.带权无向图的最小生成树不一定是惟一的
3.下面的各种图中,哪个图的邻接矩阵一定是对称的 (3) 。
(3):A.AOE网 B.AOV网 C.无向图 D.有向图
4.在AOE网中关于关键路径叙述正确的是 (4) 。
(4):A.从开始顶点到完成顶点的具有最大长度的路径,关键路径长度是完成整个工程所需的最短时间
B.从开始顶点到完成顶点的具有最小长度的路径,关键路径长度是完成整个工程所需的最短时间
C.从开始顶点到完成顶点的具有最大长度的路径,关键路径长度是完成整个工程所需的最长时间
D.从开始顶点到完成顶点的具有最小长度的路径,关键路径长度是完成整个工程所需的最短时间
5.一个具有n个顶点e条边的图中,所有顶点的度数之和等于 (5)。
(5):A.n B.2n C.e D.2e
6.具有8个顶点的无向图最多有 (6) 条边。
(6):A.8 B.28 C.56 D.72
7.具有8个顶点的有向图最多有 (7) 条边。
(7):A.8 B.28 C.56 D.78
8.深度优先遍历类似于二叉树的 (8) 。
(9):A.前序遍历 B.中序遍历 C.后序遍历 D.层次遍历
9.广度优先遍历类似于二叉树的 (9) 。
(9):A.前序遍历 B.中序遍历 C.后序遍历 D.层次遍历
10.任一个连通图的生成树 (10) 。
(l0):A.可能不存在 B.只有一棵 C.一棵或多棵 D.一定有多棵
11.下列关于连通图的BFS和DFS生成树高度论述正确的是 (11)。
(11):A.BFS生成树高度<DFS生成树的高度
B.BFS生成树高度≤DFS生成树的高度
C.BFS生成树高度>DFS生成树的高度
数据结构试卷 数据结构试题库集及答案
D.BFS生成树高度≥DFS生成树的高度
12.G是一个非连通无向图,共有28条,则该图至少有解 (12) 个顶点。[www.61k.com)
(12):A.7 B.8 C.9 D.10
二、判断题
1.一个图的邻接矩阵表示是惟一的。 ( )
2.一个图的邻接表表示是惟一的。 ( )
3.无向图的邻接矩阵一定是对称矩阵。 ( )
4.有向图的邻接矩阵一定是对称矩阵。 ( )
5.有向图用邻接表表示,顶点vi的出度是对应顶点vj链表中结点个数。 ( )
6.有向图用邻接表表示,顶点vi的度是对应顶点vj链表中结点个数。 ( )
7.有向图用邻接矩阵表示,删除所有从顶点i出发的弧的方法是,将邻接矩阵的i行全部元素置为0。 ( )
8.若从无向图中任一顶点出发,进行一次深度优先搜索,就可以访问图中所有顶点,则该图一定是连通的。
( )
9.在非连通图的遍历过程中,调用深度优先搜索算法的次数等于图中连通分量的个数。 ( )
10.具有n个顶点的有向强连通图的邻接矩阵中至少有n个小于∞的非零元素。 ( )
11.一个连通图的生成树是一个极小连通子图。 ( )
12.在有数值相同的权值存在时,带权连通图的最小生成树可能不惟一。 ( )
13.在AOE网中仅存在一条关键路径。 ( )
14.若在有向图的邻接矩阵中,主对角线以下的元素均为0,则该图一定存在拓扑有序序列。 ( )
15.若图C的邻接表表示时,表中有奇数个边结点,则该图一定是有向图。 ( )
16.在AOE网中,任何一个关键活动提前完成,整个工程都会提前完成。 ( )
17.图的深度优先遍历序列一定是惟一的。 ( )
18.有向无环图的拓扑有序序列一定是惟一的。 ( )
19.拓扑排序输出的顶点个数小于图中的顶点个数,则该图一定存在环。 ( )
三、填空题
1.在一个具有n个顶点的完全无向图和完全有向图中分别包含有 (1) 和 (2) 条边。
2.具有n个顶点的连通图至少具有 (3) 条边。
3.具有n个顶点e条边的有向图和无向图用邻接表表示,则邻接表的边结点个数分别为(4)和 (5) 条。
4.在有向图的邻接表和逆邻接表中,每个顶点链表中链接着该顶点的所有 (6) 和 (7)结点。
5.若n个顶点的连通图是一个环,则它有 (8) 棵生成树。
6.图的逆邻接表存储结构只适用于 (9) 。
7.n个顶点e条边的图采用邻接矩阵存储,深度优先遍历算法的时间复杂度是 (10) ,广度优先算法的时间复杂度是 (11) 。
8.n个顶点e条边的图,采用邻接表存储,广度优先遍历算法的时间复杂度是 (12) ,深度优先遍历算法的时间复杂度是 (13) 。
9.若要求一个稀疏图的最小生成树,最好用 (14) 算法求解。
10.若要求一个稠密图的最小生成树,最好用 (15) 算法求解。
四、应用题
1.已知图C=(V,E),其中V={a,b,c,d,e},E={(a,b),{a,c},{a,d},(b,c),(d,c),(b,e),(c,e),(d,e)}要求:
(1)画出图G;
(2)给出图G的邻接矩阵;
(3)给出图G的邻接表;
(4)给出图G的所有拓扑有序序列。
2.已知带权无向图的邻接表见下图,要求:
0 1
2 3 4 5
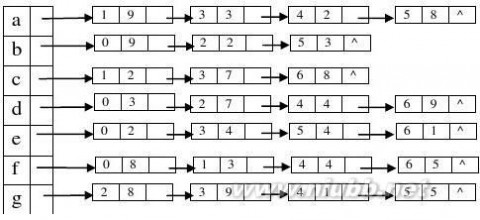
6
数据结构试卷 数据结构试题库集及答案
(1)画出图G。[www.61k.com]
(2)各画一棵从顶点a出发的深度优先生成树和广度优先生成树。
(3)给出用prim算法从顶点a出发构造最少生成树的过程。
(4)给出用Kruscal算法构造最小生成树的过程。
3.已知带权有向图如右图所示,要求:
(1)给出图G的邻接矩阵;
(2)给出图G的一个拓扑有序序列;
(3)求从顶点a出发到其余各顶点的最短路径。
4.已知带权有向图G见下图,图中边上的权
数,要求:
(1)求每项活动的最早和最晚开工时间;
(2)完成此项工程最少需要多少天;
(3)给出图G的关键路径。
值为完成活动ai需要的天
四、算法题
1.编写根据无向图G的邻接表,判断图G是否连通的算法。
2.编写根据有向图的邻接表,分别设计实现以下要求的算法:
(1)求出图G中每个顶点的出度;
(2)求出图G中出度最大的一个顶点,输出该顶点编号;
(3)计算图G中出度为0的顶点数;
(4)判断图G中是否存在边〈i,j〉。
第七章 查找
一、单项选择题
1.在长度为n的线性表中进行顺序查找,在等概率的情况下,查找成功的平均查找长度是 (1) 。
(1):A.n B.n(n+1)/2 C.(n-1)/2 D.(n+1)/2
2.在长度为n的顺序表中进行顺序查找,查找失败时需与键值比较次数是 (2) 。
(2):A.n B.1 C.n-1 D.n+l
3.对线性表进行顺序查找时,要求线性表的存储结构是 (3) 。
(3):A.倒排表 B.索引表 C.顺序表或链表 D.散列表
4.对线性表用二分法查找时要求线性表必须是 (4) 。
(4):A.顺序表 B.单链表 C.顺序存储的有序表 D.散列表
5.在有序表A[80]上进行二分法查找,查找失败时,需对键值进行最多比较次数是 (5) 。
(5):A.20 B.40 C.10 D.7
6.在长度为n的有序顺序表中,采用二分法查找,在等概率的情况下,查找成功的平均查找长度是 (6)。
2 (6):A. O(n) B.O(nlog2n) C.O(n) D.O(log2n)
7.设顺序表为{4,6,12,32,40,42,50,60,72,78,80,90,98},用二分法查找72,需要进行的比较次数是 (7) 。
(7):A.2 B.3 C.4 D.5
8.如果要求一个线性表既能较快地查找,又能适应动态变化的要求,则应采用的查找方法是 (8) 。
(8):A.顺序查找 B.二分法查找 C.分块查找 D.都不行
9.在采用线性探查法处理冲突的散列表中进行查找,查找成功时所探测位置上的键值 (9) 。
(9):A.一定都是同义词 B.一定都不是同义词
C.不一定是同义词 D.无任何关系
10.在查找过程中,若同时还要做插入、删除操作,这种查找称为 (10) 。
(10):A.静态查找 B.动态查找 C.内部查找D. 外部查找
二、填空题
1.在有序表A[30]上进行二分查找,则需要对键值进行4次、5次比较查找成功的记录个数分别为 (1) 、 (2) ,在等概率的情况下,查找成功的平均查找长度是 (3) 。

数据结构试卷 数据结构试题库集及答案
2.散列法存储的基本思想是由 (4) ,确定记录的存储地址。[www.61k.com)
3.对一棵二叉排序树进行 (5) 遍历,可以得到一个键值从小到大次序排列的有序序列。
4.对有序表A[80]进行二分查找,则对应的判定树高度为 (6) .,判定树前6层的结点个数为 (7) ,最高一层的结点个数是 (8) ,查找给定值K,最多与键值比较 (9) 次。 5.对于表长为n的线性表要进行顺序查找,则平均时间复杂度为 (10) ,若采用二分查找,则平均时间复杂度为 (11) 。
6.在散列表中,装填因子。值越大,则插入记录时发生冲突的可能性 (12) 。
7.在散列表的查找过程中与给定值K进行比较的次数取决于 (13) 、 (14) 和 (15)。
8.在使用分块查找时,除表本身外,尚需建立一个 (16) ,用来存放每一块中最高键值及 (17) 。
9.若表中有10000个记录,采用分块查找时,用顺序查找确定记录所在的块,则分成 (18)块最好,每块的最佳长度 (19) ,在这种情况下,查找成功的平均检索长度为 (20) 。
10.用n个键值构造一棵二叉排序树,最低高度是 (21) 。
11.设有散列函数H和键值k1、k2,若k1≠k2,且H(k1)= H(k2),则称k1、k2是 (22)。
12.设有n个键值互为同义词,若用线性探查法处理冲突,把这n个键值存于表长为m(m>n)的散列表中,至少要进行 (23) 次探查。
13.高度为6的平衡二叉排序树,其每个分支结点的平衡因子均为0,则该二叉树共有 (24)个结点。
14.m阶B-树,除根结点外的分支结点最多有 (25) 棵子树,最少有 (26) 棵子树,最多有 (27) 个键值,最少有 (28) 个键值。
15.m阶B+树,除根结点外的每个结点最多有 (29) 棵子树值,最少有 (30) 棵子树。
三、应用题
1.画出对长度为13的有序表进行二分查找的一棵判定树,并求其等概率时查找成功的平均查找长度。查找失败时需对键值的最多比较次数。
2.将整数序列{8,6,3,1,2,5,9,7,4}中的数依次插入到一棵空的二叉排序树中,求在等概率情况下,查找成功的平均查找长度,查找失败时对键值的最多比较次数。再画出从二叉排序树中删除结点6和8的结果。
3.将整数序列{8,6,3,1,2,5,9,7,41中的数依次插入到一棵空的平衡二叉排序树中,求在等概率情况下,查找成功的平均检索长度,查找失败时对键值的最多比较次数o
4.按不同的输入顺序输入4,5,6,建立相应的不同形态的二叉排序树。
5.设有键值序列{25,40,33,47,12,66,72,87,94,22,5,58}散列表长为12,散列函数为H(key)=key%11,用拉链法处理冲突,请画出散列表,在等概率情况下,求查找成功的平均查找长度和查找失败的平均查找长度。
6.已知一个散列函数为H(key)=key%13,采用双散列法处理冲突,H1(key)=key%11+1,探查序列为di=(H(key)+i* H1(key))%m,i=1,2,?m-1,散列表见表1,要求回答下列问题:
(1)对表中键值21,57,45和50进行查找时,所需进行的比较次数各为多少?
(2)在等概率情况下查找时,查找成功的平均查找长度是多少?
0 1 2 3 4 5 6 7 8 9 10 11 12
表1 散列表
四、算法设计题
1.设二叉树用二叉链表表示,且每个结点的键值互不相同,请编写判别该二叉树是否为二叉排序树的非递归算法。
第八章 排序
一、单项选择题
1.对n个不同的记录按排序码值从小到大次序重新排列,用冒泡(起泡)排序方法,初始序列在 (1) 情况下,与排序码值总比较次数最少,在 (2) 情况下,与排序码值总比较次数最多;用直接插入排序方法,初始序列在 (3) 情况下,与排序码值总比较次数最少,在 (4) 情况下,与排序码值总比较次数最多;用快速排序方法在 (5) 情况下,与排序码值总比较次数最少,在 (5) 情况下与排序码值总比较次数最多。
(1)-(6):
A.按排序码值从小到大排列 B.按排序码值从大到小排列
C.随机排列(完全无序) D.基本按排序码值升序排列
2.用冒泡排序方法对n个记录按排序码值从小到大排序时,当初始序列是按排序码值从大到小排列时,与码值总比较次数是 (7) 。
(7):A.n-1 B.n C.n+1 D.n(n-1)/2
3.下列排序方法中,与排序码值总比较次数与待排序记录的初始序列排列状态无关的是 (8) 。
(8):A.直接插入排序 B.冒泡排序 C.快速排序 D.直接选择排序
4.将6个不同的整数进行排序,至少需要比较 (9) 次,至多需要比较 (10) 次。
(9)-(10):A.5 B.6 C.15 D.21
5.若需要时间复杂度在O(nlog2n)内,对整数数组进行排序,且要求排序方法是稳定的,则可选择的排序方法是

数据结构试卷 数据结构试题库集及答案
(11) 。(www.61k.com)
(11):A.快速排序 B.归并排序 C.堆排序 D.直接插入排序
6.当待排序的整数是有序序列时,采用 (12) 方法比较好,其时间复杂度为O(n),而采用 (13)方法却正好相
22反,达到最坏情况下时间复杂度为O(n);无论待排序序列排列是否有序,采用 (14)方法的时间复杂度都是O(n)。
(12)-(14):A.快速排序 B.冒泡排序 C.归并排序 D.直接选择排序
7.堆是一种 (15) 排序。
(15):A.插入 B.选择 C.交换 D.归并
8.若一组记录的排序码值序列为{40,80,50,30,60,70},利用堆排序方法进行排序,初建的大顶堆是 (16) 。
(16):A.80,40,50,30,60,70 B.80,70,60,50,40,30
C.80,70,50,40,30,60 D.80,60,70,30,40,50
9.若一组记录的排序码值序列为{50,80,30,40,70,60}利用快速排序方法,以第一个记录为基准,得到一趟快速排序的结果为 (17) 。
(17):A.30,40,50,60,70,80 B.40,30,50,80,70,60
C.50,30,40,70,60,80 D.40,50,30,70,60,80
10.下列几种排序方法中要求辅助空间最大的是 (18) 。
(18):A.堆排序 B.直接选择排序 C.归并排序 D.快速排序
11.已知A[m]中每个数组元素距其最终位置不远,采用下列 (19) 排序方法最节省时间。
(19):A.直接插入 B.堆 C.快速 D.直接选择 12.设有10000个互不相等的无序整数,若仅要求找出其中前10个最大整数,最好采用 (20) 排序方法。
(20):A.归并 B.堆 C.快速 D.直接选择
13.在下列排序方法中不需要对排序码值进行比较就能进行排序的是 (21) 。
(21):A:基数排序 B.快速排序 C.直接插入排序 D.堆排序
14.给定排序码值序列为{F,B,J,C,E,A,I,D,C,H},对其按字母的字典序列的次序进行排列,希尔(Shell)排序的第一趟(d1=5)结果应为 (22) ,冒泡排序(大数下沉)的第一趟排序结果应为 (23) ,快速排序的第一趟排序结果为 (24) ,二路归并排序的第一趟排序结果是 (25) 。
(22)-(25):A.{B,F,C,J,A,E,D,I,C,H}
B.{C,B,D,A,E,F,I,C,J,H}
C.{B,F,C,E,A,I,D,C,H,J}
D.{A,B,D,C,E,F,I,J,C,H}
二、填空题
1.内部排序方法按排序采用的策略可划分为五类: (1)、 (2)、 (3)、 (4)、 (5)。
2.快速排序平均情况下的时间复杂度为 (6) ,其最坏情况下的时间复杂度为 (7)。
3.当待排序的记录个数n很大时,应采用平均时间复杂度为 (8)即 (9)、 (10)、 (11),在这些方法中当排序码值是随机分布时,采用 (12) 排序方法的平均时间复杂度最小。当希望排序方法是稳定时,应采用 (13) 排序方法,若只从节省空间考虑,最节省空间的是 (14) 方法。
4.对一组整数{60,40,90,20,10,70,50,80}进行直接插入排序时,当把第7个整数50插入到有序表中时,为寻找插人位置需比较 (15)次。
5.从未排序序列中挑选最小(最大)元素,并将其依次放到已排序序列的一端,称为 (16)排序。
6.对n个记录进行归并排序,所需要的辅助存储空间是 (17) ,其平均时间复杂度是 (18) ,最坏情况下的时间复杂度是 (19) 。
7.对n个记录进行冒泡排序,最坏情况下的时间复杂度是 (20) 。
8.对20个记录进行归并排序时,共需进行 (21) 趟归并,在第三趟归并时是把最大长度为 (22) 的有序表两两归并为长度为 (23) 的有序表。
三、应用题
1.举例说明本章介绍的排序方法中哪些是不稳定的?
2.已知排序码值序列{17,18,60,40,7,32,73,65,85},请写出冒泡排序每一趟的排序结果。
3.对于排序码值序列{10,18,14,13,16,12,11,9,15,8},给出希尔排序(dl=5,d2=2,d3=1)的每一趟排序结果。
4.判断下列序列是否为大顶堆?若不是,则把它们调整为大顶堆。
(1){90,86,48,73,35,40,42,58,66,20}
(2){12,70,34,66,24,56,50,90,86,36}
四、算法设计题
1.在带表头结点的单链表上,编写一个实现直接选择排序的算法。
2.请编写一个快速排序的非递归算法。
数据结构试卷 数据结构试题库集及答案
附录:
大连理工大学2002年硕士入学试题
数据结构部分(共50分)
一、算法填空题(20分)
1.对以下函数填空,实现将头指针为h的单链表逆置,即原链表的第一个结点变成逆置后新链表的最后一个结点,原链表的第二个结点变成新链表的倒数第二个结点,如此等等,直到最后一个结点作为新链表的第一个结点,并返回指向该结点的指针。(www.61k.com]设单链表结点类型的定义为
typedefstructnode
{int data;
strcutnode *next;
}NODE;
NODE *dlbnz(NODE*h)
{NODE*p,*q;
q=NULL;
while(h)
p=h;
h=h->next;
;
;
}
return q;
}
2.假设算术表达式由字符串b表示,其中可以包含三种括号:圆括号和方括号及花括号,其嵌套的顺序随意,如{[]([])}。请对以下函数填空,实现判别给定表达式中所含括号是否正确配对出现的算法。
#define M 10
int khjc(char *b)
{ charsM};
int i,j=0,f=1;
j=0;
for(i=0;f&&b[i]!=?\0?;i++)
{ switch(b[i])
{ case ?(?:;break;
case ?[?:;break;
case?{?:;break;
case ?)?:
case ?]?:
case ?[?:if(j==0;||b[I]!=) f=0;
}
}
return f&&;
}
3.对以下函数填空,实现以带头结点的单链表h为存储结构的直接选择排序。设单链表结点类型的定义为
typedef structnode
{ intkey;
structnode *next;
}NODE;
void pxx(NODE *h)
{ NODE*p,*q,*m;
int z;
p=h->next;
while(p!=NULL)
{ q=p->next;
m=p;
while(q!=NULL)
{ if(m->key>q->key);
;
}
数据结构试卷 数据结构试题库集及答案
if(p!=m)
{x=p->key;
p->key=m->key;
m->key=x;
}
;}
}
二、算法设计题(30分)
请用类C或类PASCAL语言设计实现下列功能的算法。[www.61k.com)
1.设二叉排序树以二叉链表为存储结构,请编写一个非递归算法,从大到小输出二叉排序树中所有其值不小于X的键值。(10分)
2.设由n个整数组成一个大根堆(即第一个数是堆中的最大值),请编写一个时间复杂度为O(log2n)的算法,实现将整数X插入到堆中,并保证插入后仍是大根堆。(10分)
3.请编写一个算法,判断含n个顶点和e条边的有向图中是否存在环。并分析算法的时间复杂度。(10分)
大连理工大学2003年硕士入学试题
数据结构部分(共75分)
一、回答下列问题(20分)
1.循环队列用数组A[0..m—1)存放其数据元素。设tail指向其实际的队尾,front指向其实际队首的前一个位置,则当前队列中的数据元素有多少个?如何进行队空和队满的判断?
2.设散列表的地址空间为0~10,散列函数为H(key)=key%11(%为求余函数),采用线性探查法解决冲突,并将键值序列{15,36,50,27,19,48}依次存储到散列表中,请画出相应的散列表;当查找键值48时需要比较多少次?
3.什么是m阶B-树?在什么情况下向一棵m阶B-树中插入一个关键字会产生结点分裂?在什么情况下从一棵m阶B-树中删除一个关键字会产生结点合并?
4.什么是线索二叉树?一棵二叉树的中序遍历序列为由djbaechif,前序遍历序列为abdjcefhi,请画出该二叉树的后序线索二叉树。
二、请用类C或类PASCAL语言进行算法设计,并回答相应问题。(45分)
1.设计一非递归算法采用深度优先搜索对无向图进行遍历,并对算法中的无向图的存储结构予以简单说明。
2.用链式存储结构存放一元多项式Pn(x)=P1xel+P2xe2+…+Pnxen,其中Pi是指数为ei的项的非零系数,且满足0≤e1≤e2…<en=n。请设计算法将多项式B=Pn2(x)加到多项式A=Pn1(x),同时对算法及链表的结点结构给出简单注释。要求利用Pnl(x)和Pn2(x)的结点产生最后求得的和多项式,不允许另建和多项式的结点空间。
3.(1){Rl,R2,?,Rn}为待排序的记录序列,请设计算法对{R1,R2,?,Rn}按关键字的非递减次序进行快速排序。
(2)若待排序的记录的关键字集合是{30,4,48,25,95,13,90,27,18),请给出采用快速排序的第一趟、第二趟排序结果。
(3)若对(2)中给出的关键字集合采用堆排序,请问初建的小根堆是什么?
(4)当给定的待排序的记录的关键字基本有序时,应采用堆排序还是快速排序?为什么?
三、算法填空(10分)
1.一棵树以孩子兄弟表示法存储,递归算法numberofleaf计算并返回根为r的树中叶子结点的个数(NULL代表空指针)。
typedefstructnode{structnode *firstchild,*nextbrother;}TFNNode;
int numberofleaf(TFNNode *r)
{intnum;
if(r==NULL)num=0;
else
if(r->firstchild==NULL)
num=+numberofleaf;
(r->nextbrother);
else;
return(num);
}
2.在根结点为r的二叉排序树中,插人数据域值为x的结点,要求插入新结点后的树仍是一棵二叉排序树(NULL代表空指针)。
二叉排序树的结点结构为
typedef struct node
{ int key;
structnode *lc,*rc;
数据结构试卷 数据结构试题库集及答案
}BiNode;
BiNode *insert(BiNode *r,int x)
{ BiNode *p,*q,*s;
s=(BiNode*)malloc(sizeof(BiNode));
s->key=x;
s->lc=NULL;s->rc=NULL;
q=NULL;
if(r==NULL) {r=s;return(r);}
p=r;
while()
{ q=p;
if() p=p->lc;
else p=p->rc
}
if(x<q->key) ;
else ;
return;
}
清华大学2001年数据结构与程序设计试题
试题内容:
一、试给出下列有关并查集(mfsets)的操作序列的运算结果:
union(1,2),union(3,4),union(3,5),union(1,7),union(3,6),
union(8,9),union(1,8),union(3,10),union(3,11),union(3,12),
union(3,13),union(14,15),union(16,0),union(14,16),union(1,3),
union(1,14)。[www.61k.com](union是合并运算,在以前的书中命名为merge)
要求:
(1)对于union(i,j),以i作为j的双亲;(5分)
(2)按i和j为根的树的高度实现union(i,j),高度大者为高度小者的双亲;(5分)
(3)按i和j为根的树的结点个数实现union(i,j),结点个数大者为结点个数小者的双亲。(5分)
二、设在4地(A,B,C,D)之间架设有6座桥,如下图所示:

要求从某一地出发,经过每座桥恰巧一次,最后仍回到原地。
(1)试就以上图形说明:此问题有解的条件是什么?(5分)
(2)设图中的顶点数为n,试用C或Pascal描述与求解此问题有关的数据结构并编写一个算法,找出满足要求的一条回路。(10分)
三、针对以下情况确定非递归的归并排序的运行时间(数据比较次数与移动次数):
(1)输人的n个数据全部有序;(5分)
(2)输入的n个数据全部逆向有序;(5分)
(3)随机地输入几个数据。(5分)
四、简单回答有关AVL树的问题。
(1)在有N个结点的AVL树中,为结点增加一个存放结点高度的数据成员,那么每一个结点需要增加多少个字位(bit)?(5分)
(2)若每一个结点中的高度计数器有8bit,那么这样的AVL树可以有多少层?最少有多少个关键码?(5分)
五、一个散列表包含hashSize=13个表项,其下标从0到12,采用线性探查法解决冲突。请按以下要求,将下列关键码散列到表中。
10 100 32 45 58 126 3 29 200 400 0
(1)散列函数采用除留余数法,用%hashSize(取余运算)将各关键码映像到表中。请指出每一个产生冲突的关键码可能产生多少次冲突。(7分)
(2)散列函数采用先将关键码各位数字折叠相加,再用%hashSize将相加的结果映像到表中的办法。请指出每一个产生冲突的关键码可能产生多少次冲突。(8分)
数据结构试卷 数据结构试题库集及答案
六、设一棵二叉树的结点定义为
struct BinTreeNode{
ElemType data;
BinTreeNode *leftChild,*rightChild;
}
现采用输入广义表表示建立二叉树。[www.61k.com]具体规定如下:
(1)树的根结点作为由子树构成的表的表名放在表的最前面;
(2)每个结点的左子树和右子树用逗号隔开。若仅有右子树,没有左子树,逗号不能省略。
(3)在整个广义表表示输入的结尾加上一个特殊的符号(例如“#”)表示输入结果。;
例如,对于如右图所示的二叉树,其广义表表示为A(B(D,E(G,)),C(,F))
此算法的基本思路是:依次从保存广义表的字符串ls中输入每个字符。若遇到的是字母(假定以字母作为结点的值),则表示是结点的值,应为它建立一个新的结点,并把该结点作为左子女当(k=1)或右子女(当k=2)链接到其双亲结点上。若遇到的是左括号”(”,则表明子表的开始,将A置为1;若遇到的是右括号”)”,则表明子表结束。若遇到的是逗号”,”,则表示以左子女为根的子树处理完毕,应接着处理以右子女为根的子树,将A置为2。
在算法中使用了一个栈s,在进入子表之前,将根结点指针进栈,以便括号内的子女链接之用。在子表处理结束时退栈。相关的栈操作如下:
MakeEmpty(s)置空栈
Push(s,p)元素p进栈
Pop(s)退栈
Top(s)存取栈顶元素的函数
下面给出了建立二叉树的算法,其中有5个语句缺失。请阅读此算法并把缺失的语句补上。(每空3分)
Void CreateBinTree(BinTreeNode *&BT,char ls)
{ Stack<BinTreeNode*>s;MakeEmpty(s);
BT=NULL; //置二叉树
BinTreeNode *p;
int k;
istream ins(ls); //把串ls定义为输入字符串流对象ins
charch;
ins>>ch;//从ins顺序读入一个字符
while(ch!=”#”)
{ //逐个字符处理,直到遇到?#?为止
switch(ch)
{ case?(?:k=1;
break;
case ?)?:pop(s);
break;
case ?,? break;
default:p=newBinTreeNode;
p->leftChild=NULL;
p->rightChfild=NULL;
if(BT==NULL)
else if(k==1)top(s)->leftChild=p;
else top(8)->rightChild=p;
}
}
}|
七、下面是一个用C编写的快速排序算法。为了避免最坏情况,取基准记录pivot采用从left,right和mid=? (1eft+right)/2?中取中间值,并交换到right位置的办法。数组a存放待排序的一组记录,数据类型为Type,left和right是待排序子区间的最左端点和最右端点。
Void quicksort(Type a&#, int lefl,int right)
{ Type temp;
数据结构试卷 数据结构试题库集及答案
if(left<right)
{ Typepivot=medlian3(a,left,right);
int i=left,j=right-1;
for(;;)
{ while(i<j&&s[I]<pivot) i++;
while(i<j&&pivot<a[j] j--;
if(i<j)
{ temp=a[i];a[j]=a[i];a[i]=temp;
i++;j--;
}
else break;
}
if(s[i]>pivot)
{ temp=a[i];a[i]=a[right];a[right]=temp;}
quicksort(a,left,i-1); //递归排序左子区间
quicksort(a,i+1,right);//递归排序右子区间
}
}
(1)用C或Pascal实现三者取中子程序median3(a,left,right);(5分)
(2)改写quicksoft算法,不用栈消去第二个递归调用quicksort(a,j+1,right);(5分)
(3)继续改写quicksort算法,用栈消去剩下的递归调用。(www.61k.com)(5分)
上海交通大学2001年数据结构及程序设计试题
注意:程序设计请采用C语言,程序应有注解及说明。回答问题简洁、清晰全面。不得采用类C之类的语言写程序。
一、参见下图,该有向图是AOE网络。该图上已标出了源点及汇点,并给出了活动(边)的权值。
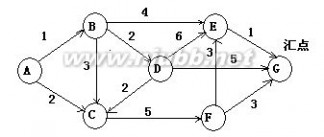
请求出该AOE网络的关键路径,以及事件(结点)的最早发生时间及最迟发生时间。(本题8分)
二、已知某二叉树的每个结点,要么其左、右子树皆为空,要么其左、右子树皆不空。又知该二叉树的前序序列为(即先根次序):J、F、D、B、A、C、E、H、X、I、K;后序序列为(即后根次序):A、C、B、E、D、X、I、H、F、K、Jo请给出该二叉树的中序序列(即中根次序),并画出相应的二叉树树形。(本题8分)
三、回答下列问题:(本题10分)
1)具有N个结点且互不相似的二叉树的总数是多少?
2)具有N个结点且不同形态的树的总数是多少?
3)对二叉树而言,如果它的叶子结点总数为N0,度为2的结点的总为N2,则N0和N2之间的关系如何?
4)二叉树是否是结点的度最多为2的树?请说明理由。
5)具有n片叶子的哈夫曼树(即赫夫曼树)中,结点总数为多少?
四、在外部分类时,为了减少读、写的次数,可以采用k路平衡归并的最佳归并树模式。当初始归并段的总数不足时,可以增加长度为零的“虚段”。请问增加的“虚段”的数目为多少?请推导之。设初始归并段的总数为m。(本题8分)
五、对平衡的排序二叉树进行删除结点的操作,必须保证删除之后平衡树中的每个结点的平衡因子是+1,-1,0三种情况之一,且该树仍然是排序二叉树。现假定删除操作是在p结点的左子树上进行的,且该左子树原高为h-l,现变为h-2。因此,必须从p的左子树沿着到根的方向回溯调整结点的平衡因子,并进行树形的调整。设p是调整时遇到的第一个平衡因子力图由-1变成-2的最年轻的“前辈”结点。我们知道,以p为根的子树经调整后,高度有可能减少1。试用图形把调整前及调整后的相关结点的平衡因子、树形表示出来;仅仅针对调整后子树的高度减少1的情况即可。注意,罗列出所有可能的情况。上图可供参考。(本题10分)
六、某算法由下述方程表示。请求出该算法的时间复杂性的级别(以大O形式表示)。注意n>7求解问题的规模,设n是3的正整数幂。(本题8分)
1 如果n=1 5T(n/3)+n 如果n>1
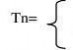
数据结构试卷 数据结构试题库集及答案
七、如右图所示,该二叉树是某棵有序树变换成的相对应的二叉树。(www.61k.com]试给出原来的有序树的形状。并回答以下问题:
1)原有序树是度为多少的树?
2)原有序树的叶子结点有哪几个?
3)是否所有的二叉树都可以找到相对应的有序树?必须满足什么条件?(本题5分)
八、在排序二叉树上进行查找操作时,设对树中的每个结点查找概率相同。设由n个结点构成的序列生成的排序二叉树是“随机”的。试求出在成功查找的情况下,平均查找长度是多少?为了简单起见,最后得到的递推式可不予求解。(本题8分)
九、设从键盘每次输入两个字符。如A、B,则表示存在着一条由数据场之值为字符A的结点到数据场之值为字符B的结点的有向边。依此输入这些
有向边,直至出现字符!为止。试设计一个程序,生成该有向图的邻接表及逆邻接表。必须交待所用的结构、变量、加以适当注解。(本题20分) ·
十、设二叉树中结点的数据场之值为一字符。采用二叉链表的方式存储该二叉树中的所有结点,设p为指向树根结点的指针。设计一个程序在该二叉树中寻找数据场之值为key(key为一变量,变量内容为一字符)的那个结点的所有祖先。设二叉树中结点数据场之值互不重复。(本题15分)
注意:有些书上将二叉树的二叉链表存储形式称之为标准存储形式。
南开大学2001年数据结构试题
一、选择题(每小题3分,共21分)
在下列各题中,每题之后均有若干个备选答案,请选出所有正确的答案,填人“”处。答案请写在答题纸上。
1.任何一个无向连通图的最小生成树。
①只有一棵②有一棵或多棵
③一定有多棵④可能不存在
2.已知一棵非空二叉树的,则能够惟一确定这棵二叉树。
①先序遍历序列和后序遍历序列
②先序遍历序列和中序遍历序列
③先序遍历序列
④中序遍历序列,
3.使用指针实现二叉树时,如果结点的个数为n,则非空的指针域个数为。
①n-1 ②2n-1 ③n+1 ④2n+1
4.设队列存储于一个一维数组中,数组下标范围是1-n,头尾指针分别为f和r,f指向第一个元素的前一个位置,r指向队列中的最后一个元素,则队列中元素个数为。
①r-f ②r-f+1 ③(r-f+1)mod n ④(r-f+n)mod n
5.任意一个AOE网络的关键路径。
①一定有多条②只有一条③可能不只一条④可能不存在.
6.下列排序算法中,在每一趟都能选出一个元素放到其最终位置上的是。
①插入排序②希尔排序③快速排序④堆排序
7.任意一个有向图的拓扑排序序列。
①一定有多种②只有一种③可能不存在④以上都不对
二、(7分)已知散列表地址空间为0-8,哈希函数为H(k)=kmod7,采用线性探测再散列法解决冲突。将下面关键字数据依次填入该散列表中,同时将查找每个关键字所需的比较次数m填入下表中,并求等概率下的平均查找长度。
关键字值:100,20,21,35,3,78,99,45

A
m
三、(12分)回答下列问题:
(1)(3分)什么叫基数排序?
(2)(3分)什么是AVL树中的平衡因子,它有什么特点?
(3)(6分

)n

个元素的序列{k1,k2,…kn}满足什么条件才能称之为堆?简述对它进行堆排序的过程。
四、(10分)顺序给出以下关键字:63、23、31、26、7、91、53、15、72、52、49、68,构造3阶B-树。要求从空树开始,每插入一个关键字,画出一个树形。
五、(6分)设有向无环图G如下图所示:
数据结构试卷 数据结构试题库集及答案
试写出图G的六种不同的拓扑排序序列。(www.61k.com)
六、(10
其中为存储关键字值的整数域,subsum中存储以该结点为根的子树中所有关键字值之和。试使用C或C++语言设计算法,计算所给树T中所有结点的subsum值。
七、(12分)给出一个带表头的单链表L,L的每个结点中存放一个整数。现给定一个阈值K,将L分成两个子表L1和L2,其中L1中存放L中所有关键字值大于等于是的结点,L2中存放L中所有关键字值小于K的结点。试编程实现这个过程。要求,使用C或C++语言实现算法,L1和L2仍占用L的存储空间。
八、(10分)设有一维整数数组A,试使用C或C++语言设计算法,将A中所有的奇数排在所有偶数之前。要求,时间复杂度尽可能地少,结果仍放在A原来的存储空间。
九、(12分)简述哈夫曼编码的构造过程。
华东理工大学2001年数据结构与程序设计试题
一、单选题(10分)
1.若某线性表中最常用的操作是在最后一个元素之后插入一个元素和删除第一个元素,则采用——存储方式最节省运算时间。
A.单链表 B.仅有头指针的单循环链表
C.双链表 D.仅有尾指针的单循环链表
2.若在线性表中采用折半查找法查找元素,该线性表应该。
A.元素按值有序 B.采用顺序存储结构
C.元素按值有序,且采用顺序存储结构
D.元素按值有序,且采用链式存储结构
3.对于给定的结点序列abcdef,规定进栈只能从序列的左端开始。通过栈的操作,能得到的序列为。
A.abcfed B.cabfed C.abcfde D.cbafde
4.已知一算术表达式的中缀形式为A+B*C-D/E,后缀形式为ABC*+DE/-,其前缀形式为。
A.-A+B*C/DE B.-A+B*CD/E
C.-+*ABC/DE D.-+A*BC/DE
5.如果n1和n2是二叉树T中两个不同结点,n2为n1的后代,那么按遍历二叉树T时,结点n2一定比结点n1先
被访问。
A.前序 B.中序 C.后序 D.层次序
6.具有65个结点的完全二叉树其深度为。(根的层次号为1)
A.8 B.7 C.6 D.5
7.已知二叉树的前序遍历序列是abdgcefh,中序遍历序列是dgbaechf,它的后序遍历序列是。
A.bdgcefha B. gdbecfha C.bdgechfa D.gdbehfca
8.对于前序遍历和后序遍历结果相同的二叉树为。
A.一般二叉树
B.只有根结点的二叉树
C.根结点无左孩子的二叉树
D.根结点无右孩子的二叉树
9.对于前序遍历与中序遍历结果相同的二叉树为。
A.根结点无左孩子的二叉树
B.根结点无右孩子的二叉树
C.所有结点只有左子树的二叉树
D.所有结点只有右子树的二叉树
10.在有n个叶子的哈夫曼树中,其结点总数为。
A.不确定 B.2n C.2n+1 D.2n-1
数据结构试卷 数据结构试题库集及答案
二、是非题(10分)
1.顺序存储方式只能用于存储线性结构。(www.61k.com)
2.消除递归不一定需要使用栈。
3.将一棵树转换成相应的二叉树后,根结点没有右子树。
4.完全二叉树可以采用顺序存储结构实现,存储非完全二叉树则不能。
5.在前序遍历二叉树的序列中,任何结点的子树的所有结点都是直接跟在该结点之后。
6.邻接表法只能用于有向图的存储,而邻接矩阵法对于有向图和无向图的存储都适用。
7.在一个有向图的邻接表中,如果某个顶点的链表为空,则该顶点的度一定为零。
8.二叉树为二叉排序树的充分必要条件是其任一结点的值均大于其左孩子的值,小于其右孩子的值。
9.最佳二叉排序树的任何子树都是最佳二叉排序树。
10.对两棵具有相同关键字集合的而形状不同的二叉排序树,按中序遍历它们得到的序列的顺序是一样的。
三、问答题
(应届生限做2,3,4,5题;在职生任选做四题;共40分)
1.(10分)什么是广义表?请简述广义表与线性表的主要区别。
2.(10分)下图表示一个地区的通讯网,边表示城市间的通讯线路,边上的权表示架设线路花费的代价。
①请分别给出该图的邻接表和邻接矩阵,要求每种存储结构能够表达出该图的全部信息,并分别对这二种形式中每个部分的含义(物理意义)予以简要说明。
②若假设每个域(包括指针域)的长度为一个字节,请分别计算出这二种结构所占用的空间大小。
3.(10分)已知如下所示长度为12的表:
(Jan,Feb,Mar,Apr,May,June,July,Aug,Sep,Oct,Nov,Dec)
①试按表中元素的顺序依次插入一棵初始为空的二叉排序树,请画出插入完成之后的二叉排序树,并求其在等概率的情况下查找成功的平均查找长度。
②若对表中元素先进行排序构成有序表,求在等概率的情况下对此有序表进行折半查找时查找成功的平均查找长度。 ③按表中元素顺序构造一棵平衡二叉排序树,并求其在等概率的情况下查找成功的平均查找长度。
4.(10分)在起泡排序过程中,有的关键字在某趟排序中可能朝着与最终排序相反的方向移动,试举例说明之。快速排序过程中有没有这种现象?
5.(10分)调用下列函数f(n),回答下列问题:
①试指出f(n)值的大小,并写出f(n)值的推导过程;
②假定n=5,试指出f(5)值的大小和执行f(5)的输出结果。
C函数
int f(int n)
{int i,j,k,sum=0;
for(j=1;i<n+1 i++)
{ for(j=n;j>i-1;j--)
for(k=1;k<j+1;k++)
suni++;
prinft(”sum=%d\n”,sum);
}
return(sum);
}
Pascal函数
FUNCTIONf(n:integer):integer;
VAR i,j,k,sum,integer;
BEGIN .
sum:=0;
FOR i:=1 TO n DO
BEGIN
FOR j:=nDOWN i DO
FOR k:=1 TO j DO
sum:=sum+1
writeln(?sum=?,sum)
END;
f:=sum
END;
四、编写算法
(应届生限做1、2、3、4题,在职生任选四题,每题10分,共40分)
数据结构试卷 数据结构试题库集及答案
1.(10分)利用两个栈S1和S2模拟一个队列,写出入队和出队的算法(可用栈的基本操作)。[www.61k.com)
栈的操作有:
makeEmpty(s:stack);置空栈
push(s:stack;value:datatype);新元素value进栈
pop(s:stack):datatype;出栈,返回栈顶值
isEmpty(s:stack):boolean;判栈空否
队列的操作有
enQtleue(s1:stack;s2:stack;value:datatype);元素value进队
deQueue(s1:stack;s2:stack):datatype;出队列,返回队头值
2.(10分)试写出给定的二叉树进行层次遍历的算法,在遍历时使用一个链接队列。
3.(10分)试写一个算法,判别以邻接表方式存储的有向图中是否存在由顶点vi到顶点vj的路径(i<>j)。假设分别基于下述策略:
1)图的深度优先搜索;
2)图的广度优先搜索;
4.(10分)设二叉排序树中关键字由1至1000的整数构成,现要检索关键字为531的结点,下述关键字序列中哪些可能是二叉排序树上搜索到的序列,哪些不可能是二叉排序树上搜索到的序列,哪些不可能是二叉排序树上搜索到的序列?
a)800,399,588,570,500,520,566,531
b)730,355,780,390,701,401,530,531
c)732,321,712,385,713,392,531
d)8,578,555,340,433,551,550,450,531
通过对上述序列的分析,试写一个算法判定给定的关键字序列(假定关键字互不相同)是否可能是二叉排序树的搜索序列。若可能则返回真,否则返回假。可假定被判定的序列已存入数组中。
5.(10分)编写一个在非空的带表头结点的单链表上实现就地排序的程序。(不额外申请新的链表空间)
华中理工大学2001年数据结构试题
说明:在有数据类型定义和算法设计的各题中,任取C语言、PASCAL语言之一作答,但不许使用所谓“类C”或“类PASCAL”。
一、选择题(从下列各题四个备选答案中选出一至四个正确答案,将其代号(A,B,C,D)写在题干前面的括号内。答案选错或未选全者,该题不得分。每小题1分,共计20分)
( )1.一个算法具有等特点。
A.可行性 B.至少有一个输入量
C.确定性 D.健壮性
( )2.是一个线性表。
A.(A,B,C,D) B.{?A?,?B?,?C?,?D?}
C.(1,2,3,…) D.(40,-22,88)
( )3.可使用作压缩稀疏矩阵的存储结构。
A.邻接矩阵 B.三元组表
C.邻接表 D.十字链表
( )4.采用一维数组表示顺序存储结构时,可用它来表示。
A.字符串 B.2度树 C.二叉树 D.无向图
( )5.假设进入栈的元素序列为d,c,a,b,e,那么可得到出栈的元素序列。
A.a,b,c,d,e B.a,b,e,d,c
C.d,b,a,e,c D.d,b,a,c,e
( )6.对队列的操作有。
A.在队首插入元素B.删除值最小的元素
C.按元素的大小排序 D.判断是否还有元素
( )7.假设有60行70列的二维数组a[1..60,1..70],以列序为主序顺序存储,其基地址为10000,每个元素占2个存储单元,那么第32行第58列的元素a[32,58]的存储地址为。(无第0行第0列元素)
A.16902 B.16904
C.14454 D.答案A,B,C均不对
( )8.是C语言中"abcd321ABCD"的子串。
A.abed B.32lAB C.”abeABC” D.”2lAB”
( )9.在下列各广义表中,长度为3的广义表有。
A.(a,b,c,()) B.((g),(a,b,c,d,f),())
C.(a,(b,(c))) D.((()))
数据结构试卷 数据结构试题库集及答案
( )10.一个堆(heap)又是一棵。(www.61k.com]
A.二叉排序树 B.完全二叉树
C.平衡二叉树 D.哈夫曼(Huffman)树
( )11.折半查找有序表(4,6,10,20,30,50,70,88,100),若查找元素58,则它将依次与表中元素比较大小,查找结果是失败。
A.20,70,30,50 B.30,88,70
C.20,50 D.30,88,50,70
( )12.对27个记录的有序表作折半查找,当查找失败时,至少需要比较次关键字。
A.3 B.4 C.5 D.6
( )13.具有12个结点的完全二叉树有。
A.5个叶子B.5个度为2的结点
C.7个分支结点 D.2个度为1的结点
( )14.具有n(n>0)个结点的完全二叉树的深度为。
A.?log2(n)? B.?log2(n+1)?
C.?log2(n)?+1 D.?loge(n) +1?
( )15.用5个权值{3,2,4,5,1}构造的哈夫曼(Huffman)树的带权路径长度是。
A.32 B.33 C.34 D.15
( )16.对14个记录的表进行2路归并排序,共需移动次记录。
A.42 B.56 C.91 D.84
( )17.对有n个记录的表作快速排序,在最坏情况下,算法的时间复杂度是。
A.O(n) B.O(n2) C.O(nlog2n) D.O(2n)
( )18.在最好情况下,下列算法中排序算法所需比较关键字次数最少。
A.冒泡 B.归并 C.快速 D.直接插入
( )19.置换选择排序的功能是。
A.选出最大的元素 B.产生初始归并段
C.产生有序文件 D.置换某个记录
( )20.可在构造一个散列文件。
A.内存 B.软盘 C.磁带 D.硬盘
二、试用2种不同表示法画出下列二叉树B1的存储结构,并评述这2种表示法的优、缺点。(共10分)


二题图B1 三题图G
三、对图G:
1. 从顶点A出发,求图G的一棵深度优先生成树;
2. 从顶点B出发,求图G的一棵广度优先生成树;
3.求图G的一棵最小生成树。(共12分)
四、设哈希(Hash)函数为:H(k)=kMODl4,其中k为关键字(整数),MOD为取模运算,用线性探测再散列法处理冲突,在地址范围为0~14散列区中,试用关键字序列(19,27,26,28,29,40,64,21,15,12)造一个哈希表,回答下列问题:
1.画出该哈希表的存储结构图;
2.若查找关键字40,必须依次与表中哪些关键字比较大小?
3.假定每个关键字的查找概率相同,试求查找成功时的平均查找长度。(共13分)
五、给定头指针为ha的单链表A,和头指针为hb的递增有序单链表B。试利用表A和表B的结点,将表A和表B归并为递增有序表C,其头指针为hc,允许有相同data值(数据元素)的结点存在,表A,B,C均带表头结点。
例如,给定:
数据结构试卷 数据结构试题库集及答案
{if(pa->data<=qc->data)
;
else
{ pc=qc;
qc=;
}
}
fa=;
pa=;
fa->next=;
;
}
}
六、设下图二叉树B2的存储结构为二叉链表,root为根指针,结点结构为:(1child,data,rchild)其中:lchild,rchild分别为指向左右孩子的指针,data为字符型。(www.61k.com](共10分)
1. 对下列二叉树B2,执行下列算法traversel(root),试指出其输出结果;
2.假定二叉树B2共有n个结点,试分析算法traversal的时间复杂度。结点类型定义如下:
struct node
{ chardata;
struct node *lchild,*rchild;
};
算法如下:
voidtraversal(structnode *root)
{if(root)
{ prinft(“%c”,root->data);
traversal(root->lchild); 二叉树B2 prinft(”%c”,root->data);
traversal(root->rchild);
} }
数据结构试卷 数据结构试题库集及答案
七、算法设计题(要求:(1)写出所用数据结构的类型定义和变量说明;(2)写出算法,并在相关位置加注释,以提高算法的可读性。(www.61k.com))
1.试设计一算法:输入一个有m行n列的整数矩阵,然后将每一行的元素按非减次序输出。例如,若输入:
4,3,5,6,2
9,8,1,2,8
7,1,2,3,8
则输出如下结果:
2,3,4,5,6
1,2,8,8,9
1,2,3,7,8
2.如果字符串的一个子串(其长度大于1)的各个字符均相同,则称之为等值子串。试设计一算法:输入字符串S,以’!’为结束标志,如果串S中不存在等值子串,则输出信息:”无等值子串”,否则求出(输出)一个长度最大的等值子串。
例如,若S=”abcl23abcl23!”,则输出:”无等值子串”;
又如,若S=”abcaabcccdddddaaadd!”,则输出等值子串:”ddddd”。(共20分)
北京理工大学2001年程序设计(含数据结构)试题
第二部分 数据结构(共50分)
一、选择题(12分,每题2分)
1.下列数据中哪些是非线性数据结构。
A.栈 B.队列 C.完全二叉树 D.堆
2.静态链表中指针表示的是。
A.内存地址 B.数组下标
C.下一元素地址 D.左、右孩子地址
3.用不带头结点的单链表存储队列时,其队头指针指向队头结点,其队尾指针指向队尾结点,则在进行删除操作时。
A.仅修改队头指针
B.仅修改队尾指针
C.队头,队尾指针都要修改
D.队头,队尾指针都可能要修改
4.在下列排序算法中,哪一个算法的时间复杂度与初始排列无关。
A.直接插入排序 B.起泡排序
C.快速排序 D.直接选择排序
5.二叉树第i层结点的结点个数最多是(设根的层数为1)。
A.2i-1 B.2i-1 C.2i D.2i-1
6.树的后根遍历序列等同于该树对应的二叉树的。
A.先序序列 B.中序序列 C.后序序列
二、填空(8分,每空1分)
1.数据结构中评价算法的两个重要指标是——。
2.顺序存储结构是通过表示元素之间的关系的。链式存储结构是通过表示元素之间的关系的。
3.AOV网中,结点表示,边表示。AOE网中,结点表示,边表示。
4.哈夫曼树是。
三、求解下列问题(25分,每题5分)
1.请用C语言给出线性链表的类型定义。
2.已知二叉树的先序序列:CBHEGAF,中序序列:HBGEACF,试构造该二叉树。
3.设散列表的地址空间为0到12的存储单元,散列函数为:h(key)=key mod 13,用链地址法解决冲突,初始时散列表为空。现依次将关键字25,33,48,25,43,38,39插入散列表,试画出完成上述所有插入操作后散列表的状态,并计算在等概率的情况下,在该表中查找成功的平均查找长度。
4.给出如下图所示的图形。
1)试写出该图的邻接表;
2)试写出该图从结点0出发的深度优先遍历序列和广度优先遍历序列,并画出遍历过程中所经的路径。
数据结构试卷 数据结构试题库集及答案
{ p=NULL;q=L;
while(q!=NULL)
{
q->next=p;
p=q;
}
}
2.全国统考答题
设二叉树用二叉链表存储,试编写按层输出二叉树结点的算法。[www.61k.com]
3.单独考试答题(可在2或3中任选一题做)
试编写在带头结点的单链表中删除(一个)最小值结点的(高效)算法。
voiddelete(Linklist &L)
北京邮电大学2001年数据结构试题
一、选择题(10分,每题2分)
1.B+树是应用在( )文件系统中。
①ISAM ②VSAM
2.将一棵树t转换为孩子-兄弟链表表示的二叉树h,则t的后根遍历是h的( )。
①前序遍历②中序遍历③后序遍历
3.一个有向无环图的拓扑排序序列( )是惟一的。
①一定②不一定
4.将10个元素散列到100000个单元的哈希表中,则( )产生冲突。
①一定会②一定不会③仍可能会
5.若要求尽可能快地对序列进行稳定的排序,则应选( )。
①快速排序②归并排序③冒泡排序
二、填空题(20分,每空2分)
1.数据的逻辑结构是指。
2.区分循环队列的满与空,只有两类办法,它们是和。
3.用一维数组B以列优先存放带状矩阵A中的非零元素A[i,j](1≤i≤n,i-2≤j≤i+2),B中的第8个元素是A中第行、第列的元素。
4.字符串’ababaaab’的nextval函数值为——。
5.下图中的强连通分量的个数为个。
6.外部

7.若不考虑基数排序,则在排序过程中,主要进行的两种基本操作是关键字的和记录的
三、简答题(15分,每题5分)
1.特殊矩阵和稀疏矩阵哪种压缩存储后会失去随机存取的功能?为什么?
数据结构试卷 数据结构试题库集及答案
2.试问线索二叉树的目的何在?
3.在多关键字排序时,LSD和MSD两种方法的特点是什么?
四、应用题(25分,每题5分)
1.画出按下表中元素的顺序构造的平衡二叉排序树,并求其在等概率的情况下查找成功的平均查找长度。[www.61k.com) {15,12,24,3,27,21,18,6,36,33,30,26,3}
2.假设用于通信的电文由字符集{a,b,c,d,e,f,g}中的字母构成,它们在电文中出现的频率分别为{0.31,0.16,0.10,0.08,0.11,0.20,0.04}。
(1)为这7个字母设计哈夫曼编码;
(2)对这7个字母进行等长编码,至少需要几位二进制数?哈夫曼编码比等长编码使电文总长压缩多少?
3.试推导当总盘数为n时的Hanoi塔的移动次数。
4.一棵满k叉树,按层次遍历存储在一维数组中,试计算结点下标为u的结点的第i个孩子的下标以及结点下标为v的结点的父母结点的下标。
5.有一图的邻接矩阵如下,试给出用弗洛伊德算法求各点间最短距离的矩阵序列A(1)、A(2)、A(3)和A(4)。
五、算法(30
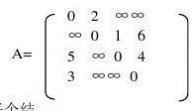
每题10分)
1点含有5个正整型的数据元素(若最后一个结点的数据元素不满5个,以值0填充),试编写一算法查找值为n(n>0)的数据元素所在的结点指针以及在该结点中的序号,若链表中不存在该数据元素则返回空指针。
2.将一组数据元素按哈希函数H(key)散列到哈希表m(0..m)中,用线性探测法处理冲突(H(key)+1、H(key)+2、?、H(key)-1,假设空单元用EMPTY表示,删除操作是将哈希表中结点标志位从INUSE标记为DELETED,试写出该散列表的查找、插入和删除三个基本操作算法。
3.给出算法将二叉链表表示的表达式二叉树按中缀表达式输出,并加上相应的括号。
北京航空航天大学2001年 数据结构与程序设计试题
一、问答题(本题10分)
一般情况下,线性表可以采用哪几种存储结构?请分别叙述每一种存储结构的构造原理与特点。
二、(本题10分)
已知AOE网为G=(V,E),V={v1,v2,v3,v4,v5,v6,v7,v8,V9,vl0},E={a1,a2,a3,a4,a5,a6,a7,a8,a9,al0,a11,a12,a13,a14},其中:
a1:(v1,v2)5 a2:(v1,v3)6 a3:(v2,v5)3 a4:(v3,V4)3
a5:(v3,v5)6 a6:(v4,v5)3a7:(v4,v7)1 a8:(v4,v8)4
a9:(v5,v6)4 al0:(v5,v7)1 a11:(v6,vl0)4 a12:(v7,v9)5
a13:(v8,v9)2 a14:(v9,v10)2
注:顶点偶对右下角的数字表示边上的权值。
请按下述过程指出所有关键路径:
ee[1:10]:
le[1:10]:
e[1:14]:
l[1:14]:
其中,ee[i]与le[i]分别表示事件vi的最早发生时间与最晚发生时间;e[i]与l[i]分别表示活动ai的最早开始时间与最晚开始时间。
三、(本题共30分,每小题10分)
欲建立一文献库,其正文(文献本身)存放在一个双向循环链表的各个链结点中。
1.为便于链结点的插入、删除操作,以及按题目、发表日期、发表者名称、主题词(假设每文最多给出三个主题词)进行检索,请设计该链表的链结点结构(给出链结点每个域的名称,并说明该域内存放什么信息。注:以下各小题设计链结点结构也这样要求)。画出整个链表结构的示意图。
2.设计一个三级索引结构,其中第三级索引称为题目索引,是按文献题目构造的稠密索引,通过该级索引并根据给定题目可得到每个文献的存放地址;该级索引按文献学科类分类存放。第二级索引称为中类索引,是题目索引的索引,指出同一中类的文献题目索引的存放位置(例如农林类、气象类??,古代史类、近代史类??)。第一级索引称为大类索引,指出同一大类(如:自然科学类、历史类??)的文献的中类索引的存放位置。请设计每一级索引的结点结构,并画出该索引的整体示意图。
3.再设计一种三级索引结构,其中第三级索引仍是题目索引(与2题所述相同),第二级索引把具有相同主题词的文献题目索引地址组织在一个单链表中。第一级索引称为主题词索引,用文献给出的主题词作关键字组成杂凑表,即该级索引为一个杂凑表,能够指出具有同一主题词的文献题目索引的索引链表的第一个链结点的存储位置。该杂凑表采用链
数据结构试卷 数据结构试题库集及答案
地址法处理冲突。[www.61k.com]请设计每一
级索引的结点结构,并画出该索引的整体示意图。
四、(本题10分)
已知非空线性链表由list指出,链结点的构造为

五、(本题15分,第1小题5分,第2小题10分)
已知求两个正整数m与n的最大公因子的过程用自然语言可以表述为反复执行如下动作:
第一步:若n等于零,则返回m;
第二步:若m小于n,则m与n相互交换;否则,保存m,然后将n送m,将保存的m除以n的余数送n。
1.将上述过程用递归函数表达出来(设求x除以y的余数可以用xMODy形式表示)。
2.写出求解该递归函数的非递归算法。
六、(本题10分)
函数voidinsert(char *s,char *t,int pos)将字符串t插入到字符串s中,插入位置为pos。请用C语言实现该函数。假设分配给字符串s的空间足够认字符串t插入。(说明:不得使用任何库函数。)
七、(本题15分) 。
命令sgrep用来在文件中查找给定字符串,并输出串所在行及行号。
命令格式为:sgrep[-i]filenamesearchstring
其中:-i:表示查找的大小写无关,省略时表示大小写相关。
filename:给定文件名。
searchstring:所要查找的串。
用C语言实现该程序,该程序应具有一定的错误处理能力。(提示:使用命令行参数)
注意:除文件及输入/出操作可使用库函数外,其他不允许使用库函数。
西安交通大学2001年数据结构试题
一、判断下列叙述是否正确,正确的填√,不正确的填×(10分)
1.数据对象就是一组数据元素的集合。 ( )
2.任何一棵前序线索二叉树,都可以不用栈实现前序遍历。 ( )
3.就平均查找长度而言,分块查找最小,折半查找次之,顺序查找最大。 ( )
4.用shell方法排序时,若关键字的排列杂乱无序,则效率最高。 ( )
5.在m阶B-树中,所有非终端结点至少包含?m/2?。 ( )
二、选择填空题(15分)
1.假设以数组A[m..n]存放循环队列的元素,其头指针是front,当前队列有k个元素,则队列的尾指针为( )。
A.(front+k)mod(n-m+1)
B.(m+k)mod n+front
C.(front-m+k)mod(n-m+1)+m
D.(front-m+k)mod(n-m+1)
2. 已知二叉树如右图所示,此二叉树的顺
序存储的结点序列是( )。
A.123□45 B.12345
C.12□435 D.□24153
3.若用冒泡排序对关键字序列{20,17,11,8,6,2}从小到大进行排序,则需要交换的总次数为( )。
A.3 B.6 C.12 D.15
4.对于一个头指针为head的带头结点的单链表,判定该表为空表的条件是( )。
A.head=NULL B.head->next=NULL
C.head->next==head D.head!=NULL
5.已知串s=“ABCDEFGH'’,则s的所有不同子串的个数为( )。
A.8 B.9 C.36 D.37
三、填空题(15分)
1.假设一个12阶的上三角矩阵A按行优先顺序压缩存储在一维数组B中,则非零元素a8,9,在B中的存储位置k=。
2.在拓扑排序中,拓扑序列的第一个顶点必定是的顶点。

3.由六个分别带权值为5,12,9,30,7,16的叶子结点构造一棵哈夫曼(Huffinan)树,该树的结点个数为,树的带权路径长度为。
数据结构试卷 数据结构试题库集及答案
4.在的情况下,链队列的出队操作需要修改尾指针。[www.61k.com]
5.对表长为n的顺序表进行分块查找,若以顺序查找确定块,且每块长度为s,则在等概率查找的情况下,查找成功时的平均查找长度为。
四、简答题(50分)
1.(6分)已知广义表L:((a,b),(c,(d,(e))),f)。
(1)试利用广义表取表头head(L)和取表尾tail(L)的基本运算,将原子c从下列广义表中分解出来,请写出运算表达式。
(2)请给出下列表达式的运算结果:
①hem(tail(head(tail(L)))) ②tail(tail(head(L)))
2.(10分)已知一个图G=(V,E),其中:
V={a,b,c,d,e,f};
E={<a,b>,<a,d>,<a,e>,<d,e>,<e,b>,<c,b>,<c,e>,<c,f>,<f,e>}
(1)请画出该图,并写出邻接矩阵。
(2)根据邻接矩阵,分别同从顶点a出发的深度优先和广度优先遍历序列。
(3)画出由此得到的深度优先和广度优先生成树(或森林)。
3.(6分)已知一个栈s的输入序列为abcd,下面两个序列能否通过栈的PUSH和POP操作输出;如果能,请写出操作序列;如果不能,请说明原因。
①dbca ②cbda
4.(5分)设模式串t=”abaabacababa”,试求出t的next和nextval函数值。
5.(7分)已知一组关键字K={20,15,4,18,9,6,25,12,3,22},请判断此序列是否为堆?如果不是,请调整为堆。
6.(8分)对于表达式(a-b+c)*d/(e+f)
(1)画出它的中序二叉树,并标出该二叉树的前序线索;
(2)给出它的前缀表达式和后缀表达式。
7.(8分)设散列长度为9,散列函数为H(k)=k mod 9,给出关键字序列:23,45,14,17,9,29,37,18,25,41,33,采用链地址法解决冲突。
(1)请画出散列表;
(2)求出查找各关键字的比较次数;
(3)计算在等概率情况下,查找成功的平均查找长度。
五、算法填空(10分)
已知图的邻接表存储结构描述如下:
CONST N=图的顶点数:
TYPE arcprt=↑arcnode;
arcnode=RECORD
adjvex:integer;
nextarc:acrptr
END;
vexnode=RECORD
vexdata:char;
firstarc:arcptr
END;
Graph=ARRAY[1..N]ofvexnode;
下面是一个图的深度优先遍历的非递归算法,请在处填上适当内容,使其成为一个完整算法。
PROCEDURE traver_dfs(g:graph);
VARvisited:ARRAY[1..N]ofBOOLEAN;
s:STACK;{s为一个栈}
p:arcptr:
BEGIN
FORi:=1 TO N DO visited[i]:= INISTACK(S);
FOR i=1 TO NDO
BEGIN ②
BEGIN
visited[i]:=true;
visit(i); //访问第i个顶点
数据结构试卷 数据结构试题库集及答案
IF g[i].firstarc≠NILTHEN
PUSH(d,g[i].firstarc)
END
WHILE ③DO
BECIN
p:POP(s);
IF p↑.nextarc≠NILTHEN
PUSH(s,p↑.nextarc);
j:=p↑.adjvex;
IF NOTvisited[i] THEN
BEGIN
visited[j]:=true;
visit(j);
IF e[j].firstarc≠NILTHEN ④
END
END
END
END
中国科学院软件研究所2001年数据结构试题
一、单项选择题(每空2分,共20分)
1.下列函数中渐近时间复杂度最小的是( )。(www.61k.com)
A.T1(n)=nlog2n+5000n B.T2(n)=n2-8000n
C.T3(n)=nlog221-6000n D.T4(n)=2nlog2n-7000n
2.线性表的静态链表存储结构与顺序存储结构相比优点是( )。
A.所有的操作算法实现简单
B.便于随机存取
C.便于插入和删除
D.便于利用零散的存储器空间
3.设栈的输入序列为1,2,?,n,输出序列为a1,a2,?,an,若存在1≤k≤n使得ak=n,则当k≤i≤n时,ai为( )。
A.n-i+l B.n-(i-k) C.不确定
4.设高度为h的二叉树(根的层数为1)上只有度为0和度为2的节点,则此类二叉树中所包含的节点数至少为
( )。
A.2h B.2h-1 C.2h+l D.h+l
5.设指针p指向线索树中的某个结点,则查找*p在某种次序下的前驱或后继不能获得加速的是( )。
A.前序线索树中查找*p的前序后继
B.中序线索树中查找*p的中序后继
C.中序线索树中查找*p的中序前继
D.后序线索树中查找*p的后序前继
6.假定有k个关键字互为同义词,若用线性探测法将这k个关键字存入散列表中,至少需要进行( )次探测。
A.k-1 B.k C.k+l D.k(k+1)/2
7.若待排序元素基本有序,则下列排序中平均速度最快的排序是( );若要求辅助空间为O(1),则平均速度最快的排序是( );若要求排序是稳定的,且关键字为实数,则平均速度最快的排序是( )。
A.直接插入排序 B.直接选择排序 C.Shell排序
D.冒泡排序 E.快速排序 F.堆排序
C.归并排序 H.基数排序
8.对于多关键字而言,( )是一种方便而又高效的文件组织文式。
A.顺序文件 B.索引文件 C.散列文件 D.倒排文件
二、问答题(共25分)
1.设A[-2:6;-3:6]是一个用行主序存储的二维数组,已知A[-2,-3]的起始存储位置为loc(-2,-3)=1000,每个数组元素占用4个存储单元,求:(6分)
1)A[4,5]的起始存储位置loc(4,5);
2)起始存储位置为1184的数组元素的下标。
2.给定二叉树的先序和后序遍历序列,能否重构出该二叉树?若能,试证明之,否则给出反例。(6分)
3.在含有n个关键字的m阶B-树中进行查找,至多读盘多少次?完全平衡的二叉排序树的读盘次数大约比它大多少
数据结构试卷 数据结构试题库集及答案
倍?(设两种树中的每个节点均是一个存储块)。(www.61k.com)(8分)
4.用向量表示的循环队列的队首和队尾位置分别为1和max_size,试给出判断队列为空和为满的边界条件。(5分)
三、阅读程序题(共10分)
1.设G是一个有向无环图,试指出下述算法的功能,输出的序列是G的什么序列?(10分)
voidDemo(ALGraph G)
{//G是图的逆邻接表,向量outdegree的各分量初值为0。
for(i=0;i<G.NodeNum;i++)
for(p=G.adjlist[i].firstedge;p;p=p->next)
//扫描i的入边表
outdegree[p->adjvex]++; //设p->adjvex=j,则将<i,j>的起点
j的出度加1
initStack(&s); //设置空栈s
for(i=0;i<G.NodeNum;i++)
if(outdegree[i]==0)
Push(&s,i); //出度为0的顶点i入栈
while(!StackEmpty(s)) //栈s非空
{ i=Pop(&Q); //出栈,相当于删去顶点i
prinft(“%c”,G.adjlist[i].vertex);//输出顶点i
for(p=G.adjlist[i].firstedge;p;p=p->next)
{ //扫描i的入边表
j=p->adjvex;//j是i的入边<j,i>的起点
outdegree[j]--; //j的出度减1,即删去i的入边<j,i>
if(!outdegree[j])
Push(&s?,j); //若j的出度为0,则令其入栈
}//endfor
}//endwhile
}//endDemo
四、算法题(每题15分,共45分)
1.试设计算法在O(n)时间内将数组A[1..n]划分为左右两个部分,使得左边的所有元素值均为奇数,右边的所有元素值均为偶数,要求所使用的辅助存储空间大小为O(1)。
2.试写一递归算法,从大到小输出二叉排序中所有的值不小于x的关键字,要求算法的时间为O(h+m),其中h为树的高度,m为输出的关键字个数。
3.设G是以邻接表表示的无向图,v0是G中的一个顶点,k是一个正的常数。要求写一算法打印出图中所有与v0有简单路径相通,且路径长度小于等于k的所有顶点(不含v0),路径长度由路径上的边数来定义。
参考答案
第一章
1.(a)是线性结构,对应的数据逻辑结构图见图1-2。
(b)是树形结构,对应的数据逻辑结构图见图1-3。
(c)是有向图,其数据逻辑结构图见图1-4。
2.(a)O(m×n)
2 (b)s+=b[i][j]的重复执行次数是n(n+1)/2,时间复杂度是O(n)
(c)O(log2n)
3.D 4.D 5.D
第二章
一、单项选择题
(1) ~(5) DACAA (6)~(10) BAAAD
二、填空题
(1)链域 (2)插入 (3)删除 (4)n-i+1 (5)n-I (6)n/2 (7)(n-1)/2
(8)h=NULL (9)h->next=NULL (10)p->next=h (11) p->next->prior=s
(12)p->next=s (13)p->prior->next (14)p->prior=s (15)p->next->prior=p
(16)p->prior->next=p (17)p->next->prior=p->prior (18)r->next=p
(19)r=p (20)r->next=q->next
三、应用题
1.顺序表:逻辑上相邻的数据元素其物理存储位置必须紧邻。其优点是:节省存储,可以随机存取。
链表:逻辑上相邻的数据元素其物理存储位置不要求紧邻,用指针来描述结点间的逻辑关系,故插入和删除运算比
数据结构试卷 数据结构试题库集及答案
较方便。(www.61k.com]
2.在带表头结点的单链表中,头指针指向表头结点,不带表头结点的单链表中,头指针指向表中第一个结点(又称首元),当进行查找运算时,必须从头指针开始去顺次访问表中每一个元素。
头结点是另设一个结点,其指针域指向存放表中第一个元素的结点,设置头结点的好处是:无需对在第一个结点前插入一个结点或删除一个结点时进行特殊处理,也可以对空表和非空表的运算进行统一处理。
四、算法设计题
1. 先判断表满否,若表未满,则从最后一个元素an开始,逐个与x进行比较,若ai>x(1≤i≤n),则将ai后移一个位置,直到ai≤x,最后把x插入到这个位置,表长+1。算法描述如下:
#define M 100
int insort(Slist *L,int z)
{int i;
if(L->n>=M)
{printf(“overflow");
return 0;}
else
for(i=L->n;i>=0;i--)
if(L->data[i]>x
L->data[i+1]=L->data[i];
else break;
L->data[i+1]=x;
L->n++;
return 1;
}
2.逐个查找单链表中的结点x,并计数。
int number(lnode *h,int x)
{ int n=0;
while(h)
{if(h->data==x)
n++;
h=h->next;
}
return s;
}
3.前插法建立带表头结点的单链表算法中的tag为输人数据结束标志。
Lnode *createhh(int tag)
{ int x;
Lnode *p,*h=(Lnode *)malloc(sizeof(Lnode));
h->next=NULL;
printf(“input x:”);
scanf(“%d”,&x);
while(x!=tag)
{p=(Lnode*)malloc(sizeof(Lnode));
p->data=x;
p->next=h->next;
h->next=p;
scanf(“%d”,&x);
}
return h;
}
4.先建立一个表头结点,用尾插法建立该单链表。然后将尾结点的指针域值置为表中第一个结点的首地址,最后释放表头结点。算法描述如下:
Lnode *createht(int tag)
{ int x;
Lnode *p,*r,*h=(Lnode *)malloc(sizeof(Lnode));
r=h;
数据结构试卷 数据结构试题库集及答案
printf(“input x:”);
scanf(“%d”,&x);
while(x!=tag)
{p=(Lnode*)malloc(sizeof(Lnode));
p->data=x;
r->next=p;
r=p;
scanf(“%d”,&x);
}
r->next=h->next;
free(h);
return r;
}
5.设p指向待逆置链表中的第一个结点,先将表头结点的链域置空。[www.61k.com)顺次取出待逆置链表中的第一个结点,用前插法插入到带表头结点的单链表中。
Void reverseh(Lnode *h)
{ Lnode *s,*p=h->next;
h->next=NULL;
while(p)
{s=p;p=p->next;
s->next=h->next;
h->next=s;
}
}
6.逐个检测顺序表中其值在x和y之间的元素,并计数k,再将其值大于y的元素向前移动k个元素。算法描述如下:
void deletexy(Slist *a,int x,int y)
{ int i,k=0;
for(i=0;i<a->n;i++)
if(a->data[i]>=x&&a->data[i]<=y)
k++;
else
a->data[i-k]=a->data[i];
a->n=a->n-k;}
第三章
一、单项选择题
(1)-(5) CACCB (6)-(7)BC
二、填空题
(1)栈顶 (2)栈底 (3)队尾 (4)队首 (5)O(n) (6)O(1) (7)O(1)
(8)O(1) (9)front=rear (10)(rear+1)%m=front (11)(rear-front+m)%m
(12) 向是的两端
三、应用题
1.栈和队列是操作位置受限的线性表,即对插入和删除运算的位置加以限制。栈是仅允许在表的一端进行插入和删除运算的线性表,因而是后进先出表。而队列是只允许在表的一端插入,另一端进行删除运算的线性表,因而是先进先出表。
2.循环队列的优点是解决了“假上溢”问题。
设用数组A[m]来存放循环队列,设front指向实际队首,rear指向新元素应插入的位置时,front=rear即可能是队空,又可能是队满,为了区分队空和队满可采用下列三种方案:
(1)用“少用一个元素空间”的方案,初态fron=rear=0,判断队空的条件是fron=rear,判断队满的条件是(reaf+1)%m=front。
(2)用“设队空标志”的方法,如设front=-1时为队空标志,初态是front=-1,rear=0。当front=rear时则队满。
(3)用count存放表中元素个数,当count=0时为队空,当count=m时为队满。
3.若进栈序列为a,b,c,d,全部可能的出栈序列是:
abcd,abdc,acbd,acdb,adcb,bacd,badc,bcad,bcda,bdca,cbad,
cbda,cdba,dcba,
数据结构试卷 数据结构试题库集及答案
不可能的出栈序列为:adbc,bdac,cdab,cadb,cadb,dabc,dacb,
dbac,dbca,dcab。(www.61k.com)
4.由于队列中操作遵循的原则是先进先出,出队元素的顺序是bdcfea,故元素进队的顺序也是bdcfea,元素进队的顺序与元素出栈的顺序相同,在栈中存取数据遵循的原则是后进先出,要得到出栈序列bdcfea,栈的容量至少是应该存放3个元素的空间。
5. 3 4 25 6 15+-/8*+
四、算法设计题
1.解本题的基本思想是:先将顺序队列q中所有元素出队,并依次进入顺序栈s中,然后出栈,再依次入队。设队列中的元素为a1,a2,…,an,出队并进栈的序列为a1,a2,…,an,出栈并入队的序列为an,an-1,…,a1,可见顺序队列q中所有元素已逆置了。顺序队列的类型定义为:
#define MAX 100
typedef struct
{int data[MAX];
int front,rear;
}Squeue;
算法描述如下:
void invert(Squeue *q)
{int s[MAX],top=0;
while(q->front<q->rear)
s[top++]=q->data[++q->front];
q->front=-1;q->rear=0;
while(top>0)
q->data[q->rear++]=s[--top];
}
2.
(1)递归算法:
int f1(int n)
{ int f;
if(n==0) return (1);
else
return(n*f1(n/2));
}
(2)将上述递归函数转换成非递归函数时,使用了一个栈,用于存储调用参数和函数值,这里采用一维数组s[n]作为栈,用一个栈顶指针top。算法如下:
#define maxlen 200;
int f2(int n)
{ int s[maxlen];
int top=0,fval=1;
while(n!=0)
{s[top]=n;
n=n/2;
top++;
}
while(top>=0)
{fval=fval*s[top];
top--;
}
return fval;
}
3.仅设队尾指针的带表头结点的循环链表,找队首结点为rear->next->next。
(1)初始化
Lnode *int queue()
{Lnode *rear;
rear=(Lnode*)malloc(sizeof(Lnode));
rear->next=rear;
数据结构试卷 数据结构试题库集及答案
return rear;
}
(2)入队算法
Lnode *enqueue(Lnode *rear,int x)
{ Lnode *p=(Lnode*)malloc(sizeof(Lnode));
p->data=x;
p->next=rear->next;
rear->next=p;
return p;
}
(3)出队算法
int outqueue(Lnode *rear,int *x)
{ Londe *p;
if(rear->next=rear)
{printf(“queue is empty”);
return 0;
}
p=rear->next->next;
*x=p->data;
rear->next->next=p->next;
free(p);
return 1;
}
第四章
一、单项选择题
(1)一(5)DBDBD (6)-(10)BDBBA (11)-(13)CAA
二、填空题
(1)两个串的长度相等且对应位置上的字符相同。(www.61k.com]
(2)是由零个字符组成的串 (3)0
(4)”goodmorning” (5)”nin” (6)4 (7)”goto” (8)m
(9)m(n-m+1) (10)Loc(a[0][0])=1000-88=912
(11)n(n+1)/2+1 (12) n(n+1)/2 (13)i(i-1)/2+j-1
(14)(2n-j+2)(j-1)/2+i-j (15)3 (16)4 (17)a(18)((b),((c,(d))))
(19)三元组表 (20)十字链表 (21)子表 (22)子表
三、应用题
1.用联接、取子串、置换运算将串S=”(xyz)+*”转化为T=”(x+z)*y”。
C1=substr(S,3,1)=”y” C2=substr(S,6,1)=”+”
C3=substr(S,7,1)=”*” C4=concat(C3,c11)=”*y”
T=replace(S,3,1,C2)=replace(S,3,1,substr(S,6,1))=”(x+z)+x”
T=replace(T,6,2,concat(C3,C1))=replace(T,6,2,concat(substr(S,7,1)),substr(S,3,1)))=”(x+z)*y”。 若只用取子串和联接操作进行的转换过程是:
C1=concat(substr(S,1,2),substr(S,6,1))=”(x+”
C2=concat(substr(S,7,1),substr(S,3,1))=”*y”
T=concat(concat(concat(substr(S,1,2),substr(S,6,1)),substr(S,4,2)),concat(substr(S,7,1),substr(S,3,1)))
2.串S的长度为n,其中的字符各不相同,所以S=”(x+z)*y”中含1个字符的子串有n个,2个字符的子串有n-1个……,含n-2个字符的子串有3个,含n-1个字符的子串有2个,共有非平凡子串的个数是n(n+1)/2-1。

素aij的下标I和j与其在一维数中存放的下标k之间存在一一对应关系,故不会失去随机存取功能。
数据结构试卷 数据结构试题库集及答案
稀疏矩阵中零元素的分布没有一定规律,可以将非零元素存于三元组表中,非零元素aij在三元组中的存放位置与i、j没有对应关系,故失去随机存取功能。(www.61k.com]
5.N阶对称矩阵A中,aij=aji,可以仅存放下三角元素(或上三角元素)。设r=max(i,j),c=min(i,j),
k=r(r-1)/2+c-1;
例如,4阶对称矩阵A,按行优先顺序存于一维数组F[10]中,

当i=2,j=3时,k=4
(2)当对称矩阵A按列优先顺序压缩存放,若仅存放上三角元素,则有:
k=r(r-1)/2+c-1
例如,4阶对称矩阵A,按列优先顺序存于一维数组F[10]中,

第五章
一、单项选择题
(1)-(5)BBCDC (6)-(10)BCABC (11)—(15)DABBD (16)-(19)CCABB
(20)-(24) BBBAC (25)-(27)DBC
二、填空题
(1)有零个或多个 (2)有且仅有一个
(3)根据树的广义表表示,可以画出这棵村,该树的度为4。
(4)树的深度为4
(5)树中叶子结点个数为8
ki-1(6)n0=14 (7)n-2m+1 (8)2-1 (9)2 (10)133 (11)59
55(12)2=32 (13)?log2(n+1)?=?log269?=7 (14) 2-1+6=37 (15) 19
7(16)2-1-20=107 (17)右 (18)m+1 (19)n+1 (20) 2m-1
(21)中序 (22)直接前驱结点 (23)直接后继结点
三、应用题
1.具有n个结点的满二叉树中只有度为2和度为0的结点,故n=2n0-1,n0=(n+1)/2。
5.构造一棵二叉树应该先确定根结点,由后序序列最后一个字母A确定根结点,可将前序序列的第一个字母*改为A。在中序遍历序列中A的左子树中含4

个字母,右子树中含3个字母,在后序遍历序列中左子树的后序遍历子序列为*EDB,可将左子树的后序遍历序列和中序遍历序列互相补足,分别是CEDB和CBDE。由这两个子序列可知左子树的根结点为B,D又为以B为根结点的右子树的根结点,E为D的右孩子,所以在前序序列中A的左子树的前序序列为:BCDE,在根结点A的右子树中,由后序遍历序列可确定其根结点为F,再确定其中序序列为GHF,进一步确定其前序序列为FGH,补足*处后,三个遍历序列为:
(1)前序遍历序列是:ABCDEFGH
(2)中序遍历序列是:CBDEAGHF
(3)后序遍历序列是:CEDBHGFA
由前序遍历序列和中序遍历序列可构造一棵二叉树如右图。
四、算法设计题
1.求叶子结点个数。
算法描述如下:
int leafnum(Csnode *t,int n)
{Gsnode *p;
if(t==NULL) return 0;
p=t->fc;
if(p==NULL)
n++;
while(p)
{n=leaf(p,n);
p=p->ns;
}
return n;
数据结构试卷 数据结构试题库集及答案
}
2.交换左右孩子。[www.61k.com]算法如下:
void exchange(Btnode *t)
{Btnode *p;
if(t)
{exchange(t->lchild);
exchange(t->rchild);
if(t->lchild||t->rchild)
{p=t->lchild;
t->lchild=t->rchild;
t->rchild=p;}
}
}
3.void printbtree(Btnode *r)
{if(r)
{printf(“%c”,r->data);
if(r->lchild||r->rchild)
printf(“(”);
printbtree(r->lchild);
if(r->rchild)
printf(“,”);
printbtree(t->rchild);
printf(“)”);
}
}
4. #define MAX 100
int checkt(Btnode *t)
{Btnode *s[MAX];
int i,n=0;
for(i=0;i<MAX,i++)
s[i]=NULL;
if(t==NULL)
return 0;
i=0;
S[0]=t;
While(I<=n)
{if(!s[i])
return 0;
if(s[i]->lchild)
{n=2*i+1;
s[n]=s[i]->lchild;
}
if(s[i]->rchild)
{n=2*i+2;
s[n]=s[i]->rchild;
}
i++;
}
return 1;
}
5.(1)前序遍历二叉树的非递归算法的基本思想是:从二叉树的根结点开始,沿左支一直走到没有左孩子的结点为止,在走的过程中访问所遇结点,并把非空右孩子进栈。当找到没有左孩子的结点时,从栈顶退出某结点的右孩子,此时该结点的左子树已遍历结束,然后按上述过程遍历该结点的右子树,如此重复,直到二叉树中所有结点都访问完毕为上。算法如下:
void preorder(Btnode *t)
数据结构试卷 数据结构试题库集及答案
{ int I=0;
Btnode *p,*s[M];
P=t;
Do
{ while(p)
{printf(“%c\t”,p->data);
if(p->rchild!=NULL)
s[i++]=p->rchild;
p=p->lchild;
}
if(i>0)
p=s[--i];
}while(i>0||p!=NULL);
}
(2)后序遍历二叉树的非递归算法的基本思想:采用一个栈保存返回的结点,先遍历根节点的所有结节点并入栈,出栈一个结点,然后遍历该结点的右结点并入栈,再遍历该右结点的所有左结点并入栈,当一个结点的左右子树均访问后再访问该结点,如此这样,直到栈为空为止。[www.61k.com)其中的难点是如何判断一个结点t的右结点已访问过,为此用p保存已访问过的结点(初值为NULL),若t->right=p成立(在后序遍历中,t的右节点一定是在t之前访问),说明t的左右子树均已访问,现在应访问t。算法如下:
void postorder(Btree *t)
{ Btree *s[maxsize];
Btree *p;
int flag,top=-1;
Do
{ while(t)
{ top++;
s[top]=t;
t=t->left;
}
p=NULL;
flag=1;
while(top=-1&&flag)
{ t=s[top];
if(t->right==p)
{ printf(“%d””,t->data);
top--;
p=t;
}
else
{ t=t->right;
flag=1;
}
}
}while(top!=-1)
}
6.求二叉树中从根结点到p结点之间路径长度的算法描述如下:
#define MAX 100
void path(Btnode *t,Btnode *p)
{ Btnode *s[MAX],*q=t;
int b[MAX],top=-1;
do {
while(q)
{s[++top]=q;
b[top]=0;
q=q->lchild;
数据结构试卷 数据结构试题库集及答案
}
if(top->-1&&b[top]==1)
{q=s[top];
if(q==p)
{printf(“根结点到q结点的路径是:”);
for(I=0;I<=top;I++)
printf(“%c”,s[I]->data);
return;
}
else top--;
}
if(top>-1)
{ p=s[top]->rchild;
b[top]=1;
}
}while(top>0);
}
7.判断以二叉链表存储的二叉树是否为完全二叉树的算法描述如下:
#define MAX 100
void checkt(BTnode *t)
{ Btnode *s[MAX];
int i,n=0;
for(i=0;i<MAX;i++)
s[i]=MAX;
if(t==NULL)
return 0;
s[0]=t;
while(i<=n)
{ if(!s[i])
return 0;
if(s[i]->lchild)
{ n=2*i+1;
s[n]=s[i]->lchild;
}
if(s[i]->rchild)
{ n=2*i+2;
s[n]=s[i]->rchild;
}
i++;
}
return 1;
}
第六章
一、单项选择题
(1)-(4)AACA (5)-(9)DBCAD (10)-(11)CB
(12)图G是一个非连通分量,至少有两个连通分量。[www.61k.com]含8个顶点的完全无向图共需28条边,另外一个顶点构成一个连通分量,所以至少含9个顶点。
二、判断题
1.正确2.错误3.正确 4.错误5.正确6.错误 7.正确 8.正确 9.正确
10.正确(若n个顶点依次首尾相接构成一个环的有向强连通图,至少含n条边,即邻接矩阵中至少有n个小于u的非零元素)。
11.错误 12.正确 13.错误 14.正确 15.正确
16.错误 17.错误 18.错误 19.正确
三、填空题
数据结构试卷 数据结构试题库集及答案
22(1)n(n-1)/2 (2)n(n-1) (3)n-1 (4)e (5)2e (6)出边 (7)人边 (8)n (9)有向图 (10)O(n) (11)O(n)
(12)O(n+e) (13)O(n+e) (14)Kruscal (15)prim
四、算法题
1.将图的深度优先遍历或广度优先遍历算法稍加改造,另设m保存访问的顶点个数,若已访问顶点个数m小于图中顶点个数n,则图G不连通,否则为连通。(www.61k.com]现将深度优先遍历的非递归算法改造如下:
采用邻接表表示,类型定义如下:
#define MaxV 20
typedef struct node
{int adjvex;
struct node *next;
}Enode;
typedef struct
{int data;
Enode *firste;
}Vnode;
typedef struct
{Vnode adjlist[MaxV];
int n;
int e;
}ALGraph;
int connect(ALGraph *G)
{int i,j,Visited[MaxV],m=0,top=0;
Enode *p,*S[MaxV];
For(i=0;i<n;i++)
Visited[i]=0;
Visited[0]=0;
Printf(“%c”,G->adjlist[0].data);
m++;
S[top++]=p->next;
j=p->adjvex;
if(visited[j]==0)
{visited[j]=1;
printf(“%c”,G->adjlist[j].data);
m++;
s[top++]=G->adjlist[j]->firste;
}
}
}
if(m<G->a)
return(0);
else
return(1);}
2. (1)解:顺序计算每个顶点链表的表中结点个数,就是该顶点的出度.
算法如下:
void outdegree(graph g,int v)
{arcnode *p;
int n=0;
p=g.adjlist[v].firstarc;
while(p)
{ n++;
p=p->nextarc;}
}
return n;
}
void outds(graph g)
数据结构试卷 数据结构试题库集及答案
{ int i;
printf(“各顶点出度:、\n”);
for(i=0;i<g.vexnum;i++)
printf(“顶点%d:%d\n”,i,outdegree(g,i));
}
(2)void maxoutds(graph g)
{ int maxv=0,maxds=0i,x;
for(i=0;i<g.vexnum;i++)
{ x=outdegredd(g,i);
if(x>maxds)
{maxds=x;maxv=1;}
}
printf(“最大出度:顶点%d的出度%d”,maxv,maxds);
}
(3)void zerods(graph g)
{ int i,x;
printf(“出度为0的顶点:\n”);
for(i=0;i<g.vexnum;i++)
{ x=outdegree(g,i);
if(x==0)
printf(“%d”,i);
}
}
(4)void arc(graph g)
{ int i,j;
arcnode *p;
printf(“输入边:\n”);
scanf(“%d,%d”,i,j);
p=g.adjlist[i].firstarc;
while(p!=NULL&&p->adjvex!=j)
p=p->nextarc;
if(p==NULL)
printf(“不存在!”);
else
printf(“存在<%d,%d>边:\n”,i,j);
}
第七章
一、单项选择题
(1) 一(5) DDCCD (6)一(9) DCCC
二、填空题
(1)8 (2)15 (3) 4.3 (4)中序 (5)记录的键值 (6)7
(7)63 (8)17 (9)17 (10)O(n) (11)O(log2n) (12)越大
(13)散列函数 (14)处理冲突方法 (15) 装填因子 (16)索引表
(17)该块的起始地址 (18) 100 (19)100 (20)101 (21)?log2(n+1)?
(22)同义词 (23)n(n+1)/2 (24) 63 (25) m (26)?m/2? (27)m-1
(28) ?m/2?-1 (29)m (30)?m/2?
三、应用题
1.判定树见下图。[www.61k.com)
查找成功的平均查找长度
ASL=(1+2*2+3*4+4*6)/13=41/13
查找失败时与键值最多比较次数为4。
2.二叉排序树见右图。在等概率情况下,


数据结构试卷 数据结构试题库集及答案
查找成功的平均查找长度ASL=29/9≈3.2
查找失败时,与键值最多比较次数是5。(www.61k.com]
3.构造一棵平衡二叉排序树
的过程见右图。
等概率情况下,查找成功的平均查
ASL=(1+2*2+3*4+4*2)/9≈2.8
查找失败时,与键值的最多比较次
4.按不同的输入顺序输入4、
二叉排序树见下图。
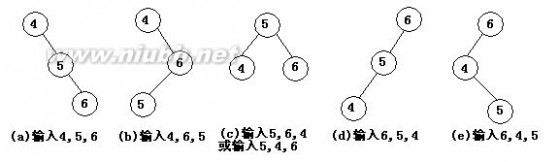
找长度 数是4。 5、6,建立相应的不同形态的
5.键值序列:{25,40,33,47,12,66,72,87,94,22,5,58} 散列地址: 3 7 0 3 1 0 6 10 6 0 5 3
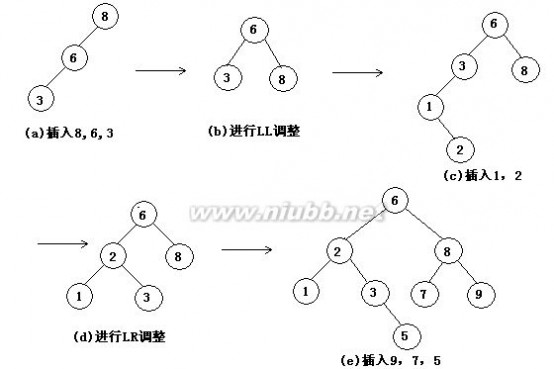

ASL=(4+2*1+3*2)/12=1
6.已知散列表是:

查找key = 21 57 45 50
h0=key%13 = 8 5 6 11
d=key%11+1 = 11 3 2 7
h1=(h0+d)%13 = 6 8 8 5
数据结构试卷 数据结构试题库集及答案
h2=(h1+d)%13 = 10
查找成功比较次数 2 2 3 2
查找成功的平均查找长度ASL=(1+2+2+2+3)/5=2
四、算法设计
1.按中序遍历二叉排序树可得到一个按键值从小到大排列的有序表,利用这个特点来判别二叉树是否为二叉排序树,算法如下:
#define max 99
#define min 0
int judge(BTnode *bt)
{ BTnode *s[max],*p=bt;
int top=0,preval=min;
do {
while(p)
{s[top++]=p;
p=p->lchild;
}
if(top>0)
{p=s[--top];
if(p->data<preval)
return 0;
preval=p->data;
p=p->rchild;
}
}while(p||top>0)
return 1;
}
第八章
一、单项选择题
(2) 一(5) DDCCD (6)一(9) DCCC
二、填空题
(1)8 (2)15 (3) 4.3 (4)中序 (5)记录的键值 (6)7
(7)63 (8)17 (9)17 (10)O(n) (11)O(log2n) (12)越大
(13)散列函数 (14)处理冲突方法 (15) 装填因子 (16)索引表
(17)该块的起始地址 (18) 100 (19)100 (20)101 (21)?log2(n+1)?
(22)同义词 (23)n(n+1)/2 (24) 63 (25) m (26)?m/2? (27)m-1
(28) ?m/2?-1 (29)m (30)?m/2?
三、应用题
1.判定树见下图。(www.61k.com)
查找成功的平均查找长度
ASL=(1+2*2+3*4+4*6)/13=41/13
查找失败时与键值最多比较次数为4。
2.二叉排序树见右图。在等概率情况下,
查找成功的平均查找长度ASL=29/9≈3.2
查找失败时,与键值最多比较次数是5。
3.构造一棵平衡二叉排序树
的过程见右图。
等概率情况下,查找成功的平均查找长度
ASL=(1+2*2+3*4+4*2)/9≈2.8
查找失败时,与键值的最多比较次数是4。
4.按不同的输入顺序输入4、5、6


,建立相应的不同形态的
数据结构试卷 数据结构试题库集及答案
二叉排序树见下图。(www.61k.com)
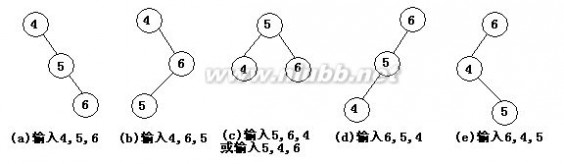
5.键值序列:{25,40,33,47,12,66,72,87,94,22,5,58}
散列地址: 3 7 0 3 1 0 6 10 6 0 5 3
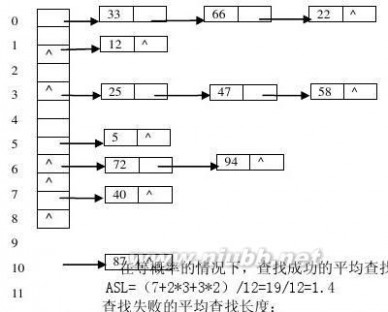
ASL=(4+2*1+3*2)/12=1
6.已知散列表是:

查找key = 21 57 45 50
h0=key%13 = 8 5 6 11
d=key%11+1 = 11 3 2 7
h1=(h0+d)%13 = 6 8 8 5
h2=(h1+d)%13 = 10
查找成功比较次数 2 2 3 2
查找成功的平均查找长度ASL=(1+2+2+2+3)/5=2
四、算法设计
1.按中序遍历二叉排序树可得到一个按键值从小到大排列的有序表,利用这个特点来判别二叉树是否为二叉排序树,算法如下:
#define max 99
#define min 0
int judge(BTnode *bt)
{ BTnode *s[max],*p=bt;
int top=0,preval=min;
do {
while(p)
{s[top++]=p;
p=p->lchild;
}
if(top>0)
{p=s[--top];
if(p->data<preval)
数据结构试卷 数据结构试题库集及答案
return 0;
preval=p->data;
p=p->rchild;
}
}while(p||top>0)
return 1;
}
第九章
一、单项选择题
(1)-(5) ABABC (6)-(10) ADDAC (11)-(15) BBADB
(16)-(20) DBCAB (21)-(25) ADCBA
二、填空题
(1)插人排序 (2)交换排序 (3)选择排序 (4)归并排序 (5)基数排序
(6)O(nlogn) (7)O(n2
2) (8)O(nlog2n) (9)快速 (10)堆 (11)归并
(12)快速 (13)归并 (14)堆 (15)3 (16)选择 (17)O(n) (18)O(nlog2
2n) (19)O(nlog2n) (20) n
5 (23)4 (24) 8
三、应用题
1.解 不稳定的排序方法有快速排序、直接选择排序、堆排序,分别举例说明如下:
(1)快速排序
给定键值序列{9,6,6}进行快速排序。[www.61k.com] 排序结果为{6,6

,9}。
(2)堆排序 给定键值序列为{9,7,6,6}进行堆排序(小顶堆)的过程见下图。
9 9 9 (9)
6 6 (6) (7) (6)
堆排序的结果为{6,6,7,9}。
(3{6,6,4},直接选择排序后结果为{4,6,6}。
(4)希尔排序,例给定排序码值序列为{4,2,2,5},设d1=2,d2=1时,排序结果为{2,2,4,5}。
2.解: 冒泡排序:
第一趟:17,18,40,7,32,60,65,73,85
第二趟:17,18,7,32,40,60,65,73
第三趟:17,7,18,32,40,60,65
第四趟:7,17,18,32,40,60
第五趟:7,17,18,32,40(没有发生交换,结束排序)
3.解:希尔排序:
一趟排序 10 11 9 13 8 12 18 14 15 16 d2=2
结果
二趟排序结果
三趟排序结果 {8,9,10,11,12,13,14,15,16,18}
4.初始序列(1){90,86,48,73,35,40,42,58,66,20}对应的完全二叉树见下图:
(22)
数据结构试卷 数据结构试题库集及答案
它是一个大顶堆。(www.61k.com]
初始序列(2){12,70,34,66,24,56,90,86,36}对应的完全二叉树不是堆,将其调整成堆的过程见左图:
四、算法设计题
1. 单链表结点类型定义为:
typedef struct node
{int key;
struct node *next;
}Lnode;
直接选择排序是每次从n-i+1个结点中选择码值最小者,与第i个结点的码值进行交换,设p指向第i个结点,min指向无序表中码值最小的结点,算法描述如下:
Void selesort1(Lnode *h)
{Lnode *p,*q,*min;
int x;
p=h->next;
while(p)
{min=p;
q=p->next;
while(q)
{if(q->key<min->key)
m=q;
q=q->next;
}
if(min!=p)
{x=p->key;
p->key=min->key;
min->key=x;
}
p=p->next;
}
}
2.快速排序非递归算法描述如下(其中s为顺序栈):
void Quicksort1(RecType t[],int n)
{int top,low=0,high=n,i,j,*s;
RecType x;
S=(int *)malloc(sizeof(int)*2*n);
Top=0;
Do{
while(low<high)
{i=low;j=high;x=r[i];
do{
while((r[i].key>=x.key)&&(i<j))
j--;
if(i<j){
r[j]=r[i];j--;}
}while(i<j);
r[i]=x;
if((i+1)<high)
{s[++top]=i+1;
s[++top]=high;}
high=i-1;
if(top>0)

{low=s[top--];
数据结构试卷 数据结构试题库集及答案
high=s[top--];}
}while(top>0||low<high);
}
目录
目录...................................................................................................................................1
说明: .................................................................................................................................1
第一章 绪论.....................................................................................................................2
第二章 线性表.................................................................................................................5
第三章 栈与队列...........................................................................................................19
第四章 串.......................................................................................................................30
第五章 数组和广义表...................................................................................................42
第六章 树和二叉树.......................................................................................................56
第七章 图.......................................................................................................................75
第八章 动态存储管理...................................................................................................96
第九章 查找.................................................................................................................100
第十章 内部排序......................................................................................................... 111
说明:
1. 本文是对严蔚敏《数据结构(c 语言版)习题集》一书中所有算法设计题目的解决方案,主要作者为一具.以 下网友:biwier,szm99,siice,龙抬头,iamkent,zames,birdthinking,lovebuaa 等为答案的修订和完善工作提出了宝 贵意见,在此表示感谢;
2. 本解答中的所有算法均采用类c 语言描述,设计原则为面向交流、面向阅读,作者不保证程序能够上机正 常运行(这种保证实际上也没有任何意义);
3. 本解答原则上只给出源代码以及必要的注释,对于一些难度较高或思路特殊的题目将给出简要的分析说 明,对于作者无法解决的题目将给出必要的讨论.目前尚未解决的题目有: 5.20, 10.40;
4. 请读者在自己已经解决了某个题目或进行了充分的思考之后,再参考本解答,以保证复习效果;
5. 由于作者水平所限,本解答中一定存在不少这样或者那样的错误和不足,希望读者们在阅读中多动脑、勤 思考,争取发现和纠正这些错误,写出更好的算法来.请将你发现的错误或其它值得改进之处向作者报告:
第一章 绪论
1.16
void print_descending(int x,int y,int z)//按从大到小顺序输出三个数
{
scanf("%d,%d,%d",&x,&y,&z);
if(x<y) x<->y; //<->为表示交换的双目运算符,以下同
if(y<z) y<->z;
if(x<y) x<->y; //冒泡排序
printf("%d %d %d",x,y,z);
}//print_descending
数据结构试卷 数据结构试题库集及答案
1.17
Status fib(int k,int m,int &f)//求k 阶斐波那契序列的第m 项的值f
{
int tempd;
if(k<2||m<0) return ERROR;
if(m<k-1) f=0;
else if (m==k-1 || m==k) f=1;
else
{
for(i=0;i<=k-2;i++) temp[i]=0;
temp[k-1]=1;temp[k]=1; //初始化
sum=1;
j=0;
for(i=k+1;i<=m;i++,j++) //求出序列第k 至第m 个元素的值
temp[i]=2*sum-temp[j];
f=temp[m];
}
return OK;
}//fib
分析: k 阶斐波那契序列的第m 项的值f[m]=f[m-1]+f[m-2]+......+f[m-k]
=f[m-1]+f[m-2]+......+f[m-k]+f[m-k-1]-f[m-k-1]
=2*f[m-1]-f[m-k-1]
所以上述算法的时间复杂度仅为O(m). 如果采用递归设计,将达到O(k^m). 即使采用暂存中 间结果的方法,也将达到O(m^2).
1.18
严蔚敏《数据结构习题集》解答
typedef struct{
char *sport;
enum{male,female} gender;
char schoolname; //校名为'A','B','C','D'或'E'
char *result;
int score;
} resulttype;
typedef struct{
int malescore;
int femalescore;
int totalscore;
} scoretype;
void summary(resulttype result[ ])//求各校的男女总分和团体总分,假设结果已经储存在result[ ] 数组中
{
scoretype score[MAXSIZE];
i=0;
数据结构试卷 数据结构试题库集及答案
while(result[i].sport!=NULL)
{
switch(result[i].schoolname)
{
case 'A':
score[ 0 ].totalscore+=result[i].score;
if(result[i].gender==0) score[ 0 ].malescore+=result[i].score; else score[ 0 ].femalescore+=result[i].score;
break;
case 'B':
score[ 0 ].totalscore+=result[i].score;
if(result[i].gender==0) score[ 0 ].malescore+=result[i].score; else score[ 0 ].femalescore+=result[i].score;
break;
…… …… ……
}
i++;
}
for(i=0;i<5;i++)
{
printf("School %d:\n",i);
printf("Total score of male:%d\n",score[i].malescore);
printf("Total score of female:%d\n",score[i].femalescore); printf("Total score of all:%d\n\n",score[i].totalscore);
}
}//summary
1.19
Status algo119(int a[ARRSIZE])//求i!*2^i 序列的值且不超过maxint {
last=1;
for(i=1;i<=ARRSIZE;i++)
{
a[i-1]=last*2*i;
if((a[i-1]/last)!=(2*i)) reurn OVERFLOW;
last=a[i-1];
return OK;
}
}//algo119
分析:当某一项的结果超过了maxint 时,它除以前面一项的商会发生异常.
1.20
void polyvalue()
{
float temp;
float *p=a;
printf("Input number of terms:");
数据结构试卷 数据结构试题库集及答案
scanf("%d",&n);
printf("Input value of x:");
scanf("%f",&x);
printf("Input the %d coefficients from a0 to a%d:\n",n+1,n);
p=a;xp=1;sum=0; //xp 用于存放x 的i 次方
for(i=0;i<=n;i++)
{
scanf("%f",&temp);
sum+=xp*(temp);
xp*=x;
}
printf("Value is:%f",sum);
}//polyvalue
第二章 线性表
2.10
Status DeleteK(SqList &a,int i,int k)//删除线性表a 中第i 个元素起的k 个元素
{
if(i<1||k<0||i+k-1>a.length) return INFEASIBLE;
for(count=1;i+count-1<=a.length-k;count++) //注意循环结束的条件
a.elem[i+count-1]=a.elem[i+count+k-1];
a.length-=k;
return OK;
}//DeleteK
2.11
Status Insert_SqList(SqList &va,int x)//把x 插入递增有序表va 中
{
if(va.length+1>va.listsize) return ERROR;
va.length++;
for(i=va.length-1;va.elem[i]>x&&i>=0;i--)
va.elem[i+1]=va.elem[i];
va.elem[i+1]=x;
return OK;
}//Insert_SqList
2.12
int ListComp(SqList A,SqList B)//比较字符表A 和B,并用返回值表示结果,值为1,表示A>B; 值为-1,表示A<B;值为0,表示A=B
{
for(i=1;i<=A.length&&i<=B.length;i++)
if(A.elem[i]!=B.elem[i])
return A.elem[i]>B.elem[i]?1:-1;
if(A.length==B.length) return 0;
数据结构试卷 数据结构试题库集及答案
return A.length>B.length?1:-1; //当两个字符表可以互相比较的部分完全相同时,哪个较长, 哪个就较大
}//ListComp
2.13
LNode* Locate(LinkList L,int x)//链表上的元素查找,返回指针
{
for(p=l->next;p&&p->data!=x;p=p->next);
return p;
}//Locate
2.14
int Length(LinkList L)//求链表的长度
{
for(k=0,p=L;p->next;p=p->next,k++);
return k;
}//Length
2.15
void ListConcat(LinkList ha,LinkList hb,LinkList &hc)//把链表hb 接在ha 后面形成链表hc {
hc=ha;p=ha;
while(p->next) p=p->next;
p->next=hb;
}//ListConcat
2.16
见书后答案.
2.17
Status Insert(LinkList &L,int i,int b)//在无头结点链表L 的第i 个元素之前插入元素b {
p=L;q=(LinkList*)malloc(sizeof(LNode));
q.data=b;
if(i==1)
{
q.next=p;L=q; //插入在链表头部
}
else
{
while(--i>1) p=p->next;
q->next=p->next;p->next=q; //插入在第i 个元素的位置
}
数据结构试卷 数据结构试题库集及答案
}//Insert
2.18
Status Delete(LinkList &L,int i)//在无头结点链表L 中删除第i 个元素
{
严蔚敏《数据结构习题集》解答
if(i==1) L=L->next; //删除第一个元素
else
{
p=L;
while(--i>1) p=p->next;
p->next=p->next->next; //删除第i 个元素
}
}//Delete
2.19
第 7 页 共 124 页
Status Delete_Between(Linklist &L,int mink,int maxk)//删除元素递增排列的链表L 中值大于 mink 且小于maxk 的所有元素
{
p=L;
while(p->next->data<=mink) p=p->next; //p 是最后一个不大于mink 的元素
if(p->next) //如果还有比mink 更大的元素
{
q=p->next;
while(q->data<maxk) q=q->next; //q 是第一个不小于maxk 的元素
p->next=q;
}
}//Delete_Between
2.20
Status Delete_Equal(Linklist &L)//删除元素递增排列的链表L 中所有值相同的元素 {
p=L->next;q=p->next; //p,q 指向相邻两元素
while(p->next)
{
if(p->data!=q->data)
{
p=p->next;q=p->next; //当相邻两元素不相等时,p,q 都向后推一步
}
else
{
while(q->data==p->data)
{
数据结构试卷 数据结构试题库集及答案
free(q);
q=q->next;
}
p->next=q;p=q;q=p->next; //当相邻元素相等时删除多余元素
}//else
}//while
}//Delete_Equal
2.21
void reverse(SqList &A)//顺序表的就地逆置
{
for(i=1,j=A.length;i<j;i++,j--)
A.elem[i]<->A.elem[j];
}//reverse
2.22
第 8 页 共 124 页
void LinkList_reverse(Linklist &L)//链表的就地逆置;为简化算法,假设表长大于2
{
p=L->next;q=p->next;s=q->next;p->next=NULL;
while(s->next)
{
q->next=p;p=q;
q=s;s=s->next; //把L 的元素逐个插入新表表头
}
q->next=p;s->next=q;L->next=s;
}//LinkList_reverse
分析:本算法的思想是,逐个地把L 的当前元素q 插入新的链表头部,p 为新表表头.
2.23
void merge1(LinkList &A,LinkList &B,LinkList &C)//把链表A 和B 合并为C,A 和B 的元素间 隔排列,且使用原存储空间
{
p=A->next;q=B->next;C=A;
while(p&&q)
{
s=p->next;p->next=q; //将B 的元素插入
if(s)
{
t=q->next;q->next=s; //如A 非空,将A 的元素插入
}
p=s;q=t;
}//while
}//merge1
数据结构试卷 数据结构试题库集及答案
2.24
第 9 页 共 124 页
void reverse_merge(LinkList &A,LinkList &B,LinkList &C)//把元素递增排列的链表A 和B 合 并为C,且C 中元素递减排列,使用原空间
{
pa=A->next;pb=B->next;pre=NULL; //pa 和pb 分别指向A,B 的当前元素
while(pa||pb)
{
if(pa->data<pb->data||!pb)
{
pc=pa;q=pa->next;pa->next=pre;pa=q; //将A 的元素插入新表
}
else
{
pc=pb;q=pb->next;pb->next=pre;pb=q; //将B 的元素插入新表
}
pre=pc;
}
C=A;A->next=pc; //构造新表头
}//reverse_merge
分析:本算法的思想是,按从小到大的顺序依次把A 和B 的元素插入新表的头部pc 处,最后处 理A 或B 的剩余元素.
2.25
void SqList_Intersect(SqList A,SqList B,SqList &C)//求元素递增排列的线性表A 和B 的元素 的交集并存入C 中
{
i=1;j=1;k=0;
while(A.elem[i]&&B.elem[j])
{
if(A.elem[i]<B.elem[j]) i++;
if(A.elem[i]>B.elem[j]) j++;
if(A.elem[i]==B.elem[j])
{
C.elem[++k]=A.elem[i]; //当发现了一个在A,B 中都存在的元素,
i++;j++; //就添加到C 中
}
}//while
}//SqList_Intersect
2.26
void LinkList_Intersect(LinkList A,LinkList B,LinkList &C)//在链表结构上重做上题
{
p=A->next;q=B->next;
pc=(LNode*)malloc(sizeof(LNode));
数据结构试卷 数据结构试题库集及答案
C=pc;
while(p&&q)
{
if(p->data<q->data) p=p->next;
else if(p->data>q->data) q=q->next;
else
{
s=(LNode*)malloc(sizeof(LNode));
s->data=p->data;
pc->next=s;pc=s;
p=p->next;q=q->next;
}
}//while
}//LinkList_Intersect
2.27
第 10 页 共 124 页
void SqList_Intersect_True(SqList &A,SqList B)//求元素递增排列的线性表A 和B 的元素的交 集并存回A 中
{
i=1;j=1;k=0;
while(A.elem[i]&&B.elem[j])
{
if(A.elem[i]<B.elem[j]) i++;
else if(A.elem[i]>B.elem[j]) j++;
else if(A.elem[i]!=A.elem[k])
{
A.elem[++k]=A.elem[i]; //当发现了一个在A,B 中都存在的元素
i++;j++; //且C 中没有,就添加到C 中
}
else {i++;j++;}
}//while
while(A.elem[k]) A.elem[k++]=0;
}//SqList_Intersect_True
2.28
void LinkList_Intersect_True(LinkList &A,LinkList B)//在链表结构上重做上题
{
p=A->next;q=B->next;pc=A;
while(p&&q)
{
if(p->data<q->data) p=p->next;
else if(p->data>q->data) q=q->next;
else if(p->data!=pc->data)
严蔚敏《数据结构习题集》解答
数据结构试卷 数据结构试题库集及答案
pc=pc->next;
pc->data=p->data;
p=p->next;q=q->next;
}
}//while
}//LinkList_Intersect_True
2.29
void SqList_Intersect_Delete(SqList &A,SqList B,SqList C)
{
i=0;j=0;k=0;m=0; //i 指示A 中元素原来的位置,m 为移动后的位置
while(i<A.length&&j<B.length&& k<C.length)
{
if(B.elem[j]<C.elem[k]) j++;
else if(B.elem[j]>C.elem[k]) k++;
else
{
same=B.elem[j]; //找到了相同元素same
while(B.elem[j]==same) j++;
while(C.elem[k]==same) k++; //j,k 后移到新的元素
while(i<A.length&&A.elem[i]<same)
A.elem[m++]=A.elem[i++];
} //需保留的元素移动到新位置 while(i<A.length&&A.elem[i]==same) i++; //跳过相同的元素
}//while
while(i<A.length)
A.elem[m++]=A.elem[i++]; //A 的剩余元素重新存储。(www.61k.com)
A.length=m;
}// SqList_Intersect_Delete
分析:先从B 和C 中找出共有元素,记为same,再在A 中从当前位置开始, 凡小于same 的 元素均保留(存到新的位置),等于same 的就跳过,到大于same 时就再找下一个same.
2.30
void LinkList_Intersect_Delete(LinkList &A,LinkList B,LinkList C)//在链表结构上重做上题 {
p=B->next;q=C->next;r=A-next;
while(p&&q&&r)
{
if(p->data<q->data) p=p->next;
else if(p->data>q->data) q=q->next;
else
{
严蔚敏《数据结构习题集》解答
u=p->data; //确定待删除元素u
while(r->next->data<u) r=r->next; //确定最后一个小于u 的元素指针r
数据结构试卷 数据结构试题库集及答案
{
s=r->next;
while(s->data==u)
{
t=s;s=s->next;free(t); //确定第一个大于u 的元素指针s
}//while
r->next=s; //删除r 和s 之间的元素
}//if
while(p->data=u) p=p->next;
while(q->data=u) q=q->next;
}//else
}//while
}//LinkList_Intersect_Delete
2.31
Status Delete_Pre(CiLNode *s)//删除单循环链表中结点s 的直接前驱
{
p=s;
while(p->next->next!=s) p=p->next; //找到s 的前驱的前驱p
p->next=s;
return OK;
}//Delete_Pre
2.32
Status DuLNode_Pre(DuLinkList &L)//完成双向循环链表结点的pre 域
{
for(p=L;!p->next->pre;p=p->next) p->next->pre=p;
return OK;
}//DuLNode_Pre
2.33
Status LinkList_Divide(LinkList &L,CiList &A,CiList &B,CiList &C)//把单链表L 的元素按类 型分为三个循环链表.CiList 为带头结点的单循环链表类型.
{
s=L->next;
A=(CiList*)malloc(sizeof(CiLNode));p=A;
B=(CiList*)malloc(sizeof(CiLNode));q=B;
C=(CiList*)malloc(sizeof(CiLNode));r=C; //建立头结点
while(s)
严蔚敏《数据结构习题集》解答
{
if(isalphabet(s->data))
{
p->next=s;p=s;
数据结构试卷 数据结构试题库集及答案
else if(isdigit(s->data))
{
q->next=s;q=s;
}
else
{
r->next=s;r=s;
}
}//while
p->next=A;q->next=B;r->next=C; //完成循环链表
}//LinkList_Divide
2.34
void Print_XorLinkedList(XorLinkedList L)//从左向右输出异或链表的元素值
{
p=L.left;pre=NULL;
while(p)
{
printf("%d",p->data);
q=XorP(p->LRPtr,pre);
pre=p;p=q; //任何一个结点的LRPtr 域值与其左结点指针进行异或运算即得到其右结点指 针
}
}//Print_XorLinkedList
2.35
Status Insert_XorLinkedList(XorLinkedList &L,int x,int i)//在异或链表L的第i 个元素前插入元 素x
{
p=L.left;pre=NULL;
r=(XorNode*)malloc(sizeof(XorNode));
r->data=x;
if(i==1) //当插入点在最左边的情况
{
p->LRPtr=XorP(p.LRPtr,r);
r->LRPtr=p;
L.left=r;
return OK;
严蔚敏《数据结构习题集》解答
}
j=1;q=p->LRPtr; //当插入点在中间的情况
while(++j<i&&q)
{
q=XorP(p->LRPtr,pre);
pre=p;p=q;
数据结构试卷 数据结构试题库集及答案
}//while //在p,q 两结点之间插入
if(!q) return INFEASIBLE; //i 不可以超过表长
p->LRPtr=XorP(XorP(p->LRPtr,q),r);
q->LRPtr=XorP(XorP(q->LRPtr,p),r);
r->LRPtr=XorP(p,q); //修改指针
return OK;
}//Insert_XorLinkedList
2.36
第 14 页 共 124 页
Status Delete_XorLinkedList(XorlinkedList &L,int i)//删除异或链表L 的第i 个元素 {
p=L.left;pre=NULL;
if(i==1) //删除最左结点的情况
{
q=p->LRPtr;
q->LRPtr=XorP(q->LRPtr,p);
L.left=q;free(p);
return OK;
}
j=1;q=p->LRPtr;
while(++j<i&&q)
{
q=XorP(p->LRPtr,pre);
pre=p;p=q;
}//while //找到待删结点q
if(!q) return INFEASIBLE; //i 不可以超过表长
if(L.right==q) //q 为最右结点的情况
{
p->LRPtr=XorP(p->LRPtr,q);
L.right=p;free(q);
return OK;
}
r=XorP(q->LRPtr,p); //q 为中间结点的情况,此时p,r 分别为其左右结点
p->LRPtr=XorP(XorP(p->LRPtr,q),r);
r->LRPtr=XorP(XorP(r->LRPtr,q),p); //修改指针
free(q);
return OK;
}//Delete_XorLinkedList
2.37
第 15 页 共 124 页
void OEReform(DuLinkedList &L)//按1,3,5,...4,2 的顺序重排双向循环链表L 中的所有结点 {
p=L.next;
while(p->next!=L&&p->next->next!=L)
数据结构试卷 数据结构试题库集及答案
{
p->next=p->next->next;
p=p->next;
} //此时p 指向最后一个奇数结点
if(p->next==L) p->next=L->pre->pre;
else p->next=l->pre;
p=p->next; //此时p 指向最后一个偶数结点
while(p->pre->pre!=L)
{
p->next=p->pre->pre;
p=p->next;
}
p->next=L; //按题目要求调整了next 链的结构,此时pre 链仍为原状
for(p=L;p->next!=L;p=p->next) p->next->pre=p;
L->pre=p; //调整pre 链的结构,同2.32 方法
}//OEReform
分析:next 链和pre 链的调整只能分开进行.如同时进行调整的话,必须使用堆栈保存偶数结点 的指针,否则将会破坏链表结构,造成结点丢失.
2.38
DuLNode * Locate_DuList(DuLinkedList &L,int x)//带freq 域的双向循环链表上的查找 {
p=L.next;
while(p.data!=x&&p!=L) p=p->next;
if(p==L) return NULL; //没找到
p->freq++;q=p->pre;
while(q->freq<=p->freq&&p!=L) q=q->pre; //查找插入位置
if(q!=p->pre)
{
p->pre->next=p->next;p->next->pre=p->pre;
q->next->pre=p;p->next=q->next;
q->next=p;p->pre=q; //调整位置
}
return p;
}//Locate_DuList
2.39
第 16 页 共 124 页
float GetValue_SqPoly(SqPoly P,int x0)//求升幂顺序存储的稀疏多项式的值
{
PolyTerm *q;
xp=1;q=P.data;
sum=0;ex=0;
while(q->coef)
{
while(ex<q->exp) xp*=x0;
数据结构试卷 数据结构试题库集及答案
sum+=q->coef*xp;
q++;
}
return sum;
}//GetValue_SqPoly
2.40
void Subtract_SqPoly(SqPoly P1,SqPoly P2,SqPoly &P3)//求稀疏多项式P1 减P2 的差式P3 {
PolyTerm *p,*q,*r;
Create_SqPoly(P3); //建立空多项式P3
p=P1.data;q=P2.data;r=P3.data;
while(p->coef&&q->coef)
{
if(p->exp<q->exp)
{
r->coef=p->coef;
r->exp=p->exp;
p++;r++;
}
else if(p->exp<q->exp)
{
r->coef=-q->coef;
r->exp=q->exp;
q++;r++;
}
else
{
if((p->coef-q->coef)!=0) //只有同次项相减不为零时才需要存入P3 中
{
r->coef=p->coef-q->coef;
r->exp=p->exp;r++;
}//if
p++;q++;
}//else
}//while
while(p->coef) //处理P1 或P2 的剩余项
{
r->coef=p->coef;
r->exp=p->exp;
p++;r++;
}
while(q->coef)
{
r->coef=-q->coef;
r->exp=q->exp;
q++;r++;
数据结构试卷 数据结构试题库集及答案
}
}//Subtract_SqPoly
2.41
void QiuDao_LinkedPoly(LinkedPoly &L)//对有头结点循环链表结构存储的稀疏多项式L 求 导
{
p=L->next;
if(!p->data.exp)
{
L->next=p->next;p=p->next; //跳过常数项
}
while(p!=L)
{
p->data.coef*=p->data.exp--;//对每一项求导
p=p->next;
}
}//QiuDao_LinkedPoly
2.42
void Divide_LinkedPoly(LinkedPoly &L,&A,&B)//把循环链表存储的稀疏多项式L 拆成只含 奇次项的A 和只含偶次项的B
{
p=L->next;
A=(PolyNode*)malloc(sizeof(PolyNode));
B=(PolyNode*)malloc(sizeof(PolyNode));
pa=A;pb=B;
while(p!=L)
{
if(p->data.exp!=2*(p->data.exp/2))
{
pa->next=p;pa=p;
严蔚敏《数据结构习题集》解答
}
else
{
pb->next=p;pb=p;
}
p=p->next;
}//while
pa->next=A;pb->next=B;
}//Divide_LinkedPoly
第三章 栈与队列
数据结构试卷 数据结构试题库集及答案
3.15
typedef struct{
Elemtype *base[2];
Elemtype *top[2];
}BDStacktype; //双向栈类型
Status Init_Stack(BDStacktype &tws,int m)//初始化一个大小为m 的双向栈tws
{
tws.base[0]=(Elemtype*)malloc(sizeof(Elemtype));
tws.base[1]=tws.base[0]+m;
tws.top[0]=tws.base[0];
tws.top[1]=tws.base[1];
return OK;
}//Init_Stack
Status push(BDStacktype &tws,int i,Elemtype x)//x 入栈,i=0 表示低端栈,i=1 表示高端栈 {
if(tws.top[0]>tws.top[1]) return OVERFLOW; //注意此时的栈满条件
if(i==0) *tws.top[0]++=x;
else if(i==1) *tws.top[1]--=x;
else return ERROR;
return OK;
}//push
Status pop(BDStacktype &tws,int i,Elemtype &x)//x 出栈,i=0 表示低端栈,i=1 表示高端栈 {
if(i==0)
{
if(tws.top[0]==tws.base[0]) return OVERFLOW;
x=*--tws.top[0];
}
else if(i==1)
{
if(tws.top[1]==tws.base[1]) return OVERFLOW;
x=*++tws.top[1];
}
else return ERROR;
return OK;
}//pop
3.16
void Train_arrange(char *train)//这里用字符串train 表示火车,'H'表示硬席,'S'表示软席 {
p=train;q=train;
InitStack(s);
while(*p)
数据结构试卷 数据结构试题库集及答案
{
if(*p=='H') push(s,*p); //把'H'存入栈中
else *(q++)=*p; //把'S'调到前部
p++;
}
while(!StackEmpty(s))
{
pop(s,c);
*(q++)=c; //把'H'接在后部
}
}//Train_arrange
3.17
int IsReverse()//判断输入的字符串中'&'前和'&'后部分是否为逆串,是则返回1,否则返回0 {
InitStack(s);
while((e=getchar())!='&')
{
if(e==?@?) return 0;//不允许在?&?之前出现?@?
push(s,e);
}
while( (e=getchar())!='@')
{
if(StackEmpty(s)) return 0;
pop(s,c);
if(e!=c) return 0;
}
if(!StackEmpty(s)) return 0;
return 1;
}//IsReverse
3.18
Status Bracket_Test(char *str)//判别表达式中小括号是否匹配
{
count=0;
for(p=str;*p;p++)
{
if(*p=='(') count++;
else if(*p==')') count--;
if (count<0) return ERROR;
}
if(count) return ERROR; //注意括号不匹配的两种情况
return OK;
}//Bracket_Test
数据结构试卷 数据结构试题库集及答案
3.19
Status AllBrackets_Test(char *str)//判别表达式中三种括号是否匹配
{
InitStack(s);
for(p=str;*p;p++)
{
if(*p=='('||*p=='['||*p=='{') push(s,*p);
else if(*p==')'||*p==']'||*p=='}')
{
if(StackEmpty(s)) return ERROR;
pop(s,c);
if(*p==')'&&c!='(') return ERROR;
if(*p==']'&&c!='[') return ERROR;
if(*p=='}'&&c!='{') return ERROR; //必须与当前栈顶括号匹配
}
}//for
if(!StackEmpty(s)) return ERROR;
return OK;
}//AllBrackets_Test
3.20
typedef struct {
. int x;
int y;
} coordinate;
void Repaint_Color(int g[m][n],int i,int j,int color)//把点(i,j)相邻区域的颜色置换为color {
old=g[i][j];
InitQueue(Q);
EnQueue(Q,{I,j});
while(!QueueEmpty(Q))
{
DeQueue(Q,a);
x=a.x;y=a.y;
严蔚敏《数据结构习题集》解答
if(x>1)
if(g[x-1][y]==old)
{
g[x-1][y]=color;
EnQueue(Q,{x-1,y}); //修改左邻点的颜色
}
if(y>1)
if(g[x][y-1]==old)
数据结构试卷 数据结构试题库集及答案
{
g[x][y-1]=color;
EnQueue(Q,{x,y-1}); //修改上邻点的颜色
}
if(x<m)
if(g[x+1][y]==old)
{
g[x+1][y]=color;
EnQueue(Q,{x+1,y}); //修改右邻点的颜色
}
if(y<n)
if(g[x][y+1]==old)
{
g[x][y+1]=color;
EnQueue(Q,{x,y+1}); //修改下邻点的颜色
}
}//while
}//Repaint_Color
第 22 页 共 124 页
分析:本算法采用了类似于图的广度优先遍历的思想,用两个队列保存相邻同色点的横坐标和 纵坐标.递归形式的算法该怎么写呢?
3.21
void NiBoLan(char *str,char *new)//把中缀表达式str 转换成逆波兰式new
{
p=str;q=new; //为方便起见,设str 的两端都加上了优先级最低的特殊符号
InitStack(s); //s 为运算符栈
while(*p)
{
if(*p 是字母)) *q++=*p; //直接输出
else
{
c=gettop(s);
if(*p 优先级比c 高) push(s,*p);
else
{
while(gettop(s)优先级不比*p 低)
严蔚敏《数据结构习题集》解答
{
pop(s,c);*(q++)=c;
}//while
push(s,*p); //运算符在栈内遵循越往栈顶优先级越高的原则
}//else
}//else
p++;
}//while
数据结构试卷 数据结构试题库集及答案
}//NiBoLan //参见编译原理教材
3.22
int GetValue_NiBoLan(char *str)//对逆波兰式求值
{
p=str;InitStack(s); //s 为操作数栈
while(*p)
{
if(*p 是数) push(s,*p);
else
{
pop(s,a);pop(s,b);
r=compute(b,*p,a); //假设compute 为执行双目运算的过程
push(s,r);
}//else
p++;
}//while
pop(s,r);return r;
}//GetValue_NiBoLan
3.23
第 23 页 共 124 页
Status NiBoLan_to_BoLan(char *str,stringtype &new)//把逆波兰表达式str 转换为波兰式new {
p=str;Initstack(s); //s 的元素为stringtype 类型
while(*p)
{
if(*p 为字母) push(s,*p);
else
{
if(StackEmpty(s)) return ERROR;
pop(s,a);
if(StackEmpty(s)) return ERROR;
pop(s,b);
c=link(link(*p,b),a);
push(s,c);
严蔚敏《数据结构习题集》解答
}//else
p++;
}//while
pop(s,new);
if(!StackEmpty(s)) return ERROR;
return OK;
}//NiBoLan_to_BoLan
第 24 页 共 124 页
数据结构试卷 数据结构试题库集及答案
分析:基本思想见书后注释.本题中暂不考虑串的具体操作的实现,而将其看作一种抽象数据 类型stringtype,对其可以进行连接操作:c=link(a,b).
3.24
Status g(int m,int n,int &s)//求递归函数g 的值s
{
if(m==0&&n>=0) s=0;
else if(m>0&&n>=0) s=n+g(m-1,2*n);
else return ERROR;
return OK;
}//g
3.25
Status F_recursive(int n,int &s)//递归算法
{
if(n<0) return ERROR;
if(n==0) s=n+1;
else
{
F_recurve(n/2,r);
s=n*r;
}
return OK;
}//F_recursive
Status F_nonrecursive(int n,int s)//非递归算法
{
if(n<0) return ERROR;
if(n==0) s=n+1;
else
{
InitStack(s); //s 的元素类型为struct {int a;int b;}
while(n!=0)
{
a=n;b=n/2;
push(s,{a,b});
严蔚敏《数据结构习题集》解答
n=b;
}//while
s=1;
while(!StackEmpty(s))
{
pop(s,t);
s*=t.a;
}//while
}
数据结构试卷 数据结构试题库集及答案
return OK;
}//F_nonrecursive
3.26
float Sqrt_recursive(float A,float p,float e)//求平方根的递归算法
{
if(abs(p^2-A)<=e) return p;
else return sqrt_recurve(A,(p+A/p)/2,e);
}//Sqrt_recurve
float Sqrt_nonrecursive(float A,float p,float e)//求平方根的非递归算法
{
while(abs(p^2-A)>=e)
p=(p+A/p)/2;
return p;
}//Sqrt_nonrecursive
3.27
第 25 页 共 124 页
这一题的所有算法以及栈的变化过程请参见《数据结构(pascal 版)》,作者不再详细写出.
3.28
void InitCiQueue(CiQueue &Q)//初始化循环链表表示的队列Q
{
Q=(CiLNode*)malloc(sizeof(CiLNode));
Q->next=Q;
}//InitCiQueue
void EnCiQueue(CiQueue &Q,int x)//把元素x 插入循环链表表示的队列Q,Q 指向队尾元 素,Q->next 指向头结点,Q->next->next 指向队头元素
{
p=(CiLNode*)malloc(sizeof(CiLNode));
p->data=x;
p->next=Q->next; //直接把p 加在Q 的后面
严蔚敏《数据结构习题集》解答
Q->next=p;
Q=p; //修改尾指针
}
第 26 页 共 124 页
Status DeCiQueue(CiQueue &Q,int x)//从循环链表表示的队列Q 头部删除元素x
{
if(Q==Q->next) return INFEASIBLE; //队列已空
p=Q->next->next;
数据结构试卷 数据结构试题库集及答案
x=p->data;
Q->next->next=p->next;
free(p);
return OK;
}//DeCiQueue
3.29
Status EnCyQueue(CyQueue &Q,int x)//带tag 域的循环队列入队算法
{
if(Q.front==Q.rear&&Q.tag==1) //tag 域的值为0 表示"空",1 表示"满"
return OVERFLOW;
Q.base[Q.rear]=x;
Q.rear=(Q.rear+1)%MAXSIZE;
if(Q.front==Q.rear) Q.tag=1; //队列满
}//EnCyQueue
Status DeCyQueue(CyQueue &Q,int &x)//带tag 域的循环队列出队算法
{
if(Q.front==Q.rear&&Q.tag==0) return INFEASIBLE;
Q.front=(Q.front+1)%MAXSIZE;
x=Q.base[Q.front];
if(Q.front==Q.rear) Q.tag=1; //队列空
return OK;
}//DeCyQueue
分析:当循环队列容量较小而队列中每个元素占的空间较多时,此种表示方法可以节约较多的 存储空间,较有价值.
3.30
Status EnCyQueue(CyQueue &Q,int x)//带length 域的循环队列入队算法
{
if(Q.length==MAXSIZE) return OVERFLOW;
Q.rear=(Q.rear+1)%MAXSIZE;
Q.base[Q.rear]=x;
Q.length++;
严蔚敏《数据结构习题集》解答
return OK;
}//EnCyQueue
Status DeCyQueue(CyQueue &Q,int &x)//带length 域的循环队列出队算法
{
if(Q.length==0) return INFEASIBLE;
head=(Q.rear-Q.length+1)%MAXSIZE; //详见书后注释
x=Q.base[head];
Q.length--;
}//DeCyQueue
数据结构试卷 数据结构试题库集及答案
3.31
第 27 页 共 124 页
int Palindrome_Test()//判别输入的字符串是否回文序列,是则返回1,否则返回0 {
InitStack(S);InitQueue(Q);
while((c=getchar())!='@')
{
Push(S,c);EnQueue(Q,c); //同时使用栈和队列两种结构
}
while(!StackEmpty(S))
{
Pop(S,a);DeQueue(Q,b));
if(a!=b) return ERROR;
}
return OK;
}//Palindrome_Test
3.32
void GetFib_CyQueue(int k,int n)//求k 阶斐波那契序列的前n+1 项
{
InitCyQueue(Q); //其MAXSIZE 设置为k
for(i=0;i<k-1;i++) Q.base[i]=0;
Q.base[k-1]=1; //给前k 项赋初值
for(i=0;i<k;i++) printf("%d",Q.base[i]);
for(i=k;i<=n;i++)
{
m=i%k;sum=0;
for(j=0;j<k;j++) sum+=Q.base[(m+j)%k];
Q.base[m]=sum; //求第i 项的值存入队列中并取代已无用的第一项 printf("%d",sum);
}
}//GetFib_CyQueue
严蔚敏《数据结构习题集》解答
3.33
Status EnDQueue(DQueue &Q,int x)//输出受限的双端队列的入队操作 {
if((Q.rear+1)%MAXSIZE==Q.front) return OVERFLOW; //队列满
avr=(Q.base[Q.rear-1]+Q.base[Q.front])/2;
if(x>=avr) //根据x 的值决定插入在队头还是队尾
{
Q.base[Q.rear]=x;
Q.rear=(Q.rear+1)%MAXSIZE;
} //插入在队尾
else
数据结构试卷 数据结构试题库集及答案
Q.front=(Q.front-1)%MAXSIZE;
Q.base[Q.front]=x;
} //插入在队头
return OK;
}//EnDQueue
Status DeDQueue(DQueue &Q,int &x)//输出受限的双端队列的出队操作
{
if(Q.front==Q.rear) return INFEASIBLE; //队列空
x=Q.base[Q.front];
Q.front=(Q.front+1)%MAXSIZE;
return OK;
}//DeDQueue
3.34
第 28 页 共 124 页
void Train_Rearrange(char *train)//这里用字符串train 表示火车,'P'表示硬座,'H'表示硬卧,'S'表 示软卧,最终按PSH 的顺序排列
{
r=train;
InitDQueue(Q);
while(*r)
{
if(*r=='P')
{
printf("E");
printf("D"); //实际上等于不入队列,直接输出P 车厢
}
else if(*r=='S')
{
printf("E");
EnDQueue(Q,*r,0); //0 表示把S 车厢从头端入队列
严蔚敏《数据结构习题集》解答
}
else
{
printf("A");
EnDQueue(Q,*r,1); //1 表示把H 车厢从尾端入队列
}
}//while
while(!DQueueEmpty(Q))
{
printf("D");
DeDQueue(Q);
}//while //从头端出队列的车厢必然是先S 后H 的顺序
数据结构试卷 数据结构试题库集及答案
}//Train_Rearrange
第 29 页 共 124 页
严蔚敏《数据结构习题集》解答
第四章 串
4.10
void String_Reverse(Stringtype s,Stringtype &r)//求s 的逆串r
{
StrAssign(r,' ); //初始化r 为空串
for(i=Strlen(s);i;i--)
{
StrAssign(c,SubString(s,i,1));
StrAssign(r,Concat(r,c)); //把s 的字符从后往前添加到r 中
}
}//String_Reverse
4.11
第 30 页 共 124 页
void String_Subtract(Stringtype s,Stringtype t,Stringtype &r)//求所有包含在串s 中而t 中没有的 字符构成的新串r
{
StrAssign(r,'');
for(i=1;i<=Strlen(s);i++)
{
StrAssign(c,SubString(s,i,1));
for(j=1;j<i&&StrCompare(c,SubString(s,j,1));j++); //判断s 的当前字符c 是否第一次出现 if(i==j)
{
for(k=1;k<=Strlen(t)&&StrCompare(c,SubString(t,k,1));k++); //判断当前字符是否包含在 t 中
if(k>Strlen(t)) StrAssign(r,Concat(r,c));
}
}//for
}//String_Subtract
4.12
int Replace(Stringtype &S,Stringtype T,Stringtype V);//将串S 中所有子串T 替换为V,并返回置 换次数
{
for(n=0,i=1;i<=Strlen(S)-Strlen(T)+1;i++) //注意i 的取值范围
if(!StrCompare(SubString(S,i,Strlen(T)),T)) //找到了与T 匹配的子串
{ //分别把T 的前面和后面部分保存为head 和tail
StrAssign(head,SubString(S,1,i-1));
StrAssign(tail,SubString(S,i+Strlen(T),Strlen(S)-i-Strlen(T)+1));
StrAssign(S,Concat(head,V));
StrAssign(S,Concat(S,tail)); //把head,V,tail 连接为新串
i+=Strlen(V); //当前指针跳到插入串以后
n++;
数据结构试卷 数据结构试题库集及答案
}//if
return n;
严蔚敏《数据结构习题集》解答
}//Replace
第 31 页 共 124 页
分析:i+=Strlen(V);这一句是必需的,也是容易忽略的.如省掉这一句,则在某些情况下,会引起 不希望的后果,虽然在大多数情况下没有影响.请思考:设 S='place', T='ace', V='face',则省掉 i+=Strlen(V);运行时会出现什么结果?
4.13
int Delete_SubString(Stringtype &s,Stringtype t)//从串s 中删除所有与t 相同的子串,并返回删除 次数
{
for(n=0,i=1;i<=Strlen(s)-Strlen(t)+1;i++)
if(!StrCompare(SubString(s,i,Strlen(t)),t))
{
StrAssign(head,SubString(S,1,i-1));
StrAssign(tail,SubString(S,i+Strlen(t),Strlen(s)-i-Strlen(t)+1));
StrAssign(S,Concat(head,tail)); //把head,tail 连接为新串
n++;
}//if
return n,
}//Delete_SubString
4.14
Status NiBoLan_to_BoLan(Stringtype str,Stringtype &new)//把前缀表达式 str 转换为后缀式 new
{
Initstack(s); //s 的元素为Stringtype 类型
for(i=1;i<=Strlen(str);i++)
{
r=SubString(str,i,1);
if(r 为字母) push(s,r);
else
{
if(StackEmpty(s)) return ERROR;
pop(s,a);
if(StackEmpty(s)) return ERROR;
pop(s,b);
StrAssign(t,Concat(r,b));
StrAssign(c,Concat(t,a)); //把算符r,子前缀表达式a,b 连接为新子前缀表达式c push(s,c);
}
}//for
pop(s,new);
if(!StackEmpty(s)) return ERROR;
return OK;
}//NiBoLan_to_BoLan
分析:基本思想见书后注释3.23.请读者用此程序取代作者早些时候对3.23 题给出的程序.
数据结构试卷 数据结构试题库集及答案
4.15
严蔚敏《数据结构习题集》解答
第 32 页 共 124 页
void StrAssign(Stringtype &T,char chars&#;)//用字符数组chars 给串T 赋值,Stringtype 的定义 见课本
{
for(i=0,T[0]=0;chars[i];T[0]++,i++) T[i+1]=chars[i];
}//StrAssign
4.16
char StrCompare(Stringtype s,Stringtype t)//串的比较,s>t 时返回正数,s=t 时返回0,s<t 时返回负 数
{
for(i=1;i<=s[0]&&i<=t[0]&&s[i]==t[i];i++);
if(i>s[0]&&i>t[0]) return 0;
else if(i>s[0]) return -t[i];
else if(i>t[0]) return s[i];
else return s[i]-t[i];
}//StrCompare
4.17
int String_Replace(Stringtype &S,Stringtype T,Stringtype V);//将串S 中所有子串T 替换为V,并 返回置换次数
{
for(n=0,i=1;i<=S[0]-T[0]+1;i++)
{
for(j=i,k=1;T[k]&&S[j]==T[k];j++,k++);
if(k>T[0]) //找到了与T 匹配的子串:分三种情况处理
{
if(T[0]==V[0])
for(l=1;l<=T[0];l++) //新子串长度与原子串相同时:直接替换
S[i+l-1]=V[l];
else if(T[0]<V[0]) //新子串长度大于原子串时:先将后部右移
{
for(l=S[0];l>=i+T[0];l--)
S[l+V[0]-T[0]]=S[l];
for(l=1;l<=V[0];l++)
S[i+l-1]=V[l];
}
else //新子串长度小于原子串时:先将后部左移
{
for(l=i+V[0];l<=S[0]+V[0]-T[0];l++)
S[l]=S[l-V[0]+T[0]];
for(l=1;l<=V[0];l++)
S[i+l-1]=V[l];
}
S[0]=S[0]-T[0]+V[0];
i+=V[0];n++;
}//if
数据结构试卷 数据结构试题库集及答案
严蔚敏《数据结构习题集》解答
}//for
return n;
}//String_Replace
4.18
typedef struct {
char ch;
int num;
} mytype;
void StrAnalyze(Stringtype S)//统计串S 中字符的种类和个数
{
mytype T[MAXSIZE]; //用结构数组T 存储统计结果
for(i=1;i<=S[0];i++)
{
c=S[i];j=0;
while(T[j].ch&&T[j].ch!=c) j++; //查找当前字符c 是否已记录过
if(T[j].ch) T[j].num++;
else T[j]={c,1};
}//for
for(j=0;T[j].ch;j++)
printf("%c: %d\n",T[j].ch,T[j].num);
}//StrAnalyze
4.19
第 33 页 共 124 页
void Subtract_String(Stringtype s,Stringtype t,Stringtype &r)//求所有包含在串s 中而t 中没有的 字符构成的新串r
{
r[0]=0;
for(i=1;i<=s[0];i++)
{
c=s[i];
for(j=1;j<i&&s[j]!=c;j++); //判断s 的当前字符c 是否第一次出现
if(i==j)
{
for(k=1;k<=t[0]&&t[k]!=c;k++); //判断当前字符是否包含在t 中
if(k>t[0]) r[++r[0]]=c;
}
}//for
}//Subtract_String
4.20
int SubString_Delete(Stringtype &s,Stringtype t)//从串s 中删除所有与t 相同的子串,并返回删除 次数
{
for(n=0,i=1;i<=s[0]-t[0]+1;i++)
{
for(j=1;j<=t[0]&&s[i+j-1]==t[i];j++);
严蔚敏《数据结构习题集》解答
数据结构试卷 数据结构试题库集及答案
if(j>m) //找到了与t 匹配的子串
{
for(k=i;k<=s[0]-t[0];k++) s[k]=s[k+t[0]]; //左移删除
s[0]-=t[0];n++;
}
}//for
return n;
}//Delete_SubString
4.21
typedef struct{
char ch;
LStrNode *next;
} LStrNode,*LString; //链串结构
void StringAssign(LString &s,LString t)//把串t 赋值给串s
{
s=malloc(sizeof(LStrNode));
for(q=s,p=t->next;p;p=p->next)
{
r=(LStrNode*)malloc(sizeof(LStrNode));
r->ch=p->ch;
q->next=r;q=r;
}
q->next=NULL;
}//StringAssign
第 34 页 共 124 页
void StringCopy(LString &s,LString t)//把串t 复制为串s.与前一个程序的区别在于,串s 业已存 在.
{
for(p=s->next,q=t->next;p&&q;p=p->next,q=q->next)
{
p->ch=q->ch;pre=p;
}
while(q)
{
p=(LStrNode*)malloc(sizeof(LStrNode));
p->ch=q->ch;
pre->next=p;pre=p;
}
p->next=NULL;
}//StringCopy
char StringCompare(LString s,LString t)//串的比较,s>t 时返回正数,s=t 时返回0,s<t 时返回负数 {
for(p=s->next,q=t->next;p&&q&&p->ch==q->ch;p=p->next,q=q->next);
if(!p&&!q) return 0;
else if(!p) return -(q->ch);
严蔚敏《数据结构习题集》解答
数据结构试卷 数据结构试题库集及答案
else if(!q) return p->ch;
else return p->ch-q->ch;
}//StringCompare
int StringLen(LString s)//求串s 的长度(元素个数)
{
for(i=0,p=s->next;p;p=p->next,i++);
return i;
}//StringLen
LString * Concat(LString s,LString t)//连接串s 和串t 形成新串,并返回指针
{
p=malloc(sizeof(LStrNode));
for(q=p,r=s->next;r;r=r->next)
{
q->next=(LStrNode*)malloc(sizeof(LStrNode));
q=q->next;
q->ch=r->ch;
}//for //复制串s
for(r=t->next;r;r=r->next)
{
q->next=(LStrNode*)malloc(sizeof(LStrNode));
q=q->next;
q->ch=r->ch;
}//for //复制串t
q->next=NULL;
return p;
}//Concat
第 35 页 共 124 页
LString * Sub_String(LString s,int start,int len)//返回一个串,其值等于串s 从start 位置起长为 len 的子串
{
p=malloc(sizeof(LStrNode));q=p;
for(r=s;start;start--,r=r->next); //找到start 所对应的结点指针r
for(i=1;i<=len;i++,r=r->next)
{
q->next=(LStrNode*)malloc(sizeof(LStrNode));
q=q->next;
q->ch=r->ch;
} //复制串t
q->next=NULL;
return p;
}//Sub_String
4.22
void LString_Concat(LString &t,LString &s,char c)//用块链存储结构,把串s 插入到串t 的字符c 之后
{
严蔚敏《数据结构习题集》解答
数据结构试卷 数据结构试题库集及答案
p=t.head;
while(p&&!(i=Find_Char(p,c))) p=p->next; //查找字符c
if(!p) //没找到
{
t.tail->next=s.head;
t.tail=s.tail; //把s 连接在t 的后面
}
else
{
q=p->next;
r=(Chunk*)malloc(sizeof(Chunk)); //将包含字符c 的节点p 分裂为两个
for(j=0;j<i;j++) r->ch[j]='#'; //原结点p 包含c 及其以前的部分
for(j=i;j<CHUNKSIZE;j++) //新结点r 包含c 以后的部分
{
r->ch[j]=p->ch[j];
p->ch[j]='#'; //p 的后半部分和r 的前半部分的字符改为无效字符'#'
}
p->next=s.head;
s.tail->next=r;
r->next=q; //把串s 插入到结点p 和r 之间
}//else
t.curlen+=s.curlen; //修改串长
s.curlen=0;
}//LString_Concat
第 36 页 共 124 页
int Find_Char(Chunk *p,char c)//在某个块中查找字符c,如找到则返回位置是第几个字符,如没 找到则返回0
{
for(i=0;i<CHUNKSIZE&&p->ch[i]!=c;i++);
if(i==CHUNKSIZE) return 0;
else return i+1;
}//Find_Char
4.23
int LString_Palindrome(LString L)//判断以块链结构存储的串L 是否为回文序列,是则返回1, 否则返回0
{
InitStack(S);
p=S.head;i=0;k=1; //i 指示元素在块中的下标,k 指示元素在整个序列中的序号(从1 开始) for(k=1;k<=S.curlen;k++)
{
if(k<=S.curlen/2) Push(S,p->ch[i]); //将前半段的字符入串
else if(k>(S.curlen+1)/2)
{
Pop(S,c); //将后半段的字符与栈中的元素相匹配
严蔚敏《数据结构习题集》解答
if(p->ch[i]!=c) return 0; //失配
数据结构试卷 数据结构试题库集及答案
}
第 37 页 共 124 页
if(++i==CHUNKSIZE) //转到下一个元素,当为块中最后一个元素时,转到下一块
{
p=p->next;
i=0;
}
}//for
return 1; //成功匹配
}//LString_Palindrome
4.24
void HString_Concat(HString s1,HString s2,HString &t)//将堆结构表示的串s1 和s2 连接为新串 t
{
if(t.ch) free(t.ch);
t.ch=malloc((s1.length+s2.length)*sizeof(char));
for(i=1;i<=s1.length;i++) t.ch[i-1]=s1.ch[i-1];
for(j=1;j<=s2.length;j++,i++) t.ch[i-1]=s2.ch[j-1];
t.length=s1.length+s2.length;
}//HString_Concat
4.25
int HString_Replace(HString &S,HString T,HString V)//堆结构串上的置换操作,返回置换次数 {
for(n=0,i=0;i<=S.length-T.length;i++)
{
for(j=i,k=0;k<T.length&&S.ch[j]==T.ch[k];j++,k++);
if(k==T.length) //找到了与T 匹配的子串:分三种情况处理
{
if(T.length==V.length)
for(l=1;l<=T.length;l++) //新子串长度与原子串相同时:直接替换
S.ch[i+l-1]=V.ch[l-1];
else if(T.length<V.length) //新子串长度大于原子串时:先将后部右移
{
for(l=S.length-1;l>=i+T.length;l--)
S.ch[l+V.length-T.length]=S.ch[l];
for(l=0;l<V.length;l++)
S[i+l]=V[l];
}
else //新子串长度小于原子串时:先将后部左移
{
for(l=i+V.length;l<S.length+V.length-T.length;l++)
S.ch[l]=S.ch[l-V.length+T.length];
for(l=0;l<V.length;l++)
S[i+l]=V[l];
严蔚敏《数据结构习题集》解答
}
S.length+=V.length-T.length;
数据结构试卷 数据结构试题库集及答案
i+=V.length;n++;
}//if
}//for
return n;
}//HString_Replace
4.26
第 38 页 共 124 页
Status HString_Insert(HString &S,int pos,HString T)//把T 插入堆结构表示的串S 的第pos 个字 符之前
{
if(pos<1) return ERROR;
if(pos>S.length) pos=S.length+1;//当插入位置大于串长时,看作添加在串尾
S.ch=realloc(S.ch,(S.length+T.length)*sizeof(char));
for(i=S.length-1;i>=pos-1;i--)
S.ch[i+T.length]=S.ch[i]; //后移为插入字符串让出位置
for(i=0;i<T.length;i++)
S.ch[pos+i-1]=T.ch[pos]; //插入串T
S.length+=T.length;
return OK;
}//HString_Insert
4.27
int Index_New(Stringtype s,Stringtype t)//改进的定位算法
{
i=1;j=1;
while(i<=s[0]&&j<=t[0])
{
if((j!=1&&s[i]==t[j])||(j==1&&s[i]==t[j]&&s[i+t[0]-1]==t[t[0]]))
{ //当j==1 即匹配模式串的第一个字符时,需同时匹配其最后一个
i=i+j-2;
j=1;
}
else
{
i++;j++;
}
}//while
if(j>t[0]) return i-t[0];
}//Index_New
4.28
void LGet_next(LString &T)//链串上的get_next 算法
{
p=T->succ;p->next=T;q=T;
while(p->succ)
严蔚敏《数据结构习题集》解答
{
if(q==T||p->data==q->data)
{
数据结构试卷 数据结构试题库集及答案
p=p->succ;q=q->succ;
p->next=q;
}
else q=q->next;
}//while
}//LGet_next
4.29
第 39 页 共 124 页
LStrNode * LIndex_KMP(LString S,LString T,LStrNode *pos)//链串上的KMP 匹配算法,返回 值为匹配的子串首指针
{
p=pos;q=T->succ;
while(p&&q)
{
if(q==T||p->chdata==q->chdata)
{
p=p->succ;
q=q->succ;
}
else q=q->next;
}//while
if(!q)
{
for(i=1;i<=Strlen(T);i++)
p=p->next;
return p;
} //发现匹配后,要往回找子串的头
return NULL;
}//LIndex_KMP
4.30
void Get_LRepSub(Stringtype S)//求S 的最长重复子串的位置和长度
{
for(maxlen=0,i=1;i<S[0];i++)//串S2 向右移i 格
{
for(k=0,j=1;j<=S[0]-i;j++)//j 为串S2 的当前指针,此时串S1 的当前指针为i+j,两指针同步移 动
{
if(S[j]==S[j+i]) k++; //用k 记录连续相同的字符数
else k=0; //失配时k 归零
if(k>maxlen) //发现了比以前发现的更长的重复子串
{
lrs1=j-k+1;lrs2=mrs1+i;maxlen=k; //作记录
严蔚敏《数据结构习题集》解答
}
}//for
}//for
if(maxlen)
数据结构试卷 数据结构试题库集及答案
{
printf("Longest Repeating Substring length:%d\n",maxlen);
printf("Position1:%d Position 2:%d\n",lrs1,lrs2);
}
else printf("No Repeating Substring found!\n");
}//Get_LRepSub
第 40 页 共 124 页
分析:i 代表"错位值".本算法的思想是,依次把串S 的一个副本S2 向右错位平移1 格,2 格,3 格,... 与自身 S1 相匹配, 如果存在最长重复子串, 则必然能在此过程中被发现. 用变量
lrs1,lrs2,maxlen 来记录已发现的最长重复子串第一次出现位置,第二次出现位置和长度.题目 中未说明"重复子串"是否允许有重叠部分,本算法假定允许.如不允许,只需在第二个for 语句 的循环条件中加上k<=i 即可.本算法时间复杂度为O(Strlen(S)^2).
4.31
void Get_LPubSub(Stringtype S,Stringtype T)//求串S 和串T 的最长公共子串位置和长度
{
if(S[0]>=T[0])
{
StrAssign(A,S);StrAssign(B,T);
}
else
{
StrAssign(A,T);StrAssign(B,S);
} //为简化设计,令S 和T 中较长的那个为A,较短的那个为B
for(maxlen=0,i=1-B[0];i<A[0];i++)
{
if(i<0) //i 为B 相对于A 的错位值,向左为负,左端对齐为0,向右为正
{
jmin=1;jmax=i+B[0];
}//B 有一部分在A 左端的左边
else if(i>A[0]-B[0])
{
jmin=i;jmax=A[0];
}//B 有一部分在A 右端的右边
else
{
jmin=i;jmax=i+B[0];
}//B 在A 左右两端之间.
//以上是根据A 和B 不同的相对位置确定A 上需要匹配的区间(与B 重合的区间)的端 点:jmin,jmax.
for(k=0,j=jmin;j<=jmax;j++)
{
严蔚敏《数据结构习题集》解答
if(A[j]==B[j-i]) k++;
else k=0;
if(k>maxlen)
{
lps1=j-k+1;lps2=j-i-k+1;maxlen=k;
数据结构试卷 数据结构试题库集及答案
}//for
}//for
if(maxlen)
{
if(S[0]>=T[0])
{
lpsS=lps1;lpsT=lps2;
}
else
{
lpsS=lps2;lpsT=lps1;
} //将A,B 上的位置映射回S,T 上的位置
printf("Longest Public Substring length:%d\n",maxlen);
printf("Position in S:%d Position in T:%d\n",lpsS,lpsT);
}//if
else printf("No Repeating Substring found!\n");
}//Get_LPubSub
第 41 页 共 124 页
分析:本题基本思路与上题同.唯一的区别是,由于A,B 互不相同,因此B 不仅要向右错位,而且 还要向左错位,以保证不漏掉一些情况.当B 相对于A 的位置不同时,需要匹配的区间的计算
公式也各不相同,请读者自己画图以帮助理解.本算法的时间复杂度是o(strlrn(s)*strlen(t))。(www.61k.com] 严蔚敏《数据结构习题集》解答
第五章 数组和广义表
5.18
第 42 页 共 124 页
void RSh(int A[n],int k)//把数组A 的元素循环右移k 位,只用一个辅助存储空间
{
for(i=1;i<=k;i++)
if(n%i==0&&k%i==0) p=i;//求n 和k 的最大公约数p
for(i=0;i<p;i++)
{
j=i;l=(i+n-k)%n;temp=A[i];
while(l!=i)
{
A[j]=A[l];
j=l;l=(j+n-k)%n;
}// 循环右移一步
A[j]=temp;
}//for
}//RSh
分析:要把A 的元素循环右移k 位,则A[0]移至A[k],A[k]移至A[2k]......直到最终回到A[0].
然而这并没有全部解决问题,因为有可能有的元素在此过程中始终没有被访问过,而是被跳了
过去.分析可知,当n 和k 的最大公约数为p 时,只要分别以A[0],A[1],...A[p-1]为起点执行上述
数据结构试卷 数据结构试题库集及答案
算法,就可以保证每一个元素都被且仅被右移一次,从而满足题目要求.也就是说,A
素分别处在p 个"循环链"上面.举例如下:
n=15,k=6,则p=3.
第一条链:A[0]->A[6],A[6]->A[12],A[12]->A[3],A[3]->A[9],A[9]->A[0].
第二条链:A[1]->A[7],A[7]->A[13],A[13]->A[4],A[4]->A[10],A[10]->A[1].
第三条链:A[2]->A[8],A[8]->A[14],A[14]->A[5],A[5]->A[11],A[11]->A[2].
恰好使所有元素都右移一次.
虽然未经数学证明,但作者相信上述规律应该是正确的.
5.19
void Get_Saddle(int A[m][n])//求矩阵A 中的马鞍点
{
for(i=0;i<m;i++)
{
for(min=A[i][0],j=0;j<n;j++)
if(A[i][j]<min) min=A[i][j]; //求一行中的最小值
for(j=0;j<n;j++)
if(A[i][j]==min) //判断这个(些)最小值是否鞍点
{
for(flag=1,k=0;k<m;k++)
if(min<A[k][j]) flag=0;
if(flag)
printf("Found a saddle element!\nA[%d][%d]=%d",i,j,A[i][j]);
严蔚敏《数据结构习题集》解答
的所有元
}
}//for
}//Get_Saddle
5.20
int exps[MAXSIZE]; //exps 数组用于存储某一项的各变元的指数
int maxm,n; //maxm 指示变元总数,n 指示一个变元的最高指数
第 43 页 共 124 页
void Print_Poly_Descend(int *a,int m)//按降幂顺序输出m 元多项式的项,各项的系数已经按 照题目要求存储于m 维数组中,数组的头指针为a
{
maxm=m;
for(i=m*n;i>=0;i--) //按降幂次序,可能出现的最高项次数为mn
Get_All(a,m,i,0); //确定并输出所有次数为i 的项
}//Print_Poly_Descend
void Get_All(int *a,int m,int i,int seq)//递归求出所有和为i 的m 个自然数
{
if(seq==maxm) Print_Nomial(a,exps); //已经求完时,输出该项
else
{
min=i-(m-1)*n; //当前数不能小于min
if(min<0) min=0;
max=n<i?n:i; //当前数不能大于max
for(j=min;j<=max;j++)
{
数据结构试卷 数据结构试题库集及答案
Get_All(a,m-1,i-j,seq+1); //取下一个数
}
}//else
exps[seq]=0; //返回
}//Get_All
void Print_Nomial(int *a,int exps[ ])//输出一个项,项的各变元的指数已经存储在数组exps 中 {
pos=0;
for(i=0;i<maxm;i++) //求出该项的系数在m 维数组a 中低下标优先的存储位置pos {
pos*=n;
pos+=exps[i];
}
coef=*(a+pos); //取得该系数coef
if(!coef) return; //该项为0 时无需输出
else if(coef>0) printf("+"); //系数为正时打印加号
else if(coef<0) printf("-"); //系数为负时打印减号
if(abs(coef)!=1) printf("%d",abs(coef)); //当系数的绝对值不为1 时打印系数
for(i=0;i<maxm;i++)
if(exps[i]) //打印各变元及其系数
严蔚敏《数据结构习题集》解答
{
printf("x");
printf("%d",i);
printf("E");
if(exps[i]>1) printf("%d",exp[i]); //系数为1 时无需打印
}
}//Print_Nomial
第 44 页 共 124 页
分析:本算法的关键在于如何按照降幂顺序输出各项.这里采用了一个递归函数来找到所有满 足和为i 的m 个自然数作为各变元的指数.只要先取第一个数为j,然后再找到所有满足和为
i-j 的m-1 个自然数就行了.要注意j 的取值范围必须使剩余m-1 个自然数能够找到,所以不能 小于 i-(m-1)*maxn,也不能大于 i.只要找到了一组符合条件的数,就可以在存储多项式系数的 数组中确定对应的项的系数的位置,并且在系数不为0 时输出对应的项.
5.21
void TSMatrix_Add(TSMatrix A,TSMatrix B,TSMatrix &C)//三元组表示的稀疏矩阵加法 {
C.mu=A.mu;C.nu=A.nu;C.tu=0;
pa=1;pb=1;pc=1;
for(x=1;x<=A.mu;x++) //对矩阵的每一行进行加法
{
while(A.data[pa].i<x) pa++;
while(B.data[pb].i<x) pb++;
while(A.data[pa].i==x&&B.data[pb].i==x)//行列值都相等的元素
{
数据结构试卷 数据结构试题库集及答案
{
ce=A.data[pa].e+B.data[pb].e;
if(ce) //和不为0
{
C.data[pc].i=x;
C.data[pc].j=A.data[pa].j;
C.data[pc].e=ce;
pa++;pb++;pc++;
}
}//if
else if(A.data[pa].j>B.data[pb].j)
{
C.data[pc].i=x;
C.data[pc].j=B.data[pb].j;
C.data[pc].e=B.data[pb].e;
pb++;pc++;
}
else
{
严蔚敏《数据结构习题集》解答
C.data[pc].i=x;
C.data[pc].j=A.data[pa].j;
C.data[pc].e=A.data[pa].e
pa++;pc++;
}
}//while
while(A.data[pa]==x) //插入A 中剩余的元素(第x 行) {
C.data[pc].i=x;
C.data[pc].j=A.data[pa].j;
C.data[pc].e=A.data[pa].e
pa++;pc++;
}
while(B.data[pb]==x) //插入B 中剩余的元素(第x 行) {
C.data[pc].i=x;
C.data[pc].j=B.data[pb].j;
C.data[pc].e=B.data[pb].e;
pb++;pc++;
}
}//for
C.tu=pc;
}//TSMatrix_Add
5.22
第 45 页 共 124 页
void TSMatrix_Addto(TSMatrix &A,TSMatrix B)//将三元组矩阵B 加到A 上
数据结构试卷 数据结构试题库集及答案
{
for(i=1;i<=A.tu;i++)
A.data[MAXSIZE-A.tu+i]=A.data[i];/把A 的所有元素都移到尾部以腾出位置 pa=MAXSIZE-A.tu+1;pb=1;pc=1;
for(x=1;x<=A.mu;x++) //对矩阵的每一行进行加法
{
while(A.data[pa].i<x) pa++;
while(B.data[pb].i<x) pb++;
while(A.data[pa].i==x&&B.data[pb].i==x)//行列值都相等的元素
{
if(A.data[pa].j==B.data[pb].j)
{
ne=A.data[pa].e+B.data[pb].e;
if(ne) //和不为0
{
A.data[pc].i=x;
A.data[pc].j=A.data[pa].j;
A.data[pc].e=ne;
pa++;pb++;pc++;
严蔚敏《数据结构习题集》解答
}
}//if
else if(A.data[pa].j>B.data[pb].j)
{
A.data[pc].i=x;
A.data[pc].j=B.data[pb].j;
A.data[pc].e=B.data[pb].e;
pb++;pc++;
}
else
{
A.data[pc].i=x;
A.data[pc].j=A.data[pa].j;
A.data[pc].e=A.data[pa].e
pa++;pc++;
}
}//while
while(A.data[pa]==x) //插入A 中剩余的元素(第x 行)
{
A.data[pc].i=x;
A.data[pc].j=A.data[pa].j;
A.data[pc].e=A.data[pa].e
pa++;pc++;
}
while(B.data[pb]==x) //插入B 中剩余的元素(第x 行)
{
A.data[pc].i=x;
数据结构试卷 数据结构试题库集及答案
A.data[pc].j=B.data[pb].j;
A.data[pc].e=B.data[pb].e;
pb++;pc++;
}
}//for
A.tu=pc;
for(i=A.tu;i<MAXSIZE;i++) A.data[i]={0,0,0}; //清除原来的A 中记录
}//TSMatrix_Addto
5.23
typedef struct{
int j;
int e;
} DSElem;
typedef struct{
DSElem data[MAXSIZE];
第 46 页 共 124 页
int cpot[MAXROW];//这个向量存储每一行在二元组中的起始位置 int mu,nu,tu;
严蔚敏《数据结构习题集》解答
第 47 页 共 124 页 } DSMatrix; //二元组矩阵类型
Status DSMatrix_Locate(DSMatrix A,int i,int j,int &e)//求二元组矩阵的元素A[i][j]的值e {
for(s=A.cpot[i];s<A.cpot[i+1]&&A.data[s].j!=j;s++);//注意查找范围
if(s<A.cpot[i+1]&&A.data[s].j==j) //找到了元素A[i][j]
{
e=A.data[s];
return OK;
}
return ERROR;
}//DSMatrix_Locate
5.24
typedef struct{
int seq; //该元素在以行为主序排列时的序号
int e;
} SElem;
typedef struct{
SElem data[MAXSIZE];
int mu,nu,tu;
} SMatrix; //单下标二元组矩阵类型
Status SMatrix_Locate(SMatrix A,int i,int j,int &e)//求单下标二元组矩阵的元素A[i][j]的值e {
s=i*A.nu+j+1;p=1;
while(A.data[p].seq<s) p++; //利用各元素seq 值逐渐递增的特点
if(A.data[p].seq==s) //找到了元素A[i][j]
{
e=A.data[p].e;
数据结构试卷 数据结构试题库集及答案
}
return ERROR;
}//SMatrix_Locate
5.25
typedef enum{0,1} bool;
typedef struct{
int mu,nu;
int elem[MAXSIZE];
bool map[mu][nu];
} BMMatrix; //用位图表示的矩阵类型
void BMMatrix_Add(BMMatrix A,BMMatrix B,BMMatrix &C)//位图矩阵的加法 {
C.mu=A.mu;C.nu=A.nu;
pa=1;pb=1;pc=1;
for(i=0;i<A.mu;i++) //每一行的相加
for(j=0;j<A.nu;j++) //每一个元素的相加
严蔚敏《数据结构习题集》解答
{
if(A.map[i][j]&&B.map[i][j]&&(A.elem[pa]+B.elem[pb]))//结果不为0 {
C.elem[pc]=A.elem[pa]+B.elem[pb];
C.map[i][j]=1;
pa++;pb++;pc++;
}
else if(A.map[i][j]&&!B.map[i][j])
{
C.elem[pc]=A.elem[pa];
C.map[i][j]=1;
pa++;pc++;
}
else if(!A.map[i][j]&&B.map[i][j])
{
C.elem[pc]=B.elem[pb];
C.map[i][j]=1;
pb++;pc++;
}
}
}//BMMatrix_Add
5.26
第 48 页 共 124 页
void Print_OLMatrix(OLMatrix A)//以三元组格式输出十字链表表示的矩阵 {
for(i=0;i<A.mu;i++)
{
if(A.rhead[i])
for(p=A.rhead[i];p;p=p->right) //逐次遍历每一个行链表
数据结构试卷 数据结构试题库集及答案
printf("%d %d %d\n",i,p->j,p->e;
}
}//Print_OLMatrix
5.27
void OLMatrix_Add(OLMatrix &A,OLMatrix B)//把十字链表表示的矩阵B 加到A 上 {
for(j=1;j<=A.nu;j++) cp[j]=A.chead[j]; //向量cp 存储每一列当前最后一个元素的指针 for(i=1;i<=A.mu;i++)
{
pa=A.rhead[i];pb=B.rhead[i];pre=NULL;
while(pb)
{
if(pa==NULL||pa->j>pb->j) //新插入一个结点
{
p=(OLNode*)malloc(sizeof(OLNode));
if(!pre) A.rhead[i]=p;
严蔚敏《数据结构习题集》解答
else pre->right=p;
p->right=pa;pre=p;
p->i=i;p->j=pb->j;p->e=pb->e; //插入行链表中
if(!A.chead[p->j])
{
A.chead[p->j]=p;
p->down=NULL;
}
else
{
while(cp[p->j]->down) cp[p->j]=cp[p->j]->down;
p->down=cp[p->j]->down;
cp[p->j]->down=p;
}
cp[p->j]=p; //插入列链表中
}//if
else if(pa->j<pb->j)
{
pre=pa;
pa=pa->right;
} //pa 右移一步
else if(pa->e+pb->e)
{
pa->e+=pb->e;
pre=pa;pa=pa->right;
pb=pb->right;
} //直接相加
else
{
if(!pre) A.rhead[i]=pa->right;
数据结构试卷 数据结构试题库集及答案
else pre->right=pa->right;
p=pa;pa=pa->right; //从行链表中删除
if(A.chead[p->j]==p)
A.chead[p->j]=cp[p->j]=p->down;
else cp[p->j]->down=p->down; //从列链表中删除
free (p);
}//else
}//while
}//for
}//OLMatrix_Add
分析:本题的具体思想在课本中有详细的解释说明.
5.28
第 49 页 共 124 页
void MPList_PianDao(MPList &L)//对广义表存储结构的多元多项式求第一变元的偏导 {
严蔚敏《数据结构习题集》解答
for(p=L->hp->tp;p&&p->exp;pre=p,p=p->tp)
{
if(p->tag) Mul(p->hp,p->exp);
else p->coef*=p->exp; //把指数乘在本结点或其下属结点上
p->exp--;
}
pre->tp=NULL;
if(p) free (p); //删除可能存在的常数项
}//MPList_PianDao
void Mul(MPList &L,int x)//递归算法,对多元多项式L 乘以x
{
for(p=L;p;p=p->tp)
{
if(!p->tag) p->coef*=x;
else Mul(p->hp,x);
}
}//Mul
5.29
第 50 页 共 124 页
void MPList_Add(MPList A,MPList B,MPList &C)//广义表存储结构的多项式相加的递归算法 {
C=(MPLNode*)malloc(sizeof(MPLNode));
if(!A->tag&&!B->tag) //原子项,可直接相加
{
C->coef=A->coef+B->coef;
if(!C->coef)
{
free(C);
C=NULL;
}
数据结构试卷 数据结构试题库集及答案
}//if
else if(A->tag&&B->tag) //两个多项式相加 {
p=A;q=B;pre=NULL;
while(p&&q)
{
if(p->exp==q->exp)
{
C=(MPLNode*)malloc(sizeof(MPLNode)); C->exp=p->exp;
MPList_Add(A->hp,B->hp,C->hp); pre->tp=C;pre=C;
p=p->tp;q=q->tp;
}
严蔚敏《数据结构习题集》解答
else if(p->exp>q->exp)
{
C=(MPLNode*)malloc(sizeof(MPLNode)); C->exp=p->exp;
C->hp=A->hp;
pre->tp=C;pre=C;
p=p->tp;
}
else
{
C=(MPLNode*)malloc(sizeof(MPLNode)); C->exp=q->exp;
C->hp=B->hp;
pre->tp=C;pre=C;
q=q->tp;
}
}//while
while(p)
{
C=(MPLNode*)malloc(sizeof(MPLNode)); C->exp=p->exp;
C->hp=p->hp;
pre->tp=C;pre=C;
p=p->tp;
}
while(q)
{
C=(MPLNode*)malloc(sizeof(MPLNode)); C->exp=q->exp;
C->hp=q->hp;
pre->tp=C;pre=C;
q=q->tp;
数据结构试卷 数据结构试题库集及答案
} //将其同次项分别相加得到新的多项式,原理见第二章多项式相加一题 }//else if
else if(A->tag&&!B->tag) //多项式和常数项相加
{
x=B->coef;
for(p=A;p->tp->tp;p=p->tp);
第 51 页 共 124 页
if(p->tp->exp==0) p->tp->coef+=x; //当多项式中含有常数项时,加上常数项 if(!p->tp->coef)
{
free(p->tp);
p->tp=NULL;
}
严蔚敏《数据结构习题集》解答
else
{
q=(MPLNode*)malloc(sizeof(MPLNode));
q->coef=x;q->exp=0;
q->tag=0;q->tp=NULL;
p->tp=q;
} //否则新建常数项,下同
}//else if
else
{
x=A->coef;
for(p=B;p->tp->tp;p=p->tp);
if(p->tp->exp==0) p->tp->coef+=x;
if(!p->tp->coef)
{
free(p->tp);
p->tp=NULL;
}
else
{
q=(MPLNode*)malloc(sizeof(MPLNode));
q->coef=x;q->exp=0;
q->tag=0;q->tp=NULL;
p->tp=q;
}
}//else
}//MPList_Add
5.30
int GList_Getdeph(GList L)//求广义表深度的递归算法
{
if(!L->tag) return 0; //原子深度为0
else if(!L) return 1; //空表深度为1
m=GList_Getdeph(L->ptr.hp)+1;
数据结构试卷 数据结构试题库集及答案
n=GList_Getdeph(L->ptr.tp);
return m>n?m:n;
}//GList_Getdeph
5.31
void GList_Copy(GList A,GList &B)//复制广义表的递归算法
{
if(!A->tag) //当结点为原子时,直接复制
{
B->tag=0;
B->atom=A->atom;
}
第 52 页 共 124 页
严蔚敏《数据结构习题集》解答
else //当结点为子表时
{
B->tag=1;
if(A->ptr.hp)
{
B->ptr.hp=malloc(sizeof(GLNode));
GList_Copy(A->ptr.hp,B->ptr.hp);
} //复制表头
if(A->ptr.tp)
{
B->ptr.tp=malloc(sizeof(GLNode));
GList_Copy(A->ptr.tp,B->ptr.tp);
} //复制表尾
}//else
}//GList_Copy
5.32
第 53 页 共 124 页
int GList_Equal(GList A,GList B)//判断广义表A 和B 是否相等,是则返回1,否则返回0 { //广义表相等可分三种情况:
if(!A&&!B) return 1; //空表是相等的
if(!A->tag&&!B->tag&&A->atom==B->atom) return 1;//原子的值相等
if(A->tag&&B->tag)
if(GList_Equal(A->ptr.hp,B->ptr.hp)&&GList_Equal(A->ptr.tp,B->ptr.tp))
return 1; //表头表尾都相等
return 0;
}//GList_Equal
5.33
void GList_PrintElem(GList A,int layer)//递归输出广义表的原子及其所在层次,layer 表示当前 层次
{
if(!A) return;
if(!A->tag) printf("%d %d\n",A->atom,layer);
else
{
数据结构试卷 数据结构试题库集及答案
GList_PrintElem(A->ptr.hp,layer+1);
GList_PrintElem(A->ptr.tp,layer); //注意尾表与原表是同一层次 }
}//GList_PrintElem
5.34
void GList_Reverse(GList A)//递归逆转广义表A
{
GLNode *ptr[MAX_SIZE];
if(A->tag&&A->ptr.tp) //当A 不为原子且表尾非空时才需逆转 {
for(i=0,p=A;p;p=p->ptr.tp,i++)
严蔚敏《数据结构习题集》解答
{
if(p->ptr.hp) GList_Reverse(p->ptr.hp); //逆转各子表 ptr[i]=p->ptr.hp;
}
for(p=A;p;p=p->ptr.tp) //重新按逆序排列各子表的顺序
p->ptr.hp=ptr[--i];
}
}//GList_Reverse
5.35
Status Create_GList(GList &L)//根据输入创建广义表L,并返回指针 {
scanf("%c",&ch);
if(ch==' ')
{
L=NULL;
scanf("%c",&ch);
if(ch!=')') return ERROR;
return OK;
}
L=(GList)malloc(sizeof(GLNode));
L->tag=1;
if(isalphabet(ch)) //输入是字母
{
p=(GList)malloc(sizeof(GLNode)); //建原子型表头
p->tag=0;p->atom=ch;
L->ptr.hp=p;
}
else if(ch=='(') Create_GList(L->ptr.hp); //建子表型表头
else return ERROR;
scanf ("%c",&ch);
if(ch==')') L->ptr.tp=NULL;
else if(ch==',') Create_GList(L->ptr.tp); //建表尾
else return ERROR;
return OK;
}//Create_GList
数据结构试卷 数据结构试题库集及答案
分析:本题思路见书后解答.
5.36
void GList_PrintList(GList A)//按标准形式输出广义表
{
if(!A) printf("()"); //空表
else if(!A->tag) printf("%d",A->atom);//原子
else
{
printf("(");
第 54 页 共 124 页
严蔚敏《数据结构习题集》解答
for(p=A;p;p=p->ptr.tp)
{
GList_PrintList(p->ptr.hp);
if(p->ptr.tp) printf(","); //只有当表尾非空时才需要打印逗号 }
printf(")");
}//else
}//GList_PrintList
5.37
第 55 页 共 124 页
void GList_DelElem(GList &A,int x)//从广义表A 中删除所有值为x 的原子 {
if(A&&A->ptr.hp)
{
if(A->ptr.hp->tag) GList_DelElem(A->ptr.hp,x);
else if(!A->ptr.hp->tag&&A->ptr.hp->atom==x)
{
q=A;
A=A->ptr.tp; //删去元素值为x 的表头
free(q);
GList_DelElem(A,x);
}
}
if(A&&A->ptr.tp) GList_DelElem(A->ptr.tp,x);
}//GList_DelElem
5.39
void GList_PrintElem_LOrder(GList A)//按层序输出广义表A 中的所有元素 {
InitQueue(Q);
for(p=L;p;p=p->ptr.tp) EnQueue(Q,p);
while(!QueueEmpty(Q))
{
DeQueue(Q,r);
if(!r->tag) printf("%d",r->atom);
else
for(r=r->ptr.hp;r;r=r->ptr.tp) EnQueue(Q,r);
数据结构试卷 数据结构试题库集及答案
}//GList_PrintElem_LOrder
分析:层序遍历的问题,一般都是借助队列来完成的,每次从队头取出一个元素的同时把它下 一层的孩子插入队尾.这是层序遍历的基本思想.
严蔚敏《数据结构习题集》解答
第六章 树和二叉树
6.33
第 56 页 共 124 页
int Is_Descendant_C(int u,int v)//在孩子存储结构上判断u 是否v 的子孙,是则返回1,否则返回 0
{
if(u==v) return 1;
else
{
if(L[v])
if (Is_Descendant(u,L[v])) return 1;
if(R[v])
if (Is_Descendant(u,R[v])) return 1; //这是个递归算法
}
return 0;
}//Is_Descendant_C
6.34
int Is_Descendant_P(int u,int v)//在双亲存储结构上判断u 是否v 的子孙,是则返回1,否则返回
{
for(p=u;p!=v&&p;p=T[p]);
if(p==v) return 1;
else return 0;
}//Is_Descendant_P
6.35
这一题根本不需要写什么算法,见书后注释:两个整数的值是相等的.
6.36
int Bitree_Sim(Bitree B1,Bitree B2)//判断两棵树是否相似的递归算法
{
if(!B1&&!B2) return 1;
else if(B1&&B2&&Bitree_Sim(B1->lchild,B2->lchild)&&Bitree_Sim(B1->rchild,B2->rchild)) return 1;
else return 0;
}//Bitree_Sim
6.37
void PreOrder_Nonrecursive(Bitree T)//先序遍历二叉树的非递归算法
{
InitStack(S);
Push(S,T); //根指针进栈
数据结构试卷 数据结构试题库集及答案
{
while(Gettop(S,p)&&p)
{
严蔚敏《数据结构习题集》解答
visit(p->data);
push(S,p->lchild);
} //向左走到尽头
pop(S,p);
if(!StackEmpty(S))
{
pop(S,p);
push(S,p->rchild); //向右一步
}
}//while
}//PreOrder_Nonrecursive
6.38
typedef struct {
BTNode* ptr;
enum {0,1,2} mark;
} PMType; //有mark 域的结点指针类型
void PostOrder_Stack(BiTree T)//后续遍历二叉树的非递归算法,用栈
{
PMType a;
InitStack(S); //S 的元素为PMType 类型
Push (S,{T,0}); //根结点入栈
while(!StackEmpty(S))
{
Pop(S,a);
switch(a.mark)
{
case 0:
Push(S,{a.ptr,1}); //修改mark 域
if(a.ptr->lchild) Push(S,{a.ptr->lchild,0}); //访问左子树
break;
case 1:
Push(S,{a.ptr,2}); //修改mark 域
if(a.ptr->rchild) Push(S,{a.ptr->rchild,0}); //访问右子树
break;
case 2:
visit(a.ptr); //访问结点,返回
}
}//while
}//PostOrder_Stack
第 57 页 共 124 页
分析:为了区分两次过栈的不同处理方式,在堆栈中增加一个mark 域,mark=0 表示刚刚访问此 结点,mark=1 表示左子树处理结束返回,mark=2 表示右子树处理结束返回.每次根据栈顶元素
数据结构试卷 数据结构试题库集及答案
的mark 域值决定做何种动作.
6.39
typedef struct {
严蔚敏《数据结构习题集》解答
int data;
EBTNode *lchild;
EBTNode *rchild;
EBTNode *parent;
enum {0,1,2} mark;
第 58 页 共 124 页
} EBTNode,EBitree; //有mark 域和双亲指针域的二叉树结点类型 void PostOrder_Nonrecursive(EBitree T)//后序遍历二叉树的非递归算法,不用栈
{
p=T;
while(p)
switch(p->mark)
{
case 0:
p->mark=1;
if(p->lchild) p=p->lchild; //访问左子树
break;
case 1:
p->mark=2;
if(p->rchild) p=p->rchild; //访问右子树
break;
case 2:
visit(p);
p->mark=0; //恢复mark 值
p=p->parent; //返回双亲结点
}
}//PostOrder_Nonrecursive
分析:本题思路与上一题完全相同,只不过结点的mark 值是储存在结点中的,而不是暂存在堆 栈中,所以访问完毕后要将mark 域恢复为0,以备下一次遍历.
6.40
typedef struct {
int data;
PBTNode *lchild;
PBTNode *rchild;
PBTNode *parent;
} PBTNode,PBitree; //有双亲指针域的二叉树结点类型
void Inorder_Nonrecursive(PBitree T)//不设栈非递归遍历有双亲指针的二叉树
{
p=T;
while(p->lchild) p=p->lchild; //向左走到尽头
while(p)
{
visit(p);
数据结构试卷 数据结构试题库集及答案
{
严蔚敏《数据结构习题集》解答
p=p->rchild;
while(p->lchild) p=p->lchild; //后继就是在右子树中向左走到尽头
}
第 59 页 共 124 页
else if(p->parent->lchild==p) p=p->parent; //当自己是双亲的左孩子时后继就是双亲 else
{
p=p->parent;
while(p->parent&&p->parent->rchild==p) p=p->parent;
p=p->parent;
} //当自己是双亲的右孩子时后继就是向上返回直到遇到自己是在其左子树中的祖先 }//while
}//Inorder_Nonrecursive
6.41
int c,k; //这里把k 和计数器c 作为全局变量处理
void Get_PreSeq(Bitree T)//求先序序列为k 的结点的值
{
if(T)
{
c++; //每访问一个子树的根都会使前序序号计数器加1
if(c==k)
{
printf("Value is %d\n",T->data);
exit (1);
}
else
{
Get_PreSeq(T->lchild); //在左子树中查找
Get_PreSeq(T->rchild); //在右子树中查找
}
}//if
}//Get_PreSeq
main()
{
...
scanf("%d",&k);
c=0; //在主函数中调用前,要给计数器赋初值0
Get_PreSeq(T,k);
...
}//main
6.42
int LeafCount_BiTree(Bitree T)//求二叉树中叶子结点的数目
{
if(!T) return 0; //空树没有叶子
数据结构试卷 数据结构试题库集及答案
else if(!T->lchild&&!T->rchild) return 1; //叶子结点
严蔚敏《数据结构习题集》解答
第 60 页 共 124 页
else return Leaf_Count(T->lchild)+Leaf_Count(T->rchild);//左子树的叶子数加上右子树的叶 子数
}//LeafCount_BiTree
6.43
void Bitree_Revolute(Bitree T)//交换所有结点的左右子树
{
T->lchild<->T->rchild; //交换左右子树
if(T->lchild) Bitree_Revolute(T->lchild);
if(T->rchild) Bitree_Revolute(T->rchild); //左右子树再分别交换各自的左右子树
}//Bitree_Revolute
6.44
int Get_Sub_Depth(Bitree T,int x)//求二叉树中以值为x 的结点为根的子树深度
{
if(T->data==x)
{
printf("%d\n",Get_Depth(T)); //找到了值为x 的结点,求其深度
exit 1;
}
else
{
if(T->lchild) Get_Sub_Depth(T->lchild,x);
if(T->rchild) Get_Sub_Depth(T->rchild,x); //在左右子树中继续寻找
}
}//Get_Sub_Depth
int Get_Depth(Bitree T)//求子树深度的递归算法
{
if(!T) return 0;
else
{
m=Get_Depth(T->lchild);
n=Get_Depth(T->rchild);
return (m>n?m:n)+1;
}
}//Get_Depth
6.45
void Del_Sub_x(Bitree T,int x)//删除所有以元素x 为根的子树
{
if(T->data==x) Del_Sub(T); //删除该子树
else
{
if(T->lchild) Del_Sub_x(T->lchild,x);
if(T->rchild) Del_Sub_x(T->rchild,x); //在左右子树中继续查找
}//else
}//Del_Sub_x
数据结构试卷 数据结构试题库集及答案
严蔚敏《数据结构习题集》解答
void Del_Sub(Bitree T)//删除子树T
{
if(T->lchild) Del_Sub(T->lchild);
if(T->rchild) Del_Sub(T->rchild);
free(T);
}//Del_Sub
6.46
void Bitree_Copy_Nonrecursive(Bitree T,Bitree &U)//非递归复制二叉树 {
InitStack(S1);InitStack(S2);
push(S1,T); //根指针进栈
U=(BTNode*)malloc(sizeof(BTNode));
U->data=T->data;
q=U;push(S2,U);
while(!StackEmpty(S))
{
while(Gettop(S1,p)&&p)
{
q->lchild=(BTNode*)malloc(sizeof(BTNode));
q=q->lchild;q->data=p->data;
push(S1,p->lchild);
push(S2,q);
} //向左走到尽头
pop(S1,p);
pop(S2,q);
if(!StackEmpty(S1))
{
pop(S1,p);pop(S2,q);
q->rchild=(BTNode*)malloc(sizeof(BTNode));
q=q->rchild;q->data=p->data;
push(S1,p->rchild); //向右一步
push(S2,q);
}
}//while
}//BiTree_Copy_Nonrecursive
分析:本题的算法系从6.37 改写而来.
6.47
void LayerOrder(Bitree T)//层序遍历二叉树
{
InitQueue(Q); //建立工作队列
EnQueue(Q,T);
while(!QueueEmpty(Q))
{
DeQueue(Q,p);
第 61 页 共 124 页
严蔚敏《数据结构习题集》解答
数据结构试卷 数据结构试题库集及答案
visit(p);
if(p->lchild) EnQueue(Q,p->lchild);
if(p->rchild) EnQueue(Q,p->rchild);
}
}//LayerOrder
6.48
int found=FALSE;
第 62 页 共 124 页
Bitree* Find_Near_Ancient(Bitree T,Bitree p,Bitree q)//求二叉树T 中结点p 和q 的最近共同祖 先
{
Bitree pathp[ 100 ],pathq[ 100 ] //设立两个辅助数组暂存从根到p,q 的路径
Findpath(T,p,pathp,0);
found=FALSE;
Findpath(T,q,pathq,0); //求从根到p,q 的路径放在pathp 和pathq 中
for(i=0;pathp[i]==pathq[i]&&pathp[i];i++); //查找两条路径上最后一个相同结点
return pathp[--i];
}//Find_Near_Ancient
void Findpath(Bitree T,Bitree p,Bitree path[ ],int i)//求从T 到p 路径的递归算法
{
if(T==p)
{
found=TRUE;
return; //找到
}
path[i]=T; //当前结点存入路径
if(T->lchild) Findpath(T->lchild,p,path,i+1); //在左子树中继续寻找
if(T->rchild&&!found) Findpath(T->rchild,p,path,i+1); //在右子树中继续寻找
if(!found) path[i]=NULL; //回溯
}//Findpath
6.49
int IsFull_Bitree(Bitree T)//判断二叉树是否完全二叉树,是则返回1,否则返回0
{
InitQueue(Q);
flag=0;
EnQueue(Q,T); //建立工作队列
while(!QueueEmpty(Q))
{
DeQueue(Q,p);
if(!p) flag=1;
else if(flag) return 0;
else
{
EnQueue(Q,p->lchild);
EnQueue(Q,p->rchild); //不管孩子是否为空,都入队列
严蔚敏《数据结构习题集》解答
数据结构试卷 数据结构试题库集及答案
}
}//while
return 1;
}//IsFull_Bitree
第 63 页 共 124 页
分析:该问题可以通过层序遍历的方法来解决.与6.47 相比,作了一个修改,不管当前结点是否 有左右孩子,都入队列.这样当树为完全二叉树时,遍历时得到是一个连续的不包含空指针的 序列.反之,则序列中会含有空指针.
6.50
Status CreateBitree_Triplet(Bitree &T)//输入三元组建立二叉树
{
if(getchar()!='^') return ERROR;
T=(BTNode*)malloc(sizeof(BTNode));
p=T;p->data=getchar();
getchar(); //滤去多余字符
InitQueue(Q);
EnQueue(Q,T);
while((parent=getchar())!='^'&&(child=getchar())&&(side=getchar()))
{
while(QueueHead(Q)!=parent&&!QueueEmpty(Q)) DeQueue(Q,e);
if(QueueEmpty(Q)) return ERROR; //未按层序输入
p=QueueHead(Q);
q=(BTNode*)malloc(sizeof(BTNode));
if(side=='L') p->lchild=q;
else if(side=='R') p->rchild=q;
else return ERROR; //格式不正确
q->data=child;
EnQueue(Q,q);
}
return OK;
}//CreateBitree_Triplet
6.51
Status Print_Expression(Bitree T)//按标准形式输出以二叉树存储的表达式
{
if(T->data 是字母) printf("%c",T->data);
else if(T->data 是操作符)
{
if(!T->lchild||!T->rchild) return ERROR; //格式错误
if(T->lchild->data 是操作符&&T->lchild->data 优先级低于T->data)
{
printf("(");
if(!Print_Expression(T->lchild)) return ERROR;
printf(")");
} //注意在什么情况下要加括号
else if(!Print_Expression(T->lchild)) return ERROR;
严蔚敏《数据结构习题集》解答
数据结构试卷 数据结构试题库集及答案
if(T->rchild->data 是操作符&&T->rchild->data 优先级低于T->data)
{
printf("(");
if(!Print_Expression(T->rchild)) return ERROR;
printf(")");
}
else if(!Print_Expression(T->rchild)) return ERROR;
}
else return ERROR; //非法字符
return OK;
}//Print_Expression
6.52
typedef struct{
BTNode node;
int layer;
} BTNRecord; //包含结点所在层次的记录类型
int FanMao(Bitree T)//求一棵二叉树的"繁茂度"
{
int countd; //count 数组存放每一层的结点数
InitQueue(Q); //Q 的元素为BTNRecord 类型
EnQueue(Q,{T,0});
while(!QueueEmpty(Q))
{
DeQueue(Q,r);
count[r.layer]++;
if(r.node->lchild) EnQueue(Q,{r.node->lchild,r.layer+1});
if(r.node->rchild) EnQueue(Q,{r.node->rchild,r.layer+1});
} //利用层序遍历来统计各层的结点数
h=r.layer; //最后一个队列元素所在层就是树的高度
for(maxn=count[0],i=1;count[i];i++)
if(count[i]>maxn) maxn=count[i]; //求层最大结点数
return h*maxn;
}//FanMao
第 64 页 共 124 页
分析:如果不允许使用辅助数组,就必须在遍历的同时求出层最大结点数,形式上会复杂一些, 你能写出来吗?
6.53
int maxh;
Status Printpath_MaxdepthS1(Bitree T)//求深度等于树高度减一的最靠左的结点
{
Bitree pathd;
maxh=Get_Depth(T); //Get_Depth 函数见6.44
if(maxh<2) return ERROR; //无符合条件结点
Find_h(T,1);
return OK;
严蔚敏《数据结构习题集》解答
}//Printpath_MaxdepthS1
数据结构试卷 数据结构试题库集及答案
void Find_h(Bitree T,int h)//寻找深度为maxh-1 的结点
{
path[h]=T;
if(h==maxh-1)
{
for(i=1;path[i];i++) printf("%c",path[i]->data);
exit; //打印输出路径
}
else
{
if(T->lchild) Find_h(T->lchild,h+1);
if(T->rchild) Find_h(T->rchild,h+1);
}
path[h]=NULL; //回溯
}//Find_h
6.54
第 65 页 共 124 页
Status CreateBitree_SqList(Bitree &T,SqList sa)//根据顺序存储结构建立二叉链表 {
Bitree ptr[sa.last+1]; //该数组储存与sa 中各结点对应的树指针
if(!sa.last)
{
T=NULL; //空树
return;
}
ptr[1]=(BTNode*)malloc(sizeof(BTNode));
ptr[1]->data=sa.elem[1]; //建立树根
T=ptr[1];
for(i=2;i<=sa.last;i++)
{
if(!sa.elem[i]) return ERROR; //顺序错误
ptr[i]=(BTNode*)malloc(sizeof(BTNode));
ptr[i]->data=sa.elem[i];
j=i/2; //找到结点i 的双亲j
if(i-j*2) ptr[j]->rchild=ptr[i]; //i 是j 的右孩子
else ptr[j]->lchild=ptr[i]; //i 是j 的左孩子
}
return OK;
}//CreateBitree_SqList
6.55
int DescNum(Bitree T)//求树结点T 的子孙总数填入DescNum 域中,并返回该数 {
if(!T) return -1;
else d=(DescNum(T->lchild)+DescNum(T->rchild)+2); //计算公式
严蔚敏《数据结构习题集》解答
T->DescNum=d;
return d;
数据结构试卷 数据结构试题库集及答案
}//DescNum
第 66 页 共 124 页
分析:该算法时间复杂度为 O(n),n 为树结点总数.注意:为了能用一个统一的公式计算子孙数 目,所以当T 为空指针时,要返回-1 而不是0.
6.56
BTNode *PreOrder_Next(BTNode *p)//在先序后继线索二叉树中查找结点p 的先序后继,并返 回指针
{
if(p->lchild) return p->lchild;
else return p->rchild;
}//PreOrder_Next
分析:总觉得不会这么简单.是不是哪儿理解错了?
6.57
Bitree PostOrder_Next(Bitree p)//在后序后继线索二叉树中查找结点p 的后序后继,并返回指 针
{
if(p->rtag) return p->rchild; //p 有后继线索
else if(!p->parent) return NULL; //p 是根结点
else if(p==p->parent->rchild) return p->parent; //p 是右孩子
else if(p==p->parent->lchild&&p->parent->rtag)
return p->parent; //p 是左孩子且双亲没有右孩子
else //p 是左孩子且双亲有右孩子
{
q=p->parent->rchild;
while(q->lchild||!q->rtag)
{
if(q->lchild) q=q->lchild;
else q=q->rchild;
} //从p 的双亲的右孩子向下走到底
return q;
}//else
}//PostOrder_Next
6.58
Status Insert_BiThrTree(BiThrTree &T,BiThrTree &p,BiThrTree &x)//在中序线索二叉树T 的结 点p 下插入子树x
{
if(p->ltag) //x 作为p 的左子树
{
s=p->lchild; //s 为p 的前驱
p->ltag=Link;
p->lchild=x;
q=x;
while(q->lchild&&!q->ltag) q=q->lchild;
严蔚敏《数据结构习题集》解答
q->lchild=s; //找到子树中的最左结点,并修改其前驱指向s
x->rtag=Thread;
x->rchild=p; //x 的后继指向p
数据结构试卷 数据结构试题库集及答案
}
else if(p->rtag) //x 作为p 的右子树
{
s=p->rchild; //s 为p 的后继
p->rtag=Link;
p->rchild=x;
q=x;
while(q->lchild&&!q->ltag) q=q->lchild;
q->lchild=p; //找到子树中的最左结点,并修改其前驱指向p
x->rtag=Thread;
x->rchild=s; //x 的后继指向p 的后继
}
else//x 作为p 的左子树,p 的左子树作为x 的右子树
{
s=p->lchild;t=s;
while(t->lchild&&!t->ltag) t=t->lchild;
u=t->lchild; //找到p 的左子树的最左节点t 和前驱u
p->lchild=x;
x->rtag=Link;
x->rchild=s; //x 作为p 的左子树,p 的左子树s 作为x 的右子树 t->lchild=x;
q=x;
while(q->lchild&&!q->ltag) q=q->lchild;
q->lchild=u; //找到子树中的最左结点,并修改其前驱指向u
}
return OK;
}//Insert_BiThrTree
6.59
void Print_CSTree(CSTree T)//输出孩子兄弟链表表示的树T 的各边 {
for(child=T->firstchild;child;child=child->nextsib)
{
printf("(%c,%c),",T->data,child->data);
Print_CSTree(child);
}
}//Print_CSTree
6.60
int LeafCount_CSTree(CSTree T)//求孩子兄弟链表表示的树T 的叶子数目 {
if(!T->firstchild) return 1; //叶子结点
else
第 67 页 共 124 页
严蔚敏《数据结构习题集》解答
{
count=0;
for(child=T->firstchild;child;child=child->nextsib)
count+=LeafCount_CSTree(child);
数据结构试卷 数据结构试题库集及答案
return count; //各子树的叶子数之和
}
}//LeafCount_CSTree
6.61
int GetDegree_CSTree(CSTree T)//求孩子兄弟链表表示的树T 的度 {
if(!T->firstchild) return 0; //空树
else
{
degree=0;
for(p=T->firstchild;p;p=p->nextsib) degree++;//本结点的度 for(p=T->firstchild;p;p=p->nextsib)
{
d=GetDegree_CSTree(p);
if(d>degree) degree=d; //孩子结点的度的最大值
}
return degree;
}//else
}//GetDegree_CSTree
6.62
int GetDepth_CSTree(CSTree T)//求孩子兄弟链表表示的树T 的深度 {
if(!T) return 0; //空树
else
{
for(maxd=0,p=T->firstchild;p;p=p->nextsib)
if((d=GetDepth_CSTree(p))>maxd) maxd=d; //子树的最大深度 return maxd+1;
}
}//GetDepth_CSTree
6.63
int GetDepth_CTree(CTree A)//求孩子链表表示的树A 的深度 {
return SubDepth(A.r);
}//GetDepth_CTree
int SubDepth(int T)//求子树T 的深度
{
if(!A.nodes[T].firstchild) return 1;
for(sd=1,p=A.nodes[T].firstchild;p;p=p->next)
if((d=SubDepth(p->child))>sd) sd=d;
第 68 页 共 124 页
严蔚敏《数据结构习题集》解答
return sd+1;
}//SubDepth
6.64
int GetDepth_PTree(PTree T)//求双亲表表示的树T 的深度
{
数据结构试卷 数据结构试题库集及答案
maxdep=0;
for(i=0;i<T.n;i++)
{
dep=0;
for(j=i;j>=0;j=T.nodes[j].parent) dep++; //求每一个结点的深度
if(dep>maxdep) maxdep=dep;
}
return maxdep;
}//GetDepth_PTree
6.65
char Pred,Ind; //假设前序序列和中序序列已经分别储存在数组Pre 和In 中
第 69 页 共 124 页
Bitree Build_Sub(int Pre_Start,int Pre_End,int In_Start,int In_End)//由子树的前序和中序序列建 立其二叉链表
{
sroot=(BTNode*)malloc(sizeof(BTNode)); //建根
sroot->data=Pre[Pre_Start];
for(i=In_Start;In[i]!=sroot->data;i++); //在中序序列中查找子树根
leftlen=i-In_Start;
rightlen=In_End-i; //计算左右子树的大小
if(leftlen)
{
lroot=Build_Sub(Pre_Start+1,Pre_Start+leftlen,In_Start,In_Start+leftlen-1);
sroot->lchild=lroot;
} //建左子树,注意参数表的计算
if(rightlen)
{
rroot=Build_Sub(Pre_End-rightlen+1,Pre_End,In_End-rightlen+1,In_End);
sroot->rchild=rroot;
} //建右子树,注意参数表的计算
return sroot; //返回子树根
}//Build_Sub
main()
{
...
Build_Sub(1,n,1,n); //初始调用参数,n 为树结点总数
...
}
分析:本算法利用了这样一个性质,即一棵子树在前序和中序序列中所占的位置总是连续的.
因此,就可以用起始下标和终止下标来确定一棵子树.Pre_Start,Pre_End,In_Start
严蔚敏《数据结构习题集》解答
第 70 页 共 124 页
和In_End 分
别指示子树在前序子序列里的起始下标,终止下标,和在中序子序列里的起始和终止下标.
6.66
typedef struct{
CSNode *ptr;
CSNode *lastchild;
数据结构试卷 数据结构试题库集及答案
Status Build_CSTree_PTree(PTree T)//由树T 的双亲表构造其孩子兄弟链表 {
NodeMsg Tree[MAXSIZE];
for(i=0;i<T.n;i++)
{
Tree[i].ptr=(CSNode*)malloc(sizeof(CSNode));
Tree[i].ptr->data=T.node[i].data; //建结点
if(T.nodes[i].parent>=0) //不是树根
{
j=T.nodes[i].parent; //本算法要求双亲表必须是按层序存储
if(!(Tree[j].lastchild)) //双亲当前还没有孩子
Tree[j].ptr->firstchild=Tree[i].ptr; //成为双亲的第一个孩子
else //双亲已经有了孩子
Tree[j].lastchild->nextsib=Tree[i].ptr; //成为双亲最后一个孩子的下一个兄弟 Tree[j].lastchild=Tree[i].ptr; //成为双亲的最后一个孩子
}//if
}//for
}//Build_CSTree_PTree
6.67
typedef struct{
char data;
CSNode *ptr;
CSNode *lastchild;
} NodeInfo; //结点数据,结点指针和最后一个孩子的指针
Status CreateCSTree_Duplet(CSTree &T)//输入二元组建立树的孩子兄弟链表 {
NodeInfo Treed;
n=1;k=0;
if(getchar()!='^') return ERROR; //未按格式输入
if((c=getchar())=='^') T=NULL; //空树
Tree[0].ptr=(CSNode*)malloc(sizeof(CSNode));
Tree[0].data=c;
Tree[0].ptr->data=c;
while((p=getchar())!='^'&&(c=getchar())!='^')
{
Tree[n].ptr=(CSNode*)malloc(sizeof(CSNode));
Tree[n].data=c;
Tree[n].ptr->data=c;
严蔚敏《数据结构习题集》解答
for(k=0;Tree[k].data!=p;k++); //查找当前边的双亲结点
if(Tree[k].data!=p) return ERROR; //未找到:未按层序输入
r=Tree[k].ptr;
if(!r->firstchild)
r->firstchild=Tree[n].ptr;
else Tree[k].lastchild->nextsib=Tree[n].ptr;
Tree[k].lastchild=Tree[n].ptr; //这一段含义同上一题
数据结构试卷 数据结构试题库集及答案
}//while
return OK;
}//CreateCSTree_Duplet
6.68
第 71 页 共 124 页
Status CreateCSTree_Degree(char node[ ],int degree[ ])//由结点的层序序列和各结点的度构造 树的孩子兄弟链表
{
CSNode * ptr[MAXSIZE]; //树结点指针的辅助存储
ptr[0]=(CSNode*)malloc(sizeof(CSNode));
i=0;k=1; //i 为当前结点序号,k 为当前孩子的序号
while(node[i])
{
ptr[i]->data=node[i];
d=degree[i];
if(d)
{
ptr[k]=(CSNode*)malloc(sizeof(CSNode)); //k 为当前孩子的序号
ptr[i]->firstchild=ptr[k]; //建立i 与第一个孩子k 之间的联系
for(j=2;j<=d;j++)
{
ptr[k]=(CSNode*)malloc(sizeof(CSNode));
ptr[k-1]->nextsib=ptr[k]; //当结点的度大于1 时,为其孩子建立兄弟链表
k++;
}//for
ptr[k-1]->nextsib=NULL;
}//if
i++;
}//while
}//CreateCSTree_Degree
6.69
void Print_BiTree(BiTree T,int i)//按树状打印输出二叉树的元素,i 表示结点所在层次,初次调 用时i=0
{
if(T->rchild) Print_BiTree(T->rchild,i+1);
for(j=1;j<=i;j++) printf(" "); //打印i 个空格以表示出层次
printf("%c\n",T->data); //打印T 元素,换行
严蔚敏《数据结构习题集》解答
if(T->lchild) Print_BiTree(T->rchild,i+1);
}//Print_BiTree
第 72 页 共 124 页
分析:该递归算法实际上是带层次信息的中序遍历,只不过按照题目要求,顺序为先右后左.
6.70
Status CreateBiTree_GList(BiTree &T)//由广义表形式的输入建立二叉链表
{
c=getchar();
数据结构试卷 数据结构试题库集及答案
if(c=='#') T=NULL; //空子树
else
{
T=(CSNode*)malloc(sizeof(CSNode));
T->data=c;
if(getchar()!='(') return ERROR;
if(!CreateBiTree_GList(pl)) return ERROR;
T->lchild=pl;
if(getchar()!=',') return ERROR;
if(!CreateBiTree_GList(pr)) return ERROR;
T->rchild=pr;
if(getchar()!=')') return ERROR; //这些语句是为了保证输入符合A(B,C)的格式
}
return OK;
}//CreateBiTree_GList
6.71
void Print_CSTree(CSTree T,int i)//按凹入表形式打印输出树的元素,i 表示结点所在层次,初次 调用时i=0
{
for(j=1;j<=i;j++) printf(" "); //留出i 个空格以表现出层次
printf("%c\n",T->data); //打印元素,换行
for(p=T->firstchild;p;p=p->nextsib)
Print_CSTree(p,i+1); //打印子树
}//Print_CSTree
6.72
void Print_CTree(int e,int i)//按凹入表形式打印输出树的元素,i 表示结点所在层次
{
for(j=1;j<=i;j++) printf(" "); //留出i 个空格以表现出层次
printf("%c\n",T.nodes[e].data); //打印元素,换行
for(p=T.nodes[e].firstchild;p;p=p->next)
Print_CSTree(p->child,i+1); //打印子树
}//Print_CSTree
main()
{
...
Print_CTree(T.r,0); //初次调用时i=0
...
严蔚敏《数据结构习题集》解答
}//main
6.73
char c; //全局变量,指示当前字符
第 73 页 共 124 页
Status CreateCSTree_GList(CSTree &T)//由广义表形式的输入建立孩子兄弟链表
{
c=getchar();
T=(CSNode*)malloc(sizeof(CSNode));
T->data=c;
数据结构试卷 数据结构试题库集及答案
{
if(!CreateCSTree_GList(fc)) return ERROR; //建第一个孩子
T->firstchild=fc;
for(p=fc;c==',';p->nextsib=nc,p=nc) //建兄弟链
if(!CreateCSTree_GList(nc)) return ERROR;
p->nextsib=NULL;
if((c=getchar())!=')') return ERROR; //括号不配对
}
else T->firtchild=NULL; //叶子结点
return OK;
}//CreateBiTree_GList
分析:书后给出了两个间接递归的算法,事实上合成一个算法在形式上可能更好一些.本算法 另一个改进之处在于加入了广义表格式是否合法的判断.
6.74
void PrintGlist_CSTree(CSTree T)//按广义表形式输出孩子兄弟链表表示的树
{
printf("%c",T->data);
if(T->firstchild) //非叶结点
{
printf("(");
for(p=T->firstchild;p;p=p->nextsib)
{
PrintGlist_CSTree(p);
if(p->nextsib) printf(","); //最后一个孩子后面不需要加逗号
}
printf(")");
}//if
}//PrintGlist_CSTree
6.75
char c;
int pos=0; //pos 是全局变量,指示已经分配到了哪个结点
Status CreateCTree_GList(CTree &T,int &i)//由广义表形式的输入建立孩子链表
{
c=getchar();
T.nodes[pos].data=c;
严蔚敏《数据结构习题集》解答
i=pos++; //i 是局部变量,指示当前正在处理的子树根
if((c=getchar())=='(') //非叶结点
{
CreateCTree_GList();
p=(CTBox*)malloc(sizeof(CTBox));
T.nodes[i].firstchild=p;
p->child=pos; //建立孩子链的头
for(;c==',';p=p->next) //建立孩子链
{
CreateCTree_GList(T,j); //用j 返回分配得到的子树根位置
数据结构试卷 数据结构试题库集及答案
p->next=(CTBox*)malloc(sizeof(CTBox));
}
p->next=NULL;
if((c=getchar())!=')') return ERROR; //括号不配对
}//if
else T.nodes[i].firtchild=NULL; //叶子结点
return OK;
}//CreateBiTree_GList
第 74 页 共 124 页
分析:该算法中,pos 变量起着"分配"结点在表中的位置的作用,是按先序序列从上向下分配,因 此树根T.r 一定等于0,而最终的pos 值就是结点数T.n.
6.76
void PrintGList_CTree(CTree T,int i)//按广义表形式输出孩子链表表示的树
{
printf("%c",T.nodes[i].data);
if(T.nodes[i].firstchild) //非叶结点
{
printf("(");
for(p=T->firstchild;p;p=p->nextsib)
{
PrintGlist_CSTree(T,p->child);
if(p->nextsib) printf(","); //最后一个孩子后面不需要加逗号
}
printf(")");
}//if
}//PrintGlist_CTree
严蔚敏《数据结构习题集》解答
第七章 图
7.14
第 75 页 共 124 页
Status Build_AdjList(ALGraph &G)//输入有向图的顶点数,边数,顶点信息和边的信息建立邻 接表
{
InitALGraph(G);
scanf("%d",&v);
if(v<0) return ERROR; //顶点数不能为负
G.vexnum=v;
scanf("%d",&a);
if(a<0) return ERROR; //边数不能为负
G.arcnum=a;
for(m=0;m<v;m++)
G.vertices[m].data=getchar(); //输入各顶点的符号
for(m=1;m<=a;m++)
数据结构试卷 数据结构试题库集及答案
t=getchar();h=getchar(); //t 为弧尾,h 为弧头
if((i=LocateVex(G,t))<0) return ERROR;
if((j=LocateVex(G,h))<0) return ERROR; //顶点未找到
p=(ArcNode*)malloc(sizeof(ArcNode));
if(!G.vertices.[i].firstarc) G.vertices[i].firstarc=p;
else
{
for(q=G.vertices[i].firstarc;q->nextarc;q=q->nextarc);
q->nextarc=p;
}
p->adjvex=j;p->nextarc=NULL;
}//while
return OK;
}//Build_AdjList
7.15
//本题中的图G 均为有向无权图,其余情况容易由此写出
Status Insert_Vex(MGraph &G, char v)//在邻接矩阵表示的图G 上插入顶点v {
if(G.vexnum+1)>MAX_VERTEX_NUM return INFEASIBLE;
G.vexs[++G.vexnum]=v;
return OK;
}//Insert_Vex
Status Insert_Arc(MGraph &G,char v,char w)//在邻接矩阵表示的图G 上插入边(v,w) {
if((i=LocateVex(G,v))<0) return ERROR;
if((j=LocateVex(G,w))<0) return ERROR;
严蔚敏《数据结构习题集》解答
if(i==j) return ERROR;
if(!G.arcs[i][j].adj)
{
G.arcs[i][j].adj=1;
G.arcnum++;
}
return OK;
}//Insert_Arc
第 76 页 共 124 页
Status Delete_Vex(MGraph &G,char v)//在邻接矩阵表示的图G 上删除顶点v {
n=G.vexnum;
if((m=LocateVex(G,v))<0) return ERROR;
G.vexs[m]<->G.vexs[n]; //将待删除顶点交换到最后一个顶点
for(i=0;i<n;i++)
{
G.arcs[i][m]=G.arcs[i][n];
G.arcs[m][i]=G.arcs[n][i]; //将边的关系随之交换
}
数据结构试卷 数据结构试题库集及答案
G.vexnum--;
return OK;
}//Delete_Vex
分析:如果不把待删除顶点交换到最后一个顶点的话,算法将会比较复杂,而伴随着大量元素 的移动,时间复杂度也会大大增加.
Status Delete_Arc(MGraph &G,char v,char w)//在邻接矩阵表示的图G 上删除边(v,w) {
if((i=LocateVex(G,v))<0) return ERROR;
if((j=LocateVex(G,w))<0) return ERROR;
if(G.arcs[i][j].adj)
{
G.arcs[i][j].adj=0;
G.arcnum--;
}
return OK;
}//Delete_Arc
7.16
//为节省篇幅,本题只给出Insert_Arc 算法.其余算法请自行写出.
Status Insert_Arc(ALGraph &G,char v,char w)//在邻接表表示的图G 上插入边(v,w) {
if((i=LocateVex(G,v))<0) return ERROR;
if((j=LocateVex(G,w))<0) return ERROR;
p=(ArcNode*)malloc(sizeof(ArcNode));
p->adjvex=j;p->nextarc=NULL;
if(!G.vertices[i].firstarc) G.vertices[i].firstarc=p;
严蔚敏《数据结构习题集》解答
else
{
for(q=G.vertices[i].firstarc;q->q->nextarc;q=q->nextarc)
if(q->adjvex==j) return ERROR; //边已经存在
q->nextarc=p;
}
G.arcnum++;
return OK;
}//Insert_Arc
7.17
第 77 页 共 124 页
//为节省篇幅,本题只给出较为复杂的Delete_Vex 算法.其余算法请自行写出.
Status Delete_Vex(OLGraph &G,char v)//在十字链表表示的图G 上删除顶点v
{
if((m=LocateVex(G,v))<0) return ERROR;
n=G.vexnum;
for(i=0;i<n;i++) //删除所有以v 为头的边
{
if(G.xlist[i].firstin->tailvex==m) //如果待删除的边是头链上的第一个结点
{
数据结构试卷 数据结构试题库集及答案
G.xlist[i].firstin=q->hlink;
free(q);G.arcnum--;
}
else //否则
{
for(p=G.xlist[i].firstin;p&&p->hlink->tailvex!=m;p=p->hlink);
if(p)
{
q=p->hlink;
p->hlink=q->hlink;
free(q);G.arcnum--;
}
}//else
}//for
for(i=0;i<n;i++) //删除所有以v 为尾的边
{
if(G.xlist[i].firstout->headvex==m) //如果待删除的边是尾链上的第一个结点 {
q=G.xlist[i].firstout;
G.xlist[i].firstout=q->tlink;
free(q);G.arcnum--;
}
else //否则
{
严蔚敏《数据结构习题集》解答
for(p=G.xlist[i].firstout;p&&p->tlink->headvex!=m;p=p->tlink);
if(p)
{
q=p->tlink;
p->tlink=q->tlink;
free(q);G.arcnum--;
}
}//else
}//for
for(i=m;i<n;i++) //顺次用结点m 之后的顶点取代前一个顶点
{
G.xlist[i]=G.xlist[i+1]; //修改表头向量
for(p=G.xlist[i].firstin;p;p=p->hlink)
p->headvex--;
for(p=G.xlist[i].firstout;p;p=p->tlink)
p->tailvex--; //修改各链中的顶点序号
}
G.vexnum--;
return OK;
}//Delete_Vex
7.18
数据结构试卷 数据结构试题库集及答案
第 78 页 共 124 页
Status Delete_Arc(AMLGraph &G,char v,char w)////在邻接多重表表示的图G 上删除边(v,w) {
if((i=LocateVex(G,v))<0) return ERROR;
if((j=LocateVex(G,w))<0) return ERROR;
if(G.adjmulist[i].firstedge->jvex==j)
G.adjmulist[i].firstedge=G.adjmulist[i].firstedge->ilink;
else
{
for(p=G.adjmulist[i].firstedge;p&&p->ilink->jvex!=j;p=p->ilink);
if (!p) return ERROR; //未找到
p->ilink=p->ilink->ilink;
} //在i 链表中删除该边
if(G.adjmulist[j].firstedge->ivex==i)
G.adjmulist[j].firstedge=G.adjmulist[j].firstedge->jlink;
else
{
for(p=G.adjmulist[j].firstedge;p&&p->jlink->ivex!=i;p=p->jlink);
if (!p) return ERROR; //未找到
q=p->jlink;
p->jlink=q->jlink;
free(q);
} //在i 链表中删除该边
严蔚敏《数据结构习题集》解答
G.arcnum--;
return OK;
}//Delete_Arc
7.19
第 79 页 共 124 页
Status Build_AdjMulist(AMLGraph &G)//输入有向图的顶点数,边数,顶点信息和边的信息建 立邻接多重表
{
InitAMLGraph(G);
scanf("%d",&v);
if(v<0) return ERROR; //顶点数不能为负
G.vexnum=v;
scanf(%d",&a);
if(a<0) return ERROR; //边数不能为负
G.arcnum=a;
for(m=0;m<v;m++)
G.adjmulist[m].data=getchar(); //输入各顶点的符号
for(m=1;m<=a;m++)
{
t=getchar();h=getchar(); //t 为弧尾,h 为弧头
if((i=LocateVex(G,t))<0) return ERROR;
if((j=LocateVex(G,h))<0) return ERROR; //顶点未找到
数据结构试卷 数据结构试题库集及答案
p->ivex=i;p->jvex=j;
p->ilink=NULL;p->jlink=NULL; //边结点赋初值
if(!G.adjmulist[i].firstedge) G.adjmulist[i].firstedge=p;
else
{
q=G.adjmulist[i].firstedge;
while(q)
{
r=q;
if(q->ivex==i) q=q->ilink;
else q=q->jlink;
}
if(r->ivex==i) r->ilink=p;//注意i 值既可能出现在边结点的ivex 域中,
else r->jlink=p; //又可能出现在边结点的jvex 域中
}//else //插入i 链表尾部
if(!G.adjmulist[j].firstedge) G.adjmulist[j].firstedge=p;
else
{
q=G.adjmulist[i].firstedge;
while(q)
{
r=q;
严蔚敏《数据结构习题集》解答
if(q->jvex==j) q=q->jlink;
else q=q->ilnk;
}
if(r->jvex==j) r->jlink=p;
else r->ilink=p;
}//else //插入j 链表尾部
}//for
return OK;
}//Build_AdjList
7.20
第 80 页 共 124 页
int Pass_MGraph(MGraph G)//判断一个邻接矩阵存储的有向图是不是可传递的,是则返回否则返回0
{
for(x=0;x<G.vexnum;x++)
for(y=0;y<G.vexnum;y++)
if(G.arcs[x][y])
{
for(z=0;z<G.vexnum;z++)
if(z!=x&&G.arcs[y][z]&&!G.arcs[x][z]) return 0;//图不可传递的条件 }//if
return 1;
}//Pass_MGraph 1,
数据结构试卷 数据结构试题库集及答案
7.21
int Pass_ALGraph(ALGraph G)//判断一个邻接表存储的有向图是不是可传递的,是则返回 1, 否则返回0
{
for(x=0;x<G.vexnum;x++)
for(p=G.vertices[x].firstarc;p;p=p->nextarc)
{
y=p->adjvex;
for(q=G.vertices[y].firstarc;q;q=q->nextarc)
{
z=q->adjvex;
if(z!=x&&!is_adj(G,x,z)) return 0;
}//for
}//for
}//Pass_ALGraph
int is_adj(ALGraph G,int m,int n)//判断有向图G 中是否存在边(m,n),是则返回1,否则返回0 {
for(p=G.vertices[m].firstarc;p;p=p->nextarc)
if(p->adjvex==n) return 1;
return 0;
}//is_adj
严蔚敏《数据结构习题集》解答
7.22
int visited[MAXSIZE]; //指示顶点是否在当前路径上
第 81 页 共 124 页
int exist_path_DFS(ALGraph G,int i,int j)//深度优先判断有向图G 中顶点i 到顶点j 是否有路 径,是则返回1,否则返回0
{
if(i==j) return 1; //i 就是j
else
{
visited[i]=1;
for(p=G.vertices[i].firstarc;p;p=p->nextarc)
{
k=p->adjvex;
if(!visited[k]&&exist_path(k,j)) return 1;//i 下游的顶点到j 有路径
}//for
}//else
}//exist_path_DFS
7.23
int exist_path_BFS(ALGraph G,int i,int j)//广度优先判断有向图G 中顶点i 到顶点j 是否有路径, 是则返回1,否则返回0
{
int visited[MAXSIZE];
InitQueue(Q);
EnQueue(Q,i);
数据结构试卷 数据结构试题库集及答案
{
DeQueue(Q,u);
visited[u]=1;
for(p=G.vertices[i].firstarc;p;p=p->nextarc)
{
k=p->adjvex;
if(k==j) return 1;
if(!visited[k]) EnQueue(Q,k);
}//for
}//while
return 0;
}//exist_path_BFS
7.24
void STraverse_Nonrecursive(Graph G)//非递归遍历强连通图G {
int visited[MAXSIZE];
InitStack(S);
Push(S,GetVex(S,1)); //将第一个顶点入栈
visit(1);
visited =1;
严蔚敏《数据结构习题集》解答
while(!StackEmpty(S))
{
while(Gettop(S,i)&&i)
{
j=FirstAdjVex(G,i);
if(j&&!visited[j])
{
visit(j);
visited[j]=1;
Push(S,j); //向左走到尽头
}
}//while
if(!StackEmpty(S))
{
Pop(S,j);
Gettop(S,i);
k=NextAdjVex(G,i,j); //向右走一步
if(k&&!visited[k])
{
visit(k);
visited[k]=1;
Push(S,k);
}
}//if
}//while
数据结构试卷 数据结构试题库集及答案
第 82 页 共 124 页
分析:本算法的基本思想与二叉树的先序遍历非递归算法相同,请参考
所以从第一个结点出发一定能够访问到所有结点.
7.25
见书后解答.
7.26
Status TopoNo(ALGraph G)//按照题目要求顺序重排有向图中的顶点
{
int new[MAXSIZE],indegree[MAXSIZE]; //储存结点的新序号
n=G.vexnum;
FindInDegree(G,indegree);
InitStack(S);
for(i=1;i<G.vexnum;i++)
if(!indegree[i]) Push(S,i); //零入度结点入栈
count=0;
while(!StackEmpty(S))
{
Pop(S,i);
new[i]=n--; //记录结点的拓扑逆序序号
严蔚敏《数据结构习题集》解答
6.37.由于是强连通图, count++;
for(p=G.vertices[i].firstarc;p;p=p->nextarc)
{
k=p->adjvex;
if(!(--indegree[k])) Push(S,k);
}//for
}//while
if(count<G.vexnum) return ERROR; //图中存在环
for(i=1;i<=n;i++) printf("Old No:%d New No:%d\n",i,new[i])
return OK;
}//TopoNo
分析:只要按拓扑逆序对顶点编号,就可以使邻接矩阵成为下三角矩阵.
7.27
int visited[MAXSIZE];
第 83 页 共 124 页
int exist_path_len(ALGraph G,int i,int j,int k)//判断邻接表方式存储的有向图G 的顶点i 到j 是 否存在长度为k 的简单路径
{
if(i==j&&k==0) return 1; //找到了一条路径,且长度符合要求
else if(k>0)
{
visited[i]=1;
for(p=G.vertices[i].firstarc;p;p=p->nextarc)
{
l=p->adjvex;
if(!visited[l])
数据结构试卷 数据结构试题库集及答案
}//for
visited[i]=0; //本题允许曾经被访问过的结点出现在另一条路径中
}//else
return 0; //没找到
}//exist_path_len
7.28
int path[MAXSIZE],visited[MAXSIZE]; //暂存遍历过程中的路径
int Find_All_Path(ALGraph G,int u,int v,int k)//求有向图G 中顶点u 到v 之间的所有简单路径,k 表示当前路径长度
{
path[k]=u; //加入当前路径中
visited[u]=1;
if(u==v) //找到了一条简单路径
{
printf("Found one path!\n");
for(i=0;path[i];i++) printf("%d",path[i]); //打印输出
}
else
严蔚敏《数据结构习题集》解答
for(p=G.vertices[u].firstarc;p;p=p->nextarc)
{
l=p->adjvex;
if(!visited[l]) Find_All_Path(G,l,v,k+1); //继续寻找
}
visited[u]=0;
path[k]=0; //回溯
}//Find_All_Path
main()
{
...
Find_All_Path(G,u,v,0); //在主函数中初次调用,k 值应为0
...
}//main
7.29
第 84 页 共 124 页
int GetPathNum_Len(ALGraph G,int i,int j,int len)//求邻接表方式存储的有向图G 的顶点i 到j 之间长度为len 的简单路径条数
{
if(i==j&&len==0) return 1; //找到了一条路径,且长度符合要求
else if(len>0)
{
sum=0; //sum 表示通过本结点的路径数
visited[i]=1;
for(p=G.vertices[i].firstarc;p;p=p->nextarc)
{
l=p->adjvex;
数据结构试卷 数据结构试题库集及答案
sum+=GetPathNum_Len(G,l,j,len-1)//剩余路径长度减一
}//for
visited[i]=0; //本题允许曾经被访问过的结点出现在另一条路径中
}//else
return sum;
}//GetPathNum_Len
7.30
int visited[MAXSIZE];
int path[MAXSIZE]; //暂存当前路径
int cycles[MAXSIZE][MAXSIZE]; //储存发现的回路所包含的结点
int thiscycle[MAXSIZE]; //储存当前发现的一个回路
int cycount=0; //已发现的回路个数
void GetAllCycle(ALGraph G)//求有向图中所有的简单回路
{
for(v=0;v<G.vexnum;v++) visited[v]=0;
for(v=0;v<G.vexnum;v++)
if(!visited[v]) DFS(G,v,0); //深度优先遍历
严蔚敏《数据结构习题集》解答
}//DFSTraverse
void DFS(ALGraph G,int v,int k)//k 表示当前结点在路径上的序号
{
visited[v]=1;
path[k]=v; //记录当前路径
for(p=G.vertices[v].firstarc;p;p=p->nextarc)
{
w=p->adjvex;
if(!visited[w]) DFS(G,w,k+1);
else //发现了一条回路
{
for(i=0;path[i]!=w;i++); //找到回路的起点
for(j=0;path[i+j];i++) thiscycle[j]=path[i+j];//把回路复制下来
第 85 页 共 124 页
if(!exist_cycle()) cycles[cycount++]=thiscycle;//如果该回路尚未被记录过,就添加到记录中 for(i=0;i<G.vexnum;i++) thiscycle[i]=0; //清空目前回路数组
}//else
}//for
path[k]=0;
visited[k]=0; //注意只有当前路径上的结点visited 为真.因此一旦遍历中发现当前结点visited 为真,即表示发现了一条回路
}//DFS
int exist_cycle()//判断thiscycle 数组中记录的回路在cycles 的记录中是否已经存在
{
int temp[MAXSIZE];
for(i=0;i<cycount;i++) //判断已有的回路与thiscycle 是否相同
{ //也就是,所有结点和它们的顺序都相同
j=0;c=thiscycle�; //例如,142857 和857142 是相同的回路
数据结构试卷 数据结构试题库集及答案
第一个结点的元素
if(cycles[i][k]) //有与之相同的一个元素
{
for(m=0;cycles[i][k+m];m++)
temp[m]=cycles[i][k+m];
for(n=0;n<k;n++,m++)
temp[m]=cycles[i][n]; //调整cycles 中的当前记录的循环相位并放入temp 数组中 if(!StrCompare(temp,thiscycle)) //与thiscycle 比较
return 1; //完全相等
for(m=0;m<G.vexnum;m++) temp[m]=0; //清空这个数组
}
}//for
return 0; //所有现存回路都不与thiscycle 完全相等
}//exist_cycle
分析:这个算法的思想是,在遍历中暂存当前路径,当遇到一个结点已经在路径之中时就表明
存在一条回路;扫描路径向量path 可以获得这条回路上的所有结点.把结点序列(例如,142857) 严蔚敏《数据结构习题集》解答
第 86 页 共 124 页
存入 thiscycle 中;由于这种算法中,一条回路会被发现好几次,所以必须先判断该回路是否已 经在cycles 中被记录过,如果没有才能存入cycles 的一个行向量中.把cycles 的每一个行向量 取出来与之比较.由于一条回路可能有多种存储顺序,比如 142857 等同于285714 和571428, 所以还要调整行向量的次序,并存入temp 数组,例如,thiscycle 为142857 第一个结点为1,cycles 的当前向量为857142,则找到后者中的1,把1 后部分提到1 前部分前面,最终在temp 中得到
142857,与thiscycle 比较,发现相同,因此142857 和857142 是同一条回路,不予存储.这个算法 太复杂,很难保证细节的准确性,大家理解思路便可.希望有人给出更加简捷的算法.
7.31
int visited[MAXSIZE];
int finished[MAXSIZE];
int count; //count 在第一次深度优先遍历中用于指示finished 数组的填充位置
void Get_SGraph(OLGraph G)//求十字链表结构储存的有向图G 的强连通分量
{
count=0;
for(v=0;v<G.vexnum;v++) visited[v]=0;
for(v=0;v<G.vexnum;v++) //第一次深度优先遍历建立finished 数组
if(!visited[v]) DFS1(G,v);
for(v=0;v<G.vexnum;v++) visited[v]=0; //清空visited 数组
for(i=G.vexnum-1;i>=0;i--) //第二次逆向的深度优先遍历
{
v=finished(i);
if(!visited[v])
{
printf("\n"); //不同的强连通分量在不同的行输出
DFS2(G,v);
}
}//for
}//Get_SGraph
数据结构试卷 数据结构试题库集及答案
{
visited[v]=1;
for(p=G.xlist[v].firstout;p;p=p->tlink)
{
w=p->headvex;
if(!visited[w]) DFS1(G,w);
}//for
finished[++count]=v; //在第一次遍历中建立finished 数组
}//DFS1
void DFS2(OLGraph G,int v)//第二次逆向的深度优先遍历的算法
{
visited[v]=1;
printf("%d",v); //在第二次遍历中输出结点序号
for(p=G.xlist[v].firstin;p;p=p->hlink)
{
严蔚敏《数据结构习题集》解答
w=p->tailvex;
if(!visited[w]) DFS2(G,w);
}//for
}//DFS2
第 87 页 共 124 页
分析:求有向图的强连通分量的算法的时间复杂度和深度优先遍历相同,也为O(n+e).
7.32
void Forest_Prim(ALGraph G,int k,CSTree &T)//从顶点k 出发,构造邻接表结构的有向图G 的 最小生成森林T,用孩子兄弟链表存储
{
for(j=0;j<G.vexnum;j++) //以下在Prim 算法基础上稍作改动
if(j!=k)
{
closedge[j]={k,Max_int};
for(p=G.vertices[j].firstarc;p;p=p->nextarc)
if(p->adjvex==k) closedge[j].lowcost=p->cost;
}//if
closedge[k].lowcost=0;
for(i=1;i<G.vexnum;i++)
{
k=minimum(closedge);
if(closedge[k].lowcost<Max_int)
{
Addto_Forest(T,closedge[k].adjvex,k); //把这条边加入生成森林中
closedge[k].lowcost=0;
for(p=G.vertices[k].firstarc;p;p=p->nextarc)
if(p->cost<closedge[p->adjvex].lowcost)
closedge[p->adjvex]={k,p->cost};
}//if
else Forest_Prim(G,k); //对另外一个连通分量执行算法
数据结构试卷 数据结构试题库集及答案
}//Forest_Prim
void Addto_Forest(CSTree &T,int i,int j)//把边(i,j)添加到孩子兄弟链表表示的树T 中 {
p=Locate(T,i); //找到结点i 对应的指针p,过程略
q=(CSTNode*)malloc(sizeof(CSTNode));
q->data=j;
if(!p) //起始顶点不属于森林中已有的任何一棵树
{
p=(CSTNode*)malloc(sizeof(CSTNode));
p->data=i;
for(r=T;r->nextsib;r=r->nextsib);
r->nextsib=p;
p->firstchild=q;
} //作为新树插入到最右侧
严蔚敏《数据结构习题集》解答
else if(!p->firstchild) //双亲还没有孩子
p->firstchild=q; //作为双亲的第一个孩子
else //双亲已经有了孩子
{
for(r=p->firstchild;r->nextsib;r=r->nextsib);
r->nextsib=q; //作为双亲最后一个孩子的兄弟
}
}//Addto_Forest
main()
{
...
T=(CSTNode*)malloc(sizeof(CSTNode)); //建立树根
T->data=1;
Forest_Prim(G,1,T);
...
}//main
第 88 页 共 124 页
分析:这个算法是在Prim 算法的基础上添加了非连通图支持和孩子兄弟链表构建模块而得到 的,其时间复杂度为O(n^2).
7.33
typedef struct {
int vex; //结点序号
int ecno; //结点所属的连通分量号
} VexInfo;
VexInfo vexs[MAXSIZE]; //记录结点所属连通分量号的数组
void Init_VexInfo(VexInfo &vexs[ ],int vexnum)//初始化
{
for(i=0;i<vexnum;i++)
vexs[i]={i,i}; //初始状态:每一个结点都属于不同的连通分量
}//Init_VexInfo
int is_ec(VexInfo vexs[ ],int i,int j)//判断顶点i 和顶点j 是否属于同一个连通分量
数据结构试卷 数据结构试题库集及答案
if(vexs[i].ecno==vexs[j].ecno) return 1;
else return 0;
}//is_ec
void merge_ec(VexInfo &vexs[ ],int ec1,int ec2)//合并连通分量ec1 和ec2
{
for(i=0;vexs[i].vex;i++)
if(vexs[i].ecno==ec2) vexs[i].ecno==ec1;
}//merge_ec
void MinSpanTree_Kruscal(Graph G,EdgeSetType &EdgeSet,CSTree &T)//求图的最小生成树的 克鲁斯卡尔算法
{
Init_VexInfo(vexs,G.vexnum);
ecnum=G.vexnum; //连通分量个数
严蔚敏《数据结构习题集》解答
while(ecnum>1)
{
GetMinEdge(EdgeSet,u,v); //选出最短边
if(!is_ec(vexs,u,v)) //u 和v 属于不同连通分量
{
Addto_CSTree(T,u,v); //加入到生成树中
merge_ec(vexs,vexs[u].ecno,vexs[v].ecno); //合并连通分量
ecnum--;
}
DelMinEdge(EdgeSet,u,v); //从边集中删除
}//while
}//MinSpanTree_Kruscal
第89 页 共 124 页
void Addto_CSTree(CSTree &T,int i,int j)//把边(i,j)添加到孩子兄弟链表表示的树T 中 {
p=Locate(T,i); //找到结点i 对应的指针p,过程略
q=(CSTNode*)malloc(sizeof(CSTNode));
q->data=j;
if(!p->firstchild) //双亲还没有孩子
p->firstchild=q; //作为双亲的第一个孩子
else //双亲已经有了孩子
{
for(r=p->firstchild;r->nextsib;r=r->nextsib);
r->nextsib=q; //作为双亲最后一个孩子的兄弟
}
}//Addto_CSTree
分析:本算法使用一维结构体变量数组来表示等价类,每个连通分量所包含的所有结点属于一 个等价类.在这个结构上实现了初始化,判断元素是否等价(两个结点是否属于同一个连通分
量),合并等价类(连通分量)的操作.
7.34
Status TopoSeq(ALGraph G,int new[ ])//按照题目要求给有向无环图的结点重新编号,并存入数 组new 中
数据结构试卷 数据结构试题库集及答案
int indegree[MAXSIZE]; //本算法就是拓扑排序
FindIndegree(G,indegree);
Initstack(S);
for(i=0;i<G.vexnum;i++)
if(!indegree[i]) Push(S,i);
count=0;
while(!stackempty(S))
{
Pop(S,i);new[i]=++count; //把拓扑顺序存入数组的对应分量中
for(p=G.vertices[i].firstarc;p;p=p->nextarc)
{
k=p->adjvex;
严蔚敏《数据结构习题集》解答
if(!(--indegree[k])) Push(S,k);
}
}//while
if(count<G.vexnum) return ERROR;
return OK;
}//TopoSeq
7.35
int visited[MAXSIZE];
void Get_Root(ALGraph G)//求有向无环图的根,如果有的话
{
for(v=0;v<G.vexnum;v++)
{
for(w=0;w<G.vexnum;w++) visited[w]=0;//每次都要将访问数组清零 DFS(G,v); //从顶点v 出发进行深度优先遍历
for(flag=1,w=0;w<G.vexnum;w++)
第 90 页 共 124 页
if(!visited[w]) flag=0; //如果v 是根,则深度优先遍历可以访问到所有结点 if(flag) printf("Found a root vertex:%d\n",v);
}//for
}//Get_Root,这个算法要求图中不能有环,否则会发生误判
void DFS(ALGraph G,int v)
{
visited[v]=1;
for(p=G.vertices[v].firstarc;p;p=p->nextarc)
{
w=p->adjvex;
if(!visited[w]) DFS(G,w);
}
}//DFS
7.36
void Fill_MPL(ALGraph &G)//为有向无环图G 添加MPL 域
{
FindIndegree(G,indegree);
数据结构试卷 数据结构试题库集及答案
if(!indegree[i]) Get_MPL(G,i);//从每一个零入度顶点出发构建MPL 域 }//Fill_MPL
int Get_MPL(ALGraph &G,int i)//从一个顶点出发构建MPL 域并返回其MPL 值 {
if(!G.vertices[i].firstarc)
{
G.vertices[i].MPL=0;
return 0; //零出度顶点
}
else
{
严蔚敏《数据结构习题集》解答
max=0;
for(p=G.vertices[i].firstarc;p;p=p->nextarc)
{
j=p->adjvex;
if(G.vertices[j].MPL==0) k=Get_MPL(G,j);
if(k>max) max=k; //求其直接后继顶点MPL 的最大者
}
G.vertices[i]=max+1;//再加一,就是当前顶点的MPL
return max+1;
}//else
}//Get_MPL
7.37
int maxlen,path[MAXSIZE]; //数组path 用于存储当前路径
int mlp[MAXSIZE]; //数组mlp 用于存储已发现的最长路径
void Get_Longest_Path(ALGraph G)//求一个有向无环图中最长的路径
{
maxlen=0;
FindIndegree(G,indegree);
for(i=0;i<G.vexnum;i++)
{
for(j=0;j<G.vexnum;j++) visited[j]=0;
if(!indegree[i]) DFS(G,i,0);//从每一个零入度结点开始深度优先遍历
}
printf("Longest Path:");
for(i=0;mlp[i];i++) printf("%d",mlp[i]); //输出最长路径
}//Get_Longest_Path
void DFS(ALGraph G,int i,int len)
{
visited[i]=1;
path[len]=i;
if(len>maxlen&&!G.vertices[i].firstarc) //新的最长路径
{
for(j=0;j<=len;j++) mlp[j]=path[j]; //保存下来
maxlen=len;
数据结构试卷 数据结构试题库集及答案
else
{
for(p=G.vertices[i].firstarc;p;p=p->nextarc)
{
j=p->adjvex;
if(!visited[j]) DFS(G,j,len+1);
}
}//else
path[i]=0;
第 91 页 共 124 页
严蔚敏《数据结构习题集》解答
visited[i]=0;
}//DFS
7.38
第 92 页 共 124 页
void NiBoLan_DAG(ALGraph G)//输出有向无环图形式表示的表达式的逆波兰式 {
FindIndegree(G,indegree);
for(i=0;i<G.vexnum;i++)
if(!indegree[i]) r=i; //找到有向无环图的根
PrintNiBoLan_DAG(G,i);
}//NiBoLan_DAG
void PrintNiBoLan_DAG(ALGraph G,int i)//打印输出以顶点i 为根的表达式的逆波兰式 {
c=G.vertices[i].data;
if(!G.vertices[i].firstarc) //c 是原子
printf("%c",c);
else //子表达式
{
p=G.vertices[i].firstarc;
PrintNiBoLan_DAG(G,p->adjvex);
PrintNiBoLan_DAG(G,p->nexarc->adjvex);
printf("%c",c);
}
}//PrintNiBoLan_DAG
7.39
void PrintNiBoLan_Bitree(Bitree T)//在二叉链表存储结构上重做上一题
{
if(T->lchild) PrintNiBoLan_Bitree(T->lchild);
if(T->rchild) PrintNiBoLan_Bitree(T->rchild);
printf("%c",T->data);
}//PrintNiBoLan_Bitree
7.40
int Evaluate_DAG(ALGraph G)//给有向无环图表示的表达式求值
{
FindIndegree(G,indegree);
数据结构试卷 数据结构试题库集及答案
if(!indegree[i]) r=i; //找到有向无环图的根
return Evaluate_imp(G,i);
}//NiBoLan_DAG
int Evaluate_imp(ALGraph G,int i)//求子表达式的值
{
if(G.vertices[i].tag=NUM) return G.vertices[i].value;
else
{
p=G.vertices[i].firstarc;
严蔚敏《数据结构习题集》解答
v1=Evaluate_imp(G,p->adjvex);
v2=Evaluate_imp(G,p->nextarc->adjvex);
return calculate(v1,G.vertices[i].optr,v2);
}
}//Evaluate_imp
分析:本题中,邻接表的vertices 向量的元素类型修改如下: struct {
enum tag{NUM,OPTR};
union {
int value;
char optr;
};
ArcNode * firstarc;
} Elemtype;
7.41
void Critical_Path(ALGraph G)//利用深度优先遍历求网的关键路径 {
FindIndegree(G,indegree);
for(i=0;i<G.vexnum;i++)
if(!indegree[i]) DFS1(G,i); //第一次深度优先遍历:建立ve for(i=0;i<G.vexnum;i++)
if(!indegree[i]) DFS2(G,i); //第二次深度优先遍历:建立vl for(i=0;i<=G.vexnum;i++)
if(vl[i]==ve[i]) printf("%d",i); //打印输出关键路径
}//Critical_Path
void DFS1(ALGraph G,int i)
{
if(!indegree[i]) ve[i]=0;
for(p=G.vertices[i].firstarc;p;p=p->nextarc)
{
dut=*p->info;
if(ve[i]+dut>ve[p->adjvex])
ve[p->adjvex]=ve[i]+dut;
DFS1(G,p->adjvex);
}
}//DFS1
数据结构试卷 数据结构试题库集及答案
{
if(!G.vertices[i].firstarc) vl[i]=ve[i];
else
{
for(p=G.vertices[i].firstarc;p;p=p->nextarc)
{
DFS2(G,p->adjvex);
第 93 页 共 124 页
严蔚敏《数据结构习题集》解答
dut=*p->info;
if(vl[p->adjvex]-dut<vl[i])
vl[i]=vl[p->adjvex]-dut;
}
}//else
}//DFS2
7.42
第 94 页 共 124 页
void ALGraph_DIJ(ALGraph G,int v0,Pathmatrix &P,ShortestPathTable &D)//在邻接表存储结 构上实现迪杰斯特拉算法
{
for(v=0;v<G.vexnum;v++)
D[v]=INFINITY;
for(p=G.vertices[v0].firstarc;p;p=p->nextarc)
D[p->adjvex]=*p->info; //给D 数组赋初值
for(v=0;v<G.vexnum;v++)
{
final[v]=0;
for(w=0;w<G.vexnum;w++) P[v][w]=0; //设空路径
if(D[v]<INFINITY)
{
P[v][v0]=1;
P[v][v]=1;
}
}//for
D[v0]=0;final[v0]=1; //初始化
for(i=1;i<G.vexnum;i++)
{
min=INFINITY;
for(w=0;w<G.vexnum;w++)
if(!final[w])
if(D[w]<min) //尚未求出到该顶点的最短路径
{
v=w;
min=D[w];
}
final[v]=1;
数据结构试卷 数据结构试题库集及答案
{
w=p->adjvex;
if(!final[w]&&(min+(*p->info)<D[w])) //符合迪杰斯特拉条件
{
D[w]=min+edgelen(G,v,w);
P[w]=P[v];
P[w][w]=1; //构造最短路径
严蔚敏《数据结构习题集》解答
}
}//for
}//for
}//ALGraph_DIJ
第 95 页 共 124 页
分析:本算法对迪杰斯特拉算法中直接取任意边长度的语句作了修改.由于在原算法中,每次 循环都是对尾相同的边进行处理,所以可以用遍历邻接表中的一条链来代替.
严蔚敏《数据结构习题集》解答
第八章 动态存储管理
8.11
typedef struct {
char *start;
int size;
} fmblock; //空闲块类型
char *Malloc_Fdlf(int n)//遵循最后分配者最先释放规则的内存分配算法
{
while(Gettop(S,b)&&b.size<n)
{
Pop(S,b);
Push(T,b); //从栈顶逐个取出空闲块进行比较
}
if(StackEmpty(S)) return NULL; //没有大小足够的空闲块
Pop(S,b);
b.size-=n;
if(b.size) Push(S,{b.start+n,b.size});//分割空闲块
while(!StackEmpty(T))
{
Pop(T,a);
Push(S,a);
} //恢复原来次序
return b.start;
}//Malloc_Fdlf
mem_init()//初始化过程
{
数据结构试卷 数据结构试题库集及答案
InitStack(S);InitStack(T); //S 和T 的元素都是fmblock 类型
Push(S,{MemStart,MemLen}); //一开始,栈中只有一个内存整块
...
}//main
8.12
void Free_Fdlf(char *addr,int n)//与上一题对应的释放算法
{
while(Gettop(S,b)&&b.start<addr)
{
Pop(S,b);
Push(T,b);
} //在按地址排序的栈中找到合适的插入位置
if(Gettop(T,b)&&(b.start+b.size==addr)) //可以与上邻块合并
{
Pop(T,b);
第 96 页 共 124 页
严蔚敏《数据结构习题集》解答
addr=b.start;n+=b.size;
}
if(Gettop(S,b)&&(addr+n==b.start)) //可以与下邻块合并
{
Pop(S,b);
n+=b.size;
}
Push(S,{addr,n}); //插入到空闲块栈中
while(!StackEmpty(T))
{
Pop(T,b);
Push(S,b);
} //恢复原来次序
}//Free_Fdlf
8.13
第 97 页 共 124 页
void Free_BT(Space &pav,Space p)//在边界标识法的动态存储管理系统中回收空闲块p {
n=p->size;
f=p+n-1; //f 指向空闲块底部
if((p-1)->tag&&(f+1)->tag) //回收块上下邻块均为占用块
{
p->tag=0;f->tag=0;
f->uplink=p;
if(!pav)
{
p->llink=p;
p->rlink=p;
}
数据结构试卷 数据结构试题库集及答案
{
q=pav->llink;
p->llink=q;p->rlink=pav;
q->rlink=p;pav->llink=p;
}
pav=p;
}//if
else if(!(p-1)->tag&&(f+1)->tag) //上邻块为空闲块
{
q=(p-1)->uplink;
q->size+=n;
f->uplink=q;
f->tag=0;
}
else if((p-1)->tag&&!(f+1)->tag) //下邻块为空闲块
严蔚敏《数据结构习题集》解答
{
q=f+1;
s=q->llink;t=q->rlink;
p->llink=s;p->rlink=t;
s->rlink=p;t->llink=p;
p->size+=q->size;
(q+q->size-1)->uplink=p;
p->tag=0;
}
else //上下邻块均为空闲块
{
s=(p-1)->uplink;
t=f+1;
s->size+=n+t->size;
t->llink->rlink=t->rlink;
t->rlink->llink=t->llink;
(t+t->size-1)->uplink=s;
}
}//Free_BT,该算法在课本里有详细的描述.
8.14
void Free_BS(freelist &avail,char *addr,int n)//伙伴系统的空闲块回收算法 {
buddy=addr%(2*n)?(addr-n):(addr+n); //求回收块的伙伴地址
addr->tag=0;
addr->kval=n;
for(i=0;avail[i].nodesize<n;i++); //找到这一大小的空闲块链
if(!avail[i].first) //尚没有该大小的空闲块
{
addr->llink=addr;
addr->rlink=addr;
数据结构试卷 数据结构试题库集及答案
}
else
{
for(p=avail[i].first;p!=buddy&&p!=avail[i].first;p=p->rlink);//寻找伙伴
if(p==buddy) //伙伴为空闲块,此时进行合并
{
if(p->rlink==p) avail[i].first=NULL;//伙伴是此大小的唯一空闲块
else
{
p->llink->rlink=p->rlink;
p->rlink->llink=p->llink;
} //从空闲块链中删去伙伴
new=addr>p?p:addr; //合并后的新块首址
第 98 页 共 124 页
严蔚敏《数据结构习题集》解答
Free_BS(avail,new,2*n); //递归地回收新块
}//if
else //伙伴为占用块,此时插入空闲块链头部
{
q=p->rlink;
p->rlink=addr;addr->llink=p;
q->llink=addr;addr->rlink=q;
}
}//else
}//Free_BS
8.15
第 99 页 共 124 页
FBList *MakeList(char *highbound,char *lowbound)//把堆结构存储的的所有空闲块链接成可 利用空间表,并返回表头指针
{
p=lowbound;
while(p->tag&&p<highbound) p++; //查找第一个空闲块
if(p>=highbound) return NULL; //没有空闲块
head=p;
for(q=p;p<highbound;p+=cellsize) //建立链表
if(!p->tag)
{
q->next=p;
q=p;
}//if
p->next=NULL;
return head; //返回头指针
}//MakeList
8.16
void Mem_Contract(Heap &H)//对堆H 执行存储紧缩
{
数据结构试卷 数据结构试题库集及答案
for(i=0;i<Max_ListLen;i++)
if(H.list[i].stadr->tag)
{
s=H.list[i].length;
p=H.list[i].stadr;
for(k=0;k<s;k++) *(q++)=*(p++); //紧缩内存空间
H.list[j].stadr=q;
H.list[j].length=s; //紧缩占用空间表
j++;
}
}//Mem_Contract
严蔚敏《数据结构习题集》解答
第九章 查找
9.25
第 100 页 共 124 页
int Search_Sq(SSTable ST,int key)//在有序表上顺序查找的算法,监视哨设在高下标端 {
ST.elem[ST.length+1].key=key;
for(i=1;ST.elem[i].key>key;i++);
if(i>ST.length||ST.elem[i].key<key) return ERROR;
return i;
}//Search_Sq
分析:本算法查找成功情况下的平均查找长度为ST.length/2,不成功情况下为ST.length.
9.26
int Search_Bin_Recursive(SSTable ST,int key,int low,int high)//折半查找的递归算法 {
if(low>high) return 0; //查找不到时返回0
mid=(low+high)/2;
if(ST.elem[mid].key==key) return mid;
else if(ST.elem[mid].key>key)
return Search_Bin_Recursive(ST,key,low,mid-1);
else return Search_Bin_Recursive(ST,key,mid+1,high);
}
}//Search_Bin_Recursive
9.27
int Locate_Bin(SSTable ST,int key)//折半查找,返回小于或等于待查元素的最后一个结点号 {
int *r;
r=ST.elem;
if(key<r .key) return 0;
else if(key>=r[ST.length].key) return ST.length;
low=1;high=ST.length;
while(low<=high)
数据结构试卷 数据结构试题库集及答案
mid=(low+high)/2;
if(key>=r[mid].key&&key<r[mid+1].key) //查找结束的条件
return mid;
else if(key<r[mid].key) high=mid;
else low=mid;
} //本算法不存在查找失败的情况,不需要return 0;
}//Locate_Bin
9.28
typedef struct {
int maxkey;
int firstloc;
严蔚敏《数据结构习题集》解答
} Index;
typedef struct {
int *elem;
int length;
第 101 页 共 124 页
Index idx[MAXBLOCK]; //每块起始位置和最大元素,其中idx[0]不利用,其内 容初始化为{0,0}以利于折半查找
int blknum; //块的数目
} IdxSqList; //索引顺序表类型
int Search_IdxSeq(IdxSqList L,int key)//分块查找,用折半查找法确定记录所在块,块内采用顺
序查找法
{
if(key>L.idx[L.blknum].maxkey) return ERROR; //超过最大元素
low=1;high=L.blknum;
found=0;
while(low<=high&&!found) //折半查找记录所在块号mid
{
mid=(low+high)/2;
if(key<=L.idx[mid].maxkey&&key>L.idx[mid-1].maxkey)
found=1;
else if(key>L.idx[mid].maxkey)
low=mid+1;
else high=mid-1;
}
i=L.idx[mid].firstloc; //块的下界
j=i+blksize-1; //块的上界
temp=L.elem[i-1]; //保存相邻元素
L.elem[i-1]=key; //设置监视哨
for(k=j;L.elem[k]!=key;k--); //顺序查找
L.elem[i-1]=temp; //恢复元素
if(k<i) return ERROR; //未找到
return k;
}//Search_IdxSeq
分析:在块内进行顺序查找时,如果需要设置监视哨,则必须先保存相邻块的相邻元素,以免数
数据结构试卷 数据结构试题库集及答案
9.29
typedef struct {
LNode *h; //h 指向最小元素
LNode *t; //t 指向上次查找的结点
} CSList;
LNode *Search_CSList(CSList &L,int key)//在有序单循环链表存储结构上的查找算法,假定每 次查找都成功
{
if(L.t->data==key) return L.t;
else if(L.t->data>key)
严蔚敏《数据结构习题集》解答
for(p=L.h,i=1;p->data!=key;p=p->next,i++);
else
for(p=L.t,i=L.tpos;p->data!=key;p=p->next,i++);
L.t=p; //更新t 指针
return p;
}//Search_CSList
第 102 页 共 124 页
分析:由于题目中假定每次查找都是成功的,所以本算法中没有关于查找失败的处理.由微积 分可得,在等概率情况下,平均查找长度约为n/3.
9.30
typedef struct {
DLNode *pre;
int data;
DLNode *next;
} DLNode;
typedef struct {
DLNode *sp;
int length;
} DSList; //供查找的双向循环链表类型
DLNode *Search_DSList(DSList &L,int key)//在有序双向循环链表存储结构上的查找算法,假 定每次查找都成功
{
p=L.sp;
if(p->data>key)
{
while(p->data>key) p=p->pre;
L.sp=p;
}
else if(p->data<key)
{
while(p->data<key) p=p->next;
L.sp=p;
}
return p;
}//Search_DSList
数据结构试卷 数据结构试题库集及答案
9.31
int last=0,flag=1;
int Is_BSTree(Bitree T)//判断二叉树T 是否二叉排序树,是则返回1,否则返回0
{
if(T->lchild&&flag) Is_BSTree(T->lchild);
if(T->data<last) flag=0; //与其中序前驱相比较
last=T->data;
if(T->rchild&&flag) Is_BSTree(T->rchild);
return flag;
严蔚敏《数据结构习题集》解答
}//Is_BSTree
9.32
int last=0;
第 103 页 共 124 页
void MaxLT_MinGT(BiTree T,int x)//找到二叉排序树T 中小于x 的最大元素和大于x 的最小 元素
{
if(T->lchild) MaxLT_MinGT(T->lchild,x); //本算法仍是借助中序遍历来实现
if(last<x&&T->data>=x) //找到了小于x 的最大元素
printf("a=%d\n",last);
if(last<=x&&T->data>x) //找到了大于x 的最小元素
printf("b=%d\n",T->data);
last=T->data;
if(T->rchild) MaxLT_MinGT(T->rchild,x);
}//MaxLT_MinGT
9.33
void Print_NLT(BiTree T,int x)//从大到小输出二叉排序树T 中所有不小于x 的元素
{
if(T->rchild) Print_NLT(T->rchild,x);
if(T->data<x) exit(); //当遇到小于x 的元素时立即结束运行
printf("%d\n",T->data);
if(T->lchild) Print_NLT(T->lchild,x); //先右后左的中序遍历
}//Print_NLT
9.34
void Delete_NLT(BiTree &T,int x)//删除二叉排序树T 中所有不小于x 元素结点,并释放空间 {
if(T->rchild) Delete_NLT(T->rchild,x);
if(T->data<x) exit(); //当遇到小于x 的元素时立即结束运行
q=T;
T=T->lchild;
free(q); //如果树根不小于x,则删除树根,并以左子树的根作为新的树根
if(T) Delete_NLT(T,x); //继续在左子树中执行算法
}//Delete_NLT
9.35
void Print_Between(BiThrTree T,int a,int b)//打印输出后继线索二叉排序树T 中所有大于a 且 小于b 的元素
数据结构试卷 数据结构试题库集及答案
p=T;
while(!p->ltag) p=p->lchild; //找到最小元素
while(p&&p->data<b)
{
if(p->data>a) printf("%d\n",p->data); //输出符合条件的元素
if(p->rtag) p=p->rtag;
else
{
严蔚敏《数据结构习题集》解答
p=p->rchild;
while(!p->ltag) p=p->lchild;
} //转到中序后继
}//while
}//Print_Between
9.36
第 104 页 共 124 页
void BSTree_Insert_Key(BiThrTree &T,int x)//在后继线索二叉排序树T 中插入元素x {
if(T->data<x) //插入到右侧
{
if(T->rtag) //T 没有右子树时,作为右孩子插入
{
p=T->rchild;
q=(BiThrNode*)malloc(sizeof(BiThrNode));
q->data=x;
T->rchild=q;T->rtag=0;
q->rtag=1;q->rchild=p; //修改原线索
}
else BSTree_Insert_Key(T->rchild,x);//T 有右子树时,插入右子树中
}//if
else if(T->data>x) //插入到左子树中
{
if(!T->lchild) //T 没有左子树时,作为左孩子插入
{
q=(BiThrNode*)malloc(sizeof(BiThrNode));
q->data=x;
T->lchild=q;
q->rtag=1;q->rchild=T; //修改自身的线索
}
else BSTree_Insert_Key(T->lchild,x);//T 有左子树时,插入左子树中
}//if
}//BSTree_Insert_Key
9.37
Status BSTree_Delete_key(BiThrTree &T,int x)//在后继线索二叉排序树T 中删除元素x {
BTNode *pre,*ptr,*suc;//ptr 为x 所在结点,pre 和suc 分别指向ptr 的前驱和后继
数据结构试卷 数据结构试题库集及答案
while(!p->ltag) p=p->lchild; //找到中序起始元素
while(p)
{
if(p->data==x) //找到了元素x 结点
{
pre=last;
ptr=p;
严蔚敏《数据结构习题集》解答
}
else if(last&&last->data==x) suc=p; //找到了x 的后继
if(p->rtag) p=p->rtag;
else
{
p=p->rchild;
while(!p->ltag) p=p->lchild;
} //转到中序后继
last=p;
}//while //借助中序遍历找到元素x 及其前驱和后继结点
if(!ptr) return ERROR; //未找到待删结点
Delete_BSTree(ptr); //删除x 结点
if(pre&&pre->rtag)
pre->rchild=suc; //修改线索
return OK;
}//BSTree_Delete_key
第 105 页 共 124 页
void Delete_BSTree(BiThrTree &T)//课本上给出的删除二叉排序树的子树T 的算法,按照线索 二叉树的结构作了一些改动
{
q=T;
if(!T->ltag&&T->rtag) //结点无右子树,此时只需重接其左子树
T=T->lchild;
else if(T->ltag&&!T->rtag) //结点无左子树,此时只需重接其右子树
T=T->rchild;
else if(!T->ltag&&!T->rtag) //结点既有左子树又有右子树
{
p=T;r=T->lchild;
while(!r->rtag)
{
s=r;
r=r->rchild; //找到结点的前驱r 和r 的双亲s
}
T->data=r->data; //用r 代替T 结点
if(s!=T)
s->rchild=r->lchild;
else s->lchild=r->lchild; //重接r 的左子树到其双亲结点上
q=r;
数据结构试卷 数据结构试题库集及答案
free(q); //删除结点
}//Delete_BSTree
分析:本算法采用了先求出x 结点的前驱和后继,再删除x 结点的办法,这样修改线索时会比较 简单,直接让前驱的线索指向后继就行了.如果试图在删除x 结点的同时修改线索,则问题反而 复杂化了.
9.38
严蔚敏《数据结构习题集》解答
void BSTree_Merge(BiTree &T,BiTree &S)//把二叉排序树S 合并到T 中
{
if(S->lchild) BSTree_Merge(T,S->lchild);
if(S->rchild) BSTree_Merge(T,S->rchild); //合并子树
Insert_Key(T,S); //插入元素
}//BSTree_Merge
第 106 页 共 124 页
void Insert_Node(Bitree &T,BTNode *S)//把树结点S 插入到T 的合适位置上
{
if(S->data>T->data)
{
if(!T->rchild) T->rchild=S;
else Insert_Node(T->rchild,S);
}
else if(S->data<T->data)
{
if(!T->lchild) T->lchild=S;
else Insert_Node(T->lchild,S);
}
S->lchild=NULL; //插入的新结点必须和原来的左右子树断绝关系
S->rchild=NULL; //否则会导致树结构的混乱
}//Insert_Node
分析:这是一个与课本上不同的插入算法.在合并过程中,并不释放或新建任何结点,而是采取 修改指针的方式来完成合并.这样,就必须按照后序序列把一棵树中的元素逐个连接到另一棵 树上,否则将会导致树的结构的混乱.
9.39
void BSTree_Split(BiTree &T,BiTree &A,BiTree &B,int x)//把二叉排序树T 分裂为两棵二叉排 序树A 和B,其中A 的元素全部小于等于x,B 的元素全部大于x
{
if(T->lchild) BSTree_Split(T->lchild,A,B,x);
if(T->rchild) BSTree_Split(T->rchild,A,B,x); //分裂左右子树
if(T->data<=x) Insert_Node(A,T);
else Insert_Node(B,T); //将元素结点插入合适的树中
}//BSTree_Split
void Insert_Node(Bitree &T,BTNode *S)//把树结点S 插入到T 的合适位置上
{
if(!T) T=S; //考虑到刚开始分裂时树A 和树B 为空的情况
else if(S->data>T->data) //其余部分与上一题同
{
数据结构试卷 数据结构试题库集及答案
else Insert_Node(T->rchild,S);
}
else if(S->data<T->data)
{
if(!T->lchild) T->lchild=S;
严蔚敏《数据结构习题集》解答
else Insert_Node(T->lchild,S);
}
S->lchild=NULL;
S->rchild=NULL;
}//Insert_Key
9.40
typedef struct {
int data;
int bf;
int lsize; //lsize 域表示该结点的左子树的结点总数加1 BlcNode *lchild,*rchild;
} BlcNode,*BlcTree; //含lsize 域的平衡二叉排序树类型
第107 页 共 124 页
BTNode *Locate_BlcTree(BlcTree T,int k)//在含lsize 域的平衡二叉排序树T 中确定第k 小的 结点指针
{
if(!T) return NULL; //k 小于1 或大于树结点总数
if(T->lsize==k) return T; //就是这个结点
else if(T->lsize>k)
return Locate_BlcTree(T->lchild,k); //在左子树中寻找
else return Locate_BlcTree(T->rchild,k-T->lsize); //在右子树中寻找,注意要修改k 的值 }//Locate_BlcTree
9.41
typedef struct {
enum {LEAF,BRANCH} tag; //结点类型标识
int keynum;
BPLink parent; //双亲指针
int key[MAXCHILD]; //关键字
union {
BPLink child[MAXCHILD];//非叶结点的孩子指针
struct {
rectype *info[MAXCHILD];//叶子结点的信息指针 BPNode *next; //指向下一个叶子结点的链接
} leaf;
}
} BPNode,*BPLink,*BPTree;//B+树及其结点类型
Status BPTree_Search(BPTree T,int key,BPNode *ptr,int pos)//B+树中按关键字随机查找的算法, 返回包含关键字的叶子结点的指针ptr 以及关键字在叶子结点中的位置pos
{
p=T;
数据结构试卷 数据结构试题库集及答案
{
for(i=0;i<p->keynum&&key>p->key[i];i++); //确定关键字所在子树
if(i==p->keynum) return ERROR; //关键字太大
p=p->child[i];
严蔚敏《数据结构习题集》解答
}
for(i=0;i<p->keynum&&key!=p->key[i];i++); //在叶子结点中查找
if(i==p->keynum) return ERROR; //找不到关键字
ptr=p;pos=i;
return OK;
}//BPTree_Search
9.42
第 108 页 共 124 页
void TrieTree_Insert_Key(TrieTree &T,StringType key)// 在 Trie 树 T 中插入字符串 key,StringType 的结构见第四章
{
q=(TrieNode*)malloc(sizeof(TrieNode));
q->kind=LEAF;
q->lf.k=key; //建叶子结点
klen=key[0];
p=T;i=1;
while(p&&i<=klen&&p->bh.ptr[ord(key[i])])
{
last=p;
p=p->bh.ptr[ord(key[i])];
i++;
} //自上而下查找
if(p->kind==BRANCH) //如果最后落到分支结点(无同义词):
{
p->bh.ptr[ord(key[i])]=q; //直接连上叶子
p->bh.num++;
}
else //如果最后落到叶子结点(有同义词):
{
r=(TrieNode*)malloc(sizeof(TrieNode)); //建立新的分支结点
last->bh.ptr[ord(key[i-1])]=r; //用新分支结点取代老叶子结点和上一层的联系 r->kind=BRANCH;r->bh.num=2;
r->bh.ptr[ord(key[i])]=q;
r->bh.ptr[ord(p->lf.k[i])]=p; //新分支结点与新老两个叶子结点相连
}
}//TrieTree_Insert_Key
分析:当自上而下的查找结束时,存在两种情况.一种情况,树中没有待插入关键字的同义词,此 时只要新建一个叶子结点并连到分支结点上即可.另一种情况,有同义词,此时要把同义词的 叶子结点与树断开,在断开的部位新建一个下一层的分支结点,再把同义词和新关键字的叶子 结点连到新分支结点的下一层.
9.43
数据结构试卷 数据结构试题库集及答案
{
p=T;i=1;
while(p&&p->kind==BRANCH&&i<=key[0]) //查找待删除元素
严蔚敏《数据结构习题集》解答
{
last=p;
p=p->bh.ptr[ord(key[i])];
i++;
}
if(p&&p->kind==LEAF&&p->lf.k=key) //找到了待删除元素
{
last->bh.ptr[ord(key[i-1])]=NULL;
free(p);
return OK;
}
else return ERROR; //没找到待删除元素
}//TrieTree_Delete_Key
9.44
第 109 页 共 124 页
void Print_Hash(HashTable H)//按第一个字母顺序输出Hash 表中的所有关键字,其中处理冲突 采用线性探测开放定址法
{
for(i=1;i<=26;i++)
for(j=i;H.elem[j].key;j=(j+1)%hashsize[sizeindex]) //线性探测
if(H(H.elem[j].key)==i) printf("%s\n",H.elem[j]);
}//Print_Hash
int H(char *s)//求Hash 函数
{
if(s) return s[0]-96; //求关键字第一个字母的字母序号(小写)
else return 0;
}//H
9.45
typedef *LNode[MAXSIZE] CHashTable; //链地址Hash 表类型
Status Build_Hash(CHashTable &T,int m)//输入一组关键字,建立Hash 表,表长为m,用链地址法 处理冲突.
{
if(m<1) return ERROR;
T=malloc(m*sizeof(WORD)); //建立表头指针向量
for(i=0;i<m;i++) T[i]=NULL;
while((key=Inputkey())!=NULL) //假定Inputkey 函数用于从键盘输入关键字
{
q=(LNode*)malloc(sizeof(LNode));
q->data=key;q->next=NULL;
n=H(key);
if(!T[n]) T[n]=q; //作为链表的第一个结点
else
数据结构试卷 数据结构试题库集及答案
for(p=T[n];p->next;p=p->next);
p->next=q; //插入链表尾部.本算法不考虑排序问题.
严蔚敏《数据结构习题集》解答
}
}//while
return OK;
}//Build_Hash
9.46
第 110 页 共 124 页
Status Locate_Hash(HashTable H,int row,int col,KeyType key,int &k)//根据行列值在Hash 表表 示的稀疏矩阵中确定元素key 的位置k
{
h=2*(100*(row/10)+col/10); //作者设计的Hash 函数
while(H.elem[h].key&&!EQ(H.elem[h].key,key))
h=(h+1)%20000;
if(EQ(H.elem[h].key,key)) k=h;
else k=NULL;
}//Locate_Hash
分析:本算法所使用的Hash 表长20000,装填因子为50%,Hash 函数为行数前两位和列数前两 位所组成的四位数再乘以二,用线性探测法处理冲突.当矩阵的元素是随机分布时,查找的时
间复杂度为O(1).
严蔚敏《数据结构习题集》解答
第十章 内部排序
10.23
void Insert_Sort1(SqList &L)//监视哨设在高下标端的插入排序算法
{
k=L.length;
for(i=k-1;i;--i) //从后向前逐个插入排序
if(L.r[i].key>L.r[i+1].key)
{
L.r[k+1].key=L.r[i].key; //监视哨
for(j=i+1;L.r[j].key>L.r[i].key;++j)
L.r[j-1].key=L.r[j].key; //前移
L.r[j-1].key=L.r[k+1].key; //插入
}
}//Insert_Sort1
10.24
void BiInsert_Sort(SqList &L)//二路插入排序的算法
{
int d[MAXSIZE]; //辅助存储
x=L.r .key;d =x;
first=1;final=1;
数据结构试卷 数据结构试题库集及答案
{
if(L.r[i].key>=x) //插入前部
{
for(j=final;d[j]>L.r[i].key;j--)
d[j+1]=d[j];
d[j+1]=L.r[i].key;
final++;
}
else //插入后部
{
for(j=first;d[j]<L.r[i].key;j++)
d[j-1]=d[j];
d[(j-2)%MAXSIZE+1]=L.r[i].key;
第 111 页 共 124 页
first=(first-2)%MAXSIZE+1; //这种形式的表达式是为了兼顾first=1 的情况 }
}//for
for(i=first,j=1;d[i];i=i%MAXSIZE+1,j++)//将序列复制回去
L.r[j].key=d[i];
}//BiInsert_Sort
10.25
void SLInsert_Sort(SLList &L)//静态链表的插入排序算法
严蔚敏《数据结构习题集》解答
{
L.r[0].key=0;L.r[0].next=1;
L.r[1].next=0; //建初始循环链表
for(i=2;i<=L.length;i++) //逐个插入
{
p=0;x=L.r[i].key;
while(L.r[L.r[p].next].key<x&&L.r[p].next)
p=L.r[p].next;
q=L.r[p].next;
L.r[p].next=i;
L.r[i].next=q;
}//for
p=L.r[0].next;
for(i=1;i<L.length;i++) //重排记录的位置
{
while(p<i) p=L.r[p].next;
q=L.r[p].next;
if(p!=i)
{
L.r[p]<->L.r[i];
L.r[i].next=p;
}
p=q;
数据结构试卷 数据结构试题库集及答案
}//SLInsert_Sort
10.26
第 112 页 共 124 页
void Bubble_Sort1(int a[ ],int n)//对包含n 个元素的数组a 进行改进的冒泡排序 {
change=n-1; //change 指示上一趟冒泡中最后发生交换的元素
while(change)
{
for(c=0,i=0;i<change;i++)
if(a[i]>a[i+1])
{
a[i]<->a[i+1];
c=i+1; //c 指示这一趟冒泡中发生交换的元素
}
change=c;
}//while
}//Bubble_Sort1
10.27
void Bubble_Sort2(int a[ ],int n)//相邻两趟是反方向起泡的冒泡排序算法
{
low=0;high=n-1; //冒泡的上下界
严蔚敏《数据结构习题集》解答
change=1;
while(low<high&&change)
{
change=0;
for(i=low;i<high;i++) //从上向下起泡
if(a[i]>a[i+1])
{
a[i]<->a[i+1];
change=1;
}
high--; //修改上界
for(i=high;i>low;i--) //从下向上起泡
if(a[i]<a[i-1])
{
a[i]<->a[i-1];
change=1;
}
low++; //修改下界
}//while
}//Bubble_Sort2
10.28
第 113 页 共 124 页
void Bubble_Sort3(int a[ ],int n)//对上一题的算法进行化简,循环体中只包含一次冒泡 {
数据结构试卷 数据结构试题库集及答案
d=1;b[0]=0;b[ 2 ]=n-1; //d 为冒泡方向的标识,1 为向上,-1 为向下 change=1;
while(b[0]<b[ 2 ]&&change)
{
change=0;
for(i=b[1-d];i!=b[1+d];i+=d) //统一的冒泡算法
if((a[i]-a[i+d])*d>0) //注意这个交换条件
{
a[i]<->a[i+d];
change=1;
}
b[1+d]-=d; //修改边界
d*=-1; //换个方向
}//while
}//Bubble_Sort3
10.29
void OE_Sort(int a[ ],int n)//奇偶交换排序的算法
{
change=1;
while(change)
严蔚敏《数据结构习题集》解答
{
change=0;
for(i=1;i<n-1;i+=2) //对所有奇数进行一趟比较
if(a[i]>a[i+1])
{
a[i]<->a[i+1];
change=1;
}
for(i=0;i<n-1;i+=2) //对所有偶数进行一趟比较
if(a[i]>a[i+1])
{
a[i]<->a[i+1];
change=1;
}
}//while
}//OE_Sort
分析:本算法的结束条件是连续两趟比较无交换发生
10.30
typedef struct {
int low;
int high;
} boundary; //子序列的上下界类型 void QSort_NotRecurve(int SQList &L)//快速排序的非递归算法 {
low=1;high=L.length;
数据结构试卷 数据结构试题库集及答案
while(low<high&&!StackEmpty(S)) //注意排序结束的条件
{
if(high-low>2) //如果当前子序列长度大于3 且尚未排好序
{
pivot=Partition(L,low,high); //进行一趟划分
if(high-pivot>pivot-low)
{
Push(S,{pivot+1,high}); //把长的子序列边界入栈
high=pivot-1; //短的子序列留待下次排序
}
else
{
Push(S,{low,pivot-1});
low=pivot+1;
}
}//if
第 114 页 共 124 页
else if(low<high&&high-low<3)//如果当前子序列长度小于3 且尚未排好序 {
严蔚敏《数据结构习题集》解答
Easy_Sort(L,low,high); //直接进行比较排序
low=high; //当前子序列标志为已排好序
}
else //如果当前子序列已排好序但栈中还有未排序的子序列
{
Pop(S,a); //从栈中取出一个子序列
low=a.low;
high=a.high;
}
}//while
}//QSort_NotRecurve
int Partition(SQList &L,int low,int high)//一趟划分的算法,与书上相同
{
L.r[0]=L.r[low];
pivotkey=L.r[low].key;
while(low<high)
{
while(low<high&&L.r[high].key>=pivotkey)
high--;
L.r[low]=L.r[high];
while(low<high&&L.r[low].key<=pivotkey)
low++;
L.r[high]=L.r[low];
}//while
L.r[low]=L.r[0];
return low;
数据结构试卷 数据结构试题库集及答案
第 115 页 共 124 页
void Easy_Sort(SQList &L,int low,int high)//对长度小于3 的子序列进行比较排序
{
if(high-low==1) //子序列只含两个元素
if(L.r[low].key>L.r[high].key) L.r[low]<->L.r[high];
else //子序列含有三个元素
{
if(L.r[low].key>L.r[low+1].key) L.r[low]<->L.r[low+1];
if(L.r[low+1].key>L.r[high].key) L.r[low+1]<->L.r[high];
if(L.r[low].key>L.r[low+1].key) L.r[low]<->L.r[low+1];
}
}//Easy_Sort
10.31
void Divide(int a[ ],int n)//把数组a 中所有值为负的记录调到非负的记录之前
{
low=0;high=n-1;
while(low<high)
{
严蔚敏《数据结构习题集》解答
while(low<high&&a[high]>=0) high--; //以0 作为虚拟的枢轴记录
a[low]<->a[high];
while(low<high&&a[low]<0) low++;
a[low]<->a[high];
}
}//Divide
10.32
typedef enum {RED,WHITE,BLUE} color; //三种颜色
第 116 页 共 124 页
void Flag_Arrange(color a[ ],int n)//把由三种颜色组成的序列重排为按照红,白,蓝的顺序排列 {
i=0;j=0;k=n-1;
while(j<=k)
switch(a[j])
{
case RED:
a[i]<->a[j];
i++;
j++;
break;
case WHITE:
j++;
break;
case BLUE:
a[j]<->a[k];
k--; //这里没有j++;语句是为了防止交换后a[j]仍为蓝色的情况
}
数据结构试卷 数据结构试题库集及答案
分析:这个算法中设立了三个指针.其中,j 表示当前元素;i 以前的元素全部为红色;k 以后的元 素全部为蓝色.这样,就可以根据j的颜色,把其交换到序列的前部或者后部.
10.33
void LinkedList_Select_Sort(LinkedList &L)//单链表上的简单选择排序算法
{
for(p=L;p->next->next;p=p->next)
{
q=p->next;x=q->data;
for(r=q,s=q;r->next;r=r->next) //在q 后面寻找元素值最小的结点
if(r->next->data<x)
{
x=r->next->data;
s=r;
}
if(s!=q) //找到了值比q->data 更小的最小结点s->next
{
p->next=s->next;s->next=q;
严蔚敏《数据结构习题集》解答
t=q->next;q->next=p->next->next;
p->next->next=t;
} //交换q 和s->next 两个结点
}//for
}//LinkedList_Select_Sort
10.34
void Build_Heap(Heap &H,int n)//从低下标到高下标逐个插入建堆的算法
{
for(i=2;i<n;i++)
{ //此时从H.r[1]到H.r[i-1]已经是大顶堆
j=i;
while(j!=1) //把H.r[i]插入
{
k=j/2;
if(H.r[j].key>H.r[k].key)
H.r[j]<->H.r[k];
j=k;
}
}//for
}//Build_Heap
10.35
void TriHeap_Sort(Heap &H)//利用三叉树形式的堆进行排序的算法
{
for(i=H.length/3;i>0;i--)
Heap_Adjust(H,i,H.length);
for(i=H.length;i>1;i--)
{
H.r[1]<->H.r[i];
数据结构试卷 数据结构试题库集及答案
}
}//TriHeap_Sort
第 117 页 共 124 页
void Heap_Adjust(Heap &H,int s,int m)//顺序表H 中,H.r[s+1]到H.r[m]已经是堆,把H.r[s]插入 并调整成堆
{
rc=H.r[s];
for(j=3*s-1;j<=m;j=3*j-1)
{
if(j<m&&H.r[j].key<H.r[j+1].key) j++;
if(j<m&&H.r[j].key<H.r[j+1].key) j++;
H.r[s]=H.r[j];
s=j;
}
H.r[s]=rc;
}//Heap_Adjust
严蔚敏《数据结构习题集》解答
第 118 页 共 124 页
分析:本算法与课本上的堆排序算法相比,只有两处改动:1.建初始堆时,i 的上限从 开始(为什么?) 2.调整堆的时候,要从结点的三个孩子结点中选择最大的那一个,最左边的孩 子的序号的计算公式为j=3*s-1(为什么?)
10.36
void Merge_Sort(int a[ ],int n)//归并排序的非递归算法
{
for(l=1;l<n;l*=2) //l 为一趟归并段的段长
for(i=0;(2*i-1)*l<n;i++) //i 为本趟的归并段序号
{
start1=2*l*i; //求出待归并的两段的上下界
end1=start1+l-1;
start2=end1+1;
end2=(start2+l-1)>(n-1)?(n-1):(start2+l-1);//注意end2 可能超出边界
Merge(a,start1,end1,start2,end2); //归并
}
}//Merge_Sort
void Merge(int a[ ],int s1,int e1,int s2,int e2)//将有序子序列a[s1]到a[e1]和a[s2]到a[e2]归并为 有序序列a[s1]到a[e2]
{
int b[MAXSIZE]; //设立辅助存储数组b
for(i=s1,j=s2,k=s1;i<=e1&&j<=e2;k++)
{
if(a[i]<a[j]) b[k]=a[i++];
else b[k]=a[j++];
}
while(i<=e1) b[k++]=a[i++];
while(j<=e2) b[k++]=a[j++]; //归并到b 中
for(i=s1;i<=e2;i++) //复制回去 H.length/3
数据结构试卷 数据结构试题库集及答案
}//Merge
10.37
void LinkedList_Merge_Sort1(LinkedList &L)//链表结构上的归并排序非递归算法 {
for(l=1;l<L.length;l*=2) //l 为一趟归并段的段长
for(p=L->next,e2=p;p->next;p=e2)
{
for(i=1,q=p;i<=l&&q->next;i++,q=q->next);
e1=q;
for(i=1;i<=l&&q->next;i++,q=q->next);
e2=q; //求出两个待归并子序列的尾指针
if(e1!=e2) LinkedList_Merge(L,p,e1,e2); //归并
}
}//LinkedList_Merge_Sort1
void LinkedList_Merge(LinkedList &L,LNode *p,LNode *e1,LNode *e2)//对链表上的子序列进 严蔚敏《数据结构习题集》解答
行归并,第一个子序列是从p->next 到e1,第二个是从e1->next 到e2
{
q=p->next;r=e1->next; //q 和r 为两个子序列的起始位置
while(q!=e1->next&&r!=e2->next)
{
if(q->data<r->data) //选择关键字较小的那个结点接在p 的后面
{
p->next=q;p=q;
q=q->next;
}
else
{
p->next=r;p=r;
r=r->next;
}
}//while
while(q!=e1->next) //接上剩余部分
{
p->next=q;p=q;
q=q->next;
}
while(r!=e2->next)
{
p->next=r;p=r;
r=r->next;
}
}//LinkedList_Merge
10.38
第 119 页 共 124 页
void LinkedList_Merge_Sort2(LinkedList &L)//初始归并段为最大有序子序列的归并排序,采
数据结构试卷 数据结构试题库集及答案
{
LNode *end[MAXSIZE]; //设立一个数组来存储各有序子序列的尾指针
for(p=L->next->next,i=0;p;p=p->next) //求各有序子序列的尾指针
if(!p->next||p->data>p->next->data) end[i++]=p;
while(end[0]->next) //当不止一个子序列时进行两两归并
{
j=0;k=0; //j:当前子序列尾指针存储位置;k:归并后的子序列尾指针存储位置
for(p=L->next,e2=p;p->next;p=e2) //两两归并所有子序列
{
e1=end[j];e2=end[j+1]; //确定两个子序列
if(e1->next) LinkedList_Merge(L,p,e1,e2); //归并
end[k++]=e2; //用新序列的尾指针取代原来的尾指针
j+=2; //转到后面两个子序列
}
严蔚敏《数据结构习题集》解答
}//while
}//LinkedList_Merge_Sort2
第 120 页 共 124 页
void LinkedList_Merge(LinkedList &L,LNode *p,LNode *e1,LNode *e2)//对链表上的子序列进 行归并,第一个子序列是从p->next 到e1,第二个是从e1->next 到e2
{
q=p->next;r=e1->next;
while(q!=e1->next&&r!=e2->next)
{
if(q->data<r->data)
{
p->next=q;p=q;
q=q->next;
}
else
{
p->next=r;p=r;
r=r->next;
}
}//while
while(q!=e1->next)
{
p->next=q;p=q;
q=q->next;
}
while(r!=e2->next)
{
p->next=r;p=r;
r=r->next;
}
}//LinkedList_Merge,与上一题完全相同
数据结构试卷 数据结构试题库集及答案
void SL_Merge(int a[ ],int l1,int l2)//把长度分别为l1,l2 且l1^2<(l1+l2)的两个有序子序列归并 为有序序列
{
start1=0;start2=l1; //分别表示序列1 和序列2 的剩余未归并部分的起始位置
for(i=0;i<l1;i++) //插入第i 个元素
{
for(j=start2;j<l1+l2&&a[j]<a[start1+i];j++); //寻找插入位置
k=j-start2; //k 为要向右循环移动的位数
RSh(a,start1,j-1,k);//将a[start1]到a[j-1]之间的子序列循环右移k 位
start1+=k+1;
start2=j; //修改两序列尚未归并部分的起始位置
}
}//SL_Merge
严蔚敏《数据结构习题集》解答
第 121 页 共 124 页
void RSh(int a[ ],int start,int end,int k)//将a[start]到a[end]之间的子序列循环右移k 位,算法原 理参见5.18
{
len=end-start+1;
for(i=1;i<=k;i++)
if(len%i==0&&k%i==0) p=i; //求len 和k 的最大公约数p
for(i=0;i<p;i++) //对p 个循环链分别进行右移
{
j=start+i;l=start+(i+k)%len;temp=a[j];
while(l!=start+i)
{
a[j]=temp;
temp=a[l];
a[l]=a[j];
j=l;l=start+(j-start+k)%len; //依次向右移
}
a[start+i]=temp;
}//for
}//RSh
10.40
书后给出的解题思路在表述上存在问题,无法理解.比如说,"把第一个序列划分为两个子序列, 使其中的第一个子序列含有s1 个记录,0<=s1<s,第二个子序列有s 个记录."可是题目中并没有 说明,第一个序列的长度<2s.请会做的朋友提供解法.
10.41
void Hash_Sort(int a[ ])//对1000 个关键字为四位整数的记录进行排序
{
int b[10000];
for(i=0;i<1000;i++) //直接按关键字散列
{
for(j=a[i];b[j];j=(j+1)%10000);
b[j]=a[i];
数据结构试卷 数据结构试题库集及答案
for(i=0,j=0;i<1000;j++) //将散列收回a 中
if(b[j])
{
for(x=b[j],k=j;b[k];k=(k+1)%10000)
if(b[k]==x)
{
a[i++]=x;
b[k]=0;
}
}//if
}//Hash_Sort
10.42
严蔚敏《数据结构习题集》解答
typedef struct {
int gt; //大于该记录的个数
int lt; //小于该记录的个数
} place; //整个序列中比某个关键字大或小的记录个数 int Get_Mid(int a[ ],int n)//求一个序列的中值记录的位置
{
place b[MAXSIZE];
for(i=0;i<n;i++) //对每一个元素统计比它大和比它小的元素个数gt 和lt for(j=0;j<n;j++)
{
if(a[j]>a[i]) b[i].gt++;
else if(a[j]<a[i]) b[i].lt++;
}
mid=0;
min_dif=abs(b[0].gt-b[0].lt);
for(i=0;i<n;i++) //找出gt 值与lt 值最接近的元素,即为中值记录
if(abs(b[i].gt-b[i].lt)<min_dif) mid=i;
return mid;
}//Get_Mid
10.43
void Count_Sort(int a[ ],int n)//计数排序算法
{
int c[MAXSIZE];
for(i=0;i<n;i++) //对每一个元素
{
for(j=0,count=0;j<n;j++) //统计关键字比它小的元素个数
if(a[j]<a[i]) count++:
c[i]=count;
}
for(i=0;i<n;i++) //依次求出关键字最小,第二小,...,最大的记录
{
min=0;
for(j=0;j<n;j++)
数据结构试卷 数据结构试题库集及答案
a[i]<->a[min]; //与第i 个记录交换
c[min]=INFINITY; //修改该记录的c 值为无穷大以便下一次选取
}
}//Count_Sort
10.44
第 122 页 共 124 页
void Enum_Sort(int a[ ],int n)//对关键字只能取v 到w 之间任意整数的序列进行排序 {
int number[w+1],pos[w+1];
for(i=0;i<n;i++) number[a[i]]++; //计数
for(pos[0]=0,i=1;i<n;i++)
严蔚敏《数据结构习题集》解答
第 123 页 共 124 页
pos[i]=pos[i-1]+num[i]; //pos 数组可以把关键字的值映射为元素在排好的序列中的位置 for(i=0;i<n;i++) //构造有序数组c
c[pos[a[i]]++]=a[i];
for(i=0;i<n;i++)
a[i]=c[i];
}//Enum_Sort
分析:本算法参考了第五章三元组稀疏矩阵转置的算法思想,其中的pos 数组和那里的cpot 数 组起的是相类似的作用.
10.45
typedef enum {0,1,2,3,4,5,6,7,8,9} digit; //个位数类型
typedef digit[3] num; //3 位自然数类型,假设低位存储在低下标,高位存储在高下标
void Enum_Radix_Sort(num a[ ],int n)//利用计数实现基数排序,其中关键字为3 位自然数,共有 n 个自然数
{
int number ,pos ;
num c[MAXSIZE];
for(j=0;j<3;j++) //依次对个位,十位和百位排序
{
for(i=0;i<n;i++) number[a[i][j]]++; //计数
for(pos[0]=0,i=1;i<n;i++)
pos[i]=pos[i-1]+num[i]; //把关键字的值映射为元素在排好的序列中的位置
for(i=0;i<n;i++) //构造有序数组c
c[pos[a[i][j]]++]=a[i];
for(i=0;i<n;i++)
a[i]=c[i];
}//for
}//Enum_Radix_Sort
分析:计数排序是一种稳定的排序方法.正因为如此,它才能够被用来实现基数排序. 10.46
typedef struct {
int key;
int pos;
} Shadow; //影子序列的记录类型
数据结构试卷 数据结构试题库集及答案
入a 中,不移动元素
{
Shadow d[MAXSIZE];
for(i=0;i<n;i++) //生成影子序列
{
d[i].key=b[i].key;
d[i].pos=i;
}
for(i=n-1,change=1;i>1&&change;i--) //对影子序列执行冒泡排序
{
严蔚敏《数据结构习题集》解答
change=0;
for(j=0;j<i;j++)
if(d[j].key>d[j+1].key)
{
d[j]<->d[j+1];
change=1;
}
}//for
for(i=0;i<n;i++) //按照影子序列里记录的原来位置复制原序列
a[i]=b[d[i].pos];
}//Shadow_Sort
第 124 页 共 124 页
三 : 第二章 80C51的结构和原理习题及答案32
第二章 80C51的结构和原理习题及答案
1、80C514单片机在功能上、工艺上、程序存储器的配置上有哪些种类? 答:80C51单片机在功能上有两种大类:(1)、基本型;(2)、增强型;
80C51单片机在生产工艺上有两种:(1)、HMOS工艺(即高密度短沟道MOS工艺);(2)、CHMOS工艺(即互补金属氧化物的HMOS工艺);
80C51单片机在程序存储器的配置上有三种形式:(1)、掩膜ROM;(2)、EPROM;
(3)、ROMLess(无片内程序存储器)。
2、80C51单片机存储器的组织采用何种结构?存储器地址空间如何划分?各地址空间的地址范围和容量如何?在使用上有何特点?
答: 80C51单片机存储器的组织采用哈佛结构:存储器在物理上设计成程序存储器和数据存储器两个独立的空间。
基本型单片机片内程序存储器容量为4KB,地址范围是0000H~0FFFH。增强型单片机片内程序存储器容量为8KB,地址范围是0000H~0FFFH。
基本型单片机片内数据存储器均为128字节,地址范围是00H~7FH,用于存放运算的中间结果、暂存数据和数据缓冲。这128字节的低32个单元用作工作寄存器,在20H~2FH共16个单元是位寻址区,然后是80个单元的他通用数据缓冲区。
增强型单片机片内数据存储器为256字节,地址范围是00H~FFH。低128字节的配置情况与基本型单片机相同,高128字节为一般RAM,仅能采用寄存器间接寻址方式访问(而与该地址范围重叠的SFR空间采用直接寻址方式访问)。
3、80C51单片机的P0~P3口在结构上有何不同?在使用上有何特点?
答: 80C51单片机各口均由接口锁存器、输出驱动器和输入缓冲器组成,但是结构存在差异:P0、P1口有转换开关MUX,P2、P3口没有;P1~P3口都有上来电阻,但是P0没有。
4个I/O口的使用特点:
(1)、P0:P0口是一个多功能的8位口,可按字节访问也可以按位访问。用做通用的I/O口,相当于一个真正的双向口:输出锁存,输入缓冲,但输入是须先将口置1;每根口线可以独立定义输入或输出。用作地址/数据复用总线:作数据总线用时,输入/输出8位数据D0~D7;作地址总线用时,输出低8位地址A0~A7。
(2)、P1:P1口惟一的单功能口,仅能用作通用的I/O口。可按字节访问也可以按位访问,输入时需先输出1,将该口设为输入状态。
(3)、P2:P2口是一个多功能8位口,可按字节访问也可以按位访问。在单片机采用并行扩展方式时,P2口作为地址总线的高8位D8~D15。
(4)、P3:P3口是一个双功能8位口,可按字节访问也可以按位访问。除作I/O口使用(位准双向口)外,每一条接口线还具有不同的第二功能:
P3.0:RXD(串行口输入);
P3.1:TXD(串行口的输出);
P3.2:INT0’(外部中断0输入);
P3.3:INT1’(外部中断0输入);
P3.4:T0(定时/计数器0的外部输入);
P3.5:T1(定时/计数器1的外部输入);
P3.6:WR’(片外数据存储器“写”选通控制输出,输出,低电平有效); P3.7:RD’( 片外数据存储器“读”选通控制输出,输出,低电平有效)。
4、如果80C51单片机晶振频率为12MHz,时钟周期、机器周期为多少?
答:根据“一个机器周期包含12个晶荡周期或6个时钟周期”得,时钟周期是1/6us,机器周期是1us。
5、80C51单片机复位后的状态如何?复位方法有几种?
答:80C51单片机复位后的状态:单片机的复位操作使单片机进入初始化状态,PC=0000H,程序从0000H地址单元开始执行。特殊功能寄存器复位后的状态是确定的。P0~P3=FFH,PSW=00H,SFR=00H,SP=07H,SBUF不定,IP、IE和PCON的有效位为0。
6、80C51单片机的片内、片外存储器如何选择?
答:80C51单片机的EA’引脚为访问内部和外部程序存储器的选择端。
程序存储器ROM:其内部容量4KB,指令可直接访问;当容量不足时,可扩展到片外ROM,此时容量可达到64KB,但此时要注意设置EA’=0;相反,当选择片内ROM时,设置EA’=1.
数据存储器RAM:内部容量128字节,指令丰富,当要对片外RAM访问时使用指令MOVX,此时读写信号都有效,但是片外RAM不能进行堆栈操作;而访问片内RAM使用MOV指令,无读写信号产生。
7、80C51单片机的PSW寄存器各位标志的意义如何?
答:程序状态字寄存器PSW,8位,其各位含意:
CY:进位、借位标志。有进位、借位时CY=1,否则CY=0 ;
AC:辅助进位、借位标志。当进行加法或减法运算时,若低4位向高4位发生进位(或借位)时,AC将被硬件置位;否则,被清除;
F0:用户标志。开机时该位为0,用户可以根据需要,通过操作指令将F0置1或者清0;当CPU执行对F0位测试条件转移指令时,根据F0的状态实现分支转移,相当于“软开关”;
RS1、RS0:当前工作寄存器组选择位,用于设定当前寄存器的组号; OV:溢出标志位。有溢出时OV=1,否则OV=0;
P:奇偶标志位。存累加器A的运算结果有奇数个1时P=1,否则P=0;在串行通信中,常以传送奇偶检验位来检验数据的可靠性。
8、80C51单片机的当前工作寄存器组如何选择?
答:当前工作寄存器组的选择由特殊功能寄存器中的程序状态字寄存器PSW的RS1、RS0来决定。可以对这两位进行编程,以选择不同的工作寄存器组。工作寄存器组与RS1、RS0的关系及地址如表2.2所示。
当某一时刻,只能选用一个寄存器组。可以通过软件对程序状态字寄存器PSW中RS1、RS0位的设置来实现。设置RS1、RS0时,可以对PSW采用字节寻址方式,也可以采用位寻址方式,间接或直接修改RS1、RS0的内容。
9、80C51单片机的控制总线信号有哪些?各信号的作用如何?
答:控制总线:
(1) 复位信号。使单片机进入初始化状态。
(2) ALE信号,在访问片外程序存储器期间,下降沿用于控制锁存P0口输出
的低8位地址;在不访问片外程序期间,可作为对外输出的时钟脉冲或用于定时目的。
(3) PSEN信号,片外程序存储器读选通信号输出端,低电平有效。在从外部
程序存储器读取指令或常数期间,每个机器周期该信号有效两次,通过数据总线P0口读回指令或常数。在访问片外数据存储器期间,该信号不出现。
(4) EA, EA为片外程序存储器选用端,该引脚为低电平时,选用片外程序存
储器,高电平或悬空时选用片外程序存储器。
(5) 另外还有第二功能下的P3口。
10、80C51单片机的程序存储器低端的几个特殊单元的用途如何?
答:80C51单片机的程序存储器低端的特殊单元的用途:
0000H:单片机复位后的入口地址;
0003H:外部中断0的中断服务程序入口地址;
000BH:定时/计数器0溢出中断服务程序入口地址;
0013H:外部中断1的中断服务程序入口地址;
001BH:定时/计数器1溢出中断服务程序入口地址;
0023H:串行接口的中断服务程序入口地址;
002BH:定时/计时器2溢出或T2EX负跳变中断服务程序入口地址(增强型单片机)。
由于每个中断入口之间的间隔进位8个地址单元,所以在程序设计时,通常在这些中断入口处设置一条无条件转移指令,使之转向对应的中断服务子程序处执行。
四 : mid文件的数据结构以及提取音轨保存为独立文件的vb源代码
mid文件的数据结构
提示
1.要想彻底弄懂本文的内容,必须具备基础的乐理知识。
2.关键词:音轨、通道、MIDI事件、MIDI命令、时间差、瞬时。
一、概述
MIDI是英语 Music Instrument Digital Interface的缩写,中译为"数字化乐器接口",也就是说它的真正涵义是1个供不同设备进行信号传输的接口。
mid文件和常见的mp3文件的本质是完全不同的。mp3文件是把声音的模拟信号经过取样→量化处理→压缩处理,转变成与声音波形对应的数字信号,播放时,这些数字信号转化为音频流。MIDI文件不是直接记录乐器的发音,而是记录演奏乐器的各种信息或指令,如使用哪1种乐器,什么时候按某个键,力度怎么样,还有颤音、滑音、发音的方位(在左边还是右边)等等一系列复杂的信息都是可以用数字来表示的,播放时,这些数字信号转化为控制信息流,控制信息流通过播放软件转换为声音。因此MIDI文件通常比声音文件小得多。mid文件只记录演奏乐器的信息,不能记录歌手的声音。
mid文件不但可以播放,甚至可以把MIDI音乐转变成看的见的乐谱并打印出来,这即可用于音乐教学,尤其是识谱。
mid文件基本上由2大部分组成:文件头和音轨块。文件头用来描述文件格式、音轨数量等。音轨存储音符集和其它信息的数据,音符集、乐谱、文本等等,都可以分配1个音轨。
二.文件头
文件头的结构:4D 54 68 64 00 00 00 06 ff ff nn nn dd dd
前四个字节是"MThd"的ASCII码。
接着的四个字节是后面三个参数部分的长度,它≡6。注意:在MIDI文件中,有关长度、大小的数值,都是采用高位在前的方式。
参数一:ff ff,其值表示文件格式,有三种格式:
=0:单音轨
=1:同步多音轨
=2:异步多音轨
单轨,很显然就只有1个轨道。
同步多音轨表明这些音轨都在同一时间开始。这种格式的第一个音轨是全局音轨,专用于设置全局性的参数,所以这种文件至少有两个音轨。
异步多音轨表明这些音轨可以不同时开始。
参数二:nn nn,是音轨数量。
参数三:dd dd,如果第1字节最高位=0,那么表示每秒=多少个瞬时(tick),默认=120,即16进制的0078。瞬时是MIDI文件中的最小时间单位,1瞬时=多少微秒呢?1瞬时=每秒微秒数÷每秒瞬时数,默认1瞬时=1000000÷120=8333微秒。很多文章说这个参数表示每个四分音符=多少个瞬时,这是错误的,笔者用反证法来说明:如果那些文章说得对,那么这个参数值越大音乐节奏越慢,而事实上,这个值越大音乐节奏越快。
如果参数三第1字节最高位=1,那么这个参数表示的意义就不同了,这时候,参数的0—7位(也就是参数的第2字节)表示每个SMTPE帧=多少瞬时。8—14位表示每秒=多少个SMTPE帧。这个值越大音乐节奏越快。注:SMTPE帧是个什么东东,笔者找不到这方面的解释。
三、音轨块
文件头之后的文件部分是音轨块,音轨块是若干个音轨的集合。每个音轨由1个音轨头和若干个MIDI事件组成。
对于同步多音轨的MIDI文件来说,一般在文件头之后的第1个音轨是全局音轨,对其它音轨都起作用的参数在这里设置,例如标题和版权、歌曲速度和系统信息码等。全局音轨后面才是各种乐器或声部的音轨。通常都是1种乐器或1个声部占用1个音轨。这种音轨又叫为1个通道,通道可以放在任意音轨(例如通道4,可以放在第1音轨或者第4音轨或者第16音轨)。MIDI可以同时演奏十六种乐器,也就是可以同时开通十六个通道(能同时开通的音轨就不止十六个了),第10通道是专为打击乐设定的。每个通道内的乐器都可以同时发几个音,组成和弦。当然,用户也可以自行增加音轨,这只要简单地把制作好的音轨数据追加在最后1个音轨的后面即可了,不过不要忘记更改文件头中的音轨数。
对于单音轨的MIDI文件来说,1个音轨可以包含两个以上的通道。
MIDI文件可以表现出1二十八种乐器音色和7两种打击乐音色,这些音色都是以编号的形式在文件中出现的。音色名称及对应编号见表7、表8、表9。
1.音轨头的结构:4D 54 72 6B xx xx xx xx
前四个字节是"MTrk"的ASCII码,接着的四个字节是音轨的长度(不包括音轨头本身8字节)。
2.MIDI事件的结构:
在音轨头之下是MIDI事件的集合。事件可分为音符事件、元事件、控制器事件和系统信息事件几大类。这些事件中,元事件、控制器事件和系统事件一般排列在音轨的前面,例如给音轨设置初始乐器和音量,这些事件通常是时间差=00的控制事件。而音符事件就排列在音轨后面了。
MIDI事件由时间差和MIDI命令组成。1个MIDI事件中一般只含有1个MIDI命令。
时间差(delta-time,有的文章称为时间片)表示相邻2个MIDI事件的间隔时间,时间差的单位是瞬时。时间差的计算有点复杂,详见后文“四、时间差的计算”
音符事件的MIDI命令由命令码和参数组成。命令码是1个最高位为1的字节,但是命令码只占用了这个字节的高4位,低4位是将被执行命令的通道号,所以也可以说,音符事件的MIDI命令是由命令码、通道号和参数三部分组成。
音符事件的格式是:时间差+命令码+参数。命令码及参数见表1。
表1 音符事件的命令码及参数
-----------------------------------------------------------------------------------
命令码 参数 描述
-----------------------------------------------------------------------------------
8x nn vv 关闭声音设备,nn=音名编号,vv=音符力度
9x nn vv 打开声音设备,参数同上
Ax nn vv 对已产生的声音连续演奏,nn=音名编号,vv=新力度
Bx cc vv 某个控制器的控制值发生变化时发出,cc=控制器编号,vv=控制值
Cx pp音色变化信息,音色被改变时发出,pp=新的音色号。注意,只有1个参数
Dx cc通道力度信息,通道的压力发生变化时发出,cc=新力度。注意,只有1个参数
Ex tt bb 滑音信息,该信息由1个二进制数的14位(www.61k.com]描述,tt=14位数的高7位,bb=低7位
-----------------------------------------------------------------------------------
说明:
①命令码中的x表示通道号。例如:90表示0通道开放声音。
②所有参数都只有1个字节,其值均≤7F(但Ex命令是把2字节作为1个14位二进制数)。
③在9x命令之后,即可写入音符了。MIDI规定,若连续向同一通道上发送多个音符,只需要一个命令码,但是时间差必不可少。例如:0091 63 40 3C 6540,表示通道1连续演奏两个音符63和65,3C是音符65的时间差。当力度=0时,表示停止声音,但不关闭设备,如:0091 63 40 3C 63 00,最后三个字节表示在3C个瞬时后,停止63音符,没关设备,还可以在后面接续音符代码。
④Bx命令是向MIDI控制器发出指令。共有1二十八个MIDI控制器。控制器名称及对应的编号见表10。
⑤Dx命令:当有一些对力度敏感的键盘不支持上面提到的复音被触发后,可以通过发送这个信息,用以表示当前所有被按下的键中力度最大的单个键的力度信息,
⑥如果使用了非音符命令(如Bx),而后面还有音符事件时,则必须重新使用9x命令。
⑦Ex命令每滑1个半音,对应值为128,比如要滑八度音阶(共十二个半音),其值=12×128。滑音又分上滑音、下滑音,滑音的乐理范围是-8192-8191,上滑音值为正,下滑音值为负,但是用参数表示却都是正数。参数计算方法是用滑音值减去(-8192),然后用mod(求余数)计算出14位二进制的高7位,用div(求商的整数)计算出14位二进制的低7位。当参数的两个字节组成的二进制数的最高位=1,是上滑音,最高位=0,是下滑音。比如要设置滑音为中值0,则应该是0-(-8192)=8192,8192才是参数。8192的14位双字节表示成8192 mod 128=00H;8192 div 128=40H。如果通道号=6,那么代码为 00 E6 0040。由于滑音控制器的原因,滑音的范围实际上最多滑1个全音,也就是两个半音。滑音需要三个控制器:⑴滑音时间,5号控制器,数值=0—7F,数值越大滑音时间越长;⑵滑音开关,45号控制器,数值=0或7F,0为关,7F为开;⑶滑音的起始音,54号控制器,数值=音符编号,最终变化音的力度值决定滑音的持续音量。
3.元事件的结构
MIDI事件根据性质可分为通道信息和系统信息2类。通道信息用于控制器的声音产生与设定,表2所列的命令就属于通道信息。下面讲的元事件却是属于系统信息类别。对事件的不同划分在于它们的控制指令不同。
元事件(meta-event)是1种有点特殊的MIDI事件,它的特殊表现在:
①普通MIDI事件的命令码都是一个字节,而元事件的命令码是两个字节,第1字节是标识符FF,第2字节是命令码。
②普通MIDI事件的命令码中包含通道号,而元事件的命令码中没有通道号。正因为没有通道号,所以全局性的命令只能放在全局音轨(单音轨除外),而针对某个音轨的命令才能放在该音轨。
③普通MIDI事件中命令的参数长度是1个字节,且最高位均为0。而元事件命令参数长度可以大于1字节,且参数的最高位可以为1。
④由于元事件命令参数可以多于1字节,所以,元事件命令后面紧接跟着1个长度参数(长度参数本身是1个字节),指明后面参数的总长度(字节数)。
元事件用于设置歌曲的速度和节拍等基本信息。元事件的格式也是由时间差和命令码、参数三部分构成,常用的命令码及参数见表2。
表2 元事件常用的命令码及参数
-------------------------------------------------------------------------------------
命令码 参数 描述
-------------------------------------------------------------------------------------
00 02 ssss ssss=音轨序号
01 nn tt... 注释文本,nn=文本长度,tt=文本字符
02 nn tt... 版权信息,只用于第一个音轨中,参数同注释文本
03 nn tt... 歌曲标题或者音轨名,参数同注释信息
04 nn tt... 所在音轨使用的乐器名称,参数同注释信息
05 nn tt... 歌词,参数同注释信息
06 nn tt... 标记,参数同注释信息
07 nn tt... 提示,参数同注释文本
20 01 cc 通道前缀,cc=通道号(0—F)
21 未知
2F 00 音轨结束命令,必须用在每个音轨的结尾
51 03 tt tt tt 节拍速度,单位:微秒,它表示一拍=多少微秒
54 hh mm ss fr SMTPE偏移量,描述音轨开始时的SMTPE时间,参数:时/分/秒/SMTPE帧
58 04 nn dd cc bb 节拍设定
59 02 sf mi 音调设定
7F xx dd... 音序器描述,xx=被发送的字节数,dd=八位二进制数据
-------------------------------------------------------------------------------------
说明:
①00命令只能产生在第1个音轨的非零时刻之前。此命令在同步多音轨文件中,必须产生在全局音轨。此命令在异步多音轨文件中,用于识别每个音轨,如果忽略,这个序列号就用音轨出现的次序表示。
②06命令标记有意义的点(如:“诗篇1”),通常用于单独音轨或同步多音轨的第一个音轨。
③07命令用来提示场景中发生的事情,如:“幕布升起”、“退出”、“台左”等等。
④20命令关联紧跟的元事件和系统专用事件的MIDI通道,直到下1个包含通道信息的MIDI事件。
⑤51命令也意味着歌曲节奏的改变。节拍速度缺省值=07A120=0.5秒,相当于每分钟120拍。每分钟节拍数=1分钟的微秒数÷节拍速度。
⑥54命令必须产生在非零元事件之前,且在第1个事件之前。在同步多音轨的MIDI文件中,必须放在全局音轨中设置。
⑦58命令中,nn=分子(每小节多少拍)。dd=分母(几分音符为一拍),例如:0=全音符,1=二分音符,2=四分音符,3=八分音符……。cc=MIDI时钟拍包含的瞬时数目,通常=24(10进制的32)。bb==1个四分音符包含多少个MIDI时钟拍,标准数为8。
⑧59命令中,sf=升(降)调记号,其最高位=0为升调,=1为降调,低7位表示升(降)几个半音。sf=0为基准C大调,例如:在五线谱上A大调有三个升号,所以sf=03,而F大调有一个降号,所以sf=81。mi=大(小)调记号,mi=00为大调,mi=01为小调。关于简谱与五线谱的调号对应详见表5、表6。
⑨7F命令是系统高级事件,表示制造商音序器统一化的描述。数据必须以制造商ID打头。
4.系统消息事件的结构
系统消息应用于整个系统而不是特定通道,不含有通道码。
系统消息事件也是1种特殊的MIDI事件,它控制整个系统的消息,通常用于控制midi键盘。常用消息码见表3。
表3 常用系统消息码
------------------------------------------------------------
消息码 参数 描述
------------------------------------------------------------
F0 ii xx...ii=厂商标识号ID,00-7F,xx...=任意字节厂商信息
F1 未定义
F2 cc dd 歌曲位道指针,cc=位道低字节,dd=位道高字节
F3 cc 歌曲选择,cc=歌曲号
F4、F5 未定义
F6 旋律请求
F7 系统消息的结束标记
F8 用于同步整个系统的计时器
F9 未定义
FA 启动当前的序列
FB 从停止的地方继续1个序列
FC 停止1个序列
FD 未定义
FE 活动检测
FF 系统复位
-------------------------------------------------------
说明:
①F0为专用消息,F1-F7为公共消息,F8-FF为实时消息
②F0命令还有1种用法,其格式与元事件的格式相同:时间差+命令码+参数,例如XG的复位码是:00 F0 08 43 10 4C00 00 7E 00 F7,其中第1个00是时间差,F0是系统码,08是参数长度,F7是结束标记。
③几个F0命令不能写在1个事件中,如果存在F0命令集,可以分成几个事件。例如:00 F0 0D 43 10 4C 00 00 7E00 F7 F0 AA BB CC F7
内含两个F0命令,可以分成两个事件:00 F0 08 43 10 4C 00 00 7E 00 F700 F0 04 AA BBCC F7"
④F0码可以写在任何音轨,不过一般会把歌曲播放前发送的系统码写在全局音轨中,并把时间差设为0。
⑤笔者在一篇文章看到,F7命令也可以带两个参数:数据长度和数据。例一:停止1个序列用:F7 01 FC,继续1个序列用:F7 01FB,其中的01就是表示F7命令发送的数据为一个字节,而FC、FB这2个命令就是被发送的数据。例二:向1个外部设备发送1个“停止”命令,间隔4八个瞬时后再发送“继续”命令:00F7 01 FC 30 F7 01FB。这种形式与例一的性质相同,不过在F7命令之前加上了时间差。最前的00是第1个F7命令的时间差,30是第二个F7命令的时间差,表示相隔48瞬时。
5.音名编号
在一条MIDI命令的后面,可以跟着另一条MIDI命令,也可以跟着音乐的音符。在MIDI文件中,每个音符都是用音名的对应编号来表示的,例如:中央C的编号=3C。八度音阶与音名相对应的编号见表4。
表4 八度音阶与音名相对应的编号
-----------------------------------------------------
音阶| CC# DD# EF F#G G#A A# B
-----------------------------------------------------
C0 | 0001 02 0304 05 0607 08 090A 0B
C1 | 0C0D 0E 0F10 11 1213 14 1516 17
C2 | 1819 1A 1B1C 1D 1E1F 20 2122 23
C3 | 2425 26 2728 29 2A2B 2C 2D2E 2F
C4 | 3031 32 3334 35 3637 38 393A 3B
C5 | 3C3D 3E 3F40 41 4243 44 4546 47
C6 | 4849 4A 4B4C 4D 4E4F 50 5152 53
C7 | 5455 56 5758 59 5A5B 5C 5D5E 5F
C8 | 6061 62 6364 65 6667 68 696A 6B
C9 | 6C6D 6E 6F70 71 7273 74 7576 77
C10 | 78 797A 7B 7C7D 7E 7F
-----------------------------------------------------
说明:
①C5在乐理中称为"中央C"。
②五线谱中的升号(#)及降号(b)与调号的对应关系见表5
③普通钢琴的最低音是15号音,最高音是6C号音。
表5 升、降号与调号的对应关系
--------------------------------------
#数 0 1 2 3 4 5 6 7
调号 C G D A E B #F #C
b数 0 1 2 3 4 5 6 7
调号 C F bB bE bA bD bG bC
--------------------------------------
说明:例如:两个升号是D大调(简谱记为:1=D),两个降号是降B大调(简谱记为:1=bB)。
6.简谱的唱名与音名编号
为了方便不懂五线谱的初学者,笔者特地把简谱各大调的唱名与音名的编号一一对应列表(3个八度,应付一般的歌曲应该够了),为在解析MIDI文件或自己编写MIDI代码时提供参考,见表6。
表6 简谱大调唱名与音名的编号对应表
----------------------------------------------------------------------
音域 ┌───低音───┐ ┌───中音───┐┌───高音───┐
唱名 1 2 34 5 67 1 23 4 56 7 12 3 45 6 7
----------------------------------------------------------------------
C调 30 32 34 35 37 39 3B 3C 3E 40 41 43 45 47 48 4A 4C 4D 4F 5153
D调 32 34 36 37 39 3B 3D 3E 40 42 43 45 47 49 4A 4C 4E 4F 51 5355
E调 34 36 38 39 3B 3D 3F 40 42 44 45 47 49 4B 4C 4E 50 51 53 5557
F调 35 37 39 3A 3C 3E 40 41 43 45 46 48 4A 4C 4D 4F 51 52 54 5658
G调 37 39 3B 3C 3E 40 42 43 45 47 48 4A 4C 4E 4F 51 53 54 56 585A
A调 39 3B 3D 3E 40 42 44 45 47 49 4A 4C 4E 50 51 53 55 56 58 5A5C
B调 2F 31 33 34 36 38 3A 3B 3D 3F 40 42 44 46 47 49 4B 4C 4E 5052
----------------------------------------------------------------------
说明:例如简谱1=D,就看D调那一行的编号,1=A,就看A调那一行的编号。
表7 1二十八种乐器音色名称及对应编号
------------------------------------------------------------------------------------------
编号 音色名 编号 音色名 编号 音色名 编号 音色名 编号 音色名
------------------------------------------------------------------------------------------
00 原声钢琴 01 明亮大钢琴 02 电声钢琴 03 酒吧钢琴 04 电钢琴1
05 电钢琴2 06 拨弦古钢琴 07 击弦古钢琴 08 钢片琴 09 钟琴
0A 八音琴 0B 颤音琴 0C 马林巴 0D 木琴 0E 管钟
0F 大扬琴 10 拉杆风琴 11 节奏风琴 12 摇滚风琴 13 教堂风琴
14 簧风琴 15 手风琴 16 口琴 17 探戈手风琴 18 尼龙弦木吉它
19 金属弦木吉它 1A 爵士电吉它 1B 滑音电吉它 1C 闷音电吉它 1D 过载
1E 失真 1F 合唱 20 声学贝司 21 指弹贝司 22 拨片电贝司
23 无品贝司 24 击弦贝司1 25 击弦贝司2 26 合成贝司1 27 合成贝司2
28 小提琴 29 中提琴 2A 大提琴 2B 倍大提琴 2C 弦乐震音
2D 弦乐拨奏 2E 管弦乐竖琴 2F 定音鼓 30 弦乐合奏1 31 弦乐合奏2
32 合成弦乐1 33 合成弦乐2 34 合唱“啊” 35 人声“噢” 36 合成人声合唱
37 管弦乐强奏 38 小号 39 长号 3A 大号 3B 弱音小号
3C 法国号 3D 铜管合奏 3E 合成铜管1 3F 合成铜管2 40 高音萨克斯
41 次中音萨克斯 42 中音萨克斯 43 低音萨克斯 44 双簧管 45 英国管
46 大管 47 黑管 48 短笛 49 长笛 4A 竖笛
4B 排箫 4C 吹瓶声 4D 日本笛 4E 口哨声 4F 埙
50 合成方波 51 合成锯齿波 52 合成蒸汽风琴 53 合成夜莺 54 合成精灵
55 合成人声 56 合成平行五度 57 合成铜管领奏 58 新世纪音色垫 59 温暖音色垫
5A 复音音色垫 5B 合成合唱音色垫5C 弓弦音色垫 5D 金属音音色垫 5E 光环音色垫
5F 吹风音色垫 60 雨声 61 音轨 62 水晶 63 大气
64 明亮 65 诡异 66 回声 67 科幻 68 西塔尔(印度)
69 班卓琴(美洲)6A 三昧线(日本)6B 十三弦筝(日本)6C 卡林巴(非洲)6D 风笛(苏格兰)
6E 里拉提琴 6F 沙奈管 70 碰铃 71 摇摆舞铃 72 钢鼓
73 木鱼 74 太科鼓 75 旋律嗵鼓 76 合成鼓 77 反转钹
78 吉它指触杂音 79 呼吸声 7A 海浪声 7B 鸟鸣声 7C 电话铃声
7D 直升飞机声 7E 鼓掌声 7F 枪声
------------------------------------------------------------------------------------------
说明:
①有些电脑的MIDI音色可能与本表有差异,例如有的厂商用中国民族乐器的音色替代表中的某些音色。
表8 7两种打击乐音色名称及对应编号(10通道专用)
------------------------------------------------------------------------------------------
编号 音色名 编号 音色名 编号 音色名 编号 音色名 编号 音色名
------------------------------------------------------------------------------------------
11 人声 one 12 人声 Two 13 人声 Three 14 人声 four 15 人声 five
16 MC-505信号音1 17 MC-505信号音218 大乐队小军鼓 19 小军鼓滚奏 1A 响指2
1B 激光枪声 1C 合成拍音 1D 高音刷音 1E 低音刷音 1F 鼓槌
20 敲方板 21 节拍器 22 节拍器重音 23 低音大鼓 24 高音大鼓
25 鼓边 26 小鼓 27 拍手声 28 电子小鼓 29 低音落地嗵鼓
2A 合音踩镲 2B 高音落地嗵鼓 2C 踩镲 2D 低音嗵鼓 2E 开音踩镲
2F 中低音嗵鼓 30 中高音嗵鼓 31 低音镲1 32 高音嗵鼓 33 点钹1
34 中国钹 35 敲钟声 36 铃鼓 37 侧击钹 38 颈铃
39 单面钹2 3A 回响梆子 3B 敲钹2 3C 高音圆鼓 3D 低音圆鼓
3E 弱音手鼓 3F 空心手鼓 40 低音手鼓 41 高阶定音鼓 42 低阶定音鼓
43 高音碰铃 44 低音碰铃 45 沙锤 46 响葫芦 47 短哨
48 长哨 49 短音刮板 4A 长音刮板 4B 击棒 4C 高音响板
4D 低音响板 4E 弱音蟋蟀声 4F 空心蟋蟀声 50 弱音三角铁 51 空心三角铁
52 高沙锤 53 铃铛 54 铃树 55 响板 56 弱音瑟多
57 空心瑟多 58 欢呼声2
---------------------------------------------------------------------------------------
表9 打击乐器与五线谱对应表
---------------------------------------
位置 打击乐
---------------------------------------
第一线 低音鼓1
第一间 低音鼓2
第二线 不同音高的中音鼓
第二间 同上
第三线 同上
第三间 军鼓
第四线 (带×号) 轻音铜钹
第四线 不同音高的中音鼓
第四间 同上
第五线 同上
第五线 (带×号) 轻音铜钹
上加一间(带×号) 脚踏钹
上加一线 脆音铜钹
上加一间 同上
---------------------------------------
表10 控制器名称及对应编号
----------------------------------------------------------------------------------------------
编号 控制器 编号 控制器 编号 控制器 编号 控制器
----------------------------------------------------------------------------------------------
00 音色库选择 01 颤音深度粗调 02 吹管控制器粗调 03 N/A
04 踏板控制器粗调 05 连滑音速度粗调 06 高位元组数据输入 07 主音量粗调
08 平衡控制粗调 09 N/A 0A 声像调整粗调 0B 情绪控制器粗调
0C—0F N/A 10—13 一般控制器 14—1F N/A 20 插口选择
21 颤音速度微调 22 吹管控制器微调 23 N/A 24 踏板控制器微调
25 连滑音速度微调 26 低位元组数据输入 27 主音量微调 28 平衡控制微调
29 N/A 2A 声像调整微调 2B 情绪控制器微调 2C 效果FX控制1微调
2D 效果FX控制2微调 2E—3F N/A 40 延音踏板1 41 滑音
42 持续音 43 弱音踏板 44 连滑音踏板控制器 45 保持音踏板2
46 变调 47 音色 48 放音时值 49 起音时值
4A 亮音 4B—4F 声音控制 50—53 一般控制器5#—8#54 连滑音控制
55—5A N/A 5B 混响效果深度 5C 未定义的效果深度 5D 合唱效果深度
5E 未定义的效果深度 5F 移调器深度 60 数据累增 61 数据递减
62 未登记的低元组数值 63 未登记的高元组数值 64 已登记的低元组数值 65 已登记的高元组数值
66—77 N/A 78 关闭所有声音 79 关闭所有控制器 7A 本地键盘开关
7B 关闭所有音符 7C Omni模式关闭 7D Omni模式开启 7E 单音模式
7F 复音模式
----------------------------------------------------------------------------------------------
说明:
①MIDI控制器的参数变化范围都为00—7F。对于开关型的控制器,小于3F为关闭,大于40为开启,例如7A控制器,vv=00关机,vv=FF开启。而模式控制器的参数为通道号,例如7F控制器,vv=要开启复音的通道号。
②每个控制器对应于1种控制事件,但是,并不是每个编号的控制器对音源都有同样效果,还要看音源的型号。
③20—3F号控制器是为了发送提高00—1F号控制器精度的LSB数据而准备的,因为00—1F号控制器的调整效果为粗调,如果要细调,发送的参数就需要14位,这时即可利用20—3F号控制器了。
④10—13和50-53号控制器被定义为通用控制器,10—13号是两个字节,50—53号为一个字节,这些控制器号可以指定为任何控制器,用来控制内部参数。
⑤相当于踏板开关类型的控制器分布在40—5F号之间。
四、时间差的计算
时间差是1个可变长度的值,但其长度最多4字节。4字节的时间差,除了最后1个字节的最高位为0(>7F就必须进位),其余字节的最高位均为1。以下详细说明。
1.时间差长度为1字节
这个字节的最大值=7F。如果>7F,就要进位,变成2字节。
2.时间差长度为2字节
例如:时间差=B4,由于>7F,所以要用2字节表示。先确定第2字节=B4-80=34。第一个字节=81,转换成二进制就是10000001,最高位1是数值80,低7位都是进位标记,不表示数值,所以低7位的那个1表示这个字节中有一个80的一次方。进位标记可以累加,一直累加到7F,这就表示这个字节中已经有了7F个80的一次方。计算:B4=80^1×1+34。
3.时间差长度为3字节
2字节的时间差满值是FF 7F,要是再加个80,就要进位成3字节了:81 8000。这时,第1字节中的8表示80的二次方,1是进位标记,表示有一个80的二次方。要注意的是第2字节,虽然其值=0,但最高位的1不能丢:10000000,它表示有0个80的一次方。
4.时间差长度为4字节
3字节的时间差满值是FF FF 7F,要是再加个80,就要进位成4字节了:81 80 8000。这时,第1字节中的8表示80的三次方,1是进位标记,表示有一个80的三次方。注意第2、第3字节最高位的1不能丢。
例1:要表示10进制65535,可以先计算出:65535=128^2×3+128^1×127+128^0×127,然后得出结果:83 FF7F。
例2:由字节值计算出时间差,只要读到最高位=0的字节,就表示时间差结束。比如时间差有三个字节:82 C003,计算:128^2×2+128^1×64+128^0×3=40963。
提示:以上计算结果的单位是瞬时,如果要转化成微秒,那么计算结果还要乘上每瞬时的微秒数,而每瞬时的微秒数可以从文件头中的参数三计算而得。
五、实例解析
下面是MIDI钢琴曲《让我们荡起双浆》的部分代码:
-------------------------------------------------------
0000: 4D 54 68 64 00 00 00 06 00 01 00 03 00 78 4D 54
0010: 72 6B 00 00 02 45 00 FF 03 0E C8 C3 CE D2 C3 C7
0020: B5 B4 C6 F0 CB AB BD B0 00 FF 03 14 D3 B0 C6 AC
0030: A1 B6 D7 E6 B9 FA BB A8 B6 E4 A1 B7 B2 E5 C7 FA
0040: 00 FF 02 1D 43 6F 70 79 72 69 67 68 74 20 5F 20
0050: 31 39 39 38 20 62 79 20 54 61 6E 67 20 42 6F 71
0060: 69 00 FF 01 07 CC C0 B2 AE E8 BD 0A 00 FF 01 09
0070: B8 D6 C7 D9 B6 C0 D7 E0 0A 00 FF 01 0A 54 61 6E
0080: 67 20 42 6F 71 69 0A 00 FF 58 04 02 02 18 08 00
0090: FF 59 02 01 00 00 FF 51 03 09 70 3D
……
0257: 00 FF 2F 00 4D 54 72 6B 00
0260: 00 05 A6 00 FF 21 01 00 00 FF 03 0B 50 49 41 4E
0270: 4F 20 72 69 67 68 74 00 C0 00 00 B0 07 7D 00 0A
0280: 32 3C 90 40 64 3C 40 00 00 43 64 3C 43 00 00 45
0290: 64 3C 45 00 00 47 64 81 34 47 00 00 4A 64 3C 4A
02A0: 00 00 47 64 3C 47 00 00 43 64 3C 43 00 00 45 64
02B0: 78 45 00 00 40 64 81 70 40 00
……
--------------------------------------------------------
解析:
0000—000D(文件头)
4D 54 68 64:MThd
00 00 00 06:参数总长度=6字节
00 01 00 03 00 78:3条同步音轨,每秒=120瞬时
000F—025A(第1音轨,全局音轨)
4D 54 72 6B:MTrk
00 00 02 45:音轨长度=581字节(不包括音轨头)
00 FF 03 0E:设置歌曲标题,长度=14字节
C8 C3 CE D2 C3 C7 B5 B4 C6 F0 CB AB BD B0:让我们荡起双桨
00 FF 03 14:设置歌曲标题,长度=20字节
D3 B0 C6 AC A1 B6 D7 E6 B9 FA BB A8 B6 E4 A1 B7 B2 E5 C7FA:影片《祖国花朵》插曲
00 FF 02 1D:设置版权信息,长度=29字节
43 6F 70 79 72 69 67 68 74 20 5F 20 31 39 39 38 20 62 79 20 54 616E 67 20 42 6F 71 69:Copyright _ 1998 by Tang Boqi
00 FF 01 07:注释文本,长度=7字节
CC C0 B2 AE E8 BD 0A:汤伯杞(0A是换行符)
00 FF 01 09:注释文本,长度=9字节
B8 D6 C7 D9 B6 C0 D7 E0 0A:钢琴独奏(0A是换行符)
00 FF 01 0A:注释文本,长度=10字节
54 61 6E 67 20 42 6F 71 69 0A:Tang Boqi(0A是换行符)
00 FF 58 04:设置节拍,长度=4字节
02 02 18 08:每小节2拍,四分音符为一拍,每个时钟拍=24瞬时,每个四分音符包含八个时钟拍
00 FF 59 02:设置音调,长度=2字节
01 00:G大调(1=G)
00 FF 51 03:设置节拍速度,长度=3字节
09 70 3D:一拍的时长=618557微秒=618.6毫秒=0.619秒
……
00 FF 2F 00:第1音轨结束
025B—0808(第2音轨,音符音轨)
4D 54 72 6B
00 00 05 A6:音轨长=1446字节
00 FF 21 01 00:元事件21命令未知何意
00 FF 03 0B:设置音轨名,长度=11字节
50 49 41 4E 4F 20 72 69 67 68 74:PIANO right
00 C0 00:原声钢琴音色
00 B0 07 7D:0通道7#控制器(主音量控制)设置音量=7D
00 0A 32:
3C 90:3C个瞬时后(休止了半拍),0通道打开声音
40 64,3C 40 00,00 43 64,3C 43 00,00 45 64,3C 45 00:简谱 0612(力度=0的代码不必写出,下同)
00 47 64,81 34 47 00,00 4A 64,3C 4A 00:简谱 3 ˙5
00 47 64,3C 47 00 00 43 64,3C 43 00,00 45 64,78 45 00,00 40 64 8170 40 00:简谱:31 2 6 -
……
六、实例制作
下面我们自己动手,来制作1个简单的MIDI文件。我选择了歌曲《东方红》,因为该曲子既熟悉又简单,我这里只写第一句的音乐代码。
为了简单起见,尽可能采用默认值,即:C大调(1=C),四分音符为一拍,每分钟120拍,原声钢琴演奏。
《东方红》的第一句简谱是:5 56| 2 -| 1 16| 2 -|。
数据如下:
----------------------------------------------------------------------------------------
4D 54 68 64 00 00 00 06 00 00 00 01 00 78(文件头:单音轨,每秒=78瞬时)
4D 54 72 6B 00 00 00 1F(音轨头:音轨长度=1F字节)
00 90 43 64 78 43 64 3C 45 64 3C 3E 64(5 56 2 -,2后面的延长符号是由下一句的8170决定的)
81 70 3C 64 78 3C 64 3C 39 64 3C 3E 64 81 70 FF 2F 00(1 16 2-)
----------------------------------------------------------------------------------------
把这些数据复制到Hex编辑器(去掉括号内容),另存为“东方红.mid”,再点击这个文件播放,OK了!
实验1:加快节奏。
把文件头中的78改为F0(加快一倍),保存,再播放,是不是快了?
实验2:改变音色为中提琴(中提琴编号=29),代码改动一下:
------------------------------------------------------
4D 54 68 64 00 00 00 06 00 00 00 01 00 78 4D 54 72 6B
00 00 00 3A:音轨长度=3A
00 C0 29:音色=中提琴
00 90 43 64 78 43 00:打开声音设备,简谱:5(一拍)
00 43 64 3C 43 00:简谱:5(半拍)
00 45 64 3C 45 00:简谱:6(半拍)
00 3E 64 81 70 3E 00:简谱:2 -(二拍)
00 3C 64 78 3C 00:简谱:1(一拍)
00 3C 64 3C 3C 00:简谱:1(半拍)
00 39 64 3C 39 00:简谱:6(半拍,低音)
00 3E 64 81 70 3E 00:简谱:2 -(二拍)
00 FF 2F 00
------------------------------------------------------
在以上的音符代码中,每个音符经过预定的时间,都要关闭(力度=00),但发音设备不关闭。似乎除了钢琴,别的乐器都要这么写代码。
当然,如果你有兴趣,可以自己把这首曲子写完全,还可以写成同步多音轨的,再添加一些设置或信息,成为一首真正的MIDI乐曲。
七、提取1个音轨保存为1个单独的mid文件
注意三点:
1.必须是同步多音轨文件,且>两个音轨。也就是说,除了全局音轨,还必须至少有两个音符音轨。
2.一般来说,紧接着全局音轨的,是主旋律音轨,其它的音符音轨都是伴奏或副声部的。但也有一些乐曲的主旋律是各种乐器轮流担当,比方说,通道0的乐器演奏了一段时间就彻底停止,让通道1的乐器作为主旋律,由此类推……碰到这种情况,就没有提取必要了。附件中“北京的金山上.mid”就是这样的文件。
3.提取出来的mid文件中,全局音轨中那些针对其它通道的命令理论上都应删除,但这样做起来很麻烦,笔者播放了几个提取的mid文件,发现不删除那些多余的命令似乎也没有什么影响。
下面是源代码:
Option Explicit
Private Sub Command1_Click()
On Error GoTo 200
Dim DAT() As Byte, teme() As Byte, tLen1 As Long, tLen2 As Long, L1As Long, L2 As Long
Dim j1 As Long, j2 As Long, k As Long, i As Long, OpenName AsString, SaveName As String
OpenName = Text1
SaveName = Left(OpenName, Len(OpenName) - 4) & "(1).mid"
If InStr(LCase(OpenName), "mid") = 0 Then Exit Sub
ReDim DAT(FileLen(OpenName) - 1) As Byte
Open OpenName For Binary As #1
Get #1, , DAT
Close #1
If DAT(9) <> 1 Then MsgBox "不是同步多音轨MIDI文件": Exit Sub
If DAT(11) < 3 Then MsgBox "至少要有三个音轨才能提取": Exit Sub
teme = StrConv("MTrk", vbFromUnicode)
k = InStrB(DAT, teme) '查找音轨0起点(全局音轨)
tLen1 = DAT(k + 4) * 65536 + DAT(k + 5) * 256 + DAT(k + 6) +8
L1 = k - 1
k = InStrB(k + 7, DAT, teme) '查找音轨1起点
tLen2 = DAT(k + 4) * 65536 + DAT(k + 5) * 256 + DAT(k + 6) +8
L2 = k - 1
DAT(11) = 2 '修改音轨数
Open SaveName For Binary As #2
k = 0: j1 = 0: j2 = 13: GoSub 100
k = 0: j1 = L1: j2 = tLen1 - 1: GoSub 100
k = 0: j1 = L2: j2 = tLen2 - 1: GoSub 100
Close #2
MsgBox "提取完成"
Exit Sub
100
ReDim teme(j2)
For i = j1 To j2 + j1: teme(k) = DAT(i): k = k + 1: Next
Put #2, , teme
Return
200
Close
End Sub
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1