一 : 2015高三数学闸北二模 有答案
闸北区2014学年度第二学期高三数学(理科)期中练习卷
考生注意:
1. 本次测试有试题纸和答题纸,解答必须在答题纸上,写在试题纸上的解答无效.
2. 答卷前,考生务必在答题纸上将姓名、学校、考试号,以及试卷类型等填写清楚,并在规定区域内贴上条形码.
3. 本试卷共有18道试题,满分150分.考试时间120分钟.
一、填空题(60分)本大题共有10题,要求在答题纸相应题序的空格内直接填写结果,每 个空格填对得6分,否则一律得零分.
1. 设幂函数f?x?的图像经过点?8,4?,则函数f?x?的奇偶性为____________.
2. 设复数z1?2?i,z2?1?2i,在复平面的对应的向量分别为OA,OB,则向量AB对应的复数所对应的点的坐标为____________.
3. 已知定义域为R的函数y?f?x?的图像关于点??1,0?对称,y?g?x?是y?f?x?的反函数,若x1?x2?0,则g?x1??g?x2??___________.
4. 一个篮球运动员投篮一次得3分的概率为a,得2分的概率为b,不得分的概率为c,其中
a,b,c?(0,1).已知投篮一次得分的期望是2,则ab的最大值是____________.
?2n?1,1?n?2,n?N,?5. 设an??1 数列?an?的前n项和为Sn,则limSn?___________. n???n,n?3,n?N.?3
?x2?6x?6,x?0,6. 设函数f(x)??若存在互不相等的实数x1,x2,x3满足x?4,x?0.?
f(1x)?f(2x?)
nf,则(x)x1?x2?x3的取值范围是_____________. 3?7.
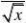
若二项式?x则这个展开式中任取一项为有理项的展开式中只有第四项的系数最大,?
概率是____________.
x2y2
2228. 从双曲线2?2?1?a?0,b?0?的左焦点F引圆x?y?a的切线,切点为T,延长ab
FT交双曲线右支于点P,若M是线段FP的中点,O为坐标原点,则MO?T的值是____________.
1
高三数学 2015高三数学闸北二模 有答案
9. 已知集合U???x,y?x?R,y?R?,M???x,y?x?y?a?,P???x,y?y?f?x??,
CUM?P,则所有满足条件的函数f?x?的编号是___________. 现给出下列函数:①y?x?a;②y?logax ;③y?sin?x?a?;④y?cosax.若0?a?1时,恒有P
10. 把正整数排列成如图?a?的三角形数阵,然后擦去第偶数行中的所有奇数、第奇数行中的所
有偶数,可得到如图?b?的三角形数阵,现将图?b?中的正整数按从小到大的顺序构成一个数列?an?,若ak?2015,则k?__________.
1 1
2 3 4 2 4
5 6 7 8 9 5 7 9
10 11 12 13 14 15 16 10 12 14 16
17 18 19 20 21 22 23 24 25 17 19 21 23 25
26 27 28 29 30 31 32 33 34 35 36 26 28 30 32 34 36 ?a? ?b?
二、选择题(15分)本大题共有3题,每题都给出四个结论,其中有且只有一个结论是正确
的,必须把答题纸上相应题序内的正确结论代号涂黑,选对得5分,否则一律得零分.
11. 下列命题中,正确的个数是???????????????????????【 】
(1) 直线上有两个点到平面的距离相等,则这条直线和这个平面平行;
(2) a、b为异面直线,则过a且与b平行的平面有且仅有一个;
(3) 直四棱柱是直平行六面体;
(4) 两相邻侧面所成角相等的棱锥是正棱锥.
A、0 B、1 C、2 D、3
12. 在极坐标系中,关于曲线C:??4sin????的下列判断中正确的是?????【 】 3?
5??A、曲线C关于直线??对称 B、曲线C关于直线??对称 63
??? C、曲线C关于点?2,?对称 D、曲线C关于极点?0,0?对称 ?3?
AC的面积与?OAB的13. 已知O是正三角形ABC内部的一点,OA?2OB?3OC?0,则?O
面积之比是???????????????????????????????【 】
A、????32 B、 C、2 D、1 23
2
高三数学 2015高三数学闸北二模 有答案
三、解答题(本题满分75分)本大题共有5题,解答下列各题必须在答题纸的规定区域(对
应的题号)内写出必要的步骤.
14. (本题满分12分,第(1)小题5分,第(2)小题7分)
如图,AB是圆柱体OO1的一条母线,已知BC过底面圆的圆心O,
D是圆O上不与点B,C重合的任意一点,AB?5,BC?5,CD?3.
(1)求直线AC与平面ABD所成角的大小;
(2)将四面体ABCD绕母线AB旋转一周,求?ACD的三边在旋
转过程中所围成的几何体的体积.
15. (本题满分13分,第(1)小题5分,第(2)小题8分)
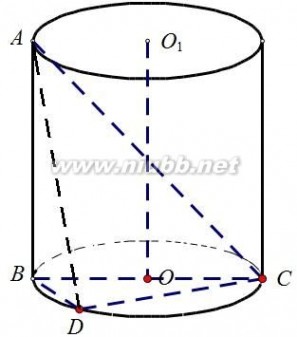
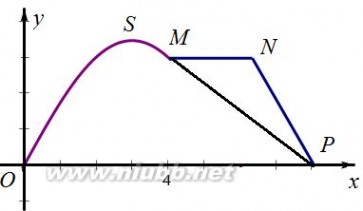
如图所示,某市拟在长为8km道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y?Asin?x?A?0,??0??x?
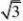
?0,4??的图像,且图像的最高点为S3,,赛道的后一部分为折线段MNP,且?MNP?120.
(1)求M、P两点间的直线距离;
(2)求折线段赛道MNP长度的最大值.
16. (本题满分14分,第(1)小题5分,第(2)小题9分)
2已知圆C1:?x?1??y?8,点C2?1,02?点Q在圆C1上运动,QC2的垂直平分线交QC1于?,
点P.
(1)求动点P的轨迹W方程;
(2)过点S?0,??且斜率为k的动直线l交曲线W于A,B两点,在y轴上是否存在定点?
?1?3?
D,使以AB为直径的圆恒过这个点?若存在,请求出点D的坐标;若不存在,请说明理由.
61阅读提醒您本文地址:
3
高三数学 2015高三数学闸北二模 有答案
17. (本题满分18分,第(1)小题4分,第(2)小题5分,第(3)小题9分)
设函数y?f?x?的定义域为D,值域为A,如果存在函数x?g?t?,使得函数y?f??g?t???的值域仍是A,那么称x?g?t?是函数y?f?x?的一个等值域变换.
(1)判断下列函数x?g?t?是不是函数y?f?x?的一个等值域变换?说明你的理由;
① f?x??log2x,x?0,x?g?t??t?,t?0;
② f?x??x2?x?1,x?R,x?g?t??2t,t?R.
(2)设函数y?f?x?的定义域为D,值域为A,函数g?t?的定义域为D1,值域为A1,
那么“D?A1”是否为“x?g?t?是y?f?x?的一个等值域变换”的一个必要条件?请说明理由; 1t
mt2?3t?n(3)设f?x??log2x的定义域为x??2,8?,已知x?g?t??是y?f?x?的2t?1
一个等值域变换,且函数y?f??g?t???的定义域为R,求实数m、n的值.
18. (本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)
我们把一系列向量ai?i?1,2,,n?按次序排成一列,称之为向量列,记作an,已知向量
1?xn?1?yn?1,xn?1?yn?1??n?2?. 2??列an满足:1??1,1?,an??xn,yn????
(1)证明:数列an是等比数列; (2)设cn?an?log2an,问数列?cn?中是否存在最小项?若存在,求出最小项;若不存
在,请说明理由;
(3)设?n表示向量an?1与an间的夹角,若b
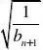
n??n2??n,对于任意正整数n
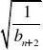
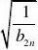
,不等式
1?loga?1?2a?恒成立,求实数a的范围.

2
4
高三数学 2015高三数学闸北二模 有答案
理科答案
一. 填空题
1、偶函数; 2、??1,1? 3、?2 4、
6、??1,6? 7、
二. 选择题
11、B 12、A 13、B
三.解答题
14、(1
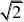
)arcsin155 5、 6184 8、b?a 9、①②④ 10、1030 7 ?????????????????????5分 10
(2)15? ????????????????????????7分
15、
解(1
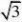
)依题意,有A? ????????????????1分 又T2???3, 而T?, ??? ?????????1分 4?6
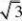
?y?six 6
2?
3?3?M?4,3 当x?
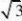
4时,y?si?,?,又P?8,0?
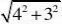
?MP?5 ???????????????3分
(2)解:法一:在?MNP中,?MNP?120,MP?5.
设?PMN??,则0???60.??????????????1分 由正弦定理得MPNPMN,?NP??,
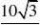
??sin120sin?sin60?
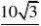
?MN??60???,????????????????????3分 ??
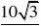
60???????60???3分
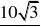
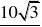
故NP?MN?5
高三数学 2015高三数学闸北二模 有答案
0???60,?当??30时,折线段赛道MNP最长为
解法二 : (2)在?MNP中,?MNP?120,MP?5.
2
2
2
.?????2分 3
由余弦定理得MN?NP?2MN?NP?COS?MNP?MP,
即MN?NP?MN?NP?25;??????????3分
2
2
32?MN?NP?
MN?NP?

25?4分 故?MN?NP??25?MNNP??,从而???42??
即MN?NP?,当且仅当MN?NP时等号成立.??????2分
3
亦即,设计为MN?NP时,折线段赛道MNP
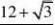
最长为.
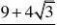
3
2
2
注:本题第(2)问答案及其呈现方式均不唯一,除了解法一、解法二给出的两种设计
方法,还可设计为:①N
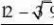
;②N
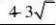
61阅读提醒您本文地址:
???
在线段MP的垂直平分线上等.
16、(1)QC2的垂直平分线交QC1于点P,?PQ?PC2.??????1分
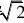
PC2?P?
③点N;?
1?
1
, C2?2C
所以动点P的轨迹W是以点C1、C2为焦点的椭圆.??????????2分
x2y

2
b2?a2?c2?1, 设椭圆的标准方程为2?2?1?a?b?0?,则2a?22c?2,
abx2
?y2?1??????????????????????2分 故椭圆的标准方程为2
y?kx?1??3,即 (2) 直线l的方程为y?kx?,联立直线和椭圆的方程得?232?x
??2
?y?1?
1
1??
9?1?2k2?x2?12kx?16?0,易知点S?0,??在椭圆内部,所以直线l与椭圆必交于两点. ?1分
3??4k16
,xx??设A?x1,y1?,B?x2,y2?,则x1?x2?,????????2分 12
31?2k291?2k2假设在y轴上存在定点D?0,m?满足题设,则DA??x1,y1?m?,DB??x2,y2?m?. 因为以AB为直径的圆恒过点D,则DA?DB??x1,y1?m???x2,y2?m??0.????????2分
11
即x1x2??y1?m??y2?m??0?*?,因为y1?kx1?,y2?kx2?,
33
所以(*)变为
1??1?11???
x1x2??y1?m??y2?m??x1x2?y1y2?m?y1?y2??m2?x1x2??kx1????kx2???m?kx1??kx2???m2
3??3?33???
222
21?18m?18?k??9m?6m?15??1?22
.???3分 ??k?1?x1x2?k??m??x?m??1x2??m?
3992k2?1?3?
6
高三数学 2015高三数学闸北二模 有答案
2??18m?18?0由假设得对于任意的k?R,DA?DB?0恒成立,即?2,解得m?1. 因此,??9m?6m?15?0
在y轴上存在点D,点D的坐标为?0,1???????????????????3分
17、(1)①不是??????????????????????????2分
1?33??3?②f?x??x?x?1??x????,即f?x?的值域为?,???, 2?44??4?22
?t1?33?3?gt?2????当t?R时,f?,即的值域仍为y?fgt??,?????????,所以x?g?t? ?????2444????2
是f?x?的一个等值域变换.??????????????????2分
(2)不必要性的反例:
f?x??x2,D?R,B??0,???
g?t??2t?1,D1?R,B1???1,???
t此时B1?D,但f??g?t?????2?1?的值域仍为B??0,???, 2
即g?t??2t?1?x?R?是f?x??x2?x?R?的一个等值域变换.(反例不唯一)??????3分
(3)f?x??log2x定义域为?2,8?,因为x?g?t?是f?x?的一个等值域变换,且函数f??g?t???的定
mt2?3t?n义域为R,所以x?g?t??,t?R的值域为?2,8?,????????2分 t2?1
mt2?3t?n2??8?2?t2?1??mt2?3t?n?8?t2?1?,??????????????1分 2t?1
?2?m?8?所以,恒有??1?9?4?m?2??n?2??0,??????????????????3分

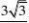
???2?9?4?m?8??n?8??0
??m?5?解得?.??????????????????????????3分 ?n?5??
18、(1)
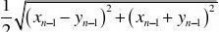
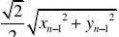

an?
?数列an是等比数列 ??????????????????3分
7
??n?1
高三数学 2015高三数学闸北二模 有答案
(2
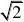
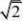
)an?2?n?1?22?n2n2?n2?2?2
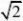
??????2分 , ?cn?2
假设 ?cn?中的第 n 项最小,由 c1? ,c2?0,?0?c2?c1. 2
2??n?1?n2?n?12?n2???当n?3时,有cn?0,又由cn?cn?1可得?22??22, 22
21?2?n2?n1???22,?即. ??1?n1?n

2??
n2
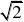
?6n?7?0,n?3n?3,?n?5.????2分
即有c5?c6?c7?;
由cn?cn?1,得3?n?5,又0?c2?c1,?c5?c4??c1;??????2分
3?3
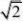
故数列?cn?中存在最小项,最小项是c5???22????????????1分 2
?a?a(3) cos?n?n?1n?,??n???????????????1分 42an?1?an
n2
?bn?????????????????????????1分 4
2221????log3?1?2a?对任意正整数n恒成立. 不等式化为:n?1n?22n2
222?? 设Tn?. n?1n?2

2n22222 又 Tn?1?Tn?数列?Tn?单?????0,2n?12n?1n?1n2?1n?22调递增????????????????????2分
??Tn?min?T1?1,要使不等式恒成立,只要1?
1log3?1?2a?,??1分 21?2a?0,
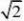
?0?a?12,1?2a?a
61阅读提醒您本文地址:
,?0?a?1 2
所以,使不等式对于任意正整数恒成立的a的取值范围是1.????2分
??
8
61阅读提醒您本文地址:
二 : 数学模型第三版)课后习题答案
2C(T0)-C(T*)=(353.33+100k)-(300+100k)=53.33. 3
50*故应改变订货策略.改变后的订货策略(周期)为T=,能节约费用约53.33元. 3 由实际意义知:当T?
《数学模型》作业解答
第四章(2008年10月28日)
1. 某厂生产甲、乙两种产品,一件甲产品用A原料1千克, B原料5千克;一件乙产品用A原料2千克, B原料4千克.现有A原料20千克, B原料70千克.甲、乙产品每件售价分别为20元和30元.问如何安排生产使收入最大?
解:设安排生产甲产品x件,乙产品y件,相应的利润为S
则此问题的数学模型为:
max S=20x+30y
?x?2y?20? s.t. ?5x?4y?70
?x,y?0,x,y?Z?
这是一个整线性规划问题,现用图解法进行求解
可行域为:由直线l1:x+2y=20, l2:5x+4y=70
l2
以及x=0,y=0组成的凸四边形区域.
第一章作业解答第
数学模型第三版 数学模型第三版)课后习题答案
直线l:20x+30y=c在可行域内
平行移动.
易知:当l过l1与l2的交点时, x S取最大值.
?x?2y?20?x?10 由? 解得? 5x?4y?70y?5??
此时 Smax=20?10?30?5=350(元)
2. 某厂拟用集装箱托运甲乙两种货物,每箱的体积、重量以及可获利润如下表: 已知这两种货物托运所受限制是体积不超过24立方米,重量不超过13百斤.试问这两种货物各托运多少箱,使得所获利润最大,并求出最大利润.
解:设甲货物、乙货物的托运箱数分别为x1,x2,所获利润为z.则问题的数学模型可表示为
max z?20x1?10x2
?5x1?4x2?24? st?2x1?5x2?13
?x,x?0,x,y?Z?12
这是一个整线性规划问题.
用图解法求解.
可行域为:由直线
l1:5x1?4x2?24
l2:2x1?5x2?13 及x1?0,x2?0组成直线 l:20x1?10x2?c在此凸四边形区域内平行移动x2 .
l1
l2
l x1
第一章作业解答第 11 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
易知:当l过l1与l2 的交点时,z取最大值
?5x1由??2x1?4x2?24?x1 解得 ??5x2?13?x2?4?1
zmax?20?4?10?1?90.
3.某微波炉生产企业计划在下季度生产甲、乙两种型号的微波炉.已知每台甲型、乙型微波炉的销售利润分别为3和2个单位.而生产一台甲型、乙型微波炉所耗原料分别为2和3个单位,所需工时分别为4和2个单位.若允许使用原料为100个单位,工时为120个单位,且甲型、乙型微波炉产量分别不低于6台和12台.试建立一个数学模型,确定生产甲型、乙型微波炉的台数,使获利润最大.并求出最大利润.
解:设安排生产甲型微波炉x件,乙型微波炉y件,相应的利润为S.
则此问题的数学模型为:
max S=3x +2y
?2x?3y?100? s.t. ?4x?2y?120
?x?6,y?12,x,y?Z?
这是一个整线性规划问题
用图解法进行求解
可行域为:由直线l1:2x+3y=100, l2:4x+2y=120
及x=6,y=12组成的凸四边形区域.
直线l:3x+2y=c在此凸四边形区域内平行移动. 易知:当l过l1与l2的交点时, S取最大值.
由??2x?3y?100 解得 ?4x?2y?120
第一章作业解答第 12 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
??x?20. ?y?20
Smax=3?20?2?20=100.
《数学模型》作业解答
第五章1(2008年11月12日)
1.对于5.1节传染病的SIR模型,证明:
(1)若s0?
至s?.
(2)若s0?1?,则i(t)先增加,在s?1?处最大,然后减少并趋于零;s(t)单调减少1
?,则i(t)单调减少并趋于零,s(t)单调减少至s?.
解:传染病的SIR模型(14)可写成 ?di?dt??i(?s?1)
? ds????si?dt
dsds由???si,知?0. s(t)单调减少. 而s(t)?0. ? lims(t)?s?存在. t??dtdt
故s(t)单调减少至s?.
(1)若s0?
当1?. 由s(t)单调减少. ?s(t)?s0. di?0,i(t)单调增加; ?dt
1di ??0,i(t)单调减少. 当s?时,?s?1?0. ?dt?s?s0时,?s?1?0. ?
即limi(t)?0. 又由书上(18)式知i??0. t??1
第一章作业解答第 13 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
di?0. ?i(t)达到最大值im. ?dt
11di从而?s-1?0. ?0. (2)若s0?,则s?t??, ??dt 当s?1时,
?i?t?单调减少且limi?t??0.即i??0. t??
4.在5.3节正规战争模型(3)中,设乙方与甲方战斗有效系数之比为
初始兵力x0与y0相同.
(1) 问乙方取胜时的剩余兵力是多少,乙方取胜的时间如何确定. a?4. b
(2) 若甲方在战斗开始后有后备部队以不变的速率r增援,重新建立模型,讨论如何判断双方的胜负.
解:用x?t?,y?t?表示甲、乙交战双方时刻t的士兵人数,则正规战争模型可近似表示为:
?dx?dt??ay
?dy???bx, ???1?
?dt?x?0??x,y?0??y00?
?0?a?现求(1)的解: (1)的系数矩阵为A??? ?b0??
?E?A??a??2?ab?0. ??1,2??ab b?
??2??2???? ,????1??1?
?2???C2??1??e????1,?2对应的特征向量分别为??x?t????2?????1?的通解为?C1??y?t???1??e????
再由初始条件,得 .
第一章作业解答第 14 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
?x?x?t???0?y0?e?2?
dybx?. dxayt?x???0?y0?e??2?t ???2? 又由?1?可得
22其解为 ay2?bx2?k, 而k?ay0?bx0 ???3?
22ay0?bx0kb3(1) 当x?t1??0时,y?t1????y0??y0. aaa2
即乙方取胜时的剩余兵力数为y0. 2
又令x?t1??0,由(2)得??x0??y0?e?2?abt1?x???0?y0?e??2?abt1?0. 注意到x0?y0,得e2abt1?x0?2y02. ?e2y0?x0abt1?3, ?t1?ln3. 4b
(2) 若甲方在战斗开始后有后备部队以不变的速率r增援.则
?dx?dt??ay?r
?dy???bx ???4? ?dt?x(0)?x,y?0??y00?
dx?ay?r?,即bxdx?aydy?rdy. 相轨线为ay2?2ry?bx2?k, dy?bx由?4?得
r?r2?222k?ay0?2ry0?bx.0或a?y???bx??k. 此相轨线比书图11中的轨线上移了a?a?2
第一章作业解答第 15 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
rr?b2r2?.乙方取胜的条件为k?0,亦即?y0???x0?2. aa?aa?2
第五章2(2008年11月14日)
6. 模仿5.4节建立的二室模型来建立一室模型(只有中心室),在快速静脉注射、恒速静脉滴注(持续时间为?)和口服或肌肉注射3种给药方式下求解血药浓度,并画出血药浓度曲线的图形.
解: 设给药速率为f0?t?

,排除速率为常数k,则x/?t??kx?t??f0?t?,x?t??VC?t?.
(1)快速静脉注射: 设给药量为D0, 则f0?t??0,C?0??D0D,解得C?t??0e?kt. VV
(2)恒速静脉滴注(持续时间为?): 设滴注速率为k0,则f0?t??k0,C?0??0,解得
?k0?kt??, 0?t??1?e?Vk C?t??? k0??1?e?kt?e?k?t???,t???Vk
(3) 口服或肌肉注射: f0?t??k01D0e?k01t?见5.4节(13)式?,解得
?k01D0?k01t?kte?e,k?k01??Vk01?k C?t??? kD?te?kt, k?k01??V??
3种情况下的血药浓度曲线如下:
第一章作业解答第 16 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
第五章3(2008年11月18日)
8. 在5.5节香烟过滤嘴模型中,
(1) 设M?800mg,l1?80mm,l2?20mm,b?0.02,??0.08,??50mm/s,a?0.3 求Q和Q1/Q2.
(2) 若有一支不带过滤嘴的香烟,参数同上,比较全部吸完和只吸到l1处的情况下,进入人体毒物量的区别. 解
aw0v?Q?/eab?l2vabl1?0.08?200.7?0.02?80??????0.3?10?5050?1?ev????229.857563e50?1?e(毫克) ????0.7?0.02????/
?其中w0?M/l1?10?, ?Q1 ?eQ2???b?l2v?e??0.08?0.02??2050
?0.97628571
第一章作业解答第 17 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
abl?aw0v?
(2) 对于一支不带过滤嘴的香烟,全部吸完的毒物量为Q3?‘?1?ev
ab??
'
?
? ??
?aw0v?v2??1?e只吸到l1处就扔掉的情况下的毒物量为Q4?'e?ab?
bl
a'bl1
v
?? ??
abl???
blabl0.02?1000.3?0.02?100e?1?ev?
??vv50Q3e?ee?e50e0.04?e0.012????bl1?0.02?80?0.032?1.256531719.abl10.3?0.02?800.0096bl1?a'bl1?Q4e?e?vvv?e50?e50e1?ev?e?e????
blv
'
Q3?295.84, Q
4
?235.44
a
?4. b
4.在5.3节正规战争模型(3)中,设乙方与甲方战斗有效系数之比为初始兵力x0与y0相同.
(1) 问乙方取胜时的剩余兵力是多少,乙方取胜的时间如何确定.
(2) 若甲方在战斗开始后有后备部队以不变的速率r增援,重新建立模型,讨论如何判断双方的胜负.
解:用x?t?,y?t?表示甲、乙交战双方时刻t的士兵人数,则正规战争模型可近似表示为:
?dx
?dt??ay?dy
???bx, ???1? ?dt
?x?0??x,y?0??y
00?
现求(1)的解: (1)的系数矩阵为A??
?0?a?
?
??b0?
?E?A?
?a
??2?ab?0. ??1,2??ab b?
第一章作业解答第 18 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
??1,?2对应的特征向量分别为???2??2???? ,????1??1?
?2???C2??1??e???x?t????2?????1?的通解为?C1??y?t???1??e????
再由初始条件,得 abtabt.
?x?x?t???0?y0?e?2?
dybx?. dxayabt?x???0?y0?e??2?abt ???2? 又由?1?可得
22其解为 ay2?bx2?k, 而k?ay0?bx0 ???3?
22ay0?bx0kb3(1) 当x?t1??0时,y?t1????y0??y0. aaa2
即乙方取胜时的剩余兵力数为y0. 2
又令x?t1??0,由(2)得??x0??y0?e?2?abt1?x???0?y0?e??2?abt1?0. 注意到x0?y0,得e2abt1?x0?2y02. ?e2y0?x01?3, ?t1?ln3. 4b
(2) 若甲方在战斗开始后有后备部队以不变的速率r增援.则
?dx?dt??ay?r
?dy???bx ???4? ?dt?x(0)?x,y?0??y00?
第一章作业解答第 19 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
由?4?得dx?ay?r?,即bxdx?aydy?rdy. 相轨线为ay2?2ry?bx2?k, dy?bx
r?r2?222k?ay0?2ry0?bx.0或a?y???bx??k. 此相轨线比书图11中的轨线上移了aa??
rr?b2r2?.乙方取胜的条件为k?0,亦即?y0???x0?2. aa?aa?
22
《数学模型》作业解答
第六章(2008年11月20日)
1.在6.1节捕鱼模型中,如果渔场鱼量的自然增长仍服从Logistic规律,而单位时间捕捞量为常数h.
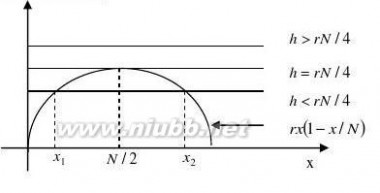
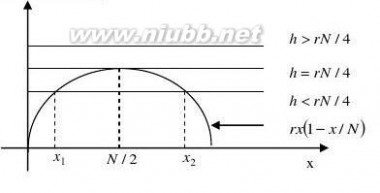
(1)分别就h?rN/4,h?rN/4,h?rN/4这3种情况讨论渔场鱼量方程的平衡点及其稳定状况.
(2)如何获得最大持续产量,其结果与6.1节的产量模型有何不同.
解:设时刻t的渔场中鱼的数量为x?t?,则由题设条件知:x?t?变化规律的数学模型为
dx(t)x?rx(1?)?h dtN
记F(x)?rx(1?
(1).讨论渔场鱼量的平衡点及其稳定性:
由F?x??0,得rx(1?
即 x)?h Nx)?h?0 . Nr2x?rx?h?0??????????1? N
??r2?4rh4h?r(r?) , NN
N??
(1)的解为:x1,2?4hNrN
2
①当h?rN/4,??0,(1)无实根,此时无平衡点;
第一章作业解答第 20 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
②当h?rN/4,??0,(1)有两个相等的实根,平衡点为x0?
N. 2
xrx2rx
,F'(x0)?0 不能断定其稳定性. )??r?
NNN
dxxrN
?0.?x0不稳定; 但?x?x0 及x?x0 均有F(x)?rx(1?)??0 ,即dtN4
F'(x)?r(1?
③当h?rN/4,??0时,得到两个平衡点:
N??x1?
易知:x1?
4h
NrN
N??
, x2?
4hNrN
22
NN''
, x2? ,F(x1)?0 ,F(x2)?0 22
?平衡点x1不稳定,平衡点x2稳定.
(2)最大持续产量的数学模型为
maxh?
?
s.t.F(x)?0?
x
即 maxh?rx(1?),
N
NrN*
易得 x0? 此时 h?, 24N*
但x0?这个平衡点不稳定.这是与6.1节的产量模型不同之处.
2
要获得最大持续产量,应使渔场鱼量x?
NNN
,且尽量接近,但不能等于.
222
'
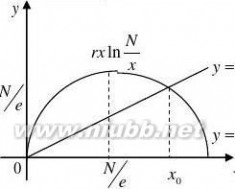
x?t??rxln2.与Logistic模型不同的另一种描述种群增长规律的是Gompertz模型:
中r和N的意义与Logistic模型相同.
N
.其x
设渔场鱼量的自然增长服从这个模型,且单位时间捕捞量为h?Ex.讨论渔场鱼量的
*
平衡点及其稳定性,求最大持续产量hm及获得最大产量的捕捞强度Em和渔场鱼量水平x0.
解:x?t?变化规律的数学模型为
dx?t?N
?rxln?Ex dtx
记 F(x)?rxln
N
?Ex x
E
?N
① 令F?x??0,得rxln?Ex?0 ?x0?Ner,x1?0.
x
第一章作业解答第 21 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
?平衡点为x0,x1 . 又?F'?x??rlnN?r?E,F'?x0???r?0,F'?x1???. x
? 平衡点xo是稳定的,而平衡点x1不稳定.
②最大持续产量的数学模型为: Ex f?x?
?maxh?Ex? N?s.t. rxln?Ex?0,x?0.?x?
由前面的结果可得 h?ENe?E
r
EE?dhEN?rdh?Ner?e,令?0. dErdE
得最大产量的捕捞强度Em?r.从而得到最大持续产量hm?rN/e,此时渔场鱼量水平*x0?N. e
dx(t)x?rx(1?) dtN
其中r为固有增长率,N`为环境容许的最大鱼量. 而单位时间捕捞量为常数h. 3.设某渔场鱼量x(t)(时刻t渔场中鱼的数量)的自然增长规律为:
1.求渔场鱼量的平衡点,并讨论其稳定性;
*2.试确定捕捞强度Em,使渔场单位时间内具有最大持续产量Qm,求此时渔场鱼量水平x0. 00
解:1.x(t)变化规律的数学模型为 dx(t)x?rx(1?)?h dtN
xxr2x?rx?h?0----(1)记f(x)?rx(1?)?h,令 rx(1?)?h?0 ,即 NNN0
??r2?4rh4h?r(r?) , (1)的解为:x1,2?NNN??24hNrN ① 当??0时,(1)无实根,此时无平衡点;
第一章作业解答第 22 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
② 当??0时,(1)有两个相等的实根,平衡点为x0?N. 2
xrx2rx)??r? ,f'(x0)?0 不能断定其稳定性. NNN
xrNdx?0 ,即?0?x0不稳定; 但?x?x0 及x?x0 均有f(x)?rx(1?)?N4dtf'(x)?r(1?
③ 当??0时,得到两个平衡点:
N?N?
x1?
易知 x1?4hrNN?N? , x2?4hrN22 NN , x2? ?f'(x1)?0, f'(x2)?0 22
?平衡点x1不稳定 ,平衡点x2稳定.
2.最大持续产量的数学模型为: ?
即 maxh?rx(1?0maxh ?s.t.f(x)?0? xNrNN**), 易得 x0? 此时 h?,但x0?这个平衡点不稳定. N242
NNN要获得最大持续产量,应使渔场鱼量x?,且尽量接近,但不能等于. 222
《数学模型》第七章作业
(2008年12月4日)
1.对于7.1节蛛网模型讨论下列问题:
(1)因为一个时段上市的商品不能立即售完,其数量也会影响到下一时段的价格,所以第k?1时段的价格yk?1由第k?1和第k时段的数量xk?1和xk决定,如果仍设xk?1仍只取决于yk,给出稳定平衡的条件,并与7.1节的结果进行比较.
2.已知某商品在k时段的数量和价格分别为xk和yk,其中1个时段相当于商品的一个生产周期.设该商品的需求函数和供应函数分别为yk?f(xk)和
第一章作业解答第 23 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
xk?1?g(yk?yk?1).试建立关于商品数量的差分方程模型,并讨论稳定平衡条件. 2
3. 已知某商品在k时段的数量和价格分别为xk和yk,其中1个时段相当于商品的一个生产周期.设该商品的需求函数和供应函数分别为yk?1?f(xk?1?xk)和2xk?1?g(yk).试建立关于商品数量的差分方程模型,并讨论稳定平衡条件.
《数学模型》作业解答
第七章(2008年12月4日)
2. 对于7.1节蛛网模型讨论下列问题:
(1)因为一个时段上市的商品不能立即售完,其数量也会影响到下一时段的价格,所以第k?1时段的价格yk?1由第k?1和第k时段的数量xk?1和xk决定,如果仍设xk?1仍只取决于yk,给出稳定平衡的条件,并与7.1节的结果进行比较.
(2)若除了yk?1由xk?1和xk决定之外,xk?1也由前两个时段的价格yk和yk?1确定.试分析稳定平衡的条件是否还会放宽.
解:(1)由题设条件可得需求函数、供应函数分别为: x?xk??yk?1?f(k?1) ? 2?xk?1?h(yk)?
在P0(x0,y0)点附近用直线来近似曲线f,h,得到 x?xk??yk?1?y0???(k?1?x0),??0 ?(1) ? 2? ??0 ?(2)?xk?1?x0??(yk?y0) ,
由(2)得 xk?2?x0??(yk?1?y0) ?(3)
第一章作业解答第 24 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
(1)代入(3)得 xk?2?x0????(xk?1?xk?x0) 2
? 2xk?2???xk?1???xk?2x0?2??x0
对应齐次方程的特征方程为 2?2????????0
特征根为?1,2????(??)2?8?? ?4
当???8时,则有特征根在单位圆外,设???8,则 ?1,2?(??)2?8?? ?()??2424??2
???2 ??1,2?1 ?
即平衡稳定的条件为 ???2与P207的结果一致.
(2)此时需求函数、供应函数在P0(x0,y0)处附近的直线近似表达式分别为: xk?1?xk??x0),??0 ?(4)?yk?1?y0???(2 ? yk?yk?1?xk?1?x0??(?y0) , ??0 ?(5)2?
由(5)得,2(xk?3?x0)?β(yk?2?y0?yk?1?y0) ?(6) 将(4)代入(6),得 2(xk?3?x0)?????(?
?xk?2?xk?1x?xk??x0)??(k?1?x0)? 22?
? 4xk?3???xk?2?2??xk?1???xk?4x0?4??x0
对应齐次方程的特征方程为 4??????2???????0 ?(7) 代数方程(7)无正实根,且???, ?
别为?1,?2,?3,则 32αβ??, ?不是(7)的根.设(7)的三个非零根分24
第一章作业解答第 25 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
??????????123?4????????????? ?1223312?????1?2?3???4?
??, 则 对(7)作变换:????12
?3?p??q?0,
1?2?218?3?3?2?2
), q?(????) 其中 p?(2???34124126
?q??1???2??q?用卡丹公式:??2?w??2??q2??3?w??2??
其中w?qpqqp()2?()3???()2?()323223qpqqp()2?()3?w2??()2?()3 23223qpqqp()2?()3?w??()2?()323223?1?i3, 2
求出?1,?2,?3,从而得到?1,?2,?3,于是得到所有特征根??1的条件.
2.已知某商品在k时段的数量和价格分别为xk和yk,其中1个时段相当于商品的一个生产周期.设该商品的需求函数和供应函数分别为yk?f(xk)和xk?1?g(关于商品数量的差分方程模型,并讨论稳定平衡条件. 解:已知商品的需求函数和供应函数分别为yk?f(xk)和xk?1?g(yk?yk?1).试建立2yk?yk?1). 2设曲线f和g相交于点P0(x0,y0),在点P0附近可以用直线来近似表示曲线f和g:
yk?y0???(xk?x0),??0 ----------------------(1)
xk?1?x0??(yk?yk?1?y0),??0 --------------------(2) 2
从上述两式中消去yk可得
第一章作业解答第 26 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
2xk?2???xk?1???xk?2(1???)x0,k?1,2,?, -----------(3) 上述(3)式是我们所建立的差分方程模型,且为二阶常系数线性非齐次差分方程. 为了寻求P0点稳定平衡条件,我们考虑(3)对应的齐次差分方程的特征方程:
2?2????????0
容易算出其特征根为
?1,2????(??)2?8?? ---------------(4) ?4
当???8时,显然有
????(??)2?8???? -----------(5) ?2???44
从而?2 ?2,?2在单位圆外.下面设???8,由(5)式可以算出 ?1,2???
2
要使特征根均在单位圆内,即 ?1,2?1,必须 ???2.
故P0点稳定平衡条件为 ???2.
3. 已知某商品在k时段的数量和价格分别为xk和yk,其中1个时段相当于商品的一个生产周期.设该商品的需求函数和供应函数分别为yk?1?f(
立关于商品数量的差分方程模型,并讨论稳定平衡条件.
解:已知商品的需求函数和供应函数分别为yk?1?f(xk?1?xk)和xk?1?g(yk).试建2xk?1?xk)和xk?1?g(yk). 2
设曲线f和g相交于点P0(x0,y0),在点P0附近可以用直线来近似表示曲线f和g:
yk?1?y0???(xk?1?xk?x0),??0 --------------------(1) 2
xk?1?x0??(yk?y0),??0 --- ----------------(2) 由(2)得 xk?2?x0??(yk?1?y0) --------------------(3)
(1)代入(3),可得xk?2?x0????(xk?1?xk?x0) 2
第一章作业解答第 27 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
? 2xk?2???xk?1???xk?2x0?2??x0,k?1,2,?, --------------(4) 上述(4)式是我们所建立的差分方程模型,且为二阶常系数线性非齐次差分方程. 为了寻求P0点稳定平衡条件,我们考虑(4)对应的齐次差分方程的特征方程:
2?2????????0
容易算出其特征根为
?1,2????(??)2?8?? ---------------(4) ?4
当???8时,显然有
????(??)2?8???? -----------(5) ?2???44
从而?2 ?2,?2在单位圆外.下面设???8,由(5)式可以算出 ?1,2???
2
要使特征根均在单位圆内,即 ?1,2?1,必须 ???2.
故P0点稳定平衡条件为 ???2.
《数学模型》作业解答
第八章(2008年12月9日)
1. 证明8.1节层次分析模型中定义的n阶一致阵A有下列性质:
(1) A的秩为1,唯一非零特征根为n;
(2) A的任一列向量都是对应于n的特征向量.
证明: (1)由一致阵的定义知:A满足
aij?ajk?aik,i,j,k?1,2,?,n
于是对于任意两列i,j,有aik?aij,?k?1,2,?,n?.即i列与j列对应分量成比例. ajk
从而对A作初等行变换可得:
第一章作业解答第 28 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
?b11b12?00初等行变换A??????????0?0
这里B?0.?秩?B??1,?b1n??0??? B ?????0??A??1
?c1n?
?0???C ?????0?再根据初等行变换与初等矩阵的关系知:存在一个可逆阵P,使PA?B,于是 ?c11c12?00?1?1PAP?BP??????0?0
易知C的特征根为c11,0,?,0(只有一个非零特征根).
又?A~C,?A与C有相同的特征根,从而A的非零特征根为c11,又?对于任意矩阵有?1??2????n?Tr?A??a11?a22???ann?1?1???1?n.故A的唯一非零特征根为n.
(2)对于A的任一列向量?a1k,a2k,?,ank?,?k?1,2,?,n? T
有
A?a1k,a2k,?,ank?T?n??n?aaa??1jjk???1k??jn?1??jn?1??na1k??aa??a??na2k?2jjk????2k?????n?a,a,?,a?T???1k2knkj?1j?1???????
?n???n???na?
??aa???a??nk?
njjknk????j?1???j?1?
?A的任一列向量?a1k,a2k,?,ank?T都是对应于n的特征向量.
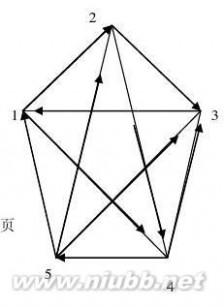
7. 右下图是5位网球选手循环赛的结果,作为竞赛图,它
是双向连通的吗?找出几条完全路径,用适当方法排出5位
选手的名次.
解:这个5阶竞赛图是一个5阶有向Hamilton图.其一个有
向Hamilton圈为3?1?4?5?2?3.所以此竞赛图
是双向连通的. 第一章作业解答第 29 页 共 57
数学模型第三版 数学模型第三版)课后习题答案
4?5?1?2?3
3?1?4?5?2
等都是完全路径.
此竞赛图的邻接矩阵为 2?4?5?3?15?3?1?2?4
?0?0?A??1??0
??1
T1010?0110??0000? ?0101?1100??令e??1,1,1,1,1?,各级得分向量为
TTS?1??Ae??2,2,1,2,3?, S?2??AS?1???4,3,2,4,5?,
TTS?3??AS?2???7,6,4,7,9? , S?4??AS?3???13,11,7,13,17?
由此得名次为5,1(4),2,3 (选手1和4名次相同).
注:给5位网球选手排名次也可由计算A的最大特征根?和对应特征向量S得到: ??1.8393,S??0.2137?T ,0.1794,0.1162,0.2137,0.2769
数学模型作业(12月16日)解答
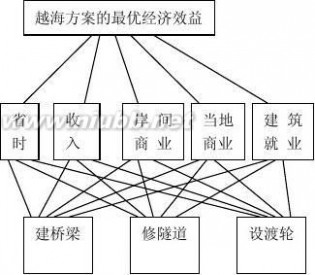
1.基于省时、收入、岸间商业、当地商业、建筑就业等五项因素,拟用层次分析法在建桥梁、修隧道、设渡轮这三个方案中选一个,画出目标为“越海方案的最优经济效益”的层次结构图.
解:目标层
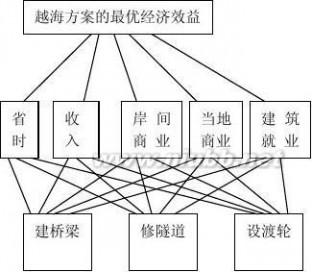
准则层
方案层
第一章作业解答第 30 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
2.简述层次分析法的基本步骤. 问对于一个即将毕业的大学生选择工作岗位的决策问题要分成哪3个层次?具体内容分别是什么?
答:层次分析法的基本步骤为:(1).建立层次结构模型;(2).构造成对比较阵;(3).计算权向量并做一致性检验;(4).计算组合权向量并做组合一致性检验. 对于一个即将毕业的大学生选择工作岗位的决策问题,用层次分析法一般可分解为目标层、准则层和方案层这3个层次. 目标层是选择工作岗位,方案层是工作岗位1、工作岗位2、工作岗位3等,准则层一般为贡献、收入、发展、声誉、关系、位置等.
3.用层次分析法时,一般可将决策问题分解成哪3个层次?试给出一致性指标的定义以及n阶正负反阵A为一致阵的充要条件.
答:用层次分析法时,一般可将决策问题分解为目标层、准则层和方案层这3个层次; 一致性指标的定义为:CI???n
n?1.n阶正互反阵A是一致阵的充要条件为:A的最大特征根
?=n.
第九章(2008年12月18日)
1.在9.1节传送带效率模型中,设工人数n固定不变.若想提高传送带效率D,一种简单的方法是增加一个周期内通过工作台的钩子数m,比如增加一倍,其它条件不变.另一种方法是在原来放置一只钩子的地方放置两只钩子,其它条件不变,于是每个工人在任何时刻可以同时触到两只钩子,只要其中一只是空的,他就可以挂上产品,这种办法用的钩子数量与第一种办法一样.试推导这种情况下传送带效率的公式,从数量关系上说明这种办法比第一种办法好.
解:两种情况的钩子数均为2m.第一种办法是2m个位置,单钩放置2m个钩子;第二种办法是m个位置,成对放置2m个钩子.
① 由9.1节的传送带效率公式,第一种办法的效率公式为
n2m??1?? D??? ?1??1?n?2m?????
当n较小,n??1时,有 2m
第一章作业解答第 31 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
D?2m??1n?n?1???n?1 1?1???1?????2n??2m4m8m??
n 4m D?1?E , E?
② 下面推导第二种办法的传送带效率公式:
对于m个位置,每个位置放置的两只钩子称为一个钩对,考虑一个周期内通过的m个钩对.
1; m
1 任一只钩对不被一名工人接触到的概率是1?; m
11 记p?,q?1?.由工人生产的独立性及事件的互不相容性.得,任一钩对为空mm 任一只钩对被一名工人接触到的概率是
的概率为qn,其空钩的数为2m;任一钩对上只挂上1件产品的概率为npqn?1,其空钩数为m.所以一个周期内通过的2m个钩子中,空钩的平均数为
2m?qn?m?npqn?1?m2qn?npqn?1
于是带走产品的平均数是 2m?m2qn?npqn?1,
未带走产品的平均数是 n?2m?m2q?npq
?此时传送带效率公式为
nn?112m?m2qn?npn?qm?1?n?1?????2?2?1????1??? D'?nn?m?m???m?????????nn?1??) ??
③ 近似效率公式:
1?nn?n?1?1n?n?1??n?2?1?由于 ?1???1?? ?23m2m6m?m?n
1?? ?1???m?n?1?1?n?1?n?1??n?2?1 ?2m2m
? D'?1??n?1??n?2? 6m2
n2
当n??1时,并令E'?1?D',则 E'? 26m
④ 两种办法的比较:
第一章作业解答第 32 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
nn2
由上知:E?,E'? 24m6m
? E'/E?2n2n?1, ? E'?E. ,当m?n时,3m3m
所以第二种办法比第一种办法好.
《数学模型》作业解答
第九章(2008年12月23日)
一报童每天从邮局订购一种报纸,沿街叫卖.已知每100份报纸报童全部卖出可获利7
元.如果当天卖不掉,第二天削价可以全部卖出,但报童每100份报纸要赔4元.报童每天售
出的报纸数r是一随机变量,其概率分布如下表:

试问报童每天订购多少份报纸最佳(订购量必须是100的倍数)?
解:设每天订购n百份纸,则收益函数为
?7r?(?4)(n?r)r?n f(r)??7nr?n?
收益的期望值为G(n) = ?(11r?4n)P(r)+7n?P(r)
r?0r?n?1n?
现分别求出 n=0,1,2,3,4,5时的收益期望值.
G(0)=0;G(1)=?4×0.05+7×0.1+7×(0.25+0.35+0.15+0.1)=6.45;
G(2)= (?8?0.05?3?0.1?14?0.25)?14?(0.35?0.15?0.1)?11.8;
G(3)=(?12?0.05?1?0.1?10?0.25?21?0.35)?21?(0.15?0.1)?14.4
G(4)=(?16?0.05?5?0.1?6?0.25?17?0.35?28?0.15)?28?0.1?13.15
G(5)=?20?0.05?9?0.1?2?0.25?13?0.35?24?0.15?35?0.1 ?10.25 当报童每天订300份时,收益的期望值最大.
数模复习资料
第一章
第一章作业解答第 33 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
1. 原型与模型
原型就是实际对象.模型就是原型的替代物.所谓模型, 按北京师范大学刘来福教授的观点:模型就是人们为一定的目的对原型进行的一个抽象.如航空模型、城市交通模型等.
??直观模型形象模型???物理模型??模型??思维模型??抽象模型?符号模型??数学模型???
2. 数学模型 如玩具、照片等如某一试验装置如某一操作 如地图、电路图
对某一实际问题应用数学语言和方法,通过抽象、简化、假设等对这一实际问题近似刻划所得的数学
d2x结构,称为此实际问题的一个数学模型. 例如力学中著名的61阅读/ www.61k.net
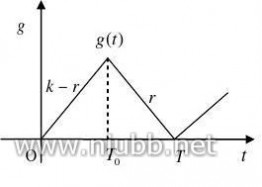
解:由题意可得贮存量g(t)的图形如下:
贮存费为
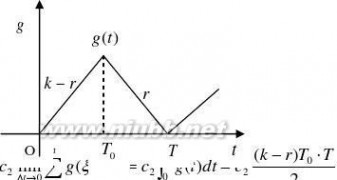
又? (k?r)T0?r(T?T0)
? T0?rr(k?r)T?TT , ? 贮存费变为 c2? k2k
于是不允许缺货的情况下,生产销售的总费用(单位时间内)为
c1c2r(k?r)T2c1r(k?r)T???c2 C(T)? T2kTT2k
第一章作业解答第 45 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
cdCr(k?r)??1
2?c2. dT2kT
dC?0 , 得T??dT
? 令2c1k c2r(k?r)2c1k c2r(k?r)? 易得函数C(T)在T处取得最小值,即最优周期为: T?
当k??r时,T??2c1 . 相当于不考虑生产的情况. c2r
当k?r时,T??? . 此时产量与销量相抵消,无法形成贮存量.
第四章(2008年10月28日)
2. 某厂生产甲、乙两种产品,一件甲产品用A原料1千克, B原料5千克;一件乙产品用A原料2千克, B原料4千克.现有A原料20千克, B原料70千克.甲、乙产品每件售价分别为20元和30元.问如何安排生产使收入最大?
解:设安排生产甲产品x件,乙产品y件,相应的利润为S
则此问题的数学模型为:
max S=20x+30y
?x?2y?20? s.t. ?5x?4y?70
?x,y?0,x,y?Z?
这是一个整线性规划问题,现用图解法进行求解
可行域为:由直线l1:x+2y=20, l2:5x+4y=70
l
以及x=0,y=0组成的凸四边形区域.
直线l:20x+30y=c在可行域内 平行移动.
易知:当l过l1与l2的交点时, x
S取最大值.
由??x?2y?20?x?10 解得? 5x?4y?70y?5??
此时 Smax=20?10?30?5=350(元)
2. 某厂拟用集装箱托运甲乙两种货物,每箱的体积、重量以及可获利润如下表:
第一章作业解答第 46 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
.试问这两种货物各托运多少箱,使得所获利润最大,并求出最大利润.
解:设甲货物、乙货物的托运箱数分别为x1,x2,所获利润为z.则问题的数学模型可表示为
max z?20x1?10x2
?5x1?4x2?24? st?2x1?5x2?13
?x,x?0,x,y?Z?12
这是一个整线性规划问题.
用图解法求解.
可行域为:由直线
l1:5x1?4x2?24
l2:2x1?5x2?13 及x1?0,x2?0组成直线 l:20x1?10x2?c在此凸四边形区域内平行移动x2 .
l1
l2
l
易知:当l过l1与l2x1 的交点时,z取最大值
由??5x1
?2x1?4x2?24?5x2?13 解得 ??x1
?x2?4?1
zmax?20?4?10?1?90.
3.某微波炉生产企业计划在下季度生产甲、乙两种型号的微波炉.已知每台甲型、乙型微波炉的销售利润分别为3和2个单位.而生产一台甲型、乙型微波炉所耗原料分别为2和3个单位,所需工时分别为4和2个单位.若允许使用原料为100个单位,工时为120个单位,且甲型、乙型微波炉产量分别不低于6台和12
第一章作业解答第 47 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
台.试建立一个数学模型,确定生产甲型、乙型微波炉的台数,使获利润最大.并求出最大利润. 解:设安排生产甲型微波炉x件,乙型微波炉y件,相应的利润为S.
则此问题的数学模型为: max S=3x +2y
?2x?3y?100? s.t. ?4x?2y?120
?x?6,y?12,x,y?Z?
这是一个整线性规划问题
用图解法进行求解
可行域为:由直线l1:2x+3y=100, l2:4x+2y=120
及x=6,y=12组成的凸四边形区域.
直线l:3x+2y=c在此凸四边形区域内平行移
动. 易知:当l过l1与l2的交点时, S取最大值.
由??2x?3y?100 解得 ?4x?2y?120
?x?20 ?. y?20?
Smax=3?20?2?20=100.
第五章2(2008年11月14日)
6. 模仿5.4节建立的二室模型来建立一室模型(只有中心室),在快速静脉注射、恒速静脉滴注(持续时间为?)和口服或肌肉注射3种给药方式下求解血药浓度,并画出血药浓度曲线的图形.
解: 设给药速率为f0?t?,中心室药量为x?t?,血药浓度为C?t?

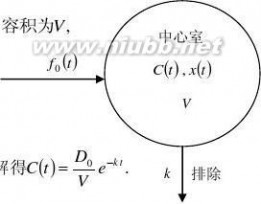
排除速率为常数k,则x/?t??kx?t??f0?t?,x?t??VC?t?. (1)快速静脉注射: 设给药量为D0, 则f0?t??0,C?0??D0,V(2)恒速静脉滴注(持续时间为?): 设滴注速率为k0,则f0?t??k0,C?0??0,解得
第一章作业解答第 48 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
?k0?kt??, 0?t??1?e?Vk C?t??? k0??1?e?kt?e?k?t???,t???Vk
(3) 口服或肌肉注射: f0?t??k01D0e?k01t?见5.4节(13)式?,解得
?k01D0?k01t?kte?e,k?k01??Vk01?k C?t???3种情况下的血药浓度曲线如kD?te?kt, k?k01??V??
下:
4.在5.3节正规战争模型(3)中,设乙方与甲方战斗有效系数之比为
初始兵力x0与y0相同.
(1) 问乙方取胜时的剩余兵力是多少,乙方取胜的时间如何确定. a?4. b
(2) 若甲方在战斗开始后有后备部队以不变的速率r增援,重新建立模型,讨论如何判断双方的胜负.
解:用x?t?,y?t?表示甲、乙交战双方时刻t的士兵人数,则正规战争模型可近似表示为:
第一章作业解答第 49 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
?dx?dt??ay
?dy???bx, ???1? ?dt?x?0??x,y?0??y00?
现求(1)的解: (1)的系数矩阵为A???0?a?? ?b0??
?a?E?A???2?ab?0. ??1,2??ab b?
??2??2???? ,????1??1?
?2???C2??1??e????1,?2对应的特征向量分别为??x?t????2?????1?的通解为?C1??y?t???1??e????
再由初始条件,得 .
?x?x?t???0?y0?e?2?
dybx?. dxayabt?x???0?y0?e??2?abt ???2? 又由?1?可得
22其解为 ay2?bx2?k, 而k?ay0?bx0 ???3?
22ay0?bx0kb3(1) 当x?t1??0时,y?t1????y0??y0. aaa2
即乙方取胜时的剩余兵力数为y0. 2
第一章作业解答第 50 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
又令x?t1??0,由(2)得??x0??y0?e?2?abt1?x???0?y0?e??2?abt1?0. 注意到x0?y0,得e21?x0?2y02. ?e2y0?x01?3, ?t1?ln3. 4b
(2) 若甲方在战斗开始后有后备部队以不变的速率r增援.则
?dx?dt??ay?r
?dy???bx ???4?
?dt?x(0)?x,y?0??y00?
dx?ay?r?,即bxdx?aydy?rdy. 相轨线为ay2?2ry?bx2?k, dy?bx由?4?得
r?r2?222k?ay0?2ry0?bx.0或a?y???bx??k. 此相轨线比书图11中的轨线上移了aa??
rr?b2r2?.乙方取胜的条件为k?0,亦即?y0???x0?2. aa?aa?
第六章(2008年11月20日)
1.在6.1节捕鱼模型中,如果渔场鱼量的自然增长仍服从Logistic规律,而单位时间捕捞量为常数h.
(1)分别就h?rN/4,h?rN/4,h?rN/4这3种情况讨论渔场鱼量方程的平衡点及其稳定状况.
(2)如何获得最大持续产量,其结果与6.1节的产量模型有何不同.
解:设时刻t的渔场中鱼的数量为x?t?,则由题设条件知:x?t?变化规律的数学模型为 22
dx(t)x?rx(1?)?h dtN
记F(x)?rx(1?
(1).讨论渔场鱼量的平衡点及其稳定性:
第一章作业解答第 51 页 共 57 页 x)?h N
数学模型第三版 数学模型第三版)课后习题答案
由F?x??0,得rx(1?
即 x)?h?0 . Nr2x?rx?h?0??????????1? N
??r2?4rh4h?r(r?) , NN
N??
(1)的解为:x1,2?4hNrN
2
①当h?rN/4,??0,(1)无实根,此时无平衡点;
②当h?rN/4,??0,(1)有两个相等的实根,平衡点为x0?N. 2
xrx2rx,F'(x0)?0 不能断定其稳定性. )??r?NNN
dxxrN?0.?x0不稳定; 但?x?x0 及x?x0 均有F(x)?rx(1?)??0 ,即dtN4F'(x)?r(1?
③当h?rN/4,??0时,得到两个平衡点:
N??
x1?
易知:x1?4hNrNN??, x2?4hNrN22 NN'' , x2? ,F(x1)?0 ,F(x2)?0 22
?平衡点x1不稳定,平衡点x2稳定.
(2)最大持续产量的数学模型为
maxh? ??s.t.F(x)?0
x),
N
NrN*易得 x0? 此时 h?, 24
N*但x0?这个平衡点不稳定.这是与6.1节的产量模型不同之处. 2即 maxh?rx(1?
要获得最大持续产量,应使渔场鱼量x?
第八章(2008年12月9日) NNN,且尽量接近,但不能等于. 222
1.基于省时、收入、岸间商业、当地商业、建筑就业等五项因素,拟用层次分析法在建桥梁、修隧道、设渡轮这三个方案中选一个,画出目标为“越海方案的最优经济效益”的层次结构
第一章作业解答第 52 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
图.
解:目标层
准则层
方案层
2.简述层次分析法的基本步骤. 问对于一个即将毕业的大学生选择工作岗位的决策问题要分成哪3个层次?具体内容分别是什么?
答:层次分析法的基本步骤为:(1).建立层次结构模型;(2).构造成对比较阵;(3).计算权向量并做一致性检验;(4).计算组合权向量并做组合一致性检验. 对于一个即将毕业的大学生选择工作岗位的决策问题,用层次分析法一般可分解为目标层、准则层和方案层这3个层次. 目标层是选择工作岗位,方案层是工作岗位1、工作岗位2、工作岗位3等,准则层一般为贡献、收入、发展、声誉、关系、位置等.
3.用层次分析法时,一般可将决策问题分解成哪3个层次?试给出一致性指标的定义以及n阶正负反阵A为一致阵的充要条件.
答:用层次分析法时,一般可将决策问题分解为目标层、准则层和方案层这3个层次; 一致性指标的定义为:CI???n
n?1.n阶正互反阵A是一致阵的充要条件为:A的最大特征根?=n.
7. 右下图是5位网球选手循环赛的结果,作为竞赛图,它是双向连通的吗?找出几条完全路径,用适当方法排出5位选手的名次.
解:这个5阶竞赛图是一个5阶有向Hamilton图.其一个有
向Hamilton圈为3?1?4?5?2?3.所以此竞赛图
是双向连通的. 4?5?1?2?32?4?5?3?15?3?1?2?4 3?1?4?5?2
等都是完全路径.
第一章作业解答第 53 页 共 57

数学模型第三版 数学模型第三版)课后习题答案
此竞赛图的邻接矩阵为
?0?0?A??1??0
??1
T1010?0110??0000? ?0101?1100??令e??1,1,1,1,1?,各级得分向量为
TTS?1??Ae??2,2,1,2,3?, S?2??AS?1???4,3,2,4,5?,
TTS?3??AS?2???7,6,4,7,9? , S?4??AS?3???13,11,7,13,17?
由此得名次为5,1(4),2,3 (选手1和4名次相同).
第九章(2008年12月23日)
一报童每天从邮局订购一种报纸,沿街叫卖.已知每100份报纸报童全部卖出可获利7
元.如果当天卖不掉,第二天削价可以全部卖出,但报童每100份报纸要赔4元.报童每天售
出的报纸数r是一随机变量,其概率分布如下表:

试问报童每天订购多少份报纸最佳(订购量必须是100的倍数)?
解:设每天订购n百份纸,则收益函数为:f(r)??
n??7r?(?4)(n?r)r?n r?n?7n
收益的期望值为G(n) = ?(11r?4n)P(r)+7n?P(r)
r?0r?n?1
现分别求出 n=0,1,2,3,4,5时的收益期望值.
G(0)=0;G(1)=?4×0.05+7×0.1+7×(0.25+0.35+0.15+0.1)=6.45;
G(2)= (?8?0.05?3?0.1?14?0.25)?14?(0.35?0.15?0.1)?11.8;
G(3)=(?12?0.05?1?0.1?10?0.25?21?0.35)?21?(0.15?0.1)?14.4
G(4)=(?16?0.05?5?0.1?6?0.25?17?0.35?28?0.15)?28?0.1?13.15
G(5)=?20?0.05?9?0.1?2?0.25?13?0.35?24?0.15?35?0.1 ?10.25 当报童每天订300份时,收益的期望值最大.
第一章作业解答第 54 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
4.在“椅子摆放问题”的假设条件中,将四脚的连线呈正方形改为呈长方形,其余条件不变.试构造模型并求解.
解:设椅子四脚连线呈长方形ABCD. AB与CD的对称轴为x轴,用中心点的转角?表示椅子的位置.将相邻两脚A、B与地面距离之和记为f(?);C、D与地面距离之和记为g(?).并旋转1800.于是,设f(0)?0,g(0)?0,就得到g????0,f????0.
数学模型:设f???、g???是?0,2??上?的非负连续函数.若????0,2??,有f???g????0,且g?0??0,f?0??0,g????0,f????0,则??0??0,2??,使f??0??g??0??0.
模型求解:令h(?)?f(?)?g(?) .就有h(0)?0, h(?)?f(?)?g(?)?0?g(?)?0.再由f???,g???的连续性,得到h???是一个连续函数. 从而h???是?0,??上的连续函数.由连续函数的介值定理:??0??0,??,使h??0??0.即??0??0,??,使f??0??g??0??0.
又因为????0,2??,有f???g????0.故f??0??g??0??0.
8. 假定人口的增长服从这样的规律:时刻t的人口为x(t),单位时间内人口的增量与xm?x(t)成正比(其中xm为最大容量).试建立模型并求解.作出解的图形并与指数增长模型、阻滞增长模型的结果比较.
解:现考察某地区的人口数,记时刻t的人口数为x?t?(一般x?t?是很大的整数),且设x?t?为连续可微函数.又设x?t?|t?0?x0.任给时刻t及时间增量?t,因为单位时间内人口增长量与xm?x(t)成正比, 假设其比例系数为常数r.则t到t??t内人口的增量为:
x?t??t??x?t??r(xm?x?t?)?t.
两边除以?t,并令?t?0,得到
?dx??r(xm?x)?rt 解为x(t)?xm?(xm?x0)e ?dt??x(0)?x0
第一章作业解答第 55 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
如图实线所示,
当t充分大时 xm
它与Logistic模型相近.
x0 t
9.为了培养想象力、洞察力和判断力,考察对象时除了从正面分析外,还常常需要从侧面 或反面思考.试尽可能迅速回答下面问题:
(1) 某甲早8:00从山下旅店出发,沿一条路径上山,下午5:00到达山顶并留宿. 次日早8:00沿同一路径下山,下午5:00回到旅店.某乙说,甲必在两天中的同一时刻经 过路径中的同一地点.为什么?
(2) 37支球队进行冠军争夺赛,每轮比赛中出场的每两支球队中的胜者及轮空者 进入下一轮,直至比赛结束.问共需进行多少场比赛,共需进行多少轮比赛.如果是n支球队比赛呢?
(3) 甲乙两站之间有电车相通,每隔10分钟甲乙两站相互发一趟车,但发车时刻 不一定相同.甲乙之间有一中间站丙,某人每天在随机的时刻到达丙站,并搭乘最先经过丙站的那趟车,结果发现100天中约有90天到达甲站,仅约10天到达乙站.问开往甲乙两站的电车经过丙站的时刻表是如何安排的?
(4) 某人家住T市在他乡工作,每天下班后乘火车于6:00抵达T市车站,他的 妻子驾车准时到车站接他回家,一日他提前下班搭早一班火车于5:30抵T市车站,随即步行回家,他的妻子象往常一样驾车前来,在半路上遇到他,即接他回家,此时发现比往常 提前了10分钟.问他步行了多长时间?
(5) 一男孩和一女孩分别在离家2 km和1 km且方向相反的两所学校上学,每天 同时放学后分别以4 km/h和2 km/h的速度步行回家.一小狗以6 km/h的速度由男孩处奔向女孩,又从女孩处奔向男孩,如此往返直至回到家中,问小狗奔波了多少路程?
如果男孩和女孩上学时小狗也往返奔波在他们之间,问当他们到达学校时小狗在何处?
解:(1)方法一:以时间t为横坐标,以沿上山路径从山下旅店到山顶的行程x为纵坐标,
第一章作业解答第 56 页 共 57 页
数学模型第三版 数学模型第三版)课后习题答案
第一章作业解答第 57 页 共 57 页
三 : 数学模型第三版_课后习题答案
《数学模型》作业解答
第二章(1)(2008年9月16日)
1. 学校共1000名学生,235人住在A宿舍,333人住在B宿舍,432人住在C宿舍.学生们
要组织一个10人的委员会,试用下列办法分配各宿舍的委员数:
(1). 按比例分配取整数的名额后,剩下的名额按惯例分给小数部分较大者;
(2). §1中的Q值方法;
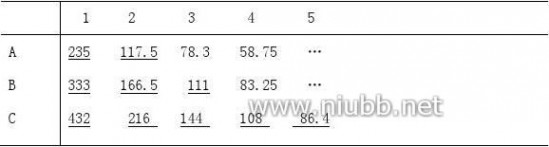
(3).d’Hondt方法:将A、B、C各宿舍的人数用正整数n=1,2,3,??相除,其商数如下表:
将所得商数从大到小取前10个(10为席位数),在数字下标以横线,表中A、B、C行有横线的数分别为2,3,5,这就是3个宿舍分配的席位.你能解释这种方法的道理吗?
如果委员会从10个人增至15人,用以上3种方法再分配名额,将3种方法两次分配的结果列表比较.
解:先考虑N=10的分配方案,
p1?235, p2?333, p3?432,
方法一(按比例分配) ?pi?13i?1000. q1?p1N
?p
i?13?2.35, 【61阅读】 q2?p2Ni?pi?13?3.33, q3?p3Ni?pi?13?4.32 i
分配结果为: n1?3, n2?3, n3?4
方法二(Q值方法)
9个席位的分配结果(可用按比例分配)为:
n1?2, n2?3, n3?4
第一章作业解答第 1 页 共 58 页
第10个席位:计算Q值为
235233324322
Q1??9204.17, Q2??9240.75, Q3??9331.2 2?33?44?5
Q3最大,第10个席位应给C.分配结果为 n1?2, n2?3, n3?5
方法三(d’Hondt方法)
此方法的分配结果为:n1?2, n2?3, n3?5
此方法的道理是:记pi和ni为各宿舍的人数和席位(i=1,2,3代表A、B、C宿 舍).pi是ni每席位代表的人数,取ni?1,2,?,从而得到的
近. pip中选较大者,可使对所有的i,i尽量接nini
再考虑N?15的分配方案,类似地可得名额分配结果.现将3种方法两次分配的结果列表如下:
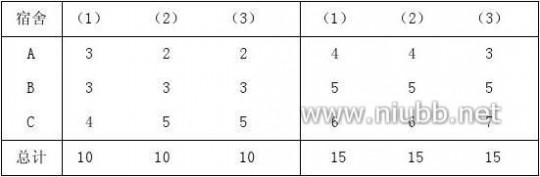
2. 试用微积分方法,建立录像带记数器读数n与转过时间的数学模型.
解: 设录像带记数器读数为n时,录像带转过时间为t.其模型的假设见课本.
考虑t到t??t时间内录像带缠绕在右轮盘上的长度,可得vdt?(r?wkn)2?kdn,两边积分,得 ?t
0vdt?2?k?(r?wkn)dn 0n
2?rk?wk2
2n2
? vt?2πk(r n ?wk) ? t?n?n. 2vv
第二章(2)(2008年10月9日)
15.速度为v的风吹在迎风面积为s的风车上,空气密度是? ,用量纲分析方法确定风车
第一章作业解答第 2 页 共 58 页
获得的功率P与v、S、?的关系.
解: 设P、v、S、?的关系为f(P,v,s,?)?0, 其量纲表达式为:
[P]=MLT2?3, [v]=LT?1,[s]=L,[?]=ML,这里L,M,T是基本量纲. 2?3
量纲矩阵为:
1?2?10A=????3?1
(P)(v)
齐次线性方程组为: 2?3?(L)01??(M) 00??(T)(s)(??
?2y1?y2?2y3?3y4?0? ?y1?y4?0
??3y?y?012?
它的基本解为y?(?1,3,1,1)
由量纲Pi定理得 ??P?1v3s1?1, ?P??v3s1?1 , 其中?是无量纲常数.
16.雨滴的速度v与空气密度?、粘滞系数?和重力加速度g有关,其中粘滞系数的定义是:运动物体在流体中受的摩擦力与速度梯度和接触面积的乘积成正比,比例系数为粘滞系数,用量纲分析方法给出速度v的表达式.
解:设v,?,?,g 的关系为f(v,?,?,g)=0.其量纲表达式为[v]=LMT,[?]=LMT,0-1-30
[?]=MLT(LTL)L=MLLTT=LMT,[g]=LMT,其中L,M,T是基本量纲. -2-1-1-1-2-2-2-1-10-2
量纲矩阵为
?1?3?11?(L)?0?(M)110?A=? ???10?1?2(T)??
(v)(?)(?)(g)
齐次线性方程组Ay=0 ,即
? y1-3y2-y3?y4?0? ?0 ?y2?y3
?-y -y-2y?034?1
的基本解为y=(-3 ,-1 ,1 ,1)
由量纲Pi定理 得
*??v?3??1?g. ?v???g,其中?是无量纲常数. ?16.雨滴的速度v与空气密度?、粘滞系数?、特征尺寸?和重力加速度g有关,其中粘
第一章作业解答第 3 页 共 58 页
滞系数的定义是:运动物体在流体中受的摩擦力与速度梯度和接触面积的乘积成正比,比例系数为粘滞系数,用量纲分析方法给出速度v的表达式.
解:设v,?,?,?,g 的关系为f(v,?,?,?,g)?0.其量纲表达式为
[v]=LMT,[?]=LMT,[?]=MLT(LTL)L=MLLTT=LMT,[?]=LM0T0 ,[g]=LMT 0-1-30-2-1-1-1-2-2-2-1-10-2其中L,M,T是基本量纲.
量纲矩阵为
?1?0A=????1
(v)
齐次线性方程组Ay=0 即 1?3?100101?(L)10??(M) ?1?2??(T)(?)(?)(?)(g)
?y1?y2?3y3?y4?y5?0?y3?y4?0 ???y1?y4?2y5?0?
的基本解为
11?y?(1,?,0,0,?)?122 ?31?y2?(0,?,?1,1,?)22?
得到两个相互独立的无量纲量
??1?v??1/2g?1/2
??3/2?1?1/2??g??2??
即 v??1) g1,?3/2?g1/2??1??2?1. 由?(?1,?2)?0 , 得 ?1??(?2
? ??
g(?3/2?g1/2??1) , 其中?是未定函数.
20.考察阻尼摆的周期,即在单摆运动中考虑阻力,并设阻力与摆的速度成正比.给出周期的表达式,然后讨论物理模拟的比例模型,即怎样由模型摆的周期计算原型摆的周期. 解:设阻尼摆周期t,摆长l, 质量m,重力加速度g,阻力系数k的关系为
f(t,l,m,g,k)?0
其量纲表达式为:
[t]?L0M0T,[l]?LM0T0,[m]?L0MT0,[g]?LM0T?2,[k]?[f][v]?1?MLT?2(LT?1)?1?L0MT?1, 其中L,M,T是基本量纲.
第一章作业解答第 4 页 共 58 页
量纲矩阵为
?0?0A=???1
(t)100?(L)0101??(M) 00?2?1??(T)1(l)(m)(g)(k)
齐次线性方程组
y2?y4?0??y3?y5?0 ??y?2y?y?045?1
的基本解为
11?Y?(1,?,0,,0)?122 ?11?Y2?(0,,?1,?,1)22?
得到两个相互独立的无量纲量
?tl?1/2g1/2??1?1/2?1?1/2?lmgk??2
∴t? kl1/2l ?1, ?1??(?2), ?2?1/2gmg
∴t?lkl1/2
(1/-好文章-2) ,其中?是未定函数 . gmg
考虑物理模拟的比例模型,设g和k不变,记模型和原型摆的周期、摆长、质量分别为
lkl?1/2
() t,t;l,l;m,m. 又t??1/2gm?g'''
当无量纲量m?lt?lgl时, 就有 ?. ???mltgll
《数学模型》作业解答
第三章1(2008年10月14日)
1. 在3.1节存贮模型的总费用中增加购买货物本身的费用,重新确定最优订货周期和订货
批量.证明在不允许缺货模型中结果与原来的一样,而在允许缺货模型中最优订货周期和订货批量都比原来结果减少.
第一章作业解答第 5 页 共 58 页
解:设购买单位重量货物的费用为k,其它假设及符号约定同课本.
10 对于不允许缺货模型,每天平均费用为:
C(T)?c1c2rT??kr T2
ccrdC??1
2?2 dT2T
2c1 c2r
2c1r c2 令dC?0 , 解得 T*?dT?? 由Q?rT , 得Q?rT?
与不考虑购货费的结果比较,T、Q的最优结果没有变.
20 对于允许缺货模型,每天平均费用为:
?c2Q2c31?2 C(T,Q)??c1??(rT?Q)?kQ? T?2r2r?
c1c2Q2c3rc3Q2kQ ?C??2???? ?T22rT2T2T2rT2
cQk?Cc2Q??c3?3? ?QrTrTT
??C?0???T 令? , 得到驻点: ?C?0???Q?
??? ??Q????T??2c1c2?c3k2?rc2c3c2c322c3kr2c1rc3kr??c2c2?c3c2(c2?c3)c2?c3
与不考虑购货费的结果比较,T、Q的最优结果减少.
2.建立不允许缺货的生产销售存贮模型.设生产速率为常数k,销售速率为常数r,
第一章作业解答第 6 页 共 58 页
k?r.在每个生产周期T内,开始的一段时间?0?t?T0?一边生产一边销售,后来的一段时间(T0?t?T)只销售不生产,画出贮存量g(t)的图形.设每次生产准备费为c1,单位时间每件产品贮存费为c2,以总费用最小为目标确定最优生产周期,讨论k??r和k?r的情况.
解:由题意可得贮存量g(t)的图形如下:
T(k?r)T0?T 2 贮存费为 c2lim?t?0?g(?i)?
ti?c2?g(t)dt?c2
i?10
又? (k?r) T0?r(T?T0)
? T0?rr(k?r)T?TT , ? 贮存费变为 c2? k2k
于是不允许缺货的情况下,生产销售的总费用(单位时间内)为
c1c2r(k?r)T2c1r(k?r)T???c2 C(T)? T2kTT2k
cdCr(k?r)??1
2?c2. dT2kT
dC?0 , 得T??dT 令2c1k c2r(k?r)
?? 易得函数C(T)在T处取得最小值,即最优周期为: T?2c1k c2r(k?r)
当k??r时,T??2c1 . 相当于不考虑生产的情况. c2r
当k?r时,T??? . 此时产量与销量相抵消,无法形成贮存量.
第一章作业解答第 7 页 共 58 页
第三网络日记章2(2008年10月16日)
3.在3.3节森林救火模型中,如果考虑消防队员的灭火速度?与开始救火时的火势b有关,试假设一个合理的函数关系,重新求解模型.
解:考虑灭火速度?与火势b有关,可知火势b越大,灭火速度?将减小,我们作如下假设: ?(b)?k, b?1
中的1是防止b?0时???而加的. 分母b?1
c1?t12c1?2t12(b?1)c2?t1x(b?1)总费用函数C?x?????c3x 22(kx??b??)kx??b??
最优解为 x?ckb12?2c2b(b?1)?(b?1)(b?1)?? k2c3k25.在考虑最优价格问题时设销售期为T,由于商品的损耗,成本q随时间增长,设q(t)?q0??t,?为增长率.又设单位时间的销售量为x?a?bp(p为价格).今将销售期分为0?t?T和T?t?T两段,每段的价格固定,记作p1,p2.求p1,p2的最优值,使销售期内的总利润最大.如果要求销售期T内的总售量为Q0,再求p1,p2的最优值. 解:按分段价格,单位时间内的销售量为
T??a?bp1,0?t? x?? Ta?bp2,?t?T??
又? q(t)?q0??t.于是总利润为
?(p1,p2)??T0?p1?q(t)?(a?bp1)dt??T?p2?q(t)?(a?bp2)dt T
T???2?2?=(a?bp1)?p1t?q0t?t?2?(a?bp2)?p2t?q0t?t?T 2?2???02?p1Tq0T?T2p2Tq0t3?T2
??)?(a?bp2)(??) =(a?bp1)(228228
??p1Tq0T?T2T??b(??)?(a?bp1) ?p12282
第一章作业解答第 8 页 共 58 页
p2Tq0t3?T2??T??b(??)?(a?bp2) ?p22282
令?????0,?0, 得到最优价格为: ?p1?p2
?1??T?p?a?b(q?)?0??12b?4?? ??p2?1?a?b(q0?3?T)?
?2b?4????
在销售期T内的总销量为
Q0??(a?bp1)dt??T(a?bp2)dt?aT?
2T20TbT(p1?p2) 2
于是得到如下极值问题:
p1Tq0T?T2p2Tq0t3?T2
max?(p1,p2)?(a?bp1)(??)?(a?bp2??) 228228
s.t aT?bT(p1?p2)?Q0 2
利用拉格朗日乘数法,解得:
aQ0?T?p??1b?bT?8 ?aQ0?T?p2???bbT8?
即为p1,p2的最优值.
第三章3(2008年10月21日)
6. 某厂每天需要角钢100吨,不允许缺货.目前每30天定购一次,每次定购的费用为2500元.每天每吨角钢的贮存费为0.18元.假设当贮存量降 到零时订货立即到达.问是否应改变订货策略?改变后能节约多少费用?
解:已知:每天角钢的需要量r=100(吨);每次订货费c1=2500(元);
每天每吨角钢的贮存费c2=0.18(元).又现在的订货周期T0=30(天)
第一章作业解答第 9 页 共 58 页
根据不允许缺货的贮存模型:C(T)?
得:C(T)?c11?c2rT?kr T22500?9T?100k T
dC2500 ??2?9dTT
令 dC?0 , 解得:T*?dT
*250050 ?935050(即订货周期为)时,总费用将最小. 33
3?250050*?9??100k=300+100k 又C(T)?503
2500?9?30?100k=353.33+100k C(T0)?30
2C(T0)-C(T*)=(353.33+100k)-(300+100k)=53.33. 3
50*故应改变订货策略.改变后的订货策略(周期)为T=,能节约费用约53.33元. 3 由实际意义知:当T?
《数学模型》作业解答
第四章(2008年10月28日)
1. 某厂生产甲、乙两种产品,一件甲产品用A原料1千克, B原料5千克;一件乙产品用A原料2千克, B原料4千克.现有A原料20千克, B原料70千克.甲、乙产品每件售价分别为20元和30元.问如何安排生产使收入最大?
解:设安排生产甲产品x件,乙产品y件,相应的利润为S
则此问题的数学模型为:
max S=20x+30y
?x?2y?20? s.t. ?5x?4y?70
?x,y?0,x,y-http://www.61k.com-?Z?
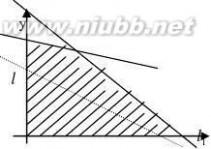
这是一个整线性规划问题,现用图解法进行求解
可行域为:由直线l1:x+2y=20, l2:5x+4y=70
l2
以及x=0,y=0组成的凸四边形区域.
第一章作业解答第
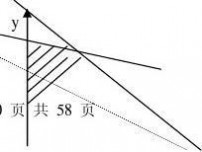
直线l:20x+30y=c在可行域内

平行移动.
易知:当l过l1与l2的交点时, x S取最大值.
?x?2y?20?x?10 由? 解得? 5x?4y?70y?5??
此时 Smax=20?10?30?5=350(元)
2. 某厂拟用集装箱托运甲乙两种货物,每箱的体积、重量以及可获利润如下表: 已知这两种货物托运所受限制是体积不超过24立方米,重量不超过13百斤.试问这两种货物各托运多少箱,使得所获利润最大,并求出最大利润.
解:设甲货物、乙货物的托运箱数分别为x1,x2,所获利润为z.则问题的数学模型可表示为
max z?20x1?10x2
?5x1?4x2?24? st?2x1?5x2?13
?x,x?0,x,y?Z?12
这是一个整线性规划问题.
用图解法求解.
可行域为:由直线
l1:5x1?4x2?24
l2:2x1?5x2?13 及x1?0,x2?0组成直线 l:20x1?10x2?c在此凸四边形区域内平行移动x2 .
l1
l2
l x1
第一章作业解答第 11 页 共 58 页
易知:当l过l1与l2 的交点时,z取最大值
?5x1由??2x1?4x2?24?x1 解得 ??5x2?13?x2?4?1
zmax?20?4?10?1?90.
3.某微波炉生产企业计划在下季度生产甲、乙两种型号的微波炉.已知每台甲型、乙型微波炉的销售利润分别为3和2个单位.而生产一台甲型、乙型微波炉所耗原料分别为2和3个单位,所需工时分别为4和2个单位.若允许使用原料为100个单位,工时为120个单位,且甲型、乙型微波炉产量分别不低于6台和12台.试建立一个数学模型,确定生产甲型、乙型微波炉的台数,使获利润最大.并求出最大利润.
解:设安排生产甲型微波炉x件,乙型微波炉y件,相应的利润为S.
则此问题的数学模型为:
max S=3x +2y
?2x?3y?100? s.t. ?4x?2y?120
?x?6,y?12,x,y?Z?
这是一个整线性规划问题
用图解法进行求解
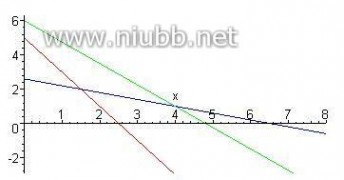
可行域为:由直线l1:2x+3y=100, l2:4x+2y=120
及x=6,y=12组成的凸四边形区域.
直线l:3x+2y=c在此凸四边形区域内 平行移动. 易知:当l过l1与l2的交点时, S取最大值.
由??2x?3y?100 解得 ?4x?2y?120
第一章作业解答第 12 页 共 58 页
??x?20. ?y?20
Smax=3?20?2?20=100.
《数学模型》作业解答
第五章1(2008年11月12日)
1.对于5.1节传染病的SIR模型,证明:
(1)若s0?
至s?.
(2)若s0?1?,则i(t)先增加,在s?1?处最大,然后减少并趋于零;s(t)单调减少1
?,则i(t)单调减少并趋于零,s(t )单调减少至s?.
解:传染病的SIR模型(14)可写成 ?di?dt??i(?s?1)
? ds????si?dt
dsds由???si,知?0. s(t)单调减少. 而s(t)?0. ? lims(t)?s?存在. t??dtdt
故s(t)单调减少至s?.
(1)若s0?
当1?. 由s(t)单调减少. ?s(t)?s0. di?0,i(t)单调增加; ?dt
1di ??0,i(t)单调减少. 当s?时,?s?1?0. ?dt?s?s0时,?s?1?0. ?
即limi(t)?0. 又由书上(18)式知i??0. t??1
第一章作业解答第 13 页 共 58 页
di?0. ?i(t)达到最大值im. ?dt
11di从而?s-1?0. ?0. (2)若s0?,则s?t??, ??dt 当s?1时,
?i?t?单调减少且limi?t??0.即i??0. t??
4.在5.3节正规战争——好文章——模型(3)中,设乙方与甲方战斗有效系数之比为
初始兵力x0与y0相同.
(1) 问乙方取胜时的剩余兵力是多少,乙方取胜的时间如何确定. a?4. b
(2) 若甲方在战斗开始后有后备部队以不变的速率r增援,重新建立模型,讨论如何判断双方的胜负.
解:用x?t?,y?t?表示甲、乙交战双方时刻t的士兵人数,则正规战争模型可近似表示为:
?dx?dt??ay
?dy???bx, ???1?
?dt?x?0??x,y?0??y00?
?0?a?现求(1)的解: (1)的系数矩阵为A??? ?b0??
?E?A??a??2?ab?0. ??1,2??ab b?
??2??2???? ,????1??1?
?2???C2??1??e????1,?2对应的特征向量分别为??x?t????2?????1?的通解为?C1??y?t???1??e????
再由初始条件,得 .
第一章作业解答第 14 页 共 58 页
?x?x?t???0?y0?e?2?
dyb61阅读球选手循环赛的结果,作为竞赛图,它是双向连通的吗?找出几条完全路径,用适当方法排出5位选手的名次.
解:这个5阶竞赛图是一个5阶有向Hamilton图.其一个有
向Hamilton圈为3?1?4?5?2?3.所以此竞赛图
是双向连通的. 4?5?1?2?32?4?5?3?15?3?1?2?4 3?1?4?5?2
等都是完全路径.
第一章作业解答第 53 页 共 58
此竞赛图的邻接矩阵为
?0?0?A??1??0
??1
T1010?0110??0000? ?0101?1100??令e??1,1,1,1,1?,各级得分向量为
TTS?1??Ae??2,2,1,2,3?, S?2??AS?1???4,3,2,4,5?,
TTS?3??AS?2???7,6,4,7,9 ? , S?4??AS?3???13,11,7,13,17?
由此得名次为5,1(4),2,3 (选手1和4名次相同).
第九章(2008年12月23日)
一报童每天从邮局订购一种报纸,沿街叫卖.已知每100份报纸报童全部卖出可获利7
元.如果当天卖不掉,第二天削价可以全部卖出,但报童每100份报纸要赔4元.报童每天售
出的报纸数r是一随机变量,其概率分布如下表:
试问报童每天订购多少份报纸最佳(订购量必须是100的倍数)?
解:设每天订购n百份纸,则收益函数为:f(r)??
n??7r?(?4)(n?r)r?n r?n?7n
收益的期望值为G(n) = ?(11r?4n)P(r)+7n?P(r)
r?0r?n?1
现分别求出 n=0,1,2,3,4,5时的收益期望值.
G(0)=0;G(1)=?4×0.05+7×0.1+7×(0.25+0.35+0.15+0.1)=6.45;
G(2)= (?8?0.05?3?0.1?14?0.25)?14?(0.35?0.15?0.1)?11.8;
G(3)=(?12?0.05?1?0.1?10?0.25?21?0.35)?21?(0.15?0.1)?14.4
G(4)=(?16?0.05?5?0.1?6?0.25?17?0.35?28?0.15)?28?0.1?13.15
G(5)=?20?0.05?9?0.1?2?0.25?13?0.35?24?0.15?35?0.1 ?10.25 当报童每天订300份时,收益的期望值最大.
第一章作业解答第 54 页 共 58 页
《数学模型》作业解答
第一章(2008年9月9日)
4.在“椅子摆放问题”的假设条件中,将四脚的连线呈正方形改为呈长方形,其余条件不变.试构造模型并求解.
解:设椅子四脚连线呈长方形ABCD. AB与CD的对称轴为x轴,用中心点的转角?表示椅子的位置.将相邻两脚A、B与地面距离之和记为f(?);C、D与地面距离之和记为g(?).并旋转1800.于是,设f(0)?0,g(0)?0,就得到g????0,f????0.
数学模型:设f???、g???是?0,2??上?的非负连续函数.若????0,2??,有f???g????0,且g?0??0,f?0??0,g????0,f????0,则??0??0,2??,使f??0??g??0??0.
模型求解:令h(?)?f(?)?g(?) .就有h(0)?0, h(?)?f(?)?g (?)?0?g(?)?0.再由f???,g???的连续性,得到h???是一个连续函数. 从而h???是?0,??上的连续函数.由连续函数的介值定理:??0??0,??,使h??0??0.即??0??0,??,使f??0??g??0??0.
又因为????0,2??,有f???g????0.故f??0??g??0??0.
8. 假定人口的增长服从这样的规律:时刻t的人口为x(t),单位时间内人口的增量与xm?x(t)成正比(其中xm为最大容量).试建立模型并求解.作出解的图形并与指数增长模型、阻滞增长模型的结果比较.
解:现考察某地区的人口数,记时刻t的人口数为x?t?(一般x?t?是很大的整数),且设x?t?为连续可微函数.又设x?t?|t?0?x0.任给时刻t及时间增量?t,因为单位时间内人口增长量与xm?x(t)成正比, 假设其比例系数为常数r.则t到t??t内人口的增量为:
x?t??t??x?t??r(xm?x?t?)?t.
两边除以?t,并令?t?0,得到
第一章作业解答第 55 页 共 58 页
?dx??r(xm?x) 解为 x(t)?xm?(xm?x0)e?rt ?dt??x(0)?x0
如图实线所示,
当t充分大时 xm
它与Logistic模型相近.
x0 t
9.为了培养想象力、洞察力和判断力,考察对象时除了从正面分析外,还常常需要从侧面 或反面思考.试尽可能迅速回答下面问题:
(1) 某甲早8:00从山下旅店出发,沿一条路径上山,下午5:00到达山顶并留宿. 次日早8:00沿同一路径下山,下午5:00回到旅店.某乙说,甲必在两天中的同一时刻经 过路径中的同一地点.为什么?
(2) 37支球队进行冠军争夺赛,每轮比赛中出场的每两支球队中的胜者及轮空者 进入下一轮,直至比赛结束.问共需进行多少场比赛,共需进行多少轮比赛.如果是n支球队比赛呢?
(3) 甲乙两站之间有电车相通,每隔10分钟甲乙两站相互发一趟车,但发车时刻 不一定相同.甲乙之间有一中间站丙,某人每天在随机的时刻到达丙站,并搭乘最先经过丙站的那趟车,结果发现100天中约有90天到达甲站,仅约10天到达乙站.问开往甲乙两站的电车经过丙站的时刻表是如何安排的?
(4) 某人家住T市在他乡工作,每天下班后乘火车于6:00抵达T市车站,他的 妻子驾车准时到车站接他回家,一日他提前下班搭早一班火车于5:30抵T市车站,随即步行回家,他的妻子象往常一样驾车前来,在半路上遇到他,即接他回家,此时发现比往常 提前了10分钟.问他步行了多长时间?
(5) 一男孩和一女孩分别在离家2 km和1 km且方向相反的两所学校上学,每天 同时放学后分别以4 km/h和2 km/h的速度步行回家.一小狗以6 km/h的速度由男孩处奔向女孩,又从女孩处奔向男孩,如此往返直至回到家中,问小狗奔波了多少路程?
如果男孩和女孩上学时小狗也往返奔波在他们之间,问当他们到达学校时小狗在何
第一章作业解答第 56 页 共 58 页
处?
解:(1)方法一:以时间t为横坐标,以沿上山路径从山下旅店到山顶的行程x为纵坐标, 第一天的行程x(t)可用曲线(?)表示 ,第二天的行程x(t)可用曲线(??)表示,(?)(??)是连续曲线必有交点p0(t0,d0),
两天都在t0时刻经过d0地点.
方法二:设想有两个人, 一人上山,一人下山,同一天同 时出发,沿同一路径,必定相遇. d0
t
早8 t0 晚5
方法三:我们以山下旅店为始点记路程,设从山下旅店到山顶的路程函数为f(t)(即t时刻走的路程为f(t)),同样设从山顶到山下旅店的路函数为g(t),并设山下旅店到山顶的距离为a(a>0).由题意知:f(8)?0,f(17)?a,g(8)?a,g(17)?0.令h(t)?f(t)?g(t),则有h(8)?f(8)?g(8)??a?0,h(17)?f(17)?g(17)?a?0,由于f(t),g(t)都是时间t的连续函数,因此h(t)也是时间t的连续函数,由连续函数的介值定理,?t0?[8,17],使h(t0)?0,即f(t0)?g(t0).
(2)36场比赛,因为除冠军队外,每队都负一场;6轮比赛,因为2队赛1轮,4队赛2轮,32队赛5轮. n队需赛n?1场,若2k?1?n?2k,则需赛k轮.
(3)不妨设从甲到乙经过丙站的时刻表是8:00,8:10,8:20,……
那么从乙到甲经过丙站的时刻表应该是8:09,8:19,8:29……
(4)步行了25分钟.设想他的妻子驾车遇到他后,先带他前往车站,再回家,汽车多行驶了10分钟,于是带他去车站这段路程汽车多跑了5分钟,而到车站的时间是6:00,所以妻子驾车遇到他的时刻应该是5:55.
(5)放学时小狗奔跑了3 km.孩子上学到学校时小狗的位置不定(可在任何位置),因为设想放学时小狗在任何位置开始跑,都会与孩子同时到家.之所以出现位置不定的结果,是
第一章作业解答第 57 页 共 58 页
由于上学时小狗初始跑动的那一瞬间,方向无法确定.
10. 某人第一天上午9:00从甲地出发,于下午6:00到达乙地.第二天上午9:00他又从乙地出发按原路返回,下午6:00回到甲地.试说明途中存在一点,此人在两天中同一时间到达该处.若第二天此人是下午4:00回到甲地,结论将如何?
答:(方法一)我们以甲地为始点记路程,设从甲地到乙地的路程函数为f(t)(即t时刻走的路程为f(t)),同样设从乙地到甲地的路函数为g(t),并设甲地到乙地的距离为a(a>0).由题意知:f(9)?0,f(18)?a,g(9)?a,g(18)?0. 令 *
h(t)?f(t)?g(t),则有h(9)?f(9)?g(9)??a?0,
h(18)?f(18)?g(18)?a?0由于f(t),g(t)都是时间t的连续函数,因此h(t)也是时间t的连续函数,由连续函数的介值定理,?t0?[9,18],使h(t0)?0,即f(t0)?g(t0). 若第二天此人是下午4:00回到甲地,则结论仍然正确,这是因为h(9)?f(9)?g(9)??a?0,h(16)?f(16)?g(16)?f(16)?0.
(方法二)此题可以不用建模的方法,而变换角度考虑:设想有两个人,一人从甲地到乙地,另一人从乙地到甲地,同一天同时出发,沿同一路径,必定相遇.若第二天此人是下午4:00回到甲地,则结论仍然正确.
第一章作业解答第 58 页 共 58 页
四 : 15数学模型第三版_课后习题答案
五 : 数学模型第三版)课后习题答案
本文标题:数学模型第三版答案-2015高三数学闸北二模 有答案61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1