| 我 | 早 | 就 | 要 | 灭 | 吴 | 了 | , | 今 | 日 | 终 | 遂 | 心 | 。 | 二 : 定积分练习题(含答案)
定积分练习题
一、单项选择题
1.
∫
1 0
e dx 与 ∫ e dx 相比 有关系式 相比,有关系式 有关系式(
x x2 0
1
).
(A) (C )
∫ ∫
1 0 1 0
e dx < ∫ e dx
x x2 0
1
(B )
∫
1 0
e dx > ∫ e dx
x x2 0
1
e dx = ∫ e dx
x x2 0
1
(D) [
∫
1 0
e dx ] = ∫ e dx
x 2 x2 0
1
答案 B
由于在 由于在区间 ( 0,1), e > e
x x2
1
2.如果 f (x) 在 [1, 1] 上连续,且平均值为 2,则 2.如果 上连续 且平均值为 则 ( A )1 ( B ) 1 (C )4
∫
1 1
f ( x)dx =(
).
( D) 4
答案: 答案 C .
1 1 因为平均值 因为平均值 2 = ∫ 1 f ( x )dx 1 ( 1)
则
∫
1 1
f ( x )dx = 4
2
d x sin t 2dt =( ). 3. dx ∫ a 2 2 ( A ) sin x sin a 2 ( C ) sin x
答案: 答案 C .
( B ) 2 x cos x ( D ) 2 x sin x
2 2
根据变上限求导公式有: 根据变上限求导公式有 变上限求导公式 d x sin t 2dt = sin x 2 dx ∫ a
3
d b 4. ∫ a arcsin xdx =( dx
(A) 0 ( C ) arcsin x (B )
).
1
2
1 x ( D ) arcsin b arcsin a
答案: 答案 A .
由于定积分是一个常数 而常数的导数等于零 由于定积分是一个常数, 常数的导数等于零 定积分 常数 等于
所以
d b ∫ a arcsin xdx = 0 dx
4
5.设 是连续函数,且 5.设 f ( x ) 是连续函数 且 F ( x ) = ( A ) e f (e ) f ( x ) ( C ) e f (e ) f ( x )
x x
x x
∫x
e x
f ( t )dt ,则 F ′( x ) =( 则
x x
).
( B ) e f (e ) + f ( x ) (D)
e x f (e x ) + f ( x )
答案: 答案 A .
因为 F ′(x) = f (e ) (e )′ f ( x)
x x
=e
x
f (e x ) f ( x )
5
6.设 的某邻域内连续,且当 6.设 f ( x ) , ( x ) 在点 x = 0 的某邻域内连续 且当 x → 0 时,
f ( x ) 是 ( x ) 的高阶无穷小 则当 x → 0 时, ∫ 的高阶无穷小,则当
是
x 0
f ( t ) sin tdt
∫
x 0
t ( t )dt 的 (
).
( A ) 低阶无穷小 ( C ) 同阶但非等价无穷小
( B ) 高阶无穷小 ( D ) 等价无穷小
答案: 答案 B .
因为
x →0
∫ lim
x 0
f ( t ) sin tdt
x 0
∫
t ( t )dt
f ( x ) sin x = lim =0 x → 0 x ( x )
6
7.设 7.设 f ( x ) =
∫
x 0
( t 1)e t dt ,则 f ( x ) 有 ( 则
).
( A ) 极小值 2 e ( C ) 极大值 2 e
( B ) 极小值 e 2 ( D ) 极大值 e 2
答案: 答案 A .
解 因为 f ′( x ) = ( x 1)e
x
所以,当 x > 1 时, f ′( x ) > 0 所以, 当 x < 1 时, f ′( x ) < 0
则 f ( x ) 有极小值 f (1) =
∫
1 0
( t 1)e t dt = 2 e
7
x x2 8.设 是连续函数, 8.设 f ( x ) 是连续函数 a ≠ 0 , F ( x ) = ∫ a f (t )dt , xa ). 则 lim F ( x ) = (
x→ a →
a2 (A)
( B ) a f (a )
2
(C ) 0
( D ) 不存在
答案: 答案 B.
因为
lim
x→ a →
∫
x a
f ( t )dt
xa
f ( x) = lim = f (a ) x →a 1
2 所以 lim F ( x ) = a f ( a ) .
x →a
8
9.
1 cos x ( A) 1 (B) 2
x →0
∫ lim
sin 2 x 0
ln(1 + t )dt
=( ). (C ) 4 ( D) 8
答案: 答案 C.
因为
x→ 0
∫ lim
sin 2 x 0
ln(1 + t )dt
1 cos x
ln(1 + sin 2 x ) 2 cos 2 x = lim x→ 0 sin x
ln( 1 + sin 2 x ) sin 2 x = lim 2 cos 2 x lim x→ 0 x→ 0 sin 2
x sin x
sin 2 x 2 sin x cos x = 4 = 2 lim x → 0 sin 2 x sin x
9
10.设 10.设 F ( x ) =
∫
x 0
1 1 1 x dt + ∫ dt ,则 ( 则 2 0 1+ t2 1+ t
).
2 ( C ) F ( x ) ≡ arctan x ( D ) F ( x ) ≡ 2 arctan x
( A ) F ( x) ≡ 0
( B ) F ( x) ≡
π
答案: 答案 B .
1 + 因为 F ′( x ) = 2 1+ x
∴ F (x) ≡ C
1
1 1 2 = 1 1 =0 1 2 x 1 + x2 1 + x2 1+ ( ) x
1 1 1 π dt + ∫ dt = 则 F ( x ) ≡ F (1) = ∫ 2 2 0 1+ t 0 1+ t 2
10
11.若 11.若
∫
k 0
3 e dx = ,则 k = ( 则 2
2x
).
(A) 1
(B ) 2
( C ) ln 2
1 ln 2 (D) 2
答案: 答案 C .
因为
∫
k 0
1 2x e dx = e 2
2x
k 0
1 2k 3 = (e 1) = 2 2
则 k = ln 2
11
12.积分 12.积分 I = t
∫
s t 0
f ( tx )dx 与(
(B ) s,t
)有关 有关. 有关 (C ) x , t (D) s
( A ) s,t , x
答案 : D
因为 I = t ( 令 t x= u) ∫ f (tx )dx = t ∫ s = ∫ f ( u)du s 所以, 所以,积分 I = t ∫ t f ( tx )dx 只与 s 有 关 0
0 s t 0
s
1 f ( u ) du t
0
12
13.设 13.设
∫
x 0
f (t )dt = 2 x 3 ,则 ∫ 2 cos xf ( sin x)dx = ( 则
0
π
).
( A)
π
3
4
(B)
π
3
4
(C ) 2
( D) 2
答案: 答案 C.
因为
∫
π
2 0
cos xf ( sin x )dx = ∫
π
3 2 0
π
2 0
f ( sin x )d( sin x )
= 2 ( sin x )
= 2
13
14.
∫
a a
x[ f ( x ) + f ( x )]dx = (
).
(A ) 4 (C ) 0
∫
a 0
xf ( x )dx
(B ) 2
∫
a 0
x[ f ( x ) + f ( x )]dx
( D ) 以上都不正确
答案: 答案 C.
函数. 因为 x [ f ( x) + f ( x) ] 是奇函数 .
所以
∫
a a
x [ f ( x ) + f ( x )] dx = 0
14
sin x 4 3 4 2 cos xdx , N = ∫ π (sin x + cos x )dx , 15.设 15.设 M = ∫ π 2 1+ x 2 2
2
π
π
P =∫
π
2
( x 2 sin 3 x cos 4 x ) dx ,则有 ( 则有 π
2
).
(A) N < P < M (C ) N < M < P
(B ) M < P < N (D) P < M < N
答案: 答案 D.
π
2
因为根据奇偶函数的性质有 因为根据奇偶函数的性质有: 奇偶函数的性质
sin x 4 M =∫ π cos xdx = 0 , 2 1+ x 2
N =∫ P=∫
π
2
(sin 3 x + cos 4 x )dx = ∫ π
2
π
2
π
2
cos 4 xdx > 0 ,
π
2
π
2
( x 2 sin 3 x cos4 x )dx = ∫ π
2
π
2
cos4 xdx < 0
15
二、填空题
1. lim
n→∞
∫
1 0
x n dx =
答案: 答案
0
.
1 0
因为
2.
lim ∫
n→ ∞
1 x dx = lim =0 n→ ∞ n + 1
n
a b
∫
b a
f ( x )d x + ∫ f ( x )d x =
答案: 答案
0
.
因为
∫
a b
f ( x )dx = ∫ f ( x )dx
a
16
b
3.
∫
1 0
( x e )′ d x =
10 x
1
答案: 答案 e .
因为
∫ (x
0
10 x
e )′dx = x e
10 x
1 0
=e
π nπ 1 2π ]= + + 1 + cos 4. lim [ 1 + cos + 1 + cos n→ ∞ n n n n
答案: 答案
2 2
因为 原式 =
π
.
∫
1
0
1 + cos πx dx =
2
∫
1 0
2 cos
π x
2
dx
17
=( 2
π
sin
πx
2
1
) =
0
2 2
π
5. 设 f ( x ) =
∫
1 x 2
0
e dt ,则 f ′( x ) = 则
t 2
2
答案: 2 xe
(1 x 2 )
.
( x)
a
根据变上限求导公式 公式: 因为, 根据变上限求导公式 ( ∫
f ( t )dt )′ = f ( ( x )) ′( x )
(1 x 2 )
2
f ′( x ) = e
6. 设
(1 x 2 )
2
(1 x )′ = 2 xe
2
.
∫
x2 + 1 0
f (t ) dt
= ln x ,其中 f (x ) 为连续函数 则 f (5) = 为连续函数,则 其中
解 从
1 答案: . 8
2
∫
x2 + 1 0
f ( t ) dt = ln x 两边求导 两边求导:
1 f ( x + 1) 2 x = x
∴
1 f ( x + 1) = 2x2
2
2
1 1 所以,由连续性有 由连续性有: = 18 所以 由连续性有 f ( 5) = lim f ( 2 x + 1) = x→2 24 8
7.设 是连续函数,且 7.设 f ( x ) 是连续函数 且 f ( x ) = sin x +
∫
π
0
f ( x )dx ,则 f ( x ) = 则
2 答案 : f ( x ) = sin x + 1π π 解: 令 ∫ f ( x )dx = a
则 f ( x ) = sin x + a
两边积分得到: 两边积分得到
0
∫
π
0
f ( x )dx = ∫ (sin x + a )dx
0
π
从而有: 从而有 a = 2 + aπ
2 故 a= 1π
2 因此 f ( x ) = sin x + 1π
19
1 0 cos t 2 dt = 8. lim ∫ x → 0 x sin x
答案: 答案
1
.
因为根据洛 因为根据洛必塔法则 根据
1 lim x→ 0 x
∫
0 sin x
cos t d t = lim
2
∫
0 sin x
cos t d t x
2
x→ 0
= lim
cos(sin
x→ 0
x ) cos x = 1 1
2
20
2 x 0 ≤ x < 1, 9.设 ,则 ∫ f ( x )dx = 9.设 f ( x ) = 则 0 1, 1 < x ≤ 2 . 3 答案: 2
分段函数的定积分, 分段函数的定积分 一般采用分段积分
则
∫
2 0
f ( x )dx = ∫ xdx + ∫ 1 dx
0 1
1
2
1 2 = x 2
1
0
1 3 +1= +1= 2 2
21
10.
∫
1 0
(e x + e x )dx =
答案:
因为. 因为.
ee
1
.
x x 1 0
∫
π
1 0
(e + e )dx = e
x
e
x
1 0
= ee
1
.
11.
∫
π
2 0
sin x dx = 2 1 + cos x
4
π
答案:
.
π sin x 1 2 2 dx = ∫ d cos x 因为. 因为. ∫ 2 2 0 1 + cos x 0 1 + cos x
= arctan(cos x )
π
2 0
=
π
4
22
12.若 12.若
∫
f ( x )dx = 2 x + C ,则 ∫ x f ( x 2 + 1)dx = 则
2
2
0
答案: 24
2
.
2
1 2 2 2 因为 ∫ x f ( x + 1)dx = ∫ f ( x + 1)d( x + 1) 0 2 0
1 2 2 = 2( x + 1) 2
2
= 25 1 = 24
0
23
13.
∫
1
1
xe
5 x2
dx =
答案: 0
.
由于被积函数是 函数. 由于被积函数是奇函数 被积函数
14.设 是连续奇函数,且 14.设 f (x ) 是连续奇函数 且
答案: 1
是连续奇函数, 因为 f ( x ) 是连续奇函数 则
从而
∫
1
0
f ( x )dx = 1 ,则 ∫ f ( x )dx = 则
1
0
∫
1 0
f ( x )dx + ∫
0 1
f ( x )dx = 0
∫
0 1
f ( x )dx =
∫
1 0
f ( x )dx = 1
24
15. 若
∫
b 1
ln xdx = 1 ,则 b = 则
答案: b = 0 .或 b = e
因为
∫
ln xdx = x (ln x 1) + C
所以
∫
b 1
ln xdx = x (ln x 1) 1 = 1
b
从而得到 从而得到 b = 0 .或 b = e
25
16.
∫
4 0
e x dx =
2
答案: 2(e
因为
+ 1)
x 2 t 0
∫
4 0
e d x = ∫ e 2 td t
2 t
(令
2 t
x =t)
= 2 ∫ t de
0
= 2t e 2t
2 0
t
2 0
2 ∫ e dt
0
= 4e 2 e
2
t
= 2 (e
2
+
1)
26
三、计算题
1. 设函数 y = f ( x ) 在
( 0 , + ∞ ) 内可导 内可导,
x 1
1 x 且 f ( x ) = 1 + ∫ f ( t )dt , 求 f ( x ) . x 1
解 由已知可得
x f ( x) = x + ∫
f ( t )dt ,
f ( x ) + x f ′( x ) = 1 + f ( x ) , 1 f ′( x ) = , 从而 f ( x ) = ln x + C , x 1 x 可得, 又从 f ( x ) = 1 + ∫ f ( t )dt 可得, f (1) = 1 x 1 故 f ( x ) = ln x + 1 27
两边求导: 两边
求导
2.求连续函数 2.求连续函数 f ( x ) ,使它满足 使它满足
1
∫
1 0
f (tx)dt = f ( x ) + x sin x .
1 x 解 因为 ∫ f ( t x )dt = ∫ f ( u)du ( 令 t x = u) . 0 x 0 x 2 所以 ∫ f ( u )d u = xf ( x ) + x sin x .
0
两边求导: 两边求导:
′( x ) + x 2 cos x + 2 x sin x . f ( x ) = f ( x ) + xf
从而 f ′( x ) = ( x cos x + 2 sin x ) .
f ( x ) = ∫ ( x cos x + 2 sin x )dx
= x sin x cos x + 2 cos x + C
= cos x x sin x + C
28
1 dx . 3. 计算 ∫ x 0 1+ e x 1 1 1 de dx = ∫ x 解 ∫ x 01+ e 0 e (1 + e x ) e dt x =∫ 令e =t 1 t (1 + t ) e 1 1 ) dt =∫ ( 1 t 1+ t
1
t = ln 1+ t
e
= 1 ln(1 + e) + ln 2
1
29
4. 计算 解
∫
2 1
2 1
x 2 x dx .
0 1
∫
2 1
x x dx = ∫ ( x 2 x ) dx +
2 2 0 1
+ ∫ ( x x )dx + ∫ ( x 2 x ) dx
1 3 1 2 =( x x ) 3 2
0
1 2 1 3 1 3 1 2 +( x x ) +( x x ) 2 3 3 2 0 1 1
1
2
1 1 1 1 8 4 1 1 11 = ( 0+ + )+( 0 )+( + ) = 3 2 2 3 3 2 3 2 6
30
5. 计算
∫
π
π
0
sin θ sin θ dθ .
3
解
∫
=
π
0
sin θ sin θ dθ = ∫
3
π
0
sin θ cos θ dθ
2
∫
=∫
π
0
sin θ cos θ d θ
2 0
sin θ cos θ dθ ∫
π π
2
sin θ cos θ dθ
=∫
π
2 0
sin θ d sin θ ∫
π
3 2 2
π π
2
3 2
sin θ d sin θ
π π
2
2 = (sin θ ) 3
0
2 (sin θ ) 3
4 = 3
31
6. 求
∫
3 4 1 2
arcsin x dx 的值 的值. x (1 x )
解
∫
3 4 1 2
arcsin x arcsin x dx = 2 ∫ d x x (1 x ) (1 x )
3 4 1 2
3 4 1 2
= 2∫
arcsin
x )
2
x d( arcsin
3 4 1 2
x)
2
= ( arcsin
7 = π 144
32
7. 设 F ( x ) =
∫
x2 0
e
t2
dt , 试求 试求:
的极值; (1) F ( x ) 的极值;
(2)曲线 拐点的横坐标;(3) (2)曲线 y = F ( x ) 拐点的横坐标;(3)
∫
3 2
x 2 F ′( x )dx 之值 之值.
解 (1)
F ′( x ) = e
x4
2x
x4
2
F ′( 0 ) = 0
F ′′( x ) = 2e
(2)
(1 4 x )
F ′ ′( 0 ) > 0
故 F ( x ) 在 x = 0 点取极小值 F ( 0) = 0 .
1 , F ′ ′( 0 ) = 0 因为在 x = ± 2 1 两侧, 并且在 x = ± 两侧, F ′′( x ) 异号 2 1 所以, 拐点横坐标 横坐标为 所以, y = F ( x ) 的拐点横坐标为 x = ± 2
33
(3)
∫
3 2
x F ′( x )dx = ∫ 2 x e
2 2
3
3 x
4
dx
1 3 x 4 4 = ∫ e d( x ) 2 2 1 x 4 3 1 81 16 = e = (e e ) 2 2 2
34
F ( x ) = ∫ t f ( x 2 t 2 )dt ,其中 f ( x ) 在 x = 0 点的 8.设 8.设 其中 0
x
F ( x) 某一邻域内可导,且 f ( 0) = 0 , f ′( 0) =1 ,求 lim 某一邻域内可导 且 求 . 4 x→ 0 → x 2 x 1 x 2 2 F ( x ) = ∫ t f ( x t )dt = ∫ f (u)du (令 x 2 t 2 = u) 解 0 2 0 F ( x) 用洛必塔法则求 用洛必塔法则求 lim , ( 注意运用条件 ) 4 x→ 0 → x 2 1 f ( x 2 ) f (0) F ( x) 1 2x f (x ) = lim lim = lim 4 3 x →0 4 x→ 0 x→ 0 2 x2 0 x 4x
1 1 = f ′( 0 ) = 4 4
35
x+2 dx . 9.计算 9.计算 ∫ 2 0 x x2 x+2 拆项计算 计算. 解 将 2 拆项计算 x x2 1 1 x+2 x+2 ∫ 0 x 2 x 2 d x = ∫ 0 ( x 2 )( x + 1) d x 4 1 1 1 1 1 dx ∫ dx = ∫ 3 0 x2 3 0 x+1 4 1 1 1 1 1 dx ∫ dx = ∫ 3
0 x2 3 0 x+1
1
4 1 5 = [ ln( 2 x ) ln( x + 1) ] = ln 2 3 3 3 0
1
36
dx 10. ∫ e x (1 ln x) ln x e e dx d( ln x ) =∫ 解. ∫ e e x (1 ln x ) ln x (1 ln x ) ln x
e
= 2∫
e e
d( ln x ) ( 1 ln x )
e e =
= 2 arcsin( ln x )
π
2
.
37
dx 11.计算 11.计算 ∫ 0 (3 + 2 x x 2 )3 / 2 2 2 dx d( x 1) 解 ∫ =∫ 2 3/ 2 0 (3 + 2 x x ) 0 [ 4 ( x 1) 2 ]3 / 2
2
dt =∫ 1 [ 4 t 2 ]3 / 2
1
(令 x 1 = t )
( 令 t = 2 sin u )
π dt 2 cos ud u 6 = 2∫ = 2∫ 2 32 0 (4 t ) 0 8 cos 3 u
1
1 = 2
∫
π
6 0
du 2 cos u
1 = tan u 2
π
6 0
=
1 2 3
38
12.计算 12.计算
解
∫
4 0
x
2
4 0
4 x x dx
2
原式= 原式=
2 2
= ∫ ( t + 2)
2 2
∫ 2
2
x
2
4 ( x 2) d( x 2)
2
2
4 t dt
2
2
(令 x 2 = t )
因为奇函数积分为零) = ∫ ( t + 4) 4 t dt (因为奇函数积分为零 因为奇函数积分为零
= 2 ∫ ( t + 4 ) 4 t dt
2 2
= 2 ∫ 2 ( 4 sin 2 u + 4)4 cos 2 u du (令 t = 2 sin u ) 令
0 π
0
= 8 ∫ 2 sin 2 ( 2u) du + 32 ∫ 2 cos 2 u du
= 4 ∫ 2 [ 1 cos( 4u) ] du + 16 ∫ 2[ 1 cos( 2u) ] du
0
π
π
0
π
0
π
0
= ( 4
π
2
0 ) + ( 16
π
2
0 ) = 10π
39
13.计算 13.计算
∫
2 2
( x 2 4 x 2 + x cos 5 x )dx
解 因为 x
所以
2
4 x 是偶函数 x cos x 是奇函数 是偶函数, 是奇函数,
2
5
∫
2 2
(x
2
4 x + x cos x )dx = ∫
2 5
2 2
x 2 4 x 2 dx
= 2∫ x
π
0
2
2
4 x
2
dx
π
= 2 ∫ 2 4 sin 2 t 4 cos 2 t dt
0
( 令 x = 2 sin t )
= 8∫
= 4
π
2 0
π
= 4∫ 2 (1 cos 4t ) dt sin ( 2 t ) d t 0
2
2
= 2π .
40
2 + 4 + x2 π 2 1 2 sec2 t dx = ∫ 4 dt (令 x = 2 tan t ) 解 ∫ 令 0 0 2 + 2 sec t 2 + 4 + x2 π π 1 1 dt = 4 ( 1 =∫ 4 0 cos 2 t + cos t ∫ 0 cos t cos t + 1 )d t
0
14.计算 14.计算
∫
2
1
dx
= ln sec t + tan t
π
4 0
∫
π
4 0
1 t 2 cos 2
2
dt
π
= ln
= ln
2 + 1 tan
t 2 + 1 tan 2 π
8
4 0
41
x sin x dx 15.计算 15.计算 ∫ 2 0 1 + cos x π π π 解 用公式 ∫ xf(x)dx = ∫ xf(x)dx ( 令 x = π t ) 0 2 0 3 π x sin x π π sin3 x dx = ∫ dx 则 ∫ 2 2 0 1 + cos x 2 0 1 + cos x π π sin 2 x
=
1 t2 dt ( 令 cos x = t ) = ∫ 2 2 1 1+ t 2 11 t dt ( 因为被积函数为偶函数 因为被积函数为偶函数) =π∫ 2 01+ t
1
π
3
π
2∫
0
1 + cos x
2
d cos x
2 π =π∫ ( 1)d t = π ( 1 ) 2 0 1 + t 2
1
42
17.计算 17.计算
∫
1 0
ln(1 x )dx
解
∫
ln(1 x )dx = x ln(1 x ) ∫
= x ln( 1 x )
∫
1 (1 )d x 1 x
1 x dx 1 x
= x ln(1 x) x ln(1 x) + C
所以
∫
1 0
ln(1 x )dx = [ ( x 1) ln(1 x ) x ] 0
1
= lim ( x 1) ln( 1 x ) 1
1 t ln t 1 = 1 = lim 1 = lim 2 t → 0+ 0 1 t t → 0+ 0 1 t
43
x →1 0
18.计算 18.计算
∫
2
π
2
tan 2 x[sin 2 2 x + ln( x + 1 + x 2 )]dx π
2
解 由于 tan x sin 2 x 是偶函数
2
2
tan x ln( x + 1 + x ) 是奇函数
2
所以 原式 =
∫
π
2
π
2
tan x sin 2 xdx + 0
2 2
= 8∫
π
2 0
sin 4 x d x
3 1 π 3π = 8 = 42 2 2
44
19.计算 9.计算 9.
1
∫
1 0
x arcta
n 1 x 2 dx
2
1 1 2 2 解 ∫ x arctan 1 x dx = ∫ arctan 1 x d(1 x ) 0 2 0 1 0 = ∫ arctan t dt ( 令 1 x 2 = t ) 2 1 1 1 = ∫ arctan t dt 2 0 1 1 1 1 1 1 dt = t arctan t ∫ t 2 2 0 1+ t 2 t 0
1 = 8 4
π
∫
1 0
t dt 1+ t
45
=
π
8 π = 8
=
=
π
8 π
8
1 1 t dt ∫ 4 0 1+ t 2 1 1 u du (令 t = u ) ∫ 令 2 2 0 1+ u 1 1 1 )du ∫ (1 2 2 0 1+ u 1 π π 1
2 + 8 = 4 2
46
20.计算 20.计算
∫
1 0
arcsin x arccos xdx
解 设 arcsin x = t ,则 arccos x =
π
2
t , dx = cos tdt
则
∫
=
1 0
arcsin x arccos xdx = ∫ t (
2 0
π
π
2
t ) cos tdt
π
2
π
2 0
∫
π
2 0
t cos t d t
∫
π
2 0
t cos t d t
2
用分部积分法,我们可以求出: 分部积分法 我们可以求出 积分 可以求出
π
2∫
t cos tdt =
π π
2 2 (
1)
, 2 0
∫
π
t cos t d t =
2
π
2
所以, 所以, 原式 = 2
π
4
47
2
2
ln t dt 在区间 [e , e2 ] 上的最大值 21.求函数 21.求函数 I ( x ) = ∫ e t 2 2t + 1 ln x I ′( x ) = 2 [e , e 2 ] 上大于零, 上大于零, 解 ,在区间 x 2x + 1 2 单调递增 递增. 所以 I ( x ) 在区间 [e , e ] 上单调 递增
x
因此函数 I ( x ) 在区间 [e , e ] 上的最大值为: 因此函数 上的最大值为
2
e2 ln t 1 2 I (e ) = ∫ dt = ln t d ( ) e t 2t + 1 e t 1
e2
∫
e2 1 1 1 ) ln t + ∫ = ( dt e t 1 t t 1 e
48
e2
e2 1 1 1 ) ln t + ∫ = ( dt e t 1 t t 1 e e2 2 1 1 1 = 2 + +∫ ( )dt e t 1 t e 1 e 1
e2
1 t 1 = + ln e+1 t e
e2
1 = + ln( e + 1 ) 1 e+1
49
22.计算积分 22.计算积分 I =
∫
1 0
x f ( x) t 2 dx ,其中 f ( x ) = ∫ 1 e dt 其中 x
采用分部积分的方法: 解 采用分部积分的方法
则 I=
∫
1 0
1 f ( x) dx = 2 ∫ f ( x )d x 0 x
= 2 f ( x) x
1 0
2∫
1 0
1 0
x df ( x )
x
= 2 f (1) 0 2 ∫
1 x 0
x e
1
1 2 x
dx
= ∫ e dx = e
1
50
三 : 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)
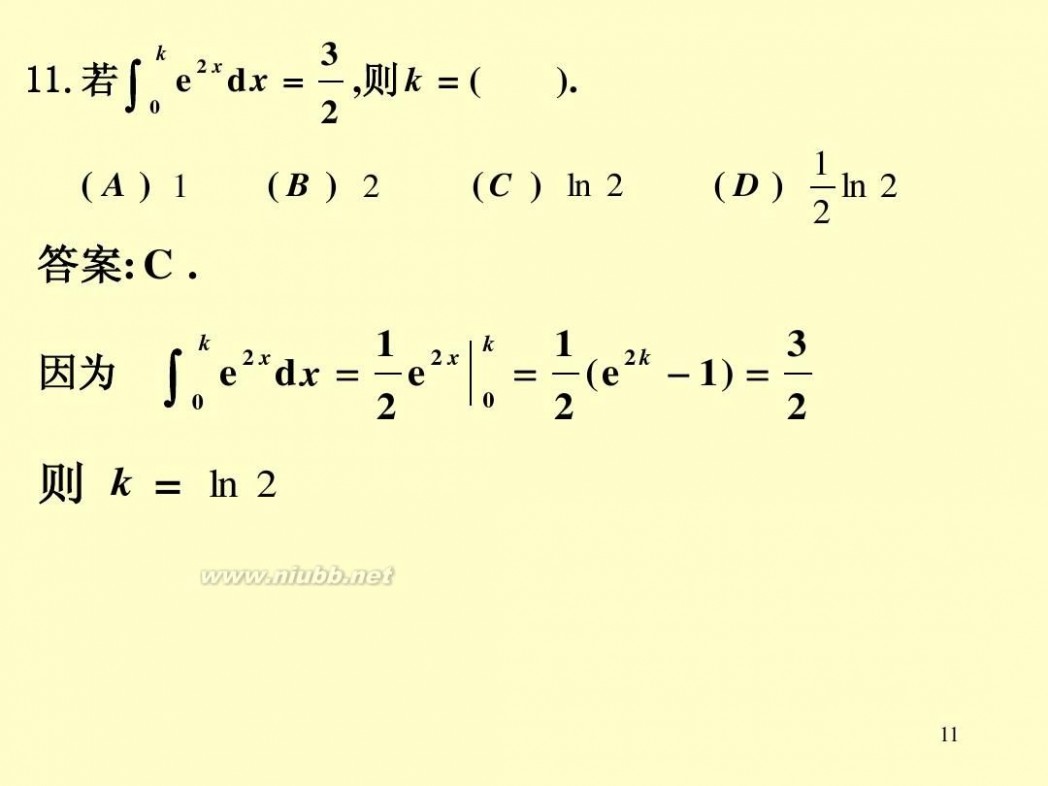
不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)
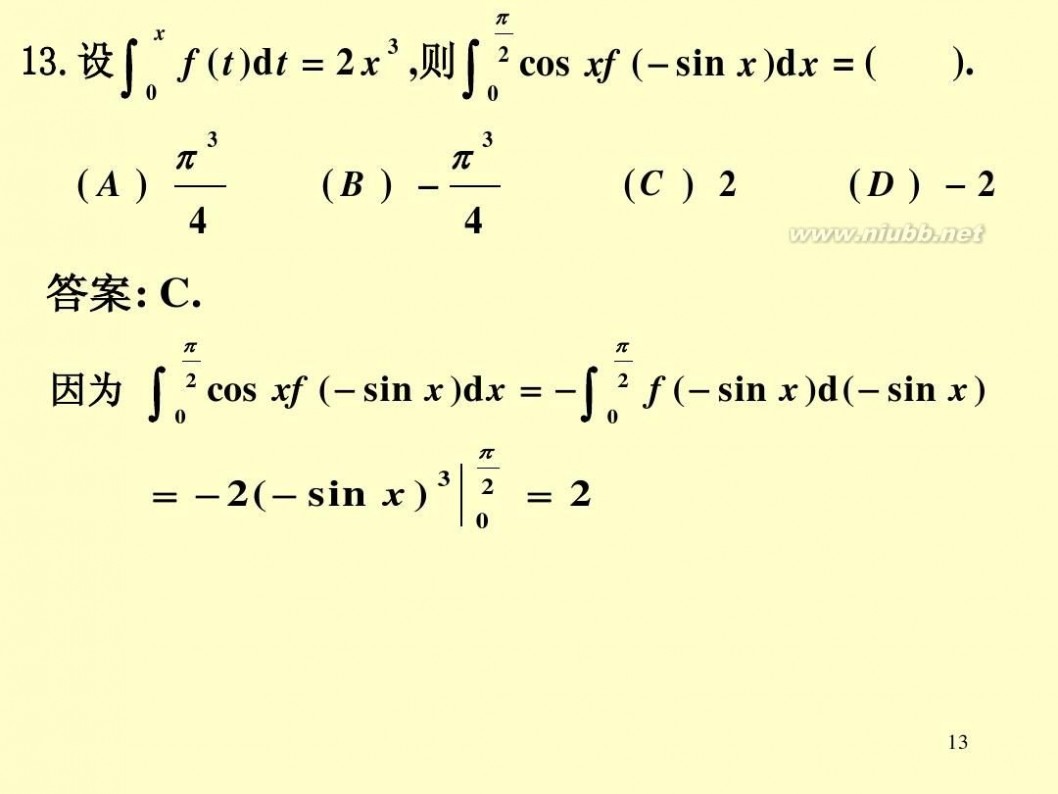
不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)
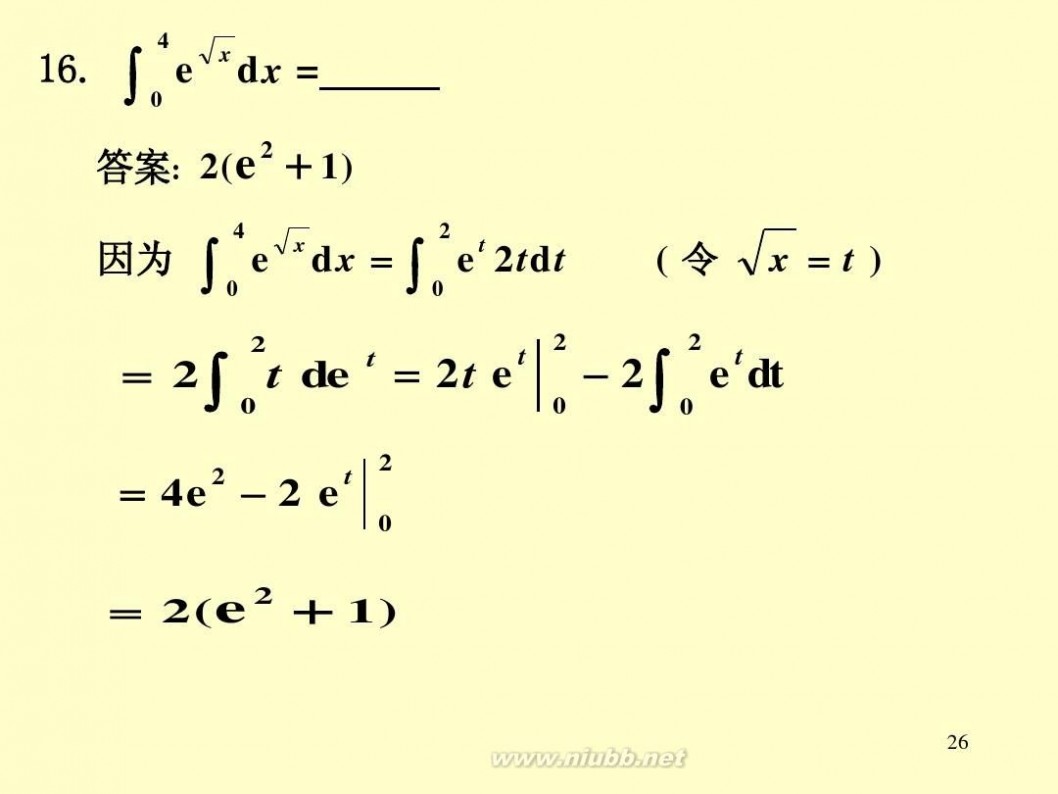
不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)
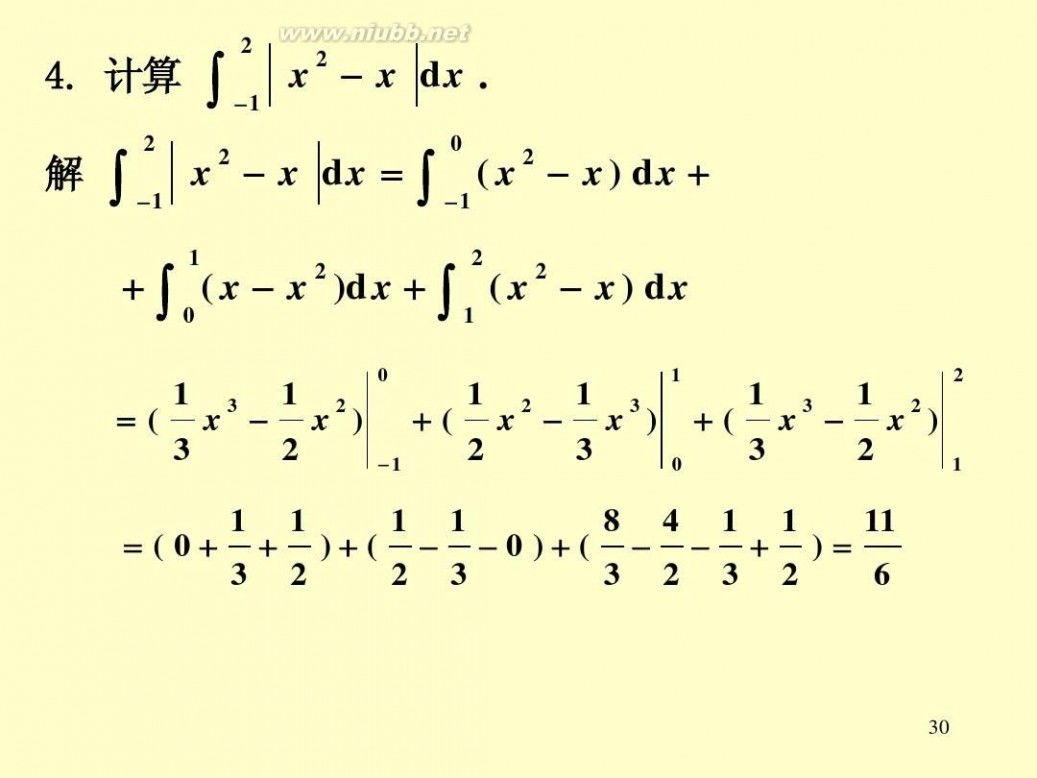
61阅读提醒您本文地址:
不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)
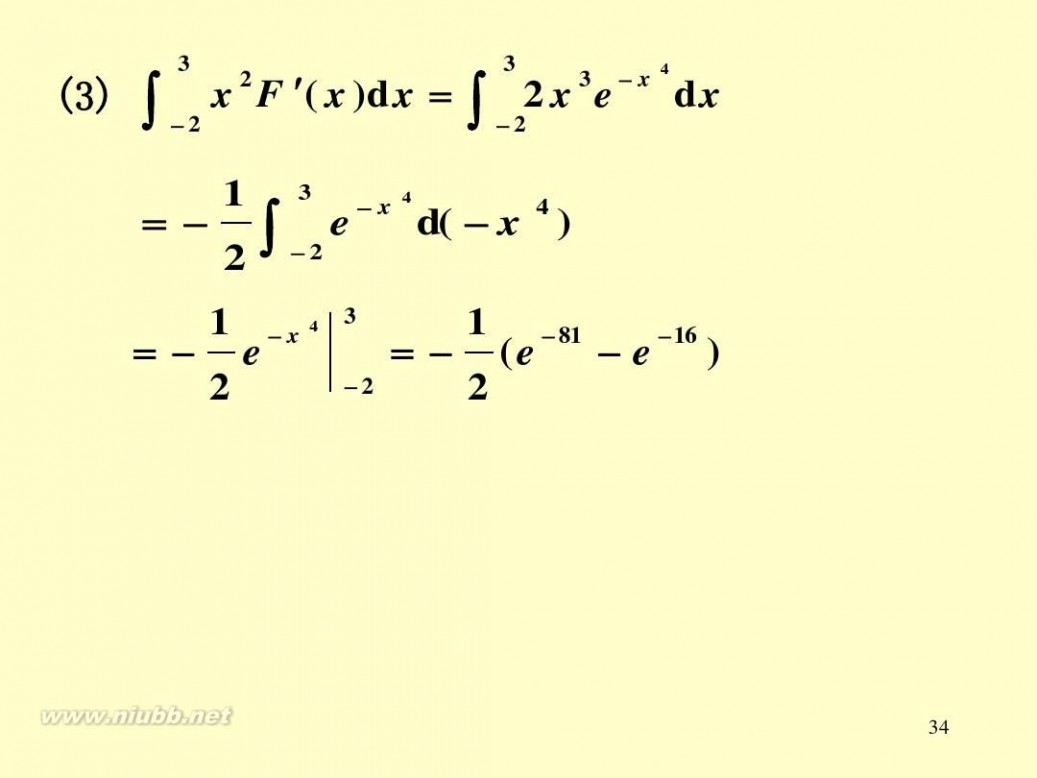
不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)
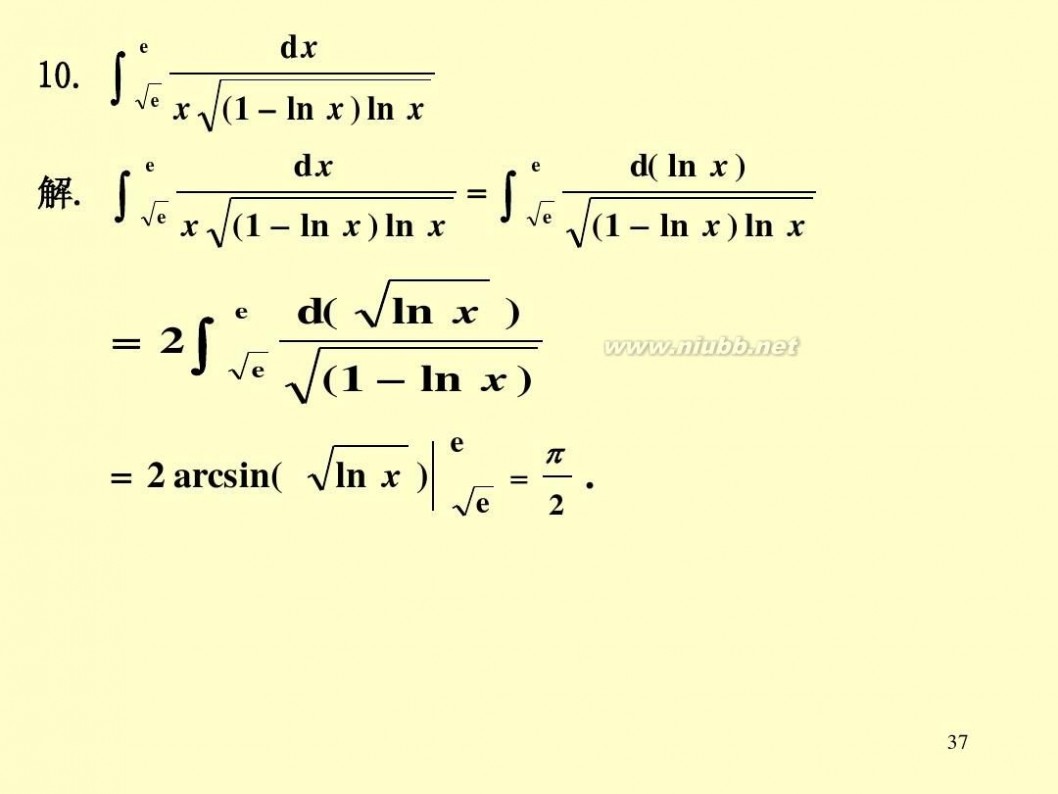
不定积分习题 定积分练习题(含答案)
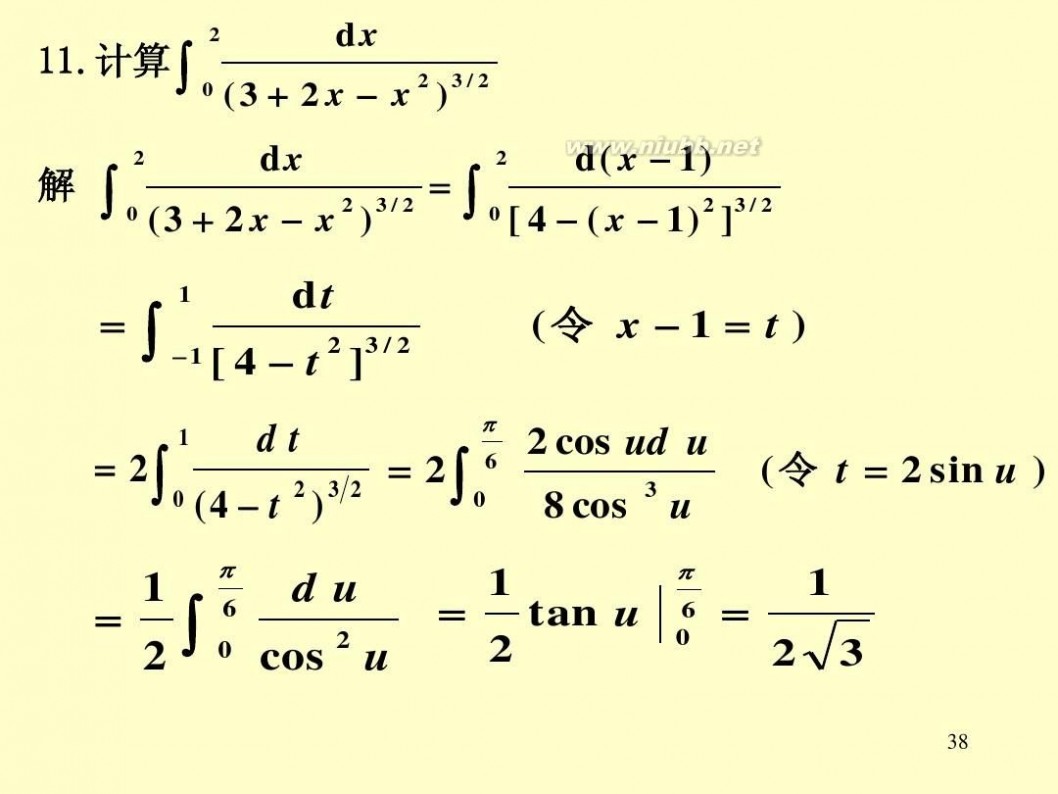
不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)
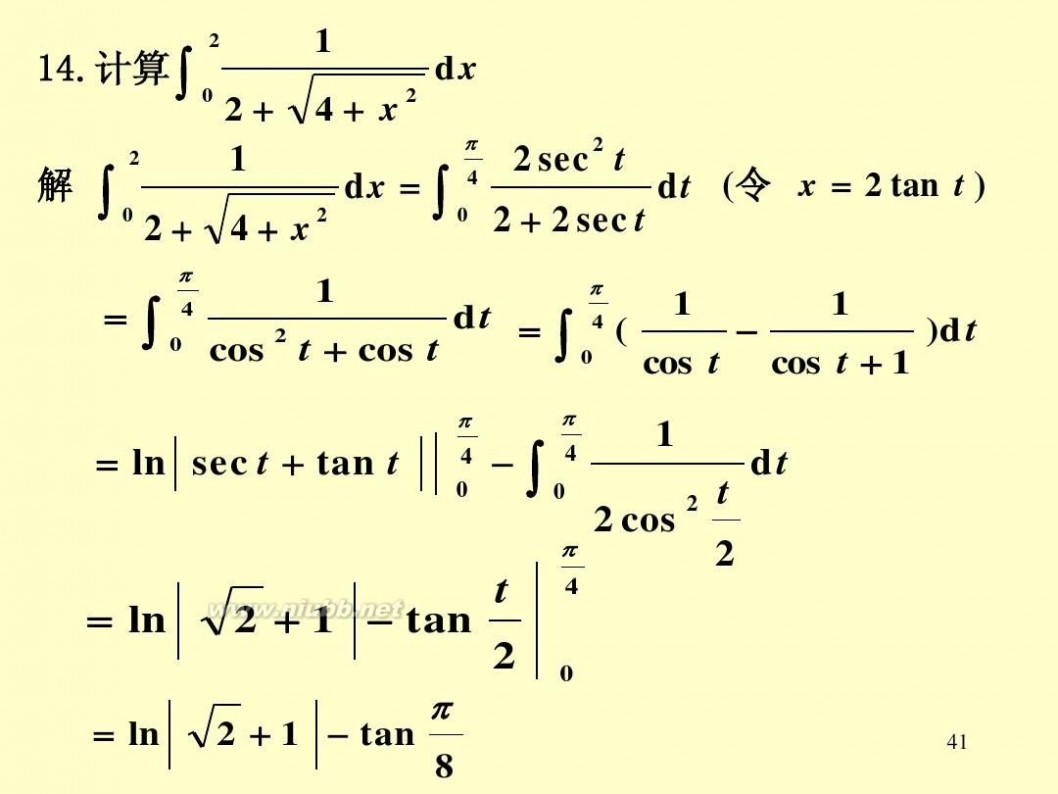
不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)
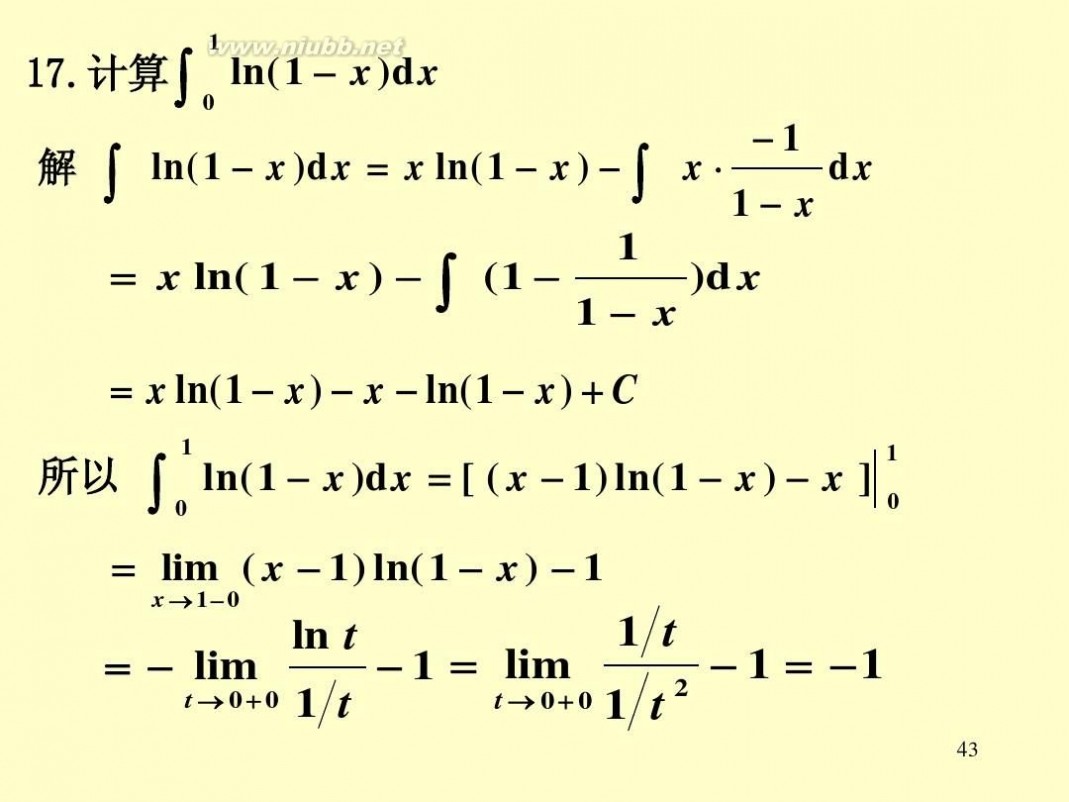
不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)
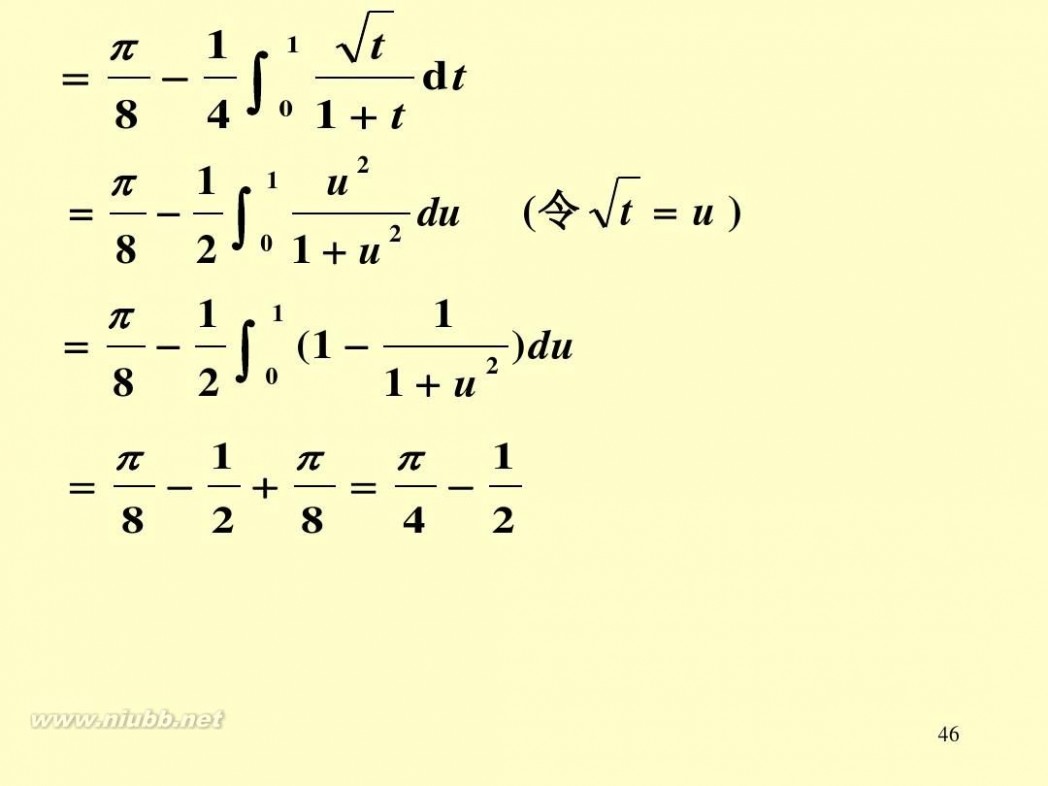
不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)

不定积分习题 定积分练习题(含答案)
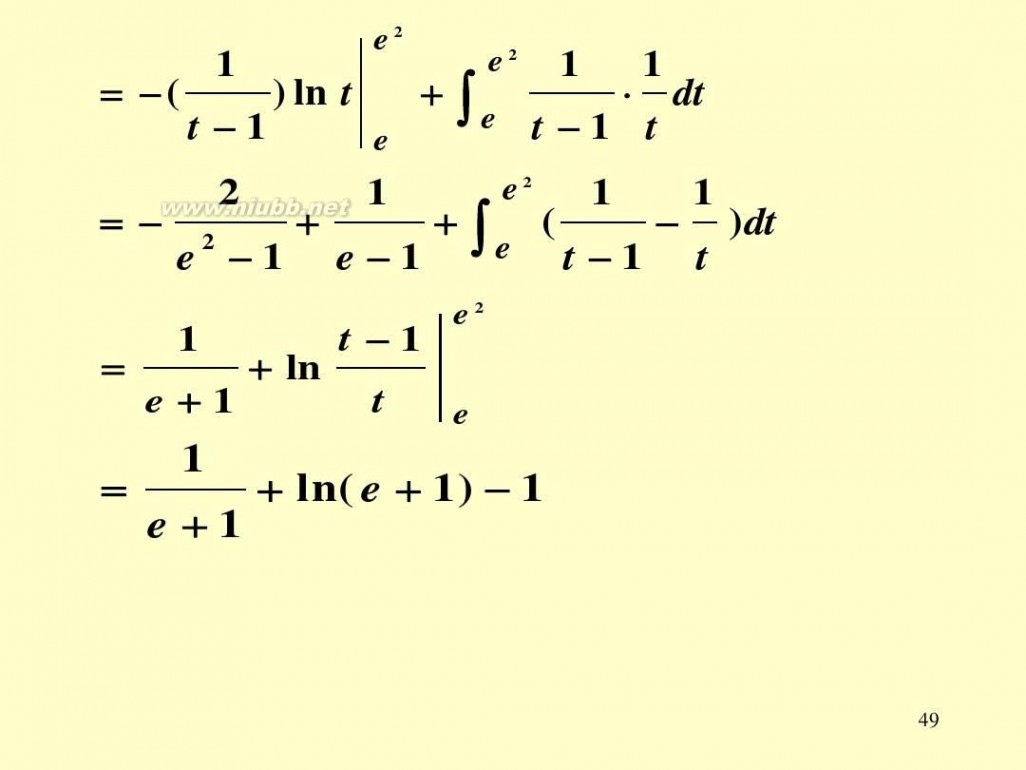
不定积分习题 定积分练习题(含答案)

61阅读提醒您本文地址:
四 : 9.2挫而不折 积极进取教案及练习题
一、 教学目标:
情感、态度、价值观:从容应对挫折和逆境,勇于克服困难,积极进取.
能力:增强调控自我、承受挫折、适应环境的能力,掌握战胜挫折的方法。
知识:知道战胜挫折、磨砺意志的基本方法。
二、重点难点:战胜挫折的途径和方法是本课的教学重点和难点。
三、课前准备:
学生准备:搜集整理勇于战胜挫折的名人、伟人故事,也可以是自己身边感人的故事。
教师准备:了解掌握中学生日常生活中普遍遇到的困难和挫折,调查了解导致中学生受到挫折的普遍因素。
四、教学流程:
六、课堂巩固:
(一)单项选择题:
1.被誉为“乐圣”的贝多芬,一声屡遭磨难,尤其是耳聋是对他最为沉重的打击,但他 发出了“要扼住命运的咽喉”,终于从 挫折中站起来。这是因为她 ( )
a吃一堑,长一智 b主动寻求帮助
c直面挫折,不畏不惧,从精神上战胜挫折。d自我疏导,自我排解
2.一次数学考试,李强.张芳均考的不理想。张芳从此以后,由害怕数学到讨厌数学,最终中考失利;而李强则分析原因,发奋努力,终于成为数学尖子。这件事告诉我们 ( )
①挫折即是坏事也是好事 ②李强更聪明些
③人们对待挫折的态度不同,结果也不一样 ④遇到挫折应积极寻找应对方法战胜挫折
a ①②③ b②③④ c①③④ d①②④
3.我国社会主义现代化建设的总设计师邓小平同志一生三起三落尤其是“文革”时期的两次沉浮,是他最痛苦的时期。他仍在为中华民族的伟大复兴而思考,他说:“我是人民的儿子,我深情的爱着我的祖国和人民。”这表明,要战胜挫折,应该 ( )
①冷静分析,从容面对 ② 学会自我疏导
③积极进取,勇于探索创新 ④ 直面挫折,不畏不惧
a ①② b①②③④ c②③ d ②③④
4.“如果生活只有晴空而没有阴语笼罩,只有幸福而没有悲哀,只有 欢乐而没有痛苦,那么,这样的生活根本就不是生活—至少不是人的生活。”这句名言说明 ( ) a生活是痛苦不堪的 b不要把生活想象的那么美好
c生活就是每天经经历欢乐痛苦 d所有的人都会经历挫折和失败
5. 2008年5月12日,四川汶川发生了强烈的地震,造成重大人员伤亡。造成此次灾难的主要原因是( )
a家庭因素 b生理因素 c社会因素 d自然因素
(二)非选择题:
【品味寓言 启迪人生】两只青蛙在觅食时不小心掉进路旁的一只牛奶罐里,罐里的牛奶不多但足以让青蛙体验到什么叫灭顶之灾。一只青蛙想:“完了!完了!这么高的牛奶罐,我永远也出不去了。”于是它很快就沉了下去。另一只青蛙看见同伴沉没于牛奶中,并没有沮丧、放弃,而是不断的告诫自己:“上帝给了发达的肌肉,我一定能够跳出去。”它鼓足力量,一次一次奋起、跳跃----生命的力量与美展现在它每一次搏击与奋斗中,最后成功脱险。
(1)从上面的寓言中,你悟出什么样的人生道理?
(2)我们在人生道路上也难免会遇到挫折,请你谈谈摆脱挫折的有效方法。
参考答案
(一)单项选择题:
1 c 2 c 3 b 4 d 5 d
(二)非选择题:
(l)人生难免有挫折;不同的人面对挫折的态度不同,将会导致不同的结果;只有意志坚强、有坚定信念的人才能实现人生的价值,享受真正的人生等。(答到两点即可)
(2)树立正确的人生;正确地认识挫折;直面挫折,不畏不惧 ;冷静分析,从容应对;自我疏导,自我排解;主动寻求帮助;积极进取,探索创新 。(须答到三点)
本文标题:面积进率练习题答案-范进中举练习(与练习册题目)有答案
本文地址: http://www.61k.com/1161057.html