一 : 初一数学上册应用题带答案

做初一数学上学期的应用题可以使人的大脑拥有更多的知识;以下是我们为大家整理的初一数学上册应用题带标准答案,希望你们喜欢。
。www.61k.com)1、运送29.5吨煤,先用一辆载重4吨的汽车运3次,剩下的用一辆载重为2.5吨的货车运.还要运几次才能完?
还要运x次才能完
29.5-3*4=2.5x
17.5=2.5x
x=7
还要运7次才能完
2、一块梯形田的面积是90平方米,上底是7米,下底是11米,它的高是几米?
它的高是x米
x(7+11)=90*2
18x=180
x=10
它的高是10米
3、某车间计划四月份生产零件5480个.已生产了9天,再生产908个就能完成生产计划,这9天中平均每天生产多少个?
这9天中平均每天生产x个
9x+908=5408
9x=4500
x=500
这9天中平均每天生产500个
4、甲乙两车从相距272千米的两地同时相向而行,3小时后两车还相隔17千米.甲每小时行45千米,乙每小时行多少千米?
乙每小时行x千米
3(45+x)+17=272
3(45+x)=255
45+x=85
x=40
乙每小时行40千米
5、某校六年级有两个班,上学期级数学平均成绩是85分.已知六(1)班40人,平均成绩为87.1分;六(2)班有42人,平均成绩是多少分?
平均成绩是x分
40*87.1+42x=85*82
3484+42x=6970
42x=3486
x=83
平均成绩是83分
6、学校买来10箱粉笔,用去250盒后,还剩下550盒,平均每箱多少盒?
平均每箱x盒
10x=250+550
10x=800
x=80
平均每箱80盒
7、四年级共有学生200人,课外活动时,80名女生都去跳绳.男生分成5组去踢足球,平均每组多少人?
平均每组x人
5x+80=200
5x=160
x=32
平均每组32人
8、食堂运来150千克大米,比运来的面粉的3倍少30千克.食堂运来面粉多少千克?
食堂运来面粉x千克
3x-30=150
3x=180
x=60
食堂运来面粉60千克
9、果园里有52棵桃树,有6行梨树,梨树比桃树多20棵.平均每行梨树有多少棵?
平均每行梨树有x棵
6x-52=20
6x=72
x=12
平均每行梨树有12棵
10、一块三角形地的面积是840平方米,底是140米,高是多少米?
高是x米
140x=840*2
140x=1680
x=12
高是12米
11、李师傅买来72米布,正好做20件大人衣服和16件儿童衣服.每件大人衣服用2.4米,每件儿童衣服用布多少米?
每件儿童衣服用布x米
16x+20*2.4=72
16x=72-48
16x=24
x=1.5
每件儿童衣服用布1.5米
12、3年前母亲岁数是女儿的6倍,今年母亲33岁,女儿今年几岁?
女儿今年x岁
30=6(x-3)
6x-18=30
6x=48
x=8
女儿今年8岁
13、一辆时速是50千米的汽车,需要多少时间才能追上2小时前开出的一辆时速为40千米汽车?
需要x时间
50x=40x+80
10x=80
x=8
需要8时间
14、小东到水果店买了3千克的苹果和2千克的梨共付15元,1千克苹果比1千克梨贵0.5元,苹果和梨每千克各多少元?
苹果x
3x+2(x-0.5)=15
5x=16
x=3.2
苹果:3.2
梨:2.7
15、甲、乙两车分别从A、B两地同时出发,相向而行,甲每小时行50千米,乙每小时行40千米,甲比乙早1小时到达中点.甲几小时到达中点?
甲x小时到达中点
50x=40(x+1)
10x=40
x=4
甲4小时到达中点
16、甲、乙两人分别从A、B两地同时出发,相向而行,2小时相遇.如果甲从A地,乙从B地同时出发,同向而行,那么4小时后甲追上乙.已知甲速度是15千米/时,求乙的速度.
乙的速度x
2(x+15)+4x=60
2x+30+4x=60
6x=30
x=5
乙的速度5
17.两根同样长的绳子,第一根剪去15米,第二根比第一根剩下的3倍还多3米.问原来两根绳子各长几米?
原来两根绳子各长x米
3(x-15)+3=x
3x-45+3=x
2x=42
x=21
原来两根绳子各长21米
18.某校买来7只篮球和10只足球共付248元.已知每只篮球与三只足球价钱相等,问每只篮球和足球各多少元?
每只篮球x
7x+10x/3=248
21x+10x=744
31x=744
x=24
每只篮球:24
每只足球:8
18小明家中的一盏灯坏了,现想在两种灯裏选购一种,其中一种是11瓦(即0.011千瓦)的节能灯,售价60元;另一种是60瓦(即0.06千瓦)的白灯,售价3元,两种灯的照明效果一样,使用寿命也相同.节能灯售价高,但是较省电;白灯售价低,但是用电多.如果电费是1元/(千瓦时),即1度电1元,试根据课本第三章所学的知识内容,给小明意见,可以根据什麼来选择买哪一种灯比较合理?
参考资料:
(1) 1千瓦=1000瓦
(2) 总电费(元)=每度电的电费(元/千瓦时)X灯泡功率(千瓦)X使用时间(小时)
(3) 1度电=1千瓦连续使用1小时
假设目前电价为1度电要3.5元
如果每只电灯泡功率为21瓦,每小时用电则为0.021度.
每小时电费= 3.5元 X 0.021 =0.0735元
每天电费=0.0735 X 24小时 =1.764元
每月电费=1.764 X 30天 =52.92元
这是一个简单的一元一次方程的求解平衡点问题,目标是从数个决策中找出各个平衡点,从不同的平衡点选择中来找出较优的决策.
解答过程:
设使用时间为A小时,
1*0.011*A+60=1*0.06*A+3
这个方程的意义就是,当使用节能灯和白灯的时间为A小时的时候,两种灯消耗的钱是相同的.解方程.
A=1163.265小时
也就是说当灯泡可以使用1163.265小时即48.47天的时候两个灯泡所花费的钱的一样多的.
那么如果灯泡寿命的时间是48.47天以下,那么白灯比较经济,寿命是48.47天以上,节能灯比较经济.
19为节约能源,某单位按以下规定收取每月电费:用电不超过140度,按每度0.43元收费;如果超过140度,超过部分按每度0.57元收费.若墨用电户四月费的电费平均每度0.5元,问该用电户四月份应缴电费多少元?
设总用电x度:[(x-140)*0.57+140*0.43]/x=0.5
0.57x-79.8+60.2=0.5x
0.07x=19.6
x=280
再分步算: 140*0.43=60.2
(280-140)*0.57=79.8
79.8+60.2=140
19某大商场家电部送货人员与销售人员人数之比为1:8.今年夏天由于家电购买量明显增多,家电部经理从销售人员中抽调了22人去送货.结果送货人员与销售人数之比为2:5.求这个商场家电部原来各有多少名送货人员和销售人员?
设送货人员有X人,则销售人员为8X人.
(X+22)/(8X-22)=2/5
5*(X+22)=2*(8X-22)
5X+110=16X-44
11X=154
X=14
8X=8*14=112
这个商场家电部原来有14名送货人员,112名销售人员
20现对某商品降价10%促销,为了使销售金额不变,销售量要比按原价销售时增加百分之几?
设:增加x%
90%*(1+x%)=1
解得: x=1/9
所以,销售量要比按原价销售时增加11.11%
21甲.乙两种商品的原单价和为100元,因市场变化,甲商品降10%,乙商品提价5%调价后两商品的单价和比原单价和提高2%,甲.乙两商品原单价各是多少/
设甲商品原单价为X元,那么乙为100-X
(1-10%)X+(1+5%)(100-X)=100(1+2%)
结果X=20元 甲
100-20=80 乙
22甲车间人数比乙车间人数的4/5少30人,如果从乙车间调10人到甲车间去,那么甲车间的人数就是乙车间的3/4.求原来每个车间的人数.
设乙车间有X人,根据总人数相等,列出方程:
X+4/5X-30=X-10+3/4(X-10)
X=250
所以甲车间人数为250*4/5-30=170.
说明:
等式左边是调前的,等式右边是调后的
23甲骑自行车从A地到B地,乙骑自行车从B地到A地,两人都均速前进,以知两人在上午8时同时出发,到上午10时,两人还相距36千米,到中午12时,两人又相距36千米,求A.B两地间的路程?(列方程)
设A,B两地路程为X
x-(x/4)=x-72
x=288
答:A,B两地路程为288
24甲、乙两车长度均为180米,若两列车相对行驶,从车头相遇到车尾离开共12秒;若同向行驶,从甲车头遇到乙车尾,到甲车尾超过乙车头需60秒,车的速度不变,求甲、乙两车的速度.
二车的速度和是:[180*2]/12=30米/秒
设甲速度是X,则乙的速度是30-X
180*2=60[X-(30-X)]
X=18
即甲车的速度是18米/秒,乙车的速度是:12米/秒
25两根同样长的蜡烛,粗的可燃3小时,细的可燃8/3小时,停电时,同时点燃两根蜡烛,来电时同时吹灭,粗的是细的长度的2倍,求停电的时间.
设停电的时间是X
设总长是单位1,那么粗的一时间燃1/3,细的是3/8
1-X/3=2[1-3X/8]
X=2.4
即停电了2.4小时.
26.甲、乙两车长度均为180米,若两列车相对行驶,从车头相遇到车尾离开共12秒;若同向行驶,从甲车头遇到乙车尾,到甲车尾超过乙车头需60秒,车的速度不变,求甲、乙两车的速度.
27.两根同样长的蜡烛,粗的可燃3小时,细的可燃8/3小时,停电时,同时点燃两根蜡烛,来电时同时吹灭,粗的是细的长度的2倍,求停电的时间.
注意:说明理由!
列一元一次方程解!
二车的速度和是:[180*2]/12=30米/秒
设甲速度是X,则乙的速度是30-X
180*2=60[X-(30-X)]
X=18
即甲车的速度是18米/秒,乙车的速度是:12米/秒
补充回答:
设停电的时间是X
设总长是单位1,那么粗的一时间燃1/3,细的是3/8
1-X/3=2[1-3X/8]
X=2.4
即停电了2.4小时.


28已知某服装厂现在有A布料70M,B布料52M,现计划用这两种布料生产M.N的服装80套.已知做一套M服装用A料0.6M,B料0.9M,做一套N服装工用A料1.1M,B 料0.4M
1)设生产M服装X件,写出关于X的不等式组
2)有哪几种符合题意的生产方案?
3)若做一套M服装可获利45元,N服装获利50元,问:那种射击方案可使厂获利最大?利润是多少?
1).设生产M服装X件
0.6x+1.1(80-x)≤70 ①
0.9x+0.4(80-x)≤52 ②
解得①x≥36
②x≤40 即36≤x≤40
2).方案一:M服装36套 N服装44套
方案二:M服装37套 N服装43套
方案三:M服装38套 N服装42套
方案四:M服装39套 N服装41套
方案五:M服装40套 N服装40套
3).方案一:45×36+50×44=3820(元)
方案二:45×37+50×43=3815(元)
方案三:45×38+50×42=3810(元)
方案四:45×39+50×41=3805(元)
方案五:45×40+50×40=3800(元)
29小王家里装修,他去商店买灯,商店柜台里现有功率为100瓦的白炽灯和40瓦的节能灯,它们的单价分别为二元和三十二元,经了解,这两种灯的照明效果和使用寿命都一样.已知小王所在地的电价为每度0.5元,请问当这两种灯的使用寿命超过多长时间时,小王选择节能灯才合算? 《用电量(度)=功率(千瓦)x时间
设时间为x小时时小王选择节能灯才合算:
0.5*100/1000x+2>0.5*40/1000x+32
0.5*0.1x+2>0.5*0.04x+32
0.05x+2>0.02x+32
0.05x-0.02x>32-2
0.03x>30
x>1000
答:当这两种灯的使用寿命超过1000个小时时,小王选择节能灯才合算.
二 : 初二下数学应用题:一根约为1米长、直径为80毫米的光纤预制棒,可
初二下数学
应用题:一根约为1长、直径为80毫米的光纤预制棒,可拉成至少400公里的光纤。试问:1平方厘米是这种光纤的横截面积的多少倍?(保留两位有效数字)
1米=100厘米
80毫米=8厘米
400公里=400*1000*100厘米
光纤的横截面积为:100*3.14*(8/2)^2/40000000
1平方厘米是这种光纤的横截面积的
1/【100*3.14*(8/2)^2/40000000】=1/0.0001256=7961.78
三 : 初中数学应用题及答案
初中数学应用题
1、随着经济的发展,尹进所在的公司每年都在元月一次性的提高员工当年的月工资。(www.61k.com]尹进2008年的月工资为2000元,在2010年时他的月工资增加到2420元,他2011年的月工资按2008到2010年的月工资的平均增长率继续增长. (1)尹进2011年的月工资为多少?
(2)尹进看了甲、乙两种工具书的单价,认为用自己2011年6月份的月工资刚好购买若干本甲种工具书和一些乙种工具书,当他拿着选定的这些工具书去付书款时,发现自己计算书款时把这两种工具书的单价弄对换了,故实际付款比2011年6月份的月工资少了242元,于是他用这242元又购买了甲、乙两种工具书各一本,并把购买的这两种工具书全部捐献给西部山区的学校.请问,尹进总共捐献了多少本工具书?
解:
(1)设尹进2008到2010年的月工资的平均增长率为x,则,2000(1+x)2=2420.解 得 ,x1=-2.1 , x2=0.1, (2分 ) x1=-2.1与题意不合,舍去.
∴尹进2011年的月工资为2420×(1+0.1)=2662元.
(2)设甲工具书单价为m元,第一次选购y本.设乙工具书单价为n元,第一次选购z本.则由题意, 可列方程:m+n=242, ①
ny+mz=2662, ②
my+nz=2662-242. ③
由②+③,整理得,(m+n)(y+z)=2×2662-242,
由①,∴242(y+z)=2×2662-242,∴ y+z=22-1=21.
答:尹进捐出的这两种工具书总共有23本.
2、【函函游园记】
函函早晨到达上海世博园D区入口处等待开园,九时整开园,D区入口处有10n条安全检查通道让游客通过安检入园,游客每分钟按相同的人数源源不断到达这里等待入园,直到中午十二时D区入口处才没有排队人群,游客一到就可安检入园。九时二十分函函通过安检进入上海世博园时,发现平均一个人通过安全检查通道入园耗时20秒。
【排队的思考】
(1)若函函在九时整排在第3000位,则这时D区入口安检通道可能有多少条?
(2)若九时开园时等待D区入口处的人数不变:当安检通道是现有的1.2倍且每分钟到达D区入口处的游客人数不变时,从中午十一时开始游客一到D区入口处就可安检入园;当每分钟到达D区入口处的游客人数增加了50%,仍要求从十二时开始游客一到D区入口处就可安检入园,求这时需要增加安检通道的数量。
解:设九时开园时,等待在D区入口处的人数为x,每分钟到达D区入口处的游客人数为y, 增加的安检通道数量为k .
1?x?(11?9)?60y?1.2?(10n)??(11?9)?60?60,① ?20?1? 依题意有?x?(12?9)?60y?10n??(12?9)?60?60,② · 8分 20?1?x?(12?9)?60(1?50%)y?(k?10n)??(12?9)?60?60.③ ?20?
初三数学试题及答案 初中数学应用题及答案
??x?(11?9)?60y?(11?9)?60,?1?12n??6020???x?(12?9)?60y 或者? ?(12?9)?60,?10n??6020??x?(12?9)?60(1?50%)y?(12?9)?60.??(k?10n)??60?20?
(
x?2160n, 由①,②解之得:???y?18n,
代入③,解之得k=3n.
增加通道的数量为3n
解法二:
设九时开园时,等待在D区入口处的人数为x,每分钟到达D区入口处的游客人数为y, 增加安检通道后的数量为m.
依据题意,有:
1?x?(11?9)?60y?1.2?(10n)??(11?9)?60?60,① ?20?1? ?x?(12?9)?60y?10n??(12?9)?60?60,② 20??1x?(12?9)?60(1?50%)y?m??(12?9)?60?60.③ ?20?
x?2160n,由①,②解之得:?代入③,解之得m?13n, ??y?18n,
增加通道的数量为m?10n?3n.
(说明:若把10n当作50,再每列出一个方程评1分,共可给3分;再得到结果增加通道为15条时,又评1分. 即把“10n=50”作条件时,视为笔误.)
3、【实际背景】
预警方案确定: 当月的500克猪肉价格设W?.如果当月W<6,则下个月要采取措施防止“猪贱伤农”. ...当月的500克玉米价格
【数据收集】
今年2月~5月玉米、猪肉价格统计表
月 份
玉米价格(元/500克)
猪肉价格(元/500克)
【问题解决】 2 0.7 7.5 3 0.8 m 4 0.9 6.25 5 1 6
初三数学试题及答案 初中数学应用题及答案
(1)若今年3月的猪肉价格比上月下降的百分数与5月的猪肉价格比上月下降的百分数相等,求3月的猪肉价格m;
(2)若今年6月及以后月份,玉米价格增长的规律不变,而每月的猪肉价格按照5月的猪肉价格比上月下降的百分数继续下降,请你预测7月时是否要采取措施防止“猪贱伤农”;
(3)若今年6月及以后月份,每月玉米价格增长率是当月猪肉价格增长率的2倍,而每月的猪肉价格增长率都为a,则到7月时只用5.5元就可以买到500克猪肉和500克玉米.请你预测8月时是否要采取措施防止“猪贱伤农”. 解:
(1)由题意,
m?7.57.5
?
6?6.256.25
,
解得: m=7.2.
(2)从2月~5月玉米的价格变化知,后一个月总是比前一个月价格每500克增长0.1元.
(或:设y=kx+b,将(2,0.7),(3,0.8)代入,得到y=0.1x+0.5,把(4,0.9), (5,1)代入都符合,可评2分,再得到(6,1.1)时不再给分) ∴6月玉米的价格是:1.1元/500克;
∵5月增长率:∴W=
5.761.1
6?6.256.25
??
125
,∴6月猪肉的价格:6(1-
125
)=5.76元/500克.
=5.24<6, 要采取措施.
说明:若答:∵5月的W=6,而6月时W的分子(猪肉价格下降)减小,且分母(六月的玉米价格增长)增大,∴6月的W<6,未叙述减小和增大理由时可扣1分. (3)7月猪肉价格是:6(1?a)2元/500克;
7月玉米价格是:1(1?2a)元/500克; 由题意,6(1?a)+1(1?2a)=5.5, 解得,a??6(1?
1)
2
2
22
110
或a?? .(7分) a??不合题意,舍去.
2
2
33
∴W?
10, (9分), W(?7.59)?6,∴不(或:不一定)需要采取措施.
12
1(1?)
5
4、用煤燃烧发电时,所说的标准煤是指含热量为7 000大卡/千克的煤.生产实际中,一般
根据含热量相等,把所需标准煤的用煤量折合成含相同热量的实际用煤量来计算.(“大卡/千克”为一种热值单位)
光明电厂生产中每发一度电需用标准煤0.36千克,现有煤矸石和大同煤两种可选为生产
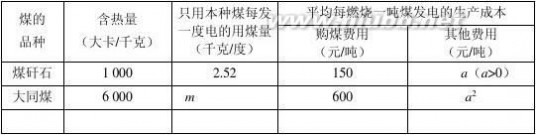
初三数学试题及答案 初中数学应用题及答案
(1)求生产中只用大同煤每发一度电的用煤量(即表中m的值);
(2)根据环保要求,光明电厂在大同煤中掺混煤矸石形成含热量为5 000大卡/千克的混
合煤来燃烧发电,若使用这种混合煤比全部使用大同煤每发1 000度电的生产成本增加了5.04元,求表中a的值.(生产成本=购煤费用+其它费用)
解:(1)光明电厂生产1度电所用的大同煤为m千克,而标准煤用量为0.36千克,
由题意,得0.36×7 000=m×6 000,解得 m=0.42
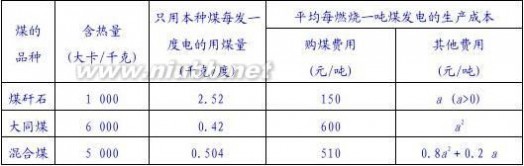
(2)设1吨含热量为5000大卡/千克的混合煤中含p吨大同煤和q吨煤矸石.
则??p?q?1,?p?0.8, ,解得?,
?6000p?1000q?5000?q?0.2
故购买1吨混合煤费用为0.8×600+0.2×150=510(元),
其他费用为0.8a+0.2 a2 元.
设光明电厂生产1度电用的混合煤为h千克,
则0.365000=, 解得h=0.504(千克). h7000
[或:设生产1千度电用的混合煤中含x吨大同煤和y吨煤矸石.
(x?y),?6000x?1000y?5000?x?0.4032,则? ,解得?, 6000x?1000y?0.36?7000.y?0.1008.??
生产1千度电用的大同煤:1 000×0.42=420 (千克)=0.42(吨),
生产1千度电用的混合煤:1 000×0.504=504(千克)=0.504(吨),
由题意可知数量关系:
5.04=平均每燃烧1吨混合煤发电的生产成本×生产1千度电所用混合煤
-平均每燃烧1吨大同煤发电的生产成本×生产1千度电所用大同煤
即:(510+0.8a2+0.2 a)×0.504-(600+a2)×0.42=5.04
(所列方程正确,※未叙述仍评8分)
化简并整理,得 0.1008 a—0.0168 a2=0.
(也可以直接写出方程:
1000?0.5041000?0?4222???80%?(600+a)+20%?(150+a)??(600+a)?5.04??10001000
)
解得 a1=6, a2=0,(不合题意,应舍去)
初三数学试题及答案 初中数学应用题及答案
所以表中a的值为6.
四 : 94分数、百分数应用题及答案
分数、百分数应用题
知识梳理:
1、求一个数是另一个数的几分之几(或百分之几),用等式表示三种量得关系:分量÷单位“1”的量=分率(或百分率)
2、已知一个数,求它的几分之几(或百分之几)是多少,用等式表示三种量的关系:单位“1”的量×分率(或百分率)=分量
3、已知一个数的几分之几(或百分之几)是多少,求这个数,用等式表示三种量的关系:分量÷分率(或百分率)=单位“1”的量
4、工程问题
工程问题是分数应用题的特例,它是探讨工作总量、工作效率和工作时间三个数量之间相互关系的一种应用题。
工作总量、工作效率、工作时间之间的关系是:
工作总量=工作效率×工作时间
工作时间=工作总量÷工作效率
工作效率=工作总量÷工作时间
工作总量÷工作效率之和=工作时间
5、浓度问题
浓度问题是一种研究溶液配比的百分数应用题。
基本数量关系有:
溶液质量=溶质质量/溶液质量×100%=溶质质量/(溶质质量+溶剂质量)×100%
溶质质量=溶液浓度×溶液质量
溶液质量=溶质质量÷溶液浓度
6、纳税与银行利息问题
依法纳税是每个公民应有的义务。把应缴纳的税款叫做应纳税额,应纳税额与收入的百分比叫做利率。基本数量关系有:
总利息=本金×利率×时间
个人应得利息=总利息×(1-利息税税率)
利率=总利息÷本金÷时间×100%
本金=总利息÷利率÷时间
7、折扣与商品利润问题
工厂或商店有时减价出售商品,通常我们把它称为“打折”出售,几折就是百分之几十。 利润问题亦是一种常见的百分数应用题。一般情况下,从厂家购进商品的价格称为成本价。商家在成本价的基础上提高价格出售,所赚的钱称为利润,利润与成本价的百分比就称为利润率。 基本数量关系:
利润率=(售价-成本价)/成本价×100%
售价=成本价×(1+利润率)
成本价=售价÷(1+利润率)
定价=成本价×(1+期望利润率)
期望利润=成本价×期望利润率
基础练习
1、一桶油第一次取出总数的10%,第二次取出剩下的20%,两次共取出28升。这桶油共有多少升?
2、一桶柴油,第一次用了全桶的20%,第二次用去20千克,第三次用了前两次的和,这时桶里还剩8千克油.问这桶油有多少千克?
3、服装厂一车间人数占全厂的25%,二车间人数比一车间少`1/5`,三车间人数比二车间多`3/10`,三车间是156人,这个服装厂全厂共有多少人?
4、加工一批零件,甲乙二人合作需12天完成;现由甲先工作3天,然后由乙工作2天还剩这批零件的`4/5`没完成. 已知甲每天比乙少加工4个,这批零件共有多少个?
5、某商店同时卖出两件商品,每件各得60元,但其中一件赚20%,另一件亏本20%,问这个商店卖出这两件商品是赚钱还是亏本?赚多少,亏多少?
6、甲、乙两只装有糖水的桶,甲桶有糖水60千克,含糖率4%,乙桶有糖水40千克,含糖率为20%,两桶互相交换多少千克才能使两桶糖水的含糖率相等?
7、现有浓度为10%的盐水20千克,再加入多少千克浓度为30%的盐水,可以得到浓度为22%的盐水?
8、在浓度为40%的酒精溶液中加入5千克水,浓度变为30%,再加入多少千克酒精,浓度变为50%?
9、一批商品,按期望获得 50%的利润来定价。结果只销掉 70%的商品。为尽早销掉剩下的商品,商店决定按定价打折扣销售。这样所获得的全部利润,是原来期望利润的91%,问:打了多少折扣
10、一列火车从甲地开往乙地,如果将车速提高20%,可以比原计划提前1小时到达;如果先以原速度行驶240千米后,再将速度提高25%,则可提前40分钟到达.求甲、乙两地之间的距离及火车原来的速度。
过关演练:
1、一堆煤,第一次用去了40%,第二次用去了它的1/5,两次共用去36吨。这堆煤共有多少吨?
2、王师傅加工一批零件,原计划每小时加工30个,6小时可以完成,实际每小时比原计划多加工20%,实际加工这批零件比原计划提前几小时?
3、大象最快每小时可以跑35千米,比猎豹的1/2少20千米。猎豹最快每小时能跑多少千米?
4、有一桶油,第一次取出全部的1/4,第二次取出全部的40%,第二次比第一次多取出75千克,第一次取出多少千克?
5、农药厂去年计划生产某种农药5吨,实际上半年生产的比全年计划生产的60%还多0.4吨,下半年生产了三又五分之三吨,全年完成计划的百分之几?
6、甬江机床厂五月份生产机床650台,比四月份多生产机床150台。五月份增长百分之几?
7、某修路队修一条路,第一天修了全长的1/4,第二天修了余下的1/3,正好是150米。洗一天修了多少米?
8、学校阅览室里有36名学生在看书,其中女生占4/9,后来又来了几名女生,这时女生人数占所有看书人数的9/10.问:后来又有几名女生来看书?
9、在某市举办的一次数学竞赛中,获一、二等奖的人数占获奖人数的2/5,获二、三等奖的人数占获总人数的3/4,那么,获一、二、三等奖的人数各占获奖总人数的几分之几?
10、六(1)班同学乘汽车到人工湖去春游,从学校出发,6/7小时行了全程的3/4,这时距离人工湖边还有4千米。照这样的速度,行完全程公用多少小时?
11、新华书店为四川灾区学生捐赠了一批课本,第一次运走了1600本,第二次运走的本数比第一次多12.5%,余下总数的3/7第三次全部运完。求捐出的这批书共有多少本?
12、冰化成水,体积减少1/11。
(1)现有15立方分米的水,结成冰后,体积是多少立方分米?
(2)一块15立方分米的冰化成水后,体积是多少立方分米?(得数保留两位小数)
13、某校原有学生325人,新学年男生增加25人,女生减少5%,总人数增加了16人。那么下着男生有多少人?
14、有一堆糖果,其中奶糖占45%,再放入16块水果糖后,奶糖就只占25%,那么,这堆糖中有奶糖多少块?
15、某实验小学四年级学生比三年级学生多1/4,五年级学生比四年级学生少10%,六年级学生比五年级学生多10%,六年级学生比三年级学生多38人,那么三、四、五、六年级共有多少人?
16、小强骑自行车从家到学校去,平常只用20分钟。由于途中有2千米正在修路,他只好推车步行,步行速度是骑车的1/3,结果用了36分钟才到学校。问:小强家到学校有多少千米?
17、学校图书馆有科技书一共3000本,其中科技书占2/5,由于同学们对科技书特别感兴趣,学校后来又买来一些科技书,这时科技书占总数的3/5。问:学校后来又买来科技书多少本?
18、把一堆皮球分别装入四个盒子中,其中1/5放在甲盒,1/3放入乙盒,放入丙盒的皮球是甲、乙两盒皮球总数的75%,丁盒放入10个,问:这堆皮球共多少个?
19、现有浓度为25%的糖水溶液100克,要把它变成浓度为40%的糖水,需要加糖多少千克?
20、爸爸今年存入银行20000元,定期两年,年利率是2.25%,到期时,按利息的20%缴纳利息税。存款到期时,爸爸从银行可取到多少元?
21、晓明妈妈的商店里进了两批水果,都售出后得到同样多的钱。妈妈说:“第一批水果热销,以比成本价高20%卖出,第二批水果滞销,在成本价的基础上降价1/5卖出,总算是这两批水果的买卖没有赔钱。”小朋友,小明的妈妈说的对吗?
22、师徒两人共同加工一批零件要12天完成,由徒弟单独加工要30天完成,师徒合作若干天后,师傅因公出差,余下的任务由徒弟继续加工17.5天完成。问:师傅是加工了几天后离开的?
23、一项工程,甲、乙两队合作需12天完成;乙、丙合作需15天完成;甲、丙两队合作,需20天完成。如果由甲、乙、丙三队合作,需要几天完成?
24、一个水池上有甲、乙两根主水管放水。水池空时,单开甲管5分钟可以注满,单开乙管10分钟
94分数、百分数应用题及答案_百分数应用题
可以注满;水池装满水后,单开丙管15分钟可以将水全部放完。如果在吃空时,将甲、乙、丙三管奇开,2分钟后关闭乙管,还要几分钟可以注满水池?
本文标题:初二数学应用题及答案-初一数学上册应用题带答案61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1