一 : 2014一元二次方程应用题经典题型汇总

一元二次方程应用题经典题型汇总

同学们知道，学习了一元二次方程的解法以后，就会经常遇到解决与一元二次方程有关的生活中的应用问题，即列一元二次方程解应用题，不少同学遇到这类问题总是左右为难，难以下笔，事实上，同学们只要能认真地阅读题目，分析题意，并能学会分解题目，各个击破，从而找到已知的条件和未知问题，必要时可以通过画图、列表等方法来帮助我们理顺已知与未知之间的关系，找到一个或几个相等的式子，从而列出方程求解，同时还要及时地检验答案的正确性并作答.现就列一元二次方程解应用题中遇到的常见的十大典型题目，举例说明.

一、增长率问题

例1 恒利商厦九月份的销售额为200万元，十月份的销售额下降了20%，商厦从十一月份起加强管理，改善经营，使销售额稳步上升，十二月份的销售额达到了193.6万元，求这两个月的平均增长率.

解 设这两个月的平均增长率是x.，则根据题意，得200(1－20%)(1+x)2＝193.6，

即(1+x)2＝1.21，解这个方程，得x1＝0.1，x2＝－2.1（舍去）.

答 这两个月的平均增长率是10%.

说明 这是一道正增长率问题，对于正的增长率问题，在弄清楚增长的次数和问题中每一个数据的意义，即可利用公式m(1+x)2＝n求解，其中m＜n.对于负的增长率问题，若经过两次相等下降后，则有公式m(1－x)2＝n即可求解，其中m＞n.

二、商品定价

例2 益群精品店以每件21元的价格购进一批商品，该商品可以自行定价，若每件商品售价a元，则可卖出（350－10a）件，但物价局限定每件商品的利润不得超过20%，商店计划要盈利400元，需要进货多少件？每件商品应定价多少？

解 根据题意，得(a－21)(350－10a)＝400，整理，得a2－56a+775＝0， 解这个方程，得a1＝25，a2＝31.

因为21×(1+20%)＝25.2，所以a2=31不合题意，舍去.

所以350－10a＝350－10×25＝100（件）.

答 需要进货100件，每件商品应定价25元.

说明 商品的定价问题是商品交易中的重要问题，也是各种考试的热点.

三、储蓄问题

例3 王红梅同学将1000元压岁钱第一次按一年定期含蓄存入“少儿银行”，到期后将本金和利息取出，并将其中的500元捐给“希望工程”，剩余的又全部按一年定期存入，这时存款的年利率已下调到第一次存款时年利率的90%，这样到期后，可得本金和利息共530元，求第一次存款时的年利率.（假设不计利息税）

解 设第一次存款时的年利率为x.

则根据题意，得[1000(1+x)－500](1+0.9x)＝530.整理，得90x2+145x－3＝0. 解这个方程，得x1≈0.0204＝2.04%，x2≈－1.63.由于存款利率不能为负数，所以将x2≈－1.63舍去.

答 第一次存款的年利率约是2.04%.

说明 这里是按教育储蓄求解的，应注意不计利息税.

四、趣味问题

例4 一个醉汉拿着一根竹竿进城，横着怎么也拿不进去，量竹竿长比城门宽4米，旁边一个醉汉嘲笑他，你没看城门高吗，竖着拿就可以进去啦，结果竖着比城门高2米，二人没办法，只好请教聪明人，聪明人教他们二人沿着门的对角斜着拿，二人一试，不多不少刚好进城，你知道竹竿有多长吗？

解 设渠道的深度为xm，那么渠底宽为(x+0.1)m，上口宽为(x+0.1+1.4)m. 则根据题意，得1(x+0.1+x+1.4+0.1)·x＝1.8，整理，得x2+0.8x－1.8＝0. 2

解这个方程，得x1＝－1.8（舍去），x2＝1.

所以x+1.4+0.1＝1+1.4+0.1＝2.5.

答 渠道的上口宽2.5m，渠深1m.

说明 求解本题开始时好象无从下笔，但只要能仔细地阅读和口味，就能从中找到等量关系，列出方程求解.

五、古诗问题

例5 读诗词解题：（通过列方程式，算出周瑜去世时的年龄）.

大江东去浪淘尽，千古风流数人物；

而立之年督东吴，早逝英年两位数；

十位恰小个位三，个位平方与寿符；

哪位学子算得快，多少年华属周瑜？

解 设周瑜逝世时的年龄的个位数字为x，则十位数字为x－3.

则根据题意，得x2＝10(x－3)+x，即x2-11x+30＝0，解这个方程，得x＝5或x＝6.

当x＝5时，周瑜的年龄25岁，非而立之年，不合题意，舍去；

当x＝6时，周瑜年龄为36岁，完全符合题意.

答 周瑜去世的年龄为36岁.

说明 本题虽然是一道古诗问题，但它涉及到数字和年龄问题，通过求解同学们应从中认真口味.

六、象棋比赛

例6 象棋比赛中，每个选手都与其他选手恰好比赛一局，每局赢者记2分，输者记0分.如果平局，两个选手各记1分，领司有四个同学统计了中全部选 手的得分总数，分别是1979，1980，1984，1985.经核实，有一位同学统计无误.试计算这次比赛共有多少个选手参加.

解 设共有n个选手参加比赛，每个选手都要与(n－1)个选手比赛一局，共计n(n－1)局，但两个选手的对局从每个选手的角度各自统计了一次，因此实际比赛总局数应为1n(n－1)局.由于每局共计2分，所以全部选手得分总共为n(n－1)分.显2

然(n－1)与n为相邻的自然数，容易验证，相邻两自然数乘积的末位数字只能是0，2，6，故总分不可能是1979，1984，1985，因此总分只能是1980，于是由n(n－

1)＝1980，得n2－n－1980＝0，解得n1＝45，n2＝－44（舍去）.

答 参加比赛的选手共有45人.

说明 类似于本题中的象棋比赛的其它体育比赛或互赠贺年片等问题，都可以仿照些方法求解.

七、情景对话

例7 春秋旅行社为吸引市民组团去天水湾风景区旅游，推出了如图1对话中收费标准.

某单位组织员工去天水湾风景区旅游，共支付给春秋旅行社旅游费用27000元.请问该单位这次共有多少员工去天水湾风景区旅游？

解 设该单位这次共有x名员工去天水湾风景区旅游.因为1000×25＝25000＜27000，所以员工人数一定超过25人.

则根据题意，得[1000－20(x－25)]x＝27000.

整理，得x2－75x+1350＝0，解这个方程，得x1＝45，x2＝30.

当x＝45时，1000－20(x－25)＝600＜700，故舍去x1；

当x2＝30时，1000－20(x－25)＝900＞700，符合题意.

答：该单位这次共有30名员工去天水湾风景区旅游.

说明 求解本题要时刻注意对话框中的数量关系，求得的解还要注意分类讨论，从中找出符合题意的结论.

图

1

八、等积变形

例8 将一块长18米，宽15米的矩形荒地修建成一个花园（阴影部分）所占的面积为原来荒地面积的三分之二.（精确到0.1m）

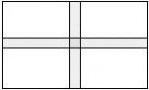
（1）设计方案1（如图2）花园中修两条互相垂直且宽度相等的小路.

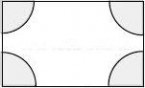
（2）设计方案2（如图3）花园中每个角的扇形都相同.

以上两种方案是否都能符合条件?若能，请计算出图2中的小路的宽和图3中扇形的半径；若不能符合条件，请说明理由.

解 都能.（1）设小路宽为x，则18x+16x－x2＝

＝0， 2×18×15，即x2－34x+1803

解这个方程，得x

＝34?，即x≈6.6. 2

2×18×15，即r2≈57.32，所以r≈7.6. 3（2）设扇形半径为r，则3.14r2＝

说明 等积变形一般都是涉及的是常见图形的体积，面积公式；其原则是形变积不变；或形变积也变，但重量不变，等等.

B

九、动态几何问题 例9 如图4所示，在△ABC中，∠C＝90°，AC＝6cm，BC＝8cm，点P从点A出发沿边AC向点C以1cm/s

的速度移动，点Q从C点出发沿CB边向点B以2cm/s的速度移动.

（1）如果P、Q同时出发，几秒钟后，可使△PCQ的面积为8平方厘米？

（2）点P、Q在移动过程中，是否存在某一时刻，使得△PCQ的面积等于△ABC的面积的一半.若存在，求出运动的时间；若不存在，说明理由. QCPwww.61k.com图4 图2 图3

解 因为∠C＝90°，所以AB10（cm）.

（1）设xs后，可使△PCQ的面积为8cm2，所以 AP＝xcm，PC＝(6－x)cm，CQ＝2xcm.

则根据题意，得

2，x2＝4.

所以P、Q同时出发，2s或4s后可使△PCQ的面积为8cm2.

（2）设点P出发x秒后，△PCQ的面积等于△ABC面积的一半. 1·(6－x)·2x＝8.整理，得x2－6x+8＝0，解这个方程，得x1＝2

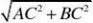
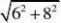
则根据题意，得111(6－x)·2x＝××6×8.整理，得x2－6x+12＝0. 222

由于此方程没有实数根，所以不存在使△PCQ的面积等于ABC面积一半的时刻. 说明 本题虽然是一道动态型应用题，但它又要运用到行程的知识，求解时必须依据路程＝速度×时间.

十、梯子问题

例10 一个长为10m的梯子斜靠在墙上，梯子的底端距墙角6m.

（1）若梯子的顶端下滑1m，求梯子的底端水平滑动多少米？

（2）若梯子的底端水平向外滑动1m，梯子的顶端滑动多少米？

（3）如果梯子顶端向下滑动的距离等于底端向外滑动的距离，那么滑动的距离是多少米？

解

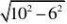
8（m）.

（1）若梯子顶端下滑1m，则顶端距地面7m.设梯子底端滑动xm.

则根据勾股定理，列方程72+(6+x)2＝102，整理，得x2+12x－15＝0， 解这个方程，得x1≈1.14，x2≈－13.14（舍去），

所以梯子顶端下滑1m，底端水平滑动约1.14m.

（2）当梯子底端水平向外滑动1m时，设梯子顶端向下滑动xm.

则根据勾股定理，列方程(8－x)2+(6+1)2＝100.整理，得x2－16x+13＝0. 解这个方程，得x1≈0.86，x2≈15.14（舍去）.

所以若梯子底端水平向外滑动1m，则顶端下滑约0.86m.

（3）设梯子顶端向下滑动xm时，底端向外也滑动xm.

则根据勾股定理，列方程 (8－x)2+(6+x)2＝102，整理，得2x2－4x＝0， 解这个方程，得x1＝0（舍去），x2＝2.

所以梯子顶端向下滑动2m时，底端向外也滑动2m.

说明 求解时应注意无论梯子沿墙如何上下滑动，梯子始终与墙上、地面构成直角三角形.

十一、航海问题

例11 如图5所示，我海军基地位于A处，在其正南

方向200海里处有一重要目标B，在B的正东方向200海A

里处有一重要目标C，小岛D恰好位于AC的中点，岛上

有一补给码头；小岛F位于BC上且恰好处于小岛D的正

南方向，一艘军舰从A出发，经B到C匀速巡航．一艘补BEwww.61k.com

图5

给船同时从D出发，沿南偏西方向匀速直线航行，欲将一批物品送往军舰.

（1）小岛D和小岛F相距多少海里？

（2）已知军舰的速度是补给船的2倍，军舰在由B到C的途中与补给船相遇于E处，那么相遇时补给船航行了多少海里？（精确到0.1海里）

解（1）F位于D的正南方向，则DF⊥BC.因为AB⊥BC，D为AC的中点，所以DF＝1AB＝100海里，所以，小岛D与小岛F相距100海里. 2

（2）设相遇时补给船航行了x海里，那么DE＝x海里，AB+BE＝2x海里，EF＝AB+BC－(AB+BE)－CF＝(300－2x)海里.

在Rt△DEF中，根据勾股定理可得方程x2＝1002+(300－2x)2，整理，得3x2－1200x+100000＝0.

解这个方程，得x1＝200

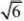
－118.4，x2＝

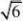
200+33

去）.所以，相遇时补给船大约航行了118.4海里.

说明 求解本题时，一定要认真地分析题意，及时发现题目中的等量关系，并能从图形中寻找直角三角形，以便正确运用勾股定理布列一元二次方程.

十二、图表信息

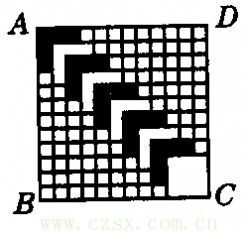
例12 如图6所示，正方形ABCD的边长为12，划分成12×12个小正方形格，将边长为n（n为整数，且2≤n≤11）的黑白两色正方形纸片按图中的方式，黑白相间地摆放，第一张n×n的纸片正好盖住正方形ABCD左上角的n×n个小正方形格，第二张纸片盖住第一张纸片的部分恰好为(n－1)×(n－1)个小正方形.如此摆放下去，直到纸片盖住正方形ABCD的右下角为止.

请你认真观察思考后回答下列问题：

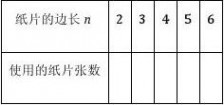
（1）由于正方形纸片边长n的取值不同，?完成摆放时所使用正方形纸片的张数也不同，请填写下表：

（2）设正方形ABCD被纸片盖住的面积（重合部分只计一次）为S1，未被盖住的面积为S2.

①当n＝2时，求S1∶S2的值；

②是否存在使得S1＝S2的n值？若存在，请求出来；若不存在，请说明理由. 解（1）依题意可依次填表为：11、10、9、8、7.

（2）S1＝n2+(12－n)[n2－(n－1)2]＝－n2+25n－12.

①当n＝2时，S1＝－22+25×2－12＝34，S2＝12×12－34＝110.

所以S1∶S2＝34∶110＝17∶55.

②若S1＝S2，则有－n2+25n－12＝图6 1×122，即n2－25n+84＝0， 2

解这个方程，得n1＝4，n2＝21（舍去）.

所以当n＝4时，S1＝S2.所以这样的n值是存在的.

说明 求解本题时要通过阅读题设条件及提供的图表，及时挖掘其中的隐含条件，对于求解第（3）小题，可以先假定问题的存在，进而构造一元二次方程，看得到的一元二次方程是否有实数根来加以判断.

十三、探索在在问题

例13 将一条长为20cm的铁丝剪成两段，并以每一段铁丝的长度为周长做成一个正方形.

（1）要使这两个正方形的面积之和等于17cm2，那么这段铁丝剪成两段后的长度分别是多少

?

（2）两个正方形的面积之和可能等于12cm2吗? 若能，求出两段铁丝的长度；若不能，请说明理由.

解（1）设剪成两段后其中一段为xcm，则另一段为（20－x）cm. 22?x??20?x?则根据题意，得??+??＝17，解得x1＝16，x2＝4， 44????

当x＝16时，20－x＝4，当x＝4时，20－x＝16，

答 这段铁丝剪成两段后的长度分别是4cm和16cm.

（2）不能.理由是：不妨设剪成两段后其中一段为ycm，则另一段为（20－y）

?y??20?y?2cm.则由题意得??+??＝12，整理，得y－20y+104＝0，移项并配方，?4??4?

得(y－10)2＝－4＜0，所以此方程无解，即不能剪成两段使得面积和为12cm2.

说明 本题的第（2）小问也可以运用求根公式中的b2－4ac来判定.若b2－4ac≥0，方程有两个实数根，若b2－4ac＜0，方程没有实数根，本题中的b2－4ac＝－16＜0即无解.

十四、平分几何图形的周长与面积问题

例14 如图7，在等腰梯形ABCD中，AB＝DC＝5，AD＝4，BC＝10.点E?在下底边BC上，点F在腰AB上.

（1）若EF平分等腰梯形ABCD的周长，设BE长为x，试用含x的代数式表示△BEF的面积； 22

（2）是否存在线段EF将等腰梯形ABCD的周长和面积同时平分？若存在，求出此时BE的长；若不存在，请说明理由；

（3）是否存在线段EF将等腰梯形ABCD的周长和面积同时分成1∶2的两部分？若存在，求此时BE的长；若不存在，请说明理由.

解（1）由已知条件得，梯形周长为12，高4，面积为28. A

D

过点F作FG⊥BC于G，过点A作AK⊥BC于K.

则可得，FG＝12?x×4， 5BG K ECwww.61k.com图7

所以S△BEF＝12224BE·FG＝－x+x（7≤x≤10）. 255

2224x+x＝14，解这个方程，得x1＝7，x2＝5（不合55（2）存在.由（1）得－

题意，舍去），

所以存在线段EF将等腰梯形ABCD的周长与面积同时平分，此时BE＝7.

（3）不存在.假设存在，显然有S△BEF∶S多边形AFECD ＝1∶2，

即(BE+BF)∶(AF+AD+DC)＝1∶2.则有－221628x+x＝， 553

整理，得3x2－24x+70＝0，此时的求根公式中的b2－4ac＝576－840＜0， 所以不存在这样的实数x.即不存在线段EF将等腰梯形ABCD的周长和面积同时分成1∶2的两部分.

说明 求解本题时应注意：一是要能正确确定x的取值范围；二是在求得x2＝5时，并不属于7≤x≤10，应及时地舍去；三是处理第（3）个问题时的实质是利用一元二次方程来探索问题的存在性.

十五、利用图形探索规律

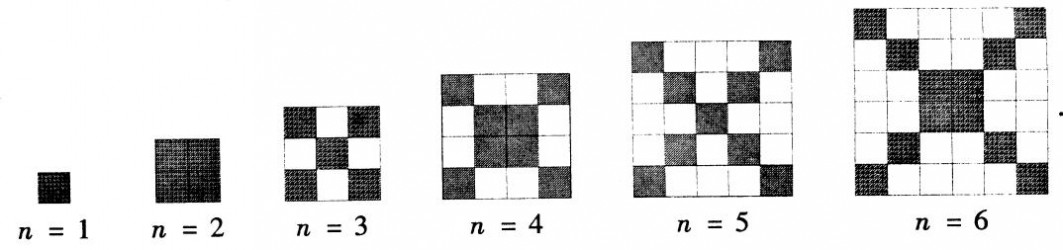
例15 在如图8中，每个正方形有边长为1 的小正方形组成：

图8

（1）观察图形，请填写下列表格： 正方形边长 黑色小正方形个数

正方形边长 黑色小正方形个数

2

4

6

8

? ?

n（偶数）

1

3

5

7

? ?

n（奇数）

（2）在边长为n（n≥1）的正方形中，设黑色小正方形的个数为P1，白色小正方形的个数为P2，问是否存在偶数．．n，使P2＝5P1？若存在，请写出n的值；若不存在，请说明理由

.

解（1）观察分析图案可知正方形的边长为1、3、5、7、?、n 时，黑色正方形的个数为1、5、9、13、2n－1（奇数）；正方形的边长为2、4、6、8、?、n 时，黑色正方形的个数为4、8、12、16、2n（偶数）.

（2）由（1）可知n为偶数时P1＝2n，所以P2＝n2－2n.根据题意，得n2－2n＝5×2n，即n2－12n＝0，解得n1＝12，n2＝0（不合题意，舍去）.所以存在偶数n＝12，使得P2＝5P1.

说明 本题的第（2）小问是属于存在性问题，求解时，可以先假设结论存在，进而从中找到数量关系，使问题获解.

综上所言，列一元二次方程解应用题是列一元一次方程、二元一次方程组解应用题的延续和发展，列方程解应用题就是先把实际问题抽象为方程模型，然后通过解方程获得对实际问题的解决.列一元二次方程解应用题的关键是：找出未知量与已知量之间的联系，从而将实际问题转化为方程模型，要善于将普通语言转化为代数式，在审题时，要特别注意关键词语，如“多少、快、慢、和、差、倍、分、超过、剩余、增加、减少”等等，此外，还要掌握一些常用的公式或特殊的等量关系，如特殊图形的面积公式、行程问题、工程问题、增长率问题中的一些特殊关系等等.

二 : 二元一次方程应用题  某通讯器材商场，计划用

二元一次方程应用题

  某器材商场，计划用60000元从厂家购进若干部新型手机，以满足市场需求，已知该厂家生产三种不同型号的手机，出厂价分别为甲种型号手机每部1800元，乙种型号手机每部600元，丙种型号手机每部1200元。若商场同时购进两种不同型号的手机共40部，并将60000元钱恰好用完。请你帮助商场价算一下如何购买。
  请写明计算过程。
  谢谢！

---

设甲乙丙种型号手机分别要购买x y z部。

x+y=40

1800x+600y＝60000，解得x=30y=10；

或y+z=40

600y+1200z＝60000，解得y=-20舍去z=60；

或x+z=40

1800x+1200z=60000，解得x=20z=20

购进甲种手机30部，乙种手机10部；或购进甲种手机20部，丙种手机20部．

三 : 一元二次方程应用题一只鸡得了禽流感，经过两轮传染后，共有625只

一元二次方程应用题

一只得了禽流感，经过两轮传染后，共有625只鸡得了禽流感。一轮传染中平均一只鸡传给多少只鸡？

---

设一轮传染中平均一只鸡传x只鸡，

则第一轮有1+x只感染，

第二轮有1+x+x(1+x)＝(1+x)^2只感染.

而两轮传染后有625只鸡感染，

故列方程：

(1+x)^2＝625

→1+x＝±25,

∴x＝24(只取正根)

答：一轮传染中平均一只鸡可传给24只鸡。

四 : 一元二次方程应用题(含答案)整理版

1：某种服装，平均每天可以销售20件，每件盈利44元，在每件降价幅度不超过10元的情况下，若每件降价1元，则每天可多售出5件，如果每天要盈利1600元，每件应降价多少元？

解：设没件降价为x，则可多售出5x件，每件服装盈利44-x元，

依题意x≤10

∴(44-x)(20+5x)=1600

展开后化简得：x2-44x+144=0

即(x-36)(x-4)=0

∴x=4或x=36(舍)

即每件降价4元

要找准关系式

2.游行队伍有8行12列，后又增加了69人，使得队伍增加的行·列数相同，增加了多少行多少列？

解：设增加x (8+x)(12+x)=96+69 x=3

增加了3行3列

3.某化工材料经售公司购进了一种化工原料,进货价格为每千克30元.物价部门规定其销售单价不得高于每千克70元,也不得低于30元.市场调查发现：单价每千克70元时日均销售60kg；单价每千克降低一元,日均多售2kg。（www.61k.com]在销售过程中,每天还要支出其他费用500元（天数不足一天时,按一天计算）.如果日均获利1950元,求销售单价

解: (1)若销售单价为x元,则每千克降低了(70-x)元,日均多售出2(70-x)千克,日均销售量为[60+2(70-x)]千克,每千克获利(x-30)元.

依题意得:

y=(x-30)[60+2(70-x)]-500

=-2x^2+260x-6500

(30<=x<=70)

(2)当日均获利最多时：单价为65元，日均销售量为60+2（70-65）＝70kg，那么获总利为1950*7000/70＝195000元,当销售单价最高时：单价为70元，日均销售60kg，将这批化工原料全部售完需7000/60约等于117天,那么获总利为（70-30）*7000-117*500＝221500

元,而221500>195000时且221500-195000=26500元.

∴销售单价最高时获总利最多,且多获利26500元.

一元二次方程应用题 一元二次方程应用题(含答案)整理版

4.一辆警车停在路边,当警车发现一辆一8M/S的速度匀速行驶的货车有违

章行为,决定追赶,经过2.5s,警车行驶100m追上货车.试问

(1)从开始加速到追上货车,警车的速度平均每秒增加多少m?

(2)从开始加速到行驶64m处是用多长时间?

解：

2.5*8=20 100-20=80 80/8=10

100/【（0+10a）/2】=10解方程为2

64/【（0+2a)/2】=a解方程为8

5.用一个白铁皮做罐头盒，每张铁皮可制作25个盒身，或制作盒底40个，

一个盒身和两个盒底配成一套罐头盒。[www.61k.com）现在有36张白铁皮，用多少张制盒身，

多少张制盒底可以使盒身和盒底正好配套？

6、解：设用 X 张制罐身 用 Y 张制罐底 则X+Y=36 X=36-Y 25X=40Y/2 X=4Y/5 4Y/5=36-Y Y=20 X=16

7.现有长方形纸片一张，长19cm，宽15cm，需要剪去边长多少的小正方形

才能做成底面积为77平方cm的无盖长方形的纸盒？

解：设边长x

则(19-2x)(15-2x)=77

4x^2-68x+208=0

x^2-17x+52=0

(x-13)(x-4)=0,当x=13时19-2x<0不合题意,舍去

故x=4

8. 某超市一月分销售额是20万元，以后每月的利润都比上个月的利润增长

10%，则二月分销售额是多少？ 3月的销售额是多少？

解：二月20*（1+0.1）=22 三月22*（1+0.1）=24.2

9. 某企业2007年利润为50万元，如果以后每年的利润都比上年的利润增

长x%。那么2009年的年利润将达到多少万元？

一元二次方程应用题 一元二次方程应用题(含答案)整理版

解：50*（1+x%）^2

10. 某厂经过两年体制改革和技术革新，生产效率翻了一番，求平均每年的增长率（精确到0.1%）

解：设平均每年的增长率x

(x+1)^2=2

x=0.414

11. 一拖拉机厂，一月份生产出甲、乙两种新型拖拉机，其中乙型16台，从二月份起，甲型每月增产10台，乙型每月按相同的增长率逐月递增，又知二月份甲、乙两型的产量之比为3：2，三月份甲、乙两型产量之和为65台，求乙型拖拉机每月增长率及甲型拖拉机一月份的产量。（www.61k.com]

解：设乙的增长率为X，那么二月乙就是16（1+X）台，甲就是16（1+X）×3÷2；三月乙就是16（1+X）2台，甲就是16（1+X）×3÷2+10台，所以列出算式16（1+X）2+16（1+X）×3÷2+10=65 求解，然后可以分别算出一月二月乙的产量，然后就可以解得甲的产量了17.

12.如图，出发沿BC匀速向点C运动。已知点N的速度每秒比点M快1cm，运动的速度。 两点同时出发，运动3秒后相距10cm。求点M和点N

解:设M速度x，则N为（x+1），（BC—3x）的

平方=10的平方，解得x=1或x=5/3又因为AC=7，所

1m/s，N的速度2m/s 13.用长为100cm的金属丝做一个矩形框.面积为400平方厘米，而王宁做的矩形框的面积为600平方厘米，什么吗？

解：设矩形一边长为X厘米，则相邻一边长为1/2（100-2X）厘米，即（50-X）厘米，依题意得：

X*(50-X)=400 解之得：X1=40,X2=10;

X*(50-X)=600 解之得：X1=20,X2=30；

所以李明做的矩形的长是40厘米，宽是10厘米；

王宁做的矩形的长是30厘米，宽是20厘米。

一元二次方程应用题 一元二次方程应用题(含答案)整理版

14.某商品进价为每件40元，如果售价为每件50元，每个月可卖出210件，如果售价超过50元，但不超过80元，每件商品的售价每上涨10元，每个月少卖1件，如果售价超过80元后，若再涨价，每件商品的售价每涨1元，每个月少卖3件。［www.61k.com]设该商品的售价为X元。

61阅读提醒您本文地址：

（1）、每件商品的利润为 元。若超过50元，但不超过80元，每月售 件。

若超过80元，每月售 件。（用X的式子填空。）

（2）、若超过50元但是不超过80元，售价为多少时 利润可达到7200元

(3)、若超过80元，售价为多少时利润为7500元。

解： 1)x-40 210-(x-40)10 210-(x-40)10-3(x-80)

(2)设售价为a (a-40)[210-(a-40)10=7200

(3)设售价为b (b-40)[210-(b-40)10-3(b-80)=7500 （第2 、3问也可设该商品的售价为X1 x2元）

15.某商场销售一批衬衫，平均每天可出售30件，每件赚50元，为扩大销售，加盈利，尽量减少库存，商场决定降价，如果每件降1元，商场平均每天可多卖2件，若商场平均每天要赚2100元，问衬衫降价多少元

解：衬衫降价x元

2100=(50-x)(30+2x)=1500+70x-x^2

x^2-70x+600=0

(x-10)(x-60)=0

x-60=0 x=60>50 舍去

x-10=0 x=10

16.在一块面积为888平方厘米的矩形材料的四角，各剪掉一个大小相同的正方形（剪掉的正方形作废料处理，不再使用），做成一个无盖的长方体盒子，要求盒子的长为25cm，宽为高的2倍，盒子的宽和高应为多少？

解：设剪去正方形的边长为x,x同时是盒子的高，则盒子宽为2x;

矩形材料的尺寸：

长：25+2x

一元二次方程应用题 一元二次方程应用题(含答案)整理版

宽：4x;

(25+2x)*4x=888,

解得：x1=6,x2=-18.5(舍去）

盒子的宽：12cm；盒子的高：6cm。［www.61k.com)

17.某公司生产开发了960件新产品，需要经过加工后才能投放市场，现在有A，B两个工厂都想参加加工这批产品，已知A工厂单独加工这批产品比B工厂单独加工这批产品要多用20天，而B工厂每天比A工厂多加工8件产品，公司需要支付给A工厂每天80元的加工费，B工厂每天120元的加工费。

1. A，B两个工厂每天各能加工多少件新产品？

2. 公司制定产品方案如下：可以由每个厂家单独完成；也可以由两个厂家同时合作完成。在加工过程中，公司需要派一名工程师每天到厂进行技术指导，并负担每天5元的午餐补助费。请帮助公司选择哪家工厂加工比较省钱，并说明理由。

解：1.设A每天加工x件产品，则B每天加工x+8件产品

由题意得960/x-960/(x+8)=20

解得x=16件

所以A每天加工16件产品，则B每天加工24件产品

2.设让A加工x件，B加工960-x件

则公司费用为x/16*(80+5)+(960-x)/24*(120+5)

化简为5/48*x+5000

所以x=0时最省钱，即全让B厂加工

18.一元二次方程解应用题 将进货单价为40元的商品按50元出售时，能卖500个，如果该商品每涨价1元，其销售量就减少10个。商店为了赚取8000元的利润，这种商品的售价应定为多少?应进货多少？

解：利润是标价-进价

设涨价x元,则:

(10+x)(500-10x)=8000

5000-100x+500x-10x^2=8000

x^2-40x+300=0

(x-20)^2=100

x-20=10或x-20=-10

x=30或x=10

经检验,x的值符合题意

所以售价为80元或60元

所以应进8000/(10+x)=200个或400个

一元二次方程应用题 一元二次方程应用题(含答案)整理版

所以应标价为80元或60元

应进200个或400个

19.参加一次聚会的每两个人都握了一次手，所有人共握手10次，有多少人参加聚会？

34.参加一次足球联赛的每两个队之间都进行两次比赛，共要比赛90场，共有多少个队参加比赛？

35.要组织一次篮球联赛，赛制为单循环形式（每两个队之间赛一场），计划安排15场比赛，应邀请多少个球队参加比赛？

解：34、n（n-1）2=10

n=5

35、x（x-1）2*2=90

x=10

36、y（y-1)2=15

y=6

20.在某场象棋比赛中，每位选手和其他选手赛一场，胜者记2分，败者记0分，平局各记1分，今有四位统计员统计了全部选手的得分之和分别是2025分、2027分、2080分、2085分，经核实，只有一位统计员的结果是正确的，问这场比赛有几位选手参加？

解： 无论如何，每一局两人合计都应得2分，所以最终的总得分一定是偶数，由于2025、2027、2085都是奇数，所以都不符合题意，所以正确的是第三个记分员

设有x人参加，则一共比了x（x-1）/2局

你的数字似乎有错，请确认是否为2070，而不是2080（2080得不出整数解）

x（x-1）/2=2070/2

x2-x-2070=0

（x-46）（x+45）=0

x1=46，x2=-45（舍）

答：一共有46位选手参加.

一元二次方程应用题 一元二次方程应用题(含答案)整理版

21．将进货单价为40元的商品按50元出售时，能卖出500个，已知该商品每降价1元，其销售量就要减少10个，为了赚8000元利润，售价应定为多少？这时进货应为多少个？

22．某商店如果将进货价8元的商品按每件10元出售，每天可销售200件，现采用提高售价，减少进货量的方法增加利润，已知这种商品每涨0.5元，其销售量就可以减少10元，问应将售价定为多少时，才能使所赚利润最大，并求出最大利润

23解：设售价应定为x元，根据题意列方程得?500?10(x?50)??(x?40)?8000整理得x2?140x?480?0

（x－60）（x－80）＝0

解得x1＝60，x2＝80

答：当x1＝60时，进货量为400个

当x2＝80时，进货量为200个

44解：由题意列方程得，a(350-10a)-21(350-10a)=400

a2?56a?775?0

（a-25）(a-31)=0

解得，a1＝25，a2＝31 31?21?20%21∵∴a2＝31不合题意,舍去

350-10a＝100

答：需要卖出100品，商品售价25元

一元二次方程应用题 一元二次方程应用题(含答案)整理版

分析：根据表格可以看出每件的售价每降1元时，每日就多销售1件，根据这个隐含条件就可以得出此类型题和以上的练习非常相似了

45.解：若定价为m元时，售出的商品为

［70－（m－130）］件

列方程得

?70?(m?130)??(m?120)?1600

2整理得m?320m?25600?0

(m?160)2?0

∴m1＝m2＝160

答：m的值是160

61阅读提醒您本文地址：

24解：设售价定为x元，则每件的利润为

[200?x?10x?10?10][200??10]0.50.5件，列式得（x－8） （x－8）元，销售量为

?20(x2?28x?160)

2??20(x?14)?720 整理得，

即当x＝14时，所得利润有最大值，最大利润是720元

61阅读提醒您本文地址：

五 : 73一元二次方程应用题(含答案)[1][1]

1：某种服装，平均每天可以销售20件，每件盈利44元，在每件降价幅度

不超过10元的情况下，若每件降价1元，则每天可多售出5件，如果每天要盈

利1600元，每件应降价多少元？

解：设没件降价为x，则可多售出5x件，每件服装盈利44-x元，

依题意x≤10

∴(44-x)(20+5x)=1600

展开后化简得：x2-44x+144=0

即(x-36)(x-4)=0

∴x=4或x=36(舍)

即每件降价4元

要找准关系式

2.游行队伍有8行12列，后又增加了69人，使得队伍增加的行·列数相同，

增加了多少行多少列？

解：设增加x (8+x)(12+x)=96+69 x=3

增加了3行3列

3.某化工材料经售公司购进了1种化工原料,进货价格为每千克30元.物价

部门规定其销售单价不得高于每千克70元,也不得低于30元.市场调查发现：单

价每千克70元时日均销售60kg；单价每千克降低一元,日均多售2kg。在销售过

程中,每天还要支出其他费用500元（天数不足一天时,按一天计算）.如果日均

获利1950元,求销售单价

解: (1)若销售单价为x元,则每千克降低了(70-x)元,日均多售出2(70-x)

千克,日均销售量为[60+2(70-x)]千克,每千克获利(x-30)元.

依题意得:

y=(x-30)[60+2(70-x)]-500

=-2x^2+260x-6500

(30<=x<=70)

(2)当日均获利最多时：单价为65元，日均销售量为60+2（70-65）＝70kg，那

么获总利为1950*7000/70＝195000元,当销售单价最高时：单价为70元，日均

销售60kg，将这批化工原料全部售完需7000/60约等于117天,那么获总利为

（70-30）*7000-117*500＝221500

元,而221500>195000时且221500-195000=26500元.

∴销售单价最高时获总利最多,且多获利26500元.

4..运动员起跑20m后速度才能达到最大速度10m/s,若运动员的速度是均匀

增加的,则他起跑开始到10m处时需要多少s?

解：

（0+10)除2为平均增加为5

（0+5a）除2乘a

5.一辆警车停在路边,当警车发现一辆一8M/S的速度匀速行驶的货车有违

章行为,决定追赶,经过2.5s,警车行驶100m追上货车.试问

(1)从开始加速到追上货车,警车的速度平均每秒增加多少m?

(2)从开始加速到行驶64m处是用多长时间?

解：

2.5*8=20 100-20=80 80/8=10

100/【（0+10a）/2】=10解方程为2

64/【（0+2a)/2】=a解方程为8

6.一容器装满20L纯酒精，第一次倒出若干升后，用水加满，第二次又倒出

同样升数的混合液，再用水加满，容器里只有5L的纯酒精，第一次倒出的酒精

多少升？（过程）

解：设第一次倒出x升，则第二次为x（20-x）/20.(此处为剩下的酒精占

总体积20升的多少即比率然后乘上倒出的升数即为倒出的纯酒精数

则20-x-x(20-x)/20=5

解得x=10

6.11个长方体的长与宽的比为5：2，高为5厘米，表面积为40平方厘米。

画出这个长方体的展开图，及其过程（设未知数）

解：设宽为2x，长为5x。

2*（2x*5x+2x*5+5x*5）=40

10x的平方+35x-20=0

x=1/2

宽为1厘米，长为2.5厘米

7.用1个白铁皮做罐头盒，每张铁皮可制作二十五个盒身，或制作盒底40个，

1个盒身和2个盒底配成一套罐头盒。现在有36张白铁皮，用多少张制盒身，

多少张制盒底可以使盒身和盒底正好配套？

8. 用含30%和75%的2种防腐药水，配置含药50%的防腐药水18kg，2种药水各

需取多少？

7、解：设用 X 张制罐身 用 Y 张制罐底 则X+Y=36 X=36-Y 25X=40Y/2 X=4Y/5 4Y/5=36-Y Y=20 X=16

8、解：设30%的取 X 75%的取 Y 则 30%*X+75%Y=50%*18 6X+15Y=180

X+Y=18 X=18-Y

6*18-6Y+15Y=180

Y=8 X=10

9.印度古算术书中有这样一首诗：“一群猴子分两队，高高兴兴在游戏，八

分之一再平方，蹦蹦跳跳树林里；其余使二叽喳喳，伶俐活泼又调皮，告我总数

共多少，两队猴子在一起。”

解：设共有x只猴子，列方程得

x-(x/8)^2=12

解得：X=48

10.现有长方形纸片一张，长19cm，宽15cm，需要剪去边长多少的小正方形

才能做成底面积为77平方cm的无盖长方形的纸盒？

解：设边长x

则(19-2x)(15-2x)=77

4x^2-68x+208=0

x^2-17x+52=0

(x-13)(x-4)=0,当x=13时19-2x<0不合题意,舍去

故x=4

11. 某超市一月分销售额是20万元，以后每月的利润都比上个月的利润增

长10%，则二月分销售额是多少？ 3月的销售额是多少？

解：二月20*（1+0.1）=22 三月22*（1+0.1）=24.2

12. 某企业2007年利润为50万元，如果以后每年的利润都比上年的利润增长x%。那么2009年的年利润将达到多少万元？

解：50*（1+x%）^2

13. 某种药品两次降价，价格降低了36%，求每次降价的百分率

解：设每次降价的百分率x

x^2=36%

x=60%

14. 某厂经过两年体制改革和技术革新，生产效率翻了一番，求平均每年的增长率（精确到0.1%）

解：设平均每年的增长率x

(x+1)^2=2

x=0.414

15.学校组织一次兵乓球比赛,参赛的每2个选手都要比赛一场,所有比赛一共有36场,问有多少名同学参赛？用一元二次方程，化成一般形式。

解：设有X名同学参赛，X*(X-1)/2=36，

一般形式： X方-X-72=0

答案： X=9

16. 一拖拉机厂，一月份生产出甲、乙2种新型拖拉机，其中乙型16台，从二月份起，甲型每月增产10台，乙型每月按相同的增长率逐月递增，又知二月份甲、乙两型的产量之比为3：2，三月份甲、乙两型产量之和为65台，求乙型拖拉机每月增长率及甲型拖拉机一月份的产量。

解：设乙的增长率为X，那么二月乙就是16（1+X）台，甲就是16（1+X）×3÷2；三月乙就是16（1+X）2台，甲就是16（1+X）×3÷2+10台，所以列出算式16（1+X）2+16（1+X）×3÷2+10=65 求解，然后可以分别算出一月二月乙的产量，然后即可解得甲的产量了17.

17.如图，出发沿BC匀速向点C运动。已知点N的速度每秒比点M快1cm，运动的速度。

两点同时出发，运动3秒后相距10cm。求点M和点N

解:设M速度x，则N为（x+1），（BC—3x）的平方加上3（x+1）的平方=10的平方，解得x=1或x=5/3又因为AC=7，所以x=1，M的速度为1m/s，N的速度2m/s

18.用长为100cm的金属丝做1个矩形框.李明做的矩形框的面积为400平方厘米，而王宁做的矩形框的面积为600平方厘米，你知道这是为什么吗？

解：设矩形一边长为X厘米，则相邻一边长为1/2（100-2X）厘米，即（50-X）厘米，依题意得：

X*(50-X)=400 解之得：X1=40,X2=10;

X*(50-X)=600 解之得：X1=20,X2=30；

所以李明做的矩形的长是40厘米，宽是10厘米；

王宁做的矩形的长是30厘米，宽是20厘米。

19.某商品进价为每件40元，如果售价为每件50元，每个月可卖出210件，如果售价超过50元，但不超过80元，每件商品的售价每上涨10元，每个月少卖1件，如果售价超过80元后，若再涨价，每件商品的售价每涨1元，每个月少卖3件。设该商品的售价为X元。

（1）、每件商品的利润为 元。若超过50元，但不超过80元，每月售 件。

若超过80元，每月售 件。（用X的式子填空。）

（2）、若超过50元但是不超过80元，售价为多少时 利润可达到7200元

(3)、若超过80元，售价为多少时利润为7500元。

解： 1)x-40 210-(x-40)10 210-(x-40)10-3(x-80)

(2)设售价为a (a-40)[210-(a-40)10=7200

(3)设售价为b (b-40)[210-(b-40)10-3(b-80)=7500 （第2 、3问也可设该商品的售价为X1 x2元）

20.某商场销售一批衬衫，平均每天可出售30件，每件赚50元，为扩大销售，加盈利，尽量减少库存，商场决定降价，如果每件降1元，商场平均每天可多卖2件，若商场平均每天要赚2100元，问衬衫降价多少元

解：衬衫降价x元

2100=(50-x)(30+2x)=1500+70x-x^2

73一元二次方程应用题(含答案)[1][1]_一元二次方程应用题

x^2-70x+600=0

(x-10)(x-60)=0

x-60=0 x=60>50 舍去

x-10=0 x=10

21.在一块面积为888平方厘米的矩形材料的四角，各剪掉1个大小相同的正方形（剪掉的正方形作废料处理，不再使用），做成1个无盖的长方体盒子，要求盒子的长为25cm，宽为高的2倍，盒子的宽和高应为多少？

解：设剪去正方形的边长为x,x同时是盒子的高，则盒子宽为2x;

矩形材料的尺寸：

长：25+2x

宽：4x;

(25+2x)*4x=888,

解得：x1=6,x2=-18.5(舍去）

盒子的宽：12cm；盒子的高：6cm。

22.甲乙二人分别从相聚20千米的A、B两地以相同的速度同时相向而行，相遇后，二人继续前进，乙的速度不变，甲每小时比原来多走1千米，结果甲到达B地后乙还需30分钟才能到达A地，求乙每小时走多少千米？

解：可以设乙每小时走a千米

乙从中点相遇后到A地需要时间10/a

甲从中点相遇后到B地需要时间10/a-0.5

根据题意建立方程

(10/a-0.5)(a+1)=10

a=4

即乙每小时走4千米

23.某企业2005年初投资100万元生产适销对路的产品，2005年底，将获得的利润与年初的投资和作为2006年初的投资。道2006年底，两年共获得56

万元，已知2006年的年获利率比2005年的年获利率多十个百分点，求2005和2006年的年获利率各是多少

解设2005年获利率是x

100x+100(1+x)(x+0.1)=56

100x+100x平方+110x+10-56=0

100x平方+210x-46=0

(20x+46)(5x-1)=0

x1=-2.3(舍）x2=0.2

0.2+0.1=0.3

2005年获利率是20%，2006年获利率是30%

24.某公司生产开发了960件新产品，需要经过加工后才能投放市场，现在有A，B2个工厂都想参加加工这批产品，已知A工厂单独加工这批产品比B工厂单独加工这批产品要多用20天，而B工厂每天比A工厂多加工8件产品，公司需要支付给A工厂每天80元的加工费，B工厂每天120元的加工费。

1. A，B2个工厂每天各能加工多少件新产品？

2. 公司制定产品方案如下：可以由每个厂家单独完成；也可以由2个厂家同时合作完成。在加工过程中，公司需要派一名工程师每天到厂进行技术指导，并负担每天5元的午餐补助费。请帮助公司选择哪家工厂加工比较省钱，并说明理由。

解：1.设A每天加工x件产品，则B每天加工x+8件产品

由题意得960/x-960/(x+8)=20

解得x=16件

所以A每天加工16件产品，则B每天加工24件产品

2.设让A加工x件，B加工960-x件

则公司费用为x/16*(80+5)+(960-x)/24*(120+5)

化简为5/48*x+5000

所以x=0时最省钱，即全让B厂加工

27.某学校以21元的价格购进一批计算器，该学校自行定价，但每只加价不能超过进价的50％，若每只以a元出售，可卖出（3400—50a）。请根据上列条件，并提出1个问题，并解答

某商店以每件21元的价格购进一批商品，该商品可以自行定价，但物价局限定每件商品加价不能超过进价的30%。若每件商品售价为a元，则可卖出（350-10a）。商品计划要赚400元，则需要卖出多少件商品？每件商品售价多少元？

解：

(a-21)*（350-10a）=400

-10a^2+560a=-7350

a^2-56a=-735

配方得：

a^2-56a+28^2=-735+28^2

(a-28)^2=9

解得：

a=31或25

验证：

a=31时，（31-21）/21=47.6% 不合法，

a=25时，（25-21）/21=19.0% 合法。

答：每件商品售价25元，需要卖出100件。

28.一张桌子的桌面长6米 宽为4米。长方形台布的面积是桌面面积的两倍 。若将台布铺在桌子上四边（4个角除外）垂下的长度相同，求这块台布的长和宽 。

解：设垂下的长度为a，

则：（6+a）*（4+a）＝2*4*6

解得：a＝2或a＝-12(舍去)，

台布的长、宽分别为8、6

29.一元二次方程解应用题 将进货单价为40元的商品按50元出售时，能卖500个，如果该商品每涨价1元，其销售量就减少十个。商店为了赚取8000元的利润，这种商品的售价应定为多少?应进货多少？

解：利润是标价-进价

设涨价x元,则:

(10+x)(500-10x)=8000

5000-100x+500x-10x^2=8000

x^2-40x+300=0

(x-20)^2=100

x-20=10或x-20=-10

x=30或x=10

经检验,x的值符合题意

所以售价为80元或60元

所以应进8000/(10+x)=200个或400个

所以应标价为80元或60元

应进200个或400个

30.甲、乙两名职工接受相同数量的生产任务，开始时，乙比甲每天少做四件，乙比甲多用了2天时间，这样甲、乙两人各剩624件；随后，乙改进了生产技术，每天比原来多做6件，而甲每天的工作量不变，结果两人完成全部生产任务所用的时间相同。原来甲乙两人每天各做多少件？没人的全部生产任务是多少? 应用题过程 谢谢

解：设每人的全部生产任务是y件，甲每天做X+4件，乙原来每天做X件，依题意得：

(y-624)/x=(y-624)/(x+4)+2 1式 （因为开始时，乙比甲每天少做4件，乙比甲多用了2天的时间，这样甲、乙两人各剩624件~~即根据时间关系列等式）

（y-624）/x + 624/(x+6)=y/(x+4) 2式 （结果两人完成全部生产任务所用的时间相同~~~也是根据时间关系列等式）

由1，2式得：（X+30）*（X-20）=0

解之得：X=20,X+4=24，，y=864

答：每人的全部生产任务是864件，甲每天做24件，乙原来每天做20件。

31.用22厘米长的铁丝，折成1个面积为30平方厘米的长方形，求这个长方形的长和宽。又问：能否折成面积是32平方厘米的长方形呢？为什么？

解：设长方形的长为x厘米，那么宽为11-x厘米

x(11-x)=32

-x2+11x-32=0

由根的判别式：112-4×1×32=121-128=-7<0

没有实数根

所以无法折成面积是32平方厘米的长方形

长方形的长宽多少？

解：x(11-x)=30

-x2+11x-30=0

x2-11x+30=0

(x-5)(x-6)=0

x=5或6

这个长方形的长和宽为6厘米和5厘米

32.1个自行车队进行训练，训练时所有队员都以35千米/时的速度前进，突然，1号队员以45千米/时的速度独自前进，行进10千米后调转车头，仍以45千米/时的速度往回骑，直到与其他队员会合，1号队员从离队开始到与队员重新会合，经过了多少时间

解：设一共用了x小时，得：

35x=10-45(x-10/45)

35x=10-45x+10

80x=20

x=1/4答：1号队员从离队开始到与队员重新会合，经过了1/4小时。

33.参加一次聚会的每2个人都握了一次手，所有人共握手10次，有多少人参加聚会？

34.参加一次足球联赛的每2个队之间都进行两次比赛，共要比赛90场，共有多少个队参加比赛？

35.要组织一次篮球联赛，赛制为单循环形式（每2个队之间赛一场），计划安排15场比赛，应邀请多少个球队参加比赛？

解：34、n（n-1）2=10

n=5

35、x（x-1）2*2=90

x=10

36、y（y-1)2=15

y=6

37.某公司生产开发了960件新产品，需要经过加工后才能投放市场，现在有A，B2个工厂都想参加加工这批产品，已知A工厂单独加工这批产品比B工厂单独加工这批产品要多用20天，而B工厂每天比A工厂多加工8件产品，公司需要支付给A工厂每天80元的加工费，B工厂每天120元的加工费。

1. A，B2个工厂每天各能加工多少件新产品？

2. 公司制定产品方案如下：可以由每个厂家单独完成；也可以由2个厂家同时合作完成。在加工过程中，公司需要派一名工程师每天到厂进行技术指导，并负担每天5元的午餐补助费。请帮助公司选择哪家工厂加工比较省钱，并说明理由。

73一元二次方程应用题(含答案)[1][1]_一元二次方程应用题

解：1.设A每天加工x件产品，则B每天加工x+8件产品

由题意得960/x-960/(x+8)=20

解得x=16件

所以A每天加工16件产品，则B每天加工24件产品

2.设让A加工x件，B加工960-x件

则公司费用为x/16*(80+5)+(960-x)/24*(120+5)

化简为5/48*x+5000

所以x=0时最省钱，即全让B厂加工

37.在某场象棋比赛中，每位选手和其他选手赛一场，胜者记2分，败者记0分，平局各记1分，今有四位统计员统计了全部选手的得分之和分别是2025分、2027分、2080分、2085分，经核实，只有一位统计员的结果是正确的，问这场比赛有几位选手参加？

解： 无论如何，每一局两人合计都应得2分，所以最终的总得分一定是偶数，由于2025、2027、2085都是奇数，所以都不符合题意，所以正确的是第3个记分员

设有x人参加，则一共比了x（x-1）/2局

你的数字似乎有错，请确认是否为2070，而不是2080（2080得不出整数解）

x（x-1）/2=2070/2

x2-x-2070=0

（x-46）（x+45）=0

x1=46，x2=-45（舍）

答：一共有46位选手参加.

39.如图，在一块长35M，宽26M的矩形地面上，修剪同样宽的两条互相垂直的道路，（两条道路与矩形的一条边平行），剩余部分栽种花草，要使剩余部分的面积为850M2，道路的宽应为多少？

40.游行队伍有8行12列，后又增加69人，使得队伍增加的行、列数相同，你知道增加了多少行或多少列吗？

图是39题的。

据转换思想

1解：可设道路的宽为Xm

（35-x）（26-x)=850

x^2-61x+60=0

(x-1)(x-60)=0

x1=1，x2=60

x2=60与题意不符

所以x1=1

道路的宽为1m

40解：设增加x行，即x列

8*12+69=（8+x）（12+x）

69=x^2+20x

x^2+20x-69=0

(x-3)(x+23)=0

x1=-23

x2=3

x1=-23与题意不符

所以x=3

41.随着人民生活水平的不断提高，我市家庭轿车的拥有量逐年增加.据统计，某小区2006年底拥有家庭轿车64辆，2008年底家庭轿车的拥有量达到100辆.

（1） 若该小区2006年底到2009年底家庭轿车拥有量的年平均增长率都相同，求该小区到2009年底家庭轿车将达到多少辆？

（2） 为了缓解停车矛盾，该小区决定投资15万元再建造若干个停车位.据测算，建造费用分别为室内车位5000元/个，露天车位1000元/个，考虑到实际因素，计划露天车位的数量不少于室内车位的2倍，但不超过室内车位的2.5倍，求该小区最多可建2种车位各多少个？试写出所有可能的方案.

(1). 解：设增长率是x.

64(1+x)2=100

x=0.25

2009年有

100(1+0.25)=125

（2）解：设室内车位为X，则室外车位为(150000-5000X)/1000

有条件得到：0<=2X<=(150000-5000X)/1000<=2.5X

得到20<=X<=21.4

X为整数

所以X取20或21

当X=20是，室内车位为50

当X=21时，室内车位45

所以最多能有70个车位

42.为一副长20CM 宽16CM的照片配1个镜框，要求镜框的四条边宽度相等，且镜框所占面积为照片面积的二分之一，镜框边的宽度应为多少

解：方法一：

镜框边的宽度为xcm,照片长加2个宽度，宽加2个宽度，外部变成1个大长方形，故大长方形的长为(20+2x)cm，宽为(16+2x)cm，大长方形面积减去照片（小长方形）面积就是镜框的面积。

(20+2x)(16+2x)-20*16=20*16/2

4x^2+72x-160=0

x^2+18x-40=0

(x+20)(x-2)=0

x=2,x=-20(舍去）

镜框边的宽度应为2cm

方法二：

镜框的面积就是2个以照片长为长、镜框边的宽度为宽的长方形面积，2个以照片宽为长、镜框边的宽度为宽的长方形面积，4个以镜框边的宽度为边长的小正方形面积三部分组成。

2(20x)+2(16x)+4x^2=20*16/2

4x^2+72x-160=0

x^2+18x-40=0

(x+20)(x-2)=0

x=2,x=-20(舍去）

镜框边的宽度应为2cm

43．将进货单价为40元的商品按50元出售时，能卖出500个，已知该商品每降价1元，其销售量就要减少十个，为了赚8000元利润，售价应定为多少？这时进货应为多少个？

44．某商店从厂家以每件21元的价格购进一批商品，该商店可以自行定价，

若每件商品售价为a元，可以卖出（350－10a）件，但物价局限定每件商品加价不能超过进价的20％，商店计划要赚400元，需要卖出多少件商品？每件商品售价多少？

45.目标P16实践与探究

每件商品的成本是120元，在试销阶段发现每件售价（元）与产品的日销售量（件）始终存在下表中的数量关系，但每天的盈利（元）却不一样。为找到每件产品的最佳定价，商场经理请一位营销策划员通过计算，在不改变每件售价（元）与日销售量（件）之间的数量关系的情况下，每件定价为m元时，每日盈利可以达到最佳值1600元。请你做营销策划员，m的值应为多少？

46．某商店如果将进货价8元的商品按每件10元出售，每天可销售200件，现采用提高售价，减少进货量的方法增加利润，已知这种商品每涨0.5元，其销售量即可减少10元，问应将售价定为多少时，才能使所赚利润最大，并求出最大利润

43解：设售价应定为x元，根据题意列方程得?500?10(x?50)??(x?40)?8000整理得x2?140x?480?0

（x－60）（x－80）＝0

解得x1＝60，x2＝80

答：当x1＝60时，进货量为400个

当x2＝80时，进货量为200个

44解：由题意列方程得，a(350-10a)-21(350-10a)=400

a2?56a?775?0

（a-25）(a-31)=0

73一元二次方程应用题(含答案)[1][1]_一元二次方程应用题

解得，a1＝25，a2＝31 31?21?20%21∵∴a2＝31不合题意,舍去

350-10a＝100

答：需要卖出100品，商品售价25元

分析：根据表格可以看出每件的售价每降1元时，每日就多销售1件，根据这个隐含条件即可得出此类型题和以上的练习非常相似了

45.解：若定价为m元时，售出的商品为

［70－（m－130）］件

列方程得

?70?(m?130)??(m?120)?1600

2整理得m?320m?25600?0

(m?160)2?0

∴m1＝m2＝160

答：m的值是160

46解：设售价定为x元，则每件的利润为

[200?x?10x?10?10][200??10]0.50.5件，列式得（x－8） （x－8）元，销售量为

?20(x2?28x?160)

2??20(x?14)?720 整理得，

即当x＝14时，所得利润有最大值，最大利润是720元

本文标题：一元二次方程应用题-2014一元二次方程应用题经典题型汇总
本文地址： http://www.61k.com/1112214.html