一 : 测量钢丝的杨氏模量
05级数学系 PB05001067 胡鑫 ?
? 测量钢丝的杨氏模量
实验目的
?
?
学会利用光杠杆法测定微小形变; 学会使用逐差法和作图法进行数据处理。 5
实验原理
宏观物体在外力作用下都会发生形变,在弹性限度内,材料的应强与应变之比为一常数,称弹性模量。杨氏模量(用E表示)是条形物体沿纵向的弹性模量,定义为弹性限度 内应力与应变之比(注:应力是力与作用的面积之比,应变是长度的变化与原长之比),即
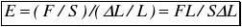
(1)
在胡克定律成立的范围内,E为常数,它仅决定于材料的属性,用于度量材料的刚性。测量杨氏模量可用拉伸法、梁德弯曲法、振动法、内耗法等。
本实验采用拉伸法测量钢丝的样式模量,即,在截面积为S的样品上的作用应力F,测量引起的相对伸长量ΔL/L,即可计算出材料的杨氏模量E。
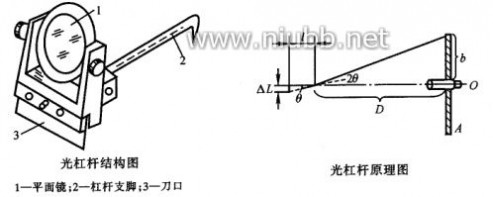
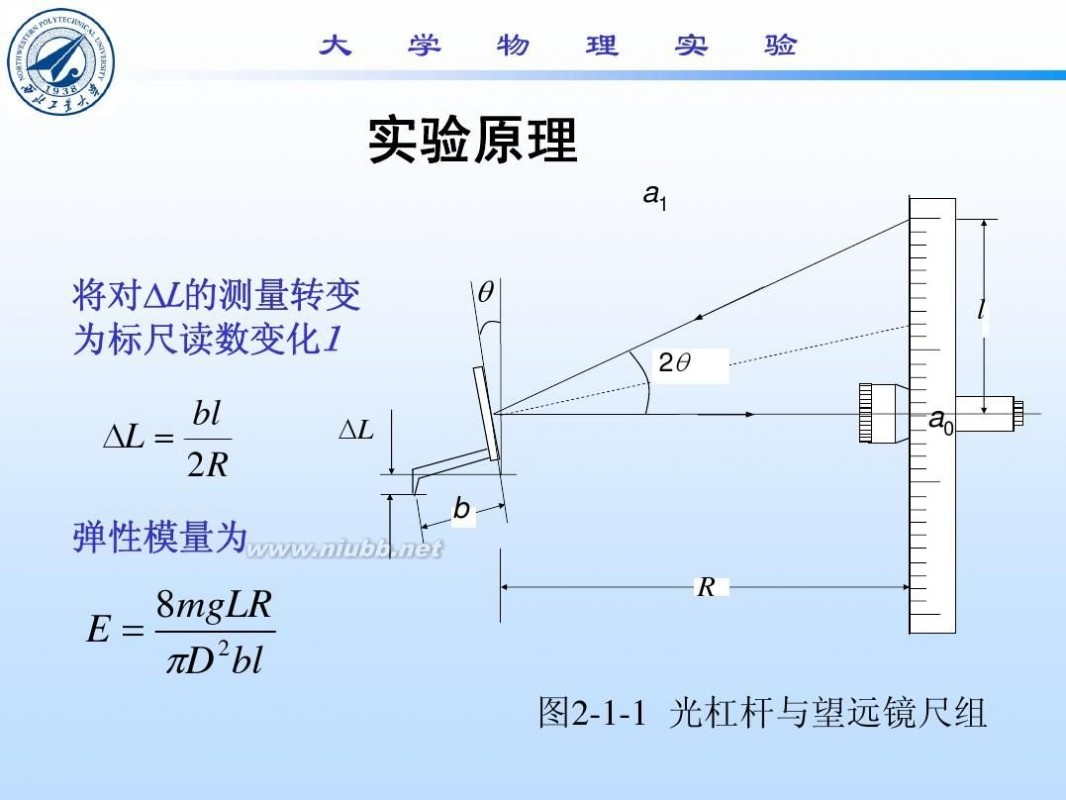
因伸长量ΔL一般很小,常用光杠杆法先放大ΔL再测量。光杠杆装置是带有一个可旋转的平面镜的支架,平面镜的镜面与三个足尖决定的平面垂直,杠杆支脚与待测物接触。当杠杆支脚随钢丝下降微小距离ΔL时,镜面法线转过θ角,反射光线转动2θ角,当θ趋于0时(臂长为l)
??tan???L/l (2)
tan2??2??b
(
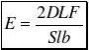
3) D
(D为镜面到标尺的距离,b是从望远镜中观察到的标尺移动的距离)
由以上三式得到
(4) 1
05级数学系 PB05001067 胡鑫 ?
只要测量出L、D、l和d(S??d2/4)及F与b ,就可确定钢丝的杨氏模量E。
实验仪器
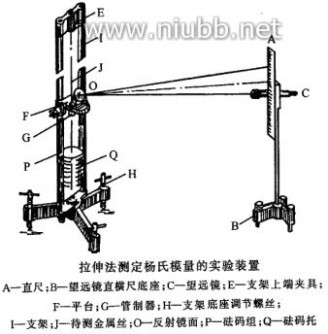
杨氏模量的测量装置包括光杠杆、砝码、望远镜和标尺。实验装置如图所示,钢丝长约1m ,上端夹紧悬挂于支架顶部,下端夹在一个管制器底部,支架中部有一平台,平台中有一圆孔,管制器能在孔中上下移动,砝码加在管制器下的砝码托上,使金属丝伸长。
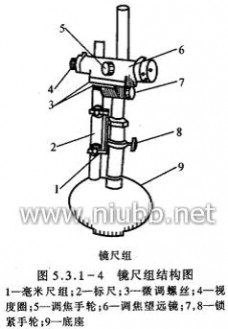
实验步骤
1. 调节仪器
(1) 调节平台与望远镜的相对位置,使光杠杆镜面法线与望远镜轴线重合。
(2) 调节支架底脚螺丝,使平台水平;调节平台的竖直位置,使其上表面与管制器顶部共面。
(3) 调节光杠杆,使其镜面与刀口平行。使用时,刀口置于平台的槽内,支脚置于管制器的槽
内,刀口和支脚尖须共面。
(4) 镜尺组的调节,调节望远镜、直尺和光杠杆三者之间的相对位置,使望远镜与平面镜等高,
调节望远镜目镜视度圈,使目镜内分划板刻线(叉丝)清晰,用手轮调焦,使标尺像清晰。 注意
——牛宝宝日记本——? 在调好光杠杆和镜尺组之后,必须防止刀口、望远镜和竖尺的位置发生变动,特别在加减
砝码时要轻取轻放。
? 先粗调后微调:通过望远镜筒上的准星看反射镜,应能看到标尺,然后微调望远镜。调目
镜可以看清叉丝,调聚焦旋钮可以看清标尺。
2. 测量数据
(5) 测量砝码托的质量m0,记录望远镜中标尺的读数r0作为钢丝的起始长度。
2
05级数学系 PB05001067 胡鑫 ?
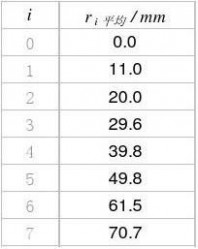
(6) 在砝码托上逐个增加500g砝码到3500g,记录望远镜中标尺上的读数ri,再将砝码逐个减
去,记下读数r'i,取两组对应数据的平均值ri。
(7) 用米尺测量金属丝的长度L和平面镜与标尺之间的距离D,以及光杠杆的臂长l。 3. ?
处理数据
用螺旋测微仪测量金属丝直径d,上、中、下各测2次,取平均值。将ri每隔四项相减,得到相当于每次加2000g的四次测 量数据,bi?ri?4?ri (i =0,1,2,3),再求平均值和误差。将测得的各量代入式(4)计算E,并求出其误差(ΔE/E和ΔE),正确表述E的测量结果。 ?
回归法
令M?2DL/(SlE),则有
ri?2DLFi/(SlE)?MFi (5)
若以ri为纵坐标,Fi为横坐标作图,因实验中M不变,故拟合得斜率为M的直线,则

(6)
数据记录
(本次实验在1409实验室○7号实验台完成)
测量钢丝的直径d数据如下表所示:

在增减砝码过程中,标尺的读数如下表所示:

L?100.50cmD?98.50cm
3
l?72.0mm
05级数学系 PB05001067 胡鑫 ?
逐差法:将d的测量值列和b的测量值列代入平均值公式和标准差公式
1n1n2?xi????xi ?x??n?1i?1ni?1
得
?40.3mm ?0.293mm
??b??1.2mm ??d??0.005mm
查表知修正因子
t?0.683,4??1.20 t?0.683,6??1.11
于是
uA?b??t?0.683,4????b?
n1.20?1.2?mm?0.7mm 2
t?0.683,6????d?1.11?0.005uA?d???mm?0.002mm n6
已给出的一些数据:
?500g
故最大不确定度为 ?m?5g?L??D?2mm?l?0.2mm ?E?D?L?d?l?b?F???2???EDLdlbF
220.0020.20.75???2????985.01005.00.29372.040.3500
?0.048
又(取g?9.7947kg?m/s2)
8DL8?985.0?1005.0?0.500?4?9.79472??N/mm?2l3.1416?0.2932?72.0?40.3
?1.98?105N/mm2
?1.98?1011N/m2
?E?0.48?1.98?1011N/m2?0.09?1011N/m2
4
05级数学系 PB05001067 胡鑫 ?
所以最终结果为
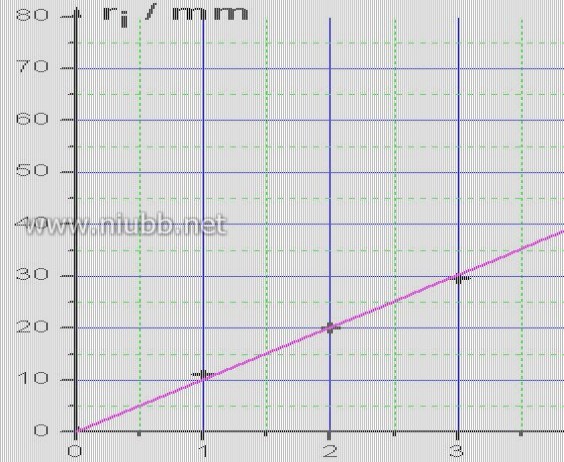
作图法:

不妨以砝码个数和伸长量两列数据进行作图,由于 ri?2DLimg/(SlE)?Ki 故有拟合直线的斜率 K?8DLmg/(?d2lE) 所以 E?8DLmg/(?d2lK)
作图如下:
拟合的曲线类型为直线
用最小二乘法求得:
参数
A
B ri?Ki 值0.00252
0.3328标准偏差5.52E-041.30E-03相关系数r样本数N置信概率P标准差5>0.99994.12E-04 0.99998
5
05级数学系 PB05001067 胡鑫 ?
即:
K?10.08
故
8DLmg8?985.0?1005.0?0.500?9.79472??N/mm?2lK3.1416?0.2932?72.0?10.08
?1.98?10N/m
不确定度 112
?E?D?L?d?l?K?m???2???EDLdlKm
220.0020.20.115???2????985.01005.00.29372.010.08500 ?0.041
?E?0.041?1.98?1011N/m2?0.08?1011N/m2
于是

比较总结:分析得不错
思考题
? 利用光杠杆把测微小长度ΔL变成测b,光杠杆的放大率为2D/L,根据此式能否以增加D减
小l来提高放大率,这样做有无好处?有无限度?应怎样考虑这个问题? 答:这样做有好处,但也有限度:设放大率为k,于是
b?L?k UB?Lwww.61k.comBb?k
显然当UBb一定时,k增大,UB?L减小,但
(1)砝码加至七个时,望远镜中标尺移动距离可能已超出测量范围,无法观测;
(2)当?较小时才有 ??tan?,而减小l会使?增大,从而增大误差。
? 报告结束 ?
6
二 : 光杠杆原理在钢丝杨氏模量测定中的近似

2007年第3期??????????????????????????物理通报??????????????????????????????实验教学研究
??
光杠杆原理在钢丝杨氏模量测定中的近似
李
霞??赵树民??贾鹏英??庞学霞
(河北大学物理科学与技术学院??河北保定??071002)
摘要:针对现行大学物理实验教材,对光杠杆测量微小长度变化的原理描述中的近似条件进行了详细地分析,并给出了严格的计算公式.
关键词:光杠杆??
系统误差??杨氏模量
????微小长度变化的测量是大学普通物理实验课程中一项重要内容,如静力拉伸法测量杨氏模量,固体线胀系数等实验,都涉及到微小长度变化.对于这些量,用一般测量长度的工具,不容易测量.宜采用光杠杆镜尺组放大法测量(光杠杆镜尺组包括光杠杆、望远镜和米尺),但在一般的物理实验教材中,对光杠杆放大原理描述都进行了近似,是一种理想的状态.而事实上,由于光杠杆系统本身的误差和实验者对仪器使用(主要是望远镜的调节)的熟练程度不够,实验过程中,或多或少会出现误操作,使得实验结果不理想.
本文以拉伸法杨氏模量的测定为例,详细分析了光杠杆放大原理中的近似,给出了严格的计算公式,并提出光杠杆测量原理应用在杨氏模量的测定实验中一些应该注意的地方.
1??光杠杆放大原理的简单描述
????光杠杆是根据几何光学的原理设计的一套装置,光杠杆的两前足放在固定位置上,后足尖搁在被测点上并使镜面法线M与望远镜光轴平行.在拉伸法杨氏模量的测定实验中,一般的光杠杆放大原理如图1所示

.
图1??光杠杆放大原理图
望远镜和米尺组成的镜尺组置于镜面前方离镜面D处.米尺平行于镜面,便于用望远镜观察映入
4??合理应用多媒体必须关注的问题4.1??考虑形象思维和抽象思维相结合
多媒体能带给学生形象直观的感性材料,有利于学生的感性认识的形成.但是要把感性认识通过抽象思维上升到理性认识,即必须依靠学生自身感知、思考、分析、推理、归纳和总结.4.2??要注意教学手段和教学目的相结合
多媒体技术只是一种教学手段,它的运用必须要服务于教学目的,促进教学目的的最佳实现.4.3??要注意多媒体技术和传统教学手段相结合
多媒体技术的优点在于它形象、直观、生动,有利于激发学生的学习积极性.??一块黑板、一只粉笔、一本书、一本教案 也有不可替代的价值.尤其是系统的黑板板书,对学生整理所学的内容,构建知识体系更具有不可替代的作用.
因此,多媒体技术和其他教学手段一样,它有自己的生命力和存在价值,同时也有自己的局限性;作为新课程改革的实施者,不能因为多媒体技术的局限就抹杀了它在教学中的巨大作用.我们应研究怎样更加合理的使用多媒体技术,使之扬长避短,让这个时代的产物更好地服务于我们的教学.
光杠杆放大原理 光杠杆原理在钢丝杨氏模量测定中的近似
2007年第3期??????????????????????????物理通报??????????????????????????????实验教学研究
镜内的米尺刻度.由于光杠杆后足将随被测点的下移而变动它的位置,从而,映入镜内的刻度也随着变化,经过光杠杆放大,反映在镜内的刻度变化??h=h-h0,将远远大于被测点的移动,这样就便于观测长度的微小变化.
被测点上下移动一微小距离??L,则镜面转动一小角度??,这时从望远镜中所见米尺上的刻度变化一个较大的读数??h,设镜面至米尺之距离为D,光杠杆前后足之距离为b,现由L(钢丝原长),D,b,??h推得出??L.
当??甚小时,tan???sin?????,则有
(1)
b
据反射定律,当反射镜转动??角时,由于反射角???????????tan??=
等于入射角,反射线转过的角度为2??,同理tan2???2??,所以
????????2???tan2??=D
由(1)、(2)式可得
=b2D
即
(3)
2D
这样,微小量??L就被放大成了??h,即两次米尺????????????????L=
读数之差.当钢丝在纵向拉力F的作用下,并忽略钢丝直径 的变化,根据杨氏模量的定义,有
????????????E=
! b??h
(4)(2)
那么,我们带入公式中的镜面至米尺之距离D,就应该是D#.由图2可知,D#=(D-?)上,(3)、(4)式就变成了
??????????????L=(5)
2D#????????????E=(6)2
! b??h
显然若以(3)式计算微小量??L,不可避免地增大了杨氏模量.但是,究竟镜面至米尺之距离D对杨氏模量所产生的误差有多大,完全取决于实验中对D的相对误差的要求.通过计算,知D的相对误差为
=(7)????#=D#D-?
一般情况下,米尺与望远镜之间的间距2?是固
2
21/2
,实际
定的,也是可测量的.考虑到2?=10.50cm(不同厂家生产的镜尺组,此参数可能有所不同),
光杠杆放大原理 光杠杆原理在钢丝杨氏模量测定中的近似
2007年第3期??????????????????????????物理通报???????????????????????100%
tan???100%
sin??
????tan??=??则
??L=
????????实验教学研究
??tan??%=??sin??%=
2R+??h
(10)
其中,?是??的弧度表示.可以从三角函数表中查出此范围内的??与tan??和sin??以及取近似值后的相对误差百分比.此时近似带来的正切和正弦取近似值后的最大相对误差百分比分别在2.295140%~2.613019%,1.151514%~1.311622%之间.2.3??假设镜面与米尺之间的距离D#不随??的改变而变化
事实上,镜面与米尺之间的距离D#将随着??的改变而有一个微小的变化,如图4所示.实验时,设法使平面镜在中心位置的法线与望远镜光轴重合,令光轴到光杠杆底角水平线距离为R,取R=5.85cm(在实际调节望远镜时,这个量很难测量).则改变??角后,D#将有一增量?D#,?D#=Rtan??.由第2.2小节的假设,这个增量最大可达1.62cm,最大相对误差为4.08%.当然,这种情况属于极端条件,实验中一般不会达到

61阅读提醒您本文地址:
.
??)
2
22b(2
(2R+??h)2+2D2-2?+2R??h+(??h)2-
2
1/2
(D-?)[D-?+2R??h+(??h)]
(11)
由此可见,不做任何近似情况下的公式(11)在计算上是非常麻烦的,因此就要根据实验的具体情况对(11)式进行适当的简化.一般情况下,(11)式中所包含的变量b、D、?、??h是很容易测量的,只有R具有很大的不确定性,但是由于?D#相对于D#或D来说非常小,可以忽略.因此(11)式的相对误差将很大程度上取决于D的大小,而不是取决于R的大小.4??结论
????通过对一般的光杠杆放大原理中的近似进行详细分析,给出了严格的光杠杆放大原理计算微小长度变化的公式(11).同时注意到,在将光杠杆放大原理应用到钢丝杨氏模量的测定中时,镜面至米尺之距离D是整个实验中最容易引起误差(D同时是影响tan??和sin??向??近似的相对误差最大的量),也是调节幅度比较大的一个参数.因此,在钢丝杨氏模
图4
量的测定中,必须D%40.00cm,且在实验室空间允许的范围内,D越大,就越容易对(11)式进行简化.
3??严格的光杠杆放大原理
????通过第2节详细地分析光杠杆放大原理中的三个近似,我们再重新推导一下严格的光杠杆放大原理.
首先,(1)式应为??????????????sin??=其次,(2)式应为
tan2??==
D#+?D#由(9)式得到
-?+Rtan??
(9)
b
(8)
更????正
2007年第2期第19页?如何揭示隐藏着的空间维数+一文在??Sktanov 后应加上??如是说.他们建议发射一艘空间飞船,该飞船 18个字.特此更正,并向作者、读者深表歉意!
编辑部??
61阅读提醒您本文地址:
三 : 钢丝杨氏模量的测定

钢丝的杨氏模量 钢丝杨氏模量的测定

钢丝的杨氏模量 钢丝杨氏模量的测定

钢丝的杨氏模量 钢丝杨氏模量的测定

钢丝的杨氏模量 钢丝杨氏模量的测定
钢丝的杨氏模量 钢丝杨氏模量的测定
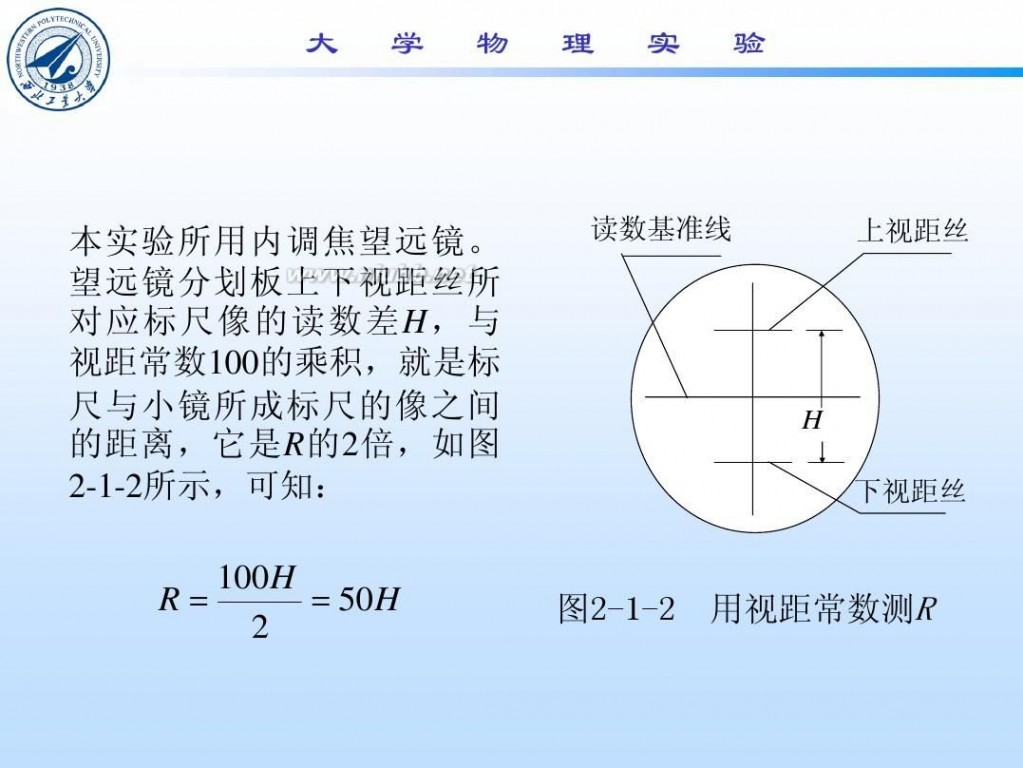
钢丝的杨氏模量 钢丝杨氏模量的测定

钢丝的杨氏模量 钢丝杨氏模量的测定

钢丝的杨氏模量 钢丝杨氏模量的测定
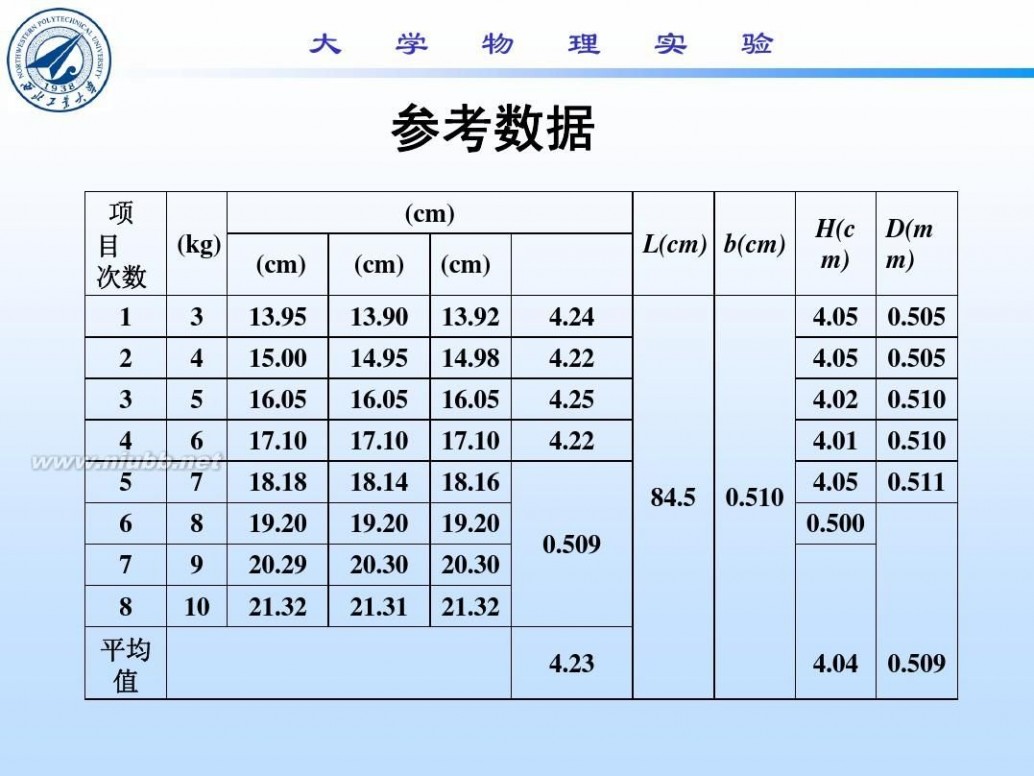
钢丝的杨氏模量 钢丝杨氏模量的测定

钢丝的杨氏模量 钢丝杨氏模量的测定
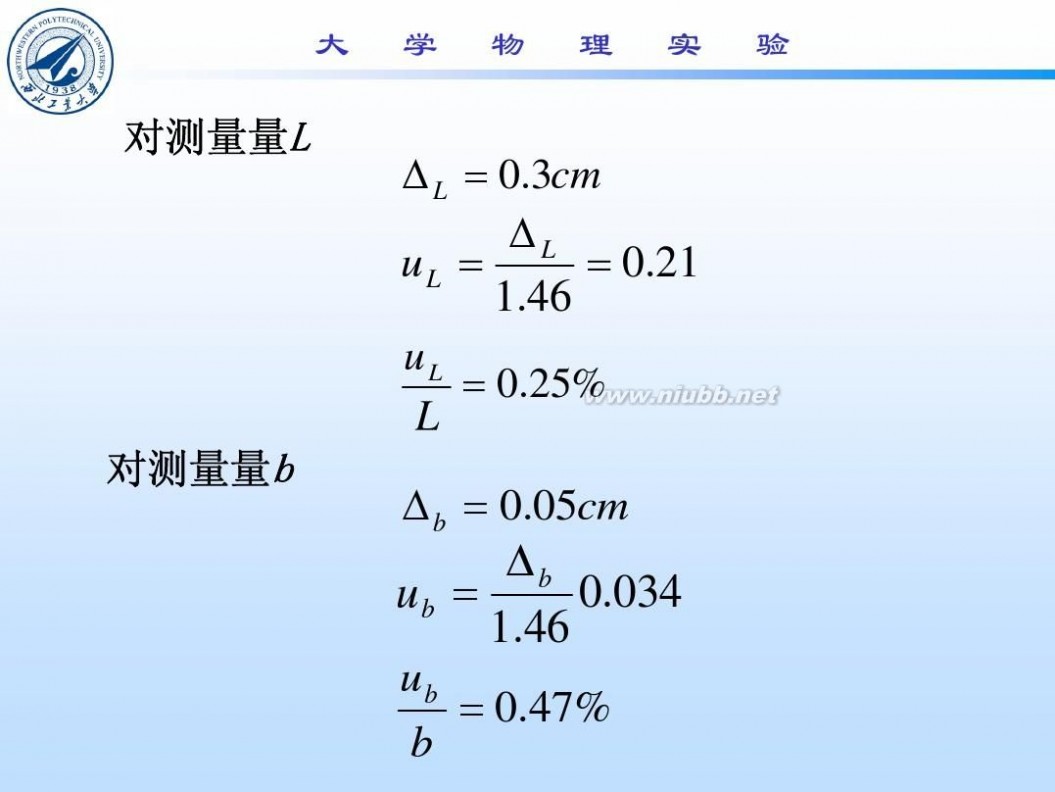
钢丝的杨氏模量 钢丝杨氏模量的测定

钢丝的杨氏模量 钢丝杨氏模量的测定

钢丝的杨氏模量 钢丝杨氏模量的测定

钢丝的杨氏模量 钢丝杨氏模量的测定

61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1