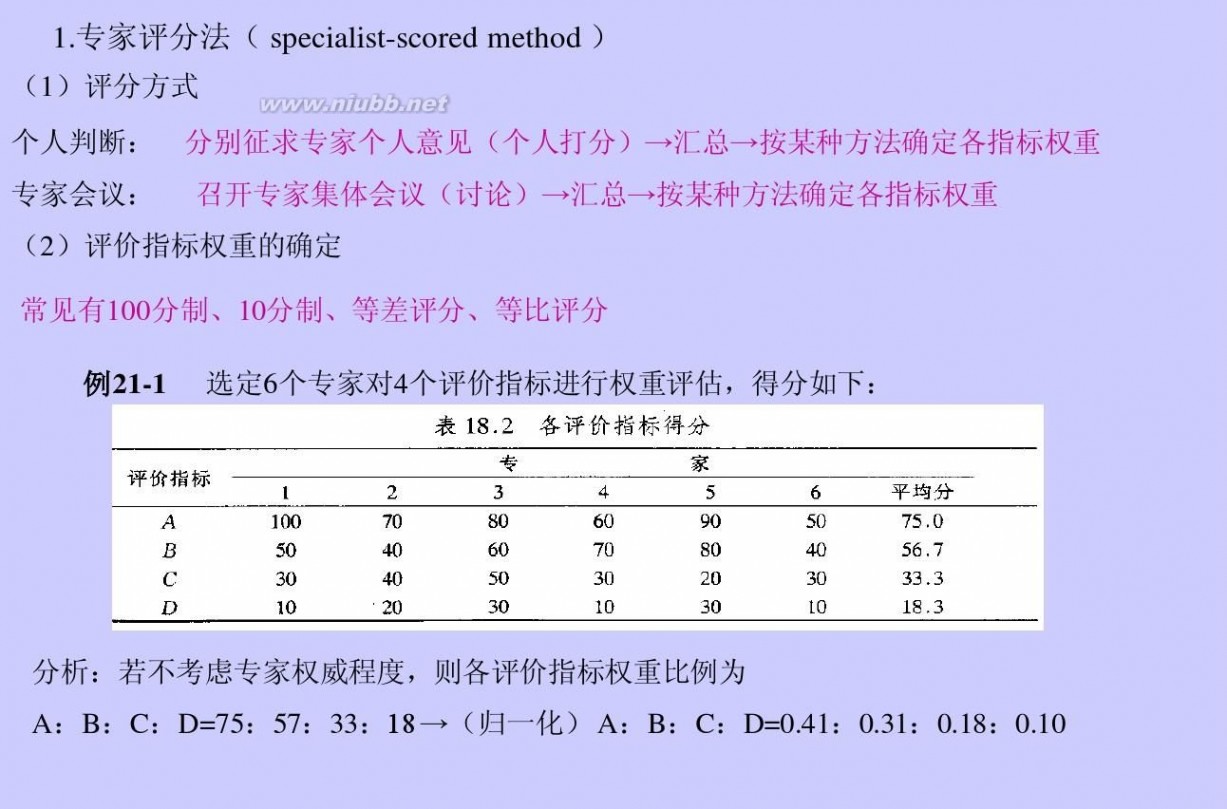
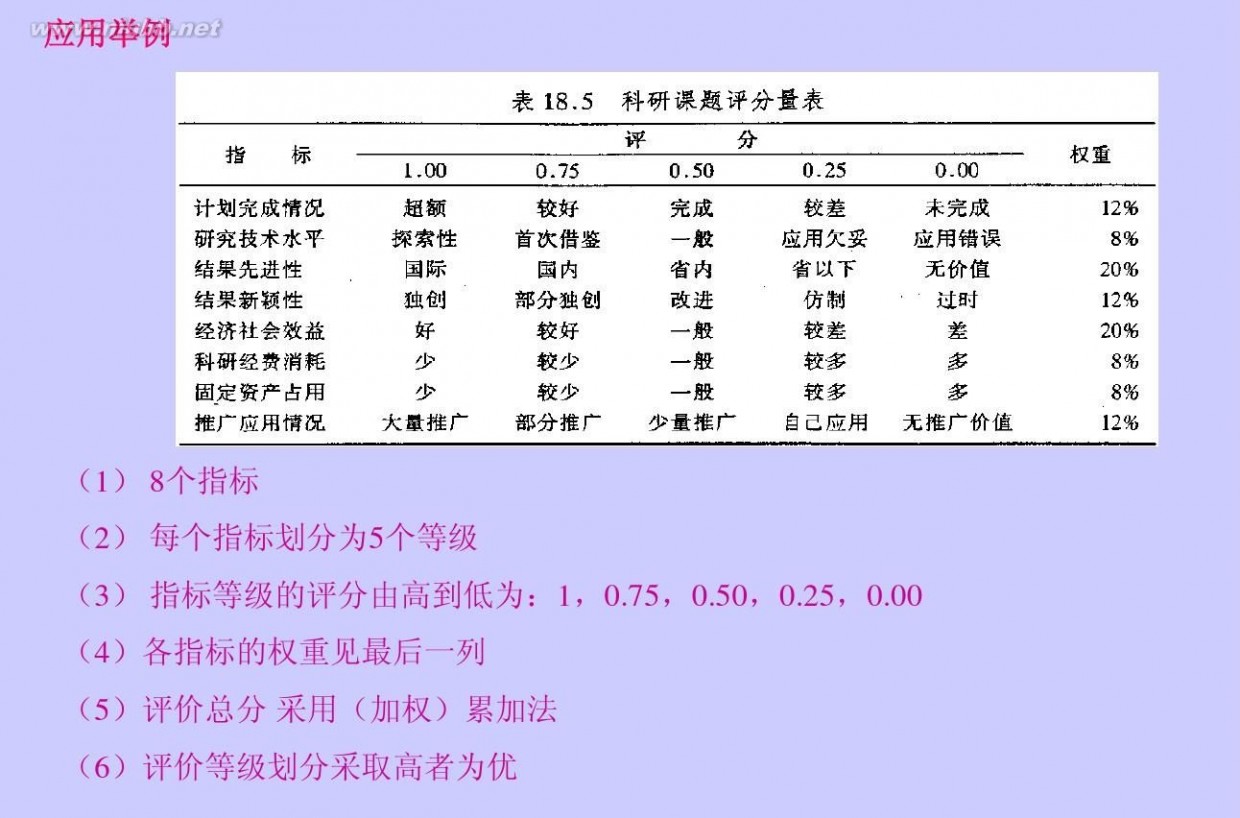
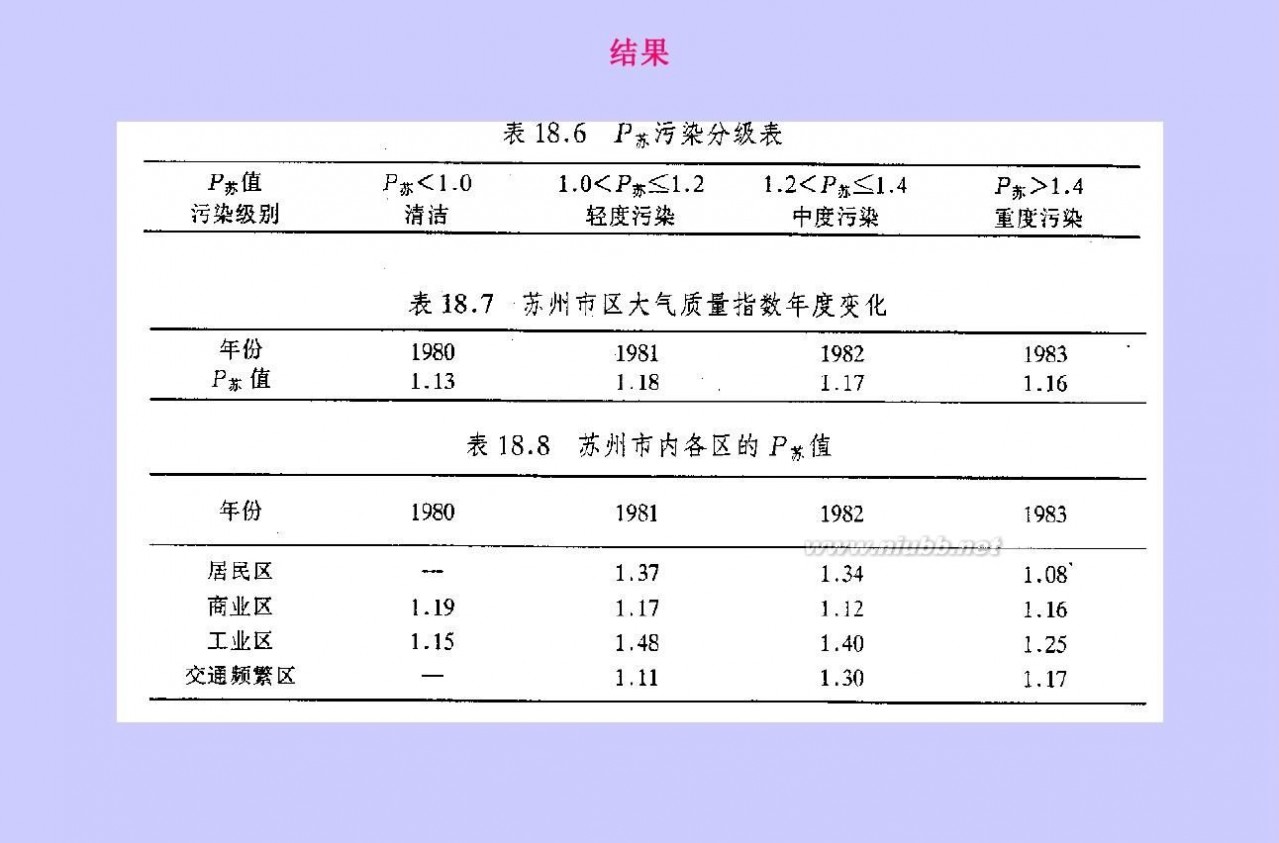
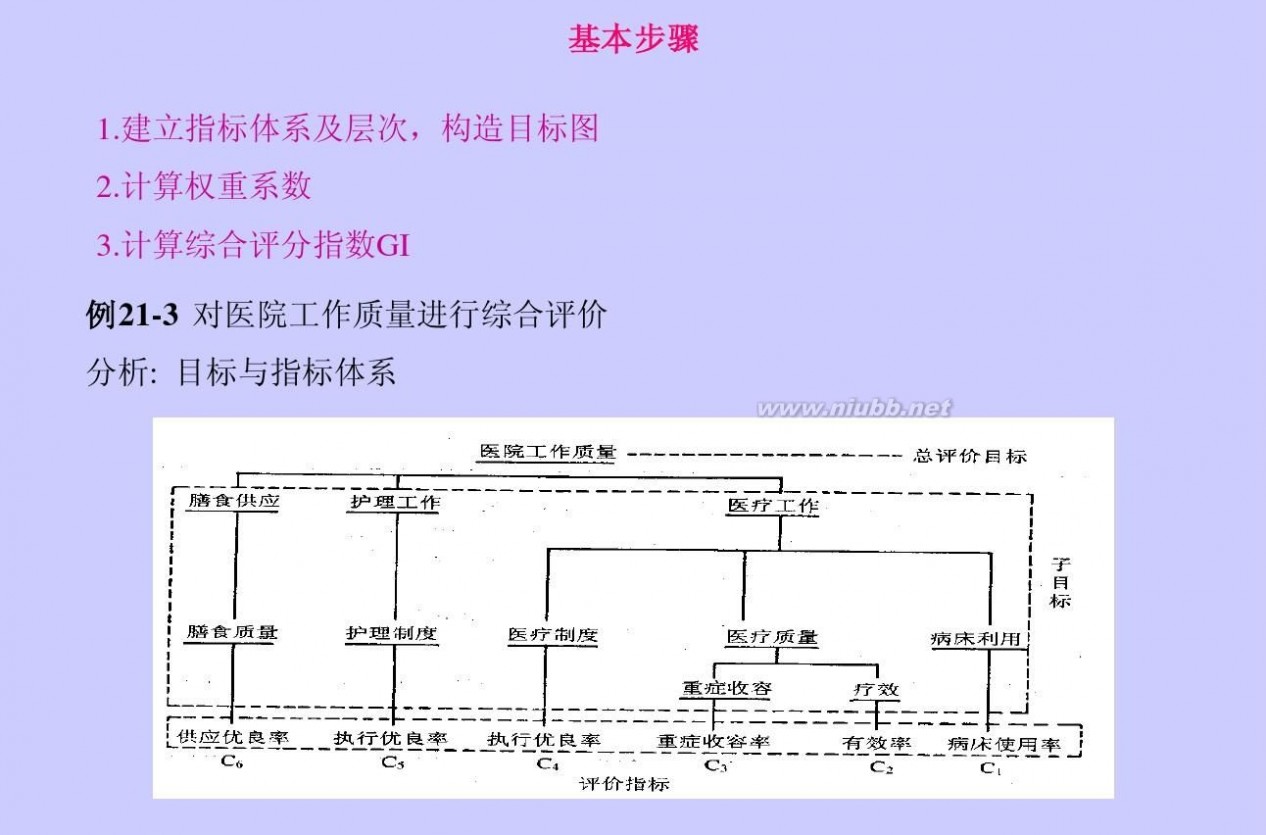
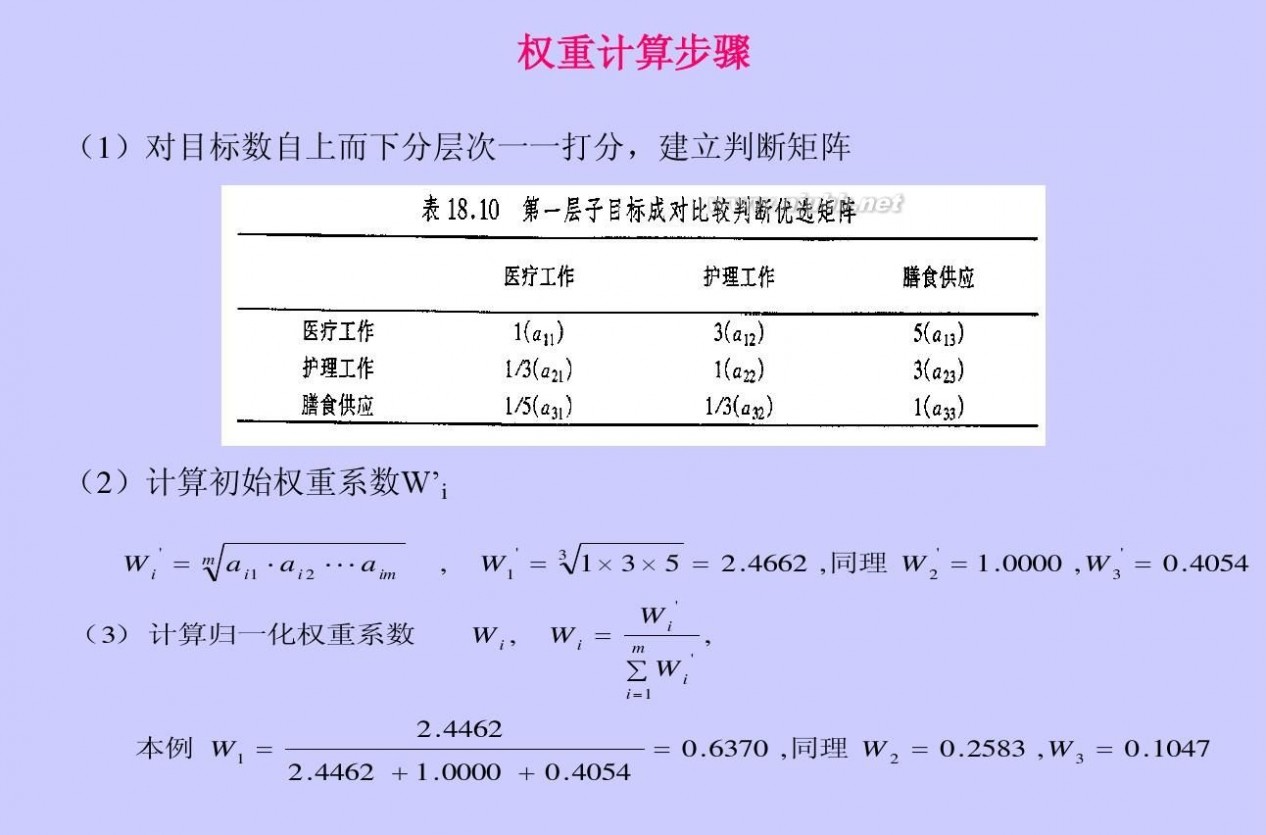
一 : 秩和比法综合评价
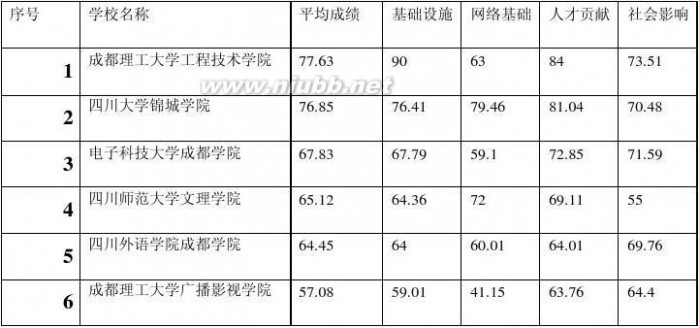

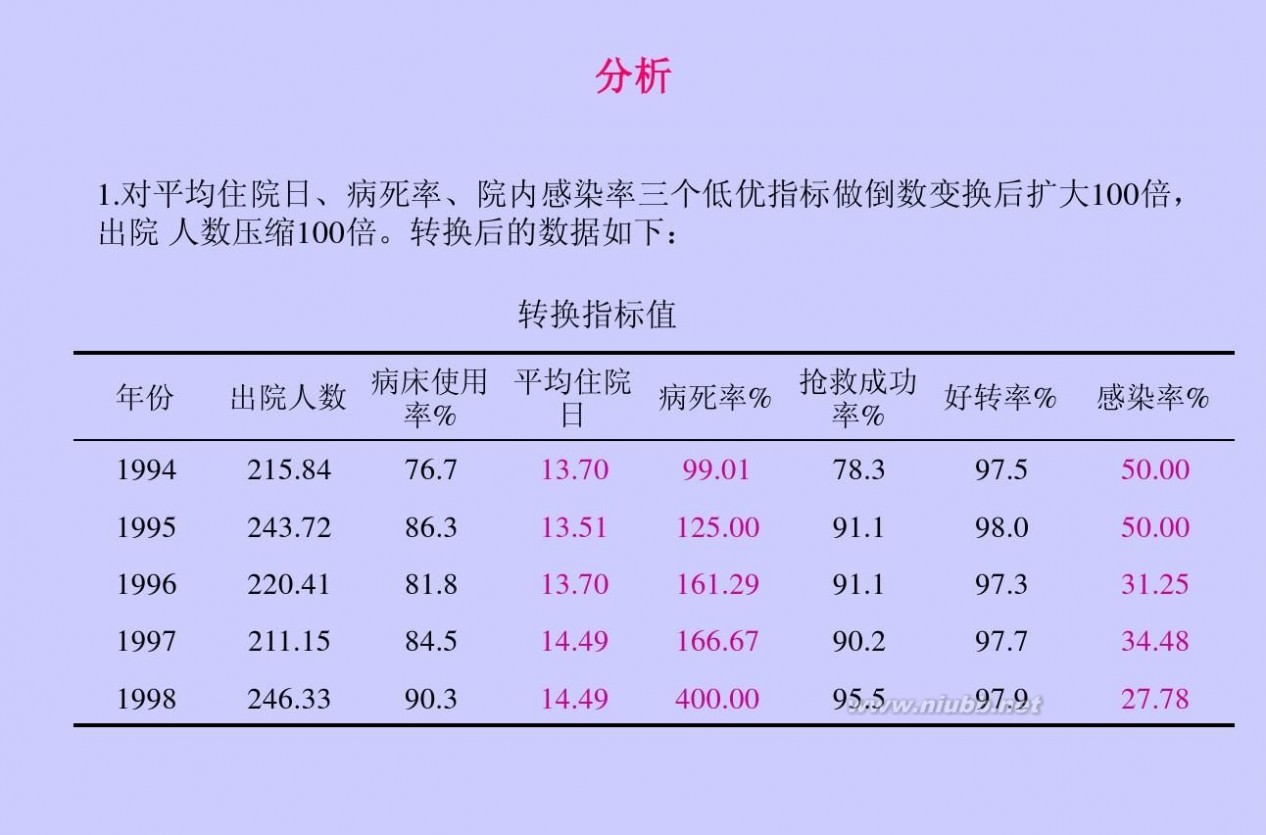
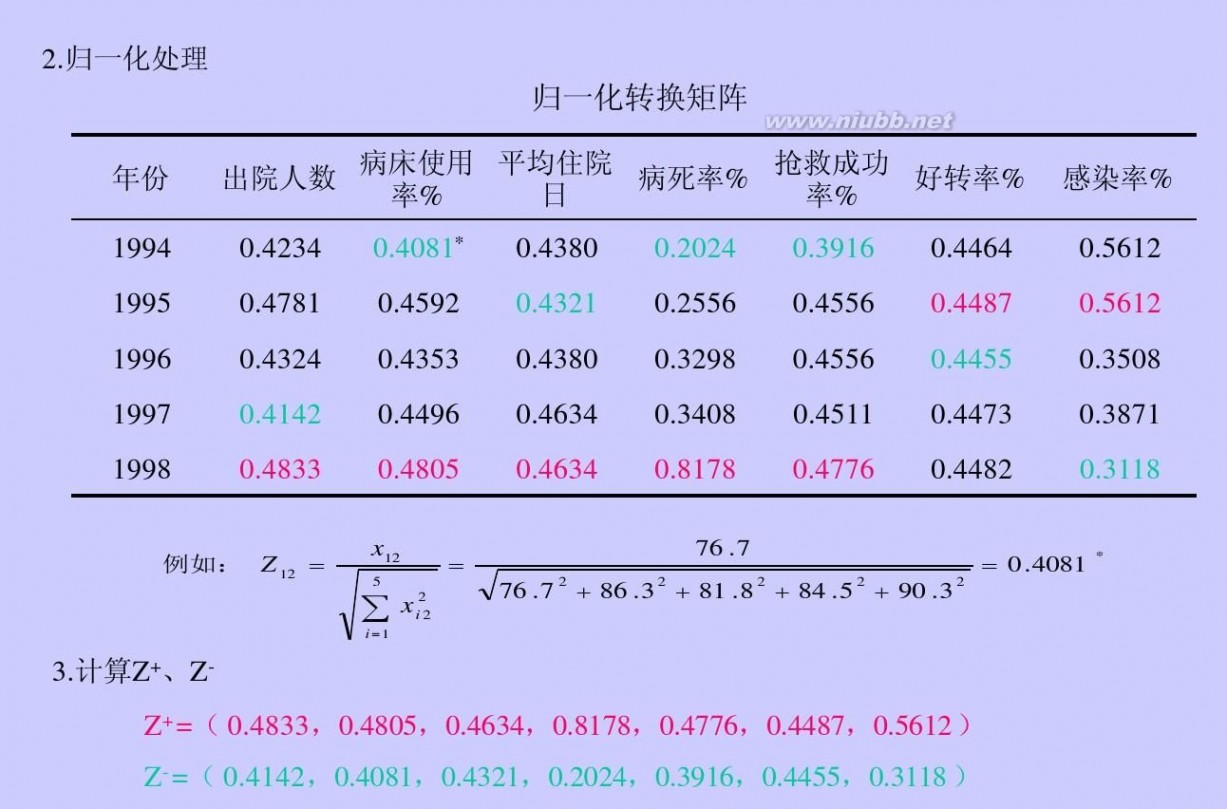
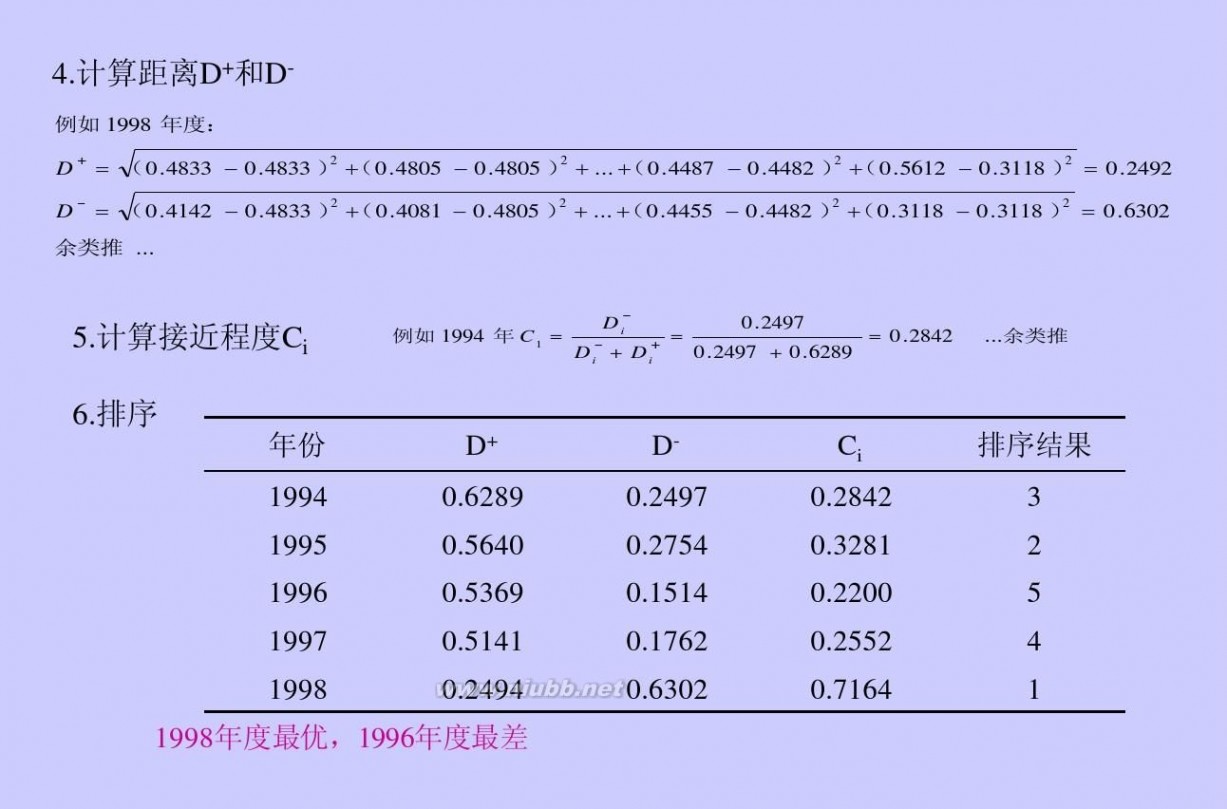
1.由于数据较少,可借助dps软件采用TOPSIS法来进行综合评价,进而对省三本院校排名。(www.61k.com) 各个样本排序指标值
样本 D+ D- 指标CI 名次 N1 0.10569 N2 0.08206 N3 0.20208 N4 0.22131
0.30283 0.32009 0.18033 0.20827
0.74129 0.79594 0.47156 0.48483
2 1 4 3
N5 0.23907 0.15915 0.39966 5
N6 0.35086 0.05665 0.13901 6
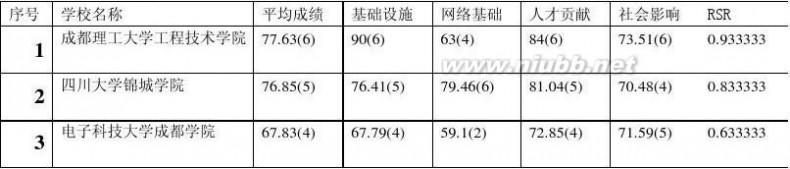
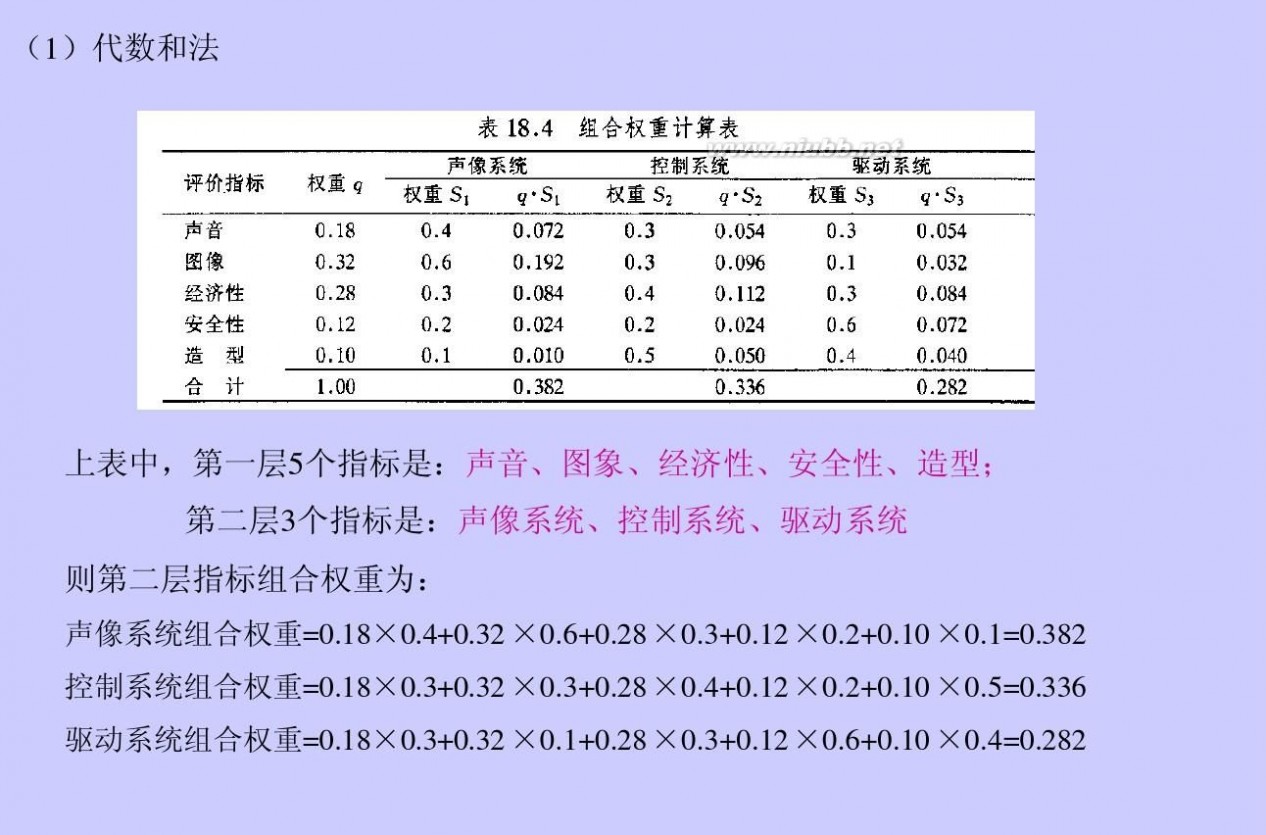
2. 可以采用秩和比(RSR)法对评价指标做综合评价,进而对省三本院校排名。 第一步,分别对要评价的各项指标进行编秩 第二步,计算各指标的秩和比(RSR)
其中:m为指标个数,n为分组数,Ri为各指标的秩次,RSR值即为多指标的平均秩次,其值越大越优
秩和比法 秩和比法综合评价


学校名称
RSR
f
成都理工大学工程技术学院 0.933333 四川大学锦城学院 0.833333 电子科技大学成都学院 四川师范大学文理学院 四川外语学院成都学院
0.633333 0.5 0.4
累积频数 1 1 1 1 1 1
1 2 3 4 5 6
秩号范围
1 2 3 4 5 6
成都理工大学广播影视学院 0.2
在spss软件里检验RSR是否符合正态分布,输出结果
平均秩次 Y
16.67% 4.0299 33.33% 4.5656 50.00% 5 66.67% 5.4289 83.33% 5.9621 95.83% 6.7169
从上表可知,RSR值正态性检验:Z=0.374,双侧检验P=0.9767,说明RSR值呈正态分布。[www.61k.com)
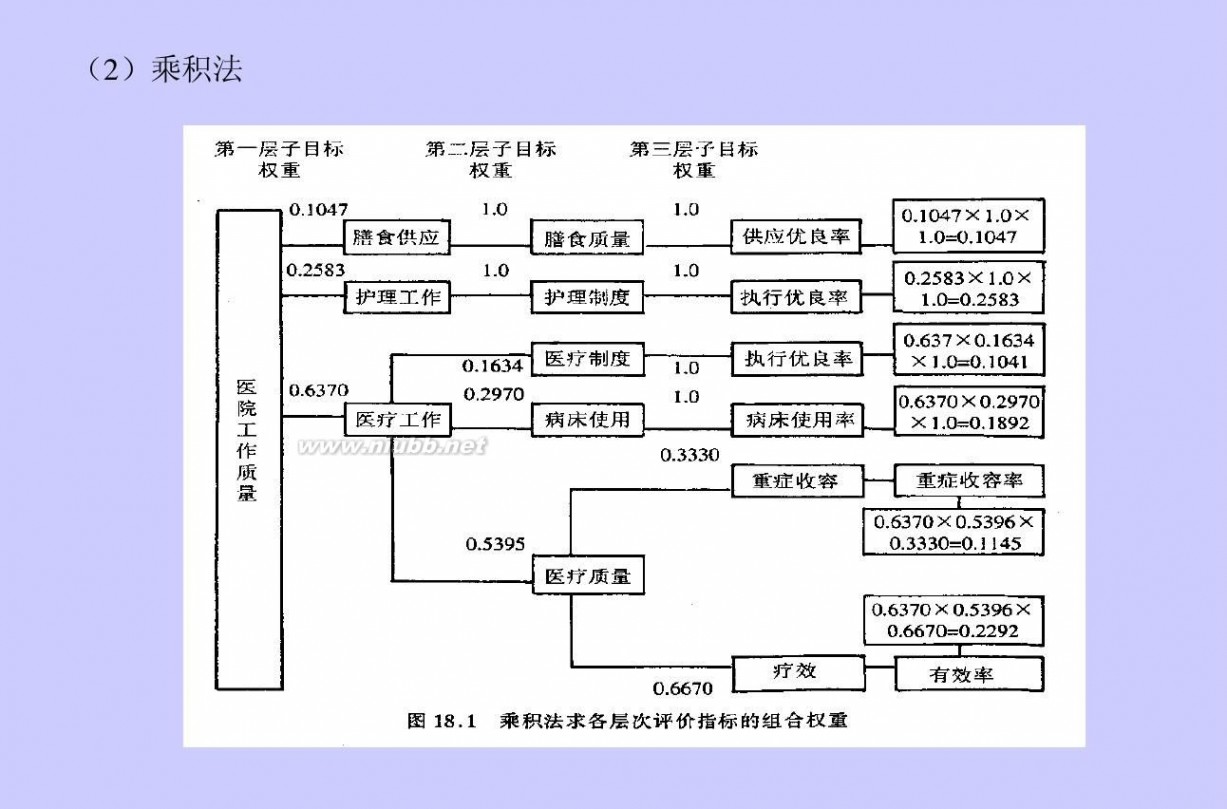
通过秩和比(RSR)值的大小,就可对评价对象进行综合排序,这种利用RSR综合指标进行排序的方法称为直接排序。 学校名称 RSR
成都理工大学工程技术学院 0.933333 四川大学锦城学院 电子科技大学成都学院 四川师范大学文理学院 四川外语学院成都学院
0.833333 0.633333 0.5 0.4
排名
1 2 3 4 5
秩和比法 秩和比法综合评价
成都理工大学广播影视学院 0.2 6
二 : 基于DRASTIC的含水层脆弱性模糊评价方法与应用
??#??112????#????水文地质工程地质2008年第3期??
基于DRASTIC的含水层脆弱性模糊评价方法与应用
李绍飞,孙书洪,王勇
(1??天津农学院,天津??300384;2??天津市水文水资源勘测管理中心,天津??300061)
摘要:通过分析目前广泛采用的DRASTIC方法存在的主要问题,将含水层脆弱性定义为模糊概念,结合模糊分析评价理论及三标度分两步的层次分析法建立了一套改进的含水层脆弱性评价模型。为测试其可靠性,分别将改进模型和传统DRASTIC模型应用于祁县东观镇含水层脆弱性评价中。研究结果表明:改进模型得到的脆弱性等级变化较后者更灵敏,分布范围及变化情况更精确,更能真实反映含水层脆弱性在空间上的连续变化,且计算简便、脆弱性分区图效果直观,丰富和完善了地下水脆弱性评价方法。
关键词:含水层;脆弱性;DRASTIC法;模糊评价
中图分类号:P641??8????????文献标识码:A????????文章编号:1000??3665(2008)03??0112??06
1
1
2
????在我国北方,地下水资源在国民经济和社会发展中占有重要地位,一旦水源被污染,其治理恢复的难度和代价都是极其巨大的。地下水脆弱性是指由于自然条件变化和人类活动影响遭受到破坏带来一系列问题的敏感程度,它反映了地下水环境的易污染性。1968年法国人Margat
[1]
toWater,D)、含水层净补给量(NetRechargeR)、含水层岩性(AquiferMedia,A)、土壤类型(SoilMedia,S)、地形坡度(Topography,T)、不饱和介质影响(ImpactoftheVadoseZoneMedia,I)、含水层水力传导系数(ConductivityofAquiferHydraulic,C)。其中,D、R、T、C属性值指标,可直接定量测得;A、S、I属类型指标,不可直接定量测得。根据各指标的重要性赋予权重指标。权重赋值分为正常和农田喷洒农药两种情况,对地下水脆弱性最具影响的指标权重为5,影响程度最小的指标权重为1(见表1)。
应用该模型时,首先将每一项指标划分为不同级别。同一级别内的指标赋予相同的定额,这样对不同级别便有了定量的区别,以此来反映指标对含水层易污染性影响的差异。据此对水文地质区段的易污染性进行排序,易污染性特征值越大,表示含水层越容易受污染;反之,越不易受污染。可直接定量测得的4项评价指标的分级范围和定额见表2;不可直接测量的3项类型指标的分类和定额见表3。
对某地区,地下水脆弱性评价值为:
Pi=
式中:
??j!!!指标j的权重;
Rij!!!评价地区i指标j的定额,据此可进行易污染性排序。
DRASTIC法属于经验性方法,且其评价模型是线性的,确切地说对于复杂的含水层脆弱性评价而言,该方法是一种评估方法,缺乏理论上的严谨性。在实i=1
首次提出含水层脆弱性概念及其评
价需考虑的因素,归纳起来可以从水文地质本身的内部因素、人类活动污染等外部因素两方面来考虑。与此相适应,其评价也分为本质脆弱性评价与特殊脆弱性评价两类。目前,含水层脆弱性评价应用最广泛的方法是美国环境保护署(USEPA)于1987年提出的DRASTIC模型,但该模型属于经验性方法,而地下水系统是个非常复杂的综合体,因此,综合运用AHP(层次分析)技术和模糊分析理论是地下水环境脆弱性评价的重要手段之一。本文以模糊分析评价理论为基础,采用三标度分两步的改进层次分析法计算指标权重,试拟建立一套较为完善合理的地下水脆弱性评价方法,并将其应用到实例计算中。
[2,3]
1??DRASTIC模型及存在问题
该模型选取影响和控制地下水流与污染物运移的7项主要因素作为脆弱性评价指标:含水层埋深(Depth
收稿日期:2007??10??19;修订日期:2007??12??25
基金项目:国家自然科学基金资助项目(50679055)和天津市科
技攻关计划重点项目(06YFGZNC06700)
作者简介:李绍飞(1979??),女,博士,讲师,主要从事水资源水
环境问题研究。
E??mail:lishaofei79@126??com
????
j
n
Rij(1)
??2008年第3期水文地质工程地质
表1??DRASTIC方法评价指标权重值Table1??WeightofindexofDRASTICmethod
????#??113????#??
????
评价指标权重
正常农药
含水层埋深(D)
55
净补给量(R)
44
岩性(A)
33
土壤类型(S)
25
坡度(T)
13
不饱和介质影响(I)
54
水力传导系数(C)
32
表2??数值指标的分级范围与定额Table2??Gradeandquotaofnumericalindex
含水层埋深(D)D??m0~1??51??5~4??64??6~9??19??1~15??215??2~22??922??9~30??5
?30??5
定额10975321
净补给量(R)R??(mm??a)
>254213~254150~213100~15075~10051~750~51
定额10975321
水力传导系数(C)C??(m??d)>81??540??7~81??528??5~40??712??2~28??54??1~12??20~4??1
定额1086421
地形坡度(T)T??(%)0~22~66~1212~18>18
定额109531
表3??类型指标的分级与定额Table3??Gradeandquotaoftypicalindex
含水层岩性(A)类型块状页岩变质岩??火成岩
冰渍岩层状砂岩、灰岩块状砂岩、灰岩、砂砾岩
玄武岩岩溶灰岩
定额1~32~54~65~94~92~109~10
土壤类型(S)类型薄层或无、砾
砂泥炭
胀缩或凝聚性粘土
亚粘土垃圾
非胀缩非凝聚粘土
定额109873~621
不饱和介质影响(I)类型承压层粉砂、粘土、页岩含粉砂、粘土的砂砾层状灰岩、砂岩、页岩
砂砾玄武岩岩溶灰岩
定额12~64~84~86~9910
离散值,同一级别内不同属性值被赋予相同的定额,因而忽略了指标本身连续变化这一客观事实;%各项指标权重被视为定值,不随研究区具体水文地质条件的不同而改变,统一按照表1赋予权值,影响了评价结果
的客观准确性。含水层易污染性及其评价的本质特征具有模糊性,可用模糊集理论进行研究。为克服DRASTIC模型的上述缺陷,本文将模糊分析评价理论和三标度分两步的层次分析法引入DRASTIC模型,建立一套较完善的地下水脆弱性评价方法。
含水层脆弱性的大小是相对的,从大到小之间没有明显的界限,是典型的模糊概念,因此可以用模糊分析评价理论解决评价指标连续变化这一问题,计算步骤如下:
2??1??1??划分评价级别
在Lobo??FerreiraJP等人在葡萄牙、大连、广州的地下水脆弱性评价中,将评价结果划分为8级,本文
[4]
考虑到DRASTIC法中指标定额分为10级,为与此相对应,本文将含水层脆弱性评价结果划分为&~?级,共10个级别(表4)。
2??1??2??构建指标评价标准特征值
通过对研究区水文地质条件特征、各评价因子的????
[4]
2??基于模糊理论与改进层次分析法的改进评
价模型
2??1??相对隶属度的确定
表4??评价结论与级别的对应关系
Table4??Thecorrespondingrelationofcalculationresultandgrade
级别易污染性脆弱性
&极难极低
(很难很低
)较难较低
?略难略低
+稍难稍低
,稍易稍高
?略易略高
.较易较高
/很易很高
?极易极高
??#??114????#????水文地质工程地质2008年第3期??
次级影响因素分析,参照前面各数值指标和类型指标的分级及定额标准值,可将地下水脆弱性评价的样本
集依据7个指标按10个级别的指标标准特征值进行识别,则有7 10阶评价标准特征值矩阵(式2)。
????????????????&????(????)?????????+????,?????????.????/?????
D30??526??722??915??212??19??16??84??61??50??0
R
Y=(yih)=
ASTI
010101810
5199179
71??48815812??2
91??8117??2147??67713720??3
66116
5595
1784474
2163343
2352222
2541101
C04??1
式中:yih!!!级别h、指标i的标准特征值
i=1,2,0,7;h=1,2,0,10
????从中可看出指标又分为两种不同类型:
28??534??640??761??171??581??值,不随研究区域含水层具体情况的变化而发生改变,这就使得评价结果的客观性受到影响。
AHP法确定权重的特点即考虑评价者的主观判断,又将评价对象的各种复杂因素用递阶层次结构表达出来,逐层进行评价分析。传统的AHP法在指标两两比较时,一般采用九标度,而本文采用三标度分两步的层次分析法,具体方法是:采用0,1,2三个标度值构建比较矩阵,将比较矩阵中元素按下式计算,可得判断矩阵:
bm=
i=1
[5]
?正向指标:指标标准特征值yih随级别h的增大而增大;
%负向指标:指标标准特征值hih随级别h的增大而减小。
2??1??3??构建指标集对评价级别的相对隶属度
设评价样本的指标特征值矩阵X=(xij)。其中,xij为样本j中指标i的特征值;i=1,2,0,7,j=1,2,0,n,n为样本个数。根据分明指标模糊化方法,利用样本的指标特征值X、评价标准特征值矩阵Y,将单项指标评价表达为评价级别上的模糊子集:
Sij={0,0,0,a,1-a,0,0}
式中:
Sij!!!样本j中指标i的单因素评价向量;a!!!第h分量,即对第h级别的隶属程度;
1-a!!!第h+1分量,即对第h+1级别的隶属程度
a由式(4)确定:
yih#a+yi,h+1#(1-a)=xij
(4)(3)
??K
n
max
+
??K
i=1
n
min
(6)
式中:
Pij!!!判断矩阵中元素;
Kij!!!比较矩阵中
i=1
??
n
元素(ki、Kj分别为第i、j
行的行累加值),行累加值中的最大、最小值一般按下式计算:
n
??K
n
i
--
i=1
??K
ni=1
??K??K
i
n
j
#(bm-1)+1(
man
i=1
??K
n
i
?
j=1
??K)
j
n
max
Pij=
1
????对于评价样本j,分别以7个评价指标的单因素评价向量Sij为行向量,组成矩阵,即可得样本j中指标集对评价级别的相对隶属度矩阵Sj。
2??1??4??计算样本指标集的评价级别向量
采用式(5)进行模糊综合计算,求得样本j中各项指标的评价级别向量:
Rj=Sj#C
转置矩阵。
2??2??权重系数的确定
T
T
i=1
??K
n
--n
n
i=1
??K
i
j=1i=1
??K??K
j
n
j
#(1+bm)+1
min
max
(
i=1
??K
<
j=1
??K)
????判断矩阵最大特征值对应的特征向量,经归一化后即为指标权向量。为确保计算准确,还须进行一致性检验,该方法更适用于地下水脆弱性评价这样影响因子较多的情况。
2??3??改进的DRASTIC模型
对于某一评价对象,根据以上求得的指标集评价j(5)
其中:C=(1,2,3,0,10)为评价级别矩阵,C为C的
??2008年第3期水文地质工程地质????#??115????#??
本j的地下水脆弱性评价级别:
Fj=A#Rj
式中:A为评价指标的权向量。
(6)
干旱气候,年均降雨量433mm,有昌源河和伏西河流经过。研究区包括山前倾斜平原区(地形标高760~800m)和黄土丘陵台地区(地形标高800~1000m),地
势从东南向西北依次变平缓。本区地下水主要储存在中下更新统的砂层、砾石层中,在古洪积扇和古河道地段形成富水性较强储水构造,孔隙水主要靠基岩山前地下径流补给。本文以第四系划分为基础,根据开采现状、参照1山西省祁县农田供水水文地质详查报告2中第四系含水层划分标准,将含水层划分为如下含水组,见表5。
表5??研究区含水组划分情况
Table5??Partitionofaquiferinresearcharea
3??实例应用
本文以山西省祁县东观镇为研究区,分别利用上述改进模糊评价模型和DRASTIC模型进行含水层脆
弱性评价,并对评价结果加以比较分析。3??1??水文地质条件概述
祁县地处太原盆地东南、汾河中游东岸,属内陆半
含水组
黄土丘陵区
浅层含水组中层含水组深层含水组
倾斜平原区
浅层含水组
中层含水组深层含水组
含水组底板小于50米,
含水层分布
含水层顶板埋深50米左右,底板埋深100米左右
含水组顶板埋深100米左右,厚度多为150米左右,个别可达200米含水组底板埋深40~70米,多为50米左右含水组底板埋深85~120米,多为100米左右含水组底板埋深多为150米左右,有的可达180米
地层时代
相当于上更新统和中更新统上部相当于中更新统的下部
相当于下更新统,或下更新统的中上部相当于全新统和上更新统,(Q3~4)相当于中更新统(Q2)相当于下更新统一部分(Q1

)
中层含水组由若干含水层组成,总厚度、单层厚度、层数、岩性,各地不同,受更新世河流变迁控制,总厚度变化在3~46m,多数地方为15~25m;层数变化在2~11m层间,多为5层;单层最薄不足1m,最厚达5m;岩性主要为粉细砂,有时为中砂。深层含水组水力联系密切,为孔隙承压水,总厚度变化在4~48??5m,最薄为零米,一般15~30m;含水层的层数3~7层;含水层岩性多为粉砂、细砂,有些井孔见中砂。浅层地下水矿化度,东南部矿化度较低,向西北逐渐增高,张庄东南东西炮以北、白圭村西北矿化度是全区最高地段。中深层地下水矿化度,北部区最高,其余广大地区均小于1g??L。
为描述研究区内水文地质条件变化规律及空间分
图1??东观镇水文地质分区图
Fig.1??HydrogeohgicalzoningofgroundwaterinDongguan
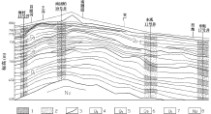
布差异,本文根据东观镇地貌类型和水文地质特征,将进一步划分成亚区,由此可得到东观镇水文地质分区图,(见图1),涧村(昌河河谷)!南团柏(黄土丘陵)!东观(倾斜平原)一线的水文地质剖面图(见图2)。3??2??实例计算与结果分析
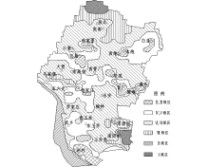
结合东观镇水文地质特点,本文用正方形网格(22 31)应用MapGIS将该区剖分成394个有效节点,根据实测钻孔资料,分别利用前述改进DRASTIC方法和DRASTIC模型,进行地下水脆弱性等级评价,将等级相同的相邻缓冲区连接起来并细化分区,即分别得到东观镇地下水脆弱性评价分区图(图3~4)。其中,根据(????在黄土丘陵区和倾斜平原区,虽然同一含水组所属地质时代不同,但储存条件、埋深特征相近,且具有水力联系,故其特征基本相同。浅层含水组由若干含水组组成,含水层总厚度、单层厚度、层数、含水层岩性,各地不同,受晚更新世以来的河流变迁控制,总厚度变化在5~40m;单层厚度最厚达15m,最薄不足1m;含水层层数4~7层;含水组岩性多为细砂、粉细砂,在,
??#??116????#????水文地质工程地质2008年第3期??
地段;级别为.级的脆弱性较高区域占11??9%,该地区上覆土层多为颗粒比较大的砂或砂质亚粘土,透水性较强,且地下水位埋深较浅,抗污能力较弱;级别为
/、?级的脆弱性很高或极高区域占10??9%,分布在昌源河河谷、张庄以北及南团柏以东等地,属极易受污染、脆弱性极强地段,该区域地下水埋深浅,上覆土层一般为较粗的粗砂,透水性强,有利于地表污染物的渗透和迁移,包气带的自净能力比较弱,地下水补给强度大,同时,这一带又是人类活动最为强烈的地区,排污、
图2??涧村-南团-东观一线水文地质剖面图Fig.2??Hydro??geologicalprofileofjiancun??
nantuan??dongguanline
过量施肥和污水灌溉等污染现象很严重,是地下水重
点保护区。在考虑建设项目时,应尽量避免兴建污染性强的项目,或者采取治理措施遏制污染的发生。以上结论与当地地下水系统实际情况基本吻合。
应用传统DRASTIC模型得到的含水层脆弱性评价值在88~205之间,主要集中在120~180范围内,依据DRASTIC的脆弱性划分原则,结合研究区具体情况,将结果划分为五个评价级别(图4)。
降水入渗补给、渠系渗漏补给、灌溉水回归补给和区域净补给四部分。在改进模糊评价模型中,计算权重时,在农药区和正常区,分别结合表1给定数据,利用三标度分两步的改进AHP
法确定权系数。
图3??由改进模型得到的脆弱性分区图
Fig.3??Zoningofgroundwatervulnerabilitybymodified
图4??由DRASTIC模型得到的脆弱性分区图Fig.4??Zoningofgroundwatervulnerability
byDRASTICmodel
从改进模型的评价结果可看出,祁县东观地下水脆弱性级别分布在(~?级之间,地下水系统整体状况不容乐观。脆弱性级别为(、)级的地区占11??2%,主要分布在南部小山丘、瓦屋村、嘉乐、东观和白圭镇一带,这些地区上覆土层颗粒小,地下水埋深大,属难污染的低脆弱性地段;级别为?、+级的地区占27??1%,该地区上覆土层颗粒较小,包气带自净能力较强,属不太易受污染的脆弱性略低地段;需引起有关部门注意的是,级别为,、?级的略高脆弱性地区占总区域的38??9%,表明研究区内有相当一部分地区地下水易受污染,这些区域土层颗粒较大,地下水埋深较
浅,总体上,两种方法得到的含水层脆弱性等级分布范围和变化走势大致相似,仅在较小范围内出现一定
的差异。前者得到的不同地段含水层脆弱性等级的变化较后者更灵敏,分布范围及变化情况更精确,与当地地下水环境实际情况更吻合;而后者评价结果相对较粗略,脆弱性等级变化缺乏连续性,相同等级的地区分布面积较大。这主要是因为传统DRASTIC模型没有考虑到各评价因子连续变化的特点,同一个较大区间的不同属性值被赋予相同的评价值,致使许多地段不同的含水层实际情况,却得出相同的脆弱性评价等级。
??2008年第3期水文地质工程地质????#??117????#??
另外,DRASTIC模型各评价指标的权重为定值(表1),没有考虑到研究区的具体情况,也使得评价结果受到影响,而改进的模糊评价模型基于三标度分两步的
AHP法确定权系数,在运算过程中指标两两比较时,考虑了实测资料所反映的数据本身对评价结果的影响。从而,本文提出的改进模糊评价模型更能真实反映含水层脆弱性在空间上的连续变化性。
镇地下水系统,整体上倾向于易受污染、脆弱性偏高,与研究区实际情况吻合较好。通过对两种方法的评价结果进行比较,可看出改进模型得到的含水层脆弱性等级变化较后者更灵敏,分布范围及变化情况更精确,与当地地下水环境实际情况更吻合;而传统DRASTIC模型评价结果相对较粗略,脆弱性等级变化缺乏连续性,相同等级的地区分布面积较大。因而,改进模糊评价模型更能真实反映含水层脆弱性在空间上的连续变化性,在我国北方丘陵、山前平原地区具有更好的应用效果,且计算简便、脆弱性分区图效果直观,丰富和完善了地下水脆弱性评价方法和理论体系。参考文献:
[1]??JaroslavVrba,
Alexander
Zaporozec.Guidebookon
4??结论
含水层脆弱性评价是对研究区域地下水系统潜在的易污染性做出定量的评估并进行区划,可为指导产业合理布局、保护地下水资源提供依据。本文针对DRASTIC模型在应用中的局限性,对其加以改进:首先,将DRASTIC模型中可直接定量获得的评价指标用模糊理论的概念进行定额,考虑了评价指标在数量上和空间上的连续变化,使评价结果更符合实际情况;另外,在确定指标权重时引入三标度分两步的层次分析法,使得权重的确定具有一定的理论依据。
为测试其可靠性,本文分别将改进的模糊评价模型和传统DRASTIC模型应用于祁县东观镇的含水层脆弱性评价中,两种方法得到的含水层脆弱性等级分布范围和变化走势大致相似。改进模型的研究结果表明:东观镇含水层脆弱性大致呈正态分布,其中,(~+级的不易污染、偏低脆弱性地区占38??3%,,~?级的易受污染、偏高脆弱性地区占61??7%,祁县东观
MappingGroundwaterVulnerability[M].InternationalContributionstoHydro??geologyFoundedbyG.Castany,E.Groba,E.Romijn.Volume(16).Hanover:Heise,1994,131.
[2]??孙才志,潘俊.地下水脆弱性的概念、评价方法与研
究前景[J].水科学进展,1999,33(4):444-449.[3]??钟佐桑.地下水防污性能评价方法探讨[J].地学前
缘,2005(4):3-11.
[4]??陈守煜,伏广淘,周惠成,等.含水层脆弱性模糊分析
评价模型与方法[J].水利学报,2002(7):23-30.[5]??徐肇忠.城市环境规划[M].武汉:武汉大学出版社,
1999:154-155.
Applicationofthemethodforfuzzyassessmentof
aquifervulnerabilitybasedonDRASTIC
LIShao??fei,SUNShu??hong,WANGYong
1
1
2
(1??TianjinAgricultureCollege,Tianjin??300384,China;
2??TianjinSurveyandManagementCenterofHydrologyandWaterResources,Tianjin??300061,China)Abstract:AccordingtotheanalysisofthemainproblemsinDRASTICmodel,whichisusedforassessinggroundwatervulnerability,thegroundwatervulnerabilityisregardedasafuzzyandstochasticconcept.Amodifiedgroundwatervulnerabilityassessmentmodelwasdeveloped,whichbasedonfuzzytheoryandanimprovedAHPmethod.ThemodifiedmodelandDRASTICmodelwerebothappliedtoassesstheaquifervulnerabilityinDongguanTown.Theresultsderivedfromthetwomethodsaresimilarinthewhole,butthegradechangingofthemodifiedmodelismoresensitiveandthedistributionismoreprecise,whichshowsthespacialcontinuousofaquifervulnerability.Soitisconsistentwiththepracticalsituationandeasytouse.Keywords:aquifer;vulnerability;DRASTICmodel;fuzzyassessment
责任编辑:王宏
三 : 综合评价方法综述与比较18
综合评价方法综述与比较
综合评价的概念: 所谓统计综合评价,通常就是指多指标综合评价技术,它是利用一定的统计指标体系,采用特定的评价模型和方法,对被评价对象多个方面的数量特征进行高度的抽象和综合,转化为综合评价值,进而确定现象的优劣、类型或对现象进行排序的一种统计方法。 目前常用的方法有层次分析法、盗用函数法、多元统计综合评价技术法(包括主成分分析法、因子分析法、聚类分析法等)。此外像人工神经网络综合评价法、模糊综合评判法、灰色系统理论等新兴综合评价技术还在源源不断地涌现。
一 简易的综合评价方法
(一),综合指数法
1,直接综合法 概念:直接综合法是在确定一套合理的指标体系基础上,对各项指标个体指数进行相加,直接计算出综合评价指数。 优点:公式简单易懂,指标数值计算简便。 缺点:得到的数值比较粗糙,以此得到的数据进行评价结果精确度不高 。
2,加权综合法 概念:加权综合法是在确定一套合理的指标体系的基础上,对各项指标个体指数进行加权平均,计算出综合评价数值。 优点:与直接综合法相比,加权综合法指标数值的计算考虑到了各指标的比重问题,将各指标赋予不同的权重,以体现不同指标的不同重要程度。 缺点:各指标的重要程度的判断具有很大主观性。
(二) 功效系数法 概念:功效系数综合评价法是指根据多目标规划的原理,把所要考核的各项指标按照多档次标准,通过功效函数转化为可以度量的评价分数,据以对被评价对象进行总体评价得分的一种方法。 优点:方法简便和可操作性强是这种方法的优点所在。 缺点:竞争力评价中,不同行业各指标的重要程度有所不同,而权数是由评判人员主观确定,因此科学性有所欠缺,往往评价结果与实际状况出入较大。
(三)综合积分法 概念:综合积分法是对构成评价指标体系的每个指标评分,将所有得分相加算出总分,作为综合评价数值的一种评价方法。适用范围:适用于定量分析且变量指标可以用数字表达的评价分析。优点:此法操作简单,结果与、易于理解。缺点:对各指标变量的评分比较主观,没有客观精确地评分公式。
二 运筹学中综合评分法
(一) 层次分析法 概念: AHP法(Analytic Hierarchy Process, AHP),即层次分析法,是美国著名运筹学家,匹兹堡大学萨蒂教授于本世纪七十年代创立的一种实用的多准则决策方法。它把一个复杂决策问题表示为一个有序的递阶层次结构,通过人们的比较判断,计算各种决策方案在不同准则及总准则之下的相对重要性量度,从而据之对决策方案的优劣进行排序。 优点: 1,系统性的分析方法; 2,简洁实用的决策方法; 3,所需定量数据信息较少;缺点: 1,不能为决策提供新方案; 2,定量数据较少,定性成分多,不易令人信服; 3,指标过多时数据统计量大,且权重难以确定; 4,特征值和特征向量的精确求法比较复杂;
(二) 模糊评价法 概念:模糊评价法是根据模糊数学的隶属度理论把定性评价转化为定量评价的一种方法。 优点: (1)为定性指标定量化提供了有效的方法,实现了定性和定量方法的集合。(2)在客观事物中,一些问题往往不是绝对的肯定或绝对的否定,涉及到模糊的因素,而且模糊综合判别评价法则很好的解决了判别的模糊和不确定的问题。 (3)所得结果为一向量,即评语集在其论语上的子集,克服了传统数字学方法结果单一的缺陷,结果包含的信息丰富。缺点:(1)不能解决评价指标间相关造成的信息重复的问题。(2)各因素权重的确定带有一定的主观性。(3)在某些情况下,隶属函数的确定有一定困难,尤其是多目标评价模型,要对每一目标,每一个因素确定隶属函数,过于繁琐,实用性不强。 应用领域:模糊综合评价方法也是目前多指标综合评价实践中应用最广的方法之一,由于我国
二十多年来模糊数学普及与发展相当有成效,使得模糊综合评价的应用领域比之多元统计方法、效用函数法还要广,涉及到经济问题评价、管理问题评价、环境评价、教育评价、科技评价、地质(如岩石可钻性模糊评价)、采矿(如开采场稳定性评价、爆破效果评价、开采方式评价等)、工程技术(如生产工艺综合评价、港口选址评价)、医学等众多领域。
(三)DEA综合评价法 概念:DEA,即数据包络分析(Data Envelopment Analysis ),是著名运筹学家查恩斯、库伯、罗兹等在研究部门之间“相对有效性评价”基础之上提出的一种新的系统分析方法。自1978年第一个分析模型C2R提出以来,经过许多学者的发展,已经成为管理科学与系统工程领域的一种重要而有效的分析工具,被应用于不同领域的效率评价。 在应用DEA法时应注意以下几点: 第一,由于DEA技术是通过对多个投入指标(输入指标)与多个产出指标(输出指标)的系统分析来比较同类型单位(企业或部门)相对效率的,因此它具有某些领域多指标综合评价所需要的一些基本要素,完全可以认为是一种“独特的综合评价技术”。 第二,DEA法是一种水平评价而不是规模评价,因为相对有效性系数(效率评价指数)与样本单位的投入指标规模和产出指标规模没有直接关系。因此,当我们需要进行规模综合分析时,就不能直接采用DEA法。 第三,DEA法既可以在一定程度上用于综合评价排序,也可以用于“分类评价”。 第四,相对有效性系数(效率评价指数)与参加评价的单位情况有关。
三 多元统计分析中的综合评价方法
(一)主成分分析
概念:主成分分析就是设法将原来众多的具有一定相关性的指标(比如P个指标),重新组合成一组新的相互无关的综合指标来代替原来的指标。通常数学上的处理就是将原来P个指标作线性组合,若没有限制条件作为新的综合指标,这样的线性组合会有很多,那么如何去选取呢?主成分分析的基本思想是:如果将选取的第一个线性组合即第一个综合指标记为F1,自然希望尽可能多的反映原来指标的信息。这里的“信息”最经典的方法就是用F1的方差来表达,即 Var(F1)越大,表 示F1包含的信息越多。因此在所有的线性组合中所选取的F1应该是方差最大的,故称F1为第一主成分。如果第一主成分不足以代表原来P个指标的信息,再考虑选取F2 即选第二个线性组合,为了有效地反映原来信息,F1已有的信息就不再需要出现在F2中,用数学语言表达就是Cov(F1,F2)=0,称F2为第二主成分,依次类推可以造出第三,第四…第P个主成分。不难想象这些主成分之间不仅不相关,而且它们的方差依次递减,因此在实际工作中,就挑选前几个最大主成分。虽然这样做会损失一部分信息,但是由于抓住了主要矛盾,并从原始数据中进一步提取了某些新的信息,这种既减少了变量的数目又抓住了主要矛盾的做法有利于问题的分析和处理。 适用范围:适用于研究中所涉及的变量指标较多,且各指标间有一定的相关性。 缺点:主成分和因子法有一个固有缺陷,当存在严重的多重相关时,会严重夸大重复变量的作用。 优点:(1)主成分分析法解决了通常方法的变量太多会增加计算量和增加分析问题的复杂性的不足,使得在进行定量分析的过程中,涉及的变量较少,得到的信息量较多。 (2)它是一种程式化的东西,不会得不出结果,当然这个结果就看你怎么解释它。 不足:(1)在将数据正态标准化的时候会存在信息丢失。(2)在现代,在进行主成分向量求解时,运用不同的统计软件会的到不同的结果。(3)在主成分综合值计算过程中,主成分权重的设定有很大的主观性。
(二)因子分析 概念:是主成分分析法的推广和发展,它是由研究原始数据相关矩阵的内部依赖关系出发,把一些具有错综复杂的多个变量(或样品)综合为少数几个因子,并给出原始变量与综合因子之间的相关关系的方法。 适用范围:如何选择适当的方法来解决实际问题,需要对问题进行综合考虑。 优点:因子分析法最大优势在于各综合因子的权重不是主观赋值而是根据各自的方差贡献率大小来确定的,方差越大的变量越重要,从而具有较大的权重;相反,方差越小的变量所对应的权重也就越小。这就避免了人为确定权重的随意性,
使得评价结果唯一,而且较为客观合理。此外,因子分析的整个过程都可以运用计算机软件方便快捷地进行,可操作性强。因此,与其他方法相比,因子分析法是一种科学、实用、简便的综合评价方法。 不足:因子分析的概念起源于本世纪初Karl Pearson和Charles Spearmer等人关于智力测验的统计分析。近年来,随着现代高速电子计算机的出现,人们将因子分析的理论成功地应用于心理学、医学、气象、地质、经济学等领域,使得因子分析的理论和方法更加丰富。因子分析法是从研究相关矩阵内部的依赖关系出发,根据相关性大小把变量分组(使得同组内的变量之间相关性不高,而不同组内的变量之间相关性较低),这样,在尽量减少信息丢失的前提下,从众多指标中提取出少量的不相关指标,然后再根据方差贡献率确定权重,进而计算出综合得分的一种方法。
(三)聚类分析概念:聚类分析法是将样品或变量按照它们在性质上的亲疏程度进行分类的多元统计分析方法。在聚类分析中,通常我们将根据分类对象的不同分为Q型聚类分析和R型聚类分析两大类。R型聚类分析是对变量进行分类处理,Q型聚类分析是对样本进行分类处理。方法:直接聚类法;最短聚类法;最长聚类法。聚类分析的基本步骤第一步,对原始数据进行无量处理,通常用标准化。第二步,计算聚类统计量。若是对样品进行分类,则计算距离系数矩阵,若是对指标进行分类,则计算相似系数矩阵。第三步,按最近或最相似原则进行聚类,并计算新类到旧类之间的距离或相似系数,给出新的聚类统计量矩阵。第四步,重复第三步,直到所有的指标或样品聚到一个类。第五步,根据聚类过程,绘制聚类谱系图,完成聚类工作。
(四)判别分析法 概念:判别分析(Discriminant analysis)是产生于二十世纪三+年代的一种多元统计方法。其基本思想就是根据已有的有明确分类的样本指标,构造一个或一组判别函数及判别规则,从而判断某一特定个体究竞是属于哪一类。 四 其他综合评分法(一)神经网络分析法 概念:神经网络分析法是从神经心理学和认知科学研究成果出发,应用数学方法发展起来的一种具有高度并行计算能力、自学能力和容错能力的处理方法。 优点:具有较强的自学习和自适应能力,高度的非线性映射能力、记忆联想能力等,它能够进行复杂的逻辑操作和非线性映射。缺点:(1)最严重的是没有能力解释自己的推理过程和推理依据。 (2)不能向用户提出必要的询问,而且数据不充分的时候,神经网络无法进行操作。
(3)把一切问题的特征都要变为数字,把一切推理都变为数值计算,其结果势必丢失部分信息。 (4)理论和学习算法还有待进一步完善和提高。 应用范围:主要用于分类和预测,类似于贝叶斯网络和决策树。(二)效用函数综合评价法 概念:将每一个评价指标按一定方法量化,变成对评价问题测量的一个量化值,即效用数值,然后按一定的合成模型加权合成求得总评价值。 优点:评价结论真实性,通俗性,评价过程各环节之间没有信息传递关系,各环节都有众多方法可共选择,这些方法可供多方位的组合,因此从理论上讲,这种方法最为丰富。
(三)灰色系统理论
概念:1982年,中国学者邓聚龙教授创立的灰色系统理论,是一种研究少数据、贫信息不确定性问题的新方法。灰色系统理论以“部分信息已知,部分信息未知”的“小样本”、“贫信息”不确定性系统为研究对象,主要通过对“部分”已知信息的生成、开发,提取有价值的信息,实现对系统运行行为、演化规律的正确描述和有效监控。 应用范围:灰色系统的应用范畴大致分为以下几方面:(1)、灰色预测 ①、人口预测;②、初霜预测;③、灾 变预测等(2)、灰色关联度分析(3)、灰色决策(4)、灰色预测控制优点:(1)、不需要大量的样本。(2)、样本不需要有规律性分布。(3)、计算工作量小。(4)、定量分析结果与定性分析结果不会一 致。 (5)、可用于近期、短期,和中长期预测。(6)、灰色预测精准度高。缺点:(1)灰色预测理论仅仅以预测精度(误差)来检验预测模型或预测结果的好坏,如此欠妥当。(2)当预测所用样本量较大时,预测长期趋势较好,但预测短期趋势较差,当所用
样本量较小时,预测短期趋势较好,预测长期趋势较差,二者无法达到两全其美。
四 : TOPSIS_综合评价法

topsis法 TOPSIS_综合评价法

topsis法 TOPSIS_综合评价法

topsis法 TOPSIS_综合评价法

topsis法 TOPSIS_综合评价法

topsis法 TOPSIS_综合评价法

topsis法 TOPSIS_综合评价法
topsis法 TOPSIS_综合评价法

topsis法 TOPSIS_综合评价法

topsis法 TOPSIS_综合评价法

topsis法 TOPSIS_综合评价法
topsis法 TOPSIS_综合评价法
topsis法 TOPSIS_综合评价法

topsis法 TOPSIS_综合评价法

topsis法 TOPSIS_综合评价法

topsis法 TOPSIS_综合评价法

topsis法 TOPSIS_综合评价法
topsis法 TOPSIS_综合评价法

topsis法 TOPSIS_综合评价法

topsis法 TOPSIS_综合评价法

topsis法 TOPSIS_综合评价法

topsis法 TOPSIS_综合评价法

topsis法 TOPSIS_综合评价法
topsis法 TOPSIS_综合评价法

topsis法 TOPSIS_综合评价法
topsis法 TOPSIS_综合评价法

topsis法 TOPSIS_综合评价法
topsis法 TOPSIS_综合评价法
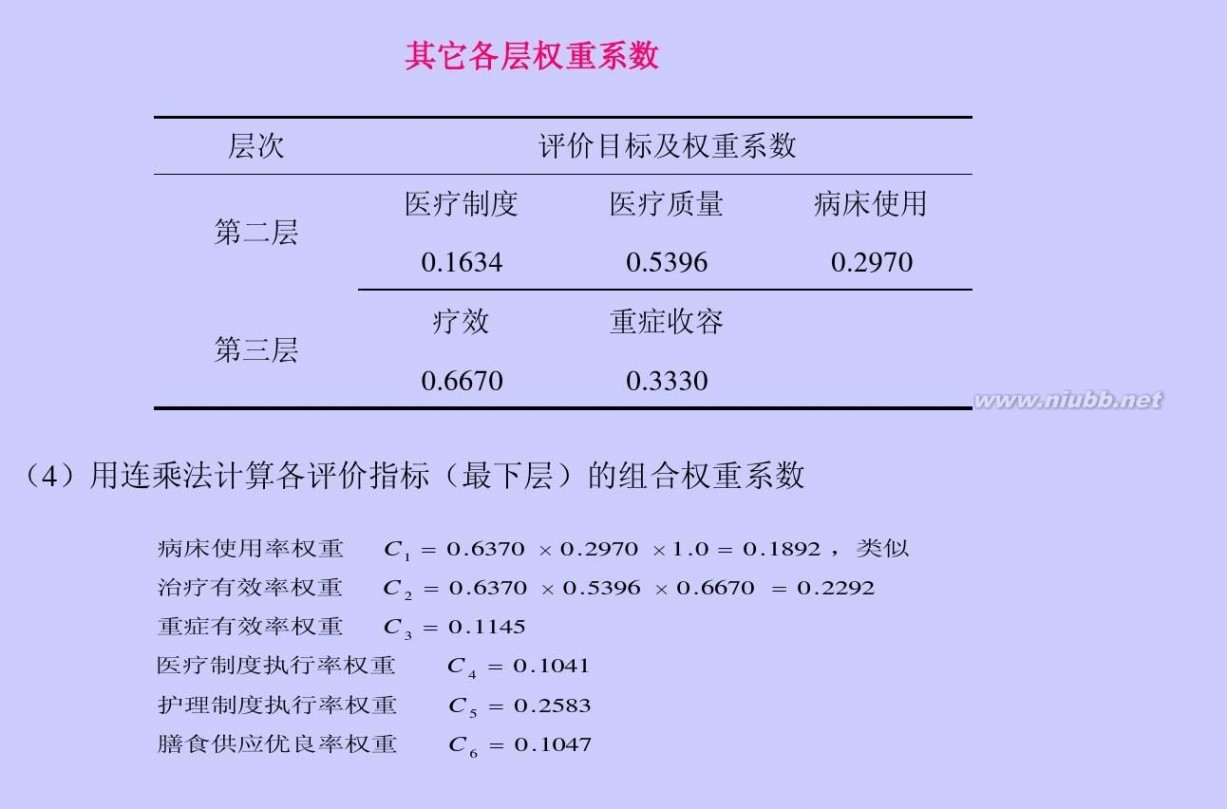
topsis法 TOPSIS_综合评价法
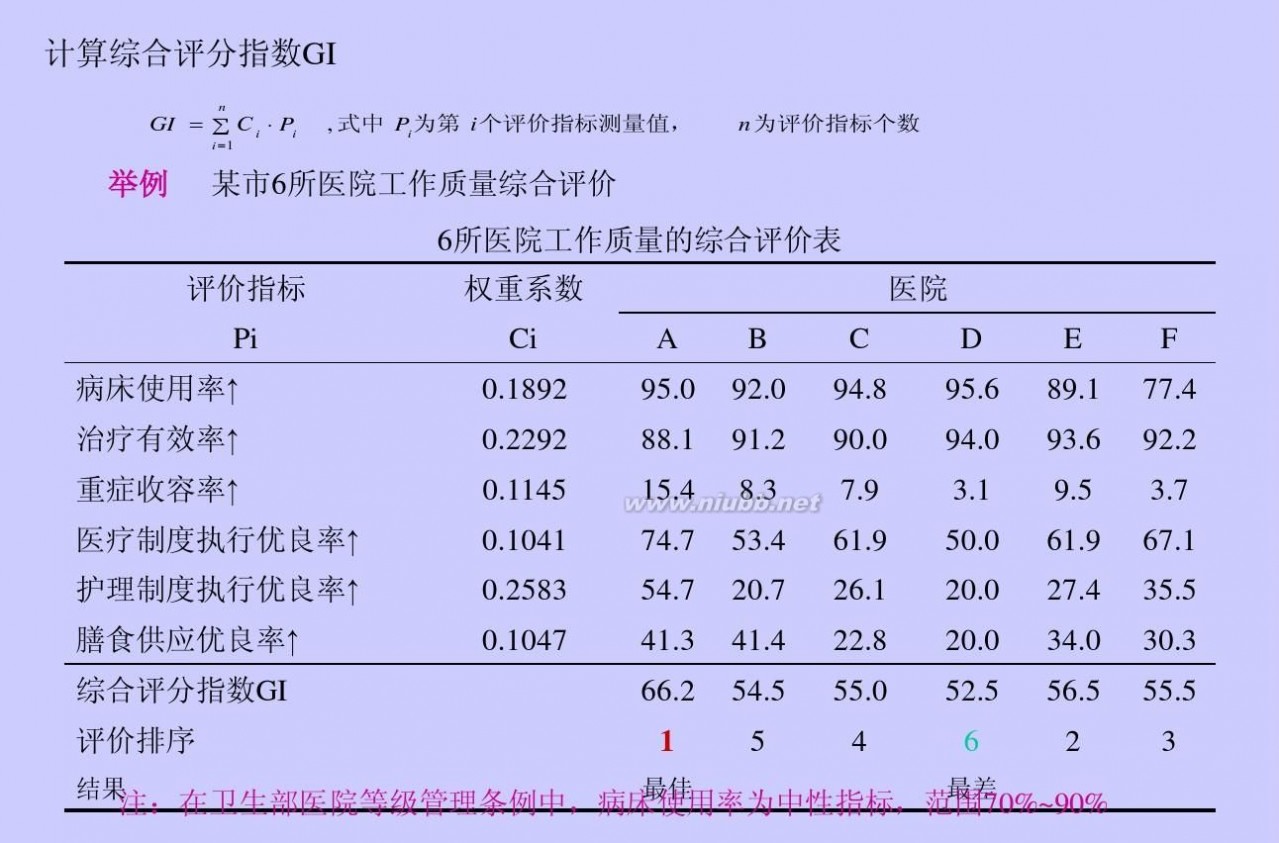
topsis法 TOPSIS_综合评价法

topsis法 TOPSIS_综合评价法
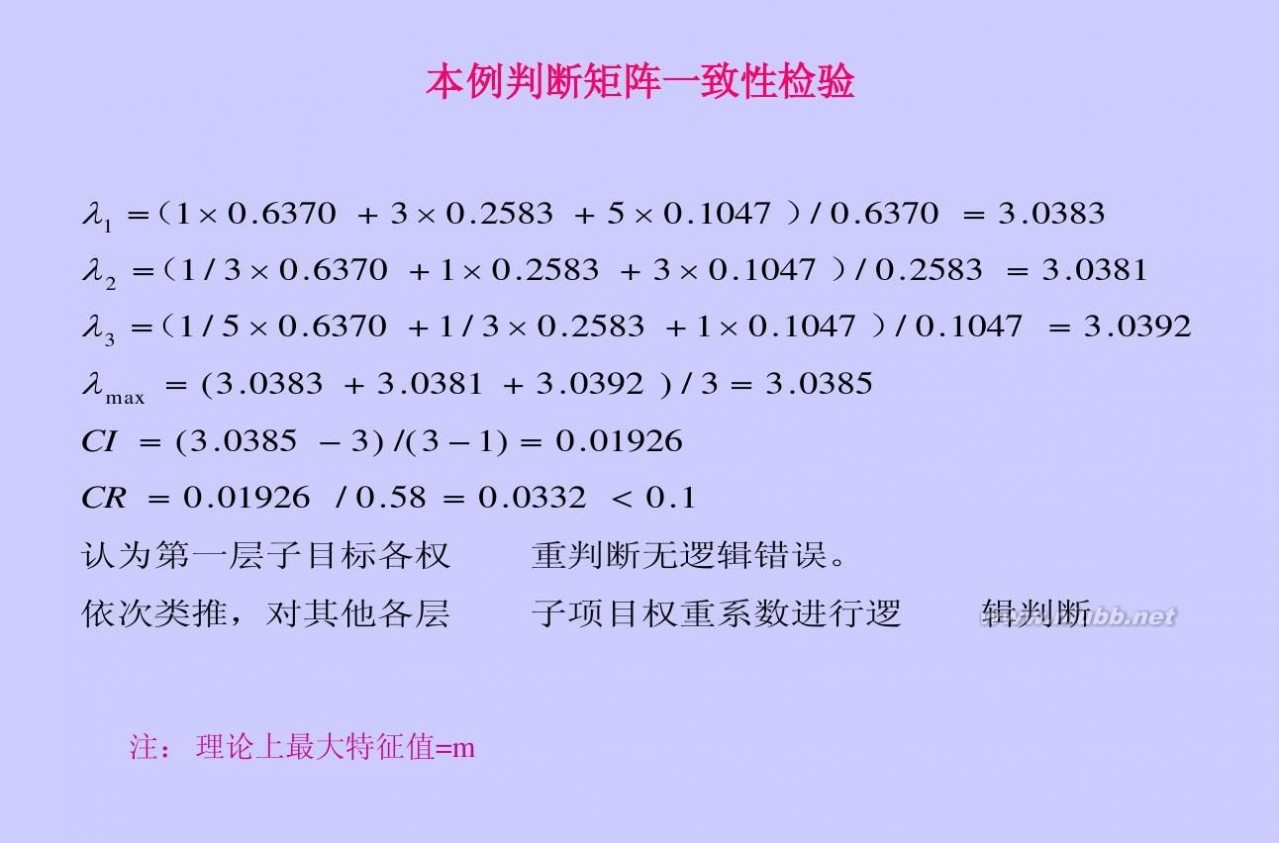
topsis法 TOPSIS_综合评价法

topsis法 TOPSIS_综合评价法
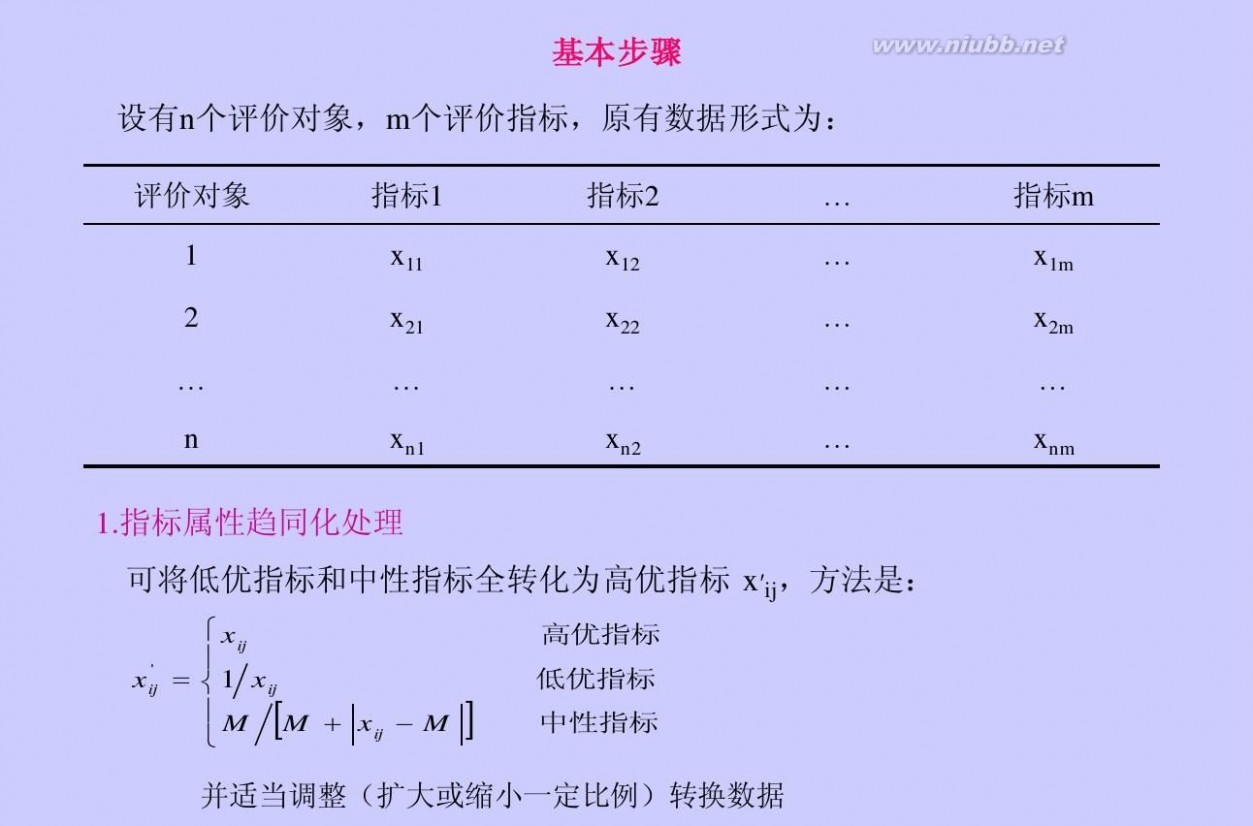
扩展:topsis法 / topsis分析法 / 熵权topsis法
topsis法 TOPSIS_综合评价法

topsis法 TOPSIS_综合评价法

topsis法 TOPSIS_综合评价法
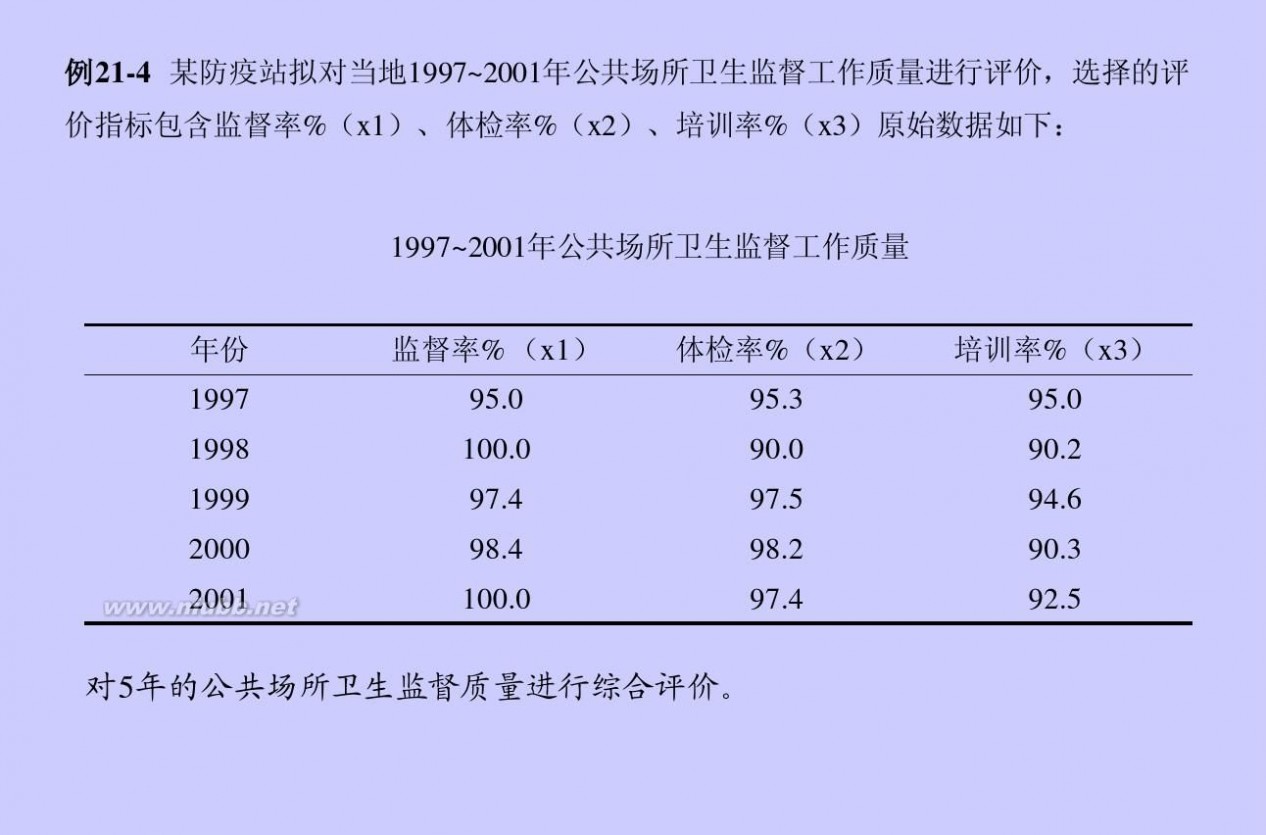
topsis法 TOPSIS_综合评价法
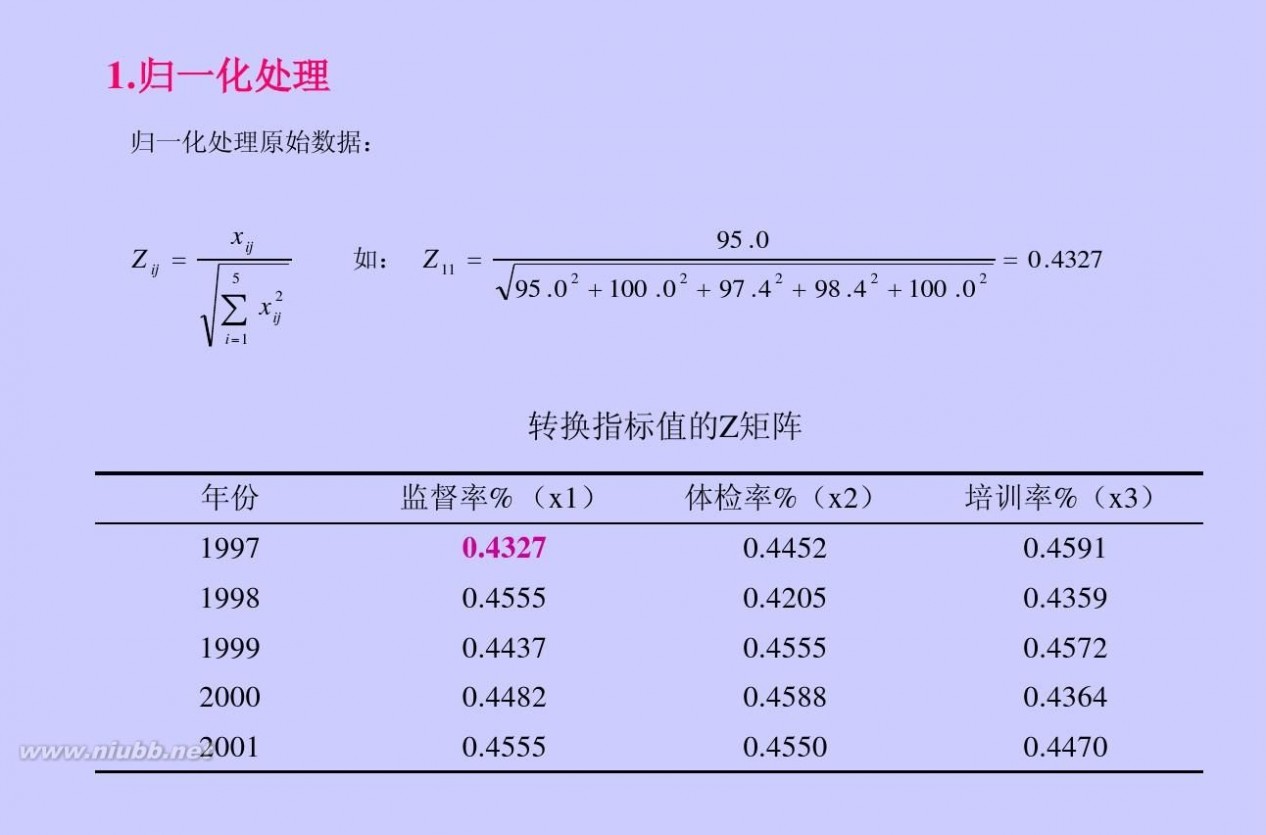
topsis法 TOPSIS_综合评价法

topsis法 TOPSIS_综合评价法
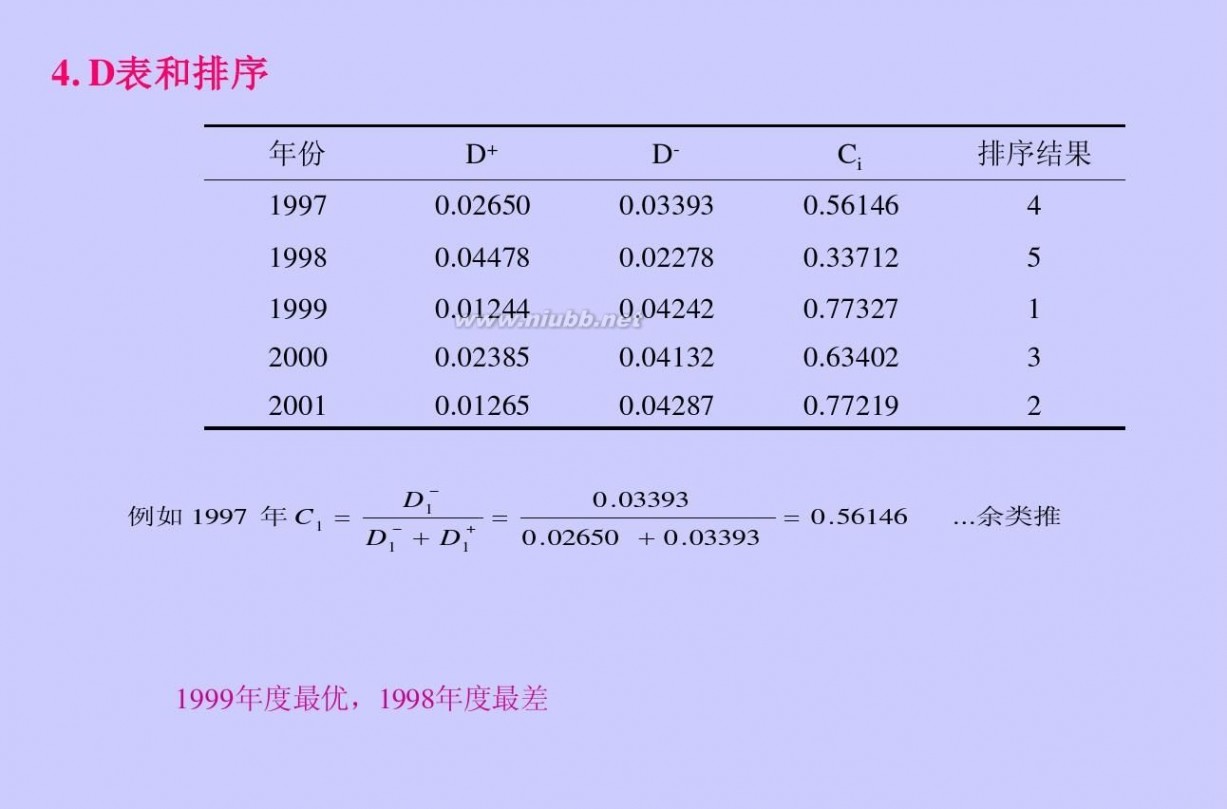
topsis法 TOPSIS_综合评价法
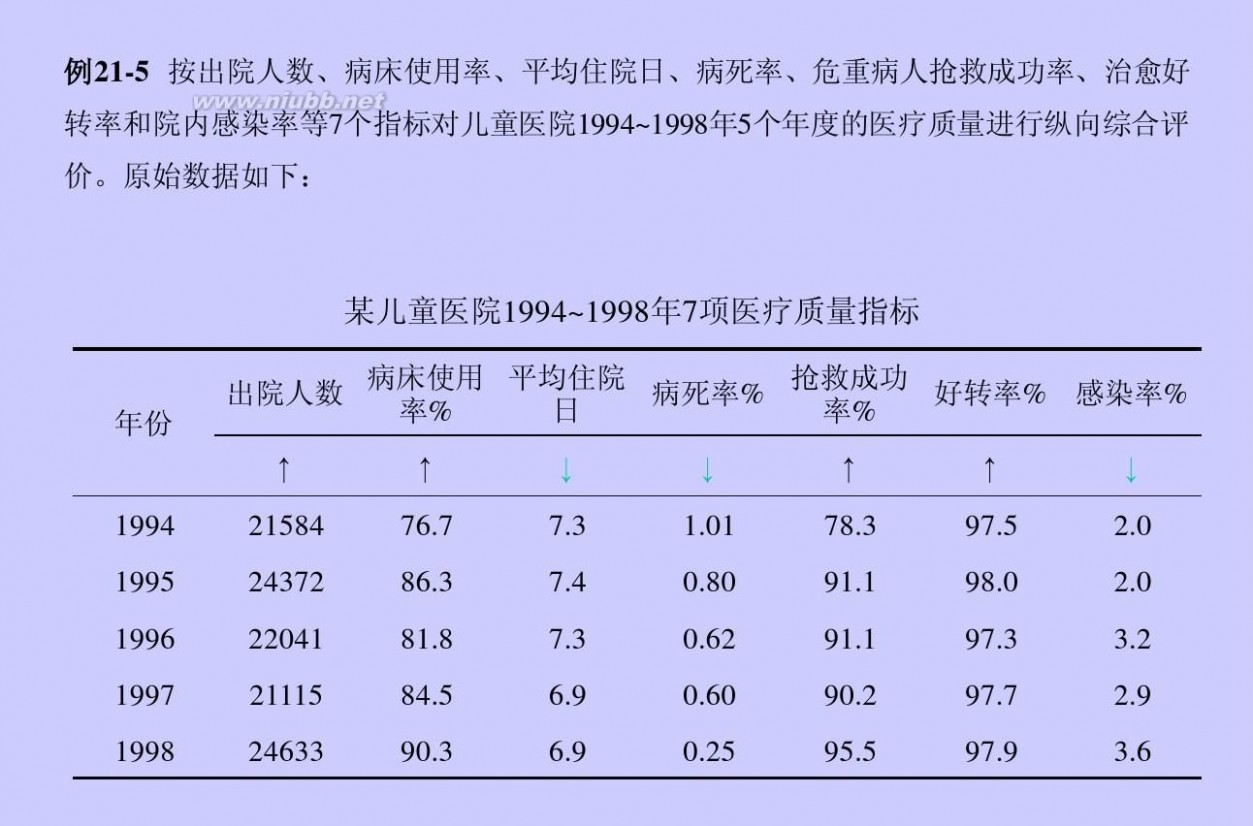
topsis法 TOPSIS_综合评价法
topsis法 TOPSIS_综合评价法
topsis法 TOPSIS_综合评价法
扩展:topsis法 / topsis分析法 / 熵权topsis法
本文标题:模糊综合评价法-秩和比法综合评价61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1